CHSE Odisha Class 12 Math Solutions Chapter 6 Probability Additional Exercise

Odisha State Board CHSE Odisha Class 12 Math Solutions Chapter 6 Probability Additional Exercise Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 6 Probability Additional Exercise

(A) Multiple Choice Questions (Mcqs) With Answers

Question 1.
If \(\left|\begin{array}{ccc}
1+x & x & x^2 \\
x & 1+x & x^2 \\
x^2 & x & 1+x
\end{array}\right|\) = a + bx + cx² + dx³ + ex⁴ + fx⁵ then write the value of a.
(a) 0
(b) 2
(c) 1
(d) 3
Answer:
(c) 1

Question 2.
If every element of a third order determinant of value 8 is multiplied by 2, then write the value of the new determinant.
(a) 32
(b) 64
(c) 16
(d) 128
Answer:
(b) 64

Question 3.
If A is a 4 x 5 matrix and B is a matrix such that A^TB and BA^T both are defined, then write the order of B
(a) 4 x 5
(b) 1 x 5
(c) 5 x 4
(d) None of these
Answer:
(a) 4 x 5

Question 4.
If \(\left[\begin{array}{lll}
3 & 5 & 3 \\
2 & 4 & 2 \\
\lambda & 7 & 8
\end{array}\right]\) is a singular matrix, write die value of 1.
(a) λ = 2
(b) λ = 1
(c) λ = 4
(d) λ = 8
Answer:
(d) λ = 8

Question 5.
Determine the maximum value of \(\left|\begin{array}{rl}
\cos x & \sin x \\
-\sin x & \cos x-1
\end{array}\right|\)
(a) 1
(b) 2
(c) 3
(d) 0
Answer:
(b) 2

Question 6.
If \(\left[\begin{array}{cc}
x & y \\
x & \frac{x}{2}+t
\end{array}\right]\) + \(\left[\begin{array}{cc}
y & x+t \\
x+2 & \frac{x}{2}
\end{array}\right]\) = \(\left[\begin{array}{ll}
1 & 4 \\
2 & 3
\end{array}\right]\) then find x.
(a) x = 1
(b) x = 0
(c) x = 2
(d) x = -1
Answer:
(b) x = 0

Question 7.
If \(\left[\begin{array}{cc}
x & y \\
x & \frac{x}{2}+t
\end{array}\right]\) + \(\left[\begin{array}{cc}
y & x+t \\
x+2 & \frac{x}{2}
\end{array}\right]\) = \(\left[\begin{array}{ll}
1 & 4 \\
2 & 3
\end{array}\right]\) then find y.
(a) y = 1
(b) y = 3
(c) y = 2
(d) y = 0
Answer:
(a) y = 1

Question 8.
If \(\left[\begin{array}{cc}
x & y \\
x & \frac{x}{2}+t
\end{array}\right]\) + \(\left[\begin{array}{cc}
y & x+t \\
x+2 & \frac{x}{2}
\end{array}\right]\) = \(\left[\begin{array}{ll}
1 & 4 \\
2 & 3
\end{array}\right]\) then find t.
(a) t = 1
(b) t = 2
(c) t = 3
(d) t = 0
Answer:
(c) t = 3

Question 9.
Which matrix is a unit matrix?
(a) \(\left(\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right)\)
(b) \(\left(\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right)\)
(c) \(\left(\begin{array}{ll}
1 & 1 \\
0 & 1
\end{array}\right)\)
(d) \(\left(\begin{array}{ll}
1 & 1 \\
1 & 1
\end{array}\right)\)
Answer:
(b) \(\left(\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right)\)

Question 10.
If \(\left(\begin{array}{cc}
\mathbf{x}_1 & \mathbf{x}_2 \\
\mathbf{y}_1 & \mathbf{y}_2
\end{array}\right)\) – \(\left(\begin{array}{ll}
2 & 3 \\
0 & 1
\end{array}\right)\) = \(\left(\begin{array}{ll}
3 & 5 \\
1 & 2
\end{array}\right)\) then find x₁, x₂, y₁, y₂.
(a) x₁ = 8, x₂ = 5, y₁ = 3, y₂ = 1
(b) x₁ = 1, x₂ = 8, y₁ = 5, y₂ = 3
(c) x₁ = 5, x₂ = 8, y₁ = 1, y₂ = 3
(d) x₁ = 3, x₂ = 1, y₁ = 8, y₂ = 5
Answer:
(c) x₁ = 5, x₂ = 8, y₁ = 1, y₂ = 3

Question 11.
If \(\left|\begin{array}{ll}
2 & 4 \\
k & 6
\end{array}\right|\) = 0, what is the value of k?
(a) 3
(b) 4
(c) 2
(d) 6
Answer:
(a) 3

Question 12.
If \(\left|\begin{array}{ll}
\mathbf{a}_1 & \mathbf{b}_1 \\
\mathbf{c}_1 & \mathbf{d}_1
\end{array}\right|\) = k \(\left|\begin{array}{ll}
a_1 & c_1 \\
b_1 & d_1
\end{array}\right|\) hen what is the value of k?
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(d) 4

Question 13.
If A = \(\left(\begin{array}{lll}
1 & 0 & 2 \\
5 & 1 & x \\
1 & 1 & 1
\end{array}\right)\) is a singular matrix then what is the value of x?
(a) 6
(b) 7
(c) 8
(d) 9
Answer:
(d) 9

Question 14.
Evaluate \(\left|\begin{array}{ccc}
-6 & 0 & 0 \\
3 & -5 & 7 \\
2 & 8 & 11
\end{array}\right|\)
(a) 66
(b) 666
(c) 6666
(d) 6
Answer:
(b) 666

Question 15.
Evaluate \(\left|\begin{array}{lll}
1 & 1 & b+c \\
1 & b & c+a \\
1 & c & a+b
\end{array}\right|\)
(a) 0
(b) 1
(c) 11
(d) 2
Answer:
(a) 0

Question 16.
Evaluate \(\left|\begin{array}{ccc}
1^2 & 2^2 & 3^2 \\
2^2 & 3^2 & 4^2 \\
3^2 & 4^2 & 5^2
\end{array}\right|\)
(a) 54
(b) 58
(c) -54
(d) 60
Answer:
(c) -54

Question 17.
If A and B are square matrices of order 3, such that |A| = -1, |B| = 3 then |3 AB| = –
(a) 1
(b) 11
(c) 9
(d) 81
Answer:
(d) 81

Question 18.
For what k
x + 2y – 3z = 2
(k + 3)z = 3
(2k + 1)y + z = 2 is inconsistent?
(a) -3
(b) -6
(c) 3
(d) 6
Answer:
(a) -3

Question 19.
The sum of two nonintegral roots of \(\left|\begin{array}{lll}
x & 2 & 5 \\
3 & x & 3 \\
5 & 4 & x
\end{array}\right|\) = 0 is ______.
(a) 5
(b) -5
(c) 3
(d) 15
Answer:
(b) -5

Question 20.
The value of \(\left|\begin{array}{ccc}
1 & 2 & 3 \\
3 & 5 & 2 \\
8 & 14 & 20
\end{array}\right|\) is ______.
(a) 1
(b) 2
(c) 0
(d) 3
Answer:
(c) 0

Question 21.
If [x 1] \(\left[\begin{array}{cc}
1 & 0 \\
-2 & 0
\end{array}\right]\) = 0, then x equals:
(a) 0
(b) -2
(c) -1
(d) 2
Answer:
(d) 2

Question 22.
The number of all possible matrices of order 3 × 3 with each entry 0 or 1 is:
(a) 27
(b) 18
(c) 81
(d) 512
Answer:
(d) 512

Question 23.
If A = \(\left[\begin{array}{cc}
\cos \alpha & -\sin \alpha \\
\sin \alpha & \cos \alpha
\end{array}\right]\) , and A + A’ = I, then the value of α is
(a) \(\frac{\pi}{6}\)
(b) \(\frac{\pi}{3}\)
(c) π
(d) \(\frac{3 \pi}{2}\)
Answer:
(b) \(\frac{\pi}{3}\)

Question 24.
Matrix A and B will be inverse of each other only if
(a) AB = BA
(b) AB = BA = 0
(c) AB = 0, BA = I
(d) AB = BA = I
Answer:
(d) AB = BA = I

Question 25.
The matrix P = \(\left[\begin{array}{lll}
0 & 0 & 4 \\
0 & 4 & 0 \\
4 & 0 & 0
\end{array}\right]\) is a
(a) square matrix
(b) diagonal matrix
(c) unit matrix
(d) None of these
Answer:
(a) square matrix

Question 26.
If A and B are symmetric matrices of same order, then AB – BA is a
(a) Skew-symmetric matrix
(b) Symmetric matrix
(c) Zero matrix
(d) Identity
Answer:
(a) Skew-symmetric matrix

Question 27.
If A is a square matrix of order 3, such that A(adj A) = 10I, then |adj A| is equal to
(a) 1
(b) 10
(c) 100
(d) 1000
Answer:
(c) 100

Question 28.
Let A be a square matrix of order 2 × 2, then |KA| is equal to
(a) K|A|
(b) K²|A|
(c) K³|A|
(d) 2K|A|
Answer:
(b) K²|A|

Question 29.
If A and B are invertible matrices then which of the following is not correct
(a) Adj A = |A|. A^-1
(b) det (A^-1) = (det A)^-1
(c) (AB)^-1 = B^-1A^-1
(d) (A + B)^-1 = A^-1 + B^-1
Answer:
(d) (A + B)^-1 = A^-1 + B^-1

Question 30.
If A is a skew-symmetric matrix of order 3, then the value of |A| is
(a) 3
(b) 0
(c) 9
(d) 27
Answer:
(b) 0

Question 31.
If A is a square matrix of order 3, such that A(adjA) = 10I, then ladj Al is equal to
(a) 1
(b) 10
(c) 100
(d) 1000
Answer:
(c) 100

Question 32.
Let A be a non-angular square matrix of order 3 x 3, then |A. adj Al is equal to
(a) |A|³
(b) |A|²
(c) |A|
(d) 3|A|
Answer:
(a) |A|³

Question 33.
Let A be a square matrix of order 3 × 3 and k a scalar, then |kA| is equal to
(a) k|A|
(b) |k||A|
(c) k³|A|
(d) none of these
Answer:
(c) k³|A|

Question 34.
If a, b, c are all distinct, and \(\left|\begin{array}{lll}
a & a^2 & 1+a^3 \\
b & b^2 & 1+b^3 \\
c & c^2 & 1+c^3
\end{array}\right|\) = 0 then the value of abc is
(a) 0
(b) -1
(c) 3
(d) -3
Answer:
(b) -1

Question 35.
If a, b, c are in AP, then the value of \(\left|\begin{array}{lll}
x+1 & x+2 & x+a \\
x+2 & x+3 & x+b \\
x+3 & x+4 & x+c
\end{array}\right|\) is:
(a) 4
(b) -3
(c) 0
(d) abc
Answer:
(c) 0

Question 36.
If A is a skew-symmetric matrix of order 3, then the value of |A| is
(a) 3
(b) 0
(c) 9
(d) 27
Answer:
(b) 0

Question 37.
A bag contains 3 white, 4 black and 2 red balls. If 2 balls are choosen at random (without replacement), then the probability that both the balls are white is:
(a) \(\frac{1}{18}\)
(b) \(\frac{2}{9}\)
(c) \(\frac{1}{12}\)
(d) \(\frac{1}{24}\)
Answer:
(c) \(\frac{1}{12}\)

Question 38.
Three diece are thrown simultaneously. The probability of obtaining a total score of 5 is:
(a) \(\frac{5}{216}\)
(b) \(\frac{1}{6}\)
(c) \(\frac{1}{36}\)
(d) \(\frac{1}{49}\)
Answer:
(c) \(\frac{1}{36}\)

Question 39.
An urn contains 6 balls of which two are red and four are black. Two balls are drawn at random. Probability that they are of the different colour is:
(a) \(\frac{2}{5}\)
(b) \(\frac{1}{15}\)
(c) \(\frac{8}{15}\)
(d) \(\frac{4}{15}\)
Answer:
(d) \(\frac{4}{15}\)

Question 40.
The probability of obtaining an even prime number on each die when a pair of dice is rolled is:
(a) 0
(b) \(\frac{1}{3}\)
(c) \(\frac{1}{12}\)
(d) \(\frac{1}{36}\)
Answer:
(d) \(\frac{1}{36}\)

Question 41.
Two events A and B are said to be independent if:
(a) A and B are mutually exclusive
(b) P (A’B’) = [1 – P(A)][1 – P(B)]
(c) P(A) = P(B)
(d) P(A) + P(B) = 1
Answer:
(b) P (A’B’) = [1 – P(A)][1 – P(B)]

Question 42.
A die is. thrown once, then the probability of getting number greater than 3 is:
(a) \(\frac{1}{2}\)
(b) \(\frac{2}{3}\)
(c) 6
(d) 0
Answer:
(a) \(\frac{1}{2}\)

Question 43.
If P(A) = \(\frac{6}{11}\), P(B) = \(\frac{5}{11}\) and P(A ∪ B) = \(\frac{7}{11}\), then P(A/B) is:
(a) \(\frac{2}{5}\)
(b) \(\frac{3}{5}\)
(c) \(\frac{4}{5}\)
(d) 1
Answer:
(c) \(\frac{4}{5}\)

Question 44.
Let the target be hit A and B: the target be hit by B and C: the target be hit by A and C. Then the probability that A, B and C all will hit, is:
(a) \(\frac{4}{5}\)
(b) \(\frac{3}{5}\)
(c) \(\frac{2}{5}\)
(d) \(\frac{1}{5}\)
Answer:
(c) \(\frac{2}{5}\)

Question 45.
What is the probability that ‘none of them will hit the target’?
(a) \(\frac{1}{30}\)
(b) \(\frac{1}{60}\)
(c) \(\frac{1}{15}\)
(d) \(\frac{2}{15}\)
Answer:
(b) \(\frac{1}{60}\)

(B) Very Short Type Questions With Answers

Question 1.
If \(\left|\begin{array}{ccc}
1+\mathbf{x} & \mathbf{x} & \mathbf{x}^2 \\
\mathbf{x} & 1+\mathbf{x} & \mathbf{x}^2 \\
\mathbf{x}^2 & \mathbf{x} & 1+\mathbf{x}
\end{array}\right|\) = a + bx + cx² + dx³ + ex⁴ + fx⁵ then write the value of a.
Solution:
\(\left|\begin{array}{ccc}
1+\mathbf{x} & \mathbf{x} & \mathbf{x}^2 \\
\mathbf{x} & 1+\mathbf{x} & \mathbf{x}^2 \\
\mathbf{x}^2 & \mathbf{x} & 1+\mathbf{x}
\end{array}\right|\)
= a + bx + cx² + dx³ + ex⁴ + fx⁵
which is an identity
Putting x = 0 we get
a = \(\left|\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right|\) = 1

Question 2.
If every element of a third order determinant of value 8 is multiplied by 2, then write the value of the new determinant.
Solution:
According to the question
|A| = 8
Now |KA| = Kⁿ|A|
⇒ |2A| = 2³|A| = 8 × 8 = 64
Value of the new determinant is 64.

Question 3.
If I is an identity matrix of order n, then k being a natural number, write the matrix I^k_n.
Solution:
If I is an identity matrix of order n, then I^k_n = I_n

Question 4.
If A is a 4 × 5 matrix and B is a matrix such that A^TB and BA^T both are defined, then write the order of B.
Solution:
Order of A = 4 × 5
Order of A^T = 5 × 4
Let order of B = m × n
A^TB is well defined ⇒ m = 4
BA^T is well defined ⇒ n = 5
Order of B = 4 × 5

Question 5.
Write the matrix which when added to the matrix \(\left[\begin{array}{cc}
2 & -3 \\
-4 & 7
\end{array}\right]\) gives the matrix \(\left[\begin{array}{ll}
4 & 1 \\
3 & 2
\end{array}\right]\)
Solution:
Let the required matrix is A.
\(\left(\begin{array}{cc}
2 & -3 \\
-4 & 7
\end{array}\right)\) + A = \(\left(\begin{array}{ll}
4 & 1 \\
3 & 2
\end{array}\right)\)
A = \(\left(\begin{array}{ll}
4 & 1 \\
3 & 2
\end{array}\right)\) – \(\left(\begin{array}{cc}
2 & -3 \\
-4 & 7
\end{array}\right)\) = \(\left(\begin{array}{cc}
2 & 4 \\
7 & -5
\end{array}\right)\)

Question 6.
Determine the maximum value of \(\left|\begin{array}{rl}
\cos x & \sin x \\
-\sin x & \cos x-1
\end{array}\right|\)
Solution:
Let f(x) = \(\left|\begin{array}{rl}
\cos x & \sin x \\
-\sin x & \cos x-1
\end{array}\right|\)
= cos²x – cos x + sin²x = 1 – cos x
As – 1 < cos x ≤ 1
⇒ 1 >- cos x ≥ – 1
⇒ 2 > 1 – cos x ≥ 0
The maximum value of f(x) = 2.

Question 7.
Write the value of k if:
\(\left|\begin{array}{lll}
\mathbf{a a _ { 1 }} & \mathbf{a a}_2 & \mathbf{a} \mathbf{a}_3 \\
\mathbf{a b _ { 1 }} & \mathbf{a b}_2 & \mathbf{a b} \\
\mathbf{a c _ { 2 }} & \mathbf{a c}_2 & \mathbf{a c _ { 3 }}
\end{array}\right|\) = k\(\left|\begin{array}{lll}
\mathbf{a}_1 & \mathbf{b}_1 & \mathbf{c}_1 \\
\mathbf{a}_2 & \mathbf{b}_2 & \mathbf{c}_2 \\
\mathbf{a}_3 & \mathbf{b}_3 & \mathbf{c}_3
\end{array}\right|\)
Solution:
\(\left|\begin{array}{lll}
\mathbf{a a _ { 1 }} & \mathbf{a a}_2 & \mathbf{a} \mathbf{a}_3 \\
\mathbf{a b _ { 1 }} & \mathbf{a b}_2 & \mathbf{a b} \\
\mathbf{a c _ { 2 }} & \mathbf{a c}_2 & \mathbf{a c _ { 3 }}
\end{array}\right|\) = k\(\left|\begin{array}{lll}
\mathbf{a}_1 & \mathbf{b}_1 & \mathbf{c}_1 \\
\mathbf{a}_2 & \mathbf{b}_2 & \mathbf{c}_2 \\
\mathbf{a}_3 & \mathbf{b}_3 & \mathbf{c}_3
\end{array}\right|\)
k = a³.

Question 8.
If A is a 3 × 3 matrix and |A| = 3, then write the matrix represented by A × adj A.
Solution:
|A| = 3 ⇒ A × Adj A = \(\left(\begin{array}{lll}
3 & 0 & 0 \\
0 & 3 & 0 \\
0 & 0 & 3
\end{array}\right)\)

Question 9.
If ω is a complex cube root of 1, then for what value of λ the determinant
\(\left|\begin{array}{ccc}
1 & \omega & \omega^2 \\
\omega & \lambda & 1 \\
\omega^2 & 1 & \omega
\end{array}\right|\) = 0?
Solution:

⇒ for any value of ‘A,’ the given determinant is ‘0’

Question 10.
If [1 2 3] A = [0], then what is the der of the matrix A?
Solution:
If [1 2 3] A = [0]
A is a 3 × 1 matrix

Question 11.
What is A + B if A = \(\left(\begin{array}{cc}
1 & 2 \\
3 & -1
\end{array}\right)\), B = \(\left(\begin{array}{cc}
0 & -1 \\
-2 & 1
\end{array}\right)\)?
Solution:
For A = \(\left(\begin{array}{cc}
1 & 2 \\
3 & -1
\end{array}\right)\), B = \(\left(\begin{array}{cc}
0 & -1 \\
-2 & 1
\end{array}\right)\)
A + B = \(\left(\begin{array}{ll}
1 & 1 \\
1 & 0
\end{array}\right)\)

Question 12.
Give an example of a unit matrix.
Solution:
\(\left(\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right)\) is a unit matrix of 2nd order.

Question 13.
Construct a 2 × 3 matrix having elements defined by a_ij = i – j.
Solution:
a_ij = i – j
a₁₁ =0, a₁₂ = 1 – 2 = – 1, a₁₃ = 1 – 3 =- 2
a₂₁ = 2 – 1 = 1, a₂₂ = 2 – 2 = 0, a₂₃ = 2 – 3 = -1
∴ The required matrix is \(\left(\begin{array}{ccc}
0 & -1 & -2 \\
0 & 0 & -1
\end{array}\right)\).

Question 14.
Find x, y if A = A’ where A = \(\left(\begin{array}{ll}
5 & \mathbf{x} \\
\mathbf{y} & 0
\end{array}\right)\)
Solution:
A = A’
⇒ \(\left(\begin{array}{ll}
5 & \mathbf{x} \\
\mathbf{y} & 0
\end{array}\right)\) = \(\left(\begin{array}{ll}
5 & \mathbf{y} \\
\mathbf{x} & 0
\end{array}\right)\) ⇒ x = y
∴ x and y are any real number where x = y

Question 15.
Cana matrix be constructed by taking 29 elements?
Solution:
Only two matrices can be formed by taking 29 elements. They are of order 1 × 29 and 29 × 1.

Question 16.
If \(\left|\begin{array}{ll}
2 & 4 \\
k & 6
\end{array}\right|\) = 0 , what is the value of k?
Solution:
\(\left|\begin{array}{ll}
2 & 4 \\
k & 6
\end{array}\right|\) = 0 ⇒ 12 – 4k = 0 ⇒ k = 3

Question 17.
If \(\left|\begin{array}{ll}
\mathbf{a}_1 & \mathbf{b}_1 \\
\mathbf{c}_{\mathbf{1}} & \mathbf{d}_1
\end{array}\right|\) = k = \(\left|\begin{array}{ll}
\mathbf{a}_1 & \mathbf{c}_1 \\
\mathbf{b}_1 & \mathbf{d}_1
\end{array}\right|\) then what is the value of k?
Solution:
k = 1

Question 18.
If A and B are square matrices of order 3, such that |A| = -1, |B| = 3 then |3 AB| = ______.
Solution:
|3 AB| = 27 |A| |B| = 81

Question 19.
Solve: \(\left|\begin{array}{ccc}
2 & 2 & x \\
-1 & x & 4 \\
1 & 1 & 1
\end{array}\right|\) = 0
Solution:
\(\left|\begin{array}{ccc}
2 & 2 & x \\
-1 & x & 4 \\
1 & 1 & 1
\end{array}\right|\) = 0 => \(\left|\begin{array}{ccc}
0 & 2 & x \\
-1-x & x & 4 \\
0 & 1 & 1
\end{array}\right|\) = 0
⇒ – (- 1 – x) (2 – x) = 0 ⇒ x = -1, x = 2.

(C) Short Type Questions With Answers

Question 1.
If A = \(\left[\begin{array}{ccc}
1 & 2 & 3 \\
3 & -2 & 1 \\
4 & 2 & 1
\end{array}\right]\) then show that A³ – 23A – 40I = 0
Solution:

Question 2.
Solve: \(\left|\begin{array}{ccc}
\mathbf{x + 1} & \omega & \omega \\
\omega & x+\omega^2 & 1 \\
\omega^2 & 1 & x+\omega
\end{array}\right|\) = 0
Solution:

Question 3.
If A = \(\left[\begin{array}{ccc}
1 & 2 & 0 \\
0 & 1 & 3 \\
-2 & 5 & 3
\end{array}\right]\), then verify that A + A’ is symmetric and A – A’ is skew symmetric.
Solution:

Question 4.
If A, B, C are matrices of order 2 × 2 each and 2A + B + C = \(\left[\begin{array}{ll}
1 & 2 \\
3 & 0
\end{array}\right]\), A + B + C = \(\left[\begin{array}{ll}
0 & 1 \\
2 & 1
\end{array}\right]\) and A + B – C = \(\left[\begin{array}{ll}
1 & 2 \\
1 & 0
\end{array}\right]\), then find A, B and C.
Solution:

Question 5.
Find the inverse of the following matrix: \(\left[\begin{array}{lll}
1 & 1 & 2 \\
0 & 1 & 2 \\
1 & 2 & 1
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{lll}
1 & 1 & 2 \\
0 & 1 & 2 \\
1 & 2 & 1
\end{array}\right]\)
Method – I
Let us find A^-1 by using elementary row transformation.
Let A = IA

Method – II
|A| = 1(1 – 4) – 1(0- 2) + 2(0- 1)
= 1(-3) – 1(-2) + 2(-1)
= -3 ≠ 0
∴ A^-1 exists.
A₁₁ = -3, A₁₂ = 2, A₁₃ = -1

Question 6.
Show that \(\left|\begin{array}{ccc}
a-b-c & 2 a & 2 a \\
2 b & b-c-a & 2 b \\
2 c & 2 c & c-a-b
\end{array}\right|\) = (a+b +c)³
Solution:

= (a + b + c)³ (1 – 0) = (a + b + c)³

Question 7.
Find the inverse of the following matrix: \(\left[\begin{array}{lll}
0 & 0 & 2 \\
0 & 2 & 0 \\
2 & 0 & 0
\end{array}\right]\)
Solution:
A = \(\left[\begin{array}{lll}
0 & 0 & 2 \\
0 & 2 & 0 \\
2 & 0 & 0
\end{array}\right]\)
|A| = 2(- 4) = – 8 ≠ 0
∴ A^-1 exists.
A₁₁ = 0, A₁₂ = 0, A₁₃ = – 4
A₂₁ = 0, A₂₂ = – 4, A₂₃ = 0
A₃₁ = 0,A₃₂ = 0, A₃₃ = – 4
∴ The matrix of cofactors

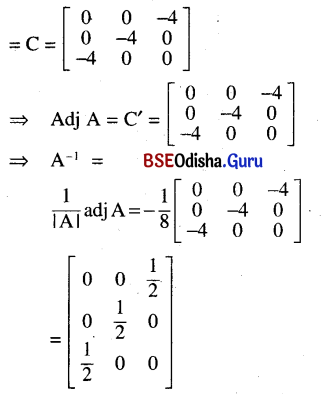
Question 8.
If the matrix A is such that \(\left[\begin{array}{cc}
1 & -1 \\
2 & 3
\end{array}\right]\)A = \(\left[\begin{array}{cc}
-4 & 1 \\
7 & 7
\end{array}\right]\), find A.
Solution:

Question 9.
Show that (a + 1) is a factor of \(\left|\begin{array}{ccc}
a+1 & 2 & 3 \\
1 & a+1 & 3 \\
3 & -6 & a+1
\end{array}\right|\).
Solution:

= (a + 1) (a² + 2a + 1 + 18) – 2(a + 1 – 9) + 3(-6 – 3a – 3)
= (a + 1)(a² + 2a + 19) – 2a + 16 – 27 – 9a
= (a + 1) (a² + 2a + 19) – 11a – 11
= (a + 1) (a² + 2a + 19) – 11(a + 1)
= (a + 1) (a² + 2a + 8)
⇒ (a + 1) is a factor of the given determinant.

Question 11.
If A = \(\left[\begin{array}{ll}
\alpha & 0 \\
1 & 1
\end{array}\right]\) and B = \(\left[\begin{array}{ll}
1 & 0 \\
5 & 1
\end{array}\right]\) show that for no values of α, A² = B.
Solution:

⇒ α2 = 1 and α + 1 = 5
⇒ α = ± 1 and α = 4
Which is not possible.
There is no α for which A² = B

Question 12.
If A = \(\left[\begin{array}{ll}
3 & -4 \\
1 & -1
\end{array}\right]\), then show that A^k = \(\left[\begin{array}{cc}
1+2 \mathrm{k} & -4 \mathrm{k} \\
\mathrm{k} & 1-2 \mathrm{k}
\end{array}\right]\), k ∈ N.
Solution:

Question 13.
If A = \(\left[\begin{array}{ccc}
1 & -2 & 2 \\
3 & 1 & -1
\end{array}\right]\), B = \(\left[\begin{array}{cc}
2 & 4 \\
1 & 2 \\
3 & -1
\end{array}\right]\), verify that (AB)^T = B^TA^T.

Question 14.
Show that for each real value of λ the system of equations
(λ + 3) + λy = 0
x + (2λ + 5)y = 0 has a unique solution.
Solution:
Given system of equations is a
homogeneous system of linear
equations.
Now
Δ = \(\left|\begin{array}{cc}
\lambda+3 & \lambda \\
1 & 2 \lambda+5
\end{array}\right|\)
= (λ + 3)(2λ + 5) – λ
= 2λ² + 11λ + 15 – λ
= 2λ² + 10λ + 15
As for 2λ² + 10A + 15, D = 100 – 120 < 0
the polynomial 2λ² + 10λ + 15 has no roots i.e. Δ ≠ 0.
Thus the system has a unique trivial solution for every real value of λ.

Question 15.
If A and B are square matrices of same order then show by means of an example that AB ≠ BA in general.
Solution:

∴ AB ≠ BA we have AB ≠ BA in general.

Question 16.
If A = \(\left|\begin{array}{cc}
0 & -\tan \frac{\theta}{2} \\
\tan \frac{\theta}{2} & 0
\end{array}\right|\), then prove that det{(I + A)(I – A)-1} = 1
Solution:

Question 17.
Solve for x: \(\left|\begin{array}{ccc}
15-2 x & 11 & 10 \\
11-3 x & 17 & 16 \\
7-x & 14 & 13
\end{array}\right|\) = 0
Solution:

Question 18.
If A = \(\left[\begin{array}{ccc}
-1 & 3 & 5 \\
1 & -3 & -5 \\
-1 & 3 & 5
\end{array}\right]\) find A³ – A².
Solution:

A² = A ⇒ A²A = A²
⇒ A³ – A² = 0

Question 19.
Prove that: A = \(\left|\begin{array}{ccc}
2 & 3 & 4 \\
1 & -2 & -3 \\
3 & 1 & -8
\end{array}\right|\) ⇒ A² – 5A + 71 = 0.
Solution:

Question 20.
Test whether the following system of equations have non-zero solution.
Write the solution set:
2x + 3y + 4z = 0,
x – 2y – 3z = 0,
3x + y – 8z = 0.
Solution:
Given equations are
2x + 3y + 4z = 0
x – 2y – 3z = 0
3x + y – 8z = 0
Now \(\left|\begin{array}{ccc}
2 & 3 & 4 \\
1 & -2 & -3 \\
3 & 1 & -8
\end{array}\right|\)
= 2(19) – 3(1) + 4(7) 0
∴ The system has no non-zero solution.
The solution set is x = 0; y = 0, z = 0.