CHSE Odisha Class 12 Math Solutions Chapter 6 Probability Ex 6(a)

Odisha State Board CHSE Odisha Class 12 Math Solutions Chapter 6 Probability Ex 6(a) Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 6 Probability Exercise 6(a)

Question 1.
Two balls are drawn from a bag containing 5 white and 7 black balls. Find the probability of selecting 2 white balls if
Solution:
Two balls are drawn from a bag containing 5 white and 7 black balls.
∴ |S| = 12.

(i) the first ball is replaced before drawing the second.
Solution:
The 1st ball is replaced before the 2nd ball is drawn. We are to select 2 white balls. So in both the draws we will get white balls. Drawing a white ball in 1st draw and in 2nd draw are independent events.
Probability of getting 2 white balls = \(\frac{5}{12}\) × \(\frac{5}{12}\) = \(\frac{25}{144}\)

(ii) the first ball is not replaced before drawing the second.
Solution:
Here the 1st ball is not replaced before the 2nd ball is drawn. Since we are to get 2 white balls in each draw, we must get a white ball.
Now probability of getting a white ball in 1st draw = \(\frac{5}{12}\).
Probability of getting a white ball in 2nd = \(\frac{4}{11}\).
Since the two draws are independent, we have the probability of getting 2 white balls
= \(\frac{5}{12}\) × \(\frac{4}{11}\) = \(\frac{20}{132}\).

Question 2.
Two cards are drawn from a pack of 52 cards; find the probability that
(i) they are of different suits.
(ii) they are of different denominations.
Solution:
Two cards are drawn from a pack of 52 cards. The cards are drawn one after another. Each suit has 13 cards.
|S| = ⁵²C₂
(i) As the two cards are of different suits, their probability
= \(\frac{52}{52}\) × \(\frac{39}{51}\)
(ii) Each denomination contains 4 cards. As the two cards drawn are of different denominations, their probability
= \(\frac{52}{52}\) × \(\frac{48}{51}\)

Question 3.
Do both parts of problem 2 if 3 cards drawn at random.
Solution:
(i) 3 cards are drawn one after another. As they are of different suits, we have their probability
= \(\frac{52}{52}\) × \(\frac{39}{51}\) × \(\frac{26}{50}\).
(ii) As the 3 cards are of different denominations, we have their probability
= \(\frac{52}{52}\) × \(\frac{48}{51}\) × \(\frac{44}{50}\).

Question 4.
Do both parts of problem 2 if 4 cards are drawn at random.
Solution:
(i) 4 cards are drawn one after another. As they are of different suits, we have their probability
= \(\frac{52}{52}\) × \(\frac{39}{51}\) × \(\frac{26}{50}\) × \(\frac{13}{49}\).
(ii) As the cards are of different denominations, we have their probability
= \(\frac{52}{52}\) × \(\frac{48}{51}\) × \(\frac{44}{50}\) × \(\frac{40}{49}\).

Question 5.
A lot contains 15 items of which 5 are defective. If three items are drawn at random, find the probability that
(i) all three are defective
(ii) none of the three is defective.
Do this problem directly.
Solution:
(i) A lot contains 15 items of which 5 are defective. Three items are drawn at random. As the items are drawn one after another.
Their probability = \(\frac{5}{15}\) × \(\frac{4}{14}\) × \(\frac{3}{13}\)
(ii) As none of the 3 items are defective, we have to draw 3 non-defective items one after another.
Their probability = \(\frac{10}{15}\) × \(\frac{9}{14}\) × \(\frac{8}{13}\)

Question 6.
A pair of dice is thrown. Find the probability of getting a sum of at least 9 if 5 appears on at least one of the dice.
Solution:
A pair of dice is thrown. Let A be the event of getting at least 9 points and B, the event that 5 appears on at least one of the dice.
∴ B = {(1, 5), (2, 5), (3, 5), (4, 5), (5, 5), (6, 5), (5, 1), (5, 2), (5, 3), (5, 4), (5, 6)}
A = {(3, 6), (4, 5), (5, 4), (6, 3), (4, 6), (5, 5), (6, 4), (5, 6), (6, 5), (6, 6)}
∴ A ∩ B = {(4, 5), (5, 4), (5, 5), (5, 6), (6, 5)}
∴ P (A | B) = \(\frac{\mathrm{P}(\mathrm{A} \cap \mathrm{B})}{\mathrm{P}(\mathrm{B})}\) = \(\frac{\frac{5}{36}}{\frac{31}{36}}\) = \(\frac{5}{11}\)

Question 7.
A pair of dice is thrown. If the two numbers appearing are different, find the probability that
(i) the sum of points is 8.
(ii) the sum of points exceeds 8.
(iii) 6 appears on one die.
Solution:
A pair of dice is thrown as two numbers are different
We have |S| = 30
(i) Let A be the. event that the sum of points on the dice is 8, where the numbers on the dice are different.
A = {(2, 6), (3, 5), (5, 3), (6, 2)}
P(A) = \(\frac{|\mathrm{A}|}{|\mathrm{S}|}\) = \(\frac{4}{30}\)
(ii) Let B be the event that sum of the points exceeds 8.
B = {(3, 6), (4, 5), (5, 4), (6, 3), (5, 6), (6, 5), (4, 6), (6, 4)}
P(B) = \(\frac{|\mathrm{B}|}{|\mathrm{S}|}\) = \(\frac{8}{30}\)
(iii) Let C be the event that 6 appears on one die.
C = {(1, 6), (2, 6), (3, 6), (4, 6), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5)}
P(C) = \(\frac{|\mathrm{C}|}{|\mathrm{S}|}\) = \(\frac{10}{30}\) = \(\frac{1}{3}\)

Question 8.
In a class 30% of the students fail in Mathematics, 20% of the students fail in English and 10% fail in both. A student is selected at random.
Solution:
In a class 30% of the students fail in Mathematics, 20% of the students fail in English and 10% fail in both. Let A be the event that a student fails in Mathematics and B be the events that he fails in English.
P(A) = \(\frac{30}{100}\), P(B) = \(\frac{20}{100}\)
Where |S| = 100, P (A ∩ B) = \(\frac{10}{100}\)

(i) If he has failed in English, what is the probability that he has failed in Mathematics?
Solution:
If he has failed in English, then the probability that he has failed in Mathematics.
i.e., P\(\left(\frac{A}{B}\right)\) = \(\frac{P(A \cap B)}{P(B)}\) = \(\frac{\frac{10}{100}}{\frac{20}{100}}\) = \(\frac{1}{2}\)

(ii) If he has failed in Mathematics, what is the probability that he has failed in English?
Solution:
If he has failed in Mathematics, then the probability that he has failed in English
i.e., P\(\left(\frac{B}{A}\right)\) = \(\frac{P(A \cap B)}{P(A)}\) = \(\frac{\frac{10}{100}}{\frac{30}{100}}\) = \(\frac{1}{3}\)

(iii) What is the probability that he has failed in both?
Solution:
Probability that he has failed in both
i.e., P (A ∩ B) = \(\frac{10}{100}\) = \(\frac{1}{10}\)

Question 9.
IfA, B are two events such that
P(A) = 0.3, P(B) = 0.4, P (A ∪ B) = 0.6
Find
(i) P (A | B)
(ii) P (B | A)
(iii) P (A | B^c)
(iv) P (B | A^c)
Solution:
A and B are two set events such that
P(A) = 0.3, P(B) = 0.4, P (A ∪ B) = 0.6
We have
P (A ∪ B) = P(A) + P(B) – P (A ∩ B)
or, 0.6 = 0.3 + 0.4 – P (A ∩ B)
or, P (A ∩ B) = 0.7 – 0.6 = 0.1

Question 10.
If A, B are events such that P(A) = 0.6, P(B) = 0.4 and P (A ∩ B) = 0.2, then find
(i) P (A | B)
(ii) P (B | A)
(iii) P (A | B^c)
(iv) P (B | A^c)
Solution:
A and B are events such that
P(A) = 0.6, P(B) = 0.4, P (A ∩ B) = 0.2

Question 11.
If A and B are independent events, show that
(i) A^c and B^c are independent,
(ii) A and B^c are independent,
(iii) A^c and B are independent.
Solution:
A and B are independent events.
(i) We have P (A ∩ B) = P(A). P(B)
P (A’ ∩ B’) = P (A ∪ B)’ = 1 – P (A ∪ B)
= 1 – [P(A) + P(B) – P (A ∩ B)]
= 1 – P(A) – P(B) + P(A) P(B)
= 1 [1 – P(A)] – P(B) [1 – P(A)]
= [1 – P(A)] [1 – P(B)] = P(A’) P(B’)
∴ A’ and B’ are independent events.

(ii) P (A ∩ B^c) = P (A – B)
= P(A) – P (A ∩ B)
= P(A) – P(A) P(B)
= P(A) [1 – P(B)]
= P(A). P(B^c).
∴ A and B^c are independent events.

(iii) P (A^c ∪ B) = P (B – A)
= P(B) – P (A ∩ B)
= P(B) – P(A) P(B)
= P(B) [1 – P(A)] = P(B) P(A^c)
∴ A^c and B are independent events.

Question 12.
Two different digits are selected at random from the digits 1 through 9.
(i) If the sum is even, what is the probability that 3 is one of the digits selected?
(ii) If the sum is odd, what is the probability that 3 is one of the digits selected?
(iii) If 3 is one of the digits selected, what is the probability that the sum is odd?
(iv) If 3 is one of the digits selected, what is the probability that the sum is even?
Solution:
Two different digits are selected at random from the digits 1 through 9.
(i) Let A be the event that the sum is even and B be the event that 3 is one of the number selected.
We have to find P (B | A).
There are 4 even digits and 5 odd digits.
∴ The sum is even if both the numbers are odd or both are even.
∴ |A| = ⁴C₂ + ⁵C₂ = 6 + 10 = 16
∴ P(A) = \(\frac{16}{{ }^9 \mathrm{C}_2}\) = \(\frac{16}{36}\)
Also B = {(1, 3), (5, 3), (7, 3), (9, 3), (3, 2), (3, 4), (3, 8), (3, 6)}
∴ A ∩ B = {(1, 3), (5, 3), (7, 3), (9, 3)}
P(B) = \(\frac{8}{36}\) P (A ∩ B) = \(\frac{4}{36}\)
P(\(\frac{B}{A}\)) = \(\frac{P(A \cap B)}{P(A)}\) = \(\frac{\frac{4}{36}}{\frac{16}{36}}\) = \(\frac{1}{4}\)

(ii) Let A be the event that the sum is odd. The sum is odd if one of the numbers selected is odd and other is even.
∴ P(A) = \(\frac{5}{9}\) × \(\frac{4}{8}\) + \(\frac{4}{9}\) × \(\frac{5}{8}\) = \(\frac{20}{36}\)
Let B be the event that one of the numbers selected is 3.
∴ B = {(1, 3), (2, 3), (4, 3), (5, 3), (6, 3), (7, 3), (8, 3), (9, 3)}
∴ A ∩ B = {(2, 3), (4, 3), (6, 3), (8, 3)}

Question 13.
If P(A) = 0.4, P (B | A) = 0.3 and P (B^c | A^c) = 0.2. find
(i) P (A | B)
(ii) P (B | A^c)
(iii) P(B)
(iv) P(A^c)
(v) P (A ∪ B)
Solution:
P(A) = 0.4, P (B | A) = 0.3 and P (B^c | A^c) = 0.2.


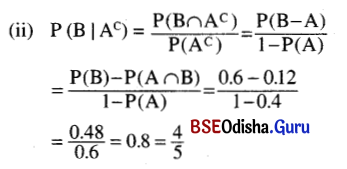
(iii) P(B) = 0.6
= \( \frac{6}{10} \)
= \( \frac{3}{5} \)

(iv) P(A^c) = 1 – P(A)
= 1 – 0.4 = 0.6
= \( \frac{6}{10} \) = \( \frac{3}{5} \)

(v) P (A ∪ B) = P(A) + P(B) – P (A ∩ B)
= 0.4 + 0.6 – 0.12
= 1.0 – 0.12 = 0.88

Question 14.
If P(A) = 0.6, P (B | A) = 0.5, find P (A ∪ B) if A, B are independent.
Solution:
P(A) = 0.6, P (B | A) = 0.5
We have P (B | A) = \(\frac{\mathrm{P}(\mathrm{B} \cap \mathrm{A})}{\mathrm{P}(\mathrm{A})}\) = 0.5
or, P (B ∩ A) = 0.5 × P(A)
= 0.5 × 0.6 = 0.3
As A and B are independent events, we have
P (B ∩ A) = P(B) P(A) = 0.3
or, P(B) = \(\frac{0.3}{\mathrm{P}(\mathrm{A})}\)
= \(\frac{0.3}{0.6}\)
= \(\frac{1}{2}\) = 0.5
P (A ∪ B) = P(A) + P(B) – P(A ∩ B)
= 0.6 + 0.5 – 0.3 = 0.8

Question 15.
Two cards are drawn in succession from a deck of 52 cards. What is the probability that both cards are of denomination greater than 2 and less than 9?
Solution:
Two cards are drawn in succession from a deck of 52 cards.
There are 6 denominations which are greater than 2 and less than 9. So there are 24 cards whose denominations are greater than 2 and less than 9.
∴ Their probability = \(\frac{24}{52}\) × \(\frac{23}{51}\).

Question 16.
From a bag containing 5 black and 7 white balls, 3 balls are drawn in succession. Find the probability that
(i) all three are of the same colour.
(ii) each colour is represented.
Solution:
From a bag containing 5 black and 7 white balls, 3 balls are drawn in succession.
(i) The 3 balls drawn are of same colour.
∴ Probability of drawing 3 balls of black colour
= \(\frac{5}{12}\) × \(\frac{4}{11}\) × \(\frac{3}{10}\) = \(\frac{1}{22}\)
Probability of drawing 3 white balls
= \(\frac{7}{12}\) × \(\frac{6}{11}\) × \(\frac{5}{10}\) = \(\frac{7}{44}\)
∴ Probability of drawing 3 balls of same colour
= \(\frac{5}{12}\) × \(\frac{4}{11}\) × \(\frac{3}{10}\) + \(\frac{7}{12}\) × \(\frac{6}{11}\) × \(\frac{5}{10}\) = \(\frac{9}{44}\)

(ii) Balls of both colour will be drawn. If B represents black ball and W represents the white ball.
∴ The possible draws are WWB, WBW, BWW.

Question 17.
A die is rolled until a 6 is obtained. What is the probability that
(i) you end up in the second roll
(ii) you end up in the third roll.
Solution:
A die is rolled until a 6 is obtained
(i) We are to end up in the 2nd roll i.e., we get 6 in the 2nd roll. Let A be the event of getting a 6 in one roll of a die.
∴ P(A) = \(\frac{1}{6}\) ⇒ P(A’) = 1 – \(\frac{1}{6}\) = \(\frac{5}{6}\)
∴ Probability of getting a 6 in the 2nd roll
= \(\frac{5}{6}\) × \(\frac{1}{6}\) = \(\frac{5}{36}\)
(ii) Probability of getting a 6 in the 3rd roll
= \(\frac{5}{6}\) × \(\frac{5}{6}\) × \(\frac{1}{6}\) = \(\frac{25}{216}\)

Question 18.
A person takes 3 tests in succession. The probability of his (her) passing the first test is 0.8. The probability of passing each successive test is 0.8 or 0.5 according as he passes or fails the preceding test. Find the probability of his (her) passing at least 2 tests.
Solution:
A person takes 3 tests in succession. The probability of his passing the 1st test is 0.8. The probability of passing each successive test is 0.8 or 0.5 according as he passes or fails the preceding test.
Let S denotes the success (passing) in a test and F denotes the failure in a test.
∴ P(S) = 0.8
∴ P(F) = 1 – P(S) = 1 – 0.8 = 0.2
We have the following mutually exclusive cases:

Event			Probability
S	S	S	0.8 × 0.8 × 0.8 = 0.512
S	S	F	0.8 × 0.8 × 0.2 = 0.128
S	F	S	0.8 × 0.2 × 0.5 = 0.080
F	S	S	0.2 × 0.5 x 0.8 = 0.080

∴ Probability of atleast 2 successes
= 0.512 + 0.128 + 0.080 + 0.080
= 0.8 = \(\frac{4}{5}\)

Question 19.
A person takes 4 tests in succession. The probability of his passing the first test is p, that of his passing each succeeding test is p or y depending on his passing or failing the preceding test. Find the probability of his passing
(i) at least three test
(ii) just three tests.
Solution:
A person takes 4 tests in succession. The probability of his passing the 1st test is P, that of his passing each succeeding test is P or P/2 depending bn his passing or failing the preceding test. Let S and F denotes the success and failure in the test.
∴ P(S) = P, P(F) = 1 – P
We have the following mutually exclusive tests:

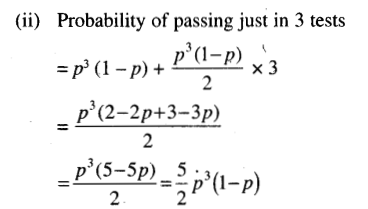
Question 20.
Given that all three faces are different in a throw of three dice, find the probability that
(i) at least one is a six
(ii) the sum is 9.
Solution:
Three dice are thrown once showing different faces in a throw.
|S| = 6³ = 216
Let A be the event that atleast one is a six.
Let B be the event that all three faces are different.
|B| = ⁶6₃
(i) Now A^c is the event that there is no six. A^c ∩ B is the event that all 3 faces are different and 6 does not occur.
|A^c ∩ B| = ⁵C₃
P (A^c | B) = \(\frac{P\left(A^C \cap B\right)}{P(B)}\)
= \(\frac{{ }^5 \mathrm{C}_3 / 216}{{ }^6 \mathrm{C}_3 / 216}\) = \(\frac{1}{2}\)

(ii) Let A be the event that the sum is 9.
A ∩ B = {(1,3, 5), (1,5, 3), (3, 5,1), (3, 1, 5), (5, 1, 3), (5, 3, 1), (1, 2, 6), (1, 6, 2), (2, 1, 6), (2, 6, 1), (6, 2, 1), (6, 1, 2), (2, 3, 4), (2, 4, 3), (3, 2, 4), (2, 3, 4), (3, 4, 2), (4, 3, 2)}
|A ∩ B| = 18
P (A | B) = \(\frac{P(A \cap B)}{P(B)}\)
= \(\frac{18 / 216}{20 / 216}\) = \(\frac{9}{10}\)

Question 21.
From the set of all families having three children, a family is picked at random.
(i) If the eldest child happens to be a girl, find the probability that she has two brothers.
(ii) If one child of the family is a son, find the probability that he has two sisters.
Solution:
A family is picked up at random from a set of families having 3 children.
(i) The eldest child happens to be a girl. We have to find the probability that she has two brothers. Let G denotes a girl and B denotes a boy.
∴ P(B) = \(\frac{1}{2}\), P(G) = \(\frac{1}{2}\)
P(BB | G) = P(B) × P(G) = \(\frac{1}{2}\) × \(\frac{1}{2}\) = \(\frac{1}{4}\)

(ii) The one child of the family is a son. We have to find the probability that he has two sisters. We have the following mutually exclusive events:
BGG, GBG, GGB.
∴ The required probability
= P(B) × P(G) × P(G) + P(G) × P(B) + P(G) + P(G) × P(G) × P(B)
= \(\frac{1}{2}\) × \(\frac{1}{2}\) × \(\frac{1}{2}\) + \(\frac{1}{2}\) × \(\frac{1}{2}\) × \(\frac{1}{2}\) + \(\frac{1}{2}\) × \(\frac{1}{2}\) × \(\frac{1}{2}\) = \(\frac{3}{8}\)

Question 22.
Three persons hit a target with probability \(\frac{1}{2}\), \(\frac{1}{3}\) and \(\frac{1}{4}\) respectively. If each one shoots at the target once,
(i) find the probability that exactly one of them hits the target
(ii) if only one of them hits the target what is the probability that it was the first person?
Solution:
Three persons hit a target with probability
\(\frac{1}{2}\), \(\frac{1}{3}\) and \(\frac{1}{4}\)
Let A, B, C be the events that the 1st person, 2nd person, 3rd person hit the target respectively.

(i) As the events are independent, the probability that exactly one of them hit the target
= P(AB’C’) + P(A’BC’) + P(A’B’C)
= P(A) P(B’) P(C’) + P(A’) P(B) P(C’) + P(A’) P(B’) P(C)

(ii) Let E₁ be the event that exactly one person hits the target.
∴ P(E₁) = \(\frac{11}{24}\)
Let E₂ be the event that 1st person hits the target
∴ P(E₂) = P(A) = \(\frac{1}{2}\)
∴ E₁ ∩ E₂ = AB’C’
⇒ P(E₁ ∩ E₂)
= P(A) × P(B’) P(C’) = \(\frac{6}{24}\)
∴ P(E₂ | E₁) = \(\frac{6 / 24}{11 / 24}\) = \(\frac{6}{11}\)