CHSE Odisha Class 12 Math Solutions Chapter 7 Continuity and Differentiability Ex 7(a)

Odisha State Board Elements of Mathematics Class 12 CHSE Odisha Solutions Chapter 7 Continuity and Differentiability Ex 7(a) Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 7 Continuity and Differentiability Exercise 7(a)

Question 1.
Examine the continuity of the following functions at indicated points.
(i) f(x) = \(\left\{\begin{array}{cl}
\frac{x^2-a^2}{x-a} & \text { if } x \neq a \\
a & \text { if } x=a
\end{array}\right.\) at x = a
Solution:

(ii) f(x) = \(\left\{\begin{aligned}
\frac{\sin 2 x}{x} & \text { if } x \neq 0 \\
2 & \text { if } x=0
\end{aligned}\right.\) at x = 0
Solution:

(iii) f(x) = \(\begin{cases}(1+2 x)^{\frac{1}{x}} & \text { if } x \neq 0 \\ e^2 & \text { if } x=0\end{cases}\) at x = 0
Solution:

(iv) f(x) = \(\left\{\begin{array}{l}
x \sin \frac{1}{x} \text { if } x \neq 0 \\
0
\end{array}\right.\) at x = 0
Solution:

(v) f(x) = \(\left\{\begin{array}{l}
\frac{x^2-1}{x-1} \text { if } x \neq 1 \\
2
\end{array}\right.\) at x = 1
Solution:

(vi) f(x) = \(\begin{cases}\sin \frac{1}{x} & \text { if } x \neq a \\ 0 & \text { if } x=0\end{cases}\) at x = 0
Solution:

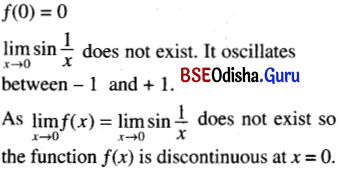
(vii) f(x) = [3x + 11] at x = –\(\frac{11}{3}\)
Solution:

(viii) f(x) = \(\left\{\begin{array}{l}
\frac{e^{\frac{1}{x}}-1}{e^{\frac{1}{x}}+1} \text { if } x \neq 0 \\
0
\end{array}\right.\) at x= 0
Solution:

(ix) f(x) = \(\left\{\begin{array}{l}
\frac{1}{x+[x]} \text { if } x<0 \\
-1 \quad \text { if } x \geq 0
\end{array}\right.\) at x = 0
Solution:

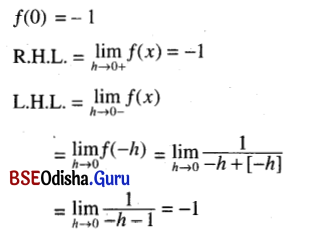
because [- h]is the greatest integer not exceeding – h
and so [- h ] = – 1
As L.H.L. = R.H.L. = f(0)
f(x) is cntinuous at x = 0.

(x) f(x) = \(\begin{cases}\frac{|x|}{x} & \text { if } x \neq 0 \\ 0 & \text { if } x=0\end{cases}\) at x = 0
Solution:

(xi) f(x) = \(\left\{\begin{array}{l}
2 x+1 \text { if } x \leq 0 \\
x \quad \text { if } 0<x<1 \\
2 x-1 \text { if } x \geq 1
\end{array}\right.\) at x = 0, 1
Solution:

(xii) f(x) = \(\left\{\begin{array}{l}
\frac{1}{e^{\frac{1}{x}}-1} \text { if } x>0 \\
0
\end{array} \text { if } x \leq 0\right.\) at x = 0
Solution:

(xiii) f(x) = sin\(\frac{\pi[x]}{2}\) at x = 0
Solution:

(xiv) f(x) = \(\frac{g(x)-g(1)}{x-1}\) at x = 1
Solution:
g(x) = |x – 1|
Then g(1) = |1 – 11| = 0
Now f(1) = \(\frac{g(1)-f(1)}{1-1}\) = 0/0
which we cannot determine.
Hence f(x) is discontinuous at x = 1.

Question 2.
If a function is continuous at x = a, then find
(i) \(\lim _{h \rightarrow 0}+\frac{1}{2}\{f(a+h)+f(a-h)\}\)
(ii) \(\lim _{h \rightarrow 0}+\frac{1}{2}\{f(a+h)-f(a-h)\}\)
Solution:

Question 3.
Find the value ofa such that the function f defined by \(\begin{cases}\frac{\sin a x}{\sin x} & \text { if } x \neq 0 \\ \frac{1}{a} & \text { if } x=0\end{cases}\)
is continuous at x = 0.
Solution:

Question 4.
If f(x) = \(\left\{\begin{array}{l}
a x^2+b \text { if } x<1 \\
1 \quad \text { if } x=1 \\
2 a x-b \text { if } x>1
\end{array}\right.\)
is continuous at x = 1, then find a and b.
Solution:
Let f(x) be continuous at x = 1
Then L.H.L. = R.H.L. = f(1)

Question 5.
Show that sin x is continuous for every real x.
Solution:
Let f(x) = sin x
Consider the point x = a, where ‘a’ is any real number.
Then f(a) = sin a

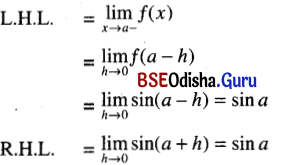
Thus L.H.L. = R.H.L. = f(a)
Hence f(x) = sin x is continuous for every real x.
(Proved)

Question 6.
Show that the function f defined by \(\left\{\begin{array}{l}
1 \text { if } x \text { is rational } \\
0 \text { if } x \text { is irrational }
\end{array}\right.\) is discontinuous ∀ ≠ 0 ∈ R.
Solution:
Consider any real point x = a
If a is rational then f(a) = 1.
Again lim_x→a+f(x) = lim_h→0f(a + h)
which does not exist because a + h may be rational or irrational
Similarly lim_x→a-f(x) does not exist.
Thus f(x) is discontinuous at any rational point. Similarly we can show that f(x) is discontinuous at any irrational point.
Hence f(x) is discontinuous for all x ∈ R
(Proved)

Question 7.
Show that the function f defined by f(x) = \(f(x)=\left\{\begin{array}{l}
x \text { if } x \text { is rational } \\
-x \text { if } x \text { is irrational }
\end{array}\right.\)
is continuous at x = 0 and discontinuous ∀ x ≠ 0 ∈ R.
Solution:
f(0) = 0
L.H.L. = lim_x→0f(x) = lim_h→0f(-h)
= \(\lim _{h \rightarrow 0} \begin{cases}-h & \text { if } h \text { is rational } \\ h & \text { if } h \text { is irrational }\end{cases}\) = 0
Similarly R.H.L. = 0
Thus L.H.L. = R.H.L. = f(0)
Hence f(x) is continuous at x = 0.
We can easily show that f(x) is discontinuous at all real points x ≠ 0.

Question 8.
Show that the function f defined by
f(x) = \(\left\{\begin{array}{l}
x \text { if } x \text { is rational } \\
0 \text { if } x \text { is irrational }
\end{array}\right.\)
is discontinuous everywhere except at x = 0.
Solution:
f(0) = 0
L.H.L. = lim_h→0f(-h)
= lim_h→0\(\begin{cases}-h & \text { if }-h \text { is rational } \\ 0 & \text { if }-h \text { is irrational }\end{cases}\)
Similarly R.H.L. = 0
Thus L.H.L. = R.H.L = f(0)
Hence f(x) is continuous at x = 0.
Let a be any real number except 0.
If a is rational then f(a) = a.
L.H.L. = lim_h→0f(a – h) which does not exist because a – h may be rational or may be irrational.
Similarly R.H.L. does not exist.
Thus f(x) is discontinuous at any rational point x – a ≠ 0.
Similarly f(x) is discontinuous at any irrational point.
Hence f(x) is discontinuous everywhere except at x = 0.
(Proved)

Question 9.
Show that f(x) = \(\begin{cases}x \sin \frac{1}{x}, & x \neq 0 \\ 0, & x=0\end{cases}\) is continuous at x = 0.
Solution:
Refer to No. 1(iv) of Exercise – 7(a).

Question 10.
Prove that e^x – 2 = 0 has a solution between 0 and 1. [Hints: Use continuity of e^x– 2 and fact – 2]
Solution:

∴ f(x) is continuous in [0, 1]
f(0). f(1) = (-1) (e – 2) < 0
∴ f(x) has a zero between 0 and 1
i.e. e^x – 2 = 0 has a solution between 0 and 1

Question 11.
So that x⁵ + x +1 = 0 for some value of x between -1 and 0.
Solution:
Let f(x) = x⁵ + x + 1 and any a ∈ (-1, 0)
f(a) = a⁵ + a + 1

= -1 = f(-1)
∴ f is continuous on [-1, 0]
But f(-1) f(0) = 1 × -1 < 0
∴ f has a zero between -1 and 0
⇒ x5 + x + 1 = 0 for some value of x between -1 and 0.