CHSE Odisha Class 12 Math Solutions Chapter 7 Continuity and Differentiability Ex 7(k)

Odisha State Board Elements of Mathematics Class 12 CHSE Odisha Solutions Chapter 7 Continuity and Differentiability Ex 7(k) Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 7 Continuity and Differentiability Exercise 7(k)

Question 1.
State True (T) or False (F).
(i) There is no function whose derivative is log π.
Solution:
False

(ii) There is no function which is its own derivative.
Solution:
False

(iii) A function is not differentiable at x = c ⇒ f is not continuous at x = c.
Solution:
False

(iv) |x²| is differentiable on (- 1, 1).
Solution:
True

(v) |x + 2| is not differentiable at x = 2.
Solution:
False

(vi) Derivative of e^{3 log x} w.r.t. x is 3x².
Solution:
True

(vii) The derivative of a non constant even function is always an odd function.
Solution:
True

(viii) If f and g are not derivable at x₀ then f + g is not derivable at x₀.
Solution:
False

Question 2.
Fill up the gaps by using the correct answer.
(i) If a is a constant and v is a variable then \(\frac{d u^v}{d v}\) = _______. (u^v In v, vu^{v – 1}, u^v In u, uv^{v – 1})
Solution:
u^v In v

(ii) If t = e^a then \(\frac{d}{d x}\)x^t = _______. (tx^{t – 1}, x^t, x^t In a, tx^t)
Solution:
tx^{t – 1}

(iii) If u = t² and v= sin t² then \(\frac{d v}{d u}\) = _______. (cos² t, \(\frac{\sin }{t}\), sec t², cos t²)
Solution:
cos t²

(iv) The tangent to the curve y = (1 + x²)² at x = -1 has slope _______. (4, -4, 8, -8)
Solution:
-8

(v) If v = (gof) (x) then \( \frac{d y}{d x}\) = _______. (\(\frac{d g}{d x} \frac{d x}{d f}\), \(\frac{d g}{d f} \frac{d f}{d x}\), \(\frac{d f}{d x} \frac{d x}{d g}\), \(\frac{d f}{d g} \frac{d g}{d x}\))
Solution:
\(\frac{d g}{d f}\frac{d f}{d x}\)

(vi) If y = sec^-1 \(\frac{\sqrt{x}+1}{\sqrt{x}}\) + \(\frac{\sqrt{x}}{\sqrt{x}+1}\) then \(\frac{d y}{d x}\) = _______. (0, undefined, \(\frac{\pi}{2}\), 1)
Solution:
0

(vii) If (x) = \(\sqrt{x^2-2 x+1}\), x ∈ [0, 2] then at x = 1, f(x) = _______. (1, 0, -1, does not exist)
Solution:
does not exist

(viii) If f(x) = |x²| then f'(\(\frac{3}{2}\)) = _______. (0, 2, 3, does not exist)
Solution:
0

Question 3.
Differentiate from first principles.
(i) e^2x
Solution:
Let y = e^2x

(ii) sin² x
Solution:
Let y = sin² x

(iii) cos x²
Solution:
Let y = cos x²

(iv) \(\boldsymbol{e}^{x^2} \)
Solution:

(v) \(\sqrt{\tan x} \)
Solution:

(vi) x² sin x
Solution:
Let y = x² sin x

(vii) In sin x
Solution:
Let y = In sin x
Then e^y = sin x  … (1)
Let dx be an increment of x and δv be the corresponding increment of y.
Then e^{y + δy} = sin (x + δx)  … (2)
Subtracting (1) from (2) we get,

(viii) sin √x
Solution:
y = sin √x
Put u = √x
Then y = sin u
Let δx be an increment of x and δu, δy be the corresponding increment of u and y respectively.

(ix) cos In x
Solution:
Let y = cos (In x)
Let u = In x
Then y = cos u
Suppose that δx be an increment of x and δu, δy be corresponding increments of u and y respectively.
Then y + δy = cos (u + δu)  ….(3)
and u + δu = In (x + δx)  ….(4)
Subtracting (2) from (3) and (1) from (4) we get
δy = cos (u + δu) – cos u
and δu = In (x + δx) – In x

Question 4.
Test differentiability of the following functions at the indicated points.
(i) f(x) =[x² + 1] at x = –\(\frac{1}{2}\)
Solution:

(ii) f(x) = \(\begin{cases}1-2 x, & x \leq \frac{1}{2} \\ x-\frac{1}{2}, & x>\frac{1}{2}\end{cases}\) at x = \(\frac{1}{2}\)
Solution:

(iii) f(x) = x + |cos x| at x = \(\frac{\pi}{2}\)
Solution:
f(x) = x + |cos x| at c = \(\frac{\pi}{2}\)

Hence onwards domain of a function is to be understood to be its natural domain unless stated otherwise.

Question 5.
Differentiate.
(i) \(\frac{1}{\ln (x \sqrt{x+1})}\)
Solution:

(ii) \(\frac{\ln x}{e^x \sin x}\)
Solution:

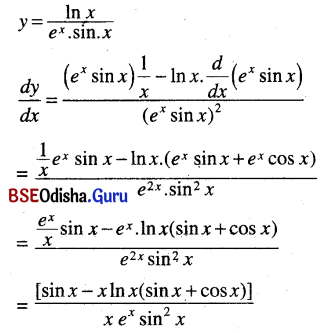
(iii) e^x (tan x – cot x)
Solution:
y = e^x (tan x – cot x)
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\) (e^x) (tan x – cot x) + e^x \(\frac{d}{d x}\) (tan x – cot x)
= e^x (tan x – cot x) + e^x (sec² x + cosec² x)

(iv) \(\left(\sqrt{x}+\frac{1}{\sqrt{x}}\right)\)x tan x
Solution:

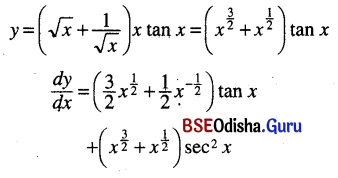
(v) \(\frac{\cos 3 x-\cos x}{\cos 5 x-\cos 3 x}\)
Solution:

(vi) x² e^x cosec x
Solution:
y = x² e^x cosec x
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\) (x²) e^x . cosec x + x² \(\frac{d}{d x}\) (e^x) . cosec x + x² e^x \(\frac{d}{d x}\)
= 2x e^x cosec x + x² e^x cosec x – x² e^x . cosec x . cot x

(vii) \(\frac{(x+1) \ln x}{\sqrt{x+2}}\)
Solution:

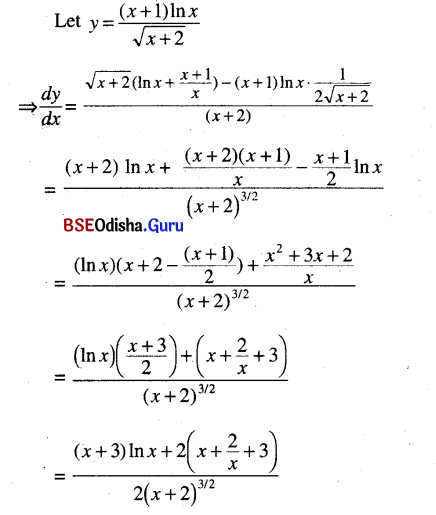
(viii) (x³ – 1)⁹ sec² x
Solution:

(ix) sin² (cos^-1 x)
Solution:

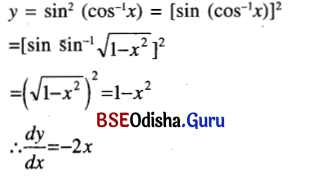
(x) a^x \(\left(x+\frac{1}{x}\right)^{10}\)
Solution:

(xi) In \(\frac{\sqrt{x+4}-2}{\sqrt{x+4}+2}\)
Solution:

(xii) In \(\frac{4 x^2(2 x-7)^3}{\left(3 x^2-7\right)^5}\)
Solution:

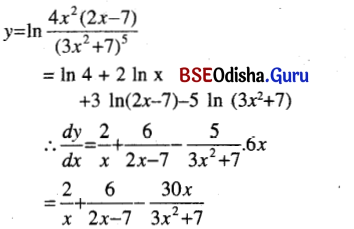
(xiii) 5^{ln sin x}
Solution:

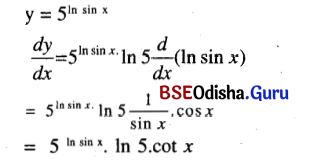
(xiv) \(\sqrt{\sin \sqrt{x}}\)
Solution:

(xv) x^{sin x} + (tan x)^x
Solution:
Let y = x^{sin x} + (tan x)^x
Put u = x^{sin x} , v = (tan x)^x
Then y = u + v

(xvi) \(e^{e^x}\)
Solution:

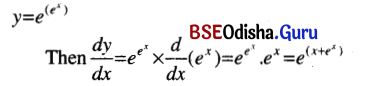
(xvii) \(x^{\sqrt{x}}\)
Solution:

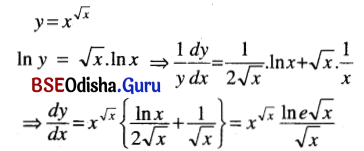
(xviii) sec^-1(e^x + x)
Solution:

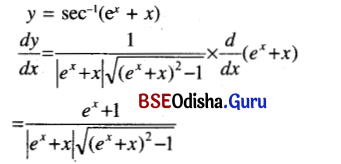
(xix) ln cos e^x
Solution:

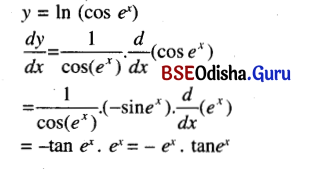
(xx) \(a^{\sin ^{-1} x^2}\)
Solution:

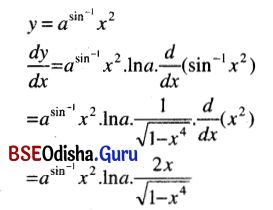
(xxi) cos^-1 \(\left(\frac{x^4-1}{x^4+1}\right)\)
Solution:

(xxii) \(\left(\mathbf{x}^{\mathbf{e}}\right)^{\mathbf{e}^{\mathrm{x}}}\) + \(\left(\mathrm{e}^{\mathrm{x}}\right)^{\mathrm{x}^e}\)
Solution:

(xxiii) \(\boldsymbol{x}^{\left(\boldsymbol{x}^x\right)}\)
Solution:

(xxiv) \(\frac{\left(x+1^2\right) \sqrt{x-1}}{\left(x^2+3\right)^3 3^x}\)
Solution:

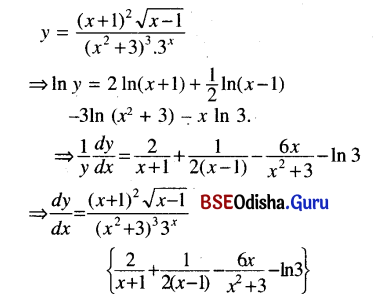
(xxv) [5 In (x³ + 1) – x⁴]^2/3
Solution:

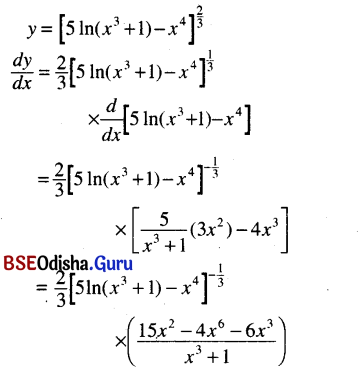
(xxvi) log₁₀ sin x + log_x 10, 0 < x > π.
Solution:

Question 6.
Differentiate
(i) sec^-1 \(\left(\frac{x^2+1}{x^2-1}\right)\)
Solution:

(ii) \(e^{\tan ^{-1} x^2}\)
Solution:

(iii) \(\frac{x \sin ^{-1} x}{\sqrt{1+x^2}}\)
Solution:

(iv) tan^-1 e^2x
Solution:

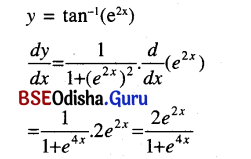
(v) tan^-1 \(\frac{\cos x}{1+\sin x}\)
Solution:

(vi) tan^-1 \(\left(\frac{\cos x-\sin x}{\cos x+\sin x}\right) \)
Solution:

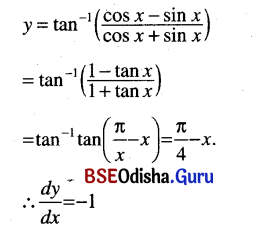
(vii) tan^-1 \(\frac{7 a x}{a^2-12 x^2}\)
Solution:

(viii) tan^-1 \(\frac{\sqrt{1+x^2}+\sqrt{1-x^2}}{\sqrt{1+x^2}-\sqrt{1-x^2}}\) (Put x² = cos θ)
Solution:

(ix) x² cos \(\frac{\sqrt{x}-1}{\sqrt{x}+1}\) = x² cosec^-1 \(\frac{\sqrt{x}+1}{\sqrt{x}-1}\)
Solution:

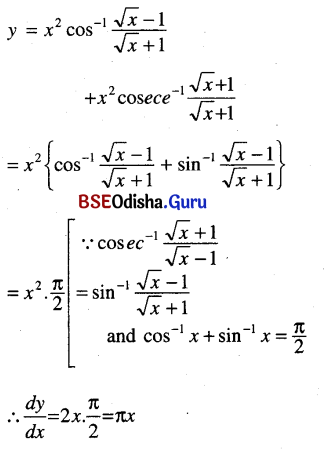
(x) tan^-1 \(\frac{x}{1+\sqrt{1-x^2}}\)
Solution:

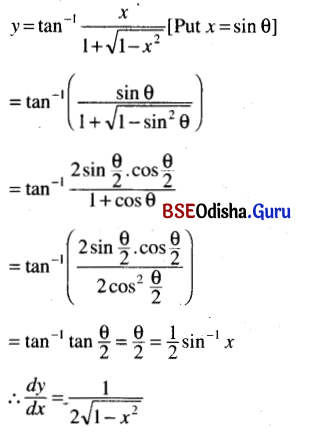
(xi) tan^-1 \(\left(\frac{x \sin \alpha}{1-x \cos \alpha}\right)\)
Solution:

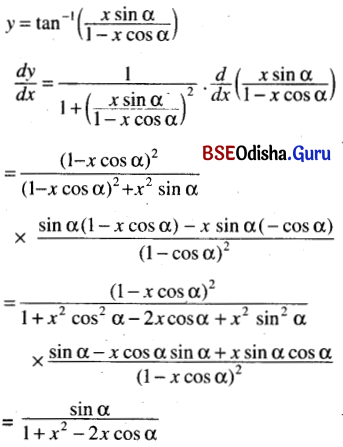
Question 7.
Find \(\frac{d y}{d x}\) if
(i) x³ + y³ = 12xy
Solution:

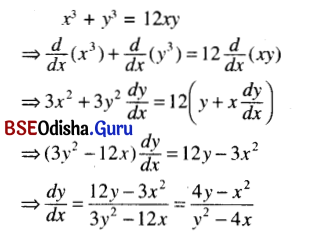
(ii) \(\left(\frac{x}{a}\right)^{2 / 3}\) + \( \left(\frac{y}{b}\right)^{2 / 3}\) = 1
Solution:

(iii) x^y = c
Solution:

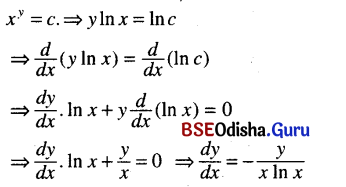
(iv) y^x = c
Solution:
y^x = c ⇒ x In y = In c
⇒ in y + \(\frac{x}{y} \frac{d y}{d x}\) = 0
⇒ \(\frac{d y}{d x}\) = –\(\frac{y \ln y}{x}\)

(v) x cot y + cosec x = 0
Solution:

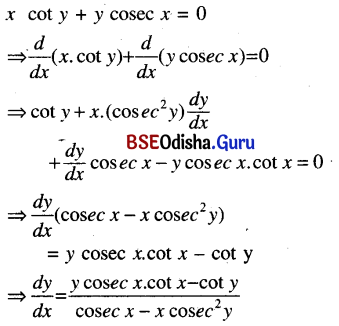
(vi) y² + x² = In (xy) + 1
Solution:

(vii) (cos x)^y = sin y
Solution:

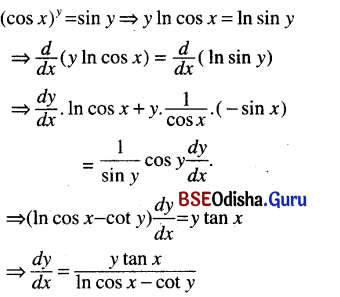
(viii) y² =a^√x
Solution:

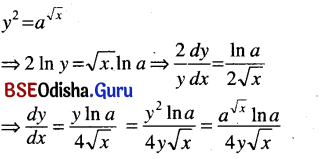
(ix) x^m yⁿ = \(\left(\frac{x}{y}\right)^{m+n}\)
Solution:

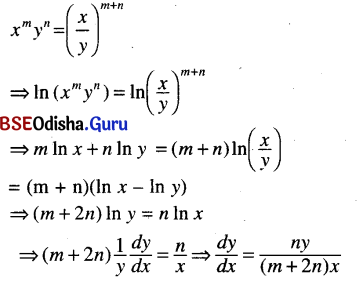
(x) y = x cot ^-1 \(\left(\frac{x}{y}\right)\)
Solution:

(xi) y = (sin y)^{sin 2x}
Solution:

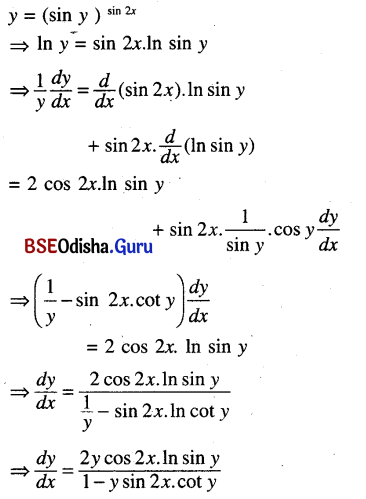
(xii) y² = x^y
Solution:

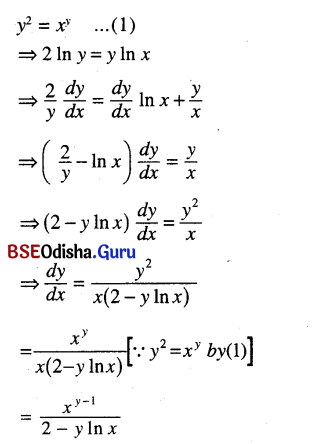
(xiii) (x + y)^{cos x} = e ^{x + y}
Solution:

(xiv) x tan y + y tan x = 0
Solution:

(xv) \(\sqrt{x^2+y^2}\) k tan^-1 \(\left(\frac{y}{x}\right)\)
Solution:

Question 8.
Differentiate
(i) tan^-1 \(\frac{2}{1-x^2}\) w.r.t. sin^-1 \(\frac{2}{1+x^2}\)
Solution:

(ii) sec^-1 \(\left(\frac{1}{2 x^2-1}\right)\) w.r.t. \(\sqrt{1-x^2}\)
Solution:

(iii) tan^-1 \(\left(\frac{1+\sin x}{1-\sin x}\right)\) w.r.t. log \(\left(\frac{1+\cos x}{1-\cos x}\right)\)
Solution:

Question 9.
Find the \(\frac{d y}{d x}\) when
(i) x = a [cos t + log tan ( t/2)], y = a sin t
Solution:

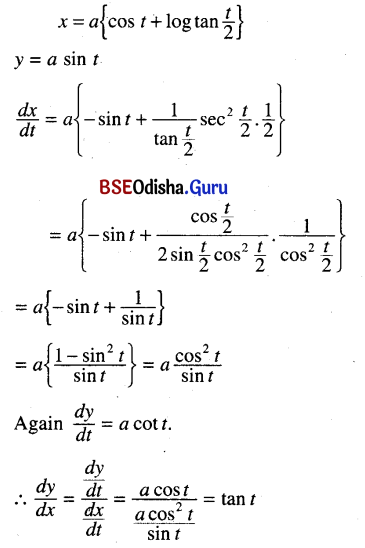
(ii) sin x = \(\frac{2 t}{1+t^2}\), tan y = \(\frac{2 t}{1-t^2}\)
Solution:

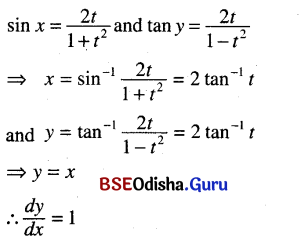
(iii) cos x= \(\sqrt{\frac{1}{1+t^2}}\), siny = \(\frac{2 t}{1+t^2}\)
Solution:

(iv) cos x = \(\sqrt{\sin 2 u}\), y = \(\sqrt{\cos 2 u}\)
Solution:

(v) x = \(\frac{\cos ^3 t}{\sqrt{\cos 2 t}}\), y = \(\frac{\sin ^3 t}{\sqrt{\cos 2 t}}\)
Solution:

Question 10.
Assuming the validity of the operations on the r.h.s. find \(\frac{d y}{d x}\).
(i) y = [ sin x + { sin x + (sin x +….)}]
Solution:

(ii) y = 1 ÷ [ x + 1 ÷ (x + 1 ÷ (x + 1 ÷ …))]
Solution:

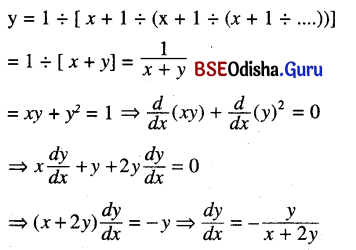
(iii) y = In [x + In (x + In (x + ….))]
Solution:

Question 11.
If cos y = x cos (a + y) then prove that
(i) \(\frac{d y}{d t}\) = \(\frac{\cos ^2(a+y)}{\sin a}\)
Solution:

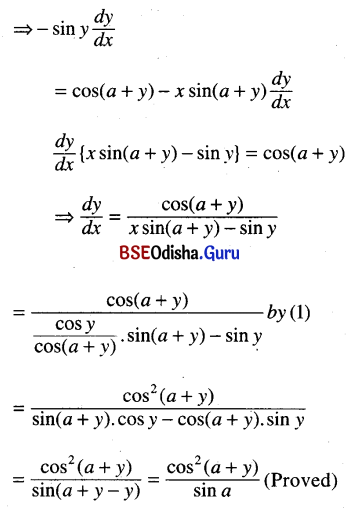
(ii) If e^θΦ = c + 4 θΦ , show that Φ + θ \(\frac{d \phi}{d \theta}\) = 0.
Solution:

Question 12.
Can you differentiate log log |sin x|? Justify your answer.
Solution:
Clearly for all x ∈ R
sin x ∈ [- 1, 1]
⇒ |sin x| ∈ [ 0,1]
⇒ log |sin x| ∈ (-∞ , 0]
⇒ log log |sin x| is not well defined for all x ∈ R
∴ Log log |sin x| is not a differentiable function.

Question 13.

Solution:

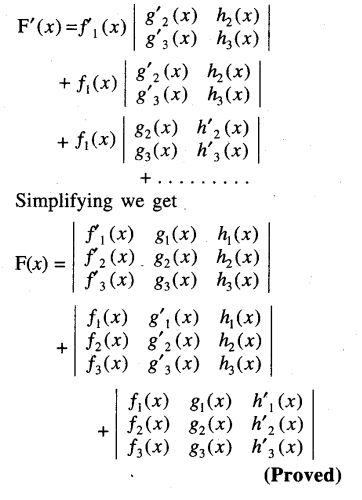
Question 14.
If x = \(\frac{1-\cos ^2 \theta}{\cos \theta}\), y = \(\frac{1-\cos ^{2 n} \theta}{\cos ^n \theta}\) then show that \(\left(\frac{d y}{d x}\right)^2\) = n²\(\left(\frac{y^2+4}{x^2+4}\right)\)
Solution:

Question 15.
Show the \(\frac{d y}{d x}\) is independent of t if.
x = cos^-1\(\frac{1}{\sqrt{t^2+1}}\), y = sin^-1\(\frac{t}{\sqrt{t^2+1}}\)
Solution:

Question 16.
If y \(\sqrt{x^2+1}\) = {\(\sqrt{x^2+1}\) – x} then prove that (x² + 1) \(\frac{d y}{d x}\) + xy + 1 = 0
Solution:

Question 17.
If e^y/x = \(\frac{x}{a+b x}\), then show that x3 \(\frac{d}{d x}\) \(\left(\frac{d y}{d x}\right)\) = \(\left(x \frac{d y}{d x}-y\right)^2\)
Solution:

Question 18.
Find the points where the following functions are not differentiable.
(i) e^|x|
Solution:
e^|x| is not differentiable at x = 0 because |x| is not differentiable at x = 0

(ii) |x² – 4|
Solution:
|x² – 4| is not differentiable at the points where x² – 4 = 0 i.e, x =± 2.

(iii) |x – 1| + |x – 2|
Solution:
|x – 1| + |x – 2| is not differentiable at x = 1 and x = 2.

(iv) sin |x|
Solution:
sin |x| is not differentiable at x = 0.