Odisha State Board Elements of Mathematics Class 11 CHSE Odisha Solutions Chapter 13 Introduction To Three-Dimensional Geometry Ex 13 Textbook Exercise Questions and Answers.
CHSE Odisha Class 11 Math Solutions Chapter 13 Introduction To Three-Dimensional Geometry Exercise 13
Question 1.
Fill in the blanks in each of the following questions by choosing the appropriate answer from the given ones.
(a) The distance of the point P(x0, y0, z0) from z – axis is [\(\sqrt{x_0^2+y_0^2}, \sqrt{y_0^2+z_0^2}, \sqrt{x_0^2+z_0^2},\)\(\sqrt{\left(x-x_0\right)^2+\left(y-y_0\right)^2}\)]
Solution:
\(\sqrt{x^2+y^2}\)
(b) The length of the projection of the line segment joining (1, 3, -1) and (3, 2, 4) on z – axis is ___________. [1, 3, 4, 5]
Solution:
5
(c) the image of the point (6, 3, -4) with respect to yz – plane is _____________. [(6, 0, -4), (6, -3, 4), (-6, -3, -4), (-6, 3, -4)]
Solution:
(-6, 3, -4)
(d) If the distance between the points (-1, -1, z) and (1, -1, 1) is 2 then z = _______________. [1, √2, 2, 0]
Solution:
1
Question 2.
(a) identify the axis on which the given points lie : (1, 0, 0), (0, 1, 0), (0, 0, 1)
Solution:
x-axis, y-axis, z-axis
(b) Identify the planes containing the points! (7, 0, 4), (2, -5, 0), (0, √2, -3)
Solution:
xz-plane, xy-plane, yz-plane.
![]()
Question 3.
(a) Determine, which of the following points have the same projection on x-axis. (2, -5, 7), (2, √2, -3), (-2, 1, 1), (2, -1, 3)
Solution:
(2, -5, 7), (2, √2, -3) and (2, -1, 3) have the same projection on x-axis.
(b) Find the projection of the point (7, -5, 3) on:
(i) xy-plane
Solution:
(7, -5, 0)
(ii) yz-plane,
Solution:
(0, -5, 3)
(iii) zx-plane
Solution:
(7, 0, 3)
(iv) x-axis
Solution:
(7, 0, 0)
(v) y-axis,
Solution:
(0, -5, 0)
(vi) z-axis.
Solution:
(0, 0, 3)
Question 4.
When do you say two lines in space are skewed? Do they intersect?
Solution:
A pair of non-co-planar lines are called skew lines. Skew lines do not intersect.
Question 5.
From the three pairs of lines given below, identify those which uniquely determine a plane:
(i) intersecting pair,
(ii) parallel pair,
(iii) a pair of skew lines.
Solution:
Out of given three pairs
(i) Intersecting pair and
(ii) Parallel pair of lines determine a plane.
Question 6.
Determine the unknown coordinates of the following points if :
(i) P(a, 2, -1)∈ yz – plane
Solution:
a = 0
(ii) Q(-1, y, 3) ∈ zx-plane
Solution:
y = 0
(iii) R(√2, -3, c) ∈ xy-plane
Solution:
c = 0
(iv) S(7, y, z) ∈ x-axis
Solution:
y = 0, z = 0
(v) T(x, 0, z) ∈ y-axis
Solution:
x = 0 , z = 0
(vi) V(a, b, -3) ∈ z-axis
Solution:
a = b = 0
![]()
Question 7.
Which axis is determined by the intersection of:
(i) xy-plane and yz-plane
Solution:
y-axis
(ii) yz-plane and zx-plane
Solution:
z-axis
(iii) zx-plane and xy-plane
Solution:
x-axis
Question 8.
Which axis is represented by a line passing through origin and normal to:
(i) xy-plane
Solution:
z-axis
(ii) yz-plane
Solution:
x-axis
(iii) zx-plane.
Solution:
y-axis
Question 9.
What are the coordinates of a point which is common to all the coordinate planes?
Solution:
Origin 0(0, 0, 0) is common to all coordinate planes.
Question 10.
If A, B, and C are projections of P(3, 4, 5) on the coordinate planes, find PA, PB, and PC.
Solution:
PA = 5, PB = 3, PC = 4.
Question 11.
(a) Find the perimeter of the triangle whose vertices are (0, 1, 2) (2, 0, 4) and (-4, -2, 7).
Solution:

(b) Show that the points (a, b, c), (b, c, a), and (c, a, b) form an equilateral triangle.
Solution:

(c) Show that the points (3, -2, 4) (1, 1, 1) and (-1, 4, -1) are collinear.
Solution:
Let A = (3, -2, 4), B = (1, 1, 1) and C = (-1, 4, -2)
D. rs of AB are < -2, 3, -3 >
D. rs of BC are < -2, 3, -3 >
As D. rs of AB is the same as d.rs of
BC it follows that A, B, and C lie on the same straight line.
So the points are collinear. (Proved)
(d) Show that points (0, 1, 2), (2, 5, 8), (5, 6, 6), and (3, 2, 0) form a parallelogram.
Solution:

(e) Show that the line segment joining (7, -6, 1) (17, -18, -3) intersect the line segment joining (1, 4, -5), (3, -4, 11) at (2, 0, 3).
Solution:

D.rs of AP are < -5, 6, 2 >
D.rs of PB are < -15, 18, 6>
i.e., < -5, 6, 2 >
Thus d.r.s. of AP are the same as the d.r.s. of PB.
So A.P.B. are collinear.
Again d.rs. of CP are < 1, -4, 8 >
D. rs. of PD are < 1, -4, 8 >
Thus d.rs. of CP and d.rs. of PD are equal.
So the points C.P.D. are collinear.
Hence line AB intersects the line CD at P. (Proved)
(f) Find the locus of points that are equidistant from points (1, 2, 3) and (3, 2, -1).
Solution:
Let A = (1, 2, 3), B = (3, 2, -1)
Let P (x, y, z) be equidistant from A and B.
Then PA = DB
(x – 1 )2 + (y – 2)2 + (z – 3)2
= (x – 3)2 + (y – 2)2 + (z + 1)2
⇒ (x – 1)2 – (x – 3)2 + (y – 2)2 – (y – 2)2 + (z – 3)2 – (z + 1)2 = 0
⇒ (x – 1 + x – 3) (x – 1 – x + 3) + (z – 3 + z + 1)(z – 3 – z – 1) = 0
⇒ (2x – 4) . 2 + (2z – 2) . (- 4) = 0
⇒ x – 2 – 2z + 2 = 0
⇒ x – 2z = 0 This is the required locus.
Question 12.
(a) Find the ratio in which the line segment through (1, 3, -1) and (2, 6, -2) is divided by zx-plane.
Solution:

(b) Find the ratio in which the lines segment through (2, 4, 5), (3, 5, -4) is divided by xy-plane.
Solution:

(c) Find the coordinates of the centroid of the triangle with its vertices at (a1, b1, c1), (a2, b2, c2), and (a3, b3, c3)
Solution:
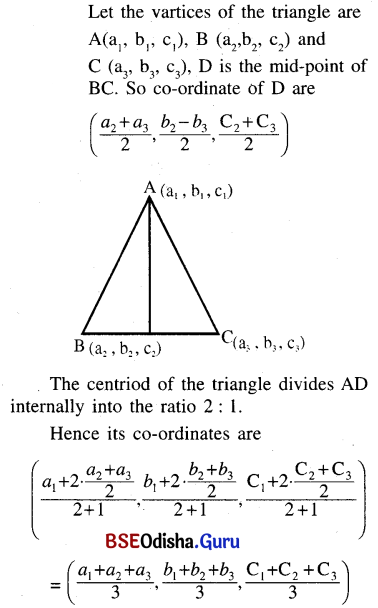
(d) If A (1, 0, -1), B (-2, 4, -2), and C (1, 5, 10) be the vertices of a triangle and the bisector of the angle BAC, meets BC at D, then find the coordinates of the point D.
Solution:
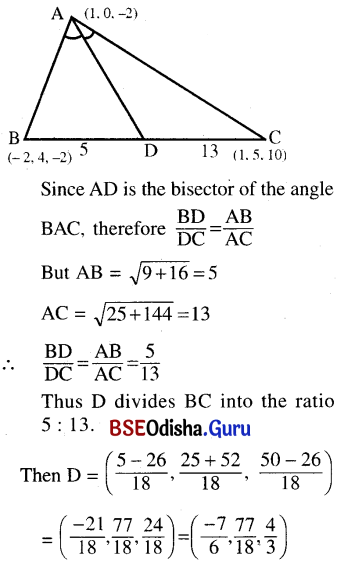
(e) Prove that the points P(3, 2, -4), Q(5, 4, -6) and R(9, 8, -10) are collinear. Find the ratio in which point Q divides the line segment PR.
Solution:
Given that P = (3, 2, -4)
Q = (5, 4, -6), R = (9, 8, -10)
D. rs. of PQ are < 2, 2, -2 >
D. rs. of QR are < 4, 4, -4 >
i.e., < 2, 2, -2 >
Thus D.rs. of PQ and QR are the same.
So P, Q, R lie on the same straight line.
Hence P, Q, and R are collinear. (Proved)
Let Q divides the join of PR in ratio k: 1
∴ \(\frac{9 k+3}{k+1}\) = 5, \(\frac{8 k+2}{k+1}\) = 4, \(\frac{-10 k-4}{k+1}\) = -6
⇒ k = \(\frac{1}{2}\)
Thus the ratio is 1: 2
