Odisha State Board Elements of Mathematics Class 12 CHSE Odisha Solutions Chapter 7 Continuity and Differentiability Ex 7(l) Textbook Exercise Questions and Answers.
CHSE Odisha Class 12 Math Solutions Chapter 7 Continuity and Differentiability Exercise 7(l)
Question 1.
If y = tan-1 x Prove that (1 + x2) y2 + 2xy1 = 0
Solution:
y = tan-1 x ⇒ y1 = \(\frac{1}{1+x^2}\)
⇒ (1 + x2) y1 = 1
⇒ (1 + x2) y2 + 2xy1 = 0
Question 2.
If 2y = x (1 + \(\frac{d y}{d x}\)) show that y2 is a constant.
Solution:

![]()
Question 3.
If y = ax sin x show that x2y2 – 2xy1 + (x2 + 2) y = 0
Solution:
y = ax sin x
⇒ y1 = a sin x + ax cos x
⇒ y2 = a cos x + a cos x – ax sin x
= 2a cos x – ax sin x
Now x2y2 – 2xy1 + (x2 + 2)y
= 2ax2 cos x – ax3 sin x – 2ax sin x – 2ax2 cos x + ax3 sin x + 2ax sin x = 0
Question 4.
If y = \(e^{m \cos ^{-1} x}\) (1 – x2) y2 – xy1= m2y
Solution:
y = \(e^{m \cos ^{-1} x}\)
⇒ In y1 = m cos-1 x
⇒ \(\frac{1}{y}\) . y = \(\frac{-m}{\sqrt{1-x^2}}\)
(\(\sqrt{1-x^2}\)) . y1 = -my
⇒ (1 – x2) (y1)2 = m2y2
⇒ (1 – x2) 2y1y2 – 2x (y1)2 = 2m2yy1
⇒ (1 – x2) y2 – xy1 = m2y
Question 5.
If x = sin t, y = sin 2t then prove that, (1 – x2)\(\frac{d^2 y}{d x^2}\) – x\(\frac{d y}{d x}\) + 4y = 0
Solution:
x= sin t, y= sin 2t

![]()
Question 6.
If y = \(\left(\sin ^{-1} x\right)^2\) , prove that (1 – x2) y2 – xy1 – 2 = 0
Solution:
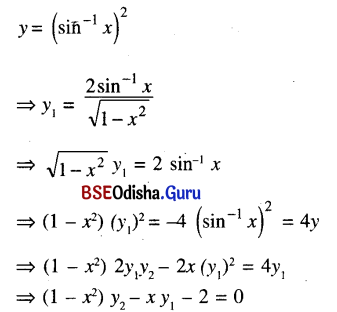
Question 7.
If y = tan-1 x, Prove that (1 + x2) y2 + 2xy1 = 0
Solution:
Same as No. 1
