Odisha State Board CHSE Odisha Class 12 Math Solutions Chapter 8 Application of Derivatives Ex 8(b) Textbook Exercise Questions and Answers.
CHSE Odisha Class 12 Math Solutions Chapter 8 Application of Derivatives Exercise 8(b)
Question 1.
Find the equations to the tangents and normals to the following curves at the indicated points.
(i) y = 2x2 + 3 at x = -1
Solution:
y = 2x2 + 3 at x = -1
⇒ \(\frac{d y}{d x}\) = 4 ∴\(\left.\frac{d y}{d x}\right]_{-1}\) = -4
Thus slope of the tangent at x = -1 is -4.
Angin for x = -1 , y = 2 + 3 = 5
The point of contact is (-1, 5).
Equation of the tangent is y – 5 = -4 (x + 1)
⇒ 4x + y – 1 = 0
Slope of the normal = \(\frac{1}{4}\)
Eqn. of the normal is y – 5 = \(\frac{1}{4}\) (x + 1)
⇒ 4y – 20 = x + 1
⇒ x – 4y + 21 = 0
(ii) y = x3 – x at x = 2
Solution:
y = x3 – x at x = 2
When x = 2, y = 23 – 2 = 6
The point is (2, 6).
Again \(\frac{d y}{d x}\) = 3x2 – 1
\(\left.\frac{d y}{d x}\right]_{x=2}\) = 12 – 1 = 11
Slope of the tangent = 11.
Slope of the normal = –\(\frac{1}{11}\)
Equation of the tangent is
y – 6 = 11 (x – 2)
⇒ 11x – y – 16 = 0
Equation of the normal is
y – 6 = –\(\frac{1}{11}\)
⇒ 11y – 66 = – x + 2
⇒ x + 11y – 68 = 0
![]()
(iii) y = √x + 2x + 6 at x = 4
Solution:
y = √x + 2x + 6 at x = 4
For x = 4, y = 2 + 8 + 6 = 16
The point is (4, 16)
Again \(\frac{d y}{d x}\) = \(\frac{1}{2 \sqrt{x}}\) + 2
\(\left.\frac{d y}{d x}\right]_{x=4}\) = \(\frac{1}{4}\) + 2 = \(\frac{9}{4}\)
Slope of the tangent = \(\frac{9}{4}\)
Slope of the normal = –\(\frac{4}{9}\)
Equation of the tangent is
y – 16 = \(\frac{9}{4}\)(x – 4)
⇒ 9x – 4y + 28 = 0
Equation of the normal is
y – 16 = – \(\frac{4}{9}\)(x – 4)
⇒ 9y – 144 = -4x + 16
⇒ 4x + 9y – 160 = 0
(iv) y = √3 sin x + cos x at x = \(\frac{\pi}{3}\)
Solution:

(v) y = (log x)2 at x = \(\frac{1}{e}\)
Solution:

(vi) y = \(\frac{1}{\log x}\) at x = 2
Solution:

(vii) y = xe-x at x = 0
Solution:
y = xe-x at x = 0
For x = 0, y = 0
The point is (0, 0).
\(\frac{d y}{d x}\) = e-x + x . (-e-x)
\(\left.\frac{d y}{d x}\right]_{x=0}\) = 1
Slope of the tangent = 1
Slope of the normal = -1
Equation of the tangent is y = x and equation of the normal is y = -x
(viii) y = a (θ – sin θ), y = a (1 – cos θ) at θ = \(\frac{\pi}{2}\)
Solution:
y = a (θ – sin θ), y = a (1 – cos θ) at θ = \(\frac{\pi}{2}\)

![]()
(ix) \(\left(\frac{x}{a}\right)^{2 / 3}\) + \(\left(\frac{y}{b}\right)^{2 / 3}\) = 1 at (a cos3 θ, b sin3 θ)
Solution:
\(\left(\frac{x}{a}\right)^{2 / 3}\) + \(\left(\frac{y}{b}\right)^{2 / 3}\) = 1 at (a cos3 θ, b sin3 θ)

Question 2.
Find the point on the curve y2 – x2 + 2x – 1 = 0 where the tangent is parallel to the x – axis.
Solution:
Given curve is y2 – x2 + 2x – 1 = 0 … (1)
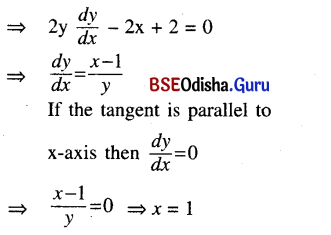
Putting x = 1 in (1) we get
y2 – 1 + 2 – 1 = 0 ⇒ y = 0
∴ The point is (1, 0).
Question 3.
Find the point (s) on the curve x = \(\frac{3 a t}{1+t^2}\), y = \(\frac{3 a t^2}{1+t^2}\) where the tangent is perpendicular to the line 4x + 3y + 5 = 0.
Solution:

Question 4.
Find the point on the curve x2 + y2 – 4xy + 2 = 0 where the normal is parallel to the x axis.
Solution:
x2 + y2 – 4xy + 2 = 0

Question 5.
Show that the line y = mx + c touches the parabola y2 = 4ax if c = \(\frac{a}{m}\).
Solution:
Given line is y = mx + c … (1)
Given parabola is y2 = 4ax

![]()
Question 6.
Show that the line y = mx + c touches the ellipse
\(\frac{x^2}{a^2}\) + \(\frac{y^2}{b^2}\) = 1 if c2 = a2m2 + b2
[Hints: Find equation to tangent at a point (x’, y’) of the curve and compare it with
y = mx + c].
Solution:

Question 7.
Show that the sum of the intercepts on the coordinate axes of any tangent to the curve
√x + √y = √a is constant.
Solution:

Question 8.
Show that the curves y = 2x and y = 5x intersect at an angle
tan-1 \(\left|\frac{\ln \left(\frac{5}{2}\right)}{1+\ln 2 \ln 5}\right|\)
(Note: Angle between two curves is the angle between their tangents at the point of intersection)
Solution:
Given curves are
y = 2x … (1)
and y = 5x … (2)
Differentiating (1) we get \(\frac{d y}{d x}\) = 2x . In 2
Differentiating (2) we get \(\frac{d y}{d x}\) = 5x . In 2
Slope of the tangent to the first curve at (x, y) = 2x . In 2
Slope of the tangent to the second curve at (x, y) = 5x . In 2
Solving (1) and (2) we get 2x = 5x ⇒ x = 0
For x = 0, y = 1
∴ The point of intersection is (0, 1).
At (0, 1) slope of the 1st tangent = In 2
Slope of the second tangent = In 5
If θ is the angle between two tangents
then \(\frac{\ln 5-\ln 2}{1+\ln 5 \cdot \ln 2}\) = \(\frac{\ln \frac{5}{2}}{1+\ln 5 \cdot \ln 2}\)
= tan-1 \(\left(\frac{\ln \frac{5}{2}}{1+\ln 5 \cdot \ln 2}\right)\)
We know that angle between two curves is the angle between their tangents at the point of intersection.
Hence the two curves intersect at an angle.
\(\left(\tan ^{-1} \cdot \frac{\ln \frac{5}{2}}{1+\ln 5 \cdot \ln 2}\right)\)
Question 9.
Show that the curves ax2 + by2 =1 and a’x2 + b’y2 = 1. Intersect at right angles if
\(\frac{1}{a}\) – \(\frac{1}{a}\) = \(\frac{1}{a^{\prime}}\) – \(\frac{1}{b^{\prime}}\).
Solution:
Given curves are
ax2+ by2= 1 … (1)
and a’x2 + b’y2 = 1 … (2)
Differentiating (1) we get


![]()
Question 10.
Find the equation of the tangents drawn from the point (1, 2) to the curve.
y2 – 2x3 – 4y + 8 = 0
Solution:
Given curve is
y2 – 2x3 – 4y + 8 = 0 … (1)

⇒ -(k – 2)2 = 3h2 – 3h3
⇒ (k – 2)2 = 3h3 – 3h2
Putting it in (2) we get
k2 – 2h3 – 4k + 8 = 0
⇒ k2 – 4k + 4 – 2h3 + 4 = 0
⇒ (k – 2)2 – 2h3 + 4 = 0
⇒ 3h3 – 3h2 – 2h3 + 4 = 0
⇒ h3 – 3h2 + 4 = 0
⇒ h3 + h2 – 4h2 + 4 = 0
⇒ h2 (h + 1) – 4 (h2 – 1) = 0
⇒ h2 (h + 1) – 4 (h + 1) (h – 1) = 0
⇒ (h + 1) (h2 – 4h + 4) = 0
⇒ (h + 1) (h – 2)2 = 0
⇒ h = -1, 2.
For h = -1, k is imaginary.
For h = 2, k = 2 + 2√3
The point at which the tangent is drawn is (2, 2 + 2√3).
Slope of the tangents
= \(\frac{3 h^2}{k-2}\) = \(\frac{12}{\pm 2 \sqrt{3}}\) = ± 2√3
Equations of the tangental
y – (2 ± 2√3) = ± 2√3(x – 2)
Question 11.
Show that the equation to the normal to x2/3 + y2/3 = a2/3 is y cos θ – x sin θ = a cos 2θ where θ is the inclination of the normal to x – axis.
Solution:

The point is (a2 sin3 θ, a2 cos3 θ).
Equation of the normal is
y – a2 cos3 θ = tan θ (x – a2 sin3 θ)
⇒ y cos θ – a2 cos4 θ = x sin θ – a2 sin4 θ
⇒ y cos θ – x sin θ = a2 (cos4 θ – sin4 θ)
= a2 (cos2 θ + sin2 θ) (cos2 θ – sin2 θ)
= a2 cos 2θ.
∴ Equation of the normal is
y cos θ – x sin θ = a2 cos 2θ.(Proved)
Question 12.
Show that the length of the portion of the tangent to x2/3 + y2/3 = a2/3 intercepted between the axes is constant.
Solution:


![]()
Question 13.
Find the tangent to the curve y = cos (x + y), 0 < x ≤ 2π which is parallel to the line
x + 2y = 0.
Solution:
y = cos (x + y) … (1)

Question 14.
If tangents are drawn from the origin to the curve y = sin x then show that the locus of the points of contact is x2y2 = x2 – y2
Solution:
Given curve is
y = sin x … (1)
\(\frac{d y}{d x}\) = cos x
Slope of the tangent to the cure (1) at any point (x, y) is cos x.
Let (h, k) be the point of contact.
Then slope of the tangent at (h, k) = cos h.
Equation of the tangent to the curve (1) at (h, k) is
y – k = cos h (x – h) … (2)
If the tangent is drawn from the origin then -k = -h cos h
⇒ k = h cos h … (3)
As (h, k) is the poitn of contact then we have
k = sin h … (4)
From (3) we get,
k = h\(\sqrt{1-\sin ^2 h}\) = h\(\sqrt{1-k^2}\) by (4).
Squaring both sides we get
k2 = h2 (1 – k2)
⇒ k2 = h2 – h2k2
⇒ h2k2 = h2 – k2
The locus of (h, k) is x2.y2 = x2 – y2 (Proved)
Question 15.
Find the equation of the normal to the curve given by
x = 3 cos θ – cos3 θ
y = 3 sin θ – sin3 θ at θ = \(\frac{\pi}{4}\)
Solution:
x = 3 cos θ – cos3 θ
y = 3 sin θ – sin3 θ
Differentiating we get
\(\frac{d x}{d \theta}\) = -3 sin θ + 3 cos2 θ . sin θ
\(\frac{d x}{d \theta}\) = 3 cos θ – 3 sin2 θ . cos θ

Question 16.
If x cos α + y sin α = p is a tangent to the curve \(\left(\frac{x}{a}\right)^{\frac{n}{n-1}}\) + \(\left(\frac{y}{b}\right)^{\frac{n}{n-1}}\) = 1
then show that (a cos α)n + (b sin α)n = pn
Solution:
Given straight line is x cos α + y sin α = p … (1)
Given curve is


![]()
Question 17.
Show that the tangent to the curve
x = a (t – sin t), y = at (1 + cos t) at t = \(\frac{\pi}{2}\) has slope. (1 – \(\frac{\pi}{2}\))
Solution:
Given curve is x = a (t – sin t)
y = at (1 + cos t)

