CHSE Odisha Class 12 Math Solutions Chapter 8 Application of Derivatives Ex 8(d)

Odisha State Board CHSE Odisha Class 12 Math Solutions Chapter 8 Application of Derivatives Ex 8(d) Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 8 Application of Derivatives Exercise 8(d)

Question 1.
Find the extreme points of the following functions. Specify if the extremum is a maximum or minimum.
Find the extreme values.
(i) y = x² + 2x + 3
Solution:

(ii) y = 5x² – 2x⁵
Solution:

∴ The function attains minimum at x = 0.
and maximum at x = 1 .
The minimum value = 0
The maximum value = 5 – 2 = 3

(iii) y = \(\frac{3 x}{x^2+1}\)
Solution:

(iv) y = x²\(\sqrt{1-x^2}\)
Solution:

(v) y = 2x³ – 15x² – 36x + 18
Solution:

The function attains maximum at x = -1 and minimum at x = 6.
Maximum value
= -2 – 15 + 36 + 18 = 37
Minimum value
= 2 × 216 – 15 × 36 – 36 × 6 + 13
= 432 – 540 – 216 + 18
= 450 – 756
= -306

(vi) y = 60/(x⁴ – x² + 25)
Solution:

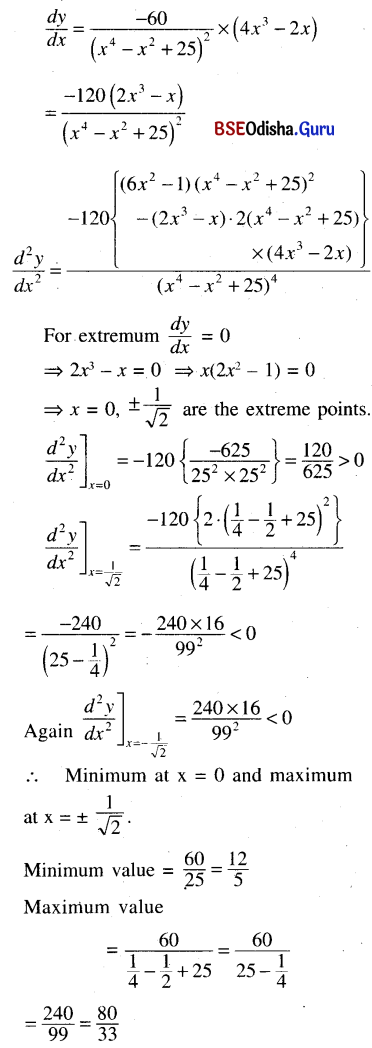
(vii) y = (x – 1)³
Solution:

So the point x = 1 is neither a point of maximum nor a point of minimum. It is an inflexion point.

(viii) y = (x – 2)³ (x + 3)⁴
Solution:

(ix) y = x + \(\frac{1}{x}\)
Solution:

∴ Maximum at x = -1
and minimum at x = 1
Maximum value = -1 – 1 = -2
Minimum value = 2.

(x) y = 4 cos 2x – 3 sin 2x, x ∈ (-\(\frac{\pi}{2}\), \(\frac{\pi}{2}\))
Solution:

(xi) y = sin x cos x, x ∈ (\(\frac{\pi}{8}\), \(\frac{\pi}{2}\))
Solution:

But there is no minimum in the domain.

(xii) y = cos x (1 + sin x), x ∈ [0, 2π]
Solution:

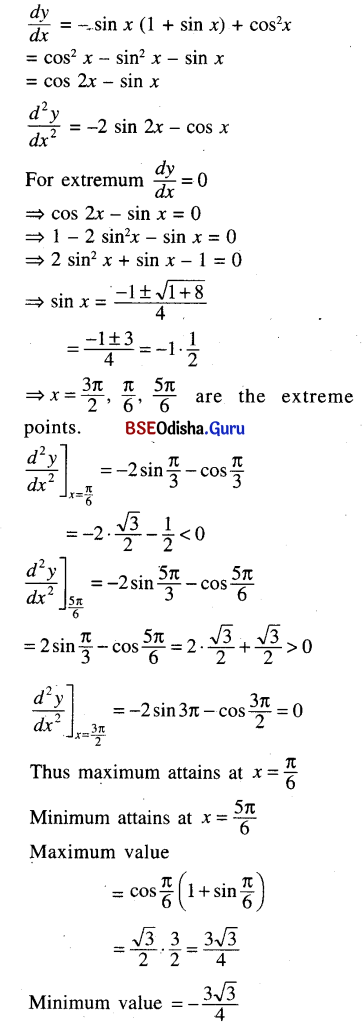
(xiii) y = sin^p x cos^q x; p, q > 0, x ∈ [0, \(\frac{\pi}{2}\))
Solution:

(xiv) y = x e^-x ; x ∈ (-2, 2)
Solution:

Question 2.
Show that the following functions do not possess maximum or minimum.
(i) x³
Solution:
y = x³

Thus the function does not possess a maximum or a minimum. (Proved)

(ii) x⁵
Solution:
Processed as in (i)

(iii) 3x³ – 12x² + 16x – 15
Solution:
Let y = 3x³ – 12x2 + 16x – 5

So the function does not possess a maximum or a minimum. (Proved)

(iv) 4 – 3x + 3x² – x³
Solution:
Processed as in (iii).

(v) ln |x|, x ≠ 0
Solution:
y = ln |x|, x ≠ 0

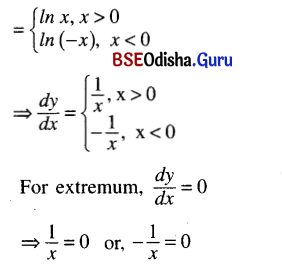
Which have no solution. Hence the function has neither a maximum nor a minimum.
(Proved)

Question 3.
Use the function f(x) = \(x^{\frac{1}{x}}\), x > 0 to show that e^x > π^c.
Solution:
f(x) = \(x^{\frac{1}{x}}\), x > 0

Question 4.
Prove the inequality x² \(e^{-x^2}\) ≤ e^-1, x ∈ R.
Solution:

Question 5.
If f(x) = a ln x + bx² + x has extreme values at x = -1 and x = 2 then find a and b.
Solution:
f(x) = a ln x + bx² + x
f'(x) = \(\frac{a}{x}\) + 2b x + 1
Given that f(x) attains extreme values at x = -1 and x = 2
Then f(-1) = 0 and f(2) = 0
⇒ -a – 2b + 1 = 0 … (1)
\(\frac{a}{2}\) + 4b + 1 = 0 … (2)
From (1) we get a = -2b + 1
Putting it in (2)
we get \(\frac{1-2 b}{2}\) + 4b + 1 = 0
⇒ 1 – 2b + 8b + 2 = 0
⇒ 3 + 6b = 0
⇒ b = \(-\frac{3}{6}\) = \(-\frac{1}{2}\)
Again a = 1 – 2b = 1 + 1 = 2
∴ a = 2, b = \(-\frac{1}{2}\)

Question 6.
Show that \(\frac{x}{1+x \tan x}\), x ∈ (0, \(\frac{\pi}{2}\)) is maximum when x = cos x.
Solution:

Thus the function attains maximum when x = cos x. (Proved)

Question 7.
Determine the absolute maximum and absolute minimum of the following function on [-1, 1]
f(x) = \(\left\{\begin{array}{l}
(x+1)^2, x \leq 0 \\
(x-1)^2, x>0
\end{array}\right.\)
Solution:
f(x) = \(\left\{\begin{array}{l}
(x+1)^2, x \leq 0 \\
(x-1)^2, x>0
\end{array}\right.\)
f(x) = \(\left\{\begin{array}{l}
2(x+1), x \leq 0 \\
2(x-1), x>0
\end{array}\right.\)
For extremum f'(x) = 0
⇒ x + 1 = 0 if x < 0
or, x – 1 = 0 if x > 0
⇒ x = -1 or x = 1
Now f(-1) = 0, f(1) = 0
Again f is not differentiable at x = 0 and f(0) = 1
The function attains absolute minimum at x = ±1. Absolute minimum value = 0.
The function attains absolute maximum at x = 0. Absolute Maximum value = 1.

Question 8.
Find extreme values of
f(x) = \(\left\{\begin{array}{l}
\frac{x}{1-x^2},-1<x<0 \\
x^3-x, 0 \leq x<2
\end{array}\right.\) on (-1, 2)
Solution:
Given that

Question 9.
Find two numbers x and y whose sum is 15 such that xy² is maximum.
Solution:
Let z = xy²
Given that x + y = 15
Then y = 15 – x
Thus z = x (15 – x)²
\(\frac{d z}{d x}\) = (15 – x)² + x² (15 – x) . (-1)
= (15 – x) (15 – x – 2x)
= (15 – x) (15 – 3x)
= 3(15 – x) (5 – x)
\(\frac{d^2 z}{d x^2}\) = -3(5 – x) – 3(15 – x)
= -3 (20 – 2x)
= -6 (10 – x)
For extreme points
\(\frac{d z}{d x}\) = 0
⇒ 3(15 – x) (5 – x) = 0
⇒ x = 15 or 5.
\(\left.\frac{d^2 z}{d x^2}\right]_{x=15}\) = 30 > 0
\(\left.\frac{d^2 z}{d x^2}\right]_{x=5}\) = 30 < 0
∴ z = xy² is maximum when x = 5.
In this case y = 10
∴The two numbers are 5, 10.

Question 10.
If the sum of two positive numbers in constant then show that their product is maximum when they are equal.
Solution:
Let x and y be two positive numbers such that x + y = c (constant)
Then y = c – x
Let p = xy = x(c – x) = cx – x²

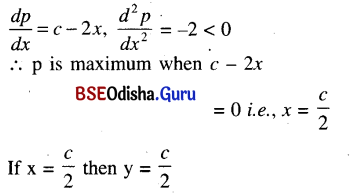
∴ The two numbers are equal. (Proved)

Question 11.
Determine a rectangle of area 25 sq. units which has minimum perimeter.
Solution:
Let x and y be the length and breadth of a rectangle of area 25 sq. units.

∴ The perimeter is minimum when the rectangle is a square of side 5 units.

Question 12.
Find the altitude of a right circular cylinder of maximum volume inscribed in a sphere of radius r.
Solution:
Let ABCD be a right circular cylinder inscribed in a sphere with centre at O and radius ‘r’. Let x be the altitude of the cylinder.

Question 13.
Show that the radius of the right circular cylinder of greatest curved surface that can be inscribed in a given cone is half the radius of the base of the cone.

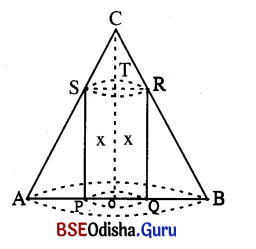
Solution:
Let ABC be a cone, Let r be the radius of the base and h be the height of the cone. Let PQRS be a cylinder inscribed in the cone whose height is x.
In the diagram OT = x.
Then CT = h – x
Now Δ CTR and Δ RQB are similar.

∴ Radius of the right circular cylinder of greatest curved surface is half the base of the cone. (Proved)

Question 14.
Show that the semi vertical angle of a cone of given slant height is tan^-1√2 when its volume is maximum.
Solution:

Question 15.
A cylindrical open water tank with a circular base is to be made out of 30 sq. metres of metal sheet. Find the dimensions so that it can hold maximum water. (Neglect thickness of sheet)
Solution:

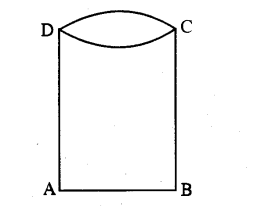
Let ABCD be an open cylindrical tank with circular base.
Let r be the radius of the base and x be the height of the tank.
Given that the tank is made out of 30 square metres of metal sheet.
The surface area of the tank
= 27πrx + πr² [∵ The tank is open.
So 2πrx + πr² = 30
⇒ 2πrx = 30 – πr²

Question 16.
A cylindrical vessel of capacity 500 cubic metres open at the top is to be constructed. Find the dimensions of the vessel if the material used is minimum given that the thickness of the material used is 2 cm.
Solution:

Question 17.
Find the coordinates of the point on the curve x²y – x + y = 0 where the slope of the tangent is maximum.
Solution:
Let (x, y) be the point on the curve
x²y – x + y = 0.

The slope is maximum when x = 0. when x = 0, y = 0
The point is (0, 0) at which the slope of the tangent is maximum.

Question 18.
Find the points on the curve y = x² + 1 which are nearest to the point (0, 2).
Solution:
Let A = (0, 2)
Let P (x, y) be any point on the curve
y = x² + 1. …(1)

Question 19.
Show that the minimum distance of a point on the curve \(\frac{a^2}{x^2}\) + \(\frac{b^2}{y^2}\) = 1
from the origin is a + b.
Solution:
Let P(x, y) be any point on the curve

Question 20.
Show that the vertical angle of a right circular cone of minimum curved surface that circumscribes a given sphere is 2 sin^-1(√2 – 1).
Solution:

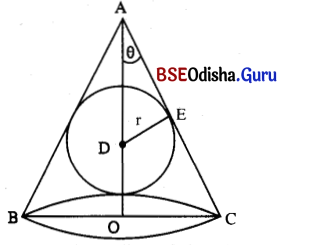
Let r is the radius of the given sphere, R is the radius of the base, H is the height and l is the C lant height of the cone ABC. Let θ is the semi vertical angle.

Question 21.
Show that the semi-vertical angle of a right circular cone of minimum volume that circumscribes a given sphere is sin^-1(\(\frac{1}{3}\)).
Solution:

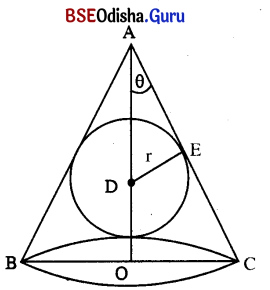
Let ABC be a right circular cone which circumscribes a sphere of radius ‘r’.
Let θ be the semi-vertical angle of the cone.
Let D be the centre of the sphere. By symmetry D must lie on AO, where O is the centre of the base.
In the diagram DO = r.
Again in the Δ ADE

Question 22.
Show that the shortest distance of the point (0, 8a) from the curve ax² = y³ is 2a√11.
Solution:
Given curve is 2x² = y³ … (1)
Let any point on it is P(x, y)
Distance of P from A (0, 8a)

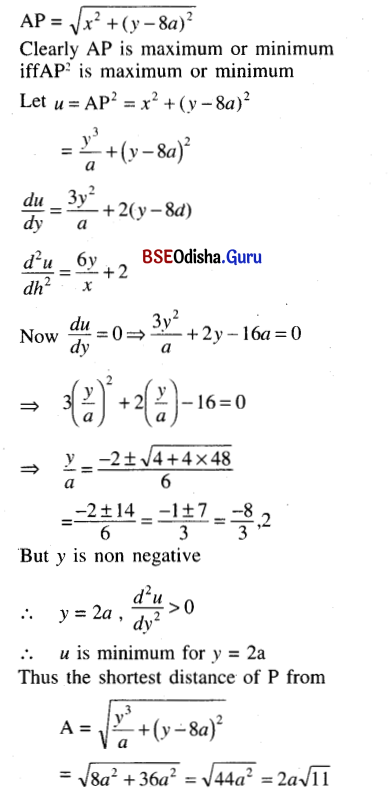
Question 23.
Show that the triangle of greatest area that can be inscribed in a circle is equilateral.
Hints: It BC is any chord then for the Δ ABC to have maximum area, the point A must be on the perpendicular bisector of BC so as to have the largest height AD. Let mDBAD = a. Let BO = OA = r. Then area of Δ ABC = \(\frac{1}{2}\)|BC| |AD| = \(\frac{1}{2}\) . 2r sin 2α (r + r + cos 2α) = r² sin 2a . (1 + cos 2a). Then maximise Δ to obtain 2a = \(\frac{\pi}{3}\)
Solution:

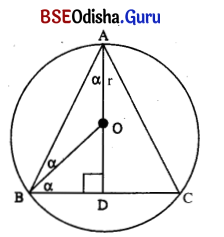
Let ABC be a triangle inscribed in a circle with centre at O and radius ‘r’.
The triangle ABC has maximum area if the point A is on the perpendicular bisector of BC.
Let ∠BAD = α, Let BO = AO = r,
Then ∠BOD = 2α.
In Δ OBD, sin 2α = \(\frac{\mathrm{BD}}{\mathrm{OB}}\)
⇒ BD = OB sin 2α = r sin 2α
Again OD = r cos 2α.
Thus AD = r + r cos 2α
Let Z be the area of the triangle ABC.