Odisha State Board Elements of Mathematics Class 12 Solutions CHSE Odisha Chapter 9 Integration Ex 9(k) Textbook Exercise questions and Answers.
CHSE Odisha Class 12 Math Solutions Chapter 9 Integration Exercise 9(k)
Evaluate the following Integrals:
Question 1.
(i) \(\int_0^{\frac{\pi}{2}} \frac{d x}{1+\tan x}\)dx
Solution:

(ii) \(\int_0^{\frac{\pi}{2}} \frac{\sqrt{\sin x}}{\sqrt{\sin x}+\sqrt{\cos x}}\)dx
Solution:

![]()
(iii) \(\int_0^1 \frac{\ln (1+x)}{2+x^2}\)dx (x = tan θ)
Solution:

(iv) \(\int_0^\pi \frac{x d x}{1+\sin x}\)
Solution:

Question 2.
(i) \(\int_{-a}^a\)x4 dx
Solution:

(ii) \(\int_{-a}^a\)(x5 + 2x2 + x) dx
Solution:
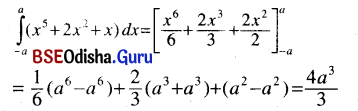
![]()
(iii) \(\int_{-\frac{\pi}{4}}^{\frac{\pi}{4}}\)cos2 x dx
Solution:
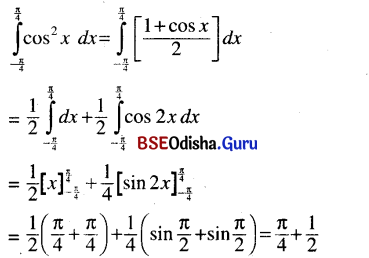
(iv) \(\int_{-\frac{\pi}{6}}^{\frac{\pi}{6}}\)sin5 x dx
Solution:
Let f(x) = sin5 x
Then f(-x) = sin5 (-x)
= -sin5 x = -f(x)
So f(x) is an odd function.
Thus \(\int_{-a}^a\)f(x) dx = 0
\(\int_{-\frac{\pi}{6}}^{\frac{\pi}{6}}\)sin5 x dx = 0
Question 3.
(i) \(\int_0^\pi\)cos3 x dx
Solution:

(ii) \(\int_0^\pi\)cos2 x dx
Solution:
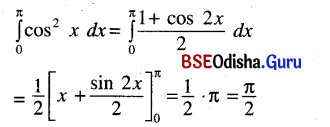
(iii) \(\int_0^\pi\)sin3 x cos x dx
Solution:
\(\int_0^\pi\)sin3 x cos x dx
[Put sin x = t, then cos x dx = dt
When x = 0, t = 0, when x = π, t = 0
\(\int_0^\pi\)t3 dt = 0
(iv) \(\int_0^\pi\)sin x cos2 x dx
Solution:
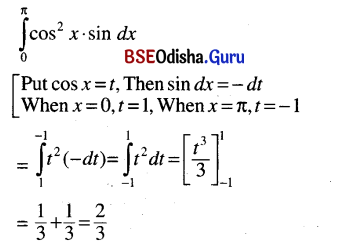
![]()
Question 4.
Show that
(i) \(\int_0^1 \frac{\ln x}{\sqrt{1-x^2}}\) dx = \(\frac{\pi}{2} \ln \frac{1}{2}\)
Solution:

(ii) \(\int_0^{\frac{\pi}{2}} \frac{\cos x-\sin x}{1+\sin x \cos x}\) dx = 0
Solution:

(iii) \(\int_0^\pi\)x ln sin x dx = \(\frac{\pi^2}{2} \ln \frac{1}{2}\)
Solution:

Question 5.
(i) \(\int_0^{\pi / 2}\)ln (tan x + cot x) dx
Solution:
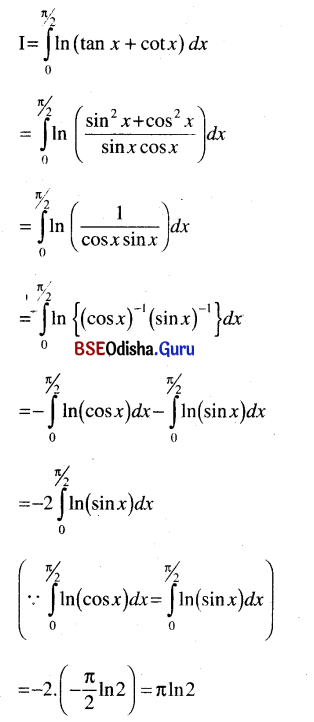
![]()
(ii) \(\int_0^\pi \frac{x \tan x-\sin x}{1+\sin x \cos x}\) dx
Solution:

(iii) \(\int_1^3 \frac{\sqrt{x} d x}{\sqrt{4-x}+\sqrt{x}}\)
Solution:

(iv) \(\int_0^\pi \frac{x \sin x d x}{1+\cos ^2 x}\)
Solution:

(v) \(\int_0^1\)x (1 – x)100 dx
Solution:

![]()
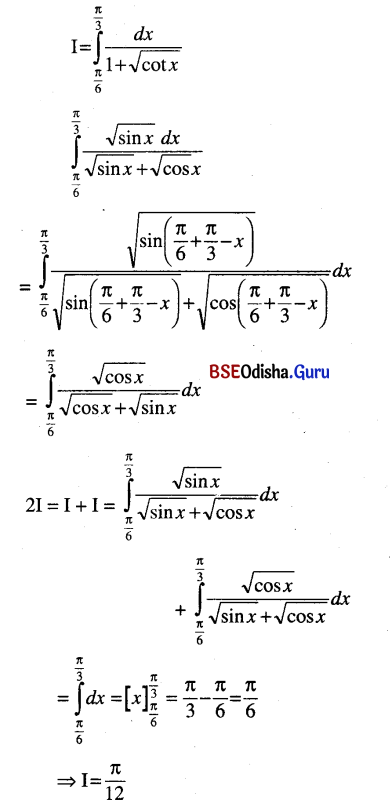
(vi) \(\int_{\pi / 6}^{\pi / 3} \frac{d x}{1+\sqrt{\cot x}}\)
Solution:
(vii) \(\int_0^{50}\)ex-[x] dx
Solution:

