BSE Odisha 10th Class Maths Solutions Algebra Chapter 7 ସଡ଼କ ସୁରକ୍ଷା ଶିକ୍ଷା Ex 7

Odisha State Board BSE Odisha 10th Class Maths Solutions Algebra Chapter 7 ସଡ଼କ ସୁରକ୍ଷା ଶିକ୍ଷା Ex 7 Textbook Exercise Questions and Answers.

BSE Odisha Class 10 Maths Solutions Algebra Chapter 7 ସଡ଼କ ସୁରକ୍ଷା ଶିକ୍ଷା Ex 7

Question 1.
ସଡ଼କ ସୁରକ୍ଷା ଶିକ୍ଷାରେ ସମାନ୍ତର ପ୍ରଗତିର ପ୍ରୟୋଗ କିପରି ହୋଇପାରେ ଲେଖ ।
Solution:
ସଡ଼କ ସୁରକ୍ଷା ଶିକ୍ଷାରେ ସମାନ୍ତର ପ୍ରଗତିର ପ୍ରୟୋଗ ହେଲା – ଟ୍ରାଫିକ୍ ସଂକେତଗୁଡ଼ିକ ମଧ୍ୟରେ ଦୂରତା ଓ ସେଗୁଡ଼ିକୁ ଅତିକ୍ରମ କରିବାର ସମୟକୁ ନେଇ ଏକ ସମାନ୍ତର ଅନୁକ୍ରମ ସୃଷ୍ଟିକରି ଏହି ପ୍ରକ୍ରିୟାକୁ ଏକ ଗାଣିତିକ ଭିଭିଦେବା ।

Question 2.
ଏକ କିଲୋମିଟର ବ୍ୟବଧାନରେ ଗୋଟିଏ ସଡ଼କରେ ଟ୍ରାଫିକ୍ ସଂକେତ ସବୁ ରହିଛି । ଏକ କାର୍ 15 ମିନିଟ୍‌ରେ 15ଟି ଟ୍ରାଫିକ୍ ସଂକେତକୁ ଅତିକ୍ରମ କଲା । କାର୍‌ର ଘଣ୍ଟା ପ୍ରତି ବେଗ କେତେ ନିର୍ଣ୍ଣୟ କର ।
Solution:
1 କି.ମି. ବ୍ୟବଧାନରେ ଟ୍ରାଫିକ୍ ସଂକେତ ଅଛି ।
15 ଟି ଟ୍ରାଫିକ୍ ଖୁଣ୍ଟି ମଧ୍ୟରେ ବ୍ୟବଧାନ 15 – 1 = 14
∴ କାର୍‌ର ଘଣ୍ଟାପ୍ରତି ବେଗ = 14 × 1 କି.ମି. = 14 କି.ମି.

Question 3.
ଏକ ଟ୍ରକ୍ ରାସ୍ତାରେ ଥ‌ିବା ଟ୍ରାଫିକ୍ ଲାଇଟ୍‌କୁ 10 ମିନିଟ୍, 20 ମିନିଟ୍, 30 ମିନିଟ୍ କ୍ରମରେ ଅତିକ୍ରମ କଲା । 15 ଟି ଲାଇଟ୍‌କୁ ଅତିକ୍ରମ କରିବାକୁ ଟ୍ରକ୍‌କୁ କେତେ ସମୟ ଲାଗିଥ୍ ?
Solution:
ଟ୍ରକ୍‌ଟି ଟ୍ରାଫିକ୍ ଲାଇଟ୍‌ଗୁଡ଼ିକୁ 10 ମିନିଟ୍, 20 ମିନିଟ୍, 30 ମିନିଟ୍ କ୍ରମରେ ଅତିକ୍ରମ କରୁଛି ।
ଏହା ସମାନ୍ତର ଅନୁକ୍ରମରେ ଅଛି ।
∴ ଅନୁକ୍ରମଟି = 10, 20, 30
ଏଠାରେ ଅନୁକ୍ରମର ପ୍ରଥମରେ = a = 10
ସାଧାରଣ ଅନ୍ତର = d = 20 – 10 = 30 – 20 = 10
ପଦସଂଖ୍ୟା = n = 15
∴ t_n = a + (n – 1) d
⇒ t₁₅ = 10 + (15 – 1) × 10
= 10 + (14 × 10)
= 10 + 140 = 150 ମିନିଟ୍
= 2 ଘଣ୍ଟା 30 ମିନିଟ୍ ।
∴ 15 ଟି ଲାଇଟ୍‌କୁ ଅତିକ୍ରମ କରିବାପାଇଁ 2 ଘଣ୍ଟା 30 ମିନିଟ୍ ସମୟ ଲାଗିବ ।

Question 4.
ଏକ ସଡ଼କରେ ଲାଗିଥ‌ିବା LED ଲାଇଟ୍ ପୋଷ୍ଟ୍ରଗୁଡ଼ିକର ଯାତ୍ରା ଆରମ୍ଭ ସ୍ଥାନରୁ ଦୂରତା ଏକ ସମାନ୍ତର ଶ୍ରେଣୀ ଅନ୍ତର୍ଭୁକ୍ତ । 5ମ ଲାଇଟ୍ ପୋଷ୍ଟ୍ର ଦୂରତା 45 କି.ମି. ଓ 8ମ ଲାଇଟ୍‌ ପୋଷ୍ଟ୍ର ଦୂରତା 75 କି.ମି. । 10 ଟି ଲାଇଟ୍ ପୋଷ୍ଟ୍ ପାର୍ ହେବାକୁ ଯଦି ଏକ ବସ 2 ଘଣ୍ଟା ସମୟ ନିଏ ତେବେ ବସର ଘଣ୍ଟା ପ୍ରତି ବେଗ ନିର୍ଣ୍ଣୟ କର ।
Solution:
ଲାଇଟ୍ ପୋଷ୍ଟ୍ଗୁଡ଼ିକର ଦୂରତା ଏକ ସମାନ୍ତର ଶ୍ରେଣୀ ଅନ୍ତର୍ଭୁକ୍ତ ।
5ମ ଲାଇଟ୍ ପୋଷ୍ଟର ଦୂରତା = a + 4d = 45 କି.ମି.
8 ମ ଲାଇଟ୍ ପୋଷ୍ଟର ଦୂରତା = a + 7d = 75 କି.ମି.
∴ (a + 7d) – (a + 4d) = 75 – 45 = 30 କି.ମି.
⇒ 3d = 30 କି.ମି.
⇒ d = 10 କି.ମି.
ପୁନଶ୍ଚ a + 4d = 45 କି.ମି.
⇒ a + (4 × 10) = 45 କି.ମି.
⇒ a = 45 – 40 = 5 କି.ମି.
10 ମ ଲାଇଟ୍ ପୋଷ୍ଟର ଦୂରତା = a + 9d
= (5 + 9 × 10) କି.ମି.
= 5 + 90
= 95 କି.ମି.
⇒ ଅତିକ୍ରାନ୍ତ ଦୂରତା = 95 କି.ମି.
ସମୟ = 2 ଘଣ୍ଟା
ବସ୍‌ର ଘଣ୍ଟା ପ୍ରତି ବେଗ = \(\frac{95}{2}\) = 47.5 କି.ମି./ଘଣ୍ଟା

Question 5.
ଦତ୍ତ ସ୍ତମ୍ଭ ଲେଖରେ କୌଣସି ସହରର ବିଗତ ବର୍ଷମାନଙ୍କରେ ସଡ଼କ ଦୁର୍ଘଟଣାରେ ମୃତ୍ୟୁବରଣ କରିଥିବା ବ୍ୟକ୍ତିମାନଙ୍କ ସଂଖ୍ୟା ବ୍ୟକ୍ତ କରାଯାଇଛି ।

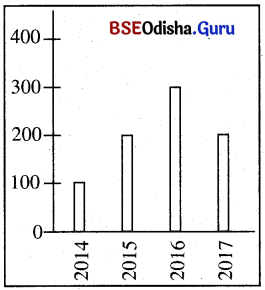
(a) 2014 – 2015 ବର୍ଷରେ ମୃତ୍ୟୁବରଣ କରିଥିବା ବ୍ୟକ୍ତିଙ୍କ ଅଭିବୃଦ୍ଧି ହାର କେତେ?
Solution:
2014 ମସିହାରେ ମୃତ୍ୟୁବରଣ କରିଥିବା ବ୍ୟକ୍ତିଙ୍କ ସଂଖ୍ୟା = 100
2015 ମସିହାରେ ମୃତ୍ୟୁବରଣ କରିଥିବା ବ୍ୟକ୍ତିଙ୍କ ସଂଖ୍ୟା = 200
∴ ଅଧ୍ଵ ମୃତ୍ୟୁବରଣ କରିଥିବା ବ୍ୟକ୍ତିଙ୍କ ସଂଖ୍ୟା = 200 – 100 = 100
∴ 2014 – 15 ବର୍ଷରେ ମୃତ୍ୟୁବରଣ କରିଥିବା ବ୍ୟକ୍ତିଙ୍କ ଅଭିବୃଦ୍ଧି ହାର

(b) 2016 – 2017 ବର୍ଷମାନଙ୍କରେ ମୃତ୍ୟୁବରଣ କରିଥିବା ବ୍ୟକ୍ତିଙ୍କ ଅଭିବୃଦ୍ଧି ବା ହ୍ରାସ ହାର କେତେ ?
Solution:
2016 ମସିହାରେ ମୃତ୍ୟୁବରଣ କରିଥିବା ବ୍ୟକ୍ତିଙ୍କ ସଂଖ୍ୟା = 300
2017 ମସିହାରେ ମୃତ୍ୟୁବରଣ କରିଥିବା ବ୍ୟକ୍ତିଙ୍କ ସଂଖ୍ୟା = 200
ହ୍ରାସ = 300 – 200 = 100
ହ୍ରାସ % = \(\frac{100}{300}\) × 100%
= \(\frac{100}{3}\)%
= \(33 \frac{1}{3}\)%

Question 6.
ଦତ୍ତ ବୃତ୍ତ ଲେଖରେ 2018 ମସିହାରେ କୌଣସି ସହରର ବିଭିନ୍ନ କାରଣରୁ ସଡ଼କ ଦୁର୍ଘଟଣାରେ ମୃତ୍ୟୁବରଣ କରିଥିବା ବ୍ୟକ୍ତିମାନଙ୍କ ସଂଖ୍ୟା ଡିଗ୍ରୀରେ ଦିଆଯାଇଛ ।
ଯଦି ସହରରେ ସେହିବର୍ଷ ମୋଟ 72000 ବ୍ୟକ୍ତି ମୃତ୍ୟୁବରଣ କରିଥି’ନ୍ତି କେତେ ?

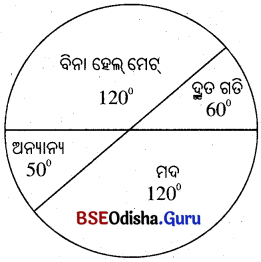
(a) ମଦ୍ୟପାନ ଜନିତ ମୃତ୍ୟୁର ସଂଖ୍ୟା କେତେ ?
Solution:
ସହରରେ ମୋଟ ମୃତ୍ୟୁ ସଂଖ୍ୟା 72,000 ।
ଏହାର ଡିଗ୍ରୀ ପରିମାପ = 360°
ମଦ୍ୟପାନ ଜନିତ ମୃତ୍ୟୁସଂଖ୍ୟାର ଡିଗ୍ରୀ ପରିମାପ = 120°

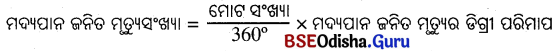
= \(\frac{72000}{360°}\) × 120° = 24,000

(b) ଅନ୍ୟାନ୍ୟ କାରଣରୁ ମୃତ୍ୟୁ ସଂଖ୍ୟା କେତେ ?
Solution:

= \(\frac{72000}{360°}\) × 50° = 10,000

(c) ବିନା ହେଲ୍‌ମେଟ୍ ଯୋଗୁଁ ମୃତ୍ୟୁସଂଖ୍ୟା କେତେ ?

= \(\frac{72000}{360°}\) × 120° = 24,000

Question 7.
ଏକ ବସଷ୍ଟାଣ୍ଡରେ ଏକ ଖମ୍ବ ଉପରେ CCTV କ୍ୟାମେରାଟିଏ ଲଗାଯାଇଛି । ଖମ୍ବର ପାଦଦେଶରୁ 30 ମିଟର ଦୂରସ୍ଥ ପ୍ଲାଟଫର୍ମର ଏକ ବିନ୍ଦୁଠାରୁ CCTV କ୍ୟାମେରାର କୌଣିକ ଉନ୍ନତି 60 ହେଲେ ଖମ୍ବର ଉଚ୍ଚତା ନିଶ୍ଚୟ କର ।
Solution:
AB ହେଉଛି ଖମ୍ବ ।
AB ଖମ୍ବର A ଠାରେ CCTV କ୍ୟାମେରା ଖଞ୍ଜାଯାଇଛି ।
ଖମ୍ବର ପାଦଦେଶ B ଠାରୁ C ପର୍ଯ୍ୟନ୍ତ ଦୂରତା 30 ମିଟର ।

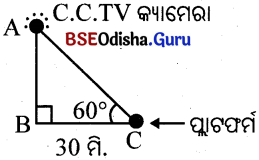
⇒ BC= 30 ମିଟର
C ଠାରେ ରହିଛି ପ୍ଲାଟଫର୍ମ । ∠C = 60°
ABC ସମକୋଣୀ A ରେ tan 60° = \(\frac{A B}{B C}\)
⇒ √3 = \(\frac{A B}{B C}\)
⇒ AB = 30√3 ମି.
ଖମ୍ବର ଉଚ୍ଚତା = 30√3 ମି.

Question 8.
24 ମିଟର ଉଚ୍ଚ ଏକ ଖୁଣ୍ଟିର ଶୀର୍ଷଦେଶରେ ଏକ CCTV କ୍ୟାମେରା ଏପରି ଲଗାଯାଇଛି ଯେପରି ଖୁଣ୍ଟିର ଶୀର୍ଷରୁ 25 ମିଟର ଦୂର ଦୃଷ୍ଟିରେଖାର ଆଗକୁ ଯାତାୟତ ଦୃଷ୍ଟିଗୋଚର ହୋଇପାରେ ।
(a) ଯେଉଁ ସ୍ଥାନଠାରୁ ଆଗକୁ ଯାତାୟତ ଦୃଷ୍ଟିଗୋଚର ହୁଏ ଖୁଣ୍ଟିର ପାଦଦେଶରୁ ସେ ସ୍ଥାନର ଦୂରତା କେତେ ?
Solution:
ଖୁଣ୍ଡରୁ ଦୃଷ୍ଟିଗୋଚର ହୁଏ = AB
AB = 25 ମି.

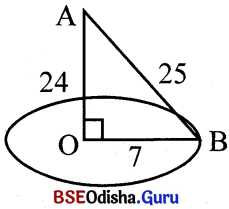
ଖୁଣ୍ଟୁର ଉଚ୍ଚତା = AO = 24 ମି.
ଯେଉଁ ସ୍ଥାନରୁ ଆଗକୁ ଯାତାୟାତ ଦୃଷ୍ଟିଗୋଚରହୁଏ,
ଖୁଣ୍ଟିଠାରୁ ପାଦଦେଶରୁ ସେ ସ୍ଥାନର ଦୂରତା = OB
= \(\sqrt{AB^2 – AO^2}\) = \(\sqrt{25^2 – 24^2}\)
= \(\sqrt{625-576}\) = \(\sqrt{49}\) = 7 ମିଟର

(b) ଖୁଣ୍ଟି ଚାରିପାଖ ସବୁଜ କ୍ଷେତ୍ରର (ଦେଖାଯାଉ ନଥ‌ିବା କ୍ଷେତ୍ର) କ୍ଷେତ୍ରଫଳ କେତେ ?
Solution:
π × (OB)² = π × (7)² = 49 π ବର୍ଗମିଟର ।
= 49 × \(\frac{22}{7}\) ବର୍ଗମିଟର (π = \(\frac{22}{7}\) ନେଲେ)
= 154 ବର୍ଗମିଟର

Question 9.
ଏକ ଚାରିଛକି ଉପରେ 10 ମିଟର ଉଚ୍ଚ ଏକ ଖମ୍ବ ଉପରେ ଏକ CCTV କ୍ୟାମେରା ଲଗାଯାଇଛି । ଗୋଟିଏ କାର ଭକ୍ତ ଖମ୍ବ ଆଡ଼କୁ ଆସୁଅଛି । ଯଦି କ୍ୟାମେରାଠାରୁ ସେହି କାରର କୌଣିକ ଅବନତି 45 ରୁ ବଦଳି 60 ହୋଇଯାଏ, ତେବେ ଏହି ସମୟ ଭିତରେ କାର୍‌ଟି କେତେ ବାଟ ଅତିକ୍ରମ କରିଥବ ?
Solution:
AB = ଖମ୍ବର ଉଚ୍ଚତା = 10 ମିଟର ।
A ଠାରେ CCTV ଲାଗିଛି ।
C ହେଉଛି କାରର ପ୍ରଥମ ଅବସ୍ଥାନ, ∠ACB = 45°
D ହେଉଛି କାରର ଦ୍ଵିତୀୟ ଅବସ୍ଥାନ, ∠ADB = 60°
କାରଟି ଅତିକ୍ରମ କରିଥିବା ଦୂରତା = CD

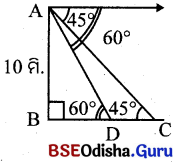
ABC ସମକୋଣୀ A ରେ, tan 45° = \(\frac{A B}{B C}\)
⇒ 1 = \(\frac{10}{B C}\)
⇒ BC = 10 ମିଟର ।
ପୁନଶ୍ଚ ABD ସମକୋଣୀ ∆ ରେ
tan 60° = \(\frac{A B}{B D}\) ⇒ √3 = \(\frac{10}{B D}\) ⇒ BD√3 = 10
⇒ BD = \(\frac{10}{√3}=\frac{10√3}{3}\) ମିଟର ।

∴ ଅତିକ୍ରାନ୍ତ ଦୂରତା = CD = BC – BD
(10 – \(\frac{10√3}{3}\)) ମି. = (\(\frac{30-10√3}{3}\)) ମି.
= \(\frac{10√3(√3-1)}{3}=\frac{10(√3-1)}{√3}\) ମି.

Question 10.
ଏକ ଛକଠାରେ ୫ ମିଟର ଉଚ୍ଚ ଖମ୍ବ ଉପରେ ଏକ CCTV କ୍ୟାମେରାରୁ ଖମ୍ବ ଆଡ଼କୁ ଆସୁଥିବା ଏକ ସ୍କୁଟର ଦେଖାଯାଉଛି । ଯଦି ସ୍କୁଟରଠାରୁ CCTV କ୍ୟାମେରାର କୌଣିକ ଉନ୍ନତି 30 ରୁ 45 ରେ ପହଞ୍ଚିବା ପାଇଁ 1 ମିନିଟ୍ ସମୟ ଲାଗେ, ତେବେ ସ୍କୁଟରର ଘଣ୍ଟା ପ୍ରତି ବେଗ ନିର୍ଣ୍ଣୟ କର ।
Solution:
AB ଖମ୍ବର ଉଚ୍ଚତା = 8 ମିଟର ।
C ହେଉଛି ସ୍କୁଟରର ପ୍ରଥମ ଅବସ୍ଥାନ, ∠ACB = 30°
D, ହେଉଛି ସ୍କୁଟରର ଦ୍ବିତୀୟ ଅବସ୍ଥାନ । ∠ADB = 45°
CD ଦୂରତା ଅତିକ୍ରମ କରିବାକୁ ସ୍ଫୁଟରକୁ ଲାଗେ = 1 ମିନିଟ୍ ।

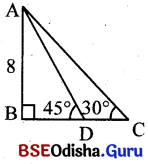
ABC ସମକୋଣୀ ∆ ରେ tan 45° = \(\frac{A B}{B D}\)
⇒ 1 = \(\frac{8}{B D}\) ⇒ BD = 8 ମିଟର ।
ପୁନଶ୍ଚ ABC ସମକୋଣୀ ∆ ରେ, tan 30° = \(\frac{A B}{B C}\)
⇒ \(\frac{1}{√3}=\frac{8}{B D}\)
⇒ BC = 8 √3
∴ CD = BC – BD
= (8√3 – 8) ମିଟର ।
= 8(√3-1) ମିଟର ।
1 ଘଣ୍ଟା = 60 ମିନିଟ୍
1 ମିନିଟ୍‌ରେ ସ୍କୁଟରଟି ଯାଏ = 8(√3 – 1) ମିଟର ।
60 ମିନିଟ୍‌ରେ ସ୍କୁଟରଟି ଯାଏ = 8(√3 – 1) × 60 = 480(√3 – 1) ମିଟର ।
∴ ସ୍ଫୁଟରର ଘଣ୍ଟା ପ୍ରତି ବେଗ = 480(√3 – 1) ମିଟର ।

Question 11.
ଏକ କାର ଘଣ୍ଟ ପ୍ରତି 60 କି.ମି. ବେଗରେ ଚାଲୁଛି । ବ୍ରେକ ଦେବା ପରେ ଯଦି ସ୍ଥିର ହେବାର ଦୂରତା 50 ମିଟର ଓ ମନ୍ଦିତ ବେଗ ସେକେଣ୍ଡ ପ୍ରତି 5 ମିଟର ହୁଏ, ତେବେ କାର୍‌ଟିର ପହଞ୍ଚିବା ସମୟ ନିର୍ଣ୍ଣୟ କର ।
Solution:
କାରର ପ୍ରାରମ୍ଭିକ ପରିବେଗ = u = 60 କି.ମି./ଘଣ୍ଟା = (60 × \(\frac{5}{8}\)) ମି./ସେ. = \(\frac{50}{3}\)
ସମୟ = t = ?
କାରର ଅନ୍ତିମ ପରିବେଗ = V = 0 ମି./ସେ.
ଅତିକ୍ରାନ୍ତ ଦୂରତା = 50 m., a = ମନ୍ଦନ = – 5ମି./ସେ.²

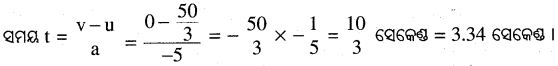
କାରଟିର ପହଞ୍ଚିବା ସମୟ \(\frac{10}{3}\) ସେକେଣ୍ଡ ବା 3.34 ସେକେଣ୍ଡ ଲାଗିବ ।

Question 12.
ଏକ ସ୍ତମ୍ଭ ଉପରେ CCTV କ୍ୟାମେରା ଲଗାଯାଇଛି । ତାହା 25 ମିଟର ଦୂର ଦୃଷ୍ଟିରେଖାରେ ଯେଉଁ ସ୍ଥାନ ପର୍ଯ୍ୟନ୍ତ ଯାତାୟତ ଲକ୍ଷ୍ୟ କରିପାରେ, ସ୍ତମ୍ଭର ପାଦ ଦେଶରୁ ସେହି ସ୍ଥାନର ଦୂରତା 24 ମିଟର । ସ୍ତମ୍ଭର ଉଚ୍ଚତା ଓ କ୍ୟାମେରା ସ୍ତମ୍ଭର ଚାରିପାଖେ ଯେଉଁ କ୍ଷେତ୍ର ମଧ୍ୟରେ ଯାତାୟତ ଦେଖୁପାରୁଛି, ତାହାର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
Solution:

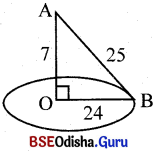
AB = ଦୃଷ୍ଟିଗୋ (LOS) = 25 ମି.
ସ୍ତମ୍ଭର ପାଦଦେଶରୁ ଯେଉଁ ସ୍ଥାନ ପରେ ଟ୍ରାଫିକ୍ ଦୃଷ୍ଟିଗୋଚର ହୁଏ, ସେ ପର୍ଯ୍ୟନ୍ତ ଦୂରତା = 24 ମି.
⇒ OB = 24 ମି.
ସ୍ତମ୍ଭର ଉଚ୍ଚତା = AO
AOB ସମକୋଣୀ ∆ ରେ
AO = \(\sqrt{AB^2 – OB^2}\)
= \(\sqrt{25^2 – 24^2}\) = \(\sqrt{625-576}\) = \(\sqrt{49}\) = 7 ମି.
କ୍ୟାମେରା, ସ୍ତମ୍ଭର ଚାରିପାଖେ ଯେଉଁ କ୍ଷେତ୍ର ମଧ୍ୟରେ ଯାତାୟତ ଦେଖିପାରୁଛି, ତାହାର କ୍ଷେତ୍ରଫଳ = π × (OB)²
= 3.14 × (24)² = (3.14 × 576) ବର୍ଗମିଟର = 1,808.64 ବର୍ଗମିଟର

Question 13.
ନିମ୍ନ ସାରଣୀରେ ଥ‌ିବା ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

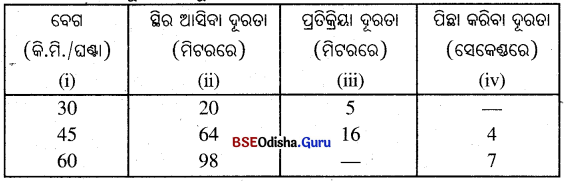
Solution:

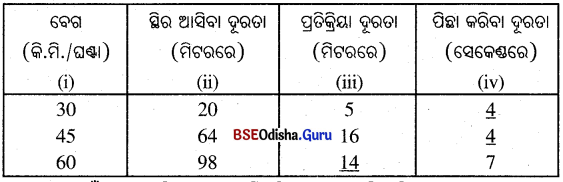
Question 14.
ସଡ଼କ ସୁରକ୍ଷା ପାଇଁ ତୁମେ ପରିସଂଖ୍ୟାନକୁ କିପରି ପ୍ରୟୋଗ କରିପାରିବ ବୁଝାଅ ।
Solution:
ବିଭିନ୍ନ ପ୍ରଦୂଷଣ ତଥା ସଡ଼କ ଦୁର୍ଘଟଣା ବିଷୟନ ତଥ୍ୟ ସଂଗ୍ରହ କରି, ତାହାର ପରିସଂଖ୍ୟାନ ଭିତ୍ତିକ ଲେଖଚିତ୍ର ପ୍ରସ୍ତୁତ କରି ତାହା ମାଧ୍ୟମରେ ଜନ ସଚେତନତା ସୃଷ୍ଟି କରାଯାଇ ସଡ଼କ ସୁରକ୍ଷା କ୍ଷେତ୍ରରେ ପ୍ରୟୋଗ କରାଯାଇପାରିବ ।

Question 15.
ବାୟୁ ପ୍ରଦୂଷଣ ରୋକିବା ପାଇଁ ସରକାରଙ୍କ କାର୍ଯ୍ୟକ୍ରମ ସମ୍ବନ୍ଧରେ ଧାରଣା ଦିଅ ।
Solution:
1989 ଭାରତ ସରକାରଙ୍କ ମୋଟର ଯାନ ଆଇନ ଅନୁସାରେ ସବୁ ପ୍ରକାର ଡ଼ିଜେଲ ଓ ପେଟ୍ରୋଲ ଚାଳିତ ଯାନ ପାଇଁ ପ୍ରଦୂଷଣ ନିୟନ୍ତ୍ରଣ ପ୍ରମାଣ ପତ୍ର (PUC) ବ୍ୟବସ୍ଥା କରିଥିଲେ ମଧ୍ୟ ଏହା ସେତେଟା କଡାକଡ଼ି ଭାବେ ଲାଗୁ ନ ହେବାରୁ ବର୍ତ୍ତମାନ ଅକ୍ଟୋବର 1, 2019 ଠାରୁ Online ପ୍ରଦୂଷଣ ନିୟନ୍ତ୍ରଣ ପ୍ରମାଣ ପତ୍ର ଦିଆଯାଉଛି ।

Question 16.
ସଡ଼କ ସୁରକ୍ଷାରେ ତ୍ରିକୋଣମିତିର କିଭଳି ପ୍ରୟୋଗ କରାଯାଇପାରେ ଲେଖ ।
Solution:
ସାଧାରଣତଃ ବଡ ବଡ ଖୁଣ୍ଟ ଉପରେ ବା ରାସ୍ତା କଡ଼ରେ ଥିବା ବଡ଼ ବଡ଼ ଅଟ୍ଟାଳିକା ଉପରେ ଆଲୋକ ଓ CCTV ବ୍ୟବସ୍ଥା କରାଯାଇଥାଏ । ତ୍ରିକୋଣମିତିରେ ଥ‌ିବା ଉଚ୍ଚତା ଓ ଦୂରତା ସମ୍ବନ୍ଧୀୟ ପାଠକୁ ଟ୍ରାଫିକ୍ ବ୍ୟବସ୍ଥା ସହିତ ସମ୍ପର୍କିତ କରାଯାଇ, ବହୁ ପରିମାଣରେ ରାସ୍ତା ଦୁର୍ଘଟଣା ରୋକାଯାଇପାରିବ ।

Question 17.
ନିମ୍ନ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଦିଅ ।
(a) ଦୃଷ୍ଟିରେଖା କ’ଣ ?
Solution:
ଦର୍ଶକର ଚକ୍ଷୁ ସହିତ ବସ୍ତୁ ବା CCTV କୁ ବିନା ବାଧାରେ ଯୋଗକରୁଥିବା ରେଖାଖଣ୍ଡକୁ ଦୃଷ୍ଟିରେଖା କୁହାଯାଏ ।

(b) CCTV କ୍ୟାମେରା ଚାରିପଟେ ସବୁଜ ବଳୟ (green belt) କ’ଣ ?
Solution:
CCTV ସ୍ତମ୍ଭ ଚାରିପଟେ ଥ‌ିବା ବୃତ୍ତାକାର କ୍ଷେତ୍ର,ଯେଉଁଠି ଟ୍ରାଫିକ୍ ଦୃଶ୍ୟମାନ ହୁଏ ନାହିଁ ଓ ଏକ୍ଷେତ୍ରକୁ ଘାସ ଆଚ୍ଛାଦିତ କରାଯାଇଥ‌ିବାରୁ ତାହାକୁ ସବୁଜ ବଳୟ କୁହାଯାଏ ।

(c) ପ୍ରତିକ୍ରିୟା ଦୂରତା କ’ଣ ?
Solution:
ପ୍ରତିକ୍ରିୟା ଦୂରତା = ସ୍ଥିରତା ଆସିବା ଦୂରତା – ବେଗକ୍ଷୟ ଦୂରତା
କିମ୍ବା, ପ୍ରତିକ୍ରିୟା ଦୂରତା = ସ୍ଥିରତା ଆସିବା ଦୂରତା / ପିଛା କରିବା ଦୂରତା ।

(d) ବେଗ କ୍ଷୟ ଦୂରତା କ’ଣ ?
Solution:
ବେଗକ୍ଷୟ ଦୂରତା = ସ୍ଥିରତା ଆସିବା ଦୂରତା – ପ୍ରତିକ୍ରିୟା ଦୂରତା ।

(e) ସ୍ଥିରତା ଆସିବା ଦୂରତା କ’ଣ ?
Solution:
ସ୍ଥିରତା ଆସିବା ଦୂରତା = ପ୍ରତିକ୍ରିୟା ଦୂରତା + ବେଗକ୍ଷୟ ଦୂରତା
କିମ୍ବା, ସ୍ଥିରତା ଆସିବା ଦୂରତା = ପ୍ରତିକ୍ରିୟା ଦୂରତା × ପିଛାକରିବା ଦୂରତା ।

(f) ପିଛା କରିବା ଦୂରତା କ’ଣ ?
Solution:
ପିଛା କରିବା ଦୂରତା = ସ୍ଥିରତା ଆସିବା ଦୂରତା | ପ୍ରତିକ୍ରିୟା ଦୂରତା

Question 18.
ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(a) ବିନା ହେଲମେଟ୍‌ରେ ଗାଡ଼ି ଚଳାଇଲେ ଜୋରିମାନା ରାଶି
(b) ସିଟ୍ ବେଲ୍ସ ନବାନ୍ଧିଲେ ଜୋରିମାନା ରାଶି ……………. ଟଙ୍କା ।
(c) ସିଗନାଲ ନ ମାନିଲେ ଜୋରିମାନା ରାଶି ……… ଟଙ୍କା ।
(d) ବିନା ଲାଇସେନ୍ସରେ ଗାଡ଼ି ଚଳାଇଲେ ଜୋରିମାନା ରାଶି ……………. ଟଙ୍କା ।
(e) ନିଶାସକ୍ତ ହୋଇ ଗାଡ଼ି ଚଳାଇଲେ ଜୋରିମାନା ରାଶି ……………. ଟଙ୍କା ।
(f) ମୋବାଇଲରେ କଥା ହୋଇ ଗାଡ଼ି ଚଳାଇଲେ ଜୋରିମାନା ରାଶି ……………. ଟଙ୍କା ।
(g) ଆମ୍ବୁଲାନ୍ସକୁ ରାସ୍ତା ନ ଛାଡ଼ିଲେ ଜୋରିମାନା ……………. ।
Solution:
(a) 1000
(b) 1000
(c) 5000
(d) 5000
(e) 10,000
(f) 10,000
(g) 10,000