BSE Odisha 10th Class Maths Notes Algebra Chapter 1 ସରଳ ସହସମୀକରଣ

Odisha State Board BSE Odisha 10th Class Maths Notes Algebra Chapter 1 ସରଳ ସହସମୀକରଣ will enable students to study smartly.

BSE Odisha Class 10 Maths Notes Algebra Chapter 1 ସରଳ ସହସମୀକରଣ

ଉପକ୍ରମଣିକା (Introduction) :

→ ଗୋଟିଏ ଅଜ୍ଞାତ ରାଶି x ରେ ଏକ ସରଳ ସମୀକରଣର ସାଧାରଣ ରୂପ ହେଉଛି ax + b = 0, ଯେଉଁଠାରେ a ≠ 0 ।
ଏଠାରେ à ଓ b ବାସ୍ତବ ସଂଖ୍ୟା ଏବଂ a କୁ xର ସହଗ (Coefficient) ଓ bକୁ ଧ୍ରୁବକ ରାଶି କୁହାଯାଏ ।
ଏଠାରେ ସମୀକରଣଟିର ସମାଧାନ (ମୂଳ) = \(\frac{-b}{2}\) ।

→ ଦୁଇଟି ଅଜ୍ଞାତ ରାଶି x ଓ y ରେ ସରଳରେଖୀୟ ସମୀକରଣର ସାଧାରଣ ରୂପ ax + by + c = 0 ……. (1)
ଯେଉଁଠାରେ a ଓ b ଯଥାକ୍ରମେ x ଓ yର ସହଗ ଓ c ଧ୍ରୁବକ ରାଶି ଏବଂ a, b ଓ ୯ ବାସ୍ତବ ସଂଖ୍ୟା ଅଟନ୍ତି । ଏଠାରେ a ≠ 0 ଓ b ≠ 0 ।

→ xy- ସମତଳରେ y = mx + c ର ଲେଖଚିତ୍ର ଏକ ସରଳରେଖା ହେତୁ ଏହାକୁ ସରଳରେଖୀୟ ସମୀକରଣ (Linear Equation) କୁହଯାଏ ।

→ x = α ଓ y = ß ହେଲେ ଏବଂ ଯଦି ସମୀକରଣଟି aα + bß + c = 0 ହୁଏ, ତେବେ x = α ଓ y = ß ସମୀକରଣର ଏକ ସମାଧାନ ହେବ । ସମାଧାନଟି (α, ß) । xy-ସମତଳରେ (α, ß) ଏକ ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (Co-ordinate) ହୋଇଥାଏ ।

ସହ-ସମୀକରଣଦ୍ଵୟର ଜ୍ୟାମିତିକ ପରିପ୍ରକାଶ (Geometrical Representation) :
→ ମନେକର ଦଉ ସହ-ସମୀକରଣଦ୍ଵୟ
a₁x + b₁y + c₁ = 0 … (1)
ଓ a₂x + b₂y + c₂ = 0 … (2)

→ ପ୍ରତ୍ୟେକ ସମୀକରଣ ପାଇଁ ଦୁଇଗୋଟି ସମାଧାନ ନିର୍ଣ୍ଣୟ କରାଯାଏ ।

→ ମନେକର ସମୀକରଣ (1) ଓ (2)ର ଲେଖଚିତ୍ର xy-ସମତଳରେ ଗୋଟିଏ ଗୋଟିଏ ସରଳରେଖା ଯଥାକ୍ରମେ L₁ ଓ L₂ ହେଉ ।
L₁ : a₁x + b₁y + c₁ = 0 ଏବଂ L₂ : a₂x + b₂y + c₂ = 0

→ L₁ ଓ L₂ ସରଳରେଖାଦ୍ବୟର ଛେଦବିନ୍ଦୁ P ନେଇ ଉକ୍ତ ବିନ୍ଦୁର x-ସ୍ଥାନାଙ୍କ ଓ y-ସ୍ଥାନାଙ୍କ ନିର୍ଣ୍ଣୟ କରାଯାଉ ।

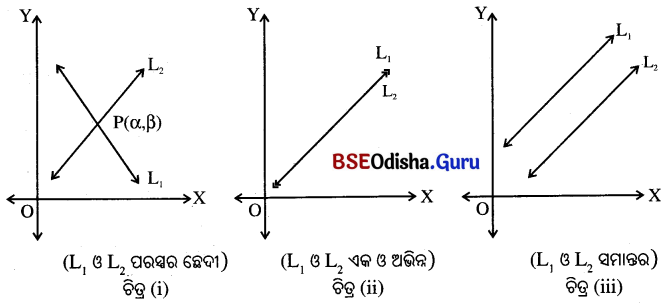
→ ଚିତ୍ର (i)ରେ L₁ ଓ L₂, ସରଳରେଖାଦ୍ୱୟ ପରସ୍ପର ଛେଦୀ, ସେମାନଙ୍କର କେବଳ ଗୋଟିଏ ଛେଦବିନ୍ଦୁ P ଓ ଏହି ବିଦୁଟି ଉଭୟ L₁ ଓ L₂; ଉପରେ ଅବସ୍ଥିତ । ଏହାର ସ୍ଥାନାଙ୍କ (α, ß) ଅର୍ଥାତ୍‌ x = α ଓ y = ß ଦ୍ବାରା ଉଭୟ ସମୀକରଣ (1) ଓ (2) ସିଦ୍ଧ ହୁଅନ୍ତି ।
ସମୀକରଣ (1) ଓ (2)ର କେବଳ ଗୋଟିଏ (ଅନନ୍ୟ) ସମାଧାନ ରହିବ; ଯଦି ଓ କେବଳ ଯଦି ସମୀକରଣ ଦ୍ବୟ ଦ୍ବାରା ସୂଚିତ ସରଳରେଖାଦ୍ବୟ ପରସ୍ପର ଛେଦୀ ହେବେ ।

→ ଚିତ୍ର (ii)ରେ L₁ ଓ L₂ ସରଳରେଖା ଦ୍ଵୟ ଏକ ଓ ଅଭିନ୍ନ (coincident) ଅର୍ଥାତ୍ ଏକ ଏବଂ ଅଭିନ୍ନ ଅଟନ୍ତି ।
ତେଣୁ ସେମାନଙ୍କର ସାଧାରଣ ବିନ୍ଦୁ ଅସଂଖ୍ୟ । ଅତଏବ ଏ କ୍ଷେତ୍ରରେ ସମୀକରଣ ଦ୍ବୟର ଅସଂଖ୍ୟ ସମାଧାନ ସମ୍ଭବ ।

→ ଚିତ୍ର (iii)ରେ L₁ ଓ L₂ ସରଳରେଖା ଦ୍ଵୟ ପରସ୍ପର ସହ ସମାନ୍ତର । ଅର୍ଥାତ୍ ସରଳରେଖାଦ୍ଵୟ ପରସ୍ପର ଛେଦୀ ହେବେ ନାହିଁ । ସହ ସମୀକରଣଦ୍ଵୟ ଦ୍ବାରା ସୂଚିତ ସରଳରେଖା ଦୁଇଟି ସମାନ୍ତର ହେଲେ, ସହ-ସମ୍ଭବ। ସମୀକରଣଦ୍ୱୟର ସମାଧାନ ସମ୍ଭବ ନୁହେଁ ।

ଲେଖଚିତ୍ର ଦ୍ବାରା ସହ-ସମୀକରଣଦ୍ଵୟର ସମାଧାନ (Solution of Simultaneous equations by use of Graphs) :
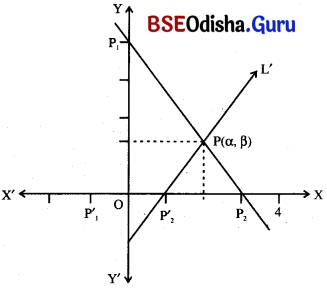
ଏକଘାତୀ ସମୀକରଣର ଲେଖଚିତ୍ର ଏକ ସରଳରେଖା । ଦୁଇଗୋଟି ଏକଘାତୀ ସମୀକରଣ a₁x + b₁y + c₁ = 0 ଏବଂ a₂x + b₂y + c₂ = 0 ର ଲେଖଚିତ୍ର ଅଙ୍କନ କରି ସେମାନଙ୍କ ଛେଦବିନ୍ଦୁ (α, ß) ନିର୍ଣ୍ଣୟ କଲେ, ଦତ୍ତ ସହସମୀକରଣ ଦ୍ଵୟର ସମାଧାନ (α, ß) ହେବ ।

ଲେଖଚିତ୍ର ଅଙ୍କନ ପ୍ରଣାଳୀ :

→ ପ୍ରତ୍ୟେକ ସମୀକରଣ ପାଇଁ ଅତି କମ୍‌ରେ ଦୁଇଟି ସମାଧାନ ନିର୍ଣ୍ଣୟ କରାଯାଏ ।

• ସମୀକରଣଗୁଡ଼ିକୁ y = mx + c ରୂପରେ ଲେଖାଯାଏ ।
• ପ୍ରତି xର ଏପରି ପୂର୍ଣ୍ଣସଂଖ୍ୟାମାନ ନେଇ yର ମଧ୍ୟ ଏକ ଅନୁରୂପ ପୂର୍ଣସଂଖ୍ୟା ନିର୍ଣ୍ଣୟ କରାଯାଏ ।
• ମାନଗୁଡ଼ିକୁ ନେଇ କ୍ରମିତ ଓ ଯୋଡ଼ିମାନ ସ୍ଥିର କରାଯାଏ ।

→ ଲେଖ କାଗଜରେ XOX’ ଓ YOY’ ଅକ୍ଷ – ଅଙ୍କନ କରାଯାଏ ।

→ ପ୍ରତ୍ୟେକ ସମୀକରଣର ସ୍ଥିରୀକୃତ କ୍ରମିତ ଯୋଡ଼ିମାନଙ୍କୁ ନେଇ ଅତି କମ୍‌ରେ ଦୁଇଟି ବିନ୍ଦୁ L₁ ଓ L₂ ସରଳରେଖା ଅଙ୍କନ କରାଯାଏ ।

→ ଯଦି ସେମାନେ (α, ß) ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି, ତେବେ ସମୀକରଣଦ୍ଵୟର ସମାଧାନ (α, ß) ହେବ ।

ସହ-ସମୀକରଣଦ୍ଵୟର ସମାଧାନ ପାଇଁ ସର୍ଭ (Conditions of solvability of two Linear simultaneous equations) :

→ xy-ସମତଳରେ ଦୁଇଟି ସରଳରେଖା ଦତ୍ତ ଥିଲେ ସେମାନେ ଯଦି ପରସ୍ପରକୁ ଛେଦ କରିବେ, ସେମାନଙ୍କର ଗୋଟିଏ ଛେଦବିନ୍ଦୁ ରହିବ । ସରଳରେଖାଦ୍ବୟର ସମୀକରଣ ଦ୍ଵୟ ହେଲେ,
a₁x + b₁y + c₁ = 0 … (1)
a₂x + b₂y + c₂ = 0 … (2)

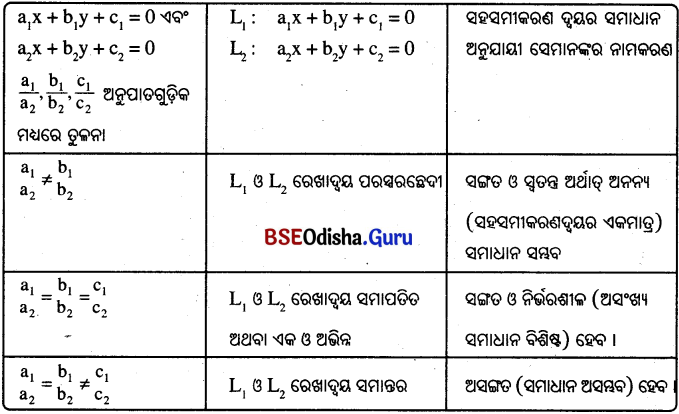
→ ସରଳରେଖାଦ୍ବୟ ପରସ୍ପରଛେଦୀ ହେଲେ ସେମାନଙ୍କର ଅନନ୍ୟ ସମାଧାନ ରହିବ । ଏ କ୍ଷେତ୍ରରେ ସହ- ସମୀକରଣଦ୍ବୟ ସଙ୍ଗୀତ ଓ ସ୍ବତନ୍ତ୍ର (consistent and independent), ତେବେ \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\) ହେବ ।

→ ଯଦି ସରଳରେଖାଦ୍ଵୟ ଏକ ଓ ଅଭିନ୍ନ ହୁଅନ୍ତି ତେବେ \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\) ସମୀକରଣଦ୍ଵୟ ସଙ୍ଗୀତ ଓ ପରସ୍ପର ନିର୍ଭରଶୀଳ (consistent and dependent) ହେବେ । ଏ କ୍ଷେତ୍ରରେ ସହ-ସମୀକରଣ ଦ୍ଵୟର ଅସଂଖ୍ୟ ସମାଧାନ ରହିବ ।

→ ଯଦି ସରଳରେଖାଦ୍ବୟ ପରସ୍ପରକୁ ଛେଦ ନ କରିବେ ଏବଂ ସେମାନେ ପରସ୍ପର ସମାନ୍ତର ହେବେ ଓ \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\) ସର୍ଭ ପୂରଣ ହେବ ଏବଂ ସହ-ସମୀକରଣଦ୍ଵୟ ଅସଙ୍ଗତ (inconsistent) ହେବେ ଅର୍ଥାତ୍ ସହ-ସମୀକରଣଦ୍ୱୟର କୌଣସି ସମାଧାନ ରହିବ ନାହିଁ ।

ମନେରଖ :

ଦ୍ରଷ୍ଟବ୍ୟ : ସମୀକରଣ a₁x + b₁y + = 0 ଓ a₂x + b₂y = 0 ଦ୍ବୟର ଅନନ୍ୟ ସମାଧାନଟି (0, 0);
ଯଦି \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\) ଓ ଅସଂଖ୍ୟ ସମାଧାନ ସମ୍ଭବ; ଯଦି \(\frac{a_1}{a_2}=\frac{b_1}{b_2}\)। ଏ କ୍ଷେତ୍ରରେ ସମୀକରଣଦ୍ଵୟ ସର୍ବଦା ସଙ୍ଗତ ଅଟନ୍ତି ।

→ (ସହ-ସମୀକରଣ ଦ୍ବୟର ବୀଜଗାଣିତିକ ସମାଧାନ) :
(Algebraic solution of Simultaneous Equations):
a₁x + b₁y + c₁ = 0 ଓ a₂x + b₂y + c₂ = 0 … (2)
ମନେକର ଦତ୍ତ ସହ-ସମୀକରଣ ଦ୍ବୟ ସଙ୍ଗତ ଓ ସ୍ବତନ୍ତ୍ର ।

(a) ପ୍ରତିକଳ୍ପନ ପ୍ରଣାଳୀ (Method of Substitution) :
(b) ଅପସାରଣ ପ୍ରଣାଳୀ (Method of Elimination)
(c) ବକ୍ରଗୁଣନ ପକ୍ଷିଣ (Method of Cross Multiplication)
ଏହି ଦୁଇ ସହସମୀକରଣ 3ଟି ବୀଜଗାଣିତିକ ପ୍ରଣାଳୀ/ପଦ୍ଧତି ସାହାଯ୍ୟରେ ସମାଧାନ କରାଯାଇ ପାରିବ । ଯଥା-

(a) ପ୍ରତିକଳ୍ପନ ପ୍ରଣାଳୀ (Method of Substitution) :
ପ୍ରତିକଳ୍ପନ ପ୍ରଣାଳୀରେ ସହସମୀକରଣଦ୍ଵୟର ସମାଧାନ କରିବାକୁ ହେଲେ, ପ୍ରଥମେ ଏମାନଙ୍କ ମଧ୍ୟରୁ ଯେକୌଣସି ଗୋଟିଏ ସମୀକରଣରୁ y କିମ୍ବା x ର ମାନ ନେଇ ଦ୍ୱିତୀୟ ସମୀକରଣରେ ପ୍ରୟୋଗ କଲେ x କିମ୍ବା y ର ମାନ ନିର୍ଣ୍ଣୟ ହେବ ।
ଉଦାହରଣ : a₁x + b₁y + c₁ = 0 … (1)
ଓ a₂x + b₂y + c₂ = 0 … (2)
ସମାଧାନ :
(i) ମନେକର ସମୀକରଣ (1)କୁ ବିଚାର କରାଯାଇ yକୁ x ମାଧ୍ୟମରେ ପ୍ରକାଶ କରିବା
ଯଦି b₁≠ 0, a₁x + b₁y + c = 0 ⇒ b₁y = -c₂ – a₁x
⇒ y = \(\frac{1}{b_1}(-c_1-a_1 x)\) ……. (3)

(ii) yର ମାନ \(\frac{1}{b_1}(-c_1-a_1 x)\) କୁ ସମୀକରଣ (2) ରେ ବ୍ୟବହାର କଲେ,

→ ଅପସାରଣ ପ୍ରଣାଳୀ (Method of Elimination) :
ଏହି ପ୍ରଣାଳୀରେ ସହସମୀକରଣଦ୍ୱୟର x କିମ୍ବା yର ସହଗମାନଙ୍କୁ ଅପସାରଣ କରାଯାଏ ।
a₁x + b₁y + c₁ = 0 ଓ a₂x + b₂y + c₂ = 0
(i) ମନେକର ଆମେ xକୁ ଅପସାରଣ କରିବା । ସମୀକରଣ (1)ରେ xର ସହଗ a1 କୁ ସମୀକରଣ (2)ର ଉଭୟ ପାର୍ଶ୍ଵରେ ଗୁଣନ କଲେ ଏବଂ ସମୀକରଣ (2)ରେ xର ସହଗ a1କୁ ସମୀକରଣ (1)ର ଉଭୟ ପାର୍ଶ୍ଵରେ ଗୁଣନ କରି ବିୟୋଗ କଲେ,

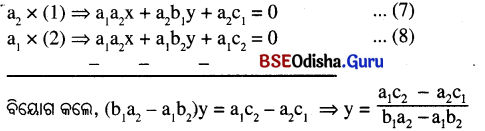
(ii) y ର ମାନକୁ ସମୀକରଣ (1) [କିମ୍ବା ସମୀକରଣ (2)]ରେ ବ୍ୟବହାର କଲେ,
x = \(\frac{b_1 c_2-b_2 c_1}{a_1 b_2-a_2 b_1}\) ଲବ୍‌ଧ ହେବ ।
x = \(\frac{b_1 c_2-b_2 c_1}{a_1 b_2-a_2 b_1}, \quad y=\frac{c_1 a_2-c_2 a_1}{a_1 b_2-a_2 b_1}\) ହେବ ।

(c) ବକ୍ରଗୁଣନ ପକ୍ଷିଣ (Cross Multiplication) :

ଏଠାରେ ସ୍ମରଣ ରହିବା ଉଚିତ ଯେ a₁b₂ – a₂b₁ ≠ 0, ଅର୍ଥାତ୍ \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2} \)
ସମୀକରଣ (4)ରେ ପ୍ରଦତ୍ତ ଉକ୍ତିକୁ ବଜ୍ରଗୁଣନ କୁହାଯାଏ । ଏହାକୁ ସହଜରେ ମନେରଖ୍ ପାଇଁ ନିମ୍ନଲିଖୂ ପଦ୍ଧତି ଅବଲମ୍ବନ କରାଯାଇଥାଏ ।

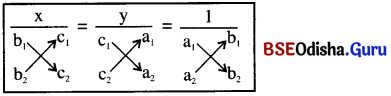
c₁ = c₂ = 0 ଓ a₁b₂ – a₂b₁ ≠ 0 ହେଲେ, aa₁x + b₁y = 0, a₂x + b₂y = 0 ସମୀକରଣଦ୍ଵୟର ସମାଧାନଟି (0, 0) ଅଟେ । ଏଠାରେ ସମୀକରଣଦ୍ଵୟକୁ ସମ ସହ-ସମୀକରଣ (Homogeneous Simultaneous equation) କୁହାଯାଏ I a₁b₂ – a₂b₁ = 0 ହେଲେ, ସରଳରେଖାଦ୍ଵୟ ଏକ ଓ ଅଭିନ୍ନ ହେବେ ଓ ଦତ୍ତ ସହ-
ଦୁଇଗୋଟି ସହ-ସମୀକରଣ ସମାଧାନ କରିବାକୁ ଦିଆଯାଇଥିଲେ ପ୍ରଥମେ a₁b₂ – a₂b₁ ≠ 0 ସର୍ଭଟି ସତ୍ୟ ବୋଲି ପରୀକ୍ଷା କରିବା ଆବଶ୍ୟକ ।

→ ଅଣ ସରଳରେଖ୍ୟ ସହସମୀକରଣ (Non-Collinear Equation) :
ଅନେକ ସହ-ସମୀକରଣ ଯାହାକି ଏକଘାତୀ ନୁହେଁ, ସେମାନଙ୍କୁ ଆବଶ୍ୟକୀୟ ପରିବର୍ତ୍ତନ କରି ଏକଘାତୀ ରୂପକୁ ଅଣାଯାଇ ପାରିବ ଓ ଉପରେ ଆଲୋଚିତ ବୀଜଗାଣିତିକ ପ୍ରଣାଳୀର ଅବଲମ୍ବନରେ ସମାଧାନ କରିହେବ ।

→ କ୍ରାମରଙ୍କ ନିୟମ (Cramer’s Rule) :
ଦତ୍ତ ଚିତ୍ରଟିକୁ ବିଚାର କର : A = \(\left(\begin{array}{ll}
5 & 7 \\
2 & 1
\end{array}\right)\)

ଏହି ଚିତ୍ରରେ ଲେଖାଯାଇଥ‌ିବା ସଂଖ୍ୟାଗୁଡ଼ିକୁ ଦୁଇଗୋଟି ଧାଡ଼ି (row) ଓ ଦୁଇଗୋଟି ସ୍ତମ୍ଭ (column) ରେ ଲେଖାଯାଇଛି । ସମସ୍ତ ଧାଡ଼ି ଓ ସ୍ତମ୍ଭଗୁଡ଼ିକୁ ଦୁଇଟି ବନ୍ଧନୀ ମଧ୍ଯରେ ରଖାଯାଇଛି । ଏହାକୁ A ରୂପେ ନାମିତ କରାଯାଇଛି । ଏଠାରେ Aକୁ ଏକ 2 × 2 ମାଟ୍ରିକ୍‌ (Matrix) କୁହାଯାଏ । ଆମେ ମଧ୍ୟ 3 × 3, 4 × 4 ମାଟ୍ରିକ୍‌ ଲେଖୁରିବା । ଉଚ୍ଚତର ଗଣିତରେ ମାଟ୍ରିକ୍‌ସର ବ୍ୟବହାର ବହୁଳ ଭାବେ କରାଯାଏ । ଯେହେତୁ ଏଠାରେ ଧାଡ଼ି ସଂଖ୍ୟା ସହ ସ୍ତମ୍ଭ ସଂଖ୍ୟା ସମାନ, ତେଣୁ ଏହି ମାଟ୍ରିକ୍‌ଗୁଡ଼ିକୁ ବର୍ଗ ମାଟ୍ରିକ୍‌ (Square matrix) କୁହାଯାଏ । କେବଳ 2 × 2 ମାଟ୍ରିକ୍‌ସକୁ ଏଠାରେ ବିଚାର କରାଯାଉଛି । ପ୍ରତି ବର୍ଗ ମାଟ୍ରିକ୍‌ସ ସହ ଗୋଟିଏ ନିର୍ଦ୍ଦିଷ୍ଟ ସଂଖ୍ୟା ସଂପୃକ୍ତ ଓ ଏହାକୁ ବର୍ଗ ମାଟ୍ରିକ୍‌ସର ଡିଟରମିନାଣ୍ଟ (determinant) କୁହାଯାଏ । ଯଦି ମାଟ୍ରିକ୍‌ A = \(\left(\begin{array}{ll}
a & b \\
c & d
\end{array}\right)\) ହୁଏ,

ଉଦାହରଣ \(\frac{1}{x}+\frac{2}{y}\) = 5 (x ≠ 0, y ≠ 0) ଏକ ଅଣସରଳରେଖୀୟ ସମୀକରଣ ।

ଅର୍ଥାତ୍ a + 2b = 5 (ଯେଉଁଠାରେ \(\frac{1}{x}\) = a ଏବଂ \(\frac{1}{y}\) = b)
ତେବେ ଏହାର ଡିଟରମିନାଣ୍ଟ୍ | |A| = \(\left|\begin{array}{ll}
a & b \\
c & d
\end{array}\right|=a d-b c\) ।

ଉଦାହରଣ :
A = \(\left(\begin{array}{ll}
5 & 7 \\
2 & 1
\end{array}\right)\) ହେଲେ |A| = 5 × 1 – 7 × 2 = 5 – 14 = -9 ଅଟେ ।
ସେହିପରି,

∴ ଡିଟରମିନାଣ୍ଟ ମାଧ୍ୟମରେ ନିର୍ଦେୟ ସମାଧାନ :

x = \(\frac{Δ_x}{Δ}\), y = \(\frac{Δ_y}{Δ}\) ଯେଉଁଠାରେ Δ ≠ 0 କାରଣ ସମୀକରଣଦ୍ଵୟ ସଙ୍ଗତ ହେବା ଆବଶ୍ୟକ ।
ବଜ୍ରଗୁଣନ ପଦ୍ଧତିରେ ଲବ୍‌ଧ ସମାଧାନକୁ ଡିଟରମିନାଣ୍ଟ ମାଧ୍ୟମରେ ଲେଖିଲେ,

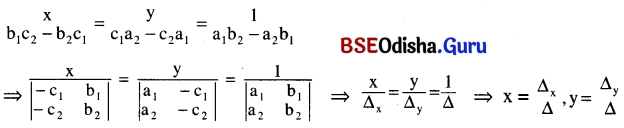
ଏହାକୁ ସୁପରିଚିତ Cramer’s ନିୟମ କୁହାଯାଏ । ବଜ୍ରଗୁଣନ ସୂତ୍ର ହିଁ Cramer’s Rule ର ଅନ୍ୟରୂପ ।

→ ପାଟିଗଣିତ ପ୍ରଶ୍ନର ସମାଧାନରେ ପ୍ରୟୋଗ :
ଏକ ଅଜ୍ଞାତ ରାଶି ବିଶିଷ୍ଟ ଏକଘାତୀ ସମୀକରଣ ପ୍ରୟୋଗ କରି ଅନେକ ପାଟିଗଣିତ ପ୍ରଶ୍ନମାନଙ୍କ ସମାଧାନ ସହଜରେ କରାଯାଏ । ସେହିପରି ଦୁଇ ଅଜ୍ଞାତ ରାଶିବିଶିଷ୍ଟ ଏକଘାତୀ ସହ ସମାଧାନରେ ପ୍ରୟୋଗରେ ଜଟିଲ ପାଟିଗଣିତ ପ୍ରଶ୍ନମାନଙ୍କ ସହଜ ସମାଧାନ ହୋଇପାରିବ ।