BSE Odisha 10th Class Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(d)

Odisha State Board BSE Odisha 10th Class Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(d) Textbook Exercise Questions and Answers.

BSE Odisha Class 10 Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(d)

Question 1.
ଗୋଟିଏ ସରଳ ପ୍ରିଜିମ୍ ର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ 2520 ବର୍ଗମିଟର । ଏହାର ତ୍ରିଭୁଜାକାର ଆଧାରର ବହୁମାନକର ଦେଶ୍ୟ 20 ମି., 21 ମି. ଓ 29 ମି. ହେଲେ, ଆୟତନ ମିଶ କର |
Solution:
ତ୍ରିଭୁଜାକାର ଭୂମିବିଶିଷ୍ଟ ପ୍ରିଜିମ୍‌ର ଭୂମିର ବାହୁତ୍ରୟର ଦୈର୍ଘ୍ୟ 20 ମି., 21 ମି. ଓ 29 ମି. ।
∵ 20² + 21² = 29² ⇒ ପ୍ରିଜିମ୍‌ର ଭୂମି ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜ ।
∴ ପ୍ରିଜିମ୍‌ର ଭୂମିର କ୍ଷେତ୍ରଫଳ = \(\frac { 1 }{ 2 }\) × 20 × 21 = 210 ବଗମି.
ମନେକର ପ୍ରିଜିମ୍ର ଉଚ୍ଚତା = h ମି.
ପ୍ରିଜିମ୍ର ସମଗ୍ରପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = ଭୂମିର ପରିସୀମା × ଉଚ୍ଚତା + 2 × ଭୂମିର କ୍ଷେତ୍ରଫଳ
= (20 + 21 + 29) × h + 2 × 210 = (70 h + 420) ବଗମି.
ପଣାକୁପାରେ, 70h + 420 = 2500
⇒ 70h = 2520 – 420 ⇒ 70h = 2100 ⇒ h = \(\frac { 2100 }{ 70 }\) = 30 ମି.
∴ ପ୍ରିଜିମୂର ଆୟତନ = ଭୂମିର କ୍ଷେତ୍ରଫଳ × ଉଚ୍ଚତା = 210 × 30 ଘନ ମି. = 6300 ଘନ ମି.

Question 2.
ଗୋଟିଏ ସରଳ ପ୍ରିଜିମୂର ଭୂମି, 8√2 ସେ.ମି. ଦୀର୍ଘ କଣ୍ଠ ବିଶିଷ୍ଟ ସମକୋଣୀ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜ । ଉଚ୍ଚତା 14 ସେ.ମି. ହେଲେ ଆୟତନ ନିର୍ଣ୍ଣୟ କର ।
Solution:
ସରଳ ପ୍ରିଜିମ୍‌ର ଆଧାର ଗୋଟିଏ ସମକୋଣୀ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜ ।
ଏହି ତ୍ରିଭୁଜର କର୍ପୂର ଦୈର୍ଘ୍ୟ = 8√2 ସେ.ମି., ପ୍ରିଜିମ୍‌ର ଉଚ୍ଚତା (h) = 14 ସେ.ମି.
ତେବେ ତ୍ରିଭୁଜର ସମାନ ବାହୁର ଦୈର୍ଘ୍ୟ = \(\frac{8 \sqrt{2}}{\sqrt{2}}\) = 8 ସେ.ମି.
ପ୍ରିଜିମୂର ଭୂମିର କ୍ଷେତ୍ରଫଳ = \(\frac { 1 }{ 2 }\) × 8 × 8 ସେ.ମି. = 32 ବ ସେ.ମି.
∴ ପ୍ରିଜିମ୍ର ଆୟତନ = ଭୂମିର କ୍ଷେତ୍ରଫଳ × ଉଚ୍ଚତା = (32 × 14) ଘନ ସେ.ମି. = 448 ଘନ ସେ.ମି.

Question 3.
ଗୋଟିଏ ସରଳ ପ୍ରିଜିମୂର ଆୟତନ 2520 ଘନ ମିଟର । ଏହାର ଆଧାର ଗୋଟିଏ ସମକୋଣୀ ତ୍ରିଭୁଜ ଯାହାର ସମକୋଣ ସଂଲଗ୍ନ ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ 7 ମି. ଓ 24 ମି. । ପ୍ରିଜିମ୍ବର ଉଚ୍ଚତା ଓ ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ ସ୍ଥିର କର ।
Solution:
ସରଳ ପ୍ରିଜିମ୍ବର ଆଧାର ଗୋଟିଏ ସମକୋଣୀ ତ୍ରିଭୁଜ । ଏହି ତ୍ରିଭୁଜର ସମକୋଣ ସଂଲଗ୍ନ ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ 7ମି. ଓ 24 ମି. |
କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = \(\sqrt{7^2+24^2}\) = \(\sqrt{49+576}\) = \(\sqrt{625}\) = 25 ମି.
∴ ପ୍ରିଜିମ୍‌ର ଭୂମିର କ୍ଷେତ୍ରଫଳ = \(\frac { 1 }{ 2 }\) × 7 × 24 = 84 ବ.ମି.
ପ୍ରିଲିମର ରଳତା = ପ୍ରିଲିମ୍ଭ ଆୟତନ / କୁମିତ ଯେତ୍ରଫଳ = \(\frac { 2520 }{ 84 }\) ମି. = 30 ମି.
∴ ପ୍ରିଜମ୍‌ର ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = ଭୂମିର ପରିସୀମା × ଉଚ୍ଚତା
= (7 +24 + 25) × 30 = 56 × 30 = 1680 ବ.ମି.

Question 4.
15 ସେ.ମି. ଉଚ୍ଚ ଗୋଟିଏ ସରଳ ପ୍ରିଜିମ୍‌ ଆଧାର ଗୋଟିଏ ସମକୋଣୀ ତ୍ରିଭୁଜ ଯାହାର କଣ୍ଠର ଦୈର୍ଘ୍ୟ 10 ସେ.ମି., ଆୟତନ 360 ଘନ ସେ.ମି. ହେଲେ ଆଧାରର ଅନ୍ୟ ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
Solution:
ପ୍ରିଜିମ୍‌ ଆଧାର ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜ । ମନେକର ଆଧାରର ଅନ୍ୟ ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ a ସେ.ମି. ଓ b ସେ.ମି. |
ତ୍ରିଭୁଜର କର୍ପୂର ଦୈର୍ଘ୍ୟ = 10 ସେ.ମି. ।
∴ a² + b² = 10² ⇒ a² + b² = 100
ପ୍ରିଜିମ୍‌ର ଭୂମିର କ୍ଷେତ୍ରଫଳ = \(\frac { 1 }{ 2 }\) ab ବ. ସେ.ମି.
∴ ପ୍ରିଜିମ୍‌ର ଭୂମିର କ୍ଷେତ୍ରଫଳ = ଆୟତନ / ଭଳତା = \(\frac { 360 }{ 15 }\) = 24 ବ. ସେ.ମି.
∴ \(\frac { 1 }{ 2 }\) ab = 24 ⇒ ab = 48
(a + b)² = a² + b² + 2ab ⇒ (a + b)² = 100 + 2 × 48 = 196
⇒ a + b = √196 ⇒ a + b = 14
ସେହିପରି (a – b)² = a² + b² – 2ab ⇒ (a−b)² = 100 – 2 × 48
⇒ (a – b)² ⇒ 4 a – b = 2
(i) ଓ (ii) କୁ ଯୋଗକଲେ, 2a = 16 ⇒ a = 8 ସେ.ମି.
∴b = 14 – 8 = 6 ସେ.ମି.
∴ ଆଧାରର ଅନ୍ୟ ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ 8 ସେ.ମି. ଓ 6 ସେ.ମି. ।

Question 5.
ଗୋଟିଏ ସରଳ ପ୍ରିଜିମ୍‌ର ପାର୍ଶ୍ଵତଳର କ୍ଷେତ୍ରଫଳ, ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳର \(\frac { 8 }{ 9 }\) କ୍ଷେତ୍ରଫଳ 96 ବର୍ଗମିଟର ଏବଂ ଆୟତନ 48 ଘନ ମିଟର ହେଲେ ଉଚ୍ଚତା ନିର୍ଣ୍ଣୟ କର ।
Solution:
ପ୍ରିଜିମ୍‌ର ପାର୍ଶ୍ଵତଳର କ୍ଷେତ୍ରଫଳ = 9 ବ.ମି.
∴ସମଗ୍ରପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 96 × \(\frac { 9 }{ 8 }\) = 108 ବ.ମି.
⇒ ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ + 2 × ଭୂମିର କ୍ଷେତ୍ରଫଳ = 108 ବ.ମି.
⇒ 96 + 2 × ଭୂମିର କ୍ଷେତ୍ରଫଳ = 108 ବ.ମି. ⇒ 2 × ଭୂମିର କ୍ଷେତ୍ରଫଳ = 108 – 96 = 12 ବ.ମି.
⇒ ଭୂମିର କ୍ଷେତ୍ରଫଳ = \(\frac { 12 }{ 2 }\) ବ.ମି. = 6 ବ.ମି. |
⇒ ପ୍ରିଜିମ୍‌ର ଆୟତନ = 48 ଘନ ମି.
∴ ପ୍ରିଜିମ୍‌ର ଉଚ୍ଚତା = ଆୟତନ / ଭୂମିର କ୍ଷେତ୍ରଫଳ = \(\frac { 48 }{ 6 }\) ମି. = 8 ମି.

Question 6.
ଗୋଟିଏ ସରଳ ପ୍ରିଜିମ୍‌ର ଆଧାର ପରିସୀମା 56 ମିଟର । ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ 1680 ବର୍ଗମିଟର ଏବଂ ଆୟତନ 2520 ଘନମିଟର ହେଲେ ଆଧାରର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
Solution:
ସରଳ ପ୍ରିଜିମ୍‌ର ଆଧାରର ପରିସୀମା = 56 ମି. । ପ୍ରିଜିମ୍‌ର ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 1680 ବ.ମି.
ଆଧାରର ପରିସୀମା × ଉଚ୍ଚତା = 1680 ବ.ମି.
⇒ ଉଚ୍ଚତା = \(\frac { 1680 }{ 56 }\) ମି. = 30 ମି.
ପ୍ରିଜିମ୍‌ର ଶଳତା = 30 ମି. | ପ୍ରିଜିମ୍‌ର ଆଧାରର = 2520ଘ.ମି.
⇒ ଆଧାରର କ୍ଷେତ୍ରଫଳ × ଉଚ୍ଚତା = 2520 ଘ.ମି.
⇒ ଆଧାରର କ୍ଷେତ୍ରଫଳ = \(\frac { 2520 }{ 30 }\) ବ.ମି. = 84 ବ.ମି.
∴ ପ୍ରିଜିମ୍‌ର ଆଧାରର କ୍ଷେତ୍ରଫଳ 84 ବର୍ଗମିଟର ।

Question 7.
ଗୋଟିଏ ସରଳ ପ୍ରିଜିମ୍‌ ଆୟତନ 84√3 ଘ. ସେ.ମି. । ଉଚ୍ଚତା 7 ସେ.ମି. ଏବଂ ଆଧାର ଏକ ସମବାହୁ ତ୍ରିଭୁଜ ହେଲେ ଆଧାରର ପ୍ରତ୍ୟେକ ବାହୁର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
Solution:
ପ୍ରିଜିମ୍‌ର ଉଚ୍ଚତା = 7 ସେ.ମି. ।
ପ୍ରିଜିମ୍ବର ଆୟତନ = 84√3 ଘ. ସେ.ମି.
ଆଧାରର କ୍ଷେତ୍ରଫଳ × ଉଚ୍ଚତା = 84√3 ଘ. ସେ.ମି.
⇒ ଆଧାରର କ୍ଷେତ୍ରଫଳ = \(\frac{84 \sqrt{3}}{7}\) = 12√3 ବ. ସେ.ମି.
ସରଳ ପ୍ରିଜିମ୍‌ର ଆଧାର ଏକ ସମବାହୁ ତ୍ରିଭୁଜ । ମନେକର ତ୍ରିଭୁଜର ବାହୁର ଦୈର୍ଘ୍ୟ a ସେ.ମି. ।
∴ ଆଧାରର କ୍ଷେତ୍ରଫଳ = \(\frac{\sqrt{3}}{4}\)a² ବ. ସେ.ମି. |
ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର, \(\frac{\sqrt{3}}{4}\)a² = 12√3 ⇒ a² = 12√3 × \(\frac{4}{\sqrt{3}}\) = 48 = a = √48 = 4√3 ସେ.ମି.
∴ ଆଧାରର ପ୍ରତ୍ୟେକ ବାହୁର ଦୈର୍ଘ୍ୟ 4√3 ସେ.ମି. ।

Question 8.
ଗୋଟିଏ ସରଳ ପ୍ରିଜିମ୍ବର ଉଚ୍ଚତା 336 ସେ.ମି. । ଏହାର ଭୂମିର ବାହୁମାନଙ୍କର ଦୈର୍ଘ୍ୟ 21 ସେ.ମି., 72 ସେ.ମି.,ଓ 75 ସେ.ମି. । 288 ସେ.ମି. ଉଚ୍ଚତା ଏବଂ 42√2 ସେ.ମି. ଦୀର୍ଘ କଣ୍ଠିଥିବା ସମକୋଣୀ ତ୍ରିଭୁଜାକାର ଭୂମି ବିଶିଷ୍ଟ ଅନ୍ୟ ଏକ ସରଳ ପ୍ରିଜିମ୍‌ ଘନଫଳ ଯଦି ଏହି ପ୍ରିଜିମ୍‌ର ଘନଫଳ ସହିତ ସମାନ ହୁଏ, ତେବେ ଭୂମିର ବାହୁମାନଙ୍କର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
Solution:
ପ୍ରଥମ ତ୍ରିଭୁଜାକାର ଭୂମିବିଶିଷ୍ଟ ପ୍ରିଜିମୂର ଭୂମିର ବାହୁତ୍ରୟର ଦୈର୍ଘ୍ୟ 21 ସେ.ମି., 72 ସେ.ମି. ଓ 75 ସେ.ମି. ।
ଏଠାରେ 21² + 72² = 75² ⇒ ପ୍ରିଜିମ୍‌ ଭୂମି ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜ ।
ପ୍ରିଜିମ୍‌ର ଭୂମିର କ୍ଷେତ୍ରଫଳ \(\frac{1}{2}\) = × 21× 72 = 756 ବ. ସେ.ମି. |
ପ୍ରଥମ ପ୍ରିଜିମ୍ବର ଆୟତନ = ଭୂମିର କ୍ଷେତ୍ରଫଳ × ଉଚ୍ଚତା = 756 × 336 = 254016 ଘ. ସେ.ମି.
ମନେକର ଦ୍ୱିତୀୟ ସମକୋଣୀ ତ୍ରିଭୁଜାକାର ଭୂମିର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ a ସେ.ମି. ଓ b ସେ.ମି. ।
ତ୍ରିକୁଲାର କାଣ୍ଡର ଦେଶ୍ୟ = 42√2 ସେ.ମି. a² + b² = (42√2)² ⇒ a² + b² = 3528
ପ୍ରିଜିମ୍‌ର ଭୂମିର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\)ab ବ.ସେ.ମି.
ପ୍ରଶ୍ନନୁସାରେ, ଦ୍ୱିତୀୟ ପ୍ରିଜିମ୍‌ ଆୟତନ = ପ୍ରଥମ ପ୍ରିଜିମୂର ଆୟତନ = 254016 ବ.ସେ.ମି. ଓ ଉଚ୍ଚତା = 288 ସେ.ମି.
କମିର ଯେତ୍ରଫଳ = ଆୟତନ / ଭଲଭା = \(\frac{254016}{288}\) = 882 ବ. ସେ.ମି. |
∴ \(\frac{1}{2}\)ab = 882 ⇒ ab = 1764
(a + b)² = a² + b² +2ab ⇒ (a + b)² = 3528 + 2 × 1764 = 3528 + 3528
⇒ (a+b)² = 7056 ⇒ a+ b = 84 …(i)
ସେହିପରି (a – b)² = a² + b² – 2ab ⇒ (a – b)² = 3528 – 2 × 1764
⇒ (a – b)² = 0 ⇒ a – b = 0 …(ii)
(i) ଓ (ii)ରୁ 2a = 84 ⇒ a = 42
∴ b = 84 – 42 = 42
∴ କମିର ଯେତ୍ରଫଳ ଦେଶ୍ୟ 42 ସେ.ମି. ଓ 42 ସେ.ମି. ।

Question 9.
8√3 ମିଟର ଉଚ୍ଚତା ବିଶିଷ୍ଟ ଗୋଟିଏ ସରଳ ପ୍ରିଜିମ୍ର ଭୂମି ଗୋଟିଏ ସମବାହୁ ତ୍ରିଭୁଜ । ଏହି ପ୍ରିଜିମୂର ଆୟତନ 864 ଘନମିଟର ହେଲେ ଏହାର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
Solution:
ପ୍ରିଜିମ୍‌ର ଭୂମି ଏକ ସମବାହୁ ତ୍ରିଭୁଜ ।
ମନେକର ତ୍ରିଭୁଜର ବାହୁର ଦୈର୍ଘ୍ୟ = a ମି. | ∴ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac{\sqrt{3}}{4}\)a² ଦି.ମି.
ପ୍ରିଜିମ୍‌ର ଉଚ୍ଚତା = 8√3 ମି., ଫିଲିମ୍ୟର ଆୟତନ = 864 ମି.ମି.
⇒ ଭୂମିର କ୍ଷେତ୍ରଫଳ × ଉଚ୍ଚତା = 864 ଘ.ମି.
⇒ ଭୂମିର କ୍ଷେତ୍ରଫଳ = \(\frac{864}{8 \sqrt{3}}\) ଦି.ମି. = 36√3 ଦି.ମି.
∴ \(\frac{\sqrt{3}}{4}\)a² = 36√3 ⇒ a² = 36 × 4 ⇒ a = 12 ମି.
ଭୂମିର ବାହୁର ଦୈର୍ଘ୍ୟ 12 ମି. ।
ପ୍ରିଜିମୂର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = ଭୂମିର ପରିସୀମା × ଉଚ୍ଚତା + 2 × ଭୂମିର କ୍ଷେତ୍ରଫଳ
∴ ପହ କ୍ଷେତ୍ରଫଳ = (12 + 12 + 12) × 8√3 + 2 × 36√3 = 288√3 + 72√3 = 360√3 ଜଗ ମିଟର |

Question 10.
4 ମିଟର ବ୍ୟାସ ଓ 9 ମିଟର ଗଭୀର କୂଅଟିଏ ଖୋଳାଯାଇ ସେଥୁରୁ ବାହାରିଥିବା ମାଟିକୁ 12 ମିଟର ବ୍ୟାସର ଏକ ସିଲିଣ୍ଡର ଆକୃତି ବିଶିଷ୍ଟ ସ୍ତୂପରେ ଗଦାକଲେ, ସ୍ତୂପଟିର ଉଚ୍ଚତା କେତେ ହେବ ?
Solution:
କୁଅଟିର ବ୍ୟାସ = 4 ମି. ⇒ ବ୍ୟାସାଦି = r = \(\frac { 4 }{ 2 }\) = 2 ମି.
ଓ ଗଭୀରତା (h) = 9 ମି.
∴ କୁଅରୁ ବାହାରିଥିବା ମାଟିର ଆମଦାନ = πr²h = (\(\frac { 22 }{ 7 }\) × (2)² × 9) = \(\frac { 22 }{ 7 }\) × 36 ଘ.ମି.
ସ୍ପପର ଦ୍ୟାପ = 12 ମି. ⇒ ବ୍ୟାସାଦି = \(\frac { 12 ମି. }{ 2 }\) = 6 ମି.
ମନେକର ସ୍ତୂପର ଉଚ୍ଚତା h ମି. । ∴ ସ୍ତୂପର ଆୟତନ = \(\frac { 22 }{ 7 }\) × (6)² × h ଘ.ମି.
ପୂଜାକୁ ପାରେ, \(\frac { 22 }{ 7 }\) × 36 × h = \(\frac { 22 }{ 7 }\) × 36 ⇒ h = 1 ମି.
∴ ସ୍ତୂପଟିର ଉଚ୍ଚତା 1 ମିଟର |

Question 11.
ଗୋଟିଏ ସିଲିଣ୍ଡର ଆକାରର ସ୍ତମ୍ଭ ତିଆରି କରିବାକୁ ପ୍ରତି 100 ଘନ ଡେ.ମି.କୁ 8 ଟଙ୍କା ହିସାବରେ 352 ଟଙ୍କା ଖର୍ଜ ହୁଏ । ସ୍ତମ୍ଭଟିର ଭୂମିର ବ୍ୟାସ 20 ଡେ.ମି. ହେଲେ ଏହାର ଉଚ୍ଚତା ହିସାବ କର । (π ≃ \(\frac { 22 }{ 7 }\))
Solution:
ପ୍ରତି 100 ଘନ ଡେ.ମି.କୁ 8 ଟଙ୍କା ହିସାବରେ 352 ଖର୍ଚ୍ଚ ହେବ = \(\frac { 100 }{ 8 }\) × 352 = 4400 ଘ.ଡେ.ମି.
∴ ସ୍ତମ୍ଭଟିର ଆୟତନ = 4400 ଘ.ଡେ.ମି.
ସ୍ତମ୍ଭଟିର ଭୂମିର ବ୍ୟାସ = 20 ଡେ.ମି. ⇒ ବ୍ୟାସାଦି = \(\frac { 20 }{ 2 }\) = 10 ଡେ.ମି.
ମନେକର ସ୍ତମ୍ଭଟିର ଉଚ୍ଚତା = h ଡେ.ମି.
ସ୍ତମ୍ଭଟିର ଆୟତନ = π × (10)² h ଘ.ଡେ.ମି. = π × 100h ଘ.ଡେ.ମି.
(∵ ସିଲିଣ୍ଡରାକୃତି ସ୍ତମ୍ଭର ଆକୃତି = ଭୂମିର କ୍ଷେତ୍ରଫଳ × ଉଚ୍ଚତା)
ପୂଜାକୁପାରେ, л × 100h = 4400 ⇒ h = \(\frac { 4400 }{ 100 }\) × \(\frac { 7 }{ 22 }\) = 14 ଡେ.ମି.
∴ ସ୍ତମ୍ଭଟିର ଉଚ୍ଚତା 14 ଡେ.ମି. ।

Question 12.
28 ମିଟର ଉଚ୍ଚ ଗୋଟିଏ ସିଲିଣ୍ଡରର ଆୟତନ 5\(\frac { 1 }{ 2 }\) ମିଟର ଦୀର୍ଘ ବାହୁ ବିଶିଷ୍ଟ ଗୋଟିଏ ସଙ୍ଗେ ସମାନ । ସିଲିଣ୍ଡରର ଭୂମିର ବ୍ୟାସ ନିର୍ଣ୍ଣୟ କର । (π ≃ \(\frac { 22 }{ 7 }\))
Solution:
ଗମଶନାର ବାଦୁଇ ଦେଶ୍ୟ = 5\(\frac { 1 }{ 2 }\) ମି. = \(\frac { 11 }{ 2 }\) ମି. |
ସମଘନର ଆୟତନ = (\(\frac { 11 }{ 2 }\))³ ଘ.ମି.
ମନେକର ସିଲିଣ୍ଡରର ଭୂମିର ବ୍ୟାସାର୍ଦ୍ଧ = r ମି., ସିଲିଣ୍ଡରର ଉଚ୍ଚତା = 28 ମି.
ମିଲିଣ୍ଡରର ଆୟତନ = πr²h = \(\frac { 22 }{ 7 }\) × r² × 28 ଘ.ମି. = 88r² ଘ.ମି.
ପୂଜାକୁପାରେ, 88r² = (\(\frac { 11 }{ 2 }\))³ ⇒ r² = \(\frac{11 \times 11 \times 11}{8}\)

Question 13.
ଗୋଟିଏ ସିଲିଣ୍ଡରର ଘନଫଳ 9504 ଘନ ସେ.ମି. । ବଜ୍ରପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ 1584 ବ.ସେ.ମି. । ଏହାର ଉଚ୍ଚତା ନିର୍ଣ୍ଣୟ କର । (π ≃ \(\frac { 22 }{ 7 }\))
Solution:
ମନେକର ସିଲିଣ୍ଡରର ଭୂମିର ବ୍ୟାସାର୍ଦ୍ଧ = r ସେ.ମି. ଓ ଉଚ୍ଚତା = h ସେ.ମି.
∴ ସିଲିଣ୍ଡରର ଆପଣନ = πr²h = 9504 ଘନ ସେ.ମି.
∴ ସିଲିଣ୍ଡରର ବଜ୍ରପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 2πrh = 1584 ବ.ସେ.ମି.
∴ \(\frac{\pi \mathrm{r}^2 \mathrm{~h}}{2 \pi \mathrm{r} h}\) = \(\frac { 9504 }{ 1584 }\) ⇒ \(\frac { r }{ 2 }\) = 6 ⇒ r = 12 ଡେ.ମି.
∴ 2πrh = 1584
⇒ 2 × \(\frac { 22 }{ 7 }\) × 12 × h = 1584 ⇒ h = \(\frac{1584 \times 7}{44 \times 12}\) = 21 ସେ.ମି.
∴ ସିଲିଣ୍ଡରର ଉଚ୍ଚତା 21 ସେ.ମି. ।

Question 14.
ଗୋଟିଏ ସିଲିଣ୍ଡରର ଉଚ୍ଚତା ଭୂମିର ବ୍ୟାସର ଦୁଇଗୁଣ । ଏହାର ଘନଫଳ 539 ଘ.ଡେ.ମି. ହେଲେ ସମଗ୍ର ତ୍ପକତଲଭ ଯେତ୍ତପଳ କେତେ ?
Solution:
ମନେକର ସିଲିଣ୍ଡରର ବ୍ୟାସ = x ଡେ.ମି., ତେବେ ଉଚ୍ଚତା (h) = 2x ଡେ.ମି.
⇒ ବ୍ୟାସାର୍ଦ୍ଧ (r) = \(\frac { x }{ 2 }\) ଡେ.ମି.
ସିଲିଣ୍ଡରର ଆପଣନ = πr²h = \(\frac { 22 }{ 7 }\) × (\(\frac { x }{ 2 }\))² × 2x = \(\frac { 22 }{ 7 }\) × \(\frac{x^2}{4}\) × 2x = \(\frac{22 x^3}{14}\) ଘ. ସେ.ମି.
ପୂଜାକୁପାରେ, \(\frac{22 x^3}{14}\) = 539 ⇒ x³ = 539 × \(\frac { 14 }{ 22 }\) = 343 ⇒ x = \(\sqrt[3]{343}\) = 7 ସେ.ମି.
∴ ବ୍ୟାସାର୍ଦ୍ଧ = \(\frac { x }{ 2 }\) = \(\frac { 7 }{ 2 }\) ସେ.ମି. ଉଚ୍ଚତା = 2x = 2 x 7 = 14 ସେ.ମି.
ସିଲିଣ୍ଡରର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 2πr (h + r)
∴ ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 2 × \(\frac { 22 }{ 7 }\) × \(\frac { 7 }{ 2 }\) (14 + \(\frac { 7 }{ 2 }\)) = 22 (\(\frac { 28 + 7 }{ 2 }\)) = 11 × 35 = 385 ଡେ.ମି.

Question 15.
ଗୋଟିଏ ନିଦା ସମବର୍ଭୁଳର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ 701\(\frac { 1 }{ 4 }\) ବ.ସେ.ମି. ଓ ବଜ୍ରପୃଷ୍ଠତଳ 528 ବ. ସେ.ମି.
ହେଲେ ଆୟତନ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ : ମନେକର ନିଦା ସମବର୍ଭୁଳର ଭୂମିର ବ୍ୟାସାର୍ଦ୍ଧ = 1 ସେ.ମି. ଓ ଉଚ୍ଚତା = h ସେ.ମି. |
∴ ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 2πr (h + r) ବ.ସେ.ମି.
ଓ ବକ୍ରପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 2πrh ବ.ସେ.ମି. = 528 ବ. ସେ.ମି.
ପୂଜାକୁପାରେ, 2πr (h + r) = 701\(\frac { 1 }{ 4 }\) ବ. ସେ.ମି. ବ| \(\frac { 2805 }{ 4 }\) ବ. ସେ.ମି. |
⇒ 2πrh + 2πr² = \(\frac { 2805 }{ 4 }\) ⇒ 2πr² = \(\frac { 2805 }{ 4 }\) – 528 = \(\frac{2805-2112}{4}\) = \(\frac { 693 }{ 4 }\)
⇒ 2 × \(\frac { 22 }{ 7 }\) × r² = \(\frac { 693 }{ 4 }\) ⇒ r² = \(\frac { 693 }{ 4 }\) × \(\frac{7}{22 \times 2}\) = \(\frac { 441 }{ 16 }\) ⇒ r = \(\sqrt{\frac{441}{16}}\) = \(\frac { 21 }{ 4 }\)
କିନ୍ତୁ ଦଉ 2πrh = 528 ⇒ 2 × \(\frac { 22 }{ 7 }\) × \(\frac { 21 }{ 4 }\) × h = 528 ⇒ h = \(\frac{528 \times 7 \times 4}{2 \times 22 \times 21}\) = 16
⇒ h = 16 ସେ.ମି.
ସମୟକୂଳର ଆୟତନ = πr²h = \(\frac { 22 }{ 7 }\) × (\(\frac { 21 }{ 4 }\))² × 16 = 1386 ଘ. ସେ.ମି.
∴ ସମୟକୂଳର ଆୟତନ 1386 ଘ. ସେ.ମି. |

Question 16.
ଗୋଟିଏ ସରଳ ବୃତ୍ତଭୂମିକ ସିଲିଣ୍ଡରର ଉଚ୍ଚତା ଓ ବ୍ୟାସର ଅନୁପାତ 3 : 2। ଏହାର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ 1232 ବ.ସେ.ମି. ହେଲେ ଏହାର ଘନଫଳ ନିଶ୍ଚୟ କର । (π ≃ \(\frac { 22 }{ 7 }\))
Solution:
ମନେକର ପଲିପ୍ରହର କଳତା = 3x ସେ.ମି. ଓ ବ୍ୟାସ = 2x ସେ.ମି.
⇒ ସିଲିଣ୍ଡରର ବ୍ୟାସାର୍ଦ୍ଧ = \(\frac { 2x }{ 2 }\) = x ସେ.ମି.
∴ ସିଲିଣ୍ଡରର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 2πr (h + r)
= 2 × \(\frac { 22 }{ 7 }\) × x (3x + x) = \(\frac { 44 }{ 7 }\) × 4x² ବ. ସେ.ମି.
ପ୍ରଶାନୁସାରେ, \(\frac { 44 }{ 7 }\) × 4x² = 1232
⇒ x² = 1232 × \(\frac { 7 }{ 44 }\) × \(\frac { 1 }{ 4 }\) = 49 ⇒ x = √49 = 7 ସେ.ମି.
⇒ ସିଲିଣ୍ଡରର କଳତା = 3x = 3 × 7 = 21 ସେ.ମି. ଓ ବୃତ୍ତଭୂମିକ = 7 ସେ.ମି.
∴ ସିଲିଣ୍ଡରର ଘନଫଳ = πr²h = \(\frac { 22 }{ 7 }\) × 7 × 7 × 21 = 3234 ସେ.ମି.

Question 17.
ଉଭୟ ପ୍ରାନ୍ତ ବନ୍ଦ ହୋଇଥିବା ଗୋଟିଏ ଫମ୍ପା ସିଲିଣ୍ଡରରେ ବ୍ୟବହୃତ ଧାତୁର ଘନଫଳ 4928 ଘ.ସେ.ମି. ଏବଂ ଏହାର ପୃଷ୍ଠତଳଦ୍ୱୟର କ୍ଷେତ୍ରଫଳର ଅନ୍ତର 352 ବ.ସେ.ମି. । ସିଲିଣ୍ଡରର ଉଚ୍ଚତା 28 ସେ.ମି. ହେଲେ, ଏହାର ଭିତର ଓ ବାହାର ବ୍ୟାସାର୍ଦ୍ଧ କେତେ ? (π ≃ \(\frac { 22 }{ 7 }\))
Solution:
ମନେକର ସିଲିଣ୍ଡରର ବହିଃ ଏବଂ ଅନ୍ତଃବ୍ୟାସାର୍ଦ୍ଧ ଦ୍ବୟ ଯଥାକ୍ରମେ R ସେ.ମି. ଏବଂ r ସେ.ମି. ।
ପ୍ରଶ୍ନନୁସାରେ, ଧାତୁର ଘନଫଳ = 4928 .60..
⇒ лR²h – лr²h = 4928 ⇒ лh (R² – r²) = 4928
⇒ \(\frac { 22 }{ 7 }\) × 28 (R² – r²) = 4928
⇒ R² – r² = 56 … (i)

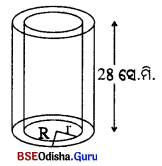
ପୁନଶ୍ଚ, ପାର୍ଶ୍ଵପୃଷ୍ଠତଳଦ୍ୱୟର କ୍ଷେତ୍ରଫଳର ଅନ୍ତର 352 ବ.ସେ.ମି. ।
⇒ 2лRh – 2лгh = 352 ⇒ 2лh (R − r) = 352
⇒ 2 × \(\frac { 22 }{ 7 }\) × 28 (R – r) = 352 ⇒ R – r = \(\frac{352 \times 7}{2 \times 22 \times 28}\) = 2
⇒ R – r = 2 …(ii)
(i) ରୁ ପାଇବା (R + r)(R – r) = 56 ⇒ (R + r) × 2 = 56
⇒ R – r = 28 …(iii)
(i) ଓ (iii) ରୁ ପାଇବା 2R = 30 ⇒ R = 15 ସେ.ମି.
ଏବଂ r = 13 ସେ.ମି.
∴ ଫମ୍ପା ସିଲିଣ୍ଡରର ଭିତର ବ୍ୟାସାର୍ଦ୍ଧ ।3 ସେ.ମି. ଓ ବାହାର ବ୍ୟାସାର୍ଦ୍ଧ 15 ସେ.ମି. |