BSE Odisha 8th Class Maths Solutions Algebra Chapter 5 ସୂଚକ ତତ୍ତ୍ଵ Ex 5(a)

Odisha State Board BSE Odisha 8th Class Maths Solutions Algebra Chapter 5 ସୂଚକ ତତ୍ତ୍ଵ Ex 5(a) Textbook Exercise Questions and Answers.

BSE Odisha Class 8 Maths Solutions Algebra Chapter 5 ସୂଚକ ତତ୍ତ୍ଵ Ex 5(a)

Question 1.
ନିମ୍ନ ରାଶିଗୁଡ଼ିକୁ xⁿ (ଘାତରାଶି) ରୂପେ ପ୍ରକାଶ କର ।
(i) 2 × 2 × 2 × 2
(ii) (-2) × (-2) × (-2) × (-2) × (-2)
(iii) \(\left(\frac{3}{4}\right) \times\left(\frac{3}{4}\right) \times\left(\frac{3}{4}\right)\)
(iv) \(\left(-\frac{1}{7}\right)\left(-\frac{1}{7}\right)\left(-\frac{1}{7}\right)\left(-\frac{1}{7}\right)\)
(v) \(\frac{5}{3} \times \frac{5}{3} \times \frac{5}{3}\)
(vi) y × y × y × y × y
(vii) (-p) (-p) (-p)
(viii) (a – b)(a – b)(a – b)(a – b)
(ix) (a + b)(a + b)(a + b)
(x) \((\frac{a}{b})(\frac{a}{b})(\frac{a}{b})(\frac{a}{b})(\frac{a}{b})\)
ସମାଧାନ :
(i) 2⁴
(ii) (-2)⁵
(iii) \(\left(\frac{3}{4}\right)^4\)
(iv) \(\left(-\frac{1}{7}\right)^4\)
(v) \((\frac{5}{3})^4\)
(vi) y⁵
(vii) (-p)^-3
(viii) (a – b)⁴
(ix) (a + b)³
(x) \((\frac{a}{b})^5\)

Question 2.
ନିମ୍ନ ଘାତରାଶିମାଈଁଙ୍କର ଆଧାର ଓ ଘାତାଙ୍କ ଦର୍ଶାଇ ମାନ ନିର୍ଣ୍ଣୟ କର ।
(i) (1)¹⁵
(ii) (-1)¹¹
(iii) (-1)¹⁸
(iv) (9)⁵
(v) (-2)⁵
(vi) \(\left(\frac{1}{2}\right)^6\)
(vii) \(\left(\frac{2}{3}\right)^5\)
(viii) (5 × 2)⁴
(ix) (10)⁷
(x) (-10)⁵
ସମାଧାନ :
(i) (1)¹⁵ ରେ ଆଧାର 1 ଓ ଘାତାଙ୍କ 15 ଅଟେ ।
(1)¹⁵ ର ମାନ = 1 × 1 × 1 × 1 × ….× 1 (15 ଥର) = 1 ।

(ii) (-1)¹¹ ରେ ଆଧାର -1 ଓ ଘାତାଙ୍କ 11 ।
(-1)¹⁵ ର ମାନ = -1
[∵ (-1)^m = -1, ଯେଉଁଠାରେ m ଏକ ଅଯୁଗ୍ମ ସଂଖ୍ୟା]

(iii) (-1)¹⁸ ରେ ଆଧାର -1 ଓ ଘାତାଙ୍କ 18 ।
(-1)¹⁸ ର ମାନ = 1
[∵ (-1)^m = 1, ଯେଉଁଠାରେ m ଏକ ଯୁଗ୍ମ ସଂଖ୍ୟା]

(iv) (9)⁵ ରେ ଆଧାର 9 ଓ ଘାତାଙ୍କ 5 ।
(9)⁵ = 9 × 9 × 9 × 9 × 9 = 59049
(9)⁵ ର ମାନ = 59049

(v) (-2)⁵ ରେ ଆଧାର -2 ଓ ଘାତାଙ୍କ 5 ।
(-2)⁵ = (-2) × (-2) × (-2) × (-2) × (-2) = -32
(-2)⁵ ର ମାନ = – 32

(vi) \(\left(\frac{1}{2}\right)^6\) ରେ ଆଧାର \(\frac{1}{2}\) ଓ ଘାତାଙ୍କ 6 ।
\(\left(\frac{1}{2}\right)^6=\left(\frac{1}{2}\right)\left(\frac{1}{2}\right)\left(\frac{1}{2}\right)\left(\frac{1}{2}\right)\left(\frac{1}{2}\right)\left(\frac{1}{2}\right)=\frac{1}{64}\)
\(\left(\frac{1}{2}\right)^6\) ରେ ମାନ = \(\frac{1}{64}\)

(vii) \(\left(\frac{2}{3}\right)^5\) ରେ ଆଧାର \(\frac{2}{3}\) ଓ ଘାତାଙ୍କ 5 ।
\(\left(\frac{1}{2}\right)^5=\left(\frac{2}{3}\right)\left(\frac{2}{3}\right)\left(\frac{2}{3}\right)\left(\frac{2}{3}\right)\left(\frac{2}{3}\right)=\frac{32}{243}\)
∴ \(\left(\frac{2}{3}\right)^5\) ରେ ମାନ = \(\frac{32}{243}\)

(viii) (5 × 2)⁴ = (10)⁴ = 10 × 10 × 10 × 10 = 10000
(5 × 2)⁴ ରେ ଆଧାର 10 ଓ ଘାତାଙ୍କ 4 । ∴ ମାନ = 10000

(ix) (10)⁷ ରେ ଆଧାର 10 ଓ ଘାତାଙ୍କ 7 ।
(10)⁴ = 10 × 10 × 10 × 10 × 10 × 10 × 10 = 10000000
(10)⁷ ର ମାନ = 10000000

(x) (-10)⁵ ରେ ଆଧାର -10 ଓ ଘାତାଙ୍କ 5 ।
(-10)⁵ = (-10)(-10)(-10)(-10)(-10) = -100000
(-10)⁵ ର ମାନ = -100000

Question 3.
ନିମ୍ନ ସାରଣୀରେ ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

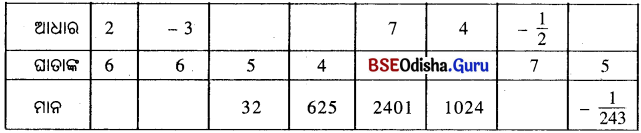
ସମାଧାନ :

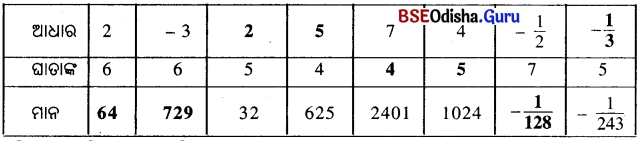
Question 4.
ନିମ୍ନ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଦିଅ ।
(i) 10 ର ଚତୁର୍ଥ ଘାତ କେତେ ?
(ii) 5 ର କେଉଁ ଘାତ 625 ?
(iii) \(\frac{1}{8},\left(\frac{1}{2}\right)\)ର କେଉଁ ଘାତ ?
(iv) କେଉଁ ଆଧାରର ତୃତୀୟ ଘାତ \(\frac{-27}{8}\)
ସମାଧାନ :
(i) 10 ର ଚତୁର୍ଥ ଘାତ = (10)⁴ = 10 × 10 × 10 × 10 = 10000
(ii) 625 = 5 × 5 × 5 × 5 = (5)⁴ ∴ 5 ର ଚତୁର୍ଥ ଘାତ 625 ।
(iii) \(\frac{1}{8}=\frac{1}{2} \times \frac{1}{2} \times \frac{1}{2}=\left(\frac{1}{2}\right)^3\) ∴ \(\frac{1}{8},\left(\frac{1}{2}\right)\) ର ତୃତୀୟ ଘାତ ।
(iv) \(\frac{-27}{8}=\left(\frac{-3}{2}\right) \times\left(\frac{-3}{2}\right) \times\left(\frac{-3}{2}\right)=\left(\frac{-3}{2}\right)^3\)
ବିକଳ୍ପ ପ୍ରଣାଳୀ : \(-\frac{27}{8}=\frac{(-3)^3}{2^3}=\left(\frac{-3}{2}\right)^3\)

Question 5.
ନିମ୍ନ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଦିଅ ।
(i) \(\frac{2}{3}\) ଆଧାରର ଷଷ୍ଠ ଘାତ, \(\frac{4}{9}\) ଆଧାରର କେଉଁ ଘାତ ସହ ସମାନ ?
(ii) 5 ଆଧାରର ଚତୁର୍ଥ ଘାତ, କେଉଁ ଆଧାରର ଦ୍ବିତୀୟ ଘାତ ସହ ସମାନ ?
(iii) 256 ଯେଉଁ ଆଧାରର ଚତୁର୍ଥ ଘାତ, ତାହାର ତୃତୀୟ ଘାତ କେତେ ?
ସମାଧାନ :
(i) \(\frac{2}{3}\) ଆଧାରର ଷଷ୍ଠ ଘାତ = \(\left(\frac{2}{3}\right)^6=\frac{2}{3} \times \frac{2}{3} \times \frac{2}{3} \times \frac{2}{3} \times \frac{2}{3} \times \frac{2}{3}\)
= \(\left(\frac{2}{3} \times \frac{2}{3}\right) \times\left(\frac{2}{3} \times \frac{2}{3}\right) \times\left(\frac{2}{3} \times \frac{2}{3}\right)=\frac{4}{9} \times \frac{4}{9} \times \frac{4}{9}=\left(\frac{4}{9}\right)^3\)
∴ \(\frac{2}{3}\) ଆଧାରର ଷଷ୍ଠ ଘାତ, \(\frac{4}{9}\) ଆଧାରର ତୃତୀୟ ଘାତ ସହ ସମାନ ।

(ii) 5 ଆଧାରର ଚତୁର୍ଥ ଘାତ = (5)⁴
= 5 × 5 × 5 × 5 = (5 × 5) × (5 × 5) = 25 × 25 = (25)²
∴ 5 ଆଧାରର ଚତୁର୍ଥ ଘାତ, 25 ଆଧାରର ତୃତୀୟ ଘାତ ସହ ସମାନ ।

(iii) 256 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
= (2 × 2) × (2 × 2) × (2 × 2) × (2 × 2) = 4 × 4 × 4 × 4 = (4)⁴
∴ 256, 4 ର ଚତୁର୍ଥ ଘାତ ।
∴ 4 ର ତୃତୀୟ ଘାତ = (4)³ = 4 × 4 × 4