BSE Odisha 8th Class Maths Solutions Algebra Chapter 9 ଚଳନ Ex 9(b)

Odisha State Board BSE Odisha 8th Class Maths Solutions Algebra Chapter 9 ଚଳନ Ex 9(b) Textbook Exercise Questions and Answers.

BSE Odisha Class 8 Maths Solutions Algebra Chapter 9 ଚଳନ Ex 9(b)

Question 1.
ନିମ୍ନ ଚଳରାଶିମାନଙ୍କ ମଧ୍ୟରେ କେଉଁଟି ସଳଖ ଚଳନ ଓ କେଉଁଟି ପ୍ରତିଲୋମୀ ଚଳନ ସମ୍ବନ୍ଧୀୟ ?
(i) କମଳା ସଂଖ୍ୟା x ଓ ତାହାର ମୂଲ୍ୟ y ଟଙ୍କା ।
(ii) ପାରିଶ୍ରମିକ x ଟଙ୍କା ଓ ଶ୍ରମ ସମୟ y ଦିନ ।
(iii) ନିର୍ଦ୍ଦିଷ୍ଟ ଦୂରତା ଅତିକ୍ରମ କରିବା ସମୟ x ଘଣ୍ଟା ଓ ବେଗ y କି.ମି. ପ୍ରତି ଘଣ୍ଟା ।
(iv) ନିର୍ଦ୍ଦିଷ୍ଟ କାମ ସମ୍ପନ୍ନ କରୁଥିବା ଶ୍ରମିକ ସଂଖ୍ୟା x ଓ ଶ୍ରମ ସମୟ y ଘଣ୍ଟା ।
(v) ସମାନ କ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ଆୟତାକାରକ୍ଷେତ୍ରର ଦୈର୍ଘ୍ୟ x ମି. ଓ ପ୍ରସ୍ଥ Y ମି. ।
(vi) ଗୋଟିଏ ଘର ରଙ୍ଗ କରିବାପାଇଁ ଶ୍ରମିକ ସଂଖ୍ୟା
(vii) ଗୋଟିଏ ମହମବତି ଦୈନିକ x ଘଣ୍ଟା ଜଳିଲେ y ଦିନ ଯାଏ ।
Solution:
(i), (ii) ସଳଖ ଚଳନ ।
(iii), (iv), (v), (vi), (vii) – ପ୍ରତିଲୋମୀ ଚଳନ |

Question 2.
ଗୋଟିଏ ନିର୍ଦ୍ଦିଷ୍ଟ କାର୍ଯ୍ୟ ସମାପନ ପାଇଁ ନିମ୍ନ ସାରଣୀର ଶୂନ୍ୟସ୍ଥାନଗୁଡ଼ିକ ପୂରଣ କର ।

Solution:

ସୂଚନା :
ଲଶ୍ୟକର, ଚଳନର ଧଦ୍ବାଜ [K = x × y = 20 × 6 = 120]
ତେଣୁ ତୃତୀୟ ଧାଡ଼ିର ସମସ୍ତ ଶୂନ୍ୟସ୍ଥାନ 120 ଦ୍ୱାରା ପୂରଣ ହେବ । x ଓ y ଚଳରାଶିଦ୍ଵୟ ମଧ୍ୟରୁ ଗୋଟିଏ ଦ୍ଵାରା 120 କୁ ଭାଗକଲେ, ଅନ୍ୟଟି ନିର୍ଣ୍ଣୟ କରିହେବ ।

Question 3.
ଦତ୍ତ ସାରଣୀମାନଙ୍କରୁ କେଉଁଗୁଡ଼ିକ ପ୍ରତିଲୋମୀ ଚଳନର ଅନ୍ତର୍ଗତ ?

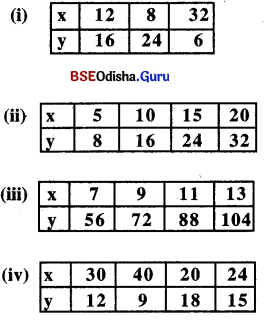
Solution:
(i) ପ୍ରତିଲୋମୀ ଚଳନ
(ii) ସଳଖ ଚଳନ
(iii) ସଳଖ ଚଳନ
(iv) ପ୍ରତିଲୋମୀ ଚଳନ

Question 4.
ଗୋଟିଏ ଶ୍ରେଣୀଗୃହରେ 30 ଜଣ ଛାତ୍ର ବସିଲେ ଜଣପିଛା 4 ବର୍ଗମିଟର ସ୍ଥାନ ମିଳେ । ଯଦି ସେହି ଶ୍ରେଣୀରେ ଆଉ 15 ଜଣ ଛାତ୍ର ନାମ ଲେଖାଇଥା’ନ୍ତି; ତେବେ ଜଣପିଛା କେତେ ବର୍ଗମିଟର ସ୍ଥାନ କମିଯିବ ?
Solution:
ଦତ୍ତ ତଥ୍ୟକୁ ନିମ୍ନ ସାରଣୀରେ ପ୍ରକାଶ କଲେ

ଏଠାରେ ଛାତ୍ର ସଂଖ୍ୟା ଏବଂ ପ୍ରତ୍ୟେକଙ୍କ ପାଇଁ ଆବଶ୍ୟକ ବସିବା ସ୍ଥାନ, ପ୍ରତିଲୋମୀ ଚଳନର ଅନ୍ତର୍ଭୁକ୍ତ ।
∴ ପ୍ରତିଲୋମୀ ଚଳନର ସୂତ୍ରାନୁଯାୟୀ x₁ y₁ = x₂y₂
⇒ 30 × 4 = 45 × y₂ ⇒ y₂ = \(\frac { 120 }{ 45 }\) = \(\frac { 8 }{ 3 }\) ବର୍ଗମିଟର
କମିଯାଇଥିବା ସ୍ଥାନର ପରିମାଣ = 4 – \(\frac { 8 }{ 3 }\) = \(\frac { 12 – 8 }{ 3 }\) ବ.ମି. = \(\frac { 4 }{ 3 }\) ବ.ମି. = 1\(\frac { 1 }{ 3 }\) ବର୍ଗମିଟର
∴ ଜଣପିଛା 1\(\frac { 1 }{ 3 }\) ବର୍ଗମିଟର ସ୍ଥାନ କମିଯିବ ।

Question 5.
ଗୋଟିଏ ସ୍କୁଲ୍‌ଘର ରଙ୍ଗ କରିବାପାଇଁ 6 ଜଣ ଶ୍ରମିକ 15 ଦିନ ନିଅନ୍ତି; ତେବେ କାମଟି 5 ଦିନରେ ଶେଷ କରିବାପାଇଁ କେତେ ଅଧ୍ଵ ଶ୍ରମିକ ଆବଶ୍ୟକ ?
Solution:
ଦତ୍ତ ତଥ୍ୟକୁ ନିମ୍ନ ସାରଣୀରେ ପ୍ରକାଶକଲେ,

ଶ୍ରମିକ ସଂଖ୍ୟା ଓ ଶେଷ କରିବା ଦିନ ସଂଖ୍ୟା ପ୍ରତିଲୋମୀ ଚଳନର ଅନ୍ତର୍ଭୁକ୍ତ ।
∴ ପ୍ରତିଲୋମୀ ଚଳନର ସୂତ୍ରାନୁଯାୟୀ x₁ y₁ = x₂y₂
⇒ 6 × 15 = x₂ × 5 ⇒ 5x₂ = 90 ⇒ x₂ = \(\frac { 90 }{ 5 }\) = 18
କାମଟିକୁ ଶେଷ କରିବାପାଇଁ 18 ଜଣ ଶ୍ରମିକ ଆବଶ୍ୟକ । କିନ୍ତୁ 6 ଜଣ ଶ୍ରମିକ ଆଗରୁ ଅଛନ୍ତି ।
ତେଣୁ ଆବଶ୍ୟକ ଅଧ‌ିକ ଶ୍ରମିକ ସଂଖ୍ୟା = 18 – 6 = 12 ଜଣ ।
କାମଟି 5 ଦିନରେ ଶେଷ କରିବାପାଇଁ 12 ଜଣ ଅଧ୍ବକ ଶ୍ରମିକ ଆବଶ୍ୟକ ।

Question 6.
ଅଂଶୁମାନର ଜନ୍ମଦିନରେ ତାହାର 6 ଜଣ ସାଙ୍ଗ ଆସିଥିଲେ । ପ୍ରତି ସାଙ୍ଗ ପାଇଁ 10ଟି ଲେଖାଏଁ ଚକୋଲେଟ୍‌ର ବ୍ୟବସ୍ଥା ଥିଲା । କିନ୍ତୁ ତା’ର ଆଉ 4 ଜଣ ଅଧ୍ଵ ସାଙ୍ଗ ଆସି ପହଞ୍ଚିଲେ; ତେବେ ପ୍ରତ୍ୟେକ କେତୋଟି କରି ଚକୋଲେଟ୍ ପାଇବେ ?
Solution:
ଦତ୍ତ ତଥ୍ୟକୁ ନିମ୍ନ ସାରଣୀରେ ପ୍ରକାଶକଲେ,

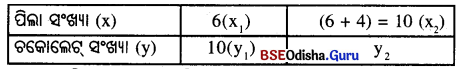
ଏଠାରେ ପିଲା ସଂଖ୍ୟା ଓ ଆସିଥିବା ଚକୋଲେଟ୍ ସଂଖ୍ୟା ପ୍ରତିଲୋମୀ ଚଳନର ଅନ୍ତର୍ଭୁକ୍ତ ।
∴ ପ୍ରତିଲୋମୀ ଚଳନର ସୂତ୍ରାନୁଯାୟୀ x₁ y₁ = x₂y₂
⇒ 6 × 10 = 10y₂ ⇒ y₂ = \(\frac{10 \times 6}{10}\) = 6
∴ ପ୍ରତ୍ୟେକ ଟି କରି ଚକୋଲେଟ୍ ପାଇବେ ।

Question 7.
ଗୋଟିଏ କାର୍ଯ୍ୟର ଅର୍ଦ୍ଧେକକୁ 12 ଜଣ ଶ୍ରମିକ 15 ଦିନରେ ଶେଷ କରନ୍ତି । ସେହି କାମଟିକୁ 30 ଜଣ ଶ୍ରମିକ କେତେ ସମୟରେ ଶେଷକରିବେ ?
Solution:
ଗୋଟିଏ କାର୍ଯ୍ୟର ଅର୍ଦ୍ଧେକକୁ 12 ଜଣ ଶ୍ରମିକ 15 ଦିନ ନିଅନ୍ତି ।
ତେବେ ସମ୍ପୂର୍ଣ୍ଣ କାର୍ଯ୍ୟକୁ 12 ଜଣ ଶ୍ରମିକ 15 × 2 = 30 ଦିନରେ ଶେଷକରିବେ ।
ଦତ୍ତ ତଥ୍ୟକୁ ନିମ୍ନ ସାରଣୀରେ ପ୍ରକାଶକଲେ,

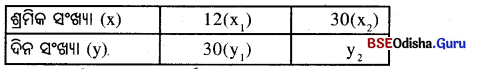
ଏଠାରେ ଶ୍ରମିକ ସଂଖ୍ୟା ଓ କାର୍ଯ୍ୟ ସରିବାର ଦିନ ସଂଖ୍ୟା ପ୍ରତିଲୋମୀ ଚଳନର ଅନ୍ତର୍ଭୁକ୍ତ ।
∴ ପ୍ରତିଲୋମୀ ଚଳନର ସୂତ୍ରାନୁଯାୟୀ x₁ y₁ = x₂y₂
⇒ 12 × 30 = 30 × y₂ ⇒ y₂ = \(\frac{12 \times 30}{30}\) = 12
∴ କାମଟିକୁ 30 ଜଣ ଶ୍ରମିକ 12 ଦିନରେ ଶେଷକରିବେ ।

Question 8.
ନିର୍ଦ୍ଦିଷ୍ଟ ପରିମାଣ ବୁନ୍ଦିରେ 50 ପଇସା ମୂଲ୍ୟର 100ଟି ମିଠାଇ ତିଆରି ହୁଏ; ତେବେ ସେହି ବୁନ୍ଦାରେ ଦୁଇଟଙ୍କା ମୂଲ୍ୟର କେତୋଟି ମିଠାଇ ତିଆରି ହେବ ?
Solution:
ଦତ୍ତ ତଥ୍ୟକୁ ନିମ୍ନ ସାରଣୀରେ ପ୍ରକାଶକଲେ,

ଏଠାରେ ଶ୍ରମିକ ସଂଖ୍ୟା ଓ କାର୍ଯ୍ୟ ସରିବାର ଦିନ ସଂଖ୍ୟା ପ୍ରତିଲୋମୀ ଚଳନର ଅନ୍ତର୍ଭୁକ୍ତ ।
∴ ପ୍ରତିଲୋମୀ ଚଳନର ସୂତ୍ରାନୁଯାୟୀ x₁ y₁ = x₂y₂
⇒ \(\frac{1}{2}\) × 100 = 2.y₂ ⇒ 50 = 2y₂ ⇒ y₂ = \(\frac{50}{2}\) = 25
∴ ସେହି ବୁନ୍ଦିରେ ଦୁଇଟଙ୍କା ମୂଲ୍ୟର 25ଟି ମିଠାଇ ତିଆରି ହେବ ।

Question 9.
ସମାନ କ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ତିନୋଟି ଆୟତକ୍ଷେତ୍ରର ଦୈର୍ଘ୍ୟ ଯଥାକ୍ରମେ 24, 12 ଓ 8 ମିଟର ହେଲେ,
(i) ସେମାନଙ୍କର ଅନ୍ୟ ବାହୁର ଦୈର୍ଘ୍ୟ ସ୍ଥିର କର ।
(ii) ଆୟତକ୍ଷେତ୍ର ତିନୋଟିର ପ୍ରସ୍ଥମାନଙ୍କର ଅନୁପାତ ସ୍ଥିର କର । ପ୍ରଥମ ପ୍ରଶ୍ନର ଏକାଧିକ ଉତ୍ତର ସମ୍ଭବ କି ? ଯଦି ସମ୍ଭବ, କାହିଁକି ?
Solution:
(i) ମନେକର ଆୟତକ୍ଷେତ୍ରତ୍ରୟର ଅନ୍ୟ ବାହୁର ଦୈର୍ଘ୍ୟ ଯଥାକ୍ରମେ a, b ଓ ୯ ମିଟର ।
ଦତ୍ତ ତଥ୍ୟକୁ ନିମ୍ନ ସାରଣୀରେ ପ୍ରକାଶକଲେ,

ଏଠାରେ ଶ୍ରମିକ ସଂଖ୍ୟା ଓ କାର୍ଯ୍ୟ ସରିବାର ଦିନ ସଂଖ୍ୟା ପ୍ରତିଲୋମୀ ଚଳନର ଅନ୍ତର୍ଭୁକ୍ତ ।
∴ ପ୍ରତିଲୋମୀ ଚଳନର ସୂତ୍ରାନୁଯାୟୀ x₁ y₁ = x₂y₂ = z₁z₂ ⇒ 24 . a = 12 . b = 8 . c
ଦରମାନ 24 a = 12b ⇒ \(\frac { a }{ b }\) = \(\frac { 12 }{ 24 }\) = \(\frac { 1 }{ 2 }\) …(i)
ପ୍ରଥମ 12b = 8c ⇒ \(\frac { b }{ c }\) = \(\frac { 8 }{ 12 }\) = \(\frac { 2 }{ 3 }\) …(ii)
∴ Eqⁿ. (i) ଓ Eqⁿ. (ii) ରୁ ପାଇଲେ, a = 1, b = 2, c = 3
∴ ଆୟତକ୍ଷେତ୍ର ତିନୋଟିର ଅନ୍ୟ ବାହୂତ୍ରୟର ଦୈର୍ଘ୍ୟ ପାଇଲେ1 ମି. 2 ମି. ଓ 3 ମି. |

(ii) ଆୟତକ୍ଷେତ୍ର ତିନୋଟିର ବାହୂତ୍ରୟର ପାଇଲେ 1 ମି. 2 ମି. ଓ 3 ମି. |
∴ ସେମାନଙ୍କର ଅନୁପାତ 1 : 2 : 3 ହେବ ।
ପ୍ରଥମ ପ୍ରଶ୍ନ ବା (i)ର ଏକାଧିକ ଉତ୍ତର ସମ୍ଭବ, କାରଣ ଦୈର୍ଘ୍ୟଗୁଡ଼ିକ ବିଭିନ୍ନ ନେଲେ ଉତ୍ତରଗୁଡ଼ିକ ବିଭିନ୍ନ ହେବ ।

Question 10.
ଗୋଟିଏ ବନ୍ୟା ଆଶ୍ରୟସ୍ଥଳରେ 120 ଜଣ ଲୋକଙ୍କ ପାଇଁ ୨ ଦିନର ଚୁଡ଼ା ଓ ଗୁଡ଼ର ବ୍ୟବସ୍ଥା ଥିଲା । ସେଠାକୁ ଆଶ୍ରୟ ନେବାପାଇଁ 180 ଜଣ ଲୋକ ଆସିଲେ । ସେହି ଖାଦ୍ୟ ସେମାନଙ୍କର କେତେ ଦିନ ଯିବ ?
Solution:
ଦତ୍ତ ତଥ୍ୟକୁ ନିମ୍ନ ସାରଣୀରେ ପ୍ରକାଶକଲେ,

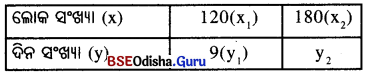
ଏଠାରେ ଶ୍ରମିକ ସଂଖ୍ୟା ଓ କାର୍ଯ୍ୟ ସରିବାର ଦିନ ସଂଖ୍ୟା ପ୍ରତିଲୋମୀ ଚଳନର ଅନ୍ତର୍ଭୁକ୍ତ ।
ତେଣୁ ତ୍ପତିଲୋମା ଭଲନ ସତ ଅନୁଯାୟୀ x₁ y₁ = x₂y₂ ⇒ 120 × 9 = 180 × y₂ ⇒ y₂ = \(\frac{12 0\times 9}{180}\) = 6
∴ ସେହି ଖାଦ୍ୟ ସେମାନଙ୍କର 6 ଦିନ ଯିବ ।

Question 11.
ରବି ସାଇକେଲ୍‌ରେ 10 କି.ମି. ପ୍ରତି ଘଣ୍ଟା ବେଗରେ ଯାଇ ସ୍କୁଲରେ 12 ମିନିଟ୍‌ରେ ପହଞ୍ଚେ ! ସେ ତାହାର ଘଣ୍ଟାପ୍ରତି ବେଗ ଆଉ 2 କି.ମି. ବଢ଼ାଇଲେ ସ୍କୁଲ୍‌ରେ କେତେ ସମୟରେ ପହଞ୍ଚିବ ? ଘରଠାରୁ ତାହାର ସ୍କୁଲ୍ କେତେ ବାଟ ?
Solution:
ଦତ୍ତ ତଥ୍ୟକୁ ନିମ୍ନ ସାରଣୀରେ ପ୍ରକାଶକଲେ,

ଏଠାରେ ଘଣ୍ଟାପ୍ରତି ବେଗ ଓ ସମୟ ପ୍ରତିଲୋମୀ ଚଳନର ଅନ୍ତର୍ଭୁକ୍ତ ।
ପ୍ରତିଲୋମୀ ଚଳନ ସୂତ୍ର ଅନୁଯାୟୀ x₁ y₁ = x₂y₂
⇒ 10 × \(\frac { 12 }{ 60 }\) = 12 × y₂ ⇒ 2 = 12y₂ ⇒ y₂ = \(\frac { 2 }{ 12 }\) = \(\frac { 1 }{ 6 }\) ଣଣ ଦା 10 ମିନିଟ୍
∴ଏଠାରେ ଚଳନର ଧ୍ରୁବାଙ୍କ xy = ଘରଠାରୁ ସ୍କୁଲର ଦୂରତା
∴ ରବି 10 ମିନିଟ୍‌ରେ ଘରେ ପହଞ୍ଚିବ ଓ ଘରଠାରୁ ତାହାର ସ୍କୁଲର ଦୂରତା 2 କି.ମି. ।