CHSE Odisha Class 11 Math Solutions Chapter 4 Trigonometric Functions Ex 4(a)

Odisha State Board Elements of Mathematics Class 11 CHSE Odisha Solutions Chapter 4 Trigonometric Functions Ex 4(a) Textbook Exercise Questions and Answers.

CHSE Odisha Class 11 Math Solutions Chapter 4 Trigonometric Functions Exercise 4(a)

Question 1.
State which of the following is positive.
(i) cos 271°
Solution:
cos 271° is + ve as 271° lies in 4th quadrant.

(ii) sec 73°
Solution:
sec 73° is + ve as sec +ve in the 1st quadrant.

(iii) sin 302°
Solution:
sin 302° is- ve as sin is -ve in the 4th quadrant

(iv) cosec 159°
Solution:
cosec 159° is + ve as 159° lies in 2nd quadrant and cosec is +ve there.

(v) sec 199°
Solution:
sec 199° is – ve as 199° lies in the 3rd quadrant and sec is -ve there.

(vi) cosec 126°
Solution:
cosec 126° is + ve as cosec is +ve in 2nd quadrant.

(vii) cos 315°
Solution:
cos 315° is +ve as 315° lies in 4th quadrant and cos is +ve there.

(viii) cot 375°
Solution:
cot 375° is +ve as 375° lies in 1st quadrant.

Question 2.
Express the following as trigonometric ratios of some acute angles.
(i) sin 1185°
Solution:
sin 1185° = sin\(\left(13 \frac{\pi}{2}+15^{\circ}\right)\)
=(- 1) ^{\(\frac{13-1}{2}\)} cos 15° = cos 15°

(ii) tan 235°
Solution:
tan 235° = tan (180° + 45°) = tan 45°

(iii) sin (- 3333°)
Solution:
sin (-3333°) – -sin 3333°
= – sin\(\left(37 \frac{\pi}{2}+3^{\circ}\right)\)
= – (- 1) ^{\(\frac{27-1}{2}\)} cos 3° =- cos 3°

(iv) cot (- 3888°)
Solution:
cot (-3888°) = – cot 3888°
= – cot\(\left(43 \frac{\pi}{2}+18^{\circ}\right)\)
= – (- tan 18°) = tan 18°

(v) tan 458°
Solution:
tan 458° = tan\(\left(5 \frac{\pi}{2}+8^{\circ}\right)\) = – cot 8°

(vi) cosec (- 60°)
Solution:
cosec (- 60°) = – cosec 60°

(vii) cos 500°
Solution:
cos 500° = cos\(\left(5 \frac{\pi}{2}+50^{\circ}\right)\)
= – (-1) ^{\(\frac{5+1}{2}\)} sin 55° – sin 50°

(viii)sec 380°
Solution:
sec 380° = sec (360° + 20°)
= sec 20°

Question 3.
Find the domain of tangent and cotangent functions.
Solution:
Domain of tan x is R – \(\left\{\frac{(2 n+1) \pi}{2}, n \in Z\right\}\) as tangent is not defined for
x = \(\frac{(2 n+1) \pi}{2}\)
The domain of cot x is R – {nπ, n ∈ Z} as cotangent is not defined for x = nπ.

Question 4.
Determine the ranges of sine and cosine functions.
Solution:
The maximum and minimum values of sine and cosine are 1 and -1, respectively.
∴ Ranges of sine and cosine are [-1, 1].

Question 5.
Find a value of A when cos 2A = sin 3A
Solution:
cos 2A = sin 3A = cos (90° – 3A)
or, 2A = 90° – 3A
or, 5A = 90° or, A = 18°

Question 6.
Find the value of
cos 1°. cos 2° …..cos 100°
Solution:
cos 1° cos 2° …..cos 100°
= 0 as cos 90° is there which is zero.

Question 7.
Find the value of
cos 24° + cos 5° + cos 175° + cos 204° + cos 300°
Solution:
cos 24° + cos 5° + cos 175° + cos 204° + cos 300°
= cos 24° + cos 5° + cos (180° – 5°) + cos (180° + 24°) + cos (360°- 60°)
= cos 24° + cos 5° – cos 5° – cos 24° + cos 60° = cos 60° = 1/2

Question 8.
Evaluate
tan\(\frac{\pi}{20}\).tan\(\frac{3 \pi}{20}\).tan\(\frac{5 \pi}{20}\).tan\(\frac{7 \pi}{20}\).tan\(\frac{9 \pi}{20}\)
Solution:
tan\(\frac{\pi}{20}\).tan\(\frac{3 \pi}{20}\).tan\(\frac{5 \pi}{20}\).tan\(\frac{7 \pi}{20}\).tan\(\frac{9 \pi}{20}\)
= tan 9° tan 27° tan 45° tan 63° tan 81°
= tan 9°. tan 27°. 1 tan (90° – 27°). tan (90° – 9°)
= tan 9° tan 27° cot 27° cot 9°
= (tan 9°. cot 9°) x (tan 27°. cot 27°)
=1 × 1=1

Question 9.
Show that
\(\frac{\sin ^3\left(180^{\circ}+\mathbf{A}\right) \cdot \tan \left(360^{\circ}-\mathbf{A}\right) \sec ^2\left(180^{\circ}-\mathbf{A}\right)}{\cos ^2\left(90^{\circ}+\mathbf{A}\right){cosec}^2 A \cdot \sin \left(180^{\circ}-A\right)}\) = tan³ A
Solution:
L.H.S

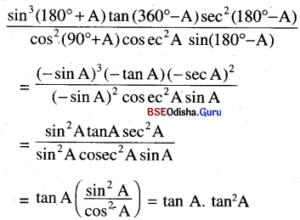
= tan³A      (R.H.S)

Question 10.
If A = cos² θ + sin⁴ θ then prove that for all values of θ, 3/4 ≤ A ≤ 1.
Solution:
A = cos² θ + sin⁴ θ =1 – sin² θ sin⁴ θ
or, sin⁴ θ – sin² θ + (1 – A) = 0 …(1)
Eqn. (I) is quadratic in sin² θ.
∴ sin² θ = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
\(=\frac{1 \pm \sqrt{1-4(1-\mathrm{A})}}{2 \times 1}\)
Where a=1, b = – 1, c = 1 – A
∴ sin² θ = \(\frac{1 \pm \sqrt{4 A-3}}{2}\)
We know that sin20 is not negative and lies in [0, 1]
So, \(\sqrt{4 \mathrm{~A}-3}\) ≤ 1
⇒ 4A – 3 ≤ 1 ⇒ 4A ≤ 4 ⇒ A ≤ 1  …(2)
Again, since sin² θ is real,
b² – 4ac must be +ve
i.e., 4A – 3 ≥ 0 ⇒ A ≥ 3/4
∴ From (2) and (3),
We have 3/4 ≤ A ≤ 1          (Proved)