CHSE Odisha Class 12 Math Solutions Chapter 4 Matrices Ex 4(a)

Odisha State Board Elements of Mathematics Class 12 CHSE Odisha Solutions Chapter 4 Matrices Ex 4(a) Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 4 Matrices Exercise 4(a)

Question 1.
State the order of the following matrices.
(i) [abc]
(ii) \(\left[\begin{array}{l}
1 \\
2
\end{array}\right]\)
(iii) \(\left[\begin{array}{ll}
x & y \\
y & z \\
z & x
\end{array}\right]\)
(iv) \(\left[\begin{array}{cccc}
1 & 0 & 1 & 4 \\
2 & 1 & 3 & 0 \\
-3 & 2 & 1 & 3
\end{array}\right]\)
Solution:
(i) (1 x 3)
(ii) (2 x 1)
(iii) (3 x 2)
(iv) (3 x 4)

Question 2.
How many entries are there in a
(i) 3 x 3 matrix
(ii) 3 x 4 matrix
(iii) p x q matrix
(iv) a sqare matrix of order p?
Solution:
(i) 9
(ii) 12
(iii) pq
(iv) p²

Question 3.
Give an example of
(i) 3 x 1 matrix
(ii) 2 x 2 matrix
(iii) 4 x 2 matrix
(iv) 1 x 3 matrix
Solution:
(i) \(\left(\begin{array}{l}
a \\
b \\
c
\end{array}\right)\)
(ii) \(\left(\begin{array}{ll}
a & b \\
c & d
\end{array}\right)\)
(iii) \(\left(\begin{array}{ll}
a & b \\
c & d \\
e & f \\
g & h
\end{array}\right)\)
(iv) (1, 2, 3)

Question 4.
Let A = \(\left[\begin{array}{lllll}
1 & 2 & 3 & 4 & 1 \\
4 & 5 & 6 & 1 & 2 \\
3 & 9 & 1 & 1 & 6
\end{array}\right]\)
(i) What is the order of A?
(ii) Write down the entries a₃₁, a₂₅, a₂₃
(iii) Write down A^T.
(iv) What is the order of A^T?
Solution:
A = \(\left[\begin{array}{lllll}
1 & 2 & 3 & 4 & 1 \\
4 & 5 & 6 & 1 & 2 \\
3 & 9 & 1 & 1 & 6
\end{array}\right]\)
(i) Order of A is (3 x 5)
(ii) a₃₁ = 3, a₂₅= 2, a₂₃ = 6
(iii) A^T = \(\left[\begin{array}{lll}
1 & 4 & 3 \\
2 & 5 & 9 \\
3 & 6 & 1 \\
4 & 1 & 1 \\
1 & 2 & 6
\end{array}\right]\)
(iv) Order of A^T is (5 x 3).

Question 5.
Matrices A and B are given below. Find A + B, B + A, A – B and B – A. Verify that A + B = B + A and B – A = -(A – B)
(i) A = \(\left[\begin{array}{l}
7 \\
1
\end{array}\right]\), B = \(\left[\begin{array}{c}
-6 \\
9
\end{array}\right]\)
Solution:

(ii) A = \(\left[\begin{array}{cc}
1 & 2 \\
3 & -1
\end{array}\right]\), B = \(\left[\begin{array}{cc}
4 & 1 \\
-3 & 2
\end{array}\right]\)
Solution:

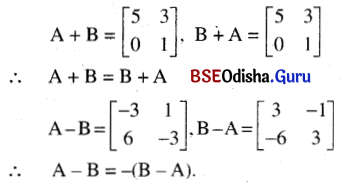
(iii) A = \(\left[\begin{array}{ll}
\frac{1}{2} & \frac{1}{4} \\
\frac{1}{3} & \frac{1}{5}
\end{array}\right]\), B = \(\left[\begin{array}{ll}
\frac{1}{3} & \frac{1}{2} \\
\frac{1}{2} & \frac{4}{5}
\end{array}\right]\)
Solution:

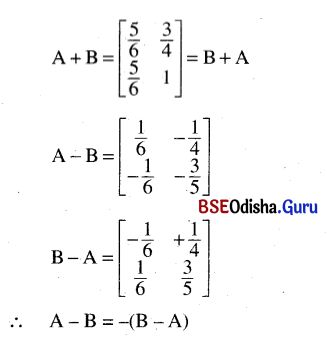
(iv) A = \(\left[\begin{array}{cc}
1 & a-b \\
a+b & -3
\end{array}\right]\), B = \(\left[\begin{array}{cc}
1 & b \\
-a & 5
\end{array}\right]\)
Solution:

(v) \(\left[\begin{array}{rrr}
1 & -2 & 5 \\
-1 & 4 & 3 \\
1 & 2 & -3
\end{array}\right]\), B = \(\left[\begin{array}{rrr}
-1 & 2 & -5 \\
1 & -3 & -3 \\
1 & 2 & 4
\end{array}\right]\)
Solution:

Question 6.
(i) Find the 2×2 matrix X
if X + \(\left[\begin{array}{ll}
0 & 1 \\
1 & 0
\end{array}\right]\) = \(\left[\begin{array}{ll}
2 & 0 \\
0 & 2
\end{array}\right]\)
Solution:

(ii) Given
[x y z] – [-4 3 1] = [-5 1 0] derermine x, y, z.
Solution:
[x y z] – [-4 3 1] = [-5 1 0]
∴ (x y z) = (-4 3 1) + (-5 1 0) = (-9 4 1)
∴ x = -9, y = 4, z = 1

(iii) If \(\left[\begin{array}{ll}
x_1 & x_2 \\
y_1 & y_2
\end{array}\right]\) – \(\left[\begin{array}{ll}
2 & 3 \\
0 & 1
\end{array}\right]\) = \(\left[\begin{array}{ll}
3 & 5 \\
1 & 2
\end{array}\right]\) determine x₁, x₂, y₁, y₂.
Solution:

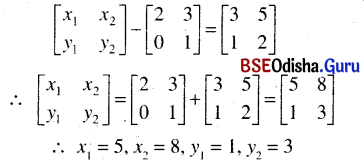
(iv) Find a matrix which when added to \(\left[\begin{array}{cc}
2 & -3 \\
-4 & 7
\end{array}\right]\) gives \(\left[\begin{array}{ll}
4 & 1 \\
3 & 2
\end{array}\right]\)
Solution:

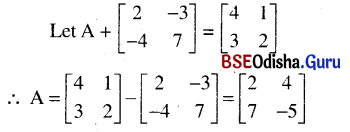
Question 7.
Calculate whenever possible, the following products.
(i) \(\left[\begin{array}{ll}
1 & 2 \\
3 & 4
\end{array}\right]\left[\begin{array}{l}
2 \\
3
\end{array}\right]\)
Solution:

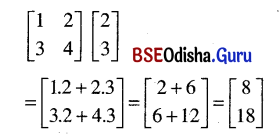
(ii) \(\left[\begin{array}{l}
2 \\
3
\end{array}\right]\left[\begin{array}{ll}
1 & 2 \\
4 & 3
\end{array}\right]\)
Solution:
\(\left[\begin{array}{l}
2 \\
3
\end{array}\right]\left[\begin{array}{ll}
1 & 2 \\
4 & 3
\end{array}\right]\) is impossible because number of columns of 1st ≠ number of rows of second.

(iii) \(\left[\begin{array}{ll}
1 & 2 \\
2 & 1
\end{array}\right]\left[\begin{array}{ll}
3 & 1 \\
1 & 1
\end{array}\right]\)
Solution:

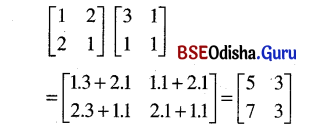
(iv) \(\left[\begin{array}{cc}
1 & -2 \\
-2 & 3
\end{array}\right]\left[\begin{array}{lll}
1 & 2 & 3 \\
2 & 3 & 4
\end{array}\right]\)
Solution:

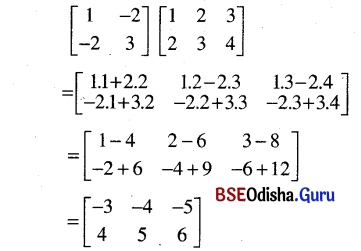
Question 8.
If A = \(\left[\begin{array}{ll}
1 & 2 \\
3 & 4
\end{array}\right]\), B = \(\left[\begin{array}{ll}
3 & 2 \\
1 & 4
\end{array}\right]\), C = \(\left[\begin{array}{ll}
2 & 2 \\
1 & 3
\end{array}\right]\)
Calculate (i) AB (ii) BA (iii) BC (iv) CB (v) AC (vi) CA
Solution:

Question 9.
Find the following products.
(i) \(\left[\begin{array}{ll}
1 & 2 \\
3 & 4
\end{array}\right]\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\)
Solution:

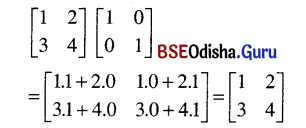
(ii) \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\left[\begin{array}{ll}
1 & 2 \\
3 & 4
\end{array}\right]\)
Solution:

(iii) \(\left[\begin{array}{ll}
1 & 2 \\
3 & 4
\end{array}\right]\left[\begin{array}{ll}
1 & 3 \\
1 & 4
\end{array}\right]\)
Solution:

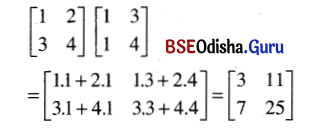
(iv) \(\left[\begin{array}{ll}
1 & 3 \\
1 & 4
\end{array}\right]\left[\begin{array}{ll}
1 & 2 \\
3 & 4
\end{array}\right]\)
Solution:

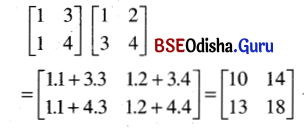
(v) \(\left[\begin{array}{cc}
1 & i \\
i & -1
\end{array}\right]^2\) where i = √-1
Solution:

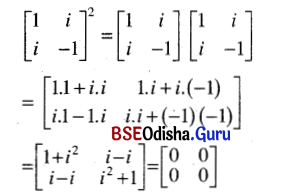
(vi) \(\left[\begin{array}{ll}
\mathbf{0} & \mathbf{1} \\
\mathbf{1} & \mathbf{0}
\end{array}\right]\left[\begin{array}{ll}
a & b \\
c & d
\end{array}\right]\)
Solution:

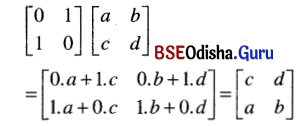
(vii) \(\left[\begin{array}{ll}
0 & k \\
1 & 0
\end{array}\right]\left[\begin{array}{ll}
a & b \\
c & d
\end{array}\right]\)
Solution:

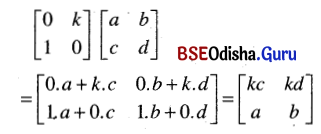
(viii) \(\left[\begin{array}{ll}
a & b \\
c & d
\end{array}\right]\left[\begin{array}{ll}
0 & 1 \\
1 & 0
\end{array}\right]\)
Solution:

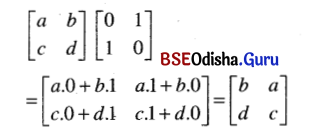
(ix) \(\left[\begin{array}{ll}
1 & 0 \\
0 & k
\end{array}\right]\left[\begin{array}{ll}
a & b \\
c & d
\end{array}\right]\)
Solution:

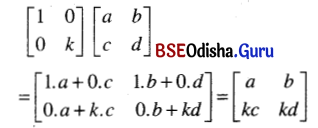
(x) \(\left[\begin{array}{lll}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9
\end{array}\right]\left[\begin{array}{lll}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0
\end{array}\right]\)
Solution:
\(\left[\begin{array}{lll}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9
\end{array}\right]\left[\begin{array}{lll}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0
\end{array}\right]\) = \(\left[\begin{array}{lll}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0
\end{array}\right]\)

Question 10.
Write true or false in the following cases:
(i) The sum of a 3 x 4 matrix with a 3 x 4 matrix is a 3 x 3 matrix.
Solution:
False

(ii) k[0] = 0, k ∈ R
Solution:
False

(iii) A – B = B – A, if one of A and B is zero and A and B are of the same order.
Solution:
False

(iv) A + B = B + A, if A and B are matrices of the same order.
Solution:
True

(v) \(\left[\begin{array}{cc}
1 & 0 \\
-2 & 0
\end{array}\right]\) + \(\left[\begin{array}{cc}
-1 & 0 \\
2 & 0
\end{array}\right]\) = 0
Solution:
True

(vi) \(\left[\begin{array}{ll}
3 & 1 \\
6 & 2
\end{array}\right]\) = 3 \(\left[\begin{array}{ll}
1 & 1 \\
2 & 2
\end{array}\right]\)
Solution:
False

(vii) With five elements a matrix can not be constructed.
Solution:
False

(viii)The unit matrix is its own transpose.
Solution:
True

Question 11.
If A = \(\left[\begin{array}{cc}
2 & 4 \\
3 & 13
\end{array}\right]\) and I = \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\) find A – α I, α ∈ R.
Solution:

Question 12.
Find x and y in the following.
(i) \(\left[\begin{array}{cc}
x & -2 y \\
0 & -2
\end{array}\right]=\left[\begin{array}{cc}
1 & -8 \\
0 & -2
\end{array}\right]\)
Solution:

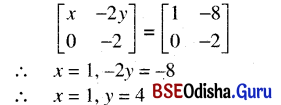
(ii) \(\left[\begin{array}{c}
x+3 \\
2-y
\end{array}\right]=\left[\begin{array}{c}
1 \\
-3
\end{array}\right]\)
Solution:

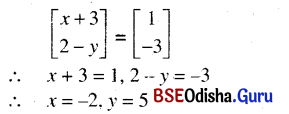
(iii) \(\left[\begin{array}{c}
2 x-y \\
x+y
\end{array}\right]=\left[\begin{array}{c}
3 \\
-9
\end{array}\right]\)
Solution:

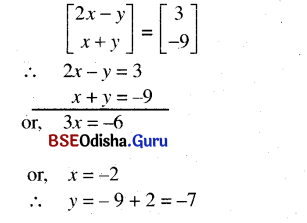
(iv) \(\left[\begin{array}{l}
x \\
y
\end{array}\right]+\left[\begin{array}{l}
3 \\
4
\end{array}\right]=\left[\begin{array}{c}
2 \\
-1
\end{array}\right]\)
Solution:

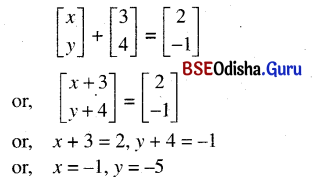
(v) [2x -y] + [y 3x] = 5 [1 0]
Solution:

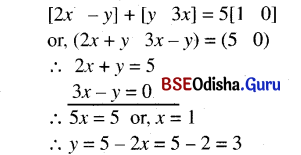
Question 13.
The element of ith row and ith column of the following matrix is i +j. Complete the matrix.

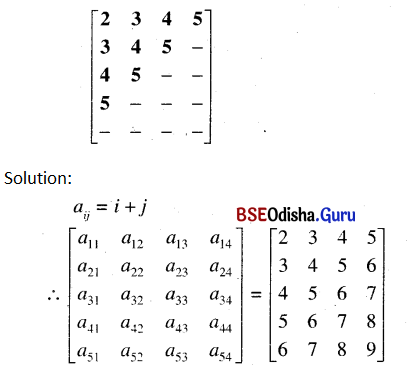
Question 14.
Write down the matrix

Question 15.
Construct a 2 x 3 matrix having elements given by
(i) a_ij = i + j
(ii) a_ij = i – j
(iii) a_ij = i × j
(iv) a_ij = i / j
Solution:

Question 16.
If \(\left[\begin{array}{cc}
2 x & y \\
1 & 3
\end{array}\right]+\left[\begin{array}{cc}
4 & 2 \\
0 & -1
\end{array}\right]=\left[\begin{array}{ll}
8 & 3 \\
1 & 2
\end{array}\right]\)
Solution:

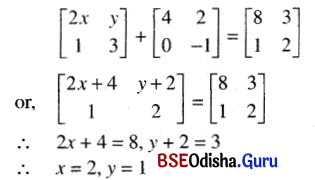
Question 17.
Find A such that
\(\left[\begin{array}{ccc}
2 & 3 & 4 \\
1 & 0 & -2 \\
3 & 1 & -1
\end{array}\right]+A=\left[\begin{array}{ccc}
1 & 2 & -1 \\
2 & -1 & 0 \\
1 & 3 & 2
\end{array}\right]\)
Solution:

Question 18.
If

Question 19.
What is the order of the matrix B if [3 4 2] B = [2 1 0 3 6]
Solution:
(3 4 2) B = (2 1 0 3 6)
Let A = (3 4 2), C = (2 1 0 3 6)
∴ Order of A = (1 x 3)
Order of C = (1 x 5)
∴ Order of B = (3 x 5)

Question 20.
Find A if \(\left[\begin{array}{l}
4 \\
1 \\
3
\end{array}\right]\) A = \(\left[\begin{array}{rrr}
-4 & 8 & 4 \\
-1 & 2 & 1 \\
-3 & 6 & 3
\end{array}\right]\)
Solution:

Question 21.
Find B if B² = \(\left[\begin{array}{cc}
17 & 8 \\
8 & 17
\end{array}\right]\)
Solution:

∴ a² + bc = 17, ab + bd= 8
ca + cd = 8, bc + d² = 17
∴ a² + bc = bc + d²
or, a² + d² or, a = d
or, ca + cd = ab + bd
or, cd + cd – bd + bd
or, 2cd = 2bd = 8
or, b = c and bd = 4 = cd
∴ ab + bd= 8
or, ab + 4 = 8
or, ab = 4
Again, a² + bc = 17
or, a² + b . b = 17 (∵ b = c)
or, a² + b² = 17
Also (a + b)² = a² + b² + 2ab
∴ (a + b)² = 17 + 8 = 25
or, a + b = 5
And (a – b)² = 17 – 8 = 9
or, a – b = 3
∴ a = 4, b = 1, So d = 4, c = 1
∴ B = \(\left[\begin{array}{ll}
4 & 1 \\
1 & 4
\end{array}\right]\)

Question 22.
Find x and y when

Question 23.
Find AB and BA given that:

Question 24.
Evaluate

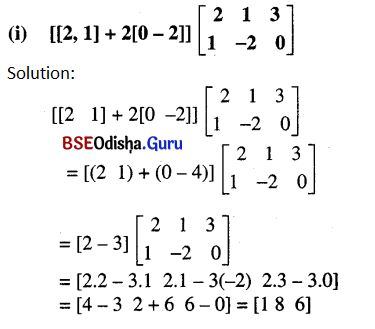
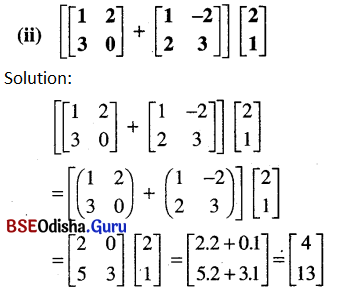
Question 25.
If

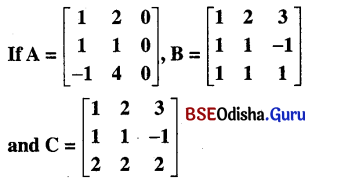
Show that AB = AC though B ≠ C. Verify that
(i) A + (B + C) = (A + B) + C
(ii) A(B + C) = AB + AC
(iii) A(BC) = (AB)C
Solution:

Question 26.
Find A and B where

Question 27.
If A = \(\left[\begin{array}{cc}
4 & 2 \\
-1 & 1
\end{array}\right]\) and I be the 2 × 2 unit matrix find (A – 2I) (A – 3I)
Solution:

Question 28.
Verify that [AB]^T = B^TA^T where

Question 29.
Verify that A = \(\left[\begin{array}{ll}
a & b \\
c & d
\end{array}\right]\) satisfies the equation x² – (a + d)x + (ad – bc)I = 0 where I is the 2 x 2 matrix.
Solution:

Question 30.
If A = \(\left[\begin{array}{rrr}
1 & 2 & 3 \\
3 & -2 & 1 \\
4 & 2 & 1
\end{array}\right]\), show that A³ – 23 A – 40 I = 0
Solution:

Question 31.

Question 32.
If A and B are matrices of the same order and AB = BA, then prove that
(i) A² – B² = (A – B) (A + B)
(ii) A² + 2AB + B² = (A + B)²
(iii) A² – 2AB + B² = (A – B)²
Solution:
(i) (A – B) (A + B)
= A² + AB – BA – B²
= A² + AB – AB- B²(∵ AB = BA)
= A² – B²
(ii) (A + B)² = (A + B) (A + B)
= A² + AB + BA + B²
= A² + AB + AB + B² (∵ AB = BA)
= A² + 2AB + B²
(iii) (A – B)² = (A – B) (A – B)
= A² – AB – BA + B²
= A² – AB – AB + B² (∵ AB = BA)
= A² – 2AB + B²

Question 33.
If α and β are scalars and A is a square matrix then prove that
(A – αI) . (A – βI) = A² – (α + β) A + αβI, where I is a unit matrix of same order as A.
Solution:
(A – αI) (A – βI)
= A² – AβI – αIA + αβI²
= A² – βAI – αA + αβI
(∵ IA = A, I² = I)
= A² – βA – αA + αβI) (∵ AI = A)
= A² – (α + β) A + αβI

Question 34.
If α and β are scalars such that A = αβ + βI, where A, B and the unit matrix I are of the same order, then prove that AB = BA.
Solution:
We have A = αβ + βI
AB (αβ + βI) B
= α βB + βI B
= α βB + βB = (α + I) βB
= βB (α + 1)
(∵ Scalar mltiβlication is associative)
= Bβ (α + 1)
= Bβα + Bβ = Bαβ + BIβ
(∵ BI = B)
= B (αβ + βi) = BA
AB = BA
(proved)

Question 35.

Question 36.

Question 37.

Question 38.

Question 39.

Question 40.

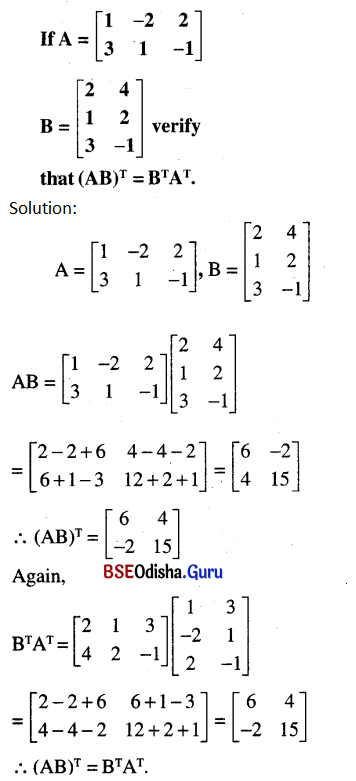
Question 41.

Question 42.

Question 43.

	Men	Women	Children
Family A →	4	6	2
Family B →	2	2	4

	Family B
	Calory	Proteins
Men	2400	45
Women	1900	55
Children	1800	33

Solution:
The given informations can be written in matrix form as

∴ Calory requirements for families A and B are 24600 and 15800 respectively and protein requirements are 576 gm and 332 gm respectively.

Question 44.
Let the investment in first fund = ₹x and in the second fund is ₹(50000-x)
Investment matrix A=[x  50000-x]

⇒ 300000 – x = 278000
⇒ x = 22000
∴ He invests ₹22000 in first bond and ₹28000 in the second bond.