Odisha State Board Elements of Mathematics Class 12 Solutions CHSE Odisha Chapter 5 Determinants Ex 5(b) Textbook Exercise Questions and Answers.
CHSE Odisha Class 12 Math Solutions Chapter 5 Determinants Exercise 5(b)
Question 1.
Write the number of solutions of the following system of equations.
(i) x – 2y = 0
Solution:
No solution
(ii) x – y = 0 and 2x – 2y = 1
Solution:
Infinite
(iii) 2x + y = 2 and -x – 1/2y = 3
Solution:
No solution
(iv) 3x + 2y = 1 and x + 5y = 6
Solution:
One
(v) 2x + 3y + 1 = 0 and x – 3y – 4 = 0
Solution:
One
![]()
(vi) x + y + z = 1
x + y + z = 2
2x + 3y + z = 0
Solution:
No solution
(vii) x + 4y – z = 0
3x – 4y – z = 0
x – 3y + z = 0
Solution:
One
(viii) x + y – z = 0
3x – y + z = 0
x – 3y + z = 0
Solution:
One
(ix) a1x + b1y + c1z = 0
a2x + b2y + c2z = 0
a3x + b3y + c3z = 0
and \(\left|\begin{array}{lll}
a_1 & b_1 & c_1 \\
a_2 & b_2 & c_2 \\
a_3 & b_3 & c_3
\end{array}\right|\) = 0
Solution:
Infinite solutions as Δ = Δ1 = Δ2 = Δ3 = 0
Question 2.
Show that the following system is inconsistent.
(a – b)x + (b – c)y + (c – a)z = 0
(b – c)x + (c – a)y + (a – b)z = 0
(c – a)x + (a – b)y + (b – c)z =1
Solution:

Question 3.
(i) The system of equations
x + 2y + 3z = 4
2x + 3y + 4z = 5
3x + 4y + 5z = 6 has
(a) infinitely many solutions
(b) no solution
(c) a unique solution
(d) none of the three
Solution:
(a) infinitely many solutions
(ii) If the system of equations
2x + 5y + 8z = 0
x + 4y + 7z = 0
6x + 9y – z = 0
has a nontrivial solution, then is equal to
(a) 12
(b) -12
(c) 0
(d) none of the three
Solution:
(b) -12
(iii) The system of linear equations
x + y + z = 2
2x + y – z = 3
3x +2y + kz = 4
has a unique solution if
(a) k ≠ 0
(b) -1 < k < 1
(c) -2 < k < 2
(d) k = 0
Solution:
(a) k ≠ 0
(iv) The equations
x + y + z = 6
x + 2y + 3z = 10
x + 2y + mz = n
give infinite number of values of the triplet (x, y, z) if
(a) m = 3, n ∈ R
(b) m = 3, n ≠ 10
(c) m = 3, n = 10
(d) none of the three
Solution:
(c) m = 3, n = 10
(v) The system of equations
2x – y + z = 0
x – 2y + z = 0
x – y + 2z = 0
has infinite number of nontrivial solutions for
(a) = 1
(b) = 5
(c) = -5
(d) no real value of
Solution:
(c) = -5
(vi) The system of equations
a1x + b1y + c1z = 0
a2x + b2y + c2z = 0
a3x + b3y + c3z =0
with has
(a) more than two solutions
(b) one trivial and one nontrivial solutions
(c) No solution
(d) only trivial solutions
Solution:
(a) more than two solutions
![]()
Question 4.
Can the inverses of the following matrices be found?
(i) \(\left[\begin{array}{ll}
0 & 0 \\
0 & 0
\end{array}\right]\)
Solution:
|A| = 0
∴ A-1 can not be found.
(ii) \(\left[\begin{array}{ll}
1 & 2 \\
3 & 4
\end{array}\right]\)
Solution:
∴ |A| = 4 – 6 = -2 ≠ 0
∴ A-1 exists.
(iii) \(\left[\begin{array}{ll}
1 & 1 \\
1 & 1
\end{array}\right]\)
Solution:
|A| = \(\left[\begin{array}{ll}
1 & 1 \\
1 & 1
\end{array}\right]\) = 1 – 1 = 0
∴ A-1 does not exist.
(iv) \(\left[\begin{array}{ll}
1 & 2 \\
2 & 4
\end{array}\right]\)
Solution:
|A| = \(\left[\begin{array}{ll}
1 & 2 \\
2 & 4
\end{array}\right]\) = 4 – 4 = 0
∴ A-1 does not exist.
(v) \(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]\)
Solution:
|A| = \(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]\) = 1 ≠ 0
∴ A-1 exists.
Question 5.
Find the inverse of the following:
(i) \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\)
Solution:

(ii) \(\left[\begin{array}{cc}
2 & -1 \\
1 & 3
\end{array}\right]\)
Solution:

(iii) \(\left[\begin{array}{cc}
4 & -2 \\
3 & 1
\end{array}\right]\)
Solution:

![]()
(iv) \(\left[\begin{array}{ll}
2 & 5 \\
1 & 3
\end{array}\right]\)
Solution:

(v) \(\left[\begin{array}{cc}
1 & 0 \\
2 & -3
\end{array}\right]\)
Solution:

(vi) \(\left[\begin{array}{cc}
1 & 0 \\
0 & -1
\end{array}\right]\)
Solution:

(vii) \(\left[\begin{array}{cc}
i & -i \\
i & i
\end{array}\right]\)
Solution:

(viii) \(\left[\begin{array}{ll}
x & -x \\
x & x^2
\end{array}\right]\), x ≠ 0, x ≠ -1
Solution:

![]()
Question 6.
Find the adjoint of the following matrices.
(i) \(\left[\begin{array}{ccc}
1 & 1 & -1 \\
2 & -1 & 2 \\
1 & 3 & -2
\end{array}\right]\)
Solution:

(ii) \(\left[\begin{array}{ccc}
-2 & 2 & 3 \\
1 & 4 & 2 \\
-2 & -3 & 1
\end{array}\right]\)
Solution:
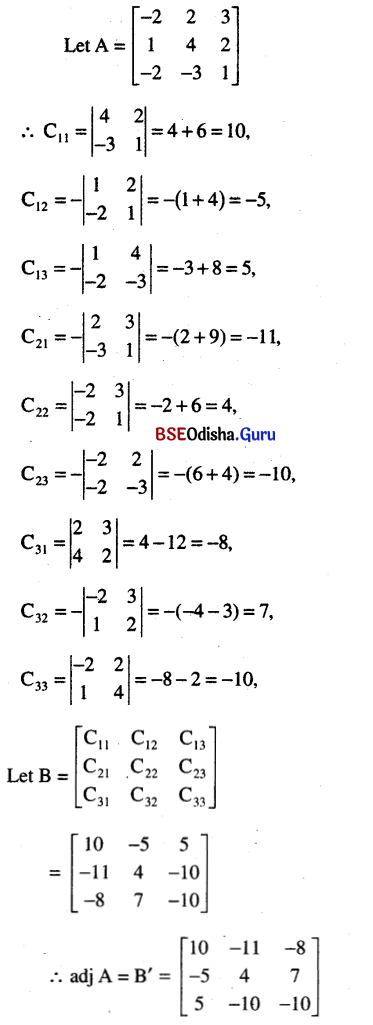
(iii) \(\left[\begin{array}{lll}
2 & 1 & 2 \\
2 & 2 & 1 \\
1 & 2 & 2
\end{array}\right]\)
Solution:

(iv) \(\left[\begin{array}{ccc}
1 & 3 & 0 \\
2 & -1 & 6 \\
5 & -3 & 1
\end{array}\right]\)
Solution:
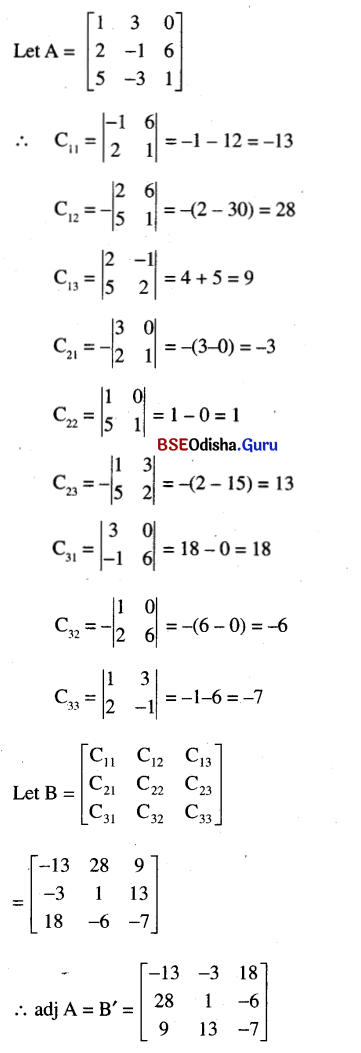
![]()
Question 7.
Which of the following matrices are invertible?
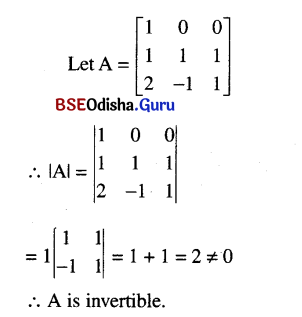
(i) \(\left[\begin{array}{ccc}
1 & 0 & 0 \\
1 & 1 & 1 \\
2 & -1 & 1
\end{array}\right]\)
Solution:
(ii) \(\left[\begin{array}{ccc}
2 & 1 & -2 \\
1 & 2 & 1 \\
3 & 6 & 4
\end{array}\right]\)
Solution:

(iii) \(\left[\begin{array}{ccc}
-1 & -2 & 3 \\
2 & 1 & -4 \\
-1 & 0 & 2
\end{array}\right]\)
Solution:

(iv) \(\left[\begin{array}{ccc}
1 & 0 & 1 \\
2 & -2 & 1 \\
3 & 2 & 4
\end{array}\right]\)
Solution:

Question 8.
Examining consistency and solvability, solve the following equations by matrix method.
(i) x – y + z = 4
2x + y – 3z = 0
x + y + z = 2
Solution:

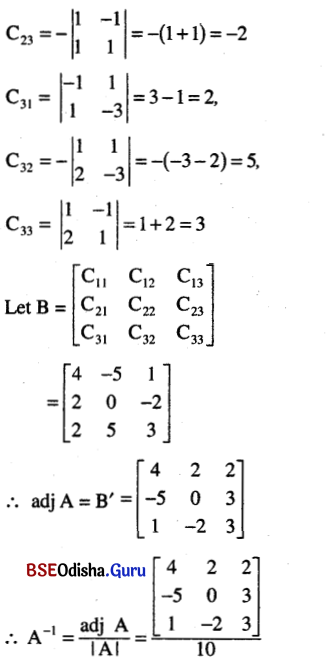
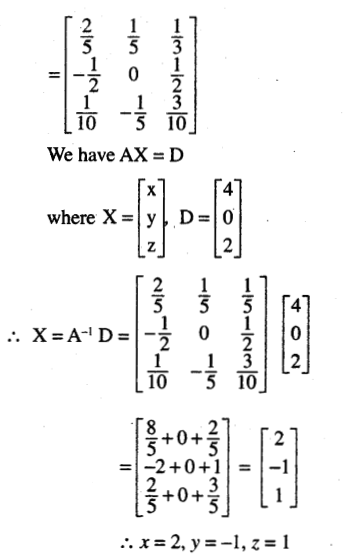
(ii) x + 2y – 3z = 4
2x + 4y – 5z = 12
3x – y + z = 3
Solution:
Let

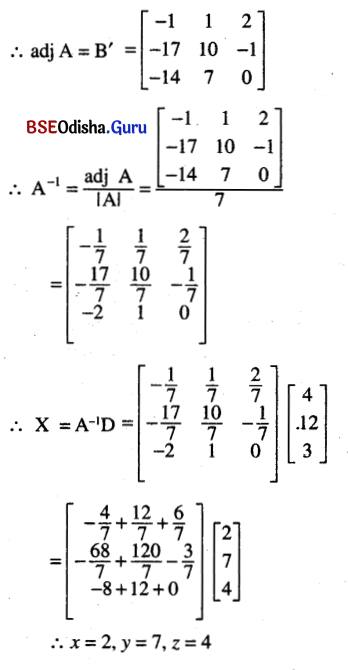
![]()
(iii) 2x – y + z = 4
x + 3y + 2z = 12
3x + 2y + 3z = 16
Solution:


(iv) x + y + z = 4
2x + 5y – 2x = 3
x + 7y – 7z = 5
Solution:
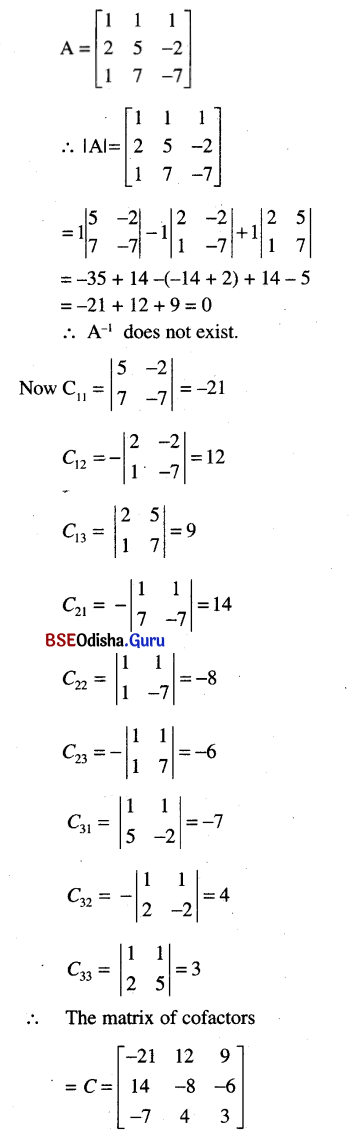

(v) x + y + z = 4
2x – y + 3z = 1
3x + 2y – z = 1
Solution:

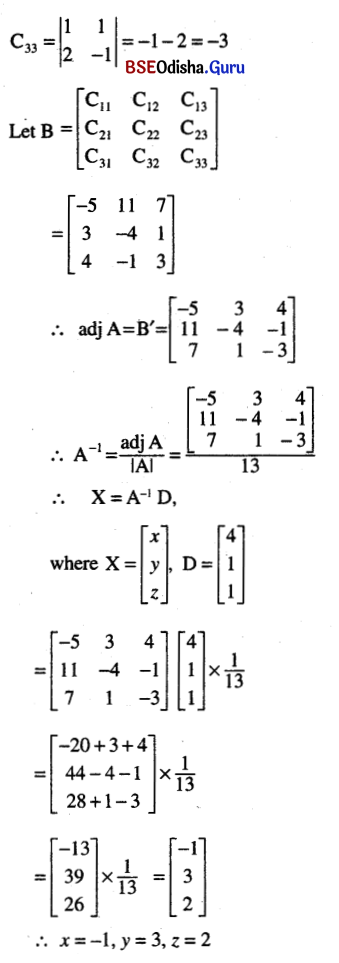
(vi) x + y – z = 6
2x – 3y + z = 1
2x – 4y + 2z = 1
Solution:

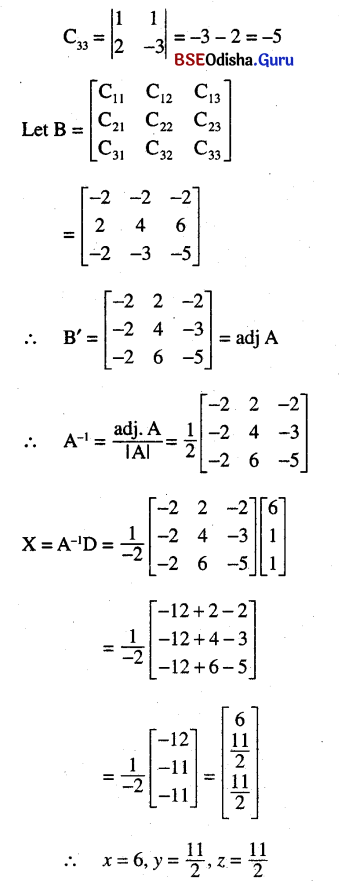
![]()
(vii) x – 2y = 3
3x + 4y – z = -2
5x – 3z = -1
Solution:


(viii) x + 2y + 3z = 14
2x – y + 5z = 15
2y + 4z – 3x = 13
Solution:


(ix) 2x + 3y +z = 11
x + y + z = 6
5x – y + 10z = 34
Solution:

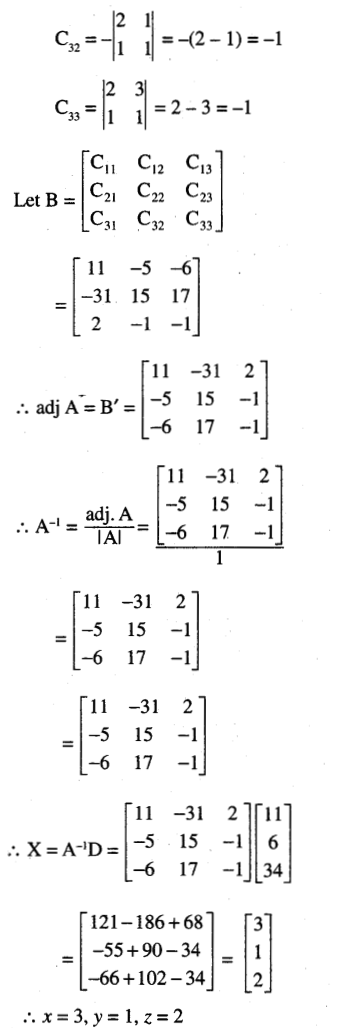
![]()
Question 9.
Given the matrices
A = \(\left[\begin{array}{ccc}
1 & 2 & 3 \\
3 & -2 & 1 \\
4 & 2 & 1
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) and C = \(\left[\begin{array}{l}
1 \\
2 \\
3
\end{array}\right]\)
write down the linear equations given by AX = C and solve it for x, y, z by matrix method.
Solution:

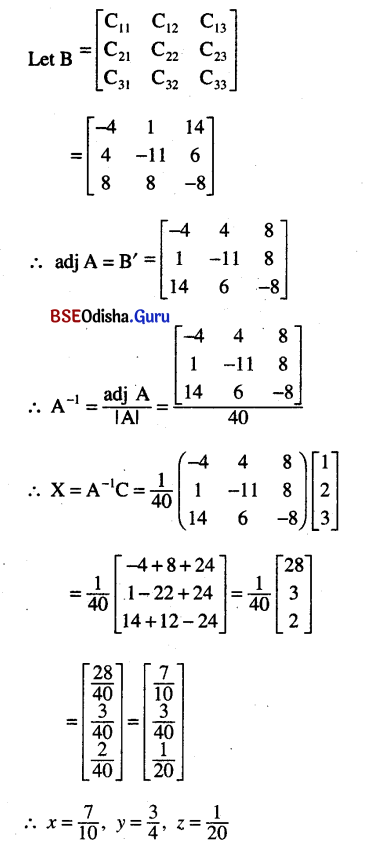
Question 10.
Find X, if \(\left[\begin{array}{ccc}
1 & 1 & 1 \\
1 & 1 & -1 \\
2 & 1 & -1
\end{array}\right]\) X = \(\left[\begin{array}{l}
6 \\
0 \\
1
\end{array}\right]\) where X = \(\left[\begin{array}{l}
x_1 \\
x_2 \\
x_3
\end{array}\right]\)
Solution:


Question 11.
Answer the following:
(i) If every element of a third order matrix is multiplied by 5, then how many times its determinant value becomes?
Solution:
125
(ii) What is the value of x if \(\left|\begin{array}{ll}
4 & 1 \\
2 & 1
\end{array}\right|^2=,\left|\begin{array}{ll}
3 & 2 \\
1 & x
\end{array}\right|-\left|\begin{array}{cc}
x & 3 \\
-2 & 1
\end{array}\right|\) ?
Solution:
x = 6
(iii) What are the values of x and y if \(\left|\begin{array}{ll}
x & y \\
1 & 1
\end{array}\right|=2,\left|\begin{array}{ll}
x & 3 \\
y & 2
\end{array}\right|=1\) ?
Solution:
x = 5, y = 3
(iv) What is the value of x if \(\left|\begin{array}{ccc}
x+1 & 1 & 1 \\
1 & 1 & -1 \\
-1 & 1 & 1
\end{array}\right|\) = 4?
Solution:
x = 0
(v) What is the value of \(\left|\begin{array}{ccc}
\mathbf{o} & -\mathbf{h} & -\mathbf{g} \\
\mathbf{h} & \mathbf{0} & -\mathbf{f} \\
\mathbf{g} & \mathbf{f} & \mathbf{0}
\end{array}\right|\)?
Solution:
0
(vi) What is the value of \(\left|\begin{array}{l}
\frac{1}{a} 1 \mathrm{bc} \\
\frac{1}{b} 1 c a \\
\frac{1}{c} 1 a b
\end{array}\right|\)
Solution:
0
(vii) What is the co-factor of 4 in the determinant \(\left|\begin{array}{rrr}
1 & 2 & -3 \\
4 & 5 & 0 \\
2 & 0 & 1
\end{array}\right|\)
Solution:
-2
(viii)In which interval does the determinant \(\left|\begin{array}{ccc}
1 & \sin \theta & 1 \\
-\sin \theta & 1 & \sin \theta \\
-1 & -\sin \theta & 1
\end{array}\right|\) lie?
Solution:
[2, 4]
(ix) Ifx + y + z = n, what is the value of Δ = \(\left|\begin{array}{ccc}
\sin (x+y+z) & \sin B & \cos C \\
-\sin B & 0 & \tan A \\
\cos (A+B) & -\tan A & 0
\end{array}\right|\) Where A, B, C are the angles of triangle.
Solution:
0
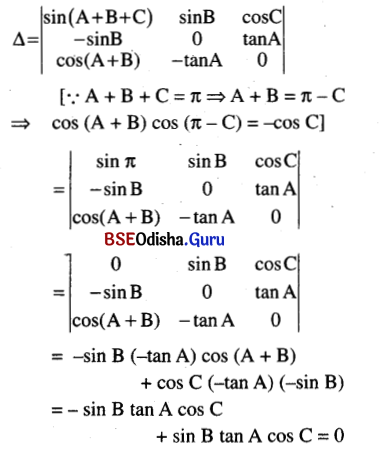
![]()
Question 12.
Evaluate the following determinants:
(i) \(\left|\begin{array}{ccc}
14 & 3 & 28 \\
17 & 9 & 34 \\
25 & 9 & 50
\end{array}\right|\)
Solution:
\(\left|\begin{array}{ccc}
14 & 3 & 28 \\
17 & 9 & 34 \\
25 & 9 & 50
\end{array}\right|\)
= 2\(\left|\begin{array}{ccc}
14 & 3 & 28 \\
17 & 9 & 34 \\
25 & 9 & 50
\end{array}\right|\) = 0
(∵ C1 = C3)
(ii) \(\left|\begin{array}{ccc}
16 & 19 & 13 \\
15 & 18 & 12 \\
14 & 17 & 11
\end{array}\right|\)
Solution:
\(\left|\begin{array}{ccc}
16 & 19 & 13 \\
15 & 18 & 12 \\
14 & 17 & 11
\end{array}\right|\) = \(\left|\begin{array}{ccc}
1 & 1 & 1 \\
1 & 1 & 1 \\
14 & 17 & 11
\end{array}\right|\)
( R1 = R1 – R2, R2 = R2 – R3)
= 0 (∵ R1 = R2)
(iii) \(\left|\begin{array}{ccc}
224 & 777 & 32 \\
735 & 888 & 105 \\
812 & 999 & 116
\end{array}\right|\)
Solution:
\(\left|\begin{array}{ccc}
224 & 777 & 32 \\
735 & 888 & 105 \\
812 & 999 & 116
\end{array}\right|\)
= 7\(\left|\begin{array}{ccc}
32 & 777 & 32 \\
105 & 888 & 105 \\
116 & 999 & 116
\end{array}\right|\) = 0
(∵ C1 = C2)
(iv) \(\left|\begin{array}{lll}
1 & 1 & 1 \\
2 & 3 & 4 \\
3 & 4 & 6
\end{array}\right|\)
Solution:

(v) \(\left|\begin{array}{ccc}
1 & 2 & 3 \\
3 & 5 & 7 \\
8 & 14 & 20
\end{array}\right|\)
Solution:

(vi) \(\left|\begin{array}{ccc}
1^2 & 2^2 & 3^2 \\
2^2 & 3^2 & 4^2 \\
3^2 & 4^2 & 5^2
\end{array}\right|\)
Solution:

= 225 – 256 – 4(100 – 144) + 9(64 – 81)
= -31 – 4(-44) + 9(-17)
= -31 + 176 – 153 = -184 + 176
= -8
(vii) \(\left|\begin{array}{ccc}
1 & 0 & -5863 \\
-7361 & 2 & 7361 \\
1 & 0 & 4137
\end{array}\right|\)
Solution:
\(\left|\begin{array}{ccc}
1 & 0 & -5863 \\
-7361 & 2 & 7361 \\
1 & 0 & 4137
\end{array}\right|\)
= 2\(\left|\begin{array}{cc}
1 & -5863 \\
1 & 4137
\end{array}\right|\)
(expanding along 2nd column)
= 2(4137 + 5863)
= 2 × 10000 = 20000
(viii) \(\left|\begin{array}{lll}
265 & 240 & 219 \\
240 & 225 & 198 \\
219 & 198 & 181
\end{array}\right|\)
Solution:

(ix) \(\left|\begin{array}{ccc}
0 & a^2 & b \\
b^2 & 0 & a^2 \\
a & b^2 & 0
\end{array}\right|\)
Solution:
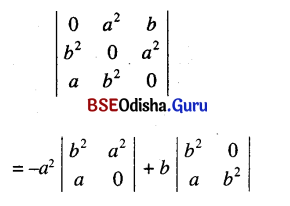
= -a2 (0 – a2) + b (b4 – 0) = a5 + b5
(x) \(\left|\begin{array}{ccc}
a-b & b-c & c-a \\
\boldsymbol{x}-\boldsymbol{y} & \boldsymbol{y}-\boldsymbol{z} & z-\boldsymbol{x} \\
\boldsymbol{p}-\boldsymbol{q} & \boldsymbol{q}-\boldsymbol{r} & \boldsymbol{r}-\boldsymbol{p}
\end{array}\right|\)
Solution:
\(\left|\begin{array}{lll}
a-b & b-c & c-a \\
x-y & y-z & z-x \\
p-q & q-r & r-p
\end{array}\right|\)
= \(\left|\begin{array}{lll}
0 & b-c & c-a \\
0 & y-z & z-x \\
0 & q-r & r-p
\end{array}\right|\) (C1 = C1 + C2 + C3)
= 0 ( ∵ C1 = 0)
![]()
(xi) \(\left|\begin{array}{lll}
a-b & b-c & c-a \\
b-c & c-a & a-b \\
c-a & a-b & b-c
\end{array}\right|\)
Solution:
\(\left|\begin{array}{lll}
a-b & b-c & c-a \\
b-c & c-a & a-b \\
c-a & a-b & b-c
\end{array}\right|\)
= \(\left|\begin{array}{lll}
0 & b-c & c-a \\
0 & c-a & a-b \\
0 & a-b & b-c
\end{array}\right|\) (C1 = C1 + C2 + C3)
= 0
(xii) \(\left|\begin{array}{ccc}
-\cos ^2 \theta & \sec ^2 \theta & -0.2 \\
\cot ^2 \theta & -\tan ^2 \theta & 1.2 \\
-1 & 1 & 1
\end{array}\right|\)
Solution:

(Expanding along 3rd row)
= (-cos2 θ + sec2 θ) (-tan2 θ – 1.2) – (sec2 θ + 0.2) (cot2 θ – tan2 θ)
= sin2 θ – 1.2 cos2 θ – sec2 θ tan2 θ – 1.2 sec2 θ – cosec2 θ + sec2 θ tan2 θ – 0.2 cot2 θ + 0.2 tan2 θ
= sin2 θ – cosec2 θ + 1.2 (cos2 θ – sec2 θ) + 0.2 (tan2 θ – cot2 θ) ≠ 0
The question seems to be wrong.
Question 13.
If \(\left|\begin{array}{ccc}
1 & 1 & 1 \\
1 & 1+x & 1 \\
1 & 1 & 1+y
\end{array}\right|\) = 0 what are x and y?
Solution:

or, xy – 0 = 0 ⇒ xy = 0, ⇒ x = 0, or y = 0
Question 14.
For what value of x \(\left|\begin{array}{ccc}
2 x & 0 & 0 \\
0 & 1 & 2 \\
-1 & 2 & 0
\end{array}\right|\) = \(\left|\begin{array}{lll}
1 & 0 & 0 \\
2 & 3 & 4 \\
0 & 3 & 5
\end{array}\right|\)?
Solution:

Question 15.
Solve \(\left|\begin{array}{ccc}
x+a & 0 & 0 \\
a & x+b & 0 \\
a & 0 & x+c
\end{array}\right|\) = 0
Solution:
\(\left|\begin{array}{ccc}
x+a & 0 & 0 \\
a & x+b & 0 \\
a & 0 & x+c
\end{array}\right|\) = 0
or, (x – a) \(\left|\begin{array}{cc}
x+b & 0 \\
0 & x+c
\end{array}\right|\) = 0
or, (x + a) (x + b) (x + c) = 0
x = -a, x = -b, x = -c
Question 16.
Solve \(\left|\begin{array}{lll}
a+x & a-x & a-x \\
a-x & a+x & a-x \\
a-x & a-x & a+x
\end{array}\right|\) = 0
Solution:

Question 17.
Solve \(\left|\begin{array}{ccc}
x+a & b & c \\
a & x+b & c \\
a & b & x+c
\end{array}\right|\) = 0
Solution:

![]()
Question 18.
Show that x = 2 is a root of \(\left|\begin{array}{ccc}x & -6 & -1 \\ 2 & -3 x & x-3 \\ -3 & 2 x & x+2\end{array}\right|\) = 0 Solve this completely.
Solution:
Putting x = 2,

= (x – 1) (-15x + 30 – 5x2 + 10x)
= (x – 1) (-5x2 – 5x + 30)
= -5(x – 1) (x2 + x – 6)
= -5(x – 1) (x + 3) (x – 2) = 0
⇒ x = 1 or, -3 or 2.
Question 19.
Evaluate \(\left|\begin{array}{ccc}
1 & a & b c \\
1 & b & c a \\
1 & c & a b
\end{array}\right|\) – \(\left|\begin{array}{lll}
1 & a & a^2 \\
1 & b & b^2 \\
1 & c & c^2
\end{array}\right|\)
Solution:
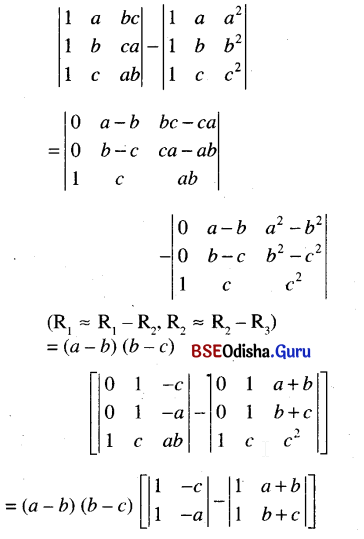
= (a – b) (b – c) [(-a + c) – (b + c – a – b)]
= (a – b) (b – c) (-a + c – c + a) = 0
Question 20.
\(\left|\begin{array}{lll}
a & a^2-b c & 1 \\
b & b^2-a c & 1 \\
c & c^2-a b & 1
\end{array}\right|\)
Solution:

Question21.
For what value of X the system of equations
x + y + z = 6, 4x + λy – λz = 0, 3x + 2y – 4z = -5 does not possess a solution?
Solution:

= 24 – 6λ – 2λ = 24 – 8λ
when Δ = 0
We have 24 – 8λ, = 0 or, λ = 3
The system of equations does not posses solution for λ = 3.
Question 22.
If A is a 3 × 3 matrix and |A| = 2, then which matrix is represented by A × adj A?
Solution:
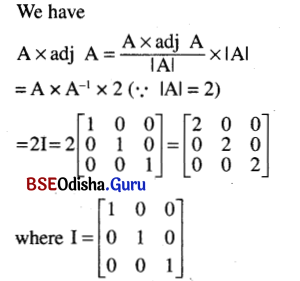
Question 23.
If A = \(\left[\begin{array}{cc}
0 & -\tan \frac{\alpha}{2} \\
\tan \frac{\alpha}{2} & 0
\end{array}\right]\)
show that (I + A) (I – A)-1 = \(\left[\begin{array}{cc}
\cos \alpha & -\sin \alpha \\
\sin \alpha & \cos \alpha
\end{array}\right]\) where I = \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\)
Solution:

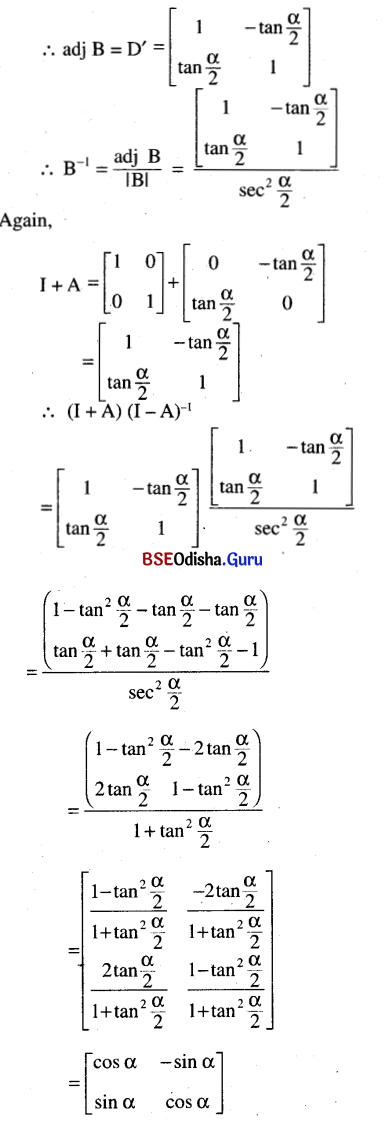
Question 24.
Prove the following:
(i) \(\left|\begin{array}{ccc}
a^2+1 & a b & a c \\
a b & b^2+1 & b c \\
a c & b c & c^2+1
\end{array}\right|\) = 1 + a2 + b2 + c2
Solution:

(ii) \(\left|\begin{array}{ccc}
1 & 1 & 1 \\
a & b & c \\
a^3 & b^3 & c^3
\end{array}\right|\) = (b – c) (c – a) (a – b) (a + b + c)
Solution:

= (a – b) (b – c) (b2 + bc + c2 – a2 – ab – b2)
= (a – b) (b- c) (c2 – a2 + bc – ab)
= (a – b) (b – c) {(c – a) (c + a) + b(c – a)}
= (a – b) (b – c) (c – a) (a + b + c) = R.H.S.
(Proved)
![]()
(iii) \(\left|\begin{array}{lll}
\boldsymbol{a} & \boldsymbol{b} & \boldsymbol{c} \\
\boldsymbol{b} & \boldsymbol{c} & \boldsymbol{a} \\
\boldsymbol{c} & \boldsymbol{a} & \boldsymbol{b}
\end{array}\right|\) = 3abc – a3 – b3 – c3
Solution:

= (a + b + c) {(b – c) (a – b) – (c – a)2}
= (a + b + c) (a + b + c) (ab – b2 – ca + bc – c2 – a2 + 2ca)
= (a + b + c) (-a2 – b2 – c2 + ab + bc + ca)
= -(a + b + c) (a2 + b2 + c2 – ab – bc – ca)
=- (a3 + b3 + c3 – 3abc)
= 3abc – a3 – b3 – c3
(iv) \(\left|\begin{array}{lll}
b^2-a b & b-c & b c-a c \\
a b-a^2 & a-b & b^2-a b \\
b c-a c & c-a & a b-a^2
\end{array}\right|\) = 0
Solution:

= (b2 – a2 + bc – ac) (a – b) {(-a + b) (c – a) – (bc – ac – ab + a2)}
= (b2 – a2 + bc – ac) (a – b) (- ca + a2 + bc – ab – bc + ac + ab – a2)
= (b2 – a2 + bc – ac) (a – b) × 0 = 0
= R.H.S.
(Proved)
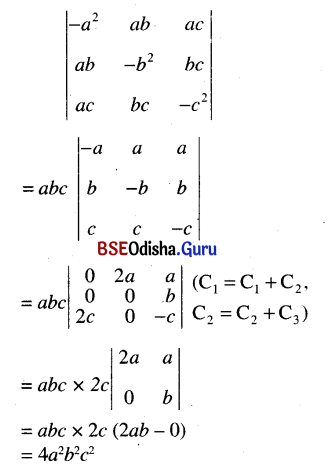
(v) \(\left|\begin{array}{ccc}
-a^2 & a b & a c \\
a b & -b^2 & b c \\
a c & b c & -c^2
\end{array}\right|\) = 4a2b2c2
Solution:
(vi) \(\left|\begin{array}{lll}
(b+c)^2 & a^2 & b c \\
(c+a)^2 & b^2 & c a \\
(a+b)^2 & c^2 & a b
\end{array}\right|\) = (a2 + b2 + c2 ) (a + b + c) (b – c) (c – a) (a – b)
Solution:

= (a – b) (b – c) (a2 + b2 + c2) (-a2 – ab + bc + c2)
= (a – b) (b – c) (a2 + b2 + c2) {(c2 – a2) + b(c – a)}
= (a2 + b2 + c2) (a – b) (b – c) (c – a) (c + a + b)
(vii) \(\left|\begin{array}{lll}
b+c & a+b & a \\
c+a & b+c & b \\
a+b & c+a & c
\end{array}\right|\) = a3 + b3 + c3 – 3abc
Solution:

= (a + b +c) {(a – b) (a – c) – (c – b) (b – c)}
= (a + b + c) (a2 – ac – ab + bc – bc + c2 + b2 – bc)
= (a + b + c) (a2 + b2 + c2 – ab – bc – ca)
= (a3 + b3 + c3 – 3abc)
(viii) \(\left|\begin{array}{ccc}
a+b+c & -c & -b \\
-c & a+b+c & -a \\
-b & -a & a+b+c
\end{array}\right|\) = 2(b + c) (c + a) (a + b)
Solution:

= -2(a + b) (b + c) (-a – b – c + b)
= 2(a + b) (b + c) (c + a)
(ix) \(\left|\begin{array}{ccc}
a x-b y-c z & a y+b x & a z+c x \\
b x+a y & b y-c z-a x & b z+c y \\
c x+a z & a y+b z & c z-a x-b y
\end{array}\right|\) = (a2 + b2 + c2) (ax + by + cz) (x2 + y2 + z2)
Solution:


![]()
Question 25.
If 2s = a + b + c show that \(\left|\begin{array}{ccc}
a^2 & (s-a)^2 & (s-a)^2 \\
(s-b)^2 & b^2 & (s-b)^2 \\
(s-c)^2 & (s-c)^2 & c^2
\end{array}\right|\) = 2s3 (s – a) (s – b) (s – c)
Solution:
Let s – a = A, s – b = B, s – c = C
A + B + C = 3s – (a + b + c)
= 3s – 2s = s
Also B + C = s – b + s – c = 2s – (b + c)
= (a + b + c) – b + c = a
Similarly C + A = b, A + B = c

= 2 ABC (A + B + C)2
[Refer Q.No.9 (xii) of Exercise 5(a)]
= 2(s – a) (s – b)(s – c) s3
Question 26.
if \(\left|\begin{array}{ccc}
x & x^2 & x^3-1 \\
y & y^2 & y^3-1 \\
z & z^2 & z^3-1
\end{array}\right|\) = 0 then prove that xyz =1 when x, y, z are non zero and unequal.
Solution:

= (x – y) (y – z) (z – x) (xyz – 1)
It is given that
(x – y) (y – z) (z – x) (xyz – 1) = 0
⇒ xyz – 1 (as x ≠ y ≠ z)
Question 27.
Without expanding show that the following determinant is equal to Ax + B where A and B are determinants of order 3 not involving x.
\(\left|\begin{array}{ccc}
x^2+x & x+1 & x-2 \\
2 x^2+3 x-1 & 3 x & 3 x-3 \\
x^2+2 x+3 & 2 x-1 & 2 x-1
\end{array}\right|\)
Solution:

Question 28.
If x, y, z are positive and are the pth, qth and rth terms of a G.P. then prove that \(\left|\begin{array}{lll}
\log x & p & 1 \\
\log y & q & 1 \\
\log z & r & 1
\end{array}\right|\) = 0
Solution:
Let the G.P. be
a, aR, aR2, aR3 …..aRn-1
p th term = aRp-1
q th term = aRq-1
r th term = aRr-1
x = aRp-1, y= aRq-1, z = aRr-1
log x = log a + (p – 1) log R,
log y = log a + (q – 1) log R,
log z = log a + (r – 1) log R

![]()
Question 29.
If Dj = \(\left|\begin{array}{ccc}
j & a & n(n+2) / 2 \\
j^2 & b & n(n+1)(2 n+1) / 6 \\
j^3 & c & n^2(n+1)^2 / 4
\end{array}\right|\) then prove that \(\sum_{j=1}^n\)Dj = 0.
Solution:

Question 30.
Ifa1, a2,……an are in G.P. and ai > 0 for every i, then find the value of
\(\left|\begin{array}{ccc}
\log a_n & \log a_{n+1} & \log a_{n+2} \\
\log a_{n+1} & \log a_{n+2} & \log a_{n+3} \\
\log a_{n+2} & \log a_{n+3} & \log a_{n+4}
\end{array}\right|\)
Solution:

Question 31.
If f(x)= \(\left|\begin{array}{ccc}
1+\sin ^2 x & \cos ^2 x & 4 \sin ^2 x \\
\sin ^2 x & 1+\cos ^2 x & 4 \sin 2 x \\
\sin ^2 x & \cos ^2 x & 1+4 \sin ^2 x
\end{array}\right|\) what is the least value of f(x)?
Solution:

As minimum value of sin 2x is 0. So the minimum value of above function f(x) is 2.
Question 32.
If fr(x), gr(x), hr(x), r = 1, 2, 3 are polynomials in x such that fr(a) = gr(a) = hr(a) and
F(x) = \(\left[\begin{array}{lll}
f_1(x) & f_2(x) & f_3(x) \\
g_1(x) & g_2(x) & g_3(x) \\
h_1(x) & h_2(x) & h_3(x)
\end{array}\right]\) find F'(x) at x = a.
Solution:
We have

[Since f1a) = g1(a) = h1(a), f2(a) = g2(a) = h2(a) and f3(a) = g3(a) = h3(a) So that each determinant is zero due to presence of two identical rows.]
![]()
Question 33.
If f(x) = \(\left[\begin{array}{ccc}
\cos x & \sin x & \cos x \\
\cos 2 x & \sin 2 x & 2 \cos 2 x \\
\cos 3 x & \sin 3 x & 3 \cos 3 x
\end{array}\right]\) find f'(\(\frac{\pi}{2}\)).
Solution:

