Odisha State Board Elements of Mathematics Class 11 CHSE Odisha Solutions Chapter 7 Linear Inequalities Ex 7(c) Textbook Exercise Questions and Answers.
CHSE Odisha Class 11 Math Solutions Chapter 7 Linear Inequalities Exercise 7(c)
Solve the following systems of linear inequalities graphically.
Question 1.
2x – y ≥ 0, x – 2y ≤ 0, x ≤ 2, y ≤ 2 [Hint: You may consider the point (2, 2) to determine the SR of the first two inequalities.]
Solution:
2x – y ≥ 0
x – 2y ≤ 0
x ≤ 2
y ≤ 2
Step – 1: Let us draw the lines.
2x – y = 0, x – 2y = 0, x = 2, y = 2
2x – y = 0
| X | 0 | 1 |
| y | 0 | 2 |
x – 2y = 0
| X | 0 | 2 |
| y | 0 | 1 |
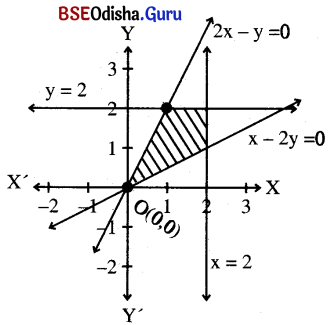
Step – 2: Let us consider point (1, 0) which does not line on any of these lines.
Putting x = 1, y = 0 in the inequations we get
2 ≥ 0 (True)
1 ≤ 0 (False)
1 ≤ 2 (True)
0 ≤ 2 (True)
Point (1, 0) satisfies all inequality except x – 2y < 0.
∴ Thus the shaded region is the solution region.
![]()
Question 2.
x – y < 1, y – x < 1
Solution:
x – y < 1
y – x < 1
Step – 1: Let us draw the dotted lines.
x – y = 1 and y – x = 1
x – y = 1 ⇒ y = x – 1
| X | 1 | 0 |
| y | 0 | -1 |
y – x = 1 ⇒ y = x + 1
| X | 0 | -1 |
| y | 1 | 0 |
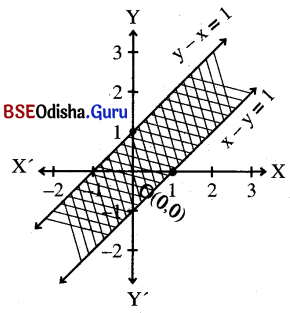
Step – 2: Let us consider the point (0, 0) which does not lie on these lines.
Putting x = 0, y = 0 in the inequations
we get
0 < 1 (True)
0 < 1 (True)
∴ (0, 0) satisfies both the inequations.
∴ Thus the shaded region is the feasible region.
Question 3.
x – 2y + 2 < 0, x > 0
Solution:
x – 2y + 2 < 0, x > 0
Step – 1: Let us draw the dotted line x – 2y + 2 = 0
⇒ y = \(\frac{x+2}{2}\)
| X | -2 | 0 |
| y | 0 | 1 |
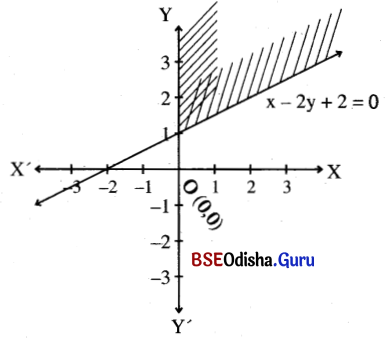
Step – 2: Let us consider the point (1, 0) that does not lie on the lines putting x = 0, y = 0 in the inequation, we get
2 < 0 (false)
1 > 0 (True)
⇒ (1, 0) satisfies x > 0 and does not satisfy x – 2y + 2 < 0.
∴ Thus the shaded region is the solution region.
Question 4.
x – y + 1 ≥ 0, 3x + 4y ≤ 12, x ≥ 0, y ≥ 0
Solution:
x – y + 1 ≥ 0
3x + 4y ≤ 12
x ≥ 0, y ≥ 0
Step – 1: Let us draw the lines.
x – y + 1 = 0
3x + 4y = 12
Now, x – y + 1 = 0 ⇒ y = x + 1
| X | 0 | -1 |
| y | 1 | 0 |
3x + 4y = 12
| X | 4 | 0 |
| y | 0 | 3 |
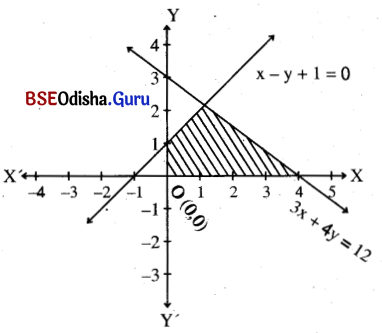
Step – 2: Let us consider the point (0, 0) which does not lie on these lines.
Putting x = 0, y = 0 in the inequations
we get
1 ≥ 0 (True)
0 ≤ 12 (False)
∴ (0, 0) satisfies both the inequations and x > 0, y > 0 is the first quadrant.
∴ Thus the shaded region is the solution region.
![]()
Question 5.
x + y > 1, 3x – y < 3, x – 3y + 3 > 0
Solution:
x + y > 1
3x – y < 3
x – 3y + 3 > 0
Step – 1: Let us draw the lines.
x + y = 1
3x – y = 3
x – 3y + 3 = 0
Now x + y = 1
⇒ y = 1 – x
| X | 1 | 0 |
| y | 0 | 1 |
3x – y = 3
⇒ y = 3x – 3
| X | 1 | 0 |
| y | 0 | -3 |
x – 3y + 3 = 0
⇒ y = \(\frac{x+3}{3}\)
| X | -3 | 0 |
| y | 0 | 1 |
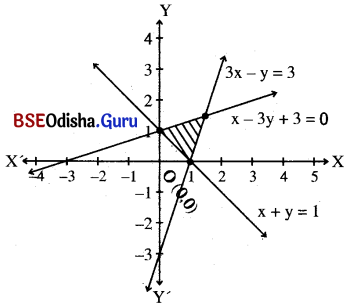
Step – 2: Let us consider the point (0, 0) that does not lie on these lines. Putting x = 0, y = 0 in the inequations we get,
0 > 1 (False)
0 < 3 (True)
3 > 0 (True)
Thus (0, 0) satisfies 3x – y < 3 and x – 3y + 3 > 0 but does not satisfy x + y > 1
∴ The shaded region is the solution region.
Question 6.
x > y, x < 1, y > 0
Solution:
x > y, x < 1, y > 0
Step – 1: Let us draw the dotted lines.
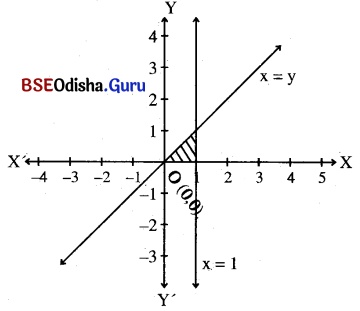
Step – 2: Let us consider a point (2, 1) that does not lie on any of the lines.
Putting x = 2, y = 2 in the inequations
we get,
2 > 1 (True)
2 < 1 (False)
1 > 0 (True)
⇒ (2, 1) satisfies x > y and y > 0 but does not satisfy x < 1.
∴ Thus the shaded region is the solution region.
Question 7.
x < y, x > 0, y < 1
Solution:
x < y
x > 0
y < 1
Step – 1: Let us draw the dotted lines.
x = y
x = 0
and y = 1
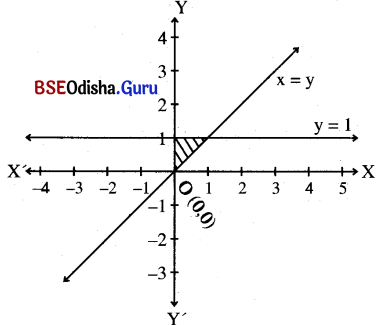
Step – 2: Let us consider point (1, 0) that does not lie on these lines.
Putting x = 0, y = 0 in the inequations
we get
1 < 0 (False)
1 > 0 (True)
0 < 1 (True)
Clearly (1, 0) satisfies x > 0, y < 1 but does not satisfy x < y.
∴ The shaded region is the solution region.
