BSE Odisha 10th Class Maths Solutions Algebra Chapter 1 ସରଳ ସହସମୀକରଣ Ex 1(a)

Odisha State Board BSE Odisha 10th Class Maths Solutions Algebra Chapter 1 ସରଳ ସହସମୀକରଣ Ex 1(a) Textbook Exercise Questions and Answers.

BSE Odisha Class 10 Maths Solutions Algebra Chapter 1 ସରଳ ସହସମୀକରଣ Ex 1(a)

Question 1.
ବନ୍ଧନୀ ମଧ୍ଯରୁ ଠିକ୍ ଉତ୍ତରଟି ବାଛି ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(i) x + y = 0 ସମୀକରଣର ଅନ୍ୟତମ ସମାଧାନ ___________ । [(4, 5), (5, 5), (- 4, 4), (-4, 5)]
(ii) x – 2y = 0 ସମୀକରଣର ଅନ୍ୟତମ ସମାଧାନ ___________ । [(4, 2), (- 4, 2), (4, – 2), (- 4, – 2)]
(iii) 2x + y + 2 = 0 ସମୀକରଣର ଅନ୍ୟତମ ସମାଧାନ ___________ । [(0, 2), (2, 0), (- 2, 0), (0, – 2)]
(iv) x – 4y + 1 = 0 ହେଲେ x = ______ । [4y-1, 4y+1,-4y + 1, -4y – 1]
(v) 2x-y+2 = 0 ହେଲେ y = ______ । [2x – 2, 2x + 2, 2x – 2, – 2x – 2]
(vi) x-2y + 3 = 0 ହେଲେ y = ______ । [½(x + 3), – ½(x – 3), – ½(-x + 3), – ½(x + 3)]
ଜ –
(i) (- 4, 4), (ii) (4, 2), (iii) (0, – 2), (iv) 4y – 1, (v) 2x + 2, (vi) 1⁄2 (x + 3)
ବ୍ୟାଖ୍ୟା ସହ ଉତ୍ତର :
(i) x + y = 0 ସମୀକରଣର ଅନ୍ୟତମ ସମାଧାନ (- 4, 4) । (କାରଣ -x = y)

(ii) x – 2y = 0 ସମୀକରଣର ଅନ୍ୟତମ ସମାଧାନ (4, 2) ଓ (- 4, -2) (କାରଣ x = 2y)

(iii) 2x + y + 2 = 0 ସମୀକରଣର ଅନ୍ୟତମ ସମାଧାନ (0, -2) (କାରଣ 2x = -(y+2))

(iv) x – 4y + 1 = 0 ⇒ x = 4y – 1

(v) 2x – y + 2 = 0 ⇒ 2x +2 = y ⇒ y = 2x + 2

(vi) x-2y+3 = 0 ⇒ x + 3 = 2y ⇒ y = ½(x +3)

Question 2.
ନିମ୍ନରେ ଦତ୍ତ ସହସମୀକରଣ ଯୋଡ଼ିରୁ କେଉଁ ସମୀକରଣ ଯୋଡ଼ି କ୍ଷେତ୍ରରେ
(i) ଅନନ୍ୟ ସମାଧାନ ସମ୍ଭବ
(ii) ଅସଂଖ୍ୟ ସମାଧାନ ସମ୍ଭବ ଏବଂ
(iii) ସମାଧାନ ସମ୍ଭବ ନୁହେଁ ?
(i) x + y + 1 = 0, x – y + 1 = 0
(ii) x + y + 1 = 0, 2x + 2y + 2 = 0
(iii) x + y + 1 = 0, x + y + 3 = 0
(iv) 2x – y + 3 = 0, – 4x + 2y – 6=0
(v) 2x – y + 3 = 0, 2x + y -3 = 0
(vi) 2x – y+3 = 0, – 6x + 3y+5=0
ସମାଧାନ :
a₁x+by+ c₂ = 0 ଏବଂ a₂x + b2y + c2 = 0 ସମୀକରେ
(i) ଅନନ୍ୟ ସମାଧାନ ସମ୍ଭବ, ଯଦି \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\) ହେବ
(ii) ଅସଂଖ୍ୟ ସମାଧାନ ସମ୍ଭବ, ଯଦି \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\) ହେବ ଏବଂ
(iii) ସମାଧାନ ଅସମ୍ଭବ, ଯଦି \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\) ହେବ ।

(i) ସହସମୀକରଣହଊ (a) x + y + 1 = 0 ଏଠାରେ a₁ = 1, b₁ = 1, c₁ = 1
(b) x – y + 1 = 0 ଏବଂ a₂ = 1, b₂ = – 1, c₂ = 1
∴ \(\frac{a_1}{a_2}=\frac{1}{1}=1\), \(\frac{b_1}{b_2}=\frac{1}{-1}=-1\)
ଏଠାରେ \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\) ହେତୁ ସମୀକରଣ ଦ୍ଵୟର ଅନନ୍ୟ ସମାଧାନ ରହିବ ।

(ii) ସମୀକରଣଦ୍ଵୟ x + y + 1 = 0 ଓ 2x + 2y + 2 = 0
ଏଠାରେ a₁ = 1, b₁ = 1, c₁ = 1 ଏବଂ a₂ = 2, b₂ = 2, c₂ = 2
∴ \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\) ହେତୁ ସମୀକରଣ ଦ୍ଵୟର ଅନନ୍ୟ ସମାଧାନ ସମ୍ଭବ।

(iii) ସମୀକରଣଦ୍ଵୟ x + y + 1 = 0 ଓ x + y + 3 = 0
ଏଠାରେ a₁ = 1, b₁ = 1, c₁ = 1 ଏବଂ a₂ = 1, b₂ = 1, c₂ = 3
∴ \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\) ହେତୁ ସମାଧାନ ସମ୍ଭବ ନୁହେଁ ।

(iv) 2x – y + 3 = 0 ଓ – 4x + 2y – 6 = 0
ଏଠାରେ a₁ = 2, b₁ = -1, c₁ = 3; a₂ = -4, b₂ = 2, c₂ = -6
∴ \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\) ହେତୁ ସମୀକରଣ ଦ୍ଵୟର ଅନନ୍ୟ ସମାଧାନ ରହିବ ।

(v) 2x – y + 3 = 0, 2x + y – 3 = 0
ଏଠାରେ a₁ = 2, b₁ = -1, c₁ = 3; a₂ = 2, b₂ = 1, c₂ = -3
∴ \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\) ହେତୁ ଅନନ୍ୟ ସମାଧାନ ସମ୍ଭବ ।

(vi) 2x – y + 3 = 0, -6x + 3y + 5 = 0
ଏଠାରେ a₁ = 2, b₁ = -1, c₁ = 3; a₂ = -6, b₂ = 3, c₂ = 5
∴ \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\) ହେତୁ ସମାଧାନ ସମ୍ଭବ ନୁହେଁ ।

Question 3.
ନିମ୍ନଲିଖୂତ ସମୀକରଣଗୁଡ଼ିକର ଲେଖଚିତ୍ର ଅଙ୍କନ ପାଇଁ ଯେକୌଣସି ତିନିଗୋଟି ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ନିରୂପଣ କର ।
(i) x – y = 0
(ii) x + y = 0
(iii) x – 2y = 0
(iv) x + 2y – 4 = 0
(v) x – 2y – 4 = 0
(vi) 2x – y + 4 = 0
ସମାଧାନ : ଏକଘାତୀ ଦୁଇ ଅଜ୍ଞାତ ରାଶିବିଶିଷ୍ଟ ସମୀକରଣର ଅସଂଖ୍ୟ ସମାଧାନ ଥାଏ ।
(i) x – y = 0
⇒ x = y ⇒ y = x

x	1	-2	3
y	1	-2	3

‘x’ର ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ମାନପାଇଁ yର ଆନୁସଙ୍ଗିକ ମାନ ସାରଣୀରେ ନିର୍ଣ୍ଣୟ କରାଯାଇଛି ।
∴ ଦତ୍ତ ସମୀକରଣର ଲେଖଚିତ୍ର ପାଇଁ ତିନୋଟି ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (1, 1), (- 2, · 2) ଏବଂ (3, 3) ।

(ii) x + y = 0
⇒ y = -x

x	-1	2	-3
y	1	-2	3

‘x’ର ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ମାନପାଇଁ yର ଆନୁସଙ୍ଗିକ ମାନ ସାରଣୀରେ ନିର୍ଣ୍ଣୟ କରାଯାଇଛି ।
∴ ଦତ୍ତ ସମୀକରଣର ଲେଖଚିତ୍ର ପାଇଁ ତିନୋଟି ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (- 1, 1), (2, − 2) ଏବଂ (-3, 3) ।

(iii) x – 2y = 0 ⇒ x = 2y
⇒ y = \(\frac{1}{2}\)x

x	2	-2	4
y	1	-1	2

‘x’ର ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ମାନପାଇଁ ଦୂର ଆନୁସଙ୍ଗିକ ମାନ ସାରଣୀରେ ନିର୍ଣ୍ଣୟ କରାଯାଇଛି ।
∴ ଦତ୍ତ ସମୀକରଣର ଲେଖଚିତ୍ର ପାଇଁ ତିନୋଟି ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (2, 1), (- 2, – 1) ଏବଂ (4, 2) ।

(iv) x + 2y – 4 = 0 ⇒ 2y = 4 – x
⇒ y = \(\frac{1}{2}\)(4 – x)

x	0	4	2
y	2	0	1

‘x’ର ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ମାନପାଇଁ yର ଆନୁସଙ୍ଗିକ ମାନ ସାରଣୀରେ ନିର୍ଣ୍ଣୟ କରାଯାଇଛି ।
∴ ଦତ୍ତ ସମୀକରଣର ଲେଖଚିତ୍ର ପାଇଁ ତିନୋଟି ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (0, 2), (4, 0) ଏବଂ (2, 1) ।

(v) x – 2y – 4 = 0 ⇒ x – 4 = 2y
⇒ y = \(\frac{1}{2}\) (x – 4)

x	0	4	2
y	-2	0	-1

‘x’ର ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ମାନପାଇଁ yର ଆନୁସଙ୍ଗିକ ମାନ ସାରଣୀରେ ନିର୍ଣ୍ଣୟ କରାଯାଇଛି ।
∴ ଦତ୍ତ ସମୀକରଣର ଲେଖଚିତ୍ର ପାଇଁ ତିନୋଟି ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (0, -2), (4, 0) ଏବଂ (2, -1) ।

(vi) 2x – y + 4 = 0 ⇒ 2x + 4 = y
⇒ y = 2x + 4

x	-2	0	1
y	0	4	6

‘x’ର ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ମାନପାଇଁ yର ଆନୁସଙ୍ଗିକ ମାନ ସାରଣୀରେ ନିର୍ଣ୍ଣୟ କରାଯାଇଛି ।
∴ ଦତ୍ତ ସମୀକରଣର ଲେଖଚିତ୍ର ପାଇଁ ତିନୋଟି ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (-2, 0), (0, 4) ଏବଂ (1, 6) ।

Question 4.
ନିମ୍ନଲିଖୂତ ପ୍ରଶ୍ନଗୁଡ଼ିକର ସଂକ୍ଷିପ୍ତ ଉତ୍ତର ଆବଶ୍ୟକ ।
(i) kx + my + 4 = 0 ଓ 2x + y + 1 = 0 ସମୀକରଣଦ୍ଵୟ ଅସଙ୍ଗତ ହେଲେ k : m କେତେ ?
(ii) 2x + 3y – 5 = 0 ଓ 7x – 6y – 1 = 0 ସହସମୀକରଣଦ୍ୱୟର ସମାଧାନ (1, ß) ହେଲେ ßର ମୂଲ୍ୟ କେତେ ?
(ii) ‘t’ ର କେଉଁ ମାନ ପାଇଁ (1, 1), ସମୀକରଣ 3x + ty – 6 = 0 ଅନ୍ୟ ଏକ ସମାଧାନ ହେବ ?
(iv) ‘t’ ର କେଉଁ ମାନ ପାଇଁ (1, 1), tx – 2y – 10 = 0 ର ଅନ୍ୟତମ ସମାଧାନ ହେବ ?
(v) ‘t’ର କେଉଁ ମାନ ପାଇଁ tx + 2y = 0 ଓ 3x + ty = 0 ସହସମୀକରଣଦ୍ୱୟର ଅସଂଖ୍ୟ ସମାଧାନ ସମ୍ଭବ ?
(vi) ଦର୍ଶାଅ ଯେ, 6x – 3y + 10 = 0 ଓ 2x – y + 9 = 0 ସହସମୀକରଣଦ୍ଵୟର ସମାଧାନ ଅସମ୍ଭବ।
(vi) ଦର୍ଶାଅ ଯେ, 2x + 5y = 17 ଏବଂ 5x + 3y = 14 ସହସମୀକରଣଦ୍ଵୟ ସଙ୍ଗୀତ ଓ ସ୍ୱତନ୍ତ୍ର ।
(viii) ଦର୍ଶାଅ ଯେ, 3x – 5y – 10 = 0 ଏବଂ 6x – 10y = 20 ସହସମୀକରଣଦ୍ୱୟର ଅସଂଖ୍ୟ ସମାଧାନ ରହିଛି ।
ସମାଧାନ :
(i) kx + my + 4 = 0 ଏବଂ 2x + y + 1 = 0
ସମୀକରଣଦ୍ୱୟରେ a₁ = k, b₁ = m, c₁ = 4 ଏବଂ a₂ = 2, b₂ = 1, c₁ = 1
ଏଠାରେ ସମୀକରଣ ଦ୍ଵୟ ଅସଙ୍ଗତ ହେବାର ସର୍ଭ,
\(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)
∴ ନିଶ୍ଚେୟ ଅନୁପାତ k:m = 2:1

(ii) 2x + 3y – 5 = 0 8 7x – 6y – 1 = 0 APANIMNAGAR AFIUIA (1, ß)
ଏଠାରେ ‘x’ର ମାନ 1 ଓ yର ମାନ ‘B’ ପାଇଁ ସମୀକରଣଦ୍ଵୟ ସିଦ୍ଧ ହେବ ।
.. 2(1) + 3(B) −5 = 0 ⇒ 2 + 3ß – 5 = 0
⇒3ß – 3 = 0 ⇒ ß \(\frac{3}{3}\) = 1⇒ ß = 1
∴ ß ର ମୂଲ୍ୟ 1 ପାଇଁ ସହସମୀକରଣର ସମାଧାନ (1, ß) ହେବ ।

(iii) ଦତ୍ତ ସମୀକରଣ 3x + ty – 6 = 0 ର ଏକ ସମାଧାନ (1, 1) ହେଲେ
x = 1 ଓ y = 1 ପାଇଁ ସମୀକରଣଦ୍ଵୟ ସିଦ୍ଧ ହେବ ।
∴ 3(1) + t (1) – 6 = 0 ⇒ 3 + t – 6 = 0 ⇒ t – 3 = 0 ⇒ t = 3
∴ ର ମୂଲ୍ୟ 3 ପାଇଁ (1, 1), ସମୀକରଣ 3x + ty – 6 = )ର ଏକ ସମାଧାନ ହେବ ।

(iv) ଦର ସମୀକରଣ tx – 2y – 10 = 0 ର ସମାଧାନ (1,1) ହେଲେ,
x = 1 ଓ y = 1 ପାଇଁ ସମୀକରଣଦ୍ଵୟ ସିଦ୍ଧ ହେବ ।
∴ t(1) – 2(1) – 10 = 0 ⇒ t – 2 – 10 = 0 ⇒ t – 12 = 0 ⇒ t = 12
∴ t ର ମାନ 12 ପାଇଁ (1, 1), ଦତ୍ତ ସମୀକରଣର ଏକ ସମାଧାନ ହେବ ।

(v) tx + 2y = 0 ଓ 3x + ty = 0
ସହସମୀକରଣଦ୍ଵୟର ଅସଂଖ୍ୟ ସମାଧାନ ସମ୍ଭବ ହେବାର ସର୍ଭ
\(\frac{a_1}{a_2}=\frac{b_1}{b_2}\)
⇒ \(\frac{t}{3}=\frac{2}{t}\) ⇒ t² = 6 ⇒ t = ±√6
∴ t ର ମାନ ±√6 ପାଇଁ ସହସମୀକରଣ ଦ୍ଵୟର ଅସଂଖ୍ୟ ମାନ ସମ୍ଭବ ।

(vi)

(vii) 2x + 5y = 17 ⇒ 2x + 5y – 17 = 0….. ..(1)
5x + 3y = 14 ⇒ 5x + 3y – 14 = 0………(2)
ସମୀକରଣ (1) ଓ (2) ରୁ a₁ = 2, b₁ = 5, c₁ = – 17 ଓ a₂ = 5, b₂ = 3, c₂ = – 14
∴ \(\frac{a_1}{a_2}=\frac{2}{5}\), \(\frac{b_1}{b_2}=\frac{5}{3}\), \(\frac{c_1}{c_2}=\frac{-17}{-14}=\frac{17}{14}\)
ଏଠାରେ ଲକ୍ଷ୍ୟ କର ଯେ \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)
∴ ସହସମୀକରଣ ଦ୍ଵୟ ସଙ୍ଗତ ଓ ସ୍ୱତନ୍ତ୍ର

(viii) 3x – 5y – 10 = 0;
6x – 10y = 20 ⇒ 6x – 10y – 20 = 0

Question 5.
ଲେଖଚିତ୍ର ଅଙ୍କନ କରି ନିମ୍ନଲିଖ୍ ସହସମୀକରଣଦ୍ଵୟର ସମାଧାନ କର ।
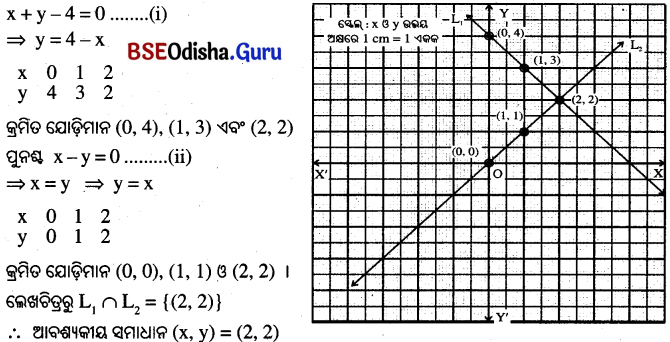
(i) x + y – 4 = 0 ଓ x − y = 0
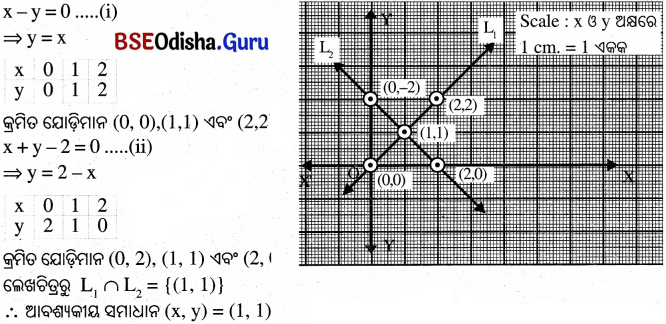
(i) x − y = 0 ଓ x + y – 2 = 0
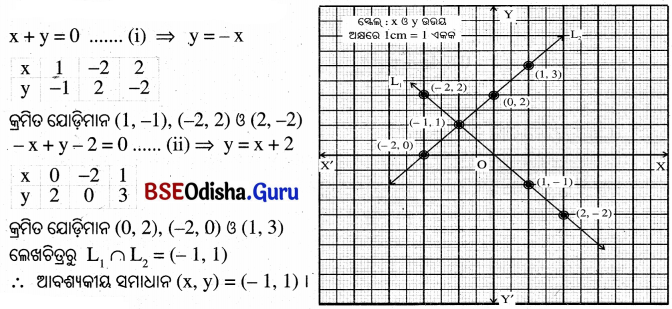
(iii) x + y = 0 ଓ – x + Y – 2 = 0
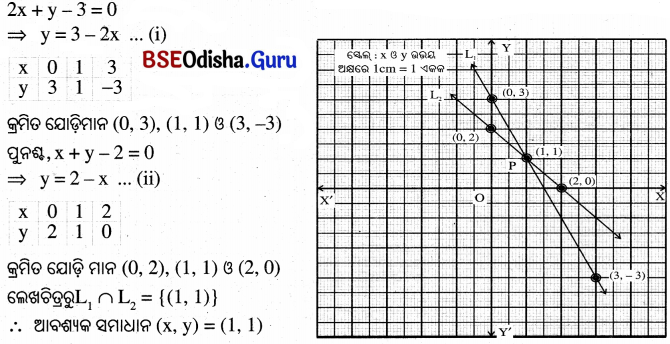
(iv) 2x + y − 3 = 0 6 x + y − 2 = 0
(v) 3x + y + 2 = 0 ଓ 2x + y + 1 = 0
(vi) x + 2y + 3 = 0 ଓ 2x + y + 3 = 0
(vii) 2x + y = 6 = 0 ଓ 2x − y + 2 = 0
(viii)x + y − 1 = 0 ଓ 2x + y − 8 = 0
(ix) 3x + y – 11 = 0 ଓ x – y – 1 = 0
(x) 2x – 3y – 5 = 0 ଓ – 4x + 6y – 3 = 0
(xi) 2x + y + 2 = 0 ଓ 4x – y – 8 = 0
(xii) 3x + 4y – 7 = 0 ଓ 5x + 2y – 7 = 0
ସମାଧାନ :
(i) ଦୁଇ ଅଜ୍ଞାତ ରାଶିବିଶିଷ୍ଟ ଏକଘାତୀ ସମୀକରଣରେ y ର ମାନକୁ x ମାଧ୍ୟମରେ ପ୍ରକାଶ କର ।
(ii) ‘x’ର ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ମାନକୁ ନେଇ ‘y’ର ଆନୁସଙ୍ଗିକ ମାନ ସ୍ଥିର କର । ଅତି କମ୍‌ରେ ତିନିଯୋଡା ମାନ ସ୍ଥିର କରିବାକୁ ହେବ ।
(iii) ପରବର୍ତୀ ସମୟରେ ତିନିଯୋଡା ମାନକୁ ନେଇ R² ସମତଳରେ ତିନୋଟି ବିନ୍ଦୁ ସ୍ଥାପନ କର ।
(iv) ଏକ ଲେଖଚିତ୍ର (ସରଳରେଖା) ଅଙ୍କନ କର ।
(i)

(ii)

(iii)

(iv)

(v)

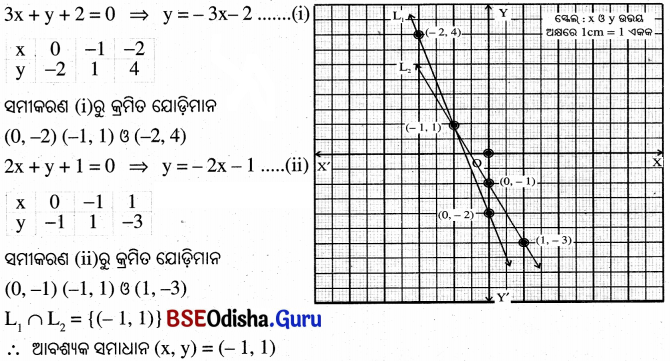
(vi)

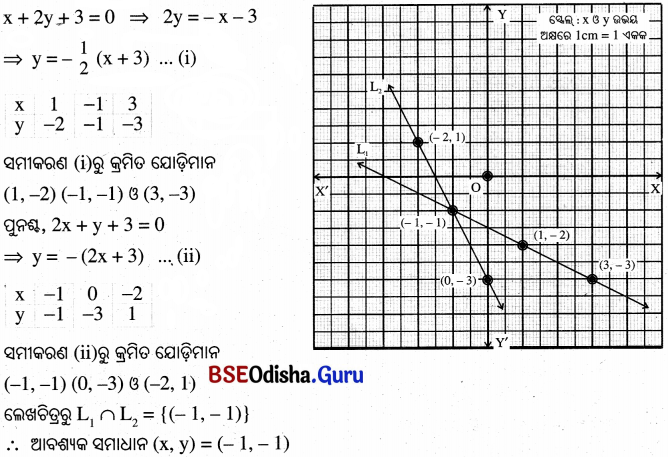
(vii)

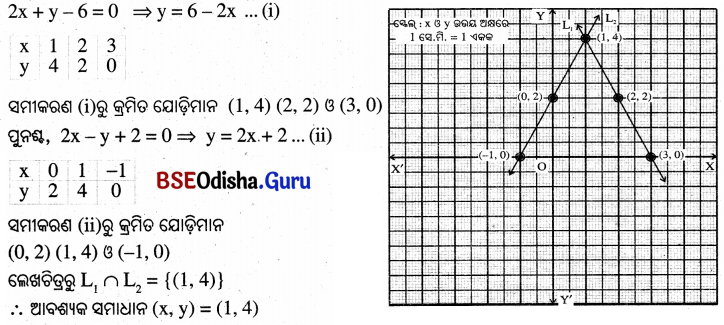
(viii)

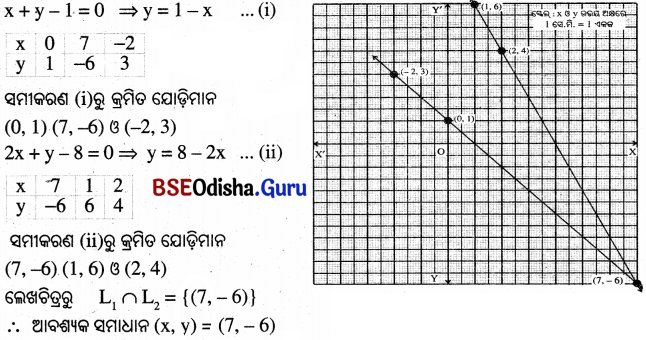
(ix)

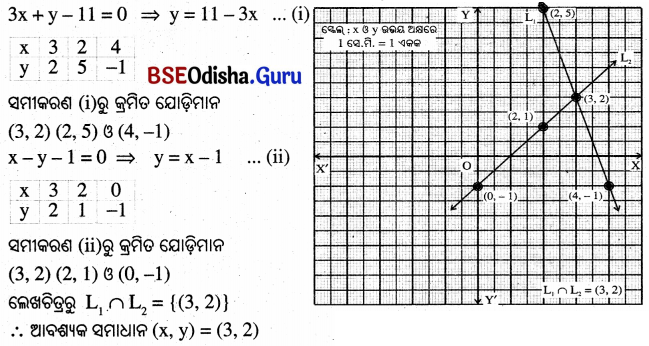
(x)

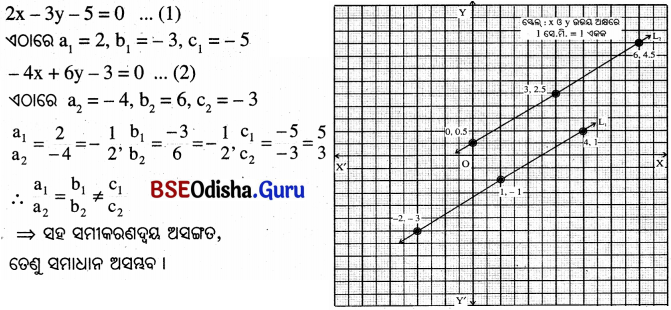
(xi)

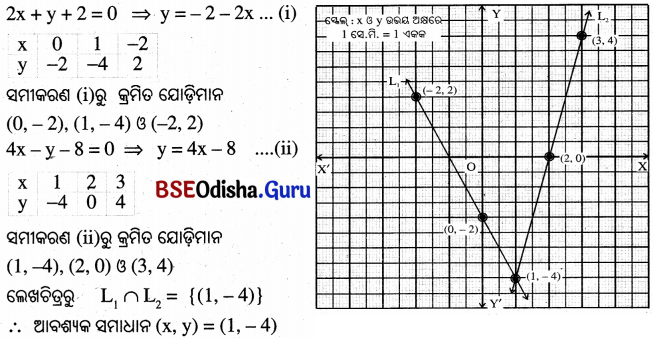
(xii)

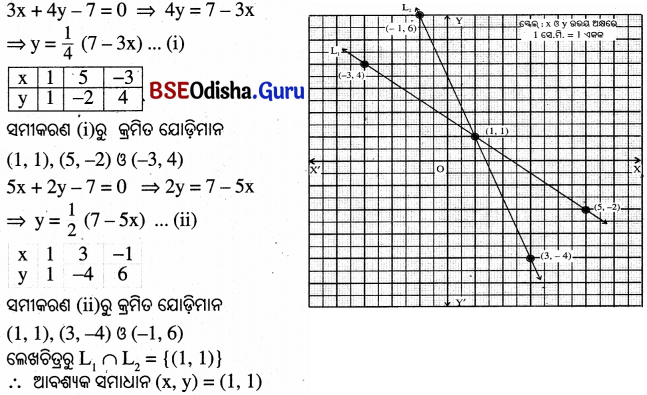
Question 6.
(i) ଲେଖଚିତ୍ର ସାହାଯ୍ୟରେ ଦର୍ଶାଅ ଯେ, 2x – 2y = 2 ଏବଂ 4x – 4y – 8 = 0 ସହସମୀକରଣଦ୍ୱୟର ସମାଧାନ ଅସମ୍ଭଵ ।
(ii) ଲେଖଚିତ୍ର ସାହାଯ୍ୟରେ ଦର୍ଶାଅ ଯେ, 2x – 3y = 1 ଏବଂ 3x-4y = 1 ସହସମୀକରଣଦ୍ୱୟର ଏକ ଅନନ୍ୟ ସମାଧାନ ଅଛି ।
(iii) ଲେଖଚିତ୍ର ସାହାଯ୍ୟରେ ଦର୍ଶାଅ ଯେ, 9x + 3y + 12 = 0 18x + 6y+ 24 = 0 ସହସମୀକରଣଦ୍ୱୟର ଏକ ଅନନ୍ୟ ସମାଧାନ ଅଛି ।
(iv) ଲେଖଚିତ୍ର ସାହାଯ୍ୟରେ 2x – y = 1 ଏବଂ x + 2y = 8 ସହସମୀକରଣଦ୍ୱୟର ପ୍ରତ୍ୟେକର y-ଛେଦଂଶ ନିରୂପଣ କର ।
ସମାଧାନ :
(i)

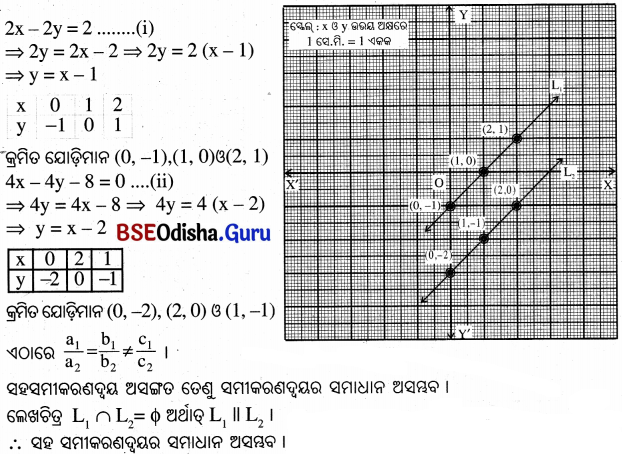
(ii)

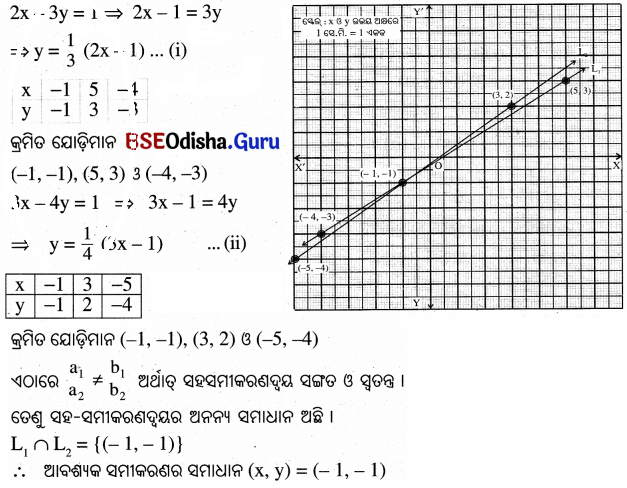
(iii)

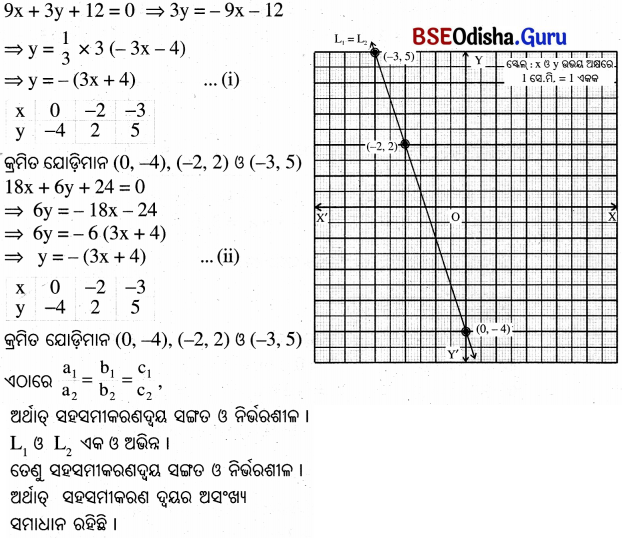
(iv)

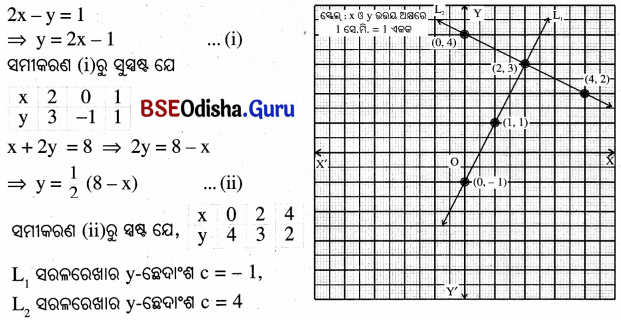
Question 7.
ନିମ୍ନରେ ପ୍ରଦତ୍ତ ସହ-ସମୀକରଣ ଦ୍ଵୟର ଅନନ୍ୟ ସମାଧାନ ସମ୍ଭବ ହେଲେ ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ରରେ k ର ମାନ ସ୍ଥିର କର ।
(i) x – 2y – 3 = 0, 3x + ky – 1 = 0
(ii) kx – y – 2 = 0, 6x + 2y – 3 = 0
(iii) kx + 3y + 8 = 0, 12x + 5y – 2 = 0
(iv) kx + 2y = 5, 3x + y = 1
(v) x – ky = 2, 3x + 2y + 5 = 0
(vi) 4x – ky = 5, 2x – 3y = 12
ସମାଧାନ :
a₁x + b₁y + c₁ = 0 ଓ a₂x + b₂y + c₂ = 0
(i) ସହସମୀକରଣଦ୍ଵୟ x – 2y – 3 = 0 ଓ 3x + ky – 1 = 0
ଏଠାରେ a₁ = 1, b₁ = – 2, c₁ = -3 ଓ a₂ = 3, b₂ = k, c₂ = – 1
ଦତ୍ତ ସହ-ସମୀକରଣ ଦ୍ଵୟର ଅନନ୍ୟ ସମାଧାନ ସର୍ତ୍ତ ଅନୁଯାୟୀ \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)
⇒ \(\frac{1}{3} \neq \frac{-2}{k}\) ⇒ k ≠ -6
k ≠ -6 ହେଲେ ସହ-ସମୀକରଣ ଦ୍ବୟର ସମାଧାନ ଅନନ୍ୟ ହେବ ।

(ii) ସହସମୀକରଣଦ୍ବୟ kx – y – 2 = 0 ଓ 6x + 2y – 3 = 0
ଏଠାରେ a₁ = k, b₁ = -1, c₁ = -2 ଓ a₂ = 6, b₂ = 2, c₂ = -3
ଦତ୍ତ ସହ-ସମୀକରଣ ଦ୍ଵୟର ଅନନ୍ୟ ସମାଧାନ ସର୍ତ୍ତ ଅନୁଯାୟୀ \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)
⇒ \(\frac{k}{6} \neq \frac{-1}{2}\) ⇒ k ≠ \(\frac{-6}{2}\) k ≠ -3
k ≠ -3 ହେଲେ ସହ-ସମୀକରଣ ଦ୍ବୟର ସମାଧାନ ଅନନ୍ୟ ହେବ ।

(iii) kx + 3y + 8 = 0 ଓ 12x + 5y – 2 = 0
ଏଠାରେ a₁ = k, b₁ = 3, c₁ = 8 ଓ a₂ = 12, b₂ = 5, c₂ = – 2
ସର୍ତ୍ତ ଅନୁଯାୟୀ
⇒ \(\frac{k}{12} \neq \frac{3}{5}\) ⇒ k ≠ \(\frac{36}{5}\)
k ≠ \(\frac{36}{5}\) ହେଲେ ସହ-ସମୀକରଣ ଦ୍ବୟର ସମାଧାନ ଅନନ୍ୟ ହେବ ।

(iv) kx + 2y = 5 ⇒ kx + 2y – 5 = 0
3x + y = 1 ⇒ 3x + y – 1 = 0
ଏଠାରେ a₁ = k, b₁ = 2, c₁ = -5 ଓ a₂ = 3, b₂ = 1, c₂ = – 1
ଦତ୍ତ ସହ-ସମୀକରଣ ଦ୍ଵୟର ଅନନ୍ୟ ସମାଧାନ ସର୍ତ୍ତ ଅନୁଯାୟୀ \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)
⇒ \(\frac{k}{3} \neq \frac{2}{1}\) ⇒ k ≠ 6
k ≠ 6 ହେଲେ ସହ-ସମୀକରଣ ଦ୍ବୟର ସମାଧାନ ଅନନ୍ୟ ହେବ ।

(v) x – ky = 2 ⇒ x – ky – 2 = 0
3x + 2y + 5 = 0
ଏଠାରେ a₁ = 1, b₁ = -k, c₁ = -2 ଓ a₂ = 3, b₂ = 2, c₂ = 5
ଦତ୍ତ ସହ-ସମୀକରଣ ଦ୍ଵୟର ଅନନ୍ୟ ସମାଧାନ ସର୍ତ୍ତ ଅନୁଯାୟୀ \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)
⇒ \(\frac{1}{3} \neq \frac{-k}{2}\) ⇒ -k ≠ \(\frac{2}{3}\) ⇒ k ≠ \(– \frac{2}{3}\)
k ≠ \(– \frac{2}{3}\) ହେଲେ ସହ-ସମୀକରଣ ଦ୍ବୟର ସମାଧାନ ଅନନ୍ୟ ହେବ ।

(vi) 4x – ky = 5 ⇒ 4x – ky – 5 = 0
2x – 3y = 12 ⇒ 2x – 3y – 12 = 0
ଏଠାରେ a₁ = 4, b₁ = -k, c₁ = -5 ଓ a₂ = 2, b₂ = -3, c₂ = -12
ଦତ୍ତ ସହ-ସମୀକରଣ ଦ୍ଵୟର ଅନନ୍ୟ ସମାଧାନ ସର୍ତ୍ତ ଅନୁଯାୟୀ \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)
\(\frac{4}{2} \neq \frac{-k}{-3}\) ⇒ -k ≠ -6 ⇒ k ≠ 6
k ≠ 6 ହେଲେ ସହ-ସମୀକରଣ ଦ୍ବୟର ସମାଧାନ ଅନନ୍ୟ ହେବ ।

Question 8.
ନିମ୍ନରେ ଦତ୍ତ ସହସମୀକରଣ ଦ୍ଵୟର ଅସଂଖ୍ୟ ସମାଧାନ ରହିଲେ ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ରରେ k ର ମାନ ସ୍ଥିର କର ।
(i) 7x – y – 5 = 0, 21x – 3y – k = 0
(ii) 8x + 5y – 9 = 0, kx + 10y – 18 = 0
(iii) kx – 2y + 6 = 0, 4x – 3y + 9 = 0
(iv) 2x + 3y = 5, 6x + ky = 15
(v) 5x + 2y = k, 10x + 4y = 3
(vi) kx – 2y – 6 = 0, 4x + 3y + 9 = 0
ସମାଧାନ :
ଯଦି \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\) ହୁଏ, ତେବେ ସହ-ସମୀକରଣଦ୍ଵୟ a₁x + b₁y + c₁ = 0 ଓ a₂x + b₂y + c₂ = 0 ର ଅସଂଖ୍ୟ ସମାଧାନ ସମ୍ଭବ ।
(i) ସମୀକରଣଦ୍ଵୟ 7x – y – 5 = 0; ଏବଂ 21x – 3y – k = 0
ଏଠାରେ a₁ = 7, b₁ = -1, c₁ = -5 ଓ a₂ = 21, b₂ = -3, c₂ = -k
ଦତ୍ତ ସର୍ତ୍ତ ଅନୁଯାୟୀ \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)
⇒ \(\frac{7}{21}=\frac{-1}{-3}=\frac{-5}{-k}\) ⇒ \(\frac{1}{3}=\frac{5}{k}\) ⇒ k = 15
∴ k ର ମାନ 15 ହେଲେ ସହ-ସମୀକରଣଦ୍ୱୟର ଅସଂଖ୍ୟ ସମାଧାନ ରହିବ ।

(ii) ସମୀକରଣଦ୍ଵୟ 8x + 5y – 9 = 0; ଓ kx + 10y – 18 = 0
ଏଠାରେ a₁ = 8, b₁ = 5, c₁ = -9; ଓ a₂ = k, b₂ = 10, c₂ =- 18
ଦତ୍ତ ସର୍ତ୍ତ ଅନୁଯାୟୀ \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)
⇒ \(\frac{8}{k}=\frac{5}{10}=\frac{-9}{-18}\) ⇒ \(\frac{8}{k}=\frac{1}{2}\) ⇒ k = 16
∴ k ର ମାନ 16 ହେଲେ ସହ-ସମୀକରଣଦ୍ୱୟର ଅସଂଖ୍ୟ ସମାଧାନ ରହିବ ।

(iii)

(iv)

(v)

(vi)

Question 9.
k ର କେଉଁ ମୂଲ୍ୟ ପାଇଁ ନିମ୍ନରେ ଦତ୍ତ ସହସମୀକରଣଦ୍ଵୟ ଅସଙ୍ଗତ ହେବେ ?
(i) 8x + 5y – 9 = 0, kx + 10y – 15 = 0
(ii) kx – 5y – 2 = 0, 6x + 2y – 7 = 0
(iii) kx + 2y – 3 = 0, 5x + 5y – 7 =
(iv) kx – y – 2 = 0, 6x – 2y – 3 = 0
(v) x + 2y – 5 = 0, 8x + ky – 10 = 0
(vi) 3x – 4y + 7 = 0, kx + 3y – 5 = 0
ସମାଧାନ :
ଏବଂ a₁x + b₁y + c₁ = 0 ଓ a₂x + b₂y + c₂ = 0
(i)

(ii)

(iii)

(iv)

(v)

(vi)