Veerendra

Odisha State Board Elements of Mathematics Class 12 CHSE Odisha Solutions Chapter 1 Relation and Function Ex 1(a) Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 1 Relation and Function Exercise 1(a)

Question 1.
If A = {a,b,c,d} mention the type of relations on A given below, which of them are equivalence relations?
(i) {(a, a), (b, b)}
(ii) {(a, a), (b, b), (c, c), (d, d)}
(iii) {(a, b), (b, a), (b, d), (d, b)}
(iv) {(b, c), (b, d), (c, d)}
(v) {(a, a), (b, b), (c, c), (d, d), (a, d), (a, c), (d, a), (c, a), (c, d), (d, c)}
Solution:
(i) Symmetric and transitive but not reflexive.
(ii) Reflexive, symmetric as well as transitive. Hence it is an equivalence relation.
(iii) Only symmetric
(iv) Only transitive
(v) Reflexive, symmetric and transitive. Hence it is an equivalence relation.

Question 2.
Write the following relations in tabular form and determine their type.
(i) R = {(x, y) : 2x – y = 0] on A = {1,2,3,…, 13}
(ii) R = {(x, y) : x divides y} on A = {1,2,3,4,5,6}
(iii) R = {(x, y) : x divides 2 – y} on A = {1,2,3,4,5}
(iv) R = {(x, y) : y ≤, x ≤, 4} on A = {1,2,3,4,5}.
Solution:
(i) R = {(x, y) : 2x- y = 0} on A
= {(x, y) : y = 2x} on A
= {(1, 2), (2, 4), (3, 6), (4, 8), (5, 10), (6, 12)}
R is neither reflexive nor symmetric nor transitive.

(ii) R = {(1, 1), (1, 2), (1, 3), (1, 4), (1,5), (1, 6), (2, 2), (2, 4), (2, 6), (3, 3), (3, 6), (4, 4), (5,5), (6, 6)}
R is reflexive transitive but not symmetric.

(iii) R = {(x, y) : x divides 2 – y} on A
= {1, 2, 3, 4, 5}
= {(x, y) : 2-y is a multiple of x}
= {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (2, 2), (2, 4), (3, 2), (3, 5), (4, 2), (5, 2)}
R is neither reflexive nor symmetric nor transitive.

(iv) R = {(x, y) : y ≤ x ≤ 4} on A
= {1, 2, 3, 4, 5}
= {(1, 1), (2, 1), (2, 2), (3, 1), (3, 2), (3, 3), (4, 1), (4, 2), (4, 3), (4, 4)}
R is neither reflexive nor symmetric but transitive.

Question 3.
Test whether the following relations are reflexive, symmetric or transitive on the sets specified.
(i) R = {(m,n) : m-n ≥ 7} on Z.
(ii) R = {(m,n) : 2|(m+n)} on Z.
(iii) R = {(m,n) : m+n is not divisible by 3} Z.
(iv) R = {(m,n) : is a power of 5} on Z – {0}.
(v) R = {(m,n) : mn is divisible by 2} on Z.
(vi) R = {(m,n) : 3 divides m-n} on {1,2,3…,10}.
Solution:
(i) R = {{m, n) : m- n ≥ 7} on Z
Reflexive:
∀ m ∈ Z, m – m = 0 < 7
⇒ (m, m) ∉ R
Thus, R is not reflexive.
Symmetry:
Let (m, n) ∈ R
⇒ m – n ≥ 7
⇒ n – m < 7
∴ (n, m) ∉ R
⇒ R is not symmetric.
Transitive:
Let (m, n), (n, p) ∈ R
m – n ≥ 7
and n – p > 7
⇒ m – p ≥ 7
⇒ (m, p) ∈ R
⇒ R is transitive.

(ii) R = {(m, n) : 2 | (m + n)} on Z
Reflexive:
∀ m ∈ Z, m + m = 2m
which is divisible by 2.
⇒ 2 | (m + m)
⇒ (m, m) ∈ R
⇒ R is reflexive.
Symmetry:
Let (m, n) ∈ R
⇒ 2 | (m + n)
⇒ 2 | (n + m)
(n, m) ∈ R
⇒ R is symmetric.
Transitive:
Let (m, n), (n, p), ∈ R
⇒ 2 | (m + n) and 2 | (n + p)
⇒ m + n = 2k₁
⇒ n + p = 2k₂
⇒ m + 2n + p = 2k₁ + 2k₂
⇒ m + p = 2(k₁ + k₂ – 1)
⇒ 2 | (m + p)
⇒ (m, p) ∈ R
⇒ R is transitive.
Thus, R is an equivalence relative.

(iii) R = {(m, n) : m + n is not divisible by 3} on Z
Reflexive:
As 3 + 3 is divisible by 3
we have (3, 3) ∉ R
⇒ R is not reflexive.
Symmetric:
Let (m, n) ∈ R
⇒ m + n is not divisible by 3
⇒ n + m is not divisible by 3
⇒ (n, m) ∈ R
⇒ R is symmetric.
Transitive:
(3, 1), (1, 6) ∈ R
But (3, 6) ∉ R
⇒ R is not transitive.

(iv) R = {(m, n) : \(\frac{m}{n}\) is a power of 5} on Z – {0}
Reflexive:
∀ m ∈ Z – {0}
\(\frac{m}{m}\) = 1 = 5°
⇒ (m, m) ∈ R
⇒ R is reflexive.
Symmetric:
Let (m, n) ∈ R
\(\frac{m}{n}\) = 5^k
\(\frac{n}{m}\) = 5^-k
⇒ (n, m) ∈ Z
⇒ R is symmetric.
Transitive:
Let (m, n), (n, p) ∈ R
⇒ \(\frac{m}{n}\) = 5^k1 , \(\frac{n}{p}\) = 5^k2
⇒ \(\frac{m}{n}\) . \(\frac{n}{p}\) = 5^k1 . 5^k2
⇒ \(\frac{m}{p}\) = 5 ^k1+k2
⇒ (m, p) ∈ R
⇒ R is transitive.
Thus R is an equivalence relation.

(v) R = {(m, n) : mn is divisible by 2} on Z
Reflexive:
3 ∈ Z
3 x 3 = 9
which is not divisible by 2.
∴ (3, 3) ∉ R
⇒ R is not reflexive.
Symmetric:
Let (m, n) ∈ R
⇒ mn is divisible by 2
⇒ nm is divisible by 2
⇒ (n, m) ∈ R
⇒ R is symmetric.
Transitive:
⇒ (3, 2), (2, 5) ∈ R
⇒ But 3 x 5 = 15,
⇒ which is not divisible by 2.
⇒ (3, 5) ∉ R
R is not transitive.

(vi) R = {(m, n) : 3 divides m-n} on A = {1, 2, 3……,10}
Reflexive:
Clearly ∀ m ∈ A, m – m = 0
which is divisible by 3
⇒ (m, m) ∈ R
⇒ R is reflexive
Symmetric:
Let (m, n) ∈ R
⇒ m – n is divisible by 3
⇒ n – m is also divisible by 3
⇒ (n, m) ∈ R
⇒ R is symmetric
Transitive:
Let (m, n), (n, p) ∈ R
⇒ m – n and n – p are divisible by 3
⇒ m – n + n – p is also divisible by p.
⇒ m – p is divisible by p.
⇒ (m, p) ∈ R
⇒ R is transitive.
Thus R is an equivalence relation.

Question 4.
List the members of the equivalence relation defined by the following partitions on X= {1,2,3,4}. Also find the equivalence classes of 1,2,3 and 4.
(i) {{1},{2},{3, 4}}
(ii) {{1, 2, 3},{4}}
(iii) {{1,2, 3, 4}}
Solution:
(i) The equivalence relation is
R = {(1, 1), (2, 2), (3, 3), (4, 4), (3, 4), (4, 3)}
[1] = {1}, [2] = {2}, [3] = {3, 4} and [4] = {3, 4}

(ii) The equivalence relation is
R = {(1, 1), (2, 2), (3, 3), (4, 4), (1, 2), (1, 3), (2, 1), (2, 3), (3, 1), (3, 2)}
[1] = [2] = [3] = {1, 2, 3}
[4] = {4}

(iii) The equivalence relation is
R = A x A, [1] = [2] = [3] = [4] = A

Question 5.
Show that if R is an equivalence relation on X then dom R = rng R = X.
Solution:
Let R is an equivalence relation on X.
⇒ R is reflexive
⇒ (x, x) ∈ R ∀ x ∈ X
⇒ Dom R = Rng R = X

Question 6.
Give an example of a relation which is
(i) reflexive, symmetric but not transitive.
(ii) reflexive, transitive but not symmetric.
(iii) symmetric, transitive but not reflexive.
(iv) reflexive but neither symmetric nor transitive.
(v) transitive but neither reflexive nor symmetric.
(vi) an empty relation.
(vii) a universal relation.
Solution:
(i) The relation R = {(a, b), (b, a), (a, c), (c, a), (a, a), (b, b), (c, c)} defined on the set {a, b, c} is reflexive, symmetric but not transitive.
(ii) “The relation x ≤ y on z” is reflexive, transitive but not symmetric.
(iii) The relation R = {(a, a), (a, b), (a, c), (b, a), (b, b), (b, c), (c, a), (c, b), (c, c)} defined on the set {a, b, c, d} is symmetric, transitive but not reflexive.
(iv) The relation R = {(a, a), (b, b), (c, c), (a, b), (b, c)} defined on the set A = {a, b, c} is reflexive but neither symmetric nor transitive.
(v) R = {(a, b), (b, c), (a, c)} on A = {a, b, c} is transitive but neither reflexive nor symmetric.
(vi) On N the relation R= {(x, y) : x + y = – 5} is an empty relation.
(vii) On N the relation R = {(x, y) : x + y > 0} is an universal relation.

Question 7.
Let R be a relation on X, If R is symmetric then xRy ⇒ yRx. If it is also transitive then xRy and yRx ⇒ xRx. So whenever a relation is symmetric and transitive then it is also reflexive. What is wrong in this argument?
Solution:
Let R is a relation on X.
If R is symmetric then xRy ⇒ yRx
If R is also transitive then xRy and yRx ⇒ xRx
⇒ Whenever a relation is symmetric and transitive, then it is reflexive. This argument is wrong because the symmetry of R does not imply dom R = X and for reflexive xRx ∀ x ∈ X.

Question 8.
Suppose a box contains a set of n balls (n ≥ 4) (denoted by B) of four different colours (may have different sizes), viz. red, blue, green and yellow. Show that a relation R defined on B as R={(b1, b2): balls b1 and b2 have the same colour} is an equivalence relation on B. How many equivalence classes can you find with respect to R?
[Note: On any set X a relation R={(x, y): x and y satisfy the same property P} is an equivalence relation. As far as the property P is concerned, elements x and y are deemed equivalent. For different P we get different equivalence relations on X]
Solution:
On B, R = {(b1, b2) : balls b1 and b2 have the same colour}

Reflexive:
∀ b ∈ B, b and b are of same colour
⇒ (b, b) ∈ R
⇒ R is reflexive.

Symmetric:
Let (b1, b2) ∈ R
⇒ b1 and b2 are of same colour
⇒ b2 and b1 are of same colour
⇒ (b2, b1) ∈ R
⇒ R is symmetric.

Transitive :
Let (b1, b2) and (b2, b3) ∈ R
⇒ b1 and b2 are of same colour
b2 and b3 are of same colour
⇒ b1, b3 are of same colour
⇒ (b1, b3) ∈ R
⇒ R is transitive
∴ R is an equivalence relation.
As there are 4 types of balls there are 4 equivalence relations with respect to R.

Question 9.
Find the number of equivalence relations on X={1,2,3}. [Hints: Each partition of a set gives an equivalence relation.]
Solution:
Method – 1: Number of equivalence relations on a set A with | A | = n.
= The number of distinct partitions of A
= B_n
where B_n+1 = \(\sum_{k=0}^n \frac{n !}{k !(n-k) !} \mathrm{B}_k\)
with B₀ = 1
Here n = 3
B₁ = 1
B_{2 =} \(\frac{1 !}{0 ! 1 !}\) B₀ + \(\frac{1 !}{1 ! 1 !}\) B₁
= 1 + 1 = 2
B₃ = \(\frac{2 !}{0 ! 2 !}\) B₀ + \(\frac{2 !}{1 ! 1 !}\) B₁ + \(\frac{2 !}{2 ! 0 !}\) B₂
= 1 + 2 + 2 = 5
Thus there are 5 equivalence relations.

Method – 2:
X= {1, 2, 3}
Number of equivalence relations = number of distinct partitions.
Different partitions of X are
{{1} {2}, {3}}
{{1}, {2, 3}}, {{2}, {1,3}},
{{3}, {1,2}} and {{1, 2,3}}
Thus number of equivalence relations = 5.

Question 10.
Let R be the relation on the set R of real numbers such that aRb iff a-b is an integer. Test whether R is an equivalence relation. If so find the equivalence class of 1 and ½ w.r.t. this equivalence relation.
Solution:
The relation R on the set of real numbers is defined as
R = {(a, b) : a – b ∈ Z}

Reflexive:
∀ a ∈ R (set of real numbers)
a – a = 0 ∈ Z
⇒ (a, a) ∈ R
⇒ R is reflexive.

Symmetric:
Let (a, b) ∈ R
⇒ a – b ∈ Z
⇒ b – a ∈ Z
⇒ (b, a) ∈ R
⇒ R is symmetric.

Transitive:
Let (a, b), (b, c) ∈ R
⇒ a – b and b – c ∈ Z
⇒ a – b + b – c ∈ Z
⇒ a – c ∈ Z
⇒ (a, c) ∈ R
⇒ R is transitive.
Thus R is an equivalence relation.
[1] = {x ∈ R : x -1 ∈ Z} = Z
\(\begin{aligned}
{\left[\frac{1}{2}\right] } &=\left\{x \in \mathrm{R}: x-\frac{1}{2} \in \mathrm{Z}\right\} \\
&=\left\{x \in \mathrm{R}: x=\frac{2 k+1}{2}, k \in \mathrm{Z}\right\}
\end{aligned}\)

Question 11.
Find the least positive integer r such that
(i) 185 ∈ [r]₇
(ii) – 375 ∈ [r]₁₁
(iii) -12 ∈ [r]₁₃
Solution:
(i) 185 ∈ [r]₇
⇒ 185 – r = 7k, k ∈ z and r < 7
⇒ r = 3
(ii) – 375 ∈ [r]₇
⇒ – 375 – r = 11k, k ∈ z and r < 11
⇒ r = 10
(iii) – 12 ∈ [r]₁₃
⇒ – 12 – r = 13k, k ∈ z and r < 13
⇒ r= 1

Question 12.
Find least non negative integer r such that
(i) 7 x 13 x 23 x 413 r (mod 11)
(ii) 6 x 18 x 27 x (- 225) = r (mod 8)
(iii) 1237(mod 4) + 985 (mod 4) = r (mod 4)
(iv) 1936 x 8789 = r (mod 4)
Solution:
(i) 7 x 13 x 23 x 413 ≡ r (mod 11)
Now 7 x 13 ≡ 3 mod 11
23 ≡ 1 mod 11
413 ≡ 6 mod 11
∴ 7 x 13 x 23 x 413 ≡ 3 x 1 x 6 mod 11
≡ 18 mod 11
≡ 7 mod 11
∴ r = 7

(ii) 6 x 18 x 27 x – 225 ≡ r (mod 8)
Now 6 x 18 ≡ 108 = 4 mod 8
27 ≡ 3 mod 8
– 225 ≡ 7 mod 8
⇒ 6 x 18 x 27 x – 225 ≡ 4 x 3 x 7 mod 8
≡ 84 mod 8
≡ 4 mod 8
∴ r = 4

(iii) 1237 (mod 4) + 985 (mod 4) r (mod 4)
Now 1237 ≡ 1 mod 4
985 ≡ 1 mod 4
⇒ 1237 (mod 4) + 985 (mod 4)
≡ (1 + 1) mod 4
≡ 2 mod 4
⇒ r = 2

(iv) 1936 x 8789 ≡ r (mod 4)
1936 x 8789 ≡ 0 mod 4
∴ r = 0

Question 13.
Find least positive integer x satisfying 276x + 128 ≡ (mod 7)
[Hint: 276 ≡ 3, 128 ≡ 2 (mod 7)]
Solution:
Now 128 ≡ 2 mod 7
Now 176 x + 128 ≡ 4 mod 7
⇒ 176 x ≡ (4 – 2) mod 7
⇒ 176 x ≡ 2 mod 7
176 x x ≡ 2 mod 7,
But 276 ≡ 3 mod 7
Thus x = 3.

Question 14.
Find three positive integers x_i, i =1, 2, 3 satisfying 3x ≡ 2 (mod 7)
[Hint: If X₁ is a solution then any member of [X₁] is also a solution]
Solution:
3x ≡ 2 mod 7
Least positive value of x ≡ 3
Each member of [3] is a solution
∴ x = 3, 10, 17 …..

BSE Odisha 11th Class Biology Important Questions (+2 1st Year)

• Chapter 1 Biodiversity Important Questions
• Chapter 2 Classification of Living World Important Questions
• Chapter 3 Classification of Plant Kingdom Important Questions
• Chapter 4 Classification of Animal Kingdom Important Questions
• Chapter 5 Morphology of Flowering Plants Important Questions
• Chapter 6 Anatomy of Flowering Plants Important Questions
• Chapter 7 Animal Tissues and Gross Anatomical Organisation of Cockroach Important Questions
• Chapter 8 Cell: Structure and Function Important Questions
• Chapter 9 Chemical Constituents of Living Cells Important Questions
• Chapter 10 Cell Division Cycle Important Questions
• Chapter 11 Transport in Plants Important Questions
• Chapter 12 Mineral Nutrition Important Questions
• Chapter 13 Photosynthesis in Higher Plants Important Questions
• Chapter 14 Respiration Important Questions
• Chapter 15 Plant Growth and Development Important Questions
• Chapter 16 Digestion and Absorption Important Questions
• Chapter 17 Breathing and Exchange of Gases Important Questions
• Chapter 18 Body Fluids and Circulation Important Questions
• Chapter 19 Excretory Products and Their Elimination Important Questions
• Chapter 20 Locomotion and Movement Important Questions
• Chapter 21 Neural Control and Coordination Important Questions
• Chapter 22 Chemical Coordination and Regulation Important Questions

CHSE Odisha Class 11 Textbook Solutions

CHSE Odisha 11th Class Biology Book Solutions (+ 2 1st Year)

• Chapter 1 Biodiversity
• Chapter 2 Classification of Living World
• Chapter 3 Classification of Plant Kingdom
• Chapter 4 Classification of Animal Kingdom
• Chapter 5 Morphology of Flowering Plants
• Chapter 6 Anatomy of Flowering Plants
• Chapter 7 Animal Tissues and Gross Anatomical Organisation of Cockroach
• Chapter 8 Cell: Structure and Function
• Chapter 9 Chemical Constituents of Living Cells
• Chapter 10 Cell Division Cycle
• Chapter 11 Transport in Plants
• Chapter 12 Mineral Nutrition
• Chapter 13 Photosynthesis in Higher Plants
• Chapter 14 Respiration
• Chapter 15 Plant Growth and Development
• Chapter 16 Digestion and Absorption
• Chapter 17 Breathing and Exchange of Gases
• Chapter 18 Body Fluids and Circulation
• Chapter 19 Excretory Products and Their Elimination
• Chapter 20 Locomotion and Movement
• Chapter 21 Neural Control and Coordination
• Chapter 22 Chemical Coordination and Regulation

CHSE Odisha Class 11 Textbook Solutions

Odisha State Board CHSE Odisha Class 12 Biology Important Questions Chapter 1 Reproduction in Organisms Important Questions and Answers.

CHSE Odisha 12th Class Biology Important Questions Chapter 1 Reproduction in Organisms

Reproduction in Organisms Class 12 Important Questions CHSE Odisha

Very Short Answer Type Questions

Choose the correct option

Question 1.
The factors which determine type of reproduction in an organism are
(a) habitat
(b) internal physiology
(c) environmental conditions
(d) All of the above
Answer:
(d) All of the above

Question 2.
A division which occurs at an angle to the transverse axis is called
(a) transverse binary fission
(b) longitudinal binary fission
(c) oblique binary fission
(d) simple binary fission
Answer:
(c) oblique binary fission

Question 3.
Conidia formation is seen in
(a) Amoeba
(b) Paramecium
(c) Aspergillus
(d) Planaria
Answer:
(c) Aspergillus

Question 4.
Sponges reproduce asexually by forming
(a) external buds
(b) gemmules
(c) merozoites
(d) None of these
Answer:
(b) gemmules

Question 5.
Cell division itself is a mode of reproduction in
(a) Amoeba
(b) Paramecium
(c) Both (a) and (b)
(d) None of these
Answer:
(c) Both (a) and (b)

Question 6.
Which one group of plants is propagated through underground roots?
(a) Bryophyllum and Kalanchoe
(b) Pistia and pineapple
(c) Ginger, potato and onion
(d) Sweet potato, Dahlia and Tapioca
Answer:
(d) Sweet potato, Dahlia and Tapioca

Question 7.
Vegetative propagation in mint occurs by
(a) offset
(b) rhizome
(c) sucker
(d) runner
Answer:
(c) sucker

Question 8.
A horizontal underground stem is a
(a) corm
(b) phylloclade
(c) rhizome
(d) rhizoid
Answer:
(c) rhizome

Question 9.
The process by which scion is inserted successfully into the stock to form a new plant is called
(a) layering
(b) cutting
(c) grafting
(d) budding
Answer:
(c) grafting

Question 10.
Micropropagation is a technique
(a) of production of true plants
(b) of production of mutants
(c) of production of variant species
(d) All of the above
Answer:
(a) of production of true plants

Question 11.
Bryophyllum undergoes vegetative propagation by means of
(a) leaf buds
(b) bulbil
(c) stem
(d) nodes
Answer:
(a) leaf buds

Correct the statements, if required, by changing the underlined word(s)

Question 1.
Yeasts generally reproduce asexually by fission.
Answer:
Yeasts generally reproduce asexually by budding.

Question 2.
External budding is the characteristic feature of Spongilla.
Answer:
External budding is the characteristic feamre of Hydra.

Question 3.
Bacteria mostly reproduce by gemmules.
Answer:
Bacteria mostly reproduce by transverse binary fission.

Question 4.
In higher organisms, cell division in itself is a mode of reproduction.
Answer:
lower

Question 5.
Onion and garlic are examples of corm.
Answer:
Onion and garlic are examples of bulb.

Question 6.
Almonds can be grown successfully if stock and scion are of different species.
Answer:
Almonds can be grown successfully if stock and scion are of related species.

Question 7.
In layering, roots are artificially induced to grow on the branches before they are detached from the parent plant.
Answer:
gootee

Question 8.
Rhizome, runner and bulb are the examples of underground stem.
Answer:
tuber

Fill in the blanks

Question 1.
The morphologically and genetically identical offsprings produced by asexual reproduction are called ………… .
Answer:
clones

Question 2.
A type of binary fission, occurring in the Euglena is called …………. .
Answer:
longitudinal binary fission

Question 3.
An.organism reproducing by fragmentation is …………… .
Answer:
Planaria

Question 4.
In Euglena, ………… binary fission is observed. (simple/longitudinal/transverse/oblique)
Answer:
longitudinal

Question 5.
Non-motile, exogenous spores of Penicillium are …………. (zoospores/oospores/conidia/ascospores)
Answer:
conidia

Question 6.
Transverse binary fission is observed in …………… . (Euglena, Paramecium, Amoeba)
Answer:
Paramecium

Question 7.
…………. is commonly practiced for root induction.
Answer:
Layering

Question 8.
In grafting, the rooted-plant is called stock and stem cutting of donor plant is called ………. .
Answer:
scion

Question 9.
Conifer cutting is practiced for propagating …………….. .
Answer:
pine

Question 10.
Rooting in stem cuttings is stimulated by using ………….. .
Answer:
auxin

Question 11.
The vegetative propagule in Agave is …………. .
Answer:
bulbil

Express the following in one or two word(s)

Question 1.
The process by which a living organism produces its offspring.
Answer:
Reproduction

Question 2.
Binary fission is seen in which phylum?
Answer:
Protozoa

Question 3.
An organism which performs internal budding.
Answer:
Spongilla

Question 4.
A process by which an organism develops its lost body part.
Answer:
Regeneration

Question 5.
What are the totipotent cells of Planaria called?
(Neoblasts, Sertoli cells, Follicular cells, Helper cells)
Answer:
Neoblasts

Question 6.
Name the biological process that enables continuity of species.
Answer:
Reproduction

Question 7.
The process of formation of spores in Aspergillus.
Answer:
Sporulation

Question 8.
Formation of 2-3 layered strong envelope around cyst.
Answer:
Encystment

Question 9.
Mode of vegetative propagation in Pistia.
Answer:
Offset

Question 10.
Name the undifferentiated mass of cells formed during culturing of cells.
Answer:
Callus

Question 11.
The alternative term used for air layering.
Answer:
Gootee

Question 12.
In which plant, air layering is done?
Answer:
Lemon

Question 13.
Name the vegetative propagules in Chrysanthemum.
Answer:
Sucker

Question 14.
A medicinal plant propagated by micropropagation.
Answer:
Atropa belladona

Short Answer Type Questions

Question 1.
Why is reproduction essential for the organisms?
Answer:
Reproduction is an important biological process that is essential for the organisms because

• it maintains life on earth.
• it results in addition of new individuals to the population, which finally leads to perpetuation of species.
• it creates variation among populations, which plays an important role in evolution.

Question 2.
Write a short note on multiple fission.
Answer:
Fission is a phenomenon of asexual reproduction in which the parent body divides into two or more daughter individuals. Multiple fission is a type of fission in which parent body divides into many small daughter individuals simultaneously, e.g. Plasmodium (the malarial parasite), Amoeba (during unfavourable conditions).

Question 3.
How does multiple fission occur in Amoeba?
Answer:
Amoeba reproduces by multiple fission during unfavourable conditions. It secretes three-layered protective cyst around itself. Its nucleus divides repeatedly to form several daughter nuclei.
Each daughter nucleus with a small amount of cytoplasm forms a daughter Amoeba called amoebae. Under favourable conditions, the cyst wall breaks up releasing young amoebae. Each young one develops pseudopodia, feeds and grows into an adult Amoeba.

Question 4.
Why is it that there is no natural death in single-celled organisms like Amoeba and bacteria?
Answer:
In single-celled organisms like Amoeba and bacteria, the parental body itself divides into two parts and becomes daughter cells. Each of these divided cell rapidly grows into an adult organism. Therefore, the parent cannot be said to have died, it continues its life as daughter cells.

Question 5.
Write a short note on sporulation.
Answer:
Spoliation
Sometimes the products of multiple fission become individually surrounded by resistant coats, i.e. cyst walls before their release from parent, the process is known as sporulation and the encysted products are known as spores.
It is not only the fastest method of reproduction but also helps to overcome unfavourable conditions. Sporulation is generally found in monerans, protistans, algae and lower fungi.

Question 6.
Draw the sketches of a zoospore and a conidium. Mention two dissimilarities between them and at least one feature common to both the structures.
Answer:
Sketches of a zoospore and a conidium are given below

The two dissimilarities between them (zoospore and conidium) are as follows

Zoospore	Conidium
It is found usually in algae.	It is found usually in fungi.
Flagellated	Non-flagellated
Formed inside a sporangium (endogenously).	Formed at the tip of conidiophores (exogenously).

The feature that is common in zoospores and conidia is that both of these spores facilitate the process of reproduction in asexually reproducing organisms.

Question 7.
Write a short note on budding in Hydra
Answer:
Budding is an asexual method of reproduction that takes place in Hydra. In this, the ectodermal interstitial cells multiply to form an outgrowth called bud, The bud grows consisting of ectoderm, endoderm and gastrovascular cavity. The bud develops mouth and tentacles at its free end. The fully grown bud separates from the parent body of the Hydra and grows into an adult.

Question 8.
Write a short note on gemmules.
Answer:
Gemmules They are internal buds formed during unfavourable condition. They give rise to new individuals in favourable conditions.
They are formed inside the body of sponges. Their formation is called as internal budding or endogenous budding.

Gemmule in sponge

Question 9.
How does asexual reproduction take place in sponges?
Answer:
Freshwater sponges (e.g. Spongilla) reproduce asexually by forming gemmules.
Gemmules They are internal buds formed during unfavourable condition. They give rise to new individuals in favourable conditions.
They are formed inside the body of sponges. Their formation is called as internal budding or endogenous budding.

Gemmule in sponge

Question 10.
How will an organism be benefitted if it reproduces through spores?
Answer:
There are some benefits for the organism which reproduces through spore formation such as

• Reproduction through spores is a simple as well as faster mode of reproduction.
• The spores are light in weight, thus keep floating in the water/air. This helps in their dispersal.
• The spores are covered with a thick layer which enables them to survive in unfavourable conditions.

Question 11.
Briefly discuss different types of fission in organisms.
Answer:
Fission It is the phenomenon of division of the parent body into two or more daughter individuals.
Fission can be of following types

1. Binary fission It is the type of fission in which parent body divides into two small, nearly equal ‘ sized daughter individuals. Each grows into an adult, e.g. Amoeba, Paramecium, etc.
2. Multiple fission It is the type of fission in which parent body divides into many small daughter individuals simultaneously, e.g. Plasmodium (the malarial parasite), Amoeba (during unfavourable conditions).

Question 12.
Why vegetative propagation is considered as a type of asexual reproduction?
Answer:
Vegetative propagation is considered as a type of asexual reproduction because .

• it is uniparental reproduction.
• cells divide by mitosis and no reductional division occurs.
• it does not involve genetic variations.

Question 13.
Write short note on air layering.
Answwer:
Air layering (gootee) In this method, about 3.5 cm ring of bark is removed from the base of an aerial shoot. This area is then covered by a thick plaster of grafting clay. It consists of hay, cowdung, clay and water with small quantity of root promoting hormone (such as NAA or IBA).

A set up for micropropagation requires an explant. The most commonly used explants are the meristematic ends of the plants, i.e. stem tip, root tip, axillary bud, etc. This is because meristematic cells have high rate of cell division. These explants, along with culture vessel, cell division media and instruments, etc., are sterilised. The explant is then inoculated into a semi-solid nutrient medium contained in a culture vessel. This is followed by incubation of culture vessel at room temperature. After some time, multiple shoots start developing from the axillary buds. This is called axillary bud proliferation.

Question 14.
Why do internodal segments of sugarcane fail to propagate vegetatively even when they are in contact with damp soil?
Answer:
On the stems, new buds develop from the nodes. So, for vegetative reproduction of a plant through stem cutting it should have atleast one node. As internodal segments of the sugarcane do not have nodes, they fail to propagate vegetatively even when they are in contact with the damp soil.

Question 15.
Is it possible to consider vegetative propagation observed in certain plants like Bryophyllum, water hyacinth, ginger, etc., as a type of asexual reproduction? Give two/three reasons.
Answer:
The formation of new plants from vegetative units (vegetative propagules) such as buds, tubers, rhizomes, etc., is called vegetative propagation (vegetative reproduction).
Vegetative propagation is considered as a type of asexual reproduction because

• it is uniparental reproduction.
• cells divide by mitosis and no reductional division occurs.
• it does not involve genetic variations.

Question 16.
Observe the diagram given below and answer the questions that follows

(i) What does the given diagram show?
(ii) Name any two plants (other than the one shown in fig.) which reproduce by the same method.
(iii) What are these plant parts referred to?
Answer:
(i) The given diagram shows a bulbil of Agave.
(ii) Two other plants which reproduce by the same method are Oxalis and lily.
(iii) These plant parts which help in vegetative (asexual) reproduction are referred to as vegetative propagules.

Question 17.
Write a short note on bulbils.
Answer:
Bulbils
These are fleshy buds produced in the axil of foliage leaves in place of axillary buds. They grow to form new plants, when shed/fall on the ground, e.g. Agave, Oxalis, Allium sativum, lily, etc.
Adventitious buds

Vegetative propagules (a) Leaf buds of Bryophyllum , (b) Bulbil of Agave

The new plantlets in the plants like potato, sugarcane, banana, Dahlia, ginger, etc., arise invariably from the nodes present in the modified stems of these plants. When these nodes come in the contact of damp soil or water, they produce roots and new plants because of the presence of meristematic cells.

Question 18.
Write a short note on micropropagation.
Answer:
Micropropagation (Propagation by plant tissue culture) This method includes propagation of plants by culturing the cells, tissues and organs. It is called as tissue culture. Initially, the culturing of cells or tissues results in the formation of an undifferentiated mass of cells called callus, which later differentiates to form a large number of plantlets.

These plantlets are transferred to separate pots or nursery to grow them into plants. Tissue culture technique is useful in obtaining virus-free plants, disease-free plants, homozygous diploids and in quick commercial propagation of orchids, Gladiolus, Chrysanthemum, other ornamental plants.

Question 19.
Mention the advantages and disadvantages of vegetative propagation.
Answer:
Advantages of Vegetative Propagation

1. It is the only method of multiplication (rapid) in seedless plants, e.g. sugarcane, banana, seedless grape, seedless orange, etc.
2. The important advantage of vegetative propagation is that a plant can be retained and multiplied indefinitely without any change or variation.
3. Vegetative propagation by plant tissue culture (micropropagation) has been applied for the production of disease-free plants.

Disadvantages of Vegetative Propagation

1. Vegetative propagules get easily decayed and are prone to viral, bacterial and fungal diseases.
2. There are no variations. Therefore, the plants may show degeneration and in such plants there is a less adaptability to changed environment.
3. There is no dispersal of vegetative propagules. Therefore, it causes overcrowding.

Differentiate between the following (for complete chapter)

Question 1.
Binary fission and Multiple fission.
Answer:
Differences between binary fission and multiple fission are as follows

Binary fission	Multiple fission
It is the process of division of the parent body into two small, nearly equal sized daughter individuals where each grows into an adult.	It is the process of division of the parent body into many small daughter individuals simultaneously.
The nucleus divides once and is immediately followed by cytoplasmic division.	The nucleus several times. Thus, it is  not followed cytoplasmic division.
It occurs under favourable conditions.	It occurs under unfavourable conditions.
e.g. Amoeba, Paramecium.	e.g. Plasmodium, Amoeba

Question 2.
Sporogony and Budding.
Answer:
Differences between sporogony and budding are as follows

Sporogony	Budding
In this, reproduction takes place by spore formation.	In this reproduction, an outgrowth or bud developing on the parent body develops into a new individual.
Spores are single-celled, reproductive bodies released from the parent body and are capable of growing into a new organism themselves, e.g. Penicillium, etc.	The daughter individual or bud remains attached tathe parent body until it is fully grown, e.g. Hydra, etc.

Question 3.
Simple binary Fission and Transverse binary fission.
Answer:
Differences between simple binary fission and transverse binary fission are as follows

Simple binary fission	Transverse binary fission
In this, fission of a parent into two daughter cells takes place along any possible plane.	In this, fission of a parent cell into two daughter cells takes place along the transverse or horizontal.
Plane of fission is not predetermined.	Plane of fission is predetermind.
The nucleus divides by mitosis, e.g. Amoeba.	The meganucleus divides by amitosis while the micronucleus divides by mitosis, e.g. Paramecium. Differentiate between the following (for complete chapter)

BSE Odisha 12th Class Biology Important Questions (+2 2nd Year)

• Chapter 1 Reproduction in Organisms Important Questions
• Chapter 2 Sexual Reproduction in Flowering Plants Important Questions
• Chapter 3 Human Reproduction Important Questions
• Chapter 4 Reproductive Health Important Questions
• Chapter 5 Heredity and Variation Important Questions
• Chapter 6 Sex Determination Important Questions
• Chapter 7 Molecular Basis of Inheritance Important Questions
• Chapter 8 Evolution Important Questions
• Chapter 9 Health and Diseases Important Questions
• Chapter 10 Improvement in Food Production Important Questions
• Chapter 11 Microbes in Human Welfare Important Questions
• Chapter 12 Principles and Processes of Biotechnology Important Questions
• Chapter 13 Applications of Biotechnology Important Questions
• Chapter 14 Organisms and Environment Important Questions
• Chapter 15 Ecosystem Important Questions
• Chapter 16 Biodiversity and its Conservation Important Questions
• Chapter 17 Environmental Issues Important Questions

CHSE Odisha Class 12 Textbook Solutions

Odisha State Board CHSE Odisha Class 11 Sociology Solutions Unit 1 ସମାଜ ବିଜ୍ଞାନ ଏବଂ ଏହାର ସମ୍ପର୍କ Questions and Answers.

CHSE Odisha 11th Class Sociology Unit 1 Question Answer ସମାଜ ବିଜ୍ଞାନ ଏବଂ ଏହାର ସମ୍ପର୍କ

‘କ’ ବିଭାଗ

ଅତି ସଂକ୍ଷିପ୍ତ ପ୍ରଶ୍ନୋତ୍ତର
ସମ୍ଭାବ୍ୟ ବିକଳ୍ପ ମଧ୍ୟରୁ ଉତ୍ତର ଚୟନ କର :

Question ୧।
ସମାଜ ବିଜ୍ଞାନର ଜନକ କିଏ
(i) ଇମାଇଲ୍ ଦୁର୍ଖମ୍
(ii) ଅଗଷ୍ଟ କମ୍‌
(iii) ହରବର୍ଟ ସେନ୍ସର
(iv) କାର୍ଲ ମାର୍କସ୍‌
Answer:
(ii) ଅଗଷ୍ଟ କମ୍

Question ୨।.
(i) ୧୯୨୦
(ii) ୧୭୨୯
(iii) ୧୮୩୯
(iv) ୧୯୨୦
Answer:
(iii) ୧୮୩୯

Question ୩।
ଅଗଷ୍ଟ କମ କେଉଁ ଦେଶର ଦାର୍ଶନିକ ଅଟନ୍ତି ?
(i) ଜର୍ମାନ
(ii) ଫରାସୀ
(iii) ଆମେରିକା
(iv) ଜାପାନ
Answer:
(ii) ଫରାସୀ

Question ୪।
(i) ସାଧାରଣ ବିଜ୍ଞାନ ଅଟେ
(ii) ନିର୍ଦ୍ଦିଷ୍ଟ ବିଜ୍ଞାନ ଅଟେ
(iii) ପ୍ରତିମାନୀୟ ବିଜ୍ଞାନ
(iv) ଏ ସମସ୍ତ
Answer:
(ii) ନିର୍ଦ୍ଦିଷ୍ଟ ବିଜ୍ଞାନ ଅଟେ

Question ୫।
ଔପସ୍ପରିକ ମତବାଦର ମୁଖ୍ୟ ପୁଷ୍ଟପୋଷକ କିଏ ?
(i) ଆଲେକସି ଆଙ୍କିଲେ
(ii) ଜର୍ଜ ସିମେଲ
(iii) ପି. ସରୋକିନ୍
(iv) ଏ ସମସ୍ତ
Answer:
(ii) ଜର୍ଜ ସିମେଇ

Question ୬।
ସମାଜବିଜ୍ଞାନ କେଉଁ ଦୁଇଟି ଶବ୍ଦରୁ ଆସିଅଛି ?
(i) ଗ୍ରୀକ୍ ଓ ଜର୍ମାନୀ
(ii) ଲାଟିନ୍ ଓ ଗ୍ରୀକ୍
(iii) ଲାଟିନ୍ ଓ ଫ୍ରାନସ
(iv) ଏ ସମସ୍ତ
Answer:
(ii) ଲାଟିନ୍ ଓ ଗ୍ରୀକ୍

Question ୭।
ସମାଜବିଜ୍ଞାନ ସାମାଜିକ ସମ୍ପର୍କ ସମ୍ବନ୍ଧରେ ସୂଚନା ଦେଇଥାଏ ଏବଂ ଜାଲଭଳି ବୁଣା ହୋଇଥିବା ସାମାଜିକ ସମ୍ପର୍କକୁ ଆମେ ସମାଜ କହିଥାଉ, ଏହି ଉକ୍ତିଟି କେଉଁ ସମାଜବିଜ୍ଞାନୀ କହିଥିଲେ?
(i) ଅଗଷ୍ଟ କମିଟେ
(ii) କାର୍ଲମାକୁ
(iii) ମକାଇଭର ଓ ପେଜ୍
(iv) ମିକ୍ସ ୱେବର
Answer:
(iii) ମକାଇଭର ଓ ପେଜ୍

Question ୮।
ସଙ୍ଗବଦ୍ଧ ଜୀବନଯାପନ କରୁଥିବା ମନୁଷ୍ୟମାନଙ୍କର ପାରସ୍ପରିକ କ୍ରିୟାର ଅଧ୍ୟୟନକୁ ସମାଜବିଜ୍ଞାନ କୁହାଯାଏ। ଏହା କାହାର ମତ ?
(i) ମୋରିସ୍ ଜିନିସ୍‌ବର୍ଗ
(ii) ମାକାଇଭର ଓ ପେଜ୍
(iii) ଗିଲିନ ଏବଂ ଗିଲିନ୍
(iv) ଏ ସମସ୍ତ ଉ.
Answer:
(iii) ଗିଲିନ ଏବଂ ଗିଲିନ

Question ୯।
ସାଂଶ୍ଳେଷିକ ମତବାଦ ଅନୁସାରେ ସମାଜବିଜ୍ଞାନ ଏକ –
(i) ନିର୍ଦ୍ଦିଷ୍ଟ ବିଜ୍ଞାନ ଅଟେ
(ii) ସାଧାରଣ ବିଜ୍ଞାନ ଅଟେ
(iii) ପ୍ରତିମାନୀୟ ବିଜ୍ଞାନ
(iv) ଏ ସମସ୍ତ
Answer:
(ii) ସାଧାରଣ ବିଜ୍ଞାନ ଅଟେ

Question ୧୦।
ସାଂଶ୍ଳେଷିକ ମତବାଦର ମୁଖ୍ୟ ପ୍ରବକ୍ତା ହେଲେ –
(i) କାର୍ଲ ମାଙ୍କସ୍
(ii) ହରବର୍ଟ ସେନସର
(iii) ଇମାଇଇ ଦୁର୍ଖମ୍
(iv) ଏ ସମସ୍ତ
Answer:
(iii) ଇମାଇଲ ଦୁମ୍‌

Question ୧୧।
ପଜିଟିଭ ଫଲୋସଫି ପୁସ୍ତକରେ କେଉଁ ଶବ୍ଦଟି ପ୍ରଥମେ ବ୍ୟବହାର କରାଯାଇଥିଲା ?
(i) ସମାଜବିଜ୍ଞାନ
(ii) ରାଜନୀତିବିଜ୍ଞାନ
(iii) ଇତିହାସ
(iv) ନୃତତ୍ତ୍ଵ
Answer:
(i) ସମାଜବିଜ୍ଞାନ

Question ୧୨।
କିଏ ସମାଜବିଜ୍ଞାନକୁ ସାମାଜିକ ଅନୁଷ୍ଠାନଗୁଡ଼ିକର ବିଜ୍ଞାନ ଅଟେ ?
(i) ଅଗଷ୍ଟ କମ୍
(ii) ଇମାଇଲଦୁର୍ଖମ୍
(iii) ସ୍କୁଲ
(iv) ମାର୍କସ୍
Answer:
(ii) ଇମାଇଲଦୁର୍ଖମ୍

Question ୧୩।
ସମାଜବିଜ୍ଞାନର ପରିସରକୁ କେତୋଟି ଭାଗରେ ବିଭକ୍ତ କରାଯାଇଛି ?
(i) ୨
(ii) ୩
(iii) ୪
(iv) ୫.
Answer:
(i) ୨

Question ୧୪।
ମାନନୀୟ ପାରସ୍କରିକ ସମ୍ପର୍କ, ସେଗୁଡ଼ିକର ଅବସ୍ଥା ଓ ଫଳାଫଳର ଅଧ୍ୟୟନକୁ ସମାଜବିଜ୍ଞାନ କୁହାଯାଏ। ଏହା କିଏ କହିଥିଲେ ?
(i) ଅଗଷ୍ଟ କମଟେ
(ii) ଜିନିସ୍ ବର୍ଗ
(iii) ଦୁର୍ଗମ
(iv) ସ୍କୁଲ
Answer:
(ii) ଜିନିସ୍‌ ବର୍ଗ

Question ୧୫।
ନିମ୍ନୋକ୍ତ କେଉଁ କାରଣ ଯୋଗୁଁ ସମାଜବିଜ୍ଞାନ ଏକ ବିଜ୍ଞାନ ନୁହେଁ ?
(i) ସମାଜ ପର୍ଯ୍ୟବେକ୍ଷଣ କରିଥାଏ
(ii) ପରିମାପକତା
(iii) ସମାଜବିଜ୍ଞାନ ପ୍ରାକୃତିକ ବିଜ୍ଞାନ ପରି ପରିକ୍ଷା କରିଥାଏ।
(iv) ଏ ସମସ୍ତ
Answer:
(ii) ପରିମାପକତା

Question ୧୬।
ନିମ୍ନୋକ୍ତ ମଧ୍ୟରୁ କେଉଁଟି ଭାରତୀୟ ସମାଜବିଜ୍ଞାନୀ
(i) ଅଗଷ୍ଟ କମ୍‌
(ii) ସ୍କୁଲ
(iii) ଏମ୍. ଏନ୍. ଶ୍ରୀନିବାସ
(iv) ଏ ସମସ୍ତ
Answer:
(iii) ଏମ୍. ଏନ୍. ଶ୍ରୀନିବାସ

Question ୧୭।
ଲାଟିନ୍ ଶବ୍ଦ ସୋସିଅସ୍‌ର ଅର୍ଥ କ’ଣ ?
(i) ସମୁଦାୟ
(ii) ସମାଜ
(iii) ଅନୁଷ୍ଠାନ
(iv) ସଙ୍ଗ

Question ୧୮।
ଗ୍ରୀକ୍ ଶବ୍ଦ ଲୋଗସ୍ତର ଅର୍ଥ କ’ଣ ?
(i) କଳା
(ii) ବିଜ୍ଞାନ
(iii) ସାହିତ୍ୟ
(iv) ହିନ୍ଦୀ
Answer:
(ii) ବିଜ୍ଞାନ

Question ୧୯।
ସୋସିଅସ୍ ବା ସୋସାଇଟସ୍ କେଉଁ ଶବ୍ଦ ଅଟେ ?
(i) କର୍ମାନ
(ii) ଗ୍ରୀକ୍
(iii) ଲାଟିନ୍
(iv) ଫ୍ରାନସ୍
Answer:
(iii) ଲାଟିନ୍

Question ୨୦।
ନିମ୍ନଲିଖତ କେଉଁ ବିଜ୍ଞାନ ସହ ସମାଜବିଜ୍ଞାନର ଘନିଷ୍ଠ ସମ୍ପର୍କ ରହିଛି ?
(i) ରାଜନୀତି ବିଜ୍ଞାନ
(ii) ଇତିହାସ
(iii) ଅର୍ଥଶାସ୍ତ୍ର
(iv) ଏ ସମସ୍ତ
Answer:
(iv) ଏ ସମସ୍ତ

Question ୨୧।
ସମାଜବିଜ୍ଞାନ ଶବ୍ଦଟି ପ୍ରଥମେ କେଉଁ ପୁସ୍ତକରେ ବ୍ୟବହାର ହୋଇଥିଲା ?
(i) ଧର୍ମ ସମ୍ବନ୍ଧୀୟ ସମାଜବିଜ୍ଞାନ
(ii) ପଜଟିଭ ଫିଲୋସଫ
(iii) ସମାଜବିଜ୍ଞାନର ନିୟମ
(iv) ଏସମସ୍ତ
Answer:
(ii) ପଜିଟିଭ୍ ଫିଲୋସଫି

Question ୨୨।
ସମାଜବିଜ୍ଞାନ ଏକ ସ୍ଵତନ୍ତ୍ର ବିଷୟବସ୍ତୁ ରୂପେ ଗ୍ରହଣ ହୋଇଥିଲା
(i) ୧୯୩୦
(ii) ୧୯୨୦
(iii) ୧୮୨୦
(iv) ୧୯୨୦
Answer:
(i) ୧୯୩୦

Question ୨୩।
ସମାଜବିଜ୍ଞାନ ପ୍ରଥମେ ଭାରତ କେଉଁ ବିଶ୍ବବିଦ୍ୟାଳୟରେ ଆରମ୍ଭ ହେଲା ?
(i) ଦିଲ୍ଲୀ
(ii) ବମ୍ବେ
(iii) ପୁନେ
(iv) କଲିକତା
Answer:
(ii) ବମ୍ବେ

Question ୨୪।
ବମ୍ବେ ବିଶ୍ଵବିଦ୍ୟାଳୟ ସମାଜବିଜ୍ଞାନ କେବେ ଆରମ୍ଭ ହୋଇଥିଲା ?
(i) ୧୯୧୯
(ii) ୧୯୨୦
(iii) ୧୮୧୯
(iv) ୧୯୧୭
Answer:
(i) ୧୯୧୯

Question ୨୫।
ଅର୍ଥଶାସ୍ତ୍ର ପ୍ରକୃତିରେ ସମାଜବିଜ୍ଞାନରେ ଏକ ବ୍ୟାପକ ବା ବିସ୍ତ୍ରୁତ ବିଭାଗ ଅଟେ ଏହା କିଏ କହିଥିଲେ ?
(i) ଥୋମାସ୍
(ii) ଲୁଇ
(iii) ମାର୍ଶାଲ
(iv) ରବିନ୍‌ସନ୍
Answer:
(i) ଥୋମାସ୍

Question ୨୬।
ନିମ୍ନୋକ୍ତ ମଧ୍ଯରୁ କିଏ ହେଉଛନ୍ତି ଐତିହାସିକ ?
(i) ଗେଟେଲ
(ii) ଭୋୱାର୍ଡ
(iii) ରାଜନୀତିବିଜ୍ଞାନ
(iv) ଏ ସମସ୍ତ
Answer:
(iv) ଏ ସମସ୍ତ

Question ୨୭।
ସମାଜବିଜ୍ଞାନ ବ୍ୟକ୍ତିର ବ୍ୟକ୍ତିତ୍ବ ସମ୍ବନ୍ଧରେ ଜାଣିବାରେ ନିର୍ଭର କରିଥାଏ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ବିଜ୍ଞାନ ଉପରେ –
(i) ରାଜନୀତି ବିଜ୍ଞାନ
(ii) ନୃ-ବିଜ୍ଞାନ
(iii) ମନୋବିଜ୍ଞାନ
(iv) ଅର୍ଥଶାସ୍ତ୍ର
Answer:
(iii) ମନୋବିଜ୍ଞାନ

Question ୨୮।
ପ୍ରାଣୀମାନଙ୍କର ପରିବେଶନାମ ସମ୍ବନ୍ଧୀୟ କ୍ରିୟାକଳାରେ ବିଜ୍ଞାନସମ୍ମତ ଅଧ୍ୟୟନକୁ କୁହାଯାଏ
(i) ସମାଜବିଜ୍ଞାନ
(ii) ମନୋବିଜ୍ଞାନ
(iii) ଜନ୍ସିଲି
(iv) ଏ ସମସ୍ତ
Answer:
(ii) ମନୋବିଜ୍ଞାନ

(ii) ମନୋବିଜ୍ଞାନ

Question ୨୯।
ରାଜନୀତି ବିଜ୍ଞାନର ବିଷୟବସ୍ତୁ ଅଟେ
(i) ରାଷ୍ଟ୍ର
(ii) ସଂସ୍କୃତି
(iii) ଲୋକନୀତି
(iv) ଏସମସ୍ତ
Answer:
(i) ରାଷ୍ଟ୍ର

Question ୩୦।
ଇତିହାସ ହେଉଛି ଅତୀତ ସମାଜବିଜ୍ଞାନ ଓ ସମାଜବିଜ୍ଞାନ ହେଉଛି ବର୍ତ୍ତମାନର ଇତିହାସ ଏହା କିଏ କହିଥିଲେ ?
(i) ମାର୍କସ୍ ୱେବର
(ii) ଭୋୱାର୍ଡ଼
(iii) କୁଲେ
(iv) ଏ ସମସ୍ତ
Answer:
(ii) ଭୋୱାର୍ଡ଼

Question ୩୧।
ସମାଜବିଜ୍ଞାନ ବ୍ୟତୀତ ଇତିହାସର କୌଣସି ଫଳ ନାହିଁ ବା ଇତିହାସ ଅଧ୍ୟୟନ ବ୍ୟତୀତ ସମାଜବିଜ୍ଞାନର କୌଣସି ମୂଳ ନାହିଁ-ଏହି ଉକ୍ତିଟି କିଏ କହିଥିଲେ ?
(i) ମାକର୍ସ ୱେବର
(ii) ଗେଟେଲ
(iii) କନସିଲି
(iv) ଏସମସ୍ତ
Answer:
(iii) ଜନସିଲି

Question ୩୨।
ସମାଜବିଜ୍ଞାନ ଆର୍ଥନୀତିକ କାର୍ଯ୍ୟକଳାପକୁ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଦୃଷ୍ଟିକୋଣରୁ ବିଚାର କରିଥାଏ।
(i) ସାଂସ୍କୃତିକ
(ii) ସାମାଜିକ
(iii) ଐତିହାସିକ
(iv) ଏସମସ୍ତ
Answer:
(ii) ସାମାଜିକ

Question ୩୩।
ଶାରୀରିକ ନୂ-ବିଜ୍ଞାନ ଆଦିମାନବ ଏକ ନିଦ୍ଧିଷ୍ଟ ଦିଗକୁ ଅଧ୍ୟୟନ କରେ।
(i) ଶାରୀରିକ
(ii) ସାଂସ୍କୃତିକ
(iii) ସାମାଜିକ
(iv) ଏସମସ୍ତ
Answer:
(i) ଶାରୀରିକ

Question ୩୪।
ସମାଜବିଜ୍ଞାନର କେଉଁ ବିଭାଗଟି ପୁରାତନ ମାନବର ଜୈବିକ ବ୍ୟବହାରକୁ ଅଧ୍ୟୟନ କରେ ?
(i) ରାଜନୀତି ବିଜ୍ଞାନ
(ii) ନୃ-ବିଜ୍ଞାନ ଉ.
(iii) ଅର୍ଥଶାସ୍ତ୍ର
(iv) ଇତିହାସ
Answer:
(ii) ନୃ-ବିଜ୍ଞାନ ଉ.

Question ୩୫।
ସମାଜବିଜ୍ଞାନ ଏକ ସ୍ଥିତିସ୍ଥାପକ ବିଜ୍ଞାନ ହୋଇଥିବାରୁ ଏହାର ସୀମା କେଉଁଠାରୁ ଆରମ୍ଭ ହୋଇ କେଉଁଠାରେ ଶେଷ ହୋଇଅଛି ତାହା ନିର୍ଦ୍ଧାରଣ କରିବା କଷ୍ଟ ମାଧ୍ଯ -ଏ ଭକ୍ତି କିଏ ପ୍ରଦାନ କରିଥିଲେ?
(i) କାଇଁ ମୁଲର
(ii) ଭି. ଏଫ. କାଲବର୍ଟନ୍
(iii) ଏସ୍. କେ ୱାକ
(iv) ଏ ସମସ୍ତ
Answer:
(ii) ଭି.ଏଫ. କାଲବର୍ଟନ

ଗୋଟିଏ ଶବ୍ଦରେ ଉତ୍ତର ଦିଅ :

Question ୧।
ସମାଜ ବିଜ୍ଞାନର ଜନକ କିଏ ?
Answer:
ଅଗଷ୍ଟ କମ୍‌

Question ୨।.
ସମାଜବିଜ୍ଞାନ ଶବ୍ଦଟି ପ୍ରଥମେ କିଏ ବ୍ୟବହାର କରିଥିଲେ?
Answer:
ଅଗଷ୍ଟ କମ୍

Question ୩।
ସମାଜବିଜ୍ଞାନ ଶବ୍ଦଟି ପ୍ରଥମେ କେଉଁ ମସିହାରେ ପ୍ରଣୟ ନ ହୋଇଥୁଲା?
Answer:
୧୮୩୯

Question ୪।
ଅଗଷ୍ଟ କମଟେ ପ୍ରଥମେ କେଉଁ ପୁସ୍ତକରେ ସମାଜବିଜ୍ଞାନ ଶବ୍ଦଟିକୁ ବ୍ୟବହାର କରିଥିଲା?
Answer:
ପଜିଟିଭ ଫିଲୋସଫି

Question ୫।
ଭାରତରେ କେଉଁ ମସିହାରେ ସମାଜବିଜ୍ଞାନର ଅଧ୍ୟୟନ ଆରମ୍ଭ ହୋଇଥିଲା ?
Answer:
୧୯୧୯ ମସିହା

Question ୬।
ଅଗଷ୍ଟ କମଟେ କେଉଁ ଦେଶର ବ୍ୟକ୍ତି ଅଟନ୍ତି ?
Answer:
ଫ୍ରାନସ୍

Question ୭।
ସମାଜ ବିଜ୍ଞାନ କେତୋଟି ଶବ୍ଦର ମିଶ୍ରଣରେ ଗଠିତ ?
Answer:
୨ଟି

Question ୮।
ସୋସିଅସ୍‌ ଅର୍ଥ କ’ଣ ?
Answer:
ସମାଜ

Question ୯।
ଲୋଗସ୍‌ର ଅର୍ଥ କ’ଣ ?
Answer:
ବିଜ୍ଞାନ ବା ଅଧ୍ୟୟନ

Question ୧୦।
ସମାଜବିଜ୍ଞାନର ପରିସରକୁ କେତୋଟି ସ୍କୁଲ୍ ଅଧ୍ୟୟନ କରିଛନ୍ତି ?
Answer:
୨ଟି

Question ୧୧।
ଜଣେ ସ୍ଵତନ୍ତ୍ର ମତବାଦୀଙ୍କର ନାମ ଲେଖ ?
Answer:
ଜର୍ଜ ସିମେଇ

Question ୧୨।
ଜଣେ ସାଂଶ୍ଳେଷିକ ମତବାଦୀଙ୍କର ନାମ ଲେଖ
Answer:
ଇମାଇଲ ଦୁର୍ଖମ୍

Question ୧୩।
ଜଣେ ଭାରତୀୟ ସମାଜବିଜ୍ଞାନୀଙ୍କର ନାମ ଲେଖ ?
Answer:
ଏମ୍. ଏନ. ଶ୍ରୀନିବାସ

Question ୧୪।
ଅଗଷ୍ଟ କମଟେ କେଉଁ ପୁସ୍ତକରେ ସମାଜବିଜ୍ଞାନ ଶବ୍ଦଟିକୁ ବ୍ୟବହାର କରିଥିଲେ ?
Answer:
ପଜିଟିଭି ଫିଲୋସଫ

Question ୧୫।
ରାଜନୀତି ବିଜ୍ଞାନର କନକ କିଏ ?
Answer:
ଆରିଷ୍ଟୋଟଲ

Question ୧୬।
ଇତିହାସ ହେଉଛି ଅତୀତର ସମାଜବିଜ୍ଞାନ ଓ ସମାଜବିଜ୍ଞାନ ହେଉଛି ବର୍ତ୍ତମାନର ଇତିହାସ ଏହା କାହାର ଭକ୍ତି ?
Answer:
ଜି.ଇ. ହାଓ୍ବାର୍ଡ

Question ୧୭।
କିଏ ସମାଜବିଜ୍ଞାନ ଓ ରାଜନୀତିର୍ବିଜ୍ଞାନକୁ ଗୋଟିଏ ମୁଦ୍ରାର ଦୁଇଟି ପାର୍ଶ୍ବ ବୋଲି କହିଥିଲେ ?
Answer:
କ୍ୟାଟ୍‌ଲିନ୍

Question ୧୮।
ସମାଜବିଜ୍ଞାନର କେଉଁ ଶବ୍ଦ ଦୁଇଟିର ମିଶ୍ରଣ ଅଟେ ?
Answer:
ସୋସିଆସ୍ ଓ ଲୋଗସ୍

Question ୧୯।
ଲୋଗସ୍ ଶବ୍ଦଟି କେଉଁ ଦେଶୀୟ ଶବ୍ଦ ଅଟେ ?
Answer:
ଗ୍ରୀକ୍

Question ୨୦।
କାହା ମତରେ, “ ସମାଜବିଜ୍ଞାନ ଏକ ବିଜ୍ଞାନ ଅଟେ । ଯାହାଙ୍କ ସାମାଜିକ ମାନବର ବ୍ୟାଖ୍ୟାମୂଳକ ବୋଧଗମ୍ୟତା ପାଇଁଚେଷ୍ଟା କରିଥାଏ। ”
Answer:
ମାର୍କସ୍ ୱେବର

Question ୨୧।
ସମାଜବିଜ୍ଞାନ କେଉଁ ପ୍ରକାର ବିଜ୍ଞାନ ଅଟେ ?
Answer:
ସାମାଜିକ ବିଜ୍ଞାନ

Question ୨୨।
ସମାଜ ବିଜ୍ଞାନକୁ ଏକ ବିଶୁଦ୍ଧ ଓ ସ୍ଵାଧୀନ ବିଜ୍ଞାନ ଭାବରେ କେଉଁ ମତବାଦ ଉଲ୍ଲେଖ କରେ ?
Answer:
ସ୍ଵତନ୍ତ୍ର ମତବାଦ

Question ୨୩।
କେଉଁ ମତବାଦ ଅନୁସାରେ ସମାଜବିଜ୍ଞାନ ସମାଜରେ ଥିବା ସମସ୍ତ ସାମାଜିକ ବିଜ୍ଞାନର ସମ୍ମିଶ୍ରଣକୁ ବୁଝାଇଥାଏ
Answer:
ସାଂଶ୍ଳେଷିକ ମତବାଦ

Question ୨୪।
ଇମାଇଲ ଦୁର୍ଖମକର ଏକ ଅବଦାନ ଲେଖ ?
Answer:
ଶ୍ରମବିଭାଜନ

Question ୨୫।
ପ୍ରାଗ୍ଲିପିକ ସମାଜର ବିଭିନ୍ନ ପ୍ରକାର ସାଂସ୍କୃତିକ ସମୂହ। ଏହାର ଗୁଣ ଓ ପରିବର୍ତ୍ତନ ସମ୍ବନ୍ଧରେ ଅଧ୍ୟୟନ କରୁଥିବା ବିଜ୍ଞାନକୁ କ’ଣ କୁହାଯାଏ ?
Answer:
ନୂ–ବିଜ୍ଞାନ

Question ୨୬।
ବ୍ୟକ୍ତିର ମସ୍ତିଷ୍କ ଓ ବ୍ୟବହାର ସମ୍ବନ୍ଧରେ ଅଧ୍ୟୟନ କରୁଥିବା ବିଜ୍ଞାନକୁ କ’ଣ କୁହାଯାଏ ?
Answer:
ମନୋବିଜ୍ଞାନ

Question ୨୭।
କିଏ Principle ପୁସ୍ତକର ଲେଖକ କିଏ ?
Answer:
ହରବର୍ଟ ସ୍ଟେନସର

Question ୨୮।
କିଏ Positive ପୁସ୍କକର ଲେଖକ କିଏ ?
Answer:
ଅଗଷ୍ଟ କମଟେ

Question ୨୯।
ଆକୃତିଗତ ମତବାଦଟି ଅନ୍ୟ ବାକ୍ୟରେ କ’ଣ କୁହାଯାଏ ?
Answer:
ଔପଚାରିକ ବା ସ୍ନାତନ୍ତ୍ର୍ୟ

Question ୩୦।
ସମାଜବିଜ୍ଞାନ ଓ ବୃ-ବିଜ୍ଞାନ ଦୁଇଟି ଯାଆଁଳା ଭଉଣୀ କିଏ କହିଛନ୍ତି ?
Answer:
ଏ.ଏଲ କ୍ରୋଏବର

Question ୩୧।
ଜଣେ ନୃ-ବିଜ୍ଞାନଙ୍କ ନାମ ଲେଖ।
Answer:
ଏ. ଏଲ. କ୍ଲୋଜେର

Question ୩୨।
ଜଣେ ଔତିହାସିକ ବିତ୍‌ଙ୍କ ନାମ ଲେଖ ?
Answer:
ଟୟନଜା

Question ୩୩।
ଜଣେ ରାଜନିତିଙ୍କ ନାମ ଲେଖ।
Answer:
ଆରିଷ୍ଟ୍ରେଟର

Question ୩୪।
ଇତିହାସର ଜନକ କିଏ ?
Answer:
ଲେରୋଟଟସ୍

Question ୩୫।
ଅର୍ଥଶାସ୍ତ୍ରରେ ଜନକ କିଏ ?
Answer:
ଆଡାମ୍ ସ୍ମିଥ୍

ଭ୍ରମ ଥିଲେ ସଂଶୋଧନ କର :

Question ୧।
ସମାଜବିଜ୍ଞାନର ଜନକ ଇମାଇଲ୍ ଦୁର୍ଖମ୍।
Answer:
ସମାଜବିଜ୍ଞାନର ଜନକ ଅଗଷ୍ଟ କମ୍‌। ସମାଜବିଜ୍ଞାନର ଦ୍ବିତୀୟ ଜନକ ଜର୍ଜ ସିଦ୍ଧେଲ।

Question ୨।
ସମାଜବିଜ୍ଞାନରେ ଦ୍ଵିତୀୟ ଜନକ ଇମାଇଲ।
Answer:
ସମାଜବିଜ୍ଞାନରେ ଦ୍ଵିତୀୟ ଜନକ ଇମାଇଲ ଦୁର୍ଖମ୍।

Question ୩।
ସମାଜବିଜ୍ଞାନ ଶବ୍ଦର ଉତ୍ପରି ୧୮୩୦ ମସିହାରେ ହୋଇଥିଲା।
Answer:
ସମାଜବିଜ୍ଞାନ ଶବ୍ଦର ଉତ୍ପତ୍ତି ୧୮୩୯ ମସିହାରେ ହୋଇଥିଲା।

Question ୪।
ମାକସ୍ ୱେବର ହେଉଛନ୍ତି ସାଂଶ୍ଳେଷିକ ମତବାଦର ପ୍ରବକ୍ତା।
Answer:
ମାକସ୍ ୱେବର ହେଉଛନ୍ତି ସ୍ବାତନ୍ତ୍ର୍ୟ ମତବାଦର ପ୍ରବକ୍ତା।

Question ୫।
ସ୍ବାତନ୍ତ୍ର୍ୟ ମତବାଦରେ ସମାଜ ବିଜ୍ଞାନର ପରିସର ବ୍ୟାପକ ଅଟେ।
Answer:
ସାଂଶ୍ଳେଷିକ ମନୋଦରେ ସମାଜ ବିଜ୍ଞାନର ପରିସର ବତବାଦ ବ୍ୟାପକ ଅଟେ।

Question ୬।
ସମାଜ ବିଜ୍ଞାନ ଏକ ପ୍ରାକୃତିକ ବିଜ୍ଞାନ ଅଟେ।
Answer:
ସମାଜବିଜ୍ଞାନ ଏକ ଆଧୁନିକ ବିଜ୍ଞାନ ଅଟେ।

Question ୭।
ସମାଜ ବିଜ୍ଞାନ ଓ ମନୋବିଜ୍ଞାନ ଦୁଇଟି ଜାଆଁଳା ଭଉଣୀ ସଦୃଶ୍ୟ।
Answer:
ସମାଜ ବିଜ୍ଞାନ ଓ ନୂ–ବିଜ୍ଞାନ ଜାଆଁଳା ଭଉଣୀ ସଦୃଶ୍ୟ ।

Question ୮।
ସମାକବିଜ୍ଞାନ ଓ ରାଜନୀତିର୍ବିଜ୍ଞାନ ସହିତ ସମ୍ପର୍କ ନାହିଁ ।
Answer:
ଉ. ସମାଜ ବିଜ୍ଞାନ ଓ ରାଜନୀତି ରାଜ୍ଞାନ ସହିତ ଅନ୍ଧି ନିବିଡ଼ ସମ୍ପର୍କ ରହିଛି।

Question ୯।
ସୋସିଅସ୍‌ ଅର୍ଥ ବିଜ୍ଞାନ ଅଟେ।
Answer:
ସୋସିଅସ୍‌ର ଅର୍ଥ ସମାନ ଅଟେ।

Question ୧୦।
ଲୋଗସ୍‌ର ଅର୍ଥ ସମାଜ ଅଟେ।
Answer:
ଲୋଗସର ଅର୍ଥ ବିଜ୍ଞାନ ଅଟେ।

Question ୧୧।
ଆକୃତିଗତ ମତବାଦ ଅନୁସାରେ ସମାଜବିଜ୍ଞାନ ଏକ ପ୍ରତିମାନିୟ ବିଜ୍ଞାନ ଅଟେ।
Answer:
ଆକୃତିଗତ ମତବାଦ ଅନୁସାରେ ସମାଜବିଜ୍ଞାନ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ବିଜ୍ଞା’ ଅଟେ।

Question ୧୨।
ସାଂଶ୍ଳେଷିକ ମତବାଦ ଅନୁସାରେ ସମାଜବିଜ୍ଞାନ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ବିଜ୍ଞାନ ଅଟେ।
Answer:
ସାଂଶ୍ଲେଷିକ ମତବାଦ ଅନୁସାରେ ସମାଜବିଜ୍ଞାନ ଏକ ନିର୍ଦ୍ଧିଷ୍ଟ ବିଜ୍ଞାନ ନୁହେଁ।

Question ୧୩।
ସ୍କୁଲ ସାଂଶ୍ଳେଷିକ ମତବାଦୀ ଅଟନ୍ତି।
Answer:
ସ୍କଲ୍ ସାଂଶ୍ଲେଷିକ ମତବାଦୀ ନୁହଁନ୍ତି।

Question ୧୪।
ସମାଜବିଜ୍ଞାନ ବ୍ୟକ୍ତିର ଅଧ୍ୟୟନ ଅଟେ।
Answer:
ସମାଜବିଜ୍ଞାନ ସମାଜର ଅଧ୍ୟୟନ ଅଟେ।

Question ୧୫।
ପ୍ରିନସିଫୁଲସ ଅଫ୍ ସୋସିଅଲୋଜି ଗ୍ରନ୍ଥ କମ୍‌ ରଚନା କରିଥିଲେ।
Answer:
ପ୍ରିନ୍‌ସିଫୁଳସ ଅଫ୍ ସୋସିଅଲୋଜି ଗ୍ରନ୍ଥ ସ୍ଟେନସର ରଚନା କରିଥିଲେ।

Question ୧୬।
ଅଗଷ୍ଟ କମଟେ ହେଉଛନ୍ତି ଔପଚାରିକ ଗୋଷ୍ଠୀର ମୁଖ୍ୟ ପ୍ରବକ୍ତା।
Answer:
ଜର୍ଜ ସିମେଲ ହେଉଛନ୍ତି ଔପଚାରିକ ଗୋଷ୍ଠୀର ମୁଖ୍ୟ ପ୍ରବକ୍ତା।

Question ୧୭।
ଭିରକାଣ୍ଡ ସାଂଶ୍ଳେଷିକ ମତବାଦର ଜଣେ ପ୍ରବକ୍ତା
Answer:
ଭିରକାଣ୍ଡ ଔପରିକ ମତ ଦର ଜଣେ ପ୍ରବକ୍ତା

Question ୧୮।
ଏଲ୍‌. ଟି. ନବହାରସ୍ ସାଂଶ୍ଳେଷିକ ମତବାଦର ପ୍ରବକ୍ତା ନୁହନ୍ତି ।
Answer:
ଏଲ୍. ଟି. ନବହାସ୍ ସାଂଶ୍ଲେଷିକ ମତବାଦର ପ୍ରବକ୍ତା ଅଟନ୍ତି ।

Question ୧୯।
ଫ୍ରଏଡ଼ ଜଣେ ନୃତତ୍ବବିତ
Answer:
ଫ୍ରଏଡ଼ ଜଣେ ମନୋସ୍ତତତ୍ତ୍ୱବିତ୍

Question ୨୦।
ଲୁଇ ଜଣେ ରାଜନୀତି ବିଜ୍ଞାନ।
Answer:
ଲୁଇ ଜଣେ ନୃତତ୍ତ୍ୱବିତ୍

ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର :

Question ୧।
ସମାଜବିଜ୍ଞାନ ଶବ୍ଦଟି ଲାଟିନ୍ ଶବ୍ଦ _____ ଓ ଗ୍ରୀକ୍ ଶବ୍ଦର _____ ର ସମ୍ମିଶ୍ରଣରେ ଗଠିତ।
Answer:
ସୋସିଅସ୍ ଓ ଲୋଗସ୍

Question ୨।
ସମାଜବିଜ୍ଞାନ ଶବ୍ଦଟି ପ୍ରଥମେ _____ ପୁସ୍ତକରେ ବ୍ୟବହାର ହୋଇଥିଲା।
Answer:
ପଜିଟିଭ୍ ଫିଲୋସଫି

Question ୩।
_____ ମସିହାରେ ସମାଜବିଜ୍ଞାନ ଶବ୍ଦଟି ପ୍ରଥମେ ବ୍ୟବହାର ହୋଇଥିଲା।
Answer:
୧୮୩୯

Question ୪।
_____ ସମାଜବିଜ୍ଞାନର ଜନକ ଅଟନ୍ତି।
Answer:
ଅଗଷ୍ଟ କମଟେ

Question ୫।
ସମାଜିଜ୍ଞାନ ଶବ୍ଦଟି _____ ଶବ୍ଦ ସୋସିଅସ୍ ଓ ଶବ୍ଦ ଲୋଗସ୍ତର ସମ୍ମିଶ୍ରଣରେ ଗଠିତ।
Answer:
ଲାଟିନ୍ ଓ ଗ୍ରୀକ୍

Question ୬।
ଅଗଷ୍ଟ କମଟେ _____ ଦେଶର ବ୍ୟକ୍ତି ଅଟନ୍ତି।
Answer:
ଫ୍ରାନ୍ସ

Question ୭।
ସୋସାଇଟସ୍ ବା ସୋସିଆସ୍ ଶବ୍ଦ ଅର୍ଥ _____ ଅଟେ।
Answer:
ସମାଜ

Question ୮।
ଲୋଗସ୍ ଶବ୍ଦ ଅର୍ଥ _____ ଅଟେ।
Answer:
ଅଧ୍ୟୟନ ବା ବିଜ୍ଞାନ

Question ୯।
ସମାଜବିଜ୍ଞାନ ଶବ୍ଦ ପରିବର୍ତ୍ତେ _____ ଶବ୍ଦ ବ୍ୟବହାର ପାଇଁ କମ୍‌ ଓ ସାଇମନ ସ୍ଥିର କରିଥିଲେ।
Answer:
ସୋସିଆଲ ଫିଜିକ୍‌ସ

Question ୧୦।
ସମାଜବିଜ୍ଞାନ ପରିସର ସମ୍ବନ୍ଧରେ _____ ଟି ମତାବାଦ ରହିଛି।
Answer:
ଦୁଇଟି,

Question ୧୧।
ସମାଜବିଜ୍ଞାନ ପରିସର ସମ୍ବନ୍ଧରେ ଦୁଇଟି ମତବାଦ ହେଲା _____ଓ _____।
Answer:
ସ୍ଵତନ୍ତ୍ର ମତବାଦ, ସାଂଶ୍ଲେଷିକ ମତବାଦ

Question ୧୨।
କର୍ଜ ସିମେଇ _____ ମତବାଦର ସମର୍ଥକ ଅଟନ୍ତି।
Answer:
ସ୍ଵତନ୍ତ୍ର ମତବାଦ

Question ୧୩।
ଇମାଇଲ _____ ଟି ପ୍ରକାରର ପରିସରକୁ ବିଭକ୍ତ କରିଛନ୍ତି ।
Answer:
ତିନୋଟି

Question ୧୪।
ସରୋକିନ୍ _____ ମତବାଦର ସମର୍ଥକ ଅଟନ୍ତି।
Answer:
ସାଂଶ୍ଳେଷିକ ମତବାଦ

Question ୧୫।
ଭାରତରେ ସମାଜବିଜ୍ଞାନ ପ୍ରଥମେ _____ ମସିହାରେ ଅଧ୍ୟୟନ ଆରମ୍ଭ ହୋଇଥିଲା।
Answer:
୧୯୧୯

Question ୧୬।
ଭାରତରେ _____ ବିଶ୍ବବିଦ୍ୟାଳୟରେ ପ୍ରଥମେ ସମାଜବିଜ୍ଞାନ ଅଧ୍ୟୟନ ଆରମ୍ଭ ହୋଇଥିଲା।
Answer:
ବମ୍ବେ

Question ୧୭।
ଭାରତରେ _____ ମସିହାରେ ସମାଜବିଜ୍ଞାନ ଏକ ସ୍ବତନ୍ତ୍ର ବିଷୟଭାବେ ବିଶ୍ବବିଦ୍ୟାଳୟ ଓ ମହାବିଦ୍ୟାଳୟରେ ଅଧ୍ୟୟନ ହୋଇଥିଲା।
Answer:
୧୯୩୦

Question ୧୮।
ସ୍ବତନ୍ତ୍ର ମତବାଦକୁ ମଧ୍ୟ _____ମତବାଦ କୁହାଯାଏ।
Answer:
ଆକୃତିଗତ ମତବାଦ

Question ୧୯।
ସମାଜବିଜ୍ଞାନ ଏକ _____ ବିଜ୍ଞାନ ଅଟେ।
Answer:
ସାମାଜିକ

Question ୨୦।
ଜନ୍ ସେଲିଙ୍କ ମତରେ ସମାଜବିଜ୍ଞାନ ବ୍ୟତୀତ ଇତିହାସ ଅଧ୍ୟୟନରେ କୌଣସି _____ ନାହିଁ ଏବଂ ଇତିହାସ ବ୍ୟତୀତ ସମାଜବିଜ୍ଞାନର _____ ନାହିଁ।
Answer:
ଫଳ, ମୂଳ

Question ୨୧।
ହାୱାଡ଼ଙ୍କ ମତରେ ‘ଇତିହାସ ହେଉଛି _____ ର ସମାଜବିଜ୍ଞାନ ଓ ସମାଜବିଜ୍ଞାନ ହେଉଛି _____ ର ଇତିହାସ।
Answer:
ଅତୀତ, ବର୍ତ୍ତମାନ

Question ୨୨।
କ୍ୟାଟ୍‌ଲିନ୍‌ଙ୍କ ମତରେ ସମାଜବିଜ୍ଞାନ ଓ _____ ଗୋଟିଏ ମୁଦ୍ରାର ଦୁଇଟି ପାର୍ଶ୍ୱ।
Answer:
ସ୍ଵତନ୍ତ୍ର

Question ୨୩।
ପଜିଟିଭ୍ ଫିଲୋସଫି ପୁସ୍ତକର ରଚୟିତା _____ ଅଟନ୍ତି।
Answer:
ଗଷ୍ଟ କମିଟେ

Question ୨୪।
ସମାଜବିଜ୍ଞାନର ମୂଳନୀତି ଜାଣି ନଥିବା ବ୍ୟକ୍ତିକୁ ତତ୍ତ୍ଵ ଶିକ୍ଷା ଦେବା ଯାହା ନିଉଟନ୍‌ଙ୍କ ଗତି ସମ୍ବନ୍ଧୀୟ ନିୟମ ଜାଣ ନ ଥିବା ବ୍ୟକ୍ତିକୁ ଶାସ୍ତ୍ରର ଜ୍ୟୋତିଷ ଓ ତାପର ଗତିଶୀଳତା ଶିକ୍ଷାଦେବା ତାହା ଅଟେ। ଏହା _____ କହିଥିଲେ।
Answer:
ଏଫ. ଏଚ୍. ଗିଡ଼ିଙ୍ଗସ୍‌

Question ୨୫।
ସମାଜବିଜ୍ଞାନ ଓ ନୃତତ୍ତ୍ଵକୁ ଯମଜ ଭଉଣୀ ବୋଲି _____ କହିଥିଲେ।
Answer:
ଏ. ଏଲ. କ୍ରୋବର

Question ୨୬।
ମାନବୀୟ ପାରସ୍ପରିକ କ୍ରିୟା ଏବଂ _____ ସେଗୁଡ଼ିକ ଅବସ୍ଥା ଏବଂ ଫଳାଫଳ ଅଧ୍ୟୟନକୁ ସମାଜବିଜ୍ଞାନ କୁହାଯାଏ।
Answer:
ପାରସ୍ପରିକ ସମ୍ପର୍କ

‘ଖ’ ବିଭାଗ

ସଂକ୍ଷିପ୍ତ ପ୍ରଶ୍ନୋତ୍ତର ଦୁଇଟି କିମ୍ବା ତିନୋଟି ବାକ୍ୟରେ ଉତ୍ତର ଦିଅ :

Question ୧।
ସମାଜବିଜ୍ଞାନ କହିଲେ କ’ଣ ବୁଝ ?
Answer:
ସମାଜବିଜ୍ଞାନ ଏକ ସାମାଜିକ ବିଜ୍ଞାନଭାବେ। ଏହି ସମାଜବିଜ୍ଞାନ ଶବ୍ଦଟି ଲାଟିନ୍ ଶବ୍ଦ ସୋସିଅସ୍ ଏବଂ ଗ୍ରୀକ୍ ଶବ୍ଦ ଲୋଗସ୍‌ର ସମ୍ମିଶ୍ରଣରେ ଗଠିତ ! ସୋସିଅସ୍ ବା ସୋସାଇଟିସ୍ ଅର୍ଥ ହେଉଛି ସମାଜ ଏବଂ ଲୋଗସ୍ ଅର୍ଥ ଅଧ୍ୟୟନ ବା ବିଜ୍ଞାନ । ତେଣୁ ଏହି ଅର୍ଥରେ ସମାଜବିଜ୍ଞାନର ଅର୍ଥ ହେଉଛି ସମାଜ ବିଜ୍ଞାନ । ଅନ୍ୟ ଅର୍ଥରେ ସମାଜବିଜ୍ଞାନ ହେଉଛି ମାନବର ସୁବ୍ୟସ୍ଥିତ ଜ୍ଞାନର ଅଧ୍ୟୟନ।

Question ୨।
ସମାଜବିଜ୍ଞାନର ସଂଜ୍ଞା ନିରୂପଣ କର।
Answer:
ମୋରିସ୍ ଜିନ୍ସବର୍ଗଙ୍କ ମତରେ, “ମାନବୀୟ ପାରସ୍ପରିକ କ୍ରିୟା ଓ ପାରସ୍ପରିକ ସମ୍ପର୍କ, ସେଗୁଡ଼ିକର ଅବସ୍ଥା ଏବଂ ଫଳାଫଳର ଅଧ୍ୟୟନକୁ ସମାଜବିଜ୍ଞାନ କୁହାଯାଏ ।”

Question ୩।
ସମାଜବିଜ୍ଞାନ ପରିସର ସମ୍ପର୍କରେ କେଉଁ ପ୍ରକାରର ମତବାଦମାନ ପ୍ରଚଳିତ ?
Answer:
ସମାଜବିଜ୍ଞାନକୁ ନେଇ ଦୁଇଗୋଟି ମତବାଦ ରହିଛି । ସେଗୁଡ଼ିକ ହେଲା ଯଥା – ( ା ) ସ୍ୱାତନ୍ତ୍ର୍ୟ, ଆକୃତିଗତ ମତବାଦ ଏବଂ (୨) ସାଂଶ୍ଲେଷିକ ମତବାଦ।

Question ୪।
ସାଂସ୍କୃତିକ ନୃତତ୍ତ୍ଵ କହିଲେ କ’ଣ ବୁଝ ?
Answer:
ସାଂସ୍କୃତିକ ନୃତତ୍ତ୍ଵ ଆଦିମ ମାନବର ଉଭୟ ବସ୍ତୁଭିଭିକ ଏକ ବସ୍ତୁତ୍ଵର ସାଂସ୍କୃତିକ ଉପାଦାନଗୁଡ଼ିକ ସଂପର୍କରେ ଆଲୋକପାତ କରିଥାଏ।

Question ୫।
ସ୍ୱତନ୍ତ୍ର ମତବାଦ କ’ଣ ?
Answer:
ସମାଜବିଜ୍ଞାନର ପରିସର ସମ୍ବନ୍ଧୀୟ ମତବାଦ ଅନୁସାରେ ସମାଜବିଜ୍ଞାନ ଏକ ବିଶୁଦ୍ଧ ଓ ସ୍ଵତନ୍ତ୍ର ବିଜ୍ଞାନ ଅଟେ। ଏହି ମତବାଦ ଅନୁସାରେ ସମାଜବିଜ୍ଞାନ ଏବଂ ସ୍ଵାଧୀନ ଓ ନିର୍ଦ୍ଦିଷ୍ଟ ବିଜ୍ଞାନ ଅଟେ। ଯାହାକି ସାମାଜିକ ସମ୍ପର୍କର। ବିଭିନ୍ନ ଆକୃତି ଅଧ୍ୟୟନ କରିଥାଏ।

Question ୬।
ସାଂଶ୍ଳେଷିକ ମତବାଦ କ’ଣ ?
Answer:
ସାଂଶ୍ଳେଷିକ ମତାମତର ସମାଜବିଜ୍ଞାନୀମାନେ ସମାଜବିଜ୍ଞାନକୁ ଏକ ବିଶୁଦ୍ଧ ବା ସ୍ଵତନ୍ତ୍ର ବିଜ୍ଞାନ ମନେକରି ନ ଥା’ନ୍ତି। ଯେହେତୁ ସାମାଜିକ ଘଟଣାଗୁଡି଼କ ପରସ୍ପର ନିର୍ଭରଶୀଳ। ତେଣୁ ସ୍ଵତନ୍ତ୍ର ଭାବରେ କୌଣସି ବିଷୟ ବା ଘଟଣାକୁ ଅଧ୍ୟୟନ କରିବା ଠିକ୍ ନୁହେଁ। ତେଣୁ ସେମାନେ ସମାଜବିଜ୍ଞାନକୁ ସାମାଜିକ ବିଜ୍ଞାନ କହନ୍ତି।

Question ୭।
ସମାଜବିଜ୍ଞାନର ପ୍ରକୃତି କ’ଣ ?
Answer:
ସମାଜବିଜ୍ଞାନ ଏକ ସ୍ଵାଧୀନ ଓ ସାଧାରଣ ବିଜ୍ଞାନ ଅଟେ। ଏହା ଏକ ତାନ୍ତ୍ରିକ ବା ବିଶୁଦ୍ଧ ବିଜ୍ଞାନ ଅଟେ; ମାତ୍ର ପ୍ରୟୋଗାତ୍ମକ ବିଜ୍ଞାନ ନୁହେଁ। ଏହା ଏକ ସାମାଜିକ ବିଜ୍ଞାନ ଅଟେ। ଏହା ଏକ ନିରପେକ୍ଷ ବିଜ୍ଞାନ ଅଟେ।

Question ୮।
ସ୍ୱତନ୍ତ୍ର ମତବାଦ ସମାଲୋଚିତ ହେବାର କାରଣ ଦର୍ଶାଅ।
Answer:
ସ୍ଵତନ୍ତ୍ର ମତବାଦ ସମାଜବିଜ୍ଞାନର ପରିସରକୁ ସଂକୀର୍ଣ୍ଣ କରିଛି। ସେହିପରି ମତବାଦ ଏକ ବିଶୁଦ୍ଧ ବିଜ୍ଞାନର ପରିକଳ୍ପନା କରିଅଛି। ଯାହାକି ଅସମ୍ଭବ ଅଟେ। ସେହିପରି ସ୍ଵତନ୍ତ୍ର ମତବାଦୀମାନଙ୍କ ମତରେ ସମାଜବିଜ୍ଞାନ କେବଳ ସାମାଜିକ ସମ୍ପର୍କର ବିଭିନ୍ନ ଆକୃତିକୁ ଅଧ୍ୟୟନ କରିଥାଏ।

Question ୯।
ସମାଜବିଜ୍ଞାନକୁ ଏକ ବିଜ୍ଞାନଭାବେ ବିବେଚନା କରିବାର କାରଣ ଦର୍ଶାଅ !
Answer:
ସମାଜବିଜ୍ଞାନକୁ ଏକ ବିଜ୍ଞାନଭାବେ ବିବେଚନା କରୁଥିବା ମତବାଦୀମାନଙ୍କ ମତରେ ସମାଜବିଜ୍ଞାନରେ ପ୍ରାକୃତିକ ବିଜ୍ଞାନ ଭଳି ବୈଜ୍ଞାନିକ ପଦ୍ଧତି ପ୍ରୟୋଗ କରିବା ସଙ୍ଗେ ସଙ୍ଗେ ଭବିଷ୍ୟବାଣୀ ମଧ୍ୟ କରିଥାଏ। ସେହିପରି ସମାଜବିଜ୍ଞାନୀମାନେ ପର୍ଯ୍ୟବେକ୍ଷଣ ସାକ୍ଷାତ୍‌କାର, ପ୍ରଶ୍ନୋତ୍ତର, ଅନୁସୂଚୀ ଆଦି ପଦ୍ଧତିମାନ ବ୍ୟବହାର କରିଥାନ୍ତି । ତେଣୁ ପ୍ରାକୃତିକ ବିଜ୍ଞାନ ଭଳି ସମାଜ ବିଜ୍ଞାନ ଏକ ବିଜ୍ଞାନ ଅଟେ।

Question ୧୦।
ସମାଜବିଜ୍ଞାନର ପରିସର କ’ଣ ?
Answer:
ସମାଜବିଜ୍ଞାନର ପରିସର ସମାଜର ଅଧ୍ୟୟନର କ୍ଷେତ୍ରକୁ ବୁଝାଇଥାଏ। ପରିସର କହିଲେ ବିଷୟବସ୍ତୁକୁ ବୁଝାଇଥାଏ। କୌଣସି ବିଜ୍ଞାନର କ୍ଷେତ୍ର, କେଉଁ ବିଷୟରେ ଅଧ୍ୟୟନ କରାଯିବା ଉଚିତ ଓ ସେହି ବିଜ୍ଞାନର ପରିସୀମାକୁ ପରିସର କୁହାଯାଏ।

ବ୍ୟାଖ୍ୟା କର ଛଅଟି ବାକ୍ୟରେ ଉତ୍ତର ଦିଅ :

Question ୧।
ସମାଜବିଜ୍ଞାନ କହିଲେ କ’ଣ ବୁଝ ?
Answer:
ରାଜନୀତି ବିଜ୍ଞାନ ଏବଂ ସମାଜବିଜ୍ଞାନ ମଧ୍ୟରେ କେତେକ କ୍ଷେତ୍ରରେ ସମାନତା ପରିଲକ୍ଷିତ ହେଉଥିଲେ ମଧ୍ୟ ଏହି ଦୁଇଟି ସାମାଜିକ ବିଜ୍ଞାନ ପରସ୍ପରଠାରୁ କେତେକ କ୍ଷେତ୍ରରେ ପୃଥକ୍ ଅଟନ୍ତି।
(i) ସମାଜବିଜ୍ଞାନ ସଂପୂର୍ଣ୍ଣ ସମାଜର ବିଜ୍ଞାନରୂପେ ପରିଚିତ; କିନ୍ତୁ ରାଜନୀତି ବିଜ୍ଞାନ ରାଷ୍ଟ୍ରର ବିଜ୍ଞାନରୂପେ ପରିଚିତ।
(ii) ସମାଜବିଜ୍ଞାନ ପରିସର ରାଜନୀତି ବିଜ୍ଞାନ ପରିସରଠାରୁ ବ୍ୟାପକ ଅଟେ।
(iii) ରାଜନୀତି ବିଜ୍ଞାନ ଏବଂ ସମାଜବିଜ୍ଞାନ ସେମାନଙ୍କର ଅଧ୍ୟୟନ ପଦ୍ଧତିରେ ପରସ୍ପରଠାରୁ ପୃଥକ୍ ଅଟନ୍ତି।
(iv) ସମାଜବିଜ୍ଞାନ ଉଭୟ ସଙ୍ଗଠିତ ଏବଂ ବିଜ୍ଞାନ ସମୁଦାୟକୁ ଅଧ୍ୟୟନ କରୁଥିବାବେଳେ ରାଜନୀତି ବିଜ୍ଞାନ କେବଳ ସଙ୍ଗଠିତ ସମୁଦାୟକୁ ଅଧ୍ୟୟନ କରିଥାଏ।

Question ୨।
ସମାଜବିଜ୍ଞାନ ଏବଂ ଅର୍ଥଶାସ୍ତ୍ର ମଧ୍ୟରେ ସଂପର୍କ ବିଶ୍ଳେଷଣ କର।
Answer:
ସମାଜବିଜ୍ଞାନ ଏବଂ ଅର୍ଥଶାସ୍ତ୍ର ମଧ୍ୟରେ ଅତି ଘନିଷ୍ଠ ସଂପର୍କ ରହିଛି। ଏହି ଦୁଇଟି ସାମାଜିକ ବିଜ୍ଞାନର ପରସ୍ପରକୁ ବହୁକ୍ଷେତ୍ରରେ ପ୍ରଭାବିତ କରିଥା’ନ୍ତି। ସମାଜ ଅଧିକ ମାତ୍ରାରେ, ଅର୍ଥନୈତିକ କାରଣଗୁଡ଼ିକ ଦ୍ଵାରା ପ୍ରଭାବିତ ହୋଇଥାଏ ଏବଂ ଅର୍ଥନୈତିକ ପ୍ରକ୍ରିୟାମାନ ସମାଜର ପାରିପାର୍ଶ୍ଵକ ଅବସ୍ଥା ଦ୍ଵାରା ନିର୍ଦ୍ଧାରିତ ହୋଇଥା’ନ୍ତି। ଏଥରୁ ସମାଜବିଜ୍ଞାନ ଏବଂ ଅର୍ଥଶାସ୍ତ୍ର ମଧ୍ୟରେ ଥିବା ନିବିଡ଼ ସଂପର୍କର ସୂଚନା ପରିପୃଷ୍ଠ ହୋଇଥାଏ। ଅର୍ଥନୈତିକ କାର୍ଯ୍ୟକଳାପ ସାମାଜିକ କାର୍ଯ୍ୟକଳାପ ସହିତ ଓତଃପ୍ରୋତଭାବେ ଜଡ଼ିତ। ଥୋମାସ୍ (Thomas)ଙ୍କ ମତରେ “ଅର୍ଥଶାସ୍ତ୍ର ପ୍ରକୃତିରେ ସମାଜଶାସ୍ତ୍ରର ବ୍ୟାପକ ଶାଖା ମଧ୍ୟରୁ ଏକ ମୁଖ୍ୟ ଶାଖା। ଯଦିଓ ସମାଜବିଜ୍ଞାନ ଏବଂ ଅର୍ମଶାସ୍ତ୍ର ମଧ୍ୟରେ ଘନିଷ୍ଠ ସଂପର୍କ ନିହିତ, ତଥାପି ଏହି ଦୁଇଟି ସାମାଜିକ ବିଜ୍ଞାନ ସେମାନଙ୍କର ବିଷୟବସ୍ତୁ ପରିସର। ଦୃଷ୍ଟିକୋଣ ଏବଂ ଅଧ୍ୟୟନ ପଦ୍ଧତିରେ ପରସ୍ପରଠାରୁ ଭିନ୍ନ ଅଟନ୍ତି।”

Question ୩।
ସମାଜବିଜ୍ଞାନ ଏବଂ ଇତିହାସ ମଧ୍ୟରେ ଘନିଷ୍ଠ ସମ୍ପର୍କ,ଉଲ୍ଲେଖ କର।
Answer:
ସମାଜବିଜ୍ଞାନ ଏବଂ ଇତିହାସ ମଧ୍ୟରେ ଘନିଷ୍ଠ ସମ୍ପର୍କ ରହିଛି। ପ୍ରଫେସର ଜି, ଇ, ହୋୱାର୍ଡ (G. E. Howard) କହିଛନ୍ତି “ ଇତିହାସ ଅତୀତର ସମାଜବିଜ୍ଞାନ ଏବଂ ସମାଜବିଜ୍ଞାନ ହେଉଛି ବର୍ତ୍ତମାନର ଇତିହାସ। (History is the past Sociology and Sociology is the present History) ଜନ୍ ସେଲି (John Selly)ଙ୍କ ମତରେ, ସମାଜଶାସ୍ତ୍ର ବ୍ୟତୀତ ଇତିହାସ ଅଧ୍ୟୟନ କୌଣସି ଫଳ ନାହିଁ ଏକ ଇତିହାସ ବ୍ୟତୀତ ସମାଜଶାସ୍ତ୍ରର ମୂଳ ନାହିଁ। (History without Sociology has no fruit, Sociology without History has no root) ଇତିହାସ ଅତୀତର ଘଟଣାବଳୀ ସହିତ ଜଡ଼ିତ। ଅତୀତର ଘଟଣାବଳୀକୁ ସମୟାନୁକ୍ରମିକ ଭାବରେ ସଜାଡ଼ି ରଖୁଥାଏ ଇତିହାସ। ଅତୀତର ସାମାଜିକ, ରାଜନୈତିକ, ଧାର୍ମିକ ଏବଂସାଂସ୍କୃତିକ ଘଟଣାଗୁଡ଼ିକୁ ଅଧ୍ୟୟନ କରିଥାଏ। ଗେଟେଲ (Gettle)ଙ୍କ ମତରେ, ଇତିହାସ ହେଉଛି ଅତୀତର ଘଟଣାବଳୀ। ଆନ୍ଦୋଳନ ଏବଂ ସେଗୁଡ଼ିକର କାରଣ ଓ ଆନ୍ତଃ- ସମ୍ପର୍କ ଏକ ନଥପତ୍ର। ଇତିହାସ ମଧ୍ଯ ସମାଜବିଜ୍ଞାନ ଉପରେ ନିର୍ଭରଶୀଳ ଅଟେ।

Question ୪।
ସମାଜବିଜ୍ଞାନ ଏବଂ ଅର୍ଥଶାସ୍ତ୍ର ମଧ୍ୟରେ ପାର୍ଥକ୍ୟ ଦର୍ଶାଅ।
Answer:
ଅର୍ଥଶାସ୍ତ୍ର ମନୁଷ୍ୟର ଅର୍ଥନୈତିକ କାର୍ଯ୍ୟକଳାପ ସହିତ ଜଡ଼ିତ। ଏହା ମୁଖ୍ୟତଃ ସମାଜରେ ଦ୍ରବ୍ୟ, ଉତ୍ପାଦନ, ଉପଭୋଗ ବିନିମୟ ଏବଂ ବଣ୍ଟନ ପ୍ରକ୍ରିୟା ସହିତ ସଂପୃକ୍ତ ଅଟେ। କିନ୍ତୁ ସମାଜବିଜ୍ଞାନ ସାମାଜିକ ଜୀବନର ସମସ୍ତ ଦିଗଗୁଡ଼ିକୁ ଅଧ୍ୟୟନ କରିଥାଏ।

1. ସମାଜବିଜ୍ଞାନ ସମସ୍ତ ପ୍ରକାର ସାମାଜିକ ଅର୍ଥକୁ ତା’ର ଅଧ୍ୟୟନର ପରିସରଭୁକ୍ତ କରିବାବେଳେ ଅର୍ଥଶାସ୍ତ୍ର କେବଳ ମନୁଷ୍ୟର ଅର୍ଥନୈତିକ ସଂପର୍କ ବିଷୟରେ ଆଲୋକପାତ କରିଥାଏ।
2. ଅର୍ଥଶାସ୍ତ୍ର ସମାଜବିଜ୍ଞାନଠାରୁ ବହୁ ପୁରାତନ ଅଟେ। ଅର୍ଥଶାସ୍ତ୍ର ପୁରୁଣା ସାମାଜିକ ବିଜ୍ଞାନରୂପେ ପରିଗଣିତ ହେଉଥିବାବେଳେ ସମାଜବିଜ୍ଞାନ ବର୍ତ୍ତମାନ ମାତ୍ର ତା’ର ଶୈଶବ ସ୍ତର ଅତିକ୍ରମ କରିଛି।
3. ସମାଜବିଜ୍ଞାନରେ ଅଧ୍ୟୟନର ମୁଖ୍ୟ ପରିସର ହେଉଛି ସମାଜ, ମାତ୍ର ଅର୍ଥଶାସ୍ତ୍ରରେ ବ୍ୟକ୍ତିକୁ ଅଧ୍ୟୟନର ପରିସରଭାବେ ନିଆଯାଇଥାଏ। କାରଣ ସମାଜବିଜ୍ଞାନ ସମ୍ପୂର୍ଣ୍ଣରୂପେ ସମାଜକୁ ଅଧ୍ୟୟନ କରିଥାଏ।
4. ଏହି ଦୁଇଟି ସାମାଜିକ ବିଜ୍ଞାନ ଅଧ୍ୟୟନ ପଦ୍ଧତି ପରସ୍ପରଠାରୁ ପୃଥକ୍ ଅଟନ୍ତି।

Question ୫।
ସାମାଜବିଜ୍ଞାନ ଏବଂ ମନସ୍ତତ୍ତ୍ଵ ମଧ୍ଯରେ ସଂପର୍କ ଆଲୋଚନା କର।
Answer:
ସମାଜବିଜ୍ଞାନ ଏବଂ ମନସ୍ତତ୍ତ୍ଵ ମଧ୍ଯରେ ସଂପର୍କ ଅତି ନିବିଡ଼ ଅଟେ। ପରସ୍ପର ଆନ୍ତଃ–ସଂପୃକ୍ତ ଏବଂ ଆନ୍ତଃ- ନିର୍ଭରଶୀଳ ଅଟନ୍ତି। ସମାଜବିଜ୍ଞାନ ମାନବ ସମାଜକୁ ଅଧ୍ୟୟନ କରୁଥିବାବେଳେ ମନସ୍ତତ୍ତ୍ଵ ମନୁଷ୍ୟର ମସ୍ତିଷ୍କ ଏବଂ ତା’ର ବ୍ୟବହାରକୁ ଅଧ୍ୟୟନ କରିଥାଏ। ମନସ୍ତତ୍ତ୍ବ ତା’ର ଅଧ୍ୟୟନ ପାଇଁ ଆବଶ୍ୟକ ହେଉଥିବା କେତେକ ଉପାଦାନ ସମାଜବିଜ୍ଞାନଠାରୁ ପାଇଥାଏ। ମନୁଷ୍ୟର ଚରିତ୍ର ଏବଂ ବ୍ୟବହାରକୁ ସଠିକ୍ ରୂପେ ବୁଝିବା ପାଇଁ ମନସ୍ତତ୍ତ୍ଵ ସମାଜବିଜ୍ଞାନ ଉପରେ ନିର୍ଭର କରିଥାଏ। ବ୍ୟକ୍ତିର ମାନସିକ ବିକାଶ କ୍ଷେତ୍ର ଉପରେ ସମାଜ ଗଭୀର ପ୍ରଭାବ ପକାଇଥାଏ। ମନୋବିଜ୍ଞାନୀମାନେ ଏହି ସମାଜଶାସ୍ତ୍ର ଜରିଆରେ ବିଭିନ୍ନ ସାମାଜିକ ସମସ୍ୟାଗୁଡ଼ିକୁ ଅଧ୍ୟୟନ କରିଥା’ନ୍ତି । ମନୋବିଜ୍ଞାନ ଆବଶ୍ୟକ ତଥ୍ୟ ବା ଆଧାର ସମାଜବିଜ୍ଞାନକୁ ପ୍ରଦାନ କରିବାରେ ସାହାଯ୍ୟ କରିଥାଏ। ସାମାଜିକ ମନସ୍ତତ୍ତ୍ଵ ସଂପର୍କରେ ଆବଶ୍ୟକ ଜ୍ଞାନ ନ ଥିଲେ ମନୁଷ୍ୟ ମଧ୍ୟରେ ଥିବା ପାରସ୍ପରିକ ସଂପର୍କ ଏବଂ କାର୍ଯ୍ୟକଳାଗୁଡ଼ିକୁ ବୁଝିବା ଅସମ୍ଭବ ହୋଇପଡ଼ିବ।

Question ୬।
ସମାଜବିଜ୍ଞାନକୁ ଏକ ବିଜ୍ଞାନ ଭାବରେ ବିବେଚନା କରାଯିବାର କାରଣମାନ ଦର୍ଶାଅ।
Answer:
ପ୍ରାକୃତିକ ବିଜ୍ଞାନ ଭଳି ସମାଜବିଜ୍ଞାନରେ ବସ୍ତୁନିଷ୍ଟ। ନିରପେକ୍ଷତା ବା ସମ୍ପୂର୍ଣ୍ଣ ବାସ୍ତବତା ରକ୍ଷା କରାଯାଇପାରେ ନାହିଁ। ସେହିପରି ମାନବୀୟ ଘଟଣାବଳୀ ସମ୍ପର୍କରେ ଭବିଷ୍ୟବାଣୀ କରିବା ମଧ୍ୟ ଅସମ୍ଭବ ଅଟେ। ସମାଜବିଜ୍ଞାନରେ ବ୍ୟବହୃତ ଶବ୍ଦମାନ ସମ୍ପୂର୍ଣ୍ଣ ସମର୍ଥନ ବହନ କରି ନ ଥା’ନ୍ତେ। ସମାଜବିଜ୍ଞାନର ବିଷୟବସ୍ତୁ ମାନବିକ ସମ୍ପର୍କ ଓ ବ୍ୟବହାର ଉପରେ ପ୍ରତିଷ୍ଠିତ। ଏହାକୁ କୌଣସି ପରୀକ୍ଷାଗାରରେ ପରୀକ୍ଷା କରାଯାଇ ପାରିବ ନାହିଁ ବା ନିରପେକ୍ଷ ଅଧ୍ୟୟନ କରି ହେବ ନାହିଁ। ତେଣୁ ଏହିସବୁ କାରଣ ଯୋଗୁଁ ସମାଜବିଜ୍ଞାନକୁ ଏକ ବିଜ୍ଞାନ କୁହାଯାଇ ନ ପାରେ।

Question ୭।
ସମାଜବିଜ୍ଞାନ ଓ ନୃତ୍ବଗ୍ଧ ମଧ୍ୟରେ ଥିବା ସମ୍ପର୍କ ସଂକ୍ଷେପରେ ଦର୍ଶାଅ।
Answer:
ସମାଜବିଜ୍ଞାନ ଏବଂ ନୃତତ୍ତ୍ଵ ପରସ୍ପର ସହିତ ଘନିଷ୍ଠଭାବେ ସଂପୃକ୍ତ। ନୃତତ୍ତ୍ଵ ଇଂରାଜୀ ନାମ ହେଉଛି () ଏହି ଦୁଇଟି ଗ୍ରୀକ୍ ଯଥା – (Anthropos) ଏବଂ Logosରୁ ଆନୀତ । ଏହି Anthropology ଶବ୍ଦର ଅର୍ଥ ମାନବ (Man) ଏବଂ Logos ଶବ୍ଦର ଅର୍ଥ ବିଜ୍ଞାନ (Science) ବା ଅଧ୍ୟୟନ Study। ତେଣୁ ନୃତତ୍ତ୍ଵର ପ୍ରକୃତ ଅର୍ଥ ହେଉଛି ମାନବ ସମ୍ବନ୍ଧୀୟ ଅଧ୍ୟୟନ ବା ମାନବ ଶରୀର ସମ୍ବନ୍ଧୀୟ ବିଜ୍ଞାନ। ଏହି ନୃତତ୍ତ୍ଵକୁ ମୁଖ୍ୟତଃ ଚାରି ଭାଗରେ ବିଭକ୍ତ କରାଯାଇପାରେ।

1. ଶାରୀରିକ ନୃତତ୍ତ୍ଵ (Physical Anthropology) : ଏହି ଶାରୀରିକ ନୃତତ୍ତ୍ଵ ଆଦିମ ମାନବର ଶାରୀରିକ ଗୁଣାବଳୀକୁ ଅଧ୍ୟୟନ କରିଥାଏ।
2. ସାମାଜିକ ନୂତତ୍ତ୍ଵ (Social Anthropology) : ଏହି ସାମାଜିକ ନୂତରୁ ସାମାଜିକ ପରିବେଶରେ ମନୁଷ୍ୟର ବ୍ୟବହାର ସହିତ ସଂପୃକ୍ତ।
3. ସାଂସ୍କୃତିକ ନୃତତ୍ତ୍ଵ (Cultural Anthropology) : ଏହି ସାଂସ୍କୃତିକ ନୃତତ୍ତ୍ଵ ଆଦିମ ମାନବର ବୟସ୍କ ବସ୍ତୁଭିଭିକ ଏବଂ ଅବସ୍ତୁଭିରିକ ସଂସ୍କୃତି ସହିତ ସଂପୃକ୍ତ।
4. ପ୍ରାଗ୍-ଐତିହାସିକ ପ୍ରତ୍ନତତ୍ତ୍ବ (Pre-Historric Anthropology) : ପ୍ରାଗ୍ଐତିହାସିକ ପ୍ରାଗୈତିହାସିକ ସମୟର ସଂସ୍କୃତିକୁ ଅଧ୍ୟୟନ କରିଥାଏ।

Question ୮।
ସମାଜବିଜ୍ଞାନର ଆବିର୍ଭାବ ଆଲୋଚନା କର।
Answer:
ସମାଜବିଜ୍ଞାନ ସମାଜର ବିଜ୍ଞାନ ଏବଂ ସାମାଜିକ ଅନୁଷ୍ଠାନର ବିଜ୍ଞାନ ଅଟେ। ଏହା ସମାଜ ଏକ ସାମାଜିକ ଅନୁଷ୍ଠାନଗୁଡ଼ିକୁ ଅଧ୍ୟୟନ କରେ। ଏହା ସାମାଜିକ ସମୂହର ପ୍ରକୃତି ଏବଂ ରକ୍ଷଣ ସାମାଜିକ ଧାରଣାଗୁଡ଼ିକୁ ସାମାଜିକ ଅନୁଷ୍ଠାନଗୁଡ଼ିକୁ ସାମାଜିକ ଆକୃତି ସମୂହ। ଜଟିଳତା ଏବଂ ପଦ୍ଧତିଗୁଡ଼ିକୁ ସାମାଜିକ ବ୍ୟବସ୍ଥାଗୁଡ଼ିକ ସାମାଜିକ ସ୍ତରୀକରଣ । ସାମାଜିକ ପ୍ରକ୍ରିୟା ଏବଂ ଏହାର ଲକ୍ଷଣ ଏବଂ ସେମାନଙ୍କର ପାରସ୍ପରିକ ସମ୍ପର୍କକୁ ବୈଜ୍ଞାନିକ ପଦ୍ଧତିରେ ଆଲୋଚନା କରେ। ସମାଜଶାସ୍ତ୍ରବିତ୍ ଅଗଷ୍ଟ କମ୍‌ ୧୮୩୯ରେ ନୂତନ ଶବ୍ଦ ସୋସିଓଲର୍ଜିକୁ ତାଙ୍କ ପୁସ୍ତକ କୋର୍ସ ଡି ଫିଲୋସଫି ପଜିଟିଭ୍ (Course de Philosophic Positive)ରେ ପ୍ରୟୋଗ କରିଥିଲେ। ସେ ଅତି ପ୍ରାଞ୍ଜଳ ଭାବରେ ଏକ ସ୍ଵତନ୍ତ୍ର ସମାଜବିଜ୍ଞାନ ସୃଷ୍ଟିର ଆବଶ୍ୟକତା ରହିଅଛି ବୋଲି ସ୍ପଷ୍ଟ କରିଦେଇଅଛନ୍ତି। ଏହି ନୂତନ ବିଜ୍ଞାନ ନିଶ୍ଚିତ ଭାବରେ ସାମାଜିକ ଘଟଣାଗୁଡ଼ିକର ବିଶ୍ଳେଷଣ ଏବଂ ବର୍ଣ୍ଣନା କରିବାରେ ସହାୟକ ହୋଇପାରିବ। ସମାଜର ଅଜ୍ଞତା ସମସ୍ତ ସାମାଜିକ ବ୍ୟାଧର ମୂଳଉତ୍ସ ଥିଲା। ଅଗଷ୍ଟ କମ୍‌ ବିଶ୍ଵାସ କରୁଥିଲେ ଯେ ଉତ୍ତମ ସମାଜର ଉନ୍ନତିରେ ସମାଜ ସମ୍ବନ୍ଧୟ ଜ୍ଞାନବିଜ୍ଞାନ, ପଦ୍ଧତି ଉପରେ ପର୍ଯ୍ୟବସିତ ହେବା ନିତାନ୍ତ ଜରୁରୀ।

Question ୯।
ସ୍ୱତନ୍ତ୍ର ମତବାଦ ଓ ସାଂଶ୍ଳେଷିକ ମତବାଦ ମଧ୍ୟରେ ପାର୍ଥକ୍ୟ ଦର୍ଶାଅ ।
Answer:
ସ୍ଵତନ୍ତ୍ର ମତବାଦ ଅନୁସାରେ ସମାଜବିଜ୍ଞାନ ଏକ ସ୍ଵାଧୀନ ଏବଂ ବିଶୁଦ୍ଧ ସହ ସମ୍ପୃକ୍ତ ସମସ୍ତ ଘଟଣାକୁ ଅଧ୍ୟୟନ କରି ନ ଥାଏ। ଏହି ମତବାଦ ଅନୁସାରେ ସମାଜବିଜ୍ଞାନର ପରିସର ସଂକୀର୍ଣ୍ଣ ଅଟେ। ସାଂଶ୍ଲେଷିକ ମତବାଦର ସମାଜବିଜ୍ଞାନୀମାନେ ସମାଜବିଜ୍ଞାନକୁ ସ୍ଵତନ୍ତ୍ର ଓ ବିଶୁଦ୍ଧ ବିଜ୍ଞାନ ଭାବରେ ବିବେଚନା କରିବା ପରିବର୍ତ୍ତେ ଏହାକୁ ଏକ ସମାଜିକ ବିଜ୍ଞାନ ଭାବରେ ବିବେଚନା କରିଛନ୍ତି। ଏହି ମତବାଦୀମାନଙ୍କ ମତାନୁସାରେ ସାମାଜିକ ଘଟଣାଗୁଡି଼କ ପରସ୍ପର ନିର୍ଭରଶୀଳ ଏବଂ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଅଂଶର ଅଧ୍ୟୟନ ସମ୍ପୂର୍ଣ ସାମାଜିକ ଜୀବନ ସମ୍ବନ୍ଧରେ ଧାରଣା ଦିଏ ନାହିଁ। ତେଣୁ ଏହି ମତବାଦର ସମାଜ ବିଜ୍ଞାନୀମାନେ ସମାଜବିଜ୍ଞାନର ପରିସର ବ୍ୟାପକ ବୋଲି ବିଚାର କରିଥା’ନ୍ତି।

‘ଗ’ ବିଭାଗ

ଦୀର୍ଘ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର

Question ୧।
ସମାଜ ବିଜ୍ଞାନର ବିକାଶ ପ୍ରତିପାଦନ କର।
Answer:
ବିଜ୍ଞାନ ଜଗତରେ ଅନ୍ୟାନ୍ୟ ସହୋଦର ବିଜ୍ଞାନୀଙ୍କ ମଧ୍ୟରେ ସାମଜ ବିଜ୍ଞାନ ଏକ ଅର୍ବାଚୀନ କିଶୋର । ବିଜ୍ଞାନ ଜଗତରେ ଏହାର ଏକ ନିଜସ୍ଵ ପୃଥକ୍ କାମ ନେଇ ଆସନ ପାଇବାର ଇତିହାସକୁ ଶତାବ୍ଦୀର ମାପକାଠିରେ ନୁହେଁ ବରଂ ଦଶକର ମାପକାଠିରେ ମାପିବା ଅଧିକ ଯୁକ୍ତିସଂଗତ ହେବ । ଏ ପରିପ୍ରେକ୍ଷୀରେ ବିଖ୍ୟାତ ସମାଜ ବିଜ୍ଞାନ ମାକାଇଭର ଲେଖୁଛନ୍ତି ~ ‘Sociology is a more or less definite body of systematic knowledge with a distinct place and name among the family of science must be dated by decades rather than by Centuries.” ୧୮୩୯ ମସିହାରେ ଫରାସୀ ଦାର୍ଶନିକ ଓ ସମାଜଶାସ୍ତ୍ରୀ ଅଗଷ୍ଟ କମ୍‌ (Auguste Comte) ପ୍ରଥମ କରି “ ସମାଜବିଜ୍ଞାନୀ ” (Sociology) ଶବ୍ଦଟି ପ୍ରଣୟନ କରିଥିଲେ ଏବଂ ଏହାର ଅଧ୍ୟୟନ ପରିସର ନିର୍ଣ୍ଣୟ କରିବା ସଂଗେ ସଂଗେ ଏହା କେଉଁ ପଦ୍ଧତି ଗ୍ରହଣ କରିବ ତାହା ମଧ୍ୟ ବ୍ୟାଖ୍ୟା କରିଥିଲେ । ତେଣୁ ତାଙ୍କୁ ସମାଜ ବିଜ୍ଞାନର ଜନ୍ମଦାତା ବୋଲି କୁହାଯାଏ ।

ସମାଜ ବିଜ୍ଞାନର ବିକାଶ :
ବିକାଶର ପ୍ରଥମ ଅବସ୍ଥା – ସାମାଜିକ ଜୀବନ ବିଷୟରେ କ୍ରମବଦ୍ଧି ତଥା ଏକ ବ୍ୟବସ୍ଥିତ ଢଙ୍ଗରେ ବିଚାର ଆଲୋଚନା ପାଶ୍ଚାତ୍ୟଜଗତରେ ପ୍ରଥମେ ଗ୍ରୀକ୍ ଦାର୍ଶନିକମାନଙ୍କ ଦ୍ଵାରା ଆରମ୍ଭ ହୋଇଥିଲା। ଗ୍ରୀକ୍ ଦାର୍ଶନିକ ପ୍ଲାଟୋ ନିଜର ପୁସ୍ତକ ”The Republic’’ ଏବଂ ଆରିଷ୍ଟୋଟଲ୍ ନିଜର ପୁସ୍ତକ “Ethics and Politics”ରେ ବିଭିନ୍ନ ପ୍ରକାର ସାମାଜିକ ଘଟଣା ଯଥା – ପାରିବାରିକ ଜୀବନ, ପରମ୍ପରା, ସମାଜରେ ନାରୀର ସ୍ଥାନ ଇତ୍ୟାଦିର ବିସ୍ତୃତ ବର୍ଣ୍ଣନା କରିଅଛନ୍ତି। ଏହି ବିଦ୍ଵାନ୍‌ମାନଙ୍କର ବିଚାରକୁ ସମାଜ, ସମୁଦାୟ, ରାଷ୍ଟ୍ର ଆଦି ମଧ୍ୟରେ କୌଣସି ପ୍ରଭେଦ ଥ‌ିବାର ସ୍ପଷ୍ଟ ହୁଏ ନାହିଁ। ପୁଣି ସେମାନେ ନିଜର ଲେଖାରେ ଏକ ଆଦର୍ଶ ସମାଜ ବ୍ୟବସ୍ଥା ଉପରେ ଅଧିକ ଜୋର୍ ଦେଇଥିଲେ। କିନ୍ତୁ ସାମାଜିକ ଜୀବନର ବାସ୍ତବତା, ଏହାର କାରଣ ନିର୍ଣ୍ଣୟ ଆଦି ଗୁରୁତ୍ଵପୂର୍ଣ୍ଣ ବିଭାଗମାନ ସେମାନଙ୍କ ଲେଖାରୁ ବାଦ୍ ପଡ଼ିଥିଲା। ନିଜର ସମାଜ ବ୍ୟବସ୍ଥାକୁ ସେମାନେ ତୀବ୍ର ସମାଲୋଚନା କରୁଥିଲେ ଅଥବା ଉଚ୍ଛସିତ ପ୍ରଶଂସା କରୁଥିଲେ। ଏଣୁ ସେମାନଙ୍କର ବିଚାରଧାରା ନିରପେକ୍ଷ ନ ହୋଇ ପକ୍ଷପାତିତା ଦୋଷରେ ଲିପ୍ତ ଥିଲା। ପ୍ଲୁଟୋ ଏବଂ ଆରିଷ୍ଟୋଟଲଙ୍କ ପରେ ସମାଜବିଜ୍ଞାନ, ସିସେରୋ, ମାରାକସ୍ ଆଲୋଲିୟସ୍, ସେଷ୍ଟ ଅଗଷ୍ଟିନ୍ ଆଦିଙ୍କ ଅବଦାନ ଉଲ୍ଲେଖଯୋଗ୍ୟ।

ସମାଜ ବିଜ୍ଞାନ ବିକାଶର ଦ୍ଵିତୀୟ ଅବସ୍ଥା : ଷଷ୍ଠ ଶତାବ୍ଦୀଠାରୁ ଚତୁର୍ଦ୍ଦଶ ଶତାବ୍ଦୀ ପର୍ଯ୍ୟନ୍ତ ସମୟକୁ ସମାଜ ବିଜ୍ଞାନ ବିକାଶର ଦ୍ଵିତୀୟ ଅବସ୍ଥା ରୂପେ ଧରାଯାଏ। ଏହି ସମୟରେ ଦୀର୍ଘଦିନ ଧରି ଧର୍ମ ଓ ଦର୍ଶନର ପ୍ରଭାବ ପ୍ରଚଳିତ ଥଲା । ତ୍ରୟୋଦଶ ବିକାଶର ଦ୍ଵିତୀୟ ଅବସ୍ଥା ରୂପେ ଧରାଯାଏ । ଏହି ସମୟରେ ଦୀର୍ଘଦିନ ଧରି ଧର୍ମ ଓ ଦର୍ଶନର ପ୍ରଭାବ ପ୍ରଚଳିତ ଥିଲା। ତ୍ରୟୋଦଶ ଶତାବ୍ଦୀବେଳକୁ ଧୀରେ ଧୀରେ ଯୁକ୍ତିବାଦର ବିକାଶ ଯୋଗୁଁ ସାମାଜିକ ଘଟଣାର ଅଧ୍ୟୟନର ଯୁକ୍ତି ମହତ୍ଵ ଲାଗିଲା। ଥୋମାସ୍ ଏକ୍ୟୁନ୍ସ (Thomas Acqwines)ଙ୍କ ପୁସ୍ତକ De-Regmine Principum ତଥା ଦାନ୍ତେଙ୍କ ପୁସ୍ତକ Monarchiaରୁ ଏହା ସ୍ପଷ୍ଟ ସଂକେତ ମିଳିଥାଏ। ଏହି ବିଦ୍ଵାନମାନେ ମନୁଷ୍ୟକୁ ଏକ ସାମାଜିକ ପ୍ରାଣୀ ଏବଂ ସମାଜକୁ ଏକ ବ୍ୟବସ୍ଥିତ ରୂପରେ ପରିଚାଳିତ କରିବା ପାଇଁ ସରକାରର ଆବଶ୍ୟକତା ଉପରେ ଗୁରୁତ୍ବ ଆରୋପ କରିଥିଲେ। ଏକ୍ୟୁସ୍‌ ସାମାଜିକ ସହଯୋଗ, ନ୍ୟାୟ, ଶ୍ରଦ୍ଧା, ଏକତା ଈଶ୍ଵର ଇତ୍ୟାଦିର ଅଧ୍ୟୟନ କରିଥିଲେ। ଏହି ସମୟରେ ପ୍ରାକୃତିକ ଘଟଣା ଓ ତଥା ଅଧ୍ୟୟନ ବିଧିକୁ ମଧ୍ଯ ସମାଜର ଅଧ୍ୟୟନରେ ପ୍ରୟୋଗ କରାଯିବାରେ ଲାଗିଲା। ଏଣୁ ସମାଜ ଅଧ୍ୟୟନରେ କାରଣ -ପରିଣାମ ସମ୍ପର୍କ (Cause effect relationship) ଉପରେ ଅଧ୍ଵକ ପ୍ରାଧାନ୍ୟ ଦିଆଗଲା।

ସମାଜ ବିଜ୍ଞାନ ବିକାଶର ତୃତୀୟ ଅବସ୍ଥା :
ପଞ୍ଚଦଶ ଶତାବ୍ଦୀ ବେଳକୁ ସାମାଜିକ ଘଟଣା ଅଧ୍ୟୟନରେ ବୈଜ୍ଞାନିକ ପଦ୍ଧତିରେ ପ୍ରୟୋଗ ହେବାକୁ ଲାଗିଲା। ଏହି ସମୟରେ ସାମାଜିକ ଜୀବନରେ ବିଭିନ୍ନ ବିଭବ, ରାଜନୈତିକ, ଧର୍ମଗତ, ସାମାଜିକ ଇତ୍ୟାଦିର ସ୍ଵତନ୍ତ୍ର ଅଧ୍ୟୟନ କରାଯିବାରେ ଲାଗିଲା। ପରିଣାମ ସ୍ଵରୂପ ବିଶିଷ୍ଟ ସମାଜିକ ବିଜ୍ଞାନ ଯଥା ଅର୍ଥଶାସ୍ତ୍ରର, ମନୋବିଜ୍ଞାନ, ରାଜନୀତି ବିଜ୍ଞାନ, ଇତିହାସ ଇତ୍ୟାଦିରେ ବିଜ୍ଞାନ ହୋଇଥିଲା। ଏହି ସମୟରେ ବିଦ୍ଵାନଗଣଙ୍କର ବୈଦ୍ଧିକଚିନ୍ତନ ଫଳରେ ସମାଜ ବିଜ୍ଞାନର ବିକାଶ ପାଇଁ ପୃଷ୍ଟଭୂମି ନିର୍ମିତ ହୋଇଥିଲା। ଏହି ଯୁଗର ପ୍ରମୁଖ ବିଚାରକଗଣ ହେଉଛନ୍ତି- ମାଥସ୍ (Malthus), ଥମାସ୍ ହବସ୍ (Thoms Hobbes), ଜନ ଲକ୍ (John Locke), ଋଷୋ (Rousseau), ମଣ୍ଡେସ୍କୁ (Montesqueu) ଇତ୍ୟାଦି। ଏ ସମସ୍ତ ବିଦ୍ଵାନଗଣଙ୍କ ସମାଜ ବିଚ୍ଛନାରେ ବିକାଶ ଦିଗରେ ଯଦିଓ ଅବଦାନ ଥିଲା ତଥାପି ଏମାନଙ୍କର ଅଧ୍ୟୟନରେ ଏକ ରୂପତା ଏବଂ ବିଶେଷୀକରଣର ଅଭାବ ଦେଖିବାକୁ ମିଳିଥାଏ।

ସମାଜ ବିଜ୍ଞାନ ବିକାଶର ଚତୁର୍ଥ ଅବସ୍ଥା : ଫରାସୀ ବିଦ୍ଵାନ ଅଗଷ୍ଟ କମ୍‌ଙ୍କ ସମୟରୁ ହିଁ ସମାଜବିଜ୍ଞାନ ବିକାଶର ଚତୁର୍ଥ ଅବସ୍ଥା ଗଣନା କରାଯାଏ। ଅଗଷ୍ଟ କମଟେ ନିଜର ଗୁରୁ ସେଣ୍ଟସାଇମନଙ୍କୁ ଭୌତିକ ବା ପଦାର୍ଥ ବିଜ୍ଞାନ ପରି ସମାଜ ବିଜ୍ଞାନକୁ ଏପରି ଏକ ବିଜ୍ଞାନରୂପେ ଗଢିବାକୁ ଇଚ୍ଛା କରିଥିଲେ । ଯାହାଦ୍ବାରା ସାମାଜିକ ଘଟଣାଗୁଡ଼ିକ ବ୍ୟବସ୍ଥିତ ଓ କ୍ରମବଦ୍ଧ ଭାବରେ ଅଧ୍ୟୟନ ତଥା ବିଶ୍ଳେଷଣ କରାଯିବା ସଙ୍ଗେ ସଙ୍ଗେ ଏହା ଫଳସ୍ଵରୂପ ସାମାଜିକ ନିୟମାମାନ ନିରୂପଣ କରାଯାଇପାରିବ। ସେଥ‌ିପାଇଁ କମଟେ ବିଶେଷ ଯତ୍ନବାନ ଥିଲେ। ସେ ପ୍ରଥମେ ସମାଜର ଅଧ୍ୟୟନକୁ ସାମାଜିକ ପଦାର୍ଥ ବିଜ୍ଞାନ (Social Physics) ନାମ ଦେଇଥିଲେ। କିନ୍ତୁ ପରେ ଏହି ନାମ ପରିବର୍ତ୍ତେ ସମାଜ ବିଜ୍ଞାନ (Sociology) ନାମ ରଖେଲେ। ସେ ସର୍ବପ୍ରଥମେ ସାମାଜିକ ଦର୍ଶନ ଏବଂ ସାମାଜିକ ବିଜ୍ଞାନ ମଧ୍ୟରେ ଥ‌ିବା ପ୍ରଭେଦ ସ୍ପଷ୍ଟ କରିଥିଲେ। ପ୍ରାକୃତିକ ଘଟଣାପରି ସାମାଜିକ ଘଟଣାଗୁଡିକ ମଧ୍ୟ ବସ୍ତୁନିଷ୍ଟତା (Objectivity) ଏବଂ ପ୍ରତ୍ୟକ୍ଷ ପ୍ରଣାଳୀ (Direct Method) ସାହାର୍ଯ୍ୟରେ ଅଧ୍ୟୟନ କରାଯାଇପାରେ ବୋଲି ସେ ମତପୋଷଣ କରିଥିଲେ। ତାଙ୍କ ସାମାଜିକ ଜୀବନରେ ସମସ୍ତ ବିଭବ ଏକ ସ୍ଵତ୍ରରେ ପନ୍ଥା ଏବଂ ଏହି ଏକତ୍ଵ ଉଦ୍ବର୍ତ୍ତନ କ୍ରିୟାର ପ୍ରଭାବରେ ସମ୍ପୂର୍ଣ୍ଣରୂପେ ପ୍ରଭାବିତ ଅଟେ।

୧୮୪୩ ଜନଷ୍ଟୁଆଟ୍ ମିଲ୍ ଇଂଲଣ୍ଡରେ ସମାଜ ଶାସ୍ତ୍ରକୁ ପରିଚିତ କରାଇଥିଲେ । ଏହାପରେ ପ୍ରସିଦ୍ଧ ବ୍ରିଟିଶ ସମାଜତତ୍ତ୍ବ ହରବର୍ଟ ସେନସର (Herbat Spencer) ସମାଜ ବିଜ୍ଞାନର ବିକାଶରେ ସକ୍ରିୟ ଭାଗ ନେଇଥିଲେ । ସେ ନିଜର ରଚନା (Synthectic Philosophy)ର ଏକ ଭାଗ Principle of Sociologyରେ କମ୍ପେଙ୍କ ବିଚାରକୁ ବିବର୍ତ୍ତନ ଦେବା ପାଇଁ ଚେଷ୍ଟା କରିଥିଲେ। ତାଙ୍କର ପ୍ରସିଦ୍ଧ ନାନା ଅଙ୍ଗ ତତ୍ତ୍ଵ (Theory of Organiastion) ଦ୍ବାରା ସେ ସମାଜର ତୁଳନା ମାନବ ଶରୀର ସହିତ କରିଥିଲେ। ମାତ୍ର ତାଙ୍କର ସାମାଜିକ ଘଟଣାଗୁଡିକର ଜୈବତରୁ ବାଖ୍ୟା ଶତାଦ୍ଦୀରେ ପ୍ରାରମ୍ଭରେ ମନୋବୈଜ୍ଞାନିକ ବାଖ୍ୟ ଦ୍ଵାରା ସ୍ଥାନାନ୍ତରିତ ହେଲା। ମଣିଷ ମନର ଉଦବର୍ତ୍ତନ କିପରି ଅଙ୍ଗାଙ୍ଗୀଭାବେ ଜଡିତ ତାହା ସେନସରଙ୍କ ଉତ୍ତର ପୁରୁଷମାନେ ଯଥା — ଗ୍ରାହାମ୍, ୱାଲାମୂଳ, ମାଡ୍ୟୁଗଲ, ୱର୍ଡଗଡିସ୍, କୁଲେ, ମିଡି ଆଦି ଦର୍ଶାଇଥିଲେ।

ଅଗଷ୍ଟ କମକେଟଙ୍କ ପରେ ଅନ୍ୟ ଫରାସୀ ବିଦ୍ଵାନଙ୍କ ମଧ୍ୟରେ ସମାଜ ବିଜ୍ଞନାକୁ ଅନ୍ୟ ସାମାଜିକ ବିଜ୍ଞାନଠାରୁ ପୃଥକ୍ ଏବଂ ଏକ ସ୍ଵତନ୍ତ୍ର ଓ ବସ୍ତୁନିଷ୍ଠ ବିଜ୍ଞାନ ରୂପେ ଗଢିବାରେ ଇମାଇଲ୍ ଦୁଖିମ୍‌ଙ୍କ ଉଲ୍ଲେଖଯୋଗ୍ୟ ! ସମାଜ . ବିଜ୍ଞାନଙ୍କୁ ସେ ସାମୂହିକ ପ୍ରତିନିଧୁତ୍ଵ ବିଜ୍ଞାନ ଉପର ନିର୍ଭର କରି ସମାଜ ବିଜ୍ଞାନ ତା’ର ଜ୍ଞାନର ଗନ୍ତାଘରକୁ ସମ୍ବନ୍ଧ କରିବା ଉଚିତ ବୋଲି ସେ ସ୍ଵୀକାର କରିଛନ୍ତି” ଏ ପରିପ୍ରେକ୍ଷୀରେ ସେ କହିଛନ୍ତି- ଆମ୍ଭର ବିଶ୍ବାସ ଅଟେ ଯେ, ଅନ୍ୟାନ୍ୟ ସାମାଜିକ ବିଜ୍ଞାନମାନ ଯଥା : ଇତିହାସ, ସାମାଜିକ ଅର୍ଥଶାସ୍ତ୍ର ଇତ୍ୟାଦିରେ ଅନୁସନ୍ଧାନଗୁଡିକୁ ନିୟମିତ ରୂପେ ଅବଗତ ହେବା ପାଇଁ ଅର୍ଥଶାସ୍ତ୍ର ନିତାନ୍ତ ଆବଶ୍ୟକ ଅଟେ ।” କାରଣ ଏହାଦ୍ଵାରା ଉପଲବ୍ଧ ସାମଗ୍ରୀ ଦ୍ବାରା ହିଁ ସମାଜ ବିଜ୍ଞାନର ନିର୍ମାଣ ହେବା ଉଚିତ

ଜର୍ମାନ୍ ସମାଜଶାସ୍ତ୍ରୀ ମାକ୍ସ ୱେବର, ଟିନସ୍ ସିଜେଲ ଆଦିଙ୍କର ସମାଜ ବିଜ୍ଞାନକୁ ଅବଦାନ ମହତ୍ତ୍ଵପୂର୍ଣ୍ଣ ଅଟେ। ସମାଜ ବିଜ୍ଞାନର ବିଜ୍ଞାନରେ ବିଶ୍ବର ବିଭିନ୍ନ ଦେଶର ବିଦ୍ଵାନଗଣଙ୍କର ମହତ୍ତ୍ଵପୂର୍ଣ୍ଣ ଅବଦାନ ରହିଅଛି। ସେମାନଙ୍କ ଉଦ୍ୟମରେ ସମାଜ ବିଜ୍ଞାନ ବିଶ୍ବର ବିଭିନ୍ନ କୋଣରେ ଉତ୍ପତ୍ତିଲାଭ କରିଥିଲା। ସମ୍ଭବତଃ ବିଶଂ ଶତାଦ୍ଦୀରେ ଫ୍ରାନ୍ସ, ଜର୍ମାନୀ ଏବଂ ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକାରେ ଏହି ବିଷୟରେ ବିକାଶ ଘଟିଥିଲା। ଏକ ସ୍ଵତନ୍ତ୍ର ବିଷୟ ହିସାବରେ ସର୍ବପ୍ରଥମେ ଏହା ୧୮୭୯ ମସିହାରେ ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକାର ୟେଲ୍ ବିଶ୍ଵବିଦ୍ୟାଳୟରେ ଆରମ୍ଭ ହୋଇଥିଲା। ଏହାପରେ ୧୮୮୯ରେ ଫ୍ରାନ୍ସ, ୧୯୦୭ରେ ଇଂଲଣ୍ଡ, ୧୯୨୦ରେ ପୋଲାଣ୍ଡ, ୧୯୨୪ରେ ମିଶର, ୧୯୪୭ରେ ସ୍ଵିଡେନ୍, ଶ୍ରୀଲଙ୍କା ଏବଂ ୧୯୫୪ ମସିହାରେ ରେଙ୍ଗୁନ୍ ବିଶ୍ଵବିଦ୍ୟାଳୟରେ ସମାଜ ବିଜ୍ଞନାର ଅଧ୍ୟୟନ ଓ ଅଧ୍ୟାପନା କାର୍ଯ୍ୟ ଆରମ୍ଭ ହୋଇଥିଲା। ଭାରତରେ ୧୯୧୪ରେ ବମ୍ବେ ବିଶ୍ଵବିଦ୍ୟାଳୟରେ, ୧୯୧୭ରେ କଲିକତା ବିଶ୍ବବିଦ୍ୟାଳୟ, ୧୯୨୦ରେ ମହୀଶୂର ବିଶ୍ଵବିଦ୍ୟାଳୟ, ୧୯୨୧ରେ ଲକ୍ଷ୍ନୌ ବିଶ୍ଵବିଦ୍ୟାଳୟ ଓ ଏହାପରେ ଅନ୍ୟ ବିଶ୍ବବିଦ୍ୟାଳୟଗୁଡିକରେ ଏକ ସ୍ଵତନ୍ତ୍ର ବିଷୟ ରୂପେ ଆର୍ବିଭାବ ହୋଇଥିଲା।

ସମାଜ ବିଜ୍ଞାନରେ ବିକାଶରେ ବିଭିନ୍ନ ଦେଶର ମହାନ ସମାଜ ବିଜ୍ଞାନୀମାନଙ୍କରେ ଅବଦାନ ରହିଅଛି ସେମାନଙ୍କ ମଧ୍ୟରୁ ଇଂଲଣ୍ଡରେ ହରବର୍ଟ ସେନସର, ଚାଲର୍ସ ହୁଅ, ହବହାଉସ୍, ୱେଷ୍ଟରମାର୍କ ମାନହୀନ, ଜିସ୍‌ବର୍ଗ, ଇବର୍ଟସନ୍ ଜିକଲ ଫ୍ରାନସର ହୁର୍ଦସ ବ୍ରେଡ ଲିଙ୍କ୍, ଜର୍ମାନରେ ଟନିଜ, ଉନଜ୍, ମାଇସ୍ ୱେବର, କାଲମାକ୍ସ, ଭିରକାଣ୍ଡ ସିଟେଲ୍, ଆମେରିକାର ଗଡ଼ିକମ୍ ସମନର ାକପାର୍କ ବର୍ଗେସ୍‌ ସରୋକିନ୍, ଜିମରମ୍ୟାନ, ମାକ୍‌ଆଇଭର ଅଗବର୍ଷ ପାରସନସ, ମର୍ଟନ କୋଜର, ରସ ବାର୍ଲସ୍ ଇତ୍ୟାଦିଙ୍କୁ ଅବଦାନଗୁଡିକୁ ସମାଜ ବିଜ୍ଞାନ ଜ୍ଞାନରେ ଅଶେଷ ସମୃଦ୍ଧି ଆଣିପାରିଛି।

Question ୨।
ସମାଜ ବିଜ୍ଞାନରେ ମୁଖ୍ୟ ତାତ୍ତ୍ଵିକ ଦୃଷ୍ଟିକୋଣମାନ ଆଲୋଚନା କର।
Answer:
ପ୍ରତ୍ୟେକ ବିଷୟରେ ଅନ୍ତର୍ଗତ ବିଷୟବସ୍ତୁ ବିଶ୍ଳେଷଣକରିବା ପାଇଁ କେତେକ ଦୃଷ୍ଟିରେ ରହିଥାଏ। ଏହାଦ୍ଵାରା ଆମ୍ଭେ କୌଣସି ସମସ୍ୟାର ଅଧ୍ୟୟନ କରିପାରିଥାଉ। ସମାଜ ଶାସ୍ତ୍ରର ବିକାଶ ସମାଜବିଜ୍ଞାନୀମାନେ ସମାଜବିଜ୍ଞାନର ବିଷୟବସ୍ତୁକୁ ସରଳ ଓ ସହଜସାଧ୍ୟ ଭାବରେ ବୁଝିବା ପାଇଁ ଆନେକ ସିଦ୍ଧାନ୍ତମାନ ପ୍ରତିଦାନ କରିଛନ୍ତି। ଏହି ସିଦ୍ଧାନ୍ତ ପରିପ୍ରେକ୍ଷୀରେ ସେମାନେ ସମାଜର ବିଭିନ୍ନ ପକ୍ଷକୁ ବିଶ୍ଳେଷଣ କରିବାକୁ ଚେଷ୍ଟା କରିଛନ୍ତି। ସମାଜବିଜ୍ଞାନର ପରିପୃଷ୍ଟ କେତେକ ଦୃଷ୍ଟିକୋଣ ନିମ୍ନରେ ବର୍ଣ୍ଣନା କରାଗଲା।

(୧) ବିବର୍ତ୍ତନବାଦ ଦୃଷ୍ଟିକୋଣ (Evolutionary Perspective): ସ୍ପେନସରଙ୍କ ମତେରେ, “ ସମାଜବିଜ୍ଞାନ ବିବର୍ତ୍ତନରେ ଜଟିଳ ସ୍ଵରୂପକୁ ଅଧ୍ୟୟନ କରିଥାଏ । “ ଏହି ବିବର୍ତ୍ତନ ବିଭିନ୍ନ ରୂପରେ ସଙ୍ଗଠିତ ହୋଇଥାଏ। ଏହା ଏକ ରେଖୀୟ ବା ବହୁରେଖୀୟ ହୋଇପାରେ। କେତେକ ସମାଜବିଜ୍ଞାନୀ ସାମାଜିକ ପରିବର୍ତ୍ତନକୁ ବୃତ୍ତାକର ବା ଚକ୍ରାକାର ଭାବରେ ସୃଷ୍ଟି କରିଛନ୍ତି। ସମାଜବିଜ୍ଞାନର ଜନକ ଅଗଷ୍ଟ କମ୍‌ ଜ୍ଞାନ ଓ ସମାଜର ବିକାଶକୁ ବିବର୍ତ୍ତନର ମାଧ୍ୟମରେ ବୁଝାଇବା ପାଇଁ ଚେଷ୍ଟା କରିଥିଲେ। ସମାଜବିଜ୍ଞାନମାନେ ସେମାନଙ୍କର ଅଧ୍ୟୟନରେ ଐତିହାସିକ ପକ୍ଷ ଉପରେ ଅଧିକ ମହତ୍ଵ ଦେଇ ସାମାଜିକ ସଂସ୍ଥା, ସାମାଜିକ ମୂଲ୍ୟ, ସାମାଜିକ ପ୍ରକିୟା, ସାମାଜିକ ନୟନ୍ତ୍ରଣ ଏବଂ ଏଥିରୁ ସୃଷ୍ଟି ପ୍ରଭାବଶାଳୀ ସାମାଜିକ ସମ୍ବନ୍ଧରେ ଅଧ୍ୟୟନରେ ବିବର୍ତ୍ତନବାଦୀ ଦୃଷ୍ଟିକୋଣରୁ ସୃଷ୍ଟି କରିଛନ୍ତି।

(୨) ସଂରଚନାତ୍ମକ-ପ୍ରକାର୍ଯ୍ୟାତ୍ମକ ଦୃଷ୍ଟିକୋଣ (Strucure Functional Perspective): ସଂରଚନାତ୍ମକ ଦୃଷ୍ଟିକୋଣ ଦ୍ଵାରା ବୃତ୍ତି ସ୍ଥାନରେ ତା’ର ପ୍ରସ୍ଥିତି ଓ ଭୂମିକାକୁ ବିଶ୍ଳେଷଣ କରାଯାଇଥାଏ। ଏହି ଦୃଷ୍ଟିକୋଣରେ ସମାଜର ବିଭିନ୍ନ ଭାଗ ମଧ୍ୟରେ ଥିବା ପରସ୍ପର ସମ୍ବନ୍ଧକୁ ଅଧ୍ୟୟନ କରାଯାଇଥାଏ। ଏଣୁ ସଂରଚନାତ୍ମକ ପ୍ରକାର୍ଯ୍ୟତ୍ମିକ ସମାଜବିଜ୍ଞାନୀମାନଙ୍କ ମତରେ ସମାଜର ଗୋଟିଏ ଭାଗରେ ପରିବର୍ତ୍ତନ ଘଟିଲେ ଅନ୍ୟ ଭାଗରେ ଅନ୍ୟ ଭାଗରେ ମଧ୍ୟ ତଦନୁରୂପ ପ୍ରଭାବ ପଡିଥାଏ। ଦ୍ଵିତୀୟତଃ, ସଂରଚନାର ବିଭିନ୍ନ ଏକକ କିଭଳି ଭାବରେ ପରସ୍ପର ସହିତ ସମ୍ବନ୍ଧିତ ଏବଂ ଏଗୁଡିକ କିପରି ପରସ୍ପର ସହିତ ସମ୍ବନ୍ଧିତ ହୋଇଥା’ନ୍ତି। ଯାହାଫଳରେ ସମାଜ ଜଟିଳ ରୂପରେ ତିଷ୍ଠି ରହିଅଛି। ତୃତୀୟତଃ ଏହି ଉପାଗମ ଦ୍ଵାରା କୌଣସି ଘଟଣାର ସମାଜ ଉପରେ ପଡ଼ୁଥିବା ପ୍ରଭାକୁ ବିଶ୍ଳେଷଣ କରାଯାଏ। ଏହି ଉପାଗମର ପ୍ରଣେତାମାନଙ୍କ ମତରେ ପ୍ରତ୍ୟେକ ବସ୍ତୁର ସମାଜର ଅନ୍ୟ ଅଙ୍ଗ ଉପରେ ପ୍ରଭାବ ପଡିଥାଏ। ସମାଜବିଜ୍ଞାନୀମାନେ ସଙ୍ଗଠନାତ୍ମକ ପରିଣାମକୁ ପ୍ରକାର୍ଯ୍ୟତ୍ମିକ (Functional) ଏବଂ ବିଘଟନାତ୍ମକ ପ୍ରଭାବକୁ ଅପ୍ରକାର୍ଯ୍ୟ (Dysfunctional) ବୋଲି ବିବେଚନା କରିଛନ୍ତି। ମର୍ଟନ ଏହି ଉପାଗମକୁ ଅଧିକ ସ୍ପଷ୍ଟ କରି ପ୍ରକାର୍ଯ୍ୟକୁ ମର୍ଟନ ଏହି ଉପାଗମକୁ ଅଧ‌ିକ ସ୍ପଷ୍ଟ କରି ପ୍ରକାର୍ଯ୍ୟକୁ ଦୁଇ ଭାଗରେ ବିଭକ୍ତ କରିଛନ୍ତି। ଟଥା : ପ୍ରକଟ ପ୍ରାକର୍ଯ୍ୟ (Manifested functions) ଏବଂ ଅପ୍ରକଟ ପ୍ରକାର୍ଯ୍ୟ (Laten functions)

ସମାଜବିଜ୍ଞାନୀମାନଙ୍କ ବିଚାରରେ ଶରୀରର ବିଭିନ୍ନ ଅଙ୍ଗପ୍ରତ୍ୟଙ୍ଗ ଯେପରି ପରସ୍ପର ସମ୍ବନ୍ଧିତ ଏବଂ ଏହାର କୌଣସି ଅଙ୍ଗ ଯେପରି ଶରୀରରୁ ଅଲଗା କରି ପୂର୍ଣବିଶ୍ଳେଷଣ ଅସମ୍ଭବ। ଠିକ୍ ସେହିପରି ସମାଜର ବିଭିନ୍ନ ଅଂଶ ଯଥା : ପରିବାର, ଧର୍ମ ଇତ୍ୟାଦିର ଭିନ୍ନ ଭିନ୍ନ ଅଧ୍ୟୟନ ତ୍ରୁଟିପୂର୍ଣ୍ଣ। ପ୍ରକାର୍ଯ୍ୟବାଦୀଙ୍କ ଦୃଷ୍ଟିରେ ସାମାଜିକ ବ୍ୟବସ୍ଥାର ସମସ୍ତ ଏକକଗୁଡିକ ପରସ୍ପର ସହିତ ଏକତାର ସ୍ଵତ୍ରରେ ବାନ୍ଧି ହୋଇଥାନ୍ତି। ସମାଜ ସଂରଚନାର ଅସ୍ଥିତ୍ଵକୁ ସ୍ପଷ୍ଟ କରିବା ପରେ ପ୍ରାକର୍ଯ୍ୟବାଦୀମାନେ ଏହି ସଂରଚନା କିଭଳି କାର୍ଯ୍ୟ କରିଥାଏ, ତାହାକୁ ବାଖ୍ୟା କରିଛନ୍ତି। ସେମାନଙ୍କ ମତରେ ସମାଜ ତିଷ୍ଠି ରହିବା ପାଇଁ କେତେକ ମୌଳିକ ଆବଶ୍ୟକତାର ପ୍ରୟୋଜନ ଥାଏ। ଏହି ଆବଶ୍ୟକତାକୁ ପ୍ରକାର୍ଯ୍ୟତ୍ମକ ପ୍ରୟୋଜନ (Functional Prerequisities) କୁହାଯାଏ। ପୁନଶ୍ଚ ପ୍ରକାର୍ଯ୍ୟାତ୍ମକ ଦୃଷ୍ଟିକୋଣରେ ସମାଜକୁ ଏକ ବ୍ୟବସ୍ଥା ଭାବରେ ବିଚାର କରାଯାଇଥାଏ।

ଏହି ପରିପ୍ରେକ୍ଷୀରେ ବ୍ୟବସ୍ଥାକୁ ବଜାୟ ରଖୁବାକୁ ହେଲେ ଏହାର ବିଭିନ୍ନ ଭାଗ ମଧ୍ଯରେ ମାତ୍ରାରେ ସୁସଂଘଠିତ ଆବଶ୍ୟକତା ପଡିଥାଏ। ଅନେକ ପ୍ରକାର୍ଯ୍ୟବାଦୀଙ୍କ ଯୁକ୍ତି ଯେ, ଏହି ଏକୀକରଣ ସମାଜର ସଭ୍ୟସମାନଙ୍କ ସହମତି ଦ୍ଵାରା ସମ୍ଭବ ହୋଇଥାଏ। ମୂଲ୍ୟବୋଧ ସହ ସହମତି ସହଯୋଗୀ ଭିତ୍ତିସ୍ତମ୍ଭ ଭଳି କାର୍ଯ୍ୟ କରିଥାଏ ଏବଂ ଏହା ସାଧାରଣ ଲକ୍ଷ୍ୟ ପ୍ରାପ୍ତି ବ୍ୟକ୍ତିତ୍ଵ ପ୍ରେରଣା ହୋଇଥାଏ। ମୂଲ୍ୟବୋଧ ପ୍ରତି ସହମତି ଉପରେ ପ୍ରାଧାନ୍ୟ ନେଇ ପ୍ରକାର୍ଯ୍ୟବାଦୀମାନେ ଏହି ସହମତି କିପରି ବଜାୟ ରହିଛି, ଏହାକୁ ବୁଝାଇବାକୁ ଯାଇ ପ୍ରକାର୍ଯ୍ୟବାଦୀମାନେ ସାମାଜିକରଣ ପ୍ରକିୟାକୁ ମହତ୍ତ୍ଵପୂର୍ଣ୍ଣ ସାଧନ ବୋଲି ବିଚାର କରିଥାନ୍ତି। ସେମାନଙ୍କ ବିଚାରରେ ସାମାଜିକୀକରଣ ପ୍ରକ୍ରିୟା ଦ୍ଵାରା ସାମାଜିକ ମୂଲ୍ୟବୋଧଗୁଡ଼ିକ ବ୍ୟକ୍ତି ଆତ୍ମୀକରଣ କରିଦେବା ପରେ ଗୋଟିଏ ପିଢ଼ିରୁ ଅନ୍ୟ ପିଢ଼ିକୁ ହସ୍ତାନ୍ତରିତ କରିଥାଏ। ଏ କ୍ଷେତ୍ରରେ ପରିବାର ସାମାଜିକ ସଂରଚନାର ଏକ ମହତ୍ତ୍ଵପୂର୍ଣ୍ଣ ପକ୍ଷ ହୋଇ ସମସ୍ତ କାର୍ଯ୍ୟ ସମ୍ପାଦନ କରିଥାଏ। ସାମାଜିକରୀକରଣ ପ୍ରକ୍ରିୟା ସହିତ ସାମାଜିକ ନିୟନ୍ତ୍ରର, ସାମାଜିକ ସ୍ଥିରତା ରକ୍ଷା କରିବା ଦିଗରେ ଅତ୍ୟନ୍ତ ସହାୟକ ହୋଇଥାଏ।

(୩) ସଂଘର୍ଷ ଦୃଷ୍ଟିକୋଣ (Conflict Persective): ସଂରଚନାତ୍ମକ ପ୍ରକାର୍ଯ୍ୟବାଦୀମାନେ ସମାଜକୁ ଏକ ସନ୍ତୁଳିତ ବ୍ୟବସ୍ଥା (Balanced System) ରୂପେ ଗ୍ରହଣ କରିଥାନ୍ତି। ଅନ୍ୟ ପକ୍ଷରେ ସଂଘର୍ଷ ଦୃଷ୍ଟିକୋଣରେ ବିଚାର କରୁଥିବା ସମାଜବିଜ୍ଞାନୀମାନେ ସମାଜକୁ ଏକ ସନ୍ତୁଳିତ ବ୍ୟବସ୍ଥା ଭାବରେ ଗ୍ରହଣ କରିବା ଏକ ଭ୍ରମରୂପ ଧାରଣା ବୋଲି ଯୁକ୍ତି କରିଥାନ୍ତି। ସେମାନେ ସାଧାରଣ ସହମତିକୁ ଜୀବନର ଭିତ୍ତିଭୂମି ରୂପେ ଗ୍ରହଣ ନକରି ଅସହମତିକୁ ଆଧାର ମନେକରି ବିଶ୍ଳେଷଣ କରିଥାନ୍ତି। ସେମାନେ ସାଧାରଣ ସହମତିକୁ ଜୀବନର ଭିତ୍ତିଭୂମି ରୂପେ ଗ୍ରହଣ ନକରି ଅସହମତିକୁ ଆଧାର ମନେକରି ବିଶ୍ଳେଷଣ କରିଥାନ୍ତି । ସଂଘର୍ଷ ଦୃଷ୍ଟିକୋଣକୁ ମାକ୍ସବାଦୀ ଦୃଷ୍ଟିକୋଣ (Marxian perspective) ମଧ୍ୟ କୁହାଯାଏ।

(୪) ଅନ୍ତଃକ୍ରିୟାବାଦ (Interactionism) : ପ୍ରକାର୍ଯ୍ୟାତ୍ମକ ଓ ମାର୍କ୍ସବାଦ ମଧ୍ୟରେ ଅନେକ ପାର୍ଥକ୍ୟ ପରିଲିକ୍ଷିତ ହୋଇଥାଏ। ତଥାପି ଉଭୟ ସମାଜକୁ ଏକ ବ୍ୟବସ୍ଥାରୂପ ବିବେଚନା କରି ତାହାର ସାଧାରଣ ସାମଗ୍ରିକ ବିଶ୍ଳେଷଣ କରିଥାନ୍ତି। ଏହି ବ୍ୟବସ୍ଥାରେ ମାନବର ବ୍ୟବହାର କିଭଳି ରୂପ ଧାରଣ କରିଥାଏ ତାହା ସ୍ପଷ୍ଟ କରିଥା’ନ୍ତି । ମାର୍କ୍ସବାଦ ଦୃଷ୍ଟିକୋଣରେମାନବର ବ୍ୟବହାର ଅର୍ଥନୈତିକ ଭିତ୍ତିଭୂମି ଦ୍ଵାରା ନିର୍ଦ୍ଧାରିତ ହୋଇଥାଏ; ମାତ୍ର ଅନ୍ତଃକ୍ରିୟାବାଦ ପରିପ୍ରେକ୍ଷୀରେ ବିଶ୍ଵାସ କରୁଥିବା ସମାଜବିଜ୍ଞାନୀମାନେ ପ୍ରକାର୍ଯ୍ୟତ୍ମକ ଓ ମାର୍କ୍ସବାଦରେ ବିଶ୍ଵାସ କରୁଥିବା ସମାଜବିଜ୍ଞାନୀମାନଙ୍କଠାରୁ ପ୍ରକାର୍ଯ୍ୟତ୍ମିକ ଓ ମାକ୍ସବାଦରେ ବିଶ୍ଵାସ ରଖୁଥ‌ିବା ସମାଜବିଜ୍ଞାନୀମାନଙ୍କଠାରୁ କେତେକାଶଂରେ ଭିନ୍ନମତ ପୋଷଣ କରିଥା’ନ୍ତି।

(୫) ପ୍ରତ୍ୟକ୍ଷବାଦ (Positionism) : ସମାଜବିଜ୍ଞାନର ଜନକ ଅଗଷ୍ଟ କମକେଟଠାରୁ ଆରମ୍ଭ କରି ଅନେକ ସମାଜବିଜ୍ଞାନୀ ପ୍ରତ୍ୟକ୍ଷବାଦ ଦୃଷ୍ଟିକୋଣ୍ଡରେ ସମଜ ଏବଂ ବ୍ୟକ୍ତିତ୍ଵ ଅଧ୍ୟୟନ କରିବା ପାଇଁ ଯୁକ୍ତିବାଢି ଆସିଛନ୍ତି। ସେମାନଙ୍କ ବିଚାରରେ ଭୌତିକ ବା ପ୍ରାକୃତିକ ବିଜ୍ଞାନର ଅଧ୍ୟୟନ ଭଳି ସାମାଜିକ ଘଟଣାର ଅଧ୍ୟୟନ କରାଯାଇପାରିବ। ଅର୍ଥାତ୍ ମାନବ ବ୍ୟବହାର ଭୌତିକ ବା ପ୍ରାକୃତିକ ବସ୍ତୁର ବ୍ୟବହାରକୁ ବସ୍ତୁନିଷ୍ଠ ଭାବରେ ମାପ କରାଯାଇପାରିବ ଏବଂ ଏହାର କାରଣ ତଥା ଫଳାଫଳ ମଧ୍ୟରେ ସମ୍ପର୍କ ସ୍ଥାପନ କରି ପର୍ଯ୍ୟବେସିତ ବ୍ୟବହାରକୁ ବୁଝାଯାଇ ପାରିବ। ପ୍ରତ୍ୟକ୍ଷବାଦୀମାନଙ୍କ ମତରେ ଅର୍ଥ, ଅନୁଭବ ଏବଂ ଉଦ୍ଦେଶ୍ୟ ଇତ୍ୟାଦି ଯେଉଁ ଘଟଣାଗୁଡିକ ସିଧାସଳଖ ପର୍ଯ୍ୟକ୍ଷେଣ ଯୋଗ୍ୟ ନୁହେଁ ସେଗୁଡିକ ସେତେ ମହତ୍ଵପୂର୍ଣ୍ଣ ନୁହନ୍ତି। ଏଣୁ ଏମାନେ ଯେଉଁ ବ୍ୟବହାରଗୁଡିକ ସିଧାସଳଖ ପର୍ଯ୍ୟବେକ୍ଷଣ କରାଯାଇପାରୁଥିବା ବ୍ୟବହାରକୁ ଅଧିକ ଗୁରୁତ୍ଵ ଦେଇଥାନ୍ତି।

(୬) ଇନ୍ଦ୍ରିୟ ଲବ୍ଧଜ୍ଞାନ (Phenomenological) : ଏହି ଦୃଷ୍ଟିକୋଣରୁ ପୃଷ୍ଠପୋଷକମାନେ ପ୍ରତ୍ୟକ୍ଷବାଦର ଅଧ୍ୟୟନ ପଦ୍ଧତିର ଭୌତିକ ଓ ପ୍ରାକୃତିକ ବିଜ୍ଞନାର ପଦ୍ଧତି ପ୍ରୟୋଗର ସମାଲୋଚକ ଥିଲେ। ସେମାନଙ୍କ ମତରେ ଉଭୟ ବିଜ୍ଞନର ବିଷୟବସ୍ତୁ ଭିନ୍ନ। ତେଣୁ ପ୍ରାକୃତିକ ବିଜ୍ଞାନର ପଦ୍ଧତି ମାନବର ଅଧ୍ୟୟନ ପାଇଁ ଉପଯୁକ୍ତ ନୁହେଁ । ପ୍ରାକୃତିକ ବିଜ୍ଞାନରେ ବସ୍ତୁଗୁଡିକର ଅଧ୍ୟୟନ କରାଯାଇଥାଏ। ଏହି ବସ୍ତୁର ଅଧ୍ୟୟନ ଏବଂ ବାଖ୍ୟା କରିବାକୁହେଲେ ଏହାକୁ କେବଳ ବାହାରୁ ପର୍ଯ୍ୟକ୍ଷେଣ କଲେ ଯଥେଷ୍ଟ, କାରଣ ଏଗୁଡିକର ଆନ୍ତଃ-ପ୍ରତିକ୍ରିୟା ମାନବ ଭଳି ନଥାଏ। ମାନବଠାରେ ଯଥେଷ୍ଟ ସଚେତନ ଶକ୍ତି, ଭାବନା, ଅନୁଭବ କରିବାର କ୍ଷମତା କରିବାର କ୍ଷମତା ଅର୍ଥ ଏବଂ ଉଦ୍ଦେଶ୍ୟପୂର୍ଣ୍ଣ ବ୍ୟବହାର କରିଥାଏ।

(୭) ଏଥେନୋମେଥେଡୋଲୋଜି (Ethnomethodology) : ଷାଠିଏ ଏବଂ ସତୁରି ଦକରେ ଯେଉଁସବୁ ନୂତନ ଉପାଗମଗୁଡିକର ବିକାଶ ହୋଇଥିଲା। ସେଗୁଡିକ ମଧ୍ୟରୁ ଏଥେନୋମେଥେଡୋଲୋଜି ଅନ୍ୟତମ। ଗାରଫିନକେଲ୍ (Garfinkel) ତାଙ୍କର ପୁସ୍ତକStudies in Ethnomethodologyରେ ସର୍ବପ୍ରଥମ ଏହି ଉପାଗର ସୁବ୍ୟବସ୍ଥିତ ବର୍ଣ୍ଣନା କରିଥିଲେ। ସଂରଚନାତ୍ମକ ପ୍ରକାର୍ଯ୍ୟକ ଉପାଗମକରେ କେତେକ ସୀମା ରହିଅଛି। ଯେଉଁ କାରଣରୁ ସାମାଜିକ ବାସ୍ତବିକତାର ମହତ୍ଵପୂର୍ଣ୍ଣ ପକ୍ଷ ଅଧ୍ୟୟନ ପରିସରରୁ ପୃଥକ୍ ହୋଇପାରେ; କିନ୍ତୁ ଏହି ଉପାୟ ମାଧ୍ୟମରେ ସାମାଜିକ ବାସ୍ତବତାକୁ ପ୍ରତ୍ୟକ୍ଷ ଓ ଅତି ନିକଟତର ଅଧ୍ୟୟନ କରାଯାଇପରେ। ବ୍ୟକ୍ତି ଜୀବନରେ ଦୈନଦିନର ସାଧାରଣ କାର୍ଯ୍ୟପ୍ରଣାଳୀ ଓ କ୍ରିୟାକଳାପ ସହିତ ସମ୍ବନ୍ଧିତ ମାନବୀୟ ବ୍ୟବହାରରେ ଅଧ୍ୟୟନ ଏଥେନୋମେଡୋଲୋଗି ଦ୍ଵାରା କରାଯାଇଥାଏ। ଏହି ପରିପ୍ରେକ୍ଷୀରେ ପୃଷ୍ଠପୋଷକମାନେ ସାମାଜିକ ଅନ୍ତଃକ୍ରିୟାଦ୍ଵାରା ଯେଉଁ ସାମାଜିକ ବାସ୍ତବତାରେ ସ୍ଵତ୍ରପାତ କରନ୍ତି ତାହାରି ଉପେର ଗୁରୁତ୍ଵ ଦେଇଥାନ୍ତି।

Question ୩।
ସମାଜବିଜ୍ଞାନର ମହତ୍ତ୍ଵ ପ୍ରତିପାଦନ କର।
Answer:
ସମାଜବିଜ୍ଞାନୀମାନଙ୍କର ଅବଦାନର ସମାଜବିଜ୍ଞାନର ଉତ୍ତରୋତ୍ତର ଉନ୍ନତି ହେବାରେ ଲାଗିଛି। ଏହା ସହିତ ପ୍ରତ୍ୟେକ ସମାଜରେ ଏହି ବିଜ୍ଞାନରେ ପ୍ରୟୋଗ ଦିନକୁ ଦିନ ଚଢି ଚାଲିଛି। ସମାଜବିଜ୍ଞାନୀମାନେ ପ୍ରତ୍ୟେକ ବିଭବ ସମ୍ବନ୍ଧରେ ଜ୍ଞାନ ଆହରଣ କରିବା ସଙ୍ଗେ ସଙ୍ଗେ ଅନ୍ୟାନ୍ୟ ବିଭାଗର ବିଦ୍ଵାନମାନଙ୍କୁ ସମାଜବିଜ୍ଞନାର ଉପାଦେୟତାକୁ ହୃଦୟଙ୍ଗମ କରାଇପାରନ୍ତି। ଆଜିକାଲି ଏହି ବିଜ୍ଞାନରେ ସିଦ୍ଧାନ୍ତ ଦ୍ଵାରା ଅନ୍ୟାନ୍ୟ ସାମାଜିକ ବିଜ୍ଞାନଗୁଡିକର ଅଧ୍ୟୟନ ସୁଗମ ହୋଇପାରୁଛି ! ଆଧୁନିକ ଜଟିଳ ସମାଜବିଜ୍ଞାନରେ ଉପାଦେୟତା ଅସୀମ। ଏଠାରେ ଅଳ୍ପ କେତେକ ଦୃଷ୍ଟିକୋଣରୁ ଏହାର ପ୍ରାଧାନ୍ୟକୁ ସ୍ପଷ୍ଟ କରାଯାଇଅଛି।

(୧) ସମାଜବିଜ୍ଞାନ ସମାଜକୁ ବୈଜ୍ଞାନିକ ପ୍ରଣାଳୀରେ ଅଧ୍ୟୟନ କରିବାରେ ସାହାର୍ଯ୍ୟ କରିଥାଏ। ସମାଜବିଜ୍ଞାନର ଉତ୍ପତ୍ତି ହେବା ପୂର୍ବରୁ ସମାଜକୁ ଏକ ଜଟିଳ ବ୍ୟବସ୍ଥା ବୋଲି ପରିଗଣିତ କରାଯାଇଥିଲା। କୌଣସି ବିଜ୍ଞାନ ଦ୍ଵାରା ଏହି ଜଟିଳ ବ୍ୟବସ୍ଥାକୁ ବୈଜ୍ଞାନିକ ଦୃଷ୍ଟିକୋଣରେ ଅଧ୍ୟୟନ କରାଯାଇ ନଥୁଲା; ମାତ୍ର ସମାଜବିଜ୍ଞାନରେ ବିକାଶ ହେବା ଦ୍ବାରା ସମାଜର ଜଟିଳ ବ୍ୟବସ୍ଥାଗୁଡିକ ବୈଜ୍ଞାନିକ ପ୍ରଣଶାଳୀରେ ଅଧ୍ୟୟନ କରାଯିବାରେ ଲାଗିଛି। ମାନବ କଲ୍ୟାଣ ଓ ପ୍ରଗତି ପାଇଁ ମାନବ ସମାଜର ବୈଜ୍ଞାନିକ ଅଧୟନର ଏକାନ୍ତ ଆବଶ୍ୟକତା ରହିଛି ବୋଲି ଆଜି ସମ୍ଭବତଃ ସମସ୍ତ ସଭ୍ୟ ସମାଜବିଜ୍ଞାନରେ ମୂଲ୍ୟକୁ ଉପଲବ୍ଧ କରିବାକୁ ଲାଗିଛନ୍ତି।

(୨) ସମାଜବିଜ୍ଞାନ ମାନବର ସାମାଜିକ ଗୁଣକୁ ସ୍ପଷ୍ଟ କରିଥାଏ। ମାନବ ଏବଂ ସମାଜରା ସମ୍ପର୍କ କ’ଣ ? ମାନବ ଉପରେ ସମାଜର ପ୍ରଭାବ କ’ଣ ? ସେ କାହିଁକି ସମାଜିକ ପ୍ରାଣୀ ? କେଉଁ କାରଣରୁ ସେ ସମାଜରେ ବସ କରେ ଇତ୍ୟାଦି ଅନେକ ପ୍ରଶ୍ନର ଉତ୍ତର ସମାଜବିଜ୍ଞନାରେ ଅଧ୍ୟୟନରୁ ସ୍ପଷ୍ଟ ହୋଇଥାଏ।

(୩) ବ୍ୟକ୍ତିର ବିକାଶରେ ସଂସ୍ଥାଗୁଡିକ ଭୂମିକା ସମାଜବିଜ୍ଞାନ ଅଧ୍ୟୟନ ଦ୍ଵାରା ସ୍ପଷ୍ଟ ହୋଇଥାଏ। ପରିବାର, ଶିକ୍ଷା. ଅନୁଷ୍ଠାନ, ରାଜ୍ୟ, ସରକାର, ଶିକ୍ଷାନୁଷ୍ଠାନ, ଧର୍ମ, ନୈତିକତା ଆଇନ୍ ଇତ୍ୟାଦି ସଂସ୍ଥାମାନଙ୍କ ସାହାର୍ଯ୍ୟରେ ଆମ ସାମଜର କାର୍ଯ୍ୟ ସମ୍ପାଦନା କରିଥାଏ। ଏହି ସଂସ୍ଥାଗୁଡିକୁ ମାନବର ବିକାଶରେ କିଭଳି ଭାବରେ ସହାୟତା କରିଥାଏ ଏବଂ କିଭଳି ଅଧ‌ିକରୁ ଅଧିକ ସାହାର୍ଯ୍ୟ କରିପାରିବ ତାହା ସମାଜବିଜ୍ଞାନ ସୂଚାଇ ଥାଏ।

(୪) ସମାଜବିଜ୍ଞାନ ଅଧ୍ୟୟନ ଫଳରେ ସମାଜ ସମ୍ବନ୍ଧରେ ଜ୍ଞାନ ବୃଦ୍ଧି ନେଇଥାଏ। ସମାଜ, ସାମାଜିକ ସମୂହ, ସାମାଜିକ ସଂସ୍ଥା, ସଂଘ ଇତ୍ୟାଦି ସମ୍ବନ୍ଧରେ ଜ୍ଞାନ ସମାଜବିଜ୍ଞାନରୁ ମିଳେ। ଏହି ଜ୍ଞାନଦ୍ଵାରା ମାନବ ନିଜକୁ ଶକ୍ତି, ଦକ୍ଷତା ଏବଂ ସୀମା ସମ୍ବନ୍ଧରେ ଯଥେଷ୍ଟ ଧାରଣା କରିପାରିଥାଏ ଏବଂ ଏ ସମସ୍ତ ଜ୍ଞାନ ସାମାଜିକ ପରିବେଶ ସହିତ ଖାପ ଖୁଆଇବାରେ ଯଥେଷ୍ଟ ସାହାର୍ଯ୍ୟ କରିଥାଏ।

(୫) ସମାଜବିଜ୍ଞାନ ଅଧ୍ୟୟନ ଦ୍ବାରା ଭିନ୍ନ ଭିନ୍ନ ସମାଜର ପ୍ରଥା, ପରମ୍ପରା ଲୋକନିୟମ, ଲୋକନିୟମ, ସ୍ତରୀକରଣ ବ୍ୟବସ୍ଥା, ସଂସ୍କୃତି ସମୁଦାୟର ସେ ସମସ୍ତ ସମାଜରେ ବାସ କରୁଥିବା ଲୋକମାନଙ୍କର ଆଶ, ଆକାଂକ୍ଷା, ବୃତ୍ତି ଇତ୍ୟାଦି ଅନେକ ତଥା ସମ୍ବନ୍ଧରେ ଜ୍ଞାନ ମିଳିଥାଏ।

(୬) ସମାଜବିଜ୍ଞାନ ଅଧ୍ୟୟନ ଦ୍ବାରା ସଙ୍କୁଚିତ ମନୋବୃତ୍ତିରୁ ମୁକ୍ତିଲାଭ କରିଥାଏ। ଜାତି, ବର୍ଣ୍ଣ, ଧର୍ମ ଇତ୍ୟାଦି ସଂକୀର୍ଣ୍ଣତାର ଊଦ୍ଧରେ ରହି ସମସ୍ତ ମାନବ ସମାଜକୁ ଏକ ତାତ୍ତ୍ଵିକ ଓ ବସ୍ତୁନିଷ୍ଠ ଦୃଷ୍ଟିକୋଣରୁ ବିଚାର କରିଥାଏ। ଏହି ବିଜ୍ଞାନର ଅଧ୍ୟୟନ ମାନବର ଜୀବନକୁ ଉନ୍ମୁକ୍ତ, ପୂର୍ଣାଙ୍ଗ ଏବଂ ସାର୍ଥକ କରିଥାଏ।

(୭ ) ସାମାଜିକ ସମସ୍ୟାଗୁଡିକର ସମାଧାନ ପାଇଁ ସମାଜବିଜ୍ଞାନର ଅବଦାନ ଅତୁଳନୀୟ। ଆଜିର ମାନବ ସମାଜ ବହୁବିଧ ସମସ୍ୟା ଯଥା : ଦାରିଦ୍ର୍ୟ, ବେକାରୀ ଜନସଂଖ୍ୟା ବୃଦ୍ଧି ଇତ୍ୟାଦିର ପ୍ରଭାବରେ ଜର୍ଜରିତ, କେତକ ସମସ୍ୟା ଏପରି ରୂପ ଧାରଣ କରିଥାଏ, ଯାହା ସମାଜର ନିତ୍ୟନୈମିତିକ କାର୍ଯ୍ୟ ପ୍ରଣାଳୀରେ ଅନେକ ବାଧା ଉପୁଯାଇଥାଏ। ସେଗୁଡିକର ଉପଯୁକ୍ତ ସମାଧାନ ବିନା ସମାଜରେ ସାମାଜିକ ଜୀବନ ଅସ୍ତବ୍ୟସ୍ତ ହୋଇପଡିଥାଏ। ଅନ୍ୟ କେତେକ ସମସ୍ୟା ବେଳେବେଳେ ମୁଣ୍ଡଟେକି ଉଠି ମାନବର ସ୍ଵକ୍ଷ୍ମ ଉଦ୍ୟମରେ ପ୍ରଶମିତ ହୋଇଥାଏ। ସମସ୍ୟାର ଯେଉଁ ରୂପ ହେଉନା କାହିଁକି, ଏହାର ପ୍ରଭାବ ଯେତେ ସ୍ଵଦୂରପ୍ରସାରୀ ହେଉନା କାହିଁକି ଏହି ସମସ୍ୟାଗୁଡିକର ବୈଜ୍ଞାନିକ ଅନ୍ଵେଷଣ ଦ୍ଵାରା ଏଗୁଡିକର କାରଣ ଓ ଫଳାଫଳ ମଧ୍ୟରେ ବୈଜ୍ଞାନିକ ସମ୍ବନ୍ଧ ସ୍ଥାପନ କରିବା ସହିତ ବିଘଟିତ ସମାଜଗୁଡିକ କିପରି ପୁର୍ନଗଠିତ କରାଯାଇପାରିବ ତା’ର ପଥ ପ୍ରଦର୍ଶନ କରିଥା’ନ୍ତି।

(୮) ସମାଜ ସଂସ୍କାର ପାଇଁ ଯୋଜନାମାନ ପ୍ରସ୍ତୁତ କରିବାରେ ସମାଜବିଜ୍ଞାନ ମଧ୍ୟ ସାହାଯ୍ୟ କରିଥାଏ। ସମାଜକୁ ପୁନର୍ଗଠନ କରିବାକୁ ହେଉ ବା ସାମାଜିକ ବିକାଶର ଗତିକୁ ତ୍ବରାନ୍ବିତ କରିବାକୁ ହେଉ ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ରରେ ଏକ ସୁଚିନ୍ତିତ ଯୋଜନାର ଆବଶ୍ୟକତା ପଡ଼ିଥାଏ। ଏହି ଯୋଜନା ପ୍ରସ୍ତୁତକାରୀ ଯଦି ସମାଜର ସମସ୍ତ ପକ୍ଷରୁ ବିଚାରକୁ ନେଇ ପକ୍ଷୀକ ଭିତ୍ତିରେ ଯୋଜନାକୁ କାର୍ଯ୍ୟକାରୀ କରିବାକୁ ଚାହାଁନ୍ତି। ତା’ର ସୁଦୂରପ୍ରସାରୀ ପ୍ରଭାବ କ’ଣ ହୋଇପାରେ ତା’ର ଭବିଷ୍ୟତବାଣୀ କରିବାରେ ସମାଜବିଜ୍ଞାନର ଉପାଦେୟତାକୁ ଏଡାଇ ଦିଆଯାଇ ନ ପାରେ। ସେଥ‌ିପାଇଁ ସମ୍ଭବତଃ ସମସ୍ତ ବିକାଶଶୀଳ ସମାଜଗୁଡ଼ିକ ସେମାନଙ୍କର ସାମାଜିକ ଯୋଜନା ପ୍ରସ୍ତୁତି ସମୟରେ ଆଜିକାଲି ବହୁଳ ଭାବରେ ସମାଜବିଜ୍ଞାନୀମାନଙ୍କର ସାହାଯ୍ୟ ଭିକ୍ଷା କରୁଛନ୍ତି।

(୯) ସମାଜବିଜ୍ଞାନ ଅପରାଧ ଓ ଅପରାଧୀମାନଙ୍କ ପ୍ରତି ମାନବର ପ୍ରଚଳିତ ହୋଇ ଆସୁଥିବା ଅଭିରୁଚିରେ ପରିବର୍ତ୍ତନ ଆଣିଛି। ପ୍ରାୟତଃ ପ୍ରତ୍ୟେକ ସମାଜରେ ଅପରାଧୀମାନଙ୍କୁ ଘୃଣ୍ୟ ଦୃଷ୍ଟିରେ ଦେଖାଯାଇଥାଏ। ପ୍ରତ୍ୟେକ ଧର୍ମ ସେମାନଙ୍କୁ ଈଶ୍ବରଙ୍କର ସୃଷ୍ଟି ବୋଲି ବିଚାର କରିଥାଏ। ସମାଜର ଦୃଷ୍ଟିକୋଣର ସେମାନେ ଲାଞ୍ଛିତ ତଥା ଅନେକ ପ୍ରକାରର ତାଡ଼ନାର ଶିକାର ହୋଇଥା’ନ୍ତି। ମାତ୍ର ମାନବର ଏହି ମନୋବୃତ୍ତିରେ ସମାଜବିଜ୍ଞାନ ଅନେକ ପରିବର୍ତ୍ତନ ଆଣିପାରିଛି। ସମାଜବିଜ୍ଞାନୀମାନେ ବୈଜ୍ଞାନିକ ଅଧ୍ୟୟନ ଦ୍ଵାରା ପ୍ରମାଣ କରିଚାଲିଛନ୍ତି ଯେ, ଅପରାଧୀମାନେ ଈଶ୍ବର କୋପ ଦୃଷ୍ଟିରୁ ବା ତାଙ୍କଦ୍ଵାରା ଦଣ୍ଡିତ ବ୍ୟକ୍ତି ନୁହଁନ୍ତି। ବରଂ ସେମାନେ କେତେକ ମାନସିକ ଓ ସାମାଜିକ ପରିସ୍ଥିତିର ଶିକାର ହୋଇ ଏଭଳି କାର୍ଯ୍ୟକଳାପରେ ଲିପ୍ତ ହେଉଛନ୍ତି। ଯଦି ସେମାନଙ୍କୁ ଉପଯୁକ୍ତ ପ୍ରଶିକ୍ଷଣ ଓ ପରିବେଶ ମଧ୍ୟରେ ରଖାଯାଏ, ତେବେ ସେମାନେ ମଧ୍ୟ ଅପରାଧ ପ୍ରବଣତାରୁ ଦୂରେଇ ସାଧାରଣ ମାନବ ଭଳି ଜୀବନଯାପନ କରିପାରିବେ।

(୧୦) ପାଠ୍ୟ ବିଷୟଗୁଡ଼ିକ ମଧ୍ୟରେ ସମାଜବିଜ୍ଞାନର ଆଦର ଆଜିକାଲି ବଢ଼ିବାରେ ଲାଗିଛି। ବିଶ୍ୱର ପ୍ରାୟ ସମସ୍ତ ରାଷ୍ଟ୍ରରେ ମହାବିଦ୍ୟାଳୟ ଏବଂ ବିଶ୍ବବିଦ୍ୟାଳୟ ସ୍ତରରେ ସମାଜବିଜ୍ଞାନ ପାଠ୍ୟଖସଡ଼ା ମଧ୍ଯରେ ସ୍ଥାନ ପାଇଅଛି। ଚିକିତ୍ସା, କାରିଗରୀ ବ୍ୟବସାୟ ଶିଳ୍ପ, ନଗର ଉନ୍ନୟନ ଯୋଜନା ଇତ୍ୟାଦି କ୍ଷେତ୍ରରେ ସମାଜବିଜ୍ଞାନର ଉପଯୋଗିତାକୁ ଉପଲବ୍ଧ କରି ଉକ୍ତ କ୍ଷେତ୍ର ସହିତ ସମ୍ବନ୍ଧିତ ପାଠ୍ୟକ୍ରମରେ ମଧ୍ଯ ସମାଜବିଜ୍ଞାନର ବିଷୟବସ୍ତୁକୁ ସ୍ଥାନ ଦିଆଯାଉଅଛି। ସେହିପରି ପ୍ରଶାସନ ଓ ପରିଚାଳନା ଆଦି କାର୍ଯ୍ୟରେ ନିଯୁକ୍ତି ଅଧିକାରୀମାନଙ୍କୁ ପ୍ରଶିକ୍ଷଣ ଦେବା ସମୟରେ ସମାଜବିଜ୍ଞାନ ସମ୍ବନ୍ଧୀୟ ଧାରଣ ପ୍ରଦାନ କରାଯାଇଅଛି।

(୧୧) ସମାଜବିଜ୍ଞାନରେ ଉପାଧ୍ଧଧାରୀମାନେ ବୃତ୍ତିଗତ କ୍ଷେତ୍ରରେ ଅନେକ ସୁବିଧାସୁଯୋଗ ପାଇଁ ପାରୁଛନ୍ତି। ଶିଳ୍ପାନୁଷ୍ଠାନ ଓ ସରକାରୀ ସ୍ତରରେ ଶ୍ରମକଲ୍ୟାଣ ଅଧିକାରୀ, ମାନବ ସମ୍ବଳ ଅଧ୍ବକାରୀ ଓ ବ୍ୟକ୍ତିଗତ ଅଧିକାରୀ, ସୁରକ୍ଷା କ୍ଷେତ୍ରରେ କର୍ମନିୟୋଜନ ଅଧୁକାରୀ, ସମାଜ କଲ୍ୟାଣ କ୍ଷେତ୍ରରେ ସମାଜ କଲ୍ୟାଣ ଅଧିକାରୀ, ଯୁଦ୍ଧ କଲ୍ୟାଣ ଅଧିକାରୀ, ପଲ୍ଲୀ ଉନ୍ନୟନ ଅଧିକାରୀ, ଶିଶୁ କଲ୍ୟାଣ ଅଧିକାରୀ, ହରିଜନ କଲ୍ୟାଣ ଅଧିକାରୀ ଓ ଆଦିବାସୀ କଲ୍ୟାଣ ଅଧିକାରୀ, ସାମାଜିକ ଶିକ୍ଷା ଓ ପୌଢ଼ଶିକ୍ଷା କ୍ଷେତ୍ରରେ ସାମାଜିକ ଶିକ୍ଷା ଅଧ୍ବକାରୀ ଓ ପ୍ରୌଢ଼ ଶିକ୍ଷା ଅଧିକାରୀ, ବିଧବା କଲ୍ୟାଣ କ୍ଷେତ୍ରରେ ସାମାଜିକ ଶିକ୍ଷା ଅଧିକାରୀ ଓ ପ୍ରୌଢ଼ଶିକ୍ଷା ଅଧୂକାରୀ, ବିଧବା କଲ୍ୟାଣ କ୍ଷେତ୍ରରେ ନାରୀ ନିକେତନରେ ଅଧୀକ୍ଷକ।

ପରିବାର ନିୟୋଜକ କ୍ଷେତ୍ରରେ ସାମାଜିକ କର୍ମକର୍ତ୍ତା ବା ଗବେଷକ। ଅପରାଧୂମାନଙ୍କର ସୁଧାର କ୍ଷେତ୍ରରେ ପରିବୀକ୍ଷା ଅଧିକାରୀ, ବାଲ୍ୟ ଅପରାଧୂ ଗୃହ ଓ ସୁଧାର ବିଦ୍ୟାଳୟମାନଙ୍କର ଅଧୀକ୍ଷକ ଆଦି ଅନେକ ଚାକିରି କେବଳ ସମାଜବିଜ୍ଞାନରେ ଉପାଧ୍ ଲାଭ କରିଥିବା ବ୍ୟକ୍ତିମାନଙ୍କୁ ଅଧିକ ସୁଯୋଗ ଦିଆଯାଉଅଛି। ସମାଜବିଜ୍ଞାନର ମହତ୍ଵକୁ ସ୍ପଷ୍ଟ କରିବାକୁ ଯାଇ ପ୍ରଫେସର ଗୀଡ଼ିଙ୍ଗସ୍‌ ଯଥାର୍ଥରେ ଲେଖୁଛନ୍ତି “ ଆମ୍ଭେ ଆମ୍ଭର ଉପସ୍ଥିତ ବସ୍ତୁକୁ କିପରି ପାଇବା ତାହା ଅର୍ଥଶାସ୍ତ୍ର ସୂଚାଇ ଦେଉଥ‌ିବାବେଳେ ଆମ୍ଭେ କ’ଣ ହେବାକୁ ଚାହୁଁଛେ ତାହା କିପରି ହେବ, ଏହା ସମାଜବିଜ୍ଞାନ ସୂଚାଇଥାଏ। ବାସ୍ତବରେ ସଜବିଜ୍ଞାନର ଉଭୟ ବ୍ୟକ୍ତି ଓ ସାମାଜିକ ଦୃଷ୍ଟିକୋଣର ମହତ୍ତ୍ଵପୂର୍ଣ୍ଣ। ଏଣୁ ଆଜିର ସମାଜରେ ସମାଜବିଜ୍ଞାନର ମହତ୍ତ୍ଵ କେବଳ ଏହା, ସମ୍ବନ୍ଧିତ ଜ୍ଞାନର ଆହରଣରେ ଯଥାର୍ଥ ହେବ ନାହିଁ। ବରଂ ଏହି ଜ୍ଞାନର ଯଥାର୍ଥ ସଦ୍‌ଉପଯୋଗ ହିଁ ସମାଜବିଜ୍ଞାନର ବାସ୍ତବ ମହତ୍ତ୍ଵ।

Question ୪।
ସମାଜ ବିଜ୍ଞାନର ସଂଜ୍ଞା ପ୍ରଦାନ କରି ଏହାର ପରିସର ଆଲୋଚନା କର।
Answer:
ଫ୍ରାନ୍ସ ସମାଜର ବିପ୍ଳବ ପରବର୍ତ୍ତୀ ଅବସ୍ଥା ଅତ୍ୟନ୍ତ ଶୋଚନୀୟ ଥିଲା। ସାମାଜିକ ବ୍ୟବସ୍ଥା କ୍ରମେ ଅବନତି ହେଉଥିଲା। ଏହି ସମୟରେ ଫ୍ରାନ୍ସର ଦାର୍ଶନିକ ଅଗଷ୍ଟକମ୍‌ ସମାଜର ଏହି ଅବ୍ୟବସ୍ଥାକୁ ଲକ୍ଷ୍ୟ କରି ଏହା କିପରି ଠିକ୍ ହୋଇପାରିବ ସେ ସମ୍ପର୍କରେ ଚିନ୍ତା କଲେ ଏବଂ ଏକ ନୂତନ ବିଜ୍ଞାନର ସନ୍ଧାନରେ ରହିଲେ। ସମାଜକୁ ସଂପୂର୍ଣ୍ଣ ଭାବରେ ଅଧ୍ୟୟନ କରି ଏହାର ସମସ୍ୟା ସମାଧାନ କରିପାରୁଥିବା ଏହି ବିଜ୍ଞାନଟିର ନାମକରଣ ପ୍ରଥମେ ସେ ସାମାଜିକ ପଦାର୍ଥ ବିଜ୍ଞାନ ରଖୁଥିଲେ। ମାତ୍ର ପରେ ୧୮୩୯ ମସିହାରେ ସେ ଏହାର ନାମ ପରିବର୍ତ୍ତନ କରି ସମାଜବିଜ୍ଞାନର ରଖୁଲେ। ଏଥ‌ିପାଇଁ ଅଗଷ୍ଟ କମ୍‌ଙ୍କୁ ସମାଜବିଜ୍ଞାନର ଜନକ କୁହାଯାଇଥାଏ। ସେ ସମାଜବିଜ୍ଞାନୀମାନଙ୍କ ମଧ୍ୟରେ ଦାର୍ଶନିକ ଓ ଦାର୍ଶନିକମାନଙ୍କ ମଧ୍ୟରେ ବିଜ୍ଞାନୀଭାବରେ ପରିଚିତ ହୋଇଥାଆନ୍ତି।

ସମାଜବିଜ୍ଞାନ ଦୁଇଟି ଶବ୍ଦର ସମ୍ମିଶ୍ରଣରେ ଗଠିତ। ତାହା ହେଲା ଲାଟିନ ଶବ୍ଦ ‘ସୋସିଅସ’ ବା ସୋସାଇଟସ୍ ଅର୍ଥାତ୍ ସମାଜ ଏବଂ ଗ୍ରୀକ୍ ଶବ୍ଦ ଲୋଗସ୍ ଅର୍ଥବିଜ୍ଞାନ ବା ଅଧ୍ୟୟନ। ତେଣୁ ସମାଜବିଜ୍ଞାନ ଶବ୍ଦର ଆକ୍ଷରିକ ଅର୍ଥ ହେଉଛି ସମାଜ ସମ୍ବନ୍ଧୀୟ ବିଜ୍ଞାନ ବା ସମାଜ ସମ୍ବନ୍ଧୀୟ ଅଧ୍ୟୟନ।
ସମାଜବିଜ୍ଞାନୀନେ ସମାଜବିଜ୍ଞାନ ସମ୍ବନ୍ଧରେ ସଂଜ୍ଞା ପ୍ରଦାନ କରିଅଛନ୍ତି। େଥ୍ ମଧ୍ୟରୁ କେତୋଟି ମୁଖ୍ୟ ସଂଜ୍ଞା ହେଲା ଭିଲିନ୍ ଏବଂ ଗିଲିନ୍‌ଙ୍କ ମତରେ, “ସଂଘବଦ୍ଧ ଜୀବନଯାପନ କରୁଥିବା ଜୀବମାନଙ୍କର ପାରସ୍ପରିକ କ୍ରିୟାର ଅଧ୍ୟୟନକୁ ସମାଜବିଜ୍ଞାନ କୁହାଯାଏ। ”

ଅଗଷ୍ଟକମ୍‌ କହନ୍ତି, “ସମାଜବିଜ୍ଞାନ ହେଉଛି ସମାଜ ସଂପର୍କୀୟ ବିଜ୍ଞାନ ଯାହା କେତେକ ପ୍ରାକୃତିକ ଏବଂ ପରିବର୍ଭନୀୟ ନିୟମକୁ ଆଖୁ ଆଗରେ ରଖ୍ ତା’ର ଅନୁସନ୍ଧାନ ଆରମ୍ଭ କରିଥାଏ। ” ମାକ୍ ଆଇଭର ଏବଂ ପେଜଙ୍କ ମତରେ, “ସମାଳବିଜ୍ଞାନ ସାମାଜିକ ସମ୍ପର୍କ ସମ୍ବନ୍ଧରେ ଅଧ୍ୟୟନ କରିଥାଏ । ଯେଉଁ ଜାଲ ଭଳି ବୁଣା ହୋଇଥିବା ସାମାଜିକ ସମ୍ପର୍କକୁ ସମାଜ କୁହାଯାଏ ।” ମାକ୍‌ସୱେବରଙ୍କ ମତରେ, “ ସମାଜବିଜ୍ଞାନ ଏକ ବିଜ୍ଞାନ ଅଟେ ଯାହାକି ସାମାଜିକ ଜୀବନ୍ତ ବ୍ୟାଖ୍ୟାତ୍ମକ ବୋଧଗମ୍ୟତା ପାଇଁ ଚେଷ୍ଟା କରିଥାଏ। ମୋରିସ୍ ଜିନିସ୍‌ବର୍ଗଙ୍କ ମତରେ, “ ମାନବିକ ପାରସ୍ପରିକ କ୍ରିୟା ଏବଂ ପାରସ୍ପରିକ ସମ୍ପର୍କ ସେଗୁଡ଼ିକର ଅବସ୍ଥା ଏବଂ ଫଳାଫଳର ଅଧ୍ୟୟନକୁ ସମାଜବିଜ୍ଞାନ କୁହାଯାଏ ।”

ସମାଜବିଜ୍ଞାନର ପରିସର:
ବିଷୟବସ୍ତୁ ବା ପରିସର କହିଲେ ଗୋଟିଏ ବିଷୟର ଅନୁସନ୍ଧାନ ଏବଂ ଅନୁଶୀଳନର ବିଷୟ କ’ଣ ହେବା ଉଚିତ୍ ତାକୁ ହିଁ ବୁଝାଇଥାଏ। ପ୍ରତ୍ୟେକ ବିଜ୍ଞାନର ନିର୍ଦ୍ଦିଷ୍ଟ ପରିସୀମା ରହିଛି। କିନ୍ତୁ ସମାଜବିଜ୍ଞାନର ପରିସୀମା ସଂପର୍କରେ ସମାଜବିତ୍‌ମାନେ ଭିନ୍ନ ଭିନ୍ନ ମତପୋଷଣ କରିଅଛନ୍ତି। ସମାଜଶାସ୍ତ୍ରର ପରିସର ଓ ବିଷୟବସ୍ତୁ ନିର୍ଣ୍ଣୟକୁ କେନ୍ଦ୍ର କରି ସମାଜବିତମାନେ ଦୁଇ ଭାଗରେ ବିଭକ୍ତ ହୋଇଛନ୍ତି। ପ୍ରଥମ ମତବାଦ ଅନୁସାରେ ସମାଜଶାସ୍ତ୍ର ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ବିଜ୍ଞାନ ଓ ଏହାର ପରିସର ସୀମିତ। ଦ୍ଵିତୀୟ ମତବାଦ ଅନୁସାରେ ସମାଜଶାସ୍ତ୍ର ଏକ ସାଧାରଣ ବିଜ୍ଞାନ ଓ ଏହର ପରିସର ଅତ୍ୟନ୍ତ ବ୍ୟାପକ। ସେ ମତବାଦ ଦୁଇଟି ହେଲା: (୧) ସ୍ଵାତନ୍ତ୍ର ମତବାଦ, (୨) ସାଂଶ୍ଲେଷିକ ମତବାଦ।

(କ) ସ୍ଵାତନ୍ତ୍ର୍ୟ ମତବାଦ ବା ଆକୃତିଗତ ମତବାଦ: ସ୍ଵାତନ୍ତ୍ର୍ୟ ମତବାଦୀମାନଙ୍କ ମତରେ ସମାଜଶାସ୍ତ୍ରର ପରିସର ସୀମିତ ଅଟେ। ସମାଜଶାସ୍ତ୍ର ଏକ ସ୍ଵତନ୍ତ୍ର ତଥା ନିର୍ଦ୍ଦିଷ୍ଟ ବିଜ୍ଞାନ, ଯାହାକି କେବଳ ସାମାଜିକ ସମ୍ପର୍କରେ ବିଭିନ୍ନ ଆକୃତିକୁ ହିଁ ଅଧ୍ୟୟନ ଅଟେ। ସ୍ଵତନ୍ତ୍ର ମତବାଦର ମୁଖ୍ୟ ପୃଷ୍ଠପୋଷକମାନେ ହେଲେ – ଜର୍ଜ ସିଟେଲ ସ୍ମୟ, ଭିରକଣ୍ଡାଟ୍, ମାକ୍ସ ୱେବର, ଉନୱାଇଜ ଏବଂ ଫଡ଼ିନାଣ୍ଡଟନିସ୍। ଏହି ମତବାଦୀମାନେ ସମାଜବିଜ୍ଞାନକୁ ଏକ ସ୍ଵତନ୍ତ୍ର ଓ ନିରପେକ୍ଷ ବିଜ୍ଞାନଭାବେ ବିଚାର କରିଥାଆନ୍ତି। ସମାଜବିଜ୍ଞାନ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ରୂପ ଦେଇ ଅନ୍ୟାନ୍ୟ ସମାଜବିଜ୍ଞାନଠାରୁ ଏହାକୁ ପୃଥକ୍ କରିବା ହେଉଛି ସ୍ଵାତନ୍ତ୍ର୍ୟ ମତବାଦୀମାନଙ୍କର ଆଭିମୁଖ୍ୟ।

(୧) ଜର୍ଜ ସିଷେଲ : ଜର୍ମାନୀ ସମାଜବିତ୍ ଜର୍ଜ ସିମେଲ ମତାନୁସାରେ ସମାଜଶାସ୍ତ୍ର ସକଳ ପ୍ରକାର ସାମାଜିକ ସମ୍ପର୍କକୁ ବର୍ଣ୍ଣନା, ବିଭାଜନ ଓଁ ବିଶ୍ଳେଷଣ ଦ୍ଵାରା ଉପସ୍ଥାପନ କରେ। ତାଙ୍କ ମତରେ ସମାଜଶାସ୍ତ୍ର ମନୁଷ୍ୟର ପ୍ରକୃତ ବ୍ୟବହାର ପରିବର୍ତ୍ତେ ସେମାନଙ୍କର ଆକୃତିଗତ ବ୍ୟବହର ଅଧ୍ୟୟନ କ୍ଷେତ୍ରରେ, ସୀମିତ ରହିବା ଆବଶ୍ୟକ। ତାଙ୍କ ମତରେ ପ୍ରତିଯୋଗିତା, ବଶ୍ୟତା, ପ୍ରଭୂତ୍ଵ, ସାମାଜିକୀକରଣ ଏବଂ ଶ୍ରମବିଭାଜନ ପ୍ରଭୃତି ହେଉଛି ସାମାଜିକ ସଂପର୍କର ମୁଖ୍ୟ ଆକୃତି। ସମାଜବିଜ୍ଞାନର ମୁଖ୍ୟ କାର୍ଯ୍ୟ ହେଲା ସେଗୁଡ଼ିକୁ ପରିସ୍କରଠାରୁ ପୃଥକ୍ କରି ଅଧ୍ୟୟନ ଏବଂ ଅନୁଶୀଳନ କରିବା।

(୨) ସ୍ଵଲ୍ : ସ୍କଲ୍‌ଙ୍କ ମତରେ ସମାଜଶାସ୍ତ୍ରରେ ସମାଜର ପ୍ରତ୍ୟେକ କାର୍ଯ୍ୟକଳାପକୁ ଅଧ୍ୟୟନ କରେ ନାହିଁ। ଏହାର କେବଳ ସମ୍ପର୍କ, ବ୍ୟବହାର ଏବଂ କ୍ରିୟାକଳାପର ଅନୁବଂଶିକ ଆକୃତିକୁ ଅଧ୍ୟୟନ କରିଥାଏ। ପ୍ରତ୍ୟେକ ବିଜ୍ଞାନର ନିର୍ଦ୍ଦିଷ୍ଟ ପରିସୀମା ପରି ଏହାର ପରିସୀମା ରହିଛି।

(୩) ଭିକାଣ୍ଡ : ତାଙ୍କ ମତରେ ସମାଜଶାସ୍ତ୍ର ଏକ ସାମାଜିକ ବିଜ୍ଞାନ। ସମାଜଶାସ୍ତ୍ର ସେହି ପ୍ରକାର ମନସ୍ତାତ୍ତତ୍ତିକ ସମ୍ପର୍କର ବିଚାର କରେ ଯାହା ସମାଜର ମନୁଷ୍ୟମାନଙ୍କୁ ଗୋଟିଏ ସୂତ୍ରରେ ବାନ୍ଧି ଦେଇପାରେ। ତାଙ୍କ ମତରେ ପ୍ରେମ, ଘୃଣା, ପ୍ରତିଯୋଗିତା, ସହଯୋଗିତା ସୂତ୍ରରେ ବାନ୍ଧି ଦେଇପାରେ। ତାଙ୍କ ମତରେ ପ୍ରେମ, ଘୃଣା, ପ୍ରତିଯୋଗିତା ଓ ସହଯୋଗିତା ପ୍ରଭୃତି ସମ୍ପର୍କରେ ଚରମ ଆକୃତିର ଅଧ୍ୟୟନ ସମାଜଶାସ୍ତ୍ରର ବିଷୟବସ୍ତୁ ହେବା ଉଚିତ। ଅତଏବ ସମାଜଶାସ୍ତ୍ରର ପରିସର ମନସ୍ତାତ୍ତ୍ଵିକ ସମ୍ପର୍କଗୁଡ଼ିକୁ ଅଧନ କରିବା ଉଚିତ, ଯାହା ଫଳରେ ବ୍ୟକ୍ତି ସମୂହ ସହିତ ପରିଚିତ ହୋଇଥାଏ।

(୪) ମ୍ୟାକସ୍ ୱେବର : ଜର୍ମାନ ସମାଜତତ୍ତ୍ୱବିତ୍ ମ୍ୟାକ୍‌ସ୍ ୱେବର କହନ୍ତି, “ସାମାଜିକ ବ୍ୟବହାରକୁ ବ୍ୟାଖ୍ୟା କରିବା ଏବଂ ଠିକ୍ ଭାବେ ବୁଝିବା ସମାଜ ଶାସ୍ତ୍ରର ପରିସରଭୁକ୍ତ।” ତାଙ୍କ ମତରେ ସାମାଜିକ ବ୍ୟବହାର ମାନସିକ ସମ୍ପର୍କରେ ସମସ୍ତ ଦିଗକୁ ଅନ୍ତର୍ଭୁକ୍ତ କରି ନ ଥାଏ। ସେହିପରି ମାନସିକ ସମ୍ପର୍କ ସାମାଜିକ ନୁହେଁ। ଏହା ଅନ୍ୟମାନଙ୍କର ସମ୍ପର୍କ ସହ ସଂପୃକ୍ତ ଏବଂ ସେମାନଙ୍କ ଦ୍ଵାରା ନିଦ୍ଧାରିତ।

(୫) ଉନ୍‌ଇଜ୍ : ତାଙ୍କ ମତରେ ସାମାଜିକ ବିଜ୍ଞାନ ସାମାଜିକ ସମ୍ପର୍କ ଆକୃତିକୁ ଅଧ୍ୟୟନ କରିବା ଉଚିତ ସେ ଏହି ସାମାଜିକ ସଂପର୍କକୁ ବିଭିନ୍ନ ପ୍ରକାରରେ ବିଭକ୍ତ କରିଛନ୍ତି।

(୬) ଫର୍ଜିନାଣ୍ଡ ଟିନସ୍‌ : ଟନିସ୍‌ଙ୍କ ମତରେ ସାମାଜିକ ବିଜ୍ଞାନ ଏକ ସ୍ଵାଧୀନ ଏବଂ ବିଶୁଦ୍ଧ ସାମାଜିକ ବିଜ୍ଞାନ ! ସେ ସାମାଜିକ ସମ୍ପର୍କର ଆକୃତିକୁ ଭିତ୍ତି କରି ସମାଜ ଓ ସମ୍ପ୍ରଦାୟ ମଧ୍ୟରେ ପାର୍ଥକ୍ୟ ଦର୍ଶାଇଛନ୍ତି ଏବଂ ଏହି ଦୁଇ ପ୍ରକାର ସାମାଜିକ ସମ୍ପର୍କକୁ ନେଇ ସମାଜ ଗଠିତ ବୋଲି ସେ ମତପୋଷଣ କରିଛନ୍ତି।

ସମାଲୋଚନା :
(୧) ସ୍ଵାତନ୍ତ୍ର୍ୟ ମତବାଦ ସାମାଜିକ ବିଜ୍ଞାନର ପରିସରକୁ ଅତ୍ୟନ୍ତ ସଂକୀର୍ଣ୍ଣ କରିଦେଇଛି। ସମାଜଶାସ୍ତ୍ର କେବଳ ସାମାଜଢି ସଂପର୍କର ଆକୃତିକ ଅଧ୍ୟୟନ କରିବା ଉଚିତ ନୁହେଁ।

(୨) ଏହି ମତବାଦ ମୂର୍ଖ ଏହି ମତବାଦ ମୂର୍ଖ ସମ୍ପର୍କକୁ ଅମୂର୍ଖ ସଂପର୍କଠାରୁ ଅଲଗା କରି ପାଠକରି ସାମାଜିକ ବିଜ୍ଞାନ ପରିସରକୁ କ୍ଷୁଦ୍ର କରିଦିଏ।

(୩) ବିଶୁଦ୍ଧ ଏବଂ ସ୍ଵାଧୀନ ସମାଜଶାସ୍ତ୍ର କଳ୍ପନା ଅସମ୍ଭବ ଅଟେ। କୌଣସି ସମାଜବିତ୍ ଏହା କରିବାରେ ଏ ପର୍ଯ୍ୟନ୍ତ ସକ୍ଷମ ହୋଇନାହାନ୍ତି।

(୪) ସମାଜଶାସ୍ତ୍ର କେବଳ ସଂପର୍କ ଓ ଏହାର ବିଭିନ୍ନ ଆକୃତିକୁ ଅଧ୍ୟୟନ କରେ ତାହା ନୁହେଁ। ରାଜନୀତିବିଜ୍ଞାନ, ମନସ୍ତତ୍ତ୍ଵ ଏବଂ ଆନ୍ତର୍ଜାତୀୟ ଆଇନ୍ ଆଦି ଅନେକ ସାମାଜିକ ବିଜ୍ଞାନ ମଧ୍ୟ ସାମାଜିକ ସମ୍ପର୍କକୁ ଅୟନ କରିଥା’ନ୍ତି।

(ଖ) ସାଂଶ୍ଳେଷିକ ମତବାଦ : ସାଂଶ୍ଳେଷିକ ମତବାଦ ଅନୁସାରେ ସମାଜ ଶାସ୍ତ୍ର ହେଉଛି ସାମାଜିକ ବିଜ୍ଞାନର ସଂଶ୍ଳେଷଣ। ଏହି ସବୁ ପ୍ରକାର ବିଜ୍ଞାନର ଏକ ମିଶ୍ରଣଫଳ। ଏହା ଏକ ସ୍ଵତନ୍ତ୍ର ବା ସ୍ଵାଧୀନ ବିଜ୍ଞାନ ନୁହେଁ। ଏହା ଏକ ସାଧାରଣ ବିଜ୍ଞାନ। ଏହି ମତବାଦର ମୁଖ୍ୟ ପ୍ରବକ୍ତାମାନେ ହେଲେ ଇମାଇଲ୍ ଦୁର୍ଖମ୍। ଏଲ.ଟି. ହହାଉସ୍, ପି.ଏ. ସରୋକିନ୍ ଏବଂ ମୋରିସ୍ ଜିନିସ୍‌ବର୍ଗ ଆଦିଙ୍କ ମତରେ ସମାଜଶାସ୍ତ୍ର ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ସାମାଜିକ ବିଜ୍ଞାନ ନୁହେଁ। ଏହା ସମାଜକୁ ସାଧାରଣଭାବେ ଅଧିନ କରେ। ତେଣୁ ସମାଜଶାସ୍ତ୍ର ପରିସର ଅତି ବ୍ୟାପକ ଓ ବିସ୍ତୃତ। ସମସ୍ତ ସାମାଜିକ ବିଜ୍ଞାନ ସମାଜଶାସ୍ତ୍ରର ପରିସରଭୁକ୍ତ ଅଟନ୍ତି।

(୧) ଇମାଇଲ୍ ଦୁର୍ଖମ୍ : ଫରାସୀ ସମାଜବିଜ୍ଞାନବିତ୍ ଇମାଇଲ୍ ଦୁର୍ଗମ ସମାଜ ବିଜ୍ଞାନକୁ ତିନି ଭାଗରେ ବିଭକ୍ତ କରିଅଛନ୍ତି। ସେଗୁଡ଼ିକ ହେଲା : (୧) ସାମାଜିକ ରୂପତତ୍ତ୍ଵ, (୨) ସାମାଜିକ ଜୀବତତ୍ତ୍ଵ ଓ (୩) ସାଧାରଣ ସାମାଜିକ ବିଜ୍ଞାନ। ସାମାଜିକ ଘଟଣା ଓ କ୍ରିୟାକଳାପରେ ସାଧାରଣ ନିୟମଗୁଡ଼ିକୁ ଅନୁଧ୍ୟାନ କରିବା ହେଉଛି ଏହାର କାର୍ଯ୍ୟ।

(୨) ଏଲ୍. ଟି ହହାଉସ୍ : ଇଂରେଜ ସମାଜତତ୍ତ୍ୱବିତ୍ ଏଲ୍.ଟି. ହବହାଉସ୍‌ଙ୍କ ମତରେ ହେଉଛି ବିଭିନ୍ନ ସାମାଜିକ ବିଜ୍ଞାନର ସଂଶ୍ଳେଷଣ ଜୀବନର ସମସ୍ତ ଦିଗଗୁଡ଼ିକ ସହ ସଂପୃକ୍ତ ।”

(୩) ପି. ଏ ସରୋକିନ୍ : ପି. ଏ. ସରୋକିନ୍‌ଙ୍କ ମତ ଅନୁସାରେ “ ସମାଜଶାସ୍ତ୍ର ବିଭିନ୍ନ ପ୍ରକାରର ସାମାଜିକ ସମ୍ପର୍କ ବିଚାର ଓ ଅନୁଶୀଳନ କରୁଥିବାରୁ ତାକୁ ସ୍ଵତନ୍ତ୍ରଭାବେ ଏକ ବିଜ୍ଞାନ କହିହେବ ନାହିଁ । ସମାଜଶାସ୍ତ୍ର ସାମାଜିକ ଘଟଣାର ବିଭିନ୍ନ ବିଭାଗଗୁଡ଼ିକ ମଧ୍ୟରେ ସମ୍ପର୍କକୁ ଅଧ୍ୟୟନ କରିଥାଏ ।”

(୪) ମୋରିସ୍ ଜିନିସ୍‌ବର୍ଗ : ଜିନିସ୍‌ବର୍ଗଙ୍କ ମତରେ ସମାଜ ବିଜ୍ଞାନ ମନୁଷ୍ୟ ସହ ସମାଜର ବିଭିନ୍ନ ପ୍ରକାର ସମ୍ପର୍କକୁ ବିଶ୍ଳେଷଣ କରେ। ଏହି ସମ୍ପର୍କ ସାଧାରଣତଃ ତିନି ପ୍ରକାରର। ସମାଜଶାସ୍ତ୍ର ସାମାଜିକ ରୂପତତ୍ତ୍ଵ, ସାମାଜିକ ନିୟନ୍ତ୍ରଣ, ସାମାଜିକ ପ୍ରକ୍ରିୟା ଏବଂ ସାମାଜିକ ବ୍ୟାଧୁତତ୍ତ୍ଵ ପ୍ରଭୃତିକୁ ଅନ୍ତର୍ଭୁକ୍ତ କରିଥାଏ।

(୫) କାର୍ଲମାନ୍‌ଭାଇସ୍‌ଙ୍କ ମତ କାର୍ଲମାନ୍‌ଭାଇସ୍ ସମାଜଶାସ୍ତ୍ରକୁ ଦୁଇଟି ମୁଖ୍ୟ ଶାଖାରେ ବିଭିକ୍ତ କରିଅଛନ୍ତି। ତାହା ହେଲା ସାଧାରଣ ସମାଜଶାସ୍ତ୍ର ଓ ଐତିହାସିକ ସମାଜଶାସ୍ତ୍ର। ତାଙ୍କ ମତରେ “ ସାଧାରଣ ସମାଜଶାସ୍ତ୍ର ସମାଜରେ ମନଷ୍ୟମାନଙ୍କର ଏକତ୍ର ସହାବସ୍ଥାନର ମୁଖ୍ୟ କାରଣଗୁଡ଼ିକ ବିଶ୍ଳେଷଣ କରିଥାଏ।

ସାଂଶ୍ଲେଷିକ ମତବାଦ ସାମାଜିକ ବିଜ୍ଞାନର ଏକ ବ୍ୟାପକ ରୂପ ହୋଇଥିବାରୁ ଏହା ବେଶ୍ ଆଦୃତ ଅଟେ। ଏ ଦୁଇଟି ମତବାଦକୁ ଅଧ୍ୟୟନ କଲେ ଜଣାଯାଏ ସେ ସମାଜ ଶାସ୍ତ୍ରର ପରିସର ଅତ୍ୟନ୍ତ ବ୍ୟାପକ ଅଟେ। ଏହା ଉଭୟ ସାଧାରଣ ଓ ସ୍ଵତନ୍ତ୍ର ବିଜ୍ଞାନ ଭାବରେ ପରିଚିତ ଅଟେ ଏବଂ ଉଭୟ ଚିନ୍ତାଧାରା ଅନ୍ତର୍ଭୁକ୍ତ କରିଥାଏ। ଅନ୍ୟାନ୍ୟ ସାମାଜିକ ବିଜ୍ଞାନ ପରି ସମାଜ ହେଉଛି ସମାଜଶାସ୍ତ୍ରର କେନ୍ଦ୍ରବିନ୍ଦୁ। ଅନ୍ୟାନ୍ୟ ବିଜ୍ଞାନ ସମାଜର ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଦିଗକୁ ଅଧ୍ୟୟନ କରୁଥିବାବେଳେ ସମାଜଶାସ୍ତ୍ର ସାମାଜିକ ସମ୍ପର୍କକୁ ଅଧ୍ୟୟନ କରିବା ସହିତ ତା’ର ସମସ୍ତ ଦିଗକୁ ଅଧ୍ୟୟନ କରିଥାଏ। ତେଣୁ ସମାଜଶାସ୍ତ୍ରର ପରିସର କଦାପି ସଂକୀର୍ଣ୍ଣ ହୋଇ ନ ପାରେ। ଏକ କ୍ରମବର୍ଦ୍ଧିଷ୍ଣୁ ସାମାଜିକ ବିଜ୍ଞାନ ହିସାବରେ ଏହାର ପରିସର ଅତ୍ୟନ୍ତ ବ୍ୟାପକ ଅଟେ।

Question ୬।
ସମାଜଶାସ୍ତ୍ର ଓ ରାଜନୀତି ବିଜ୍ଞାନ ମଧ୍ୟରେ ଥିବା ସମ୍ପର୍କ ଆଲୋଚନା କର।
Answer:
ସମାଜଶାସ୍ତ୍ର ଓ ରାଜନୀତି ବିଜ୍ଞାନ ଉଭୟ ଆନ୍ତଃନିର୍ଭରଶଳ ଓ ଆନ୍ତଃ ସଂପୃକ୍ତ। ଏହି ଦୁଇଟି ବିଜ୍ଞାନ ପରସ୍ପର ଏତେ ଘନିଷ୍ଠ ଯେ ଗୋଟିଏ ବ୍ୟତୀତ ଅନ୍ୟଟି ଅର୍ଥଶୂନ୍ୟ ଅଟେ। ତେଣୁ କ୍ୟାଟ୍‌ଲିନ୍‌ଙ୍କ ଭାଷାରେ ସମାଜଶାସ୍ତ୍ର ଓ ରାଜନୀତିବିଜ୍ଞାନ ଗୋଟିଏ ମୁଦ୍ରାର ଦୁଇଟି ପାର୍ଶ୍ଵ। ହୋଫର୍‌ଙ୍କ ମତରେ, “ରାଷ୍ଟ୍ର ଯାହାକି ରାଜନୀତି ବିଜ୍ଞାନର କେନ୍ଦ୍ରବିନ୍ଦୁ ତାହା ପ୍ରାଥମିକ ଅବସ୍ଥାରେ ଏକ ରାଜନୈତିକ ଅନୁଷ୍ଠାନ ଅପେକ୍ଷା ଏକ ସାମାଜିକ ଅନୁଷ୍ଠାନ ରୂପେ ପରିଚିତ। ସେହିପରି ମୋରିସ୍ ଜିନ୍‌ସବର୍ଗ କହନ୍ତି ଐତିହାସିକ ଭାବେ ସମାଜଶାସ୍ତ୍ରର ମୁଖ୍ୟ ଭିଭି ବା ମୌଳିକ ବସ୍ତୁ ରାଜନୀତି ଓ ଇତିହାସ ଦର୍ଶନର ନିହିତ ।”

ସମାଜଶାସ୍ତ୍ର ମନୁଷ୍ୟର ସାମାଜିକ ଜୀବନକୁ ସଂପୂର୍ଣ୍ଣଭାବରେ ଅଧ୍ୟୟନ କରିଥାଏ। ଏହା ସାମ୍ପ୍ରଦାୟିକ ଜୀବନର ତଥ୍ୟ ଓ ନିୟମଗୁଡ଼ିକ ଆବିଷ୍କାର କରିବା ପାଇଁ ପଦକ୍ଷେପ ଗ୍ରହଣ କରିଥାଏ। ମାତ୍ର ରାଜନୀତି ବିଜ୍ଞାନ ମନୁଷ୍ୟର ରାଜନୈତିକ କ୍ରିୟାକଳାପକୁ କରିଥାଏ। ଏହା ହେଉଛି ରାଷ୍ଟ୍ର ଓ ସରକାର ସମ୍ବନ୍ଧୀୟ ବିଜ୍ଞାନ। ଏହା ବିଭିନ୍ନ ପ୍ରକାର ରାଜନୈତିକ କାର୍ଯ୍ୟକଳାପ, ସମ୍ବିଧାନ, ଘଟିଯାଇଥିବା ବିଭିନ୍ନ ପ୍ରକାରର ବିପ୍ଲବ, ନିର୍ବାଚନ ପ୍ରକ୍ରିୟା, ମତଦାନ ଅଧିକାର, ନାଗରିକ କର୍ତ୍ତବ୍ୟ, ରାଷ୍ଟ୍ରର ନିୟମ ପ୍ରଣୟନ ଇତ୍ୟାଦି ସମ୍ବନ୍ଧରେ ଅଧ୍ୟୟନ କରିଥାଏ।

ସମାଜ ଶାସ୍ତ୍ର ରାଜନୀତି ବିଜ୍ଞାନ ଉପରେ ନିର୍ଭରଶୀଳ। ସମାଜର ଉନ୍ନତି ପାଇଁ ରାଷ୍ଟ୍ର ଆଇନ୍‌ମାନ ପ୍ରଣୟନ କରିଥାଏ। ସମାଜରୁ ଅପରାଧ, ଦାରିଦ୍ର୍ୟ, ବେକାର ସମସ୍ୟା, ଯୌତୁକ ପ୍ରଥା, ଅସ୍ପୃଶ୍ୟତା, ଭିକ୍ଷା ବୃତ୍ତି ଆଦି ଅନିଷ୍ଟକାରୀ ସାମାଜିକ ବ୍ୟାଧ୍ୟ ବା ସମସ୍ୟାଗୁଡ଼ିକୁ ସରକାର ହିଁ ଦୂରୀଭୂତ କରନ୍ତି। ସମାଜରେ ପ୍ରଚଳିତ ଅନାବଶ୍ୟକ ପ୍ରଥାଗୁଡ଼ିକର ମୂଳୋତ୍ପାଟନ ସରକାରଙ୍କ ଦ୍ଵାରା ହିଁ ହୋଇଥାଏ। ବନ୍ୟା, ବାତ୍ୟା, ମରୁଡ଼ି ଓ ଦୁର୍ଭିକ୍ଷ ପ୍ରଭୃତି ପ୍ରାକୃତିକ ଦୁର୍ବିପାକ ସମୟର ସରକାର ଲୋକମାନଙ୍କୁ ଆର୍ଥିକ ସାହାଯ୍ୟ ପ୍ରଦାନ କରିଥାନ୍ତି। ସାମାଜିକ ଅନୁଷ୍ଠାନଗୁଡ଼ିକ ରାଷ୍ଟ୍ର ଏବଂ ସରକାରଙ୍କ ଦ୍ଵାରା ନିୟନ୍ତ୍ରିତ ହୋଇଥାଏ। ସମାଜଶାସ୍ତ୍ର ବିଭିନ୍ନ ପ୍ରକାର ରାଜନୈତିକ ଅନୁଷ୍ଠାନ, ସଂଘ, ସଂଗଠନ ଏବଂ ବିଭିନ୍ନ ପ୍ରକାର, ରାଜନୈତିକ କାର୍ଯ୍ୟାବଳୀଗୁଡ଼ିକ ବିଜ୍ଞାନ ମାଧ୍ୟମରେ ହିଁ ଅଧ୍ୟୟନ କରେ। ବିଭିନ୍ନ ଆଇନ ମାନ ପ୍ରଣୟନ କରି ସରକାର ସମାଜରେ ସାମାଜିକ ପରିବର୍ତ୍ତନର ବେଗକୁ ତ୍ୱରାନ୍ଵିତ କରିଥା’ନ୍ତି।

ସେହପରି ରାଜନୀତିବିଜ୍ଞାନ ମଧ୍ୟ ବିଭିନ୍ନ ଦିଗରୁ ସମାଜଶାସ୍ତ୍ର ଉପରେ ନିର୍ଭର କରେ। ସମାଜଶାସ୍ତ୍ର ବିଜ୍ଞାନକୁ ବହୁ ଉପାଦାନ ଯୋଗାଇ ଦେଇଥାଏ। ଲୋକମାନଙ୍କର ରାଜନୈତିକ ଜୀବନ ତଥା କାର୍ଯ୍ୟାବଳୀ ଆଦି ରାଜନୀତି ବିଜ୍ଞାନର ବିଷୟବସ୍ତୁ ସମାଜଶାସ୍ତ୍ର ପରିସରଭୁକ୍ତ। ସୁତରାଂ କେତେକ ସମାଜଶାସ୍ତ୍ରବିତ୍ ରାଜନୀତି ବିଜ୍ଞାନକୁ ସମାଜଶାସ୍ତ୍ରର ଏକ ସ୍ଵତନ୍ତ୍ର ଶାଖାରୂପେ ଅଭିହିତ କରିଛନ୍ତି। ଏହା ନିଶ୍ଚିତ ଯେ, ସମାଜଶାସ୍ତ୍ରର ପୃଷ୍ଠଭୂମି ବ୍ୟତୀତ ରାଜନୀତି ବିଜ୍ଞାନର ଅଧ୍ୟୟନ ଅସମ୍ଭବ। ରାଷ୍ଟ୍ରର ସାର୍ବଭୌମତ୍ବ ଅଧୀନରେ ସଂଗଠିତ ସାମାଜିକ ସମୂହ ସହିତ ରାଜନୀତି ବିଜ୍ଞାନ ସଂପୃକ୍ତ ସରକାରର ପ୍ରକାରଭେଦ, ସରକାରୀ ଦଳର ପ୍ରକୃତି, ଆଇନ୍ ଏବଂ ରାଷ୍ଟ୍ରର କାର୍ଯ୍ୟାବଳୀ ପ୍ରଭୃତି ସମାଜର ପ୍ରକ୍ରିୟା ଦ୍ଵାରା ନିର୍ଦ୍ଧାରିତ। ରାଜନୀତି ବିଜ୍ଞାନ ସମାଜର ଉତ୍ପତି, ସମାଜର ଗଠନ ସମାଜର କାର୍ଯ୍ୟ ଏବଂ ସମାଜର ବିକାଶ ଆଦିକୁ ସମାଜଶାସ୍ତ୍ର ମାଧ୍ୟମରେ ହିଁ ଅର୍ଥୟନ କରିଥାଏ। ସରକାରଙ୍କ ଦ୍ଵାରା ଗଠିତ ଆଇନ୍ ସମାଜରେ ପ୍ରଚଳିତ ପ୍ରଥା, ପରମ୍ପରା, ଲୋକନିୟମ ଓ ପ୍ରତିମାନ ପ୍ରଭୃତି ବିଭିନ୍ନ ଅନୌପଚାରିକ ନୀତିନିୟମ ଉପରେ ପ୍ରତିଷ୍ଠିତ। ଅତୀତରେ ସଂଘଟିତ ହୋଇଥିବା ବିଭିନ୍ନ ରାଜନୈତିକ ତତ୍ତ୍ଵ ସମ୍ବନ୍ଧୀୟ ପରିବର୍ତ୍ତନ କେବଳ ମାତ୍ର ସମାଜଶାସ୍ତ୍ର ଦ୍ଵାରା ହିଁ ସମ୍ଭବ ହୋଇଛି। ରାଜନୈତିକ ସମସ୍ୟାର ଉତ୍ତମ ବ୍ୟାଖ୍ୟା ଏବଂ ସମାଧାନ ପାଇଁ ସମାଜଶାସ୍ତ୍ର ସମ୍ବନ୍ଧୀୟ ଏକାନ୍ତ ଜ୍ଞାନ ଅପରିହାର୍ଯ୍ୟ। କାରଣ ସମସ୍ତ ରାଜନୈତିକ ସମସ୍ୟାମାନ ମୁଖ୍ୟତଃ ସମାଜ ତଥା ସାମାଜିକ ଦିଗ ସହିତ ସଂପୃକ୍ତ।

ଅନେକ ସମସ୍ୟା ଯଥା :
ସାଂପ୍ରଦାୟିକତା, ଜାତିଗତ ସଂଘର୍ଷ, ଅପରାଧ, ବେକାରୀ ଇତ୍ୟାଦି ସାମାଜିକ ଓ ଅର୍ଥନୈତିକ ସମସ୍ୟା ଭାବେ ପରିଚିତ। ଯାହାକୁ ଉଭୟ ଅଧ୍ୟୟନ କରିଥା’ନ୍ତି। ଏହି ପରିପ୍ରେକ୍ଷାରେ ଏଫ୍. ଏଚ. ଗିଡ଼ିଙ୍ଗସ୍ କହିଛନ୍ତି, “ ସମାଜଶାସ୍ତ୍ରର ମୂଳନିୟମ ସମ୍ବନ୍ଧରେ ଅଜ୍ଞ ଥିବା ବ୍ୟକ୍ତିକୁ ରାଷ୍ଟ୍ର ବିଷୟକ ତତ୍ତ୍ବ ବିଷୟରେ ଶିକ୍ଷାଦେବା ଯେପରି ଅଟେ, ନିଉଗତି ସମ୍ବନ୍ଧୀୟ ନିୟମ ଜାଣି ନ ଥିଲା ବ୍ୟକ୍ତିକୁ ଗ୍ରହଣ ବିଜ୍ଞାନ ବିଷୟରେ ଶିକ୍ଷା ଅନୁରୂପ ଅଟେ। ତେଣୁ ସମାଜଶାସ୍ତ୍ର ଏବଂ ରାଜନୀତି ବିଜ୍ଞାନ ପରସ୍ପର ଉପରେ ନିର୍ଭରଶୀଳ ଅଟନ୍ତି। ଉଭୟ ଆନ୍ତଃ ସଂପୃକ୍ତ ଓ ଆନ୍ତଃ ନିର୍ଭରଶୀଳ। ନିବିଡ଼ ତଥା ଘନିଷ୍ଠ ସମ୍ପର୍କ ସତ୍ତ୍ଵେ ଉଭୟ ସମାଜଶାସ୍ତ୍ର ଓ ରାଜନୀତି ବିଜ୍ଞାନ କ୍ଷେତ୍ରରେ ପରସ୍ପରଠାରୁ ଭିନ୍ନ ଅଟନ୍ତି। ସମାଜଶାସ୍ତ୍ର ଓ ରାଜନୀତି ବିଜ୍ଞାନ ମଧ୍ୟରେ ବହୁ ପାର୍ଥକ୍ୟ ପରିଲକ୍ଷିତ ହୁଏ। ସମାଜଶାସ୍ତ୍ର ଓ ରାଜନୀତି ବିଜ୍ଞାନ ମଧ୍ୟରେ ଥିବା ସେହି ପାର୍ଥକ୍ୟମାନ ହେଲା

(୧) ସମାଜଶାସ୍ତ୍ର ସମାଜ ବିଜ୍ଞାନ; ମାତ୍ର ରାଜନୀତି ବିଜ୍ଞାନ ରାଷ୍ଟ୍ର ଓ ସରକାର ସମ୍ବନ୍ଧୀୟ ବିଜ୍ଞାନ। ସମାଜଶାସ୍ତ୍ର ସମାଜକୁ ସଂପୂର୍ଣ୍ଣ ଭାବରେ ଏବଂ ମନୁଷ୍ୟକୁ ଏକ ସାମାଜିକ ପ୍ରାଣୀ ରୂପେ ଅଧ୍ୟୟନ କରୁଥିବା ସମୟରେ ରାଜନୀତି ବିଜ୍ଞାନ ସମାଜର ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଦିଗ ଅର୍ଥାତ୍ ମନୁଷ୍ୟକୁ ଏକ ରାଜନୈତିକ ଜୀବ ଭାବେ ଅଧ୍ୟୟନ କରେ।

(୨) ସମାଜଶାସ୍ତ୍ରର ପରିସର ରାଜନୀତି ବିଜ୍ଞାନର ପରିସରଠାରୁ ଅଧିକ ବ୍ୟାପକ। ସମାଜଶାସ୍ତ୍ର ସମାଜର ସାମାଜିକ, ରାଜନୈତିକ, ଅର୍ଥନୈତିକ, ସାଂସ୍କୃତିକ ଓ ଧାର୍ମିକ ଦିଗ ସହିତ ସଂପୃକ୍ତ ଏବଂ ପରିବାର, ବିବାହ, ଧର୍ମ, ଜ୍ଞାତି ଓ ଜାତି ପ୍ରଭୃତି ସମସ୍ତ ସାମାଜିକ ଅନୁଷ୍ଠାନଗୁଡ଼ିକ ଅଧ୍ୟୟନ କରିଥାଏ । କିନ୍ତୁ ରାଜନୀତି ବିଜ୍ଞାନ କେବଳ ମାତ୍ର ସମାଜର ରାଜନୈତିକ ଦିଗ ସହିତ ସଂପୃକ୍ତ ଏବଂ ଏହା ରାଷ୍ଟ୍ର ଓ ସରକାର ପରି କେତେକ ନିର୍ଦ୍ଦିଷ୍ଟ ରାଜନୈତିକ ଅନୁଷ୍ଠାନକୁ ଅଧ୍ୟୟନ କରିଥାଏ।

(୩) ସମାଜଶାସ୍ତ୍ର ସମସ୍ତ ପ୍ରକାର ସଂଘ ଓ ଅନୁଷ୍ଠାନଗୁଡ଼ିକୁ ଅଧ୍ୟୟନ କରୁଥିବା ସମୟରେ ରାଜନୀତି ବିଜ୍ଞାନ କେବଳ ମାତ୍ର ରାଷ୍ଟ୍ର ଓ ସରକାର ପରି ନିର୍ଦ୍ଦିଷ୍ଟ ପ୍ରକାର ସଂଘ ଓ ସଂଗଠନକୁ ଅଧ୍ୟୟନ କରିଥାଏ।

(୪) ସମାଶାସ୍ତ୍ର ଉଭୟ ଶୃଙ୍ଖଳିତ ଏବଂ ବିଶୃଙ୍ଖଳିତ ସମାଜ ଓ ସଂଗଠନର ଆଲୋଚନା କଲାବେଳେ ରାଜନୀତି ବିଜ୍ଞାନ କେବଳ ଶୃଙ୍ଖଳାବଦ୍ଧ ରାଜନୈତିକ ସଂଗଠନ ଓ ଅନୁଷ୍ଠାନକୁ ବିଶ୍ଳେଷଣ କରିଥାଏ।

(୫) ସମାଜଶାସ୍ତ୍ର ମନୁଷ୍ୟକୁ ଏକ ସାମାଜିକ ପ୍ରାଣୀ ହିସାବରେ ଧରି ନେଇଥାଏ। ମାତ୍ର ରାଜନୀତି ବିଜ୍ଞାନ ମନୁଷ୍ୟକୁ ଏକ ରାଜନୈତିକ ଜୀବ ହିସାବରେ ଧରି ନେଇଥାଏ। ସମାଜବିଜ୍ଞାନ ମନୁଷ୍ୟ କାହିଁକି ଓ କିପରି ଏକ ରାଜନୈତିକ ପ୍ରାଣୀ ଏହାରି ଉପରେ ପର୍ଯ୍ୟବେସିତ ଅଟେ।

(୬) ସମାଜଶାସ୍ତ୍ର ସାମାଜିକ ନିୟନ୍ତ୍ରଣ ସମସ୍ତ ଉପାୟ ତଥା ଅଧ୍ୟୟନ କରିଥାଏ; ମାତ୍ର ରାଜନୀତି ବିଜ୍ଞାନ କେବଳ ମାତ୍ର ରାଷ୍ଟ୍ର ଓ ସରକାରଙ୍କ ଦ୍ଵାରା ସ୍ବୀକୃତିପ୍ରାପ୍ତ ସାମାଜିକ ନିୟନ୍ତ୍ରଣର ମାଧ୍ୟମଗୁଡ଼ିକୁ ଅଧ୍ୟୟନ କରିଥାଏ।

(୭) ସମାଜଶାସ୍ତ୍ର ଏକ ବିକଶିତ ବିଜ୍ଞାନ। ଏହାର ଏକ କ୍ଷୁଦ୍ର ଅତୀତ ରହିଛି; ମାତ୍ର ରାଜନୀତି ବିଜ୍ଞାନର ସୃଷ୍ଟି ଅତି ପୁରୁଣା କାଳରୁ।

(୮) ସମାଜଶାସ୍ତ୍ର ବିଭିନ୍ନ ପ୍ରଥା, ପରମ୍ପରା, ଲୋକନୀତି, ଲୋକନିୟମ ଉପରେ ପ୍ରତିଷ୍ଠିତ। ସମାଜ ଉଭୟ ଓ ଔପଚାରିକ (Formal) ଏବଂ ଅନୌପଚାରିକ (Informal) ନୀତିନିୟମ ସହିତ ସଂପୃକ୍ତ; କିନ୍ତୁ ରାଜନୀତି ବିଜ୍ଞାନ କେବଳ ରାଷ୍ଟ୍ର ଓ ସରକାରଙ୍କ ଦ୍ଵାରା ପ୍ରତିଷ୍ଠିତ ଔପଚାରିକ ନୀତିନିୟମ ସହିତ ସଂଶ୍ଳିଷ୍ଟ।

(୯) ରାଜନୀତି ବିଜ୍ଞାନ ମନୁଷ୍ୟର କେବଳ ସଚେତନିକ କାର୍ଯ୍ୟକଳାପକୁ ଅଧ୍ୟୟନ କରିଥାଏ। ମାତ୍ର ସମାଜ ବିଜ୍ଞାନ ଉଭୟ ସଚେତନିକ ଓ ଅଚୈତନିକ କାର୍ଯ୍ୟକଳାପକୁ ଅଧ୍ୟୟନ କରିଥାଏ।

(୧୦ ) ପ୍ରଫେସର ଗାର୍ଶ୍ଵରଙ୍କ ମତରେ ରାଜନୀତି ବିଜ୍ଞାନ କେବଳ ଗୋଟିଏ ପ୍ରକାର ସାମାଜିକ ସମିତିକୁ ଅଧ୍ୟୟନ କରିଥାଏ। ଏହା ହେଉଛି ରାଷ୍ଟ୍ର; ମାତ୍ର ସମାଜବିଜ୍ଞାନ ସମସ୍ତ ପ୍ରକାର ସମିତିଗୁଡ଼ିକୁ ଅଧ୍ୟୟନ କରିଥାଏ। ସମାଜ ବିଜ୍ଞାନ ଓ ନୃବିଜ୍ଞାନ ମଧ୍ୟରେ ସମ୍ପର୍କ ଓ ପାର୍ଥକ୍ୟମାନ ଆଲୋଚନା କର।

Question ୭।
କିମ୍ବା, ସମାଜଶାସ୍ତ୍ର ଓ ନୂତତ୍ତ୍ବ ଦୁଇ ଯଆଁଳା ଭଉଣୀ ଅଟନ୍ତି-ଆଲୋଚନା କର।
Answer:
ନୃତତ୍ତ୍ଵ ଏକ ସାମାଜିକ ବିଜ୍ଞାନ। ଏହି ସାମାଜିକ ବିଜ୍ଞାନ ମଧ୍ୟ ସମାଜବିଜ୍ଞାନ ପରି ମାନବକୁ ଅଧ୍ୟୟନ କରିଥାଏ। ନୃତତ୍ତ୍ଵ ଇଂରାଜୀ ଶବ୍ଦ Authroplogy ଦୁଇଟି ଇଂରାଜୀ ଶବ୍ଦରୁ ସୃଷ୍ଟି ହୋଇଛି। Authroploseର ଅର୍ଥ ମଣିଷ ଓ Logosର ଅର୍ଥ ଅଧ୍ୟୟନ। ତେଣୁ ବ୍ୟବହାରିକ ଦୃଷ୍ଟିରୁ ଏହାର ଅର୍ଥ ହେଲା ମାନବର ବିଜ୍ଞାନ। ଏହି ନୃତତ୍ତ୍ଵ ମଣିଷର କାର୍ଯ୍ୟବଳୀ ଓ ଅଚରଣକୁ ଅଧ୍ୟୟନ କରିଥାଏ। ଅନେକ ସାଧାରଣ ବିଷୟ ଏ ଦୁଇଟି ସାମାଜିକ ବିଜ୍ଞନାର ପରିସରଭୁକ୍ତ ଅଟେ। ସମାଜ, ସଂସ୍କୃତି, ପରିବାର, ଧର୍ମ ଇତ୍ୟାଦିକୁ ଉଭୟ ଅଧ୍ୟୟନ କରନ୍ତି। ତେଣୁ ଏ. ଏଲ୍‌. କ୍ରୋଏବର୍ (A.L. Koreber)ଙ୍କ ମତରେ “ ସମାଜ ବିଜ୍ଞାନ ଓ ନୃବିଜ୍ଞାନ ଦୁଇଟି ଯାଆଁଳା ଭଉଣୀ। ନୃତିଜ୍ଞାନ କହିଲେ ମାନବର ବିଜ୍ଞାନ କିମ୍ବା ମାନବ ସମ୍ବନ୍ଧରେ ଅଧ୍ୟୟନ ଅଟେ।”

ନୃତତ୍ତ୍ଵ ମୁଖ୍ୟତଃ ତିନି ଭାଗରେ ଭାଗ କରାଯାଇଛି । ସେଗୁଡିକ ହେଲା — (୧) ଶାରୀରିକ (Physical Authropology), ( ୨ ) ପ୍ରାକ୍ ଐତିହାସିକ ନୃତତ୍ତ୍ଵ (Pre-historic Authropology) ଏବଂ (୩) ସାମାଜିକ ସାଂସ୍କୃତିକ ନୃତତ୍ତ୍ଵ (Social d Cultural Anthropology)।

ଶରୀରିକ ନୃତତ୍ତ୍ଵ (Physical Authropology): ଶରୀରିକ ନୃତତ୍ତ୍ଵର ମନୁଷ୍ୟର ଶାରୀରିକ ଲକ୍ଷଣମାନ ଅନୁଧ୍ୟାନ କରାଯାଇଥାଏ। ଏଥ‌ିରେ ମନୁଷ୍ୟର ଶରୀରିକ ଅଶଂମାନ ତୁଳନା କରିବା ଏବଂ ସେମାନଙ୍କର ଆଙ୍ଗୁଠି ଛାପ, ଦେହର ଆକୃତି ଇତ୍ୟାଦି ଅଧ୍ୟୟନ କରାଯାଇଥାଏ । ମନୁଷ୍ୟର ସାମାଜିକ ଜୀବନ ସହ ତା’ର ଶାରୀରିକ ଗଠନ ସମ୍ପର୍କ ବିଷୟରେ ବୁଝାଉଥ‌ିବାରୁ ଏହା କେତକେଶଂରେ ସମାଜବିଜ୍ଞାନ ସହ ସମ୍ପୃକ୍ତ।

ପ୍ରାଗ୍ ଐତିହାସିକ ନୃତତ୍ତ୍ୱ (Pre-historic Authropology) : ପ୍ରତ୍ନତାତ୍ତ୍ଵତକ ନୃତତ୍ତ୍ଵ କିମ୍ବା ପ୍ଲାଗ୍ ଐତିହାସିକ ନୃତତ୍ତ୍ଵ କହିଲେ ମାନବ ସଭ୍ୟତାର ପ୍ରାଚୀନତମ ନମୁନାଗୁଡିକ ବିଭିନ୍ନ ଯୋଜନା ସାହାର୍ଯ୍ୟରେ ପ୍ରକାଶ କରାଯାଇଥାଏ। ସାମାଜିକ ଓ ସାଂସ୍କୃତିକ

ନତତ୍ତ୍ୱ (Social and Cultural Anthropology) : ସମାଜବିଜ୍ଞାନରେ ଯେଉଁସବୁ ତଥ୍ୟ ପରିସର ଅନ୍ତର୍ଭୁକ୍ତ, ସାମାଜିକ ଓ ସାଂସ୍କୃତିକ ନୃତତ୍ତ୍ଵରେ ମଧ୍ୟ ସେହିସବୁ ପରିସରକୁ ଅଧ୍ୟୟନ କରାଯାଇଥାଏ। ସମାଜବିଜ୍ଞାନ ନୃବିଜ୍ଞାନ ଉପରେ ସମ୍ପୂର୍ଣ ନିର୍ଭରଶୀଳ। ସମାଜବିଜ୍ଞାନର ଏ ଐତିହାସିକ ଦିଗ ସାଂସ୍କୃତିକ ନୃତିଜ୍ଞାନ ସହିତ ସମ୍ପୃକ୍ତ। ବର୍ତ୍ତମାନର ସାମାଜିକ ଜୀବନକୁ ବୁଝିବା ପାଇଁ ଆମକୁ ନୂବିଜ୍ଞାନର ସାହାର୍ଯ୍ୟ ନେବାକୁ ପଡିଥାଏ। ସମାଜବିଜ୍ଞାନ ସାମ୍ପ୍ରତିକ ସାଂସ୍କୃତିକ ବିଳମ୍ବନ, ସାଂସ୍କୃତିକ ପରିବର୍ତ୍ତନ ଓ ଅନ୍ୟାନ୍ୟ ସସ୍‌ତ୍ୟୟଗୁଡିକୁ ଗ୍ରହଣ କରିଥାଏ। ସେହିପରି ନୂବିଜ୍ଞାନ ମଧ୍ୟ ସମାଜବିଜ୍ଞାନ ଉପରେ ନିର୍ଭର କରିଥାଏ।

ସାମଞ୍ଜସ୍ୟ (Similarity):
ସମାଜବିଜ୍ଞାନ ଓ ନୃତତ୍ତ୍ଵ ପରସ୍ପର ଉପରେ ନିର୍ଭରଶୀଳ ଅଟନ୍ତି। ଉଭୟ ସମାଜବିଜ୍ଞାନ ଓ ନୃତତ୍ତ୍ଵ ମାନବ ସମାଜକୁ ଅଧ୍ୟୟନ କରିଥାଆନ୍ତି। ମାନବ ସମାଜର କ୍ରିୟାକଳାପ, ବ୍ୟବହାର, ଚାଲିଚଳନ, ନୀତିନୀୟମ ଇତ୍ୟାଦିକୁ ଉଭୟକୁ ବିଜ୍ଞାନ ଅଧ୍ୟୟନ କାରିଥାନ୍ତି। ସେମାନଙ୍କର ଅଧ୍ୟୟନରେ ପରିସର ମଧ୍ୟ-ପରିବାର, ଗୋଷ୍ଠୀ, ସମ୍ପ୍ରଦାୟ, ଜାତି ଆସିଥାଆନ୍ତି। ସାଂସ୍କୃତିକ ନୃତତ୍ତ୍ଵର କେତେକ ଚିନ୍ତା ଓ ଚେତନା ସମାଜବିଜ୍ଞାନରେ ଦେଖାଯାଇଥାଏ। ପ୍ରସିଦ୍ଧ ନୃତତ୍ତ୍ବବିତ୍ ରାଡକ୍ଟିଙ୍ଗ ବ୍ରାଉନ୍ (Redcdiff Browin), ବି. ମାଲିନୋକ୍ସି (B. Malinoswki), ରାଲଫ୍ ୟିନ୍ଧନ୍ (Ralph Winton), ଲୁଇ (Lowie), ରେମଣ୍ଡ ଫାର୍ଥ (Raymond Firth), ମାର୍ଗାରେଟ୍ ମିଡ (Margareat Mead) ଇତ୍ୟାଦି ଯାହାସବୁ ଅଧ୍ୟୟନ କରିଛନ୍ତି ସେସବୁ ସମାଜବିଜ୍ଞାନ ପାଇଁ ସାହାର୍ଯ୍ୟ ଯୋଗାଯାଇଛି। ତେଣୁ ସମାଜବିଜ୍ଞାନ ବିନା ନୃତତ୍ତ୍ଵର ସ୍ଥିତି ଏବଂ ନୃତତ୍ତ୍ଵ ବିନା ସମାଜବିଜ୍ଞାନର ସ୍ଥିତି ନାହିଁ । ନୃତତ୍ତ୍ବ ଓ ସମାଜ ବିଜ୍ଞାନ ଉଭୟ ପରିସ୍ପର ପରିପୂରକ ଅଟନ୍ତି । ଉଭୟେ ସମାଜ, ‘ସଂସ୍କୃତି, ଧର୍ମ, ପରିବାର, ବିବାହ ଓ ସାମାଜିକ ସମୂହକୁ ଅଧ୍ୟୟନ କରିଥାଆନ୍ତି । ସମାଜବିଜ୍ଞାନ ଓ ନୃତତ୍ତ୍ଵ ମଧ୍ଯରେ ଘନିଷ୍ଠ ସମ୍ପର୍କ ବା ସମାଞ୍ଜସ୍ୟ ରହିଛି। ମାତ୍ର ଏହି ସବୁ ସମାଞ୍ଜସ୍ୟ ଥାଇ ମଧ୍ୟ ସମାଜବିଜ୍ଞାନ ଓ ନୃତତ୍ତ୍ଵ ମଧ୍ଯରେ ଅନେକ ପାର୍ଥକ୍ୟ ପରିଲିକ୍ଷିତ ହୋଇଥାଏ। ସେଗୁଠିକ ନିମ୍ନରେ ଅଲୋଚନା କରାଗଲା।

(୧) ସମାଜବିଜ୍ଞାନ ଆଧୁନିକ ଶିଳ୍ପା ସଭ୍ୟତା, ସହରୀ ସଭ୍ୟତା ଓ ଶିକ୍ଷିତ ମାନବ ସମାଜକୁ ଅଧ୍ୟୟନ କରିଥାଏ; କିନ୍ତୁ ନୂତତ୍ତ୍ଵ ପୁରାତନ ସମାଜ। ପ୍ରାଗୈତିହାସିକ ଏବଂ ଶିକ୍ଷା ଓ ସଭ୍ୟତାର ଆଲୋକ ଦେଖୁନଥିବା ସମାଜର ଅଧ୍ୟୟନ କରିଥାଏ।

(୨) ସମାଜବିଜ୍ଞାନ ଜଟିଳ, ଆଧୁନିକ ସମାଜର କୌଣସି ଏକ ସାମାଜିକ ଅନୁଷ୍ଠାନରେ ବାଖ୍ୟ କରିଥାଏ। କିନ୍ତୁ ନୂତତ୍ତ୍ୱବିତ୍‌ମାନେ ପ୍ରାଗୈତିହାସିକ କାଳର କ୍ଷୁଦ୍ର ସମାଜକୁ ବାଖ୍ୟ କରିଥାଆନ୍ତି। ଯେପରି କି ବିବାହ, ପରିବାର ଓ ସାମାଜିକ ପରିବର୍ତ୍ତନ ଇତ୍ୟାଦି।

(୩) ସମାଜବିଜ୍ଞାନ ଏକ ଜଟିଳ ଅବସ୍ଥା ହୋଇଥିବାରୁ ଏହାର ପରିସର ବ୍ୟାପକ ଅଟେ; କିନ୍ତୁ ନୃତତ୍ତ୍ଵ ଏକ କ୍ଷୁଦ୍ର ସମାଜକୁ ଅଧ୍ୟୟନ କରୁଥିବାରୁ ଏହାର ପରିସର କ୍ଷୁଦ୍ର ଅଟେ।

(୪) ସମାଜବିଜ୍ଞାନ ପରୋକ୍ଷ ପଦ୍ଧତି ବା ନିୟମରେ ତଥ୍ୟ ସଂଗ୍ରହ କରିଥାଏ। ପରିସଂଖ୍ୟାନ, ପ୍ରଶାବଳୀ, ସାକ୍ଷାତକାର ପଦ୍ଧତି ପ୍ରୟୋଗ କରି ତଥ୍ୟ ସଂଗ୍ରହ କରିଥାଏ; କିନ୍ତୁ ନୂବିଜ୍ଞାନ ପ୍ରତ୍ୟେକ୍ଷ ପର୍ଯ୍ୟବେକ୍ଷଣ ପଦ୍ଧତିରେ ତଥ୍ୟ ସଂଗ୍ରହ କରିଥାଏ

(୫) ସମାଜବିଜ୍ଞାନ ଐତିହାସିକ ତଥ୍ୟ ଉପରେ ଗୁରୁତ୍ଵ ଦେଇଥାଏ; କିନ୍ତୁ ନୃତତ୍ତ୍ଵ ଏହି ଐତିହାସିକ ତଥ୍ୟ ଉପରେ ଗୁରୁତ୍ଵ ଦେଇ ନଥାଏ।

(୬) ସମାଜବିଜ୍ଞାନକୁ ଆଂଶିକ ଅଧ୍ୟୟନ ବୋଲି କୁହାଯାଇଥାଏ । କାରଣ ଏହା ସମାଜର ଗୋଟିଏ ବିଭାଗ ବା କେତେକ ଅନୁଷ୍ଠାନକୁ ଅଧ୍ୟୟନ କରିଥାଏ; କିନ୍ତୁ ନୂତତ୍ତ୍ୱ ଏକ କ୍ଷୁଦ୍ର ସମାଜକୁ ଅଧ୍ୟୟନ କରୁଥିବାରୁ, ସାମଗ୍ରିକ ଭାବରେ ସମାଜର ଅନୁଶୀଳନ କରିଥାଏ ।

(୭) ସମାଜବିଜ୍ଞାନୀମାନେ ବୃହତ୍ତ ସମାଜକୁ ଅନୁଧ୍ୟାନ କରିଥାଆନ୍ତି, କିନ୍ତୁ ନୃବିଜ୍ଞାନୀମାନେ କ୍ଷୁଦ୍ର ସମାଜକୁ ଅଧ୍ୟୟନ କରିଥାଆନ୍ତି।

(୮) ନୂବିଜ୍ଞାନରେ ସଂଗୃହୀତ ତଥ୍ୟାବଳୀ ଅଳ୍ପ କେତେକଙ୍କ ମତରେ ପ୍ରତିଷ୍ଠିତ; କିନ୍ତୁ ସମାଜବିଜ୍ଞାନ କ୍ଷେତ୍ରରେ ସଂଗୃହୀତ ତଥ୍ୟାବଳୀ ଅପେକ୍ଷାକୃତ ବହୁଳ ଅଧ‌ିକ ସଂଖ୍ୟକ ବ୍ୟକ୍ତିଙ୍କ ମତ ଉପରେ ପର୍ଯ୍ୟବେସିତ।

(୯) ସମାଜବିଜ୍ଞାନ ବର୍ତ୍ତମାନର ସାମାଜିକ ଘଟଣାବଳୀ ଓ କାର୍ଯ୍ୟକଳାପକୁ ଅଧ୍ୟୟନ କରିଥାଏ; ମାତ୍ର ନୃତ୍ତତ୍ଵ ଅତୀତର ସାମାଜିକ ଘଟଣାବଳୀ ଓ ପ୍ରାଚୀନ ମାନବର କାର୍ଯ୍ୟକଳାକୁ ଅଧ୍ୟୟନ କରିଥାଏ।

(୧୦) ସମାଜବିଜ୍ଞାନ ଅପରାଧ, ବାଲ୍ୟ ଅପରାଧ, ଦାରିଦ୍ର ସମସ୍ୟା, ଆତ୍ମହତ୍ୟା, ଯୌତୁକ ପ୍ରଥା, ଅସ୍ପୃଶ୍ୟତା ପ୍ରଭୃତି ଆଧୁନିକ ସାମାଜିକ ସମସ୍ୟାଗୁଡିକୁ ଅଧ୍ୟୟନ କରିବା ସହିତ ଦୂରୀକରଣ ପାଇଁ ପଦକ୍ଷେପମାନ ନେଇଥାଏ; କିନ୍ତୁ ନୂତତ୍ତ୍ଵ ଯଦିଓ ସାମାଜିକ ସମସ୍ୟାଗୁଡିକ ଅଧ୍ୟୟନ କରିଥାଏ ତଥାପି ସେଗୁଡିକର ଦୂରୀକରଣ ନିମିତ୍ତ ପଦକ୍ଷେପମାନ ନେଇ ନଥାଏ।

(୧୧) ସମାଜବିଜ୍ଞାନ ମାନବିକ ଆଚରଣକୁ ସାମାଜିକ ଦୃଷ୍ଟିକୋଣରୁ ବିଚାର କରିଥାଏ; କିନ୍ତୁ ନୁବିଜ୍ଞାନ ବା ମନୋବିଜ୍ଞାନ ମାନବିକ ଆଚରଣକୁ ମାନସିକ ଦୃଷ୍ଟିକୋଣରୁ ବିଚାର କରିଥାଏ। ଉପରୋକ୍ତ ପାର୍ଥକ୍ୟ ସତ୍ତ୍ଵେ ଏହା ସତ୍ୟ ଯେ ଉଭୟ ସମାଜଶାସ୍ତ୍ର ଓ ନୃତତ୍ତ୍ଵ ପରସ୍ପର ନିର୍ଭରଶୀଳ ଏବଂ ପରସ୍ପରକୁ ଗଭୀରଭାବେ ପ୍ରଭାବିତ କରିଥାଆନ୍ତି।

Question ୮।
ସମାଜ ବିଜ୍ଞାନ ସହିତ ରାଜନୀତି ବିଜ୍ଞାନର ସମ୍ପର୍କ ସମ୍ବନ୍ଧରେ ଆଲୋଚନା କର। କିମ୍ବ, ସମାଜବିଜ୍ଞାନ ସହିତ ରାଜନୀତି ବିଜ୍ଞାନ ମଧ୍ୟରେ ପାର୍ଥକ୍ୟ ଉଲ୍ଲେଖ କର।
Answer:
ରାଜନୀତି ବିଜ୍ଞାନ ରାଷ୍ଟ୍ର ଓ ସରକାରଙ୍କୁ ଅଧ୍ୟୟନ କରିଥାଏ। ଏହା ମୁନଷ୍ୟର ରାଜନୈତିକ କାର୍ଯ୍ୟକଳାକୁ ଅଧ୍ୟୟନ କରେ। ଏହା ରାଷ୍ଟ୍ରର ଉତ୍ପରି, ଗଠନ, କ୍ଷମତା, ପ୍ରଭତ୍ତ୍ଵ, ରାଜନୈତିକ ଦଳର କାର୍ଯ୍ୟବଳୀ ଓ ଆଦର୍ଶ ତଥା ନିର୍ବାଚନ ପଦ୍ଧତି ଇତ୍ୟାଦିକୁ ଅଧ୍ୟୟନ କରିଥାଏ। ରାଜନୀତି ବିଜ୍ଞାନର ରାଷ୍ଟ୍ର ସମାଜର କେନ୍ଦ୍ରବିନ୍ଦୁ ହୋଇଥିବାବେଳେ ସମାଜବିଜ୍ଞାନ ରାଷ୍ଟ୍ରକୁ ଏକ ସାମାଜିକ ଅନୁଷ୍ଠାନ ଆଖ୍ୟା ଦେଇଥାଏ। ରାଜନୀତି ବିଜ୍ଞାନ ସମାଜର କେବଳ ଗୋଟିଏ ଦିଗକୁ ଅନୁଶୀଳନ କଲାବେଳେ ସମାଜବିଜ୍ଞାନ ସମାଜର ସମସ୍ତ ଦିଗକୁ ଅନୁଧ୍ୟାନ କରିଥାଏ। ତେଣୁ ରାଜନୀତି ବିଜ୍ଞାନ ସମାଜବିଜ୍ଞାନର ଅଶଂ ଅଟେ। ରାଷ୍ଟ୍ର ଅଧୀନସ୍ଥ ସମସ୍ତ ସାମାଜିକ ସମୂହ, ସାମାଜିକ ଅନୁଷ୍ଠାନଗୁଡିକୁ ଅଧ୍ୟୟନ କରିବା ରାଜନୀତି ବିଜ୍ଞାନର ପ୍ରଧାନ କାର୍ଯ୍ୟ ଅଟେ। ବିଭିନ୍ନ ଆଇନ୍, ରାଜନୈତିକ ଦଳ, ସମ୍ବିଧାନ, ସରକାରୀ ଦଳରେ ପରିଚାଳନା ପ୍ରଭୃତି ରାଜନୀତି ବିଜ୍ଞନାର ପରରସରଭୁକ୍ତ ଅଟେ।

ସାମଞ୍ଜସ୍ୟ (Similarity):
ରାଜନୀତି ବିଜ୍ଞାନ ଓ ସମାଜିକ ପରସ୍ପର ଅଙ୍ଗାଙ୍ଗୀ ଭାବରେ ଜଡିତ। ବହୁ ପ୍ରାଚୀନ କାଳରୁ ଏହି ଦୁଇଟି ବିଜ୍ଞାନ ମଧ୍ୟରେ ନିବିଡ ସମ୍ପର୍କ ରହିଛି। ରାଜନୀତି ବିଜ୍ଞାନ ବିନା ସମାଜବିଜ୍ଞାନ ନରର୍ଥକ ଏବଂ ସମାଜବିଜ୍ଞାନ ବିନା ରାଜନୀତି ବିଜ୍ଞାନ ମୂଲ୍ୟହୀନ ଅଟେ। ତେଣୁ ରାଜୀନିତି ବିଜ୍ଞାନ ଓ ସମାଜବିଜ୍ଞାନ ପରସ୍ପର ନିର୍ଭରଶୀଳ। ସମାଜବିଜ୍ଞାନକୁ ଛାଡିଦେଇ ରାଜନୀତି ବିଜ୍ଞାନ ତିଷ୍ଠିପାରେ ନାହିଁ କିମ୍ବା ରାଜନୀତି ବିଜ୍ଞାନ ବ୍ୟତିରେକ ସମାଜବିଜ୍ଞାନ ଅଧୟନ ଅସମ୍ଭବ ହୋଇପଡେ। ଗିନ୍ସବର୍ଗ (Ginsberg)ଙ୍କ ମତରେ, “ ଐତିହାସିକ ଦୃଷ୍ଟିକୋଣରୁ ସମାଜବିଜ୍ଞାନର ମୂଳ ଉତ୍ସ ରାଜନୀତି ବିଜ୍ଞାନ, ଇତିହାସ ଓ ଦର୍ଶନ ମଧ୍ୟରେ ରହିଛି ।” ପ୍ଲାଟୋ (Plato)ଙ୍କ ରିପବ୍ଲିକ (Republic) ବା ଆରିଷ୍ଟୋଟଲ (Aristole} ଯେଉଁ ପଲିଟକ୍ସ ( Politics) ଗ୍ରନ୍ଥ ରଚନା କରିଛନ୍ତି, ସେଗୁଡିକ ଉଚ୍ଚ ସାମାଜିକ ଚେତନା ଉପରେ ଆଧାରିତ। ରାଜନୈତିକ କ୍ରିୟାକଳାପ ସାମାଜିକ ଜୀବନର ଅଂଶ ବିଶେଷ। ଏଥୁରୁ କରାଯାଏ ଯେ ସମାଜବିଜ୍ଞାନ ଓ ରାଜନୀତି ବିଜ୍ଞାନ ମଧ୍ୟରେ ଏକ ସାମଞ୍ଜସ୍ୟ ରହିଛି । ଯଦି ଆମର ସମାଜବିଜ୍ଞାନ ସମ୍ପର୍କରେ ଜ୍ଞାନ ନଥୁବ, ତେବେ ସମାଜରେ ଚାଲିଥିବା ରାଜନୀତିକୁ ଠିକ୍ ରୂପେ ବୁଝି ପାରିବା ନାହିଁ। ରାଷ୍ଟ୍ର ସମ୍ବିଧାନ ବା ନାଗରିକ ଅଧିକାର ସେହି ସମାଜ ପୃଷ୍ଟଭୂମିରେ ହିଁ ଜନ୍ମ ନେଇଥାଏ।

ରାଜନୀତି ବିଜ୍ଞାନ ଓ ସମାଜବିଜ୍ଞାନ ସମନ୍ଵୟରେ ଏକ ନୂତନ ବିଜ୍ଞାନର ସୃଷ୍ଟି ହୋଇଛି। ଯହାକି ରାଜନୈତିକ ସମାଜବିଜ୍ଞାନ (Poltical Sociology) ନାମରେ ନାମିତ। ଆଇନ୍, ପ୍ରଥା, ପରମ୍ପରା, ରାଜନୀତି, ରାଷ୍ଟ୍ରର କ୍ଷମତା, ପ୍ରଭୂତ୍ଵ ନେତୃତ୍ଵ, ଜାତି ଇତ୍ୟାଦି ଉଭୟ ସମାଜବିଜ୍ଞାନୀ ଓ ରାଜନୀତି ବିଜ୍ଞାନୀ ଅଧ୍ୟୟନ କରିଥାଆନ୍ତି। ରାଜନୀତି ମନୁଷ୍ୟର ରାଜନୈତିକ ଜୀବନକୁ ଅଧ୍ୟୟନ କରେ। ଏହା ମନୁଷ୍ୟର ସାମାଜିକ ଜୀବନର ଅଂଶ ବିଶେଷ। ଏଥୁରୁ ଜଣାଯାଏ ରାଜନୀତି ବିଜ୍ଞାନ ସମାଜବିଜ୍ଞାନର ପରିସରଭୁକ୍ତ ସୃଷ୍ଟି। ରାଜନୈତିକ ସମସ୍ୟାଗୁଡିକର ମଧ୍ୟ ସାମାଜିକ ଦିଗ ରହିଛି। ସେହି ଦିଗମାନ ଜାଣିବାକୁ ହେଲେ ସମାଜବିଜ୍ଞାନ ସମ୍ବନ୍ଧରେ ଧାରଣା ଥିବା ଆବଶ୍ୟକ।

ସମାଜବିଜ୍ଞାନ ଓ ରାଜନୀତି ବିଜ୍ଞାନ ମଧ୍ୟରେ ସାମଞ୍ଜସ୍ୟ ଥିବାରୁ କମ୍‌ (Comte), କାଟଲିନ୍ (Catline}, ସ୍ପେନସର (Spencer) ଇତ୍ୟାଦି ବିଦ୍ଵାନମାନେ ସମାଜବିଜ୍ଞାନ ଓ ରାଜନୀତି ବିଜ୍ଞାନକୁ ଦୁଇଗୋଟି ବିଷୟ ରୂପେ ଗ୍ରହଣ କରିନାହାନ୍ତି। ଜଣେ ରାଜନୀତି ବିଜ୍ଞାନୀ ସମାଜବିଜ୍ଞାନୀ ହେବା ପାଇଁ ବାଧ, କାରଣ ଉଭୟ ବିଜ୍ଞାନୀ ମଧ୍ୟରେ ସାମଞ୍ଜସ୍ୟ ଥ‌ିବାରୁ କୌଣସି ରାଷ୍ଟ୍ରର ନୀତି, ନିୟମ, ପ୍ରଥା, ପରମ୍ପରା, ଆଚାର, ବିଚାର, ଉପରେ ନିର୍ଭରଶୀଳ। ଯାହାକି ଏଗୁଡିକ ସମାଜବିଜ୍ଞାନର ଅଂଶବିଶେଷ। ଉଦାହରଣସ୍ୱରୂପ ପରିବାର ସମାଜର ଏକ ସ୍ଥାୟୀ ଅନୁଷ୍ଠାନ ଅଟେ । କିନ୍ତୁ ଯେତେବେଳେ ବିବାହ, ବିବାହ ସମ୍ପର୍କୀୟ ଆଇନ୍ ଇତ୍ୟାଦି କଥା ଉଠେ ସେତେବେଳେ ତାହା ରାଜନୀତି ବିଜ୍ଞାନର ଅଂଶବିଶଷ ହୋଇଥାଏ। ତେଣୁ ସମାଜବିଜ୍ଞାନ ଓ ରାଜନୀତି ବିଜ୍ଞାନ ଉପରେ ନିର୍ଭରଶୀଳ ଅଟେ। କେତେକ ବିଷୟ ଅଛି ଯାହା ଉଭୟ ସମାଜବଜ୍ଞାନ ଓ ରାଜନୀତି ବିଜ୍ଞାନୀ ଅଧ୍ୟୟନ କରନ୍ତି । ଯଥା ଭୋଟ, ଯୁଦ୍ଧ ପ୍ରଚାର, ବିପ୍ଲବ, କ୍ଷମତା ଓ ଲୋକମତ ପ୍ରଭୃତି ବିଜ୍ଞାନର ପରିସରଭୁକ୍ତ ଅଟେ। ସାମ୍ପ୍ରଦାୟିକ ଦଙ୍ଗା, ଭାତିଭେଦ ପ୍ରଥା ଇତ୍ୟାଦି ସାମାଜିକ ସମସ୍ୟା ହେଲେ ମଧ୍ୟ ଏହା ରାଜନୀତି ପ୍ରାଣୋଦିତ।

ପାର୍ଥକ୍ୟ (Difference} :
ସମାର୍ଜବିଜ୍ଞାନ ସହ ରାଜନୀତି ଯେତେ ଘନିଷ୍ଠ ସମ୍ପର୍କ ଥିଲେ ମଧ୍ୟ ଏ ଦୁହେଁ ପରସ୍ପରଠାରୁ ପୃଥକ୍ ଅଟନ୍ତି। ସେମାନଙ୍କ ମଧ୍ୟରେ ଯେଉଁ ସବୁ ପାର୍ଥକ୍ୟ ପରିଲିକ୍ଷିତ ହୁଏ ତାହା ନିମ୍ନରେ ଆଲୋଚନା କରାଗଲା।

1. ସମାଜବିଜ୍ଞାନ ସମଗ୍ର ସାମାଜିକ ଅଧ୍ୟୟନ କରିଥାଏ; କିନ୍ତୁ ରାଜନୀତି ବିଜ୍ଞାନ ରାଷ୍ଟ୍ର ଓ ସରକାରକୁ ଅଧ୍ୟୟନ କରିଥାଏ ।
2. ସମାଜବିଜ୍ଞାନ କୁହେ ମନୁଷ୍ୟ ଏକ ସାମାଜିକ ପ୍ରାଣୀ; କିନ୍ତୁ ରାଜନୀତି ବିଜ୍ଞାନ କହେ ମନୁଷ୍ୟ ଏକ ରାଜନୈତିକ ପ୍ରାଣୀ।
3. ସମାଜବିଜ୍ଞାନ ଏକ ନୂତନ ବିଜ୍ଞାନ ଅଟେ; କିନ୍ତୁ ରାଚନୀତି ବିଜ୍ଞାନ ଏକ ପୁରାତନ ବିଜ୍ଞାନ ଅଟେ।
4. ସମାଜବିଜ୍ଞାନର ପରିସର ବ୍ୟାପକ ଅଟେ; କିନ୍ତୁ ରାଜନୀତି ବିଜ୍ଞାନର ପରିସର ସଂକ୍ଷିପ୍ତ ଅଟେ।
5. ସମାଜବିଜ୍ଞାନ ଉଭୟ ଶୃଙ୍ଖଳିତ ଓ ବିଶୃଙ୍ଖଳିତ ସମାଜକୁ ଅଧନ କରେ; କିନ୍ତୁ ରାଜୀନତି ବିଜ୍ଞାନ କେବଳ ଶୃଙ୍ଖଳିତ ସମାଜକୁ ଅଧ୍ୟୟନ କରିଥାଏ।
6. ସମାଜବିଜ୍ଞାନ ସାମ୍ପ୍ରତିକ ସମାଜର ଘଟଣା, ଆଚାର ବିଚାର ଓ ରୀତିନୀତି ଅଲୋଚନା କରିଥାଏ। ଭବିଷ୍ୟତରେ ସମାଜ କି ଆକାର ଧାରଣ କରିବ ଏବଂ କିଭଳି ପରିବର୍ତ୍ତନ ହେବ ସେ ସବୁକୁ ଏହା ବିଚାର କରେ ନାହିଁ; କିନ୍ତୁ ରାଜନୀତି ବିଜ୍ଞାନ ରାଷ୍ଟ୍ରନୀତି ଓ ଶାସନ ବ୍ୟବସ୍ଥା ଭବିଷ୍ୟତରେ କିପାର ଉତ୍ତମ ରୂପେ ଚାଲିପାରିବ ସେ ସଂକ୍ରାନ୍ତରେ ମନ୍ତବ୍ୟ ଦେଇଥାଏ।
7. ଅଗଷ୍ଟ କମ୍‌ ସମାଜବିଜ୍ଞାନ ଜନକ ଅଟନ୍ତି; କିନ୍ତୁ ଆରିଷ୍ଟୋଟଲ୍ ରାଜନୀତି ବିଜ୍ଞାନର ଜନକ ଅଟନ୍ତି।
8. ସମାଜବିଜ୍ଞାନ କ’ଣ ସହିତ କିପରି ଓ କାହିଁକି ପ୍ରଶ୍ନର ଉତ୍ତର ଦେଇଥାଏ; କିନ୍ତୁ ରାଜନୀତି ବିଜ୍ଞାନ କେବଳ କ’ଣ ପ୍ରଶ୍ନର ଉତ୍ତର ଦେଇଥାଏ।
9. ସମାଜବିଜ୍ଞାନର ତଥ୍ୟାବଳୀ ଅନେଙ୍କାଶଂରେ ଅନୁଭାବ୍ୟ (empiric) ଅଟେ; କିନ୍ତୁ ରାଜନୀତି ବିଜ୍ଞାନର ତଥ୍ୟାବଳୀ ତାନ୍ତ୍ରିକ (theoretical) ଅଟେ।
10. ସମାଜ ସମାଜବିଜ୍ଞାନ ଏକ ସାଧାରଣ ବିଜ୍ଞାନ ଅଟେ; କିନ୍ତୁ ରାଜୀନତି ବିଜ୍ଞାନ ଏକ ସ୍ବତନ୍ତ୍ର ବିଜ୍ଞାନ ଅଟେ।
11. ସମାଜବିଜ୍ଞାନ ବିଭିନ୍ନ ପ୍ରଥା, ପରମ୍ପରା, ଲୋକରୀତି, ଲୋକନିୟମ ଓ ପ୍ରତିମାନ ଉପରେ ପ୍ରତିଷ୍ଠିତ; କିନ୍ତୁ ରାଜନୀତି ବିଜ୍ଞାନ କେବଳ ରାଷ୍ଟ୍ର ଓ ସରକାରଙ୍କ ଦ୍ଵାରା ପ୍ରତିଷ୍ଠିତ ହୋଇଥାଏ।

Question ୯।
ସମାଜ ବିଜ୍ଞାନ ଏବଂ ଇତିହାସ ମଧ୍ୟରେ ଥିବା ସମ୍ପର୍କକୁ ବିଶ୍ଳେଷଣ କର।
Answer:
ସମାଜବିଜ୍ଞାନ ଓ ଇତିହାସ ପରସ୍ପର ଅତି ଘନିଷ୍ଠ ଭାବେ ଜଡିତ। ସମୟ ସମାଜବିଜ୍ଞାନୀ ଐତିହାସିକ ମାନବ ସମାଜକୁ ଅଧ୍ୟୟନ କରିଥାଆନ୍ତି; ମାତ୍ର ସାର୍ବଜନୀନ ବର୍ତ୍ତମାନର ମନୁଷ୍ୟ ଓ ସେମାନଙ୍କର କାର୍ଯ୍ୟାବଳୀଗୁଡିକୁ ଅଧ୍ୟୟନ କରିଥାଏ। ଇତିହାସ ଅତୀତର ଘଟଣାବଳୀଗୁଡିକୁ ଅନୁଶୀଳନ କରିଥାଏ, ଯେଉଁଥରେ ମାନବ ସମାଜର ସାମାଜିକ, ରାଜନୈତିକ ଓ ଅର୍ଥନୈତିକ କାର୍ଯ୍ୟବଳୀମାନ ଅଧ୍ୟୟନ କରିଥାଏ। ତେଣୁ ସମାଜଶାସ୍ତ୍ର ଇତିହାସଠାରୁ ଅଲଗା ହୋଇପାରେ ନାହିଁ କି ଇତିହାସ ସମାଜଶାସ୍ତ୍ରଠାରୁ ଅଲଗା ହୋଇପାରରେ ନାହିଁ। ତେଣୁ ଜି. ଇ. ହୋବାର୍ଡ (GE. Howood)ଙ୍କ ମତରେ, “ଇତିହାସ ହେଉଛି ଅତୀତର ସମାଜଶାସ୍ତ୍ର ଏବଂ ସମାଜଶାସ୍ତ୍ର ହେଉଛି ବର୍ତମାନର ଇତିହାସ (History is the past sociology and sociology is the present history) ।” ଜନ୍ ସେଲି (John Seely)ଙ୍କ ମତରେ, “ ସମାଜଶାସ୍ତ୍ର ବ୍ୟତୀତ ଇତହିହାସ ଅଧ୍ୟୟନରେ କୌଣସି ଫଳ ନାହିଁ ଏବଂ ଇତିହାସ ବ୍ୟତୀତ, ସମାଜବିଜ୍ଞାନର ମୂଳ ନାହିଁ ।” (History without sociology has not frunt sociology without history has no root)

ସାମଞ୍ଜସ୍ୟ (Similarity):
ଯେହେତୁ ଇତିହାସ ରାଜନୈତିକ, ଅର୍ଥନୈତିକ, ସାମାଜିକ ଘଟଣାବଳୀ ଉପରେ ଆଲୋକପାତ କରିଥାଏ, ଅତୀତର ଘଟଣାର କାରଣ ଓ ଫଳାଫଳ ଉପରେ ଅଧ୍ୟୟନ କରିଥାଏ, ଇତିହାସ ଅତୀତର ଲୋକମାନଙ୍କର ଚାଲିଚଳନ ବ୍ୟବହାର, ରାଜନୀତିକୁ ଆଧାର କରି ସମାଜବିଜ୍ଞାନୀ ବର୍ତ୍ତମାନର ସମାଜକୁ ଖୁବ୍ ଭଲ ଭାବରେ ଅଧ୍ୟୟନ କରିଥାଏ। ଉଦାହରଣ ସ୍ଵରୂପ ବର୍ତ୍ତମାନ ପରିସ୍ଥିତିରେ ଧର୍ମ, ପରିବାର ତଥା ବିବାହ ଆଦି ଅନୁଷ୍ଠାନର ସାମାଜିକ ଗୁରୁତ୍ବର ଅଧ୍ୟୟନ ପାଇଁ ଏସବୁ ଅନୁଷ୍ଠାନର ଉତ୍ପତ୍ତି ବିଷୟରେ ଜାଣିବା ଆବଶ୍ୟକ। ଇତିହାସ ବର୍ତ୍ତମାନ ଅତୀତର ସାମାଜିକ ଘଟଣାବଳୀ, ଅର୍ଥନୈତିକ କାର୍ଯ୍ୟକଳାପ ଓ ସାଂସ୍କୃତିକ ଜୀବନ ଧାରାଗୁଡିକ ସମୀକ୍ଷା କରିବାରେ ବ୍ୟସ୍ତ।

ଏହିପରି ଭାବରେ ଇତିହାସ ଓ ସମାଜବିଜ୍ଞାନ ଖୁବ୍ ନିକଟତର। ଉଭୟ ସମାଜବିଜ୍ଞାନ ଓ ଇତିହାସ ସଭ୍ୟତା ଓ ସଂସ୍କୃତି ଉପରେ ଅଧ୍ୟୟନ କରିଥାଆନ୍ତି। ମାତ୍ର ବିଜ୍ଞାନରେ ଐତିହାସିକ ପଦ୍ଧତିରେ ବହୁତ ବ୍ୟବହାର କରାଯାଇଛି। ଯଥା — ଦୁର୍ଖମଙ୍କର ଅତ୍ମହତ୍ୟା, କାର୍ଲମାକ୍ସଙ୍କ ଶ୍ରେଣୀ ସଂଘର୍ଷ ଇତ୍ୟାଦିରୁ ଇତିହାସ ବିଷୟରେ ସ୍ପଷ୍ଟ ଜଣାପଡେ। ଉଭୟ ସମାଜବିଜ୍ଞାନ ଓ ଇତିହାସ ସଭ୍ୟତା ଓ ସଂସ୍କୃତି ଉପରେ ଅଧ୍ୟୟନ କରିଥାଆନ୍ତି; ମାତ୍ର ବିଜ୍ଞାନରେ ଐତିହାସିକ ପଦ୍ଧତିରେ ବହୁତ ବ୍ୟବହାର କରାଯାଇଛି। ଯଥା ଦୁର୍ଖମଙ୍କର ଆତ୍ମହତ୍ୟା, କାର୍ଲମାର୍କ୍ସଙ୍କର ଶ୍ରେଣୀ ସଂଘର୍ଷ ଇତ୍ୟାଦିରୁ ଇତିହାସ ବିଷୟରେ ସ୍ପଷ୍ଟ ଜଣାପଡେ। ଉଭୟ ସମାଜବିଜ୍ଞାନ ଓ ଇତିହାସ ପରସ୍ପର ପରିପୂରକ ଓ ନିର୍ଭରଶୀଳ ଅଟନ୍ତି। ସମାଜବିଜ୍ଞାନ ବ୍ୟତିରେକ ଇତିହାସର ମୂଲ୍ୟ କିଛି ନାହିଁ ତଥା ଇତିହାସ ବିନା ସମାଜବିଜ୍ଞାନ ଅଧ୍ୟୟନ ଅସମ୍ଭବ। ସେଥ‌ିପାଇଁ କୁହାଯାଇଛି ସମାଜବିଜ୍ଞାନ ବିନା ଇତିହାସ ଅଧ୍ୟୟନ ଅମମ୍ଭବ ନିଷ୍ପଭି ପୁଣି ଇତିହାସ ବିନା ସମାଜବିଜ୍ଞାନର କୌଣସି ଅସ୍ତିତ୍ଵ ନାହିଁ ।

ସମାଜବିଜ୍ଞାନ ଇତିହାସକୁ ମଧ୍ୟ ଅନୁକରଣ କରେ। ବିଭିନ୍ନ ସାମାଜିକ ସମସ୍ୟା ଓ ଘଟଣାବଳୀ ମଧ୍ୟରୁ ଐତିହାସିକ ଗୁରୁତ୍ବପୂର୍ଣ୍ଣ ସିଦ୍ଧାନ୍ତଗୁଡିକୁ ଖୋଜିପାଏ। ତେଣୁ ସମାଜବିଜ୍ଞାନର ପୃଷ୍ଠଭୂମିରେ ଇତିହାସକୁ ହିଁ ଅଧ୍ୟୟନ କରାଯାଏ। କାର୍ଲମାର୍କ୍ସଙ୍କର ରଚନାଗୁଡିକୁ ଏକାଧାରାରେ ଇତିହାସ ଓ ସମାଜବିଜ୍ଞାନ ଉପରେ ଆଧାରିତ। କେତେକ ପ୍ରସିଦ୍ଧ ଐତିହାସକୁ ମଧ୍ୟ ସମାଜବିଜ୍ଞାନୀ କୁହାଯାଇଥାଏ। ଯଥା – ଆନୋଇଡ ଟଏନବି (Arnold Toynbee), ଓସ୍ୟାଲଡ୍ ସେଙ୍ଗଲର୍ (Oswaldsengler) ଇତ୍ୟାଦି ଐତିହାସିକ ସମାଜବିଜ୍ଞାନ (Historical Sociology) ଏବଂ ସମାଜ ବୈଜ୍ଞାନିକ ଇତିହାସ (Sociology History) ଏହି ଦୁଇ ବିଭାଗ ବର୍ତ୍ତମାନ ଇତିହାସ ଓ ସମାଜବିଜ୍ଞାନର ନୂତନ ଓ ସ୍ଵତନ୍ତ୍ର ଅଧ୍ୟୟନ ଭାବରେ ବେଶ ପରିଚିତ । ତେଣୁ ହାର୍ଡ ଯାହା ମତ ଦେଇଛନ୍ତି ତାହା ହେଉଛି ଇତିହାସ ହେଉଛି ଅତୀତର ସମାଜବିଜ୍ଞାନ ଓ ସମାଜବିଜ୍ଞାନ ହେଉଛି ବର୍ତ୍ତମାନ ଇତିହାସ। ତାହା ଯଥାର୍ଥ ଅଟେ।

ପାର୍ଥକ୍ୟ (Difference) :
ସମାଜବିଜ୍ଞାନ ଇତିହାସ ମଧ୍ଯରେ ଯେତେ ଘନିଷ୍ଠତା ଥିଲେ ସେମାନଙ୍କ ମଧ୍ୟରେ ଅନେକଗୁଡିଏ ପାର୍ଥକ୍ୟ ପରିଲିକ୍ଷିତ ହୋଇଥାଏ। ସେଗୁଡ଼ିକ ନିମ୍ନରେ ଆଲୋଚନା କରାଗଲା।

1. ସମାଜବିଜ୍ଞାନ ବର୍ତ୍ତମାନର ସମାଜରୁ ଅନୁଧ୍ୟାନ କରିଥାଏ; କିନ୍ତୁ ଇତିହାସ ଅତୀତ ସମାଜକୁ ଅନୁଧ୍ୟାନ କରିଥାଏ।
2. ସମାଜବିଜ୍ଞାନର ପରିସର ବ୍ୟାପକ ହୋଇଥାଏ; କିନ୍ତୁ ଇତିହାସର ପରିସର କ୍ଷୁଦ୍ର ହୋଇଥାଏ।
3. ସମାଜବିଜ୍ଞାନ ଏକ ନୂତନ ବିଜ୍ଞାନ ଅଟେ; କିନ୍ତୁ ଇତିହାସ ଏକ ସ୍ଵତନ୍ତ୍ର ବିଜ୍ଞାନ ଅଟେ।
4. ସମାଜବିଜ୍ଞାନ ଏକ ସାଧାରଣ ବିଜ୍ଞାନ ଅଟେ; କିନ୍ତୁ ଇତିହାସ ଏକ ସ୍ଵତନ୍ତ୍ର ବିଜ୍ଞାନ ଅଟେ।
5. ସମାଜବିଜ୍ଞାନ ବିଶ୍ଳେଷଣ ପର୍ଯ୍ୟାଲୋଚନା ଉପରେ ଗୁରୁତ୍ବ ଦିଏ; କିନ୍ତୁ ଇତିହାସ ଘଟଣାର ବର୍ଣ୍ଣନା ଉପରେ ଗୁରୁତ୍ଵ ଦେଇଥାଏ।
6. ସମାଜବିଜ୍ଞାନ ଉଭୟ ଗୁଣାତ୍ମକ ଓ ପରିମାଣାତ୍ମକ ପଦ୍ଧତିରେ ପ୍ରୟୋଗ କରେ, କିନ୍ତୁ ଇତିହାସ କେବଳ ଗୁଣାତ୍ମକ ପଦ୍ଧତିର ପ୍ରୟୋଗ କରିଥାଏ।
7. ସମାଜବିଜ୍ଞାନ ପ୍ରତ୍ୟେକ ଯୁଦ୍ଧ, ବିପ୍ଳବକୁ ଗୁରୁତ୍ଵ ଦେଇ ନ ଥାଏ। ଏହା ଯୁଦ୍ଧ ବିପ୍ଳବକୁ ସାଧାରଣ ଭାବେ ଅଧ୍ୟୟନ କରିଥାଏ; କିନ୍ତୁ ଇତିହାସ ପ୍ରତ୍ୟେକ ଯୁଦ୍ଧକୁ ଗୁରୁତ୍ଵ ଦେଇ ସ୍ଵତନ୍ତ୍ର ରୂପେ ଅଧ୍ୟୟନ କରିଥାଏ।
8. ମାଜବିଜ୍ଞାନ ଦୃଷ୍ଟିକୋଣ ସାଧାରଣ ହୋଇଥାଏ; କିନ୍ତୁ ଇତିହାସ ଦୃଷ୍ଟିକୋଣ ସ୍ଵତନ୍ତ୍ର ହୋଇଥାଏ।
9. ସମାଜବିଜ୍ଞାନ ପର୍ଯ୍ୟବେକ୍ଷଣ ଅନୁସନ୍ଧାନ, ପରୀକ୍ଷଣ ଓ ତଥ୍ୟ ସଂଗ୍ରହ ଉପରେ ଗୁରୁତ୍ଵ ଦିଏ। ସମାଜବିଜ୍ଞାନ ନିଜେ ବିଭିନ୍ନ ଅଞ୍ଚଳରେ ଅବସ୍ଥାନ କରି ପ୍ରତ୍ୟେକ୍ଷ ବା ପରୋକ୍ଷ ଭାବେ ତଥ୍ୟ ସଂଗ୍ରହ କରିଥାଏ। କିନ୍ତୁ ଇତିହାସ ଶିଳାଲିପି, ସ୍ତୂପ ଓ ସଭ୍ୟତାର ଭଗ୍ନାଂବିଶେଷରୁ ତଥ୍ୟ ସଂଗ୍ରହ କରେ।
10. ସମାଜବିଜ୍ଞାନର ପରୀକ୍ଷା କରିବା ସମ୍ଭବପରେ ହୋଇଥାଏ। କାରଣ ଏହା ବର୍ତ୍ତମାନକୁ ଅଧ୍ୟୟନ କରିଥାଏ; କିନ୍ତୁ ଇତିହାସ ଯେହେତୁ ଅତୀତ ଘଟଣାବଳୀକୁ ଅଧ୍ୟୟନ କରିଥାଏ, ସେଥୁପାଇଁ ଏହାର ପରୀକ୍ଷା କରିବା ସମ୍ଭବପରେ ହୋଇ ନ ଥାଏ।
11. ସମାଜବିଜ୍ଞାନ ବ୍ୟକ୍ତିକୁ ଉପେକ୍ଷା କରି ସମାଜକୁ ପ୍ରାଧାନ୍ୟ ଦେଇଥାଏ; କିନ୍ତୁ ଇତିହାସ ବ୍ୟକ୍ତି ବିଶେଷକୁ ଗୁରୁତ୍ଵ ଦେଇଥାଏ।
12. ସମାଜବିଜ୍ଞାନ ତା’ର ଅଧ୍ୟୟନ ମାର୍ଗ ନିଜେ ପ୍ରସ୍ତୁତ କରେ । ମାନବିକ ଘଟଣାବଳୀରୁ ଏହା ସମାଜତାନ୍ତ୍ରିକ ଦୃଷ୍ଟିରୁ ଦେଖେ। ତା’ ଦୃଷ୍ଟିରେ ଏହି ଘଟଣାବଳୀ ମନୁଷ୍ୟର ସାମାଜିକ ସମ୍ପର୍କର ପରିଣାମ; କିନ୍ତୁ ଇତିହାସ ମାନବିକ ଘଟଣା ସମୂହର କଳାନୁକ୍ରମିକ ବିବରଣୀମାନ ଦିଏ।
13. ସମାଜବିଜ୍ଞାନ ବସ୍ତୁ ନିରପେକ୍ଷ ଅଟେ; କିନ୍ତୁ ଇତିହାସ ବସ୍ତୁମୂଳକ ଅଟେ।

Question ୧୦।
ସମାଜବିଜ୍ଞାନ ଓ ଅର୍ଥଶାସ୍ତ୍ର ମଧ୍ୟରେ ସମ୍ପର୍କ ଓ ପାର୍ଥକ୍ୟ ବିଶ୍ଳେଷଣ କର।
Answer:
ଅର୍ଥନୀତି ଏକ ସାମାଜିକ ବିଜ୍ଞାନ। କେତେକ ଅର୍ଥନୀତିକ କୁହନ୍ତି “ଅର୍ଥନୀତି ହେଉଛି ସମ୍ପଦ ବିଜ୍ଞାନ। ଅନ୍ୟ କେତେକ ଅର୍ଥନୀତିଜ୍ଞଙ୍କ ମତରେ ଅର୍ଥନୀତି ହେଉଛି ଜନମଙ୍ଗଳକାରୀ ବିଜ୍ଞାନ।” ଅର୍ଥନୀତିରେ ମଣିଷର ଅର୍ଥନୈତିକ କ୍ରିୟାକଳାପକୁ ବିଚାର ଓ ଆଲୋଚନା କରାଯାଏ। ଏହି ଅର୍ଥନୈତିକ କାର୍ଯ୍ୟକଳାପ, ସାମାଜିକ କାର୍ଯ୍ୟକଳାପର ଅଂଶବିଶେଷ ଅଟେ। ସମାଜରେ ଉତ୍ପାଦନ, ବିତରଣ, ବଣ୍ଟନ, ବୃଷ୍ଟି ଓ ଅର୍ଥ ଉତ୍ପାଦନ ଇତ୍ୟାଦି ଅର୍ଥନୀତିର ଅନ୍ତର୍ଗତ। ମଣିଷର ଚାହିଦା ବା ଆବଶ୍ୟକତା ତା’ର ପୂରଣ କରିବାର ପ୍ରଣାଳୀକୁ ଅର୍ଥନୀତି ଅଧ୍ୟୟନ କରେ। ଅର୍ଥନୀତି ଓ ସମାଜବିଜ୍ଞାନ ପରସ୍ପରର ଖୁବ୍ ନିକଟବର୍ତୀ ଅଟନ୍ତି । ଏହି ଦୁଇ ସାମାଜିକ ବିଜ୍ଞାନ ଖୁବ୍ ଘନିଷ୍ଠ ଅଟନ୍ତି।

ସାମଞ୍ଜସ୍ୟ (Similarity) :
ଅର୍ଥନୀତି ଓ ସମାଜବିଜ୍ଞାନ ପରସ୍ପର ନିର୍ଭଶୀଳ ଅଟନ୍ତି। ଅର୍ଥନୀତି ଓ ସମାଜବିଜ୍ଞାନ ପରସ୍ପର ପରିପୂରକ, ଅର୍ଥାତ୍ ଅର୍ଥନୀତି ବିନା ସମାଜବିଜ୍ଞାନର ଅଧ୍ୟୟନ ଅସମ୍ଭବ ଓ ସମାଜବିଜ୍ଞାନ ବିନା ଅର୍ଥନୀତି ଅଧ୍ୟୟନ ଅସମ୍ଭବ ଅଟେ। ମନୁଷ୍ୟର ଅର୍ଥନୈତିକ କାର୍ଯ୍ୟକଳାପ ବିଷୟରେ ଅଧ୍ୟୟନ କରିବାକୁ ହେଲେ ସମାଜବିଜ୍ଞାନୀ ଅର୍ଥନୀତିର ସାହାଯ୍ୟ ନେଇଥାଏ। ଏହି ଅର୍ଥନୈତିକ ଦିଗ ସମ୍ପୂର୍ଣ୍ଣ ରୂପେ ସମାଜବିଜ୍ଞାନ ଉପରେ ନିର୍ଭର କରେ। ଅର୍ଥନୈତିକ କାର୍ଯ୍ୟକଳାପଗୁଡ଼ିକୁ ସମ୍ପୂର୍ଣ୍ଣ ରୂପେ ବ୍ୟାଖ୍ୟା କରିବା ପାଇଁ ସମାଜବିଜ୍ଞାନର ସାହାଯ୍ୟ ନେବାକୁ ପଡ଼ିଥାଏ। ତେଣୁ ସମାଜବିଜ୍ଞାନ ଓ ଅର୍ଥନୀତି ପରସ୍ପର ଘନିଷ୍ଠଭାବେ ଜଡ଼ିତ।

କାର୍ଲାମାର୍ଚ୍ଚ (Karl Mark)ଙ୍କ ମତ ଅନୁସାରେ ମନୁଷ୍ୟର ଅର୍ଥନୈତିକ ସମ୍ପର୍କ ତା’ର ସାମାଜିକ ସମ୍ପର୍କର କାରଣ ହୋଇଥାଏ। କେତେକ ଅର୍ଥନୀତିଜ୍ଞ ତଥା ସୋମ୍ବାର୍ଟ (Sombert), ମାକସ୍‌ବର (Marxweber), ପାରେଟୋ (Pareto) ପ୍ରଭୃତି ଅର୍ଥନୈତିକ ପରିବର୍ତ୍ତନ ପରିବର୍ତ୍ତନକୁ ସାମାଜିକ ପରିବର୍ତ୍ତନ ପରିଣାମ ଭାବରେ ବିଚାର କରନ୍ତି। ମାକ୍ସୱେବର ସମାଜରେ ଅଣଅର୍ଥନୈତିକ ଉପାଦାନଗୁଡ଼ିକ କିପରି ଅର୍ଥନୈତିକ କାର୍ଯ୍ୟକଳାପକୁ ପ୍ରଭାବିତ କରନ୍ତି ତାହା ଦର୍ଶାଇଛନ୍ତି। ଏହା ବ୍ୟତୀତ ତାଙ୍କର ପୁସ୍ତକ ପ୍ରୋଟେଷ୍ଟାଣ୍ଟ ଏଥ୍କସ୍ (Protestant Ethics) ଏବଂ ସ୍ପିରିଟ୍ ଅଫ୍ କ୍ୟାପିଟାଲିଜିମ୍ (Spirit of Capitalism)ରେ ପ୍ରୋଟେଷ୍ଟାଣ୍ଟ ନିୟମାବଳୀ ଓ ଆଧୁନିକ ପୁଞ୍ଜିବାଦ ମଧ୍ୟରେ ସମ୍ପର୍କ ସ୍ଥାପନ କରିଛନ୍ତି। କେତେକ ସାମାଜିକ ସମସ୍ୟା ରହିଛି ଯାହା ଉଭୟ ଅର୍ଥନୀତିଜ୍ଞ ଓ ସମାଜବିଜ୍ଞାନ ମିଳିତ ଭାବେ ଅଧ୍ୟୟନ କରିଥାଆନ୍ତି। ଯାହା ଦାରିଦ୍ର୍ୟ, ବେକାରୀ, ଭିକ୍ଷାବୃତ୍ତି, ଜନବିସ୍ଫୋରଣଜନିତ ସମସ୍ୟା ଇତ୍ୟାଦିରେ ସମାଜବିଜ୍ଞାନୀ ଓ ଅର୍ଥନୈତିକ ବିଜ୍ଞାନୀ ଉଭୟ ସଂଶ୍ଳିଷ୍ଟ ହୋଇଥା’ନ୍ତି। କୌଣସି ସମାଜ ପ୍ରଥା, ପରମ୍ପରା ସେହି ସମାଜର ଅର୍ଥନୀତିକୁ ପ୍ରଭାବିତ କରିଥାଏ। ଅର୍ଥନୈତିକ ବିକାଶ ଓ ସାମାଜିକ ପ୍ରଗତି ଉଭୟ ଉପରେ ନିର୍ଭରଶୀଳ। ଯଥା : ଅନ୍ଧବିଶ୍ଵାସ, କୁସଂସ୍କାର ତଥା ଅପରାଧର ମାତ୍ରା ଅଧିକ ହେଲେ ଆର୍ଥିକ ବିକାଶ ସମ୍ଭବପର ହୁଏ ନାହିଁ। ସେହିଭଳି ବେକାରୀ, ପରିବାର ଏବଂ ଜନସଂଖ୍ୟାର ମାତ୍ରାଧ୍ଵକ ବୃଦ୍ଧି ଦ୍ଵାରା ସମାଜରେ ବିଘଟନ ଓ ବିପର୍ଯ୍ୟସ୍ତ ସୃଷ୍ଟି ହୋଇଥାଏ।

ଅର୍ଥଶାସ୍ତ୍ର ମନୁଷ୍ୟର ଅର୍ଥନୈତିକ ଜୀବନ ବିଷୟରେ ଅଧ୍ୟୟନ ସୃଷ୍ଟି ହୋଇଥାଏ। ଉତ୍ପାଦନ, ଉପଭୋଗ ବଣ୍ଟନ, ବିନିମୟ, ଅର୍ଥନୈତିକ ଆଇନ ପ୍ରଣୟନ, ଦେଶ ଦେଶ ମଧ୍ୟରେ ବ୍ୟବସାୟିକ ସମ୍ପର୍କ ପ୍ରଭୃତି ଅର୍ଥନୀତି ବିଜ୍ଞାନର ପରିସରଭୁକ୍ତ। ଅର୍ଥନୀତି ମନୁଷ୍ୟର ଭୌତିକ କଲ୍ୟାଣ ନିମନ୍ତେ ଦୃଷ୍ଟି ଦେଇଥାଏ। ଅର୍ଥନୈତିକ କଲ୍ୟାଣ ହିଁ ସାମାଜିକ ବିକାଶର ଏକ ଅଂଶ ଅଟେ। ସାମାଜିକ ନିୟମ ବିଷୟରେ ଉପଯୁକ୍ତ ଜ୍ଞାନ ନ ଥଲେ ଅର୍ଥନୈତିକ କଲ୍ୟାଣ ବିଷୟରେ ଅଧ୍ୟୟନ ଅସମ୍ଭବ ହୋଇପଡ଼େ। ଏହିପରି ଭାବରେ ଅର୍ଥଶାସ୍ତ୍ର ସମାଜବିଜ୍ଞାନ ଠାରୁ ସାହାଯ୍ୟ ପାଇଥାଏ। ଉଦାହରଣ ସ୍ଵରୂପ ଅର୍ଥନୀତି ଓ ସମାଜବିଜ୍ଞାନୀମାନେ ବ୍ୟବସାୟ ଚକ୍ର, ମୁଦ୍ରାସ୍ପତି ପ୍ରଭୃତି ଅର୍ଥନୈତିକ ସମସ୍ୟାଗୁଡ଼ିକୁ ସମାଧାନ କରିବା ପାଇଁ ସେହି ନିର୍ଦ୍ଦିଷ୍ଟ ସମୟରେ ସାମାଜିକ ଘଟଣାଗୁଡ଼ିକୁ ବିଚାରକୁ ନେବାକୁ ଭୁଲି ନ ଥା’ନ୍ତି। ଏଥୁରୁ ଜଣାଯାଏ ଅର୍ଥନୈତିକ ଜୀବନ ଓ ସାମାଜିକ ଜୀବନ କିପରି ପରସ୍ପର ଉପରେ ନିର୍ଭରଶୀଳ। ଅର୍ଥଶାସ୍ତ୍ରର ସାହାଯ୍ୟ ବିନା ସମାଜକୁ ସମ୍ପୂର୍ଣ୍ଣଭାବେ ଅଧ୍ୟୟନ କରିହେବ ନାହିଁ କି ସମାଜବିଜ୍ଞାନ ସାହାଯ୍ୟ ବିନା ଅର୍ଥଶାସ୍ତ୍ରକୁ ଭଲଭାବରେ ବୁଝି ହେବ ନାହିଁ । ତେଣୁ ଅର୍ଥଶାସ୍ତ୍ର ଓ ସମାଜବିଜ୍ଞାନ ପରସ୍ପର ନିର୍ଭରଶୀଳ ଅଟନ୍ତି ।

ସମାଜବିଜ୍ଞାନ ଓ ଅର୍ଥଶାସ୍ତ୍ର ମଧ୍ୟରେ ପାର୍ଥକ୍ୟ (Difference between Sociology and Economics) :

1. ସମାଜବିଜ୍ଞାନ କହେ ମନୁଷ୍ୟ ଏକ ସାମାଜିକ ପ୍ରାଣୀ। ତେଣୁ ଏହା ମନୁଷ୍ୟର ସାମାଜିକ କାର୍ଯ୍ୟକଳାପକୁ ଅଧ୍ୟୟନ କରିଥାଏ; କିନ୍ତୁ ଅର୍ଥନୀତି କହେ ମନୁଷ୍ୟ ଏକ ଅର୍ଥନୈତିକ ପ୍ରାଣୀ। ତେଣୁ ଏହା ମନୁଷ୍ୟର ଅର୍ଥନୈତିକ କାର୍ଯ୍ୟକଳାପକୁ ଅଧ୍ୟୟନ କରିଥାଏ।
2. ସମାଜବିଜ୍ଞାନ ସମଗ୍ର ସମାଜକୁ ଅନୁଧ୍ୟାନ କରିଥାଏ। ତେଣୁ ଏହା ଏକ ସାଧାରଣ ବିଜ୍ଞାନ ଅଟେ। ଅର୍ଥନୀତି ସମାଜର କେବଳ ଅର୍ଥନୈତିକ ଦିଗକୁ ଅଧ୍ୟୟନ କରିଥାଏ। ତେଣୁ ଏହା ଏକ ସ୍ଵତନ୍ତ୍ର ବିଜ୍ଞାନ ଅଟେ।
3. ଏହା ସମଗ୍ର ସମାଜକୁ ଅନୁଧ୍ୟାନ କରୁଥିବାରୁ ଏହାର ପରିସର ବ୍ୟାପକ ଅଟେ; କିନ୍ତୁ ଅର୍ଥନୀତି ସମଗ୍ର ସମାଜରୁ ଏକ ଅଂଶକୁ ଅଧ୍ୟୟନ କରୁଥିବାରୁ ଏହାର ପରିସର କ୍ଷୁଦ୍ର ଅଟେ।
4. ସମାଜବିଜ୍ଞାନ ଏକ ନୂତନ ବିଜ୍ଞାନ ଅଟେ; କିନ୍ତୁ ଅର୍ଥନୀତି ପୁରାତନ ଅଟେ।
5. ସମାଜବିଜ୍ଞାନ ସମାଜକୁ ଅଧ୍ୟୟନର ପରିସରଭୁକ୍ତ କରିଥାଏ; କିନ୍ତୁ ଅର୍ଥନୀତି ବ୍ୟକ୍ତିକୁ ଅଧ୍ୟୟନ ପରିସରଭୁକ୍ତ କରିଥାଏ।
6. ସମାଜବିଜ୍ଞାନ ସାମାଜିକ ସମ୍ପର୍କକୁ ଅଧ୍ୟୟନ କରିଥାଏ; କିନ୍ତୁ ଅର୍ଥନୀତି ଅର୍ଥନୈତିକ ସମ୍ପର୍କକୁ ଅଧ୍ୟୟନ କରିଥାଏ।
7. ସମାଜଶାସ୍ତ୍ର ମୌଳିକଭାବେ ଲୋକମାନଙ୍କର ଅର୍ଥନୈତିକ କାର୍ଯ୍ୟକଳାପର ସାମାଜିକ ଦିଗ ସହିତ ସଂଶ୍ଳିଷ୍ଟ; କିନ୍ତୁ ଅର୍ଥଶାସ୍ତ୍ର ମୁଖ୍ୟତଃ ସମ୍ପଦର ଉତ୍ପାଦନ ଉପଭୋଗ, ବଣ୍ଟନ ସମ୍ବନ୍ଧୀୟ ପଦ୍ଧତି ଓ କୌଶଳ ସହିତ ଜଡ଼ିତ। ଯାହା ମନୁଷ୍ୟର ଭୌତିକ ସୁଖ ସ୍ଵାଚ୍ଛନ୍ଦ୍ୟ ସହିତ ପ୍ରତ୍ୟେକ୍ଷ କିମ୍ବା ପରୋକ୍ଷ ଭାବରେ ସମ୍ପୃକ୍ତ।
8. ସମାଜଶାସ୍ତ୍ର ମାନବବାଦୀ (Humanistic) ଅଟେ; କିନ୍ତୁ ଅର୍ଥଶାସ୍ତ୍ର ବସ୍ତୁବାଦୀ (Materialistic) ଅଟେ।
9. ସମାଜଶାସ୍ତ୍ରରେ ପର୍ଯ୍ୟବେକ୍ଷଣ ସାକ୍ଷତକାର, ଅନୁସୂଚୀ ଓ ପ୍ରଶ୍ନବଳୀ ଆଦି ବ୍ୟବହୃତ ହୋଇଥାଏ; କିନ୍ତୁ ଅର୍ଥଶାସ୍ତ୍ରରେ ଅବରୋହମୂଳକ ସିଦ୍ଧାନ୍ତ (Deduction), ଆରୋହପଦ୍ଧତି (Induction), ଜନସଂଖ୍ୟା ଓ ପରିସଂଖ୍ୟାନ (Statistics) ପ୍ରଭୃତି ପ୍ରୟୋଗ ହୋଇଥାଏ।
10. ସମାଜଶାସ୍ତ୍ର ଉଭୟ ସାମାଜିକ ସମସ୍ୟା ସହିତ ଅର୍ଥନୈତିକ ସମସ୍ୟାକୁ ଅଧ୍ୟୟନ କରିଥାଏ; କିନ୍ତୁ ଅର୍ଥନୀତି କେବଳ ଅର୍ଥନୈତିକ ସମସ୍ୟାକୁ ଅଧ୍ୟୟନ କରିଥାଏ।

Question ୧୧।
ସମାଜଶାସ୍ତ୍ର ଓ ମନସ୍ତତ୍ତ୍ଵ ମଧ୍ଯରେ ସମ୍ପର୍କ ଆଲୋଚନା କର।
Answer:
ମନସ୍ତତ୍ତ୍ଵ ଓ ଇଂରାଜୀ ଶବ୍ଦ (Psychology) ଦୁଇଟି ଗ୍ରୀକ୍ ଶବ୍ଦର ମିଶ୍ରଣରେ ଗଠିତ। ଯଥା : ସାଇକେ (Psyche) ଏବଂ ଲୋଗସ୍ (Logos)। ସାଇକେ (Psyche) ଶବ୍ଦର ଅଇଁ ଆତ୍ମା (Soul) ଏବଂ ଲୋଗସ ଶବ୍ଦର ଅର୍ଥ ଅଧ୍ୟୟନ ବ। ବିଜ୍ଞାନ (Science)। ତେଣୁ ଆଭିଧାନିକ ଅର୍ଥରେ ମନସ୍ତତ୍ତ୍ଵକୁ (Psyche) ଶବ୍ଦର ଅର୍ଥ ଆତ୍ମାର ବିଜ୍ଞାନ (Science of soul) ଅଟେ। ମନସ୍ତତ୍ତ୍ଵ ମନୋବିଜ୍ଞାନ ମଧ୍ୟ କୁହାଯାଏ। ଅର୍ଥାତ୍ ମନୁଷ୍ୟର ମନକୁ କରିବାକୁ କିମ୍ବା ମାନସିକ କ୍ରିୟାକଳାପର ଅଧ୍ୟୟନକୁ ମନସ୍ତତ୍ତ୍ଵ କୁହାଯାଏ । ସମାଜବିଜ୍ଞାନ ଓ ମନସ୍ତତ୍ତ୍ଵ ନିବିଡ଼ ଭାବରେ ସମ୍ପକ୍ତ । ମନସ୍ତତ୍ତ୍ଵ ମନୁଷ୍ୟର ମାନବିକ କାର୍ଯ୍ୟକଳାପକୁ ଅଧ୍ୟୟନ କଲାବେଳେ ସମାଜବିଜ୍ଞାନ ମନୁଷ୍ୟର ସାମାଜିକ କ୍ରିୟାକଳାପକୁ ଅଧ୍ୟୟନ କରିଥାଏ। ଏହି ମାନବିକ ଆଚରଣ ମାଧ୍ୟମରେ ମନସ୍ତତ୍ତ୍ୱବିତ୍ ବ୍ୟକ୍ତିର ବ୍ୟବହାର, ଦୃଷ୍ଟିଭଙ୍ଗୀ, ଚାଲିଚଳନ, ମୂଲ୍ୟବୋଧ ଇତ୍ୟାଦିକୁ ଅଧ୍ୟୟନ କରିଥାଏ। ଏହାଛଡ଼ା ମନୁଷ୍ୟର ବ୍ୟକ୍ତିତ୍ଵକୁ ଅନୁଶୀଳନ କରିଥାଏ। ଏହାଦ୍ଵାରା ବିଭିନ୍ନ ସମସ୍ୟାଗୁଡ଼ିକ ପ୍ରତି ଏହାର ପ୍ରତିକ୍ରିୟା କ’ଣ ତାକୁ ଅନୁଧ୍ୟାନ କରିଥାଏ। ଏହି ମନସ୍ତତ୍ତ୍ଵ ମଧ୍ଯ ସମାଜବିଜ୍ଞାନୀକୁ ଅନେକ କ୍ଷେତ୍ରରେ ସାହାଯ୍ୟ କରିଥାଏ। ଏହି ମନସ୍ତତ୍ତ୍ଵ ବିଜ୍ଞାନ ମାନସିକ କ୍ରିୟା ଅନୁଭୂତି (Perception) ପ୍ରବର୍ତ୍ତନ (Motive) ବୋଧଶକ୍ତି (Cognition) ଓ ପ୍ରତିଶିକ୍ଷା (Learning) ଇତ୍ୟାଦି ଅଧ୍ୟୟନ କରିଥାଏ। ମଣିଷ ଶରୀର ପ୍ରତ୍ୟେକ ଅଙ୍ଗପ୍ରତ୍ୟଙ୍ଗ ଯଥା: ସ୍ନାୟବିକ ଜୀବକୋଷ, ଚେତନା ଓ ଅବଚେତନ ଅବସ୍ଥା । ମସ୍ତିଷ୍କ ସହ ଏସବୁର ସମ୍ପର୍କ ଜୀବବିଜ୍ଞାନ ସହ ଜଡ଼ିତ।

ମନସ୍ତତ୍ତ୍ଵରେ “ ବ୍ୟକ୍ତି” ହିଁ ମନୋବିଜ୍ଞାନର କେନ୍ଦ୍ରବିନ୍ଦୁ ହୋଇଥାଏ। ମାତ୍ର ସମାଜବିଜ୍ଞାନରେ “ ସମାଜ” ହିଁ କେନ୍ଦ୍ରବିନ୍ଦୁ ଅଟେ। ସାମାଜିକ ସମ୍ପର୍କଗୁଡ଼ିକ ସମାଜ ଭିତରେ କିପରି ସୃଷ୍ଟି ହୁଏ, ତାହା ସମାଜବିଜ୍ଞାନର ଅଧ୍ୟୟ ନ ବିଷୟବସ୍ତୁ ହୋଇଥାଏ। ମାତ୍ର ମନସ୍ତତ୍ତ୍ଵ ବ୍ୟକ୍ତିର ମାନସିକ ଓ ଶାରିରୀକ ପ୍ରକ୍ରିୟା ଏବଂ ବ୍ୟକ୍ତିଗତ ଅନୁଭୂତିର ବିଶ୍ଳେଷଣ କରିଥାଏ। ଦୁର୍ଖମୂଙ୍କ ମତରେ ସମାଜବିଜ୍ଞାନ କେବଳ ସାମାଜିକ ଘଟଣାକୁ ଅନୁଧ୍ୟାନ କରିବା ଉଚିତ। ମନସ୍ତାତ୍ତ୍ଵିକ ଘଟଣାକୁ ନୁହେଁ। ମନସ୍ତତ୍ତ୍ଵ ମନୁଷ୍ୟର ଆଚରଣ, ବ୍ୟବହାର, ଚାଲିଚଳନ ଇତ୍ୟାଦିକୁ ଅଧ୍ୟୟନ କରିଥାଏ। ଏହା ବ୍ୟତୀତ ବୁଦ୍ଧି, ବିବେକ, ବିଚକ୍ଷଣତା, ପ୍ରତିଶଷ୍ଟ (Learning) ଆଶା ଓ ଆଶଙ୍କ ତାଥା ଭୟ ଇତ୍ୟାଦିକୁ ଅଧ୍ୟୟନ କରିଥାଏ। ବ୍ୟକ୍ତି କ’ଣ ଭାବେ କ’ଣ ଚିନ୍ତା କରେ ? କ’ଣ ଚାହେଁ ଏସବୁ ମନସ୍ତତ୍ତ୍ଵ ଅଧ୍ୟୟନ କରିଥାଏ। ସମାଜିକ ମନୋବିଜ୍ଞାନ (Social Psychology) ସମାଜଶାସ୍ତ୍ର ଓ ମନସ୍ତତ୍ତ୍ଵ ମଧ୍ଯରେ ସମନ୍ଵୟ ପ୍ରତିଷ୍ଠା କରିଥାଏ। ଏହା ମନୁଷ୍ୟକୁ ଏକ ସାମାଜିକ ପ୍ରାଣୀ ଭାବରେ ତା’ର ବ୍ୟକ୍ତିଗତ ଓ ମାନସିକ ସ୍ତରରେ ଅଧ୍ୟୟନ କରିଥାଏ। ତେଣୁ ସମାଜବିଜ୍ଞାନ ସମ୍ପର୍କ ଖୁବ୍ ଘନିଷ୍ଠ ଅଟେ। ଏହି ଦୁଇଟିକୁ ଅଲଗା କରିବା ସମ୍ଭବପର ନୁହେଁ ।

ସାମଞ୍ଜସ୍ୟ (Similarity) :
ସମାଜବିଜ୍ଞାନ ଓ ମନୋବିଜ୍ଞାନ ମଧ୍ୟରେ ଅନେକ ସାମଞ୍ଜସ୍ୟ ଗୋଟିଏ ମୁଦ୍ରାର ଦୁଇଟି ପାର୍ଶ୍ବ ସଦୃଶ। ଅର୍ଥାତ୍ ଗୋଟିଏ ଅନ୍ୟଟି ବିନା ପରିଲକ୍ଷିତ ହୋଇଥାଏ। ଏହି ଦୁଇଟି ବିଜ୍ଞାନ ତିଷ୍ଠି ପାରିବ ନାହିଁ। କାର୍ଲ ପିଅରସନ୍ (Kart Pearson) ଓ ସିଗମଣ୍ଡ ଫ୍ରଏଡ୍‌ଙ୍କ ମତରେ “ସମସ୍ତ ସାମାଜିକ ଜୀବନ ବା ଘଟଣା, ଶେଷରେ ମନସ୍ତାତ୍ତ୍ଵିକ ଘଟଣାରେ ପରିବର୍ତ୍ତନ ହୋଇଥାଏ ।”

ଗିନସ୍‌ବର୍ଗଙ୍କ ମତରେ ଅନେକଗୁଡ଼ିଏ ସାମାଜିକ ତଥ୍ୟକୁ ଦୃଢ଼ ଭାବରେ ପ୍ରତିପାଦିତ କରିବାକୁ ହେଲେ ସେସବୁକୁ ସାଧାରଣ ମନସ୍ତାତ୍ତ୍ଵିକ ତତ୍ତ୍ଵର ସାହାଯ୍ୟ ନେବାକୁ ପଡ଼ିଥାଏ। ପ୍ରକୃତ ପକ୍ଷେ ମନସ୍ତାତ୍ତ୍ଵିକ ଘଟଣାବଳୀ ସାମାଜିକ ସମ୍ପର୍କକୁ ଉତ୍ପନ୍ନ। ଏଥୁରୁ ସ୍ପଷ୍ଟ ବୁଝାପଡ଼େ ସମାଜବିଜ୍ଞାନ ଓ ମନୋବିଜ୍ଞାନ ପରସ୍ପର ନିର୍ଭରଶୀଳ। ସମାଜବିଜ୍ଞାନ ମନୁଷ୍ୟର ସାମାଜିକ କ୍ରିୟାକଳାପକୁ ଅଧ୍ୟୟନ କଲାବେଳେ ମନସ୍ତତ୍ତ୍ଵ ବ୍ୟକ୍ତିର ମନସ୍ତାତ୍ତ୍ଵିକ କ୍ରିୟାକଳାପ ଅଧ୍ୟୟନ କରିଥାଏ। ଏଣୁ ଉଭୟ ସମାଜବିଜ୍ଞାନୀ ଓ ମନୋବିଜ୍ଞାନୀ ବ୍ୟକ୍ତିକୁ ଅଧ୍ୟୟନ କରିଥାଆନ୍ତି ଏବଂ ଉଭୟ ମଣିଷର ବ୍ୟବହାର ଉପରେ ଗୁରୁତ୍ଵ ଦେଇଥାଆନ୍ତି। ମଣିଷର ସାମାଜିକ ବ୍ୟବହାର ଓ ସମ୍ପର୍କକୁ ବୁଝିବାକୁ ହେଲେ ଉଭୟ ସମାଜବିଜ୍ଞାନ ଓ ମନସ୍ତତ୍ତ୍ଵର ଆବଶ୍ୟକତା ରହିଛ ।

ସମାଜବିଜ୍ଞାନ ଦ୍ଵାରା ମନୋବିଜ୍ଞାନକୁ ଅନେକ ସାହାଯ୍ୟ ମିଳିଥାଏ। ଯଥା : ସାମାଜିକ ଅବସ୍ଥା, ସଂସ୍କୃତି, ସାମାଜିକ ଢାଞ୍ଚାର ଉପଯୁକ୍ତ ଅଧ୍ୟୟନ ବିନା ମଣିଷର ମନସ୍ତତ୍ତ୍ଵକୁ ଠିକ୍ ରୂପେ ବୁଝି ହେବ ନାହିଁ। କେତେକ ସାଧାରଣ ବିଷୟବସ୍ତୁ ରହିଛି। ଯେଉଁଗୁଡ଼ିକ ଉଭୟ ସମାଜବିଜ୍ଞାନୀ ଓ ମନୋବିଜ୍ଞାନୀ ଅଧ୍ୟୟନ କରିଥାଆନ୍ତି। ତେଣୁ ତାଙ୍କ ଭିତରେ ଏକ ସାମଞ୍ଜସ୍ୟ ଦେଖାଯାଇଥାଏ। ଯଥା : ବ୍ୟକ୍ତିଗତ ଆଚରଣରେ ବିଶୃଙ୍ଖଳା, ଅପରାଧ, ବାଲ୍ୟ ଅପରାଧ ଜନମତ, ରାଜନୈତିକ ପ୍ରଚାର, ନେତୃତ୍ଵ, ଯୁଦ୍ଧ, କଳହ, ସାମାଜିକୀକରଣ, ଅନୁକରଣ ଓ ଫେସନ ଇତ୍ୟାଦି ଉଭୟ ସମାଜବିଜ୍ଞାନୀ ଓ ମନୋବିଜ୍ଞାନୀ ଅଧ୍ୟୟନ କରିଥାଆନ୍ତି।

ସାମାଜିକ ମନୋବିଜ୍ଞାନ (Social Psychlogy) ଅନେକ ସାମାଜିକ ସମସ୍ୟାର ସମାଧାନ କରିଥାଏ। ଯଥା : ସାମାଜିକ ଦ୍ଵନ୍ଦୁ, ଧାର୍ମିକ ପକ୍ଷପାତିତା, ଅପରାଧ, ବେଶ୍ୟାବୃତ୍ତି, ଜୁଆଖେଳ, ମଦ୍ୟପାଦ ଇତ୍ୟାଦି ସାମାଜିକ ଘଟଣାର ଅଧ୍ୟୟନ କ୍ଷେତ୍ରରେ ଏହି ମନୋବିଜ୍ଞାନର ଗୁରୁତ୍ଵପୂର୍ଣ୍ଣ ଭୂମିକା ରହିଅଛି। ବ୍ୟକ୍ତିଗତ ଚିନ୍ତା ଓ ଚେତନା, ସାମାଜିକ ଚିନ୍ତା ଓ ଚେତନାର ଏକ ଅଂଶ ବିଶେଷ ଅଟେ।

କେତେକ ମନସ୍ତତ୍ତ୍ୱବିତ୍ ଯଥା : ଫ୍ରଏଡ୍, ୟୁଙ୍ଗ, ମର୍ଫି ଇତ୍ୟାଦି ସାମାଜିକ ବିଜ୍ଞାନର ଚିନ୍ତାଧାରାକୁ ସୁଦୃଢ଼ କରିଦେଇଛନ୍ତି । କ୍ରେଟ୍ (Kretch) ଓ କୁଚୁଫିଲଡ୍ (Cruthfield)ଙ୍କ ମତରେ ସାମାଜିକ ମନୋବିଜ୍ଞାନ ହେଉଛି ସେହି ପ୍ରକାର ବିଜ୍ଞାନ ଯାହା ସମାଜ ମଧ୍ୟସ୍ଥ ବ୍ୟକ୍ତି ଆଚରଣକୁ ପ୍ରକାଶ କରିଥାଏ। ଟି.ବି. ବଟ୍‌ଟଙ୍କ ମତରେ, “ସାମାଜିକ ବିଜ୍ଞାନ ହେଉଛି ସାଧାରଣ ମନୋବିଜ୍ଞାନର ଅଂଶବିଶେଷ ଯାହା ସାମାଜିକ ଜୀବନର ମନୋସ୍ତାତ୍ତ୍ଵିକ ଦିଗକୁ ଅଧ୍ୟୟନ କରିଥାଏ ।” ଲାଏପିଏନ୍ (Lapiere)ଙ୍କ ମତରେ, “ଜୀବ ବିଜ୍ଞାନ ଓ ରାସାୟନିକ ବିଜ୍ଞାନ ମଧ୍ୟରେ ଯେଉଁପରି ସଂପର୍କ ଅଛି ଠିକ୍ ସେହିପରି ସାମାଜିକ ବିଜ୍ଞାନ ଓ ମନୋବିଜ୍ଞାନ ମଧ୍ୟରେ ସମ୍ପର୍କ ରହିଛି। ଏହିସବୁ ଦୃଷ୍ଟିରୁ ଅନୁଧ୍ୟାନ କଲେ ଜଣାଯାଏ ସମାଜବିଜ୍ଞାନ ଓ ମନୋବିଜ୍ଞାନ ପରସ୍ପରଠାରୁ ଅଲଗା ନୁହଁନ୍ତି।

Question ୧୨।
ସମାଜବିଜ୍ଞାନ ଓ ମନୋବିଜ୍ଞାନ ମଧ୍ୟରେ ପାର୍ଥକ୍ୟ ଦର୍ଶାଅ।
Answer:
ସମାଜବିଜ୍ଞାନ ଓ ମନୋବିଜ୍ଞାନ ମଧ୍ୟରେ କେତେକ ପାର୍ଥକ୍ୟ ଦେଖୁବାକୁ ଦେଖୁବାକୁ ମିଳିଥାଏ। ସେଗୁଡ଼ିକ ନିମ୍ନରେ ଆଲୋଚନା କରାଗଲା।

ସମାକବିଜ୍ଞାନ	ମନୋବିଜ୍ଞାନ
(୧) ସମାଜବିଜ୍ଞାନ ସମ୍ପୂର୍ଣ୍ଣ ସମାଜକୁ ଅଧ୍ୟୟ ନ କରିଥାଏ।	(୧) ମନସ୍ତତ୍ତ୍ଵ ବ୍ୟକ୍ତିର ମସ୍ତିଷ୍କକୁ ଅଧ୍ୟୟନ କରିଥାଏ। ଏହା ବ୍ୟକ୍ତିର ମାନସିକ ପ୍ରକ୍ରିୟା, ଆନ୍ତଃ ଓ ବାହ୍ୟ ବ୍ୟବହାରକୁ ଅଧ୍ୟୟନ କରିଥାଏ।
(୨) ସମାଜବିଜ୍ଞାନକୁ ଗଠନ କରୁଥିବା ବିଭିନ୍ନ ପ୍ରକାରର ସମୂହଗୁଡ଼ିକ ଅଧୟନ କରିଥାଏ।	(୨) ମନସ୍ତତ୍ତ୍ଵ ବ୍ୟକ୍ତିର ମାନସିକ ବିକାଶ ଉପରେ ସମୂହ ଜୀବନର ପ୍ରଭାବ; ସମୂହର ମାନସିକ ଜୀବନର ଉନ୍ନତି ଓ ସେମାନଙ୍କର ପରସ୍ପରସହ ସମ୍ପର୍କ ପ୍ରତିଷ୍ଠା କରେ।
(୩) ସମାଜ ବିଜ୍ଞାନର ପରିସର ବ୍ୟାପକ ଅଟେ। `	(୩) ମନସ୍ତତ୍ତ୍ଵର ପରିସର ସମାଜ ବିଜ୍ଞାନ ତୁଳନାରେ କ୍ଷୁଦ୍ର ଅଟେ।
(୪) ସମାଜବିଜ୍ଞାନ ଏକ ସାଧାରଣ ବିଜ୍ଞା। `	(୫) ମନୋବିଜ୍ଞାନର ତଥ୍ୟାବଳୀକୁ ପରୀକ୍ଷା କରିବା ପାଇଁ ପରୀକ୍ଷାଗାର ନ ଥାଏ।
(୫) ସମାଜବିଜ୍ଞାନର ତଥ୍ୟାବଳୀକୁ ପରୀକ୍ଷା କରିବା ପାଇଁ କୌଣସି ପରୀକ୍ଷାଗାର ନଥାଏ ।	(୬) ମନସ୍ତତ୍ତ୍ଵ ମନସ୍ତାତ୍ତ୍ଵିକ ଦୃଷ୍ଟିକୋଣରୁ ଭିଭିକରି ଆଲୋଚନା କରିଥାଏ।
(୭ ) ସମାଜବିଜ୍ଞାନରେ ସାମୂହିକ ପର୍ଯ୍ୟବେକ୍ଷଣ ପ୍ରଣାଳୀ (Group observation method) ବ୍ୟବହୃତ ହୋଇଥାଏ।	(୭) ମନସ୍ତତ୍ତ୍ଵରେ ବ୍ୟକ୍ତିଗତ ପର୍ଯ୍ୟବେକ୍ଷଣ ପ୍ରଣାଳୀ (Individual observations method)ବ୍ୟବହୃତ ହୋଇଥାଏ।
(୮) ସାମାଜବିଜ୍ଞାନ ପ୍ରତ୍ୟେକ ଘଟଣାକୁ ସାମାଜିକ ଦୃଷ୍ଟିକୋଣରୁ ଆଲୋଚନା କରିଥାଏ।	(୮) ମନୋବିଜ୍ଞାନ ମନୁଷ୍ୟର ମାନବିକ ଦୃଷ୍ଟିକୋଣରୁ ଅଧ୍ୟୟନ କରିଥାଏ ।
(୯) ବ୍ୟକ୍ତିଗତ ଜୀବନର ପରିବର୍ତ୍ତେ ଦଳଗତ ଜୀବନ, ଗୋଷ୍ଠୀର ବିକାଶ ଓ ସାମାଜିକ ସଂରଚନା ଆଲୋଚନା କରିଥାଏ।	(୯) ବ୍ୟକ୍ତି ଚରିତ୍ର ଗଠନ ଓ ବ୍ୟକ୍ତିର ବ୍ୟକ୍ତିଗତ ବିକାଶ ସାଧନକୁ ଆଲୋଚନା କରିଥାଏ।

Odisha State Board CHSE Odisha Class 11 Economics Solutions Unit 1 ଭାରତୀୟ ଅର୍ଥନୀତିର ସ୍ଥିତି Questions and Answers.

CHSE Odisha 11th Class Economics Unit 1 Question Answer ଭାରତୀୟ ଅର୍ଥନୀତିର ସ୍ଥିତି

I. ନିମ୍ନୋକ୍ତ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ପ୍ରଦତ୍ତ ବିକଳ୍ପଗୁଡ଼ିକ ମଧ୍ୟରୁ ଚୟନ କର।
[Choose the Correct answer of the followings from the alternatives as given]

Question ୧।
ଭାରତୀୟ ଅର୍ଥନୀତିର ମୌଳିକ ବୈଶିଷ୍ଟ୍ୟ :
(i) ସ୍ଵ ମୁଣ୍ଡପିଛା ଆୟ
(ii) ବେକାରୀ ସମସ୍ୟା
(iii) ଦାରିଦ୍ର୍ୟ ସମସ୍ୟା
(iv) ଉପରୋକ୍ତ ସମସ୍ତଟି
Answer:
(iv) ଉପରୋକ୍ତ ସମସ୍ତଟି

Question ୨।
ପାରଂପରିକ କ୍ଷେତ୍ର ଓ ଆଧୁନିକ କ୍ଷେତ୍ରର ସହାବସୁ ନ ଥ‌ିବା ଅର୍ଥ ବ୍ୟବସ୍ଥା :
(i) ଦ୍ବୈତ ଅର୍ଥବ୍ଯବସ୍ଥା
(iii) ଶିକ ଅର୍ଥ ବ୍ୟବସ୍ଥା
(ii) କୃଷି ଅର୍ଥବ୍ୟବସ୍ଥା
(iv) ସମସ୍ତଟି
Answer:
(i) ଦ୍ଵୈତ ଅର୍ଥବ୍ୟବସ୍ଥା

Question ୩।
ଘରୋଇ କ୍ଷେତ୍ର ଓ ଆଧୁନିକ କ୍ଷେତ୍ରର ସହାବସ୍ଥାନ ଥିବା ଅର୍ଥ ବ୍ୟବସ୍ଥା :
(i) ମିଶ୍ରିତ ଅର୍ଥବ୍ଯବସ୍ଥା
(ii) ଶିଳ୍ପ ଅର୍ଥ ବ୍ୟବସ୍ଥା
(iii) କୃଷି ଅର୍ଥ ବ୍ୟବସ୍ଥା
(iv) ସମସ୍ତଟି
Answer:
(i) ମିଶ୍ରିତ ଅର୍ଥବ୍ୟବସ୍ଥା

Question ୪।
ଭାରତୀୟ ଅର୍ଥନୀତି ଏକ :
(i) ଉନ୍ନତ ଅର୍ଥନୀତି
(ii) ଅନୁନ୍ନତ ଅର୍ଥନୀତି
(iii) ବିକାଶଙ୍ଗୋମୁଖୀ
(iv) ସମସ୍ତଟି
Answer:
(iii) ବିକାଶୋନ୍ମୁମୁଖୀ

Question ୫।
ପ୍ରତ୍ୟେକ ବ୍ୟକ୍ତି ପିଛା ଆୟକୁ କ’ଣ କୁହାଯାଏ ?
(i) ମୁଣ୍ଡପିଛା ଆୟ
(ii) ମୋଟ ଆୟ
(iii) ନିଟ୍ ଆୟ
(iv) କୌଣସିଟି ନୁହେଁ
Answer:
(i) ମୁଣ୍ଡପିଚ୍ଛା ଆୟ

Question ୬।
ଛଦ୍ମବେଶୀ ବେକାରୀ ଭାରତୀୟ ଅର୍ଥନୀତିର କେଉଁ କ୍ଷେତ୍ରରେ ଦେଖାଦେଇଥାଏ ?
(i) କୃଷି
(iii) ସେବା
(ii) ଶିଳ୍ପ
(iv) ସମସ୍ତଟି
Answer:
(i) କୃଷି

Question ୭।
ଭାରତୀୟ ଜନସଂଖ୍ୟା ଭାରତ ପାଇଁ :
(i) ବୋଝ
(ii) ପରିସଂପତ୍ତି
(iii) ଧନ
(iv) ସମସ୍ତଟି
Answer:
(i) ବୋଝ

Question ୮।
ଜନସଂଖ୍ୟାର ଦ୍ରୁତ ଅଭିବୃଦ୍ଧିକୁ କ’ଣ କୁହାଯାଏ ?
(i) ଜନ ବିସ୍ଫୋରଣ
(ii) ବେକାରୀ
(iii) ଅର୍ଥ ବେକାରୀ
(iv) ସମସ୍ତଟି
Answer:
(i) ଜନ ବିସ୍ଫୋରଣ

Question ୯।
ବୃତ୍ତି ବା କାର୍ଯ୍ୟକୁ ସାଧାରଣତଃ କେତୋଟି ଭାଗରେ ବିଭକ୍ତ କରାଯାଇଛି ?
(i) ୪
(ii) ୨
(iii) ୩
(iv) ୫
Answer:
(ii) ୩

Question ୧୦ ।
ପ୍ରକୃତି ସହିତ ସଂଶ୍ଳିଷ୍ଟ ବୃତ୍ତି :
(i) ପ୍ରାଥମିକ ବୃତ୍ତି
(ii) ମାଧ୍ୟମିକ ଚୃତ୍ତି
(iii) ସେବା ବୃତ୍ତି
(iv) ସମସ୍ତଟି
Answer:
(i) ପ୍ରାଥମିକ ବୃତ୍ତି

Question ୧୧ ।
ପ୍ରାଥମିକ ବୃଦ୍ଧିର ଅନ୍ତର୍ଭୁକ୍ତ ହୋଇଥିବା କ୍ଷେତ୍ର :
(i) କୃଷି
(ii) ଗୋ-ପାଳନ
(iii) କକଡ଼ା ଚାଷ
(iv) ସମସ୍ତଟି
Answer:
(iv) ସମସ୍ତଟି

Question ୧୨ ।
ଦ୍ଵିତୀୟତଃ ବା ମାଧ୍ୟମିକ ବୃଦ୍ଧିରେ ଅନ୍ତର୍ଭୁକ୍ତ କ୍ଷେତ୍ର :
(i) ବୃହତ୍ ଶିଳ୍ପ
(ii) ଚିନିର୍ମାଣ କ୍ଷେତ୍ର
(iii) କ୍ଷୁଦ୍ରଶିକ
(iv)ସମସ୍ତଟି
Answer:
(iv)ସମସ୍ତଟି

Question ୧୩ ।
ସେବା କ୍ଷେତ୍ରରେ ଅନ୍ତର୍ଭୁକ୍ତ କ୍ଷେତ୍ର :
(i) ପରିବହନ
(ii) ଯୋଗାଯୋଗ
(iii) ବ୍ୟାଙ୍କ ସେବା
(iv) ସମସ୍ତଟି
Answer:
(iv) ସମସ୍ତଟି

Question ୧୪ ।
୨୦୧୧ ମସିହା ଜନଗଣନା ଅନୁସାରେ ଭାରତରେ ମୋଟ ଜନସଂଖ୍ୟା :
(i) ୧୨୧.୦୨ କୋଟି
(ii) ୧୨୦ କୋଟି
(iii) ୧୩୪ କୋଟି
(iv) ୧୮୦ କୋଟି
Answer:
(i) ୧୨୧,୦୨ କୋଟି

Question ୧୫ ।
କେଉଁ ମସିହାକୁ ଭାରତୀୟ ଜନସଂଖ୍ୟାର ବୃହତ୍ ବିଭାଜନର ବର୍ଷ କୁହାଯାଏ ?
(i) ୧୯୨୧
(ii) ୧୯୨୦
(iii) ୧୯୮୧
(iv) ୧୯୨୦
Answer:
(1) ୧୯୨୧

Question ୧୬ ।
୨୦୧୧ ମସିହା ଜନଗଣନା ଅନୁସାରେ ଭାରତର ସାକ୍ଷରତା ହାର :
(i) ୭୦ ପ୍ରତିଶତ
(ii) ୭୪ ପ୍ରତିଶତ
(iii) ୮୦ ପ୍ରତିଶତ
(iv) ୪୦ ପ୍ରତିଶତ
Answer:
(ii) ୭୪ ପ୍ରତିଶତ

Question ୧୭ ।
୨୦୧୧ ମସିହା ଜନଗଣନା ଅନୁସାରେ ଭାରତର ଜନସଂଖ୍ୟାର ଘନତ୍ବ ପ୍ରତିବର୍ଗ କିଲୋମିଟର ପିଛା କେତେ ?
(i) ୩୭୦
(ii) ୩୮୨
(iii) ୯୪୦
(iv) ୯୩୦

Question ୧୮ ।
୨୦୧୧ ମସିହା ଜନଗଣନା ଅନୁସାର ଭାରତର ଲିଙ୍ଗାନୁପାତ ହାର କେତେ (ପ୍ରତି ୧୦୦୦ ପୁରୁଷରେ):
(i) ୯୪୩
(ii) ୯୬୯
(iii) ୯୪୦
(iv) ୯୫୦
Answer:
(iii) ୯୪୦

Question ୧୯ ।
୨୦୧୧ ମସିହା ଜନଗଣନା ଅନୁସାରେ ଭାରତୀୟମାନଙ୍କର ବଞ୍ଚିବାର ହାରାହାରି ବୟସ କେତେ ?
(i) ୬୮
(ii) ୭୦
(iii) ୬୯.୦୯
(iv) ୬୦
Answer:
(iii) ୬୯.୦୯

Question ୨୦ ।
ନୂତନ ଜନସଂଖ୍ୟା ନୀତି କେଉଁ ମସିହାରେ କାର୍ଯ୍ୟକାରୀ ହୋଇଥିଲା ?
(i) ୨୦୦୦
(ii) ୧୯୯୧
(iii) ୧୭୭୭
(iv) ୧୮୯୦
Answer:
(i) ୨୦୦୦

Question ୨୧ ।
ଜନସଂଖ୍ୟା ସ୍ଥିରତା କୋଷ କେବେ ଗଠନ କରାଯାଇଥିଲା ?
(i) ୨୦୦୩
(ii) ୨୦୦୦
(iii) ୨୦୦୨
(iv) ୧୭୭୬
Answer:
(i) ୨୦୦୩

Question ୨୨ ।
ଭାରତର ଜନସଂଖ୍ୟା ବୃଦ୍ଧିର କାରଣ :
(i) ଉଚ୍ଚ ଜନ୍ମହାର
(ii) ଉଚ୍ଚ ମୃତ୍ୟୁହାର
(iii) ନିମ୍ନସ୍ତରର ଜନ୍ମହାର
(iv) ସମସ୍ତଟି
Answer:
(i) ଉଚ୍ଚ ଜନ୍ମହାର

Question ୨୩ ।
ନିମ୍ନୋକ୍ତ ମଧ୍ୟରୁ କେଉଁଟି ଜନସଂଖ୍ୟା ବୃଦ୍ଧିର ପ୍ରଭାବ ?
(i) ଖାଦ୍ୟ ସମସ୍ଯ
(ii) ଦାରିଦ୍ର୍ୟ ସମସ୍ୟ
(iii) ବେକାରୀ ସମସ୍ୟା
(iv)ସମସ୍ତଟି
Answer:
(iv)ସମସ୍ତଟି

Question ୨୪ ।
ଭାରତର ପ୍ରଥମ ଜନସଂଖ୍ୟା ନୀତି କେବେ ଘୋଷଣା କରାଯାଇଥିଲା ?
(i) ୧୯୭୬
(ii) ୧୮୯୦
(iii) ୨୦୦୦
(iv) ୨୦୦୨
Answer:
(i) ୧୯୭୬

Question ୨୫ ।
ସ୍ଵାଧୀନତା ପ୍ରାପ୍ତି ସମୟରେ ଭାରତୀୟ ଅର୍ଥନୀତି କିପରି ଥୁଲା ?
(i) ଅନୁନ୍ନତ
(ii) ଉନ୍ନତ
(iii) ବିକଶିତ
(iv) ମସ୍ତଟି
Answer:
(i) ଅନୁନ୍ନତ

Question ୨୬ ।
୨୦୧୧ ମସିହା ଜନଗଣନା ଅନୁସାର ଭାରତର ଜନସଂଖ୍ୟାର ବୃଦ୍ଧି ହାର କେତେ ?
(i) ୧.୬୨ ପ୍ରତିଶତ
(ii) ୧.୯୨ ପ୍ରତିଶତ
(iii) ୧.୪୩ ପ୍ରତିଶତ
(iv) ସମସ୍ତଟି
Answer:
(i) ୧.୬୨ ପ୍ରତିଶତ

II. ନିମ୍ନୋକ୍ତ ଉକ୍ତିଗୁଡ଼ିକର ସଠିକତା ପ୍ରମାଣ କର ।
ଆବଶ୍ୟକ ସ୍ଥଳେ ରେଖାଙ୍କିତ ଅଂଶଗୁଡ଼ିକୁ ନ ବଦଳାଇ ଭ୍ରମ ସଂଶୋଧନ କର ।
[Prove the correctness of the followings, correct them if necessary without changing words underlined]

Question ୧।
ଭାରତର ଜନସଂଖ୍ୟା ଭାରତର ଅର୍ଥନୀତି ପାଇଁ ପରିସଂପରି ।
Answer:
ଭାରତର ଜନସଂଖ୍ୟା ଭାରତର ଅର୍ଥନୀତି ପାଇଁ ବୋଝ (Liabitics)

Question ୨।
ଜନ ବିସ୍ଫୋରଣର ଅର୍ଥ ହେଲା ଜନସଂଖ୍ୟାର ଦ୍ରୁତ ଅଭିବୃଦ୍ଧି ।
Answer:
ସଠିକ୍

Question ୩ ।
ଭାରତର ମୁଣ୍ଡପିଚ୍ଛା ଆୟ ଉନ୍ନତ ଦେଶର ମୁଣ୍ଡପିଛା ଆୟ ତୁଳନାରେ ଅଧିକ ।
Answer:
ଭାରତର ମୁଣ୍ଡପିଛା ଆୟ ଉନ୍ନତ ଦେଶର ମୁଣ୍ଡପିଚ୍ଛା, ଆୟ ତୁଳନାରେ କମ୍।

Question ୫ ।
୨୦୧୧ ମସିହା ଜନଗଣନା ଅନୁସାରେ ଭାରତରେ କେରଳର ସାକ୍ଷରତା ହାର ଅଧିକ ।
Answer:
ସଠିକ୍

Question ୬।
୨୦୧୧ ମସିହା ଜନଗଣନା ଅନୁସାରେ କେରଳରେ ପ୍ରତି ହଜାର ପୁରୁଷରେ ମହିଳା ମାନଙ୍କର ସଂଖ୍ୟା ୧୦୮୪ ।
Answer:

Question ୭।
କୃଷିକୁ ପ୍ରାଥମିକ ବୃଦ୍ଧିରେ ଅନ୍ତର୍ଭୁକ୍ତ କରାଯାଏ ।
Answer:
ସଠିକ୍

Question ୮।
ପ୍ରାଥମିକ କ୍ଷେତ୍ରକୁ ବିନିର୍ମାଣ କ୍ଷେତ୍ର କୁହାଯାଏ ।
Answer:
ମାଧ୍ୟମିକ କ୍ଷେତ୍ରକୁ ବିନିର୍ମାଣ କ୍ଷେତ୍ର କୁହାଯାଏ ।

Question ୯ ।
ବୀମା ସେବାକୁ ସେବା କ୍ଷେତ୍ରରେ ଅନ୍ତର୍ଭୁକ୍ତ କରାଯାଏ ।
Answer:
ସଠିକ୍

Question ୧୦ ।
ପାରଂପରିକ କ୍ଷେତ୍ର ଓ ଆଧୁନିକ କ୍ଷେତ୍ରରେ ସହାବସ୍ଥାନକୁ ଦୈତ ଅର୍ଥନୀତି କୁହାଯାଏ ।
Answer:
ସଠିକ୍

Question ୧୧ ।
ଭାରତୀୟ ଅର୍ଥନୀତିକ କୃଷି କ୍ଷେତ୍ରର ଅବଦାନ ହ୍ରାସ ପାଉଛି
Answer:
ସଠିକ୍

Question ୧୨ ।
ଭାରତୀୟ ଅର୍ଥନୀତିକୁ ଶିଳ୍ପ କ୍ଷେତ୍ରର ଅବଦାନ ବୃଦ୍ଧି ପାଇଛି ।
Answer:
ଭାରତୀୟ ଅର୍ଥନୀତିକୁ ସେବା କ୍ଷେତ୍ରର ଅବଦାନ ବୃଦ୍ଧି ପାଇଛି

Question ୧୩ ।
ଭାରତରେ ବିହାରର ଜନସଂଖ୍ୟାର ଘନତ୍ଵ ସର୍ବାଧ‌ିକ ।
Answer:
ସଠିକ୍

Question ୧୪ ।
ଭାରତରେ ପରିବାର ନିୟୋଜନ କାର୍ଯ୍ୟକ୍ରମ ୧୯୫୧ ମସିହାରେ ଆରମ୍ଭ ହୋଇଥିଲା ।
Answer:
ଭାରତରେ ପରିବାର ନିୟୋଜନ କାର୍ଯ୍ୟକ୍ରମ ୧୯୫୨ ମସିହାରେ ଆରମ୍ଭ ହୋଇଥିଲା ।

Question ୧୫ ।
ଦୁଇ ସନ୍ତାନ ପରିବାର ଗଠନ ପରିବାର ନିୟୋଜନ କାର୍ଯ୍ୟକ୍ରମର ମୁଖ୍ୟ ବୈଶିଷ୍ଟ୍ୟ |
Answer:
ସଠିକ୍

Question ୧୬ ।
୨୦୦୦ ମସିହା ଜନସଂଖ୍ୟା ନୀତିରେ ଜନ୍ମ, ମୃତ୍ୟୁ ଏବଂ ବିବାହର ବାଧ୍ୟତାମୂଳକ ପଞ୍ଜିକରଣ କରିବାର ବ୍ୟବସ୍ଥା କରାଯାଇଥିଲା ।
Answer:
ସଠିକ୍

Question ୧୭ ।
୧୯୭୬ ମସିହା ଜନନୀତିରେ ମୋଟ ପ୍ରସୂତିର ୮ ପ୍ରତିଶତ ଘରୋଇ ଡାକ୍ତରଖାନାରେ କରାଇବାର ବ୍ୟବସ୍ଥା କରାଯାଇଥିଲା ।
Answer:
୧୯୭୬ ମସିହା ଜନନୀତିରେ ମୋଟ ପ୍ରସୂତିର ୮ ପ୍ରତିଶତ ସରକାରୀ ଡାକ୍ତରଖାନାରେ କରାଇବାର ବ୍ୟବସ୍ଥା କରାଯାଇଥିଲା ।

Question ୧୮ ।
ଭାରତରେ ପରିବାର ନିୟୋଜନ ଇଚ୍ଛାଧୀନ ଅଟେ ।
Answer:
ସଠିକ୍

Question ୧୯ ।
ବିହାର ଭାରତର ପୂର୍ଣ୍ଣ ସାକ୍ଷର ରାଜ୍ୟ ଅଟେ ।
Answer:
କେରଳ ଭାରତର ପୂର୍ଣ୍ଣ ସାକ୍ଷର ରାଜ୍ୟ ଅଟେ ।

Question ୨୦ ।
ଉଚ୍ଚଜନ୍ମ ହାର ଭାରତର ଜନସଂଖ୍ୟା ବୃଦ୍ଧିର ମୁଖ୍ୟ କାରଣ ।
Answer:
ସଠିକ୍

Question ୨୧ ।
ପରିବାର ନିୟୋଜନ କାର୍ଯ୍ୟକ୍ରମର ଅନ୍ୟ ନାମ ପରିବାର ଉନ୍ନୟନ କାର୍ଯ୍ୟକ୍ରମ ।
Answer:
ସଠିକ୍

Question ୨୨ ।
୨୦୦୧ ମସିହା ଜନଗଣନା ଅନୁସାରେ ଭାରତର ମୋଟ ଜନସଂଖ୍ୟା ୧୦୨.୦୨ କୋଟି ଥିଲା ।
Answer:
ସଠିକ୍

Question ୨୩ ।
ଜନ୍ମ ଠାରୁ ୧ ବର୍ଷ ବୟସ ମଧ୍ୟରେ ମୃତ୍ୟୁବରଣ କରୁଥିବା ଶିଶୁଙ୍କର ସଂଖ୍ୟାକୁ ମୃତ୍ୟୁହାର କୁହାଯାଏ ।
Answer:
ସଠିକ୍

III. ନିମ୍ନୋକ୍ତ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଦୁଇଟିରୁ ତିନୋଟି ବାକ୍ୟରେ ମଧ୍ଯରେ ଲେଖି ।
[Answer the following questions within 2 to 3 Sentences in each case.

Question ୧ ।
ଭାରତୀୟ ଅର୍ଥନୀତିର ଦୁଇଟି ବୈଶିଷ୍ଟ୍ୟ(Features) ଲେଖ ।
Answer:
ଭାରତୀୟ ଅର୍ଥନୀତିର ଦୁଇଟି ବୈଶିଷ୍ଟ୍ୟ ହେଲା
(୧) ଦ୍ରୁତ ଜନସଂଖ୍ୟା ବୃଦ୍ଧି ଭାରତୀୟ ଅର୍ଥନୀତିର ମୁଖ୍ୟ କାରଣ ।
(୨) କୃଷିକ୍ଷେତ୍ର ଉପରେ ନିର୍ଭରଶୀଳତା ଭାରତୀୟ ଅର୍ଥନୀତିର ଅନ୍ୟ ଏକ ମୁଖ୍ୟ କାରଣ ।

Question ୨।
ଜନସଂଖ୍ୟା ବୃଦ୍ଧିର ଦୁଇଟି କାରଣ (Causes) ଲେଖ ।
Answer:
ଜନସଂଖ୍ୟା ବୃଦ୍ଧିର ଦୁଇଟି କାରଣ ହେଲା
(୧) ତ୍ରୁଟିଯୁକ୍ତ ସାମାଜିକ ବ୍ୟବସ୍ଥା ଭାରତୀୟ ଅର୍ଥନୀତିର ଜନସଂଖ୍ୟା ବୃଦ୍ଧିର ମୁଖ୍ୟ କାରଣ ।
(୨) ପ୍ରାକୃତିକ ବିପର୍ଯ୍ୟୟ ଉପରେ ନିୟନ୍ତ୍ରଣ ଜନସଂଖ୍ୟା ବୃଦ୍ଧିର ଅନ୍ୟତମ କାରଣ ।

Question ୩ ।
ପରିବାର ନିୟୋଜନ ( Family Planning) କ’ଣ ?
Answer:
ଭାରତ ସରକାରଙ୍କ ଦ୍ଵାରା ଦେଶରୁ ଦ୍ରୁତ ଜନସଂଖ୍ୟାଗ୍ରତ ସମସ୍ୟା ସମାଧାନ କରିବା ଲକ୍ଷ୍ୟରେ ଗ୍ରହଣ କରାଯାଇଥିବା ଯୋଜନାବଦ୍ଧ ପରିବାର ନିୟନ୍ତ୍ରଣ କାର୍ଯ୍ୟକ୍ରମକୁ ପରିବାର ନିୟୋଜନ କାର୍ଯ୍ୟକ୍ରମ କୁହାଯାଏ । ପରିବାରର ଆର୍ଥିକ ପରିସ୍ଥିତିକୁ ଲକ୍ଷ୍ୟକରି ପରିବାରର ଆକାର ସୀମିତ ରଖୁବା ପାଇଁ ଭାରତ ସରକାରଙ୍କ ଦ୍ବାରା ଗ୍ରହଣ କରାଯାଇଥିବା ଯୋଜନାବଦ୍ଧ କାର୍ଯ୍ୟକ୍ରମକୁ ପରିବାର ନିୟୋଜନ କାର୍ଯ୍ୟକ୍ରମ କୁହାଯାଏ । ଦୁଇ ସନ୍ତାନ ବିଶିଷ୍ଟ ପରିବାର ଗଠନ କରିବା ଏହି କାର୍ଯ୍ୟକ୍ରମର ମୁଖ୍ୟ ଲକ୍ଷ୍ୟ ।

Question ୪।
ଦ୍ୱୈତ ଅର୍ଥ ବ୍ୟବସ୍ଥା (Dualistic Economic) କ’ଣ ?
Answer:
ଯେଉଁ ଅର୍ଥ ବ୍ୟବସ୍ଥାରେ ଉଭୟ ପାରଂପରିକ କ୍ଷେତ୍ର ଏବଂ ଆଧୁନିକ କ୍ଷେତ୍ରର ସହାବସ୍ଥାନ ଥାଏ, ତାହାକୁ ଦ୍ଵୈତ ଅର୍ଥ ବ୍ୟବସ୍ଥା କୁହାଯାଏ । ଭାରତୀୟ ଅର୍ଥ ବ୍ୟବସ୍ଥା ଏକ ଦ୍ଵୈତ ଅର୍ଥ ବ୍ୟବସ୍ଥା ।

Question ୫।
ମିଶ୍ରିତ ଅର୍ଥନୀତି (Mixed Keonomy) କାହାକୁ କୁହାଯାଏ ?
Answer:
ଯେଉଁ ଅର୍ଥନୀତିରେ ଉଭୟ ସରକାରୀ (କ୍ଷତ୍ର ଓ ଘରୋଇ କ୍ଷେତ୍ରର ସହାବସ୍ଥାନ ଦେଖାଦେଇଥାଏ, ତାହାକୁ ମିଶ୍ରିତ ଅର୍ଥନୀତି ବା ବ୍ୟବସ୍ଥା କୁହାଯାଏ । ଭାରତର ଅର୍ଥ ବ୍ୟବସ୍ଥା ଏକ ମିଶ୍ରିତ ଅର୍ଥ ବ୍ୟବସ୍ଥା !

Question ୬ ।
ଲିଙ୍ଗାନୁପାତ (Sex-Ratio) କ’ଣ ?
Answer:
ପ୍ରତି ଏକ ହଜାର ପୁରୁଷରେ ମହିଳାମାନଙ୍କର ସଂଖ୍ୟାକୁ ଲିଙ୍ଗାନୁପାତ କୁହାଯାଏ । ୨୦୧୧ ମସିହା ଜନଗଣନା ତଥ୍ୟ ଅନୁସାରେ ଭାରତର ଲିଙ୍ଗାନୁପାତ ୯୪୦।

Question ୭ ।
ଜନସଂଖ୍ୟାର ଘନତ୍ଵ (Density Population) କାହାକୁ କୁହାଯାଏ ?
Answer:
ପ୍ରତିବର୍ଗ କିଲୋମିଟର ପିଛା ବସବାସ କରୁଥିବା ଲୋକମାନଙ୍କର ସଂଖ୍ୟାକୁ ଜନସଂଖ୍ୟାର ଘନତ୍ଵ କୁହାଯାଏ । ଦେଶର ମୋଟ ଜନସଂଖ୍ୟାକୁ ଦେଶର ମୋଟ ଅଂଚଳ ସହିତ ଭାଗ କରି ଜନସଂଖ୍ୟାର ଘନତ୍ଵ ନିର୍ଦ୍ଧାରଣ କରାଯାଏ । ୨୦୧୧ ମସିହା ଜନଗଣନା ଅନୁସାରେ ଭାରତର ଜନସଂଖ୍ୟାର ଘନତ୍ଵ ୩୮୨ ।

Question ୮।
ଜନ୍ମହାର (Birth Rate) କାହାକୁ କୁହାଯାଏ ?
Answer:
ପ୍ରତି ଏକ ହଜାର ଜନସଂଖ୍ୟାରେ ହାରାହାରି ଜନ୍ମଲାଭ କରୁଥିବା ଶିଶୁମାନଙ୍କର ସଂଖ୍ୟାକୁ ଜନ୍ମହାର କୁହାଯାଏ । ଉଚ୍ଚ ଜନ୍ମହାର ଭାରତର ଜନସଂଖ୍ୟା ବୃଦ୍ଧିର ମୁଖ୍ୟ କାରଣ ।

Question ୯।
ଶିଶୁ ମୃତ୍ୟୁହାର (IMR) କ’ଣ ?
Answer:
ଏକ ବର୍ଷ ବୟସ ଅତିକ୍ରମ ହେବା ପୂର୍ବରୁ ପ୍ରତି ଏକ ହଜାର ଶିଶୁ ମଧ୍ୟରୁ ମୃତ୍ୟୁବରଣ କରୁଥିବା ଶିଶୁମାନଙ୍କର ସଂଖ୍ୟାକୁ ଶିଶୁ ମୃତ୍ୟୁହାର କୁହଯାଏ । ଭାରତରେ ଶିଶୁ ମୃତ୍ୟୁହାର ଉନ୍ନତ ଦେଶମାନଙ୍କ ତୁଳନାରେ ଅଧ‌ିକ ।

Question ୧୦ ।
ସାକ୍ଷରତା ହାର (Literacy Rate) କ’ଣ ?
Answer:
କୌଣସି ରାଷ୍ଟ୍ରର ଜନସଂଖ୍ୟାର ଗୁଣାତ୍ମକ ଦିଗଟିକୁ ପ୍ରଭାବିତ କରୁଥିବା ଏକ ମୁଖ୍ୟ ଉପାଦାନ ହେଲା ସାକ୍ଷରତା ହାର । ଭାରତରେ ବିଭିନ୍ନ ଦଶନ୍ଧିରେ ସାକ୍ଷରତା ହାର କ୍ରମାଗତ ଭାବରେ ବୃଦ୍ଧି ଘଟିଅଛି । ୧୯୦୧ ମସିହାରେ ଭାରତର ସାକ୍ଷରତା ହାର ମାତ୍ର ୫.୪ ପ୍ରତିଶତ ରହିଥିଲା । ପର୍ଯ୍ୟାୟକ୍ରମେ ଏହା ବୃଦ୍ଧି ପାଇ ଚାଲିଛି । ୧୯୦୧ ମସିହାରେ ଏହା ୫.୪ ପ୍ରତିଶତରୁ ବୃଦ୍ଧି ପାଇ ୨୦୧୧ରେ ଏହା ୭୪.୦୪ ପ୍ରତିଶତରେ ପହଞ୍ଚିପାରିଛି ।

Question ୧୧।
ମୃତ୍ୟୁହାର (Death Rate) କ’ଣ ?
Answer:
ଏକ ହଜାର ଜନସଂଖ୍ୟା ୨୦୧୧ ମସିହା ଜନଗଣନା ତଥ୍ୟ ପ୍ରତି ମୃତ୍ୟୁବରଣ କରୁଥିବା ଲୋକମାନଙ୍କର ସଂଖ୍ୟାକୁ ମୃତ୍ୟୁହାର କୁହାଯାଏ । ଅନୁସାରେ ଭାରତର ମୃତ୍ୟୁହାର ପ୍ରତି ୧୦୦୦ ଜନସଂଖ୍ୟାରେ ୭.୧ ୮.

Question ୧୨ ।
ଆୟୁ ପ୍ରତ୍ୟାଶା ବା ପରମାୟୁ (life Expectancy) କ’ଣ ?
Answer:
ଜଣେ ବ୍ୟକ୍ତି ଜନ୍ମଠାରୁ ମୃତ୍ୟୁ ପର୍ଯ୍ୟନ୍ତ ଜୀବନ କାଳକୁ ପରମାୟୁ କୁହାଯାଏ । ପରମାୟୁ ଧାରଣାଟି ଜନସଂଖ୍ୟାର ଗୁଣାତ୍ମକ ଦିଗ ସହ ସଂଶ୍ଳିଷ୍ଟ ।

Question ୧୩ ।
ବୟସାନୁକ୍ରମିକ ଗଠନ ବା ବୟସ ଢାଞ୍ଚା (Age Structure) କ’ଣ ?
Answer:
କୌଣସି ଦେଶର ଜନ ଶକ୍ତି ବୟସାନୁକ୍ରମିକ ଶ୍ରେଣୀ ପ୍ରକରଣକୁ ବୟସାନୁକ୍ରମିକ ଗଠନ ବା ବୟସ ଢାଞ୍ଚା କୁହାଯାଏ । ୨୦୧୧ ମସିହା ଜନଗଣନା ତଥ୍ୟ ଅନୁସାରେ ୧୫ ରୁ ୫୯ ବର୍ଷ ବୟସ ମଧ୍ୟରେ ୬୪.୪୩ ପ୍ରତିଶତ ଲୋକ ରହିଛନ୍ତି ।

Question ୧୪ ।
୨୦୦୦ ମସିହା ଜନସଂଖ୍ୟା ନୀତିର ଦୁଇଟି ବୈଶିଷ୍ଟ୍ୟ(I’eatures) ଲେଖ ।
Answer:
୨୦୦୦ ମସିହା ଜନସଂଖ୍ୟା ଜାତିର ବୈଶିଷ୍ଟ୍ୟ
(୧) ଜନ୍ମ, ବିବାହ ଏବଂ ମୃତ୍ୟୁର ବାଧ୍ୟତାମୂଳକ ପଞ୍ଜୀକରଣ କରିବାର ବ୍ୟବସ୍ଥା କରାଯାଇଛି ।
(୨) ସଂକ୍ରମଣ ରୋଗର ପ୍ରତିକାର ଏବଂ ପ୍ରତିଷେଧକ ବ୍ୟବସ୍ଥା କରିବା ।

Question ୧୫ ।
୧୯୭୬ ମସିହା ଜନସଂଖ୍ୟା ନୀତିର ଦୁଇଟି ବୈଶିଷ୍ଟ୍ୟ (Features) ଲେଖ ।
Answer:
୧୯୭୬ ମସିହା ଜନସଂଖ୍ୟା ନୀତିର ଦୁଇଟି ବୈଶିଷ୍ଟ୍ୟ ହେଲା-
(୧) ଆଇନ୍‌ଗତ ଭାବରେ ଉଭୟ ପୁରୁଷ ଏବଂ ମହିଳାମାନଙ୍କର ବିବାହ ବୟସକୁ ଯଥାକ୍ରମେ ୨୧ ଏବଂ ୧୮ ବର୍ଷକୁ ବୃଦ୍ଧି କରିବା ।
(୨) ମୋଟ କେନ୍ଦ୍ରୀୟ ଅନୁଦାନ ୮ ପ୍ରତିଶତକୁ କେବଳ ପରିବାର ନିୟୋଜନ କାର୍ଯ୍ୟକ୍ରମରେ ବିନିଯୋଗ କରିବାର ବ୍ୟବସ୍ଥା କରାଯାଇଥିଲା ।

Question ୧୬ ।
ପ୍ରାଥମିକ କ୍ଷେତ୍ର (Primary Sector) କାହାକୁ କୁହାଯାଏ ?
Answer:
ପ୍ରକୃତି ସହିତ ସଂଶ୍ଳିଷ୍ଟ ହୋଇ ଉତ୍ପାଦନ କରାଯାଉଥିବା କ୍ଷେତ୍ରକୁ ପ୍ରାଥମିକ କ୍ଷେତ୍ର କୁହାଯାଏ । ପ୍ରାଥମିକ କ୍ଷେତ୍ରରେ, କୃଷି ଓ କୃଷି ସଂପର୍କିତ କ୍ଷେତ୍ର ଅନ୍ତର୍ଭୁକ୍ତ କରାଯାଇଥାଏ । କୃଷି, ଗୋ-ଗୋପାଳ, କୁକୁଡ଼ା ଚାଷ, ମାଛ ଚାଷ, କଦଳୀ ଚାଷ ଓ ଛତୁ ଚାଷ ଇତ୍ୟାଦିକୁ ଏହି କ୍ଷେତ୍ରରେ ଅନ୍ତର୍ଭୁକ୍ତ କରାଯାଏ ।

Question ୧୭ ।
ମାଧ୍ୟମିକ କ୍ଷେତ୍ର (Secondary Scctor) କାହାକୁ କୁହାଯାଏ ?
Answer:
ମାଧ୍ୟମିକ କ୍ଷେତ୍ର କହିଲେ ବିନିର୍ମାଣ କ୍ଷେତ୍ରକୁ ବୁଝାଏ । ଏହି କ୍ଷେତ୍ରରେ ସମସ୍ତ ପ୍ରକାରର ଶିଳ୍ପ; ଯଥା : ବୃହତ୍ ଶିଳ୍ପ, କ୍ଷୁଦ୍ର ଶିଳ୍ପ ଓ କୁଟୀର ଶିଳ୍ପକୁ ଅନ୍ତର୍ଭୁକ୍ତ କରାଯାଏ । ଏହି କ୍ଷେତ୍ରର ମଧ୍ୟ ବିନିର୍ମାଣ କ୍ଷେତ୍ର କୁହାଯାଏ ।

Question ୧୮।
ତୃତୀୟକ କ୍ଷେତ୍ର (lertiary Sector)କୁ କ’ଣ ?
Answer:
ତୃତୀୟକ କ୍ଷେତ୍ରକୁ ସେବା କ୍ଷେତ୍ର କୁହାଯାଏ । ଏଥିରେ ଉଭୟ ବ୍ୟକ୍ତିଗତ ସେବା ଓ ବ୍ୟବସାୟିକ ସେବାକୁ – ଅନ୍ତର୍ଭୁକ କରାଯାଏ। ଡାକ୍ତରଙ୍କର ରୋଗୀ ସେବା, ଶିକ୍ଷକଙ୍କର ଶିକ୍ଷକତା, ପରିବହନ, ଯୋଗାଯୋଗ, ଶିକ୍ଷା, ସ୍ୱାସ୍ଥ୍ୟ, ବୀମା ସେବା ଇତ୍ୟାଦି ଏହିକ୍ଷେତ୍ର ରହିଥାଏ ।

Question ୧୯।
ବୃତିଗତ ବଣ୍ଟନ (Occupational Structure) କାହାକୁ କୁହାଯାଏ ?
Answer:
ଦେଶର ମୋଟ ଶ୍ରମଶକ୍ତିର ବିଭିନ୍ନ ବୃତ୍ତି ବା ଧନ୍ଦା ମଧ୍ୟରେ ବଣ୍ଟନକୁ ବୃତ୍ତିଗତ ବଣ୍ଟନ କୁହାଯାଏ । ବୃତ୍ତିକୁ ସାଧାରଣତଃ, ତିନୋଟି ଶ୍ରେଣୀରେ ବିଭକତ କରାଯାଇଛି । ସେଗୁଡ଼ିକ ହେଲା– ପ୍ରାଥମିକ ବୃଦ୍ଧି, ମାଧ୍ୟମିକ ବୃଦ୍ଧି ଓ ସେବା

Question ୨୦ ।
ମୁଣ୍ଡପିଚ୍ଛା ଆୟ (Percapita Income) କ’ଣ ?
Answer:
ମୁଣ୍ଡପିଚ୍ଛା ଆୟକୁ ପ୍ରତ୍ୟେକ ବ୍ୟକ୍ତି ପିଚ୍ଛା ଆୟ କୁହାଯାଏ । ଦେଶର ମୋଟ ଜନସଂଖ୍ୟାକୁ ଦେଶର ମୋଟ ଭୂଖଣ୍ଡ ସହିତ ରାଗ କରି ମୁଣ୍ଡପିଛା ଆୟ ନିର୍ଦ୍ଧାରଣ କରାଯାଏ ।

Question ୨୧ ।
ଭାରତର ବୃତ୍ତିଗତ ଢାଞ୍ଚାର ଦୁଇଟି ତ୍ରୁଟି (lefects) ଲେଖ ।
Answer:
ଭାରତର ବୃତ୍ତିଗତ ଢାଞ୍ଚାର ଦୁଇଟି ତ୍ରୁଟି ହେଲା-
(୧) ଭାରତୀୟ ଅର୍ଥ ବ୍ୟବସ୍ଥାର ପ୍ରାଥମିକ କ୍ଷେତ୍ର ଉପରେ ଜନସଂଖ୍ୟାର ଚାପ ଅଧିକ ।
(୨) ଭାରତର ମାଧ୍ୟମିକ କ୍ଷେତ୍ର ସ୍ଵଳ୍ପ ବିକଶିତ ।

IV. ପାର୍ଥକ୍ୟ ଦର୍ଶାଅ । [Distinguish between]

Question ୧।
ଉନ୍ନତ ଦେଶ ଓ ଅନୁନ୍ନତ ଦେଶ (leveloped Country and under-developed country)
Answer:
ଉନ୍ନତ ଦେଶ :
୧. ଯେଉଁ ଦେଶର ଲୋକମାନଙ୍କର ମୁଣ୍ଡପିଛା ଆୟ ଅଧିକ ସେହି ଦେଶକୁ ଉନ୍ନତ ଦେଶ କୁହାଯାଏ ।
୨. ସହିତ ବଞ୍ଚିବାରମାନ ଉନ୍ନତ, ସହରୀକରଣ, ଶିଳ୍ପକ୍ଷେତ୍ରର ପ୍ରାଧାନ୍ୟ ଅଧିକ ଏବଂ ଉଚ୍ଚ ପୁଞ୍ଜି ଅଭିବୃଦ୍ଧି । ଏହି ଦେଶଗୁଡ଼ିକର ବୈଶିଷ୍ଟ୍ୟ !
୩. ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା, ଇଂଲଣ୍ଡ, କାନାଡ଼ା ଓ ଫ୍ରାନ୍ସ ଇତ୍ୟାଦି ଦେଶଗୁଡ଼ିକୁ ଉନ୍ନତ ଦେଶ କୁହାଯାଏ !

ଅନୁନ୍ନତ ଦେଶ :
୧. ଯେଉଁ ଦେଶର ମୁଣ୍ଡ ପିଛା ଆୟ କମ୍ ସେହି ଦେଶକୁ ଅନୁନ୍ନତ ଦେଶ କୁହାଯାଏ ।
୨. ସ୍ଵଳ୍ପ ମୁଣ୍ଡପିଚ୍ଛା ଆୟ, ନିମ୍ନ ସ୍ତରର ବଞ୍ଚିବାର ମାନ, ଜନସଂଖ୍ୟା ବୃଦ୍ଧି, ବେକାରୀ ଦ୍ଵୈତ ଅର୍ଥନୀତି ଏବଂ ସ୍ଵଳ୍ପପୁଞ୍ଜି ଅଭିବୃଦ୍ଧି ହାର ଇତ୍ୟାଦି । ଏହି ସମସ୍ତ ଦେଶର ବୈଶିଷ୍ଟ୍ୟ ।
୩. ଭାରତ, ପାକିସ୍ତାନ, ଶ୍ରୀଲଙ୍କା ଓ ବ୍ରାଜିଲ୍ ଇତ୍ୟାଦି ଦେଶଗୁଡ଼ିକୁ ଅନ୍ନନତ ଦେଶ କୁହାଯାଏ ।

୨। ପ୍ରାଥମିକ କ୍ଷେତ୍ର ଓ ମାଧ୍ଯମିକ କ୍ଷେତ୍ର । (Primary Sector and Secondary Sector)
ପ୍ରାଥମିକ କ୍ଷେତ୍ର :
୧. ପ୍ରକୃତି ସହିତ ସଂଶ୍ଳିଷ୍ଟ ହୋଇ କାର୍ଯ୍ୟ କରୁଥିବା କ୍ଷେତ୍ରକୁ ପ୍ରାଥମିକ କ୍ଷେତ୍ର କୁହାଯାଏ ।
୨. ଏହି କ୍ଷେତ୍ରରେ କୃଷି ଓ କୃଷି ସଂପର୍କିତ କ୍ଷେତ୍ରକୁ ଅନ୍ତର୍ଭୁକ୍ତ କରାଯାଏ ।
୩. ମନୁଷ୍ୟ ବଞ୍ଚି ରହିବା ପାଇଁ ଏହି କ୍ଷେତ୍ର ଉପରେ ନିର୍ଭର କରିଥାଏ ।

ମାଧ୍ୟମିକ କ୍ଷେତ୍ର:୭
୧. ବିନିର୍ମାଣ କ୍ଷେତ୍ର ସହିତ ସଂଶ୍ଳିଷ୍ଟ କ୍ଷେତ୍ରକୁ ମାଧ୍ୟମିକ କ୍ଷେତ୍ର କୁହାଯାଏ ।
୨. ଏହି କ୍ଷେତ୍ରରେ ସମସ୍ତ ପ୍ରକାରର ଶିଳ୍ପକୁ ଅନ୍ତର୍ଭୁକ୍ତ କରାଯାଏ ।
୩. ମନୁଷ୍ୟର ଅନ୍ୟାନ୍ୟ ଆବଶ୍ୟକତା ଏହି କ୍ଷେତ୍ର ଦ୍ବାରା ଉତ୍ପାଦନ କରାଯାଏ !

୩। ଜନ୍ମହାର ଓ ମୃତ୍ୟୁହାର । (Birth Rate and leath Rate)
ଜନ୍ମହାର :
୧. ପ୍ରତି ଏକ ହଜାର ଜନସଂଖ୍ୟାରେ ହାରାହାରି ଜନ୍ମ ଲାଭ କରୁଥିବା ଶିଶୁ ସଂଖ୍ୟାକୁ ଜନ୍ମହାର କୁହାଯାଏ ।
୨. ଭାରତରେ ଜନ୍ମହାର ହ୍ରାସ ପାଉଛି ।
୩. ଉଚ୍ଚ ଜନ୍ମହାର ଜନସଂଖ୍ୟା ବୃଦ୍ଧିର ମୁଖ୍ୟ କାରଣ ।

ମୃତ୍ୟୁହାର :
୧. ଏକ ହଜାର ଜନସଂଖ୍ୟା ପ୍ରତି ମୃତ୍ୟୁବରଣ କରୁଥିବା ଲୋକସଂଖ୍ୟାକୁ ମୃତ୍ୟୁହାର କୁହାଯାଏ ।
୨. ଭାରତରେ ମୃତ୍ୟୁହାର ହ୍ରାସ ପାଉଛି ।
୩. ନିମ୍ନସ୍ତରର ମୃତ୍ୟୁହାର ଜନସଂଖ୍ୟା ବୃଦ୍ଧିର ଏକ କାରଣ ।

V. ପ୍ରତ୍ୟେକଟି ଉତ୍ତର ୭୫ଟି ଶବ୍ଦର ଦେବାକୁ ହେବ । [Answer in 75 Words.]

Question ୧।
ପ୍ରାଥମିକ କ୍ଷେତ୍ର (Prinary Sector):
Answer:
ଦେଶର ସମସ୍ତ ଉତ୍ପାଦନକ୍ଷମ ଉତ୍ସଗୁଡ଼ିକୁ ମୁଖ୍ୟତଃ ତିନି ଶ୍ରେଣୀରେ ବିଭକ୍ତ କରାଯାଇଛି । ସେଗୁଡ଼ିକ ହେଲା (୧) ପ୍ରାଥମିକ କ୍ଷେତ୍ର, (୨) ମାଧ୍ୟମିକ କ୍ଷେତ୍ର ଏବଂ (୩) ସେବା କ୍ଷେତ୍ର । ପ୍ରାଥମିକ କ୍ଷେତ୍ରକୁ ବୃତ୍ତିଗତ ଢାଞ୍ଚାରେ ପ୍ରଥମ ଏବଂ ଗୁରୁତ୍ବପୂର୍ଣ୍ଣ କ୍ଷେତ୍ରଭାବେ ଗଣନା କରା ପ୍ରାଥମିକ କ୍ଷେତ୍ର କହିଲେ କୃଷିକ୍ଷେତ୍ର ଏବଂ କୃଷି ସଂପର୍କିତ ଅନ୍ୟାନ୍ୟ କ୍ଷେତ୍ରକୁ ବୁଝାଏ । ଏହି କ୍ଷେତ୍ରରେ କୃଷି, ଗୋପାଳନ, କୁକୁଡ଼ା ଚାଷ, ମାଛ ଚାଷ, କଦଳୀ ଚାଷ, ଛତୁ ଚାଷ, ଗୁଣ୍ଡୁରି ଚଢ଼େଇ ଚାଷ, ମହୁ ଚାଷ ଇତ୍ୟାଦିକୁ ଅନ୍ତର୍ଭୁକ୍ତ କରାଯାଇଥାଏ । ଏହି କ୍ଷେତ୍ର ପ୍ରକୃତି ସହିତ ସଂଶ୍ଳିଷ୍ଟ ଥାଏ । ପ୍ରାକୃତିକ ସମ୍ବଳର ବିନିଯୋଗ ଏହି କ୍ଷେତ୍ରର ଉତ୍ପାଦନ ପ୍ରକ୍ରିୟାରେ ପ୍ରାଧାନ୍ୟ ଲାଭ କରିଥାଏ । ପ୍ରାଥମିକ କ୍ଷେତ୍ରରେ ଉତ୍ପାଦିତ ଦ୍ରବ୍ୟ ଜୀବନ ଧାରଣ ପାଇଁ ଅତ୍ୟନ୍ତ ଆବଶ୍ୟକ !

Question ୨।
ଦ୍ବିତୀୟକ କ୍ଷେତ୍ର (Secondary sector):
Answer:
ଦ୍ଵିତୀୟକ କ୍ଷେତ୍ରରେ ନିୟୋଜିତ ଶ୍ରମିକମାନେ ନିର୍ମାଣ କାର୍ଯ୍ୟ କରିଥାନ୍ତି । ଏହି କ୍ଷେତ୍ରରେ ପ୍ରାକୃତିକ ସମ୍ବଳକୁ ଉପଯୋଗ କରି ବିଭିନ୍ନ ଖାଉଟି ଦ୍ରବ୍ୟ ତଥା ଉତ୍ପାଦକ ଦ୍ରବ୍ୟ ଉତ୍ପାଦନ କରାଯାଏ । ଏହି କ୍ଷେତ୍ର ପ୍ରକୃତି ସହିତ ସଂଶ୍ଳିଷ୍ଟ ନଥାଏ । ମାଧ୍ୟମିକ କ୍ଷେତ୍ରରେ ସମସ୍ତ ପ୍ରକାରର ଶିଳ୍ପ ; ଯଥା – ବୃହତ୍ ଶିଳ୍ପ, କ୍ଷୁଦ୍ର ଶିଳ୍ପ ଓ କୁଟୀର ଶିଳ୍ପ ଅନ୍ତର୍ଭୁକ୍ତ ହୋଇଥାଏ । ଏତଦ୍‌ବ୍ୟତୀତ ନିର୍ମାଣ, ବିଜୁଳି ଶକ୍ତି, ଜଳଯୋଗାଣ ଇତ୍ୟାଦି ଅର୍ଥନୈତିକ ଓ ଉତ୍ପାଦନଶୀଳ କାର୍ଯ୍ୟକଳପେକୁ ନେଇ ଦ୍ଵିତୀୟକ କ୍ଷେତ୍ର ଗଠିତ । ବୃହତ୍ ଓ କ୍ଷୁତ୍ର ନିର୍ମାଣକାରୀ ସଂସ୍ଥା ଏହି କ୍ଷେତ୍ରରେ ଅନ୍ତର୍ଭୁକ୍ତ । ଏହି କ୍ଷେତ୍ର ପ୍ରାଥମିକ କ୍ଷେତ୍ରର ଉତ୍ପାଦକୁ କଞ୍ଚାମାଲ ରୂପେ ବ୍ୟବହାର କରିଥାଏ । ତେଣୁ ଏହି କ୍ଷେତ୍ର ପୁଞ୍ଜିଭିଭିକ।

Question ୩।
ସେବା କ୍ଷେତ୍ର (Service Sector):
Answer:
ତୃତୀୟକ କ୍ଷେତ୍ର ସମସ୍ତ ସେବା କ୍ଷେତ୍ରକୁ ନେଇ ଗଠିତ । ତୃତୀୟକ କ୍ଷେତ୍ରରେ ଉଭୟ ବ୍ୟକ୍ତିଗତ ସେବା (Personal service) ଓ ବ୍ୟବସାୟିକ ସେବା ଅନ୍ତର୍ଭୁକ୍ତ ହୋଇଥାଏ । ପରିବହନ , ଯୋଗାଯୋଗ, ବ୍ୟାଙ୍କ, ବୀମା, ଶିକ୍ଷା, ସ୍ବାସ୍ଥ୍ୟ ଇତ୍ୟାଦିକୁ ବ୍ୟବସାୟିକ ସେବା କୁହାଯାଏ । ଶିକ୍ଷକଙ୍କ ଶିକ୍ଷକତା, ଡାକ୍ତରଙ୍କ ରୋଗୀସେବା, ଓକିଲଙ୍କ ଓକିଲାତି ଇତ୍ୟାକୁ ବ୍ୟକ୍ତିଗତ ସେବା କୁହାଯାଏ । ମୋଟ ଉପରେ ସମସ୍ତ ଅର୍ଥନୈତିକ କାର୍ଯ୍ୟକଳାପ ଏହି କ୍ଷେତ୍ରରେ ଅନ୍ତର୍ଭୁକ୍ତ । ଏହି କ୍ଷେତ୍ର ଉଭୟ ପ୍ରାଥମିକ ଓ ଦ୍ଵିତୀୟକ କ୍ଷେତ୍ରର ବିକାଶ ପାଇଁ ସହାୟତା କରିଥାଏ । ଏହି ତୃତୀୟକ କ୍ଷେତ୍ରରେ କେବଳ ଅର୍ଥନୈତିକ ସେବାର ଅଭିବୃଦ୍ଧି ଲକ୍ଷ୍ୟ କରାଯାଇଥାଏ । ଅର୍ଥନୈତିକ ବିକାଶ ପ୍ରକ୍ରିୟା ସହିତ ସେବାକ୍ଷେତ୍ରର ବିକାଶ ହୋଇଥାଏ ।

Question ୪।
ଭାରତର ବୃତ୍ତିଗତ ଢାଞ୍ଚା (Occupational Structure of India):
Answer:
ଭାରତର ବୃତ୍ତିଗତ ଢାଞ୍ଚା, ପ୍ରାଥମିକ, ଦ୍ଵିତୀୟକ ଓ ତୃତୀୟକ କ୍ଷେତ୍ରକୁ ନେଇ ଗଠିତ । ସ୍ଵାଧୀନତା ପ୍ରାପ୍ତି ପୂର୍ବରୁ ଭାରତର ବୃତ୍ତିଗତ ଢ଼ାଞ୍ଚା ଅସନ୍ତୁଳିତ ଥିଲା । ସ୍ଵାଧୀନତାର ପରବର୍ତୀ ସମୟରେ ଆମ ଦେଶର ବୃତ୍ତିଗତ ଢାଞ୍ଚାରେ ପରିବର୍ତ୍ତନ ଆସିଛି । କିନ୍ତୁ, ପାଶ୍ଚାତ୍ୟ ଦେଶମାନଙ୍କରେ ପରିଲକ୍ଷିତ ଢାଞ୍ଚାଗତ ପରିବର୍ତ୍ତନ ଆମ ଦେଶରେ ଅନୁଭୂତ ହୋଇନାହିଁ । କୃଷିକ୍ଷେତ୍ର ଉପରେ ନିର୍ଭରଶୀଳତା, ମନ୍ଥର ଶିଳ୍ପ ବିକାଶ, ନିମ୍ନ ବିକଶିତ ସେବାକ୍ଷେତ୍ର, ନିମ୍ନ ଆୟସ୍ତର, ଅସନ୍ତୁଳିତ ବିକାଶ ଇତ୍ୟାଦି ଆମ ଦେଶର ବୃତ୍ତିଗତ ଢ଼ାଞ୍ଚାର ବୈଶିଷ୍ଟ୍ୟ । ଭାରତର ବୃତ୍ତିଗତ ଢାଞ୍ଚାରେ ପରିବର୍ତ୍ତନ ଆଣିବାକୁ ହେଲେ ପ୍ରାଥମିକ କ୍ଷେତ୍ର ଉପରେ ନିର୍ଭରଶୀଳତାର ହ୍ରାସ, ଶିଳ୍ପ ଓ ସେବା କ୍ଷେତ୍ରର ବିକାଶସାଧନ, ଜନ ବିସ୍ଫୋରଣ ସମସ୍ୟାର ସମାଧାନ, ଫଳପ୍ରଦ ଆଞ୍ଚଳିକ ବିକାଶ କାର୍ଯ୍ୟକ୍ରମ, ଗ୍ରାମାଞ୍ଚଳରେ ଶିଳ୍ପମାନ ସ୍ଥାପନ ଇତ୍ୟାଦି କାର୍ଯ୍ୟକ୍ରମ ଗ୍ରହଣ କରିବାକୁ ହେବ ?

Question ୫।
ବୃତ୍ତିଗତ ଢାଞ୍ଚା (Occupational Structure):
Answer:
ବୃତ୍ତିଗତ ଢ଼ାଞ୍ଚା ମୋଟ୍ ଶ୍ରମଶକ୍ତିର ନିଯୁକ୍ତି ଦର୍ଶାଇଥାଏ । ବୃତ୍ତିଗତ ଢାଞ୍ଚା କହିଲେ, ଭିନ୍ନ ଭିନ୍ନ ବୃତ୍ତି ବା କ୍ଷେତ୍ରରେ ନିଯୁକ୍ତି ଥିବା ଶ୍ରମଶକ୍ତିକୁ ବୁଝାଇଥାଏ । ଦେଶର ମୋଟ ଶ୍ରମଶକ୍ତିକୁ ତିନିଗୋଟି ବୃତ୍ତିରେ ବଣ୍ଟନ କରାଯାଇଥାଏ; ଯଥା ପ୍ରାଥମିକ ବୃତ୍ତି, ଦ୍ଵିତୀୟକ ବୃତ୍ତି ଓ ତୃତୀୟକ ବୃତ୍ତି । ଅର୍ଥନୈତିକ ବିକାଶ ଓ ବୃତ୍ତିଗତ ଢାଞ୍ଚା ମଧ୍ୟରେ ନିବିଡ ସଂପର୍କ ରହିଥାଏ । ଅର୍ଥନୈତିକ ବିକାଶ ବୃତ୍ତିଗତ ଢାଞ୍ଚାରେ ପରିବର୍ତ୍ତନ ଆଣିଥାଏ । ଏହି ମୁଖ୍ୟ ତିନିଗୋଟି କ୍ଷେତ୍ର; ଯଥା ପ୍ରାଥମିକ କ୍ଷେତ୍ର, ଦ୍ଵିତୀୟକ କ୍ଷେତ୍ର ଓ ତୃତୀୟକ କ୍ଷେତ୍ରରେ ଶ୍ରମଶକ୍ତିର ନିଯୁକ୍ତିରେ ଯେଉଁ ପରିବର୍ତ୍ତନ ଦେଖାଯାଏ, ତାହା ବୃତ୍ତିଗତ ଢ଼ାଞ୍ଚାରେ ପରିବର୍ତ୍ତନ କୁହାଯାଏ । ପ୍ରଫେସର ଏ.ଜି.ବି ଫିସର୍‌ଙ୍କ ସିଦ୍ଧାନ୍ତ ଅନୁସାରେ ରାଷ୍ଟ୍ରର ବିକାଶ ସହିତ ପ୍ରାଥମିକ କ୍ଷେତ୍ରରେ ନିୟୋଜିତ ଶ୍ରମଶକ୍ତିର ଅନୁପାତ ହ୍ରାସ ପାଏ ଏବଂ ଦ୍ଵିତୀୟକ ଓ ତୃତୀୟକ କ୍ଷେତ୍ରରେ ନିଯୁକ୍ତି ଶ୍ରମଶକ୍ତିର ବୃଦ୍ଧି ଘଟେ । ଦେଶର ବୃତ୍ତିଗତ ଢାଞ୍ଚାରେ ପରିବର୍ତନ ହେଲେ ଦେଶର ଅର୍ଥନୈତିକ ବିକାଶସାଧନ ହୋଇଥାଏ ।

Question ୬।
ସାମନ୍ତବାଦୀ ଅର୍ଥବ୍ୟବସ୍ତୁ (Feudalistic Economic System):
Answer:
ସାମନ୍ତବାଦ ଏକ ସାମାଜିକ ଓ ଅର୍ଥନୈତିକ ବ୍ୟବସ୍ଥା । ମଧ୍ୟଯୁଗରେ ଇଉରୋପରେ ଏହି ବ୍ୟବସ୍ଥା ଦେଖା ଦେଇଥିଲା । ଏହି ବ୍ୟବସ୍ଥାରେ ସାମନ୍ତବାଦୀମାନେ ଚାଷୀମାନଙ୍କୁ ଚାଷ ନିମନ୍ତେ ଜମି ଦେଇ ସମସ୍ତ ସୁରକ୍ଷା ଯୋଗାଇ ଦେଉଥିଲେ ଏବଂ ପ୍ରତିବଦଳରେ ସେମାନଙ୍କୁ ନିଜ ଆବଶ୍ୟକ ନିମନ୍ତେ ବିଭିନ୍ନ କାର୍ଯ୍ୟରେ ନିୟୋଜିତ ହେବାପାଇଁ ବାଧ୍ୟ କରୁଥିଲେ । ଇଂରେଜ ଶାସନକାଳ ମଧ୍ୟରେ ସାମନ୍ତବାଦୀ ଅର୍ଥବ୍ୟବସ୍ଥାର ସମ୍ୟକ୍ ଝଲକ ଦେଖ‌ିବାକୁ ମିଳିଥିଲଶ । ଇଂରେଜମାନେ ଆମ ଦେଶର ଭୂ-ରାଜସ୍ୱ ସଂଗ୍ରହର ଅଧିକାର ହାତେଇଥିଲେ । ସେମାନେ ଜମିଦାରୀ ପ୍ରଥାର ପ୍ରଚଳନ କରିଥିଲେ । ଜମିଦାରମାନେ ଚାଷୀମାନଙ୍କଠାରୁ ଜମିର ଖଜଣା ମନଇଛା ଆଦାୟ କରୁଥିଲେ । ସେମାନେ ଚାଷୀମାନଙ୍କୁ ବିଭିନ୍ନ ଉପାୟରେ ଅତ୍ୟାଚାର ଓ ଶୋଷଣ କରୁଥିଲେ । ତେଣୁ ସ୍ଵାଧୀନତା ପ୍ରାପ୍ତି ସମୟରେ ଭାରତୀୟ ଅର୍ଥବ୍ୟବସ୍ଥାରେ କେତେକାଂଶରେ ସମାନ୍ତବାଦୀ ଅର୍ଥବ୍ୟବସ୍ଥାକୁ ରୂପାନ୍ତରିତ ହୋଇଥିଲା

Question ୭।
ଔପନିବେଶିକ ଅର୍ଥବ୍ୟବସ୍ତୁ (Colonial Economic System):
Answer:
ଯେଉଁ ଶାସନ ବ୍ୟବସ୍ଥାରେ ଗୋଟିଏ ରାଷ୍ଟ୍ର ଅନ୍ୟ ଗୋଟିଏ ରାଷ୍ଟ୍ର ଉପରେ ନିଜ ଅର୍ଥନୈତିକ, ରାଜନୈତିକ ଏବଂ ସାର୍ବଭୌମତ୍ବ ଅଧ୍ଯକାର ବିସ୍ତାର କରିଥାଏ, ତାହାକୁ ଔପନିବେଶିକ ଅର୍ଥବ୍ୟବସ୍ଥା କୁହାଯାଏ । ଏହି ବ୍ୟବସ୍ଥାରେ ସମୟ କ୍ରମେ ଶାସନ ରାଷ୍ଟ୍ର ସହିତ ଶାସିତ ରାଷ୍ଟ୍ର ଅର୍ଥନୀତି ମିଶ୍ରଣ ହୋଇଥାଏ । ଇଂରେଜ ସରକାର ଦୀର୍ଘ ୨୦୦ ବର୍ଷରୁ ଉର୍ଦ୍ଧ ଶାସନ କାଳ ସମୟରେ ଭାରତୀୟ ଅର୍ଥବ୍ୟବସ୍ଥାକୁ ଏକ ଔପନିବେଶିକ ଅର୍ଥ ବ୍ୟବସ୍ଥାରେ ପରିଣତ କରିଥିଲେ । ସମ୍ବଳର ବିନିଯୋଗ, ଭିତ୍ତିଭୂମିର ବିକାଶ ଇତ୍ୟାଦି ସମସ୍ତ କ୍ଷେତ୍ରରେ ବ୍ରିଟିଶ୍ ସରକାର ଚୂଡାନ୍ତ ନିଷ୍ପତ୍ତି ନେଉଥଳେ । ଏହି ସମସ୍ତ ନିଷ୍ପଭି ଇଂରେଜ ସରକାରଙ୍କ ସ୍ଵାର୍ଥସାଧନ ନିମନ୍ତେ ପ୍ରେରିତ ଥିଲା । ଭାରତୀୟ ଅର୍ଥବ୍ୟବସ୍ଥାରେ ଇଂରେଜ ସରକାରଙ୍କ ଆଧ‌ିପତ୍ୟ ବୃଦ୍ଧି ପାଇଥିଲା । ଇଂରେଜ ସରକାରଙ୍କର ଏହି ଔପନିବେଶିକ ନୀତି ଭାରତୀୟ ଅର୍ଥବ୍ୟବସ୍ଥାକୁ ଦୁର୍ବଳ କରି ଦେଇଥିଲା ।

Question ୮।
ଅନଗ୍ରସର ଅର୍ଥନୀତି (lackward Iconomy);
Answer:
ଦୀର୍ଘ ୨୦୦ ବର୍ଷରୁ ଉର୍ଦ୍ଧ୍ଵ ଇଂରେଜ ଶାସନ ଭାରତୀୟ ଅର୍ଥବ୍ୟବସ୍ଥାକୁ ବିପର୍ଯ୍ୟନ୍ତ କରିଥିଲା । ନିଜସ୍ଵ ସ୍ଵାର୍ଥ ସାଧନର ଅଭୀପ୍‌ସ! ଭାରତକୁ ଦିନକୁ ଦିନ ଗରିବ କରିଥିଲା । ପ୍ରଚୁର ପୁଞ୍ଜି ଓ ସମ୍ବଳର ବହିର୍ଗମନ ଭାରତୀୟ ଅର୍ଥ ବ୍ୟବସ୍ଥାକୁ ରୋଗାକ୍ରାନ୍ତ କରିଥିଲା । ନୀତି ଓ ଦିଶାହୀନ ଇଂରେଜ ଶାସନ ଅର୍ଥନୀତିର ପ୍ରତ୍ୟେକ ସ୍ତରରେ ଅଧଃପତନ ଘଟାଇଥିଲା । ଶିଳ୍ପ ଓ କୃଷି ଆଦି କ୍ଷେତ୍ରରେ ଅବହେଳା ପ୍ରଦର୍ଶନ କରାଯିବାରୁ ଦାରିଦ୍ର୍ୟ ଓ ବେକାରୀ ବୃଦ୍ଧି ପାଇଲା । ସ୍ଵାଧୀନତା ପ୍ରାପ୍ତି ସମୟରେ ସମଗ୍ର ବିଶ୍ଵରେ ଭାରତ ଏକ ଅନୁନ୍ନତ ଓ ଅନଗ୍ରସର ଅର୍ଥନୀତିଭାବେ ପରିଗଣିତ ହେଲା ।

Question ୯।
ସୁଣୁ ଅର୍ଥନୀତି (Stagnant [conomy):
Answer:
ଇଂରେଜ ଶାସନ ସମୟରେ ଭାରତର ପ୍ରାକୃତିକ ତଥା ମାନବ ସମ୍ବଳ କ୍ରମାଗତଭାବେ ଶୋଷିତ ହୋଇଥିଲା । ଭାରତର ପ୍ରାକୃତିକ ଓ ମାନବ ସମ୍ବଳ କୁ ଇଂରେଜ ସରାକର ନିଜ ଦେଶକୁ ପ୍ରେରଣ କରି ସେଠାକାର ଉତ୍ପାଦିକ ପଦାର୍ଥକୁ ଭାରତର ଲୋକମାନଙ୍କୁ କ୍ରୟ କରିବାପାଇଁ ବାଧ୍ୟ କରୁଥିଲେ ନିଜସ୍ଵ ସମ୍ବଳରେ ଉତ୍ପାଦିତ ଦ୍ରବ୍ୟକୁ ଇଂରେଜ ସରକାରଙ୍କ ଦ୍ଵାରା ଧାର୍ଯ୍ୟ ଦରରେ କ୍ରୟ କରି ଭାରତର ଲୋକମାନେ ଶୋଷିତ ହେଉଥିଲେ । ସମୟ କ୍ରମେ ଭାରତୀୟ ଶିଳ୍ପଗୁଡ଼ିକ ବନ୍ଦ ହେଲା ଏବଂ ଇଂଲଣ୍ଡର ଶିଳ୍ପଜାତ ଦ୍ରବ୍ୟର ବିକ୍ରି ବୃଦ୍ଧି ହେବା ଫଳରେ ଇଂଲଣ୍ଡର ଶିଳ୍ପିକ ବିକାଶସାଧନ ହେଲା । ଦାରିଦ୍ର୍ୟ ଓ ବେକାରୀ ବୃଦ୍ଧି ଆମ ଦେଶର ଅର୍ଥବ୍ୟବସ୍ଥାକୁ ସ୍ଥାଣୁ କରିଦେଲା ।

ବ୍ୟବସାୟିକ ଉଦ୍ଦେଶ୍ୟ ରଖୁ ଦୀର୍ଘ ୨୦୦ ବର୍ଷ ଧରି ଶାସନ କରିଥିବା ଇଂରେଜ ସରକାର ଭାରତୀୟ ଅର୍ଥନୀତିର ମେରୁଦଣ୍ଡକୁ ଦୁର୍ବଳ କରିଥିଲେ । ଷୋଡଶ ଓ ସପ୍ତଦଶ ଶତାବ୍ଦୀରେ ଯେଉଁ ଭାରତ ଏକ ଶିଳ୍ପସମୃଦ୍ଧ ରାଷ୍ଟ୍ରଭାବେ ବିଶ୍ଵ ଦରବାରରେ ପରିଗଣିତ ହେଉଥିଲା । ଅଷ୍ଟାଦଶ ଓ ଉନବିଂଶ ଶତାବ୍ଦୀବେଳକୁ ସେହି ଦେଶ ଶିଳ୍ପକ୍ଷେତ୍ରରେ ଏକ ଦୁର୍ବଳ ରାଷ୍ଟ୍ରଭାବରେ ପରିଚିତ ହେଲା । ସମଗ୍ର ବିଶ୍ବରେ ଖ୍ୟାତି ଅର୍ଜନ କରିଥିବା ଭାରତୀୟ ହସ୍ତଶିଳ୍ପ ଓ କୁଟୀର ଶିଳ୍ପ କ୍ରମଶଃ ନିଜସ୍ଵ ସତ୍ତା ହରାଇଲା । ଭାରତୀୟ ଅର୍ଥନୀତି ମୁଖ୍ୟତଃ ଏକ ଆମଦାନୀକାରୀ ଅର୍ଥନୀତିର ରୂପ ନେଲା ।

Question ୧୦ ।
ଦ୍ଵୈତ ଅର୍ଥନୀତି (Hualistic Economy):
Answer:
ଦୈତ୍ୟ ଅର୍ଥବ୍ୟବସ୍ଥାରେ ପାରମ୍ପରିକ ପଦ୍ଧତି ଓ ଆଧୁନିକ ପଦ୍ଧତିର ସହାବସ୍ଥାନ ଦେଖିବାକୁ ମିଳେ । ଏହି ଅର୍ଥବ୍ୟବସ୍ଥା ଆଧୁନିକ ମୁଦ୍ରା ବ୍ୟବସ୍ଥା ଓ ପାରମ୍ପରିକ ପଣ୍ୟ ବିନିମୟ ବ୍ୟବସ୍ଥାର ସହାବସ୍ଥାନ ଦେଖିବାକୁ ମିଳିଥାଏ । ଅନ୍ୟ ଅନୁନ୍ନତ ଅର୍ଥବ୍ୟବସ୍ଥା ଭଳି ଭାରତୀୟ ଅର୍ଥବ୍ୟବସ୍ଥାକୁ ମଧ୍ୟ ଏକ ଦ୍ଵୈତ ଅର୍ଥବ୍ୟବସ୍ଥା କୁହାଯାଏ । ପ୍ରଥମ ଧରଣର ବ୍ୟବସ୍ଥା ସହରାଞ୍ଚଳରେ ଦେଖିବାକୁ ମିଳିଥାଏ । ଦ୍ଵିତୀୟ ଧରଣର ବ୍ୟବସ୍ଥା ଗ୍ରାମାଞ୍ଜନରେ ଦେଖିବାକୁ ମିଳିଥାଏ । ସହରାଞ୍ଚଳରେ ଆଧୁନିକ ଜୀବନଯାପନ, ସଂଗଠିତ ଶ୍ରମିକ, ଶିଳ୍ପର ବିକାଶ, ଉଚ୍ଚଶିକ୍ଷା ଓ ଉନ୍ନତି ସ୍ଵାସ୍ଥ୍ୟ ବ୍ୟବସ୍ଥା ରହିଥିବାବେଳେ ଗ୍ରାମାଞ୍ଚଳରେ ଅନୁନ୍ନତ ଜୀବନଯାପନ, ଅସଂଗଠିତ ଶ୍ରମିକ, ଅନୁନ୍ନତ କୃଷିକ୍ଷେତ୍ର, ଶିକ୍ଷା, ସ୍ୱାସ୍ଥ୍ୟ, ଗମନାଗମନର ଘୋର ଅଭାବ ପରିଲକ୍ଷିତ ହୋଇଥାଏ । ଭାରତ ଭଳି ଏକ ଗ୍ରାମବହୁଳ ରାଷ୍ଟ୍ରରେ ଦ୍ଵୈତ ଅର୍ଥବ୍ୟବସ୍ଥା ଦାରିଦ୍ର୍ୟକୁ ତୀବ୍ରତର କରି ରାଷ୍ଟ୍ର ବିକାଶ ପଥରେ ପ୍ରତିବନ୍ଧକ ସୃଷ୍ଟି କରୁଛି ।

Question ୧୧।
ଅର୍ଥବ୍ୟବସ୍ଥାର ରଚନାତ୍ମକ ପରିବର୍ତ୍ତନ :
Answer:
ପ୍ରାଥମିକ, ମାଧ୍ୟମିକ ଓ ସେବା ଭଳି ଉତ୍ପାଦନର କ୍ଷେତ୍ରଗୁଡ଼ିକୁ ବୃତ୍ତିର ଉତ୍ସ ରୂପେ ବିବେଚନା କରାଯାଏ । ଯେଉଁଠାରୁ ଆୟ ଉତ୍ପତ୍ତି ସମ୍ଭବ ହୁଏ, ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ସମୟ ସୀମା ମଧ୍ୟରେ ମୋଟ ଉତ୍ପନ୍ନ ଆୟରେ ଉତ୍ପାଦନ କ୍ଷେତ୍ରର ଅବଦାନଗତ ଗୁରୁତ୍ଵକୁ ବିଚାର କରିବାକୁ ଉତ୍ପାଦନ ଢାଞ୍ଚା କୁହାଯାଏ । କିନ୍ତୁ ସମୟକୁ ସମୟ ଉତ୍ପାଦନ ଢାଞ୍ଚାରେ ପରିବର୍ତ୍ତନ ବା ଉତ୍ପାଦନ କ୍ଷେତ୍ରଗୁଡ଼ିକର ମୋଟ ଉତ୍ପନ୍ନ ଆୟରେ ତୁଳନାତ୍ମକ ଅବଦାନ ସ୍ଥିତିରେ ପରିବର୍ତ୍ତନକୁ ଅର୍ଥ ବ୍ୟବସ୍ଥାର ରଚନାତ୍ମକ ପରିବର୍ତ୍ତନ କୁହାଯାଏ ।

Question ୧୨ ।
ଭାରତରେ ବୃତ୍ତିଗତ ଢାଞ୍ଚାର ପରିବର୍ତ୍ତନ
(Changes in the occupational structure in India :
Answer:
ବୃତ୍ତି କହିଲେ ଶମଶକ୍ତି ଦ୍ଵାରା ସଂଗଠିତ ଆର୍ଥନୀତିକ କାର୍ଯ୍ୟକଳାପ ଓ ନିୟୋଜିତ ଶ୍ରମଶକ୍ତିର ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ କାଳରେ ବୃତ୍ତିଗତ ଓ ବିଭାଜନଙ୍କ ଗୁରୁତ୍ୱକୁ ଉପସ୍ଥାପନା କରିବାକୁ ବୃତ୍ତିଗତ ଢାଞ୍ଚା କୁହାଯାଏ । ସମୟାନୁକ୍ରମିକ ବୃଭିଗତ ଢାଞ୍ଚାର ଉପସ୍ଥାପନା ବା ନିୟୋଜିତ ଓ ଶ୍ରମଶକ୍ତିର ବୃଭିଗତ ବିଭାଜନ ଢାଞ୍ଚାରେ ପରିବର୍ତ୍ତନର ଉପସ୍ଥାପନାକୁ ବୃଭିଗତ ଢ଼ାଞ୍ଚାର ପରିବର୍ତ୍ତନ କୁହାଯାଏ। ଭାରତରେ ବୃତ୍ତିଗତ ଢାଞ୍ଚାର ନିଷ୍ଠୁର ପରିବର୍ତ୍ତନ ଉପଲବ୍ଧ ନହେଲେହେଁ ଏହାର ପରିବର୍ଭନୀୟ ଗୁଣ ଯାହା ପ୍ରଦର୍ଶନ କରେ ତାହାହେଲେ ପ୍ରାଥମିକ ବୃଭିର ଗୁରୁତ୍ଵ କ୍ରମାଗତ ହ୍ରାସ ପାଉଥିବାବେଳେ ସେବା କ୍ଷେତ୍ରର ଗୁରୁତ୍ଵ ମାଧ୍ୟମିକ କ୍ଷେତ୍ରଠାରୁ କ୍ରମାଗତ ଅଧ‌ିକ ବୃଦ୍ଧି ପାଇ ଆସୁଅଛି ।

Question ୧୩।
ମୁଣ୍ଡପିଛା ଉତ୍ପାଦ(Product Per capita) :
Answer:
ମୁଣ୍ଡପିଛା ଉତ୍ପାଦନ ବ୍ୟକ୍ତିପ୍ରତି ହାରାହାରି ଉତ୍ପାଦନକୁ ବୁଝାଏ । ମୋଟ ଜାତୀୟ ଉତ୍ପାଦନକୁ ଲୋକସଂଖ୍ୟା ଦ୍ଵାରା ଭାଗକରି ଏହା ନିର୍ଦ୍ଧାରଣ କରାଯାଇଥାଏ, ଯାହା ବାସ୍ତବ ମୁଣ୍ଡପିଛା ଆୟ ମଧ୍ୟ ବୁଝାଏ । ଏହା ଜୀବନଧାରଣର ମାନ ନିର୍ଦ୍ଧାରଣକାରୀ ପ୍ରକୃଷ୍ଟ ଉପାଦାନ ରୂପେ ଆର୍ଥିକ ଅଭିବୃଦ୍ଧିର ପରିମାପକ ଅଟେ ।

Question ୧୪।
ଜନ ବିସ୍ଫୋରଣ (Population explosion) :
Answer:
ଜନ ବିସ୍ଫୋରଣ କହିଲେ ଜନସଂଖ୍ୟାର ଦ୍ରୁତ ଅଭିବୃଦ୍ଧିକୁ ବୁଝାଏ । ଯେତେବେଳେ ଦେଶର ଜାତୀୟ ଆୟର ବୃଦ୍ଧି ତୁଳନାରେ ଜନସଂଖ୍ୟାର ବୃଦ୍ଧି ଅଧ‌ିକ ହୁଏ ସେତେବେଳେ ଜନସଂଖ୍ୟାର ସମସ୍ୟା ଦେଖାଦେଇଥାଏ । ସ୍ଵାଧୀନତା ପରିବର୍ତୀ ସମୟରେ ଜନଗଣନା ତଥ୍ୟକୁ ଅନୁଧ୍ୟାନ କଲେ ଜଣାଯାଏ ଯେ ଭାରତ ଜନବିସ୍ଫୋରଣର ସମସ୍ୟା ଦେଇ ଗତି କରୁଛି । ୧୯୫୧ ଜନଗଣନାରେ ଭାରତର ଜନ୍ମହାର ଓ ମୃତ୍ୟୁହାର ଯଥାକ୍ରମେ ୩୯.୯ ଏବଂ ୨୭.୪ ଥିଲା । ଜନସଂଖ୍ୟାର ବୃଦ୍ଧିହାର ୧.୨୫ ପ୍ରତିଶତ ଥିଲା । ୨୦୧୧ ଜନଗଣନାରେ, ଜନ୍ମହାର ଓ ମୃତ୍ୟୁହାର ଯଥାକ୍ରମେ ୨୦.୯୭ ଏବଂ ୭.୪୮ରେ ପହଞ୍ଚିଛି । ଜନସଂଖ୍ୟାର ବୃଦ୍ଧିହାର ୧.୬୯ ପ୍ରତିଶତକୁ ହ୍ରାସ ପାଇଛି । କିନ୍ତୁ ଜନ୍ମ ହାରର ହ୍ରାସ ମୃତ୍ୟୁହାରର ହ୍ରାସ ତୁଳନାର କମ୍ ହୋଇଥିବାରୁ ଦେଶରେ ଜନ ବିସ୍ଫୋରଣର ସମସ୍ୟା ଦେଖାଦେଇଛି । ଏହି ଜନବିସ୍ଫୋରଣର ସମସ୍ୟା ଦେଶରେ ଅନେକ ସାମାଜିକ ଓ ଆର୍ଥନୀତିକ ସମସ୍ୟା ସୃଷ୍ଟି କରିଛି !

Question ୧୫।
ପରିବାର କଲ୍ୟାଣ କାର୍ଯ୍ୟକ୍ରମ(Family Planning Programme) :
Answer:
ପଞ୍ଚମ ପଞ୍ଚବାର୍ଷିକ ଯୋଜନା ସମୟରେ ପରିବାର କଲ୍ୟାଣ କାର୍ଯ୍ୟକ୍ରମ ନାମରେ ଏକ ନୂତନ ଜନସଂଖ୍ୟା ନୀତି ପ୍ରଣୟନ କରାଗଲା । ପରିବାର ନିୟୋଜନ ସହିତ ବିଭିନ୍ନ ପରିବାର କଲ୍ୟାଣ କାର୍ଯ୍ୟକ୍ରମ ଏଥରେ ସନ୍ନିବେଶିତ ହେଲା । ଏହି ନୀତି ସ୍ଵାସ୍ଥ୍ୟ, ପୁଷ୍ଟିସାଧନ, ଶିଶୁ ଓ ମାତୃ ମଙ୍ଗଳ ଇତ୍ୟାଦି ଅନେକ କାର୍ଯ୍ୟକ୍ରମ ଉପରେ ଗୁରୁତ୍ଵ ଦେଲା । ଫଳରେ ନୂତନ ଜନସଂଖ୍ୟା ନୀତି ଅଧ୍ବକ ଲୋକପ୍ରିୟ ହୋଇପାରିଲା । ଏହି କାର୍ଯ୍ୟକ୍ରମର ଲୋକପ୍ରିୟତା ଆଦୌ ଉତ୍ସାହଜନକ ହେଲା ନାହିଁ । ୧୯୭୬-୭୭ରେ ୮୨ଲକ୍ଷ ବନ୍ଧ୍ୟାକରଣ ଅସ୍ତ୍ରୋପଚାର କରାଯାଇଥିବା ସ୍ଥଳେ ୧୯୭୭-୭୮ରେ ମାତ୍ର ୬୪ ଲକ୍ଷ ବନ୍ଧ୍ୟାକରଣ ଅସ୍ତ୍ରୋପଚାର କରାଗଲା ।

Question ୧୬।
ଜାତୀୟ ଜନସଂଖ୍ୟା ନୀତି ୨୦୦୦ ଆଲୋଚନା କର ।
Answer:
୧୯୭୬ ମସିହା ପରବର୍ତ୍ତୀ ୨୪ ବର୍ଷର ଏକ ବିରାଟ ବ୍ୟବଧାନ ପରେ ୨୦୦୦ ମସିହା ଫେବୃୟାରୀ ୧୫ ତାରିଖରେ ତତ୍କାଳୀନ NDA ସରକାର ନୂତନ ଜନସଂଖ୍ୟା ନୀତି ୨୦୦୦ ଘୋଷଣା କଲେ । ଜନସଂଖ୍ୟା ବୃଦ୍ଧିକୁ ୨୦୦୪ ମସିହା ସୁଦ୍ଧା ସ୍ଥିର ରଖୁବା ଏହାର ମୂଳ ଲକ୍ଷ୍ୟ । ଏହି ଜନସଂଖ୍ୟା ନୀତିର ଆଭିମୁଖ୍ୟଗୁଡ଼ିକ ହେଲା:-

ହାସ :
୧।୧୪ ବର୍ଷ ପର୍ଯ୍ୟନ୍ତ ସମସ୍ତଙ୍କୁ ମାଗଣା ବାଧ୍ୟତାମୂଳକ ଶିକ୍ଷା ଓ ଅଧାରୁ ପାଠ ପଢ଼ା ଛାଡ଼ୁଥିବା ପିଲାଙ୍କର ସଂଖ୍ୟା
୨ । ଶିଶୁ ମୃତ୍ୟୁହାର ଏବଂ ପ୍ରସବକାଳୀନ ମାତା ମୃତ୍ୟୁହାରକୁ ଯଥାକ୍ରମେ ୩୦ ଓ ୧୦କୁ ହ୍ରାସ କରିବା;
୩ । ବାଳିକାମାନଙ୍କ ମଧ୍ୟରେ ବିଳମ୍ବିତ ବିବାହକୁ ପ୍ରୋତ୍ସାହିତ କରିବା;
୪ ।ସଂକ୍ରାମକ ରୋଗର ପ୍ରତିରୋଧ ଓ ନିରାକରଣ;
୫ । ସାର୍ବଜନୀତ ରୋଗ ପ୍ରତିରୋଧକ ଟୀକା ପ୍ରଦାନ;
୬ । ଜନ୍ମ, ମୃତ୍ୟୁ ଓ ବିବାହର ବାଧ୍ୟତାମୂଳକ ପଞ୍ଜୀକରଣ କରିବା;
୭ । ଗର୍ଭପାତ ଆଇନ୍‌ର ସରଳୀକରଣ କରିବା ।

Question ୧୭ ।
ଜନସଂଖ୍ୟା ସଂକ୍ରମଣ ତତ୍ତ୍ବ (lemographic Iransition Theory):
Answer:
ଜନସଂଖ୍ୟା ସଂକ୍ରମଣ ତତ୍ତ୍ବ ବିକଶିତ ରାଷ୍ଟ୍ରଗୁଡ଼ିକର ଏକ ଐତିହାସିକ ଅଭିଜ୍ଞତା ଅଟେ । ଏହା ଦେଶର ଆର୍ଥିକ ବିକାଶ ଜନସଂଖ୍ୟା ବୃଦ୍ଧି ସହିତ କିପରି ସମ୍ପର୍କିତ ତାହାର ସୂଚନା ଦେଇଥାଏ । ଜନସଂଖ୍ୟା ସଂକ୍ରମଣ ତତ୍ତ୍ଵରେ ଜନସଂଖ୍ୟା ବୃଦ୍ଧିର ତିନୋଟି ଅବସ୍ଥା ଦେଖାଦେଇଥାଏ । ପ୍ରାଥମିକ ଅବସ୍ଥାରେ ଜନ୍ମହାର ଏବଂ ମୃତ୍ୟୁହାର କମ୍ ଥାଏ । ଏହା ବିଶେଷ କରି ଅନୁନ୍ନତ ରାଷ୍ଟ୍ର ସହିତ ସମ୍ପୃକ୍ତ । ଏହି ଅବସ୍ଥାରେ ଜନସଂଖ୍ୟା ବୃଦ୍ଧି ହୋଇନଥାଏ । ଦ୍ଵିତୀୟରେ ଅଧିକ ଜନ୍ମହାର ଏବଂ ସ୍ଵଚ୍ଛ ମୃତ୍ୟୁହାର ହୋଇଥାଏ । ଏହା ବିଶେଷ କରି ବିକାଶଶୀଳ ରାଷ୍ଟ୍ର ସହିତ ସଂପୃକ୍ତ । ତୃତୀୟରେ ଉଭୟ ଜନ୍ମହାର ଓ ମୃତ୍ୟୁହାର ସ୍ଵଳ୍ପ ହୋଇଥାଏ । ଏହା ବିକଶିତ ରାଷ୍ଟ୍ର ସହିତ ସମ୍ପୃକ୍ତ ।

Question ୧୮।
ଉଚ୍ଚ ଜନ୍ମହାର (High Birth Rate) :
Answer:
ଭାରତରେ ଜନ୍ମହାର ଅଧିକ ହେବାର ଅନେକ କାରଣ ରହିଛି, ଯାହା ମୁଖ୍ୟତଃ ସାମାଜିକ ଓ ଆର୍ଥନୀତିକ । ଉଚ୍ଚ ଜନ୍ମହାର ବିଭିନ୍ନ କାରଣଗୁଡ଼ିକରୁ ବୃଦ୍ଧି ହୋଇଥାଏ, ସେଗୁଡ଼ିକ ହେଲା, ସାର୍ବଜୀନନ ବିବାହ, ଅଳ୍ପ ବୟସରେ ବିବାହ, କୃଷି ଉପରେ ନିର୍ଭରଶୀଳତା, ଦାରିଦ୍ର୍ୟ, ପୁତ୍ର ସନ୍ତାନ ନିମନ୍ତେ ଅଗ୍ରାଧ‌ିକାର, ଉଚ୍ଚ ଶିଶୁ ମୃତ୍ୟୁହାର ଏବଂ ନିରକ୍ଷରତା ଓ ଅନ୍ଧବିଶ୍ଵାସ । ଭାରତରେ ବିବାହକୁ ଜୀବନ ମାର୍ଗରେ ଏକ ଗୁରୁତ୍ଵପୂର୍ଣ୍ଣ ସୋପାନ ବୋଲି ବିବେଚନା କରାଯାଏ । ଏହାକୁ ଏକ ପବିତ୍ର ବନ୍ଧନ ଓ ପରିବାର ଏବଂ ସମାଜ ପାଇଁ ମୌଳିକ ଆବଶ୍ୟକତା ବୋଲି ସମସ୍ତେ ଭାବନ୍ତି । ଏଣୁ ଆମ ଦେଶର ପ୍ରାୟ ସମସ୍ତେ ବିବାହ କରନ୍ତି, ଅବିବାହିତ ସ୍ତ୍ରୀ ପୁରୁଷଙ୍କ ସଂଖ୍ୟା ନିହାତି ନଗଣ୍ୟ । ଏଣୁ ଏହା ଉଚ୍ଚ ଜନ୍ମହାର ସୃଷ୍ଟି କରିଥାଏ ।

VI. ଦୀର୍ଘଧର୍ମୀ ପ୍ରଶ୍ନୋତ୍ତର ।
[Long Answer Type Questions.]

Question ୧।
ଭାରତରେ ଜନସଂଖ୍ୟାର ମୁଖ୍ୟ ବୈଶିଷ୍ଟ୍ୟଗୁଡ଼ିକ ଉପସ୍ଥାପନ କର ।
(Explain the important features of India’s Population.)
Answer:
ରାଷ୍ଟ୍ର, ତା’ର ଭୌଗୋଳିକ ଭୂଖଣ୍ଡ ଓ ଅଧିବାସୀଙ୍କୁ ନେଇ ଆତ୍ମପ୍ରକାଶ କରେ । ରାଷ୍ଟ୍ରର ପ୍ରତ୍ୟେକ ଆର୍ଥନୀତିକ କାର୍ଯ୍ୟକ୍ରମ ତା’ର ଅଧିବାସୀମାନଙ୍କ ଦ୍ଵାରା ଓ ସେହିମାନଙ୍କ ଉଦ୍ଦେଶ୍ୟରେ ସଂଗଠିତ ହୁଏ । ମାତ୍ର ଏହାର ପରିଚାଳନାଗତ ଦିଗ ମନୁଷ୍ୟର ବୁଦ୍ଧିମତା ଉପରେ ପର୍ଯ୍ୟବସିତ । ଏହି ଦିଗକୁ ବିଶେଷଜ୍ଞ ବା ଆର୍ଥନୀତିଜ୍ଞମାନେ ପରିଚାଳନା କରନ୍ତି । ଏଥୁରୁ ପ୍ରତ୍ୟେକ ରାଷ୍ଟ୍ରର ଅର୍ଥନୀତି ବା ଅର୍ଥବ୍ୟବସ୍ଥା ଗଢ଼ି ଉଠେ । ତେଣୁ ଅର୍ଥଶାସ୍ତ୍ରର ଅଧ୍ୟୟନ ସ୍ଥଳେ ରାଷ୍ଟ୍ରର ଅଧୂବାସୀ ବା ଜନସଂଖ୍ୟାକୁ ମୂଳପିଣ୍ଡ ରୂପେ ବିବେଚନା କରାଯାଏ । ଏହି ଦୃଷ୍ଟିକୋଣରୁ ଜନସଂଖ୍ୟାର ବିଭିନ୍ନ ଗୁଣ ବା ବୈଶିଷ୍ଟ୍ୟଗୁଡ଼ିକୁ ସ୍ଵତନ୍ତ୍ରତର ସହ ଅଧ୍ୟୟନ କରିବାର ଆବଶ୍ୟକତା ଦେଖାଯାଏ । ଜନସଂଖ୍ୟାର ବୈଶିଷ୍ଟ୍ୟଗୁଡ଼ିକୁ ଆଲୋଚନା କଲାବେଳେ ମୁଖ୍ୟତଃ ସେଗୁଡ଼ିକୁ ଦୁଇ ଭାଗରେ ବିଭକ୍ତ କରି ଆଲୋଚନା କରାଯାଏ । ତାହା ହେଲା– (କ) ପରମାଣାତ୍ମକ ଦିଗ (ଖ) ଗୁଣାତ୍ମକ ଦିଗ ।

(କ) ପରିମାଣାତ୍ମକ ଦିଗ (Quantitative Aspect):
ଜନସଂଖ୍ୟାର ପରିମାଣାତ୍ମକ ଦିଗ କହିଲେ ଏହା ସଂଖ୍ୟା ବା ଆକାର ସଂପର୍କିତ ବିଭିନ୍ନ ଗୁଣ ବା ବୈଶିଷ୍ଟ୍ୟର ଆଲୋଚନାକୁ ବୁଝାଏ । ଆକାର ବା ସଂଖ୍ୟାଭିଭିକ ଜନସଂଖ୍ୟାର ବିଭିନ୍ନ ବୈଶିଷ୍ଟ୍ୟଗୁଡ଼ିକୁ ନିମ୍ନରେ ଉପସ୍ଥାପନା କରାଗଲା।

(୧) ଜନସଂଖ୍ୟାର ଆକାର(Sure of Population):
ଜନସଂଖ୍ୟାର ଆକାର, ରାଷ୍ଟ୍ରର ମୋଟ୍ ଅଧିବାସୀ ବା ଜନସଂଖ୍ୟାର ଆକଳନକୁ ବୁଝାଏ । ଏହି ଆକଳନ ଭାରତବର୍ଷରେ ‘ଜନଗଣନା’ ଦ୍ବାରା ପ୍ରତି ଦଶ ବର୍ଷରେ ଥରେ ସଂପାଦିତ ହୁଏ ଓ ପ୍ରତି ଦଶନ୍ଧିର ପ୍ରଥମ ବର୍ଷ ହିଁ ୧୮୯୧ ଠାରୁ କ୍ରମଶଃ ସଂଗଠିତ ହୋଇ ଆସୁଛି । ଏହି ଆକାରରେ ୧୮୯୧ ଜନଗଣନାରେ ଭାରତରେ ୨୩.୬ କୋଟି ଥ‌ିବାବେଳେ ୧୯୧୧ ହିସାବରେ ୨୫.୨ କୋଟିକୁ ବୃଦ୍ଧି ପାଇଥିଲା । ୨୦୧୧ ଜନଗଣନାରେ ମୋଟ ଜନସଂଖ୍ୟା ଥୁଲା ୧୨୧.୦୨ କୋଟି । ଆକାର ଦୃଷ୍ଟିରୁ ଭାରତର ଜନସଂଖ୍ୟା ପୃଥିବୀରେ ଦ୍ଵିତୀୟ ଓ ଚୀନ୍‌ର ଜନସଂଖ୍ୟା ପ୍ରଥମ ଅଟେ । ଆକାର ଦୃଷ୍ଟିରୁ ଭାରତର ଜନସଂଖ୍ୟାକୁ ତୁଳନାତ୍ମକ ଭାବେ ବିଚାର କଲେ ଭାରତ ଏକ ଜଳବହୁଳ ରାଷ୍ଟ୍ର ଭାବରେ ପରିଚିତ । କାରଣ ପୃଥିବୀର ସ୍ଥଳ ଭାଗର ମାତ୍ର ୨.୪ ଭାଗ ଭାରତ ଅଧୀନରେ ଥିବାବେଳେ ପୃଥ‌ିବୀର ଜନସଂଖ୍ୟାର ପ୍ରାୟ ୧୩ ଭାଗ ଭାରତରେ ବସବାସ କରନ୍ତି ।

(୨) ଜନସଂଖ୍ୟାର ଘନତ୍ବ (Density of Population):
ଦେଶର ଭୌଗୋଳିକ ଅବସ୍ଥିତି ବିଚାର କରି ପ୍ରତି ବର୍ଗକିଲୋମିଟରରେ ବସବାସ କରୁଥିବା ହାରାହାରି ଅଧୂବାସୀ ସଂଖ୍ୟାକୁ ସେହି ଦେଶରେ ଜନସଂଖ୍ୟାର ଘନତ୍ଵ ବୋଲି କୁହାଯାଏ । ଦେଶର ଭୌଗୋଳିକ ଭୂଖଣ୍ଡ ଯେତେ ବର୍ଗ କିଲୋମିଟର ମାପ କରାଯାଏ, ଭାରତ ବର୍ଷରେ ଜନସଂଖ୍ୟାର ଘନତ୍ବ ଜନଗଣନାରୁ ଜନଗଣନା ବୃଦ୍ଧି ପାଇବାରେ ଲାଗିଛି । ଏହା ୧୯୦୧ କଗଣନାରେ ୩୩ ଥିବା ବେଳେ ୧୯୧୧ରେ ୮୨, ୧୯୩୧ରେ ୯୦ ଏବଂ ୨୯୧୧ରେ ୩୮୩କୁ ବୃଦ୍ଧି ପାଇଛି । ସ୍ଥଳବିଶେରେ ଜନସଂଖ୍ୟାର ଘନତ୍ବର ପାର୍ଥକ୍ୟ କେତେଗୁଡ଼ିଏ ଉପାଦାନ ଉପରେ ପର୍ଯ୍ୟବେସିତ । ସେ ସବୁ ହେଲେ ଜଳବାୟୁ, ଭୂମିର ଉର୍ବରତା, ପ୍ରାକୃତିକ ସମ୍ବଳର ଉପଲବ୍‌ଧତା ଇତ୍ୟାଦି ।

(୩) ଲିଙ୍ଗାନୁପାତ (Sex Ratio):
ଲିଙ୍ଗାନୁପାତ ଜନସଂଖ୍ୟାକୁ ସାଧାରଣତଃ ପୁରୁଷ ଓ ମହିଳା ଭାବରେ ଦୁଇ ଭାଗରେ ବିଭକ୍ତ କଲାବେଳେ ଦେଶର ପ୍ରତି ହଜାର ପୁରୁଷ ସଂଖ୍ୟା ପାଇଁ ହାରାହାରି ମହିଳା ସଂଖ୍ୟାକୁ ଲିଙ୍ଗାନୁପାତ କୁହାଯାଏ । ଏହା ପୁରୁଷ ଓ ମହିଳାଙ୍କ ମଧ୍ୟରେ ଏକ ପରିମାଶ୍ରାମକ ତୁଳନା ଅଟେ । ୨୦୦୧ ଜନଗଣନା ହିସାବରେ ଭାରତରେ ଲିଙ୍ଗାନୁପାତ ୯୩୩ ଅଟେ । ଅର୍ଥାତ୍ ଭାରତରେ ପ୍ରତି ହଜାର ପୁରୁଷ ସଂଖ୍ୟାରେ ମହିଳା ସଂଖ୍ୟା ୯୩୩ ଅଟେ । ୧୯୯୧ରେ ୯୪୦ ଥ‌ିବାବେଳେ, ୨୦୧୧ରେ ଏହା ୯୪୩ ଥିଲା । ଭାରତରେ ଏହି ଲିଙ୍ଗାନୁପାତକୁ ଜଣାପଡ଼େ ଯେ ଭାରତରେ ପୁରୁଷ ଶିଶୁ ପ୍ରତି ପ୍ରାଧାନ୍ୟ ଦିଆଯାଏ । କିନ୍ତୁ ଋଷିଆ, ଜାପାନ ଓ ଆମେରିକା ପରି ଉନ୍ନତ ରାଷ୍ଟ୍ରମାନଙ୍କରେ ପୁରୁଷ ସଂଖ୍ୟାଠାରୁ ମହିଳା ସଂଖ୍ୟା ଅଧ୍ବକ ।

(୪) ବୟସାନୁକ୍ରମିକ ଶ୍ରେଣୀ ବିଭାବ (Age Composition):
ବୟସକୁ ଭିଭିକରି ଜନସଂଖ୍ୟାକୁ ମୁଖ୍ୟତଃ ୩ ଶ୍ରେଣୀରେ ବିଭକ୍ତ କରାଯାଏ; ଯଥା ଶିଶୁ ଶ୍ରେଣୀ ୦ ରୁ ୧୪ ବର୍ଷ, ନିୟୋଜନ କ୍ଷମ ଶ୍ରେଣୀ – ୧୫ ରୁ ୫୯ ବର୍ଷ ଓ ଶେଷରେ ବାର୍ଦ୍ଧକ୍ୟ ୬୦ ରୁ ଅଧିକ ବୟସର ଜନ । ପ୍ରଥମ ଓ ଶେଷ ଶ୍ରେଣୀର ଜନସଂଖ୍ୟା ଉପାର୍ଜନକ୍ଷମ ହୋଇ ନ ଥିବାରୁ ସେମାନଙ୍କୁ ନିର୍ଭରଶୀଳ କୁହାଯାଏ ଓ ସେମାନଙ୍କର ମୋଟ ଅଂଶ ଜନସଂଖ୍ୟା ୩୯.୪ ଭାଗ ଅଟେ । ଅର୍ଥାତ୍ ଭାରତରେ ୬୦.୧ ଭାଗ ଜନସଂଖ୍ୟା ଉପାର୍ଜନକ୍ଷମ ଓ ସେମାନଙ୍କ ମଧ୍ୟରୁ ଯେଉଁମାନେ ନିୟୋଜିତ । ସେମାନଙ୍କ ଉପରେ ଆବଶ୍ୟକତା ପୂରଣ ପାଇଁ ଦେଶର ମୋଟ ଜନସଂଖ୍ୟା ନିର୍ଭରଶୀଳ ଅଟେ । ୧୯୫୧ରେ ବୟସାନୁକ୍ରମିକ ଶ୍ରେଣୀ ବିଭାଗ ଥୁଲ (୦-୧୪) ବର୍ଷରେ ୩୭.୪, (୧୫ ରୁ ୫୯) ବର୍ଷରେ ୫୬.୯ ଓ (୬୦ ରୁ ଊର୍ଷ) ରେ ୫.୭, ୨୦୧୧ରେ ଏହା ଥିଲା (୦-୧୪) ୩, ୧ (୧୫-୫୯) ରେ ୬୦.୬ ଓ (୬୦-ଊର୍ଦ୍ଧ୍ବରେ) ୮.୩ ।

(ଖ) ଗୁଣାତ୍ମକ ଦିଗ (Qualitative Aspect):
ଜନସଂଖ୍ୟାର ଗୁଣ ବା ମାନକୁ ବିଚାର କରି ମଧ୍ୟ ଜନସଂଖ୍ୟାର କେତେକ ବୈଶିଷ୍ଟ୍ୟ ପ୍ରତିପାଦିତ ହୁଏ ଓ ସେଗୁଡ଼ିକ ଜନସଂଖ୍ୟାର ଗୁଣାତ୍ମକ ଦିଗ ବୋଲି କୁହାଯାଏ ।

ଗୁଣାତ୍ମକ ବୈଶିଷ୍ଟ୍ୟଗୁଡ଼ିକ ହେଲା-
(୧) ଜୀବନ କାଳ (Life Expectancy):
ଜୀବନ କାଳ, ରାଷ୍ଟ୍ରର ହାରାହାରି ଆୟକୁ ବୁଝାଏ | ଭାରତ ବର୍ଷରେ ୯୩ ରୁ ୯୭ ମଧ୍ଯରେ ଆୟୁକାଳ ହାରାହାରି ୬୧.୧ ବର୍ଷ ବୋଲି ଆକଳନ କରାଯାଇଅଛି ଓ ଏହି ସ୍ଥଳେ ପୁରୁଷମାନଙ୍କର ୬୦.୪ ବର୍ଷ ଓ ମହିଳାମାନଙ୍କର ୬୧.୮ ବର୍ଷ । ଭାରତରେ ଆୟୁକାଳ କ୍ରମଶଃ ବୃଦ୍ଧି ଘଟୁଛି । ୧୯୫୧ ରୁ ୩୩ ରୁ ବୃଦ୍ଧି ପାଇଁ ୨୦୧୧ରେ ୬୯.୯ ବର୍ଷରେ ପହଞ୍ଚିଛି ।

(୨) ଶିକ୍ଷାହାର (Rate of literacy):
ଶିକ୍ଷାର ହାର କହିଲେ ସମୁଦାୟ ଜନସଂଖ୍ୟାର ଶିକ୍ଷିତ ବ୍ୟକ୍ତିଙ୍କ ଶତକଡ଼ା ହାରକୁ ବୁଝାଏ । ଶିକ୍ଷିତ ବ୍ୟକ୍ତିମାନଙ୍କର ମଧ୍ୟ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ସଂଜ୍ଞା ରହିଛି । ତାହା ହେଲା ଭାବବ୍ୟକ୍ତ କରି ବୁଝିପାରୁଥିବେ, ପଢ଼ି ପାରୁଥ‌ିବେ ଓ ଲେଖୁ ପାରୁଥୁବେ, ତେବେ ସେ ଜଣେ ଶିକ୍ଷିତ ବ୍ୟକ୍ତି ଅଟନ୍ତି । ଏହି ସଂଜ୍ଞା ୧୯୮୧ ଠାରୁ ପ୍ରସ୍ଖଳିତ । ମାତ୍ର ଏହା ପୂର୍ବରୁ ସର୍ବନିମ୍ନ ବୟସ ୫ ବର୍ଷ ଥିଲା । ଏହି ସଂଜ୍ଞାକୁ ଆଧାର କରି ୨୦୦୧ ଜନଗଣନା ଭାରତ ଶିକ୍ଷାହାର ୬୫.୪% । ଏହା ପୁରୁଷମାନଙ୍କ କ୍ଷେତ୍ରରେ ୭୫.୮ ଶତକଡ଼ା ଓ ମହିଳାମାନଙ୍କ କ୍ଷେତ୍ରରେ ୫୨.୨% ! ଭାରତରେ ଶିକ୍ଷାହାର, ଶିକ୍ଷାର ପ୍ରସାର ଗୁଣ ପ୍ରକାଶ କରେ । ୧୯୫୧ରେ ଶିକ୍ଷାହାର ୧୮.୩ ପ୍ରତିଶତ । ୨୦୧୧ରେ ଏହା ୭୪କୁ ବୃଦ୍ଧି ପାଇଛି ।

ଅମର୍ତ୍ତ୍ୟ ସେନ୍‌ଙ୍କ ମତରେ ଶିକ୍ଷା ଆର୍ଥିକ ପ୍ରଗତିର ଏକ ଅଙ୍ଗ ହୋଇ ଥିବାରୁ ଶିକ୍ଷାର ପ୍ରସାର ପ୍ରତି ଅବହେଳା ପ୍ରଦର୍ଶନ କରାଯାଇପାରିବ ନାହିଁ । ଭାରତୀୟ ସମ୍ବିଧାନରେ ପ୍ରାଥମିକ ଶିକ୍ଷାକୁ (୦-୧୪) ବର୍ଷ ମାଗଣା ଓ ବାଧ୍ୟତାମୂଳକ କରାଯାଇଥିବା ବେଳେ, ଏହି ଲକ୍ଷ୍ୟ ୧୯୬୦ ମଧ୍ଯରେ ପୂରଣ କରିବାକୁ ଧାର୍ଯ୍ୟ ହୋଇଥିବାବେଳେ ଭାରତରେ ଶିକ୍ଷାର ପ୍ରସାର ଯଥେଷ୍ଟ ଅଗ୍ରଗତି କରିପାରି ନାହିଁ ।

(୩) ସହରୀକରଣ (Urbanisation):
ସହରାଞ୍ଚଳ କହିଲେ ଏହା ସାଧାରତଃ ପୌରାଞ୍ଚଳ, ମହାନଗର ନିଗମ ଓ ବିଜ୍ଞାପିତ ଅଂଚଳଗୁଡ଼ିକୁ ବୁଝାଇବା ସହିତ ଅନ୍ୟାନ୍ୟ ଅଞ୍ଚଳଗୁଡ଼ିକୁ ବୁଝାଏ । ଯେଉଁ ସବୁ ଅଂଚଳର ଲୋକସଂଖ୍ୟା ସର୍ବନିମ୍ନ ୫୦୦ ହେବା ସହ ଜନସଂଖ୍ୟାର ଘନତ୍ଵ ମଧ୍ୟ ୪୦୦ ରୁ କମ୍ ହୋଇ ନ ଥାଏ ଓ ସେହି ଅଂଚଳର ୭୫ ଭାଗ ଲୋକ ଅଣକୃଷି କ୍ଷେତ୍ର ଉପରେ ନିର୍ଭର କରି ଜୀବିକା ନିର୍ବାହ କରିଥାନ୍ତି । ଏହାଛଡ଼ା ଅନ୍ୟାନ୍ୟ ଅଞ୍ଚଳଗୁଡ଼ିକୁ ଗ୍ରାମାଞ୍ଚଳ କୁହାଯାଏ । ୨୦୦୧ ଜନଗଣନା ହିସାବରେ ଭାରତରେ ମୋଟ ଜନସଂଖ୍ୟାର ମାତ୍ର ୨୭.୮ ଭାଗ ସହରାଞ୍ଚଳରେ ବାସ କରନ୍ତି ଓ ଅବଶିଷ୍ଟ ୭୨, ୨ ଭାଗ ଗ୍ରାମାଞ୍ଚଳରେ ବସବାସ କରନ୍ତି । ତେଣୁ ଭାରତକୁ ଏକ ଗ୍ରାମବହୁଳ ଦେଶ କୁହାଯାଏ । ୨୦୧୧ ଜନଗଣନାରେ ମୋଟ ଜନସଂଖ୍ୟାରେ ୬୮.୮ ଗ୍ରାମାଞ୍ଚଳରେ ଏବଂ ୩୧, ୨ ସହରାଞ୍ଚଳରେ ବସବାସ କରନ୍ତି ।

(୪) ବୃତ୍ତିଗତ ଢାଞ୍ଚା (Occupational Structure):
ବୃତ୍ତି କହିଲେ ସମ୍ବଳ ସଂଗ୍ରହ ମାଧ୍ୟମଗୁଡ଼ିକୁ ବୁଝାଏ ଓ ଏହା ମୁଖ୍ୟତଃ ପ୍ରାଥମିକ ଓ ସେବା କ୍ଷେତ୍ର ଭାବରେ ତିନି ଭାଗରେ ବିଭକ୍ତ । ଦେଶର ନିୟୋଜନ କ୍ଷମ ବ୍ୟକ୍ତିମାନେ ଏହି ସବୁ କ୍ଷେତ୍ରଗୁଡ଼ିକର ସମ୍ବଳ ସଂଗ୍ରହ କରନ୍ତି ଓ ଜିବୀକା ନିର୍ବାହ କରନ୍ତି । ତେଣୁ ପ୍ରାଥମିକ କ୍ଷେତ୍ର ମୁଖ୍ୟ ବୃଭିଗତ କ୍ଷେତ୍ର ଭାବରେ ଅବିହିତ ଓ ଏହା ମଧ୍ୟ ବହୁ ପୂର୍ବରୁ ଅନୁନ୍ନତ ହୋଇ ଆସୁଅଛି । ଯଥା : ୧୯୦୧ରେ ୭୧.୭ ଭାଗ, ୧୯୫୧ରେ ୭୨.୧ ଭାଗ ବୃତ୍ତିଗତ ଢାଞ୍ଚା ବୃଦ୍ଧି ପାଇଛି ଓ ୧୯୯୧ରେ ଏହା ୬୬.୮ ଭାଗ ପ୍ରାଥମିକ କ୍ଷେତ୍ରରେ କାର୍ଯ୍ୟ କରି ଆସୁଅଛି ଏବଂ ଏହା କ୍ରମଶଃ ହ୍ରାସ ପାଉଅଛି ।

(୫) ଜୀବନଧାରଣ ମାନ(Standard of Living):
ଭାରତର ଅଧ୍ବବାସୀ ଯେଉଁପରି ଆବଶ୍ୟକତା ପୂରଣ ପାଇଁ ସାମର୍ଥ୍ୟ ପ୍ରକାଶ କରନ୍ତି, ତାକୁ ଜୀବନଧାରଣର ମାନ କୁହାଯାଏ । ମୁଣ୍ଡପିଛା ଆୟକୁ ଏହାର ମାପକରୂପେ ମୁଖ୍ୟତଃ ବିଚାର କରାଯାଏ ଓ ଏହା ନିମ୍ନ ସ୍ତରରୁ ଅଟେ । ୧୯୯୬- ୯୭ ବର୍ଷ ଭାରତର ମୁଣ୍ଡପିଚ୍ଛା ଆୟ ଚଳିତ ଦରରେ ବାର୍ଷିକ ୧୧,୫୬୪ ଟଙ୍କା ଓ ୧୯୯୯-୨୦୦୦ ବର୍ଷ ଆକଳନରେ ୨୬.୧ ଭାଗ ଲୋକ ଦାରିଦ୍ର୍ୟ ସୀମରେଖା ତଳେ ବସବାସ କରନ୍ତି । ଅର୍ଥାତ୍‌, ୨୬.୧ ଭାଗ ଲୋକ ସର୍ବନିମ୍ନ ଆବଶ୍ୟତା ପୂରଣ କରିପାରନ୍ତି ନାହିଁ । ଏହା ସବୁ ଜନସଂଖ୍ୟାର ବିଭିନ୍ନ ପରିମାଣାତ୍ମକ ଓ ଗୁଣାତ୍ମକ ବୈଶିଷ୍ଟ୍ୟ ଅଟେ । ଓ ।

Question ୨।
୧୯୭୬ ମସିହା ଜାତୀୟ ଜନସଂଖ୍ୟା ନୀତିର ମୁଖ୍ୟ ବୈଶିଷ୍ଟ୍ୟଗୁଡ଼ିକ ଆଲୋଚନା କର ।
(Explain the main features of the Population Policy of 1976.)
Answer:
ଭାରତ ସରକାର ୧୯୭୬ ମସିହା ଏପ୍ରିଲ୍ ମାସରେ ଦେଶଲ ପ୍ରଥମ ଜନସଂଖ୍ୟା ନୀତି ଘୋଷଣା କରିଥିଲେ । ଏହି ନୀତିର କେତେକ ପ୍ରଧାନ ବୈଶିଷ୍ଟ୍ୟ ଦର୍ଶାଯାଉଛି ।
(୧) ଆଇନ୍ ଦ୍ବାରା ଉଭୟ ପୁରୁଷ ଓ ମହିଳାମାନଙ୍କ ବିବାହ ବୟସକୁ ଯଥାକ୍ରମେ ୨୧ ଓ ୧୮କୁ ବୃଦ୍ଧି କରାଯାଉଥିଲା ।
(୨) ଜନସଂଖ୍ୟା ଯୋଜନା କାର୍ଯ୍ୟକ୍ରମର ବିଭିନ୍ନ ରାଜ୍ୟରେ ସଫଳତାକୁ ବିଚାରକୁ ନେଇ କେନ୍ଦ୍ରୀୟ ଅନୁଦାନର ୮ ପ୍ରତିଶତ କେବଳ ପରିବାର ନିୟୋଜନ କାର୍ଯ୍ୟକ୍ରମରେ ବ୍ୟୟ କରିବାର ବ୍ୟବସ୍ଥା କରାଯାଇଥିଲା ।
(୩) ସବୁରାଜ୍ୟରେ ନାରୀ ଶିକ୍ଷାର ସ୍ତର ବୃଦ୍ଧି କରିବା ଉପରେ ଗୁରୁତ୍ବ ଦିଆଯାଇଥିଲା।
(୪) ବନ୍ଧ୍ୟାକରଣ ପଦ୍ଧତି ଗ୍ରହଣ କରିଥିବା ବ୍ୟକ୍ତିମାନଙ୍କୁ ଆର୍ଥିକ ପ୍ରୋତ୍ସାହନ ଓ ସାମୂହିକ ପ୍ରୋତ୍ସାହନର ପରିମାଣ ବୃଦ୍ଧି କରାଗଲା।
(୫) ଜନସଂଖ୍ୟା ଉପରେ ଗବେଷଣା, ଶିକ୍ଷା, ସ୍ବାସ୍ଥ୍ୟ ସେବା ତଥା ମା ଓ ଶିଶୁଙ୍କ ସ୍ଵାସ୍ଥ୍ୟରକ୍ଷା ଉପରେ ଅଧିକ ପ୍ରାଧାନ୍ୟ ଦିଆଯାଇଥିଲା।
(୬) ପରିବାର ନିୟୋଜନ କାର୍ଯ୍ୟକ୍ରମକୁ ଏକ ଗଣ ଆନ୍ଦୋଳନରେ ପରିଣତ କରିବା ପାଇଁ ଚିକିତ୍ସକ ଗୋଷ୍ଠୀ, ଜିଲ୍ଲା ପରିଷଦ, ପଞ୍ଚାୟତ ସମିତି, ଶିକ୍ଷକ, ମହିଳା ସମିତି ଓ ସମବାୟ ସମିତି ଆଦିକୁ ସଂଶ୍ଳିଷ୍ଟ କରି ଉପଯୁକ୍ତ ଗୋଷ୍ଠୀ ପ୍ରୋତ୍ସାହନ ଦେବାକୁ ସ୍ଥିର କରାଯାଇଥିଲା ।
(୭) ପରିବାର ଯୋଜନା ବାର୍ତ୍ତା ଘରେ ଘରେ ପହଞ୍ଚାଇବା ନିମନ୍ତେ ଗଣମାଧ୍ୟମର ଅଧିକ ବ୍ୟବହାର କରିବା ନିମନ୍ତେ ନିଷ୍ପତ୍ତି ନିଆଗଲା।

Question ୩ ।
ଜନ ବିସ୍ଫୋରଣ କ’ଣ ? ଏହା କାରଣଗୁଡ଼ିକ ଆଲୋଚନା କର ।
(What is Population Explosion ? Explain its causes.)
Answer:
ଜନସଂଖ୍ୟାର ପରିମାଣାତ୍ମକ ଦିଗ ପ୍ରତି ଧ୍ୟାନ ଦେଲେ ଏହା ପରିବର୍ତ୍ତନୀୟ ଅବସ୍ଥା ଏବଂ ଏହାର ଗତି ଦିନକୁ ଦିନ ଜନସଂଖ୍ୟାର ବୃଦ୍ଧି ଘଟାଉଅଛି । ଭାରତରେ କେବଳ ୧୯୨୧ ଜନଗଣନାକୁ ଛାଡ଼ିଦେଲେ; ଅନ୍ୟ ସମସ୍ତ ଜନଗଣନା ବର୍ଷରେ ଭାରତର ଜନସଂଖ୍ୟା ବୃଦ୍ଧିପାଇ ଆସୁଅଛି । ଜନ ବିସ୍ଫୋରଣ, ଜନସଂଖ୍ୟା ବୃଦ୍ଧିର ଏକ ଅବସ୍ଥା; ଯେଉଁ ଅବସ୍ଥାରେ ଦ୍ରୁତ ଜନସଂଖ୍ୟା ବୃଦ୍ଧି ସମ୍ଭବ ହୋଇ ଦେଶ ଲାଗି ବିପଦସଂକୁଳ ଅବସ୍ଥା ସୃଷ୍ଟି କରେ । ଜନବିସ୍ଫୋରଣ ସେହି ଅବସ୍ଥାକୁ ବୁଝାଏ । ଯେତେବେଳେ ପ୍ରତି ହଜାର ଲୋକସଂଖ୍ୟା ପ୍ରତି ଜନ୍ମଗ୍ରହଣ କରୁଥିବା ଶିଶୁ ସଂଖ୍ୟା ବା ଜନ୍ମହାର ଜାତୀୟ ସ୍ତରରେ ଅଧିକ ଏବଂ ଏହା ହରାହାରି ୩୫ ରୁ ୪୦ ମଧ୍ୟରେ ସ୍ଥିର ରହୁଥ‌ିବା ବେଳେ ପ୍ରତି ହଜାର ଲୋକସଂଖ୍ୟାରେ ହାରାହାରି ମୃତ୍ୟୁବରଣ କରୁଥିବା ଲୋକସଂଖ୍ୟା ବା ମୃତ୍ୟୁହାରର ହ୍ରାସ ଘଟି ୧୫ ରୁ ୨୦ ମଧ୍ୟରେ ସ୍ଥିର ରୁହେ ଏବଂ ଜନସଂଖ୍ୟାର ବାର୍ଷିକ ବୃଦ୍ଧିହାର ୨% ଠାରୁ ଅଧିକ ରୁହେ । ୧୯୫୦ ମସିହା ଠାରୁ ଭାରତରେ ଏହି ଅବସ୍ଥା ପରିଲକ୍ଷିତ ହେଉଅଛି ।

କାରଣ :
ଜନସଂଖ୍ୟା ବୃଦ୍ଧିର ମୁଖ୍ୟ ନିର୍ଣ୍ଣାୟକ ଉପାଦାନଗୁଡ଼ିକ ହେଲା- ଜନ୍ମହାର, ମୃତ୍ୟୁହାର ଏବଂ ଅନୁପ୍ରବେଶ । ମାତ୍ର ଜନବିସ୍ଫୋରଣ ମୁଖ୍ୟତଃ ଜନ୍ମହାର ଓ ମୃତ୍ୟୁହାରକୁ କେନ୍ଦ୍ରକରି ନିର୍ମିତ ହୋଇଥାଏ । .ଏହି ଅବସ୍ଥାରେ ଜନ୍ମହାର ଅପେକ୍ଷାକୃତ ଅଧୂକ ଓ ପ୍ରାୟ ସ୍ଥିର ରୁହେ ଏବଂ ମୃତ୍ୟୁହାରରେ ଦ୍ରୁତ ହ୍ରାସ ଘଟି ଦ୍ରୁତ ଜନସଂଖ୍ୟା ବୃଦ୍ଧି ଘଟାଇଥାଏ । ତେଣୁ ଜନ୍ମବିସ୍ଫୋରଣର ନିର୍ଣ୍ଣାୟକ କ୍ଷେତ୍ରରେ ମୃତ୍ୟୁହାରର ଗୁରୁତ୍ଵ ଯଥେଷ୍ଟ ବେଶୀ। ୧୯୨୦ରୁ ୩୦ ଏବଂ ୧୯୬୧ ରୁ ୩୦ ମଧ୍ୟରେ ଜନ୍ମହାରରେ ମାତ୍ର ୫:୨ ହ୍ରାସ ଘଟିଥିବା ବେଳେ ମୃତ୍ୟୁହାରରେ ୧୭.୩ ହ୍ରାସ ଘଟିଥିଲା ।

ଅଧୂକ ଏବଂ ପ୍ରାୟ ସ୍ଥିର ଜନ୍ମହାର :
ଜନବିସ୍ଫୋରଣର ମୁଖ୍ୟ ବୈଶିଷ୍ଟ୍ୟ ହେଲା ଅନୁନ୍ନତ ଅବସ୍ଥା । ଏହି ଅନୁନ୍ନତ ଅବସ୍ଥା ମଧ୍ୟ ସାମାଜିକ ଜୀବନକୁ ପ୍ରଭାବିତ କରିଥାଏ ଏବଂ ବିସ୍ଫୋରଣ ସମୟରେ ସାମାଜିକ କୁସଂସ୍କାର, ଅନ୍ଧବିଶ୍ବାସ ଇତ୍ୟାଦିର ପ୍ରଭାବ ପରିଲକ୍ଷିତ ହୁଏ । ଦ୍ଵିତୀୟରେ ଶିକ୍ଷାର ଅନଗ୍ରସରତା ମଧ୍ୟ ଜନମାନସରେ ସଚେତନତାର ପ୍ରଭାବ ଏବଂ ସଂକୁଚିତ ପରିବେଶ କ୍ଷେତ୍ରରୁ ଜନ୍ମହାରେ ହ୍ରାସ ଘଟାଇବାକୁ ସକ୍ଷମ ହୋଇପାରେ ନାହିଁ । ଏହି ସବୁ କ୍ଷେତ୍ରରୁ ପରିବାରକୁ ସଂକୁଚିତ କରାଇବାର ଚିନ୍ତାଧାରା ଜନ୍ମହାରରେ ହ୍ରାସ କ୍ଷେତ୍ରରେ ବିଶେଷ ପରିବର୍ତ୍ତନ ଲକ୍ଷ୍ୟ କରାଯାଇପାରେ ନାହିଁ ।

ଦ୍ରୁତ ମୃତ୍ୟୁହାର ହ୍ରାସ :
ବିସ୍ଫୋରଣ ଅବସ୍ଥା ଏକ ଅନୁନ୍ନତ ଅବସ୍ଥାରୁ ଉତ୍ପନ୍ନ ହେଲେ ମଧ୍ୟ ଆର୍ଥିକ ପ୍ରଗତି ସମ୍ଭବ ହୁଏ; ମାତ୍ର ତାହା ଯଥେଷ୍ଟ ହୋଇ ନ ଥାଏ I ଯେତିକି ପ୍ରଗତି ସମ୍ଭବ, ତାହା ଲୋକମାନଙ୍କର ଜନସାଧାରଣ ମାନରେ ପରିବର୍ତ୍ତନ ଆଣି, ଉତ୍ତମ ଖାଦ୍ୟ ଓ ଉତ୍ତମ ଯତ୍ନର ଆୟୁକାଳ ବୃଦ୍ଧି ଘଟାଇ ମୃତ୍ୟୁହାରରେ ହ୍ରାସ ଘଟାଏ ।

ଦ୍ଵିତୀୟରେ, ଶିକ୍ଷାର ପ୍ରସାର ଯେତିକି ସମ୍ଭବ ହୁଏ, ତାହା ଲୋକମାନଙ୍କ ମଧ୍ୟରେ ସଚେତନତା ବୃଦ୍ଧି ଘଟାଏ; ସ୍ଵାସ୍ଥ୍ୟଗତ ଯତ୍ନ କ୍ଷେତ୍ରରେ କିଛି ଲୋକ ଉପକାର ତଥା ଅପକାରଗତ ବ୍ୟାବହାରିକ ମୂଲ୍ୟ ପ୍ରତି ବିଚାରବନ୍ତ ହୁଅନ୍ତି । ତୃତୀୟରେ, ଡାକ୍ତରୀ ଓ ସ୍ୱାସ୍ଥ୍ୟ ସେବାଗତ କ୍ଷେତ୍ରରେ ପ୍ରସାର ହେତୁ ବ୍ୟକ୍ତିବିଶେଷ ସ୍ଵାସ୍ଥ୍ୟର ଯତ୍ନ ବୋର ସୁବିଧା ଲାଭ କରିଥାନ୍ତି ।

ଚତୁର୍ଥରେ, ଜନମଂଗଳ ରାଷ୍ଟ୍ରଗୁଡ଼ିକରେ ମହାମାରୀ ଦୂରୀକରଣ ଯୋଜନାମାନ କାର୍ଯ୍ୟକ୍ଷମ ହୋଇ ଅକାଳ ମୃତ୍ୟୁ ସବୁକୁ ରୋକାଯାଇପାରୁଅଛି । ଯଥା : ବସନ୍ତ, ମ୍ୟାଲେରିଆ, ହଇଜା ଆଦି ଦୂରୀକରଣ । ଏହିସବୁ କ୍ଷେତ୍ରରେ ଉନ୍ନତି ମୃତ୍ୟୁହାରରେ ଯଥେଷ୍ଟ ହ୍ରାସ ପରିଲକ୍ଷିତ କରାଇଥାଏ ।

ତେଣୁ ଜଳକୁଣ୍ଡରେ ଜଳ ପ୍ରବେଶ ଓ ନିଷ୍କାସନ ପ୍ରଣାଳୀ ସହାୟତାରେ ଜଳପତ ମାପିବା ସଦୃଶ ଯଦି ଜନ୍ମହାରର ବିଶେଷ ହ୍ରାସ ନ ଘଟି ମୃତ୍ୟୁ ହାରରେ ଯଥେଷ୍ଟ ହ୍ରାସ ଘଟେ । ତେବେ ଦେଶରେ ଦ୍ରୁତ ଜନସଂଖ୍ୟା ବୃଦ୍ଧି ସମ୍ଭବ ହୋଇ ବିସ୍ଫୋରଣ ସୃଷ୍ଟି କରେ ଓ ଏହି କ୍ଷେତ୍ରରେ ଦ୍ରୁତ ମୃତ୍ୟୁହାରର ହ୍ରାସ ଗୁରୁତ୍ଵପୂର୍ଣ୍ଣ ଭୂମିକା ବହନ କରେ ।

Question ୪।
ଭାରତୀୟ ଅର୍ଥ ବ୍ୟବସ୍ଥାରେ ଜନବିସ୍ଫୋରଣର ପ୍ରଭାବକୁ ଆଲୋଚନା କର ।
(Discuss the impact of Population Explosion in Indian Economy.)
Answer:
ଭାରତ ଏକ ଜନବହୁଳ ରାଷ୍ଟ୍ର । ପୁନଶ୍ଚ ଦୃତ ଜନସଂଖ୍ୟା ବୃଦ୍ଧି କାରଣରୁ ଜନବିସ୍ଫୋରଣ ଭଳି ସ୍ଥିତି ଉତ୍ପନ୍ନ ହୁଏ । ଏହି ସ୍ଥିତିକୁ ଏକ ସମସ୍ୟା ରୂପେ ବିବେଚନା କରାଯାଏ । କାରଣ ଏହା ଅର୍ଥ ବ୍ୟବସ୍ଥା ଉପରେ ବହୁବିଧ ପ୍ରତିକୂଳ ପ୍ରଭାବ ପକାଇ ଆର୍ଥିକ ପ୍ରଗତି କ୍ଷେତ୍ରରେ ପ୍ରତିବନ୍ଧକ ହୋଇଥାଏ । ଅର୍ଥ ବ୍ୟବସ୍ଥା ପ୍ରତି ଜନବିସ୍ଫୋରଣର ପ୍ରଭାବକୁ ବିଭିନ୍ନ ଦୃଷ୍ଟିକୋଣରୁ ବିଚାର କରି ଉପସ୍ଥାପନ କରାଯାଇପାରେ, ତାହା ନିମ୍ନରେ ଆଲୋଚନା କରାଗଲା ।

ଜନବିସ୍ଫୋରଣର ପ୍ରଭାବ :
(କ) ମୁଣ୍ଡପିଛା ଆୟ : ଦୃତ ଜନସଂଖ୍ୟା ବୃଦ୍ଧି ଫଳରେ ଜାତୀୟ ଆୟ ବୃଦ୍ଧି ଘଟିଲେ ହେଁ ଏହା ମୁଣ୍ଡପିଛା ଆୟ କ୍ଷେତ୍ରରେ ଯଥାର୍ଥ ପ୍ରତିଫଳିତ ହୋଇପାରେ ନାହିଁ । କାରଣ, ଆର୍ଥିକ ଅଭିବୃଦ୍ଧି ହାରଠାରୁ ଜନସଂଖା ଅଧିକ ହାରରେ ବୃଦ୍ଧି ପାଇଥାଏ । ଉଦାହରଣ ସ୍ୱରୂପ ୧୯୫୦-୫୧ ରୁ ୧୯୯୦-୯୧ ମଧ୍ୟରେ ଜାତୀୟ ଆୟ ଶତକଡ଼ା ୮-୯ ଭାଗ ବୃଦ୍ଧି ପାଇଥିଲେ ହେଁ ମୁଣ୍ଡପିଛା ଆୟକ୍ଷେତ୍ରରେ ମାତ୍ର ୨-୪ ଭାଗ ବୃଦ୍ଧି ପରିଲକ୍ଷିତ ହୁଏ । ଅନ୍ୟପକ୍ଷରେ ମୁଣ୍ଡପିଛା ଆୟକୁ ଜୀବନଧାରଣର ମାନ ନିର୍ଦ୍ଧାରକ ରୂପେ ବିଚାର କରାଯାଉଥିବା ବେଳେ ଏହାର ଆର୍ଥିକ ଅନଗ୍ରସରତା ପ୍ରତିପାଦନ କରେ ।

(ଖ) ବୃତ୍ତିଗତ ଢାଞ୍ଚାରେ ଚାପ : ଜନବିସ୍ଫୋରଣ ନିୟୋଜନ କ୍ଷମ ବ୍ୟକ୍ତି ସଂଖ୍ୟା ବୃଦ୍ଧି ପାଇବା ବେଳେ ଅନ୍ୟାନ୍ୟ ବୃତ୍ତିଗତ କ୍ଷେତ୍ରରେ ଯଥେଷ୍ଟ ଉନ୍ନତି ପରିଲକ୍ଷିତ ହୋଇ ନ ପାରିବା କାରଣରୁ କୃଷି କ୍ଷେତ୍ରରେ ଚାପ ପ୍ରତିଫଳିତ ହୁଏ ଓ ଛଦ୍ମବେଶୀ ବେକାରୀ ସହ ଅର୍ଥ ବେକାରୀ ସମସ୍ୟା ଉତ୍ପନ୍ନ ହୁଏ । ଏହା ମଧ୍ୟ ନିର୍ଭରଶୀଳତା ବୃଦ୍ଧି ଘଟାଇବା ସହ ପ୍ରଗତିର ପଥରୋଧ କରେ । ନିର୍ଭରଶୀଳତା ୧୯୬୧ରେ ୬୨.୪ ଭାଗ ଓ ୨୦୦୧ରେ ୬୮.୮ ଭାଗକୁ ବୃଦ୍ଧି ପାଇଛି ।

(ଗ) ଖାଦ୍ୟ ଯୋଗାଣ ଉପରେ ଚାପ : ଅତି ଆବଶ୍ୟକ ପଦାର୍ଥଗୁଡ଼ିକ ମଧ୍ୟରେ ଖାଦ୍ୟ ପ୍ରଥମ | କାରଣ ଏହା ବଞ୍ଚିବା ପାଇଁ ଆବଶ୍ୟକ ହୁଏ । ଜନବିସ୍ଫୋରଣ କାରଣରୁ ଭାରତରେ ଖାଦ୍ୟ ଉତ୍ପାଦନରେ ବିଶେଷ କରି ଉନ୍ନତି ପରିଲକ୍ଷିତ ହେଲେ ହେଁ ମୁଣ୍ଡପିଛା ଉପଲବ୍ଧ ପରିମାଣ ପ୍ରାୟ ଅପରିବର୍ତ୍ତନୀୟ ସ୍ଥିତି ପ୍ରଦର୍ଶନ କରେ । ଉଦାହରଣ : ଭାରତରେ ୧୯୫୬ ବର୍ଷ ନିଟ୍ ଖାଦ୍ୟଶସ୍ୟ ଉତ୍ପାଦନ ୬୩ ନିୟୁତ ଟନ୍ ଥାଇ ମୁଣ୍ଡପିଛା ଖାଦ୍ୟ ପରିମାଣ ଦୈନିକ ୪୩୧ ଗ୍ରାମ୍ ଥ‌ିବାବେଳେ ୧୯୯୦ ବର୍ଷ ୧୪୫ ନିୟୁତ୍ ଟନ୍‌କୁ ବୃଦ୍ଧି ପାଇ ମଧ୍ୟ ୪୭୬ ଗ୍ରାମ୍ ଥୁଲା ଓ ୨୦୦୦ ବର୍ଷ ମଧ୍ୟ ୧୬୮ ନିୟୁତ ଟନ୍ ଉତ୍ପାଦନ ସହ ୪୫୮ ଗ୍ରାମ ରହିଛି ।

(ଘ) ସାକ୍ଷରତା ଉପରେ ଚାପ : ଭାରତରେ ଶିକ୍ଷା ବ୍ୟୟକୁ ଯେତେବେଳେ ସାମାଜିକ ବିନିଯୋଗ ଭାବରେ ବିବେଚନା କରାଯାଏ । ଗୁରୁତ୍ବ ଦୃଷ୍ଟିକୋଣରୁ ଏହା ଉପଲବ୍‌ଧ ହୋଇ ପାରେ ନାହିଁ । କାରଣ ଭାରତ ଭଳି ଗରିବ ଦେଶରେ ଜନସଂଖ୍ୟା ବୃଦ୍ଧି କାରଣରୁ ଏହାର ମୁକାବିଲା କରାଯାଇପାରେ ନାହିଁ। ୬ ରୁ ୧୪ ବର୍ଷ ପିଲାମାନଙ୍କ ପାଇଁ ଭାରତରେ ମୁଣ୍ଡପିଛା ବାର୍ଷିକ ଆୟ ମାତ୍ର ୧୪୪ ଟଙ୍କା । ତେଣୁ ମାନବ ସମ୍ବଳର ଉପଯୁକ୍ତ ଯତ୍ନ ନେଇ ହୁଏ ନାହିଁ; ଶିକ୍ଷା ହାର ମଧ୍ୟ ବିଶେଷ ଅନଗ୍ରସରତା ପ୍ରକାଶ କଲାବେଳେ ବୃଦ୍ଧି ସ୍ଥାନାନ୍ତରଣ ଘଟେ ।

(ଙ) ଦରଦାମ୍ ଉପରେ ପ୍ରଭାବ : ବହୁଳ ଜନସଂଖ୍ୟା କାରଣରୁ ଆବଶ୍ୟକତା ବୃଦ୍ଧି ପାଏ ଓ ଅସମ ବଣ୍ଟନ ସ୍ଥିତିକୁ କିଛି ଲୋକ ଅତ୍ୟାବଶ୍ୟକ ଦ୍ରବ୍ୟ ପୂରଣ କରି ନ ପାରି ଦାରିଦ୍ର୍ୟ ସୀମା ତଳେ ବସବାସ କରୁଥିବାବେଳେ ଚାହିଦା ବୃଦ୍ଧି କାରଣରୁ ବଜାରରେ ମଧ୍ୟ ଦରଦାମ୍ ବୃଦ୍ଧି ଘଟି ମୁଦ୍ରାସ୍ପତି ସୃଷ୍ଟି କରେ ।

(ଚ) ପୁଞ୍ଜି ସୃଷ୍ଟି ପ୍ରତି ପ୍ରଭାବ : ଜନସଂଖ୍ୟା ବୃଦ୍ଧି ଫଳରେ ଉପଯୋଗ ବ୍ୟୟ ବୃଦ୍ଧି ପାଇ ସଞ୍ଚୟ ଓ ବିନିଯୋଗ ହ୍ରାସ ପାଏ। ଫଳରେ ପୁଞ୍ଜି ସୃଷ୍ଟି ସ୍ଵଳ୍ପ ହୋଇଥାଏ । ମାତ୍ର ବାସ୍ତବ ମୁଣ୍ଡପିଛା ଆୟକୁ ଅପରିବର୍ତିତ ରଖୁବା ପାଇଁ ଜାତୀୟ ଆବଶ୍ୟକ । କିନ୍ତୁ ଏଠାରେ ଦ୍ରୁତ ଜନସଂଖ୍ୟା କାରଣରୁ ଆବଶ୍ୟକ ବୃଦ୍ଧିକୁ ଆଟ୍‌ରେ ରଖୁ ଯେତିକି ପ୍ରଗତି ଘଟିବା କଥା, ତାହା ପୁଞ୍ଜି ଆୟର ବୃଦ୍ଧି ଓ ଜନସଂଖ୍ୟା ବୃଦ୍ଧି ସମହାରରେ ହେବା ଅଭିବୃଦ୍ଧି ଘଟିପାରେ ନାହିଁ । ଅନ୍ୟପକ୍ଷରେ, ଜନସଂଖ୍ୟା ସ୍ଵଳ୍ପତାକୁ ବାଧାପ୍ରାପ୍ତ ହୁଏ ।

(ଛ) ପରିବେଶ ପ୍ରତି ପ୍ରଭାବ : ଜନବିସ୍ଫୋରଣ କାରଣରୁ ପରିବେଶ ପ୍ରଦୂଷଣ ହୋଇ ସ୍ଵାସ୍ଥ୍ୟ ସମସ୍ୟାକୁ ଜଟିଳ କରି ଗଢ଼ି ତୋଳେ । ଏହା ନିଜର କବର ନିଜେ ଖୋଳିବା ସଂଗେ ସମାନ ହୁଏ ।

(କ) ସାମାଜିକ ଚାପ : ଜନବିସ୍ଫୋରଣ କାରଣରୁ ସାମାଜିକ ଶାନ୍ତି ରଂଗ ହୁଏ । କାରଣ ଏହା ଗୁଣାତ୍ମକ ବିକାଶ ପ୍ରତିରୋଧ କରିବା ସହ ସାମାଜିକ କାର୍ଯ୍ୟକଳାପକୁ ଉତ୍ସାହିତ କରେ। ଏହା ସବୁ ଜନବିସ୍ଫୋରଣର ବହୁବିଧ ଫଳ ଅଟେ । ତେଣୁ ଭାରତ ଭଳି ଅର୍ଥ ବ୍ୟବସ୍ଥାରେ ଜନସଂଖ୍ୟାର ଦ୍ରୁତବୃଦ୍ଧିକୁ ରୋକିବା ସର୍ବପ୍ରଥମ ଆବଶ୍ୟକତା ଅଟେ ।

Question ୫।
ସ୍ଵାଧୀନତା ପ୍ରାପ୍ତି ସମୟରେ ଭାରତର ଆର୍ଥନୀତିକ ସ୍ଥିତି କିପରି ଥୁଲା ? ଆଲୋଚନା କର।
(Explain the condition of Indian Economy on the eve of Independence.)
Answer:
ଇଂରେଜମାନଙ୍କର ଦୀର୍ଘ ୨୦୦ ବର୍ଷର ଶାସନ ଭାରତୀୟ ଅର୍ଥନୀତି ପାଇଁ ମହଙ୍ଗା ଥିଲା । ଏହି ସମୟ ମଧ୍ୟରେ ଭାରତୀୟ ଅର୍ଥବ୍ୟବସ୍ଥାର ମୌଳିକ ବୈଶିଷ୍ଟ୍ୟଗୁଡ଼ିକ ବିଶେଷ ପ୍ରଭାବିତ ହୋଇଥିଲା । ଶୋଷଣ ମନୋଭାବ, ସମ୍ବଳର ସ୍ଥାନାନ୍ତର, ଦେଶର ବିଭକ୍ତିକରଣ ଭାରତୀୟ ଅର୍ଥବ୍ୟବସ୍ଥାକୁ ଏକ ଅନୁନ୍ନତ ଅର୍ଥ ବ୍ୟବସ୍ଥାର ରୂପ ଦେଇଥିଲା । ୧୯୪୭ ମସିହାରେ ଭାରତ ଯେତେବେଳେ ସ୍ଵାଧୀନ ହେଲା ଏହାର ଅର୍ଥ ବ୍ୟବସ୍ଥା ସ୍ଥାଣୁ ଓ ବିପର୍ଯ୍ୟସ୍ତ ହୋଇ ପଡ଼ିଥିଲା । ସ୍ଵାଧୀନତା ପ୍ରାପ୍ତି ସମୟରେ ଭାରତୀୟ ଅର୍ଥବ୍ୟବସ୍ଥାର ଚିତ୍ର କ’ଣ ଥିଲା ନିମ୍ନରେ ତାହା ଆଲୋଚନା କରାଯାଇଛି ।

(କ) ଔପନିବେଶିକ ଅର୍ଥବ୍ୟବସ୍ଥା (Calonial Economy):
ଯେଉଁ ଶାସନ ବ୍ୟବସ୍ଥାରେ ଗୋଟିଏ ରାଷ୍ଟ୍ୟ ଅନ୍ୟ ଗୋଟିଏ ରାଷ୍ଟ୍ର ଉପରେ ନିଜର ଅର୍ଥନୈତିକ, ରାଜନୈତିକ ଏବଂ ସାର୍ବଭୌମତ୍ଵ ଅଧିକାର ବିସ୍ତାର କରିଥାଏ, ତାହାକୁ ଔପନିବେଶିକ ଅର୍ଥ ବ୍ୟବସ୍ଥା କୁହାଯାଏ । ଏହି ବ୍ୟବସ୍ଥାରେ ସମୟ କ୍ରମେ ଶାସକ ରାଷ୍ଟ୍ର ସହିତ ଶାସିତ ରାଷ୍ଟ୍ରର ଅର୍ଥନୀତି ମିଶ୍ରଣ ହୋଇଥାଏ ।

ଇଂରେଜ ସରକାର ଦୀର୍ଘ ୨୦୦ ବର୍ଷରୁ ଊର୍ଦ୍ଧ୍ୱ ଶାସନ କାଳ ସମୟରେ ଭାରତୀୟ ଅର୍ଥ ବ୍ୟବସ୍ଥାକୁ ଏକ ଔପନିବେଶିକ ଅର୍ଥବ୍ୟବସ୍ଥାରେ ପରିଣତ କରିଥିଲେ । ସମ୍ବଳର ବିନିଯୋଗ, ଭିତ୍ତିଭୂମିର ବିକାଶ ଇତ୍ୟାଦି ସମସ୍ତ କ୍ଷେତ୍ରରେ ବ୍ରିଟିଶ୍ ସରକାର ଚୂଡ଼ାନ୍ତ ନିଷ୍ପତ୍ତି ନେଉଥିଲେ । ଏହି ସମସ୍ତ ନିଷ୍ପଭି ଇଂରେଜ ସରକାରଙ୍କ ସ୍ଵାର୍ଥ ସାଧନ ନିମନ୍ତେ ପ୍ରେରିତ ଥିଲା । ଭାରତୀୟ ଅର୍ଥବ୍ୟବସ୍ଥାରେ ଇଂରେଜ ସରକାରଙ୍କ ଆଧୂପତ୍ୟ ବୃଦ୍ଧି ହେଲା । ଇଂରେଜ ସରକାରଙ୍କର ଏହି ଔପନିବେଶିକ ନୀତି ଭାରତୀୟ ଅର୍ଥ ବ୍ୟବସ୍ଥାକୁ ଦୁର୍ବଳ କରି ଦେଇଥିଲା ।

(ଖ) ସାମନ୍ତବାଦୀ ଅର୍ଥବ୍ୟବସ୍ଥା (Feudal Economy):
ସାମନ୍ତବାଦ ଏକ ସାମାଜିକ ଓ ଅର୍ଥନୈତିକ ବ୍ୟବସ୍ଥା । ମଧ୍ୟଯୁଗରେ ଇଉରୋପରେ ଏହି ବ୍ୟବସ୍ଥା ଦେଖା ଦେଇଥିଲା । ଏହି ବ୍ୟବସ୍ଥାରେ ସାମନ୍ତବାଦୀମାନେ ଚାଷୀମାନଙ୍କୁ ଚାଷ ନିମନ୍ତେ ଜମି ଦେଇ ସମସ୍ତ ସୁରକ୍ଷା ଯୋଗାଇ ଦେଉଥିଲେ ଏବଂ ପ୍ରତିବଦଳରେ ସେମାନଙ୍କୁ ନିଜ ଆବଶ୍ୟକ ନିମନ୍ତେ ବିଭିନ୍ନ କାର୍ଯ୍ୟରେ ନିୟୋଜିତ ହେବା ପାଇଁ ବାଧ୍ୟ କରୁଥିଲେ । ଇଂରେଜ ଶାସନ କାଳ ମଧ୍ୟରେ ସାମନ୍ତବାଦୀ ଅର୍ଥ ବ୍ୟବସ୍ଥାର ସମ୍ୟକ୍ ଝଲକ ଦେଖୁବା ମିଳିଥିଲା । ଇଂରେଜମାନେ ଆମ ଦେଶରେ ଭୂ-ରାଜସ୍ୱ ସଂଗ୍ରହର ଅଧିକାର ହାତେଇ ଥିଲେ । ସେମାନେ ଜମିଦାରୀ ପ୍ରଥାର ପ୍ରଚଳନ କରିଥିଲେ । ଜମିଦାରମାନେ ଚାଷୀମାନଙ୍କଠାରୁ ଜମିରେ ଖଜଣା ମନ ଇଚ୍ଛା ଆଦାୟ କରୁଥିଲେ । ସେମାନେ ଚାଷୀମାନଙ୍କୁ ଭିନ୍ନ ଭିନ୍ନ ଉପାୟରେ ଅତ୍ୟାଚାର ଓ ଶୋଷଣ କରୁଥିଲେ । ତେଣୁ ସ୍ଵାଧୀନତା ପ୍ରାପ୍ତି ସମୟରେ ଭାରତୀୟ ଅର୍ଥ ବ୍ୟବସ୍ଥାର କେତେକାଂଶରେ ସାମନ୍ତବାଦୀ ଅର୍ଥ ବ୍ୟବସ୍ଥାକୁ ରୂପାନ୍ତରିତ ହୋଇଥିଲା ।

(ଗ) ଅନଗ୍ରସର ଅର୍ଥବ୍ୟବସ୍ତା (Backward Economy):
ଦୀର୍ଘ ୨୦୦ ବର୍ଷରୁ ଊର୍ଦ୍ଧ୍ଵ ଇଂରେଜ ଶାସନ ଭାରତୀୟ ଅର୍ଥ ବ୍ୟବସ୍ଥାକୁ ବିପର୍ଯ୍ୟସ୍ତ କରିଥିଲା । ନିଜସ୍ଵ ସ୍ଵାର୍ଥ ସାଧନର ଅଭୀପ୍‌ସା ଭାରତକୁ ଦିନକୁ ଦିନ ଗରିବ କରିଥିଲା । ପ୍ରଚୁର ପୁଞ୍ଜି ଓ ସମ୍ବଳର ବହିର୍ଗମନ ଭାରତୀୟ ଅର୍ଥବ୍ୟବସ୍ଥାକୁ ରୋଗାକ୍ରାନ୍ତ କରିଥିଲା । ନୀତି ଓ ଦିଶାହୀନ ଇଂରେଜ ଶାସନ ଅର୍ଥନୀତିର ପ୍ରତ୍ୟେକ ସ୍ତରରେ ଅଧଃପତନ ଘଟାଇ ଥିଲା । ଶିଳ୍ପ ଓ କୃଷି ଆଦି କ୍ଷେତ୍ରରେ ଅବହେଳା ପ୍ରଦର୍ଶନ କରାଯିବାରୁ ଦାରିଦ୍ର୍ୟ ଓ ବେକାରୀ ବୃଦ୍ଧି ପାଇଲା । ସ୍ଵାଧୀନତା ପ୍ରାପ୍ତି ସମ୍ଭରେ ସମଗ୍ର ବିଶ୍ଵରେ ଭାରତ ଏକ ଅନୁନ୍ନତ ଓ ଅନଗ୍ରସର ଅର୍ଥନୀତି ଭାବେ ପରିଗଣିତ ହେଲା ।

(ଘ) ସ୍ଥାଣୁ ଅର୍ଥବ୍ୟବସ୍ଥା (Stagnant Economy):
ଇଂରେଜ ଶାସନ ସମୟରେ ଭାରତର ପ୍ରାକୃତିକ ତଥା ମାନବ ସମ୍ବଳ କୁମାଗତ ଭାବେ ଶୋଷିତ ହୋଇଥିଲା। ଭାରତର ପ୍ରାକୃତିକ ଓ ମାନବ ସମ୍ବଳକୁ ଇଂରେଜ ସରକାର ନିଜ ଦେଶକୁ ପ୍ରେରଣ କରି ସେଠାକାର ଉତ୍ପାଦିତ ପଦାର୍ଥକୁ ଭାରତର ଲୋକମାନଙ୍କୁ କ୍ରୟ କରିବା ପାଇଁ ବାଧ୍ୟ କରୁଥିଲେ । ନିଜସ୍ଵ ସମ୍ବଳରେ ଉତ୍ପାଦିତ ଦ୍ରବ୍ୟକୁ ଇଂରେଜ ସରକାରଙ୍କୁ ଦ୍ବାରା ଧାର୍ଯ୍ୟ ଦରରେ କ୍ରୟକରି ଭାରତର ଲୋକମାନେ ଶୋଷିତ ହେଉଥିଲେ। ସମୟ କ୍ରମେ ଭାରତୀୟ ଶିଳ୍ପଗୁଡ଼ିକ ବନ୍ଦ ହେଲା ଏବଂ ଫଳରେ ଇଂଲଣ୍ଡର ଶିଳ୍ପିକ ବିକାଶ ସାଧନ ହେଲା । ଦାରିଦ୍ର୍ୟ, ବେକାରୀ ବୃଦ୍ଧି ଆମ ଦେଶର ଅର୍ଥବ୍ୟବସ୍ଥାକୁ ସ୍ଥାଣୁ କରିଦେଲା ।

ବ୍ୟାବସାୟିକ ଉଦ୍ଦେଶ୍ୟ ରଖୁ ଦୀର୍ଘ ୨୦୦ ବର୍ଷ ଧରି ଶାସନ କରିଥିବା ଇଂରେଜ ସରକାର ଭାରତୀୟ ଆର୍ଥନୀତିକ ମେରୁଦଣ୍ଡକୁ ଦୁର୍ବଳ କରିଥିଲେ । ଷୋଡ଼ଶ ଓ ସପ୍ତଦଶ ଶତାବ୍ଦୀରେ ଯେଉଁ ଭାରତ ଏକ ଶିଳ୍ପ ସମୃଦ୍ଧ ରାଷ୍ଟ୍ରଭାବେ ବିଶ୍ଵ ଦରବାରରେ ପରିଗଣିତ ହେଉଥିଲା; ଅଷ୍ଟାଦଶ ଓ ଊନବିଂଶ ଶତାବ୍ଦୀ ବେଳକୁ ସେହି ଦେଶ ଶିଳ୍ପକ୍ଷେତ୍ରରେ ଏକ ଦୁର୍ବଳ ରାଷ୍ଟ୍ରଭାବରେ ପରିଚିତ ହେଲା । ସମଗ୍ର ବିଶ୍ଵରେ ଖ୍ୟାତ ଭାରତୀୟ ହସ୍ତଶିଳ୍ପ ଓ କୁଟୀର ଶିଳ୍ପ କ୍ରମଶଃ ନିଜସ୍ଵ ସତ୍ତା ହରାଇଲା । ଭାରତୀୟ ଅର୍ଥନୀତି ମୁଖ୍ୟତଃ ଏକ ଆମଦାନକାରୀ ଅର୍ଥନୀତିର ରୂପ ନେଲା ।

ଉପରୋକ୍ତ ଆଲୋଚନାରୁ ଏହା ସ୍ପଷ୍ଟ ଯେ, ସ୍ଵାଧୀନତା ପ୍ରାପ୍ତି ସମୟରେ ଭାରତୀୟ ଅର୍ଥନୀତି ଏକ ଔପନିବେଶିକ ଅର୍ଥ-ସାମନ୍ତବାଦୀ, ଅନଗ୍ରସର, କୃଷିପ୍ରଧାନ, ସ୍ଥାଣୁ ଅର୍ଥବ୍ୟବସ୍ଥାରେ ପରିଣତ ହୋଇଥିଲା । ଇଂରେଜ ସରକାରଭକର ଶୋଷଣ ନୀତି ଆମ ଦେଶର ଆର୍ଥିକ ଅନଗ୍ରସରତାର ମୁଖ୍ୟ କାରର ଭାବେ ଦଣ୍ଡାୟମାନ ହୋଇଥିଲା।

Question ୬ ।
ସମକାଳୀନ ଭାରତୀୟ ଅର୍ଥ ବ୍ୟବସ୍ଥାର ମୌଳିକ ବୈଶିଷ୍ଟ୍ୟଗୁଡ଼ିକ ଆଲୋଚନା କର ।
(Explain the characteristics of Contemporary Indian Economy.)
Answer:
ଭାରତ ଏକ ପ୍ରମୁଖ ତୃତୀୟ ବିଶ୍ଵ ରାଷ୍ଟ୍ର । ଦୀର୍ଘଦିନର ବ୍ରିଟିଶ୍ ସାମ୍ରାଜ୍ୟର ଏକ ଉପନିବେଶ ହିସାବରେ ଶୋଷିତ ହେବା ପରେ ଭାରତ ୧୯୪୭ ମସିହାରେ ସ୍ଵାଧୀନ ହୋଇଥିଲା । ସ୍ଵାଧୀନତାର ପରବର୍ତ୍ତୀ ସମୟରେ ଦ୍ରୁତ ଉନ୍ନତି ପାଇଁ କରାଯାଇଥିବା ପ୍ରଚେଷ୍ଟାର ଫଳ ସ୍ଵରୂପ ଭାରତୀୟ ଅର୍ଥବ୍ୟବସ୍ଥାରେ ବିଭିନ୍ନ ବିଭାଗରେ ଆଖୁ ଦୃଶିଆ ବିକାଶ ସଂଘଟିତ ହୋଇଛି । ଏଥଯୋଗୁଁ ଆମ ଅର୍ଥବ୍ୟବସ୍ଥାକୁ ଏବେ ଆଉ ଦୁର୍ବଳ ଅର୍ଥବ୍ୟବସ୍ଥା ବୋଲି ଅଭିହିତ କରା ନ ଯାଇ ବିକାଶୋନୁମୁଖୀ ବୋଲି ବର୍ଣ୍ଣନା କରାଯାଉଛି । ନ ଦୀର୍ଘ ୬୦ ବର୍ଷର ଯୋଜନା ଫଳର ଭାରତ କେତେକ କ୍ଷେତ୍ରରେ ଅଗ୍ରଗତି କରିଥିଲେ ମଧ୍ୟ ଅନେକ କ୍ଷେତ୍ରରେ ପଛୁଆ ହୋଇ ରହିଛି । ଏହି ପୃଷ୍ଠଭୂମିରେ ଭାରତୀୟ ଅର୍ଥବ୍ୟବସ୍ଥାର ମୌଳିକ ବୈଶିଷ୍ଟ୍ୟଗୁଡ଼ିକର ସଂକ୍ଷିପ୍ତ ବିବରଣୀ ନିମ୍ନୋକ୍ତ ମତେ ପ୍ରଦାନ କରାଯାଇଛି ।

(କ) ସ୍ଵଳ୍ପ ମୁଣ୍ଡପିଛା ଆୟ (Lower per Capita Income):
ମୁଣ୍ଡପିଛା ଆୟ ବିକାଶର ଏକ ମାପ କାଠି । ଜାତୀୟ ଆୟକୁ ଜନସଂଖ୍ୟାରେ ଭାଗ କରି ମୁଣ୍ଡପିଛା ଆୟ ନିର୍ଦ୍ଧାରଣ କରାଯାଏ । ପୃଥ‌ିବୀର ଅଧିକାଂଶ ବିକଶିତ ରାଷ୍ଟ୍ର ତୁଳନାରେ ଭାରତର ମୁଣ୍ଡପିଛା ଆୟ ବହୁତ କମ୍ ହୋଇଥିବାରୁ ପରିଲକ୍ଷିତ ହୁଏ । ୨୦୦୩ ମସିହା ପରିସଂଖ୍ୟାନ ଅନୁସାରେ ଭାରତର ମୁଣ୍ଡପିଚ୍ଛା ଆୟ ୫୩୦ ଆମେରିକୀୟ ଡଲାର ଥିବାବେଳେ ସୁଇଜରଲ୍ୟାଣ୍ଡ ଓ ଆମେରିକାରେ ମୁଣ୍ଡପିଚ୍ଛା ଆୟ ଯଥାକ୍ରମେ ୩୯,୮୮୦ ଓ ୩୭,୬୧୦ ଡଲାର ଥିଲା । ଭାରତ ସରକାରଙ୍କ ଦ୍ଵାରା ପ୍ରଦତ୍ତ ଅର୍ଥନୈତିକ ସର୍ବେକ୍ଷଣ ୨୦୧୦-୧୧ ରେ ପ୍ରଦତ୍ତ ପରିସଂଖ୍ୟାନ ଅନୁସାରେ ୨୦୦୩– ୦୫ରୁ ୨୦୦୯-୧୧ ମଧ୍ଯରେ ମୁଣ୍ଡପିଛା ଆୟ ପ୍ରାୟ ୩୭ ଶତାଂଶ ବୃଦ୍ଧି ପାଇଛି । ୨୦୧୫-୧୬ ଆର୍ଥିକ ସର୍ଭେ ଅନୁସାରେ ଭାରତର ମୁଣ୍ଡପିଚ୍ଛା ଆୟ ୯୩, ୨୩୧ ଟଙ୍କା ।

(ଖ) ବୃଦ୍ଧିଗତ ଢାଞ୍ଚାରେ ତ୍ରୁଟି(lefeet in the Occupational Soructure):
ଆମ ଦେଶର ବୃତ୍ତିଗତ ଢାଞ୍ଚାକୁ ଲକ୍ଷ୍ୟକଲେ ଜଣାଯାଏ ଯେ ମୋଟ ଜନସଂଖ୍ୟାର ପ୍ରାୟ ୬୭ ଶତାଂଶ ଶ୍ରମଶକ୍ତି କେବଳ କୃଷିକ୍ଷେତ୍ର ଉପରେ ନିର୍ଭରଶୀଳ । କିନ୍ତୁ ଆମେରିକା, ଇଂଲଣ୍ଡ, କାନାଡ଼ା ଭଳି ଉନ୍ନତ ଦେଶରେ ମାତ୍ର ୨ ଶତାଂଶରୁ ୩ ଶତାଂଶ ଶ୍ରମଶକ୍ତି କୃଷିକ୍ଷେତ୍ର ଉପରେ ନିର୍ଭରଶୀଳ । ଆମ ଦେଶର ଜାତୀୟ ଆୟକୁ କୃଷିକ୍ଷେତ୍ରର ଅବଦାନ କ୍ରମାଗତ ଭାବରେ ହ୍ରାସ ପାଇବାରେ ଲାଗିଛି । କୃଷିକ୍ଷେତ୍ରରେ ସ୍ଵଳ୍ପ ଉତ୍ପାଦନ କ୍ଷମତାର ସମସ୍ୟା ଦେଖାଦେଇଛି । ପ୍ରାବିଧ‌ିକ ଜ୍ଞାନ କୌଶଳ, ପୁଞ୍ଜି ଓ ଭିଭିଭୂମି ଇତ୍ୟାଦିର ଅଭାବ ଯୋଗୁଁ କୃଷିକ୍ଷେତ୍ରରେ ଉତ୍ପାଦନଶୀଳତା ଅନ୍ୟ ଦେଶ ତୁଳନାରେ ବହୁତ କମ୍ ।

(ଗ) ଜନସଂଖ୍ୟାର ଚାପ (Pressure of Population):
ଭାରତ ବିଶ୍ଵର ଦ୍ଵିତୀୟ ଜନବହୁଳ ରାଷ୍ଟ୍ର । ୨୦୧୧ ମସିହା ଜନଗଣନା ଅନୁସାରେ ଆମ ଦେଶର ମୋଟ ଜନସଂଖ୍ୟା ୧୨୧,୦୨କୋଟି ଏବଂ ଜନସଂଖ୍ୟାର ବୃଦ୍ଧି ହାର ୧.୬୪ ଶତାଂଶ । ଦ୍ରୁତ ଜନସଂଖ୍ୟା ବୃଦ୍ଧି ଭାରତୀୟ ଅର୍ଥନୀତିର ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ରରେ ପ୍ରବଳ ଚାପ ସୃଷ୍ଟି କରୁଛି । ଏହା ଦେଶର ଆର୍ଥିକ ଓ ସାମାଜିକ ବିକାଶରେ ଅନ୍ତରାୟ ହେଉଛି ।

(ଘ) ସ୍ଵଳ୍ପ ପୁଞ୍ଜି ଗଠନ (Low Rate of Capital Formation):
ଆମ ଦେଶର ଅର୍ଥନୀତିର ଅନ୍ୟତମ ବୈଶିଷ୍ଟ୍ୟ ହେଲା ପୁଞ୍ଜିର ସ୍ଵଳ୍ପତା ! ପୁଞ୍ଜିର ଅଭାବ ହେତୁ ମୁଣ୍ଡପିଛା ପୁଞ୍ଜିର ପରିମାଣ ଓ ପୁଞ୍ଜି ଗଠନର ହାର କମ୍ ହୋଇଛି । ସ୍ଵଳ୍ପ ପୁଞ୍ଜି ଗଠନ ଦେଶରେ ଶ୍ରମ ଓ ଭୂମିର ଉତ୍ପାଦନଶୀଳତା ହ୍ରାସ କରୁଛି । ସ୍ଵଳ୍ପ ପୁଞ୍ଜି ଗଠନ ଦେଶର ଆର୍ଥିକ ପ୍ରଗତିରେ ମୁଖ୍ୟ ଅନ୍ତରାୟ ଭାବେ ଦଣ୍ଡାୟମାନ ହୋଇଛି ।

(ଙ) ପ୍ରାକୃତିକ ସମ୍ବଳର ସଠିକ୍ ବିନିଯୋଗର ସମସ୍ୟା (Problems of proper utilisation of Natural Resources):
ଆମ ଦେଶରେ ପ୍ରାକୃତିକ ସମ୍ବଳର ସଠିକ୍ ଏବଂ ପୂର୍ଣ ବ୍ୟବହାର ହୋଇପାରୁ ନାହିଁ । ପୁଞ୍ଜିର ଅଭାବ ଏବଂ ପ୍ରାବିଧ‌ିକ ଜ୍ଞାନ କୌଶଳର ଅଭାବ ପ୍ରାକୃତିକ ସମ୍ବଳର ପୂର୍ଣ୍ଣ ବ୍ୟବହାର ନ କରିବାର ପ୍ରଧାନ କାରଣ ଅଟେ।

(ଚ) ସ୍ଵଳ୍ପ ଆଧାରିକ ସଂରଚନା (Inadequate Infrastrcture):
ଦେଶର ଅର୍ଥନୈତିକ ଓ ସାମାଜିକ ବିକାଶରେ ଉଭୟ ଅର୍ଥନୈତିକ ଓ ସାମାଜିକ ଆଧରିକ ସଂରଚନା ଭୂମିକା ଗୁରୁତ୍ଵପୂର୍ଣ୍ଣ । ସ୍ଵାଧୀନତା ପ୍ରାପ୍ତିର ପରବର୍ତୀ ସମୟରେ ଦେଶର ଆଧାରିକ ସଂରଚନାର ବିକାଶ କ୍ଷେତ୍ରରେ ଉଲ୍ଲେଖନୀୟ ଅଗ୍ରଗତି ହୋଇଛି କିନ୍ତୁ ଦ୍ରୁତ ଅର୍ଥନୈତିକ ବିକାଶ ପାଇଁ ଏହା ପର୍ଯ୍ୟାପ୍ତ ନୁହେଁ।

(ଛ) ଦୁର୍ବଳମାନବ ପୁଞ୍ଜି (Poor Human Capital):
କୌଣସି ଦେଶର ଆର୍ଥିକ ବିକାଶ ସେହି ଦେଶର ଦକ୍ଷ ଓ ତାଲିମପ୍ରାପ୍ତ ମାନବ ପୁଞ୍ଜି ଉପରେ ନିର୍ଭର କରିଥାଏ । ମାନବ ପୁଞ୍ଜି ଦେଶର ଶ୍ରମ ଗୁଣବତ୍ତାକୁ ବୁଝାଇଥାଏ । ଏହା ଶିକ୍ଷା, ତାଲିମ, ସ୍ଵାସ୍ଥ୍ୟ ଓ ବାସଗୃହ ଇତ୍ୟାଦି ଦ୍ଵାରା ପ୍ରଭାବିତ ହୋଇଥାଏ । ସ୍ଵାଧୀନତାର ପରବର୍ତ୍ତୀ ସମୟରେ ବିଭିନ୍ନ ପଞ୍ଚବାର୍ଷିକ ଯୋଜନାରେ ମାନବ ପୁଞ୍ଜିର ବିକାଶକୁ ଗୁରୁତ୍ଵ ଦିଆଯାଇଥିଲେ ମଧ୍ୟ ଭାରତର ସାମାଜିକ ସଂରଚନା ବା ମାନବ ସମ୍ବଳର ଗୁଣବତ୍ତାରେ ବିଶେଷ ପରିବର୍ତ୍ତନ ହୋଇନାହିଁ । ଏହା ଦେଶର ଆର୍ଥିକ ଅନଗ୍ରସରତାର ଅନ୍ୟତମ କାରଣ ଅଟେ ।

(କ) ବେକାରୀ ଓ ଦାରିଦ୍ର୍ୟ ସମସ୍ୟା (Problems of Unemployment and Roverty):
ଭାରତୀୟ ଅର୍ଥବ୍ୟବସ୍ଥାର ଦୁଇଟି ଗୁରୁତ୍ଵପୂର୍ଣ୍ଣ ସମସ୍ୟା ହେଲା ଲେକାରୀ ଓ ଦାରିଦ୍ର୍ୟ ସମସ୍ୟା । ଦୃତ ଜନସଂଖ୍ୟା ବୃଦ୍ଧି ଦେଶରେ ଶ୍ରମ ଯୋଗାଣରେ ବୃଦ୍ଧି କରୁଛି । ଦେଶର ଆର୍ଥିକ ବିକାଶ ମନ୍ଥର ହୋଇଥିବାରୁ ଶ୍ରମ ଚାହିଦା ମନ୍ଥର ଗତିରେ ବୃଦ୍ଧି ପାଉଛି । ଫଳରେ ଦେଶରେ ବେକାରୀ ସମସ୍ୟା ତୀବ୍ରତର ରୂପ ନେଇଛି । ରୋଜଗାର ସୁବିଧାର ଅଭାବ ହେତୁ ଲୋମକାନଙ୍କର ବଞ୍ଚିବାର ମାନ ହ୍ରାସ ପାଉଛି । ତେଣୁ ଦେଶରେ ଦାରିଦ୍ର୍ୟ ସମସ୍ୟା.ଉତ୍କଟତର ହୋଇଛି ।

(ଝ) ଆୟବଣ୍ଟନରେ ଅସମାନତା (Inequalities in the Distribution of Income):
ଆୟ ବଣ୍ଟନ କ୍ଷେତ୍ରରେ ଥିବା ଅସମାନତା ଭାରତୀୟ ଅର୍ଥ ବ୍ୟବସ୍ଥାର ଅନ୍ୟତମ ଗୁରୁତ୍ଵପୂର୍ଣ୍ଣ ବୈଶିଷ୍ଟ୍ୟ । ନିମ୍ନ ମୁଣ୍ଡପିଛା ଆୟ ସହିତ ଉଚ୍ଚ ଆୟ ବୈଷମ ଦାରିଦ୍ର୍ୟର ତୀବ୍ରତାକୁ ପ୍ରତିଫଳିତ କରୁଛି । ସ୍ଵଳ୍ପ ସଂଖ୍ୟକ ଭାରତୀୟ ଧନୀ ଥିଲାବେଳେ ଅଧିକାଂଶ ଅତ୍ୟନ୍ତ ଗରିବ ! ବିଶ୍ବବ୍ୟାଙ୍କ ରିପୋର୍ଟ ୨୦୧୦ ଅନୁସାରେ ଶୀର୍ଷ ୨୦ ଶତାଂଶ ଭାରତୀୟଙ୍କ ଆୟ ମୋଟେ ଆୟର ୪୫.୩ ଶତାଂଶ ହେବାବେଳେ ନିମ୍ନ ୨୦ ଶତାଂଶ ଭାରତୀୟଙ୍କ ଆୟ ମାତ୍ର ୮.୧ ଶତାଂଶ ।

(ଞ) ଦ୍ଵୈତ ଅର୍ଥନୀତି (Dualistic Economy):
ଭାରତୀୟ ଅର୍ଥନୀତିର ଅନ୍ୟତମ ବୈଶିଷ୍ଟ୍ୟ ହେଲା ଉଭୟ ପାରଂପରିକ କ୍ଷେତ୍ର ଓ ଆଧୁନିକ କ୍ଷେତ୍ରରେ ସହାବସ୍ଥାନ । ଗ୍ରାମାଞ୍ଚଳରେ ପାରମ୍ପରିକ ପଦ୍ଧତି ଏବଂ ସହରାଞ୍ଚଳରେ ଆଧୁନିକ ପଦ୍ଧତିର ବ୍ୟବହାର ଦେଖିବାକୁ ମିଳିଥାଏ । ଭାରତ ଭଳି ଏକ ଗ୍ରାମ ବହୁଳ ରାଷ୍ଟ୍ରରେ ଦ୍ଵୈତ ଅର୍ଥନୀତି ଗ୍ରାମାଞ୍ଚଳର ଦାରିଦ୍ର୍ୟକୁ ତୀବ୍ରତର କରି ଦେଶର ବିକାଶ କ୍ଷେତ୍ରରେ ପ୍ରତିବନ୍ଧକ ସୃଷ୍ଟି କରି ଆସୁଛି ।

ଉପରୋକ୍ତ ଆଲୋଚନାରୁ ଏହା ସ୍ପଷ୍ଟ ଯେ, ଏକ ନିମ୍ନ ବିକଶିତ ରାଷ୍ଟ୍ରର ସମସ୍ତ ବୈଶିଷ୍ଟ୍ୟ ଭାରତରେ ଦେଖିବାକୁ ମିଳିଥିବାରୁ ଭାରତର ଅର୍ଥନୀତିକୁ ଏକ ଅନୁନ୍ନତ ଅର୍ଥନୀତିରେ ପରିଗଣିତ କରାଯାଇଛି । କିନ୍ତୁ ଏହା ସତ୍ୟ ଯେ ସାଂପ୍ରତିକ ପରିସ୍ଥିତିରେ ଭାରତୀୟ ଅର୍ଥନୀତିରେ ଦେଖାଦେଇଥିବା ସଫଳତା ନିକଟ ଭବିଷ୍ୟତରେ ଭାରତକୁ ସମଗ୍ର ବିଶ୍ବରେ ଏକ ବୃହତ୍ ଅର୍ଥନୈତିକ ଶକ୍ତିରେ ପରିଗଣିତ ହୋଇ ବିଶ୍ବ ଅର୍ଥବ୍ୟବସ୍ଥାର ମାର୍ଗଦର୍ଶକ ହେବାର ମସ୍ତ ଲକ୍ଷଣ ଦର୍ଶାଉଅଛି ।

Question ୨। .
ଭାରତୀୟ ବୃତ୍ତିଗତ ଢାଞ୍ଚାର ଲକ୍ଷଣଗୁଡ଼ିକ କ’ଣ ? ଭାରତର ବୃତ୍ତିଗତ ଢାଞ୍ଚାରେ ପରିବର୍ତ୍ତନ ଆଣିବା ପାଇଁ କି କି ପଦକ୍ଷେପ ଗ୍ରହଣ କରାଯାଇଛି ?
(What are the chracteristics of India’s occupation – structure? What are the possible steps to change the occupational structure of India.)
Answer:
ଭାରତର ବୃତ୍ତିଗତ ଢାଞ୍ଚା ବୈଚିତ୍ରମୟ । ଏହି ବୈଚିତ୍ୟମୟ ବୃତ୍ତିଗତ ଢାଞ୍ଚାର କେତେକ ଲକ୍ଷଣ ରହିଛି । ଭାରତର ବୃତ୍ତିଗତ ଢାଞ୍ଚାରେ ପରିଦୃଷ୍ଟ ହେଉଥିବା ଲକ୍ଷଣଗୁଡ଼ିକୁ ନିମ୍ନରେ ଆଲୋଚନା କରାଯାଇଛି

(କ) କୃଷିର ପ୍ରାଧାନ୍ୟ (Importance of Agriculture):
ଭାରତ ଏକ କୃଷି ପ୍ରଧାନ ଦେଶ । ଦୀର୍ଘ ୬୦ ବର୍ଷର କୃଷିକ୍ଷେତ୍ରରେ ନିୟୋଜିତ । ଜନସଂଖ୍ୟାର ଦୃତ ବୃଦ୍ଧି ଏବଂ । କୃଷିକ୍ଷେତ୍ର ଉପରେ ନିର୍ଭରଶୀଳତା ବୃଦ୍ଧି କରିଛି । ତେଣୁ କୃଷିକ୍ଷେତ୍ରରେ ସ୍ଵଚ୍ଛ ଉତ୍ପାଦିତାର ସମସ୍ୟା

(ଖ) ଔଦ୍ୟୋଗିକ ବିକାଶ (Industrial Development):
ଯୋଜନା ପରେ ମଧ୍ୟ ଭାରତର ପ୍ରାୟ ୬୭ ଭାଗ ଶ୍ରମ ଶକ୍ତି ଦ୍ଵିତୀୟକ କ୍ଷେତ୍ର ଓ ତୃତୀୟକ କ୍ଷେତ୍ରର ମନ୍ଥର ବିକାଶ ଦେଖାଦେଇଛି ।
ଆମ ଦେଶର ମୋଟ ଶ୍ରମଶକ୍ତିର ପ୍ରାୟ ୧୩ ଶତାଂଶ ଶ୍ରମଶକ୍ତି ଶିଳ୍ପକ୍ଷେତ୍ରରେ କାର୍ଯ୍ୟରତ । ଆମେରିକା ଓ ଇଂଲଣ୍ଡପରି ଉନ୍ନତ ଦେଶରେ ଯଥାକ୍ରମେ ୩୨ ଶତାଂଶ ଓ ୪୨ ଶତାଂଶ ଶ୍ରମଶକ୍ତି ଶିଳ୍ପ କ୍ଷେତ୍ରରେ କାର୍ଯ୍ୟରତ । ଏହିପରି ସଂଖ୍ୟାକର ଏହା ସ୍ପଷ୍ଟ ଯେ ଭାରତ ଶିଳ୍ପ ବିକାଶ କ୍ଷେତ୍ରରେ ଅନଗ୍ରସର ।

(ଗ) ନିମ୍ନ ବିକଶିତ ତୃତୀୟକ କ୍ଷେତ୍ର (low levelopment in the fertiary Sector):
ଭାରତ ମୋଟ୍ ଶ୍ରମଶକ୍ତିର ମାତ୍ର ୨୫,୧ ପ୍ରତିଶତ ତୃତୀୟକ କ୍ଷେତ୍ରରେ କାର୍ଯ୍ୟରତ। ଆମେରିକା ଓ ଇଂଲଣ୍ଡ ଭଳି ଦେଶରେ ଯତାକ୍ରମେ ୬୬ ପ୍ରତିଶତ ଓ ୫୬ ପ୍ରତିଶତ ଶ୍ରମଶକ୍ତି ଦ୍ଵିତୀୟକ ଏବଂ ତୃତୀୟକ କ୍ଷେତ୍ରରେ କାର୍ଯ୍ୟରତ । ତେଣୁ ଏହି ପରିସଂଖ୍ୟାନରୁ ଏହା ସ୍ପଷ୍ଟ ହୁଏ ଯେ ଆମ ଦେଶର ତୃତୀୟକ କ୍ଷେତ୍ରର ବିକାଶ ଉଲ୍ଲେଖନୀୟ ନୁହେଁ ।

(ଘ) ନିମ୍ନ ଆୟ ସ୍ତର (low level of Income):
ଭାରତର ମୋଟ ଶ୍ରମଶକ୍ତି ପ୍ରାୟ ୬୭ ଶତାଂଶ ପ୍ରାଥମିକ କ୍ଷେତ୍ରରେ ନିୟୋଜିତ । ଦ୍ଵିତୀୟକ ଓ ତୃତୀୟକ କ୍ଷେତ୍ର ତୁଳନାରେ ପ୍ରାଥମିକ କ୍ଷେତ୍ରରେ ଆୟ ସୃଷ୍ଟିକାରୀ କ୍ଷମତା କମ୍ । ତେଣୁ ଅଧିକାଂଶ ଭାରତୀୟଙ୍କର ମୁଣ୍ଡପିଛା ଆୟ ସ୍ଵ ଏବଂ ବଞ୍ଚିବାର ମାନ ଅନୁନ୍ନତ।

(ଙ) ଅସୁନ୍ତଳିତ ବିକାଶ (Unbalanced Growth):
ଭାରତର ଶ୍ରମଶକ୍ତି ତିନିଗୋଟି କ୍ଷେତ୍ରରେ ସମାନ ଭାବରେ ନିଯୁକ୍ତ ନ ହୋଇ ପ୍ରାଥମିକ କ୍ଷେତ୍ରରେ ଅଧିକାଂଶ ଶ୍ରମଶକ୍ତି କାର୍ଯ୍ୟରତ । ତେଣୁ ଆମ ଦେଶର ସମସ୍ତ କ୍ଷେତ୍ରର ବିକାଶ ସମପରିମାଣରେ ହୋଇପାରି ନାହିଁ । ଏହା ଭାରତ ପାଇଁ ଏକ ଅସୁନ୍ତଳିତ ଅର୍ଥବ୍ୟବସ୍ଥା ସୃଷ୍ଟି କରିଛି ।

(ଚ) ଅନଗ୍ରସର ଗ୍ରାମୀଣ ଅର୍ଥନୀତି (Undervelopmed Village Economy):
ପ୍ରାଥମିକ କ୍ଷେତ୍ର ମୁଖ୍ୟତଃ ଗ୍ରାମଭିତିକ । ପ୍ରାଥମିକ କ୍ଷେତ୍ର ଉପରେ ଅତ୍ୟଧୂକ ନିର୍ଭରଶୀଳ ଅଧିକାଂଶ ଶ୍ରମଶକ୍ତି ଗ୍ରାମ ଭିତ୍ତିକ । ଭାରତର ଗ୍ରାମୀଣ ଅର୍ଥ ବ୍ୟବସ୍ଥା ପଛୁଆ ଥିବାରୁ ଭାରତୀୟ ଅର୍ଥ ବ୍ୟବସ୍ଥା ମଧ୍ୟ ପଛୁଆ ହୋଇରହିଛି । ଉପରୋକ୍ତ ଆଲୋଚନାରୁ ଏହା ସ୍ପଷ୍ଟ ହୁଏ ଯେ ସ୍ଥାଣୁପ୍ରାୟ ବୃତ୍ତିଗତ ଢାଞ୍ଚା ଭାରତୀୟ ଅର୍ଥ ବ୍ୟବସ୍ଥାର ଦୁଃଖଦ ଚିତ୍ର ପ୍ରଦାନ କରୁଛି । ଦେଶର ସମାନୁପାତିକ ବିକାଶ ପାଇଁ ଆମ ଦେଶର ବୃତ୍ତିଗତ ଢାଞ୍ଚାରେ ପରିବର୍ତ୍ତନର ଆବଶ୍ୟକତା ଦେଖାଦେଇଛି । ନିମ୍ନଲିଖିତ ପଦକ୍ଷେପ ଦ୍ବାରା ଆମ ଦେଶର ବୃତ୍ତିଗତ ଢାଞ୍ଚାରେ ପରିବର୍ତ୍ତନ ଅଣାଯାଇପାରିବ । .

୧. ନବିସ୍ଫୋରଣର ସମସ୍ୟାକୁ ନିୟନ୍ତ୍ରଣ କରିବା ପାଇଁ ଫଳପ୍ରଦ କାର୍ଯ୍ୟକ୍ରମ ହାତକୁ ନେବା ।
୨. ଗ୍ରାମାଞ୍ଚଳରେ କ୍ଷୁଦ୍ର ଶିଳ୍ପ ଓ କୁଟୀର ଶିଳ୍ପର ବିକାଶ ପାଇଁ ପଦକ୍ଷେପ ନେବା ।
୩. . କୃଷିକ୍ଷେତ୍ରରେ ଆଧୁନିକୀକରଣ କରି କୃଷିକ୍ଷେତ୍ରର ଉତ୍ପାଦନ ଏବଂ ଉତ୍ପାଦନ କ୍ଷମତା ବୃଦ୍ଧି କରିବା ।
୪. କୃଷିଭିତ୍ତିକ ଶିଳ୍ପର ବିକାଶ କରିବା ।
୫,.ଦେଶରେ ବୃହତ, ଶିଳ୍ପମାନ ସ୍ଥାପନ କରିବା ।
୬. ଦେଶରେ ତୃତୀୟକ କ୍ଷେତ୍ରର ବିକାଶ ସାଧନ କରିବା ।
୭. ଦେଶରେ ଫଳପ୍ରଦ ଗ୍ରାମାଞ୍ଚଳ ବିକାଶ କାର୍ଯ୍ୟକ୍ରମ କାର୍ଯ୍ୟକାରୀ କରିବା !
୮. ଦେଶରେ ଆତ୍ମନିଯୁକ୍ତି କାର୍ଯ୍ୟକ୍ରମକୁ ପ୍ରୋତ୍ସାହିତ କରିବା ।
୯. ଦେଶର ବିକାଶ ସାଧନ ପାଇଁ ଅନ୍ୟ ଦେଶ ଓ ଆନ୍ତର୍ଜାତୀୟ ବଜାର ଉପରେ ପ୍ରାଧାନ୍ୟ ଦେବା ।

Question ୭।.
ଭାରତରେ ପରିବାର ନିୟୋଜନ କାର୍ଯ୍ୟକ୍ରମ ଆଲୋଚନା କର।
(Discuss the family planning programme in India.)
Answer:
ଭାରତ ପୃଥ‌ିବୀରେ ପ୍ରଥମ ଦେଶ ଯେ କି ପରିବାର ନିୟନ୍ତ୍ରଣକୁ ଏକ ସରକାରୀ କାର୍ଯ୍ୟକ୍ରମ ରୂପରେ ପ୍ରଥମ ପଞ୍ଚବାର୍ଷିକ ଯୋଜନା ଆରମ୍ଭରୁ କାର୍ଯ୍ୟକାରୀ କରି ଆସୁଅଛି । ୧୯୫୨ ମସିହାରେ ଏକ ପରୀକ୍ଷାମୂଳକ ଭିଭିରେ ଜାତୀୟ ପରିବାର ନିୟୋଜନ କାର୍ଯ୍ୟକ୍ରମର ଶୁଭାରମ୍ଭ କରାଗଲା । ୧୯୫୦ ୟାକୁ ୧୯୬୧ ମସିହା ପର୍ଯ୍ୟନ୍ତ ସମୟକୁ ପରିବାର ନିୟନ୍ତ୍ରଣ କାର୍ଯ୍ୟକ୍ରମର ପରୀକ୍ଷାମୂଳକ ସମୟ ବୋଲି ଧରାଯାଏ । ଏହି କାର୍ଯ୍ୟକ୍ରମକୁ ଲୋକମାନେ ସ୍ଵଇଚ୍ଛାରେ ଗ୍ରହଣ କରିବାର ଲକ୍ଷ୍ୟ ରଖାଯାଇଥିଲା । ମାତ୍ର ୧୯୬୧ ଜନଗଣନାର ଫଳାଫଳ ସରକାର ତଥା ସଚେତନ ନାଗରିକମାନଙ୍କୁ ବିବ୍ରତ କରିଦେଲା । ୧୯୪୧:୫୧ ଦଶନ୍ଧିରେ ଜନସଂଖ୍ୟାର ବୃଦ୍ଧିହାର ୧୩.୩୪ ପ୍ରତିଶତ ଥିବାବେଳେ, ୧୯୫୧- ୬୧ ଦଶନ୍ଧିରେ ଏହା ୨୧.୬୪ ପ୍ରତିଶତକୁ ବୃଦ୍ଧି ପାଇଲା । ତେଣୁ ତୃତୀୟ ପଞ୍ଚବାର୍ଷିକ ଯୋଜନା ୯୧୯୬୧— ୬୬)ରେ ଦେଶରେ ଜନସଂଖ୍ୟାର ଦୃତ ବୃଦ୍ଧି ହାରକୁ ପ୍ରତିରୋଧ କରିବାର ଲକ୍ଷ୍ୟ କରାଗଲା | ଦମ୍ପତିମାନଙ୍କୁ ପରିବାର ଯୋଜନା ପ୍ରତି ଧ କୃଷ୍ଟ କରିବା ନିମନ୍ତେ ଏକ ବ୍ୟାପକ କାର୍ଯ୍ୟକ୍ରମ ହାତକୁ ନିଆଗଲା । ଏହି କାର୍ଯ୍ୟକ୍ରମ ଦେଶର ପ୍ରତ୍ୟେକ ଘରେ ଘରେ ପହଞ୍ଚାଇବାର ଲକ୍ଷ୍ୟ କରାଗଲା । ୧୯୬୬ ମସିହାରେ ଏକ ସ୍ଵତନ୍ତ୍ର ଜନ୍ମ ନିୟନ୍ତ୍ରଣ ବିଭାଗ ଓ କେନ୍ଦ୍ରରେ ଜନ୍ମ ନିୟନ୍ତ୍ରଣ କମିଶନର ପଦବୀ ସୃଷ୍ଟି କରାଗଲା ।

ଚତୁର୍ଥ ପଞ୍ଚବାର୍ଷିକ ଯୋଜନା କାଳରେ (୧୯୬୯-୭୪) ପରିବାର ଯୋଜନା କାର୍ଯ୍ୟକ୍ରମକୁ ସମୟ ଭିଭିକ ଓ ନିର୍ଦ୍ଦିଷ୍ଟ ଲକ୍ଷ୍ୟ ହାସଲ ମୂଳକ କରାଗଲା । ୧୯୭୬ ଏପ୍ରିଲ୍ ମଧ୍ୟଭାଗରେ ଜାତୀୟ ଜନସଂଖ୍ୟା ନୀତି (National Population Policy) କେନ୍ଦ୍ର ସରକାରଙ୍କ ଦ୍ଵାରା ଘୋଷଣା କରାଗଲା । ଏହି ନୀତିର କେତେକ ପ୍ରଧାନ ବୈଶିଷ୍ଟ୍ୟ ନିମ୍ନରେ ପ୍ରଦତ୍ତ କରାଯାଇଛି ।

ବୈଶିଷ୍ଟ୍ୟ (Features):
୧. ଆଇନ ଦ୍ବାରା ଉଭୟ ପୁଅ ଓ ଝିଅମାନଙ୍କର ବିବାହ ବୟସକୁ ଯଥାକ୍ରମେ ୨୧ ଓ ୧୮କୁ ବୃଦ୍ଧି କରାଗଲା । ଏହା ୧୯୭୮ ମସିହାଠାରୁ କାର୍ଯ୍ୟକାରୀ କରାଗଲା ।
୨. ୧୯୭୧ ମସିହା ଜନଗଣନାର ଜନସଂଖ୍ୟାକୁ ୨୦୦୦ ମସିହା ପର୍ଯ୍ୟନ୍ତ ସାଂସଦ ସଭାର ପ୍ରତିନିଧ‌ି ସଂଖ୍ୟା ନିରୂପଣର ଆଧାର ଭାବେ ଗ୍ରହଣ କରିବାର ନିଷ୍ପତ୍ତି ନିଆଗଲା ।
୩. ବିଭିନ୍ନ ରାଜ୍ୟରେ ପରିବାର ନିୟୋଜନ କାର୍ଯ୍ୟକ୍ରମର ସଫଳତାକୁ ବିଚାରକୁ ନେଇ କେନ୍ଦ୍ରୀୟ ଅନୁଦାନର ୮% ଅର୍ଥ ଯୋଗାଇ ଦେବାର ବ୍ୟବସ୍ଥା କରାଗଲା ।
୪. ସବୁ ରାଜ୍ୟରେ ନାରୀ ଶିକ୍ଷାର ସ୍ତର ବୃଦ୍ଧି କରିବା ଉପରେ ଗୁରୁତ୍ବ ଦିଆଗଲା ।
୫. ବନ୍ଧ୍ୟାକରଣ ପଦ୍ଧତି ଗ୍ରହଣ କରିଥିବା ବ୍ୟକ୍ତିମାନଙ୍କୁ ଆର୍ଥିକ ପ୍ରୋତ୍ସାହନ ଓ ସାମୂହିକ ପ୍ରୋତ୍ସାହନର ପରିମାଣ ବୃଦ୍ଧି କରାଗଲା ।
୬. ଜନସଂଖ୍ୟା ଉପରେ ଗବେଷଣା, ଶିକ୍ଷା, ସ୍ୱାସ୍ଥ୍ୟ ସେବା ତଥା ମା ଓ ଶିଶୁଙ୍କ ସ୍ଵାସ୍ଥ୍ୟ ରକ୍ଷା ଉପରେ ଅଧିକ ପ୍ରାଧାନ୍ୟ ଦିଆଗଲା ।
୭. ପରିବାର ନିୟନ୍ତ୍ରଣକୁ ଏକ ଗଣଆନ୍ଦୋଳନରେ ପରିଣତ କରିବା ପାଇଁ ଚିକିତ୍ସକ ଗୋଷ୍ଠୀ, ଜିଲ୍ଲା ପରିଷଦ, ପଞ୍ଚାୟତ ସମିତି, ଶିକ୍ଷକ, ସମବାୟ ସମିତି ଓ ଶ୍ରମିକ ସଂଘ ଆଦିକୁ ସଂଶ୍ଳିଷ୍ଟ କରି ଉପଯୁକ୍ତ ଗୋଷ୍ଠୀ ପ୍ରୋତ୍ସାହନ ଦେବାକୁ ସ୍ଥିର କରାଗଲା ।
୮. ପରିବାର ନିୟୋଜନର ବାର୍ତ୍ତା ଘରେ ଘରେ ପହଞ୍ଚାଇବା ନିମନ୍ତେ ଗଣମାଧ୍ୟମର ଅଧିକ ବ୍ୟବହାର ନିମନ୍ତେ ନିଷ୍ପତି ନିଆଗଲା ।

ସ୍ଵତନ୍ତ୍ର ଭାବେ ଏହି ପରିବାର ନିୟନ୍ତ୍ରଣ କାର୍ଯ୍ୟକ୍ରମ ପ୍ରସ୍ତୁତ ହୋଇ ଥିବାରୁ ଏହାକୁ କ୍ରାସ କାର୍ଯ୍ୟକ୍ରମ (Crash Programme) କୁହାଯାଏ । ୧୯୭୫ ମସିହା ଜୁନ୍ ୨୫ ତାରିଖ ଠାରୁ ଦେଶରେ ଜରୁରୀ ଅବସ୍ଥା ଜାରି କରାଗଲା । ଏହାର ସୁଯୋଗ ନେଇ ତତ୍‌କାଳୀନ କେନ୍ଦ୍ର ସରକାର ଘୋଷିତ ଜାତୀୟ ଜନସଂଖ୍ୟା ନୀତିକୁ କାର୍ଯ୍ୟକାରୀ କରିବା ନିମନ୍ତେ ବାଧ୍ୟତାମୂଳକ ବନ୍ଧ୍ୟାକରଣ କାର୍ଯ୍ୟକ୍ରମ ଆରମ୍ଭ କଲେ । ଏହାଫଳରେ ୧୯୬୬-୭୭ରେ ବନ୍ଧ୍ୟାକରଣ ନିର୍ଦ୍ଧାରିତ ଲକ୍ଷ୍ୟ ୪.୨ ନିୟୁତ ଥିବା ସ୍ଥଳେ ସମୁଚିତ ଉଦ୍ୟମ ଯୋଗୁ ୮.୨ ନିୟୁତ ଲୋକଙ୍କ ଠାରେ ବନ୍ଧ୍ୟାକରଣ କରାଯାଇଥିଲା । ଏହି ଲକ୍ଷ୍ୟ ହାସଲ ନିମନ୍ତେ ଲୋକମାନଙ୍କୁ ଅନେକ ସ୍ଥଳରେ ବାଧ୍ୟ କରାଯାଇଥିବାର ଅଭିଯୋଗ ହୁଏ । ଯାହାଫଳରେ, ପରିବାର ନିୟନ୍ତ୍ରଣ କାର୍ଯ୍ୟକ୍ରମ କ୍ରମେ ଜନ ସମର୍ଥନ ହରାଇଲା ଏବଂ ୧୯୭୮ ମସିହା ପର୍ଯ୍ୟନ୍ତ ଏ ଯୋଜନାର ଗତି ଯଥେଷ୍ଟ ଭାବେ ବାଧାପ୍ରାପ୍ତ ହେଲା । ଏହା ପରେ ଅବଶ୍ୟ ଏହି ପରିବାର ନିୟନ୍ତ୍ରଣ କାର୍ଯ୍ୟକ୍ରମ ନୂତନ ରୂପ ନେଇ ଜନାଦୃତ ହେବାକୁ ଲାଗିଲା ।

୧୯୭୭ ମସିହା ଜୁନ୍ ମାସରେ କେନ୍ଦ୍ରରେ ପ୍ରତିଷ୍ଠିତ ଜନତା ସରକାର ଜନସଂଖ୍ୟା ନୀତି ଘୋଷଣା କଲେ । ଏହି ନୂତନ ନୀତିରେ ପ୍ରଧାନତଃ ଦୁଇଟି ନୂତନ ଆଭିମୁଖ୍ୟ ଲକ୍ଷ୍ୟ କରାଯାଏ । ପ୍ରଥମତଃ, ଏହା ସ୍ୱେଚ୍ଛାକୃତ ପରିବାର ନିୟନ୍ତ୍ରଣ ଉପରେ ଗୁରୁତ୍ଵ ଦେଲା । ଦ୍ଵିତୀୟତଃ, ପରିବାର ନିୟନ୍ତ୍ରଣ ସହିତ ପରିବାରର ସ୍ୱାସ୍ଥ୍ୟ ସେବା ଉପରେ ଏହି ନୀତି ପ୍ରାଧାନ୍ୟ ଦେଲା ଅର୍ଥାତ୍ ଜନ୍ମ ନିୟନ୍ତ୍ରଣ ସହ ସ୍ଵାସ୍ଥ୍ୟସେବା, ମାତୃମଙ୍ଗଳ, ଶିଶୁ ପାଳନ ଓ ପୁଷ୍ଟିସାର ଖାଦ୍ୟ ଯୋଗାଣ ଆଦିକୁ ସଂଶ୍ଳିଷ୍ଟ କରିବା ନୂତନ ନୀତିର ଉଦ୍ଦେଶ୍ୟ ହେଲା । ତେଣୁ ଏହି ନୂତନ ନୀତି ଅନୁସାରେ ପରିବାର ନିୟନ୍ତ୍ରଣ କାର୍ଯ୍ୟକ୍ରମ (Family Planning Programme), ପରିବାର କଲ୍ୟାଣ (Tiamily Welfare Programme) କାର୍ଯ୍ୟକ୍ରମରେ ରୂପାନ୍ତରିତ କରାଗଲା; ମାତ୍ର ଏହାର ଫଳ ଆଦୌ ଉତ୍ସାହ ଜନକ ନ ଥିଲା । ୧୯୭୬-୭୭ରେ ୮୨ ଲକ୍ଷ ବନ୍ଧ୍ୟାକରଣ ଅସ୍ତ୍ରୋପଚାର କରାଯାଇଥିବା ବେଳେ ୧୯୭୭-୭୮ ରେ ମାତ୍ର ୬୪ ଲକ୍ଷ ବନ୍ଧ୍ୟାକରଣ ଅସ୍ତ୍ରୋପଚାର କରାଗଲା ।

ଷଷ୍ଠ ପଞ୍ଚବାର୍ଷିକ ଯୋଜନା (୧୯୮୦-୮୫) ଦେଶର ଜନସଂଖ୍ୟାକୁ ସୀମିତ ରଖୁବାର ଦୀର୍ଘକାଳୀନ ଲକ୍ଷ୍ୟ ସ୍ଥିର କରି, ଏହାର ହାସଲ ନିମନ୍ତେ ନିର୍ଦ୍ଦିଷ୍ଟ ନୀତି ନିର୍ଦ୍ଧାରଣ କରାଗଲା । ୨୦୫୦ ମସିହା ସୁଦ୍ଧା ଭାରତର ମୋଟ ଜନସଂଖ୍ୟା ୧୨୯ କୋଟିରେ ସୀମିତ ରଖୁବାର ଲକ୍ଷ୍ୟ ପରିପୂରଣ କରିବା ପାଇଁ ଆଶାପୋଷଣ କରାଗଲା । ଏଥୁ ନିମନ୍ତେ ବର୍ତ୍ତମାନର ୧.୬୭ ପ୍ରତିଶତ ନିଟ୍ ପ୍ରଜନନ ହାରିକୁ ୧୯୯୬ ମସିହା ସୁଦ୍ଧା ସାମଗ୍ରିକ ଦୃଷ୍ଟିରେ ୧.୦କୁ ଏବଂ ୨୦୦୧ ମସିହା ବେଳକୁ ଏହା, ପ୍ରତ୍ୟେକ ରାଜ୍ୟରେ ହାସଲ କରିବାରେ ଲକ୍ଷ୍ୟ ନୂତନ ସ୍ଵାସ୍ଥ୍ୟ ନୀତିରେ ଧାର୍ଯ୍ୟ କରାଗଲା । ନିଟ୍ ପ୍ରଜନନ ହାର (Nate reproduction rate)ର ଅର୍ଥ ହେଲା ଜଣେ ସନ୍ତାନ ପ୍ରସବ କରିପାରୁଥିବା ମହିଳା ୪୫ ବର୍ଷରେ ପଦାର୍ପଣ କରିସାରିବା ପରେ ହିଁ ମାତ୍ର ଜଣେ ପ୍ରଜନକ୍ଷମ ମହିଳା ସନ୍ତାନ ପ୍ରସବ ପାଇଁ ସାମର୍ଥ୍ୟ ହୋଇପାରୁଥିବ; ମାତ୍ର ଆମ ଦେଶରେ ଜଣେ ପ୍ରଜନନକ୍ଷମ ମହିଳା ୪୫ ବର୍ଷ ପଦାର୍ପଣ ନ କରୁଣୁ, ଏକରୁ ଅଧିକ ୧୫ ବର୍ଷ ପର୍ଯ୍ୟନ୍ତ ଅତିକ୍ରମ କରିପାରୁଥିବା ମହିଳା ପ୍ରଜନନକ୍ଷମ ହୋଇଯାଉଛନ୍ତି । ଏହାଦ୍ଵାରା ଜନସଂଖ୍ୟା ବଢ଼ି ଚାଲିଛି । ଅନ୍ୟପକ୍ଷରେ, ଯେତେବେଳେ ନିଟ୍ ପ୍ରଜନନ ହାର ୧ ହୁଏ, ଜଣେ ପ୍ରଜନନକ୍ଷମ ମହିଳା ୪୪ ବର୍ଷ ଅତିକ୍ରମ କରି ଆଉ ସନ୍ତାନ ପ୍ରସବ କରିବାର କ୍ଷମତା ହରାଇଲା ପରେ ପରେ; ମାତ୍ର ଜଣେ ମହିଳା ୧୫ ବର୍ଷ ଏହାରୁ ପ୍ରଜନନକ୍ଷମ ହୋଇପାରେ । ଏହି ଅବସ୍ଥାରେ ଜନସଂଖ୍ୟା ଅପରିବର୍ତ୍ତିତ ରହେ ।

ସପ୍ତମ ଯୋଜନା ସମୟ ମଧ୍ୟରେ ୯୧୯୮୫-୯୦), ୨୦୦୦ ମସିହା ସୁଦ୍ଧା ସମସ୍ତଙ୍କ ପାଇଁ ସ୍ଵାସ୍ଥ୍ୟ ସେବା ଯୋଗାଇବା ଏବଂ ୨୦୦୦ ମସିହାରୁ ନିଟ୍ ପ୍ରଜନନ ହାର ୧କୁ ହ୍ରାସ କରିବାର ଲକ୍ଷ୍ୟ କରାଯାଇଥିଲା । ଏହି ଯୋଜନାରେ, ମଧ୍ୟ ମାତୃ ଓ ଶିଶୁ ସ୍ଵାସ୍ଥ୍ୟ ଦେବା କାର୍ଯ୍ୟକ୍ରମ (Mankind and Child Icalth Care Programc)କୁ ଅଗ୍ରାଧିକାର ଦିଆଗଲା । ପରିବାର କଲ୍ୟାଣ କାର୍ଯ୍ୟକ୍ରମରେ ଉଭୟ ମାତୃ ଓ ଶିଶୁ ମୃତ୍ୟୁହାରକୁ ହ୍ରାସ, କରିବା ସପ୍ତମ ଯୋଜନାର ମୂଳଲକ୍ଷ୍ୟ ଥିଲା !

୧୯୯୨ ମସିହା ଅପ୍ରେଲ ପହିଲା ତାରିଖରେ ଅଷ୍ଟମ ପଞ୍ଚବାର୍ଷିକ ଯୋଜନା ଆରମ୍ଭ ହେଲା । ୧୯୯୧ ମସିହା ଡିସେମ୍ବର ମାସରେ ଯୋଜନା କମିଶନ ଉନ୍ନୟନ ପରିଷଦ (National Development Council)ରେ ‘ଜନସଂଖ୍ୟା ନିୟନ୍ତ୍ରଣ ଆହ୍ବାନ ଓ କୌଶଳ’ ଶୀର୍ଷକ ନାମକ ଦଲିଲ୍‌ ଦସ୍ତାବିଜ ଉପସ୍ଥାପନପ କଲେ । ଏଥିରେ ଉଲ୍ଲେଖ ଥିଲା, “ ଜନସଂଖ୍ୟା ବିସ୍ପୋଣ, ଯାହାକି ଦେଶର ସାମାଜିକ, ଅର୍ଥନୈତିକ ବିକାଶ ନିମନ୍ତେ ସମଗ୍ର ପ୍ରଚେଷ୍ଟାକୁ ପ୍ରତିହତ କରୁଛି, ତାହା ଦେଶ ପକ୍ଷରେ ଏକମାତ୍ର ଅତି ଜରୁରୀ ସମସ୍ୟା” । ତେଣୁ ସରକାର ଏକ କର୍ମ ଯୋଜନା ପ୍ରସ୍ତାବ (Action Plan) ରଖଳେ । ତା’ର ବୈଶିଷ୍ଟ୍ୟ ହେଲା-

୧. ଦେଶବାସୀଙ୍କର ଜୀବନଧାରାର ବିକାଶ ।
୨. ସହରାଞ୍ଚଳ ବସ୍ତିମାନଙ୍କରେ ପରିବାର କଲ୍ୟାଣ ସମ୍ବନ୍ଧୀୟ କାର୍ଯ୍ୟକ୍ରମର ପ୍ରଚାର ।
୩. ହଜାର ପ୍ରତି ଜନ୍ମହାର ୩୯ ରୁ ଅଧିକ ଥିବା, ରାଜ୍ୟର ୯୦ ଜିଲ୍ଲାରେ ଜନ୍ମହାର ହ୍ରାସ ପାଇଁ ଅଧିକ ଦୃଷ୍ଟି ଦେବ !
୪. ପରିବାର କଲ୍ୟାଣ କାର୍ଯ୍ୟକ୍ରମରେ ସ୍ବେଚ୍ଛାସେବୀ ଅନୁଷ୍ଠାନ ଓ ବେସରକାରୀ ସଂଗଠନଗୁଡ଼ିକର ଅଧ‌ିକ ସହଯୋଗ ନେବା ।
୫. କେନ୍ଦ୍ର ସରକାରଙ୍କ ଠାରୁ ରାଜ୍ୟମାନଙ୍କୁ ମିଳୁଥ‌ିବା ଅନୁଦାନ ସହ ରାଜ୍ୟମାନଙ୍କ ଜନ୍ମହାର ନିୟନ୍ତ୍ରଣ ସଫଳତା ସହିତ ସଂଯୋଗ ସ୍ଥାପନ କରିବା ଏବଂ
୬. ଦେଶର ଅନେକ ଅଂଚଳରେ ଲୋକମାନଙ୍କର ପୁତ୍ର ସନ୍ତାନଟିଏ ପାଇବାର ଅଦମନୀୟ ମନୋବୃତ୍ତିକୁ ହ୍ରାସ କରିବା !

ନବମ ପଞ୍ଚବାର୍ଷିକ ଯୋଜନା (୧୯୯୬-୨୦୦୨) ଜନସଂଖ୍ୟା ନୀତି ସପ୍ତମ ଦଶକର ଶେଷ ଭାଗ ନିର୍ଦ୍ଧାରିତ ନୀତି ଅପେକ୍ଷା ଅଧ‌ିକ କୋହଳ ବା ଉଦାର ପରି ମନେ ହୁଏ । ଏହାର ଫଳ ନିର୍ଣାୟକାଭିମୁଖୀ (Rcsult Oriented Approach) । ଏ ପର୍ଯ୍ୟନ୍ତ ଜନ୍ମ ନିୟନ୍ତ୍ରଣ କରାଯାଇଥିବା ସମସ୍ତ ପ୍ରଚେଷ୍ଟାର ଫଳ ଆଶାଜନକ ନୁହେଁ । ଜନ୍ମ ନିୟନ୍ତ୍ରଣ ତଥାପି ଏକ ଦିବାସ୍ୱପ୍ନ ପରି ମନେ ହୁଏ । ବିଗତ ଶତାବ୍ଦୀର ଶେଷ ବେଳକୁ ନିଟ୍ ପ୍ରଜନନ ହାର ୧କୁ ହ୍ରାସ କରିବା ନବମ ଯୋଜନାରେ ଲକ୍ଷ୍ୟ କରାଗଲା । ମୋଟ ଉପରେ ବର୍ତ୍ତମାନର ଜନସଂଖ୍ୟା ନିୟନ୍ତ୍ରଣ କାର୍ଯ୍ୟକ୍ରମକୁ ଅଧିକ ଲୋକାଭିମୁଖୀ କରାଯାଇ ଏହାକୁ କେବଳ ପ୍ରଚାରରେ ସୀମିତ ନ କରାଯାଇ ଏହାର ନିର୍ଦ୍ଧାରିତ ଲକ୍ଷ୍ୟ ହାସଲ ଦିଗରେ ଅଧ୍ଵର୍କ ଗୁରୁତ୍ଵ ଦିଆଯାଇଛି । ନିର୍ଦ୍ଧାରିତ ଲକ୍ଷ୍ୟ ହାସଲ ଦିଗରେ ଅଧିକ ଗୁରୁତ୍ବ ଦିଆଯାଇଛି । କାରଣ ଏହି ଜନସଂଖ୍ୟା ବିସ୍ଫୋରଣ ବୋମା ବିସ୍ଫୋରଣ ଠାରୁ ଯେ ଅଧିକ ଭୟଙ୍କର ତାହା ସମସ୍ତେ ଅନୁଭବ କଲେଣି।

Question ୮।
ଜାତୀୟ ଜନସଂଖ୍ୟା ନୀତି –୨୦୦୦ ଆଲୋଚନା କର ।
(Discuss the National Population Policy-2000.)
Answer:
୧୯୯୪ ମସିହା ମେ ମାସରେ ଏମ୍.ଏସ୍. ସ୍ଵାମୀନାଥନ୍ କମିଟି ଜାତୀୟ ଜନସଂଖ୍ୟା ପ୍ରସ୍ତୁତ କରି କେନ୍ଦ୍ର ସରକାରଙ୍କୁ ପ୍ରଦାନ କରିଥିଲେ । ଏହାର ୬ ବର୍ଷ ପରେ ୨୦୦୦ ମସିହା ଫେବୃଆରୀ ମାସ ୧୫ ତାରିଖରେ ନୂତନ ଜନସଂଖ୍ୟା ନୀତି ଘୋଷଣା କରାଯାଇଥିଲା । ଜନସଂଖ୍ୟା ନିୟନ୍ତ୍ରଣ ପାଇଁ ସରକାରଙ୍କର ଯେଉଁ ମୁଖ୍ୟ ଆଭିମୁଖ୍ୟ ଥିଲା ତାହା ହିଁ ଏହି ନୀତିରେ ପ୍ରତିଫଳିତ ହୋଇଥିଲା । ଉଦାହରଣ ସ୍ଵରୂପ – ପ୍ରଥମତଃ, ନାଗରିକମାନଙ୍କ ଇଚ୍ଛାନୁସାରେ ତାଙ୍କର ପରିବାର ନିୟନ୍ତ୍ରଣ ପନ୍ଥା ସ୍ଥିର କରିବେ । ଦ୍ବିତୀୟତଃ କୌଣସି ନିର୍ଦ୍ଦିଷ୍ଟ ସାଂଖ୍ୟକ ଲକ୍ଷ୍ୟ ରଖୁ ପରିବାର ନିୟନ୍ତ୍ରଣ ସେବା କରାଯିବ ନାହିଁ ।

ନୀତିର ଲକ୍ଷ୍ୟ (Objectives of the Policy):
୨୦୦୪ ମସିହାରେ ଜନସଂଖ୍ୟା ନୀତିରେ ସମୟକୁ ଆଧାର କରି ତିନି ପ୍ରକାର ମୂଳ ଲକ୍ଷ୍ୟ କରାଗଲା । ପ୍ରଥମତଃ, ଯାହାକୁ ତତ୍‌କାଳ ଲକ୍ଷ୍ୟ (Immediate Objcctive) କୁହାଗଲା। ତାହା ହେଲା — ଜନ୍ମ ନିୟନ୍ତ୍ରଣ, ସ୍ଵାସ୍ଥ୍ୟ ସେବାର ଭିଜିଭୂମି ଗଠନ, ଶିଶୁ ସ୍ଵାସ୍ଥ୍ୟ ଯତ୍ନ ଯୋଗାଣ, ନିରାପଦ ମାତୃତ୍ଵ ପ୍ରଦାନ ଓ ସ୍ଵାସ୍ଥ୍ୟକର୍ମୀମାନଙ୍କ ଅଭାବ ପୂରଣ ।

ମଧ୍ୟବର୍ତ୍ତୀକାଳୀନ ଲକ୍ଷ୍ୟ ( Mediur Term Objective) ଭାବରେ ଆନ୍ତଃ କ୍ଷେତ୍ରୀୟ (Inten Sectoral) ପରିଚାଳନା କୌଶଳ ଅବଲମ୍ବନ କରି ୨୦୧୦ ମସିହା ମଧ୍ୟରେ ମୋଟ ସନ୍ତାନ ସନ୍ତତି ଜନ୍ମ କ୍ଷମତା (‘Total Fertility Rate)ହାରରେ ସ୍ଥିରତା ଆଣିବା (୩.୩ ରୁ ୨.୧କୁ ହ୍ରାସ), ପ୍ରତିସ୍ଥାପନ ସ୍ତର ( Replacement level) କୁ ହ୍ରାସ କରିବା ଓ ପ୍ରତି ଦମ୍ପତ୍ତିଙ୍କର ଦୁଇଟି ସନ୍ତାନ ନିୟମ କଡ଼ାକଡ଼ି ଭାବେ ଭାବିବା ।

ନୂତନ ଜନସଂଖ୍ୟା ନୀତିର ଦୀର୍ଘ ମିଆଦି ଲକ୍ଷ୍ୟ (Long Term Objective) ହେଲା- ୨୦୪୫ ମସିହା ସୁଦ୍ଧ ଏକ ସ୍ଥିର ଜନସଂଖ୍ୟା ଅଣାଯିବ ଯାହାକି ନିରନ୍ତର ଅର୍ଥନୈତିକ ଅଭିବୃଦ୍ଧି (Sustainable Iconomic Growth) । ସାମାଜିକ ବିକାଶ ଓ ପରିବାର ସୁରକ୍ଷାର ଆବଶ୍ୟକତା ସହ ସମାନତା ଆଣିପାରିବ।

ତେବେ ଏହି ଲକ୍ଷ୍ୟଗୁଡ଼ିକ ହାସଲ ଦିଗରେ ସହାୟକ ହେବା ଭଳି ୧୬ଟି ଉତ୍ସାହପ୍ରଦ ଓ ପ୍ରରୋଚନା ମୂଳକ ଉପାୟମାନ ଗ୍ରହଣ କରାଯାଇଛି । ସେଗୁଡ଼ିକ ମଧ୍ୟରୁ କେତୋଟି ମୁଖ୍ୟ ଉପାୟମାନ ନିମ୍ନରେ ଉପସ୍ଥାପନ କରାଗଲା । ଲକ୍ଷ୍ୟ ହାସଲ ନିମିତ୍ତ କେତେକ ଉପାୟ (Some measures to attain the objectives):

(୧) ଯୋଜନାର ବିକେନ୍ଦ୍ରୀକରଣ ଓ କାର୍ଯ୍ୟକରିତା (Decentralisation of planning and Implemen-tation):
ଭାରତର ସମ୍ବିଧାନର ୧୯୯୯ ମସିହାର ୭୩ତମ ଓ ୭୪ତମ ସଂଶୋଧନ ସ୍ଵାସ୍ଥ୍ୟସେବା, ପରିବାର କଲ୍ୟାଣ ଓ ପ୍ରାଥମିକ ଶିକ୍ଷାକୁ ଗ୍ରାମ ପଞ୍ଚାୟତଗୁଡ଼ିକର ଅଧୁନକୁ ହସ୍ତାନ୍ତର କରିଅଛି | ଗ୍ରାମ ପଞ୍ଚାୟତ ଓ ଜିଲ୍ଲା ପରିଷଦ ଭଳି ଗଣତାନ୍ତ୍ରିକ ଅନୁଷ୍ଠାନଗୁଡ଼ିକ କ୍ଷୁଦ୍ର ପରିବାରର ବାର୍ତ୍ତା ପ୍ରଚାର କରିବାରେ ପୁରସ୍କାର ପାଇବେ ବୋଲି ସିଦ୍ଧାନ୍ତ ନିଆଯାଇଛି ।

(୨) ଗ୍ରାମ୍ୟ ସ୍ତରରେ ଆନୁଷ୍ଠାନିକ ସନ୍ତାନ ପ୍ରସବ ସୁବିଧା ( Assistance for Delivery at Village level): ତାଲିମ୍ ପ୍ରାପ୍ତ ସ୍ଵାସ୍ଥ୍ୟ କର୍ମଚାରୀଙ୍କ ଦ୍ଵାରା ସନ୍ତାନ ପ୍ରସବ ନିମିତ୍ତ ଉପଯୁକ୍ତ ସ୍ଵାସ୍ଥ୍ୟ ପରୀକ୍ଷା, ଔଷଧ ଓ ସେବା ଯୋଗାଇ ଦେବାର ବ୍ୟବସ୍ଥା ରହିଛି ।

(୩) ଉନ୍ନତ ସ୍ୱାସ୍ଥ୍ୟ ଓ ପୁଷ୍ଟିହୀନତା ଦୂର ପାଇଁ ନାରୀ ସଶକ୍ତିକରଣ (Empowering Wome for Health and Nutitition):
ସୁସ୍ଥ ଓ ନିରାପଦ ମାତୃତ୍ଵ ଲାଭ ନିମିତ୍ତ ଉନ୍ନତ ସ୍ଵାସ୍ଥ୍ୟର ଆବଶ୍ୟକ ରହିଛି । ଏଣୁ ନିରାପଦ ମାତୃତ୍ଵ, ସଂକ୍ରାମକ ବ୍ୟାଧ୍ ନିବାରଣ, ପ୍ରଜନନ ପଥ ସଂକ୍ରମଣ ଚିକିତ୍ସା ତଥା ପୁଷ୍ଟିହୀନତା ଦୂରୀକରଣ ନିମିତ୍ତ ନାରୀମାନଙ୍କୁ ଅଧିକ ସଚେତନ ଓ ଶକ୍ତିଶାଳୀ କରିବାର ବ୍ୟବସ୍ଥା ରହିଛି |

(୪) ପରିବାର କଲ୍ୟାଣ ନିମିତ୍ତ ସେବା ପ୍ରଦାନ (Meeting needs for family welfare services):
ନୂତନ ଜନସଂଖ୍ୟା ନୀତି ପରିବାର କଲ୍ୟାଣ ନିମିତ୍ତ ଅଧିକ ସେବା ଯୋଗାଇବା ଉପରେ ଗୁରୁତ୍ଵ ଦେଲା । ପଞ୍ଚାୟତ ସ୍ତରରେ ଯେଉଁ ରୋଗୀମାନଙ୍କ ସେବା ନିମିତ୍ତ ବିଶେଷଜ୍ଞମାନଙ୍କ ସେବାର ଆବଶ୍ୟକ ମନେ ହେଉଛି, ସେମାନଙ୍କୁ ଆମ୍ବୁଲାନ୍ସ ଯୋଗାଇ ବଡ଼ ଡାକ୍ତରଖାନାକୁ ପଠାଇବାର ବ୍ୟବସ୍ଥା କରାଯାଇଛି ।

(୫) ପରିବାର ନିୟନ୍ତ୍ରଣ, ନିରାପଦ ମାତୃତ୍ଵ ଓ ସୁସୁ ଶିଶୁଲାଭର ବାର୍ତ୍ତା ପ୍ରେରଣ। (The spread of the message of family control with safe motherhood and healthy child):
ଦେଶରେ ଏପରି କେତେକ ସ୍ଥାନ ଅଛି ଯଥା : ସହରୀତଳ ବସ୍ତି, ଆଦିବାସୀ ବହୁଳ ଅଂଚଳ, ପାର୍ବତ୍ୟ ଅଂଚଳ, ସ୍ଥାନଚ୍ୟୁତ ହୋଇଥିବା ଅଧିବାସୀ ଓ ପ୍ରବାସୀ ବାସିନ୍ଦା, ଯେଉଁମାନଙ୍କ ନିକଟରେ ପରିବାର ନିୟନ୍ତ୍ରଣର ବାର୍ତ୍ତା ପହଞ୍ଚିପାରି ନାହିଁ । ସେମାନଙ୍କ ନିକଟରେ ପରିବାର ନିୟନ୍ତ୍ରଣ, ନିରାପଦ ମାତୃତ୍ବ ଓ ସୁସୁ ଶିଶୁ ଲାଭର ବାର୍ତ୍ତା ପହଞ୍ଚାଇ ଜନସଂଖ୍ୟା ନୀତିର ବିଭିନ୍ନ ଲକ୍ଷ୍ୟ ପୂରଣ କରିବା ଉପରେ ଗୁରୁତ୍ବର ଆରୋପ କରାଯାଇଛି ।

(୬) ବିବିଧ ସ୍ଵାସ୍ଥ୍ୟ ସେବା ଯୋଗାଉଥ‌ିବା ଚିକିତ୍ସାଳୟ ସ୍ଥାପନ (Diverse Health Care Clinic):
ଘରୋଇ ଚିକିତ୍ସା କରୁଥିବା ବିଶେଷଜ୍ଞମାନଙ୍କୁ କେତେକ ନିର୍ଦ୍ଦିଷ୍ଟ ଶ୍ରେଣୀ ଲୋକଙ୍କୁ ବିବିଧ ସ୍ୱାସ୍ଥ୍ୟ ସେବା ଯୋଗାଇବା ନିମିତ୍ତ ସରକାରୀ ସ୍ବୀକୃତି ଦେବା ଓ ସେମାନଙ୍କୁ ଏ ଦିଗରେ ସଂଶ୍ଳିଷ୍ଟ କରିବାର ବ୍ୟବସ୍ଥା ନୂତନ ନୀତିରେ ରହିଛି । (୭) ଦେଶୀୟ ଚିକିତ୍ସା ପଦ୍ଧତି ତଥା ହୋମିଓପ୍ୟାଥ୍ ଚିକିତ୍ସା ପଦ୍ଧରେ ଜନସଂଖ୍ୟା ନିୟନ୍ତ୍ରଣ ଓ ସ୍ଵାସ୍ଥ୍ୟରକ୍ଷା ପ୍ରଦାନ କରାଯିବାର ବ୍ୟବସ୍ଥା ରହିଛି ।

(୮) ଜନ୍ମ ନିୟନ୍ତ୍ରଣର ବିଭିନ୍ନ ପଦ୍ଧତି ଉପରେ ଯେଉଁ ଗବେଷଣାମାନ କରାଯାଉଛି, ତା ପାଇଁ ସକାରୀ ଅନୁଦାନ ଦେବାର ଉପଯୁକ୍ତ ବ୍ୟବସ୍ଥା କରାଯାଛି । ଏହା ବ୍ୟତୀତ ପ୍ରଜନନ ଓ ଶିଶୁ ସ୍ଵାସ୍ଥ୍ୟ ଉପରେ ଅଧିକ ଗବେଷଣା ପାଇଁ ଆର୍ଥିକ ବ୍ୟବସ୍ଥା କରାଯାଇଛି ।

(୯) ଜନ୍ମସଂଖ୍ୟା ନୀତିର କାର୍ଯ୍ୟକାରିତାକୁ ତଦାରଖ କରିବା ପାଇଁ ଜାତୀୟ ଜନସଂଖ୍ୟା ଆୟୋଗ ସ୍ଥାପନର ପ୍ରସ୍ତାବ ମଧ୍ୟ ରଖାଗଲା।

(୧୦) ସର୍ବଶେଷରେ, ବିଭିନ୍ନ ଗଣମାଧ୍ୟମ ଦ୍ବାରା ଜନସଂଖ୍ୟା ସମ୍ବନ୍ଧୀୟ ସମସ୍ତ ବାର୍ତ୍ତା ଓ ଶିକ୍ଷା ଲୋକଙ୍କ ପାଖରେ ପହଞ୍ଚାଇ ଦେଶରେ ପ୍ରଚଳିତ ଜନସଂଖ୍ୟା ନିୟନ୍ତ୍ରଣ ଓ ସୁସୁ ପରିବାର ଗଠନର ଜାତୀୟ ଅଭିଯାନକୁ ସଫଳ କରିବାରେ ଉଦ୍ୟମ କରି ରଖୁବା ମଧ୍ୟ ଏହି ନୂତନ ନୀତିରେ ସ୍ଥାନ ପାଇଲା !

୨୦୦ ଜନସଂଖ୍ୟା ନୀତିର ସମୀକ୍ଷା (valuation of NPP 2000):
ବର୍ତ୍ତମାନ ଦେଶର ଜନସାଂଖ୍ୟକ ଅବସ୍ଥା ସହ ଉପରୋକ୍ତ ନୂତନ ନୀତିକୁ ତୁଳନା କରାଗଲେ ନିମ୍ନଲିଖତ ସିଦ୍ଧାନ୍ତରେ ଉପନୀତ ହେବାକୁ ପଡ଼େ ।
(୧) ନୂତନ ଜନସଂଖ୍ୟା ନୀତିରେ ମୋଟ ସନ୍ତାନ ଜନ୍ମ କ୍ଷମତା (Lotal Fertility Ratc) ହାକୁ ୨୦୧୦ ମସିହା ସୁଦ୍ଧା ୩.୩ ରୁ ୨.୧ ପ୍ରତିଶତ ହ୍ରାସ କରିବାର ଲକ୍ଷ୍ୟ ହାସଲ ସମ୍ଭବ ହୋଇପାରି ନାହିଁ ।

(୨) ସନ୍ତାନ ପ୍ରସବ ତାଲିମ ପ୍ରାପ୍ତ ସ୍ଵାସ୍ଥ୍ୟ କର୍ମଚାରୀଙ୍କ ଦ୍ଵାର ପ୍ରସ୍ତାବିତ ପ୍ରସବ କୁଟୀର ପ୍ରକଳ୍ପ ମାଧ୍ୟମରେ ୧୦୦ ପ୍ରତିଶତ ନିରାପଦ ମାତୃତ୍ଵ ସେବା ଯୋଗାଇବା ଏକ ଉଚ୍ଚ ଅଭିଳାଷ ବୋଲି ବହୁ ବିଶ୍ଵେଜ୍ଞ ମତପୋଷଣ କରନ୍ତି ।

(୩) ଭାରତରେ ଜନସଂଖ୍ୟା ବୃଦ୍ଧିହାର ବିଶେଷଭାବରେ ବିହାର, ଉତ୍ତରପ୍ରଦେଶ, ମଧ୍ୟପ୍ରଦେଶ, ରାଜସ୍ଥାନ ଏବଂ ଓଡ଼ିଶାରେ ଅଧିକ ଦେଖାଯାଏ । ଏହି ରାଜ୍ୟଗୁଡ଼ିକୁ ସଂକ୍ଷେପରୁ ବୀମାରୁ (BIMARU) ରାଜ୍ୟ ବୋଲି କୁହାଯାଏ । ଏହି ରାଜ୍ୟଗୁଡ଼ିକରେ ମୋଟ ଜନସଂଖ୍ୟାର ୮୭ ପ୍ରତିଶତ ଲୋକ ଅଛନ୍ତି ଏବଂ ସମୁଦାୟ ଜନ୍ମିତ ସନ୍ତାନ ସନ୍ତତିମାନଙ୍କ ମଧ୍ୟରୁ ଏହି ରାଜ୍ୟଗୁଡ଼ିକରେ ୪୫ ପ୍ରତିଶତ ଦେଖାଯାଆନ୍ତି । ନୂତନ ଜନସଂଖ୍ୟା ନୀତିରେ ଏହି ରାଜ୍ୟଗୁଡ଼ିକର ଜନସଂଖ୍ୟା ନିୟନ୍ତ୍ରଣ ନିମିତ୍ତ କୌଣସି ବିଶେଷ ପଦକ୍ଷେପ ଉଲ୍ଲେଖ ହୋଇନାହିଁ ।

(୪) ଭାରତରେ ଜନସଂଖ୍ୟାର ସ୍ଥିରତା ବା ୨୦୪୫ ମସିହା ସୁଦ୍ଧା ‘ଶୂନ୍ୟ ବୃଦ୍ଧି’ ପରିସ୍ଥିତି ହାସଲ କରିବାର ଯେଉଁ ଲକ୍ଷ୍ୟ ନୂତନ ନୀତିରେ ରହିଛି, ତାହା ହାସଲ କରିବା ଅସମ୍ଭବ ମନେହୁଏ । ଏପରିକି କେରଳ ରାଜ୍ୟ ଯାହାକି ଜନସଂଖ୍ୟା କମାଇବାରେ ସମଗ୍ର ଦେଶରେ ଏକ ଦୃଷ୍ଟାନ୍ତ ହୋଇପାରିଛି (୯୩ ପ୍ରତିଶତ ବୃଦ୍ଧି- ୨୦୦୧ ଜନଗଣନା ଅନୁସାରେ), ୨୦୩୯ ମସିହା ସୁଦ୍ଧା ଏହି ରାଜ୍ୟ ତା’ର ଜନସଂଖ୍ୟାରେ ସ୍ଥିରତା ହାସଲ କରିପାରିବ ବୋଲି ଗଣନା କରାଯାଇଛି ।

୨୦୧୧ ଜନଗଣନା ତଥ୍ୟ ଏକ ସାର୍ବଜନୀନ ହୋଇଛି । ଏଥିରେ ଦେଶର ବାର୍ଷିକ ହାରାହାରି ଜନସଂଖ୍ୟା ବୃଦ୍ଧିହାର ୧.୬୪ ପ୍ରତିଶତକୁ ହ୍ରାସ ପାଇଥିବା ବେଳେ ଜନ୍ମହାର ହଜାର ପ୍ରତି ୨୨ ସ୍ତରକୁ ହ୍ରାସ ପାଇଛି । ପୁରୁଷ- ମହିଳା ଅନୁପାତ ୯୩୩ ରୁ ୯୪୦କୁ ବୃଦ୍ଧି ପାଇଥିବା ବେଳେ ସାକ୍ଷରତା ହାର ୭୪ ପ୍ରତିଶତକୁ ବୃଦ୍ଧି ପାଇଛି । ଏ ସବୁ ୧ ପ୍ରତିଶତ ସ୍ତରର ନିମ୍ନରେ ରହିଥିବା ବେଳେ ଜନ୍ମହାର ହଜାର ପ୍ରତି ପ୍ରାୟ ୧୦-୧୨ ସ୍ତରରେ ରହିଛି । ସେ ସବୁ ଦେଶରେ ସାକ୍ଷରତା ହାର ପ୍ରାୟ ଶତ ପ୍ରତିଶତ ସ୍ତର ପାଖାପାକୁ ରହିଛି। ତେଣୁ ବ୍ୟାପକ ଜନସଚେତନତା ଓ ଗତି, ଧର୍ମ ତଥା ବର୍ଣ୍ଣ ନିର୍ବିଶେରେ ସମସ୍ତଙ୍କ ମିଳିତ ଉଦ୍ୟମରେ ଆମ୍ଭେ ଯେ ଦ୍ରୁତ ଜନସଂଖ୍ୟା ବୃଦ୍ଧିକୁ ଆଗାମୀ ଦିନରେ ନିୟନ୍ତ୍ରଣ କରିପାରିବା ଏଥିରେ ସନ୍ଦେହ ନାହିଁ ।

Question ୯।
ଜନସଂଖ୍ୟା ବୃଦ୍ଧିର କାରଣସମୂହ ଆଲୋଚନା କର ।
(Explain the Causes of Population Growth.)
Answer:
ଜନ୍ମହାର ଓ ମୃତ୍ୟୁହାର ମଧ୍ୟରେ ଥିବା ତାରତମ୍ୟକୁ ଜନସଂଖ୍ୟା ବୃଦ୍ଧି ହାର ବା ଜନସଂଖ୍ୟାର ସ୍ଵାଭାବିକ ବୃଦ୍ଧି ହାର କୁପହାଯାଏ । ଗୋଟିଏ ଦେଶର ମୃତ୍ୟୁହାର ତୁଳନାର ଜନ୍ମହାର ଅଧ‌ିକ ହେଲେ, ସେ ଦେଶର ଜନସଂଖ୍ୟା ବୃଦ୍ଧି ପରିଦୃଷ୍ଟ ହୁଏ । ୧୯୨୧ ମସିହା ପୂର୍ବରୁ ଭାରତରେ ଉଭୟ ଜନ୍ମହାର ଓ ମୃତ୍ୟହାର ଅଧିକ ଥିଲା । ଏଣୁ ଜନସଂଖ୍ୟାର ଓ ସ୍ଵାଭାବିକ ବୃଦ୍ଧି ହାର ବହୁତ ନିମ୍ନରେ ଥିଲା । କିନ୍ତୁ ୧୯୨୧ ମସିହା ପରଠାରୁ ଜନ୍ମହାର ତୁଳନାରେ ମୃତ୍ୟୁହାର ଅସାଧରଣ ଭାବେ ହ୍ରାସ ପାଇବାରେ ଲାଗିଛି । ଫଳରେ ଜନସଂଖ୍ୟାର ସ୍ଵାଭାବିକ ବୃଦ୍ଧି ହାର ବଢ଼ିବାରେ ଲାଗିଛି ।
ଭାରତର ଜନସଂଖ୍ୟା ବୃଦ୍ଧିର ଦୁଇଟି କାରଣ ରହିଛି; ଯଥା—

(୧) ଉଚ୍ଚଜନ୍ମହାର(High Birth Rate)- ଭାରତରେ ଜନ୍ମହାର ଉଚ୍ଚ ହେବାର ଅନେକଗୁଡ଼ିଏ କାରଣ ରହିଛି । ଏହା ମୁଖ୍ୟତଃ ସାମାଜିକ ଓ ଅର୍ଥନୈତିକ । ଉଚ୍ଚ ଜନ୍ମହାରର କାରଣଗୁଡ଼ିକ ନିମ୍ନରେ ଦର୍ଶାଯାଇଛି..
(କ) ଭାରତରେ ବିବାହ ସାର୍ବଜନୀନ !
(ଖ) ଭାରତର ଏକ ଗ୍ରୀଷ୍ମପ୍ରଧାନ ଦେଶ ଆମ ଦେଶରେ ବାଳିକାମାନେ ଅଛ ବସୟରେ ଗର୍ଭଧାରଣ କ୍ଷମତାର ଅଧିକାରୀ ହୋଇଥାଆନ୍ତି । ତେଣୁ ଅଳ୍ପ ବୟସରେ ବିବାହ କରିବା ଫଳରେ ସେମାନେ ଅଧୂକ ଶିଶୁ ଜନ୍ମ ଦିଅନ୍ତି ।
(ଗ) ଭାରତ ଏକ କୃଷି ପ୍ରଧାନ ଦେଶ । କୃଷି କାର୍ଯ୍ୟରେ ବିବିଧ କାର୍ଯ୍ୟ କରିବାପାଇଁ ଅନେକ ଶ୍ରମିକଙ୍କର ଆବଶ୍ୟକ ପଡ଼ିଥାଏ । ପିତାମାତା କୃଷିକାର୍ଯ୍ୟକୁ ଅଧ‌ିକ ସହଜ ଓ କାର୍ଯ୍ୟକ୍ଷମ କରିବାପାଇଁ ଅଧ୍ବକ ଶିଶୁ ଜନ୍ମଦେବା ପାଇଁ ଅଗ୍ରହ ପ୍ରକାଶ କରିଥାନ୍ତି ।
(ଘ) ଭାରତରେ ଅଧିକାଂଶ ଲୋକ ଦରିଦ୍ର । ତେଣୁ ସେମାନଙ୍କର ଆର୍ଥିକ ପରିସ୍ଥିତିର ଉନ୍ନତି ଆଣିବା ପାଇଁ ସେମାନେ ଅଧିକ ସନ୍ତାନ ଜନ୍ମ ଦେବା ପାଇଁ ପ୍ରୟାସ କରିଥାନ୍ତି ।
(ଙ) ଭାରତରେ ହିନ୍ଦୁଙ୍କ ସଂଖ୍ୟା ଅଧ‌ିକ । ହିନ୍ଦୁ ସମାଜରେ ଗୋଟିଏ ପୁତ୍ର ସନ୍ତାନ ପୂର୍ବପୁରୁଷଙ୍କର ମସ୍ତ କର୍ମ ସଂପାଦନ କରିଥାଏ । ତେଣୁ ପ୍ରତ୍ୟେକ ପିତାମାତା ଗୋଟିଏ ପୁତ୍ର ପ୍ରାପ୍ତି ପର୍ଯ୍ୟନ୍ତ ଅପେକ୍ଷା କରିଥାନ୍ତି। ଏହା ଦେଶରେ ଜନ୍ମହାର ବୃଦ୍ଧି କରିଥାଏ ।
(ଚ) ଭାରତରେ ଶିଶୁ ମୃତ୍ୟୁହାର ଅଧ‌ିକ । ତେଣୁ ପିତାମାତା ଗୋଟିଏ ଦୁଇଟି ଶିଶୁ ଜନ୍ମ ଦେଇ ଜନ୍ମ ନିୟନ୍ତ୍ରଣ ପଦ୍ଧତି ଅବଲମ୍ବନ କରିବାକୁ ଭୟ କରିଥାନ୍ତି । ସେମାନେ ଶିଶୁ ମୃତ୍ୟୁର ଆଶଙ୍କା କରି ଅଧୁକ ଶିଶୁ ଜନ୍ମ ଦେଇଥାନ୍ତି ।
(ଛ) ନିରକ୍ଷରତା ଓ ଅନ୍ଧବିଶ୍ଵାସ ଭାରତୀୟଙ୍କୁ ବାସ୍ତବତାଠାରୁ ଦୂରେ ରଖୁଛି । ସଚେତନତାର ଅଭାବ ସେମାନଙ୍କୁ ଅବାଞ୍ଛିତ ସନ୍ତାନ ଦେବାକୁ ପ୍ରେରିତ କରେ । ସେମାନେ ସନ୍ତାନକୁ ଭଗବାନଙ୍କର ବରଦାନ ଭାବେ ଗ୍ରହଣ କରିଥାନ୍ତି । ଜନ୍ମ ନିୟନ୍ତ୍ରଣ ପଦ୍ଧତିକୁ ଧର୍ମ ବିରୋଧୀ ଭାବି ଗ୍ରହଣ କରି ନ ଥାନ୍ତି ।

(୨) ମୃତ୍ୟୁ ହ୍ରାସରକlରଶ (Caues of Decreases in Death Rate) – ଆମ ଦେଶର ମୃତ୍ୟୁହାର କ୍ରମାଗତ ଭାବେ ହ୍ରାସ ପାଇବାରେ ଲାଗିଛି । ୧୯୫୧ ମସିହା ଜନଗଣନାରେ ଭାରତର ମୃତ୍ୟୁହାର ଥିଲା ୨୭.୪ ପ୍ରତିଶତ । ୨୦୧୧ ମସିହା ଜନଗଣନାରେ ଭାରତର ମୃତ୍ୟୁହାର ୭.୪୮ ପ୍ରତିଶତକୁ ହ୍ରାସ ପାଇଛି । ଭାରତର ମୃତ୍ୟୁହାର ହ୍ରାସ ପାଇବାରେ ଅନେକଗୁଡ଼ିକଏ କାଣ ରହିଛି । ସେଗୁଡ଼ିକ ହେଲା-

(୧) ସ୍ଵାଧୀନତା ପ୍ରାପ୍ତି ପରେ ଆମ ଦେଶରେ ଚିକିତ୍ସା ବିଜ୍ଞାନ ଓ ଚିକିତ୍ସାର ସୁବିଧା ସୁଯୋଗ ବୃଦ୍ଧି ହୋଇଛି । ଦେଶର ଅନୁନ୍ନତ ଅଂଚଳରେ ସରକାର ଡାକ୍ତରଖାନା ପ୍ରତିଷ୍ଠା ହେବା ସହିତ ଲୋକମାନଙ୍କୁ ମାଗଣାର ଡାକ୍ତରୀ ସେବା ଓ ଔଷଧ ପ୍ରଦାନ କରାଯାଉଛି । ତେଣୁ ଦେଶର ମୃତ୍ୟୁହାରରେ ହ୍ରାସ ପରିଲକ୍ଷିତ ହୋଇଛି ।

(୨) ସ୍ଵାଧୀନତା ପ୍ରାପ୍ତି ପରେ ଦେଶରେ ବିଭିନ୍ନ ପ୍ରକାରର ମହାମାରୀ ଯଥା : ବସନ୍ତ, ହଇଜା, ପ୍ଲେଟ୍ ଓ ମ୍ୟାଲେରିଆ ଇତ୍ୟାଦିର ସଫଳଭାବେ ନିୟନ୍ତ୍ରଣ କରାଯାଇପାରିଛି । ତେଣୁ ଦେଶର ମୃତ୍ୟୁହାର ହ୍ରାସ ପାଇଛି ।

(୩) ସ୍ଵାଧୀନତା ପ୍ରାପ୍ତି ପରେ ପ୍ରାକୃତିକ ବିପର୍ଯ୍ୟୟର ସଫଳ ନିୟନ୍ତ୍ରଣ କରାଯାଇପାରିଛି । ସରକାରୀ ବାତ୍ୟା ଆଶ୍ରୟସ୍ଥଳ ନିର୍ମାଣ, ନଦୀବନ୍ଧର ମରାମତି, ଭୂମିକମ୍ପରୁ ରକ୍ଷା ପାଇବା ପାଇଁ ସ୍ଵତନ୍ତ୍ର ଧରଣର ଗୃହ ନିର୍ମାଣ, ସୁନାମିର ରକ୍ଷା ପାଇବା ପାଇଁ ନଦୀ କୂଳରେ ରହୁଥିବା ଲୋକମାନଙ୍କ ପାଇଁ ପାଣିପାଗ ସଚେତନା ଇତ୍ୟାଦି ଅନେକଗୁଡ଼ିଏ ପ୍ରାକୃତିକ ବିପର୍ଯ୍ୟୟ ପ୍ରତିକାର ବ୍ୟବସ୍ଥା ହାତକୁ ଦେଇଛନ୍ତି । ତେଣୁ ଦେଶରୁ ମୃତ୍ୟୁହାର ହ୍ରାସ ପାଇବାରେ ଲାଗିଛି।

(୪) ସ୍ଵାଧୀନତା ପ୍ରାପ୍ତି ପରେ ଦେଶରେ ପ୍ରସୂତି ଓ ମାତୃମଙ୍ଗଳ କେନ୍ଦ୍ରର ବ୍ୟାପକ ପ୍ରତିଷ୍ଠା ଫଳରେ ପ୍ରସବକାଳୀନ ମୃତ୍ୟୁ ଯଥେଷ୍ଟ ହ୍ରାସ ପାଇଛି । ବର୍ତ୍ତମାନ ଶତ ପ୍ରତିଶତ ଆନୁଷ୍ଠାନିକ ପ୍ରସ୍ତୁତି ନିମନ୍ତେ ଉଦ୍ୟମ କରାଯାଇଛି ।

Odisha State Board CHSE Odisha Class 12 Biology Solutions Chapter 1 Reproduction in Organisms Textbook Questions and Answers.

CHSE Odisha 12th Class Biology Chapter 1 Question Answer Reproduction in Organisms

Reproduction in Organisms Class 12 Questions and Answers CHSE Odisha

Very Short Answer Type Questions

Fill in the blanks with correct answer from the choices given in the bracket

Question 1.
Non-motile asexual reproductive units are called …………….. (zoospores, buds, gametes, conidia)
Answer:
conidia

Question 2.
In …………., a living organism divides equationally. (fragmentation, fission, budding, sporulation)
Answer:
fission

Question 3.
Yeast generally reproduces by …………….. .
(fission, budding, sporulation, gametangia)
Answer:
budding

Question 4.
Dahlia propagates by …………… (roots, stem, leaf, seed)
Answer:
roots

Question 5.
The process by which one plant part is inserted into another to grow a new individual plant is called ………….. .
(layering, cutting, grafting, micropropagation)
Answer:
grafting

Answer each of the following in one word or more words

Question 6.
What is called the motile asexual reproduction units?
Answer:
Zoospores

Question 7.
In which asexual method do yeasts generally divide?
Answer:
Budding

Question 8.
What can be called to sexual reproductive units?
Answer:
Gametes

Question 9.
What is the general asexual method of reproduction in Amoeba?
Answer:
Binary fission

Question 10.
In the process of grafting, what is called to detached part?
Answer:
Scion

Question 11.
In which process can large number of adventitious buds be formed?
Answer:
Micropropagation

Correct the statements without changing underlined words only

Question 12.
In mound layering, branches at lower portion of the stem are put in the soil at many places.
Answer:
In mound layering, the shoot is pruned and lower part is covered by soil, like a mound.

Question 13.
Dahlia reproduces vegetatively by stems.
Answer:
Dahlia reproduces vegetatively by roots.

Question 14.
Aspergillus reproduces asexually by zoospores.
Answer:
Aspergillus reproduces sexually by zoospores.

Question 15.
Internal buds in sponges are called gemma cups.
Answer:
Internal buds in sponges are called gemmules.

Question 16.
In binary fission, many cells can be produced from one cell.
Answer:
In binary fission, two cells can be produced from one cell.

Fill in the blanks

Question 17.
The process of perennation of species takes place by ………
Answer:
encystment

Question 18.
Zoospores are borne inside …………….
Answer:
sporangia

Question 19.
Under unfavourable conditions when a number of tiny Amoeba are produced by multiple fission, it is called …………..
Answer:
multiple fission

Question 20.
Internal buds in Hydra are called …………..
Answer:
endogenous buds.

Question 21.
In Bryophyllum, adventitious buds are borne on …………..
Answer:
leaves

Short Answer Type Questions

Write notes on the following with at least 2 valid points

Question 1.
Asexual reproduction
Answer:
When offsprings are produced by a single parent without the involvement of gametic fusion, the reproduction is called asexual.
The resultant offsprings are similar to one another and are exact copies of their parents. Such a group of morphologically and genetically similar individuals is called clone.

Question 2.
Micropropagation
Answer:
In this method, the propagation of plants is achieved by culturing the cells, tissues and organs in laboratory. It is called tissue culture. Initially, this forms an undifferentiated mass of cells called callus. Later on, this callus differentiates to produce many small plantlcts. The tcchniquc of micropropagation is similar ro initiating the rooting in plant cuttings.
In a way it can also be called as another method of vegetative propagation in plants. However, it differs from the conventional procedure because ir is carried out under sterile condition and requires an artificial nutrient medium.

Question 3.
Cutting
Answer:
A small piece of any plant, i.e. stem, root or leaf used for vegetative propagation is called as cutting. In stem cutting, a piece of stem (20-30 cm long) is taken from parent plant. The cutting with nodes and internodes are planted in moist soil having adequate nutrients.

After a few days, roots from basal part and shoots from upper buds can be observed emerging from the planted part. The plants propagated by this method are China rose, Bougainvillea, sugarcane, etc.

Question 4.
Layering
Answer:
Layering
In this method, adventitious roots are artificially induced on the stem branches while they are still attached to the „ plant, e.g. jasmine, grapevine, litchi, orange, etc.
There are three types of layering

1. Serpentine layering The basal branches (i.e. lower portions of the stem) are pegged in the soil at several places to form new plants.
2. Mound layering In this process, the shoot is pruned and its lower part is covered by soil with the apical portion remaining outwards; in the form of a mound.
   After some time, it develops a number of shoots. Among these, rooted ones are separated and planted, e.g. gooseberry and current.
3. Air layering (gootee) In this method, about 3.5 cm ring of bark is removed from the base of an aerial shoot. This area is then covered by a thick plaster of grafting clay. It consists of hay, cowdung, clay and water with small quantity of root promoting hormone (such as NAA or IBA).

Question 5.
Fission
Answer:
It is the division of the parent body into two or more daughter individuals identical to the parent.

Fission can occur by the following methods
(i) Binary fission It is the division of the parent cell into two small, nearly equal sized daughter individuals, each of which rapidly grows into an adult. It occurs in single-celled animals like bacteria and protozoans, e.g. Amoeba, Paramecium, etc.

• Simple binary fission When division occurs in any one plane, it is known as simple binary fission, e.g. Amoeba.
• Longitudinal binary fission It takes place when division occurs along the longitudinal axis, e.g. Euglena, Vorticella.
• Transverse binary fission When division occurs along the transverse axis, right angle to the longitudinal axis of the individual, e.g. Paramecium, diatoms, bacteria, Planaria.
• Oblique binary fission When division occurs at an angle to the transverse axis, e.g. Ceratium, Gonyaulax.

Question 6.
Budding
Answer:
In this process, unequal and small projections called buds are produced from the parent cell. Initially, these buds remain attached to the parent cell and eventually get separated and mature into new organisms, e.g. yeast, Hydra, etc.

Depending on the place from where the bud arises, budding can be of two types
External budding (Hydra and yeast) During favourable conditions like presence of adequate nutrients, moisture, etc., a bud grows on the parent body.
In Hydra (multicellular organism), regenerative cells are used for reproduction during budding.
A bud develops on the median region of the body as an outgrowth. Later, due to the repeated cell divisions, these buds gradually enlarge and coelenteron of Hydra migrates ipto it.

Question 7.
Fragmentation
Answer:
It is the breaking of parental body into distinct pieces, each of which regenerates into an offspring, e.g. Hydra, Planaria, sea stars, Spirogyra, etc.
In economically important horticultural or crop plants, human beings use this method of segregating plant parts for their own benefits.

Differentiate between two words in the following pairs of words

Question 1.
Zoospores and Conidia
Answer:
Differences between zoospores and conidia are as follows

Zoospores	Conidia
They are motile asexual structures.	They are immotile asexual structures.
They are borne endogenously in sporangia.	They are borne exogenously.
They are liberated from sporangium only after it becomes mature, e.g. Ulothrix.	They can be easily disseminated by external agent like air and water, e.g. Penicillium.

 

Question 2.
Asexual reproduction and Sexual reproduction
Answer:
Differences between asexual reproduction and sexual reproduction are as follows

Asexual reproduction	Sexual reproduction
It occurs in lower organisms.	It occurs almost in all types of animals and mostly in higher plants.
It is always uniparental.	It is usually biparental.
Gametes are not formed.	Gametes are always formed.
Fertilisation does not take place.	Fertilisation takes place.
It involves only mitosis.	It involves both meiosis and mitosis.
Young ones are genetically identical to the parents.	Young ones differ genetically from the parents.
Multiplication occurs rapidly.	Multiplication is not so rapid as in asexual reproduction.
Since there is no variation, so It does not contribute in the evolution of the species.	Since there are variations, soft contributes in the evolution of the species.

 

Question 3.
Grafting and Layering
Answer:
Differences between grafting and layering are as follows

Grafting	Layering
It is a technique of connecting two parts usually a root system and a shoot system.	It is a type of root induction in which adventitious roots are induced to develop on a soft stem.
It is useful in obtaining more varieties from a single parent.	It only results in one type of offspring.
Highly desirable characters from parents can be obtained.	Same characteristics as of parents occur in offspring.
e.g. mango, lemon.	e.g. rose, jasmine.

 

Question 4.
Budding and Fission
Answer:
Differences between budding and fission are as follows

Budding	Fission (Binary)
The parent produces a small bud that gradually grows in size and then separates from the parent body.	The parent body divides into two equal and similar halves. Each half forms a new individual.
A protuberance (bud) is formed.	A protuberance is not formed.
Division is unequal.	Division is equal.
Parent body remains intact.	Parent body disappears.
e.g. yeast, Sycon, Hydra.	e.g. bacteria, Amoeba, Euglena, Paramecium, Ptanaria.

 

Question 5.
Internal budding and External budding
Answer:
Differences between internal budding and external budding are as follows

Internal budding	External budding
Buds are formed within the parent body.	Bud grows externally on parent body.
Buds or gemmules come out under favourable conditions and form a new colony.	Bud detaches from parent body and grows into a new individual.
e.g. Spongilla.	e.g. Hydra.

 

Question 6.
Fragmentation and Budding
Answer:
Differences between fragmentation and budding are as follows

Fragmentation	Budding
Parent body breaks into two or more pieces called fragments.	Parent body produces a small bud exogenously or . endogenously,
Parent identity is lost.	Parent remains intact.
e.g. flatworms, Marchantia.	e.g. yeast, Sycon.

 

Long Answer Type Questions

Question 1.
Give an account of vegetative repoduction in angiosperms.
Answer:
In plants, asexual reproduction is commonly known as vegetative propagation. It is the process of formation of a new plant from detached vegetative parts of the parent plant. These vegetative structures are called vegetative propagules. This process helps in multiplication of seedless plants, e.g. sugarcane, banana, etc. The process is asexual reproduction as it does not involve two parents. Vegetative ‘‘propagation in plants is of two types

Natural Vegetative Propagation
This type of vegetative propagation occurs in plants naturally. A fragment of the mother plant gets separated and forms an independent plant under suitable conditions.
This can take place by the following vegetative propagules
(i) By Roots
The buds present on the roots grow into leafy shoots called slips above the ground and adventitious roots at their bases. Each slip gives rise to a new plant, e.g. sweet potato, Dahlia, guava, yam, Tinospora, etc.

(a) Root tuber of sweet potato, (b) Fasciculated root of Dahlia, (c) Nodulous roots of mango ginger

(ii) By Stems
In plants, vegetative propagation can also take place by stems. They modify themselves to give rise to new plants.
This can take place by the following vegetative propagules
This can take place by the following vegatative propagules
(a) Underground stems Underground modified stems possess buds which grow into new plants.
Some of its types are given below

1. Rhizomes These are modified stems with buds and sufficient stored food. A piece of rhizome containing bud can give rise to a new plant. This method is used in the propagation of plants like ginger, turmeric, banana, lotus, etc.
2. Bulbs They are highly reduced underground stems with a number of buds, e.g. onion, lilies, garlic, etc.
3. Tubers They are the modified underground stem branches having several buds, e.g. each eye of the potato is a bud, which grows into a new potato plant when planted with a portion of swollen tuber. The potato crop is raised by the tubers, not by seeds.

(b) Subaerial stems Vegetative propagation by the means of subaerial stems, can be categorised as given below

1. Runners They are modified stems, which produce adventitious roots at nodes. Each node gives rise to an aerial shoot which becomes a new plant, e.g. Oxalis, Centella, grasses, etc.
2. Stolons These are horizontal branches that arch above the ground. They also help in vegetative propagation, e.g. strawberry, Vallisneria.
3. Suckers They arise from the base of the erect shoot, grow horizontally in the soil and then come out to form new aerial shoots. These shoots become independent when suckers break away from the parent plant, e.g. mint, Chrysanthemum, etc.
4. Offsets They are one internode long runners, which develop tuft of leaves at the apex, e.g.
   Pistia (water lettuce), Eichhornia (water hyacinth), etc.

(c) Aerial stems Aerial modified stems of cacti develop new plants when the stem segments fall on the ground. These act as the means of vegetative propagation, e.g. Opuntia, etc.

Vegetative reproduction by stem modifications (a) Runner, (b) Stolons, (c) Sucker, (d) Offset

Question 2.
Describe the process of micropropagation and its advantages.
Answer:
Micropropagatlon
In this method, the propagation of plants is achieved by culturing she cells, tissues and orgun lis Labotatory. It is called ussuc culture, Initially, this forms an undifferentiated mass of cells called calluL Liter on, this callus d.ïffescntiatcs to produce many small plantlets. The technique of micropropaganon is similar to initiating the rooting in plant cuttings.

In a way it can also be called as another method of vegetative propagation in plants. However, it differs from the conventional procedure because it is carried out under sterile condition and requires an artificial nutrient medium.

A set up for micropropagation requires an explant. The most commonly used explants are the meristematic ends of the plants, i.e. stem tip, root tip, axillary bud, etc. This is because meristematic cells have high rate of cell division. These explants, along with culture vessel, cell division media and instruments, etc., are sterilised. The explant is then inoculated into a semi-solid nutrient medium contained in a culture vessel. This is followed by incubation of culture vessel at room temperature. After some time, multiple shoots start developing from the axillary buds. This is called axillary bud proliferation.

Each growing point is subcultured to initiate shooting in callus. This process is called as adventitious shoot formation. Auxin is added in high ratio to stimulate shoot formation. Each shoot inturn develops roots.

A small plantlet is generated, which is later on transferred to an open field for hardening.
Micropropagation is generally practised for many ornamental, fruit and crop plants.
It is considered useful because

1. healthy propagules can be obtained from infected parent plants.
2. rapid rate of multiplication of plantlets.
3. plant material with desired trait and its maintenance in a small space can be easily achieved.

Also, considerable progress in commercial harvesting of medicinal plants such as Dioscorea deltoidea, D. floribunda, Atropa belladona, Solanum sp., Rauwolfia serpentina, etc., has been observed by utilising micropropagation techniques.

Examples of Micropropagation
This process is used in the production of crops such as tea, coffee, oil palm, date palm, coconut, fruit yielding plants like papaya, banana, Citrus and apples in large numbers.

Significant improvement have been achieved in developing protocols for micropropagation of tree species. Mass propagation in vitro of teak, Eucalyptus sp., sandal wood, different species of bamboo and many other trees has been successfully done.

Advantages of Micropropagation
1. Certain species of potato, Cassava, sugarcane and banana have been observed to be severely and chronically affected by pathogenic viruses. Due to this, their yields have reduced considerably. Their yields can be increased significantly by micropropagation which can be used to produced disease-free stocks from infected parent plants.

2. Potato is susceptible to many viral pathogens, some of which may be present without perceptible, symptoms. Eradication of viruses can be achieved by employing micropropagation techniques where healthy meristematic buds are .cultured.
More than 500 plants can be obtained in about 3-4 months starting from a single meristem. By varying the medium composition, light intensity and temperature, plantlets can be induced to . produce microtubers.
These disease-free microtubers can be grown under controlled conditions in soil to form minitubers. These minitubers can be planted directly in the field to raise a disease-free crop.

3. Apart from these applications of micropropagation, techniques for generating true-to type planting, material from elite genotypes, micropropagation holds special significance in situations where rapid accumulation of extremely limited stock material is required.
The desired genetic gains achieved through plant breeding can be multiplied several folds on an economic and rapid time scale.

Question 3.
Describe the process of asexual reproduction in lower animals.
Answer:
Asexual Reproduction:
When the offspring is produced by a single parent without the involvement of gamete formation, the reproduction is called as asexual reproduction.

Properties of Asexual Reproduction
The properties of asexual reproduction are as follows

1. Offsprings produced by asexual reproduction are identical to one another and exact copies of their parents. The term clone is used to describe such morphologically and genetically similar individuals.
2. Asexual reproduction occurs in plants, protozoans and some lower animals such as sponges, coelenterates, certain worms and tunicates.
3. It is absent among the higher non-vertebrates and all vertebrates.
4. Asexual reproduction is common among single-celled organisms and animals with relatively simple organisation.
5. In protists and monerans, the organism or the parent cell divides into two, to give rise to new individuals. Thus, in these organisms cell division is itself a mode of reproduction.
6. It involves only mitotic cell division. Meiosis does not occur in asexual reproduction.

Modes of Asexual Reproduction
It takes place by the following methods
Fission
It is the division of the parent body into two or more daughter individuals identical to the parent.
Fission can occur by the following methods
(i) Binary fission It is the division of the parent cell into two small, nearly equal sized daughter individuals, each of which rapidly grows into an adult. It occurs in single-celled animals like bacteria and protozoans, e.g. Amoeba, Paramecium, etc.

Binary fission is of following types

• Simple binary fission When division occurs in any one plane, it is known as simple binary fission, e.g. Amoeba.
• Longitudinal binary fission It takes place when division occurs along the longitudinal axis,
  e.g. Euglena, Vorticella.
• Transverse binary fission When division occurs along the transverse axis, right angle to the longitudinal axis of the individual, e.g. Paramecium, diatoms, bacteria, Planaria.
• Oblique binary fission When division occurs at an angle to the transverse axis, e.g. Ceratium, Gonyaulax.

(ii) Multiple fission It is the division of the parent body into many small daughter individuals simultaneously, e.g. Plasmodium, (the malarial parasite), Amoeba (during unfavourable conditions), Stanieria (an alga), etc.

At the onset of unfavourable conditions, like drying of water reservoir, extreme hot, drought, scarcity of food or condensation of water into ice, Amoeba withdraws its pseudopodia, becomes spherical and encloses itself within the 2-3 layered strong envelope. This process is known as encystment. During this phase, the metabolism of Amoeba is reduced to the minimum.

However, the nucleus divides repeatedly to form a large number of nuclei. Each nucleus remains surrounded by a small amount of cytoplasm. When the favourable environmental condition sets in the outer environment, the prolectin cyst disintegrates and premature daughter Amoeba called amoebae gets released.

Multiple fission in Amoeba Spoliation

Sometimes the products of multiple fission become individually surrounded by resistant coats, i.e. cyst walls before their release from parent, the process is known as sporulation and the encysted products are known as spores.

It is not only the fastest method of reproduction but also helps to overcome unfavourable conditions. Sporulation is generally found in monerans, protistans, algae and lower fungi.
Different organisms produce different types of spores as given below
(i) Zoospores They are microscopic motile structures with one or two flagella. The flagella help the zoospores to swim in aquatic habitat for proper dispersal.
These are the most common reproductive structures seen in the members of kingdom-Fungi and simple plants such as algae, e.g. Chlamydomonas, Albugo, Ulothrix, Saprolegnia (lower fungi), etc.

(ii) Conidia They are non-motile, exogenous spores, which develop through constriction on the tips of the conidiophore in fungi, e.g. PeniciUium, Aspergillus, etc.

Conidia of PeniciUium

Budding
In this process, unequal and small projections called buds are produced from the parent cell. Initially, these buds remain attached to the parent cell and eventually get separated and mature into new organisms, e.g. yeast,
Hydra, etc.
Depending on the place from where the bud arises, budding can be of two types
(i) External budding (Hydra and yeast) During favourable conditions like presence of adequate nutrients, moisture, etc., a bud grows on the parent body.
In Hydra (multicellular organism), regenerative cells are used for reproduction during budding.

A bud develops on the median region of the b«dy as an outgrowth. Later, due to the repeated cell divisions, these buds gradually enlarge and coelenteron of Hydra migrates ipto it.

Tentacles start developing at the terminal region of the bud’s mouth. These buds develop into tiny individuals which on getting fully matured, detach themselves from the parent body and become new independent individuals.

The same process occurs in yeast. The cell wall of parent bulges out as an outgrowth at the peripheral region and is called bud. The parent nucleus divides along with the cytoplasm and the newly formed ‘ nucleus migrates into the new bud which gets detached from the parent yeast.

(ii) Internal budding (Gemmule formation) Under the adverse conditions, several sponges form internal buds. These internal buds are called gemmules.

In this process, archaeocytes a special type of totipotent cells aggregate together and a hard coat is formed around them. It remains open to outside via a small pore, i.e. micropyle.

During favourable environmental conditions, a mass of archaeocytes comes out via micropyle (a minute pore) that grows into a colony, e.g. Spongilla, etc.

Question 4.
Describe the process of asexual reproduction in lower plants.
Answer:

In plants, asexual reproduction is commonly known as vegetative propagation. It is the process of formation of a new plant from detached vegetative parts of the parent plant. These vegetative structures are called vegetative propagules. This process helps in multiplication of seedless plants, e.g. sugarcane, banana, etc. The process is asexual reproduction as it does not involve two parents. Vegetative ‘‘propagation in plants is of two types

Natural Vegetative Propagation
This type of vegetative propagation occurs in plants naturally. A fragment of the mother plant gets separated and forms an independent plant under suitable conditions.
This can take place by the following vegetative propagules
(i) By Roots
The buds present on the roots grow into leafy shoots called slips above the ground and adventitious roots at their bases. Each slip gives rise to a new plant, e.g. sweet potato, Dahlia, guava, yam, Tinospora, etc.

(a) Root tuber of sweet potato, (b) Fasciculated root of Dahlia, (c) Nodulous roots of mango ginger

(ii) By Stems
In plants, vegetative propagation can also take place by stems. They modify themselves to give rise to new plants.
This can take place by the following vegetative propagules
This can take place by the following vegatative propagules
(a) Underground stems Underground modified stems possess buds which grow into new plants.
Some of its types are given below

1. Rhizomes These are modified stems with buds and sufficient stored food. A piece of rhizome containing bud can give rise to a new plant. This method is used in the propagation of plants like ginger, turmeric, banana, lotus, etc.
2. Bulbs They are highly reduced underground stems with a number of buds, e.g. onion, lilies, garlic, etc.
3. Tubers They are the modified underground stem branches having several buds, e.g. each eye of the potato is a bud, which grows into a new potato plant when planted with a portion of swollen tuber. The potato crop is raised by the tubers, not by seeds.

(b) Subaerial stems Vegetative propagation by the means of subaerial stems, can be categorised as given below

1. Runners They are modified stems, which produce adventitious roots at nodes. Each node gives rise to an aerial shoot which becomes a new plant, e.g. Oxalis, Centella, grasses, etc.
2. Stolons These are horizontal branches that arch above the ground. They also help in vegetative propagation, e.g. strawberry, Vallisneria.
3. Suckers They arise from the base of the erect shoot, grow horizontally in the soil and then come out to form new aerial shoots. These shoots become independent when suckers break away from the parent plant, e.g. mint, Chrysanthemum, etc.
4. Offsets They are one internode long runners, which develop tuft of leaves at the apex, e.g.
   Pistia (water lettuce), Eichhornia (water hyacinth), etc.

(c) Aerial stems Aerial modified stems of cacti develop new plants when the stem segments fall on the ground. These act as the means of vegetative propagation, e.g. Opuntia, etc.

Vegetative reproduction by stem modifications (a) Runner, (b) Stolons, (c) Sucker, (d) Offset

CHSE Odisha 12th Class Biology Book Solutions (+ 2 2nd Year)

• Chapter 1 Reproduction in Organisms
• Chapter 2 Sexual Reproduction in Flowering Plants
• Chapter 3 Human Reproduction
• Chapter 4 Reproductive Health
• Chapter 5 Heredity and Variation
• Chapter 6 Sex Determination
• Chapter 7 Molecular Basis of Inheritance
• Chapter 8 Evolution
• Chapter 9 Health and Diseases
• Chapter 10 Improvement in Food Production
• Chapter 11 Microbes in Human Welfare
• Chapter 12 Principles and Processes of Biotechnology
• Chapter 13 Applications of Biotechnology
• Chapter 14 Organisms and Environment
• Chapter 15 Ecosystem
• Chapter 16 Biodiversity and its Conservation
• Chapter 17 Environmental Issues

CHSE Odisha Class 12 Textbook Solutions

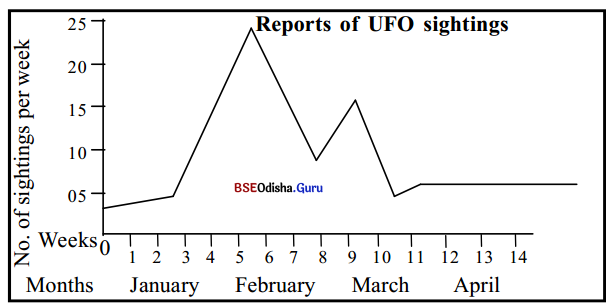
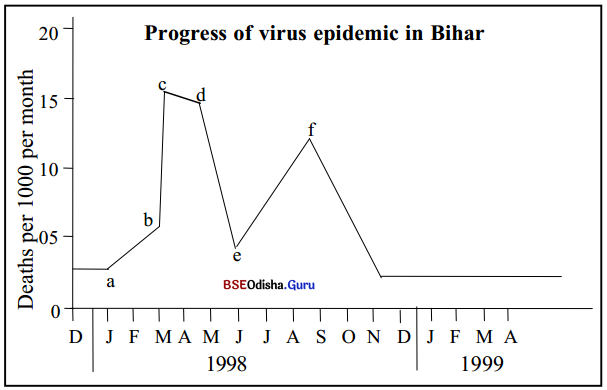
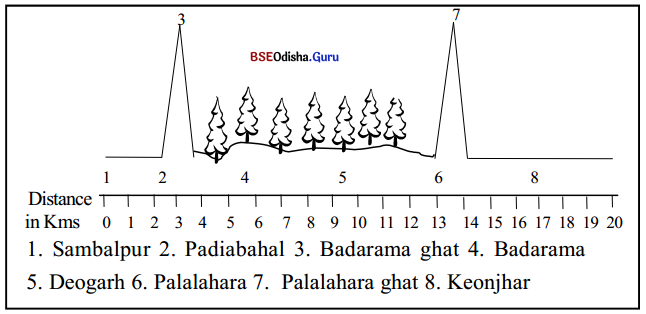
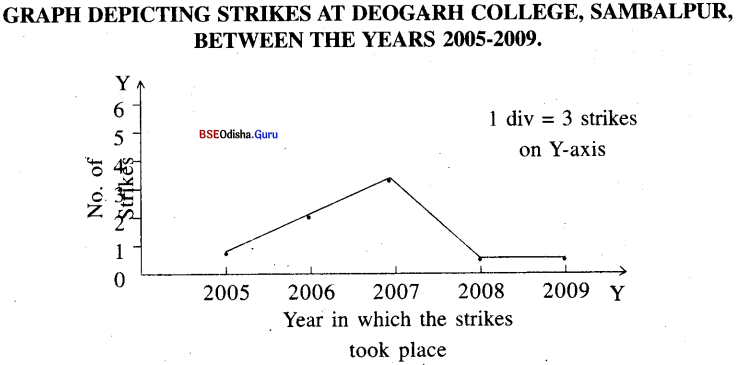
Odisha State Board BSE Odisha 8th Class Sanskrit Solutions Grammar ବ୍ୟାକରଣ ବିଭାଗ Questions and Answers.

BSE Odisha Class 8 Sanskrit Grammar ବ୍ୟାକରଣ ବିଭାଗ

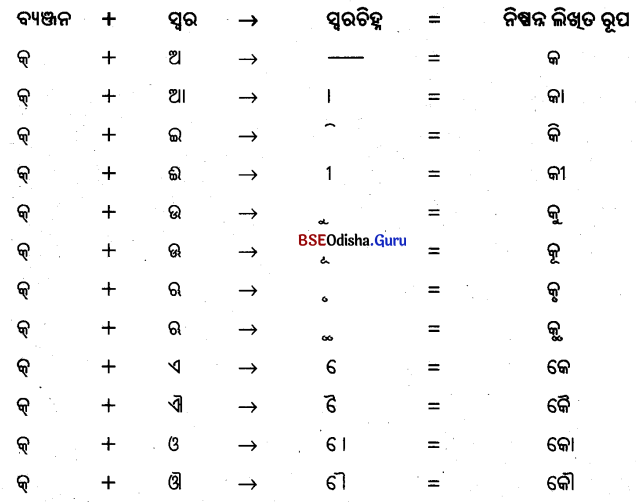
संधिविधानम् (ସନ୍ଧିବିଧାନମ୍)

• ପ୍ର + ନମତି = ପ୍ରଣମତି
• ଇତି + ଆଦୟଃ = ଇତ୍ୟାଦୟ
• ଶିଳ୍ପ + ଆଗାରସ୍ୟ = ଶିଳ୍ପୀଗାରସ୍ୟ
• ଶିଳ୍ପା + ଆଗାରାନ୍ = ଶିଳ୍ପୀଗାରାନ୍
• ଇତଃ + ତତଃ = ଇତସ୍ତତଃ
• କଃ + ଅପି = କୋଽପି
• କିମ୍ + ତୁ = = କିନ୍ତୁ
• ଅତି + ଲବ = ଅତୀବ
• ଇତି + ଇବ = ଇତୀବ
• ନିଶା + ଅର୍ଧ = ନିଶାର୍ଧ

• ମରଣାତ୍ + ପରମ୍ = ମରଣାପୂରମ୍
• ଭୂଚରଣକ + ଆଦୀନି = ଭୂଚଣକାଦୀନି
• ପ୍ର + ଆରମଃ = ପ୍ରାରମଃ
• କଃ + ଚିତ୍ = କଶ୍ଚିତ୍
• କିମ୍ + ଅପି = କିମପି
• ପରଂ + ତୁ = ପରନ୍ତୁ
• ପ୍ର + ଆପ୍ତବାନ୍ = ପ୍ରାପ୍ତବାନ୍
• ପ୍ର + ଆପ୍ରୋତି = ପ୍ରାୟୋତି
• ଅତଃ + ଏବ = ଅତଏବ
• ସମ୍ + ଭଳ = ସମ୍ମିଳ
• ଅତି + ଅନ୍ତମ୍ = ଅତ୍ୟନ୍ତମ୍
• ପରି + ଅଟକା = ପର୍ଯ୍ୟଟକା
• ପୁଷ୍ପ + ଅର୍ଘ୍ୟମ୍ = ପୁଷ୍ପାର୍ଘ୍ୟମ୍
• କଃ + ଚିତ୍ର = କଶ୍ଚିତ୍
• ପ୍ର + ଆପ୍ରୋତି = ପ୍ରାପ୍ନାତି
• ଅତ୍ର + ଅପି = ଅତ୍ରାପି।

• ବୈଦିକଗୁରୁକୁଳ + ଆଶ୍ରମଃ = ବୈଦିକଗୁରୁକୁଳାଶ୍ରମଃ
• ଅର୍ଥ + ଉପାର୍ଜନମ୍ = ଅର୍ଥୋପାର୍ଜନମ୍
• ପ୍ର + ଆସୁବତି = ପ୍ରାପ୍ଲବନ୍ତ
• ଅତି + ଆବଶ୍ୟକ = ଅତ୍ୟାବଶ୍ୟକଃ
• ତତ୍ + ଅନନ୍ତରମ୍ = ତଦନନ୍ତମ୍
• ଉପନ୍ୟାସକାରଃ + ଚ = ଉପନ୍ୟାସକାରଷ୍ଟ
• ଅତି + ଲବ = ଅତୀବ
• ନାମ + ଅନୁସାରେଣ = ନାମାନୁସାରେଣ
• ସମ୍ + ଜାତଃ = ସଞ୍ଜାତଃ
• ସ୍ଵରଃ + ଲବ = ସ୍ଵର ଇବ
• ନ + ଅସ୍ଥି = ନାସ୍ତି
• ବିଦ୍ୟା + ଆଳୟେ = ବିଦ୍ୟାଳୟ
• ଉତ୍ + ମୋଚୟତ = ଉନ୍ମୋଚୟତ
• ମୂଲ୍ୟ + ଅଙ୍କନମ୍ = ମୂଲ୍ୟାଙ୍କନମ୍ନୀ
• ତିରନ୍ + ଆବଳୀଭି = ନୀତିରଡା଼ବଳିଭି
• ଅତ୍ର + ଉପସ୍ୱାପିତା = ଅତ୍ରୋପସ୍ଥାପିତାଃ
• ବୃଦ୍ଧ + ଉପସେବିନଃ = ବୃଦ୍ଧାପସେବିନଃ
• ସର୍ପଦୁର୍ଜନୟୋ + ମଧେ = ସର୍ପଦୁର୍ଜନୟୋର୍ମଧେ
• ସର୍ପ + ନ = ସର୍ପା ନ
• ଦୁର୍ଜନଃ + ତୁ = ଦୁର୍ଜନସ୍ତୁ
• କାର୍ଯ୍ୟମ୍ + ଅଦ୍ୟ = କାର୍ଯ୍ୟମଧ୍ଯ
• ଚ + ଅପରାହ୍ନିକମ୍ = ଚାପରାନ୍ତ୍ରିକମ୍।
• କୃତମ୍ + ଅଦ୍ୟ = କୃତମଦ୍ୟ
• ପ୍ରତି + ଈକ୍ଷତେ = ପ୍ରତୀକ୍ଷତେ
• କିମ୍ + ଅପି = କିମପି
• ନ + ଏବ = : ନୈବ
• ତତ୍ + ଅପି = ତଦପି
• ଅଚ୍ଛାନାମ୍ + ଅପି = ଅଳ୍ପନାମପି
• ନାରଃ + ଅପି = ନାଗୋଽପି
• ଗୁଣବତ୍ + ଜନସୃକାଁତ୍ = ଗୁଣବଜନସୃକାଁତ୍ସ୍ଵ
• ନଃ + ଅପି = ସ୍କୋଽପି
• ପ୍ର + ଆପ୍ଳୁତି = ପ୍ରାପ୍ରୀତି
• ପୁଷ୍ପମାଳ + ଅନୁଷଙ୍ଗଣ = ପୁଷ୍ପମାଳାନୁଷଙ୍ଗଣ
• ପଞ୍ଚ + ଏବ = ପଞ୍ଚିବ
• ମନୁଷ୍ୟାନ୍ + ଚ = ମନୁଷ୍ୟ
• ଗୁରୂନ୍ + ଅତିଥୁପଞ୍ଚମାନ୍ = ଗୁରୂନତିଥପଞ୍ଚମାନ୍ତୃ
• ତିଃ + ଆରଭ୍ୟତେ = ତୃଣେରାରଭ୍ୟତେ
• ଉଦାରଚରିତାନାଂ + ତୁ = ଉଦାରଚରିତାନାନ୍ତୁ
• ବସୁଧା + ଏବ = ବସୁଧୈବ
• ହଂସ + ହି = ହଂସୋ ହି
• କ୍ଷୀରମ୍ + ଆଦରେ = କ୍ଷୀରମାଦରେ
• ତତ୍ + ମିଶ୍ରିତ୍ = ତନ୍ନିଶ୍ରାତ୍ଭ
• ବେତ୍ + ନ = ଭବେନ୍ନ
• କଦା + ଅପି = କଦାପି
• କଥମ୍ + ଅପି = କଥମପି

• ବର୍ଜୟତି + ଅପଃ = ବର୍ଜୟତ୍ୟପଃ
• ତଥା + ଏବ = ତଥୈବ
• କଃ + ବନ = କଷ୍ଟନ
• ସତ୍ + ଜନଃ = ସଜନଃ
• ପ୍ର + ଆପ୍‌ସ୍ୟାମି = ପ୍ରାପ୍‌ସ୍ୟାମି
• ନିଃ + କରୁନଃ = ନିଷ୍କରୁନଃ
• ଚ + ଆସୀତ୍ = ଚାସୀତ୍
• କଃ + ବନ = କଷ୍ଟନ
• ତତ୍ର + ଏବ = ତତ୍ରୈବ
• ସମ୍ + ଭବିଷ୍ୟତି = ସମ୍ଭବିଷ୍ୟତି
• ପ୍ର + ଆପ୍ତବାନ୍ = ପ୍ରାପ୍ତବାନ୍
• କଃ + ଚିତ୍ର = କଶ୍ଚିତ୍
• ସର୍ବ + ଆଦୌ = ସର୍ବାଦୌ
• ପ୍ର + ଆପ୍ଲୁୟାତ୍ = ପ୍ରାପ୍ତିତ୍ବ
• ହନଃ + ମଣ୍ଡୁକା = ବହବୋ ମଣ୍ଡୁକା
• ସମ୍ + ମିଳିତା = ସମ୍ମିଳିତ
• ଇତି + ଆଦିଭଃ = ଇତ୍ୟାଦିଭି
• ତଥା + ଅପି = ତଥାପି
• ପରଂ + ତୁ = ପରନ୍ତୁ
• ମନ + ବଳମ୍ = ମନୋବଳମ୍ପା
• ଦମ୍ + ଅପି = ପାଦମପି
• ପ୍ର + ଆପ୍ତବତଃ = ପ୍ରାପ୍ତବୟଃ
• କସ୍ୟ + ଅପି = କନ୍ୟାପି
• ଇତି + ଆଦୀନି = ଇତ୍ଯାଦୀନି
• ଶତଃ + ଇତି = ଶକ୍ତ ଇତି
• ପରଃ + ପରମ୍ = ପରସ୍ପରମ୍ବ
• ଚନ + ଅନୁସାରମ୍ଭ = ବଚନାନୁସାରମ୍କ
• ସ୍ୟ + ଅପି = କନ୍ୟାପି
• ସାଧୁ + ଉକ୍ତମ୍ = ସାଧୂକ୍ତମ୍ଅ
• ତି + ଉଜଃ = ଅତ୍ୟୁତଃ
• ପ୍ରଧାନ + ଅମାତ୍ୟ = ପ୍ରଧାନାମାତ୍ୟ
• ତଥା + ଏବ = ତଥୈବ
• କାଳ + ଅନ୍ତରେ = କାଳାନ୍ତରେ
• ଜନ୍ମଭୂମି + ଚ = ଜନ୍ମଭୂମିଣ୍ଟ
• ସ୍ଵର୍ଗତ୍ + ଅପି = ସ୍ବର୍ଗାଦପି
• ଭବତାଂ + ମମ = ଭବତାନୁମ
• ଯତ୍ର + ଅହିଂସା = ଯତ୍ରାହିଂସା

• ସ୍ଵତନ୍ତ୍ରତା ସାଧନମ୍ + ଅକରୋତ୍ = ସ୍ଵତନ୍ତ୍ରତାସାଧନମକରୋତ୍ର
• ବୀନ୍ଦ୍ର + ମଧୁରମ୍ = ରବୀନ୍ଦ୍ରା ମଧୁରମ୍
• କା + ଅପି = କାପି
• ସହ + ଉଦରା = ସହୋଦରଃ
• ବିହଙ୍ଗ + ଉତ୍‌ପତନେ = ବିହଙ୍ଗୋତ୍ପତନେ

संधिविच्छेद: (ସନ୍ଧିବିଚ୍ଛେଦଃ)

• ପ୍ରଣମତି = ପ୍ର + ନମତି
• ଇତ୍ୟାଦୟଃ = ଇତି + ଆଦୟ
• ଶିଳାଗାରସ୍ୟ = ଶିଳ୍ପ + ଆଗାରସ୍ୟ
• ଶିଳ୍ପୀଗାରାନ୍ = ଶିଳ୍ପ + ଆଗାରାନ୍
• ଇତସ୍ତତଃ = ଇତଃ + ତତଃ
• କୋଽପି = କଃ + ଅପି
• କିନ୍ତୁ = କିମ୍ + ତୁ
• ଅତୀବ = ଅତି + ଇବ
• ନିଶାର୍ଧ = ନିଶା + ଅର୍ଧ
• ମରଣାପୂରମ୍ = ମରଣାତ୍ + ପରମ୍
• ଭୂଚଣକାଦୀନି = ଭୂଚଣକ + ଆଦାନ
• ପ୍ରାରମ୍ଭ = ପ୍ର + ଆରମ୍ଭ
• ଶାକାଦିର୍ଭି = ଶାକ + ଆଦିରଃ
• କଶ୍ଚିତ୍ = କଃ + ଚିତ୍ର
• କିମପି = କିମ୍ + ଅପି
• ପରନ୍ତୁ = ପରଂ + ତୁ
• ପ୍ରାପ୍ତବାନ୍ = ପ୍ର + ଆପ୍ତବାନ୍
• ପ୍ରାଷ୍ଟୋତି = ପ୍ର + ଆପ୍ଳୁତି
• ଅତ ଏବ = ଅତଃ + ଏବ
• ସମୁଳ = ସମ୍ + ଉଚ୍ଚ

• ପର୍ଯ୍ୟଟକା = ପରି + ଅଟକା
• କଶ୍ଚିତ୍ର = କଃ + ଚିତ୍ର
• ପ୍ରାଷ୍ଟୋତି = ପ୍ର + ଆଜ୍ୟୋତି
• ଅତୀବ = ଅତି + ଇବ
• ପୁଷ୍ପାର୍ଘ୍ୟମ୍ = ପୁଷ୍ପ + ଅର୍ଘ୍ୟମ୍
• ଅତ୍ରାପି = ଅତ୍ର + ଅପି
• ବୈଦିକଗୁରୁକୁଳା ଶ୍ରମଃ = ବୈଦିକଗୁରୁକୁଳ + ଆଶ୍ରମ
• ଅର୍ଥୋପାର୍ଜନମ୍ = ଅର୍ଥ + ଉପାର୍ଜନମ୍
• ପ୍ରାପ୍ରୁବନ୍ତି = ପ୍ର + ଆସୁବନ୍ତି .
• ଅତ୍ୟାବଶ୍ୟକମ୍‌ = ଅତି + ଆବଶ୍ୟକମ୍
• ତଦନନ୍ତରଂ = ତତ୍ + ଅନନ୍ତରମ୍
• ଉପନ୍ୟାସକାରଷ୍ଟ = ଉପନ୍ୟାସକାରଃ + ଚ
• ଅତୀବ = ଅତି + ଇବ
• ପରନ୍ତୁ = ପରମ୍ + ତୁ
• ନାମାନୁସାରେଣ = ନାମ + ଅନୁସାରେଣ
• ସଞ୍ଜାତଃ = ସମ୍ + ଜାତଃ
• ସ୍ଵର ଇବ = ସ୍ଵରଃ + ଇବ
• ନାସ୍ତି = ନ + ଅସ୍ତି
• ନୀତିରନ୍ଧାବଳିଭଃ = ନୀତିରନ୍ + ଆବଳିଭିଂ
• ଅତ୍ରୋପସ୍ଥାପିତା = ଅତ୍ର + ଉପସ୍ଥାପିତା
• ପସେବିନଃ = ବୃଦ୍ଧ + ଉପବେସିନଃ
• ପ୍ରାଣମତ୍‌ = ପ୍ର + ଅନମତ୍
• ସର୍ପଦୁର୍ଜନୟୋର୍ମଧ୍ଯ = ସର୍ପଦୁର୍ଜନ + ମଧ୍ୟ
• ସର୍ପୋ ନ = ସପଃ + ନ
• ସର୍ପୋ ଦଶତି = ସପଃ + ଦଶତି
• ଦୁର୍ଜନସ୍ତୁ = ଦୁର୍ଜନଃ + ତୁ
• କାର୍ଯ୍ୟମଦ୍ୟ = କାର୍ଯ୍ୟମ୍ + ଅଦ୍ୟ
• ଚାପରାହ୍ନିକମ୍ = ଚ+ ଅପରାହ୍ନିକମ୍
• କୃତମସ୍ୟା = କୃତମ୍ + ଅଦ୍ୟ
• ପ୍ରତୀକ୍ଷତେ = ପ୍ରତି+ ଈକ୍ଷତେ
• କିମପି = କିମ୍ + ଅପି
• ଜୈବ = ନ + ଏବ
• ତଦପି = ତତ୍ + ଅପି
• ଅଜ୍ଞା ନାମପି = ଅଚ୍ଛାନାମ୍ + ଅପି
• ନାଗୋଽପି = ନାରଃ + ଅପି
• କିନ୍ତୁ = କିଂ + ତୁ
• ଗୁଣବଜନସ୍ମର୍କାତ୍ = ଗୁଣବତ୍ + ଜନସୃତ୍
• ସ୍ଵକପି = ସ୍ଵତଃ + ଅପି
• ପ୍ରାସ୍ମୋତି = ପ୍ର + ଆପ୍ରୋତି
• ପୁଷ୍ପମାଳା ନୁଷଙ୍ଗଣ = ପୁଷ୍ପମାଳ + ଅନୁଷଙ୍ଗଣ
• ପବ = ପଞ୍ଚ + ଏବ
• ଗୁରୂନତିଥପଞ୍ଚମାନ୍ = ଗୁରୂନ୍ + ଅତିଥପଞ୍ଚମାନ୍
• ତୃଣିରାରଭ୍ୟତେ = ତୃ + ଆରଭ୍ୟତେ
• ଉଦାରଚରିତାନାନ୍ତୁ = ଉଦାରଚରିତାନାଂ + ତୁ
• ବସୁଧୈବ = ବସୁଧା + ଏବ
• ହଂସୋ ହି = ‘ହଂସ + ହି

• କ୍ଷୀରମାଦରେ = କ୍ଷୀରମ୍ + ଆଦରେ
• ତନ୍ନିଶ୍ରାତ୍‌ = ତତ୍ + ମିଶ୍ରିତ୍ଭ
• ବେନ୍ସ = ଭବେତ୍ + ନ
• କଦାପି = କଦା + ଅପି
• କଥମପି = କଥମ୍ + ଅପି
• ବର୍ଜୟତ୍ୟପଃ = ବର୍ଜୟତି + ଅପ
• ତଥୈବ = ତଥା + ଏବ
• କଷ୍ଟନ = କଃ + ଚନ
• ସଜନଃ = ସତ୍ + ଜନଃ
• ନିଷ୍ଠାପ = ନିଃ + ପାପଃ
• .ନିଷ୍କରୁନଃ = ନିଃ + କରୁନଃ
• ପ୍ରାପ୍‌ସ୍ୟାମି = ପ୍ର + ଆପ୍‌ସ୍ୟାମି
• ପ୍ରଧାନାମାତ୍ୟ = ପ୍ରଧାନ + ଅମାତ୍ୟ
• ତଥୈବ = ତଥା + ଏବ
• କାଳାନ୍ତରେ = କାଳ + ଅନ୍ତରେ
• ଜନ୍ମଭୂମିଷ୍ଟ = ଜନ୍ମଭୂମି + ଚ
• ସ୍ବର୍ଗାଦପି = ସ୍ଵର୍ଗତ୍ + ଅପି
• କଶ୍ଚିତ୍ = କଃ + ଚିତ୍
• ସର୍ବାଦୌ = ସର୍ବ + ଆଦୌ
• ପ୍ରାପ୍ରୁୟାତ୍ = ପ୍ର + ଆପ୍‌ୟାତ୍
• ବହବୋ ମଣ୍ଡୁକା = ବହନଃ + ମଣ୍ଡୁକା
• ସମ୍ମିଳିତା = ସମ୍ + ମିଳିତଃ
• ଇତ୍ୟାଦିଭିଂ = ଇତି + ଆଦିଭି
• କ୍ରୋ ବା = କଃ + ବା
• ତଥାପି = ତଥା + ଅପି
• ମନୋବଳମ୍ = ମନଃ + ବଳମ୍
• ପୁନରପି = ପୁନଃ + ଅପି
• କୋଽପି = କଃ + ଅପି
• ପାଦମପି = ପାଦମ୍ + ଅପି
• ପ୍ରାପ୍ତିବତଃ = ପ୍ର + ଆୟୁବତଃ
• କସ୍ୟାପି = କସ୍ୟ + ଅପି
• ଇତ୍ୟାଦୀନି = ଇତି + ଆଦାନ
• ଶକ୍ତ ଇତି = ଶନ୍ତଃ + ଇତି
• ପରସ୍କରମ୍ = ପରଃ + ପରମ୍
• ବଚନାନୁସାରମ୍ = ବଚନ + ଅନୁସାରମ୍
• କନ୍ୟାପି = କସ୍ୟ + ଅପି
• ସାଧୁଲମ୍ = ସାଧୁ + ଉକ୍ତମ୍
• ଅତ୍ୟଚ୍ଚ = ଅତି + ଉଚ୍ଚ
• ବାସୀଙ୍କ = ଚ+ ଆସୀତ୍
• କଣ୍ଟନ = କଃ + ଚନ
• ଅତୀବ = ଅତି + ଇବ
• ତତ୍ରୈବ = ତତ୍ର + ଏବ
• ସମ୍ଭବିଷ୍ୟତି = ସମ୍ + ଭବିଷ୍ୟତି
• ପ୍ରାପ୍ତବାନ୍ = ପ୍ର + ଆପ୍ତବାନ୍
• ଭବତାନ୍କମ = ଭବତାଂ + ମମ
• ଯତ୍ରାହିଂସା = ଯତ୍ର + ଅହିଂସା

• ସ୍ଵତନ୍ତ୍ରତା ସାଧନମୂକରୋତ୍ = ସ୍ୱତନ୍ତ୍ରତାସାଧନମ୍ ଅକରୋତ୍
• ରବୀନ୍ଦ୍ରା ମଧୁରମ୍ = ରବୀନ୍ଦ୍ର + ମଧୁରମ୍
• କାପି = କା’ + ଅପି .
• ସହୋଦରଃ = ସହ + ଉଦରଃ
• ବିହଙ୍ଗୋପତନେ = ବିହଙ୍ଗ + ଉତ୍‌ପତନେ

क्रियापदचयनम् (କ୍ରିୟାପଦଚୟନମ୍ )

प्रश्न 1.
ପ୍ରବହତି, ଗଙ୍ଗା, ଘୋଷିତବାନ୍, ଅକରୋତ୍, ପ୍ରବର୍ଗତେ, ଭବତି ।
उत्तर:
ପ୍ରବହତି, ଘୋଷିତବାନ୍, ଅକରୋଡ୍, ପ୍ରବର୍ଗତେ, ଭବତି।

प्रश्न 2.
ହଂସ, ଆଦତ୍ତ, ଦଶତି, ସ୍ୟାତ୍, ଭବେତ୍, କୁର୍ଥାତ୍ ।
उत्तर:
ଆଦରେ, ଦଶତି, ସ୍ୟାତ୍, ଭବେତ, କୁର୍ଯ୍ୟାତ୍।

प्रश्न 3.
ମୁଞ୍ଚତି, ପ୍ରାଷ୍ଟୋତି, ଧାର୍ଯ୍ୟ, ଯାତି, ଶିରସି, ବର୍ଣୟନ୍ତି ।
उत्तर:
ମୁଞ୍ଚତି, ପ୍ରାପ୍ନାତି, ଧାର୍ଯ୍ୟତେ, ଯାତି, ବର୍ଷୟନ୍ତି।

प्रश्न 4.
ଦଶତି, କୃତବାନ୍, ଅକରୋଡ୍, ପ୍ରଖରା, ଆସୀତ୍ବ, ଭବତି ।
उत्तर: ଦଶତି, କୃତବାନ୍, ଅକରୋତ, ଆସୀତ, ଭବତି ।

प्रश्न 5.
ନିବସନ୍ତି, ଭବତି, ଅସ୍ଥି, ଭୂମି, ପ୍ରାପ୍ରୁବନ୍ତି, ଆସୀତ୍।
उत्तर:
ନିବସ୍‌ତ୍ତି, ଭବତି, ଅସ୍ଥି, ପ୍ରାପ୍ତିବନ୍ତି, ଆସୀତ୍।

प्रश्न 6.
କୁର୍ବନ୍ତ, ଜାନାତି, ଅସ୍ଥି, ଅତ୍ର, ଭବତି, ପୋଷୟତି ।
उत्तर:
କୁର୍ବନ୍ତି, ଜାନାତି, ଅସ୍ଥି, ଭବତି, ପୋଷୟତି ।

प्रश्न 7.
ଅସ୍ଥି, ନିବସତି, ଲିଖୁତବାନ୍, ଭବତି, ସମର୍ପୟତି, ମାର୍ଗମ୍ ।
उत्तर:
ଅସ୍ଥି, ନିବସନ୍ତ, ଲିଖତବାନ୍, ଭବତି, ସମର୍ପୟନ୍ତି ।

प्रश्न 8.
ପ୍ରାଷ୍ଟୋତି, ସ୍ୟାତ୍, ପୃଷ୍ଟବାନ୍, ଭକ୍ତବାନ୍, ଭବାନ୍,ଅଗଚ୍ଛତ୍ ।
उत्तर:
ପ୍ରାଷ୍ଟୋତି, ସ୍ୟାତ, ପୃଷ୍ଟବାନ, ଉକ୍ତବାନ, ଅଗଚ୍ଛତ୍।

प्रश्न 9.
ଅସ୍ଥି, ପଠତି, ଇତି, ସ, ଆଗଚ୍ଛନ୍ତୁ, ହରଡି ।
उत्तर:
ଅଗ୍ନି, ପଠରି, ସରି, ଆଗଚ୍ଛନ୍ତୁ, ହରନ୍ତି ।

प्रश्न 10.
ମଣ୍ଡୟତି, ଜୀବନ୍ତ, ଭୂମି, କର୍ଷତି, କରୋତି, ଆନୟତି ।
उत्तर:
ମଣ୍ଡୟତି, ଜୀବନ୍ତି, କର୍ଷତି, କରୋତି, ଆନୟତି ।

प्रश्न 11.
କରିଷ୍ୟାମଃ, ଅଭବତ୍, କୃତବନ୍ତୀ, ନୀତବନ୍ତୀ, ଭାଷଣମ୍, ଆସୀତ୍ ।
उत्तर:
କରିଷ୍ୟାମଃ, ଅଭିବତ୍, କୃତବନ୍ତୀ, ନୀତବନ୍ତଃ, ଆସୀତ୍।

प्रश्न 12.
ହ୍ୟାମି, ଦୀୟତେ, ଦଣ୍ଡୟତି, ଇଚ୍ଛାମି, ପଠନ୍ତି ।
उत्तर:
ସ୍ମିଥ୍ୟାମି, ଦୀୟତେ, ଦଣ୍ଡୟତି, ଇଚ୍ଛାମି, ପଠନ୍ତି ।

प्रश्न 13.
ମମ, ଭବେୟୁ, ଭବିଷ୍ୟତି, ଅସ୍ଥି, ପାଳୟତି, ନେଷ୍ୟାମି |
उत्तर:
ଉବେୟୁ, ଭବିଷ୍ୟତି, ଅସ୍ଥି, ପାଳୟତି, ନେଷ୍ୟାମି।

प्रश्न 14.
ଭବତି, ପ୍ରୟଚ୍ଛନ୍ତି, ଆଗଳନ୍ତି, ସନ୍ତ, କୁର୍ବନ୍ତ, ତତ୍ର ।
उत्तर:
ଭବତି, ପ୍ରୟଚ୍ଛନ୍ତି, ଆଗଛନ୍ତି, ସନ୍ତ, କୁର୍ବନ୍ତି।

प्रश्न 15.
ରକ୍ଷତି, ନୟତି, କୁର୍ମ, ଜାନାତି, ପୁନଃ, ପ୍ରଣମତି।
उत्तर:
ରକ୍ଷତି, ନୟତି, କୁର୍ମୁ, ଜାନାତି, ପ୍ରଣମତି।

प्रश्न 16.
ଆସୀତ୍, ସୂତ୍ରମ୍, ଅଭିବତ୍, ଅପଶ୍ୟନ, ଅଭବନ, ଆଗଛନ୍ ।
उत्तर:
ଆସୀତ, ଅଭିବତ୍, ଅପଶ୍ୟନ୍, ଅଭବନ, ଆଗଚ୍ଛନ୍।

प्रश्न 17.
ଅପୀଡୟନ୍, ଅଭିବତ, ଦୁଃଖ୍ୟତଃ, ଆସୀତ, ଅଦଦାତ୍, ଅଚିନ୍ତୟତ୍ ।
उत्तर:
ଅପୀଡୟନ, ଅଭବତ, ଆସୀତ, ଅଦଦାତ, ଅଚିନ୍ତୟତ୍।

प्रश्न 18.
ଅପଶ୍ୟତ୍, ମରିଷ୍ୟତି, ଭବତି, କିମର୍ଥ୍ୟ, ରକ୍ଷତି, ଅଗଚ୍ଛତ୍ ।
उत्तर:
ଅପଶ୍ୟତ୍, ମରିଷ୍ୟତି, ଭବତି, ରକ୍ଷତି, ଅଗଚ୍ଛତ୍।

प्रश्न 19.
ଅବଦତ୍, ଭବତଃ, ଅଭିବତ୍, କାକ, ଅଗଚ୍ଛତ୍, ଆସୀତ୍ ।
उत्तर:
ଅବଦତ, ଭବତଃ, ଅଭିବତ୍, ଅଗଚ୍ଛିତ, ଆସୀତ୍।

प्रश्न 20.
ଦେହି, ଜଳମ୍, ରକ୍ଷ, ଆସୀତ୍, ଗତବାନ୍, ଭକ୍ତବାନ୍।
उत्तर:
ଦେହି, ରକ୍ଷ, ଆସୀତ, ଗତବାନ, ଉକ୍ତବାନ୍।

प्रश्न 21.
ରକ୍ଷତଃ, କରୋତି, ଛାତ୍ରା, ଭର୍ବତି, ଭବତଃ, ପଶ୍ୟତଃ ।
उत्तर:
ରକ୍ଷତଃ, କରୋତି, ଭବତି, ଭବତଃ, ପଶ୍ୟତଃ ।

प्रश्न 22.
କୁରୁତଃ, ପଶ୍ୟତଃ, ବର୍ଷୟତଃ, ଖ୍ରୀଷ୍ଟାବ୍ଦ, ପ୍ରାପ୍ତବାନ୍, ସ୍ମାରୟତି ।
उत्तर:
କୁରୁତଃ, ପଶ୍ୟତଃ, ବର୍ଷୟତଃ, ପ୍ରାପ୍ତବାନ, ସ୍ମାରୟତି ।

प्रश्न 23.
ଆଗତବନ୍ତଃ, ମୁଣ୍ଡୁକା, କୃତବତଃ, ବର୍ଷୟନ୍ତ, ଆସୀତ୍ବ, କୁର୍ଯ୍ୟାତ୍।
उत्तर:
ଆଗତବନ୍ତଃ, କୃତବତଃ, ବର୍ଷୟନ୍ତ, ଆସୀତ, କୁର୍ଯ୍ୟାତ୍ ।

प्रश्न 24.
କୃତବନ୍ତଃ, ପତିତବନ୍ତଃ, ମନୋବଳମ୍, କୁର୍ବନ୍ତ, ପ୍ରାପ୍ତବନ୍ତୀ, ଉଦ୍ଭବତୀ ।
उत्तर:
କୃତବନ୍ତଃ, ପତିତବନ୍ତଃ, କୁର୍ବନ୍ତି, ପ୍ରାପ୍ତବନ୍ତଃ, ଉଦ୍ଭବତୀ।

प्रश्न 25.
କୁର୍ଯ୍ୟା, ଶୃଣୁମା, ପ୍ରାପ୍ରୁୟା, ଭବେ, ଆଗଚ୍ଛତ, ଶିଶୁ ।
उत्तर:
କୁର୍ଯ୍ୟା, ଶୁଣୁୟଃ, ପ୍ରାପ୍ତି, ଭବେ, ଆଗଚ୍ଛିତ।

प्रश्न 26.
ଆଗଳତ୍ବ, ଭବତଃ, ପ୍ରାପ୍ତବାନ୍, ଅଭିବତ୍, କଥ୍ୟ, ଅବଦନ୍ ।
उत्तर:
ଆଗଚ୍ଛିତ, ଭବତଃ, ପ୍ରାପ୍ତବାନ୍, ଅଭିବତ୍, ଅବଦନ୍।

प्रश्न 27.
ଅବଦତ୍, ପ୍ରାପ୍ତବନ୍ତ, ଅଭବନ୍, ପ୍ରାପ୍ତବାନ୍, ପୁତ୍ର, ଭବେ ।
उत्तर:
ଅବଦତ୍, ପ୍ରାପ୍ତବନ୍ତଃ, ଅରବନ, ପ୍ରାପ୍ତବାନ୍, ଭବେ ।

प्रश्न 28.
କ୍ରନ୍ଦସି, କ୍ରନ୍ଦାମି, ଭବିଷ୍ୟତି, କରିଷ୍ୟାମି, ପୁତ୍ର, ଭବିଷ୍ୟାମି |
उत्तर:
କୁନ୍ଦସି, କ୍ରନ୍ଦାମି, ଭବିଷ୍ୟତି, କରିଷ୍ୟାମି, ଭବିଷ୍ୟାମି ।

प्रश्न  29.
ଜ୍ଞାତବତୀ, ଅସ୍ଥି, କ୍ରନ୍ଦସି, ଚିହ୍ନମ, ଭବନ୍ତି, ପୂଛନ୍ତି ।
उत्तर:
ଜ୍ଞାତବତୀ, ଅସ୍ଥି, କୁନ୍ଦସି, ଭବନ୍ତି, ପୂଛନ୍ତି ।

प्रश्न 30.
ଭବତି, ପୂଛନ୍ତି, ବିସ୍ମରନ୍ତି, ଦୁଃଖମ୍, କଥୟତ୍ତି, ଭବିଷ୍ଯତି ।
उत्तर:
ଭବନ୍ତି, ପୂଛନ୍ତି, ବିସ୍ମରନ୍ତି, କଥୟନ୍ତି, ଭବିଷ୍ୟତି।

प्रश्न 31.
ଭବିଷ୍ୟତି, ସ୍ଵାସ୍ୟତି, ସ୍ମରିଷ୍ୟତି, ଏତଦ୍, କଥୁତବତୀ, ଅଭିବତ୍ ।
उत्तर:
ଭବିଷ୍ୟତି, ସ୍ଵାସ୍ୟତି, ସ୍ମରିଷ୍ୟତି, କଥୁତବତୀ, ଅଭିବତ୍।

प्रश्न 32.
ଅପଶ୍ୟତ୍, ମରିଷ୍ୟତି, ସଜ୍ଜନଃ, ରକ୍ଷତି, ଭବତି, ଅବଦତ୍ ।
उत्तर:
ଅପଶ୍ୟତ୍, ମରିଷ୍ୟତି, ରକ୍ଷତି, ଭବତି, ଅବଦତ୍।

प्रश्न 33.
ସମ୍ଭବିଷ୍ୟତି, ଭବତି, କୁରୁତଃ, ପଶ୍ୟତ, ବର୍ଷୟତ, ଫଳମ୍ ।
उत्तर:
ସମ୍ଭବିଷ୍ୟତି, ଭବତି, କୁରୁତଃ, ପଶ୍ୟତ, ବର୍ଷୟତ ।

प्रश्न 34.
ପ୍ରକଟିତବତୀ, ଉତ୍ପାଟିତବାନ୍, ଦୂରୀକୃତବାନ୍, ଅଭିବତ୍, ନୟନମଃ, ସ୍ଵାସ୍ୟତି ।
उत्तर:
ପ୍ରକଟିତବତୀ, ଉତ୍ପାଟିତବାନ୍, ଦୂରୀକୃତବାନ୍, ଅଭିବତ୍, ସ୍ଵାସ୍ୟତି |

प्रश्न 35.
ଭ୍ରମତି, ଖେଳତି, ଦୁଷ୍ୟନ୍ତ, ବାଳିକା, ପଶ୍ୟାମି, ଦ୍ରଷ୍ୟାମି ।
उत्तर:
ଭ୍ରମତି, ଖେଳନ୍ତି, ଦ୍ରଷ୍ୟାନ୍ତ, ପଶ୍ୟାମି, ଦ୍ରଷ୍ୟାମି ।

प्रश्न 36.
ଚିନ୍ତୟତି, ସ୍ତମଃ, ବର୍ଷୟତି, କୁର୍ଯାତ୍, ଗଚ୍ଛେତ୍, ପତେତ୍।
उत्तर:
ଚିନ୍ତୟତି, ବର୍ଷୟତି, କୁର୍ଯାତ, ଗଚ୍ଛେତ, ପତେତ୍।

प्रश्न 37.
ଦତ୍‌ଥ, କୁର୍ମ, ପ୍ରାପ୍ରୁଥ, ପିବାମଃ, ବିଦ୍ୟାଳୟ, ଶୁଣୁଥ ।
उत्तर:
ଦତ୍‌ଥ, କୁର୍ମୁ, ପ୍ରାପ୍ରୁଥ, ପିବାମଃ, ଶୁଣୁଥ।

प्रश्न 38.
ଆଗଚ୍ଛିତ, କୁରୁତ, ରକ୍ଷତ, ନିୟୋଜିତଃ, ଯୁବକ, ସ୍ଥାପିତବାନ୍ ।
उत्तर:
ଆଗଚ୍ଛିତ, କୁରୁତ, ରକ୍ଷତ, ନିୟୋଜିତଃ, ସ୍ଥାପିତବାନ୍।

प्रश्न 39.
ତିଷ୍ଠତି, ତିଷ୍ଠତଃ, ତିଷ୍ଠନ୍ତି, ବାଳିକେ, ଦଦାତି, ଜାନାତି ।
उत्तर:
ତିଷ୍ଠତି, ତିଷ୍ଠତଃ, ତିଷ୍ଠନ୍ତି, ଦଦାତି, ଜାନାତି।

प्रश्न 40.
କରୋଷି, କୁରୁଥା, କୁରୁଥ, ବୟମ, ପଶ୍ୟସି, ପଶ୍ୟଥ ।
उत्तर:
କରୋଷି, କୁରୁଥ, କୁରୁଥ, ପଶ୍ୟସି, ପଶ୍ୟଥ ।

प्रश्न 41.
ସୁରିଷ୍ୟତି, ପୁତ୍ର, କଥୁତବତୀ, ରଚିତବାନ୍, କୃତବାନ୍, ଅର୍ପିତବାନ୍ ।
उत्तर:
ସ୍ମରିଷ୍ୟନ୍ତ, କଥୁତବତୀ, ରଚିତବାନ, କୃତବାନ୍, ଅର୍ପିତବାନ୍।

प्रश्न 42.
ବୃକ୍ଷ, ଆସୀତ୍ବ, ଅଭିବତ୍, ଅପଶ୍ୟନ୍, ଅଭବନ, ଆଗଚ୍ଛନ୍ ।
उत्तर:
ଆସୀତ, ଅଭିବତ, ଅପଶ୍ୟନ୍, ଅଭବନ, ଆଗର୍ଜନ।

प्रश्न 43.
ଦୃଶ୍ୟତେ, ଚାଣକ୍ୟ, ପୂଛନ୍ତି, ବିସ୍ମରନ୍ତି, ବିସ୍ମରିଷ୍ୟସି, କଥୟତି ।
उत्तर:
ଦୃଶ୍ୟତେ, ପୃଚ୍ଛନ୍ତି, ବିସ୍ମରତି, ବିସ୍ମରିଷ୍ୟସି, କଥୟତି।

प्रश्न 44.
ପ୍ରାପ୍ରୁୟାତ୍ର, ନିର୍ଣ୍ଣୀତବନ୍ତୀ, ମୟୂକ, ଆଗତବନ୍ତୀ, କୃତବନ୍ତଃ, ବର୍ଷୟନ୍ତ ସୁ ।
उत्तर:
ପ୍ରାପ୍ୟୟାତ, ନିର୍ଣ୍ଣୀତବନ୍ତଃ, ଆଗତବନ୍ତଃ, କୃତବନ୍ତଃ, ବର୍ଣ୍ଣୟନ୍ତ

प्रश्न 45.
କୁର୍ଯ୍ୟା, ଶୁଣୁୟଃ, ପ୍ରାପ୍ରୁୟା, ବାଳିକା, ଭବେ, ଆଗଚ୍ଛତ୍ ।
उत्तर:
କୁର୍ଯ୍ୟା, ଶୃଣୁୟାଁ, ପ୍ରାପ୍ତି, ଭବେ, ଆଗଚ୍ଛିତ୍।

प्रश्न 46.
ତ୍ୟଜସି, ଲିଖନ୍ତି, ଗଚ୍ଛତୁ, ଭବତଃ, ଆଗଚ୍ଛନ, ଅପଶ୍ୟନ୍ ।
उत्तर:
ତ୍ୟଜର୍ସି, ଲିଖନ୍ତି, ଗଛତୁ, ଆଗଚ୍ଛନ, ଅପଶ୍ୟନ୍।

प्रश्न 47.
ହସସି, ତୁମ୍, ହସ, ହସଥ, ଭବସି, ଭବତଃ ।
उत्तर:
ହସସି, ହସଥା, ହସଥ, ଭବସି, ଭବତଃ ।

प्रश्न 48.
ପତିତବନ୍ତଃ, କୁର୍ବନ୍ତ, ଦର୍ଶକା, ଆରୂଢ଼ବାନ, ପ୍ରାପ୍ତବତଃ, ଉଦ୍ଭବତୀ ।
उत्तर:
ପତିତବନ୍ତଃ, କୁର୍ବନ୍ତ, ଆରୂଢ଼ବାନ, ପ୍ରାପ୍ତିବନ୍ତୀ, ଉଦ୍ଭବତୀ।

प्रश्न 49.
ଅସ୍ତି, ନୟନ୍ତି, ସନ୍ତି, ସ୍ତ୍ରୀ, ମିତ୍ରାଣି, ତିଷ୍ଠତି ।
उत्तर:
ଅସ୍ତି, ନୟନ୍ତି, ସରି, ଡଃ, ତିଷ୍ଠତି।

प्रश्न 50.
ଧାବତି, ଧାବତଃ, ଧାବନ୍ତି, କୂଜନ୍ତି, କୋକିଳ, ନୃତ୍ୟନ୍ତ ।
उत्तर:
ଧାବତି, ଧାବତଃ, ଧାବନ୍ତି, କୂଜନ୍ତି, ନୃତ୍ୟନ୍ତି।

प्रश्न 51.
ଗଚ୍ଛାବ, ପଠାବ, ହସାବ, ଭବାନଃ, ଆବାମ୍, ପଶ୍ୟାବ
उत्तर:
ଗଚ୍ଛାବାଃ, ପଠାଦଃ, ହସାବ, ଭବାନଃ, ପଶ୍ୟାବ ।

प्रश्न 52.
ଗର୍ଜତି, ଦଶତି, ଆରୋହତି, ସ୍ନିହ୍ୟତି, କର୍ଷତି, କୃଷକ।
उत्तर:
ଗର୍ଜତି, ଦଶତି, ଆରୋହତି, ସ୍ପୃହ୍ୟତି, କର୍ଷତି ।

प्रश्न 53.
ପଠସି, ପଠଥ, ପଠଥ, ଯୁବାମ, ଭବସି, ଭବତଃ ।
उत्तर:
ପଠସି, ପଠଥ୍ୟ, ପଠଥ, ଭବସି, ଭବଥ ।

प्रश्न 54.
ଧାବନ୍ତି, ରଚୟତି, ଯାତି, ପାଳୟତି, କୂଜତି, ଅହମ୍ ।
उत्तर:
ଧାବନ୍ତି, ରଚୟତି, ଯାତି, ପାଳୟତି, କୂଜତି ।

प्रश्न 55.
ଉବେୟମ୍, ଶୁଣୁୟାମ୍, ନିଷ୍ପୀତବାନ୍, ସା, କ୍ରନ୍ଦସି, କ୍ରନ୍ଦାମି ।
उत्तर:
ରବେୟମ୍, ଶୃଣୁୟାମ, ନିଶ୍ଚିତବାନ, କ୍ରନ୍ଦସି, କ୍ରନ୍ଦାମି।

प्रश्न 56.
ଦେହି, ରକ୍ଷ, କୃତବତଃ, ସୈନ୍ୟା, ଗତବାନ୍, ଭକ୍ତବାନ୍ ।
उत्तर:
ଦେହି, ରକ୍ଷ, କୃତବନ୍ତୀ, ଗତବାନ୍, ଭକ୍ତବାନ୍।

प्रश्न 57.
ଯାପୟତି, ପଠତି, ମିତ୍ର, ହସ୍ପତି, ନୟତି, ଦଦାତି ।
उत्तर:
ଯାପୟତି, ପଠତି, ହସତି, ନୟତି, ଦଦାତି ।

प्रश्न 58.
ପଶ୍ୟସି, ପଶ୍ୟଥ, ପଶ୍ୟଥ, ନୟସି, ନୟଥ, ଛାତ୍ରା ।
उत्तर:
ପଶ୍ୟସି, ପଶ୍ୟଥ, ପଶ୍ୟଥ, ନୟସି, ନୟଥା ।

प्रश्न 59.
କୃଷକ, ବିକସତି, ରକ୍ଷତି, ପଠତି, ସ୍ନିହାତି, ଜଛତି ।
उत्तर:
ବିକସତି, ରକ୍ଷତି, ପଠତି, ସ୍ନିନ୍ଦ୍ୟତି, ଜତି।

प्रश्न 60.
କ୍ରୀଣୀତଃ, ଗୃହ୍ମୀତଃ, ଚିନୁତଃ, ତ୍ୱ, ରୁଦତଃ, ନୟାବ ।
उत्तर:
କ୍ରୀଣୀତଃ, ଗୃହ୍ମୀତଃ, ଚିନୁତଃ, ରୁଦତଃ, ନୟାବ ।

प्रश्न 61.
ଈଶ୍ୱରଃ, ଆଗଚ୍ଛତି, ପଶ୍ୟତି, ଚିନ୍ତୟତି, ଜନୟତି, କରୋତି ।
उत्तर:
ଆଗଚ୍ଛତି, ପଶ୍ୟତି, ଚିନ୍ତସ୍ଥତି, ଜନୟତି, କରୋତି।

प्रश्न 62.
ହସାମି, ପିତା, ପଠାମ, ଭବତି, ଦଦାସି, ଅସ୍ଥି ।
उत्तर:
ହସାମି, ପଠାମଃ, ଭବତି, ଦଦାସି, ଅନ୍ତି।

प्रश्न 63.
କ୍ରୀଣନ୍ତି, ଗୃହୁରି, ଚିନ୍ଧତି, ରୁଦନ୍ତି, ନୟାମଃ, ପିତା ।
उत्तर:
କ୍ରୀଣନ୍ତି, ଗୃହୁରି, ଚିନ୍‌ତି, ରୁଦନ୍ତି, ନୟାମଃ ।

प्रश्न 64.
ଆରୋହତି, ବାନରଃ, ଦଶତି, ଗର୍ଜତି, ନିନ୍ଦତି, ସ୍ମରତି।
उत्तर:
ଆରୋହତି, ଦଶତି, ଗର୍ଜତି, ନିନ୍ଦତି, ସ୍ମରତି।

कर्तृ पदचयनम् (କର୍ତ୍ତୃପଦଚୟନମ୍ )

प्रश्न 1.
ଭାରତୀ, ମନୋଜଃ, ପ୍ରଣମତି, ସ୍ୱ, ମାତା, ପରିବେଶଃ ।
उत्तर:
ଭାରତୀ, ମନୋଜଃ, ସ, ମାତା, ପରିବେଶଃ ।

प्रश्न 2.
ବାୟୁ, କ୍ଷେତ୍ରାଣି, ଜୀବା, ଭବତି, ମେଘା, ପରିବେଶଃ ।
उत्तर:
ବାୟୁ, କ୍ଷେତ୍ରାଣି, ଜୀବା, ମେଘା, ପରିବେଶଃ ।

प्रश्न 3.
ଦେଶଃ, ରାଜ୍ୟ, ରାଜଧାନୀ, ରାଜାନୀ, କୁର୍ବନ୍ତ, ସରୋବରଃ ।
उत्तर:
ଦେଶ, ରାଜ୍ୟ, ରାଜଧାନୀ, ରାଜାନଃ, ସରୋବରଃ ।

प्रश्न 4.
ରାଜା, ପ୍ରଜାଃ, ସାଧବ, ତେ, ଭବାନ୍, ସ୍ୟାତ୍ ।
उत्तर:
ରାଜା, ପ୍ରଜାଃ, ସାଧବୀ, ତେ, ଭବାନ୍।

प्रश्न 5.
ଛାତ୍ରୀ, ଶିକ୍ଷକ, ସ୍ୱ, ସ୍ବୟଂ, ଆସୀତ୍ବ, ଗୋପାଳ ।
उत्तर:
ଛାତ୍ରୀ, ଶିକ୍ଷକଃ, ସ୍ୱ, ସ୍ଵୟଂ, ଗୋପାଳ ।

प्रश्न 6.
ବାଳକ, ଏଷ, ଅହଂ, ସେବକଃ, ବୟଃ, ନୀତବନ୍ତଃ ।
उत्तर:
ବାଳକଃ, ଏହିଃ, ଅହଂ, ସେବକଃ, ବୟମ୍ ।

प्रश्न 7.
ଗୁରୁ, ମୁକୁନ୍ଦଦେବୀ, ସୈନିକ, ଅଭବତ୍, ମାତୃଭୂମି ଭବାନ୍ ।
उत्तर:
ଗୁରୁ, ମୁକୁନ୍ଦଦେବାଃ, ସୈନିକ, ମାତୃଭୂମି, ଭବାନ୍ ।

प्रश्न 8.
ଜନା, ନଦ୍ୟ, ଭୂମି, ଶସ୍ୟାନି, କୃଷକ, ଭବତି ।
उत्तर:
ଜନଃ, ନଦ୍ୟ, ଭୂମି, ଶସ୍ୟାନି, କୃଷକ ।

प्रश्न 9.
ହରେକୃଷ୍ଣ, ଅହଂ, ଭବାନ୍, ପଠତି, ଛାତ୍ରା, ବୃକ୍ଷ ।
उत्तर:
ହରେକୃଷ୍ଣ, ଅହଂ, ଭବାନ, ଛାତ୍ରା, ବୃକ୍ଷା ।

प्रश्न 10.
ପଥଦଃ, ସ, ବୃଦ୍ଧ, ପୃଷ୍ଟବାନ୍, ଭବାନ୍, ଯଃ ।
उत्तर:
ପଥଦଃ, ସ, ବୃଦ୍ଧା, ଭବାନ୍, ଯଃ ।

प्रश्न 11.
ଭଲୁକ, ଗନ୍ଧମାଦନ, ପରିମଳଗିରି, ଏତତ୍ତ୍ଵ, ଭକ୍ତା, କରୋତି ।
उत्तर:
ଭଲୁକ, ଗନ୍ଧମାଦନ, ପରିମଳଗିରି, ଏତତ୍, ଭକ୍ତା|

प्रश्न 12.
ମହର୍ଷି, ସ୍ୱ, କ୍ଷେତ୍ର, ଅରଣ୍ୟ, ଜନା, ପୋଷୟତ୍ତି ।
उत्तर:
ମହର୍ଷି, ଡଃ, କ୍ଷେତ୍ର, ଅରଣ୍ୟମ୍, ଜନା ।

प्रश्न 13.
ପାଦପା, ମନ୍ଦିରମ, ଧୀବତି, ଯାତ୍ରିକା, ପର୍ଯଟକଃ, ପ୍ରାଚୀରମ୍ |
उत्तर:
ପାଦପା, ମନ୍ଦିରମ, ଯାତ୍ରିକା, ପର୍ଯଟକଃ, ପ୍ରାଚୀରମ୍।

प्रश्न 14.
ଗଙ୍ଗା, ଦେଶ, ତିଳକ, ରବୀନ୍ଦ୍ର, ପ୍ରବହିତ, ଜନଃ ।
उत्तर:
ଗଙ୍ଗା, ଦେଶଃ, ତିଳକ, ରବୀନ୍ଦ୍ର, ଜନଃ ।

प्रश्न 15.
ଆଦରେ, ହଂସ, ଦୀର୍ଘଦର୍ଶୀ, କୁଟୁମ୍ବକମ୍, ଅଙ୍ଗାରଃ, ପ୍ରତିକୂଳାନି।
उत्तर:
ହଂସ, ଦୀର୍ଘଦର୍ଶୀ, କୁଟୁମ୍ବକମ୍‌, ଅଙ୍ଗାରଃ, ପ୍ରତିକୂଳାନି।

प्रश्न 16.
ମୃତ୍ୟୁ, ବିଚକ୍ଷଣା, ସର୍ପ, ଦଶତି, ଦୁର୍ଜନୀ, ନରେଶଃ ।
उत्तर:
ମୃତ୍ଯୁ, ବିଚକ୍ଷଣା, ସର୍ପ, ଦୁର୍ଜନଃ, ନରେଶଃ ।

प्रश्न 17.
ସ୍ୱ, ତେ, ଗର୍ବାନ୍ଧ, ମହୀନ୍ଦ୍ର, ମହାପୁରୁଷା, ଜ୍ଞାତବାନ୍।
उत्तर:
ସ୍ୱ, ତେ, ଗର୍ବାନ୍ଧୀ, ମହୀନ୍ଦ୍ର, ମହାପୁରୁଷା ।

प्रश्न 18.
ଠାକୁରରାଜଃ, ମନ୍ତ୍ରୀ, ରାଜଗୁରୁ, ଜନା, ପ୍ରବିଷ୍ଟବତଃ, ନେତାରଃ ।
उत्तर:
ଠାକୁରରାଜଃ, ମନ୍ତ୍ରୀ, ରାଜଗୁରୁ, ଜନା, ନେତାରଃ ।

प्रश्न 19.
ଦେଶଃ, ଦାୟାଦଃ, ତେ, ଭାରତଂ, ନୀତବନ୍ତୀ, ଏଷା ।
उत्तर:
ଦେଶଃ, ଦାୟାଦଃ, ତେ, ଭାରତଂ, ଏଷା।

प्रश्न 20.
ବଟବୃକ୍ଷ, ପରିବାରଃ, ଶାବକ, ନୟତି, ମାତା, ଶୁକଃ ।
उत्तर:
ବଟବୃକ୍ଷ, ପରିବାରଃ, ଶାବକ, ମାତା, ଶୁକଃ ।

प्रश्न 21.
ସର୍ବେ, ବରଂ, ଶୁକଃ, ବ୍ୟାଧ୍ୟ, ପଶ୍ୟତି, ମାତା ।
उत्तर:
ସର୍ବେ, ବୟଂ, ଶୁକଃ, ବ୍ୟାଧ, ମାତା ।

प्रश्न 22.
ଆମ୍ରବୃକ୍ଷ, ଆସୀ, ସୂତ୍ର, କୋକିଳ, ସ, କାକଃ ।
उत्तर:
ଆମ୍ରବୃକ୍ଷ, ସୂତ୍ର, କୋକିଳୀ, ସ, କାକଃ ।

प्रश्न 23.
କାକା, ତେ, କ୍ରମେଣ, ସ୍ୱ, କୋକିଳ, ସଜନଃ ।
उत्तर:
କାକା, ତେ, ଡଃ, କୋକିନଃ, ସଜ୍ଜନଃ ।

प्रश्न 24.
ସୈନିକା, ଯୁବକ, ରକ୍ଷତ, ହେନେରୀ, ମାତା, ସେବିକା ।
उत्तर:
ସୈନିକଃ, ଯୁବକ, ହେନେରୀ, ମାତା, ସେବିକା।

प्रश्न 25.
ଜନମଃ, ହେନେରୀ, ଯୁବକ, ବ୍ୟବସାୟୀ, ଶ୍ରୁତମ, ସୈନିକା ।
उत्तर:
ଜନମଃ, ହେନେରୀ, ଯୁବକ, ବ୍ୟବସାୟୀ, ସୈନିକା।.

प्रश्न 26.
ଯଃ, ଭବେତ୍, ସର୍ବେ, ମଣ୍ଡୁକା, ଦର୍ଶକା, ସ୍ତମ୍ଭ।
उत्तर:
ଯଃ, ସର୍ବେ, ମଣ୍ଡୁକା, ଦର୍ଶକା, ସ୍ତମଃ ।

प्रश्न 27.
ସ୍ତତଃ, ଯଃ, ସ, ତ୍ୱ, ପତେତ, ଦର୍ଶକଃ ।
उत्तर:
ସ୍ତମଃ, ଯଃ, ସ, ବଂ, ଦର୍ଶକଃ ।

प्रश्न 28.
ପୁତ୍ର, ତ୍ୱ, ଏଷ, ଜନା, ଏଷା, ବିସ୍ମରିଷ୍ଯତି।
उत्तर:
ପୁନଃ, ବଂ, ଏଷ, ଜନଃ, ଏଷା ।

प्रश्न 29.
ବାଳ, ବାଣକ୍ୟ, ଏତତ୍ବ, ଏଷ, ଜନନୀ, ଅସ୍ଥି ।
उत्तर:
ବାଳ, ଚାଣକ୍ୟ, ଏତତ, ଏଷ, ଜନନୀ।

प्रश्न 30.
ଯୁବତଃ, ସୈନିକ, ଗ୍ରାମ, ପ୍ରାଣା, କୁରୁତ, ଧାର୍ମିକୀ ।
उत्तर:
ଯୁବତଃ, ସୈନିକ, ଗ୍ରାମଃ, ପ୍ରାଣୀ, ଧାର୍ମିକୀ।

प्रश्न 31
କୁର୍ଯ୍ୟାତ୍, ମଣ୍ଡୁକ, ଯଃ, ସ୍ତମଃ, ଶିଖରଃ, ବିଜୟୀ ।
उत्तर:
ମଣ୍ଡୁକଃ, ଯଃ, ସ୍ତମଃ, ଶିଖରଃ, ବିଜୟୀ ।

प्रश्न 32.
ବାଟିକା, ଭବତ, ଜନମଃ, ରତିଃ, ସରଳୀ, ମାର୍ଗ ।
उत्तर:
ବାଟିକା, ଜନମଃ, ରବି, ସରଜଃ, ମାର୍ଗ ।

प्रश्न 33.
କାର୍ଯ୍ୟ, ଏଷ, ପଶ୍ୟତ, ମହତ୍, ପୁରସ୍କାର, ମାନମଃ ।
उत्तर:
କାର୍ଯ୍ୟ, ଏଷ, ମହତ୍ବ, ପୁରସ୍କାରଃ, ମାନମଃ।

प्रश्न 34.
ଭାରତବର୍ଷମ, ଭବାନ୍, ଅକରୋତ୍, ତିଳକ, ଅହିଂସା, ସ୍ୱତନ୍ତ୍ରତା ।
उत्तर:
ଭାରତବର୍ଷମ, ଭବାନ, ତିଳକ, ଅହିଂସା, ସ୍ଵତନ୍ତ୍ରତା।

प्रश्न 35.
ରବୀନ୍ଦ୍ର, ମଧୁରଂ, ଗାନଂ, ଅତନୋତୁ, ଦେଶଃ, ଜନ୍ମ।
उत्तर:
ରବୀନ୍ଦ୍ର, ମଧୁରଂ, ଗାନଂ, ଦେଶଃ, ଜନ୍ମ।

प्रश्न 36.
ମନୁଜାଃ, ସର୍ବେ, ସହୋଦରା, ବିହଙ୍ଗା, ପ୍ରବର୍ତତେ, ଧର୍ମ ।
उत्तर:
ମନୁଜାଃ, ସର୍ବେ, ସହୋଦରା, ବିହଙ୍ଗା, ଧର୍ମ୍ଯ ।

प्रश्न 37.
ମନୋଜଃ, ଭବତି, ବାୟୁ, ପରିବେଶ, ମାତା, ଇୟମ୍ ।
उत्तर:
ମନୋଜଃ, ବାୟୁ, ପରିବେଶ, ମାତା, ଇୟମ୍।

प्रश्न 38.
ଇୟମ୍, କଃ, ବାୟୁ, ଜୀବା, ମେଘା, ପୂଚ୍ଛତି ।
उत्तर:
ଇୟମ୍, କଃ, ବାୟୁ, ଜୀବା, ମେଘା ।

प्रश्न 39.
ମେଘା, ବୃକ୍ଷା, ମାତା, ଭବତି, ବୃଦ୍ଧି, ରମା ।
उत्तर:
ମେଘା, ବୃକ୍ଷା, ମାତା, ବୃଦ୍ଧି, ରମା ।

प्रश्न 40.
ଦେଶଃ, ଏଷା, ପୁତ୍ର, କଥୟତି, ବାୟୁ, ସ୍ୱସାରଃ ।
उत्तर:
ଦେଶଃ, ଏଷା, ପୁନଃ, ବାୟୁ, ସ୍ଵରଃ ।

प्रश्न 41.
ସ୍ୱ, ସ୍ଵସା, ଦୁହିତା, କରୋତି, ପର୍ବତଃ, ମେଘା ।
उत्तर:
ସ, ସ୍ଵସା, ଦୁହିତା, ପର୍ବତଃ, ମେଘା ।

प्रश्न 42. ଜନଃ, ଜ୍ୟେଷ୍ଠା, ଶ୍ରେଷ୍ଠ, ଭବନ୍ତି,ଏଷା, ବାଳ ।
उत्तर:
ଜନଃ, ଜ୍ୟେଷ୍ଠା, ଶ୍ଳେଷ୍ମା, ଏଷା, ବାଜଃ ।

प्रश्न 43.
ବୃକ୍ଷ, ଜୀବା, ମେଘା, ଭ୍ରମତି, ମନୋଜଃ, ଇୟମ୍ ।
उत्तर:
ବୃକ୍ଷ, ଜୀବା, ମେଘା, ମନୋଜଃ, ଇୟମ୍ ।

प्रश्न 44.
ନିର୍ମାଣମ୍, ଅହମ୍, ଭବିଷ୍ୟସି, ଦର୍ପଣମ୍, ଚିହ୍ନମ, ଏଷ ।
उत्तर:
ନିର୍ମାଣମ୍, ଅହମ୍, ଦର୍ପଣମ୍, ଚିହ୍ନମ, ଏଷ ।

प्रश्न 45.
ଲୋକା, ନୀତିଃ, ମତଃ, ଭରି, ଶତିଃ, କୃତବାନ୍ ।
उत्तर:
ଲୋକା, ନୀତିଃ, ମତିଃ, ଭଲ୍ଲି, ଶ ।

प्रश्न 46.
ପାଦଃ, ଦର୍ଶକଃ, ଏକା, କୁର୍ଯା, ପୁତ୍ର, ସଫଳ ।
उत्तर:
ପାଦଃ, ଏକା, ଦର୍ଶକଃ, ପୁନଃ, ସଫଳ ।

प्रश्न 47.
ମୂର୍ଖ, ସର୍ବେ, ମାତରଃ, ଶିଶୁ, ଅହମ୍, ପ୍ରାପ୍ତବାନ।
उत्तर:
ମୂର୍ଖ, ସର୍ବେ, ମାତରଃ, ଶିଶୁ, ଅହଂ ।

प्रश्न 48.
ଉଜଃ, ପତେ, ଯନ୍ତ୍ର, ବଚନମ୍, ତେ, କଃ ।
उत्तर:
ଉଚ୍ଚା, ଯନ୍‌ମ, ବଚନ, ତେ, କଃ ।

प्रश्न 49.
ଏତତ୍ କୌଟିଲ୍ୟ, ନେତ୍ରୀ, ମଙ୍ଗଳ, ପଶ୍ୟ, ମାତୃଭୂମି ।
उत्तर:
ଏତତ୍, କୌଟିଲ୍ୟ, ନେତ୍ରୀ, ମଙ୍ଗଳଂ, ମାତୃଭୂମି ।

प्रश्न 50.
ମାତରଃ, ଦୁହିତରଃ, ବାୟୁ, ଯାତି, କଃ, ମାତା ।
उत्तर:
ମାତରଃ, ଦୁହିତରଃ, ବାୟୁ, କଃ, ମାତା ।

प्रश्न 51.
ମାତରଃ, ରାମଃ, ମନୋଜଃ, କରୋତି, ବୟମ୍, ଅହମ୍ ।
उत्तर:
ମାତରଃ, ରାମଃ, ମନୋଜଃ, ବୟମ୍, ଅହମ୍ ।

प्रश्न 52.
ଭ୍ରମତି, ପରିବେଶ, ଜଳମ୍, ଗଗନମ୍, ଭୂମି, ହାଃ ।
उत्तर:
ପରିବେଶ, ଜଳମ୍ବ, ଗଗନମ, ଭୂମି, ଡଃ ।

प्रश्न 53.
ଯାତ୍ରା, ଦୁହିତା, ଦୁହିତରଃ, ନନାନ୍ଦା, କରୋତି, ସ୍ଵସା ।
उत्तर:
ଯାତ୍ରା, ଦୁହିତା, ଦୁହିତରଃ, ନନାନ୍ଦା, ସ୍ଵସା ।

प्रश्न 54.
ବଂଶଃ, ଚନ୍ଦ୍ରଗୁପ୍ତା, ରାମାୟଣମ୍, ବାକ୍ୟ, ସ୍ମରତି, ମଧୁ ।
उत्तर:
ବଂଶ, ଚନ୍ଦ୍ରଗୁପ୍ତ, ରାମାୟଣମ୍, ବାକ୍ୟ, ମଧୁ।

प्रश्न 55.
ରାଷ୍ଟ୍ରମ, ପ୍ରବହତି, ବିମଳା, ଗଙ୍ଗା, ବେଦଃ, ପବିତ୍ରମ୍ |
उत्तर:
ରାଷ୍ଟ୍ରମ, ବିମଳା, ଗଙ୍ଗା, ବେଦଃ, ପବିତ୍ରମ୍ ।

प्रश्न 56.
ପୁନଃ, ମାତରଃ, ଅହମ୍, ବୟମ୍, ଫଳମ୍ ପୃଚ୍ଛତି ।
उत्तर:
ପୁନଃ, ମାତରଃ, ଅହମ୍, ବୟମ୍, ଫଳମ୍ ।

प्रश्न 57.
ମାତା, ଭୂମି, ଭବତି, ଗଗନମ, ପରିବେଶଃ, ବୃକ୍ଷା ।
उत्तर:
ମାତା, ଭୂମି, ଗଗନମ, ପରିବେଶଃ, ବୃକ୍ଷା ।

प्रश्न 58.
ଏକା, ପୁତ୍ର, ଭବୋ, ବଧୂର, ବାଳକଃ, ପ୍ରୟାସ ।
उत्तर:
ଏକା, ପୁନଃ, ବଧୂରଃ, ବାଳକ, ପ୍ରୟାତଃ ।

प्रश्न 59.
କ୍ରନ୍ଦସି, ଚାଣକ୍ୟ, ଶିଶୁ, ପୁଂ, ହସ୍ତ, ମଗଧଃ ।
उत्तर:
ଚାଣକ୍ୟ, ଶିଶୁ, ବଂ, ହସ୍ତୀ, ମଗଧଃ ।

प्रश्न 60.
ଅସ୍ଥି, ମମ, ନଦୀ, ପ୍ରଜାଃ, ନରେଶଃ, ଗ୍ରାମାଧୀଶଃ ।
उत्तर:
ମମ, ନଦୀ, ପ୍ରଜାଃ, ନରେଶଃ, ଗ୍ରାମାଧୀଶଃ ।

प्रश्न 61.
ସା, କୃଷ୍ଣବହିଃ, ଈଶ୍ୱରଃ, ସୁନ୍ଦରଃ, ଅସୁନ୍ଦରା, ଭବତି ।
उत्तर:
ସା, କୃଷ୍ଣବର୍ଶୀ, ଈଶ୍ୱରଃ, ସୁନ୍ଦରଃ, ଅସୁନ୍ଦରଃ ।

प्रश्न 62.
ଈର୍ଷା, ଆଗଛତି, ସ, ଗାନମ୍, ନେତ୍ରମ, ତୃପ୍ତି ।
उत्तर:
ଈର୍ଷା, ସା, ଗାନମ୍, ନେତ୍ରମ୍, ତୃପ୍ତି ।

प्रश्न 63.
ସୁଙ୍ଖ, ଦୁଃଖ, ଆସୀତ୍ବ, ମିତ୍ର, ଫଳ, ବନମ୍ ।
उत्तर:
ସୁଖ, ଦୁଃଖ, ମିତ୍ର, ଫଳ, ବନମ୍।

प्रश्न 64.
ସର୍ବା, ଅଭବତ୍, ଭବାନ୍, ସୂତ୍ର, ଛିନ୍ନମ୍, ଶୀଘ୍ରମ୍ ।
उत्तर:
ସର୍ବା, ଭବାନ୍, ସୂତ୍ର, ଛିନ୍ନମ, ଶୀଘ୍ରମ୍ ।

प्रश्न 65.
ପିତା, ତେ, ବୟମ୍, ଭବତି, ବୃକ୍ଷ ।
उत्तर:
ପିତା, ତେ, ବୟମ୍, ବୃକ୍ଷ ।

प्रश्न 66.
ଭବତି, କୋକିଳ, ଶୁକ, କୃପା, ପରିବାରଃ, ସୁବର୍ଷବର୍ଷ ।
उत्तर:
କୋକିଳ, ଶୁକଃ, କୃପା, ପରିବାରଃ, ସୁବର୍ଣ୍ଣବହିଃ ।

प्रश्न 67.
ବ୍ୟାଧଃ, ପିଞ୍ଜରା, ଅହଂ, ବଦତି, ସୃଷ୍ଟି, ମନଃ ।
उत्तर:
ବ୍ୟାଧଃ, ପିଞ୍ଜରା, ଅହଂ, ସୃଷ୍ଟି, ମନଃ ।

प्रश्न 68.
ଯନଂ, ସୂତ୍ର, ବନ୍ଧ, କାକା, ଚଞ୍ଚୁ, ଅଭବନ୍।
उत्तर:
ଯନଂ, ସୂତ୍ର, ବନ୍ଧ୍ୟା, କାକା, ଚଞ୍ଚୁ

प्रश्न 69.
ବଟବୃକ୍ଷ, ଏକ, ନୂତନଃ, ଶାବକ, ସା, ଅଛି ।
उत्तर:
ବଟବୃକ୍ଷ, ଏକ, ନୂତନଃ, ଶାବୟଃ, ସା।

वाक्यगठनम् (ବାକ୍ୟଗଠନମ୍)

• ଇଣ୍ଡିଂ – (ଇଏ) ଇୟଂ ମମ ଜନନୀ।
• ପ୍ରତିଦିନ – (ପ୍ରତିଦିନ) ପ୍ରତିଦିନଂ ପାଠ୍ୟ ପଠ।
• ଏକଦା – (ଥରେ) ଏକଦା ତତ୍ର ବନମ୍ ଆସୀତ୍
• ସହ – (ସହିତ) ମାତ୍ରା ସହ ମନୋଜଃ ଭ୍ରମତି ।
• ତଦା – (ସେତେବେଳେ) ତଦା ମାତ୍ରେ ନିବେଦୟତି।
• କୃପୟା – (ଦୟାକରି) କୃପୟା ବଦତୁ।
• ପରିତଃ – (ଚାରିପଟେ) ଅମ୍ଳାନ୍ ପରିତଃ ଯଃ ଦୃଶ୍ୟମାନଃ ଅସ୍ତି ଡଃ ପରିବେଶଃ ।
• ପୁନଃ – (ପୁଣି) ପୁନଃ ପୁନଃ ପୃଚ୍ଛତି।
• ଭବତି – (ହୁଏ) ଭୂମି ଦୂଷିତା ଭବତି ।
• କୁର୍ମ – (କରିବା) ବୃୟଂ ବୃକ୍ଷଣା ରୋପଣଂ କୁର୍ମା।
• ତହିଁ – (ତେବେ) ତହିଁ ପରିବେଶଃ ସୁରକ୍ଷିତଃ ଭବେତ୍।
• ବିଶ୍ଵାସ – (ବିଶ୍ଵାସ) ମାତରି ତଥ୍ୟ ବିଶ୍ୱାସ ଅସ୍ତି।
• ଇତି – (ବୋଲି) ଇତି ଡଃ ଶପଥ୍ୟ ନୟତି ।
• ଆନନ୍ଦେନ – ( ଖୁସିରେ) ମାତା ଆନନ୍ଦେନ ଆଲିଙ୍ଗତି।
• ରକ୍ଷତି – (ରକ୍ଷାକରେ) ବୃକ୍ଷ ରକ୍ଷତି ରକ୍ଷିତଃ ।
•  ସୂୟଂ – (ତୁମ୍ଭେମାନେ) ପୂୟଂ ସର୍ବେ ପଠତ।
• ଛାତ୍ରା – (ଛାତ୍ରମାନେ) ଛାତ୍ରା ପାଠ୍ୟ ପଠନ୍ତୁ ।
• ଆସୀତ୍ – (ଥିଲେ) ସ୍ୱୀ ରାଜା ଆସୀତ୍।
• ଆଗଳ୍ପ – (ଆସ) ତୁମ ଅତ୍ର ଆଗଛ ।
• ସମ୍ୟକ୍ – (ଭଲ) ଅହଂ ସମ୍ୟକ୍ ପଠାମି।
• ଅଧୂକମ୍ – (ବେଶି) ତୁମ୍ ଅଧୂକଂ ଜାନାସି।
• କିନ୍ତୁ – (କିନ୍ତୁ) କିନ୍ତୁ ମନସି ସୁଙ୍ଖ ନାସ୍ତି ।
• କଥ୍ତବାନ୍ – (କହିଲେ) ଗୁରୁଦେବ କଥ୍ତବାନ୍।
• ଉଚ୍ଚୈଃ – ( ବଡ଼ପାଟିରେ) ଛାତ୍ରା ଉଜଃ ପଠନ୍ତି ।
• ସାଧୁ – (ଧନ୍ୟବାଦ) ସାଧୁ ବାଳକ ସାଧୁ।
• କୃତେ – (ପାଇଁ) ତବ କୃତେ ନାସ୍ତି ।
• ଅତୀବ – (ଅତ୍ୟନ୍ତ) ଅହଂ ତ୍ବ ଅତୀବ ସୁହ୍ୟାମି ।
• ଏବଂ – (ହିଁ) ଏଷ ଏବ ଇଛତି।
• ତୁମ୍ – (ଦେବାକୁ) ପୁରସ୍କାରଂ ଦାତୁମ୍ ଇଚ୍ଛାମି ।
• କିଂ – (କଣ) ବଂ କିଂ ଖାଦସି ?
• ଏଷା – (ଇଏ) ଏଷା ମମ ଜନନୀ।
• ଉପରି – (ଉପରେ) ମମ ଉପରି ବଂ ତଃ ?
• ଅତ୍ର – (ଏଠାରେ) ଅତ୍ର କଃ ତିଷ୍ଠତି ?
• କ୍ରମଶଃ – (କ୍ରମେ) କ୍ରମଶଃ ଛାତ୍ରା ଗଛନ୍ତି ।
• ବହନଃ – (ବହୁତ) ବହବ ଜନଃ ଗଛନ୍ତି ।
• ଅଗ୍ରେ – (ଆଗରେ) ଅଗ୍ରେ ଅଗ୍ରେ ଆଗଛ ।
• ତଦାନୀ – (ସେତେବେଳେ) ତଦାନୀ ତୁମ୍ ଆଗଛ।
• ନୀତବାନ୍ – (ନେଉଥିଲେ) ବିଦ୍ରୋହସ୍ୟ ନେତୃତ୍ୱ ସ୍ୱ ନୀତବାନ୍ ।
• ତତଃ – (ତେଣୁ) ତତଃ ଅହଂ କଥୟାମି ।
• ଅଭବତ୍ – (ହେଲା) ଅଦ୍ୟ ଦୃଷ୍ଟି ଅଭବତ୍।
• ପ୍ରାୟତଃ – (ପ୍ରାୟ) ପ୍ରାୟତଃ ଶିକ୍ଷକ ଅସ୍ଥି ।
• ଜୀବନ୍ତ – (ବଞ୍ଚନ୍ତି) ଜନା କୃଷିଦ୍ୱାରା ଜୀବନ୍ତି ।
• ନାମ – (ନାଆଁ) ତବ ନାମ କିମ୍ ?
• କରୋତି – (କରେ) କୃଷକ କଷ୍ଟ କରୋତି।
• ନମଃ – (ନମସ୍କାର) କୃଷ୍ଣକାୟ ନମଃ ।
• ଏତସ୍ମିନ୍ – (ଏହି) ଏତସ୍ମିନ୍ ଗ୍ରାମେ କୃଷକ ତିଷ୍ଠନ୍ତି ।
• ହଳଂ – (ହଳ) ହଳଂ ନାମ ଲାଙ୍ଗଳମ୍।
• ଏତେନ – (ଏହାଦ୍ଵାରା) ଏତେନ ଭୂମି ଉର୍ବରା ଭବତି ।
• ଅସ୍ଵାକଂ – (ଆମର) ଅସ୍ମାକଂ ଦେଶସ୍ୟ ନାମ ଭାରତମ୍।

• ଭାବନ୍ତି – (ଅଟନ୍ତି) ତେ ଛାତ୍ରା ଭବନ୍ତି ।
• କଶ୍ଚିତ୍ – (କେହିଜଣେ) କଶ୍ଚିତ୍ ବୃଦ୍ଧ ଗଛତି।
• ଅଭବତ୍ – (ହେଲା) ଅଧୁନା ସୃଷ୍ଟି ଅଭବତ୍।
• ଅପଶ୍ୟତ୍ – (ଦେଖିଲା) ସା ଚନ୍ଦ୍ରମ୍ ଅପଶ୍ୟତ୍ ।
• ପୃଷ୍ଟବାନ୍ – (ପଚାରିଲା) ପୁନଃ ଜନକଂ ପୃଷ୍ଟବାନ୍ ।
• ଇତଃ – (ଏଠାରୁ) ଇତଃ କେନ୍ଦ୍ରାପଡ଼ା କିୟତ୍ ଦୂରମ୍ ?
• କିମପି – (କିଛି) ସାଂ କିମପି ନ ବଦତି।
• ପ୍ରାପ୍ତବାନ୍ – (ପାଇଲା) ଡଃ ପୁରସ୍କାରଂ ପ୍ରାପ୍ତବାନ୍।
• ଦୂରେ – (ଦୂରରେ) ଦୂରେ ପର୍ବତଃ ଅସ୍ଥି ।
• ତହିଁ – (ତେବେ) ତହିଁ ତ୍ରିଂ କଥୟ ।
• ପ୍ରାସ୍ମୋତି – (ପାଏ) ଶ୍ରମିକ ପାରିଶ୍ରମିକଂ ପ୍ରାପ୍ନାତି ।
• ଏତସ୍ୟ – (ଏହାର) ଏତସ୍ୟ ପୁସ୍ତକସ୍ୟ ନାମ ଭାଷାଜନନୀ ।
• ହରତି – (ହରଣକରେ) ପ୍ରାକୃତିକଶୋଭା ମନଃ ହରତି ।
• ଏକା – (ଗୋଟିଏ) ଏକା ବାଳିକା ଧାବତି ।
• ଆଗଚ୍ଛତି – (ଆସୁଛି) ସା ଅତ୍ର ଆଗଛତି ।
• ପ୍ରଣମନ୍ତି – (ପ୍ରଣାମ କରନ୍ତି) ଭକ୍ତା ଦେବଂ ପ୍ରଣମନ୍ତି ।
• ଉଭୟତଃ – ( ଉଭୟପଟେ) ମାର୍ଗମ୍ ଉଭୟତଃ ବୃକ୍ଷା ସତ୍ତ୍ୱେ ।
• ମନୋହରମ୍ – (ସୁନ୍ଦର) ତସ୍ୟ ଦୃଶ୍ୟ ମନୋହରମ୍ ।
• ବିନା – (ବିନା) ଧନଂ ବିନା ସୁଙ୍ଖ ନାସ୍ତି ।
• ଦର୍ଶନୀୟମ – (ଦର୍ଶନଯୋଗ୍ୟ) ଏତତ୍ ସର୍ବେଷା ଦର୍ଶନୀୟମ୍ ।
• ଅନ୍ତରେଣ – (ବିନା) ଜଳମ୍ ଅନ୍ତରେଣ ବୟଂ ନ ଜୀବାମଃ ।
• ଭକ୍ତା – ( ଭକ୍ତିରେ) ଭକ୍ତ ଭକ୍ତ ପ୍ରଣମନ୍ତି ।
• କ୍ରମେଣ – (କ୍ରମରେ) ଛାତ୍ରା କ୍ରମେଣ ଆଗଛନ୍ତି ।
• କୁଧତି – (ରାଗୁଛନ୍ତି) ପିତା ପୁତ୍ରାୟ କୃଧତି ।
• ସାକମ୍ – ( ସହିତ) ମୟା ସାକମ୍ ଆଗଛ। .
• ଅଭିତଃ – (ଆଗରେ) ପିତରମ୍ ଅଭିତଃ ସତ୍ୟ ବଦତୁ।
• ବା – (କି) ଙ୍‌ ପଠସି ବା ?
• ନ – (ନାହିଁ) ଅହଂ ନ ପଠାମି।
• ମହତ୍ – (ବଡ଼) ଅତ୍ର ମହତ୍ ଅରଣ୍ୟମ୍ ଆସୀତ୍ ।
• କ୍ରମଶଃ – (କ୍ରମେ) କ୍ରମଶଃ ଜଳ ବଦ୍ଧତେ।
• କୁର୍ବନ୍ତ – (କରନ୍ତି) ଜନଃ କାର୍ଯ୍ୟ କୁର୍ବନ୍ତି ।
• ତେନ – ( ତାହାଦ୍ୱାରା) ତେନ ପରିବାରାନ୍ ପୋଷୟନ୍ତି ।
• ଦ୍ରଷ୍ଟବ୍ୟ – (ଦେଖୁବାଉଚିତ)ଇସ୍ପାତନଗରୀ ଅବଶ୍ୟ ଦ୍ରଷ୍ଟବ୍ୟ।
• ଅବଶ୍ୟମ୍ – (ନିଶ୍ଚୟ) ତୁମ୍ ଅବଶ୍ୟମ୍ ଆଗଛ ।
• ନିବସନ୍ତି – (ରୁହନ୍ତି) ଅତ୍ର ଜନଃ ନିବସନ୍ତି।

• ଚ – (ଏବଂ) ତ୍ୱମେବ ମାତା ଚ ପିତା ତ୍ଵମ୍ ଏବ।
• ଅଭବତ୍ – (ହୋଇଥିଲେ) ଡଃ ପ୍ରଧାନମନ୍ତ୍ରୀ ଅଭବତ୍।
• ପ୍ରାପ୍ତବାନ୍ – (ପାଇଲେ) ଡଃ ପୁରସ୍କାରଂ ପ୍ରାପ୍ତବାନ୍ ।
• ଅନନ୍ତରମ୍ – (ପରେ) ଅନନ୍ତରମ୍ ଆଗଚ୍ଛତୁ।
• ପ୍ରଥମତଃ – (ପ୍ରଥମେ) ପ୍ରଥମତଃ ସ୍ଵଂ ତତ୍ର ଗଛ।
• ତସ୍ୟ – (ତାଙ୍କ) ତଥ୍ୟ ନାମ କିମ୍ ?
• ବାଲ୍ୟାତ୍ – (ପିଲାଦିନୁ) ବାଲ୍ୟାତ୍ ଅହଂ ଦୁଃଖୀ ।
• ପ୍ରଚାରାୟ – (ପ୍ରଚାରପାଇଁ) ସ୍ତ ଧର୍ମସ୍ୟ ପ୍ରଚାରାୟ କାର୍ଯ୍ୟ କରୋତି।
• ଅପି – (ମଧ୍ୟ) ମାତା ଅପି ଅହସତ୍ ।
• ଅତୀବ – (ଅତ୍ୟନ୍ତ) ଅହମ୍ ଅତୀବ ଦୁଃଖୀ ।
• କୃତବାନ୍ – (କରିଥିଲେ) ଡଃ ଦେଶସେବାଂ କୃତବାନ୍
• ଗତଃ – (ଗଲେ) ରାମଃ ବରଂ ଗତଃ ।
• ସମୀପେ – (ପାଖରେ) ଗ୍ରାମସ୍ୟ ସମୀପେ ବନମ୍ ଅଛି ।
• ପ୍ରତିବର୍ଷ – (ପ୍ରତିବର୍ଷ) ପ୍ରତିବର୍ଷମତ୍ର ମେଳା ଭବତି ।
• ନାମ୍ନା – (ନାମରେ) ଅହଂ ନାମ୍ନା ଶୁଭାଶିଷ ।
• ମହାନ୍ – (ବଡ଼) ମହାନ୍ ବଟବୃକ୍ଷ ଅନ୍ତି।
• ସାନନ୍ଦ – (ଆନନ୍ଦରେ) ଡଃ ସାନନ୍ଦ ନିବସତି ।
• ନୟତି – (ନିଏ) ଶାବକ ଜନ୍ମ ନୟତି ।
• ତସ୍ମି – (ତାକୁ) ତସ୍ମି ଭୋଜନଂ ଦଦାତି ।
• କୀଦୃଶ – (କିପରି) ଈଶ୍ଵରସ୍ୟ ପକ୍ଷପାତଃ କୀଦୃଶଃ ?
• ନାସ୍ତି – (ନାହିଁ) ମମ ସ୍ଵତଃ ନାସ୍ତି ।
• ତହିଁ – (ତେବେ) ତହିଁ ତୁମ୍ ଆଗଛ।
• କର୍ତ୍ତୃ – (କରିବାକୁ) ବରଂ ଗର୍ବଂ କର୍ଡିଂ ପାରୟାମଃ ।
• ପ୍ରତିଦିନମ୍ – (ପ୍ରତିଦିନ) ପ୍ରତିଦିନଂ ବ୍ୟାୟାମଂ କୁରୁ।
• ତତ୍ର – (ସେଠାକୁ) ଶୁନଃ ତତ୍ର ଆଗଛତି।
• ତଦା – (ସେତେବେଳେ) ତଦା ତସ୍ୟା ଈର୍ଷା ଆଗଛତି ।
• ତତ୍ – (ତାହା) ତତ୍ ମୟି ନାସ୍ତି ।
• କୃତେ – (ପାଇଁ) ଈଶ୍ଵରସ୍ୟ କୃତେ ଧନ୍ୟବାଦମ୍ ଅର୍ପୟତି ।
• ଏବଂ – (ହି) ମନଃ ଅବ୍ୟବସ୍ଥିତମ୍ ଏବ।
• ସମମ୍ – ( ସହିତ) ପରିବାରେଣ ସମଂ ତିଷ୍ଠତି।
• ନିତ୍ୟ – (ପ୍ରତିଦିନ) ନିତ୍ୟ ପାଠ୍ୟ ପଠ।
• ବରଂ – (ଭଲ) ବରମ୍ ଏକ ଗୁଣୀପୁନଃ ।
• ଦଶତି – (ଦର୍ଶନ କରେ) ସର୍ପ ଦଶତି କାଳେନ ।
• ଶଃ – (ଆସନ୍ତାକାଲି) ଶଃ ତୁମ୍ ଆଗଛ।
• ହ୍ୟୁ – (ଗତକାଲି) ହ୍ୟୁ ପିତା ଆଗଛତ୍।
• କୃତମ୍ – (କରିଛ) କୃତଂ ନ ବା ?
• ନୈବ – (କେବେନୁହେଁ) ନୈବ ତୁଲ୍ୟ କଦାଚନ।

• ଯାତି – (ଯାଏ) ଛାତ୍ର ପାଠଶାଳା ଯାତି ।
• ପ୍ରାସ୍ମୋତି – (ପାଏ) କେବଳଂ ଯଶଃ ପ୍ରାପ୍ଳୁତି ।
• ପଞ୍ଚ – (ପାଞ୍ଚ) ପଞ୍ଚ ଫଳାନି ସନ୍ତି ।
• ସମାର୍ଚ୍ଚରେଡ୍ – (କରଣୀୟ) ପରେରାଂ ନ ସମାଚରେତ୍।
• ମୁଞ୍ଚତି – (ଛାଡେ) ମଳିନବଂ ନ ମୁଞ୍ଚତି ।
• ତି– (ହିଁ) ନଂ ହି ଦୁର୍ଗା ।
• ଆତ୍ମନଃ – (ନିଜର) ଆତ୍ମନଃ ବୁଦ୍ଧି ନାସ୍ତି ।
• ଆଦରେ – (ଗ୍ରହଣ କରେ) ହଂସ କ୍ଷୀରମ୍ ଆଦରେ
• କଷ୍ଟନ – (କୌଣସି) କଣ୍ଟନ ଜନଃ ଆୟାତି ।
• ଆସୀତ୍ – (ଥ୍ଲା) ଡଃ ରାଜା ଆସୀତ୍।
• ଅଭବତ୍ – (ହେଉଥୁଲା) ଡଃ ମୁକ୍ତା ନ ଅଭିବତ୍।
• କେଚନ – (କେତେକ) କେଚନ କାମଃ ଅପଶ୍ୟନ୍।
• କ୍ରମେଣ – (କ୍ରମେ) ଛାତ୍ରା କ୍ରମେଣ ଗଛନ୍ତି ।
• ଅଧ୍ବକଂ – (ବେଶି) ଡଃ ଅଧିକାଂ ଦୁଃଖମ୍ ଅଦଦାତ୍।
• କୃପୟା – (ଦୟାକରି) କୃପୟା ବଦତୁ।
• ଅକରୋତ୍ – (କଲା) କୋକିଳସ୍ୟ ଉପରି ଆକ୍ରମଣମ ଅକରୋତ୍ ।
• ନୂନମ୍‌ – (ନିଶ୍ଚୟ ) ଅହଂ ନୂନଂ ପ୍ରାପ୍‌ସ୍ୟାମି ।
• ଭବାନ୍ – (ଆପଣ) ଭବାନ୍ ନିଷ୍କରୁନଃ ଭବତି।
• କିମର୍ଥମ୍ – (କାହିଁକି) ଭବାନ୍ କିମର୍ଥ୍ୟ ନ ରକ୍ଷତି ?
• ଦୂରମ୍ – (ଦୂର) ଦୂରଂ ଗଛତୁ ଭବାନ୍।
• ଶୀଘ୍ରମ୍ – (ଶୀଘ୍ର) ଶୀଘ୍ରମ୍ ଅତ୍ର ଆଗଛ।
• ଶ୍ରୁତମ୍ – (ଶୁଣାଗଲା) ଘୋରଗର୍ଜନଂ ଶ୍ରୁତମ୍।
• ଅନେକେ – (ଅନେକ) ଅନେକେ ସୈନ୍ୟା ଆହତା
• ଦେହି – (ଦିଅ) ଜଳଂ ଦେହି ।
• ଅତୀବ – (ଅତ୍ୟନ୍ତ) ବ୍ୟବସାୟୀ ଅତୀବ ଦୁଃଖ୍ୟତଃ ।
• ଗତବାନ୍ – (ଗଲେ) ରାମଃ ବରଂ ଗତବାନ୍।
• ରକ୍ଷ – (ରକ୍ଷାକର) ରକ୍ଷ ରକ୍ଷ ମାତରମ୍ ।
• କୁରୁତ – (କର) ଜନସେବାଂ କୁରୁତ।
• ଋତଃ – (ଗଲେ) ପିତା କଟକଂ ଗତଃ ।
• ସତତମ୍ – (ସର୍ବଦା) ମନସା ସତତଂ ସ୍ମରଣୀୟମ୍ ।
• ସର୍ବେ – ( ସମସ୍ତେ) ସର୍ବେ ତତ୍ତ୍ବ ଗଛନ୍ତି ।

• ବହନଃ – (ବହୁତ) ବହବ ଛାତ୍ରା ପଠନ୍ତି ।
• ଅସ୍ତି – (ଅଛି) ସ୍ତମ୍ଭ ଚିକ୍କଶଃ ଅସ୍ଥି ।“
• ଅଧଃ – (ତଳେ) ସ ନୂନମ୍ ଅଧଃ ପତେତ୍ ।
• ତଥାପି – (ତଥାପି) ତଥାପି ଡଃ ନ ପଠତି।
• ଶୁକ୍ଳା – (ଶୁଣି) ଅନ୍ୟତାଂ ବଚନଂ ଶ୍ରୁତ୍ବା ଅଧଃ ପତିତବହିଃ ।
• ପୁତ୍ର – (ହେ ପୁତ୍ର) ପୁତ୍ର ! ପାଠ୍ୟ ପଠ।
• ଭବେ – (ହେବାଉଚିତ) ରଂ ନୂନଂ ସଫଳଂ ଭବେ ।
• ଅତଃ – (ଏଣୁ) ଅତଃ ଡଃ ନ ପଠତି।
• ଅନ୍ୟ – (ଅନ୍ୟମାନେ) ଅନ୍ୟ ନ ଆଗଛନ୍ତି ।
• ଇତି – (ଶେଷ) ଇତି ବାହାଁ ।
• ମାତଃ – (ହେ ମା’) ମାତଃ ! ବଂ କ୍ରନ୍ଦସି ?
• କୀ ଦୃଶମ୍ – (କିପରି) କୀଦୃଶଂ ସୌଭାଗ୍ୟମ୍‌ ?
• କଥମ୍ – (କାହିଁକି) କଣଂ କ୍ରନ୍ଦତି ପୁନଃ ?
• ଜ୍ଞାତବତୀ – (ଜାଣିଲେ) ମାତା ସର୍ବଂ ଜ୍ଞାତବତୀ ।
• ଏଵମ୍ – (ଏହିପରି) ସମାଜେ ଏବଂ ଦୃଶ୍ୟତେ |
• ମଙ୍ଗଳମ୍ – (ମଙ୍ଗଳ) ମାତୃଭୂମେ ମଙ୍ଗଳଂ ଭବିଷ୍ୟତି |
• ଗରୀୟସୀ – (ବଡ଼) ଜନନୀ ଜନ୍ମଭୂମି ଚ ସ୍ବର୍ଗାଦପି ଗରୀୟସୀ ।
• ଭବିଷ୍ୟସି – (ହେବ) ତୁମ୍ ଅମାତ୍ୟ ଭବିଷ୍ୟସି ।
• ହସ୍ତେନ – (ହାତରେ) ଶିଶୁ ହସ୍ତେନ ଖାଦତି ।
• ପଶ୍ୟ – (ଦେଖ) ବଂ ଚନ୍ଦ୍ର ପଶ୍ୟ।
• ବିମଳା – (ନିର୍ମଳ) ଗଙ୍ଗା ବିମଳା ଅଣ୍ଡି।

• ପବିତ୍ରମ୍ – (ପବିତ୍ର) ସଂସ୍କୃତଂ ସଦା ପବିତ୍ରମ୍ ।
• ମଧୁରମ୍ – (ମିଠା) ରବୀନ୍ଦ୍ରଗାନଂ ମଧୁରମ୍ ଅସ୍ତି ।
• ମତମ୍ – (ମତ) ଅତ୍ର ସମସ୍ତଂ ମତଂ ସମାନମ୍ ।
• କାପି – (କିଛିହେଲେ) କାପି ବାଧା ନାସ୍ତି ।