CHSE Odisha Class 11 Math Solutions Chapter 9 Binomial Theorem Ex 9(b)

Odisha State Board CHSE Odisha Class 11 Math Solutions Chapter 9 Binomial Theorem Ex 9(b) Textbook Exercise Questions and Answers.

CHSE Odisha Class 11 Math Solutions Chapter 9 Binomial Theorem Exercise 9(b)

Question 1.
²ⁿC₀ + ²ⁿC₂ + …… + ²ⁿC_2n = 2^2n-1 and ²ⁿC₁ + ²ⁿC₃ + ….. + ²ⁿC_2n-1 = 2^2n-1
Solution:
We know that
(1 + x)²ⁿ = ²ⁿC₀ + ²ⁿC₁x + ²ⁿC₂x² + …..+ ²ⁿC_2nxⁿ …(1)
Putting x = 1
We get putting x = – 1  we get
∴ (²ⁿC₀ + ²ⁿC₂ + ²ⁿC₄ + ….. + ²ⁿC_2n) – (²ⁿC₁ + ²ⁿC₃ + ….. + ²ⁿC_2n-1) = 0
∴ ²ⁿC₀ + ²ⁿC₂ + ….. + ²ⁿC_2n
= ²ⁿC₁ + ²ⁿC₃ + ….. + ²ⁿC_2n-1
= \(\frac{2^{2 n}}{2}\) = 2^2n-1

Question 2.
Find the sum of
(i) C₁ + ²C₂ + ³C₃ + ….. + ⁿC_n
Solution:
C₁ + ²C₂ + ³C₃ + ….. + ⁿC_n

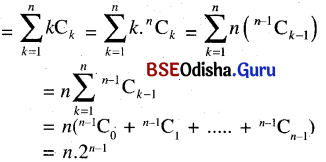
(ii) C₀ + ²C₁ + ³C₂ + ….. + ⁽ⁿ⁺¹⁾C_n Hint: write (C₀ + C₁ + ….. + C_n) + (C₁ + ²C₂ + ….. + ⁿC_n) use (5) and exercise 1.

Question 3.
Compute \(\frac{(1+k)\left(1+\frac{k}{2}\right) \ldots\left(1+\frac{k}{n}\right)}{(1+n)\left(1+\frac{n}{2}\right) \ldots\left(1+\frac{n}{k}\right)}\)
Solution:

Question 4.
Show that
(i) C₀C₁ + C₁C₂ + C₂C₃ + ….. + C_n-1C_n = \(\frac{(2 n) !}{(n-1) !(n+1) !}\)
Solution:

(ii) C₀C_r + C₁C_r+1 + C₂C_r+2 + ….. + C_n-rC_n = \(\frac{(2 n) !}{(n-r) !(n+r) !}\) Hint : Proceed as in Example 13. Compare the coefficient of a^n-1 to get (i) and the coefficient of a^n-r to get (ii)
Solution:


∴ C₀C_r + C₁C_r+1 + C₂C_r+2 + ….. + C_n-rC_n = \(\frac{(2 n) !}{(n-r) !(n+r) !}\)

(iii) 3C₀ – 8C₁ + 13C₂ – 18C₃ + ….. + (n+1)^th term = 0
Solution:
3C₀ – 8C₁ + 13C₂ – 18C₃ + ….. + (n+1)^th term
= 3C₀ – (5 + 3)C₁ + (10 + 3) C₂ – (15 + 3) C₃ + …
= 3(C₀ – C₁ + C₂ …) + 5 (- C₁ + 2C₂ – 3C₃ …..)
But (1 – x)ⁿ =C₀ – C₁x + C₂x² – C₃x³ + … + (-1)ⁿ xⁿC_n … (1)
Putting x = 1 we get
C₀ – C₁ + C₂ ….. + (-1)ⁿC_n
and differentiating (1) we get n(1 – x)^n-1 (- 1)
= – C₁ + 2C₂x – 3C₃x² +…..
Putting x = 1 we get
– C₁ + 2C₂ – 3C₃ + ….. = 0
∴ 3C0 – 8C1 +13C2 …… (n+1) terms = 0

(iv) C₀n² + C₁(2 – n)² +C₂(4 – n)² + ….. + C_n(2n – n)² = n.2ⁿ
Solution:
C₀n² + C₁(2 – n)² +C₂(4 – n)² + ….. + C_n(2n – n)² = n.2ⁿ
= n²(C₀ + C₁ + + C_n) + (2²C₁ + 4²C₂ + ….. + (2n)²C_n) – 4n (C₁ + 2C₂ + 3C₃ + ….+ nC_n)
= n² . 2ⁿ + 4n(n+l)2^n-2 – 4 n . n . 2^n-1
= 2^n-1 (2n² + 2n² + 2n – 4n²)
= 2n . 2^n-1 = n2ⁿ

(v) C₀ – 2C₁ +3C₂ + ….. + (-1)ⁿ(n+1)C_n = 0
Solution:

(vi) C₀ – 3C₁ +5C₂ + ….. + (2n+1)C_n = (n+1)²ⁿ
Solution:

Question 5.
Find the sum of the following :
(i) C₁ – 2C₂ + 3C₃ + ….. + n(-1)^n-1C_n 
Solution:

(ii) 1.2C₂ + 2.3C₃ + ….. + (n-1)nC_n
Solution:

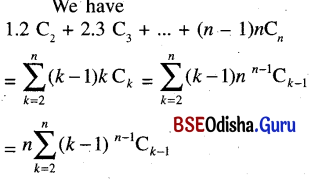
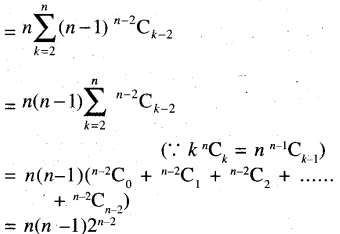
(iii) C₁ + 2²C₂ + 3²C₃ + ….. + n²C_n
Solution:

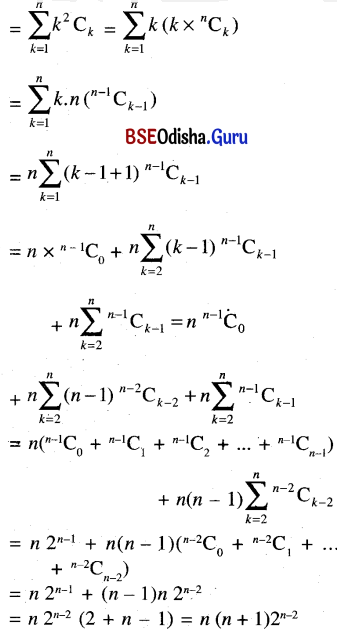
(vi) C₀ – \(\frac{1}{2}\)C₁ + \(\frac{1}{3}\)C₂ + ….. + (-1)ⁿ \(\frac{1}{n+1}\)C_n
Solution:

Question 6.
Show that
(i) C₁² + 2C₂² +3C₃² + ….. + nC_n² = \(\frac{(2 n-1) !}{\{(n-1) !\}^2}\)
Solution:

(ii) C₂ + 2C₃ + 3C₄ + ….. + (n – 1)C_n = 1 + (n – 2)2^n-1
Solution:

Question 7.
C₁ – \(\frac{1}{2}\)C₂ + \(\frac{1}{3}\)C₃ + ….. +(-1)ⁿ⁺¹ \(\frac{1}{n}\)C_n = 1 + \(\frac{1}{2}\) + …. + \(\frac{1}{n}\)
Solution:

Question 8.
C₀C₁ + C₁C₂ + ….. + C_n-1C_n = \(\frac{2^n \cdot n \cdot 1 \cdot 3 \cdot 5 \ldots(2 n-1)}{(n+1)}\)
Solution:

Question 9.
The sum \(\frac{1}{1 ! 9 !}+\frac{1}{3 ! 7 !}+\ldots+\frac{1}{7 ! 3 !}+\frac{1}{9 ! 1 !}\) can be written in the form \(\frac{2^a}{b !}\) find a and b.
Solution:

Question 10.
(a) Using binominal theorem show that 1⁹⁹ + 2⁹⁹ + 3⁹⁹ + 4⁹⁹ + 5⁹⁹ is divisible by 5 (Regional Mathematical Olympiad, Orissa – 1987)
Solution:
1⁹⁹ + 2⁹⁹ + 3⁹⁹ + 4⁹⁹ + 5⁹⁹
= 1 + (5 – 3)⁹⁹ + 3⁹⁹ + (5 – 1)⁹⁹ + 5⁹⁹
= 1 + (5⁹⁹ – ⁹⁹C₁5⁹⁸.3¹ + ⁹⁹C₂5⁹⁷.3² – …3⁹⁹) + 3⁹⁹ – (1 – ⁹⁹C₁5¹ + ⁹⁹C₂5² – …  5⁹⁹) + 5⁹⁹
= (3 × 5⁹⁹ – ⁹⁹C₁5⁹⁸.3¹ + ⁹⁹C₂5⁹⁷.3² – ….. + ⁹⁹C⁹⁸5¹.3⁹⁸) + (⁹⁹C₁5¹ – ⁹⁹C₂5² + …. – ⁹⁹C₉₈5⁹⁸) ….(1) which is divisible by 5 as each term is a multiple of 5.

(b) Using the same procedure show that 1⁹⁹ + 2⁹⁹ + 3⁹⁹ + 4⁹⁹ + 5⁹⁹ is also divisible by 3 so that it is actually divisible by 15.
Solution:
From Eqn. (1) above, it is clear that each term within the 1st bracket is divisible by 3 and the terms in the 2nd bracket are divisible by 99 and hence divisible by 3.
Each term in Eqn. (1) is divisible by 3. As it is divisible by 3 and 5, it is divisible by 3 × 5 = 15