Odisha State Board Elements of Mathematics Class 11 CHSE Odisha Solutions Chapter 10 Sequences and Series Ex 10(b) Textbook Exercise Questions and Answers.
CHSE Odisha Class 11 Math Solutions Chapter 10 Sequences and Series Exercise 10(b)
Question 1.
Expand in ascending power of x.
(i) 2x
Solution:
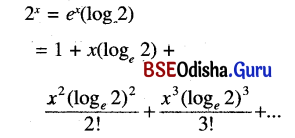
(ii) cos x
Solution:

(iii) sin x
Solution:

(iv) \(\frac{x e^{7 x}-e^{-x}}{e^{3 x}}\)
Solution:

(v) \(\boldsymbol{e}^{e^x}\) up to the term containing x4
Solution:
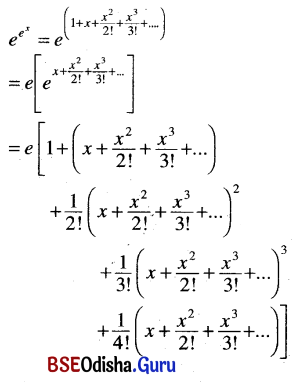
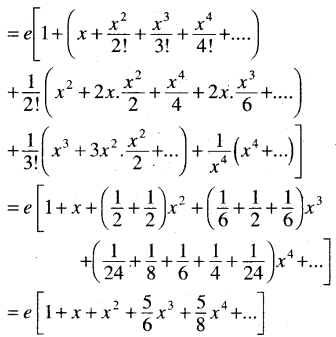
![]()
Question 2.
If x = y + \(\frac{y^2}{2 !}+\frac{y^3}{3 !}\) + ….. then show that y = x – \(\frac{x^2}{2}+\frac{x^3}{3}+\frac{x^4}{4}\) +….
Solution:

Question 3.
Find the value of \(x^2-y^2+\frac{1}{2 !}\left(x^4-y^4\right)+\frac{1}{3 !}\left(x^6-y^6\right)\) + ….
Solution:

Question 4.
Show that
(i) 2\(\left(\frac{1}{3 !}+\frac{2}{5 !}+\frac{3}{7 !}+\ldots\right)=\frac{1}{e}\)
Solution:
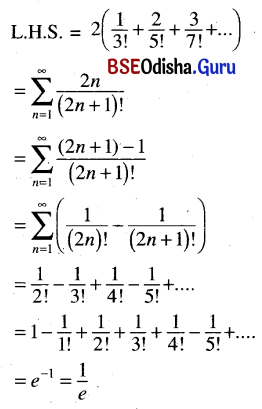
(ii) \(\frac{9}{1 !}+\frac{19}{2 !}+\frac{35}{3 !}+\frac{57}{4 !}+\frac{85}{5 !}\) + …. = 12e – 5
Solution:

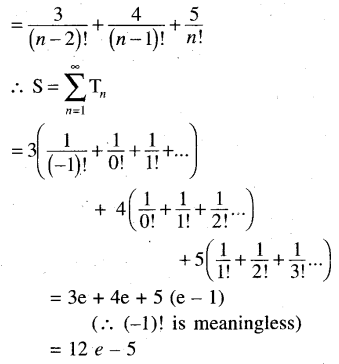
(iii) \(1+\frac{1+3}{2 !}+\frac{1+3+3^2}{3 !}+\ldots=\frac{1}{2}\left(e^3-e\right)\)
Solution:

(iv) \(\frac{1.3}{1 !}+\frac{2.4}{2 !}+\frac{3.5}{3 !}+\frac{4.6}{4 !}\) + …. = 4e
Solution:
tn for L.H.S.
= \(\frac{n(n+2)}{n !}=\frac{n^2+2 n}{n !}\)

(v) \(\frac{1}{1.2}+\frac{1.3}{1.2 .3 .4}+\frac{1.3 .5}{1.2 .3 .4 .5 .6}\) + …. = √e – 1
Solution:

![]()
Question 5.
Prove that
(i) loge(1 + 3x + 2x2) = 3x – \(\frac{5}{2}\)x2 + \(\frac{9}{3}\)x3 – \(\frac{17}{4}\)x4 + …..,|x| < \(\frac{1}{2}\)
Solution:

(ii) loge(n + 1) – loge(n – 1) = 2 \(\left[\frac{1}{n}+\frac{1}{3 n^3}+\frac{1}{5 n^5}+\ldots\right]\)
Solution:
There is a printing mistake in the question. The correct question is loge(n + 1) – loge(n – 1)
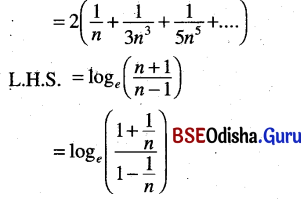
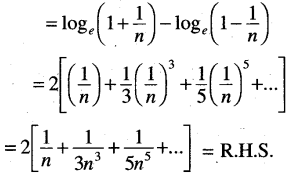
(iii) loge(n + 1) – logen = 2 \(\left[\frac{1}{2 n+1}+\frac{1}{3(2 n+1)^3}+\frac{1}{5(2 n+1)^5}+\ldots\right]\)
Solution:
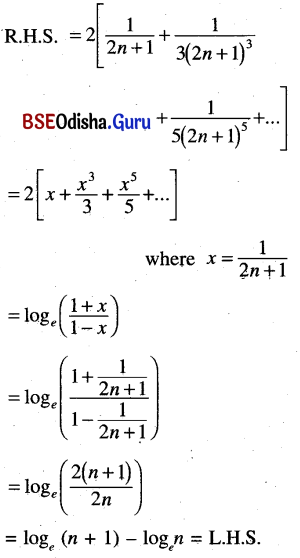
(iv) logem – logen = \(\frac{m-n}{m}+\frac{1}{2}\left(\frac{m-n}{m}\right)^2\)
Solution:
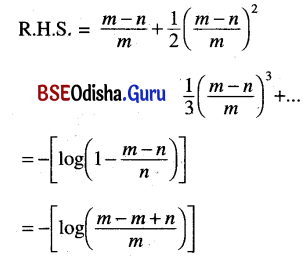
= – [log n – log m]
= log m – log n = L.H.S.
(v) logea – logeb = \(2\left[\frac{a-b}{a+b}+\frac{1}{3}\left(\frac{a-b}{a+b}\right)^3\right.\) \(\left.+\frac{1}{5}\left(\frac{a-b}{a+b}\right)^5+\ldots\right], a>b\)
Solution:
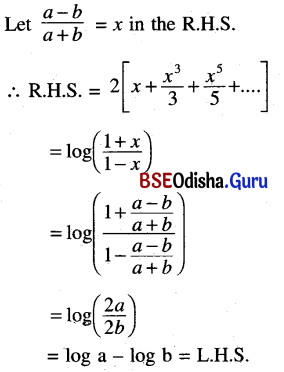
(vi) logen = \(\frac{n-1}{n+1}+\frac{1}{2} \cdot \frac{n^2-1}{(n+1)^2}\)\(+\frac{1}{3} \cdot \frac{n^2-1}{(n+1)^3}\) + …..
Solution:

