CHSE Odisha Class 12 Math Solutions Chapter 8 Application of Derivatives Additional Exercise

Odisha State Board CHSE Odisha Class 12 Math Solutions Chapter 8 Application of Derivatives Additional Exercise Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 8 Application of Derivatives Additional Exercise

(A) Multiple Choice Questions (Mcqs) With Answers

Question 1.
Write the maximum value of the function y = x⁵ in the interval [1, 5].
(a) 125
(b) 3125
(c) 625
(d) 225
Solution:
(b) 3125

Question 2.
Differentiate sin^-1 (cos x) with respect to x.
(a) -1
(b) 0
(c) 1
(d) None of the above
Solution:
(a) -1

Question 3.
Write the equation of the tangent to the curve y = |x| at the point (-2, 2).
(a) 2x + 2y = 0
(b) 2x + y = 0
(c) x + y = 1
(d) x + y = 0
Solution:
(d) x + y = 0

Question 4.
Write the value of \(\frac{d}{d x}\)(sin x)
(a) tan x
(b) sin x
(c) cos x
(d) cot x
Solution:
(c) cos x

Question 5.
Write the value of \(\frac{d}{d x}\)(cos x)
(a) cos x
(b) -sin x
(c) sin x
(d) cot x
Solution:
(b) -sin x

Question 6.
Write the value of \(\frac{d}{d x}\)(tan x)
(a) tan x
(b) sec² x
(c) sin x
(d) cot x
Solution:
(c) sin x

Question 7.
Write the value of \(\frac{d}{d x}\)(sec x)
(a) sin x cos x
(b) sin x tan x
(c) cot x tan x
(d) sec x tan x
Solution:
(d) sec x tan x

Question 8.
Write the value of \(\frac{d}{d x}\)(cot x) = -cosec²x
(a) -sin² x
(b) -cos² x
(c) -cosec² x
(d) -tan² x
Solution:
(c) -cosec² x

Question 9.
Write the value of \(\frac{d}{d x}\)(cosec x)
(a) -cosec x cot x
(b) -sin x cot x
(c) -tan x cot x
(d) -cos x cot x
Solution:
(a) -cosec x cot x

Question 10.
Write the value of \(\frac{d}{d x}\)(e^x) = ex
(a) e
(b) x
(c) e^x
(d) e^2x
Solution:
(c) e^x

Question 11.
Write the value of \(\frac{d}{d x}\)(a^x)
(a) a^2x log a
(b) a^x log a
(c) log a
(d) log a^x
Solution:
(b) a^x log a

Question 12.
Write the value of \(\frac{d}{d x}\)(log x)
(a) x
(b) \(\frac{1}{2 x}\)
(c) \(\frac{1}{x^2}\)
(d) \(\frac{1}{x}\)
Solution:
(d) \(\frac{1}{x}\)

Question 13.
Write the value of \(\frac{d}{d x}\)(log_a x)
(a) \(\frac{x}{\log a}\)
(b) \(\frac{1}{x \log a}\)
(c) \(\frac{1}{x^2 \log a}\)
(d) \(\frac{1}{2 x^2 \log a}\)
Solution:
(b) \(\frac{1}{x \log a}\)

Question 14.
Write the value of \(\frac{d}{d x}\)(cot^-1 x) = \(\frac{-1}{1+x^2}\)
(a) \(\frac{1}{1-x^2}\)
(b) \(\frac{1}{1+x^2}\)
(c) \(\frac{-1}{1-x^2}\)
(d) \(\frac{-1}{1+x^2}\)
Solution:
(d) \(\frac{-1}{1+x^2}\)

Question 15.
Find \(\frac{\mathrm{dy}}{\mathrm{dx}}\) for √x + √y = √c.
(a) \(\frac{\sqrt{y}}{\sqrt{x}}\)
(b) \(\frac{\sqrt{x}}{\sqrt{y}}\)
(c) –\(\frac{\sqrt{y}}{\sqrt{x}}\)
(d) –\(\frac{\sqrt{x}}{\sqrt{y}}\)
Solution:
(c) –\(\frac{\sqrt{y}}{\sqrt{x}}\)

Question 16.
If f(x) = \(\log _{x^2}\) (log x), then find f'(e).
(a) \(\frac{1}{e}\)
(b) \(\frac{1}{\mathrm{e}^2}\)
(c) \(\frac{1}{2 \mathrm{e}}\)
(d) \(\frac{2}{\mathrm{e}}\)
Solution:
(c) \(\frac{1}{2 \mathrm{e}}\)

Question 17.
If y = \(\sqrt{\sin x+y}\), then what is \(\frac{\mathrm{dy}}{\mathrm{dx}}\)?
(a) \(\frac{\cos x}{2 y+1}\)
(b) \(\frac{\cos x}{2 y-1}\)
(c) \(\frac{\sin x}{2 y-1}\)
(d) \(\frac{\sin x}{2 y+1}\)
Solution:
(b) \(\frac{\cos x}{2 y-1}\)

Question 18.
If y = 10^x and z = 100^x/2 then find \(\frac{\mathrm{d}}{\mathrm{dx}}\left(\frac{\mathrm{y}^2}{\mathrm{z}}\right)\)
(a) 10^x log 10
(b) 10^2x log 10
(c) x log 10
(d) x² log 10
Solution:
(a) 10^x log 10

Question 19.
Find the differential of y = sin² x.
(a) 2sinx cot x dx
(b) 2sinx tan x dx
(c) 2sinx cosx dx
(d) 2cosx sinx dx
Solution:
(c) 2sinx cosx dx

Question 20.
Differentiate \(\sqrt{\sin \sqrt{x}}\)
(a) \(\frac{\cos \sqrt{x}}{4 \sqrt{x \sin \sqrt{x}}}\)
(b) \(\frac{\sin x}{4 \sqrt{x \cos \sqrt{x}}}\)
(c) \(\frac{\sin \sqrt{x}}{4 \sqrt{x \cos \sqrt{x}}}\)
(d) \(\frac{\sin x}{4 \sqrt{x \cos x}}\)
Solution:
(a) \(\frac{\cos \sqrt{x}}{4 \sqrt{x \sin \sqrt{x}}}\)

Question 21.
If f(x) = [tan² x], what is f'(0)?
(a) 0
(b) 1
(c) -1
(d) None of the above
Solution:
(a) 0

Question 22.
If xy = e^x-y then find \(\frac{\mathrm{dy}}{\mathrm{dx}}\).
(a) \(\frac{\log x}{(1-\log x)^2}\)
(b) \(\frac{\log x}{(1+\log x)^2}\)
(c) \(\frac{\log x}{(1+\log x)}\)
(d) \(\frac{\log x}{(1-\log x)}\)
Solution:
(b) \(\frac{\log x}{(1+\log x)^2}\)

Question 23.
Find \(\frac{\mathrm{dy}}{\mathrm{dx}}\) if y = cot^-1\(\left(\frac{1+\cos x}{1-\cos x}\right)^{\frac{1}{2}}\)
(a) 0
(b) \(\frac{1}{2}\)
(c) 1
(d) \(\frac{1}{4}\)
Solution:
(b) \(\frac{1}{2}\)

Question 24.
Find the derivative of sin x° w.r.t. x.
(a) \(\frac{\pi}{90}\) cos x°
(b) π cos x°
(c) \(\frac{\pi}{180}\) cos x°
(d) π sin x°
Solution:
(c) \(\frac{\pi}{180}\) cos x°

Question 25.
The least value of a such that f(x) = x² + ax + 1 is strictly increasing on (1, 2) is
(a) -2
(b) -4
(c) 2
(d) 4
Solution:
(a) -2

Question 26.
If y = sec^-1\(\left(\frac{x+1}{x-1}\right)\) + sin^-1\(\left(\frac{x-1}{x+1}\right)\) then find \(\frac{\mathrm{dy}}{\mathrm{dx}}\).
(a) 0
(b) -1
(c) 1
(d) None of the above
Solution:
(a) 0

Question 27.
Let f(x) = e^x g(x), g(0) = 2 and g'(0) = 1, then find f'(0).
(a) 1
(b) 2
(c) 3
(d) 0
Solution:
(c) 3

Question 28.
If x ∈ (0, π/2) then find \(\frac{\mathrm{d}}{\mathrm{dx}}\)[sin x]
(a) 0
(b) 1
(c) 7C
(d) \(\frac{\pi}{2}\)
Solution:
(a) 0

Question 29.
If f(x) = [x²] then f’\(\left(\frac{3}{2}\right)\) = ________.
(a) 1
(b) \(\frac{3}{2}\)
(c) 0
(d) –\(\frac{3}{2}\)
Solution:
(c) 0

Question 30.
A differentiable function f defined for all x > 0 satisfies f(x²) = x³ for all x > 0. What is f'(b)?
(a) 3
(b) 4
(c) 6
(d) 12
Solution:
(c) 6

Question 31.
What is the derivative of f'(In x) w.r.t x where f(x) = ln x.
(a) \(\frac{1}{x^2 \ln x}\)
(b) \(\frac{1}{2 x \ln x}\)
(c) \(\frac{1}{x \ln x^2}\)
(d) \(\frac{1}{x \ln x}\)
Solution:
(d) \(\frac{1}{x \ln x}\)

Question 32.
For what value of a, f(x) = log_a (x) is increasing on R?
(a) a > 1
(c) a < 1
(b) a = 1
(d) a > 1
Solution:
(a) a ≥ 1

Question 33.
Write the points at which tangent to the curve y = x² – 3x is parallel to x – axis.
(a) \(\left(\frac{3}{2}, \frac{9}{4}\right)\)
(b) \(\left(\frac{3}{2}, \frac{-9}{4}\right)\)
(c) \(\left(\frac{-3}{2}, \frac{9}{4}\right)\)
(d) \(\left(\frac{-3}{2}, \frac{-9}{4}\right)\)
Solution:
(b) \(\left(\frac{3}{2}, \frac{-9}{4}\right)\)

Question 34.
If y = e^x + e^-x + 2 has a tangent parallel to x – axis at (α, β) then find the value of α.
(a) 0
(b) 2
(c) 1
(d) -1
Solution:
(a) 0

Question 35.
Write slope of the tangent to the curve y = √3 sin x + cos x at (\(\frac{\pi}{3}\), 2)
(a) 1
(b) -1
(c) 0
(d) None of the above
Solution:
(c) 0

Question 36.
Find the value of x for which f(x) is either a local maximum or a local minimum when
f(x) = x³ – 3x² – 9x + 6.
(a) (3, -1)
(b) (3, 1)
(c) (-1, 3)
(d) (1, -3)
Solution:
(a) (3, -1)

Question 37.
Find the x – coordinates of the extreme points of the function.
y = cos x + sin x , x ∈ [0, \(\frac{\pi}{2}\)]
(a) \(\frac{\pi}{4}\)
(b) \(\frac{2 \pi}{3}\)
(c) \(\frac{\pi}{2}\)
(d) π
Solution:
(a) \(\frac{\pi}{4}\)

Question 38.
Find the equation of tangent to the curve x = y² – 2 at the points where slope of the normal equal to (-2).
(a) x + y – 1 = 0
(b) 2x + y – 1 = 0
(c) 2x – y + 1 = 0
(d) x – y + 1 = 0
Solution:
(b) 2x + y – 1 = 0

Question 39.
f(x) = x⁴ – 62x² + ax + 9 attains its maximum value at x = 1 in the interval [0, 2]. Find the value of ‘a’.
(a) 12
(b) 120
(c) 1
(d) 1200
Solution:
(b) 120

Question 40.
If sin (x + y) = log (x + y) then \(\frac{d y}{d x}\) is:
(a) 2
(b) -2
(c) 1
(d) -1
Solution:
(d) -1

Question 41.
If f(x) = 2x and g(x) = \(\frac{x^2+1}{2}\) then which of the following can be a discontinuous function?
(a) F(x) + g(x)
(b) f(x) – g(x)
(c) f(x) . g(x)
(d) \(\frac{f(x)}{g(x)}\)
Solution:
(d) \(\frac{f(x)}{g(x)}\)

Question 42.
If f(x) = x² sin (‘) where x ≠ 0 then the value of the function f at x = 0, so that the function is continuous at x = 0 is
(a) 0
(b) -1
(c) 1
(d) none of these
Solution:
(a) 0

Question 43.
The derivative of cos^-1 (2x² – 1) with respect to cos^-1 x
(a) 2
(b) \(\frac{-1}{2 \sqrt{1-x^2}}\)
(c) \(\frac{2}{x}\)
(d) 1 – x²
Solution:
(a) 2

Question 44.
If y = \(\sqrt{\sin x+y}\) then \(\frac{d y}{d x}\) is equal to:
(a) \(\frac{\cos x}{2 y-1}\)
(b) \(\frac{\cos x}{1-2 y}\)
(c) \(\frac{\sin x}{1-2 y}\)
(d) \(\frac{\sin x}{2 y-1}\)
Solution:
(a) \(\frac{\cos x}{2 y-1}\)

Question 45.
Find the value of \(\frac{d y}{d x}\) at θ = \(\frac{\pi}{3}\) if x = asec³ θ and x = atan³ θ is:
(a) \(\frac{\sqrt{3}}{2}\)
(b) –\(\frac{\sqrt{3}}{2}\)
(c) \(\frac{1}{2}\)
(d) 1
Solution:
(a) \(\frac{\sqrt{3}}{2}\)

Question 46.
If x²y = e^x-y then \(\frac{d y}{d x}\) is:
(a) \(\frac{1+x}{1+\log x}\)
(b) \(\frac{1-x}{1+\log x}\)
(c) \(\frac{x}{1+\log x}\)
(d) \(\frac{x}{(1+\log x)^2}\)
Solution:
(d) \(\frac{x}{(1+\log x)^2}\)

Question 47.
Differential coefficient of sec (tan^-1 x) is:
(a) \(\frac{x}{1+x^2}\)
(b) \(x \sqrt{1+x^2}\)
(c) \(\frac{x}{\sqrt{1+x^2}}\)
(d) \(\frac{1}{\sqrt{1+x^2}}\)
Solution:
(c) \(\frac{x}{\sqrt{1+x^2}}\)

Question 48.
The function f(x) = x^x is decreasing in the interval:
(a) (0, e)
(b) (0, \(\frac{1}{e}\))
(c) (0, 1)
(d) none of these
Solution:
(b) (0, \(\frac{1}{e}\))

(B) Very Short Type Questions With Answers

Question 1.
If f'(2⁺) = 0 and f'(2^–) = 0, then is f(x) continuous at x = 2?
Solution:
f'(2⁺) = 0 and f'(2^–) = 0
⇒ f is differentiable at x = 2
⇒ f is continuous at x = 2.

Question 2.
If Φ(x) = f(x) + f(1 – x), f'(x) = 0 for 0 < x < 1, then is x = a point of maxima or minima of Φ(x)?
Solution:
Let Φ(x) = f(x) + f(1 – x)
⇒ Φ’ = f'(x) – f'(1 – x)
Φ”(x) = f”(x) + f”(1 – x)
Now Φ'(\(\frac{1}{2}\)) = f'(\(\frac{1}{2}\)) – f'(\(\frac{1}{2}\)) = 0
⇒ \(\frac{1}{2}\) is a critical point.
Φ”(\(\frac{1}{2}\)) = f”(\(\frac{1}{2}\)) – f”(\(\frac{1}{2}\)) = 0
⇒ x = \(\frac{1}{2}\) is neither a point of local maxima nor a point of local minima.

Question 3.
Write the interval in which the function f(x) = sin^-1 (2 – x) is differentiable.
Solution:
f(x) = sin^-1 (2 – x) is differentiable for
1 – (2 – x)² > 0.
⇒ (2 – x)² < 1
⇒ -1 < 2 – x < 1
⇒ -3 < -x < -1
⇒ 3 > x < 1
⇒ 1 < x < 3
⇒ x ∈ (1, 3)
∴ f is differentiable on (1, 3)

Question 4.
Write the set of values of x for which the function f(x) = sin x – x is increasing.
Solution:
f(x) = sin x – x
⇒ f'(x) = cos x – 1 ≤ 0 for all x ∈ R
∴ f(x) is increasing for all x ∈ R

Question 5.
Write the differential coefficient of e^{[x] ln (x + 1)} where 3 ≤ x < 4 with respect to x.
Solution:
Let y = e
= e^3ln(x+1) (∵ 3 ≤ x < 4)
= \(e^{\ln (x+1)^3}\) = (x + 1)³
\(\frac{d y}{d x}\) = 3(x + 1)²

Question 6.
Write a logarithmic function which is differentiable only in the open interval (-1, 1).
Solution:
f(x) = \(\left\{\begin{array}{l}
\ln \left|\sin ^{-1} x\right|, x \neq 0 \\
1, x=0
\end{array}\right.\) is differentiable only on (-1, 1).

Question 7.
Write a function which has both relative and absolute maximum at the point (1, 2).
Solution:
f(x) = -x² + 2x + 1 on [0, 1] has relative and absolute maximum at (1, 2).

Question 8.
Write the derivation of e^3logx with respect to x².
Solution:
Let u = e^3lnx = e^lnx = \(e^{\ln x^3}\)= x³ and v = x²
∴ \(\frac{d u}{d x}\) = 3x² and \(\frac{d v}{d x}\) = 2x
∴ Derivative of u w.r.t. v is
\(\frac{d u}{d v}\) = \(\frac{3 x^2}{2 x}\) = \(\frac{3 x}{2}\)

Question 9.
Write the maximum value of the function y = x⁵ in the interval [1, 5]:
Solution:
y = x⁵
⇒ \(\frac{d y}{d x}\) = 5x⁴ > 0 ∀ x ∈ [1, 5]
i.e y is strictly increasing in the given interval.
Thus the maximum value of
y = x⁵ = 5⁵ = 3125

Question 10.
Differentiate a^lnx with respect to x
Solution:
\(\frac{d}{d x}\)(a^{ln x}) = a^{ln x} (ln a)\(\frac{d}{d x}\)ln x
= \(\frac{a^{\ln x} \ln a}{x}\)

Question 11.
Mention the values of x for which x the function f(x) = x³ – 12x is increasing.
Solution:
Given f(x) = x³ – 12x
f is increasing if f'(x) > 0
⇒ 3x² – 12 > 0
⇒ x² > 4
⇒ -2 > x > 2
⇒ x ∈ (-∞, -2) ∪ (2, ∞)

Question 12.
Differentiate sin^-1 (cos x) with respect to x.
Solution:
\(\frac{d}{d x}\)sin^-1 (cos x) = \(\frac{d}{d x}\)sin^-1 sin (\(\frac{\pi}{2}\) – x)
= \(\frac{d}{d x}\) (\(\frac{\pi}{2}\) – x) = 1

Question 13.
Write the equation of the tangent to the curve y = |x| at the point (-2, 2).
Solution:
y = |x| = \(\left\{\begin{aligned}
x, & x \geq 0 \\
-x, & x<0
\end{aligned}\right.\)
When x < 0, \(\frac{d y}{d x}\) = -1
which is the slope of the tangent at (-2, 2).
Equation of the required tangent is
y – 2 = (-1) (x + 2)
⇒ y = -x
⇒ x + y = 0.

Question 14.
What is the derivative of sec^-1 x with respect to x if x < -1?
Solution:
Let y = sec^-1 x
⇒ \(\frac{d y}{d x}\) = \(\frac{1}{|x| \sqrt{x^2-1}}\)
when x < (-1) we have |x| = -x
∴ \(\left.\frac{\mathrm{dy}}{\mathrm{dx}}\right]_{\mathrm{x}<(-1)}\) = \(\frac{(-1)}{x \sqrt{x^2-1}}\)

Question 15.
Write the set of points where the function f(x) = x³ has relative (local) extrema.
Solution:
f(x) = x³
⇒ f'(x) = 3x²
f'(x) = 0
⇒ x = 0
But f”(x) = 6x = 0 when x = 0
∴ x = 0 is not a point of local extrema.
∴ Hence the set of points where f has relative extrema = Φ.

Question 16.
In which interval of x the function \(\frac{\ln \mathbf{x}}{x}\) is decreasing?
Solution:
Let f(x) = \(\frac{\ln x}{x}\)
⇒ f'(x) = \(\frac{x \cdot \frac{1}{x}-\ln x}{x^2}\) = \(\frac{1-\ln x}{x^2}\)
f is decreasing for
f'(x) < 0 ⇒ \(\frac{1-\ln x}{x^2}\) < 0
⇒ 1 – ln x < 0 (∵ x² > 0)
⇒ 1 < ln x
⇒ ln x > 1
⇒ x e (e, ∞).

(C) Short Type Questions With Answers

Question 1.
If y = \(e^{x^{e^{e^{e^{x^x…..}}}}}\), then find \(\frac{d \mathbf{y}}{\mathbf{d x}}\).
Solution:

Question 2.
If \(\frac{\mathbf{d}^2 \mathbf{y}}{\mathbf{d x}^2}\), if x = a cosΦ and y = b sinΦ.
Solution:
x = a cosΦ, y = b sinΦ

Question 3.
Find the point on the curve x² + y² – 4xy + 2 = 0, where the normal to the curve is parallel to the x – axis.
Solution:
Given equation of the curve is
x² + y² – 4xy + 2 = 0 … (1)
Differentiang we get

Question 4.
Find the intervals in which the function y = \(\frac{\ln x}{x}\) is increasing and decreasing.
Solution:

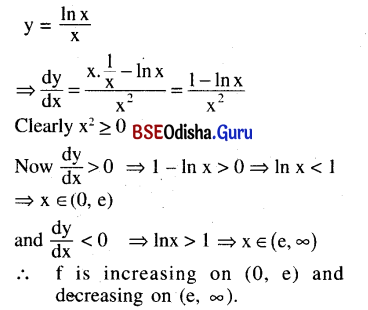
Question 5.
Differentiate y = tan^-1\(\frac{\sqrt{1+x^2}+\sqrt{1-x^2}}{\sqrt{1+x^2}-\sqrt{1-x^2}}\)
Solution:

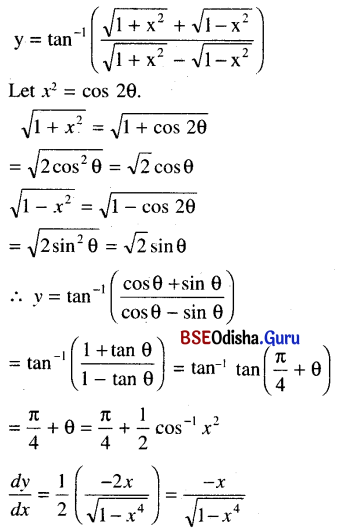
Question 6.
Differentiate y = (sin y)^{sin 2x}
Solution:
y = (sin y)^{sin 2x}
⇒ In y = sin 2x ln (sin y)

Question 7.
Test the differentiability and continuity of the following function at x = 0:
f(x) = \(\left\{\begin{array}{cc}
\frac{1-e^{-x}}{x} & x \neq 0 \\
1 & x=0
\end{array}\right.\)
Solution:
Given function is


As LHD = RHD, we have the given function is differentiable at x = 0 and f'(0) = –\(\frac{1}{2}\).

Question 8.
Show that the sum of intercepts on the co-ordinate axes of any tangent to the curve
√x + √y = √a is constant.
Solution:
Given curve √x + √y = √a … (1)

Question 9.
Find the equation of the normal to the curve y = (log x)² at x = \(\frac{1}{e}\).
Solution:
Given equation of the curve is
y = (log x)²

Question 10.
If y = x + \(\frac{1}{x+\frac{1}{x+\cdots \cdots \infty}}\), find \(\frac{\mathbf{d y}}{\mathbf{d x}}\), the rhs being a valid expression.
Solution:

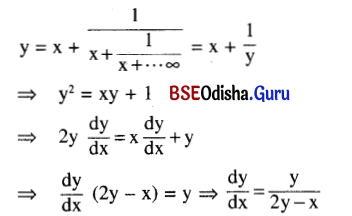
Question 11.
Differentiate sec^-1 (\(\frac{1}{2 x^2-1}\)) with respect to \(\sqrt{1-x^2}\).
Solution:

Question 12.
Find \(\frac{d \mathbf{y}}{\mathbf{d t}}\) , when y = sin^-1 \(\left(\frac{2 \sqrt{t}-1}{t^2}\right)\)
Solution:

Question 13.
Find \(\frac{\mathbf{d y}}{\mathbf{d x}}\) , if x^myⁿ = \(\left(\frac{\mathbf{x}}{\mathbf{y}}\right)^{\mathrm{m}+\mathrm{n}}\)
Solution:

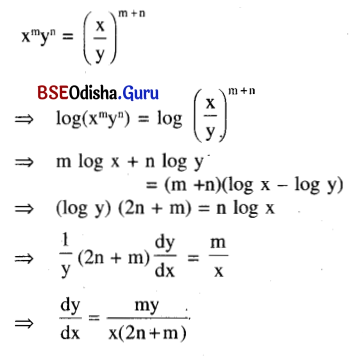
Question 14.
If x = a sec θ, y = b tan θ, prove that:
\(\frac{d^2 y}{d x^2}\) = –\(\frac{b^4}{a^2 y^3}\)
Solution:

Question 15.
Find the interval where the following function is increasing:
y = sin x + cos x, x ∈ [0, 2π].
Solution:
y = sin x + cos x, x ∈ [0, 2π].

Question 16.
Find \(\frac{d y}{d x}\), when y^x = x^{sin y}.
Solution:
y^x = x^{sin y}
Taking log of both sides we get,
x ln y = (sin y) ln x
Differentiating with respect to x we get,

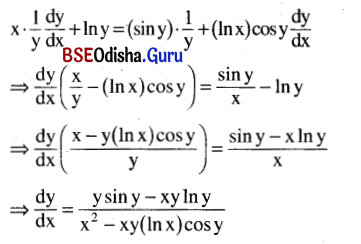
Question 17.
Show that \(\frac{d y}{d x}\) is independent of t,
if cos x = \(\sqrt{\frac{1}{1+t^2}}\), sin y = \(\frac{2 t}{1+t^2}\)
Solution:
cos x = \(\sqrt{\frac{1}{1+t^2}}\), sin y = \(\frac{2 t}{1+t^2}\)
Let t = tan θ
∴ cos x = cos θ, sin y = sin 2θ
⇒ y = 2θ, x = θ
⇒ y = 2x
⇒ \(\frac{d y}{d x}\) = 2 which is independent of t.

Question 18.
Show that 2sin x + tan x > 3x for all x ∈ (0, \(\frac{\pi}{2}\))
Solution:
Let f(x) = 2sin x + tan x – 3x
⇒ f'(x) = 2cos x + sec² x – 3
Let g(x) = f'(x) = 2cos x + sec² x – 3
⇒ g'(x) = -2sin x + 2sec² x tan x
= 2sin x (sec³ x – 1) ≥ 0
for all x ∈ (0, \(\frac{\pi}{2}\))
∴ g is an increasing function on (0, \(\frac{\pi}{2}\))
But g(0) = 0
∴ g(x) ≥ 0 for all x ∈ (0, \(\frac{\pi}{2}\))
⇒ f(x) ≥ 0 for all x ∈ (0, \(\frac{\pi}{2}\))
⇒ f is an increasing function on (0, \(\frac{\pi}{2}\))
But f(0) = 0
∴ f(x) ≥ 0 for all x ∈ (0, \(\frac{\pi}{2}\))
⇒ 2sin x + tan x ≥ 3x for x ∈ (0, \(\frac{\pi}{2}\))

Question 19.
Show that no two normals to a parabola are parallel.
Solution:
Let us consider the parabola y² = 4ax – (1) and A(at₁², 2at₁) and B (at₂², 2at₂) are any two points on its from (1)

As t₁ ≠ t₂ we have no two normals of a parabola are parallel.

Question 20.
Examine the differentiability of In x² for all real values of x.
Solution:
Let f(x) = In (x²) = 2 ln |x|
Clearly Dom f = R – {0}
Let any a ∈ Dom f.

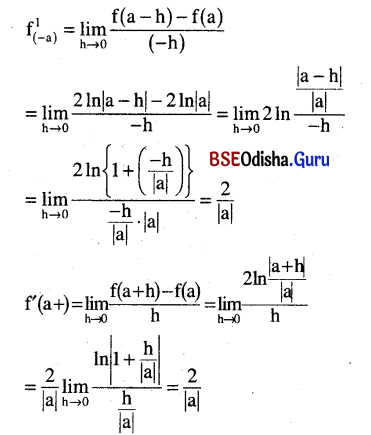
Question 21.
Find the derivative of x^{sin x} with respect to x.
Solution:
Let y = x^{sin x} = e^{(sin x)/nx}

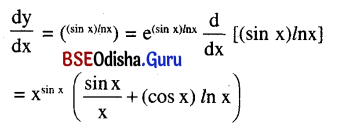
Question 22.
Differentiate sin^-1 \(\left(\frac{2 x}{1+x^2}\right)\) with respect to cos^-1 \(\left(\frac{1-x^2}{1+x^2}\right)\).
Solution:

Question 23.
Find the slope of the tangent to the curve x = 2(t – sin t), y = 2(1 – cos t) at t = \(\frac{\pi}{4}\).
Solution:

Question 24.
If cos y = x cos(a + y), then show that \(\frac{d y}{d x}\) = \(\frac{\cos ^2(a+y)}{\sin a}\).
Solution:

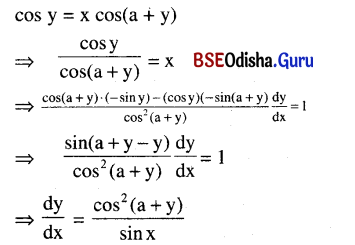
Question 25.
Find the extreme values of the function y = x + \(\frac{y}{x}\).
Solution:

Question 26.
Find the intervals where the following function is (i) increasing, (ii) decreasing:
f(x) = \(\begin{cases}\mathbf{x}^2+1, & x \leq-3 \\ x^3-8 x+13, & x>-3\end{cases}\)
Solution:
Given f(x) = \(\begin{cases}\mathbf{x}^2+1, & x \leq-3 \\ x^3-8 x+13, & x>-3\end{cases}\)
Clearly f is not differentiable at x = -3.
and f ‘(x) = \(\begin{cases}2 \mathrm{x}, & \mathrm{x}>-3 \\ 3 \mathrm{x}^2-8 & \mathrm{x}<-3 \\ \text { does not exist } & \text { for } \mathrm{x}=-3\end{cases}\)
Case – 1: x > -3
Clearly f'(x) > 0 for x > 0 and f'(x) < 0 for -3 < x < 0
∴ f is increasing in (0, ∞) and decreasing in (-3, 0).
Case – 2: x < -3
Clearly for x < -3, f(x) = 3x² – 8 > 0
i.e., f is increasing in (-∞, -3)
Thus f is increasing in (-∞, -3) ∪ (0, ∞) and decreasing in (-3, 0).

Question 27.
Prove that:
y = In tan \(\left(\frac{\pi}{4}+\frac{x}{2}\right)\) ⇒ \(\frac{d y}{d x}\) = sec x
Solution:

Question 28.
Differentiate with respect to x:
y = \(2^{x^2}\) + tan^-1 \(\left(\frac{\cos x-\sin x}{\cos x+\sin x}\right)\)
Solution:

Question 29.
Find the equation of the tangent to the curve x = y² – 1 at the point where the slope of the normal to the curve is (-2).
Solution:
Given equation of the curve is x = y² – 1.

Question 30.
Find \(\frac{d y}{d x}\) if y = \(\log _{\left(x^2\right)}\)3.
Solution:

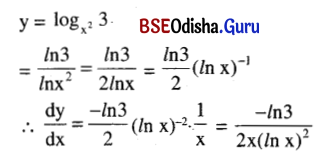
Question 31.
Write why the function sin^-1 \(\frac{1}{\sqrt{1-x^2}}\) cannot be differentiated anywhere.
Solution:

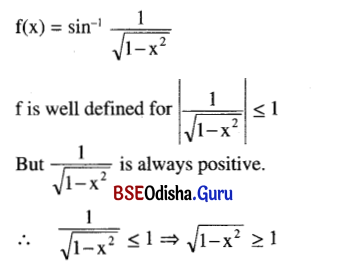
⇒ 1 – x² ≥ 1
⇒ x = 0
∴ DOM of {0 3}
But f is not defined in a deleted interval of x = 0.
Hence f is not differentiable at x = 0 and hence not differentiable anywhere.