Odisha State Board Elements of Mathematics Class 12 CHSE Odisha Solutions Chapter 7 Continuity and Differentiability Ex 7(c) Textbook Exercise Questions and Answers.
CHSE Odisha Class 12 Math Solutions Chapter 7 Continuity and Differentiability Exercise 7(c)
Find derivatives of the following functions.
Question 1.
(x2 +5)8
Solution:
y = (x2 +5)8
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\)(x2 +5)8
= 8(x2 +5)7 × \(\frac{d}{d x}\)(x2 +5) by chain rule
= 8(x2 +5)7 . 2x
= 16x (x2 +5)7
Question 2.
\(\frac{1}{\left(x^3+\sin x\right)^2}\)
Solution:
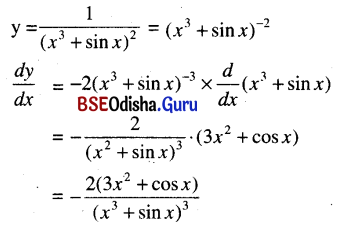
![]()
Question 3.
In (√x+1)
Solution:
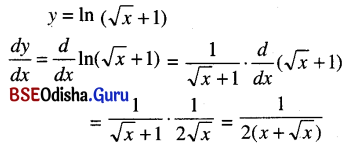
Question 4.
sin 5x + cos 7x
Solution:
sin 5x + cos 7x
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\)(sin 5x) + \(\frac{d}{d x}\)(cos 7x)
= cos 5x . \(\frac{d}{d x}\)(5x) – sin 7x . \(\frac{d}{d x}\)(7x)
= 5 cos 5x – 7 sin 7x
Question 5.
esin t
Solution:
y = esin t
\(\frac{d y}{d x}\) = \(\frac{d}{d t}\)(esin t) = esin t . \(\frac{d}{d t}\)(sin t)
= esin t . cos t
Question 6.
\(\sqrt{a x^2+b x+c}\)
Solution:
y = \(\sqrt{a x^2+b x+c}\)
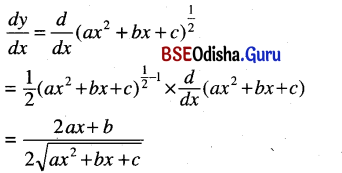
Question 7.
\(\left(\frac{x+1}{x^2+3}\right)^{-3}\)
Solution:

Question 8.
sec (tan θ)
Solution:
y = sec (tan θ)
\(\frac{d y}{d θ}\) = \(\frac{d}{d θ}\) {sec (tan θ)}
= sec (tan θ) . tan (tan θ) . \(\frac{d}{d θ}\)(tan θ)
= sec (tan θ) . tan (tan θ) . sec2 θ
Question 9.
sin \(\left(\frac{1-x^2}{1+x^2}\right)\)
Solution:

Question 10.
\(\sqrt{\tan (3 z)}\)
Solution:
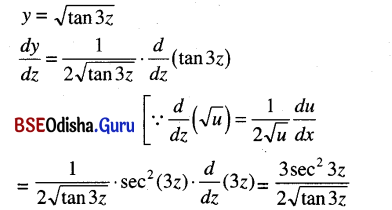
![]()
Question 11.
tan3 x
Solution:
y = tan3x = (tan x)3
\(\frac{d y}{d x}\) = 3(tan x)2. \(\frac{d}{d x}\)(tan x)
= 3tan2 x . sec2 x
Question 12.
sin4 x
Solution:
y = sin4x
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\)(sin4 x)
= 4 (sin x)3 . \(\frac{d}{d x}\)(sin x)
= 4 sin3 x . cos x
Question 13.
sin2 x cos2 x
Solution:
y = sin2 x cos2 x = \(\frac{1}{4}\)sin2 2x
\(\frac{d y}{d x}\) = \(\frac{1}{4}\) \(\frac{d}{d x}\)(sin 2x)2
= \(\frac{1}{4}\). 2sin 2x . \(\frac{d}{d x}\)(sin 2x)
= \(\frac{1}{2}\) sin 2x . cos 2x . \(\frac{d}{d x}\)(2x)
= \(\frac{1}{2}\) sin 2x cos 2x . 2 = sin 2x . cos 2x
Question 14.
sin 5x cos 7x
Solution:
y = sin 5x cos 7x
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\)(sin 5x) . cos 7x + \(\frac{d}{d x}\)sin 5x . (cos 7x)
= cos 5x . \(\frac{d}{d x}\)(5x) . cos 7x + sin 5x . (-sin 7x) . \(\frac{d}{d x}\)(7x)
= 5 cos 5x . cos 7x – 7 sin 5x . sin 7x
Question 15.
tan x cot 2x
Solution:
y = tan x. cot 2x
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\)(tan x) . cot 2x + tan x . \(\frac{d}{d x}\)(cot 2x)
= sec2 x / cot 2x + tan x . (-cosec2 x) \(\frac{d}{d x}\)(2x)
= sec2 x . cot 2x – 2 tan x . cosec2 x
Question 16.
\(\sqrt{\sin \sqrt{x}}\)
Solution:

Question 17.
\(\sqrt{\sec (2 x+1)}\)
Solution:

Question 18.
cosec (ax + b)2
Solution:
y = cosec (ax + b)2
\(\frac{d y}{d x}\) = – cosec (ax + b)2 cot (ax + b)2 . \(\frac{d}{d x}\)(ax + b)2
[ ∵ \(\frac{d}{d x}\)(cosec u) = -cosec u . cot u . \(\frac{d u}{d x}\)
= – cosec (ax + b)2 . cot (ax + b)2 . 2(ax + b) . \(\frac{d}{d x}\)(ax + b)
[ ∵ \(\frac{d}{d x}\)(u2) = 2u \(\frac{d u}{d x}\)
= – cosec (ax + b)2 . cot (ax + b)2 . 2(ax + b) . a
= – 2a (ax + b) cosec (ax + b)2 cot (ax + b)2
![]()
Question 19.
aIn x
Solution:
y = aIn x . In a . \(\frac{d}{d x}\)(In x)
[ ∵ \(\frac{d}{d x}\)(au) = au . In a . \(\frac{d u}{d x}\)
= aIn x . In a . \(\frac{1}{x}\) = \(\frac{a^{\ln x} \ln a}{x}\)
Question 20.
\(a^{x^2} b^{x^3}\)
Solution:
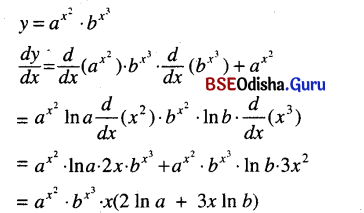
Question 21.
In tan x
Solution:
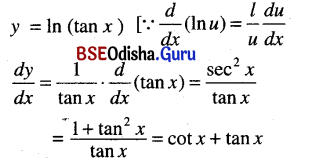
Question 22.
\(5^{\sin x^2}\)
Solution:
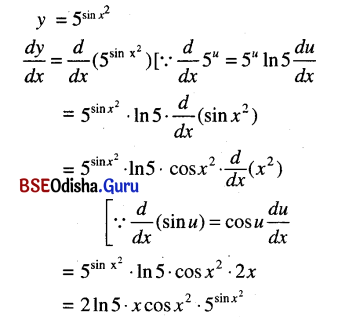
Question 23.
In tan\(\left(\frac{\pi}{4}+\frac{x}{2}\right)\)
Solution:

Question 24.
\(\sqrt{\left(a^{\sqrt{x}}\right)}\)
Solution:

Question 25.
In (enx + e-nx)
Solution:
y = In (enx + e-nx)
\(\frac{d y}{d x}\) = \(\frac{1}{e^{n x}+e^{-n x}}\) . \(\frac{d}{d x}\) (enx + e-nx)
= \(\frac{n\left(e^{n x}-e^{-n x}\right)}{e^{n x}+e^{-n x}}\)
![]()
Question 26.
\(e^{\sqrt{a x}}\)
Solution:
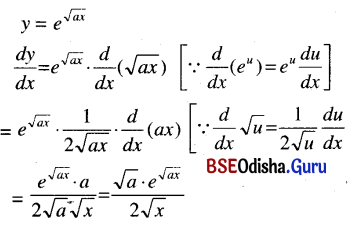
Question 27.
\(\sqrt{\log x}\)
Solution:
y = \(\sqrt{\log x}\)
\(\frac{d y}{d x}\) = \(\frac{1}{2 \sqrt{\log x}}\) . \(\frac{d}{d x}\)(log x)
= \(\frac{1}{2 \sqrt{\log x}}\) . \(\frac{1}{x}\)
Question 28.
esin x – acos x
Solution:
y = esin x – acos x
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\)(esin x) – \(\frac{d}{d x}\)(acos x)
= esin x . \(\frac{d}{d x}\)(sin x) – acos x . In a . \(\frac{d}{d x}\)(cos x)
= esin x . cos x + acos x . In a . sin x
Question 29.
\(\frac{e^{3 x^2}}{\ln \sin x}\)
Solution:

Question 30.
Prove that
\(\frac{d}{d x}\left[\frac{1-\tan x}{1+\tan x}\right]^{\frac{1}{2}}\) = 1 / \(\sqrt{\cos 2 x}\) (cos x + sin x)
Solution:

