BSE Odisha 10th Class Maths Solutions Algebra Chapter 2 ଦ୍ବିଘାତ ସମୀକରଣ Ex 2(b)

Odisha State Board BSE Odisha 10th Class Maths Solutions Algebra Chapter 2 ଦ୍ବିଘାତ ସମୀକରଣ Ex 2(b) Textbook Exercise Questions and Answers.

BSE Odisha Class 10 Maths Solutions Algebra Chapter 2 ଦ୍ବିଘାତ ସମୀକରଣ Ex 2(b)

Question 1.
ନିମ୍ନଲିଖତ ପ୍ରଶ୍ନମାନଙ୍କର ଉତ୍ତର ଦିଅ ।
(i) ଗୋଟିଏ ସଂଖ୍ୟା ଓ ଏହାର ବ୍ୟତ୍‌କ୍ରମର ସମଷ୍ଟି 2 । ସଂଖ୍ୟାଟିକୁ x ନେଇ ଏକ ଦ୍ଵିଘାତ ସମୀକରଣ ଗଠନ କର ।
(ii) ଦୁଇଗୋଟି କ୍ରମିକ ପୂର୍ଣ୍ଣ ସଂଖ୍ୟାର ଗୁଣଫଳ 20 । ସଂଖ୍ୟାଦ୍ଵୟ ମଧ୍ୟରୁ ଗୋଟିକୁ y ନେଇ ଆବଶ୍ୟକୀୟ ଦ୍ଵିଘାତ ସମୀକରଣ ଗଠନ କର ।
(iii) ଦୁଇଟି ସଂଖ୍ୟାର ସମଷ୍ଟି 18 ଏବଂ ସେମାନଙ୍କର ଗୁଣଫଳ 72 । ଗୋଟିଏ ସଂଖ୍ୟାକୁ x ନେଇ ଏକ ଦ୍ଵିଘାତ ସମୀକରଣ ଗଠନ କର ।
(iv) କୌଣସି ସଂଖ୍ୟା, ତାହାର ବର୍ଗ ସମାନ ହେଲେ ସଂଖ୍ୟାଟି ନିର୍ଣ୍ଣୟ କର ।
(v) ପ୍ରଥମ n ସଂଖ୍ୟକ ଗଣନ ସଂଖ୍ୟାର ସମଷ୍ଟି S = \(\frac{n(n+1) }{2}\)। ଯଦି S = 120 ହୁଏ, ତେବେ nର ମୂଲ୍ୟ ନିରୂପଣ କରିବା ପାଇଁ ଏକ ଦ୍ଵିଘାତ ସମୀକରଣ ଗଠନ କର ।
(vi) \(\sqrt{x}\) + x = 6 କୁ ଏକ ଦ୍ବିଘାତ ସମୀକରଣ ରୂପେ ପ୍ରକାଶ କର ।
(vii) \(\sqrt{x+9}\) + 3 = x କୁ ଏକ ସ୍ଵିଘାତ ସମୀକରଣ ରୂପେ ପ୍ରକାଶ କର ।
(viii) x – 2\(\sqrt{2}\) – 6 = 0 ସମୀକରଣକୁ ଏକ ଦ୍ଵିଘାତ ସମୀକରଣ ରୂପେ ପ୍ରକାଶ କର ।
ସମାଧାନ :
(i) ମନେକର ସଂଖ୍ୟାଟି x । ସଂଖ୍ୟାଟିର ବ୍ୟକ୍ରମ \(\frac{1}{x}\)
ପ୍ରଶ୍ନନୁସାରେ, x + \(\frac{1}{x}\) = 2 ⇒ x² + 1 = 2x ⇒ x² – 2x + 1 = 0
∴ ନିଶ୍ଚେୟ ଦ୍ବିଘାତ ସମୀକରଣ x² – 2x + 1 = 0

(ii) ମନେକର ଗୋଟିଏ ସଂଖ୍ୟା y । ଅନ୍ୟଟି = (y + 1)
ପ୍ରଶ୍ନନୁସାରେ, y (y + 1) = 20 ⇒ y² + y – 20 = 0
∴ ନିଶ୍ଚେୟ ଦ୍ବିଘାତ ସମୀକରଣ y + y – 20 = 0

(iii) ମନେକର ପ୍ରଥମ ସଂଖ୍ୟାଟି x ଓ ଦ୍ବିତୀୟ ସଂଖ୍ୟାଟି 18 – x ।
ପ୍ରଶ୍ନନୁସାରେ, x (18 – x) = 72 ⇒ 18x – x² = 72 = x² – 18x + 72 = 0
∴ ନିଶ୍ଚେୟ ଦ୍ବିଘାତ ସମୀକରଣ, x² – 18x + 72 = 0

(iv) ମନେକର ସଂଖ୍ୟାଟି x।
ପ୍ରଶ୍ନନୁସାରେ ସଂଖ୍ୟାଟି ତା’ର ବର୍ଗ ସହ ସମାନ ହେବ । ଅର୍ଥାତ୍ x = x²
⇒ x² – x = 0 ⇒ x ( x – 1 ) = 0
⇒ x = 0 ବା x – 1 = 0 ⇒ x= 0 ବା x = 1
∴ ସଂଖ୍ୟାଟି 0 କିମ୍ବା 1 ।

(v) ପ୍ରଶ୍ନନୁସାରେ \(\frac{n(n+1) }{2}\) = 120 ⇒ n² + n = 240 ⇒ n² + n – 240 = 0

(vi) √x + x = 6 ⇒ √x = 6 – x
⇒ (√x)² =(6 – x)² ⇒ x = 36 + x² – 12x
⇒ x² – 12x – x + 36 = 0 ⇒ x² – 13x + 36 = 0

(vii) √(x + 9) + 3 = x ⇒ √(x + 9) = x – 3
⇒ (\(\sqrt{x+9}\))² = (x – 3)² ⇒ x² – 6x + 9 = x + 9
⇒ x² – 6x – x + 9 – 9 = 0 = x² – 7x = 0
ବିକଳ୍ପ ସମାଧାନ :
ମନେକର \(\sqrt{x+9}\) = t
⇒ x + 9 = t² ⇒ x = t² – 9
xର ମାନ ସମୀକରଣରେ ବସାଇଲେ k + 3 = t² – 9
⇒ t – t – 9 – 3 = 0 ⇒ t – t – 12 = 0

(viii) x – 2√2 – 6 = 0 ⇒ x – 6 = 2√2
⇒ (x – 6)² = (2√2)² ⇒ x² – 12x + 36 = 8
⇒ x² – 12x + 36 – 8 = 0 ⇒ x² – 12x + 28 = 0

Question 2.
ନିମ୍ନଲିଖ ପ୍ରଶ୍ନମାନଙ୍କର ଉତ୍ତର ଦିଅ ।
(i) ଗୋଟିଏ ଧନାତ୍ମକ ସଂଖ୍ୟା ତାହାର ବର୍ଗମୂଳ ଅପେକ୍ଷା 12 ଅଧିକ ହେଲେ, ସଂଖ୍ୟାଟି ନିରୂପଣ କର ।
(ii) ଗୋଟିଏ ସଂଖ୍ୟା ଏବଂ ତାହାର ବ୍ୟତ୍‌କ୍ରମର ସମଷ୍ଟି \(\frac{41}{20}\) ହେଲେ ସଂଖ୍ୟାଟି ସ୍ଥିର କର ।
(iii) ଦୁଇଟି କ୍ରମିକ ପୂର୍ଣ ସଂଖ୍ୟାର ବ୍ୟୁତ୍‌କ୍ରମ ଭଗ୍ନସଂଖ୍ୟା ଦ୍ବୟର ଯୋଗଫଳ \(\frac{11}{30}\) ଦ୍ଵୟକୁ ନିରୂପଣ କରିବା ପାଇଁ ଆବଶ୍ୟକ ଦ୍ଵିଘାତ ସମୀକରଣଟି ଗଠନ କରି ସଂଖ୍ୟାଦ୍ଵୟ ନିରୂପଣ କର ।
(iv) ଦୁଇଟି କ୍ରମିକ ପୂର୍ଣ୍ଣ ସଂଖ୍ୟାର ବ୍ୟୁତ୍‌କ୍ରମର ସମଷ୍ଟି \(\frac{25}{123}\) ହେଲେ ସଂଖ୍ୟାଦ୍ଵୟ ନିର୍ଣ୍ଣୟ କର ।
(v) ଯଦି 51 କୁ ଦୁଇଭାଗ କଲେ ସେମାନଙ୍କର ଗୁଣଫଳ 378 ହୁଏ, ତେବେ ସଂଖ୍ୟା ଦ୍ଵୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ :
(i) ମନେକର ଧନାତ୍ମକ ସଂଖ୍ୟାଟି x² । ଏହାର ବର୍ଗମୂଳ = √x² = x
ପ୍ରଶ୍ନନୁସାରେ, x² = x + 12 = x² -x – 12 = 0
⇒ x² – 4x + 3x – 12 = 0 ⇒ x (x – 4) + 3 (x – 4) = 0
⇒ (x – 4) (x + 3) = 0 ⇒ x – 4 = 0 ବା x + 3 = 0
⇒ x = 4 ବା x = -3 (ଅସମ୍ଭବ)
∴ ଧନାତ୍ମକ ସଂଖ୍ୟାଟି x² = 4² = 16

(ii) ମନେକର ସଂଖ୍ୟାଟି x । ତାହାର ବ୍ୟତ୍‌କ୍ରମ \(\frac{1}{x}\)
ପ୍ରଶ୍ନନୁସାରେ, x + \(\frac{1}{x}=\frac{41}{20}\) = \(\frac{x²+1}{x}=\frac{41}{20}\)
⇒ 20x² + 20 = 41x ⇒ 20x² – 41x + 20 = 0
⇒ 20x² – 25x – 16x + 20 = 0 ⇒ 5x (4x – 5) – 4 (4x – 5) = 0
⇒ (4x – 5) (5x – 4)=0 = 4x – 5 = 0 ବା 5x – 4 = 0
⇒ x = \(\frac{5}{4}\)ବା x = \(\frac{4}{5}\)
∴ ସଂଖ୍ୟାଟି \(\frac{4}{5}\) ହେଲେ ଏହାର ବ୍ୟତ୍‌କ୍ରମ \(\frac{5}{4}\) ହେବ ।
ଅଥବା x = \(\frac{5}{4}\) ହେଲେ ଏହାର ବ୍ୟତ୍‌କ୍ରମ \(\frac{4}{5}\) ହେବ ।
∴ ସଂଖ୍ୟାଟି \(\frac{4}{5}\) ବା \(\frac{5}{4}\) ହେବ ।

(iii) ମନେକର କ୍ରମିକ ପୂର୍ଣ୍ଣ ସଂଖ୍ୟାଦ୍ୱୟ x ଓ x + 1
x ର ବ୍ୟୁତ୍‌କ୍ରମ \(\frac{1}{x}\) ଓ x + 1 ର ବ୍ୟକ୍ରମ \(\frac{1}{x+1}\)
ପ୍ରଶ୍ନନୁସାରେ, \(\frac{1}{x}+\frac{1}{x+1}=\frac{11}{30}\) ⇒ \(\frac{x+1+x}{x(x+1)}=\frac{11}{30}\)
⇒ \(\frac{2x+1}{x²+x)}=\frac{11}{30}\) ⇒ 11x² + 11x = 60x + 30
⇒ 11x² + 11x – 60x – 30 = 0 ⇒ 11x² – 49x – 30 = 0
⇒ 11x² – 55x + 6x – 30 = 0 ⇒ 11x (x – 5) + 6 (x – 5) = 0 ⇒ (x – 5) (11x + 6) = 0 ⇒ x – 5 = 0 ବା 11x + 6 = 0
⇒ x = 5 ବା x = \(\frac{-6}{11}\) (ଅସମ୍ଭବ)
∴ x = 5 ହେଲେ ଏହାର ପରବର୍ତ୍ତୀ
∴ ନିଶ୍ଚେୟ କ୍ରମିକ ପୂର୍ଣ୍ଣ ସଂଖ୍ୟାଦ୍ଵୟ 5 ଓ 6 । କ୍ରମିକ ସଂଖ୍ୟା x + 1 = 6

(iv) ମନେକର କ୍ରମିକ ପୂର୍ବସଂଖ୍ୟାଦ୍ୱୟ x ଓ x + 1 ।
ପ୍ରଶାନୁସାରେ, \(\frac{1}{x}+\frac{1}{x+1}=\frac{23}{132}\) ⇒ \(\frac{x+1+x}{x(x+1)}=\frac{23}{132}\)
⇒ \(\frac{2x+1}{x²+x)}=\frac{23}{132}\) ⇒ 23x² + 23x = 264x + 132
⇒ 23x² + 23x – 264x – 132 = 0 ⇒ 23x² – 241x – 132 = 0
⇒23x² – 253x + 12x – 132 = 0 ⇒ 23x (x – 11) + 12 (x – 11) = 0
⇒ (x – 11) (23x + 12) = 0 ⇒ x – 11 = 0 ବା 23x + 12 = 0
⇒ x = 11 ବା x = \(– \frac{12}{23}\) (ଅସମ୍ଭବ) ⇒ x + 1 = 11 + 1 = 12
∴ ପୂର୍ଣ୍ଣସଂଖ୍ୟାଦ୍ଵୟ 11 ଓ 12 ।

(v) ମନେକର ଗୋଟିଏ ସଂଖ୍ୟା x ଓ ଅନ୍ୟଟି 51 – x ।
ପ୍ରଶ୍ନନୁସାରେ, x (51 – x) = 378 ⇒ 51x – x² = 378
⇒ x – 51x + 378 = 0 ⇒ x² – 42x – 9x + 378 = 0
⇒x (x-42) – 9 (x – 42) = 0 ⇒ (x – 42) (x – 9) = 0
⇒ x – 42 = 0 ବା x – 9 = 0 ⇒ x = 42 ବା x = 9
∴ ଯଦି x = 9 ହୁଏ ତେବେ ଅନ୍ୟ ଭାଗଟି 42 ହେବ ।
∴ ସଂଖ୍ୟାଦ୍ୱୟ 9 ଓ 42 ସେହିପରି x = 42 ହୁଏ ତେବେ ଅନ୍ୟ ଭାଗଟି 9 ହେବ ।

Question 3.
ଏକ ଦୁଇଅଙ୍କ ବିଶିଷ୍ଟ ସଂଖ୍ୟା, ତାହାର ଅଙ୍କ ଦ୍ଵୟର ଗୁଣଫଳର 3 ଗୁଣ । ଏକକ ସ୍ଥାନରେ ଥ‌ିବା ଅଙ୍କଟି ଦଶକ ସ୍ଥାନରେ ଥ‌ିବା ଅଙ୍କଠାରୁ 2 ବୃହତ୍ତର । ସଂଖ୍ୟାଟି ନିରୂପଣ କର ।
ସମାଧାନ :
ମନେକର ଦୁଇଅଙ୍କ ବିଶିଷ୍ଟ ସଂଖ୍ୟାର ଏକକ ସ୍ଥାନୀୟ ଅଙ୍କ x ଓ ଦଶକ ସ୍ଥାନୀୟ ଅଙ୍କ y ।
∴ ସଂଖ୍ୟାଟି = 10y + x
ପ୍ରଶ୍ନନୁସାରେ 10y + x = 3xy …… (i) ଏବଂ x = y + 2 ……. (ii)
ସମୀକରଣ (ii)ରୁ x ର ମାନ ସମୀକରଣ (i) ରେ ବସାଇଲେ, 10y + y + 2 = 3y (y + 2)
⇒ 11y + 2 = 3y² + 6y ⇒ 3y² + 6y – 11y – 2 = 0
⇒ 3y² – 5y – 2 = 0 ⇒ 3y² – 6y+ y – 2 = 0
⇒ 3y (y – 2) + 1 (y – 2) = 0 ⇒ (y – 2) (3y + 1) = 0
⇒ y – 2 = 0 ବା 3y + 1 = 0 = y = 2 ବା y = (ଅସମ୍ଭବ)
∴ x = y + 2 = 2 + 2 = 4
ସଂଖ୍ୟାଟି = 10y + x = 10 × 2 + 4 = 24

Question 4.
ଗୋଟିଏ ପରିବାରରେ ଆଲ୍‌ଫାର ବୟସ, ବିଟା ଓ ଗାମାର ବୟସ୍‌ର ଗୁଣଫଳ ସହ ସମାନ । ଯଦି ବିଟା, ଗାମାଠାରୁ 1 ବର୍ଷ ବଡ଼ ହୁଏ ଏବଂ ଆଲ୍‌ଫାର ବୟସ 42 ହୁଏ, ତେବେ 5 ବର୍ଷ ପରେ ବିଟାର ବୟସ କେତେ ହେବ ?
ସମାଧାନ :
ମନେକର ପରିବାରରେ ଗାମାର ବୟସ = x ବର୍ଷ
∴ ବିଟାର ବୟସ = (x + 1) ବର୍ଷ । ଆଲ୍‌ଫାର ବୟସ = 42।
ପ୍ରଶ୍ନନୁସାରେ, x(x + 1) = 42 ⇒ x² + x = 42
⇒ x² + x – 42 = 0 ⇒ x² + 7x – 6x – 42 = 0
⇒ x(x + 7) – 6(x + 7) = 0 ⇒ (x + 7) (x – 6) = 0
⇒ x + 7 = 0 ବା x – 6 = 0 = x = -7 ବା x = 6
x = – 7 ବୟସ ଋଣାତ୍ମକ ହେବନାହିଁ ତେଣୁ ଏହା ଅସମ୍ଭବ। ତେବେ ଏଠାରେ x = 6 ଗ୍ରହଣୀୟ ।
∴ ଗାମାର ବୟସ = x ବର୍ଷ = 6 ବର୍ଷ ଏବଂ ବିଟାର ବୟସ = 6 + 1 = 7 ବର୍ଷ ।
∴ 5 ବର୍ଷ ପରେ ବିଟାର ବୟସ ହେବ = 7 + 5 = 12 ।

Question 5.
କୌଣସି ଏକ ଅରଣ୍ୟରେ ବାସ କରୁଥିବା ମର୍କଟମାନଙ୍କ ମଧ୍ୟରୁ ସେମାନଙ୍କ ସଂଖ୍ୟାର ଏକ ଅଷ୍ଟମାଂଶର ବର୍ଗ କ୍ରୀଡ଼ାରତ ଏବଂ ଅବଶିଷ୍ଟ ବାରଟି ମର୍କଟ ଏକ ଶୃଙ୍ଗ ଉପରେ ବସିଥିଲେ । ଅରଣ୍ୟରେ ସମ୍ଭବତଃ କେତେ ମର୍କଟ ଥିଲେ ?
ସମାଧାନ :
ମନେକର ଅରଣ୍ୟରେ ସମ୍ଭବତଃ xଟି ମର୍କଟ ଥିଲେ ।
ସେମାନଙ୍କ ଏକ- ଅଷ୍ଟମାଂଶର ବର୍ଗ କ୍ରିଡ଼ାରତ ଥିଲେ । କ୍ରୀଡ଼ାରତ ଥିବା ମର୍କଟଙ୍କ ସଂଖ୍ୟା = (\(\frac{x}{8}\))² = \(\frac{x²}{64}\)
ଅବଶିଷ୍ଟ 12 ଟି ମର୍କଟ ଶୃଙ୍ଗ ଉପରେ ବସିଥିଲେ ।
ପ୍ରଶ୍ନନୁସାରେ, \(\frac{x²}{64}+12\) = x = \(\frac{x²+768}{64}=x\)
⇒ x² + 768x = 64 x ⇒ x² – 64x + 768 = 0
⇒ x² -48x – 16x + 768 = 0 ⇒ x (x – 48) – 16 (x – 48) = 0
⇒ (x – 48) (x – 16)=0 = x – 48 = 0 ବା x – 16 = 0
⇒ x = 48 ବା x = 16
∴ ଅରଣ୍ୟରେ ସମ୍ଭବତଃ 48 କିମ୍ବା 16ଟି ମର୍କଟ ଥିଲେ ।

Question 6.
ଗୋଟିଏ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ 30 ବ. ସେ.ମି. । ତ୍ରିଭୁଜର ଉଚ୍ଚତା, ଭୂମିର ଦୈର୍ଘ୍ୟଠାରୁ 7 ସେ.ମି. ଅଧ୍ଵ ହେଲେ, ଭୂମିର ଦୈର୍ଘ୍ୟ ସ୍ଥିର କର ।
ସମାଧାନ :
ଗୋଟିଏ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ = 30 ବର୍ଗ ସେ.ମି.
ତ୍ରିଭୁଜର ଉଚ୍ଚତା, ଭୂମିର ଦୈର୍ଘ୍ୟଠାରୁ 7 ସେ.ମି. ଅଧ୍ଵ ।
ମନେକର ଭୂମିର ଦୈର୍ଘ୍ୟ X ସେ.ମି. । ଉଚ୍ଚତା = x + 7 ସେ.ମି.
∴ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) ଭୂମି × ଉଚ୍ଚତା = \(\frac{1}{2}\)x(x+7)
⇒ 30 = \(\frac{1}{2}\)(x² + 7x) ⇒ x² + 7x = 60
⇒ x²+7x-60 = 0 ⇒ x² + 12x – 5x – 60 = 0
⇒ x (x + 12) – 5 (x + 12) = 0 ⇒ (x + 12) (x – 5)= 0
⇒ x + 12 = 0 ବା x – 5 = 0 = x=- 12 (ଅସମ୍ଭବ) ବା x = 5
∴ ତ୍ରିଭୁଜର ଭୂମିର ଦୈର୍ଘ୍ୟ 5 ସେ.ମି. ।

Question 7.
ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜର ସମକୋଣର ସଂଲଗ୍ନ ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ 5x ସେ.ମି. ଓ (3x – 1) ସେ.ମି. ଓ କ୍ଷେତ୍ରଫଳ 60 ବର୍ଗ ସେ.ମି. । ତେବେ ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ :
ସମକୋଣ ସଂଲଗ୍ନ ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ 5x ସେ.ମି. ଏବଂ (3x – 1) ସେ.ମି. ।
ସମକୋଣୀ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ = 60 ବର୍ଗ ସେ.ମି. (ଦତ୍ତ)
⇒ \(\frac{1}{2}\) × ସମକୋଣ ସଂଲଗ୍ନ ଦୈର୍ଘ୍ୟର ବାହୁଦ୍ୱୟର ଗଣଫଳ = 60
⇒ \(\frac{1}{2}\) . 5x . (3x – 1) = 60 ⇒ x(3x – 1) = 60 × \(\frac{2}{5}\)
⇒ 3x² – x = 24 ⇒ 3x² – x – 24 = 0
ଏଠାରେ a = 3, b = -1, c = – 24

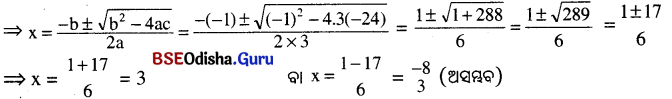
∴ ସମକୋଣୀ ତ୍ରିଭୁଜର ବାହୁ ଦ୍ୱୟର ଦୈର୍ଘ୍ୟ 5x = 5 × 3 = 15 ସେ.ମି. ।
ଓ 3x – 1 = 3 × 3 – 1 = 8 ସେ.ମି. ।
ବିକଳ୍ପ ପ୍ରଣାଳୀ : 3x² – x – 24 = 0 ର ସମାଧାନ ଉତ୍ପାଦକୀକରଣ ଦ୍ଵାରା ସମ୍ଭବ ।

Question 8.
n ବାହୁ ବିଶିଷ୍ଟ ବହୁଭୁଜର କର୍ଡ ସଂଖ୍ୟା \(\frac{n}{2}\)n(n-3)। ଯଦି ବହୁଭୁଜର 54ଟି କର୍ଣ୍ଣ ରହିବ, ତେବେ ବହୁଭୁଜର ବାହୁର ସଂଖ୍ୟା କେତେ ?
ସମାଧାନ :
n ବାହୁ ବିଶିଷ୍ଟ ବହୁଭୁଜର କର୍ଣ୍ଣ ସଂଖ୍ୟା = \(\frac{n}{2}\)n(n-3)
ଏହାର କର୍ଣ୍ଣ ସଂଖ୍ୟା 54 1
ପ୍ରଶ୍ବାନୁସାରେ, \(\frac{n}{2}\)n(n-3) = 54 ⇒ n² – 3n = 108
→n² – 3n-108 = 0 ⇒ n² – 12n + 9n – 108 = 0
→ n (n – 12) + 9 (n – 12) = 0 → (n – 12) (n + 9) = 0
→ n – 12 = 0 ବା n + 9 = 0
⇒ n =12 ବା n = -9 (ଅସମ୍ଭବ)
∴ ବହୁଭୁଜର ବାହୁ ସଂଖ୍ୟା 12 ।

Question 9.
ଦୁଇଟି ବର୍ଗକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳର ସମଷ୍ଟି 468 ବ.ମି. ଏବଂ ପରିସୀମାଦ୍ବୟର ଅନ୍ତର 24 ମି. ହେଲେ ପ୍ରତ୍ୟେକର ବାହୁର ଦୈର୍ଘ୍ୟ ନିରୂପଣ କର ।
ସମାଧାନ :
ଦୁଇଟି ବର୍ଗକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳର ସମଷ୍ଟି 468 ବର୍ଗ ମି. । ପରିସୀମାଦ୍ବୟର ଅନ୍ତର = 24 ମିଟର
ମନେକର ଗୋଟିଏ ବର୍ଗକ୍ଷେତ୍ରର ବାହୁର ଦୈର୍ଘ୍ୟ a ମି. ଓ ଅନ୍ୟଟିର ଦୈର୍ଘ୍ୟ b ମି. ।
ପ୍ରଶ୍ବାନୁସାରେ, a² + b² = 468 ଏବଂ 4a – 4b = 24
⇒ 4(a – b) = 24 ⇒ a – b = \(\frac{24}{4}\) = 6 ………(i)
2ab = (a² + b²) – (a – b)² = 468 – 36 = 432
(a + b)² = a² + b² + 2ab = 468 + 432 = 900
⇒ a + b = 30 ……..(ii)
ସମୀକରଣ (i) ଓ (ii)କୁ ଯୋଗକଲେ a – b + a + b = 6 + 30 = 36
⇒ 2a = 36 ⇒ a = = 18 ମି., b = 30 a 30 18 = 12 ମି.
∴ ବହୁଭୁଜର ବାହୁ ଦୈର୍ଘ୍ୟ 18 ମି. ଓ 12 ମି. ।

ବିକଳ୍ପ ପ୍ରଣାଳୀ : a² + b² = 468 ଏବଂ a – b = 6
a – b = 6 = b = a – 6
∴ a² + (a – b)² = 468⇒ 2a² – 12a + 36 = 468
2a² – 12a – 432 = 0 = a² – 6a – 216 = 0
⇒ (a – 18) (a + 12) = 0 ⇒ a = 18 ବା -12
ଏଠାରେ a = 18 ଗ୍ରହଣୀୟ ଏବଂ a = -12 ଅଗ୍ରହଣୀୟ
ଯଦି a = 18 ହୁଏ, ଦେବେ b = 18 – 6 = 12
∴ ବର୍ଗକ୍ଷେତ୍ର ବାହୁର ଦୈର୍ଘ୍ୟ 18 ମି. ଓ ଅନ୍ୟଟିର ଦୈର୍ଘ୍ୟ 12 ମି. ।

Question 10.
ଜଣେ ବ୍ୟକ୍ତି ତାଙ୍କ ଚାଲିବାର ବେଗକୁ ଯଦି ଘଣ୍ଟା ପ୍ରତି 1 କି.ମି. ବୃଦ୍ଧି କରେ, ତେବେ 2 କି.ମି. ରାସ୍ତା ଅତିକ୍ରମ କରିବା ପାଇଁ 10 ମିନିଟ୍ କମ୍ ସମୟ ନେଇଥା’ନ୍ତା । ତେବେ ବ୍ୟକ୍ତିର ଚାଲିବାର ଘଣ୍ଟା ପ୍ରତି ବେଗ ସ୍ଥିର କର ।
ସମାଧାନ :
ମନେକର ବ୍ୟକ୍ତିଙ୍କର ଚାଲିବାର ଘଣ୍ଟାପ୍ରତି ବେଗ = x କି.ମି. ।
ଏହି ବେଗରେ 2 କି.ମି. ରାସ୍ତା ଅତିକ୍ରମ କରିବାପାଇଁ ସମୟ ଲାଗିଲା = \(\frac{2}{x}\) ଘଣ୍ଟା ।
ଯଦି ତାଙ୍କର ଚାଲିବାର ଘଣ୍ଟାପ୍ରତି ବେଗ 1 କି.ମି. ବୃଦ୍ଧି ହୁଏ, ତେବେ ତାଙ୍କର ବେଗ = (x+1) କି.ମି. ।
ବେଗ ବୃଦ୍ଧି ହେଲେ 2 କି.ମି. ରାସ୍ତା ଅତିକ୍ରମ କରିବାକୁ ସମୟ ଲାଗିବ = \(\frac{2}{x+1}\) ଘଣ୍ଟା ।
ପ୍ରଶ୍ବାନୁସାରେ, \(\frac{2}{x}-\frac{2}{x+1}=\frac{10}{60}\) (∵ 10 ମିନିଟ = \(\frac{10}{60}\) ଘଣ୍ଟା ।)

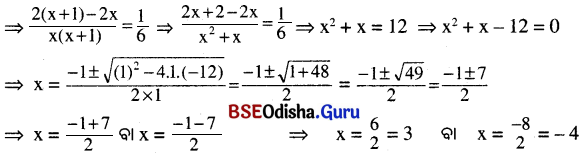
x = – 4 ଗ୍ରହଣୀୟ ନୁହେଁ (କାରଣ ବେଗ ଋଣାତ୍ମକ ହେବା ଅସମ୍ଭବ) ।
∴ ବ୍ୟକ୍ତିଙ୍କର ଚାଲିବାର ଘଣ୍ଟାପ୍ରତି ବେଗ 3 କି.ମି. ।

Question 11.
ଏକ ନୌକାର ବେଗ ସ୍ଥିର ଜଳରେ 15 କି.ମି. ପ୍ରତି ଘଣ୍ଟା । ଏହା ସ୍ରୋତର ପ୍ରତିକୂଳରେ 30 କି.ମି. ଅତିକ୍ରମ କରି ପୁନଶ୍ଚ (ଅନୁକୂଳରେ) ଫେରି ଆସିବାକୁ 4 ଘଣ୍ଟା 30 ମି. ସମୟ ନେଲା । ତେବେ ସ୍ରୋତର ଘଣ୍ଟା ପ୍ରତି ବେଗ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ :
ଗୋଟିଏ ନୌକାର ବେଗ ସ୍ଥିର ଜଳରେ 15 କି.ମି.|ଘଣ୍ଟା ।
ମନେକର ସ୍ରୋତର ବେଗ x କି.ମି./ଘଣ୍ଟା ।
ସ୍ରୋତର ଅନୁକୂଳରେ ନୌକାଟି 1 ଘଣ୍ଟାରେ ଯିବ (15 + x) କି.ମି. ।
ସ୍ରୋତର ପ୍ରତିକୂଳରେ ନୌକାଟି 1 ଘଣ୍ଟାରେ ଯିବ (15 – x) କି.ମି. ।
ସ୍ରୋତର ଅନୁକୂଳରେ 30 କି.ମି. ଯିବାକୁ ସମୟ ଲାଗିବ = \(\frac{30}{15+x}\) ଘଣ୍ଟା । ଏବଂ
ସ୍ରୋତର ପ୍ରତିକୂଳରେ 30 କି.ମି. ଯିବାକୁ ସମୟ ଲାଗିବ = \(\frac{30}{15-x}\) ଘଣ୍ଟା ।
ପ୍ରଶ୍ନ ନୁସାରେ, \(\frac{30}{15+x}+\frac{30}{15-x}=4\frac{1}{2}\)
⇒ 30(\(\frac{15-x+15+x}{(15+x)(15-x)}\)) = \(\frac{9}{2}\)
⇒ \(\frac{30×30}{225-x²}=\frac{9}{2}\) ⇒ 1800 = 9 (225 – x²)
⇒ 225 – x² = \(\frac{1800}{9}\) = 200 ⇒ 225 – 200 = x² ⇒ x² = 25 ⇒ x= √25 = 5
∴ ସ୍ରୋତର ବେଗ 5 କି.ମି./ ଘଣ୍ଟା ।

Question 12.
ଗୋଟିଏ ଶ୍ରେଣୀର ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ସଂଖ୍ୟକ ଛାତ୍ରଙ୍କ ମଧ୍ୟରେ 250 ଟଙ୍କାକୁ ସମାନ ଭାଗରେ ବଣ୍ଟାଗଲା । ଯଦି 25 ଜଣ ଛାତ୍ର ଅଧ‌ିକ ହୋଇଥା’ନ୍ତେ, ତେବେ ପ୍ରତ୍ୟେକ 0.50 ଟଙ୍କା ଲେଖାଏଁ କମ୍ ପାଇଥା’ନ୍ତେ । ଶ୍ରେଣୀର ଛାତ୍ର ସଂଖ୍ୟା ସ୍ଥିର କର ।
ମନେକର ଶ୍ରେଣୀର ଛାତ୍ର ସଂଖ୍ୟା x ଜଣ ।
x ଜଣ ଛାତ୍ରଙ୍କ ମଧ୍ୟରେ 250 ଟଙ୍କାକୁ ସମାନ ଭାଗରେ ବାଣ୍ଟିଲେ ଜଣକା ପାଇବେ = \(\frac{250}{x}\) ଟଙ୍କା
25 ଜଣ ଛାତ୍ର ଅଧ୍ଵ ହେଲେ ଛାତ୍ର ସଂଖ୍ୟା = (x + 25) ଜଣ ।
25 ଜଣ ଛାତ୍ର ଅଧ୍ୟା ହେଲେ ଜଣକା ପାଇବେ = (\(\frac{250}{x}\) – 0.50) ଟଙ୍କା
ପ୍ରଶ୍ନନୁସାରେ, (x + 25)(\(\frac{250}{x}\) – 0.50) = 250
⇒ (x + 25)(500 – x) = 500x ⇒ 500x – x² + 12500 – 25x = 500x
⇒ x² + 25x – 12500 = 0

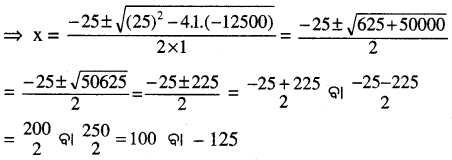
x = – 125 ଗ୍ରହଣୀୟ ନୁହେଁ, କାରଣ ଛାତ୍ର ସଂଖ୍ୟା ଋଣାତ୍ମକ ହେବନାହିଁ ।
⇒ x = 100 ∴ ଶ୍ରେଣୀର ଛାତ୍ରସଂଖ୍ୟା 100 ।

Question 13.
ଗୋଟିଏ ଆୟତକ୍ଷେତ୍ରର ଦୈର୍ଘ୍ୟ, ପ୍ରସ୍ଥ ଅପେକ୍ଷା 8 ମିଟର ଅଧୀକ । କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ 240 ବର୍ଗ ମିଟର ହେଲେ କ୍ଷେତ୍ରଟିର ପରିସୀମା କେତେ ?
ସମାଧାନ :
ଗୋଟିଏ ଆୟତକ୍ଷେତ୍ରର ଦୈର୍ଘ୍ୟ, ପ୍ରସ୍ଥ ଅପେକ୍ଷା 8 ମି. ଅଧ୍ବକ ।
ମନେକର ଆୟତକ୍ଷେତ୍ରର ପ୍ରସ୍ଥ = x ମି., ଦୈର୍ଘ୍ୟ = (x + 8) ମିଟର,
ଆୟତକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = (x + 8) x ବର୍ଗ ମିଟର ।
ପ୍ରଶ୍ନନୁସାରେ, (x + 8) x = 240
⇒x² + 8x = 240 ⇒ x² + 8x – 240 = 0
⇒ x² + 20x – 12x – 240 = 0
⇒ x(x + 20) – 12(x + 20) = 0
⇒ (x + 20) (x – 12) = 0
⇒ x + 20 = 0 ବା x – 12 = 0
⇒x = -20 (ଅସମ୍ଭବ) ବା x = 12
∴ ଆୟତକ୍ଷେତ୍ରର ପ୍ରସ୍ଥ = 12 ମି., ଦୈର୍ଘ୍ୟ = x + 8 = 12 + 8 = 20 ମି.
ଆୟତକ୍ଷେତ୍ରର ପରିସୀମା = 2 (ଦୈର୍ଘ୍ୟ + ପ୍ରସ୍ଥ) = 2 (20 + 12) = 2 × 32 = 64 ମିଟର ।

Question 14.
ଏକ ରେଳଗାଡ଼ି 300 କି.ମି. ଦୀର୍ଘ ଯାତ୍ରା ପଥରେ ସମାନ ବେଗରେ ଗତି କରୁଥିଲା । ଯଦି ଗାଡ଼ିର ବେଗ ଘଣ୍ଟାପ୍ରତି 5 କି.ମି. ଅଧ୍ଵ ହୋଇଥା’ନ୍ତା, ତେବେ ଗାଡ଼ିଟି ନିର୍ଦ୍ଦିଷ୍ଟ ସମୟର 2 ଘଣ୍ଟା ପୂର୍ବରୁ ଯଥା ସ୍ଥାନରେ ପହଞ୍ଚିନ୍ତା । ତେବେ ଗାଡ଼ିର ଘଣ୍ଟାପ୍ରତି ବେଗ ନିରୂପଣ କର ।
ସମାଧାନ :
ମନେକର ଗାଡ଼ିର ଘଣ୍ଟାପ୍ରତି ବେଗ x କି.ମି. ।
ଏହି ବେଗରେ ଗାଡ଼ିକୁ 300 କି.ମି. ଯିବାକୁ ସମୟ ଲାଗିବ \(\frac{300}{x}\) ଘଣ୍ଟା ।
ମାତ୍ର ଘଣ୍ଟାକୁ x + 5 କି.ମି. ବେଗରେ 300 କି.ମି. ଯିବାକୁ ସମୟ ଲାଗିବ \(\frac{300}{x+5}\) ଘଣ୍ଟା ।
ପ୍ରଶ୍ନନୁସାରେ, \(\frac{300}{x}-\frac{300}{x+5}=2\) ⇒ 300(\(\frac{1}{x}-\frac{1}{x+5}\) = 2

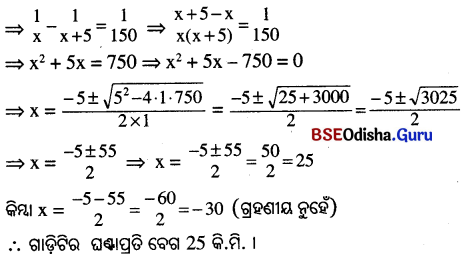
Question 15.
ଏକ ଆୟତାକାର ପଡ଼ିଆର ଦୈର୍ଘ୍ୟ 25 ମିଟର, ପ୍ରସ୍ଥ 16 ମିଟର ଓ ପଡ଼ିଆର ଚତୁଃପାର୍ଶ୍ବରେ ସମାନ ଚଉଡ଼ାର ଏକ ରାସ୍ତା ଅଛି । ଯଦି ଚତୁଃପାର୍ଶ୍ଵରେ ଥ‌ିବା ରାସ୍ତାର କ୍ଷେତ୍ରଫଳ 230 ବର୍ଗମିଟର ହୁଏ, ତେବେ ରାସ୍ତାର ଚଉଡ଼ା ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ :
ମନେକର ରାସ୍ତାର ଚଉଡ଼ା = x ମିଟର
ଆୟତାକାର ପଡ଼ିଆର ଦୈର୍ଘ୍ୟ = 25 ମିଟର, ପ୍ରସ୍ଥ = 16 ମିଟର ।
.. ବାହାର ଆୟତାକାର ପଡ଼ିଆର ଦୈର୍ଘ୍ୟ = (25 + 2x) ମି. ଓ ପ୍ରସ୍ଥ = (16 + 2x) ମି.
ପ୍ରଶ୍ନନୁସାରେ, (25 + 2x) (16 + 2x) – 25 × 16 = 230
⇒ 400 + 50x + 32x + 4x² – 400 = 230
⇒ 4x² + 82x – 230 = 0 ⇒ 2x² + 41x – 115=0
ଏଠାରେ a = 2, b = 41, c = -115

∴ ରାସ୍ତାର ଚଉଡ଼ା 2.5 ମିଟର ।
ବି.ଦ୍ର. : ଉତ୍ପାଦକୀକରଣଦ୍ୱାରା 2x² + 41x – 115 = 0 ର ସମାଧାନ ମଧ୍ୟ ସମ୍ଭବ ।

Question 16.
କେତେକ ଛାତ୍ରଛାତ୍ରୀ ଏକ ବଣଭୋଜିର ଆୟୋଜନ କଲେ । ଖାଦ୍ୟ ଅଟକଳ (Budget) 480 ଟଙ୍କା ଥିଲା । ସେମାନଙ୍କ ମଧ୍ୟରୁ 8 ଜଣ ବଣଭୋଜିକୁ ଗଲେ ନାହିଁ; ଯାହା ଫଳରେ ଖାଦ୍ୟ ବାବଦ ଖର୍ଚ୍ଚ ଜଣପିଛା 10 ଟଙ୍କା ବଢ଼ିଗଲା । ତେବେ କେତେଜଣ ଛାତ୍ରଛାତ୍ରୀ ବଣଭୋଜିକୁ ଯାଇଥିଲେ ?
ସମାଧାନ :
ମନେକର x ଜଣ ଛାତ୍ରଛାତ୍ରୀ ବଣଭୋଜିର ଆୟୋଜନ କରିଥିଲେ ।
ଖାଦ୍ୟ ଅଟକଳ = 480 ଟଙ୍କା ଥିଲା ।
ଜଣେ ପିଲା ପିଛା ଖର୍ଚ୍ଚ ପଡ଼ିଥାନ୍ତା = \(\frac{480}{x}\)
8 ଜଣ ବଣଭୋଜିକୁ ନଯିବାରୁ ପିଲା ସଂଖ୍ୟା = x – 8
∴ ବଣଭୋଜିକୁ ଯାଇଥବା ଛାତ୍ରଛାତ୍ରୀ ସଂଖ୍ୟା = x – 8
x – 8 ଜଣ ପିଲାଙ୍କ ପାଇଁ ଖର୍ଚ୍ଚ 480 ଟଙ୍କା ହେଲେ, ଜଣେ ପିଲା ପିଛା ଖର୍ଚ୍ଚ ପଡ଼ିଲା = \(\frac{480}{x-8}\) ଟଙ୍କା ।
ପ୍ରଶ୍ନନୁସାରେ, \(\frac{480}{x-8}-\frac{480}{x}=10\) ⇒ 480(\(\frac{x-x+8}{(x-8)x}\)) = 10
⇒ \(\frac{8}{x²-8x}=\frac{1}{48}\) ⇒ x² – 8x = 384
⇒ x² -8x – 384 = 0 ⇒ x² – 24x + 16x – 384 = 0
⇒ x (x – 24) + 16 (x – 24) = 0 ⇒ (x – 24) (x + 16) = 0 ⇒x-24=0 Ql x + 16 = 0
⇒x= 24 Q1 x = – 16
∴ ବଣଭୋଜିକୁ ଯାଇଥବା ଛାତ୍ରଛାତ୍ରୀ ସଂଖ୍ୟା = x – 8 = 24 – 8 = 16 ଜଣ।

Question 17.
ସମାଧାନ ଜର :
(i) (x + 1) (x + 2) (x + 3) (x + 4) = 120
(ii) \(5 \sqrt{\frac{3}{x}}+7 \sqrt{\frac{x}{3}}=22 \frac{2}{3}\)
(iii) 3x + \(\frac{5}{16x}\) – 2 = 0
(iv) \(\frac{2x+1}{x+1}^4-6\frac{2x+1}{x+1}^2+8=0\)
(v) (3x² – 8)² – 23 (3x² – 8) + 76 = 0
(vi) 5 (5^x + 5^-x) = 26
(vii) (x² – 2x)² – 4 (x² – 2x) + 3 = 0
(viii) x^-4 – 5x^-2 + 4 = 0
(ix) \(2\left(x^2+\frac{1}{x^2}\right)-3\left(x+\frac{1}{x}\right)-1=0\)
(x) \(\frac{3}{√2x}-\frac{√2x}{5}=5 \frac{9}{10}\)
(xi) \(\frac{x}{x+1}+\frac{x+1}{x}=\frac{34}{15}\) (x ≠ 0, x ≠ – 1)
(xii) x (2x + 1) (x – 2) (2x – 3) = 63
(xiii) \(\frac{x-3}{x+3}+\frac{x+3}{x-3}=6 \frac{6}{7}\) (x ≠ – 3, 3)
(xiv) \(3\left(x^2+\frac{1}{x^2}\right)+4\left(x-\frac{1}{x}\right)-6=0\)
(xv) (\(\frac{x+1}{x-1}\))² – (\(\frac{x+1}{x-1}\)) – 2 = 0
(xvi) \(\sqrt{2x+9}\) + x = 13
(xvii) \(\sqrt{2 x+\sqrt{2 x+4}}\) = 4
ସମାଧାନ :
(i) (x + 1) (x + 2) (x + 3) (x + 4) = 120
= (x+1) (x+4) (x + 2) (x + 3) = 120 ⇒ (x² + 5x + 4) (x² + 5x + 6) = 120
ମନେକର x² + 5x = p
ପ୍ରଭେ ସମୀକରଣରଟି (p + 4) (p + 6) = 120
⇒ p² + 10p+ 24 = 120 ⇒ p² + 10p + 24 – 120 = 0
⇒p² + 10p – 96 = 0 ⇒ p² + 16p – 6p – 96 = 0
⇒p(p + 16) – 6(p + 16) = 0 ⇒ (p + 16) (p – 6) = 0
⇒p + 16 = 0 କିମ୍ବା p – 6 = 0 ⇒ p = -16 କିମ୍ବା p=6
p ପରିବର୍ତ୍ତେ x + 5x ନେଲେ x² + 5x = – 16
⇒ x² + 5x + 16 = 0 ଏଠାରେ D = b² – 4ac = 25 – 64 = -39
⇒ D < 0 ବୀଜଦ୍ଵୟ ଅବାସ୍ତବ, ଗ୍ରହଣୀୟ ନୁହେଁ ।
ପୁନଶ୍ଚ x² + 5x = 6
⇒ x²+5x – 6 = 0, ଏଠାରେ a = 1, b = 5, c = – 6

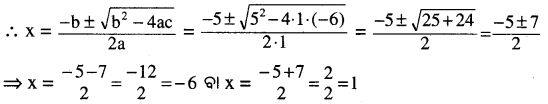
∴ ନିର୍ଦେୟ ସମାଧାନ – 6 ଓ 1 ।

(ii) \(5 \sqrt{\frac{3}{x}}+7 \sqrt{\frac{x}{3}}=22 \frac{2}{3}\)
ମନେକର \(\sqrt{\frac{3}{x}}\) = p = \(\sqrt{\frac{x}{3}}=\frac{1}{p}\)
ପ୍ରଭେ ସମୀକରଣରଟି 5p + \(\frac{7}{p}\) = \(\frac{68}{3}\) ⇒ \(\frac{5p²+7}{p}=\frac{68}{3}\)
⇒ 15p² + 21 = 68p ⇒ 15p² – 68p + 21 = 0, ଏଠାରେ a = 15, b = -68, c = 21

ବି.ଦ୍ର. : x ର ମାନ \(\frac{25}{147}\) ଦେଇ ଦତ୍ତ ସମୀକରଣଟି ସିଦ୍ଧ ହେଉଛି କି ନାହିଁ ପରୀକ୍ଷା କରି ଦେଖ । ଯଦି ନ ହେଉଥାଏ ତେବେ ସମାଧାନ କେବଳ 27 ହେବ । ଏଠାରେ \(\frac{25}{147}\) ଅଗ୍ରହଣୀୟ ।

(iii) 3x + \(\frac{5}{16x}\) – 2 = 0
⇒ \(\frac{48x²+5-32x}{16x}=0\) ⇒ 48x² + 5 – 32x = 0

(iv) \(\frac{2x+1}{x+1}^4-6\frac{2x+1}{x+1}^2+8=0\)
ମନେକର (2x+1)= p ଦଉ ସମୀକରଣ p⁴ – 6p² + 8 = 0 => p⁴ – 4p² – 2p² + 8 = 0
⇒ p²(p² – 4) – 2(p² – 4) = 0 ⇒ (p² – 4)(p² – 2) = 0
⇒ p² – 4 = 0 ବା p² – 2 = 0 ⇒ p² = 4 ବା p² = 2 ⇒ p = ±2 ବା p = ±√2
\(\frac{2x+1}{x+1}=2\), x ର ମାନ ନିର୍ଦୟ ଅସମ୍ଭବ |

ବି.ଦ୍ର. :
(\(\frac{2x+1}{x+1}\))² = p ମନେକର
ଦଉ ସମୀକରଣ p² – 6p + 8 = 0 ⇒ p = 4 ବା p = 2
\(\frac{2x+1}{x+1}\) = 4 ⇒ \(\frac{2x+1}{x+1}\) = ±2 ନେଇ x ର ମାନ ସ୍ଥିର କରାଯାଇପାରେ ।
ପୁନଶ୍ଚ (\(\frac{2x+1}{x+1}\))² = 2 = \(\frac{2x+1}{x+1}\) = ±√2 ନେଇ
x ର ମାନ ସ୍ଥିର କରାଯାଇପାରେ ।

(v) ମନେକର 3x² – 8 = p
ପ୍ରଭେ ସମୀକରଣ p² – 23p + 76 = 0 । ଏଠାରେ a = 1, b = 23, c = 76

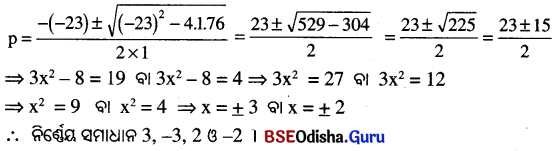
(vi) ମନେକର 5^x = p
ପ୍ରଭେ ସମୀକରଣ 5(p + \(\frac{1}{p}\)) = 26 ⇒ \(\frac{5(p²+1)}{p}\) = 26
⇒ 5p² + 5 = 26p ⇒ 5p² – 26p + 5 = 0
⇒ 5p² – 25p – p + 5 = 0 ⇒ 5p (p -5) – 1(p – 5) = 0
⇒ (p – 5) (5p – 1) = 0 ⇒ p – 5 = 0 କିମ୍ବା 5p – 1 = 0
⇒p = 5 କିମ୍ବା p = \(\frac{1}{5}\) ⇒5^x = 5¹ କିମ୍ବା 5^x = 5^-1
⇒ x = 1 କିମ୍ବା x = -1
∴ ନିର୍ଦେୟ ସମାଧାନ 1 ଓ -1 ।

(vii) ମନେକର x² – 2x = p
ପ୍ରଭେ ସମୀକରଣ, p² – 4p + 3 = 0
p² – 3p – p + 3 = 0 p(p – 3) – 1(p – 3) = 0
⇒(p – 3) (p – 1) = 0 ⇒ p – 3 = 0 ବା p – 1 = 0
⇒ p = 3 ବା p = 1
x² – 2x = 3 ⇒ x² – 2x – 3 = 0
⇒ x – 3x + x – 3 = 0 ⇒ x (x – 3) + 1 (x – 3) = 0
⇒ (x – 3) (x + 1) = 0 ⇒ x – 3 = 0 ବା x + 1 = 0
⇒ x = 3 ବା x = – 1
ପୁନଶ୍ଚ x² – 2x = 1 ⇒ x² – 2x – 1 = 0 । ଏଠାରେ a = 1, b = – 2, c = – 1 ବା

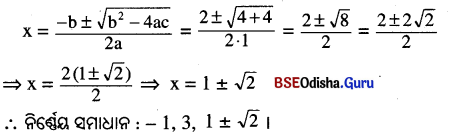
(viii) ମନେକର x^-2 = p। ଦଉ ସମୀକରଣ, p² – 5p + 4 = 0

(ix) \(2\left(x^2+\frac{1}{x^2}\right)-3\left(x+\frac{1}{x}\right)-1=0\)

ପୁନଶ୍ଚ x + \(\frac{1}{x}\) = -1 ⇒ \(\frac{x²+1}{x}\) = -1 ⇒ x² + 1 = -x ⇒ x² + x + 1 = 0
ସମୀକରଣ x² + x + 1 = 0 ରେ D < 0 ହେତୁ ବାସ୍ତବ ବୀଜ ସମ୍ଭବ ନୁହେଁ ।
∴ ନିର୍ଦେୟ ସମାଧାନ 2 ଓ \(\frac{1}{2}\) ।

(x) ମନେକର \(\frac{1}{√2x}\) = p; √2x = \(\frac{1}{p}\)
ପ୍ରଭେ ସମୀକରଣ, 3p – \(\frac{1}{5p}=\frac{59}{10}\)
⇒ \(\frac{15p²-1)}{5p}=\frac{59}{10}\) ⇒ \(\frac{15p²-1)}{p}=\frac{59}{2}\)
⇒ 30p² – 2 = 59p ⇒ 30p² – 59p – 2 = 0
⇒30p² – 60p + p – 2 = 0 ⇒ 30p (p – 2) + 1 (p – 2) = 0
⇒ (p – 2) (30p+1) = 0 ⇒ p – 2 = 0 ବା 30p + 1 = 0
⇒p = 2 ବା p = \(– \frac{1}{30}\)
p = 2 ⇒ \(\frac{1}{√2x}\) = 2 ⇒ \(\frac{1}{2x}\) = 4 ⇒ x = \(\frac{1}{8}\)
p = \(– \frac{1}{30}\) ⇒ \(\frac{1}{√2x}=- \frac{1}{30}\) = \(\frac{1}{2x}=\frac{1}{900}\)
⇒ 2x = 900 ⇒ x = 450
x = 450 ପୁନଶ୍ଚ ସମୀକରଣରେ ବସାଇଲେ ଏହା ସମୀକରଣକୁ ସିଦ୍ଧ କରିବ ନାହିଁ ।
ତେଣୁ ଏହା ଗ୍ରହଣୀୟ ନୁହେଁ ।
∴ xର ଏକମାତ୍ର ମୂଲ୍ୟ \(\frac{1}{8}\) ଅଟେ ।

(xi) \(\frac{x}{x+1}+\frac{x+1}{x}=\frac{34}{15}\)
⇒ \(\frac{x²+(x+1)²}{x(x+1)}=\frac{34}{15}\) ⇒ \(\frac{x²+x²+2x+1}{x²+x)}=\frac{34}{15}\)
⇒ \(\frac{2x²+2x+1}{x²+x}=\frac{34}{15}\) ⇒ 34 (x² + x) = 15 (2x² + 2x + 1)
⇒ 34x² + 34x = 30x² + 30x + 15
⇒ 34x² – 30×2 + 34x – 30x – 15 = 0 ⇒ 4x² + 4x – 15 = 0
⇒ 4x² + 10x – 6x – 15=0 ⇒ 2x (2x + 5) – 3 (2x + 5) = 0
⇒ (2x + 5) (2x-3)=0 ⇒ x = \(\frac{-5}{2}\) ବା x = \(\frac{3}{2}\)
∴ ନିର୍ଦେୟ ସମାଧାନ \(\frac{3}{2}\) ଓ \(\frac{-5}{2}\) ।

(xii) x (2x + 1) (x – 2) (2x – 3) = 63 ⇒ {x (2x – 3)} {(2x + 1) (x – 2)} = 63
⇒ (2x² – 3x) (2x² -3x – 2) = 63
ମନେକର 2x² – 3x = p
∴ p (p – 2) = 63 ⇒ p² – 2p – 63 = 0
⇒p² – 9p + 7p – 63 = 0 ⇒ p (p – 9) + 7 (p – 9) = 0
(p – 9) (p + 7) =0 p – 9 = 0 p + 7 = 0
⇒ p = 9 ବା p = -7
∴ p = 9 ⇒ 2x² – 3x = 9 ⇒ 2x² – 3x – 9 = 0
⇒ 2x² – 6x + 3x – 9 = 0 ⇒ 2x (x – 3) + 3 (x – 3) = 0
⇒ (x – 3) (2x + 3) = 0 ⇒ x = 3 ବା x = \(\frac{-3}{2}\)
p = -7 ⇒ 2x² – 3x + 7 = 0
ଏଠାରେ b² – 4ac = 9 – 56 = – 47
D < 0 xର ଅବାବ ମାନ ଗ୍ରହଣୀୟ ନୁହେଁ ।
∴ ନିର୍ଦେୟ ସମାଧାନ 3 ଓ \(\frac{3}{2}\) ।

(xiii) ମନେକର \(\frac{x-3}{x+3}=p\), ପ୍ରଭଦ ସମୀକରଣଟି p – \(\frac{1}{p}=\frac{48}{7}\)
⇒ \(\frac{p²-1}{p}=\frac{48}{7}\) ⇒ 7(p²-1) = 48p ⇒ 7p² – 48p – 7 = 0
ଏଠାରେ a = 7, b = -48, c = -7

∴ ନିର୍ଦେୟ ସମାଧାନ -4 ଓ \(\frac{9}{4}\) ।

(xiv) \(3\left(x^2+\frac{1}{x^2}\right)+4\left(x-\frac{1}{x}\right)-6=0\)

(xv) (\(\frac{x+1}{x-1}\))² – (\(\frac{x+1}{x-1}\)) – 2 = 0
ମନେକର \(\frac{x+1}{x-1}=p\)
ଦଉ ସମାଜରଣ p² – p – 2 = 0
ଏଠାରେ a = 1, b = -1, c = -2

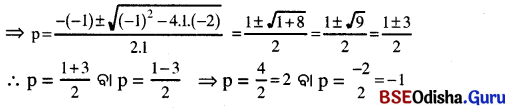
ଯଦି p = 2 ⇒ \(\frac{x+1}{x-1}\) = 2 ⇒ x + 1 = 2(x – 1) ⇒ x + 1= 2x – 2
⇒ x – 2x = -2 -1 ⇒ -x = -3 ⇒ x = 3
ଯଦି p = 1 ⇒ \(\frac{x+1}{x-1}\) = -1 ⇒ x + 1 = -1(x – 1) ⇒ x+ 1 = -x + 1
⇒ x + x = 1 – 1 ⇒ 2x = 0 ⇒ x = 0

(xvi) \(\sqrt{2x+9}\) + x = 13

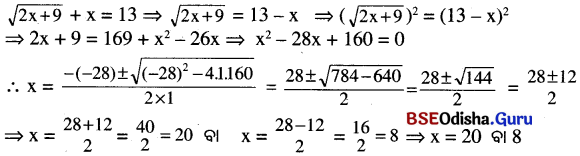
x = 8 ଦ୍ବାରା ଦତ୍ତ ସମୀକରଣଟି ସିଦ୍ଧ ହେଉଛି; ମାତ୍ର x = 20 ହେଲେ, \(\sqrt{2x+9}\) + x ≠ 13
∴ ଦତ୍ତ ସମୀକରଣର ସମାଧାନ x = 8 ।

(xvii) \(\sqrt{2 x+\sqrt{2 x+4}}\) = 4

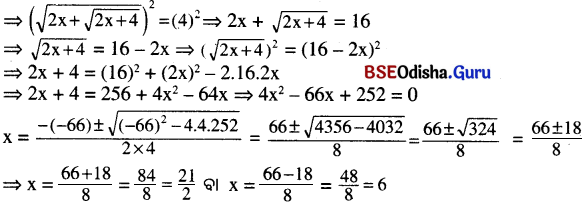
x = 6 ଦ୍ଵାରା ଦତ୍ତ ସମୀକରଣଟି ସିଦ୍ଧ ହେଉଛି; ମାତ୍ର x = \(\frac{21}{2}\) ହେଲେ,
\(\sqrt{2 x+\sqrt{2 x+4}}\) ≠ 4 (ଦତ୍ତ ସମୀକରଣଟି ସିଦ୍ଧ ହେଉନାହିଁ)
∴ ନିଶ୍ଚେ ସମୀକରଣର ସମାଧାନ 6।