Odisha State Board Elements of Mathematics Class 12 Solutions CHSE Odisha Chapter 11 Differential Equations Ex 11(a) Textbook Exercise Questions and Answers.
CHSE Odisha Class 12 Math Solutions Chapter 11 Differential Equations Exercise 11(a)
Question 1.
Determine the order and degree of each of the following differential equations.
(i) y sec2 x dx + tan x dy = 0
Solution:
Order: 1, Degree: 1
(ii) \(\left(\frac{d y}{d x}\right)^4\) + y5 = \(\frac{d^3 y}{d x^3}\)
Solution:
Order: 3, Degree: 1
(iii) a\(\frac{d^2 y}{d x^2}\) = \(\left\{1+\left(\frac{d y}{d x}\right)^2\right\}^{\frac{3}{2}}\)
Solution:
Order: 2, Degree: 2
(iv) tan-1\(\sqrt{\frac{d y}{d x}}\) = x
Solution:
Order: 1, Degree: 1
(v) ln\(\left(\frac{d^2 y}{d x^2}\right)\) = y
Solution:
Order: 2, Degree: 1
![]()
(vi) \(\frac{\frac{d y}{d t}}{y+\frac{d y}{d t}}\) = \(\frac{y t}{d y}\)
Solution:
Order: 1, Degree: 2
(vii) \(\frac{d^2 y}{d u^2}\) = \(\frac{3 y+\frac{d y}{d u}}{\sqrt{\frac{d^2 y}{d u^2}}}\)
Solution:
Order: 2, Degree: 3
(viii) \(e^{\frac{d z}{d x}}\) = x2
Solution:
Order: 1, Degree: 1
Question 2.
Form the differential equation by eliminating the arbitrary constants in each of the following cases.
(i) y = A sec x
Solution:
y = A sec x
Then \(\frac{d y}{d x}\) = A sec x tan x = y tan x
(ii) y = C tan-1 x
Solution:
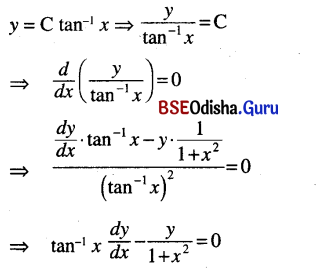
(iii) y = Aet + Be2t
Solution:

(iv) y = Ax2 + Bx
Solution:
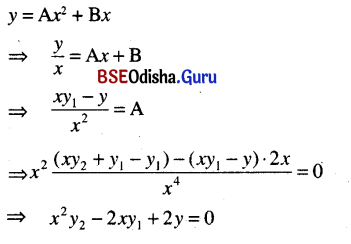
(v) y = -acos x + b sin x
Solution:
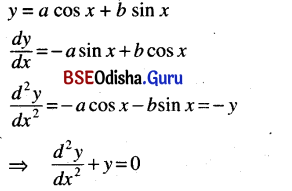
(vi) y = a sin-1 x + b cos-1 x
Solution:

![]()
(vii) y = at + bet
Solution:

(viii) y = a sin t + bet
Solution:

(ix) ax2 + by = 1
Solution:
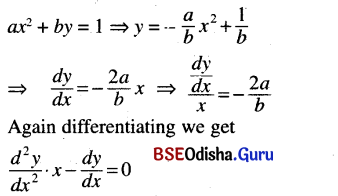
Question 3.
Find the general solution ofthe following differential equations.
(i) \(\frac{d y}{d x}\) = \(\frac{e^{2 x}+1}{e^x}\)
Solution:
\(\frac{d y}{d x}\) = \(\frac{e^{2 x}+1}{e^x}\)
⇒ y = ∫(ex + e-x) dx = ex – e-x + C
(ii) \(\frac{d y}{d x}\) = x cos x
Solution:
\(\frac{d y}{d x}\) = x cos x
⇒ y = ∫x cos x dx
= x . sin x – ∫sin x dx – x sin x + cos x + C
(iii) \(\frac{d y}{d x}\) = t5 log t
Solution:
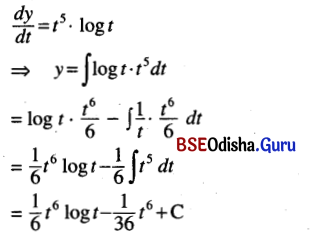
![]()
(iv) \(\frac{d y}{d x}\) = 3t2 + 4t + sec2 t
Solution:
\(\frac{d y}{d x}\) = 3t2 + 4t + sec2 t
⇒ y = t3 + 2t2 + tan t + C
(v) \(\frac{d y}{d x}\) = \(\frac{1}{x^2-7 x+12}\)
Solution:
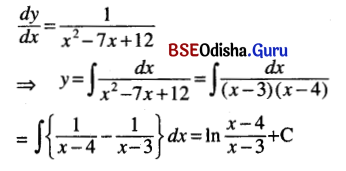
(vi) \(\frac{d y}{d u}\) = \(\frac{u+1}{\sqrt{3 u^2+6 u+5}}\)
Solution:

(vii) (x2 + 3x + 2) dy – dx = 0
Solution:

(viii) \(\frac{d y}{d t}\) = \(\frac{\sin ^{-1} t e^{\sin ^{-1} t}}{\sqrt{1-t^2}}\)
Solution:
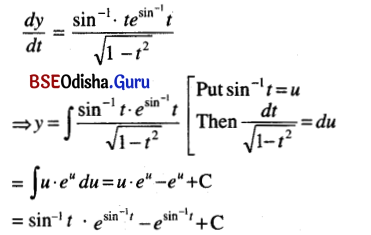
Question 4.
Solve the following differential equations.
(i) \(\frac{d y}{d x}\) = y + 2
Solution:
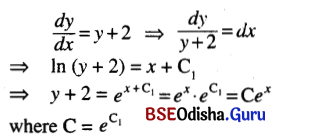
(ii) \(\frac{d y}{d t}\) = \(\sqrt{1-y^2}\)
Solution:
\(\frac{d y}{d t}\) = \(\sqrt{1-y^2}\)
⇒ \(\frac{d y}{\sqrt{1-y^2}}\) = dt
⇒ sin-1 y = t + C
(iii) \(\frac{d y}{d z}\) = sec y
Solution:
\(\frac{d y}{d z}\) = sec y
⇒ cos y dy = dz
⇒ sin y = z + C
(iv) \(\frac{d y}{d x}\) = ey
Solution:
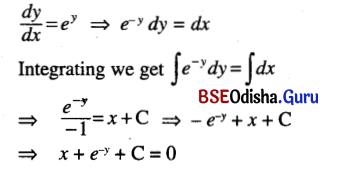
(v) \(\frac{d y}{d x}\) = y2 + 2y
Solution:
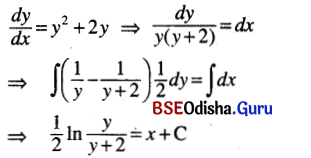
(vi) dy + (y2 + 1) dx = 0
Solution:
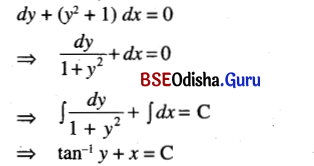
![]()
(vii) \(\frac{d y}{d x}\) + \(\frac{e^y}{y}\) = 0
Solution:

(viii) dx + cot x dt = 0
Solution:
dx + cot x dt = 0
⇒ tan x dx + dt = 0
⇒ ∫tan x dx + ∫dt = C1
⇒ In sec x + t = C1
⇒ In sec x = C1 – t
⇒ sec x = \(e^{C_1}\) . e-t
⇒ cos x = \(e^{-C_1}\) . et
⇒ cos x = Cet where C = \(e^{-C_1}\)
Question 5.
Obtain the general solution of the following differential equations.
(i) \(\frac{d y}{d x}\) = (x2 + 1) (y2 + 1)
Solution:
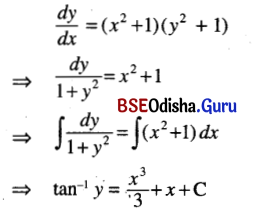
(ii) \(\frac{d y}{d t}\) = e2t+3y
Solution:
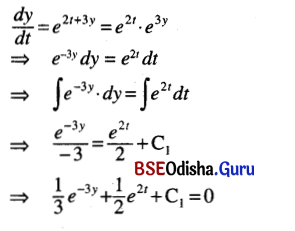
⇒ 2e-3y + 3e2t + 6C1 = 0
⇒ 2e-3y + 3e2t = C
where C = -6C1
(iii) \(\frac{d y}{d z}\) = \(\frac{\sqrt{1-y^2}}{\sqrt{1-z^2}}\)
Solution:

(iv) \(\frac{d y}{d z}\) = \(\frac{x \log x}{3 y^2+4 y}\)
Solution:
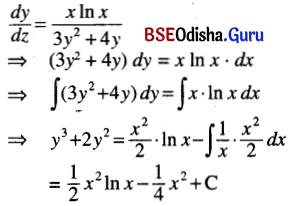
(v) x2\(\sqrt{y^2+3}\) dx + y\(\sqrt{x^3+1}\) dy = 0
Solution:

(vi) tan y dx + cot x dy = 0
Solution:
tan y dx + cot x dy = 0
⇒ tan x . dx + cot y dy = 0
⇒ ∫tan x dx + ∫cot y dy = 0
⇒ -ln cos x + ln siny = ln C
⇒ ln\(\frac{\sin y}{\cos x}\) = ln C
⇒ \(\frac{\sin y}{\cos x}\) = C
⇒ sin y = C cos x
![]()
(vii) (x2 + 7x + 12) dy + (y2 – 6y + 5) dx = 0
Solution:

(viii) y dy + e-y x sin x dx = 0
Solution:
y dy + e-y x sin x dx = 0
⇒ yey dy + x sin x dx = 0
⇒ ∫yey dy + ∫x sin dx = C
[Integrating by parts.
⇒ yey – ∫ey dy + x(-cos x) – ∫(-cos x) dx = C
⇒ yey – ey – x cos x + sin x = C
⇒ (y – 1) ey – x cos x + sin x = C
Question 6.
Solve the following second order equations.
(i) \(\frac{d^2 y}{d x^2}\) = 12x2 + 2x
Solution:

(ii) \(\frac{d^2 y}{d t^2}\) =e2t +e-t
Solution:

(iii) \(\frac{d^2 y}{d \vartheta^2}\) = -sin υ + cos υ + sec2 υ
Solution:
\(\frac{d^2 y}{d \vartheta^2}\) = -sin υ + cos υ + sec2 υ
Integrating we get
\(\frac{d y}{d υ}\) = ∫sin υ dυ + ∫cos υ dυ + ∫sec2 υ dυ
= cos υ + sin υ + tan υ + A
Again integratingwe get
y = ∫(cos υ + sin υ + tan υ + A)dυ + B
where A, B are arbritrary constants.
⇒ y = sin υ – cos υ + ln |sec υ| + A.υ. + B
(iv) cosec x \(\frac{d^2 y}{d x^2}\) = x
Solution:
cosec x \(\frac{d^2 y}{d x^2}\) = x
\(\frac{d^2 y}{d x^2}\) = x sin x
Integrating we get
\(\frac{d y}{d x}\) = ∫x sin x dx + A
= x . (-cos x) – ∫(-cos x) dx + A
= -x cos x + ∫cos x dx + A
= -x cos x + sin x + A
Again integrating we get
y = -∫x cos x dx + ∫sin x + ∫A dx + B
= -{x sin x -∫1 . sin x dx} – cos x + Ax + B
= -x sin x – 2cos x + Ax + B
(v) x2\(\frac{d^2 y}{d x^2}\) + 2 = 0
Solution:
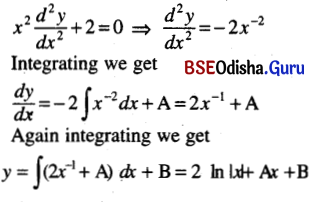
(vi) sec x \(\frac{d^2 y}{d x^2}\) = sec 3x
Solution:

![]()
(vii) \(\frac{d^2 y}{d x^2}\) = sec2 x + cos2 x
Solution:

(viii) e-x\(\frac{d^2 y}{d x^2}\) = x
Solution:
e–x\(\frac{d^2 y}{d x^2}\) = x
⇒ \(\frac{d^2 y}{d x^2}\) = xex
Integrating we get
\(\frac{d y}{d x}\) = ∫xex dx = ∫ex dx + Ax + B
= xex – ex – ex + Ax + B
= (x – 2)ex + Ax + B
Question 7.
Find the particular solutions of the following equations subject to the given conditions.
(i) \(\frac{d y}{d x}\) = cos x, given that y = 2 when x = 0.
Solution:
\(\frac{d y}{d x}\) = cos x
Integrating we get
y = ∫cos x dx = sin x + C
Given that when x = 0, y = 2
So 2 = C
∴ The particular solution is y = sin x + 2
(ii) \(\frac{d y}{d t}\) = cos2 y subject to y = \(\frac{\pi}{4}\) when t = 0.
Solution:
\(\frac{d y}{d t}\) = cos2 y
⇒ sec2 y dy = dt
∫sec2 dy = ∫dt
⇒ tan y = t + C
When t = 0, y = \(\frac{\pi}{4}\)
So tan \(\frac{\pi}{4}\) = C ⇒ C = 1
∴ The particular solution is tan y = t + 1
(iii) \(\frac{d y}{d x}\) = \(\frac{1+y^2}{1+x^2}\) given that y = √3 when x = 1.
Solution:

(iv) \(\frac{d^2 y}{d x^2}\) = 6x given that y = 1 and \(\frac{d y}{d x}\) = 2 when x = 0.
Solution:
\(\frac{d^2 y}{d x^2}\) = 6x ⇒ \(\frac{d y}{d x}\) = 3x2 + 2
When x = 0, \(\frac{d y}{d x}\) = 2
So 2 = A
∴ \(\frac{d y}{d x}\) = 3x2 + 2
Again integrating we get
y = x3 + 2x + B
When x = 0, y = 1
So B = 1.
∴ The particular solution is y = x3 + 2x + 1
Question 8.
(i) Solve : \(\frac{d y}{d x}\) = sec (x + y)
Solution:
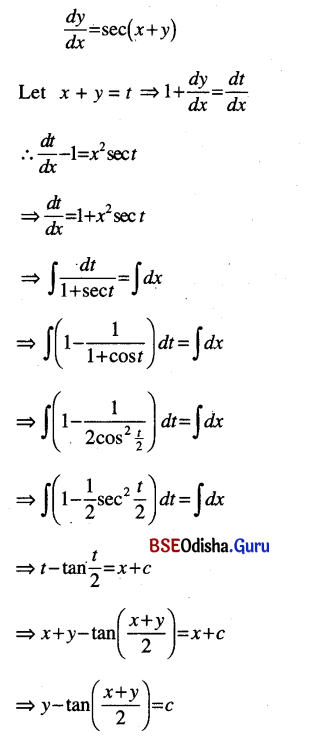
(ii) Solve : \(\frac{d y}{d x}\) = sin(x + y) + cos(x + y)
Solution:

![]()
(iii) Solve : \(\frac{d y}{d x}\) = cos (x + y)
Solution:

(iv) Solve : \(\frac{d y}{d x}\) + 1 = ex+y
Solution:

