Bhagya

Odisha State Board BSE Odisha 7th Class Odia Solutions Chapter 1 କଳାମାଣିକରେ Textbook Exercise Questions and Answers.

BSE Odisha Class 7 Odia Solutions Chapter 1 କଳାମାଣିକରେ

ପାଠ୍ୟପୁସ୍ତକସ୍ଥ ଅଭ୍ୟାସ କାର୍ଯ୍ୟର ଉତ୍ତର

Question ୧।
ଉତ୍ତର କୁହ ।
(କ) ମାତା ଯଶୋଦା କାହିଁକି ଚିନ୍ତିତ ହୋଇପଡ଼ିଛନ୍ତି ?
Answer:
ସ୍ନେହମୟୀ ମାତା ଯଶୋଦା କୃଷ୍ଣଙ୍କ ବନରୁ ଫେରିବା ବିଳମ୍ବରେ ଅଧୀରା ହୋଇପଡ଼ିଛନ୍ତି । ପ୍ରତ୍ୟହ ସନ୍ଧ୍ୟାପୂର୍ବରୁ କୃଷ୍ଣ ଗୋଚାରଣରୁ ଫେରିଆସନ୍ତି; କିନ୍ତୁ ସେଦିନ ସନ୍ଧ୍ୟା ଅତିକ୍ରାନ୍ତ ହୋଇଯାଇଛି; ତେଣୁ ମାତା ଯଶୋଦାଙ୍କ ମନ ଭୟ ଓ ନାନା ଆଶଙ୍କାରେ ବିବ୍ରତ ହୋଇପଡ଼ିଛି ।

(ଖ) ଶ୍ରୀକୃଷ୍ଣଙ୍କୁ କେଉଁ ଖାଦ୍ୟ ରୁଚୁ ନଥିଲା ?
Answer: –
ଶ୍ରୀକୃଷ୍ଣଙ୍କ ଶରୀର ଥୁଲା ଦୁର୍ବଳ । ତେଣୁ ମା’ ତାଙ୍କୁ ନାନା କ୍ଷୀରଜାତ ଦ୍ରବ୍ୟ; ଯଥା- ଗୋଟିକା, ଅଧାମ ଓ ସର ଆଦି ଯାଚି ଖୁଆଇବାକୁ ଚେଷ୍ଟା କରୁଥିଲେ । ମାତ୍ର ସେସବୁ ଖାଦ୍ୟ କୃଷ୍ଣଙ୍କୁ ରୁଚୁ ନଥିଲା । କିନ୍ତୁ ଲହୁଣି ପ୍ରତି ତାଙ୍କ ମନରେ ଗଭୀର ଆଗ୍ରହ ଥିଲା ଓ ମା’ଙ୍କୁ ସେ ଲହୁଣି ଲାଞ୍ଚ ମାଗୁଥିଲେ ।

(ଗ) ଯଶୋଦା ନିଜକୁ ଡଙ୍କୁଣୀ ବୋଲି କାହିଁକି କହିଛନ୍ତି ?
Answer:
ଯଶୋଦାଙ୍କର ବୃଦ୍ଧାବୟସରେ ଶ୍ରୀକୃଷ୍ଣ ଏକମାତ୍ର ସନ୍ତାନ ହୋଇଥିବାରୁ ସେ କ୍ଷଣମାତ୍ର ପାଖରୁ ଛାଡ଼ିବାକୁ ଇଚ୍ଛା କରୁନଥିଲେ; କିନ୍ତୁ କୃଷ୍ଣ ଗୋଚାରଣରେ ଯିବାକୁ ଜିଦ୍ କରୁଥିଲେ । ବନରୁ ଫେରିବାରେ ବିଳମ୍ବ ହେବାରୁ ଯଶୋଦା ବ୍ୟସ୍ତ ଓ ବିବ୍ରତ ହୋଇ ନିଜକୁ ଡଙ୍କୁଣୀ ବୋଲି କହି ଅନୁତାପ କରୁଥିଲେ ।

(ଘ) ଶ୍ରୀକୃଷ୍ଣଙ୍କ ପାଦରେ କଣ୍ଟା ଫୁଟିଯିବାର ଆଶଙ୍କା ମାଆଙ୍କ ମନରେ କାହିଁକି ସୃଷ୍ଟି ହୋଇଛି ?
Answer:
ଗୋଚାରଣରେ ଯିବାବେଳେ ଶ୍ରୀକୃଷ୍ଣ କଠଉ ଓ ଛତା ସଙ୍ଗରେ ନେଇଥାଆନ୍ତି । କିନ୍ତୁ ସେଦିନ ସେସବୁ ନେବାକୁ ସେ ଭୁଲି ଯାଇଥିଲେ । କଠଉ ନ ଥିବାରୁ ତାଙ୍କ କୋମଳ ପାଦରେ କଣ୍ଟା ଫୁଟି ତାଙ୍କୁ କଷ୍ଟ ହେଉଥ‌ିବ ଭାବି ମା’ ମନରେ ଆଶଙ୍କା ସୃଷ୍ଟି ହୋଇଛି । ବନ ମଧ୍ଯରେ ପଡ଼ିଥିବା ଅନାବନା କଣ୍ଟା ଫୁଟି ପାଦରୁ ରକ୍ତ ଝରିପଡ଼ୁଥ‌ିବ ଓ ସେ ଯନ୍ତ୍ରଣା ଭୋଗୁଥ‌ିବେ, ଏହିକଥା ମନରେ ଭାଳି ମା’ଙ୍କ ମନ ବିଷାଦରେ ଭରିଉଠିଛି ।

Question ୨।
ଦୁଇଟି ବା ତିନୋଟି ବାକ୍ୟରେ ଉତ୍ତର ଦିଅ ।
(କ) ଶ୍ରୀକୃଷ୍ଣଙ୍କୁ କଳାମାଣିକ କହିବାର ତାତ୍ପର୍ଯ୍ୟ କ’ଣ ?
Answer:
ମାଣିକ୍ୟ ହେଉଛି ଏକ ବହୁମୂଲ୍ୟ ରତ୍ନପଥର । ଏହା ବିଭିନ୍ନ ବର୍ଷର ହୋଇଥାଏ ଓ ବର୍ଣ୍ଣ ଅନୁସାରେ ତା’ର ନାମକରଣ ହୋଇଥାଏ । ଏହା ଚିକ୍‌କଣ, ସୁନ୍ଦର ଓ ବହୁ ମୂଲ୍ୟବାନ୍ । ଯଶୋଦାଙ୍କ ପାଇଁ ଶ୍ରୀକୃଷ୍ଣ ଥିଲେ ସର୍ବସୁନ୍ଦର ଓ ବହୁ ମୂଲ୍ୟବାନ୍ । କିନ୍ତୁ କୃଷ୍ଣଙ୍କ ଶରୀରର ରଙ୍ଗ ଶ୍ୟାମଳ ହୋଇଥିବାରୁ ଯଶୋଦା ପୁତ୍ର କୃଷ୍ଣଙ୍କୁ ସ୍ନେହରେ କଳାମାଣିକ ବୋଲି ସମ୍ବୋଧନ କରିଛନ୍ତି ।

(ଖ) ପୁଅର କେଉଁସବୁ କାର୍ଯ୍ୟ ମନେପକାଇ ମାଆ ଭାଳି ହେଉଛନ୍ତି ?
Answer:
ମା’ ମନ ସନ୍ତାନ ପାଇଁ ସତତ ବ୍ୟାକୁଳ। କୃଷ୍ଣ ଯଶୋଦାଙ୍କର ଏକମାତ୍ର ସନ୍ତାନ ଥିଲେ। ମା’ଙ୍କ ବାରଣ ସତ୍ତ୍ଵେ ଆଦରର ଧନ ତାଙ୍କର ଗୋରୁ ଚରାଇବାକୁ ବଣକୁ ଯାଇ ଫେରିବାରେ ବିଳମ୍ବ କରିଛନ୍ତି। ତେଣୁ ସ୍ନେହମୟୀ, ମମତାମୟୀ ମା’ର ହଦୟ ଅହେତୁକ ଭୟ ଓ ଆଶଙ୍କାରେ ଥରିଉଠିଛି। କୃଷ୍ଣଙ୍କୁ ଘରେ ଅଧାମ, ଗୋଟିକା, ସର ଆଦି ସୁସ୍ଵାଦୁ ଖାଦ୍ୟ ରୁଚେ ନାହିଁ । ଲହୁଣି ମାଗି ମାଗି ନୃତ୍ୟ କରିବା, ଅଳି ଅଝଟ କରି ତଳେ ଗଡ଼ିଯିବା, ଧୂଳି ଧୂସର ହୋଇ କୋଳରେ ଲୋଟିଯିବା ଭଳି କୃଷ୍ଣଙ୍କର ଶିଶୁସୁଲଭ ଚପଳତାକୁ ମା’ ମନେ ପକାଇ ଭାଳି ହେଉଛନ୍ତି । ଜଙ୍ଗଲରେ ଡାହାଣୀ ଓ ରାକ୍ଷସଙ୍କର ଉପଦ୍ରବ ହେଉଥ‌ିବ, ଟାଣଖରାରେ ଶ୍ରମଝାଳ ବୋହି ଯାଉଥବ, ପାଦରେ କଣ୍ଟା ଫୁଟି କଷ୍ଟ ହେଉଥ‌ିବ – ଏମିତି କେତେକଥା ଭାବି ଭାଳି ହେଉଛନ୍ତି ଏବଂ ଭାବି ଭାବି ମା ଯଶୋଦା ବିଳାପ କରୁଥିଲେ ।

(ଗ) ମାଆଙ୍କର ହୃଦୟ ତାପ ବିନାଶ କରିବାରେ ଶ୍ରୀକୃଷ୍ଣ ହରିଚନ୍ଦନ ପରି ଥିଲେ ବୋଲି କହିବାର କାରଣ କ’ଣ ?
Answer:
ହରିଚନ୍ଦନ ହେଉଛି ଦେବଯୋଗ୍ୟ ସୁବାସିତ ଶ୍ଵେତ ଚନ୍ଦନ । ଗ୍ରୀଷ୍ମକାଳରେ ଶରୀରକୁ ଶୀତଳତା ପ୍ରଦାନ କରିବାପାଇଁ ଚନ୍ଦନ ଲଗାଯାଏ ଯାହାକି ହୃଦୟର ସକଳ ସନ୍ତାପ, ଦୁଃଖ, ତାପ ଓ ଦିହନକୁ ଶାନ୍ତ କରେ । ଯଶୋଦାଙ୍କ ଜୀବନରେ କୃଷ୍ଣ ଥିଲେ ବାର୍ଦ୍ଧକ୍ୟର ଏକମାତ୍ର ସମ୍ବଳ, ଜୀବନର୍‌ ସର୍ବସ୍ଵ । ଯେତେବେଳେ ସେ କୃଷ୍ଣଙ୍କୁ ହୃଦୟରେ ଲଗାଇ ଆଲିଙ୍ଗନ କରନ୍ତି, ତାଙ୍କ ହୃଦୟର ସକଳ ଦୁଃଖ, ସନ୍ତାପ ଦୂରୀଭୂତ ହୁଏ । କ୍ଷଣକ ପାଇଁ ପାଖରୁ ଅନ୍ତର ହେଲେ ଭୟ ଓ ଆଶଙ୍କାରେ ତାଙ୍କ ମନରେ ବ୍ୟାକୁଳତା ଭରିଯାଏ ଏବଂ କୋଳକୁ ଫେରିଆସିଲେ ସେ ପରମ ସୁଖ ଅନୁଭବ କରନ୍ତି । ତେଣୁ ସେ କୃଷ୍ଣଙ୍କୁ ହୃଦୟର ତାପ ବିନାଶକ ହରିଚନ୍ଦନ ବୋଲି କହିଛନ୍ତି ।

(ଘ) ଶ୍ରୀକୃଷ୍ଣ କିପରି ଯଶୋଦାଙ୍କର ସୁଖର କାରଣ ଥିଲେ ?
Answer:
ବୃଦ୍ଧ ବୟସରେ ଶ୍ରୀକୃଷ୍ଣଙ୍କ ପରି ସନ୍ତାନ ଯଶୋଦାଙ୍କ ଜୀବନର ସର୍ବସ୍ବ ଏବଂ ଏକମାତ୍ର ସମ୍ବଳ ଥିଲେ । ତାଙ୍କ ପାଇଁ କୃଷ୍ଣ ଥିଲେ ନୟନ ପ୍ରତିମା ସଦୃଶ । କ୍ଷଣକ ପାଇଁ କୃଷ୍ଣ ପାଖରୁ ଅନ୍ତର ହେଲେ ସେ ବିଳାପ କରି ଉଠୁଥିଲେ । କୃଷ୍ଣ ତାଙ୍କ ପାଇଁ ଅନ୍ଧର ଲଉଡ଼ି ଓ ଦରିଦ୍ରର ଧନ ପରି ଥିଲେ । ଅଝଟ କୃଷ୍ଣ କିନ୍ତୁ ତାଙ୍କ ବାରଣ ନ ମାନି ଗୋଚାରଣରେ ବନକୁ ଚାଲି ଯାଉଥିଲେ । ଜୀବର ଜୀବନ ତଥା ହୃଦରତ୍ନହାର ସଦୃଶ କୃଷ୍ଣ ତାଙ୍କ ଜୀବନର ସମସ୍ତ ସୁଖର କାରଣ ଥିଲେ । ତାଙ୍କ ଚନ୍ଦ୍ରବଦନ ଦର୍ଶନରେ ମା’ ପାଉଥିଲେ ଅସୀମ ଆନନ୍ଦ । ଜୀବନର ସମସ୍ତ ଦୁଃଖ ପାସୋରି ସେ ତାଙ୍କୁ କୋଳେଇ ନେଉଥିଲେ ।

(ଡ) ଶ୍ରୀକୃଷ୍ଣଙ୍କର ବେଣୁସ୍ଵନକୁ କାନ ଡେରିବା ପ୍ରସଙ୍ଗରେ କେଉଁ ଭାବ ପ୍ରକାଶ ପାଇଛି ?
Answer:
ଶ୍ରୀକୃଷ୍ଣ ନିତିପ୍ରତି ଗୋଚାରଣରେ ବନକୁ ଯାଇ ସନ୍ଧ୍ୟା ପୂର୍ବରୁ ଗୃହକୁ ପ୍ରତ୍ୟାବର୍ତ୍ତନ କରୁଥିଲେ । ଗୋଧୂଳି ବେଳରେ ତାଙ୍କ ବଂଶୀସ୍ୱନକୁ କାନଡେରି ରହୁଥିଲେ ମାତା ଯଶୋଦା । ଦୂରରୁ ସୁମଧୁର ବେଣୁତାନ ତାଙ୍କ ମନରେ ଆନନ୍ଦ ଭରି ଦେଉଥିଲା । ସେ ଦାଣ୍ଡକୁ ଧାଇଁ ଯାଉଥିଲେ ପୁଅକୁ ପାଛୋଟି ଆଣିବାପାଇଁ । ସେଦିନ ସନ୍ଧ୍ୟା ଅତିକ୍ରାନ୍ତ ହୋଇଥିଲେ ମଧ୍ୟ କୃଷ୍ଣଙ୍କ ଘରବାହୁଡ଼ାରେ ବିଳମ୍ବ ଦେଖି ମା’ ଯଶୋଦାଙ୍କ ମନ ଭୟ ଓ ଆଶଙ୍କାରେ ଭରି ଉଠିଥିଲା । ବଂଶୀର ସ୍ଵନକୁ ଅପେକ୍ଷା କରି କରି ନାନା ବିପଦ ଆଶଙ୍କାରେ ବ୍ୟାକୁଳ ହୋଇଥିଲା ତାଙ୍କ ମନ । ତେଣୁ ନିଜକୁ ସ୍ଵୀକାର କରି ଦୁଃଖରେ ଭାଙ୍ଗି ପଡ଼ିଥିଲେ ସେ । ପୁତ୍ରର ଗୁଣ ସ୍ମରଣ କରି ସେ କରୁଣ ସ୍ବରରେ ବିଳାପ କରିଉଠିଥିଲେ । ଏଠାରେ ମାତା ଯଶୋଦାଙ୍କର ଅପୂର୍ବ ବାତ୍ସଲ୍ୟ-ମମତାର ଭାବ ପ୍ରକାଶ ପାଇଛି ।

Question ୩।
ପଠିତ କବିତାଟିକୁ ମନେପକାଇ କବିତାଂଶ ପୂରଣ କର ।
(କ) ଅନ୍ଧ ଲଉଡ଼ି ବାବୁରେ ………………..।
(ଖ) ………………………. ରଖି ଯାଉ ଗୋରୁ।
(ଗ) ହୃଦତାପ ବିନାଶନେ ……………….।
(ଘ) ………………………. ସର ନ ରୁଚଇ ତୋତେ।
(ଙ) ବନେ କଣ୍ଟା ଲାଗି ହୋଏ ……………….।
Answer:
(କ) ଅନ୍ଧ ଲଉଡ଼ି ବାବୁରେ ହୃଦ ରତ୍ନହାରା ।
(ଖ) ଡରୁ ଥାଉ ଅନ୍ଧାରକୁ ରଖି ଯାଉ ଗୋରୁ।
(ଗ) ହୃଦତାପ ବିନାଶନେ ହରିଚନ୍ଦନ।
(ଘ) ଗୋଟିକା, ଅଧାମ, ସର ନ ରୁଚଇ ତୋତେ।
(ଙ) ବନେ କଣ୍ଟା ଲାଗି ହୋଏ ମୃଦୁ ପାଦ ଚିନ୍ତା।

Question ୪ ।
ସରଳ ଭାଷାରେ ବୁଝାଇ ଲେଖ ।
(କ) ତୋଳି ମୁଁ ଧଇଲେ ……………………….ପଶିବଇଁ ମୁହଁ ।
Answer:
ପ୍ରଦତ୍ତ ପଦ୍ୟାଶଟି ଅଭିମନ୍ୟୁ ସାମନ୍ତସିଂହାରଙ୍କ ରଚିତ ‘କଳା ମାଣିକରେ’ ଶୀର୍ଷକ ପଦ୍ୟରୁ ଆନୀତ । ଏଠାରେ ମା’ର ବାତ୍ସଲ୍ୟପ୍ରୀତି ଏବଂ ସନ୍ତାନର ଜନନୀପ୍ରୀତି ଉଭୟର ପରିପ୍ରକାଶ ଘଟିଛି । ବାଲ୍ୟକାଳରେ ଶ୍ରୀକୃଷ୍ଣ ଅତ୍ୟନ୍ତ ଦୁର୍ବଳ ଶରୀରବିଶିଷ୍ଟ ଥିଲେ । ସେଥ‌ିପାଇଁ ମାତା ଯଶୋଦା ଚିନ୍ତିତ ଥିଲେ । ସନ୍ତାନ ଯେତେ ସୁସ୍ଥ ସବଳ ଥିଲେ ମଧ୍ୟ ଜନନୀ ଚକ୍ଷୁରେ ସେ ସଦାବେଳେ ଦୁର୍ବଳ ମନେ ହୋଇଥାଏ । କୃଷ୍ଣଙ୍କୁ କୋଳରେ ଧରି ସ୍ନେହ କଲାବେଳେ ଯଶୋଦା ପୁତ୍ରର ଅସୁସ୍ଥତା ଆଶଙ୍କା କରିଥାଆନ୍ତି । ତେଣୁ ଗୋଟିକା, ଅଧାମ ଓ ସର ଆଦି ପୁଷ୍ଟିକର ଖାଦ୍ୟ ଖାଇବାକୁ ତାଙ୍କୁ ବାଧ୍ୟ କରନ୍ତି । ଏହିପରି ଦୁର୍ବଳ କୋମଳ ଶରୀର ଧାରଣ କରି ସେ ଗୋଚାରଣ ନିମନ୍ତେ ବନକୁ ଯାଇଥିବାରୁ ମା’ ମନ ସଦା ଆତଙ୍କିତ ଥାଏ । ପୁନଶ୍ଚ ସନ୍ଧ୍ୟା ପରେ ବନରୁ ଫେରିବାରେ ବିଳମ୍ବ ହେବାରୁ ଆଶଙ୍କାରେ ଅତିଷ୍ଠ ହୋଇ ଯଶୋଦା ବ୍ୟାକୁଳ ହୋଇଉଠିଛନ୍ତି ଓ ପୁତ୍ରର ଗୁଣାବଳୀ ସ୍ମରଣ କରି ବିଳାପ କରିଛନ୍ତି ।

(ଖ) ନେଲୁ ନାର୍ହି କାର୍ହି ପାଇଁ ………………………….. ..ମୃଦୁ ପାଦ ଚିନ୍ତା ।
Answer:
ପ୍ରୋକ୍ତ ପଦ୍ୟାଶଟି ଅଭିମନ୍ୟୁ ସାମନ୍ତସିଂହାରଙ୍କ ରଚିତ ‘କଳା ମାଣିକରେ’ ଶୀର୍ଷକ ପଦ୍ୟରୁ ଆନୀତ । ସ୍ନେହମୟୀ ଜନନୀ ଯଶୋଦାଙ୍କର ବିଳାପ ବର୍ଣ୍ଣନା କରିଛନ୍ତି । ସନ୍ଧ୍ୟାରେ ଗୃହକୁ ପ୍ରତ୍ୟାବର୍ତ୍ତନ କରିବାରେ ବିଳମ୍ବ ହେବାରୁ ଯଶୋଦା କୃଷ୍ଣଙ୍କ ଚିନ୍ତାରେ ବ୍ୟାକୁଳ ହୋଇଉଠିଛନ୍ତି । ଗାଈଗୋଠ ସହ ଗଲାବେଳେ କୃଷ୍ଣ ତାଙ୍କ କଠଉ ଓ ଛତା ସଙ୍ଗରେ ନେବାକୁ ଭୁଲିଯାଇଛନ୍ତି । ସେଥ‌ିପାଇଁ ମା’ଙ୍କ ମନରେ ଅସୁମାରି ଆଶଙ୍କା ସୃଷ୍ଟି ହୋଇଛି । ସେ ଚିନ୍ତା କରିଛନ୍ତି ହୁଏତ ନିଦାଘ ଝାଞ୍ଜି ହେତୁ କୃଷ୍ଣଙ୍କ ଦେହରୁ ଝାଳ ବହି ପଡ଼ୁଥ‌ିବ । ବନ ମଧ୍ୟରେ ଅନାବନା କଣ୍ଟା ମାଡ଼ି ସୁକୋମଳ ପାଦ ଦୁଇଟିରୁ ରକ୍ତ ଝରିପଡ଼ୁଥ‌ିବ । ଯନ୍ତ୍ରଣାରେ ତାଙ୍କ ଅଲିଅଳ ପୁଅ ଅଧୀର ହୋଇପଡ଼ୁଥ୍ । ଚାଲିବାରେ କଷ୍ଟ ଅନୁଭବ କରି ହୁଏତ ଆସିବାରେ ବିଳମ୍ବ ହୋଇଛି । ଏହିପରି ନାନା ଭୟ ଓ ଆଶଙ୍କାରେ ମା’ ମନ ଶିହରି ଉଠିଛି । ବାତ୍ସଲ୍ୟ ମମତାମୟୀ ଜନନୀ ଯଶୋଦାଙ୍କର ବ୍ୟାକୁଳତା କବିଙ୍କ ଲେଖନୀରେ ଜୀବନ୍ତ ହୋଇଉଠିଛି।

Question ୫।
ଅସଜଡ଼ା ପଦକୁ ସଜାଡ଼ି ଲେଖ ।
(କ) ତୁ ତୁ ବିନାଶନେ ଏକଇ ବୃଦ୍ଧକାଳେ ନନ୍ଦ ହୃଦତାପ ହରିଚନ୍ଦନ ମୋହର ।
Answer:
ବୃଦ୍ଧକାଳେ ତୁ ମୋହର ଏକଇ ନନ୍ଦନ, ହୃଦତାପ ବିନାଶନେ ତୁ ହରିଚନ୍ଦନ ।

(ଖ) ଶ୍ରୁତିକି ଡଙ୍କୁଣୀ ବନକୁ ମାତିବାର ଶୁଭୁଛି ଛାଡ଼ିଦେଲି ନିଶାଚର କାହିଁକି ମୁଁ ।
Answer:
ନିଶାଚର ମାତିବାର ଶୁଭୁଛି ଶ୍ରୁତିକି, ମୁଁ ଡଙ୍କୁଣୀ ଛାଡ଼ିଦେଲି ବନକୁ କାହିଁକି ।

Question ୬।
ଯଶୋଦା ଶ୍ରୀକୃଷ୍ଣଙ୍କୁ କ’ଣ କ’ଣ ସମ୍ବୋଧନ କରି ଡାକିଛନ୍ତି, ସେହି ନାମଗୁଡ଼ିକ ଲେଖ ।
Answer:
ଶ୍ରୀକୃଷ୍ଣଙ୍କ ଉଦ୍ଦେଶ୍ୟରେ ଜନନୀ ଯଶୋଦା ସମ୍ବୋଧନ କରି ଡାକିଥିବା ନାମଗୁଡ଼ିକ ହେଲା କଳାମାଣିକ, ନିଧନ ସଙ୍ଖାଳି, ଦରିଦ୍ର ପସରା, ଅନ୍ଧ ଲଉଡ଼ି, ହୃଦ ରତ୍ନହାରା, ଜୀବ ଜୀବନ, ନୟନ ପ୍ରତିମା, ହରିଚନ୍ଦନ ।

Question ୭।
ରେଖାଙ୍କିତ ଶବ୍ଦଗୁଡ଼ିକର ଅର୍ଥ ଲେଖ ।
(କ) ନିଧନ ସଙ୍ଖାଳି ମୋର ଦରିଦ୍ର ପସରା ।
Answer:
ନିଧନ – ନିର୍ଜନ, ଧନହୀନ, ଦରିଦ୍ର, ଗରିବ ।

(ଖ) ବୃଦ୍ଧକାଳେ ତୁ ମୋହର ଏକଇ ନନ୍ଦନ ।
Answer:
ନିଧନ – ପୁଅ, ପୁତ୍ର ।

(ଗ) ଗୋଟିକା ଅଧାମ ସର ନ ରୁଚଇ ତୋତେ ।
Answer:
ଅଧାମ – ଦୁଗ୍ଧଜାତ ମିଷ୍ଟାନ୍ନ ବିଶେଷ, ରାବିଡ଼ି, ସରପୁଳି। ଦୁଗ୍ଧକୁ ଗରମ କରି ଏଥୁରୁ ଜଳୀୟ ଅଂଶ କମିଗଲା ପରେ ଅର୍ଦ୍ଧତରଳ ଅବସ୍ଥାରେ ଯାହା ରହେ ତାହାକୁ ଅଧାମ କୁହାଯାଏ । ଏହା ଏକ ସୁସ୍ବାଦୁ ଖାଦ୍ୟ ।.

(ଘ) ବନେ କଣ୍ଟା ଲାଗି ହୋଏ ମୃଦୁ ପାଦ ଚିନ୍ତା ।
Answer:
ମୃଦୁ – କୋମଳ, ନରମ ।

(ଙ‍) ବାର ବାର ବାରୁଥାଇ ଯିବା ପାଇଁ ବନେ ।
Answer:
ବାରୁଥାଇ – ବାରଣ କରୁଥାଇ, ମନା କରୁଥାଇ ।

Question ୮।
ତଳେ ଦିଆଯାଇଥ‌ିବା ସମୋଚ୍ଚାରିତ ଶବ୍ଦଗୁଡ଼ିକ ମଧ୍ୟରେ ଥ‌ିବା ଅର୍ଥଗତ ପାର୍ଥକ୍ୟ ଲେଖ ।
ବେଶି – ବେଶା,  ନିଧନ –  ନିଧନ,  ଶ୍ରୁତି – ଶ୍ରୁତି,  ନିଶା –  ନିଶା,  ବର – ବର
Answer:
ବେଶି – ଅଧ୍ଵ ।
ବେଶା – ବେଶଧାରା ।
ନିଧନ – ମୃତ୍ୟୁ, ବିନାଶ ।
ନିଧନ – ଧନହୀନ, ଦରିଦ୍ର ।
ଶ୍ରୁତି – କାନ, ଶ୍ରବଣ, ଶୁଣିବା ।
ଶ୍ରୁତି – ବେଦ, କିମ୍ବଦନ୍ତୀ ।
ନିଶା – ରାତ୍ରି ।
ନିଶା – ନିଶାଦ୍ରବ୍ୟ ଅଭସ୍ତ
ବର – ବୃକ୍ଷ ବିଶେଷ, ସ୍ୱାମା, ପତି।
ବର – ଆଶାର୍ବାଦା

Question ୯।
ତଳଲିଖିତ ଶବ୍ଦଗୁଡ଼ିକର ଦୁଇଟି ଲେଖାଏଁ ପ୍ରତିଶବ୍ଦ ଲେଖ ।
କାନନ, ଦରିଦ୍ର, ନୟନ, ଜନନୀ, ଲଉଡ଼ି
Answer:
କାନନ – ବଣ, ଜଙ୍ଗଲ ।,
ନୟନ – ଚକ୍ଷୁ, ଆଖି ।
ଲଉଡ଼ି – ବାଡ଼ି, ଯଷ୍ଟି ।
ଦରିଦ୍ର – ଦୀନ, ଗରିବ ।
ଜନନୀ – ମାତା, ମା’ ।

ତୁମପାଇଁ କାମ :

ଏ ଗୀତଟିକୁ ସ୍ଵର, ତାଳ ସହ ଗାନ କର ।
ସନ୍ତାନ ପ୍ରତି ସ୍ନେହ ପ୍ରକାଶ କରୁଥିବା ଏହିପରି ବିଭିନ୍ନ କବିଙ୍କର ଆଉ କେତୋଟି ଗୀତ ସଂଗ୍ରହ କର ଓ ପଢ଼ ।
Answer:
ପିଲାମାନେ ଶିକ୍ଷକ ବା ଅଭିଭାବକଙ୍କ ପରାମର୍ଶ ନେଇ ନିଜେ କର ।

ଅଭ୍ୟାସ ପାଇଁ ଅତିରିକ୍ତ ପ୍ରଶ୍ନୋତ୍ତର

ଅତିସଂକ୍ଷିପ୍ତ ପ୍ରଶ୍ନୋତ୍ତର

Question ୧ ।
‘କଳାମାଣିକରେ’ କବିତାର କବିଙ୍କ ନାମ କ’ଣ ?
Answer:
କଳାମାଣିକରେ କବିତାର କବି ହେଉଛନ୍ତି ଅଭିମନ୍ୟୁ ସାମନ୍ତସିଂହାର।

Question ୨ ।
କଳାମାଣିକରେ କବିତାଟି କେଉଁ କାବ୍ୟରୁ ଆସିଅଛି ?
Answer:
କଲାମାଶିକାରେ କବିତାଟି ଅଭିମନ୍ୟୁ ସାମନ୍ତ୍ରସିଂହାରଙ୍କ ରଚିତ ‘ବିନ୍ଦଗ୍ଧ ଚିନ୍ତ୍ର।ମଶି’ କାବ୍ୟରୁ ଆସିଅଛି।

Question ୩ ।
କୃଷ୍ଣଙ୍କୁ କିଏ ଝୁରି ହେଉଛନ୍ତି ?
Answer:
କୃଷ୍ଣଙ୍କୁ ମାଆ ଯଶୋଦା ବାତ୍ସଲ୍ୟ ସ୍ନେହହେତୁ ମନେ ମନେ ତାଙ୍କୁ ଝୁରି ହେଉଛନ୍ତି।

Question ୪ ।
ଶ୍ରୀକୃଷ୍ଣ କାହାକୁ ଡରୁଥିଲେ ?
Answer:
ଶ୍ରୀକୃଷ୍ଣ ଅନ୍ଧି।ରକୁ ଡରୁଥିଲୋ

Question ୫ ।
ମାଆ ଯଶୋଦା ଶ୍ରୀକୃଷ୍ଣଙ୍କୁ ବଣକୁ ଯିବାକୁ ବାରଣ କରୁଥିଲେ କାହିଁକି ?
Answer:
ବଣ ମଧ୍ଯରେ ଡାହାଣୀମାନେ କ୍ଷତି ଘଟାନ୍ତି। ସେଥ‌ିପାଇଁ ଶ୍ରୀକୃଷ୍ଣଙ୍କୁ ମାଆ ଯଶୋଦା ବଣକୁ ଯିବାକୁ ବାରଣ କରୁଥ୍ ଲୋ

Question ୬ ।
ଶ୍ରୀକୃଷ୍ଣ କେଉଁ ଖାଦ୍ୟକୁ ଭଲ ପାଉଥିଲେ ?
Answer:
ଶ୍ରୀକୃଷ୍ଣ ଲବଣି ଖାଇବା ପାଇଁ ଭଲ ପାଉଥ୍ ଲୋ

Question ୭ ।
ମାଆ ଯଶୋଦାଙ୍କୁ କ’ଣ ନ ଶୁଣିପାରିଥିବାରୁ ସେ ଅତ୍ୟଧୁକ ବ୍ୟସ୍ତ ହୋଇପଡ଼ିଛନ୍ତି ?
Answer:
ମାଆ ସନ୍ଧ୍ୟା ସମୟରେ ଶ୍ରୀକୃଷ୍ଣଙ୍କ ବଂଶୀ ସ୍ଵରକୁ ଶୁଣିଥା’ନ୍ତି । କିନ୍ତୁ ଆଜି ସେ ବଂଶୀ ସ୍ଵରକୁ ନ ଶୁଣି ପାରିଥବାରୁ ଅତ୍ୟଧୂକ ବ୍ୟସ୍ତ ହୋଇପଡ଼ିଛନ୍ତି।

Question ୮ ।
ଶ୍ରୀକୃଷ୍ଣଙ୍କ ପାଦରେ କଷ୍ଟ ହେଉଥ‌ିବ ବୋଲି ଯଶୋଦା କାହିଁକି ଭାବୁଥିଲେ ?
Answer:
ଶ୍ରୀକୃଷ୍ଣ ବଣକୁ ଗଲାବେଳେ ସାଙ୍ଗରେ କଠଉ ନେଇ ନ ଥିଲେ। ପାଦରେ କଣ୍ଟା ଫୁଟି କଷ୍ଟ ହେଉଥ‌ିବ ବୋଲି ଯଶୋଦା ଭାବୁଥିଲେ ।

Question ୯ ।
ଶ୍ରୀକୃଷ୍ଣଙ୍କ ଦେହରୁ ଝାଳ ବୋହୁଥ‌ିବ ବୋଲି କାହିଁକି ମାଆ ଯଶୋଦା ଭାବୁଥିଲେ ?
Answer:
ଝାଞ୍ଜି ଖରାରେ ଶ୍ରୀକୃଷ୍ଣଙ୍କ ଦେହରୁ ଝାଳ ବୋହୁଥ୍‌ବ ବୋଲି ଯଶୋଦା ଭାବୁଥ୍ ଲୋ

Question ୧୦ ।
ନିଶାଚରମାନେ କେଉଁଠି ମାତିଥିବାର ଯଶୋଦା ଶୁଣିଥିଲେ ?
Answer:
ନିଶାଚରମାନେ ବଣରେ ମାତିଥିବାର ଯଶୋଦା ଶୁଣିଥିଲେ।

ବସ୍ତୁନିଷ୍ଠ ପ୍ରଶ୍ନୋତ୍ତର:

Question ୧।
‘କଳାମାଣିକରେ’ କବିତାଟି କେଉଁ ବହିରୁ ଅଣାଯାଇଛି ?
(କ) ବିଦଗ୍‌ଧ ଚିନ୍ତାମଣି
(ଖ) ତପସ୍ବିନୀ
(ଗ) ପ୍ରଶୟବଳ୍ମରା
(ଘ) ପ୍ରେମକଳା
Answer:
(କ) ବିଦଗ୍‌ଧ ଚିନ୍ତାମଣି

Question ୨ ।
‘କଳାମାଣିକରେ’ କବିତାଟି କାହାର ରଚନା ?
(କ) ଉପେନ୍ଦ୍ର ଭଞ୍ଜ
(ଖ) ଦୀନକୃଷ୍ଣ ଦାସ
(ଗ) ଅଭିମନ୍ୟୁ ସାମନ୍ତସିଂହାର
(ଘ) ଗାଙ୍ଗଧର ମେହେର
Answer:
(ଗ) ଅଭିମନ୍ୟୁ ସାମନ୍ତସିଂହାର

Question ୩।
‘କଳାମାଣିକରେ’ କବିତା ‘ବିଦଗ୍‌ଧ ଚିନ୍ତାମଣି’ କାବ୍ୟର କେଉଁ ଛାନ୍ଦରୁ ଅଣାଯାଇଛି ?
(କ) ଚତୁର୍ଦ୍ଦଶ ଛାନ୍ଦ
(ଖ) ଷଷ୍ଠ ଛାନ୍ଦ
(ଗ) ଚଉଷଠି ଛାନ୍ଦ
(ଘ) ସତଷଠି ଛାନ୍ଦ
Answer:
(ଘ) ସତଷଠି ଛାନ୍ଦ

Question ୪।
ନିମ୍ନୋକ୍ତ ମଧ୍ୟରୁ କେଉଁଟି ଅଭିମନ୍ୟୁ ସାମନ୍ତସିଂହାରଙ୍କ ରଚନା ନୁହେଁ ?
(କ) ବାଘଗାତ
(ଖ) ଚଢ଼େଇ ଗୀତ
(ଗ) ନାନାବାୟା ଗୀତ
(ଘ) ବୋଲେ ହୁଁଟି
Answer:
(ଗ) ନାନାବାୟା ଗୀତ

Question ୫।
‘କଳାମାଣିକରେ’ କବିତାରେ ମାତାଙ୍କର କେଉଁ ମୁଖ୍ୟଭାବ କବି ପ୍ରକାଶକରିଛନ୍ତି ?
(କ) ବାତ୍ସଲ୍ୟମୟୀ ହୃଦୟର ଆବେଗ
(ଗ) ମାତୃ ହୃଦୟର ପ୍ରେମ
(ଖ) ମାତୃ ହୃଦୟର ସ୍ନେହ
(ଘ) ସନ୍ତାନର ମୋହ
Answer:
(କ) ବାତ୍ସଲ୍ୟମୟୀ ହୃଦୟର ଆବେଗ

Question ୬ ।
‘ଧୀରେ ଘେନ କାନନରେ କୃଷ୍ଣ ବିଳମ୍ବିତ’ – ଏଠାରେ ଏହି କବିତାଂଶରେ ‘ଧୀରେ’ କାହାକୁ ସମ୍ବୋଧନ କରାଯାଇଛି ?
(କ) ଯଶୋଦାଙ୍କୁ
(ଖ) ଗୋପୀମାନଙ୍କୁ
(ଗ) କବିତାଟି ଯେଉଁମାନେ ଶୁଣିବେ
(ଘ) ପଣ୍ଡିତମାନଙ୍କୁ
Answer:
(ଘ) ପଣ୍ଡିତମାନଙ୍କୁ

Question ୭।
‘କଳାମାଣିକ’ କାହାକୁ କୁହାଯାଇଛି ?
(କ) ଏକ ମୂଲ୍ୟବାନ୍ ଧାତୁ
(ଖ) ଧନସମ୍ପତ୍ତି
(ଗ) ଶ୍ରୀକୃଷ୍ଣ
(ଘ) ପଦ୍ମରାଗ ମଶି
Answer:
(ଗ) ଶ୍ରୀକୃଷ୍ଣ

Question ୮ ।
‘ବୃଦ୍ଧକାଳେ ତୁ ମୋହର ଏକଇ ନନ୍ଦନ’ ବୋଲି କାହାକୁ କୁହାଯାଇଛି ?
(କ) ଶ୍ରୀକୃଷ୍ଣଙ୍କୁ
(ଖ) ନନ୍ଦରାଜାଙ୍କୁ
(ଗ) ଅଭିମନ୍ୟୁଙ୍କୁ
(ଘ) ବଳରାମଙ୍କୁ
Answer:
(କ) ଶ୍ରୀକୃଷ୍ଣଙ୍କୁ

Question ୯୮
‘ହୃଦତାପ ବିନାଶନେ ତୁ ହରିଚନ୍ଦନ’ – ଏହି ପଦ୍ୟାଶରେ ‘ହରିଚନ୍ଦନ’ କାହାକୁ ଲକ୍ଷ୍ୟକରି କୁହାଯାଇଛି ?
(କ) ଶ୍ରୀକୃଷ୍ଣ
(ଖ) ବଳରାମ
(ଗ) କୃଷ୍ଣ ଓ ବଳରାମ
(ଘ) ବିଷ୍ଣୁଙ୍କ ଚନ୍ଦନ
Answer:
(ଘ) ବିଷ୍ଣୁଙ୍କ ଚନ୍ଦନ

Question ୧୦ ।
ନେଲୁ ନାହିଁ କାହିଁ ତୋ କଠଉ ଛତା’ ପଦ୍ୟାଶରେ ମାଆଙ୍କର କେଉଁ ମନୋଭାବ ପ୍ରକାଶ ପାଉଛି ?
(କ) ପୁଅ ପ୍ରତି ବିରକ୍ତିଭାବ
(ଖ) ପୁଅର ନିଭୀକତା ସଂପର୍କରେ ଆସ୍ଥା
(ଗ) ପୁଅର ଗୋଡ଼ରେ କଣ୍ଟା ପଶିବାର ଭୟ
(ଘ) ପୁଅର ନିରାପତ୍ତା ପ୍ରତି ସଂଶୟ
Answer:
(ଗ) ପୁଅର ଗୋଡ଼ରେ କଣ୍ଟା ପଶିବାର ଭୟ

Question ୧୧।
‘ମୁଁ ଡଙ୍କୁଣି ଛାଡ଼ିଦେଲି ବନକୁ କାହିଁକି’ ? – ଏଥରେ କେଉଁ ମୁଖ୍ୟ ଭାବଟି ପ୍ରକାଶ ପାଇଛି ?
(କ) ସ୍ନେହ
(ଖ) ବାତ୍ସଲ୍ୟ
(ଗ) ଆଶଙ୍କା
(ଘ) ଚିନ୍ତା
Answer:
(ଗ) ଆଶଙ୍କା

Question ୧୨ ।
‘ନିଶାଚର ମାତିବାର ଶୁଭୁଛି ଶ୍ରୁତିକି’ – ଏହି ପଦ୍ୟାଶରେ ‘ନିଶାଚର’ କାହାକୁ ଲକ୍ଷ୍ୟକରି କୁହାଯାଇଛି ?
(କ) ରାକ୍ଷସ
(ଖ) ରାତିଚୋର
(ଗ) ହିଂସ୍ରଜନ୍ତୁ
(ଘ) ଖଣ୍ଡ
Answer:
(କ) ରାକ୍ଷସ

Question ୧୩ ।
ହରିଚନ୍ଦନ କ’ଣ କରେ ?
(କ) ହୃଦତାପ ବିନାଶ କରେ
(ଖ) ବୃଦ୍ଧକାଳେ ସାହାଯ୍ୟ କରେ
(ଗ) ହୃଦୟରେ ଭକ୍ତିଭାବ ଆଣେ
(ଘ) ମନରେ ସାହସ ଦିଏ
Answer:
(କ) ହୃଦତାପ ବିନାଶ କରେ

Question ୧୪ ।
ଶ୍ରୀକୃଷ୍ଣ ନାଚି ନାଚି ମା’ଙ୍କୁ କ’ଣ ଲାଞ୍ଚ ମାଗନ୍ତି ?
(କ) ପେଡ଼ା
(ଖ) ରାବିଡ଼ି
(ଗ) ହୁଧସର
(ଘ) ଲହୁଣି
Answer:
(ଘ) ଲହୁଣି

Question ୧୫ ।
ନିମ୍ନୋକ୍ତ ମଧ୍ୟରୁ ବାତ୍ସଲ୍ୟ ମମତାର ଅର୍ଥ କେଉଁଟି ?
(କ) ପୁଅଝିଅମାନଙ୍କର ଉନ୍ନତି
(ଖ) ପୁଅଝିଅଙ୍କ ପ୍ରତି ପିତାମାତାଙ୍କର କର୍ତ୍ତବ୍ୟ
(ଗ) ଦୁଧସର
(ଘ) ଲହୁଣି
Answer:
(ଘ) ଲହୁଣି

Question ୧୬ ।
ନିମ୍ନୋକ୍ତ ମଧ୍ୟରୁ କେଉଁଟିକୁ କୃଷ୍ଣ ଡରନ୍ତି ବୋଲି ଯଶୋଦା କହିଛନ୍ତି ?
(କ) ଡାହାଣୀକୁ
(ଖ) ଅନ୍ଧିରକୁ
(ଗ) ନିଶାଚରକୁ
(ଘ) ହିଂସ୍ରଜନ୍ତୁଙ୍କୁ
Answer:
(ଘ) ହିଂସ୍ରଜନ୍ତୁଙ୍କୁ

Question ୧୭ ।
କୃଷ୍ଣ ବଣକୁ ଯାଇଥିଲାବେଳେ ସାଥ୍‌ରେ କେଉଁ କେଉଁ ଜିନିଷ ନେଇ ନଥ‌ିବାରୁ ମାତା ଯଶୋଦା ଭାଳି ହୋଇଛନ୍ତି ?
(କ) ଗୋଟିକା, ଅଧାମ
(ଖ) ବଂଶୀ
(ଗ) କଠଉ, ଛତା
(ଘ) ମୟୂରଚଦ୍ରିକା
Answer:
(ଗ) କଠଉ, ଛତା

Question ୧୮ ।
ଅଧାମର ଅର୍ଥ ନିମ୍ନୋକ୍ତ ମଧ୍ୟରୁ କେଉଁଟି ?
(କ) ପୋଡ଼ା
(ଖ) ରାବିଡ଼ି
(ଗ) କହିଶି
(ଘ) ରସଗୋଲା
Answer:
(ଖ) ରାବିଡ଼ି

Question ୧୯ ।
ଯଶୋଦା କ’ଣ ପାଇଁ କାନ ଡେରିଥା’ନ୍ତି ?
(କ) ଶ୍ରୀକୃଷ୍ଣଙ୍କ କଥା
(ଖ) ଶ୍ରୀକୃଷ୍ଣଙ୍କ ବଂଶୀର ସ୍ଵନ
(ଗ) ଗାଈପଲ ଫେରିବାର ଶବ୍ଦ
(ଘ) ଶ୍ରୀକୃଷ୍ଣଙ୍କ କଠଉର ଶବ୍ଦ
Answer:
(ଖ) ଶ୍ରୀକୃଷ୍ଣଙ୍କ ବଂଶୀର ସ୍ଵନ

Question ୨୦ ।
ବନକୁ ଯିବାପାଇଁ ଯଶୋଦା ଶ୍ରୀକୃଷ୍ଣଙ୍କୁ ବାରମ୍ବାର ବାରଣ କରୁଥିଲେ କାହିଁକି ?
(କ) ସାଥ୍‌ରେ କଠଉ ଓ ଛତା ନେବାକୁ ଶ୍ରୀକୃଷ୍ଣ ଭୁଲିଯା’ନ୍ତି ।
(ଖ) ବଣରେ ଅନ୍ଧାର ଘୋଟି ରହିଥାଏ ।
(ଗ) ବଣରେ ଗୋଟିକା, ଅଧାମ, ଲହୁଣି ଆଦି ମିଳିନଥାଏ ।
(ଘ) ଡାହାଣୀ ଶ୍ରୀକୃଷ୍ଣଙ୍କୁ ଲୋଭେଇଯା’ନ୍ତି ।
Answer:
(ଘ) ଡାହାଣୀ ଶ୍ରୀକୃଷ୍ଣଙ୍କୁ ଲୋଭେଇଯା’ନ୍ତି ।

Question ୨୧ ।
ମାତା ଯଶୋଦା କେଉଁ କଥା ଭାଳୁଛନ୍ତି ବୋଲି କବିତାରେ କୁହାଯାଇଛି ?
(କ) ଘରକଥା
(ଖ) ଗାଈଗୋରୁଙ୍କ କଥା
(ଗ) ବାତ୍ସଲ୍ୟମମତା କଥା
(ଘ) ପଡ଼େ।ଶାଙ୍କ ମମତା କଥା
Answer:
(ଗ) ବାତ୍ସଲ୍ୟମମତା କଥା

Question ୨୨ ।
ବନେ କଣ୍ଟା ଲାଗି ହୋଏ – ପାଦ ଚିନ୍ତା : ପାଦ ପୂରଣ କର ।
(କ) କଅଁଳ
(ଖ) ମୃଦୁ
(ଗ) ନରମ
(ଘ) କର୍କଶ
Answer:
(ଖ) ମୃଦୁ

Question ୨୩ ।
ନାଚି ଲାଞ୍ଚ ମାଗୁଥାଉ – କେମନ୍ତେ : – ପାଦ ପୂରଣ କର ।
(କ) ଲବଣି
(ଖ) ଗୋଟିକା
(ଗ) ଆଧାମ
(ଘ) ସର
Answer:
(କ) ଲବଣି

Question ୨୪ ।
ଅଭିମନ୍ୟୁ ସାମନ୍ତସିଂହାର କେଉଁ ଶତାବ୍ଦୀର କବି ?
(କ) ବିଂଶ
(ଖ) ଊନବିଂଶ
(ଗ) ସପ୍ତଦଶ
(ଘ) ଅଷ୍ଟାଦଶ
Answer:
(ଘ) ଅଷ୍ଟାଦଶ

Question ୨୫ ।
‘ତୋଳି’- ଏହା କେଉଁ ଅର୍ଥ ପ୍ରକାଶ କରେ ?
(କ) ତୋଳିବା
(ଖ) ସଂଗ୍ରହ କରିବା
(ଗ) ଟେକି ଧରି
(ଘ) ଏ ସମସ୍ତ
Answer:
(ଗ) ଟେକି ଧରି

Question ୨୬ ।
‘ସାରୁ’ – ଏହା କେଉଁ ଅର୍ଥ ପ୍ରକାଶ କରେ ?
(କ) ଶେଷକରୁ
(ଖ) ଏକପ୍ରକାର ପରିବା
(ଗ) ପରିବା
(ଘ) ଏଥିମଧ୍ୟରୁ କୌଣସିଟି ନୁହେଁ
Answer:
(କ) ଶେଷକରୁ

Question ୨୭ ।
ନିଧନସଙ୍ଖାଳି ମୋର ଦରିଦ୍ର ପସରା – ରେଖାଙ୍କିତ ଶବ୍ଦଟିର ଅର୍ଥ କ’ଣ ?
(କ) ଧନହାନ
(ଖ) ମୃତ
(ଗ) ଗରିବ
(ଘ) ପାଇବା
Answer:
(କ) ଧନହାନ

Question ୨୮ ।
ମାତା ଯଶୋଦା ନିଜକୁ ଡଙ୍କୁଣୀ ବୋଲି କାହିଁକି କହିଛନ୍ତି ?
(କ) ଶ୍ରୀକୃଷ୍ଣଙ୍କୁ କଠଉ, ଛତା ଦେଇ ନଥ‌ିବାରୁ
(ଖ) ନିଶାଚର ମାତିଥିବା ଶୁଣି ମଧ୍ୟ ଶ୍ରୀକୃଷ୍ଣଙ୍କୁ ବଣକୁ ଛାଡ଼ିଥିବାରୁ
(ଗ) ଶ୍ରୀକୃଷ୍ଣଙ୍କ ଦେହରେ ଖରାବାଜି ଝାଳ ବହୁଥ‌ିବାରୁ
(ଘ) ଶ୍ରୀକୃଷ୍ଣ ପଥଶ୍ରମ ପାଉଥିବାରୁ
Answer:
(ଖ) ନିଶାଚର ମାତିଥିବା ଶୁଣି ମଧ୍ୟ ଶ୍ରୀକୃଷ୍ଣଙ୍କୁ ବଣକୁ ଛାଡ଼ିଥିବାରୁ

Question ୨୯ ।
ଯଶୋଦା ଶ୍ରୀକୃଷ୍ଣଙ୍କୁ ଲକ୍ଷ୍ୟକରି ପ୍ରତ୍ୟକ୍ଷ ଭାବରେ କେଉଁ କଥାଟି କହିନାହାନ୍ତି ? ସେ ତାଙ୍କର-
(କ) ନିଧନସଙ୍ଖ୍।ଳି
(ଖ) ହରିଚନ୍ଦନ
(ଗ) କରିଦ୍ରପସରା
(ଘ) ନୟନପ୍ରତିମା
Answer:
(ଖ) ହରିଚନ୍ଦନ

Question ୩୦
ମା’ ପୁଅକୁ ଲବଣି ପିତୁଳା ବୋଲି କାହିଁକି କହିଛନ୍ତି ?
(କ) ସ୍ନେହବଶତଃ
(ଖ) ଦୟ।ବଶତଃ
(ଗ) କରୁଣାବଶତଃ
(ଘ) ଭୟବଶତଃ
Answer:
(କ) ସ୍ନେହବଶତଃ

Question ୩୧ ।
‘ଗୋଟିକା, ଅଧାମ, ସର ନ ରୁଚଇ ତୋତେ’ ଏଥୁ ‘ଗୋଟିକା’ ଶବ୍ଦର ଅର୍ଥ କ’ଣ ?
(କ) ସରପୁଳି
(ଖ) ରସାବଳି
(ଗ) ରାବିଡ଼ି
(ଘ) ପେଡ଼ା
Answer:
(ଘ) ପେଡ଼ା

Question ୩୨ ।
‘କଳାମାଣିକ’ କବିତାରେ ଯଶୋଦାଙ୍କର କେଉଁ ମନୋଭାବ ଉପରେ ଗୁରୁତ୍ଵ ଦିଆଯାଇଛି ?
(କ) ଉଦ୍‌ବିଗ୍ନତା
(ଖ) ଭୟାତୁରତା
(ଗ) ଅସହାୟତା
(ଘ) ସନ୍ତାନପ୍ରତି ମମତା
Answer:
(ଘ) ସନ୍ତାନପ୍ରତି ମମତା

Question ୩୩ ।
‘କଳାମାଣିକରେ’ କବିତାର ମୁଖ୍ୟ ଭାବ କ’ଣ ?
(କ) ଈଶ୍ବର ଭକ୍ତି
(ଖ) କରୁଣଭାବ
(ଗ) ବିଷାଦଭାବ
(ଘ) ସନ୍ତାନ ସ୍ନେହ
Answer:
(ଘ) ସନ୍ତାନ ସ୍ନେହ

Question ୩୪ ।
ଶ୍ରୀକୃଷ୍ଣ ବଣକୁ ଯାଇଥିବାରୁ ଯଶୋଦଙ୍କ ମନରେ କେଉଁ ଭାବ ଉଦ୍ରେକ ହୋଇ ନାହିଁ ?
(କ) ଭୟ
(ଖ) ଉଦ୍‌ବେଗ
(ଗ) ଅ।ଶଙ୍କା
(ଘ) କୌତୂହଳ
Answer:
(ଘ) କୌତୂହଳ

କବି ପରିଚୟ :

ଇତିହାସରେ ଏକ ଉଜ୍ଜ୍ବଳ ଚରିତ୍ର । ସେ ‘କାବ୍ୟଯୁଗ’ ବା ‘ରାତିକ୍ଷୁଗ’ ବା ‘ଛନ୍ଦଯୁଗ’ ନାମରେ ନାମିତ ଏକ ସ୍ଵତନ୍ତ୍ର ସାର ସ୍କୃତ ଯୁଗର ଅନ୍ୟତମ ପ୍ରତିନିଧ୍। ରାଧାକୃଷ୍ଣଙ୍କର ଅମୃତ ଜୀବନଚରିତ ଆଧାରିତ ବହୁ କାବ୍ୟକବିତାର ସେ ରଚୟିତା । ପ୍ରତ୍ୟେକ ଓଡ଼ିଆଙ୍କ ନିକଟରେ ସେ ବିଦଗ୍ଧ କବିଭାବେ ପରିଚିଦ୍ଧ । ତାଙ୍କ ରଚିତ କାବ୍ୟକବିତାଗୁଡ଼ିକ ମଧ୍ୟରେ ‘ବିଦଗ୍ଧ ଚିନ୍ତାମଣି’, ‘ପ୍ରେମକଳା’, ‘ରସବତୀ’, ‘ସୁଲକ୍ଷଣା’, ‘ବାଘଗୀତ’, ‘ଚଢ଼େଇ ଗୀତ’, ‘ବୋଲେ ହୁଁ ଟି’ ଆଦି ପ୍ରଧାନ । ବାଲ୍ୟକାଳରୁ ସେ ସରଳ ସାବଲୀଳ କରୁଥିଲେ । କବିତା ‘କଳା ମାଣିକରେ’ କବିଙ୍କର ସର୍ଚଶ୍ରେଷ୍ଠ କାବ୍ୟ ‘ବିଦଗ୍ଧ ଚିନ୍ତାମଣି’ ର ସତଷଠି ଛାନ୍ଦରୁ ଗୃହୀତ ।

କବିତାର ପୃଷ୍ଠଭୂମି :

ଶ୍ରାକୃଷ୍ଣ ପ୍ତତିଦିନ ଗୋପବାଳକମାନଙ୍କ ସହ ବନକୁ ଗୋଚାରଣରେ ଯାଉଥିଲେ । ଏକଦା ସନ୍ଧ୍ୟାରେ ଗାଈଗୋଠ ସହ ଘରକୁ ଫେରିବାରେ ତାଙ୍କର ବିଳମ୍ବ ହେବାରୁ ଯଶୋଦାଙ୍କ ମନରେ ଅନେକ ଭୟ ଓ ଆଶଙ୍କା ଯଶୋଦାଙ୍କ ମନରେ ଅନେକ ଭୟ ଓ ଆଶଙ୍କା ସୃଷ୍ଟି ହୋଇଛି । ସେ ମନରେ ପୁତ୍ର କୃଷ୍ଣଙ୍କ ଗୁଣ ଗାନକରି ବିଳାପ କରିଛନ୍ତି । ସ୍ନେହ- ବତ୍ସଳ ମାତା ମନର ବ୍ୟସ୍ତତାରେ କବିତାଟି ରସାଣିତ ହୋଇଛି । କବି ବାତ୍ସଲ୍ୟଭରା ହୃଦୟର ଆବେଗକୁ ସୁନ୍ଦର ଭାବେ କବିତାରେ ରୂପ ଦେଇଛନ୍ତି ।

କବିତାର ସାରକଥା :
ଗୋପପୁରରେ ପ୍ରତ୍ୟହ ଶ୍ରୀକୃଷ୍ଣ ଗୋପାଳ ବାଳକମାନଙ୍କ ସହ ଗାଈଗୋଠ ନେଇ ବନ ମଧ୍ୟକୁ ଗୋଚାରଣ ନିମିତ୍ତ ଯାଇଥା’ନ୍ତି ଓ ସନ୍ଧ୍ୟା ସମୟରେ ପ୍ରତ୍ୟାବର୍ତ୍ତନ କରନ୍ତି । ସେଦିନ ଫେରିବା ବିଳମ୍ବ ହେବାରୁ ମାତା ଯଶୋଦାଙ୍କ ମନ ବ୍ୟସ୍ତତାରେ ଭରି ଉଠିଛି । ମନ ମଧ୍ୟରେ ନାନା ଆଶଙ୍କା ସୃଷ୍ଟି ହୋଇଛି। କୃଷ୍ଣଙ୍କର ଗୁଣ ଓ କାର୍ଯ୍ୟକଳାପ ଆଦି ତାଙ୍କ ସ୍ମୃତିକୁ ଆସିବାରୁ ସେ ବିଳାପ କରିଉଠିଛନ୍ତି । ସ୍ନେହମୟୀ ଜନନୀଙ୍କ ବାତ୍ସଲ୍ୟ ମମତା କବିତାର ଛତ୍ରେ ଛତ୍ରେ ଫୁଟିଉଠିଛି ଯାହା କବି ସାମନ୍ତସିଂହାରଙ୍କ ଲେଖନୀରେ ଅତି ମନୋରମ ରୂପ ଲାଭ କରିଛି ।

ଯଶୋଦାଙ୍କ ବୃଦ୍ଧାକାଳର ଏକମାତ୍ର ସନ୍ତାନ ଥିଲେ ଶ୍ରୀକୃଷ୍ଣ । ସେ ପିତାମାତାଙ୍କର ଅତି ଅଲିଅଳ ଥିଲେ । ଦୀର୍ଘସମୟ ଧରି ଶ୍ରୀକୃଷ୍ଣ ଆଖୁ ଆଢୁଆଳରେ ରହିଯିବାରୁ ମା’ ମନ ତାଙ୍କର ଆତଙ୍କିତ ହୋଇପଡ଼ିଛି । ଅହେତୁକ ଭୟରେ ମନ ଶିହରି ଉଠିଛି । ମା’ଙ୍କ ପାଇଁ ସେ ସତେଯେପରି ଥୁଲେ ଅନ୍ଧର ଲଉଡ଼ି, ଦରିଦ୍ରର ପସରା ଓ ନିର୍ଜନର ଧନ ସ୍ୱରୂପ । ତାଙ୍କ ପ୍ରାଣର ପ୍ରତିମା, ନୟନର ମଣି କୃଷ୍ଣଙ୍କର ବନ ମଧ୍ୟରେ କୌଣସି ଅସୁବିଧା ହେଲା କି ? ଏହା ଚିନ୍ତାକରି ଭୟରେ ମାତା ଯଶୋଦାଙ୍କ ହୃଦୟ ବ୍ୟସ୍ତତାରେ ଭରିଉଠିଛି, ବ୍ୟାକୁଳତାରେ ଅଧୀର ହୋଇପଡ଼ିଛନ୍ତି ସେ ।

ଯେଉଁ କୃଷ୍ଣ ଅନ୍ଧାରକୁ ଭୟ କରନ୍ତି, ସେ ଗାଈଗୋଠ ସହ ସନ୍ଧ୍ୟା ପରେ କିପରି ଘରକୁ ଫେରିବେ ସେ ବିଷୟରେ ଭାବି ମା’ ମନ ବାତୁଳ ପ୍ରାୟ ହୋଇଉଠିଛି । ବାରଣ କଲେ ମଧ୍ୟ କୃଷ୍ଣ ଗାଈଗୋଠ ସହ ବନକୁ ଯିବାକୁ ଜିଦ୍ କରୁଥିଲେ । ବୃଦ୍ଧ ବୟସରେ ତାଙ୍କ ହୃଦଚନ୍ଦନ ପ୍ରାୟ ଏକମାତ୍ର ପୁତ୍ରର ଅନୁପସ୍ଥିତି ତାଙ୍କୁ ବିବ୍ରତ କରିପକାଇଛି । ତାଙ୍କର ମନେପଡ଼ିଯାଇଛି କୃଷ୍ଣଙ୍କର ଲବଣି ମାଗିବାର ଭଙ୍ଗୀ । ଗୋଟିକା, ଅଧାମ, ସର ଖାଇବାକୁ ରୁଚୁ ନଥିଲାବେଳେ ଲହୁଣି ଚୋରାଇ ଖାଇବାରେ ସେ କିପରି ପାରଙ୍ଗମ ଥିଲେ ତାହା ଯଶୋଦାଙ୍କ ଆଖି ଆଗରେ ନାଚି ଉଠିଛି ।

ମା’ ଶୁଣିଥିଲେ ଯେ ବନରେ ଡାକିନୀ, ଯୋଗିନୀ ଆଦି ନିଶାଚରମାନେ ଉପଦ୍ରବ କରିଥାଆନ୍ତି, ଯେଉଁଥପାଇଁ ସେ ଦୁର୍ବଳ ମନା କୃଷ୍ଣଙ୍କୁ ବନକୁ ପଠାଇବାକୁ ବାରଣ କରି ଆସୁଥିଲେ । ସେମାନେ ପୁଅ ପାଇଁ କିଛି ବିପତ୍ତି ସୃଷ୍ଟି କରିନାହାନ୍ତି ତ ! ମମତାମୟୀ ମା’ ମନ ସେ କଥା ଚିନ୍ତାକରି ଆତଙ୍କିତ ହୋଇପଡ଼ିଛି। ନିଦାଘ ଝାଞ୍ଜିରେ ହୁଏତ କୋମଳ ଅଙ୍ଗରୁ ଝାଳ ବୋହି ପଡ଼ୁଥ‌ିବ । କଠଉ କି ଛତା ମଧ୍ଯ ନେବାକୁ ଭୁଲିଯାଇଛନ୍ତି ସେ । ହୁଏତ ପାଦରେ କଣ୍ଟା ଫୁଟି କଷ୍ଟ ହେଉଥ‌ିବ । ଏ ସମସ୍ତ କଥା ମନରେ ଭାଳି ଯଶୋଦା ବିବ୍ରତ ହୋଇପଡ଼ିଛନ୍ତି । ଗୋଠ ବାହୁଡ଼ା ସମୟରେ ପୁଅର ବଂଶୀସ୍ବନ ନ ଶୁଣି ସେ ବ୍ୟସ୍ତ ହୋଇପଡ଼ିଛନ୍ତି । ବାତ୍ସଲ୍ୟ ମମତାରେ ଭରା ମା’ ହୃଦୟର ଉଦ୍‌ବିଗ୍ନତା କବିତାକୁ ରସାଣିତ କରିଛି ।

କଠିନ ଶବ୍ଦାର୍ଥ :

• ଭାକୁଛନ୍ତି – ଭାବୁଛନ୍ତି
• ଧୀରେ – ପଣ୍ଡିତମାନେ /ସୁଧୀଜନମାନେ ।
• ବାତ୍ସଲ୍ୟ ମମତା – ନିଜ ପୁଅଝିଅମାନଙ୍କ ପ୍ରତି ପିତାମାତାଙ୍କ ଗଭୀର ସ୍ନେହ ।
• ଘେନ – ଗ୍ରହଣ କର
• କାନନ – ବଣ / ଜଙ୍ଗଲ ।
• ନିଧନ – ଧନହୀନ / ଦରିଦ୍ର / ଗରିବ
• ଲଉଡ଼ି – ବାଡ଼ି ।
• ଅନ୍ଧ ଲଉଡ଼ି – ଅନ୍ଧଲୋକ ବାଡ଼ି ସାହାଯ୍ୟରେ ବାଟ ଖୋଜି ଚାଲେ । ବାଢ଼ିଟି ତା’ପାଇଁ ସବୁଠାରୁ ବେଶି -ପ୍ରିୟ, ବେଶି ପ୍ରୟୋଜନ ।
• ଜୀବନ – ପ୍ରାଣ
• ପାସୋରି – ଭୁଲି
• ସାରୁ – ଶେଷକରୁ
• ଜନକ – ପିତା / ବାପା ।
• ଜନନୀ – ମାତା ।
• ନନ୍ଦନ – ପୁତ୍ର ।
• ବାରବାର – ବାରମ୍ବାର
• ଡାକିନୀ – ଡାହାଣୀ
• ହରିଚନ୍ଦନ – ଶୀତଳତା ପ୍ରଦାନକାରୀ ଶ୍ଵେତ ଚନ୍ଦନ ବା ଆହ୍ଲାଦ ପ୍ରଦାନକାରୀ ଚନ୍ଦନ ।
• ବେଣୁଗୀତ – ବଂଶୀସ୍ବର
• ହୃଦତାପ – ହୃଦୟର ଦୁଃଖଜ୍ଵାଳା ।
• ଗୋଟିକା – ପେଡ଼ା / ସନ୍ଦେଶ ।
• ଅଧାମ – ସରପୁଳି / ରାବିଡ଼ି ।
• ଲବଣି – ଲହୁଣି ।
• ବାରୁଥାଇ – ମନାକରୁଥାଏ
• ମମତା – ସ୍ନେହ ।
• ବେଣୁ – ବଂଶୀ ।
• ନିଶାଚର – ରାକ୍ଷସ / ରାତ୍ରିରେ ଯେଉଁମାନେ ବିଚରଣ କରନ୍ତି ।
• ଅଙ୍ଗୁ – ଦେହରୁ
• ଶ୍ରୁତି – ଶୁଣିବା/କାନ ।
• ତରୁ – ବୃକ୍ଷ ।
• ମୃଦୁ – କୋମଳା
• ସଙ୍ଖଳି – ପ୍ରାଣଧନ / ପ୍ରିୟବ୍ ସ୍ତୁ।
• ତାଙ୍କୁଶା – ଡାହାଣା

Odisha State Board BSE Odisha 7th Class Odia Solutions Chapter 2 ତାରା-ସୂର୍ଯ୍ୟ Textbook Exercise Questions and Answers.

BSE Odisha Class 7 Odia Solutions Chapter 2 ତାରା-ସୂର୍ଯ୍ୟ

ପାଠ୍ୟପୁସ୍ତକସ୍ଥ ଅଭ୍ୟାସ କାର୍ଯ୍ୟର ଉତ୍ତର

Question ୧।
ଉତ୍ତର କୁହ ।
(କ) କେଉଁମାନଙ୍କୁ ରବି ପରି ରଶ୍ମିମାନ୍ ବୋଲି କବି କହିଛନ୍ତି ?
Answer:
ବିଦେଶୀ ଶାସକମାନଙ୍କ କଠୋର ଶାସନ ଓ ପ୍ରଚଣ୍ଡ ବଳ ବିକ୍ରମ ରବି ପରି ରଶ୍ମିମାନ୍ ଭଳି ଦେଖାଯାଉଥିଲେ ମଧ୍ୟ ଆମ ଦେଶର ବିଜ୍ଞ, ବିଦ୍ୱାନ୍ ଓ ଜ୍ଞାନୀ ଗୁଣୀମାନଙ୍କୁ ରବି ପରି ରଶ୍ମିମାନ୍ ବୋଲି କବି କହିଛନ୍ତି ।

(ଖ) ସେମାନଙ୍କ ମନରେ ଭୟ ଅଛି ବୋଲି କବି କାହିଁକି ଉପଲବ୍ଧି କରିଛନ୍ତି ?
Answer:
ସୂର୍ଯ୍ୟଙ୍କ ଦୀପ୍ତିମନ୍ତ ଆଭା ଓ ଜ୍ୟୋତି ସମ୍ମୁଖରେ ଦୂର ଗଗନର ନକ୍ଷତ୍ରମାନେ ତେଜହୀନ ଜଣା ପଡ଼ିଥାଆନ୍ତି । କବି କିନ୍ତୁ ଏଠାରେ ଦେଶବାସୀଙ୍କ ମନର ଭୟକୁ ଲକ୍ଷ୍ୟ କରି ଏହା କହିଛନ୍ତି । ବିଦେଶୀ ଶାସକଙ୍କ ନିଷ୍ଠୁର ଶାସନ ବ୍ୟବସ୍ଥା ଆଢୁଆଳରେ ସେମାନେ ଭୟାତୁର ବୋଲି କବି ଅନୁଭବ କରିଛନ୍ତି ।

(ଗ) ଆମ୍ଭ ଭାସ୍କର କାହାକୁ ଲକ୍ଷ୍ୟ
Answer:
ଦେଶବାସୀଙ୍କ ଉପରେ ବିଦେଶୀ ଶାସକଙ୍କ ବଳ ବିକ୍ରମ ତଥା ନିର୍ଦ୍ଦୟ ଶାସନକୁ କବି ଆମ୍ଭ ଭାସ୍କର ବୋଲି କହିଛନ୍ତି ।

(ଘ) ଆମ୍ଭ ଭାସ୍କରକୁ ଅନ୍ୟମାନେ କାହିଁକି କ୍ଷୁଦ୍ର ତାରା ବୋଲି କହନ୍ତି ?
Answer:
ପୃଥ୍ବା ବାସାଙ୍କୁ ସୂର୍ଯ୍ୟ ପ୍ରଚଣ୍ଡ ତେଜୋଦୀପ୍ତ ପ୍ରତାୟମାନ ହେଉଥ୍ବାବେଳେ ହର ମହାକାଶରେ ସୂର୍ଯ୍ୟସମ ଅନ୍ୟ ନକ୍ଷତ୍ରମାନଙ୍କ ମଣ୍ଡଳ ମଧ୍ୟରେ ଥ‌ିବା ଗ୍ରହାଧ‌ିବାସୀମାନଙ୍କୁ ସୂର୍ଯ୍ୟ କ୍ଷୁଦ୍ର ତାରା ପରି ପରିଦୃଷ୍ଟ ହୁଅନ୍ତି । ବାସ୍ତବରେ ସୂର୍ଯ୍ୟସମ ଆଚରଣ ପ୍ରଦର୍ଶନ କରୁଥ‌ିବା ବିଦେଶୀ ଶାସକମାନେ ଆମ ଦେଶବାସୀଙ୍କ ପାଇଁ କ୍ଷୁଦ୍ର ତଥା ନଗଣ୍ୟ ଭାବେ ଗୃହୀତ ହୋଇଥାଆନ୍ତି ।

(ଙ) ‘‘ଆମ୍ଭେ ଚାହୁଁଥାଉ ତାଙ୍କର ଉଦୟ’’- କିଏ କାହାର ଉଦୟ ଚାହୁଁଛନ୍ତି ?
Answer:
ଆମ ଦେଶବାସୀ ଏପରି ସଂସ୍କାର ପାଇଛନ୍ତି ଯେ ସେମାନେ ଉପକାରୀର ସମାଲୋଚନା କରିପାରନ୍ତି ନାହିଁ । ବିଶ୍ବ ସଭ୍ୟତା ଓ ବିଜ୍ଞାନ ବିଷୟରେ ଆମକୁ ସଭ୍ୟ ଶିକ୍ଷିତ କରାଇଥିବା, ଜ୍ଞାନଦାନ କରାଇଥିବା ରାଜାର ଜୟଗାନ କରିବା ପ୍ରଜାର ପ୍ରଥମ କର୍ତ୍ତବ୍ୟ ବୋଲି ଭାରତୀୟମାନେ ଚିନ୍ତା କରିଥାଆନ୍ତି । ତେଣୁ ତାଙ୍କର ଜୟଗାନ କରିବା ତଥା ଆମର ଉପକାର ସାଧନ କରୁଥିବା ଶାସକଙ୍କୁ ସୂର୍ଯ୍ୟ ସହ ତୁଳନା କରି ଆମେ ତାଙ୍କ ଉଦୟ କାମନା କରୁଥାଉ ବୋଲି କବି ଉଲ୍ଲେଖ କରିଛନ୍ତିା

Question ୨।
ଦୁଇଟି ବା ତିନୋଟି ବାକ୍ୟରେ ଉତ୍ତର ଲେଖ ।
(କ) ତାରାଗଣ କେବଳ ନିଜର ଜଗତକୁ ଆଲୋକିତ କରିଛନ୍ତି – ଏଥୁ କେଉଁ ଭାବ ପ୍ରକାଶ ପାଇଛି ?
Answer:
ତାରାଗଣ ସୁଦୂର ମହାକାଶରେ ଅବସ୍ଥାପିତ ଥିବାରୁ ଆମକୁ କ୍ଷୁଦ୍ର ପରିଦୃଷ୍ଟ ହୋଇଥାଆନ୍ତି । କିନ୍ତୁ ସେମାନେ ସୂର୍ଯ୍ୟଙ୍କ ପରି ଗୋଟିଏ ଗୋଟିଏ ମହାନ୍ ଆଲୋକପିଣ୍ଡ ଅଟନ୍ତି । ସେମାନେ ନିଜ ମଣ୍ଡଳରେ ଥ‌ିବା ଗ୍ରହ ଉପଗ୍ରହାଦିର ଅଧିବାସୀମାନଙ୍କୁ ଆଲୋକ ପ୍ରଦାନ କରିଥାଆନ୍ତି । ସେହିପରି ଆମ ଦେଶର ବିଜ୍ଞ, ବିଦ୍ଵାନ୍ ତଥା ପଣ୍ଡିତମଣ୍ଡଳୀ ଯଥେଷ୍ଟ ପ୍ରତିଭାବାନ୍ ହୋଇଥିଲେ ମଧ୍ୟ ସେମାନେ କେବଳ ନିର୍ଦ୍ଦିଷ୍ଟ ପରିସର ମଧ୍ୟସ୍ଥ ସମାଜରେ ପୂଜ୍ୟ ଓ ମହାନ୍ ଭାବେ ପରିଗଣିତ ହୋଇଥାଆନ୍ତି । ପ୍ରଚାର ଓ ପ୍ରସାର ଅଭାବରୁ ସେମାନେ ବହିର୍ଦେଶ ଲୋକଲୋଟନ ଅନ୍ତରାଳରେ ରହି ନଗଣ୍ୟ ଭାବେ ବିବେଚିତ ହୁଅନ୍ତି । ବିଦେଶୀ ଶାସକବର୍ଗ ବଳପୂର୍ବକ ସେମାନଙ୍କ ଉପରେ ପ୍ରଭୁତ୍ଵ ଜାହିର କରି ଅନ୍ୟ ଦେଶରେ ମଧ୍ୟ ସୂର୍ଯ୍ୟସମ ତେଜୋଦୀପ୍ତ ଜଣା ପଡ଼ିଥାଆନ୍ତି । କିନ୍ତୁ ଆମ ଦେଶର ପ୍ରଚଣ୍ଡ ପ୍ରତିଭାମାନେ କେବଳ ଆମ ନିଜ ଦେଶରେ ହିଁ ପରିଚିତ ହୋଇଥାଆନ୍ତି ।

(ଖ) ଆମ ଭାସ୍କରଙ୍କୁ ତାରାରାଜ୍ୟର ଲୋକମାନେ ଏକ କ୍ଷୁଦ୍ର ତାରା ବୋଲି କହୁଥ‌ିବାରୁ କବିଙ୍କ ମନରେ କେଉଁ ଭାବ ଉଦ୍ରେକ ହୋଇଛି ?
Answer:
ମହତ ବ୍ୟକ୍ତିମାନେ ସାଧାରଣ ଲୋକଙ୍କ କଥାରେ ପ୍ରତିକ୍ରିୟା ପ୍ରକାଶ କରନ୍ତି ନାହିଁ । ଯାହା ବାସ୍ତବ ସେମାନେ ତାରା ପରି ପ୍ରତୀୟମାନ ହୋଇଥାଏ । ତେଣୁ ସେମାନେ ଆମ ଭାସ୍କରକୁ କ୍ଷୁଦ୍ର ତାରା ବୋଲି କହିଥା’ନ୍ତି । କବି ଏ କଥାରେ ବିସ୍ମୟ ପ୍ରକାଶ କରିନାହାନ୍ତି । ତାଙ୍କ ମତରେ ଭାସ୍କରକୁ କ୍ଷୁଦ୍ର ତାରା ବୋଲି କହିଦେଲେ ସେ କ୍ଷୁଦ୍ର ହୋଇଯାଏ ନାହିଁ । ସାଧାରଣ ଚକ୍ଷୁରେ ତାରା ପରି ଦେଖାଗଲେ ମଧ୍ୟ ଭାସ୍କରର ତେଜ ଓ ଆଲୋକରେ କିଛି ପରିବର୍ତ୍ତନ ଆସି ନଥାଏ ।

(ଗ) ତାରାମାନଙ୍କ ରାଜ୍ୟରେ ଆମ ସୂର୍ଯ୍ୟ କାହିଁକି ଦେଖାଯାଆନ୍ତି ନାହିଁ ?
Answer:
ସୂର୍ଯ୍ୟ ଏକ ଜ୍ଵଳନ୍ତ ଅଗ୍ନିପିଣ୍ଡ । ଏହାର ଆଲୋକ ଓ ତେଜ ସୌରମଣ୍ଡଳରେ ଅବସ୍ଥିତ ଗ୍ରହ, ଉପଗ୍ରହାଦିଙ୍କୁ ଅନୁଭୂତ ହୁଏ । ମାତ୍ର ତାରକାମାନେ ନିଜ ମଣ୍ଡଳରେ ଥାଇ ନିଜ ଚତୁଃପାର୍ଶ୍ଵରେ ପରିକ୍ରମା କରୁଥିବା ଗ୍ରହାଦିମାନଙ୍କୁ ଆଲୋକ ପ୍ରଦାନ କରିଥାଆନ୍ତି ଯେଉଁଠାରେକି ସୂର୍ଯ୍ୟଙ୍କ ଆଲୋକ ତାରା ପରି ପରିଦୃଷ୍ଟ ହୁଏ । ଦିବସରେ ମଧ୍ୟ ସେହି ତାରକାମାନଙ୍କର ତେଜ ଓ ଆଲୋକ ପ୍ରଭାବରେ ଆମ ସୂର୍ଯ୍ୟ ସେମାନଙ୍କ ରାଜ୍ୟରେ ପରିଦୃଷ୍ଟ ହୋଇନଥାଆନ୍ତି । ପରିଦୃଷ୍ଟ ହୁଏ ସେମାନେ ସେ ସମ୍ପର୍କରେ ଅନୁରୂପ ମତ ପ୍ରଦାନ କରିଥାଆନ୍ତି ।

(ଙ) ତାରାମାନଙ୍କର ରବିପଣ କେବଳ ସେଇମାନଙ୍କ ରାଜ୍ୟରେ ସୀମିତ ବୋଲି କୁହାଯାଇଛି କାହିଁକି ?
Answer:
ସୂର୍ଯ୍ୟ ଏକ ଉଜ୍ଜ୍ଵଳ ତେଜୋମୟ ଆଲୋକପିଣ୍ଡ । ଏହାର ତେଜ ଓ ଆଲୋକ କେବଳ ସୂର୍ଯ୍ୟଙ୍କୁ ପରିକ୍ରମା କରୁଥ‌ିବା ଗ୍ରହ ଉପଗ୍ରହାଦିରେ ପରିଦୃଷ୍ଟ ହୁଏ । କିନ୍ତୁ ତାରକାମାନେ ସୂର୍ଯ୍ୟସମ ପ୍ରଚଣ୍ଡ ତେଜୋଦୀପ୍ତ ହୋଇଥିଲେ ମଧ୍ୟ ସେମାନେ ପୃଥ‌ିବୀଠାରୁ ବହୁଦୂରରେ ଅବସ୍ଥାନ କରୁଥିବାରୁ ପୃଥ‌ିବୀବାସୀ ସେମାନଙ୍କ ରବିପଣ ଅନୁଭବ କରିପାରନ୍ତି ନାହିଁ । ଅନ୍ୟ ଅର୍ଥରେ ଆମ ଦେଶର ବିଦ୍ବାନ୍, ଜ୍ଞାନୀମାନେ ଅନ୍ୟ ଦେଶରେ ନିଜର ଜ୍ଞାନ ଗରିମା ପରିପ୍ରକାଶ କରିବାର ସେମାନଙ୍କୁ ମର୍ଯ୍ୟାଦା ପ୍ରଦାନ କରିଥାଏ ।

Question ୩।
ପ୍ରସଙ୍ଗ ସହ ସରଳାର୍ଥ ଲେଖ ।
(କ) ଯାହାକୁ ଯେମନ୍ତ ଦିଶେ ତେମନ୍ତ ସେ ଭାଷେ ।
Answer:
ଯାହାକୁ ………………………………… ସେ ଭାଷେ ।
Answer:
ଶଂସିତ ପଦ୍ୟାଶଟି ସ୍ବଭାବ କବି ଗଙ୍ଗାଧର ମେହେରଙ୍କ ରଚିତ ‘ତାରା-ସୂର୍ଯ୍ୟ’ କବିତାରୁ ଆନୀତ । ଏଠାରେ କବି ଏକ ସାଧାରଣ ସତ୍ୟର ଅବତାରଣା କରିଛନ୍ତି । ସାଧାରଣତଃ ଲୋକମାନେ କୌଣସି ବସ୍ତୁକୁ ଯେପରି ଭାବେ ଦେଖୁଥାଆନ୍ତି ସେହି ଭାବେ ବର୍ଣ୍ଣନା କରିଥା’ନ୍ତି । ଚାରି ଅନ୍ଧ ସାଙ୍ଗ ହାତୀର ବର୍ଣ୍ଣନା କଲାପରି ଖାଲି ଆଖୁକୁ ଯାହାକିଛି ଯେପରି ଭାବେ ଦୃଶ୍ୟମାନ ହୁଏ ତାହା ଜନସାଧାରଣରେ ସେହିଭାବେ ବର୍ଣ୍ଣିତ ହୋଇଥାଏ । ମାତ୍ର ମହତ ଲୋକେ ସେହି ମନ୍ତବ୍ୟ ସମ୍ପର୍କରେ କୌଣସି ପ୍ରତିକ୍ରିୟା ପ୍ରକାଶ କରିନଥା’ନ୍ତି । କାରଣ ସେମାନେ ବାସ୍ତବତା ଉପଲବ୍ଧି କରିପାରନ୍ତି । ସେମାନେ ସାଧାରଣ ଚକ୍ଷୁରେ ଯାହା ଯେପରି ଦେଖାଯାଏ ତା’ର କାରଣ ଅନୁଧ୍ୟାନ କରନ୍ତି ଓ ବାସ୍ତବତାକୁ ବୁଝି ମତ ଉପସ୍ଥାପନ କରନ୍ତି । ତାରାମାନେ ସୂର୍ଯ୍ୟ ସମ ପ୍ରଚଣ୍ଡ ତେଜୋଦୀପ୍ତ ଆଲୋକପିଣ୍ଡ ବୋଲି କବି ଉପଲବ୍ଧି କରିଛନ୍ତି ଏବଂ ଦିବସରେ ତାରକାଗଣ ପରିଦୃଷ୍ଟ ନ ହେବାର କାରଣ ମଧ୍ୟ ସେ ଜାଣିଛନ୍ତି । ସେଇଥପାଇଁ ସାଧାରଣ ଲୋକଙ୍କ ପରି ମତ ପ୍ରକାଶ ନକରି ପ୍ରକୃତ କାରଣ ଅନୁଧ୍ୟାନ କରିବା ଗୁରୁତ୍ଵପୂର୍ଣ୍ଣ ବୋଲି କବି କହିଛନ୍ତି ।

(ଖ) ଯେ ଯାହାର ହିତ କରେ ନ ନେଲେ ତା’ ନାମ
ଆମ୍ଭ ଦେଶେ କହୁଁ ତାକୁ ନିମକହାରାମ ।
Answer:
ଯେ ଯାହାର …………………….. ନିମକହାରାମ ।
ପ୍ରୋକ୍ତ ପଦ୍ୟାଶଟି ସ୍ବଭାବ କବି ଗଙ୍ଗାଧର ମେହେରଙ୍କ ରଚିତ ‘ତାରା-ସୂର୍ଯ୍ୟ’ କବିତାରୁ ଆନୀତ । ଏଠାରେ କବି ଆମ୍ଭ ଦେଶବାସୀଙ୍କ ଅନ୍ୟ ଏକ ମହାନତା ବିଷୟରେ ଆଲୋକପାତ କରିଛନ୍ତି । ଉପକାରୀର ଉପକାର ସ୍ଵୀକାର କରିବା ମହତ ବ୍ୟକ୍ତିର ଲକ୍ଷଣ । ଭାରତୀୟମାନେ ଏହା ଉପଲବ୍ଧି କରି ନିଜ ମହନୀୟତାର ପରିଚୟ ଯୁଗେ ଯୁଗେ ପ୍ରଦାନ କରି ଆସିଛନ୍ତି । ତାରକାଗଣ ସୂର୍ଯ୍ୟଙ୍କ ପରି ତେଜୋଦୀପ୍ତ ହୋଇଥିଲେ ମଧ୍ୟ ଆଲୋକ ଉତ୍ତାପ ଯୋଗାଇ ସକଳ ଶକ୍ତିର ଆଧାର ଭାବେ ଗୃହୀତ ହୋଇଥାଆନ୍ତି ।

ସେଥ୍ପାଇଁ ଆମେ ପ୍ରତ୍ୟହ ତାଙ୍କର ଉଦୟ କାମନା କରିଥାଉ ଏବଂ ତାଙ୍କ ମହାନ୍ ଉପକାର ପାଇଁ ତାଙ୍କୁ ପ୍ରଣିପାତ କରିଥାଉ । ତାରାଗଣ ସୂର୍ଯ୍ୟସମ ଜ୍ଵଳନ୍ତ ଆଲୋକପିଣ୍ଡ ହୋଇଥିଲେ ମଧ୍ୟ ସେମାନେ ଆମର କୌଣସି ଉପକାରରେ ଆସୁନଥ‌ିବାରୁ ସୂର୍ଯ୍ୟ ପରି ସେମାନେ ଉପଯୁକ୍ତ ସମ୍ମାନ ଲାଭ କରନ୍ତି ନାହିଁ । ତେଣୁ ଆମ ଦେଶବାସୀ ଉପକାରୀ । ସୂର୍ଯ୍ୟଙ୍କ ମହାନତାରେ ଶତମୂଖ ହୋଇଛନ୍ତି । ତାରକାଗଣଙ୍କୁ ଲୁକ୍କାୟିତ ପ୍ରତିଭା ସେମାନଙ୍କ ଦୃଷ୍ଟି ଅନ୍ତରାଳରେ ରହିଯାଇଛି । ଅଥଚ ସେହି ତାରକାଗଣ ଦିନେ ନା ଦିନେ ପରିପ୍ରକାଶିତ ହୋଇ ନିଜର ଉଜ୍ଜଳତାର ଜଗତକୁ ଆଲୋକ ଦୀପ୍ତ କରିବେ ।

Question ୪।
ଦିଆଯାଇଥ‌ିବା ଶବ୍ଦଗୁଡ଼ିକର ଦୁଇଟି ଲେଖାଏଁ ପ୍ରତିଶବ୍ଦ ଲେଖ ।
ରଜନୀ, ଭାସ୍କର, ଗଗନ, ତମ, ତାରା
Answer:
ରଜନୀ – ରାତ୍ରି, ବିଭାବରୀ
ଭାସ୍କର – ସୂର୍ଯ୍ୟ, ରବି
ଗଗନ – ଆକାଶ, ଅମ୍ବର
ତମ – ଅଜ୍ଞାନ, ଅନ୍ଧାର
ତାରା – ନକ୍ଷତ୍ର, ଚନ୍ଦ୍ରଜାୟା

Question ୫।
ବିପରୀତ ଅର୍ଥବୋଧକ ଶବ୍ଦ ଲେଖ ।
ଲାଭ, କ୍ଷୟ, ଉଦୟ, ହିତ, ପ୍ରଚୁର, ମହତ, କ୍ଷୁଦ୍ର, ଆଲୋକ
Answer:
ଲାଭ – କ୍ଷତି
ଉଦୟ – ଅସ୍ତ
ପ୍ରଚୁର – ଅପ୍ରଚୁର, ସ୍ଵୱି
କ୍ଷୁଦ୍ର – ବୃହତ୍
କ୍ଷୟ – ବୃଦ୍ଧି
ହିତ – ଅହିତ
ମହତ – ହାନ, ଅମହତ
ଆଲେ।କ – ଅନ୍ଧକାର

Question ୬ ।
ତଳେ ଦିଆଯାଇଥ‌ିବା ଶବ୍ଦଗୁଡ଼ିକୁ ପୁରୁଷ ଭେଦରେ ସଜାଇ ଲେଖ ।
ସେ, ତାରା, ତୁମ୍ଭେ, ରବି, ଆମ୍ଭ, ତୁମ୍ଭ (ପ୍ରଥମ ପୁରୁଷ, ଦ୍ଵିତୀୟ ପୁରୁଷ, ତୃତୀୟ ପୁରୁଷ)
Answer:
ଦ୍ଵିତୀୟ ପୁରୁଷ – ଆମ୍ଭ
ତୁମ୍ଭେ ତୃତୀୟ ପୁରୁଷ – ତୁମ୍ଭ, ତୁମ୍ଭେ
ତୃତାୟ ପୁରୁଷ – ସେ, ତାରା, ରବି

Question ୭ ।
୧୦୦ ରୁ ୧୫୦ ଶବ୍ଦ ମଧ୍ଯରେ ଉତ୍ତର ଲେଖ ।
(କ) ତାରା ଓ ସୂର୍ଯ୍ୟଙ୍କ ମଧ୍ୟରେ କବି କାହାକୁ ଶ୍ରେଷ୍ଠତ୍ୱ ପ୍ରଦାନ କରିଛନ୍ତି ?
Answer:
‘ତାରା-ସୂର୍ଯ୍ୟ’ କବିତାଟି ସ୍ବଭାବ କବି ଗଙ୍ଗାଧର ମେହେରଙ୍କ ‘ଅର୍ଘ୍ୟଥାଳୀ’ କବିତା ସଂକଳନରୁ ଗୃହୀତ । କବିତାଟିରେ କବି ବିଦେଶୀ ଶାସନାଧୀନ ଦେଶବାସୀଙ୍କ ମନରେ ଆତ୍ମବିଶ୍ଵାସ ଭରିଦେଇ ହୀନମନ୍ୟତା ଦୂର କରିବାକୁ ପରାମର୍ଶ ଦେଇଛନ୍ତି । କବି ସୁଦୂର ମହାକାଶରେ ମିଞ୍ଜି ମିଞ୍ଜି ଆଲୋକ ପ୍ରଦାନ କରୁଥିବା ତାରକାଗଣଙ୍କୁ ସୂର୍ଯ୍ୟସମ ତେଜୋଦୀପ୍ତ ବୋଲି ପ୍ରକାଶ କରି ସୂର୍ଯ୍ୟ ସହ ସମକକ୍ଷ ବୋଲି ବର୍ଣ୍ଣନା କରିଛନ୍ତି । କିନ୍ତୁ ସୂର୍ଯ୍ୟ ଆମ ନିକଟରେ ରହି ଆମ ପାଇଁ ଉପକାରୀ ଭାବେ ଉତ୍ତାପ ଓ ଆଲୋକ ପ୍ରଦାନ କରୁଥିବାରୁ, ତାରକାମାନେ ସେହି ଆଲୋକ ଓ ତାପ ତୁଳନାରେ କ୍ଷୁଦ୍ର ଓ ନଗଣ୍ୟ ବିବେଚିତ ହୋଇଥାଆନ୍ତି । ସୂର୍ଯ୍ୟଙ୍କ ପ୍ରଚଣ୍ଡ କିରଣ ପ୍ରଭାବରେ ସେମାନେ ଦିବସରେ ପ୍ରତିଭାତ ହୋଇପାରନ୍ତି ନାହିଁ । ଏଠାରେ କବି ବିଦେଶୀ ଶାସକର ନିଷ୍ଠୁର ଶାସନ ଓ ଅତ୍ୟାଚାରକୁ ତେଜଭରା ସୂର୍ଯ୍ୟ ସହ ତୁଳନା କରି ଶାସିତ ଦେଶବାସୀଙ୍କ ଅବଦମିତ ପ୍ରତିଭାକୁ ତାରକାମାନଙ୍କ ସହ ତୁଳନା କରିଛନ୍ତି।

ବିଦେଶୀ ଶାସକଙ୍କ ଶୋଷଣ ଓ ଅତ୍ୟାଚାରକୁ ମଥାପାତି ସହି ନେଉଥ‌ିବା ଦେଶବାସୀଙ୍କ ମନରେ ପ୍ରେରଣା ତଥା ଉତ୍ସାହ ଭରି ଦେବାପାଇଁ ସେମାନଙ୍କୁ ଆତ୍ମପରିଚୟ ପ୍ରଦାନ କରି କବି କହିଛନ୍ତି ଯେ ସେମାନେ ବିଦେଶୀମାନଙ୍କ ତୁଳନାରେ କୌଣସି ଗୁଣରେ ନୂନ ନୁହଁନ୍ତି । ଏଠାରେ ତାରାର ଶ୍ରେଷ୍ଠତ୍ୱ ପ୍ରତିପାଦିତ ହୋଇଛି । ସେମାନେ ଅତୀତରେ ବିଶ୍ବରେ ଏକ ପ୍ରମୁଖ ବୀରଜାତି ଭାବେ ଯେପରି ପରିଗଣିତ ହୋଇଥିଲେ ତାହା ହୁଏତ ସେମାନେ ପାସୋରି ଦେଇଛନ୍ତି । କଳା, ସାହିତ୍ୟ, ଧର୍ମ, ପ୍ରତିରକ୍ଷା, ବାଣିଜ୍ୟ ବ୍ୟବସାୟ ଆଦି ସବୁକ୍ଷେତ୍ରରେ ସେମାନେ ଥିଲେ ଅଦ୍ବିତୀୟ । ସେମାନଙ୍କ ପ୍ରଚଣ୍ଡ ପ୍ରତିଭା ସମ୍ପର୍କରେ କବି ଅଗବତ ଥ‌ିବାରୁ ସେମାନଙ୍କୁ ଦୂର ଆକାଶର ତାରକା ସହ ତୁଳନା କରିଛନ୍ତି ।

କେବଳ ସେମାନଙ୍କ ପ୍ରତିଭା ନିଜ ଦେଶ ମଧ୍ୟରେ ସୀମିତ ରହିବାରୁ ଅନ୍ୟ ରାଷ୍ଟ୍ରବାସୀ ତାହା ଉପଲବ୍ଧି କରିପାରି ନାହାନ୍ତି । ପରାଧୀନତାର ଶୋଷଣ ଓ ପେଷଣ ମଧ୍ୟରେ ସେମାନେ କ୍ରମେ ଆତ୍ମବିଶ୍ଵାସ ହରାଇ ଦୁର୍ବଳ ମାନସିକତାର ଶିକାର ହୋଇଛନ୍ତି । ସେମାନଙ୍କ ଶକ୍ତି, କ୍ଷମତା ସଙ୍କୁଚିତ ହୋଇ ଦୂରଗଗନର ତାରକା ବଞ୍ଚ୍ ରହିଛି । ନିଜ ଦେଶବାସୀଙ୍କର ଏତାଦୃଶ ଅବସ୍ଥା ଲକ୍ଷ୍ୟ କରି କବି ଅଭିମାନଭରା ସଚେତନ ହେବାକୁ ଆହ୍ଵାନ କରିଛନ୍ତି । ନିଜ ଦେଶବାସୀଙ୍କର ଏତାଦୃଶ ଅବସ୍ଥା ଲକ୍ଷ୍ୟ କରି କବି ଅଭିମାନଭରା କଣ୍ଠରେ ସେମାନଙ୍କୁ ଜାଗ୍ରତ ତଥା ସଦୃଶ କେବଳ ମିଞ୍ଜି ମିଞ୍ଜି ହୋଇ କଣ୍ଠରେ ସେମାନଙ୍କୁ ଜାଗ୍ରତ ତଥା ସଚେତନ ହେବାକୁ ଆହ୍ବାନ କରିଛନ୍ତି।

(ଖ) କବି ନିଜର ଅଭିମାନକୁ କିପରି ପ୍ରକାଶ କରିଛନ୍ତି ?
Answer:
ସ୍ବଭାବ କବି ଗଙ୍ଗାଧର ମେହେର ଥିଲେ ଜଣେ ସ୍ଵାଭିମାନୀ ଓ ଦେଶପ୍ରେମୀ । କବିଙ୍କର ‘ତାରା-ସୂର୍ଯ୍ୟ’ କବିତାଟି ଏକ ଦେଶପ୍ରେମମୂଳକ କବିତା । ଦେଶବାସୀଙ୍କୁ ଜାଗରିତ କରିବା ଉଦ୍ଦେଶ୍ୟରେ ଏହି କବିତାଟି ରଚିତ ହୋଇଛି । ମାତୃଭୂମି ଓ ମାତୃଭାଷା ପ୍ରତି ତାଙ୍କ ହୃଦୟରେ ଥିଲା ଗଭୀର ମମତା। ପରାଧୀନ ଭାରତର ଦେଶବସୀଙ୍କ ଦୁରବସ୍ଥା କବିଙ୍କୁ ଗଭୀର ଦୁଃଖ ଦେଇଛି । ବିଦେଶୀ ଶାସନର ଅତ୍ୟାଚାର ଓ ଶୋଷଣରେ ଦେଶବାସୀ ନିଜର ସ୍ବାତନ୍ତ୍ର୍ୟ ହରାଇ ବାଧ୍ୟ ହୋଇ ନିଷ୍ଠୁର ଶାସନକୁ ମଥାପାତି ସହି ନେଉଥିଲେ । ଏକଦା ବିଶ୍ଵରେ ଏକ ମହାନ୍ ଜାତିର ମର୍ଯ୍ୟାଦା ଲାଭ କରିଥିବା ଆମ ଦେଶବାସୀ ଅତୀତ ଗୌରବକୁ ଭୁଲିଯାଇ ନୀରବରେ ସମସ୍ତ ଶୋଷଣ କଷଣକୁ ସହ୍ୟ କରୁଥିବା ଲକ୍ଷ୍ୟ କରି ସେମାନଙ୍କ ମନରେ ଆତ୍ମବିଶ୍ଵାସ ସୃଷ୍ଟି କରିବାକୁ କବି ତାଙ୍କ ଲେଖନୀ ଚାଳନା କରିଛନ୍ତି । ଆମ ଦେଶବାସୀ କେତେ ମହାନ୍ ଓ କେତେ କେତେ ପ୍ରତିଭାର ଅଧ୍ୟାକାରୀ ହୋଇ ମଧ୍ଯ କଠୋର ଶାସନ ତଳେ ହୀନମନ୍ୟ ହୋଇପଡ଼ିବା କବିଙ୍କ ମନରେ ବିଷାଦ ଭରି ଦେଇଛି । ତେଣୁ ସେମାନଙ୍କ ଭିତରେ ଲୁଚି ରହିଥ‌ିବା ସ୍ଵାଧୀନଚେତା ମାନବୀୟ ଗୁଣର ବିକାଶ ଘଟାଇବାପାଇଁ ସେ ସେମାନଙ୍କୁ ଆହ୍ୱାନ କରିଛନ୍ତି।

ସୂର୍ଯ୍ୟ ପ୍ରଚଣ୍ଡ ତେଜ ଓ ଆଲୋକରେ ଧରାବାସୀଙ୍କୁ ଅସ୍ତବ୍ୟସ୍ତ କରି ପକାଉଥବା ବେଳେ ସୁଦୂର ମହାକାଶରେ ଥ‌ିବା ଅସଂଖ୍ୟ ତାରାଗଣ କେବଳ କ୍ଷୀଣ ଆଲୋକ ଧରି ଚାହିଁ ରହିଛନ୍ତି । ଏପରିକି ସୂର୍ଯ୍ୟଙ୍କ ପ୍ରଚଣ୍ଡ ପ୍ରଭାରେ ସେମାନେ ଦିବସରେ ଜ୍ୟୋତିହୀନ ହୋଇ ରହିଛନ୍ତି । ଯଦିଓ ସେମାନେ ସୂର୍ଯ୍ୟଙ୍କ ପରି ଗୋଟିଏ ଗୋଟିଏ ତେଜୋମୟ ଆଲୋକପିଣ୍ଡ ତଥାପି ସୂର୍ଯ୍ୟଙ୍କ ପରାକ୍ରମ ନିକଟରେ ସେମାନେ ନିଜର ବିକ୍ରମ ପରିପ୍ରକାଶର ସୁଯୋଗ ପାଉନାହାନ୍ତି । ସେହିପରି ଆମ ଦେଶବାସୀମାନେ ପ୍ରଚଣ୍ଡ ପ୍ରତିଭାର ଅଧିକାରୀ ହେଲେ ମଧ୍ୟ କେବଳ ଦେଶ ମଧ୍ୟରେ ତାହା ସୀମିତ ରହିଛି । ପ୍ରଚାର ଓ ପ୍ରସାର ଅଭାବରୁ ସେମାନଙ୍କ ପ୍ରତିଭା ସମ୍ପର୍କରେ ବାହ୍ୟଜଗତ ଅପରିଚିତ ରହିଛି । କିନ୍ତୁ ସେମାନଙ୍କଠାରେ ଯେଉଁ ମହାନୁଭବତା , ଅଛି ତାହା ଅନ୍ୟତ୍ର ବିରଳ । ସେମାନେ ଉପକାରୀର ଉପକାରକୁ ମୁକ୍ତ କଣ୍ଠରେ ସ୍ଵୀକାର କରି ତା’ର ଉନ୍ନତି କାମନା କରିଥାଆନ୍ତି । ସେଥ୍ପାଇଁ କବି କହିଛନ୍ତି –

‘ଯେ ଯାହାର ହିତ କରେ ନ ନେଲେ ତା’ ନାମ
ଆମ୍ଭ ଦେଶେ କହୁଁ ତାକୁ ନିମକହାରାମ ।’’

(ଗ) ‘ତାରା-ସୂର୍ଯ୍ୟ’ କବିତାର ଭାବ ଆମକୁ ଏକ ମହାଶିକ୍ଷା ପ୍ରଦାନ କରେ କିପରି ?
Answer:
ସ୍ବଭାବ କବି ଗଙ୍ଗାଧର ମେହେରଙ୍କ ସମସ୍ତ କବିତାବଳୀ ପାଠକଙ୍କୁ ମହାନ୍ ଶିକ୍ଷା ପ୍ରଦାନ କରିଥାଏ । ପଠିତ ‘ତାରା-ସୂର୍ଯ୍ୟ’ କବିତାରେ କବି ତାରା କିମ୍ବା ସୂର୍ଯ୍ୟ କାହାକୁ ନୂନ ଭାବେ ବର୍ଣ୍ଣନା ନକରି ଉଭୟଙ୍କ ଗୁଣଗାନ କରିଛନ୍ତି । ଏହା କେବଳ ଜଣେ ମହତ ବ୍ୟକ୍ତିର ଲକ୍ଷଣ । ମହତ ବ୍ୟକ୍ତି ସର୍ବଦା ଉପକାରୀ ନିକଟରେ କୃତଜ୍ଞ ରହିବା ସହ ପ୍ରତ୍ଯୁପକାର ପାଇଁ ସୁଯୋଗ ଅପେକ୍ଷାରେ ରହେ । କାହାକୁ ଇତର ବା ନଗଣ୍ୟ ମନେକରିବା ମହତ ବ୍ୟକ୍ତିର ଲକ୍ଷଣ ନୁହେଁ । ତେଣୁ କବି କ୍ଷୀଣ ଆଲୋକ ଧାରଣ କରିଥିବା ତାରକାମାନଙ୍କୁ ସେମାନଙ୍କ ତେଜ ଓ ତାପ ବିଷୟରେ ସ୍ମରଣ କରାଇ ଦେଇଛନ୍ତି । ଅପର ପକ୍ଷରେ ସୂର୍ଯ୍ୟଙ୍କଠାରୁ ଲାଭ କରୁଥିବା ଉପକାରକୁ ମୁକ୍ତ କଣ୍ଠରେ ସ୍ଵୀକାର କରିବାକୁ ପଶ୍ଚାତ୍‌ପଦ ହୋଇ ନାହାନ୍ତି । ସେଥ‌ିପାଇଁ କବିତାରେ କହିଛନ୍ତି

‘‘ଆମ୍ଭ ରାଜ୍ୟ ଆମ୍ଭ ରବି କରେ ତମ କ୍ଷୟ,
ଏଣୁ ଆମ୍ଭେ ଚାହୁଁଥାଉଁ ତାଙ୍କର ଉଦୟ ।’’

ବାସ୍ତବ କ୍ଷେତ୍ରରେ କବିତାଟିରୁ କବିଙ୍କର ସ୍ଵଦେଶପ୍ରେମର ପରିଚୟ ମିଳିଥାଏ । ଦେଶବାସୀଙ୍କୁ ତାରକାଗଣ ଭାବେ ବର୍ଣ୍ଣନା କରି ସେମାନଙ୍କ ଦୀପ୍ତି, ତେଜ, ବୀରତ୍ଵ ଓ ପ୍ରତିଭା ସମ୍ପର୍କରେ ସେ ଯେ ଦେଶବାସୀ ପ୍ରଚଣ୍ଡ ପ୍ରତିଭାର ଅଧ‌ିକାରୀ ହୋଇଥିଲେ ମଧ୍ୟ ବିଦେଶୀ ପରାଧୀନ ଜୀବନ ଯାପନ କରୁଥିବା ହେତୁ ସେମାନଙ୍କର ସମସ୍ତ ପ୍ରତିଭା ଭିତରେ ହିଁ ସେମାନେ ପ୍ରତିଭାବନ୍ତ ଭାବେ ବିଦିତ । ପ୍ରଚାର ଓ ପ୍ରସାର ଅଭାବ ହେତୁ ସେମାନେ ବହିର୍ଦ୍ଦେଶରେ ପରିଚିତ ହୋଇପାରି ନାହାଁନ୍ତି । ଜଣେ ମହତ ବ୍ୟକ୍ତି ଭାବେ ତାହା କବି ଅନୁଭବ କରିଛନ୍ତି । ଦେଶବାସୀଙ୍କ ମନରେ ଜାଗରଣ ସୃଷ୍ଟି କରିବାପାଇଁ ସେ କବିତା ମାଧ୍ୟମରେ ଉତ୍ସାହ ଓ ପ୍ରେରଣା ପ୍ରଦାନ କରିଛନ୍ତି । ବିଦେଶୀ ଶାସକଙ୍କ କ୍ରୂର ଶାସନ ତଳେ ଅତ୍ୟାଚାରିତ ତଥା ଶୋଷିତ ଜାବନ ଯାପନ କରୁଥ୍ ବାରୁ ସେମାନେ ଦୂର ଆକାଶର ତାରକାମାନଙ୍କ ପରି ନାରବରେ ଚାର୍ହି ରହିଥ‌ିବା ଲକ୍ଷ୍ୟ କରି କବିଙ୍କ ମନରେ ଦୁଃଖ ଜାତ ହୋଇଛି ।

ମହତ ବ୍ୟକ୍ତି ଯେପରି ଉପକାରୀଠାରେ ସଦାକୃତଜ୍ଞ ରହିଥାଏ, ସେହିପରି ସୂର୍ଯ୍ୟସମ ବିଦେଶୀ ଶାସନକୁ ପ୍ରତ୍ୟକ୍ଷ ସମାଲୋଚନା ନକରି ବରଂ ଉପକାରୀର ଅପକାର କାମନା କରୁଥିବା ଲୋକ ଆମ ଦେଶରେ ନିମକହାରାମ ଭାବେ ବିବେଚିତ ହୁଏ ବୋଲି କବି ସ୍ପଷ୍ଟ ଉଲ୍ଲେଖ କରିଛନ୍ତି । ତଥାପି ଦେଶବାସୀଙ୍କ ମନରେ ଆତ୍ମବିଶ୍ଵାସ ସୃଷ୍ଟି କରାଇବାରେ କବିଙ୍କ ପ୍ରୟାସ ପ୍ରଣିଧାନଯୋଗ୍ୟ ।

ତୁମପାଇଁ କାମ :

ଗଙ୍ଗାଧର ମେହେରଙ୍କର ‘ତାରା-ସୂର୍ଯ୍ୟ’ ପରି ଅନ୍ୟ କେତୋଟି କବିତା ସଂଗ୍ରହ କରି ପଢ଼ ।
ତାରା ଓ ସୂର୍ଯ୍ୟଙ୍କୁ ନେଇ ଅନ୍ୟ କୌଣସି କବିଙ୍କର କେତୋଟି କବିତା ପଢ଼ି ସେଗୁଡ଼ିକର ସାରକଥା ଲେଖ ।
Answer:
ପିଲାମାନେ ଶିକ୍ଷକ ବା ଅଭିଭାବକଙ୍କ ପରାମର୍ଶ ନେଇ ନିଜେ କର ।

ଅଭ୍ୟାସ ପାଇଁ ଅତିରିକ୍ତ ପ୍ରଶ୍ଳେ।ତ୍ତର

ଅତିସଂକ୍ଷିପ୍ତ ପ୍ରଶ୍ନୋତ୍ତର

Question ୧।
‘ତାରା-ସୂର୍ଯ୍ୟ’ କବିତାରେ କବି ପ୍ରଥମେ କାହାକୁ ସମ୍ବୋଧନ କରିଛନ୍ତି ?
Answer:
ତାରା – ସୂର୍ଯ୍ୟ କବିତାର କବି ପ୍ରଥମେ ତାରାମାନଙ୍କୁ ସମ୍ବେ।ଧନ କରିଛନ୍ତି।

Question ୨ ।
ତାରାମାନଙ୍କ ମନରେ ଭୟ ଅଛି ବୋଲି କବି କାହିଁକି ଅନୁଭବ କରିଛନ୍ତି ?
Answer:
ତାରାମାନେ ଦିନରେ ଦେଖା ନ ଯାଇ ରାତିରେ ଦେଖାଦେଉଥ‌ିବାରୁ ସେମାନଙ୍କ ମନରେ ଭୟ ଅଛି ବୋଲି ଅନୁଭବ କରିଛନ୍ତି।

Question ୩ ।
ନିମକହାରାମ କାହାକୁ କୁହାଯାଏ ?
Answer:
ହିତକାରୀର ହିତକୁ ସ୍ଵୀକାର କରୁନଥିବା ଲୋକଙ୍କୁ ନିମକହାରାମ କୁହାଯାଏ ।

Question ୪ ।
“ ଆମ୍ଭେ ଚାହୁଁଥାଉ ତାଙ୍କର ଉଦୟ” — କିଏ କାହାର ଉଦୟ ଚାହୁଁଛନ୍ତି ?
Answer:
ଆମ ରାଜ୍ୟର ଲୋକମାନେ ଆମ୍ଭର ଅନ୍ଧକାରକୁ ଦୂର କରୁଥିବା ରବିଙ୍କର ଉଦୟ ଚାହୁଁଛନ୍ତି ।

Question ୫।
‘ତାରା-ସୂର୍ଯ୍ୟ’ କବିତାର କବି କିଏ ?
Answer:
‘ତାରା-ସୂର୍ଯ୍ୟ’ କବିତାର କବି ଗଙ୍ଗାଧର ମେହେର ।

Question ୬।
ଆମ୍ଭ ଭାସ୍କରଙ୍କୁ ଅନ୍ୟମାନେ କାହିଁକି କ୍ଷୁଦ୍ର ତାରା ବୋଲି କହନ୍ତି ?
Answer:
ଆମ୍ଭ ଭାସ୍କର ଅନ୍ୟମାନଙ୍କ ଆଗରେ ଭାସ୍କର ହୋଇ ଦେଖାଯାଆନ୍ତି ନାହିଁ ବୋଲି ଅନ୍ୟମାନେ ଆମ୍ଭ ଭାସ୍କରଙ୍କୁ କ୍ଷୁଦ୍ର ତାରା ବୋଲି କହନ୍ତି।

Question ୭ ।
କ’ଣ ସତ୍ୟ ବୋଲି କବି ଜାଣିଛନ୍ତି ?
Answer: -ତାରାମାନେ ସୂର୍ଯ୍ୟ ପରି ଅଟନ୍ତି ଏହା ସତ୍ୟବୋଲି କବି ଜାଣିଛନ୍ତି

Question ୮।
‘ତାରା – ସୂର୍ଯ୍ୟ’ କବିତାଟି କେଉଁ ମୂଳଗ୍ରନ୍ଥରୁ ଆନୀତ ?
Answer:
‘ତାରା – ସୂର୍ଯ୍ୟ’ କବିତାଟି କବିଙ୍କର ‘ଅର୍ଘ୍ୟଥାଳୀ’ କବିତାରୁ ଆନୀତ ।

Question ୯।
ଆମ ରାଜ୍ୟରେ କିଏ ତମ କ୍ଷୟ କରେ ?
Answer:
ଆମ ରାଜ୍ୟରେ ରବି ତମ କ୍ଷୟ କରେ ।

Question ୧୦ ।
କେଉଁମାନଙ୍କୁ ରବି ପରି ରଶ୍ମିମାନ ବୋଲି କବି କହିଛନ୍ତି ?
Answer:
ତାରାମାନଙ୍କୁ ରବିପରି ରଶ୍ମିମାନ ବୋଲି କବି କହିଛନ୍ତି ।

Question ୧୧।
ଆମ୍ଭ ତମ ନାଶିବାକୁ କାହାର ପ୍ରଭାବ ନାହିଁ ?
Answer:
ଆମ୍ଭ ତମ ନାଶିବାକୁ ତାରାମାନଙ୍କର ପ୍ରଭାବ ନାହିଁ ।

Question ୧୨।
ଆମେ କାହିଁକି ରବିଙ୍କର ଉଦୟକୁ ଚାହୁଁଛୁ ?
Answer:
ରବି ତମ କ୍ଷୟ କରୁଥିବାରୁ ଆମେ ରବିଙ୍କର ଉଦୟକୁ ଚାହୁଁଛୁ ।

Question ୧।
ନିମ୍ନୋକ୍ତ କବିତାମାନଙ୍କ ମଧ୍ୟରୁ କେଉଁଟି ଗଙ୍ଗାଧର ମେହେରଙ୍କ ରଚନା ?
(କ) ଅବକାଶ ଚିନ୍ତା
(ଖ) ଅର୍ଘ୍ୟଥାଳୀ
(ଗ) ବାଘଗାତ
(ଘ) ଅର୍ବନା
Answer:
(ଖ) ଅର୍ଘ୍ୟଥାଳୀ

Question ୨।
ଗଙ୍ଗାଧର ମେହେରଙ୍କୁ କି କବି କୁହାଯାଏ ?
(କ) ବ୍ୟାସକବି
(ଖ) ଜାତୀୟ କବି
(ଗ) ସ୍ୱଭାବ କବି
(ଘ) ଗଲ୍ଲାକବି
Answer:
(ଗ) ସ୍ୱଭାବ କବି

Question ୩ ।
‘ତାରା-ସୂର୍ଯ୍ୟ’ କବିତାର ମୁଖ୍ୟ ଭାବ କ’ଣ ?
(କ) ଦେଶପ୍ରେମର ବାର୍ତ୍ତା
(ଖ) ପ୍ରକୃତି ପ୍ରେମର ବାର୍ତ୍ତା
(ଗ) ବିଭୁପ୍ରେମର ବାର୍ତ୍ତା
(ଘ) ଅର୍ଚ୍ଚନା
Answer:
(ଘ) ଅର୍ଚ୍ଚନା

Question ୪।
ନିମ୍ନୋକ୍ତ ମଧ୍ଯରୁ କେଉଁଟି ସୂର୍ଯ୍ୟଙ୍କର ପ୍ରତିଶବ୍ଦ ନୁହେଁ ?
(କ) ପ୍ରଭାକର
(ଖ) ଭାସ୍କର
(ଗ) ଦିବାକର
(ଘ) ରବି
Answer:
(ଖ) ଭାସ୍କର

Question ୫ ।
ନିମ୍ନୋକ୍ତ କବିତା ପଂକ୍ତି ପାଇଁ କେଉଁଟି ଉପଯୁକ୍ତ ପଂକ୍ତି
(କ) ଆମ୍ଭ ତମ ନାଶିବାକୁ ନାହିଁ ତ ପ୍ରଭାବ
(ଖ) ସେକଥାରେ ମହତଙ୍କ କି ଯାଏ ଆସେ
(ଗ) ତୁମେ ପରା ଅଛ କେତେ ରବି-ରଶ୍ମିମାନ
(ଘ) ଏଶୁ ଆମ୍ଭେ ଚାହୁଁଥାଉ ତାଙ୍କର ଉଦୟ
Answer:
(ଖ) ସେକଥାରେ ମହତଙ୍କ କି ଯାଏ ଆସେ

Question ୬।
‘ଆମ୍ଭ ଦେଶେ କହୁଁ ତାକୁ ନିମକହାରାମ !’
(କ) କୃତଜ୍ଞ
(ଖ) କୃତଘ୍ନ
(ଗ) ନାଚ
(ଘ) ହିଂସ୍ର
Answer:
(ଖ) କୃତଘ୍ନ

Question ୭ ।
ନିମ୍ନୋକ୍ତ ଶବ୍ଦମାନଙ୍କ ମଧ୍ୟରୁ କେଉଁଟି ଦ୍ଵିତୀୟ ପୁରୁଷ ?
(କ) ସେ
(ଖ) ରବି
(ଗ) ଦିବାକର
(ଘ) ସ୍ଵାଭିମାନର ବାର୍ତ୍ତା
Answer:
(ଗ) ଦିବାକର

Question ୮।
ସୂର୍ଯ୍ୟଙ୍କର କେଉଁ ପ୍ରତିଶବ୍ଦ ‘ତାରା-ସୂର୍ଯ୍ୟ’ କବିତାରେ କବି ବ୍ୟବହାର କରି ନାହାନ୍ତି ?
(କ) ଭାସ୍ନର
(ଖ) ପ୍ରଭାକର
(ଗ) ରବି
(ଘ) ଦିବାକର
Answer:
(ଘ) ଦିବାକର

Question ୯ ।
‘ତାରା-ସୂର୍ଯ୍ୟ’ କବିତାରେ କବିଙ୍କ ମନର କି ଭାବ ପ୍ରକାଶପାଇଛି ?
(କ) ଘୃଣାଭାବ
(ଖ) ଆଳସ୍ୟଭାବ
(ଗ) ସ୍ଵାଭିମାନ
(ଘ) ସଂଜାର୍ଣ୍ଣ
Answer:
(ଗ) ସ୍ଵାଭିମାନ

Question ୧୦ ।
‘ତାରା-ସୂର୍ଯ୍ୟ’ କବିତାର କବି କାହାକୁ ଶ୍ରେଷ୍ଠତ୍ୱ ପ୍ରଦାନ କରିଛନ୍ତି ?
(କ) ତାରା
(ଖ) ସୂର୍ଯ୍ୟ
(ଗ) ରାଜ୍ୟ
(ଘ) ଚ୍ଚାତି
Answer:
(ଖ) ସୂର୍ଯ୍ୟ

Question ୧୧ ।
କେଉଁମାନଙ୍କୁ ନିମକହାରାମ କୁହାଯାଏ ?
(କ) ଉପକାରୀ ପ୍ରତି କୃତଜ୍ଞତା ପ୍ରକାଶ କରୁଥିବା ବ୍ୟକ୍ତିକୁ
(ଖ) ନିଜର ଜୟଗାନ କରୁଥ୍ ବା ବ୍ୟକ୍ତିକୁ
(ଗ) ନିଜର ଜୟଗାନ ନ କରୁଥିବା ବ୍ୟକ୍ତିକୁ
(ଘ) ଉପକାରୀ ପ୍ରତି କୃତଜ୍ଞତା ପ୍ରକାଶ କରୁନଥିବା ବ୍ୟକ୍ତିକୁ
Answer:
(ଘ) ଉପକାରୀ ପ୍ରତି କୃତଜ୍ଞତା ପ୍ରକାଶ କରୁନଥିବା ବ୍ୟକ୍ତିକୁ

Question ୧୨ ।
ଆମ ଭାସ୍କର କାହାକୁ ଲକ୍ଷ୍ୟ କରି କୁହାଯାଇଛି ?
(କ) ଆମର ତାରାଙ୍କୁ
(ଖ) ଆମର ସୂର୍ଯ୍ୟଙ୍କୁ
(ଗ) ଆମର ମନୋଭାବକୁ
(ଘ) ଆମର ପରମ୍ପରାକୁ
Answer:
(ଖ) ଆମର ସୂର୍ଯ୍ୟଙ୍କୁ

Question ୧୩ ।
‘‘ଆମ୍ଭ ଭାସ୍କରକୁ ତୁମ ରାଜ୍ଯଲୋକ ସାରା, ବୋଲୁଛନ୍ତି ଗଗନର କ୍ଷୁଦ୍ର ଏକ ତାରା !?? – ଏଥୁରେ କେଉଁ ଭାବ ପ୍ରକାଶପାଇଛି ?
(କ) ପ୍ରସନ୍ନତା
(ଖ) ସଂକାର୍ଣ୍ଣ ମନୋଭାବ
(ଗ) ବିବ୍ରତା
(ଘ) ଭୟ
Answer:
(ଖ) ସଂକାର୍ଣ୍ଣ ମନୋଭାବ

Question ୧୪ ।
ନିମ୍ନୋକ୍ତ ମଧ୍ୟରୁ କେଉଁଟି ଗଙ୍ଗାଧର ମେହେରଙ୍କ ଦ୍ଵାରା ରଚିତ ନୁହେଁ ?
(କ) ତପସ୍ୱିନା
(ଖ) ଅର୍ଘ୍ୟଥାଳୀ
(ଗ) ଧର୍ମପଦ
(ଘ) ପ୍ରଶୟବଲ୍ଲରା
Answer:
(ଗ) ଧର୍ମପଦ

Question ୧୫ ।
ପ୍ରକୃତରେ କାହାକୁ କବି ମହାନ ବୋଲି ଉଲ୍ଲେଖ କରିଛନ୍ତି ?
(କ) ତାରାମାନଙ୍କୁ
(ଖ) ସୂର୍ଯ୍ୟଙ୍କୁ
(ଗ) ତାରାମାନଙ୍କ ରବିପଣକୁ
(ଘ) ତାରାମାନଙ୍କର ସୂର୍ଯ୍ୟଙ୍କପ୍ରତି ଉପହାସ ଭାବକୁ
Answer:
(ଖ) ସୂର୍ଯ୍ୟଙ୍କୁ

Question ୧୬ ।
‘ରବି’ – କେଉଁ ପୁରୁଷ ?
(କ) ପ୍ରଥମ
(ଖ) ଦ୍ୱିତୀୟ
(ଗ) ତୃତାୟ
(ଘ) ମଧ୍ୟମ
Answer:
(ଗ) ତୃତାୟ

Question ୧୭।
‘ତାରା’ କେଉଁ ପୁରୁଷ ?
(କ) ପ୍ରଥମ
(ଖ) ଦ୍ୱିତାୟ
(ଗ) ତୃତୀୟ
(ଘ) ମଧ୍ୟମ
Answer:
(ଗ) ତୃତୀୟ

Question ୧୮ ।
‘ତାରା–ସୂର୍ଯ୍ୟ’ କବିତାର କବି କିଏ ?
(କ) ଗଙ୍ଗାଧର ମେହେର
(ଖ) ରାଧାନାଥ ରାୟ
(ଗ) ଗୋପବନ୍ଧୁ ଦାସ
(ଘ) ମଧୁସୂଦନ ରାଓ
Answer:
(କ) ଗଙ୍ଗାଧର ମେହେର

Question ୧୯ ।
ଆମ୍ଭେ ଚାହୁଁଥାଉଁ ତାଙ୍କର ଉଦୟ’ – କିଏ କାହାର ଉଦୟ ଚାହୁଁଛନ୍ତି?
(କ) ପୃଥ‌ିବୀ ଅଧିବାସୀଗଣ ସୂର୍ଯ୍ୟଙ୍କର ଉଦୟ
(ଖ) ପୃଥ‌ିବୀ ଅଧିବାସୀଗଣ ସୂର୍ଯ୍ୟାଙ୍କର ଉଦୟ
(ଗ) ପୃଥ‌ିବୀର ଅଧିବାସୀଗଣ ଚନ୍ଦ୍ର ଓ ସୂର୍ଯ୍ୟଙ୍କର ଉଦୟ
(ଘ) ପୃଥ‌ିବୀର ଅଧିବାସୀଗଣ ତାରାମାନଙ୍କର ଉଦୟ
Answer:
(କ) ପୃଥ‌ିବୀ ଅଧିବାସୀଗଣ ସୂର୍ଯ୍ୟଙ୍କର ଉଦୟ

Question ୨୦ ।
କେଉଁମାନଙ୍କୁ ରବିପରି ରଶ୍ମିମାନ୍ ବୋଲି କବି କହିଛନ୍ତି ?
(କ) ତାରାମାନଙ୍କୁ
(ଖ) ସୂର୍ଯ୍ୟଙ୍କୁ
(ଗ) ଚନ୍ଦ୍ରଙ୍କୁ
(ଘ) ବିଦ୍ୱାନମାନଙ୍କୁ
Answer:
(କ) ତାରାମାନଙ୍କୁ

Question ୨୧ ।
‘ଭାସ୍କର’ ଶବ୍ଦଟିର ଅର୍ଥ କ’ଣ ?
(କ) ଉଜ୍ଜ୍ବଳ
(ଖ) ଆସିବା
(ଗ) ସୂର୍ଯ୍ୟ
(ଘ) ଚନ୍ଦ୍ର
Answer:
(କ) ଉଜ୍ଜ୍ବଳ

Question ୨୨ ।
ତାରାଗଣ କେବଳ ନିଜର ଜଗତକୁ ଆଲୋକିତ କରିଛନ୍ତି – ଏଥୁରୁ କେଉଁ ଭାବ ପ୍ରକାଶପାଇଛି ?
(କ) ସଂକାର୍ଣ୍ଣ ମନେ।ଭାବ
(ଖ) ସ୍ୱାର୍ଥପର ମନେ।ଭାବ
(ଗ) ନିଃସ୍ଵାର୍ଥ ମନୋଭାବ
(ଘ) ଦୃଢ଼ ମନୋଭାବ
Answer:
(କ) ସଂକାର୍ଣ୍ଣ ମନେ।ଭାବ

Question ୨୩ ।
‘ତାରା-ସୂର୍ଯ୍ୟ’ କବିତାଟି କବିଙ୍କର କେଉଁ କାବ୍ୟରୁ ଅଣାଯାଇଛି ?
(କ) କବିତାକଲ୍ଲୋଳ
(ଖ) ଅର୍ଘ୍ୟଥାଳୀ
(ଗ) ଇନ୍ଦୁମତୀ
(ଘ) ପ୍ରଶୟବଲ୍ଲରା
Answer:
(ଖ) ଅର୍ଘ୍ୟଥାଳୀ

କବି ପରିଚୟ :

ଓଡ଼ିଆ ସାହିତ୍ୟରେ ଆଧୁନିକ ଯୁଗର ଅନ୍ୟତମ ବରେଣ୍ୟ କବି ଗଙ୍ଗାଧର ମେହେର ସ୍ୱଭାବ କବିଭାବେ ପରିଚିତ। ପ୍ରକୃତିକୁ କାବନ୍ତ୍ରଭାବେ ବର୍ଣ୍ଣନା କରିବାରେ ସେ ଥିଲେ ସିଦ୍ଧହସ୍ତ । ତେଣୁ ତାଙ୍କୁ ପ୍ରକୃତି କବି ମଧ୍ୟ କୁହାଯାଏ । ସ୍ବଭାବ କବି ବରଗଡ଼ ଜିଲ୍ଲାର ବରପାଲି ଗ୍ରାମରେ ଜନ୍ମଗ୍ରହଣ କରିଥିଲେ । ତାଙ୍କ ରଚିତ ‘ତପସ୍ବିନୀ’, ‘ଇନ୍ଦୁମତୀ’, ‘କୀଚକବଧ’ ଆଦି କାବ୍ୟ ଏବଂ ‘କୃଷକ ସଙ୍ଗୀତ’, ‘ଅର୍ଘ୍ୟଥାଳୀ’, ‘କବିତା କଲ୍ଲୋଳ’ ଆଦି କ୍ଷୁଦ୍ର କବିତା ସଙ୍କଳନ ତାଙ୍କ ଅନନ୍ୟ ସାଧାରଣ କବି ପ୍ରତିଭାର ପରିଚୟ ବହନ କରେ । ମାତୃଭୂମି ଓ ମାତୃଭାଷାକୁ ଅମୂଲ୍ୟ ଗ୍ରନ୍ଥ ଭାବେ ବିବେଚିତ ହୋଇଛି ଓ ଓଡ଼ିଆ ଶିକ୍ଷାର୍ଥୀମାନଙ୍କ ପାଠ୍ୟପୁସ୍ତକରେ ସ୍ଥାନିତ ହୋଇଛି ।

କବିତାର ପୃଷ୍ଠଭୂମି :

‘ତାରା-ସୂର୍ଯ୍ୟ’ କବିତାଟି କବିଙ୍କ ଶ୍ରେଷ୍ଠ କବିତା ‘ଅର୍ଘ୍ୟଥାଳୀ’ରୁ ଗୃହୀତ । କବି ଏହି କବିତାଟିରେ ବିଦେଶୀ ଲକ୍ଷ୍ୟକରି ‘ଆମ ସୂର୍ଯ୍ୟ ଆମ ପାଇଁ ସବୁଠୁ ଉଜ୍ଜଳ’ ବୋଲି ଅଭିମାନୀ ବାର୍ତ୍ତା ପ୍ରଦାନ କରିଛନ୍ତି । କବିତାରେ କବିଙ୍କ ସ୍ଵଦେଶପ୍ରେମ ସ୍ପଷ୍ଟ ପ୍ରତିଭାତ ହୋଇଛି । ଉତ୍କଳୀୟମାନଙ୍କୁ ଉଦ୍‌ବୋଧନ ଦେଇ ମନରୁ ହୀନମନ୍ୟତା ଦୂର କରିବାକୁ ଏବଂ ହୃଦୟରେ ଆତ୍ମବିଶ୍ଵାସ ଜାଗ୍ରତ କରିବାକୁ କବି ପରାମର୍ଶ ଦେଇଛନ୍ତି ।

କବିତାର ସାରକଥା :

ବିସ୍ମରଣ ହୋଇଥିଲା । କଳା, ଭାସ୍କର୍ଯ୍ୟ, ସାହିତ୍ୟ, ଧର୍ମ, ସାମାଜିକ ସ୍ଥିତି ଓ ବାଣିଜ୍ୟ ବ୍ୟବସାୟ ଆଦି ସବୁ କ୍ଷେତ୍ରରେ ସେମାନେ ଥିଲେ ଅଗ୍ରଗଣ୍ୟ । କିନ୍ତୁ ପରାଧୀନ ରହି ସେମାନଙ୍କ ମାନସିକତାରେ ପରିବର୍ତ୍ତନ ଦେଖା ଦେଇଥ‌ିବା ଅନୁଭବ କରି କବି ସେମାନଙ୍କୁ ଜାଗ୍ରତ କରିବାପାଇଁ ଆହ୍ବାନ ଦେଇଛନ୍ତି । ସେ ସେମାନଙ୍କୁ ତାରକାଗଣ ସହ ତୁଳନା କରି କହିଛନ୍ତି ଯେ ସେମାନେ ତାପ, ତେଜ ଓ ଜ୍ୟୋତିରେ ସୂର୍ଯ୍ୟଙ୍କ ତୁଳନାରେ କେବେ ମଧ୍ୟ ଊଣା ନୁହଁନ୍ତି । ବାସ୍ତବରେ ରାତ୍ରି ଆକାଶରେ ଦେଖାଯାଉଥ‌ିବା ନକ୍ଷତ୍ରଗୁଡ଼ିକ ସୂର୍ଯ୍ୟଙ୍କ ପରି ଗୋଟିଏ ଗୋଟିଏ ତେଜୋଦୀପ୍ତ ଜ୍ୟୋତିଷ୍କ ।

ମହାକାଶରେ ସୂର୍ଯ୍ୟଙ୍କୁ ଯେପରି ଗ୍ରହମାନେ ପରିକ୍ରମା କରିଥାଆନ୍ତି ସେହିପରି ପ୍ରତ୍ୟେକ ନକ୍ଷତ୍ରଙ୍କର ଗୋଟିଏ ଗୋଟିଏ ମଣ୍ଡଳ ରହିଅଛି ଓ ତାଙ୍କ ଚତୁଃପାର୍ଶ୍ବରେ ଗ୍ରହ ଉପଗ୍ରହାଦି ପରିକ୍ରମଣ କରୁଛନ୍ତି । ସେମାନେ ସୂର୍ଯ୍ୟଙ୍କ ପରି ରଶ୍ମିମାନ ଓ ତେଜୋବନ୍ତ । କେବଳ ଦୂର ଆକାଶରେ ଥିବାରୁ ସେମାନେ କ୍ଷୁଦ୍ର ଦେଖାଯାଆନ୍ତି ଏବଂ ଦିବସରେ ସୂର୍ଯ୍ୟଙ୍କ ଜ୍ୟୋତି ପ୍ରଭାବରେ ସେମାନେ ଦୃଷ୍ଟିଗୋଚର ହୋଇପାରନ୍ତି ନାହିଁ । ଠିକ୍ ସେହିପରି ବିଦେଶୀ ଶାସକଙ୍କ କଠୋର ଶାସନ ମଧ୍ୟରେ ଦେଶବାସୀ ଦୂରଗଗନର ନକ୍ଷତ୍ରମାନଙ୍କ ପରି ନିଜର ପରାକ୍ରମ ପ୍ରକାଶ କରିବାକୁ ସୁଯୋଗ ପାଇପାରୁ ନାହାନ୍ତି ।

ଦେଶବାସୀଙ୍କୁ ତାରକାଗଣ ଭାବେ ସମ୍ବୋଧନ କରି ସେମାନଙ୍କୁ ଦୀପ୍ତି, ତେଜ ଓ ବିକ୍ରମ ସମ୍ପର୍କରେ ସଚେତନ ହେବାକୁ କବି କହିଛନ୍ତି । ସେମାନଙ୍କଠାରେ ଅଶେଷ ପ୍ରତିଭା ଥିଲେ ମଧ୍ୟ ସେସବୁ ବିଦେଶୀ ଶାସକଙ୍କ ପରାକ୍ରମରେ ଅବଦମିତ ହୋଇ ରହିଅଛି । ତାରାମାନଙ୍କ ରାଜ୍ୟରେ ସୂର୍ଯ୍ୟ । ମଧ୍ୟ ଗଗନର ଏକ କ୍ଷୁଦ୍ରତାରା ଭାବେ ପରିଦୃଷ୍ଟ ହୋଇଥାଆନ୍ତି । ସେହିପରି ପୃଥ‌ିବୀରେ ସୂର୍ଯ୍ୟଙ୍କ ପ୍ରଚଣ୍ଡ କିରଣ ସମ୍ମୁଖରେ ତାରାମାନେ ପରିଦୃଷ୍ଟ ହୋଇପାରୁ ନାହାନ୍ତି । ମହତ ବ୍ୟକ୍ତିମାନେ କିନ୍ତୁ ବାସ୍ତବତାକୁ ଅନୁଭବ କରିଥାଆନ୍ତି । ସାଧାରଣ ଲୋକଚକ୍ଷୁରେ ତାରକାଗୁଡ଼ିକ କ୍ଷୁଦ୍ର ଦେଖାଯାଉଥିଲେ ମଧ୍ୟ ସେମାନଙ୍କ ମହାନତା ବିଷୟରେ ମହତ ବ୍ୟକ୍ତିମାନେ ଜାଣି ଥାଆନ୍ତି ।

ବିଦେଶୀ ଶାସକମାନଙ୍କ ଉଦ୍ଦେଶ୍ୟରେ କବି ଦୃଢ଼ଭାବେ କହିଛନ୍ତି। ଯେ ସେମାନେ ଯେତେ ବଳ ବିକ୍ରମଶାଳୀ ହେଲେ ମଧ୍ୟ ଆମ ଦେଶ ସମ୍ପର୍କରେ ସେମାନେ ସମ୍ପୂର୍ଣ୍ଣ ଅଜ୍ଞ । ଆମ ଦେଶ, ଆମ ଦେଶବାସୀ, ଆମ ସଂସ୍କୃତି ଓ ଆମ ପରମ୍ପରା ଆମ ପାଇଁ ମହାନ୍ । ମହାନ ବ୍ୟକ୍ତିମାନେ ଅଜ୍ଞ ନୁହଁନ୍ତି । କବି କହିଛନ୍ତି ଯେ ସୂର୍ଯ୍ୟଙ୍କ ପରି ତାରକାମାନେ ସେମାନଙ୍କ ରାଜ୍ୟରେ ମଧ୍ୟ ପ୍ରଚୁର କିରଣ ଦେଇଥାଆନ୍ତି । ତେଣୁ ସେଠାରେ ସେମାନେ ତେଜୀୟାନ ସୂର୍ଯ୍ୟ ଭାବେ ପରିଗଣିତ ହୋଇଥାଆନ୍ତି । ସେହିପରି ଆମ ଦେଶରେ ଆମ ଦେଶବାସୀଙ୍କ ମହତ୍ତ୍ବ ରହିଥିଲେ। ମଧ୍ୟ ବିଦେଶରେ ତାହା ପରିପ୍ରକାଶ ହୋଇ ନ ପାରିବାରୁ ସେମାନେ ଆମକୁ ମୂର୍ଖ ଓ ଇତର ବୋଲି ଭାବି ଆମ ଉପରେ ଶାସନ କରିବାକୁ ଆସିଛନ୍ତି ।

ଆମ ଉପରେ ସେମାନେ ନିଜ ନିଜର ପ୍ରଭୁତ୍ଵ ଜାହିର କରି ବଳପୂର୍ବକ ଆମ ଉପରେ ଏକ ବିଦେଶୀ ଶାସନକୁ ଲଦି ଦେଇଛନ୍ତି । ସାଧାରଣ ଲୋକଙ୍କ ଧାରଣା ଯେ ବିଦେଶୀ ଶାସକମାନେ ଆମଠାରୁ ବିଜ୍ଞ ଓ ଅଧ୍ବକ ଶିକ୍ଷିତ । ସେମାନେ ଆମକୁ ସଭ୍ୟତାର ଆଲୋକ ଦେଖାଉଛନ୍ତି । ତେଣୁ ସାଧାରଣ ଲୋକେ ସେମାନଙ୍କୁ ଅଧ୍ବକ ଶକ୍ତିଶାଳୀ ବୋଲି ମନେ କରିଥାଆନ୍ତି । ସେମାନଙ୍କ ପ୍ରଭାବରେ ଆମଠାରେ ଲୁକ୍‌କାୟିତ ଅବସ୍ଥାରେ ରହିଥ‌ିବା ପ୍ରତିଭା ପ୍ରକାଶ ଲାଭ କରିବା ସମ୍ଭବ ହେଉ ନାହିଁ । ଯାହା ଅପ୍ରକାଶିତ ରହିଥାଏ ତା’ର ଗୁରୁତ୍ଵକୁ କେହି ଉପଲବ୍ଧି କରିପାରି ନଥାଏ । ଅପରନ୍ତୁ ସେ ପ୍ରଭାବଶାଳୀ ବ୍ୟକ୍ତିର ଜୟଗାନ କରିଥାଏ । କାରଣ ଉପକାରୀର ଉପକାର ଅସ୍ବୀକାର କରୁଥିବା ବ୍ୟକ୍ତିକୁ ସାଧାରଣତଃ ନିମକହାରାମ ବୋଲି କୁହାଯାଏ। କବିତା ମାଧ୍ୟମରେ କବି ଦେଶବାସୀଙ୍କୁ ସେମାନଙ୍କ ଶକ୍ତି ଓ ସାମର୍ଥ୍ୟ ସମ୍ପର୍କରେ ସଚେତନ କରି ଜାଗ୍ରତ ହେବାକୁ ଆହ୍ଵାନ ଦେଇଛନ୍ତି ।

କଠିନ ଶବ୍ଦାର୍ଥ :

• ରବିରଶ୍ମି – ସୂର୍ଯ୍ୟ କିରଣ ।
• ଯେମନ୍ତ – ଯେପରି ।
• ପ୍ରଭାକର – ସୂର୍ଯ୍ୟ ।
• ଭାଷେ – କୁହେ ।
• ଦିଶ – ଦେଖାଯାଏ, ଦିଗ
• ଗଗନ – ଆକାଶ
• ହିତ – ମଙ୍ଗଳ
• ରଜନୀ’ – ରାତି ।
• ତମ – ଅନ୍ଧକାର ।
• ଭାସ୍ବର – ଉଜ୍ଜ୍ଵଳ ।
• ନିମକହାରାମ – କୃତଘ୍ନ / ଅକୃତଜ୍ଞା
• ଭାସ୍କର – ସୂର୍ଯ୍ୟ
• ଦିଶେ – ଦେଖାଯାଏ

Odisha State Board BSE Odisha 8th Class Science Solutions Chapter 17 ତାରକା ଓ ସୌରଜଗତ Textbook Exercise Questions and Answers.

BSE Odisha Class 8 Science Solutions Chapter 17 ତାରକା ଓ ସୌରଜଗତ

Question 1.
ବନ୍ଧନୀ ମଧ୍ୟରୁ ଠିକ୍ ଉତ୍ତରଟି ବାଛ ।
(a) ନିମ୍ନଲିଖ ମଧ୍ୟରୁ କିଏ ସୌରଜଗତର ଅନ୍ତର୍ଭୁକ୍ତ ନୁହେଁ (ଗ୍ରହାଣୁ, ଉପଗ୍ରହ, ତାରକାପୁଞ୍ଜ, ଧମୂକେତୁ)
(b) ନିମ୍ନଲିଖ ମଧ୍ୟରୁ କେଉଁଟି ଗୋଟିଏ ସୌରଗ୍ରହ ନୁହେଁ । ( ସିରିଅସ୍, ବୁଧ, ଶନି, ଶୁକ୍ର)
(c) ନିମ୍ନଲିଖ ମଧ୍ୟରୁ କେଉଁଟି ଗୋଟିଏ ତାରା ? (ସନ୍ଧ୍ୟାତାରା, ଧ୍ରୁବତାରା, ସୁଟିଂତାରା, ଲଞ୍ଜାତାରା )
(d) ଭୁଗର୍ଭରେ ଗଚ୍ଛିତ ତୈଳଖଣିର ସନ୍ଧାନରେ କେଉଁ ଉପଗ୍ରହର ଭୂମିକା ଗୁରୁତ୍ବପୂର୍ଣ୍ଣ ? (ସାଧାରଣ, ଭୂସ୍ଥିର, ସୁଦୂର-ସନ୍ଧାନୀ, ଏଡୁସାଟ୍)

Answers:
(a) ତାରକାପୁଞ୍ଜ
(b) ସିରିଅସ୍
(c) ଧ୍ରୁବତାରା
(d) ସୁଦୂର -ସନ୍ଧାନୀ

Question 2.
ଗୋଟିଏ ବା ଦୁଇଟି ପଦରେ ଉତ୍ତର ଦିଅ ।
(a) ଚନ୍ଦ୍ର କାହାର ଆଲୋକରେ ଆଲୋକିତ ହୁଏ ?
ଉ-
ଚନ୍ଦ୍ର ସୂର୍ଯ୍ୟର ଆଲୋକରେ ଆଲୋକିତ ହୁଏ ।

(b) ସୂର୍ଯ୍ୟଠାରୁ ଦୂରତମ ଗ୍ରହର ନାମ କ’ଣ ?
ଉ-
ସୂର୍ଯ୍ୟଠାରୁ ଦୂରତମ ଗ୍ରହର ନାମ ନେପଚୁନ୍ ।

(c) କେଉଁ ଗ୍ରହର ରଙ୍ଗ ଲାଲ୍ ଦିଶେ ?
ଉ-
ମଙ୍ଗଳ ଗ୍ରହର ରଙ୍ଗ ଲାଲ୍ ଦିଶେ ।

(d) ନିର୍ଦ୍ଦିଷ୍ଟ ଆକୃତିରେ ସଜାଯିବାଭଳି ଦେଖାଯାଉଥିବା ତାରାମାନଙ୍କୁ କ’ଣ କୁହାଯାଏ ?
ଉ
ନିର୍ଦ୍ଦିଷ୍ଟ ଆକୃତିରେ ସଜାଯିବାଭଳି ଦେଖାଯାଉଥ‌ିବା ତାରାମାନଙ୍କୁ ତାରକାପୁଞ୍ଜ କୁହାଯାଏ ।

(e) ସାଧାରଣତଃ କେଉଁ କେଉଁ ଗ୍ରହର କକ୍ଷ ମଧ୍ୟରେ ‘ଗ୍ରହାଣୁପୁଞ୍ଜ’ ଅବସ୍ଥିତ ?
ଉ-
ମଙ୍ଗଳ ଓ ବୃହସ୍ପତି ଗ୍ରହର କକ୍ଷ ମଧ୍ୟରେ ‘ଗ୍ରହାଣୁପୁଞ୍ଜ’ ଅବସ୍ଥିତ ।

Question 3.
ନିମ୍ନରେ ଦିଆଯାଇଥ‌ିବା ଉକ୍ତିଗୁଡ଼ିକ ‘ଠିକ୍‌’ ବା ‘ଭୁଲ୍’ ଲେଖ ।
(a) ଧ୍ରୁବତାରା ସୌରଜଗତର ଏକ ସଦସ୍ୟ ।
(b) ସୌରଜଗତର କ୍ଷୁଦ୍ରତମ ଗ୍ରହ ହେଉଛି ବୁଧ ।
(c) ଅମାବାସ୍ୟା ଦିନ ସୂର୍ଯ୍ୟପରାଗ ଘଟିବାର ସମ୍ଭାବନା ଅଛି ।
(d) ସିରଅସ୍ କାଳପୁରୁଷ ମଣ୍ଡଳ ନିକଟରେ ଦେଖାଯାଏ ।

Answers:
(a) ଭୁଲ୍
(b) ଠିକ୍
(c) ଠିକ୍
(c) ଠିକ୍
(d) ଠିକ୍

Question 4.
‘କ’ ସ୍ତମ୍ଭର ଉପଯୁକ୍ତ ପଦ ସହିତ ‘ଖ’ ସ୍ତମ୍ଭର ଉପଯୁକ୍ତ ପଦକୁ ମେଳ କର ।

Question 5.
(a) ଆକାଶରେ ସନ୍ଧ୍ୟାତାରା ରୂପେ କିଏ, କେତେବେଳେ ଓ କେଉଁ ଦିଗରେ ଦେଖାଯାଏ ?
ଉ-
ଆକାଶରେ ସନ୍ଧ୍ୟାତାରା ରୂପେ ଶୁକ୍ରଗ୍ରହ ସୂର୍ଯ୍ୟାସ୍ତ ପ୍ରାୟ 47 ଦିଗ୍‌ବଳୟ ମଧ୍ୟରେ ଏହାକୁ ଦେଖୁହେବ ।

(b) ସୌରଜଗତର ବୃହତ୍ତମ ଗ୍ରହର ନାମ ଓ ସର୍ବାଧ‌ିକ ଉପଗ୍ରହଧାରୀ ଗ୍ରହର ନାମ ଲେଖ ।
ଉ-
ସୌରଜଗତର ବୃହତ୍ତମ ଗ୍ରହର ନାମ ବୃହସ୍ପତି ଓ ସର୍ବାଧ‌ିକ ଉପଗ୍ରହଧାରୀ ଗ୍ରହର ନାମ ବୃହସ୍ପତି ।

(c) ତାରକାପୁଞ୍ଜ କହିଲେ କ’ଣ ବୁଝ ? ଦୁଇଟି ତାରକାପୁଞ୍ଜର ନାମ ଲେଖ ।
ଉ-
ମହାକାଶରେ ତାରାଗୁଡ଼ିକ ବିଭିନ୍ନ ଆକାରରେ ସଜ୍ଜିତ ହୋଇ ରହିଥ‌ିବାପରି ଦେଖାଯାଆନ୍ତି । ଏହାକୁ ତାରାପୁଞ୍ଜ, ତାରକାପୁଞ୍ଜ, ନକ୍ଷତ୍ରପୁଞ୍ଜ ବା ନକ୍ଷତ୍ରମଣ୍ଡଳ କୁହାଯାଏ । ଦୁଇଟି ତାରକାପୁଞ୍ଜର ନାମ ସପ୍ତର୍ଷିମଣ୍ଡଳ ଓ କାଳପୁରୁଷ ।

(d) ଧୂମକେତୁର ଗଠନ ଲେଖ । ଏହାର ଲାଞ୍ଜ ସବୁବେଳେ ଦେଖାଯାଏ କି ?
ଉ-

• ଧୂମକେତୁଗୁଡ଼ିକ ଛୋଟ ପଥରଖଣ୍ଡ, ଧୂଳିକଣା ଏବଂ ଗ୍ୟାସ୍‌ରେ ଭର୍ତ୍ତି ।
• ଲାଞ୍ଜ ଅଂଶଟି ମୁଖ୍ୟତଃ ଏମୋନିଆ, ମିଥେନ୍, ଜଳୀୟବାଷ୍ପ ଓ ବରଫକଣାରେ ପୂର୍ଣ ।
• ସୂର୍ଯ୍ୟର ନିକଟତର ହେଲେ ଏଥିରେ ଥ‌ିବା ଛୋଟ ଛୋଟ କଣିକା ବାଷ୍ପୀଭୂତ ହୋଇ ଲକ୍ଷ ଲକ୍ଷ କି.ମି. ପର୍ଯ୍ୟନ୍ତ ଲମ୍ବିଥାଏ ।
• ଧୂମକେତୁ ସୂର୍ଯ୍ୟର ନିକଟତର ହେବାବେଳେ ଲାଞ୍ଜଟି ସୂର୍ଯ୍ୟର ବିପରୀତ ଦିଗରେ ସର୍ବଦା ରହିଥାଏ ଏବଂ ସୂର୍ଯ୍ୟଠାରୁ ଅନେକ ଦୂରକୁ ଚାଲିଗଲେ ଲାଞ୍ଜଟି ପ୍ରାୟ ଦେଖାଯାଏ ନାହିଁ । ଧୂମକେତୁର ଲାଞ୍ଜ ଅଂଶ ସବୁବେଳେ ଦେଖାଯାଏ ନାହିଁ । କେବଳ ସୂର୍ଯ୍ୟର ନିକଟତର ହେଲେ ଦେଖାଯାଏ ।

(e) ଉଲ୍‌କା କହିଲେ କ’ଣ ବୁଝ ? ଉଲ୍‌କା ଓ ଉଲ୍‌କାପିଣ୍ଡ ମଧ୍ୟରେ ପ୍ରଭେଦ ଲେଖ ।
ଅନ୍ଧାର ରାତିରେ ଯେଉଁ ମହାକାଶୀୟ ବସ୍ତୁ ଆଲୋକର ଝଲକ ସୃଷ୍ଟି କରି ଭୂପୃଷ୍ଠ ଆଡ଼କୁ ପଡ଼ିବାର ଦେଖାଯାଏ, ସେଗୁଡ଼ିକୁ ଉଲ୍‌କା କହନ୍ତି; ମାତ୍ର ଯେଉଁ ଉଲ୍‌କାଗୁଡ଼ିକ ଆକାରରେ ବଡ଼, ସେଗୁଡ଼ିକ ସଂପୂର୍ଣ୍ଣ ପୋଡ଼ି ନଯାଇ ଭୂପୃଷ୍ଠରେ ଆସି ପଡ଼ନ୍ତି । ଏଗୁଡ଼ିକ ଥଣ୍ଡାହୋଇ ପଥର ଆକାରରେ ପଡ଼ିରହନ୍ତି । ସେଗୁଡ଼ିକୁ ଉଲ୍‌କାପିଣ୍ଡ କୁହାଯାଏ ।
ଉ-

(f) କୃତ୍ରିମ ଉପଗ୍ରହ ଓ ପ୍ରାକୃତିକ ଉପଗ୍ରହ ମଧ୍ୟରେ ଦୁଇଟି ପାର୍ଥକ୍ୟ ଲେଖ ।
ଉ-

Question 6.
‘ଶନିଗ୍ରହ’ ସମ୍ବନ୍ଧରେ ଏକ ସଂକ୍ଷିପ୍ତ ଟିପ୍‌ପଣୀ ଲେଖ ।

• ଶନି ଆୟତନରେ ସୌରଜଗତର ଦ୍ଵିତୀୟ ବୃହତ୍ତମ ଗ୍ରହ ଓ ଏହାର ରଙ୍ଗ ଈଷତ୍ ପୀତ ।
• ସମଗ୍ର ଗ୍ରହଟି ହାଇଡ୍ରୋଜେନ୍, ହିଲିୟମ୍, ଏମୋନିଆ, ମିଥେନ୍ ପରି ଗ୍ୟାସ୍‌ରେ ପୂର୍ଣ ।
• ଏହାର 60ଟି ଉପଗ୍ରହ ମଧ୍ୟରୁ ଟାଇଟନ୍ ବୃହତ୍ତମ ଅଟେ ।
• ଶନିର ଅନେକ ବଳୟ ରହିଛି । ଏହି ବଳୟଗୁଡ଼ିକ ଅତିକ୍ଷୁଦ୍ର ପଥର, ବରଫକଣା ଓ ଧୂଳିକଣାକୁ ନେଇ ଗଠିତ । ଏମାନେ ଶନି ଚାରିପଟେ ପତଳା ଚକ୍ର ଆକାରରେ ଘୂରିବୁଲନ୍ତି ।
• ଶନିର ସାନ୍ଦ୍ରତା ସୌରଜଗତର ଗ୍ରହମାନଙ୍କ ମଧ୍ୟରେ ସବୁଠାରୁ କମ୍ ।

Question 7.
କୃତ୍ରିମ ଉପଗ୍ରହଦ୍ଵାରା ଆମର କି କି ଉପକାର ସାଧୁତ ହୋଇପାରୁଛି ?
(a) ଏହା ବାୟୁମଣ୍ଡଳରେ ଘଟୁଥିବା ପରିବର୍ତ୍ତନ, ପାଣିପାଗ ବିବରଣୀ ଇତ୍ୟାଦି ବିଷୟରେ ସୂଚନା ପ୍ରଦାନ କରିପାରୁଛି ।
(b) ସୁଦୂର-ସନ୍ଧାନୀ ଉପଗ୍ରହଦ୍ବାରା ଖଣିଜ ପଦାର୍ଥ ତଥା ଭୂଗର୍ଭରେ ଗଚ୍ଛିତ ତୈଳ ଇତ୍ୟାଦିର ପରିମାଣ ଓ ସ୍ଥାନ ନିରୂପଣ କରାଯାଇପାରୁଛି ।
(c) ଭୂସ୍ଥିର ଉପଗ୍ରହ ଦ୍ଵାରା ଟେଲିଯୋଗାଯୋଗ ବା ଦୂର ସଂଚାରଣ, ବିଭିନ୍ନ କାର୍ଯ୍ୟକ୍ରମର ସିଧା ପ୍ରସାରଣ, ଉପଗ୍ରହ ମାଧ୍ୟମରେ ଶିକ୍ଷାଦାନ ଇତ୍ୟାଦି ସମ୍ପାଦନ କରାଯାଇପାରୁଛି ।
(d) ଜଙ୍ଗଲ ଓ ପରିବେଶ ସନ୍ତୁଳନ ନିମନ୍ତେ ନୂତନ ଜଙ୍ଗଲ ସୃଷ୍ଟିପାଇଁ ସ୍ଥାନ ନିରୂପଣ ଇତ୍ୟାଦି କ୍ଷେତ୍ରରେ ଉପଗ୍ରହ ଗୁରୁତ୍ୱପୂଣ୍ଣ ଭୂମିକା ଗ୍ରହଣକରିଛି ।

Question 8.
ତୁମ ଉତ୍ତର ଖାତାରେ ଦୁଇଟି ନକ୍ଷତ୍ର ମଣ୍ଡଳର ରେଖାଙ୍କିତ ଚିତ୍ର ଅଙ୍କନ କର ତୁମ ଉତ୍ତର ଖାତାରେ ଦୁଇଟି ନକ୍ଷତ୍ର ମଣ୍ଡଳର ରେଖାଙ୍କିତ ଚିତ୍ର ଅଙ୍କନ କର ।

Question 9.
ଗୋଟିଏ ଗ୍ରହର ବ୍ୟାସାର୍ଦ୍ଧ ଅନ୍ୟ ଏକ ଗ୍ରହର ବ୍ୟାସାର୍ଦ୍ଧର 10 ଗୁଣ । ବଡ଼ ଗ୍ରହଟିର ଆୟତନ କେତୋଟି ସାନଗ୍ରହର ଆୟତନ ସହ ସମାନ ହେବ ହିସାବ କର ।
ମନେକର ପ୍ରଥମ ସାନଗ୍ରହର ବ୍ୟାସାର୍ଦ୍ଧ = 1, ଦ୍ବିତୀୟ ବଡ଼ ଗ୍ରହର ବ୍ୟାସାର୍ଦ୍ଧ (R) = 10r,

Question 10.
ଚନ୍ଦ୍ରକଳାର ହ୍ରାସବୃଦ୍ଧି ସମ୍ବନ୍ଧରେ ଏକ ସଂକ୍ଷିପ୍ତ ଆଲୋଚନା କର ।

• ଯେଉଁ ଦିନ ଚନ୍ଦ୍ର ଥାଳିଆଭଳି ପ୍ରାୟ ବୃତ୍ତାକାର ଦେଖାଯାଏ, ତାକୁ ପୂର୍ଣ୍ଣମୀ କହନ୍ତି । ତା’ ପରଠାରୁ ପ୍ରତିଦିନ ତାର ଉଜ୍ଜ୍ବଳ ଥାଳିଆ ଭଳି ଦିଶୁଥ‌ିବା ଅଂଶ କମିବାରେ ଲାଗେ । ଏହା କ୍ରମଶଃ ସରୁ ହୋଇ ଦାଆପରି ବକ୍ରାକୃତି ଦେଖାଯାଏ ।
• ପ୍ରାୟ ପନ୍ଦର ଦିନ ବେଳକୁ ଆଦୌ ଦେଖାଯାଏନି । ଆମେ କହୁ ସେଦିନ ଅମାବାସ୍ୟା ହେଲା ।
• ତା’ପରଠୁ ପ୍ରାୟ ପନ୍ଦର ଦିନ ପର୍ଯ୍ୟନ୍ତ ଚନ୍ଦ୍ରର ଉଜ୍ଜଳ ଦିଶୁଥ‌ିବା ଅଂଶ ଧୀରେ ଧୀରେ ବୃଦ୍ଧିପାଏ ଓ ପନ୍ଦରଦିନ ବେଳକୁ ପ୍ରାୟ ଥାଳିଆଭଳି ଦେଖାଯାଏ । ଚନ୍ଦ୍ରର ଆକୃତିରେ ଏପରି ପରିବର୍ତ୍ତନକୁ ଚନ୍ଦ୍ରକଳାର ହ୍ରାସବୃଦ୍ଧି କୁହନ୍ତି ।

ଆଉ କ’ଣ କରିହେବ ?

Question 1.
ଆମ ଭୁବନେଶ୍ୱରରେ ଥ‌ିବା ସାମନ୍ତ ଚନ୍ଦ୍ରଶେଖର ପ୍ଲାନେଟାରିୟମ୍‌କୁ ବୁଲିଯାଅ । ସେଠାରେ ତାରକାମାନଙ୍କୁ କିପରି ପ୍ରଦର୍ଶନ କରାଯାଉଛି ଲକ୍ଷ୍ୟ କରି ।
ଉ-
ପିଲାମାନେ ନିଜେ କରିବାକୁ ଚେଷ୍ଟା କର ।

Question 2.
ଆକାଶରେ ଉଲ୍‌କାପାତର ଦୃଶ୍ୟ ଦେଖିବାକୁ ଚେଷ୍ଟା କର । (ସେପ୍ଟେମ୍ବରରୁ ନଭେମ୍ବର ମାସର କୌଣସି ମେଘମୁକ୍ତ ରାତି ଏଥିପାଇଁ ବେଶ୍ ଉପଯୋଗୀ)
ଉ-
ପିଲାମାନେ ନିଜେ କରିବାକୁ ଚେଷ୍ଟା କରି ।

Question 3.
ଆଉ କିଛି ତାରକାପୁଞ୍ଜର ନାମ ସଂଗ୍ରହ କର । ଆକାଶରେ ସେଗୁଡ଼ିକୁ ଠାବ କରିବାକୁ ଶିଖ ।
ଉ-
ପିଲାମାନେ ନିଜେ କରିବାକୁ ଚେଷ୍ଟା କର ।

Question 4.
ଦୂରତାର ମାନ (scale) ସହିତ ଏକ ସୌର ଜଗତର ଚିତ୍ର ଅଙ୍କନ କର ।
ଉ-
ପିଲାମାନେ ନିଜେ କରିବାକୁ ଚେଷ୍ଟା କର ।

Question 5.
ରାତିରେ ମେଘମୁକ୍ତ ଆକାଶକୁ ଦେଖ୍ ତାରା, ତାରକାପୁଞ୍ଜ, ଗ୍ରହ ଇତ୍ୟାଦିଙ୍କୁ ଚିହ୍ନିବାକୁ ଶିଖ ଓ ସେମାନଙ୍କର ଗତିବିଧୂ ଲକ୍ଷ୍ୟ କର ।
ଉ-
ପିଲାମାନେ ନିଜେ କରିବାକୁ ଚେଷ୍ଟା କର

Question 6.
ବିଭିନ୍ନ ଜ୍ୟୋତିର୍ବିଦ୍‌ମାନଙ୍କର ଫଟୋ ସଂଗ୍ରହ କରି ଆଲବମରେ ରଖ । ସେମାନଙ୍କର ଜ୍ୟୋତିର୍ବିଜ୍ଞାନ (Astronomy) କୁ ଦାନ ସମ୍ବନ୍ଧରେ ବିବରଣୀ ସଂଗ୍ରହ କରି ରଖ ।
ଉ-
ଓଡ଼ିଶାର ସାମନ୍ତ ଚନ୍ଦ୍ରଶେଖର ଜଣେ ପ୍ରସିଦ୍ଧ ଜ୍ୟୋତିର୍ବିଦ୍ ଥିଲେ । ସେ ‘ସିଦ୍ଧାନ୍ତ ଦର୍ପଣ’ ନାମକ ଏକ ଉପାଦେୟ ଗ୍ରନ୍ଥ ରଚନା କରି ଅମର ହୋଇଯାଇଛନ୍ତି । ଏଥୁରୁ ବିଭିନ୍ନ ଗ୍ରହ, ନକ୍ଷତ୍ରମାନଙ୍କର ଗତିବିଧ ତଥା ଅନ୍ୟାନ୍ୟ ମହାଜାଗତିକ ବସ୍ତୁ ସମ୍ବନ୍ଧରେ ବିଭିନ୍ନ ତଥ୍ୟ ଆମେ ପାଇପାରୁ । ଗାଲିଲିଓ ମଧ୍ୟ ଜଣେ ପ୍ରସିଦ୍ଧ ଜ୍ୟୋତିର୍ବିଦ୍ ଅଟନ୍ତି । ସେ ହେଉଛନ୍ତି ଦୂରବୀକ୍ଷଣ ଯନ୍ତ୍ରର ଉଦ୍ଭାବକ । ସେ ଦୂରବୀକ୍ଷଣ ଯନ୍ତ୍ର ସାହାଯ୍ୟରେ ଆକାଶରେ ଥିବା ବିଭିନ୍ନ ଗ୍ରହ ନକ୍ଷତ୍ରମାନଙ୍କର ଗତିବିଧ‌ିକୁ ଲକ୍ଷ୍ୟକରିଥିଲେ ଓ ସିଏ ମଧ୍ୟ ତଥ୍ୟ ପ୍ରଦାନ କରିଥିଲେ ଯେ ପୃଥ‌ିବୀ ଓ ଗ୍ରହସମୂହ ସୂର୍ଯ୍ୟ ଚାରିପଟେ ଘୂର୍ଶନ କରିଥା’ନ୍ତି ଓ ସୂର୍ଯ୍ୟ ହେଉଛି ସ୍ଥିର । ଅନ୍ୟାନ୍ୟ ପ୍ରସିଦ୍ଧ ଜ୍ୟୋତିର୍ବିଜ୍ଞାନୀମାନଙ୍କର ନାମ ହେଉଛି ଟଲେମୀ, କୋପରନିକସ୍‌, ଆର୍ଯ୍ୟଭଟ୍ଟ ଇତ୍ୟାଦି ।

Question 7.
ଜ୍ୟୋତିର୍ବିଜ୍ଞାନ ସମ୍ବନ୍ଧରେ ବାହାରୁଥ‌ିବା ଲେଖାଗୁଡ଼ିକୁ ପଢ଼ ଓ ତୁମକୁ ଭଲ ଲାଗୁଥ‌ିବା କଥା ସଂଗ୍ରହ କରି ରଖ । ଉ- ପିଲାମାନେ ନିଜେ କରିବାକୁ ଚେଷ୍ଟା କର ।
ଉ-
ପିଲାମାନେ ନିଜେ କରିବାକୁ ଚେଷ୍ଟା କର ।

ପରୀକ୍ଷା ଉପଯୋଗୀ ଅତିରିକ୍ତ ପ୍ରଶ୍ନୋତ୍ତର

ବସ୍ତୁନିଷ୍ଠ ପ୍ରଶ୍ନେ। ଭର

1. ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(i) …………………. କୁ ଶିକାରୀ ତାରା କୁହାଯାଏ ।
(ii) …………………. ଉପଗ୍ରହଦ୍ବାରା TV ପ୍ରସାରଣ ସମ୍ଭବପର ହେଉଛି ।
(iii) …………………. ତାରକାପୁଞ୍ଜ N କିମ୍ବା M ପରି ଦେଖାଯାଏ ।
(iv) …………………. ଗ୍ରହ ପୂର୍ବରୁ ପଶ୍ଚିମକୁ ଆବର୍ତ୍ତନ କରେ ।
(v) …………………. ଗ୍ରହ ପୂର୍ବରୁ ପଶ୍ଚିମକୁ ଆବର୍ତ୍ତନ କରେ ।
(vi) ସୂର୍ଯ୍ୟଠାରୁ ଆଲୋକ ଆସି ପୃଥିବୀପୃଷ୍ଠରେ ପହଞ୍ଚିବାକୁ …………………. ମିନିଟ୍ ଲାଗେ ।
(vii) ସୂର୍ଯ୍ୟର ବସ୍ତୁତ୍ଵ ପ୍ରାୟ …………………. କି.ଗ୍ରା. ।
(viii) ସର୍ବପ୍ରଥମେ ………………….
(ix) ଗ୍ରହାଣୁପୁଞ୍ଜ …………………. ଓ …………………. ଗ୍ରହଗୁଡ଼ିକର କକ୍ଷଦ୍ବୟର ମଧ୍ୟରେ ରହି ସୂର୍ଯ୍ୟକୁ ପରିକ୍ରମଣ କରୁଛି ।
(x) ହାଲିଙ୍କ ଧୂମକେତୁର ପରିକ୍ରମଣ ସମୟ ପ୍ରାୟ ……………………… ବର୍ଷ ଅଟେ ।
(xi) ସୌରଜଗତର ସବୁଠାରୁ ବଡ଼ ଉପଗ୍ରହର ନାମ ………………………ଅଟେ ।
(xii) ମହାକାଶ ଅଭିଯାନର ପ୍ରଥମ କୃତ୍ରିମ ଉପଗ୍ରହର ନାମ …………………. ଅଟେ ।
(xiii) ପ୍ରଥମ ଜୀବନ୍ତ କୋଷ …………………. ମଣ୍ଡଳରେ ସୃଷ୍ଟି ହୋଇଥିଲା ।
(xiv) …………………. ଗ୍ରହକୁ ଜଳଗ୍ରହ କହନ୍ତି
(xv) …………………. ସବୁଠାରୁ ବଡ଼ ଗ୍ରହାଣୁ ଅଟେ ।
(xvi) ଆକାଶଗଙ୍ଗା ଛାୟାପଥରେ ପ୍ରାୟ ……………………. ଟି ତାରକା ରହିଛନ୍ତି ।
(xvii) ଆମ ରାଶିଚକ୍ରରେ …………………. ଟି ରାଶି ଅଛି ।
(xviii) …………………. ସୌରଜଗତର କ୍ଷୁଦ୍ରତମ ଗ୍ରହ ।
(xix) ପୃଥ‌ିବୀର …………………. ଦିଗରେ ଥ‌ିବା ଆକାଶରେ ଧ୍ରୁବୁତାରା ଦେଖାଯାଏ ।
(xx) ସୂର୍ଯ୍ୟର ଦ୍ବିତୀୟ ନିକଟତମ ଗ୍ରହ …………………. ।

Answers:
(i) କାଳପୁରୁଷ
(ii) ଭୂସ୍ଥିର
(iii) କ୍ୟାସିଓପିଆ
(iv) ଶୁକ୍ର
(v) ହିଲିୟମ୍
(vi) 8
(vii) 2×10³⁰
(viii) ନିଲ୍ ଆମଷ୍ଟ୍ରଙ୍ଗ
(ix) ମଙ୍ଗଳ, ବୃହସ୍ପତି
(x) 76
(xi) ଟାଇଟନ୍
(xii) ସ୍ଫୁଟନିକ୍ -1
(xiii) ବାରି
(xiv) ପୃଥ‌ିବୀ
(Xv) ସିରସ୍
(xvi) 1.5 x 10¹¹
(xvii) 12
(xviii) ବୁଧ
(xix) ଉତ୍ତର
(xx) ଶୁକ୍ର

2. ବାମ ପାର୍ଶ୍ଵରେ ଥ‌ିବା ଶବ୍ଦଦ୍ୱୟର ସମ୍ପର୍କକୁ ଲକ୍ଷ୍ୟ କରି ଦକ୍ଷିଣ ପାର୍ଶ୍ଵରେ ଥ‌ିବା ଶବ୍ଦ ସହ ସଂପର୍କିତ ଶବ୍ଦଟି ଲେଖ ।
(i) ଟାଇଟନ୍‌ : ଉପଗ୍ରହ :: ହାଲି : …………………. ।
(ii) ମଙ୍ଗଳ : ଲାଲ :: ନେପ୍‌ଚ୍ୟୁନ : …………………. ।
(iii) ପୃଥ‌ିବୀ : ଚନ୍ଦ୍ର :: ଶନି : …………………. ।
(iv) ଅମାବାସ୍ୟା : ସୂର୍ଯ୍ୟପରାଗ :: ପୂର୍ଣ୍ଣିମା : …………………. ।
(v) ସାଧାରଣ ଦୂରତା : km :: ମହାକାଶ ଦୂରତା : …………………. ।
(vi) ୟୁରେନ୍ସ : ସବୁଜଗ୍ରହ :: ନେପ୍‌ଚୁନ୍ : …………………. ।
(vii) ବୁଧ : 59 ଦିନ :: ପୃଥ‌ିବୀ : …………………. ।
(viii) ପୃଥ‌ିବୀ : ଗ୍ରହ :: ଫୋବସ୍ : …………………. ।
(ix) ଶନି : ବଳୟଗ୍ରହ :: ମଙ୍ଗଳ : …………………. ।

Answers:
(i) ଧୂମକେତୁ
(ii) ନୀଳବର୍ଣ୍ଣ
(iii) ଟାଇଟାନ୍
(iv) ଚନ୍ଦ୍ରଗ୍ରହଣ
(v) ଆଲୋକ ବର୍ଷ
(vi) ଶୀତଳଗ୍ରହ
(vii) 23 ଘ . 56 ମି . 4 ସେ
(viii) ଉପଗ୍ରହ
(ix) ଲୋହିତଗ୍ରହ

3. ନିମ୍ନୋକ୍ତ ପ୍ରତ୍ୟେକ ପ୍ରଶ୍ନପାଇଁ ଦିଆଯାଇଥ‌ିବା ଚାରୋଟି ସମ୍ଭାବ୍ୟ ଉତ୍ତର ମଧ୍ୟରୁ ଠିକ୍ ଉତ୍ତରଟି ବାଛ ।
(i) ………………ର ପରିକ୍ରମଣ କାଳ ସର୍ବାଧ‌ିକ ।
(i) ବୃହସ୍ପତି
(ii) ଶନି
(iii) ୟୁରେନ୍ସ
(iv) ନେପଚୁନ୍

(ii) ବୃହସ୍ପତିରେ ………………….. ଟି ଉପଗ୍ରହ ଅଛି ।
(i) 69
(ii) 66
(iii) 63
(iv) 60

(iii) ……………………. ଗ୍ରହର ପୃଥ‌ିବୀ ସହ ସାଦୃଶ୍ୟ ଅଛି ।
(i) ମଙ୍ଗଳ
(ii) ବୁଧ
(iii) ଶନି
(iv) ଶୁକ୍ଳ

(iv) ପୃଥିବୀ ………………… ଛାୟାପଥର ଅଂଶବିଶେଷ ଅଟେ ।
(i) ହାଇଡ୍ରା
(ii) ଭିର୍‌ଗୋ
(iii) ମିଲ୍‌କ
(iv) ବ୍ୟୁଟେସ୍

(v) ସୂର୍ଯ୍ୟ ନିଜ ଅକ୍ଷ ଚାରିପଟେ …………………….. ଦିନରେ ଥରେ ଘୂରେ ।
(i) 24
(ii) 25
(iii) 59
(iv) 365

(vi) ଏକ ଆଲୋକବର୍ଷ ପ୍ରାୟ କେତେ କି.ମି. ?
(i) 9.5 x 10¹²
(iii) 0.946 x 10¹²
(ii) 91.5 x 10¹²
(iv) 946 x 10¹²

(vii) ସୂର୍ଯ୍ୟ ନିଜ ଅକ୍ଷ ଚାରିପାଖରେ କେତେ ଦିନରେ ଥରେ ଘୂରେ ?
(i) 24 ଘଣ୍ଟା
(ii) 365 69
(iii) 59 ଦିନ
(iv) 25 ଦିନ

(viii) କେଉଁ ଉପଗ୍ରହଦ୍ଵାରା ଟେଲିଭିଜନ ପ୍ରସାରଣ ସମ୍ଭବ ହୋଇପାରୁଛି ?
(i) ସାଧାରଣ
(ii) ଭୂସ୍ଥିର
(iii) ସୁଦୂର ସନ୍ଧାନୀ
(iv) ସମସ୍ତ

(ix) ବୃହସ୍ପତିରେ କେତୋଟି ଉପଗ୍ରହ ଅଛି ?
(i) 60
(ii) 63
(iii) 66
(iv) 69

(x) କେଉଁଟି ସୂର୍ଯ୍ୟର ମୁଖ୍ୟ ଉପାଦାନ ?
(i) ଏମୋନିଆ
(ii) ହିଲିୟମ୍
(iii) ନିୟନ୍
(iv) ଆରଗନ୍

Answers:
(i) ନେପଚୁନ୍
(ii) 63
(iii) ମଙ୍ଗଳ
(iv) ମିଲ୍‌କ
(v) 25
(vi) 9.5 × 10²
(vii) 25 ଦିନ
(x) ହିଲିୟମ୍
(viii) ଭୂସ୍ଥିର
(ix) 63

4. ‘କ’ ସ୍ତମ୍ଭରେ ଥ‌ିବା ଶବ୍ଦ ସହିତ ‘ଖ’ ସ୍ତମ୍ଭରେ ଥିବା ସମ୍ପର୍କିତ ଶବ୍ଦକୁ ମିଳାଅ ।

‘କ’ ସ୍ତମ୍ଭ	‘ଖ’ ସ୍ତମ୍ଭ
(i) ଚନ୍ଦ୍ର ଆକୃତିରେ ପରିବର୍ତ୍ତନ	(i) 27.3 ଦିନ
(ii) ଶୁକ୍ର	(ii)  21.07.1969
(iii) ଚନ୍ଦ୍ରର ପରିକ୍ରମଣକାଳ	(iii) ଚନ୍ଦ୍ରକଳା
(iv) ଆପେ।ଲୋ -II	(iv) ପାହାନ୍ତି ତାରା
(v) ଗବେଷଣାଗାର	(v) ଲାଲ୍ ଗ୍ରହ
(vi) ସିରିୟସର ଦୂରତା	(vi) ଦ୍ଵିତୀୟ ବୃହତ୍ତମ ଗ୍ରହ
(vii) ସପ୍ତର୍ଷିମଣ୍ଡଳ	(vii) 23 ଘଣ୍ଟା 56 ମିନିଟ୍ 4 ସେ.
(viii) ପୃଥ‌ିବୀର ଆବର୍ତ୍ତନକାଳ	(viii) ପ୍ରଶ୍ନବାଚକ ଚିହ୍ନ
(ix) ମଙ୍ଗଳ	(ix) 8.7 ଆଲୋକବର୍ଷ ମାନମନ୍ଦିର
(x) ଶନି	(x) ମାନପନ୍ଦିର

Answer:

‘କ’ ସ୍ତମ୍ଭ	‘ଖ’ ସ୍ତମ୍ଭ
(i) ଚନ୍ଦ୍ର ଆକୃତିରେ ପରିବର୍ତ୍ତନ	(iii) ଚନ୍ଦ୍ରକଳା
(ii) ଶୁକ୍ର	(iv) ପାହାନ୍ତି ତାରା
(iii) ଚନ୍ଦ୍ରର ପରିକ୍ରମଣକାଳ	(i) 27.3 ଦିନ
(iv) ଆପେ।ଲୋ -II	(ii)  21.07.1969
(v) ଗବେଷଣାଗାର	(x) ମାନପନ୍ଦିର
(vi) ସିରିୟସର ଦୂରତା	(ix) 8.7 ଆଲୋକବର୍ଷ ମାନମନ୍ଦିର
(vii) ସପ୍ତର୍ଷିମଣ୍ଡଳ	(viii) ପ୍ରଶ୍ନବାଚକ ଚିହ୍ନ
(viii) ପୃଥ‌ିବୀର ଆବର୍ତ୍ତନକାଳ	(vii) 23 ଘଣ୍ଟା 56 ମିନିଟ୍ 4 ସେ.
(ix) ମଙ୍ଗଳ	(v) ଲାଲ୍ ଗ୍ରହ
(x) ଶନି	(vi) ଦ୍ଵିତୀୟ ବୃହତ୍ତମ ଗ୍ରହ

 

Odisha State Board CHSE Odisha Class 12 Economics Solutions Chapter 17 ବଜେଟ୍ Questions and Answers.

CHSE Odisha 12th Class Economics Chapter 17 Questions and Answers in Odia Medium

ବସ୍ତୁନିଷ୍ଠ ଓ ଅତିସଂକ୍ଷିପ୍ତ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
A. ସମ୍ଭାବ୍ୟ ଚାରୋଟି ଉତ୍ତର ମଧ୍ୟରୁ ଠିକ୍ ଉତ୍ତରଟି ବାଛି ଲେଖ ।

1. କେଉଁ ବଜେଟ୍ ମୁଦ୍ରାସ୍ତୀତି ନିୟନ୍ତ୍ରଣ କରିପାରେ ?
(A) ସମତୁଲ ବଜେଟ୍
(B) ନିଅଣ୍ଟିଆ ବଜେଟ୍
(C) ବଳକା ବଜେଟ୍
(D) ଉଭୟ (A) ଓ (B)
Answer:
(C) ବଳକା ବଜେଟ୍

2. କେଉଁ ବଜେଟ୍ ରାଷ୍ଟ୍ରର ବିକାଶ ପାଇଁ ଉପଯୋଗୀ ?
(A) ସମତୁଲ ବଜେଟ୍
(B) ନିଅଣ୍ଟିଆ ବଜେଟ୍
(C) ବଳକା ବଜେଟ୍
(D) ବୁଲେଟ୍
Answer:
(B) ନିଅଣ୍ଟିଆ ବଜେଟ୍

3. ବଜେଟ୍ ଶବ୍ଦଟି କେଉଁ ଫରାସୀ ଶବ୍ଦରୁ ଆସିଅଛି ?
(A) ବଜେଟି
(B) ବିଗେଟି
(C) ବକେଟ୍
(D) ଉପରୋକ୍ତ ସମସ୍ତ
Answer:
(A) ବଜେଟି

4. ବଳକା ବଜେଟ୍ ସେହି ସମୟରେ ସୃଷ୍ଟି ହୁଏ, ଯେତେବେଳେ :
(A) ସରକାରୀ ଆୟ = ସରକାରୀ ବ୍ୟୟ
(B) ସରକାରୀ ଆୟ < ସରକାରୀ ବ୍ୟୟ
(C) ସରକାରୀ ଆୟ > ସରକାରୀ ବ୍ୟୟ
(D) ଉପରୋକ୍ତ କୌଣସିଟି ନୁହେଁ
Answer:
(C) ସରକାରୀ ଆୟ > ସରକାରୀ ବ୍ୟୟ

5. ପ୍ରସ୍ତାବିତ ଆୟ ପ୍ରସ୍ତାବିତ ବ୍ୟୟଠାରୁ କମ୍ ହେଲେ ବଜେଟ୍ କ’ଣ ହୋଇଥାଏ ?
(A) ସନ୍ତୁଳିତ
(B) ବଳକା
(C) ନିଅଣ୍ଟିଆ
(D) କୌଣସିଟି ନୁହେଁ
Answer:
(C) ନିଅଣ୍ଟିଆ

6. ପ୍ରସ୍ତାବିତ ଆୟ ପ୍ରସ୍ତାବିତ ବ୍ୟୟ ସହିତ ସମାନ ବଜେଟ୍ କ’ଣ ହୋଇଥାଏ ?
(A) ସନ୍ତୁଳିତ
(B) ବଳକା
(C) ନିଅଣ୍ଟିଆ
(D) ଉପରୋକ୍ତ କୌଣସିଟି ନୁହେଁ
Answer:
(A) ସନ୍ତୁଳିତ

7. ପ୍ରସ୍ତାବିତ ଆୟ ପ୍ରସ୍ତାବିତ ବ୍ୟୟ ସହିତ ଅଧ‌ିକ ହେଲେ ବଜେଟ୍ କ’ଣ ହୋଇଥାଏ ?
(A) ସନ୍ତୁଳିତ
(B) ବଳକା
(C) ନିଅଣ୍ଟିଆ
(D) ଉପରୋକ୍ତ କୌଣସିଟି ନୁହେଁ
Answer:
(B) ବଳକା

8. କେଉଁ ବଜେଟ୍ ଅବସ୍ତୀତି ନିୟନ୍ତ୍ରଣ କରିପାରେ ?
(A) ସନ୍ତୁଳିତ
(B) ବଳକା
(C) ନିଅଣ୍ଟିଆ
(D) ଉପରୋକ୍ତ କୌଣସିଟି ନୁହେଁ ।
Answer:
(C) ନିଅଣ୍ଟିଆ

B. ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

1. ବଜେଟ୍‌ ଶବ୍ଦ ____________ ବଜେଟିରୁ ଉତ୍ପତ୍ତି ଲାଭ କରିଛି ବୋଲି ବିଶ୍ବାସ କରାଯାଏ ।
Answer:
ଫରାସୀ

2. ____________ ସରକାରଙ୍କ ଆୟ-ବ୍ୟୟର କେବଳ ଏକ ଗାଣିତିକ ହିସାବ ନୁହେଁ; ଏହା ମଧ୍ୟ ଅନେକ ଗୁଣରେ ଜନସାଧାରଣଙ୍କ ଉନ୍ନତି ପାଇଁ ଅଭିପ୍ରେତ ।
Answer:
ବଜେଟ୍

3. ଯେଉଁ ବଜେଟ୍‌ର ଅନୁମାନିକ ଆୟ ଓ ବ୍ୟୟ ସମାନ ତାହା ____________ ବଜେଟ୍‌ ।
Answer:
ସମତୁଲ

4. ଅର୍ଥନୈତିକ ସ୍ଥିରତା ସହିତ ବିକାଶ ପାଇଁ ଆଧୁନିକ ଅର୍ଥଶାସ୍ତ୍ରୀଗଣ ____________ ବଜେଟ୍ ପ୍ରତି ଦୃଢ଼ ଆସ୍ଥା ପ୍ରକଟ କରିଛନ୍ତି ।
Answer:
ଅସମତୁଲ

5. ବଜେଟ୍ ଅବଧୂ ମଧ୍ଯରେ ଯଦି ଆୟ ବ୍ୟୟଠାରୁ କମ୍ ହୁଏ, ତାହାକୁ ____________ ବଜେଟ୍ ପ୍ରତି ଦୃଢ଼ ଆସ୍ଥା ପ୍ରକଟ କରିଛନ୍ତି ।
Answer:
ନିଅଣ୍ଟିଆ

6. ଋଣ, ନୂତନ ମୁଦ୍ରାସୃଷ୍ଟି, ପୂର୍ବ ସଂରକ୍ଷିତ ପାଣ୍ଠିରୁ ଅର୍ଥ ପ୍ରତ୍ୟାହାର ଇତ୍ୟାଦିର ସହାୟତାରେ ସରକାର ବଜେଟ୍‌ର ____________ ବଜେଟ୍ କହନ୍ତି ।
Answer:
ନିଅଣ୍ଟ

7. ____________ ବଜେଟ୍‌ର ଅଭିବୃଦ୍ଧିକାରୀ ପ୍ରଭାବ ରହିଛି ।
Answer:
ନିଅଣ୍ଟିଆ

8. ____________ ବଜେଟ୍ ଧନୀ-ଗରିବ ପ୍ରଭେଦ ହ୍ରାସ କରେ ।
Answer:
ନିଅଣ୍ଟିଆ

9. ନିଅଣ୍ଟିଆ ବଜେଟ୍ ଏକ ____________ ରାଷ୍ଟ୍ର ପାଇଁ ବରଦାନ ସଦୃଶ ।
Answer:
ବିକାଶଶୀଳ

10. ନିଅଣ୍ଟିଆ ବଜେଟ୍ ରାଷ୍ଟ୍ରରେ ____________ ସମତୁଳନ ସମସ୍ୟା ସୃଷ୍ଟି କରେ ।
Answer:
ଆଦାନପ୍ରଦାନ

11. ଯେଉଁ ବଜେଟ୍‌ରେ ରାଷ୍ଟ୍ରର ଆନୁମାନିକ ବ୍ୟୟଠାରୁ ଆୟ ଅଧ୍ବକ, ତାହାକୁ ____________ ବଜେଟ୍ କୁହାଯାଏ ।
Answer:
ବଳକା

12. ____________ ବଜେଟ୍ ମୁଦ୍ରାଷ୍ଟୀତି ନିୟନ୍ତ୍ରଣ କରିବାରେ ସହାୟତା ପ୍ରଦାନ କରେ ।
Answer:
ବଳକା

C. ନିମ୍ନଲିଖ ଉକ୍ତିଗୁଡ଼ିକ ଭୁଲ୍ କି ଠିକ୍ ଲେଖ । ରେଖାଙ୍କିତ ଅଂଶର ପରିବର୍ତ୍ତନ ନ କରି ଆବଶ୍ୟକ ସ୍ଥଳେ ସଂଶୋଧନ କର ।

1. ସଂସ୍ଥାପିତ ଅର୍ଥଶାସ୍ତ୍ରୀଗଣ ଅସମତୁଲ ବଜେଟ୍‌ର ସମର୍ଥକ ।
Answer:
ଭୁଲ୍ ।
ଠିକ୍ – ସଂସ୍ଥାପିତ ଅର୍ଥଶାସ୍ତ୍ରୀଗଣ ସମତୁଲ ବଜେଟ୍‌ର ସମର୍ଥକ ।

2. ବଳକା ବଜେଟ ଜାତୀୟ ଆୟ ବୃଦ୍ଧି କରେ ।
Answer:
ଭୁଲ୍ ।
ଠିକ୍ – ବଳକା ବଜେଟ୍ ଜାତୀୟ ଆୟ ହ୍ରାସ କରେ ।

3. ବଳକା ବଜେଟ୍ର ନୀତିକାରୀ ।
Answer:
ଭୁଲ୍ ।
ଠିକ୍ – ବଳକା ବଜେଟ୍ ଅବସ୍ତୀତିକାରୀ ।

4. ନିଅଣ୍ଟିଆ ବଜେଟ ଅନାବଶ୍ୟକ ବ୍ୟୟ ପାଇଁ ପ୍ରୋତ୍ସାହିତ କରେ ।
Answer:
ଠିକ୍ ।

5. ନିଅଣ୍ଟିଆ ବଜେଟ୍ ଋଣବୋଝ ହ୍ରାସ କରେ ।
Answer:
ଭୁଲ୍ ।
ଠିକ୍ – ବଳକା ବଜେଟ୍ ଋଣବୋଝ ହ୍ରାସ କରେ ।

6. ବଳକା ବଜେଟ୍ ସରକାରଙ୍କ ସ୍ବାଧୀନତା ହ୍ରାସ କରେ ।
Answer:
ଭୁଲ୍ ।
ଠିକ୍ – ସମତୁଲ ବଜେଟ୍ ସରକାରଙ୍କ ସ୍ବାଧୀନତା ହ୍ରାସ କରେ ।

7. ନିଅଣ୍ଟିଆ ବଜେଟର ଅଭିବୃଦ୍ଧିକାରୀ ପ୍ରଭାବ ରହିଛି ।
Answer:
ଠିକ୍ ।

8. ସମତୁଲ ବଜେଟ୍ ନିଅଣ୍ଟିଆ ବା ବଳକା ହୋଇଥାଏ ।
Answer:
ଭୁଲ୍ ।
ଠିକ୍ – ଅସମତୁଲ ବଜେଟ୍ ନିଅଣ୍ଟିଆ ବା ବଳକା ହୋଇଥାଏ ।

9. ରାଜସ୍ଵ ବାୟର ରାଜସ୍ଵ ଆୟକ ବାଦଦେଲେ ରାଜସ୍ବ ନିଅଣ୍ଟ ହିସାବ କରାଯାଏ ।
Answer:
ଠିକ୍ ।

10. ଯେଉଁ ବଜେଟରେ ପ୍ରସ୍ତାବିତ ବ୍ୟୟ ଏବଂ ପ୍ରତ୍ୟାଶିତ ଆୟ ସମାନ ହୋଇଥାଏ, ତାହାକୁ ଅସନ୍ତୁଳିତ ବଜେଟ୍ କୁହାଯାଏ ।
Answer:
ଭୁଲ୍ ।
ଠିକ୍ – ଯେଉଁ ବଜେଟ୍‌ରେ ପ୍ରସ୍ତାବିତ ବ୍ୟୟ ଓ ପ୍ରତ୍ୟାଶିତ ଆୟ ସମାନ ହୋଇଥାଏ, ତାହାକୁ ସନ୍ତୁଳିତ ବଜେଟ୍ କୁହାଯାଏ ।

D. ଗୋଟିଏ ବାକ୍ୟରେ ଉତ୍ତର ଦିଅ ।

1. ବଜେଟ୍ କ’ଣ ?
Answer:
ବଜେଟ୍, ସର୍ବସାଧାରଣ ସଂସ୍ଥାଗୁଡ଼ିକର କୌଣସି ଆର୍ଥିକ ବର୍ଷ ଆରମ୍ଭରୁ ସେହି ବର୍ଷ ଲାଗି ଏକ ଆୟ-ବ୍ୟୟର ଅଟକଳ ଅଟେ ।

2. ଭାରତରେ ଓ ଆମେରିକା ମଧ୍ୟରେ ଆର୍ଥିକବର୍ଷ ଆରମ୍ଭ ସ୍ଥଳେ ପୃଥକତା କ’ଣ ?
Answer:
ଭାରତରେ ଆର୍ଥିକ ବର୍ଷ ଏପ୍ରିଲ୍ ମାସ ପ୍ରଥମ ଦିନରୁ ଆରମ୍ଭ ହେଲାବେଳେ ତାହା ଆମେରିକାରେ ଜୁଲାଇ ମାସ ପ୍ରଥମ ଦିନରୁ ଆରମ୍ଭ ହୁଏ ।

3. ଅସମତୁଲ ବଜେଟ୍ କେତେ ପ୍ରକାରର ?
Answer:
ଅସମତୁଲ ବଜେଟ୍ ଦୁଇ ପ୍ରକାରର; ଯଥା – ନିଅଣ୍ଟିଆ ଓ ବଳକା ବଜେଟ୍ ।

4. ସମତୁଲ ବଜେଟ୍ କହିଲେ କ’ଣ ବୁଝ ?
Answer:
ଯେଉଁ ବଜେଟ୍‌ରେ ଆୟ ବ୍ୟୟ ମଧ୍ୟରେ ସମାନତା ଦେଖାଯାଏ, ତାକୁ ସମତୁଲ ବଜେଟ୍ କୁହାଯାଏ ।

5. ନିଅଣ୍ଟିଆ ବଜେଟ୍କୁ ଅଭିବର୍ଷକ କାହିଁକି କୁହାଯାଏ ?
Answer:
ନିଅଣ୍ଟିଆ ବଜେଟ୍ ଅଧୃକ କ୍ରୟ କ୍ଷମତା ସୃଷ୍ଟି କରୁଥିବାରୁ ଏହାକୁ ଅଭିବର୍ଷକ କୁହାଯାଏ ।

6. ନିଅଣ୍ଟିଆ ବଜେଟ୍‌ର ଏକ ଦୁର୍ଗୁଣ ଦର୍ଶାଅ ।
Answer:
ଋଣ ବୋଝ ବା ଅପଚୟ ବୃଦ୍ଧି, ନିଅଣ୍ଟିଆ ବଜେଟ୍‌ର ଏକ ଦୁର୍ଗୁଣ ।

7. ସମତୁଲ ବଜେଟ୍‌ର ଏକ ସୁଗୁଣ ଉପସ୍ଥାପନ କର ।
Answer:
ସମତୁଲ ବଜେଟ୍‌ର ଏକ ସୁଗୁଣ ହେଲା, ଏହା ଅପଚୟ ହ୍ରାସ କରେ ବା ଆର୍ଥନୀତିକ ସ୍ଥିରତା ରକ୍ଷା କରେ ।

8. କେଉଁ ବଜେଟ୍ ବେକାରି ନିୟନ୍ତ୍ରଣ କରିପାରେ ?
Answer:
ନିଅଣ୍ଟିଆ ବଜେଟ୍ ବେକାରି ନିୟନ୍ତ୍ରଣ କରିପାରେ ।

9. କେଉଁ ବଜେଟ୍ ମୁଦ୍ରା ସ୍ତୀତି ନିୟନ୍ତ୍ରଣ କରିପାରେ ?
Answer:
ବଳକା ବଜେଟ୍ ମୁଦ୍ରା ସ୍ତ୍ରୀତି ନିୟନ୍ତ୍ରଣ କରିପାରେ ।

10. ସଙ୍ଗଠିତ ପାଣ୍ଠି କ’ଣ ?
Answer:
ଯେଉଁ ପାଣ୍ଠି ସରକାରଙ୍କ ସମସ୍ତ ରାଜସ୍ଵ ଓ ଆଣିଥିବା ଋଣର ପରିମାଣ ଦର୍ଶାଇଥାଏ, ତାହାକୁ ସଙ୍ଗଠିତ ପାଣ୍ଠି କୁହାଯାଏ ।

11. ଆକସ୍ମିକ ପାଣ୍ଠି କ’ଣ ?
Answer:
ଯେଉଁ ପାଣ୍ଠି ରାଷ୍ଟ୍ରପତିଙ୍କ ଅଧୀନରେ ରହେ ଏବଂ ଯାହା ଆକସ୍ମିକ ବ୍ୟୟକୁ ସାମ୍ନା କରିବା ପାଇଁ ଉଦ୍ଦିଷ୍ଟ, ତାହାକୁ ଆକସ୍ମିକ ପାଣ୍ଠି କୁହାଯାଏ ।

12. ରାଜସ୍ଵ ନିଅଣ୍ଟ କ’ଣ ?
Answer:
ରାଜସ୍ବ ବ୍ୟୟରୁ ରାଜସ୍ବ ଆୟକୁ ବାଦ୍ ଦେଲେ ଯେଉଁ ଅତିରିକ୍ତ ରାଜସ୍ବ ବ୍ୟୟ ଦେଖାଯାଏ, ତାହାକୁ ରାଜସ୍ଵ ନିଅଣ୍ଟ କୁହାଯାଏ ।

13. ବଜେଟ୍ ନିଅଣ୍ଟ କ’ଣ ?
Answer:
ମୋଟ ଆୟକୁ ଓ ମୋଟ ବ୍ୟୟରୁ ବାଦ୍ ଦେଲେ ଯେଉଁ ଅତିରିକ୍ତ ବ୍ୟୟ ରହେ, ତାହାକୁ ବଜେଟ୍ ନିଅଣ୍ଟ କୁହାଯାଏ ।

14. ବିତ୍ତୀୟ ନିଅଣ୍ଟ କ’ଣ ?
Answer:
ମୋଟ ବ୍ୟୟ ଏବଂ ମୋଟ ଆୟ ମଧ୍ୟରେ ଥିବା ପାର୍ଥକ୍ୟ ସହିତ ପୁଞ୍ଜି ବିନିଯୋଗକୁ ମିଶାଇବା ସହ ମୋଟ ଋଣ ଏବଂ ଅନ୍ୟାନ୍ୟ ଦେୟକୁ ବାଦ୍ ଦେବାପରେ ଯାହା ରହେ, ତାହାକୁ ବିତ୍ତୀୟ ନିଅଣ୍ଟ କୁହାଯାଏ ।

15. ମୌଦ୍ରିକ ନିଅଣ୍ଟ କ’ଣ ?
Answer:
ମୌଦ୍ରିକ ନିଅଣ୍ଟ ହେଉଛି ଭାରତୀୟ ରିଜର୍ଭ ବ୍ୟାଙ୍କର କେନ୍ଦ୍ର ସରକାରଙ୍କୁ ଦିଆଯାଉଥିବା ବଦ୍ଧିତ ନିଟ୍ ଋଣକୁ ବୁଝାଏ ।

ସଂକ୍ଷିପ୍ତ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
A. ନିମ୍ନଲିଖୂ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଦୁଇଟି/ତିନୋଟି ବାକ୍ୟ ମଧ୍ଯରେ ଦିଅ ।

1. ବଜେଟ୍ କ’ଣ ?
Answer:
ବଜେଟ୍ ସରକାରୀ ରାଜସ୍ଵ ଓ ବ୍ୟୟର ପ୍ରାଥମିକ ଅନୁମୋଦିତ ଯୋଜନା ସମ୍ପର୍କିତ ନଥପତ୍ର । ଅର୍ଥାତ୍‌ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ବର୍ଷ ପାଇଁ ସରକାରଙ୍କ ଆୟ ଓ ବ୍ୟୟର ରୂପରେଖ ବଜେଟ୍‌ରେ ସ୍ଥାନ ପାଇଥାଏ । ସରକାରୀ ଆୟବ୍ୟୟର ଅଟକଳ ବଜେଟ୍‌ର ମୁଖ୍ୟ ଅଂଶ ହୋଇ ରହିଥାଏ ।

2. ସମତୁଲ ବଜେଟ୍ କ’ଣ ?
Answer:
ଯେଉଁ ବଜେଟ୍‌ରେ ସରକାରୀ ଆୟର ପରିମାଣ ଏହାର ବ୍ୟୟ ପରିମାଣ ସହ ସମତୁଲ ହୋଇଥାଏ, ତାହାକୁ ସମତୁଲ ବଜେଟ୍ କୁହାଯାଏ । ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ବର୍ଷ ପାଇଁ ପ୍ରସ୍ତୁତ ସରକାରୀ ବ୍ୟୟ ଅଟକଳରେ ବିଭିନ୍ନ ସୂତ୍ରରୁ ସଂଗୃହୀତ ହେବାକୁ ଥିବା ପ୍ରତ୍ୟାଶିତ ଆୟ ଓ ବିଭିନ୍ନ ଉଦ୍ଦେଶ୍ୟରେ ହେବାକୁ ଥିବା ପ୍ରସ୍ତାବିତ ବ୍ୟୟ ସହ ସମାନ ହୋଇଥାଏ ।

3. ବଳକା ବଜେଟ୍ କ’ଣ ?
Answer:
ଯେଉଁ ବଜେଟ୍‌ରେ ସରକାରୀ ଆୟ, ସରକାରୀ ବ୍ୟୟଠାରୁ ଅଧିକ ହୁଏ, ତାହାକୁ ବଳକା ବଜେଟ୍ କୁହାଯାଏ । ଏ କ୍ଷେତ୍ରରେ ସରକାରୀ ପ୍ରତ୍ୟାଶିତ ଆୟ, ପ୍ରସ୍ତାବିତ ବ୍ୟୟଠାରୁ ଅଧିକ ହୋଇଥାଏ । ଫଳରେ ସରକାରୀ ଆୟର ଏକ ଅଂଶ ସରକାରଙ୍କଦ୍ଵାରା ଉପଯୋଗ ନ ହୋଇ ଗଚ୍ଛିତ ହୋଇ ରହିଥାଏ ।

4. ନିଅଣ୍ଟିଆ ବଜେଟ୍ କ’ଣ ?
Answer:
ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ବର୍ଷ ପାଇଁ ଯଦି ସରକାରଙ୍କ ପ୍ରସ୍ତାବିତ ବ୍ୟୟ ଅଟକଳ ପ୍ରତ୍ୟାଶିତ ଆୟଠାରୁ ଅଧିକ ହୁଏ, ତେବେ ସେ ବଜେଟ୍‌କୁ ନିଅଣ୍ଟିଆ ବଜେଟ୍ କୁହାଯାଏ । ଏହା ଏକ ଅସମତୁଲ ବଜେଟ୍ ଯେଉଁଥରେ ସରକାରୀ ବ୍ୟୟ ସରକାରୀ ଆୟଠାରୁ ଅତ୍ୟଧ୍ଵ ହୋଇଥାଏ ।

5. ରାଜସ୍ଵ ନିଅଣ୍ଟ କ’ଣ ?
Answer:
ରାଜସ୍ବ ବ୍ୟୟରୁ ରାଜସ୍ଵ ଆୟକୁ ବାଦ୍ ଦେଲେ ଯେଉଁ ଅତିରିକ୍ତ ରାଜସ୍ବ ବ୍ୟୟ ଦେଖାଯାଏ, ତାହାକୁ ରାଜସ୍ୱ ନିଅଣ୍ଟ କୁହାଯାଏ । କେନ୍ଦ୍ର ସରକାରଙ୍କ ଚଳନ୍ତି ରାଜସ୍ବ ବ୍ୟୟରେ ଉଭୟ ଯୋଜନା ବ୍ୟୟ ଓ ଅଣଯୋଜନା ବ୍ୟୟ ଅନ୍ତର୍ଭୁକ୍ତ କରାଯାଇଥାଏ । ଚଳନ୍ତି ରାଜସ୍ବ ଆୟ ଯାହାକି ଉଭୟ ଟିକସ ଆୟ ଓ ଅଣଟିକସ ଆୟରୁ ମିଳେ, ତାହା ରାଜସ୍ବ ବ୍ୟୟ ବାବଦରେ ଖର୍ଚ୍ଚ କରାଯାଇଥାଏ ।

6. ବଜେଟ୍ ନିଅଣ୍ଟ କ’ଣ ?
Answer:
ମୋଟ ଆୟକୁ, ମୋଟ ବ୍ୟୟରୁ ବାଦ୍ ଦେଲେ ଯେଉଁ ଅତିରିକ୍ତ ବ୍ୟୟ ରହେ, ତାହାକୁ ବଜେଟ୍ ନିଅଣ୍ଟ କୁହାଯାଏ ।ମୋଟାମୋଟି ଭାବେ ବଜେଟ୍ ନିଅଣ୍ଟ ହିସାବ କରାଗଲାବେଳେ, ସରକାର ସବୁପ୍ରକାରର ବ୍ୟୟକୁ (ରାଜସ୍ଵ ହିସାବ ଓ ପୁଞ୍ଜିବିନିଯୋଗ ହିସାବ) ଏବଂ ସମସ୍ତ ଆୟ (ରାଜସ୍ୱ ଆୟ ଏବଂ ପୁଞ୍ଜି ବିନିଯୋଗ ବ୍ୟୟ, ଯାହାକି ଖୋଲାବଜାରରୁ ଉଠାଇଥିବା ଋଣ ଏବଂ ଅନ୍ୟାନ୍ୟ ଦେୟ)କୁ ହିସାବ ଅନ୍ତର୍ଭୁକ୍ତ କରିଥା’ନ୍ତି । ଭାରତ ସରକାରଙ୍କ ପାରମ୍ପରିକ ବଜେଟ୍ ନିଅଣ୍ଟ, ସରକାରଙ୍କ ନିଅଣ୍ଟିଆ ଅର୍ଥ ବ୍ୟବସ୍ଥାରେ ପ୍ରତିଫଳିତ ହେଉଥିଲା ।

7. ବିତ୍ତୀୟ ନିଅଣ୍ଟ କ’ଣ ?
Answer:
ବିତ୍ତୀୟ ନିଅଣ୍ଟ ହେଉଛି ବଜେଟ୍ ନିଅଣ୍ଟଯୁକ୍ତ ଖୋଲାବଜାରରୁ ଉଠାଇଥିବା ଋଣ ଏବଂ ଅନ୍ୟାନ୍ୟ ଦେୟସମୂହ । ପ୍ରକାରାନ୍ତରେ କହିଲେ ବିତ୍ତୀୟ ନିଅଣ୍ଟ (କ) ମୋଟ ବ୍ୟୟ ଏବଂ ମୋଟ ଆୟ ମଧ୍ୟରେ ଥିବା ପାର୍ଥକ୍ୟ ସହିତ ପୁଞ୍ଜି ବିନିଯୋଗକୁ ମିଶାଇବା ସହ ମୋଟ ଋଣ ଏବଂ ଅନ୍ୟାନ୍ୟ ଦେୟକୁ ବାଦ୍ ଦେବାପରେ ଯାହା ରହେ ତାହାକୁ ବୁଝାଏ, (ଖ) ଏହା ମଧ୍ୟ ମୋଟ ବଜେଟ୍ ନିଅଣ୍ଟ ସହିତ ମୋଟ ଋଣ ଓ ଅନ୍ୟାନ୍ୟ ଦେୟ ମିଶାଇଲେ, ଯାହା ମିଳେ ତାହାକୁ ବୁଝାଏ ।

8. ପ୍ରାଥମିକ ନିଅଣ୍ଟ କ’ଣ ?
Answer:
ମୋଟ ବିତ୍ତୀୟ ନିଅଣ୍ଟରୁ ମୋଟ ସୁଧ ବାବଦ ଅର୍ଥ ପ୍ରଦାନକୁ ବାଦ୍ ଦେଲେ ଯାହା ରହେ, ତାହାକୁ ପ୍ରାଥମିକ ନିଅଣ୍ଟ ବୋଲି ଧରାଯାଏ । ସଂକ୍ଷେପରେ କହିଲେ, ମୋଟ ବିତ୍ତୀୟ ନିଅଣ୍ଟରୁ ସୁଧ ବାବଦ ଅର୍ଥ ପ୍ରଦାନକୁ ବାଦ୍ ଦେଲେ ଯାହା ଉଦ୍‌ବୃତ୍ତ ଆକାରରେ ରହେ, ତାହା ହିଁ ପ୍ରାଥମିକ ନିଅଣ୍ଟ ।

9. ମୌଦ୍ରିକ ନିଅଣ୍ଟ କ’ଣ ?
Answer:
ଏହା ଭାରତୀୟ ରିଜର୍ଭ ବ୍ୟାଙ୍କର କେନ୍ଦ୍ର ସରକାରଙ୍କୁ ଦେଉଥବା ବର୍ଷିତ ନିଟ୍ ଋଣକୁ ବୁଝାଏ । ଏହା (କ) ଭାରତୀୟ ରିଜର୍ଭ ବ୍ୟାଙ୍କ ନିକଟରେ ସରକାରଙ୍କ ରାଜକୋଷୀୟ ପତ୍ରର ନିଟ୍ ବୃଦ୍ଧିର ପରିମାଣ, (ଖ) ସରକାରଙ୍କ ତରଫରୁ କେନ୍ଦ୍ରୀୟ ବ୍ୟାଙ୍କ ବଜାରରୁ ଉଠାଇଥିବା ଋଣର ପରିମାଣକୁ ବୁଝାଇଥାଏ ।

10. କିପରି ସମତୁଲ ବଜେଟ୍ ସରକାରଙ୍କ ସ୍ଵାଧୀନତା ହ୍ରାସ କରେ ?
Answer:
ଆଧୁନିକ ରାଷ୍ଟ୍ର ଜନମଙ୍ଗଳକାରୀ ରାଷ୍ଟ୍ର ହୋଇଥିବାରୁ ଜନମଙ୍ଗଳ ପାଇଁ ଏହାକୁ ବିଭିନ୍ନ ଦିଗରେ ବ୍ୟୟ କରିବାକୁ ହୋଇଥାଏ । ସ୍ବାଭାବିକଭାବେ, ସରକାରୀ ବ୍ୟୟ ବହୁଗୁଣିତ ହୁଏ । କିନ୍ତୁ ଏହା ସମତୁଲ ବଜେଟ୍ କ୍ଷେତ୍ରରେ ଅସମ୍ଭବ । ସମତୁଲ ବଜେଟ୍ ଅନୁସରଣ କରୁଥିବା ରାଷ୍ଟ୍ର ପକ୍ଷେ ଆବଶ୍ୟକ ମୁତାବକ ବ୍ୟୟ କରିବା ସମ୍ଭବ ହେଉନଥିବାରୁ ଏହା ଜନମଙ୍ଗଳ କରିପାରେ ନାହିଁ, ଫଳରେ ସରକାରଙ୍କ ଭୂମିକା ହ୍ରାସ ପାଏ ।

B. ପାଞ୍ଚଟି/ ଛଅଟି ବାକ୍ୟରେ ନିମ୍ନଲିଖୂ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଦିଅ ।

1. ବଜେଟ୍ କ’ଣ ?
Answer:
ବଜେଟ୍ ସରକାରଙ୍କର ଏକ ଗୁରୁତ୍ବପୂର୍ଣ ଅର୍ଥନୈତିକ ଦସ୍ତାବିଜ୍‌ । ଆଗାମୀ ଆର୍ଥିକ ବର୍ଷ ପାଇଁ ଏହା ସରକାରଙ୍କ ଆୟ-ବ୍ୟୟ ଅଟକଳ । ସରକାର କେଉଁ କେଉଁ ଉତ୍ସରୁ ଆୟ କରିବାପାଇଁ ଆଶା ରଖୁଛନ୍ତି ଏବଂ କେଉଁ କେଉଁ କ୍ଷେତ୍ରରେ କେତେ ବ୍ୟୟ କରିବାପାଇଁ ପ୍ରସ୍ତାବ ରଖୁଛନ୍ତି ତାହାର ବଜେଟ୍ ସୂଚନା ଦିଏ ।

ପରବର୍ତ୍ତୀ ଆର୍ଥିକ ବର୍ଷ ପାଇଁ ସରକାରଙ୍କ ଆଭିମୁଖ୍ୟ କ’ଣ, ତାହା ଏଥିରୁ ସ୍ପଷ୍ଟ ହୋଇଥାଏ । ପ୍ରତିବର୍ଷ ଫେବୃୟାରୀ ମାସର ଅନ୍ତିମ ଦିବସରେ ଭାରତର କେନ୍ଦ୍ର-ସରକାର ପାର୍ଲିଆମେଣ୍ଟରେ ବଜେଟ୍ ଉପସ୍ଥାପନ କରନ୍ତି । ପ୍ରଫେସର ଗ୍ଲାଡ଼ଷ୍ଟୋନ୍‌ଙ୍କ ମତରେ-ବଜେଟ୍ ସରକାରଙ୍କ ଆୟ-ବ୍ୟୟର ଏକ ଗାଣିତିକ ହିସାବ କେବଳ ନହେଁ, ଏହା ମଧ୍ୟ ଅନେଇ ଗଣରେ ଇରସାଧାରଣଙ୍କ ଉଇଲି ପାଇଁ ଅଭିଯୋଲ ।

2. ସମତୁଲ ବଜେଟ୍ କ’ଣ ?
Answer:
ଯେଉଁ ବଜେଟ୍‌ର ଆନୁମାନିକ ଆୟ ଓ ବ୍ୟୟ ସମାନ ତାହା ସମତୁଲ ବଜେଟ୍ । ଏହାକୁ ସନ୍ତୁଳିତ ବଜେଟ୍ ମଧ୍ୟ କୁହାଯାଏ । ପ୍ରଫେସର ଡାଲଟନ୍‌ଙ୍କ ମତରେ, ନିର୍ଦ୍ଦିଷ୍ଟ ସମୟସୀମା ମଧ୍ୟରେ ଯଦି ରାଜସ୍ବ ବ୍ୟୟଠାରୁ କମ୍ ହୁଏ ନାହିଁ, ତେବେ ତାହା ସମତୁଲ ବଜେଟ୍ । ସଂସ୍ଥାପିତ ଅର୍ଥଶାସ୍ତ୍ରୀଗଣ ସମତୁଲ ବଜେଟ୍‌ର ଦୃଢ଼ ସମର୍ଥକ ଥିଲେ ।

ସେମାନେ ସର୍ବନିମ୍ନ କର ଓ ସର୍ବନିମ୍ନ ସରକାରୀ ବ୍ୟୟରେ ବିଶ୍ୱାସ କରୁଥିବାରୁ ସ୍ବାଭାବିକ ଆର୍ଥିକ ଅବସ୍ଥା ପାଇଁ ସମତୁଲ ବଜେଟ୍ ଉପରେ ଗୁରୁତ୍ୱ ଆରୋପ କରୁଥିଲେ । ସେମାନଙ୍କ ମତରେ, ସମତୁଲ ବଜେଟ୍‌ର ନିରପେକ୍ଷ ପ୍ରଭାବ ଦରଦାମ୍ ବୃଦ୍ଧି କିମ୍ବା ହ୍ରାସ କରିପାରେ ନାହିଁ । ଫଳରେ ଅର୍ଥନୈତିକ ସ୍ଥିରତା ସହିତ ଅର୍ଥବ୍ୟବସ୍ଥା ସ୍ଵାଭାବିକ ରହେ ।

3. ନିଅଣ୍ଟିଆ ବଜେଟ୍ କ’ଣ ?
Answer:
ନିଅଣ୍ଟିଆ ବଜେଟ୍ କ୍ଷେତ୍ରରେ ଆନୁମାନିକ ବ୍ୟୟ ଆୟଠାରୁ ଅଧିକ । ଅଧ୍ୟାପକ ଟେଲରଙ୍କ ମତରେ ବଜେଟ୍ ଅବଧୂ ମଧ୍ଯରେ ଯଦି ଆୟ ବ୍ୟୟଠାରୁ କମ୍ ହୁଏ, ତାହାକୁ ନିଅଣ୍ଟିଆ ବଜେଟ୍ କହନ୍ତି । ଋଣ, ନୂତନ ମୁଦ୍ରାସୃଷ୍ଟି, ପୂର୍ବ ସଂରକ୍ଷିତ ପାଣ୍ଠିରୁ ଅର୍ଥ ପ୍ରତ୍ୟାହାର ଇତ୍ୟାଦିର ସହାୟତାରେ ସରକାର ବଜେଟ୍‌ର ନିଅଣ୍ଟ ଭରଣା କରନ୍ତି । ଏହି ନିଅଣ୍ଟ ଭରଣା ପ୍ରକ୍ରିୟାକୁ ନିଅଣ୍ଟିଆ ବିତ୍ତ ବ୍ୟବସ୍ଥା କୁହାଯାଏ ।

ନିଅଣ୍ଟିଆ ବଜେଟ୍‌ର ଅଭିବୃଦ୍ଧିକାରୀ ପ୍ରଭାବ ରହିଛି । ଯେତେବେଳେ ସରକାର ଆୟଠାରୁ ଅଧ୍ୟକ ବ୍ୟୟ କରନ୍ତି, ଜାତୀୟ ଆୟ ବହୁଗୁଣିତ ହୋଇଥାଏ । ରାଷ୍ଟ୍ରର ସର୍ବାଙ୍ଗୀନ ବିକାଶ ସାଧୁ ହୋଇପାରେ । ଏହା ମଧ୍ୟ ଅବସ୍ତୀତି ନିୟନ୍ତ୍ରଣ କରି ଅର୍ଥନୈତିକ ସ୍ଥିରତା ଆଣିପାରେ ! ତେଣୁ ଅଧିକାଂଶ ବିକାଶଶୀଳ ରାଷ୍ଟ୍ର ଉଦ୍ଦେଶ୍ୟମୂଳକ ଭାବେ ନିଅଣ୍ଟିଆ ବଜେଟ୍ ଅନୁସରଣ କରନ୍ତି ।

4. ବଳକା ବଜେଟ୍ କ’ଣ ?
Answer:
ଯେଉଁ ବଜେଟ୍‌ରେ ରାଷ୍ଟ୍ରର ଆନୁମାନିକ ଆୟ ଆନୁମାନିକ ବ୍ୟୟଠାରୁ ଅଧ୍ବକ, ତାହାକୁ ବଳକା ବଜେଟ୍ କୁହାଯାଏ । ଏଠାରେ ସରକାର ଜନସାଧାରଣଙ୍କଠାରୁ ଯେଉଁ ଅର୍ଥ ଆଦାୟ କରନ୍ତି, ତା’ଠାରୁ କମ୍ ବ୍ୟୟ କରନ୍ତି । ଫଳରେ ଜାତୀୟ ଆୟ କିଛି ଗୁଣ ହ୍ରାସ ପାଏ ଏବଂ ଏହା ମୁଦ୍ରାସ୍ପତି ନିୟନ୍ତ୍ରଣ କରିବାରେ ସହାୟତା ପ୍ରଦାନ କରେ । ଏହା ମଧ୍ୟ ଅଣଉତ୍ପାଦୀ ଓ ଅନାବଶ୍ୟକ ବ୍ୟୟ ହ୍ରାସ କରେ ।

ରାଷ୍ଟ୍ରର ଋଣଭାର ଲାଘବ ହୋଇପାରେ; କିନ୍ତୁ ବଳକା ବଜେଟ୍ ରାଷ୍ଟ୍ରର ଉତ୍ପାଦନ ଓ ନିୟୋଜନ ହ୍ରାସ କରେ । ଆୟ ହ୍ରାସ ପାଇବାରୁ ରାଷ୍ଟ୍ରର ଚାହିଦା ମଧ୍ୟ ହ୍ରାସ ପାଏ । ଫଳରେ ନିବେଶ, ନିୟୋଜନ ଏବଂ ଉତ୍ପାଦନ ହ୍ରାସ ପାଇବାରେ ଲାଗେ । ଏହା କ୍ରମଶଃ ରାଷ୍ଟ୍ରକୁ ଅବସ୍ତୀତି ଆଡ଼କୁ ଅଗ୍ରସର କରାଏ । ଆଧୁନିକ ବିଶ୍ବରେ ବଳକା ବଜେଟ୍‌ର ଗୁରୁତ୍ଵ ହ୍ରାସ ପାଇଛି ଏବଂ ଏହାର ପ୍ରଚଳନ ସୀମିତ ।

5. ନିଅଣ୍ଟିଆ ବଜେଟ୍ କିପରି ସମ୍ପଦ ଓ ଆୟ ବଣ୍ଟନରେ ଅସମାନତା ସୃଷ୍ଟି କରେ ?
Answer:
ଅଧ୍ୟାପକ ଟେଲର୍‌ଙ୍କ ମତରେ, ବଜେଟ୍ ଅବଧୂ ମଧ୍ଯରେ ଯଦି ଆୟ ବ୍ୟୟଠାରୁ କମ୍ ହୁଏ, ତାହାକୁ ନିଅଣ୍ଟିଆ ବଜେଟ୍ କହନ୍ତି । ତେଣୁ ନିଅଣ୍ଟିଆ ବଜେଟ୍ ଯୋଗୁଁ ମୁଦ୍ରାଙ୍ଗୀତି ସୃଷ୍ଟି ହୋଇଥାଏ । ଏହାଦ୍ଵାରା ବ୍ୟବସାୟୀ ଓ ଉତ୍ପାଦନକାରୀ ବ୍ୟକ୍ତି ଉପକୃତ ହୋଇଥା’ନ୍ତି । ମଜୁରି ଆକାରରେ ନିର୍ଦ୍ଦିଷ୍ଟ ପରିମାଣରେ ମୁଦ୍ରା ପାଉଥିବା ଶ୍ରମିକ ଗୋଷ୍ଠୀମାନଙ୍କୁ କ୍ଷତି ସହିବାକୁ ପଡ଼ିଥାଏ । ତେଣୁ ଧନୀ ଅଧ୍ବକ ଧନୀ ହେବା ସଙ୍ଗେ ସଙ୍ଗେ ଗରିବ ଅଧୂକ ଗରିବ ହୋଇଥାଏ । ଏହାଦ୍ଵାରା ଅର୍ଥନୈତିକ ଅସମାନତା ବୃଦ୍ଧି ପାଏ ।

6. ନିଅଣ୍ଟିଆ ବଜେଟ୍କୁ କାହିଁକି ଆର୍ଥିକ ବିଧ୍ୱଂସୀ କୁହାଯାଏ ?
Answer:
ନିଅଣ୍ଟିଆ ବଜେଟ୍ କ୍ଷେତ୍ରରେ ସରକାରୀ ବ୍ୟୟ ସରକାରୀ ଆୟଠାରୁ ଅଧ‌ିକ ହୋଇଥାଏ । ନିଅଣ୍ଟିଆ ବଜେଟ୍‌ର ମାତ୍ରା ଅଧ‌ିକ ହୋଇଗଲେ ତାହା ଦେଶକୁ ଆର୍ଥିର୍କ ବିଧ୍ୱଂସ ଆଡ଼କୁ ନେଇଥାଏ । ଦେଶରୁ ବୈଦେଶିକ ମୁଦ୍ରା ଚାଲିଯିବାକୁ ଆରମ୍ଭ କରେ । ଆନ୍ତର୍ଜାତିକ ପୁଞ୍ଜିନିବେଶକାରୀଙ୍କର ସେ ଦେଶରେ ପୁଞ୍ଜିନିବେଶ କରିବାକୁ ଇଚ୍ଛା ପ୍ରକାଶ କରନ୍ତି ନାହିଁ ।

ଦେଶ ତା’ର ଆର୍ଥିକ ସ୍ଥିତି ହରାଇଥାଏ । ଏପରି ଅବସ୍ଥା ଭାରତରେ ୧୯୯୧ ମସିହା ଜୁନ୍ ମାସରେ ଦେଖାଦେଇଥିଲା । ଯାହାଫଳରେ ନୂତନ ଆର୍ଥିକ ସଂସ୍କାର ପ୍ରଣୟନ କରାଗଲା ଏବଂ ଯାହାର ମୂଳ ଲକ୍ଷ୍ୟ ଥିଲା ବଜେଟ୍ ନିଅଣ୍ଟକୁ ହ୍ରାସ କରିବା ।

7. ସମତୁଲ ବଜେଟ୍‌ରେ ସରକାରଙ୍କ ଭୂମିକା କାହିଁକି ସୀମିତ ?
Answer:
ଯେଉଁ ବଜେଟ୍‌ର ଆନୁମାନିକ ଆୟ ଓ ବ୍ୟୟ ସମାନ ତାହା ସମତୁଲ ବଜେଟ୍ । ତେଣୁ ସମତୁଲ ବଜେଟ୍‌ରେ ବ୍ୟୟର ପ୍ରସ୍ତାବନା ଆୟ ଅନୁସାରେ କରାଯାଏ । ସରକାର ନିଜ କାର୍ଯ୍ୟକଳାପ ସୀମିତ ରଖୁବାପାଇଁ ବାଧ୍ୟ ହୁଅନ୍ତି । ଫଳରେ ଘରୋଇ ସଂସ୍ଥାର ଭୂମିକା ବୃଦ୍ଧି ପାଏ । ଅଳଂକାଂଶ ଅର୍ଥନୈତିକ କାର୍ଯ୍ୟକଳାପ ସରକାରୀ କ୍ଷେତ୍ରରୁ ଘରୋଇ କ୍ଷେତ୍ରକୁ ହସ୍ତାନ୍ତରିତ ହୁଏ ।

ସରକାରଙ୍କ ଭୂମିକା ହ୍ରାସ ପାଏ । ଆଧୁନିକ ରାଷ୍ଟ୍ରମାନଙ୍କରେ ସମୟକ୍ରମେ ସରକାରଙ୍କ ଭୂମିକା ସୀମିତ ହେଉଥିବାରୁ ଏହା ସମତୁଲ ବଜେଟ୍ ପାଇଁ ପ୍ରୋତ୍ସାହିତ କରିବ ବୋଲି କୁହାଯାଏ ।

C. ଛଅଟି ବାକ୍ୟ ମଧ୍ୟରେ ସୀମିତ ରଖି ପାର୍ଥକ୍ୟ ଦର୍ଶାଅ ।

1. ବଳକା ବଜେଟ୍ ଓ ନିଅଣ୍ଟିଆ ବଜେଟ୍ :
Answer:
ବଳକା ବଜେଟ୍‌ରେ ସରକାରୀ ଆୟ ସରକାରୀ ବ୍ୟୟଠାରୁ ଅଧିକ ହୋଇଥାଏ । ବଳକା ବଜେଟ୍ କ୍ଷେତ୍ରରେ ସରକାରଙ୍କ ଦେୟ ହ୍ରାସ ହୋଇଥାଏ । ଏହା ମୁଦ୍ରାଣ୍ଡୀତି ରୋକିବାରେ ସାହାଯ୍ୟ କରେ ଏବଂ ସରକାର ଦାୟିତ୍ୱବାନ୍ ହୋଇଥା’ନ୍ତି । ବଳକା ବଜେଟ୍ ବିକାଶଶୀଳ ଦେଶ ପାଇଁ ଉପଯୋଗୀ ନୁହେଁ । ଏହା ଆୟ ଓ ନିୟୋଜନ ବୃଦ୍ଧିରେ ସହାୟକ ହୋଇ ନ ଥାଏ । ନିଆଣ୍ଟିଆ ବଜେଟ୍‌ରେ ସରକାରୀ ବ୍ୟୟ ସରକାରୀ ଆୟଠାରୁ ଅଧିକ ହୋଇଥାଏ ।

ଏହି ବଜେଟ୍‌ରେ ସରକାରଙ୍କର ଦେୟ ବୃଦ୍ଧି ହୋଇଥାଏ । ନିଅଣ୍ଟିଆ ବଜେଟ୍ ମୁଦ୍ରାଷ୍ଟୀତିକୁ ତ୍ବରାନ୍ବିତ କରିଥାଏ, ଫଳରେ ସରକାରଙ୍କ ସଂରକ୍ଷିତ ପାଣ୍ଠି ହ୍ରାସ ପାଇଥାଏ । ଏହି ବଜେଟ୍ କ୍ଷେତ୍ରରେ ସରକାର ଦାୟିତ୍ବହୀନତାର ପରିଚୟ ଦେଇଥା’ନ୍ତି । ଏହି ବଜେଟ୍ ବିକାଶଶୀଳ ଦେଶ ପାଇଁ ବିଶେଷ ଉପଯୋଗୀ କାରଣ ଏହା ଆୟ ଓ ନିୟୋଜନ ବୃଦ୍ଧି କରିଥାଏ ।

2. ସମତୁଲ ଓ ଅସମତୁଲ ବଜେଟ୍ :
Answer:
ସମତୁଲ ବଜେଟ୍‌ରେ ପ୍ରସ୍ତାବିତ ସରକାରୀ ବ୍ୟୟ ଓ ପ୍ରସ୍ତାବିତ ସରକାରୀ ଆୟ ପରସ୍ପର ସମାନ ହୋଇଥା’ନ୍ତି । ଏହା ସରକାରଙ୍କର ଅଣଉତ୍ପାଦୀ ଓ ଅନାବଶ୍ୟକ ଖର୍ଚ୍ଚକୁ କମାଇଥାଏ । ଏହା ବିକାଶଶୀଳ ଦେଶ ପାଇଁ ଉପଯୁକ୍ତ ନୁହେଁ । କାରଣ ଏହା ଗୋଟିଏ ଦେଶକୁ ଅର୍ଦ୍ଧ-ନିୟୋଜନରୁ ପୂର୍ଣ୍ଣ ନିୟୋଜନ ଅବସ୍ଥାକୁ ନେବାରେ ସହାୟକ ହୁଏ ନାହିଁ । ଯୁଦ୍ଧ ଓ ଜରୁରୀକାଳୀନ ପରିସ୍ଥିତି ପାଇଁ ଏହା ଉପଯୁକ୍ତ ନୁହେଁ ।

ଅସମତୁଲ ବଜେଟ୍ କ୍ଷେତ୍ରରେ ପ୍ରସ୍ତାବିତ ସରକାରୀ ବ୍ୟୟ ଓ ପ୍ରସ୍ତାବିତ ସରକାରୀ ଆୟ ସମାନ ହୋଇ ନ ଥା’ନ୍ତି । ଏହା ସରକାରଙ୍କର ଅଣଉତ୍ପାଦୀ ଓ ଅନାବଶ୍ୟକ ଖର୍ଚ୍ଚକୁ ବୃଦ୍ଧି କରିଥାଏ । ଏହା ବିକାଶଶୀଳ ଦେଶ ପାଇଁ ଉପଯୁକ୍ତ ହୋଇଥାଏ କାରଣ ଏହା ଗୋଟିଏ ଦେଶକୁ ପୂର୍ଣ୍ଣ ନିୟୋଜନ ସ୍ତରରେ ପହଞ୍ଚାଇବା ପାଇଁ ଫଳପ୍ରଦ ହୋଇଥାଏ । ଯୁଦ୍ଧ ଓ ଜରୁରୀକାଳୀନ ପରିସ୍ଥିତି ପାଇଁ ଏହା ଉପଯୁକ୍ତ ହୋଇଥାଏ ।

ଦୀର୍ଘ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର

1. ବଜେଟ୍ ହେଉଛି ଆର୍ଥନୀତିକ ପ୍ରଗତିର ଏକ ଅସ୍ତ୍ର – ଆଲୋଚନା କର ।
Answer:
ବିଜେଟ୍ ସରକାରଙ୍କ ଏକ ଗୁରୁତ୍ବପୂର୍ଣ ଅର୍ଥନୈତିକ ଦସ୍ତାବିଜ୍ । ଆଗାମୀ ଆର୍ଥିକ ବର୍ଷ ପାଇଁ ଏହା ସରକାରଙ୍କ ଆୟ-ବ୍ୟୟ ଅଟକଳ । ସରକାର କେଉଁ କେଉଁ ଭତ୍ସରୁ ଆୟ କରିବା ପାଇଁ ଆଶା ରଖୁଛନ୍ତି ଏବଂ କେଉଁ କେଉଁ କ୍ଷେତ୍ରରେ କେତେ ବ୍ୟୟ କରିବାପାଇଁ ପ୍ରସ୍ତାବ ରଖୁଛନ୍ତି ତାହା ବଜେଟ୍ ସୂଚନା ଦିଏ । ପରବର୍ତ୍ତୀ ଆର୍ଥିକ ବର୍ଷ ପାଇଁ ସରକାରଙ୍କ ଆଭିମୁଖ୍ୟ କ’ଣ, ତାହା ଏଥିରୁ ସ୍ପଷ୍ଟ ହୋଇଥାଏ ।

ପ୍ରଫେସର ପ୍ଲାଡ଼ଷ୍ଟୋନ୍ ବଜେଟ୍‌ରେ ସଂଜ୍ଞା ଉପସ୍ଥାପନ କରି କହିଛନ୍ତି, ବଜେଟ୍ ସରକାରଙ୍କ ଆୟ-ବ୍ୟୟର କେବଳ ଏକ ଗାଣିତିକ ହିସାବ ନୁହେଁ, ଏହା ମଧ୍ୟ ଅନେକ ଗୁଣରେ ଜନସାଧାରଣଙ୍କ ଉନ୍ନତି ପାଇଁ ଅଭିପ୍ରେତ ।

ପୂର୍ବରୁ, ସରକାରଙ୍କ ସୀମିତ କାର୍ଯ୍ୟକ୍ରମ ସହ ବଜେଟ୍ ପ୍ରତି ବିଶେଷ ଗୁରୁତ୍ଵ ପ୍ରକାଶ ପାଉ ନ ଥିଲା । ବରଂ ଏହାକୁ ବ୍ୟବସ୍ଥାପିକା ପାଇଁ ଏକ ସାଧାରଣ ସୂଚନା ରୂପେ ବିବେଚନା କରାଯାଉଥିଲା । ମାତ୍ର ଜନମଙ୍ଗଳ ରାଷ୍ଟ୍ରଗୁଡ଼ିକରେ ରାଷ୍ଟ୍ରର ଗରତପର୍ଣ ଭୂମିକାକ ବିଚାର କରି ବଳେଟକ ଆର୍ଥଳ ପଗଡିର ମଧ୍ୟ ଆମ ରପେ ବିବେଚନା କରାଯାଏ ।

ବିକଶିତ ଦେଶମାନଙ୍କରେ ଅର୍ଥବ୍ୟବସ୍ଥା ପୂର୍ଣ୍ଣ ନିୟୋଜନ ଅବସ୍ଥାରେ ଥିବାରୁ ସେଠାରେ ସାଧନମାନ ଅନିୟୋଜିତ ନଥା’ନ୍ତି । କିନ୍ତୁ ସେସବୁ ଅର୍ଥବ୍ୟବସ୍ଥା ବାଣିଜ୍ୟ ତରଙ୍ଗରୁ ମୁକ୍ତ ହୋଇନଥିବାରୁ ମଝିରେ ମଝିରେ ମାନ୍ଦାବସ୍ଥା, ବେକାରୀ ଓ ମୁଦ୍ରାଙ୍ଗୀତି ବା ଅତ୍ୟଧୂକ କ୍ରୟଶକ୍ତିର ଚାପ ବହନ କରିଥା’ନ୍ତି । କିନ୍ତୁ ବିକାଶଶୀଳ ଦେଶମାନଙ୍କର ଅର୍ଥବ୍ୟବସ୍ଥା ପୂର୍ଣ ନିୟୋଜନଠାରୁ କମ୍ ସ୍ତରରେ ଥିବାରୁ ଆର୍ଥନୀତିକ ଅଭିବୃଦ୍ଧି ଲାଭ ସେମାନଙ୍କର ପ୍ରମୁଖ ଲକ୍ଷ୍ୟ ହୋଇଥାଏ ।

ଏହିସବୁ ଦରିଦ୍ର ଦେଶମାନଙ୍କରେ ଅଭିବୃଦ୍ଧି ଲାଭ ସମସ୍ୟା ଗୁରୁତର ହୋଇଥାଏ। ଏହିସବୁ ସମସ୍ୟାଗୁଡ଼ିକ ହେଲା ବଣ୍ଟନଜନିତ ସମସ୍ୟା, ବିତରଣଜନିତ ସମସ୍ୟା ଓ ସ୍ଥିରତା ରକ୍ଷା ସମ୍ବନ୍ଧୀୟ ସମସ୍ୟା । ଏହିସବୁ ଦେଶମାନଙ୍କରେ ଆର୍ଥନୀତିକ ବିକାଶ ହାସଲ ପାଇଁ ବଜେଟ୍‌କୁ ଏକ ପ୍ରଧାନ ଅସ୍ତ୍ର ଭାବରେ ପ୍ରୟୋଗ କରାଯାଇଥାଏ । ନିମ୍ନଲିଖ୍ ଉପାୟମାନଙ୍କ ମାଧ୍ୟମରେ ବଜେଟ୍ ଦେଶମାନଙ୍କର ଅର୍ଥବ୍ୟବସ୍ଥାକୁ ପ୍ରଭାବିତ କରିଥାଏ ।

ପ୍ରଥମତଃ, ସରକାର ତାଙ୍କର ରାଜକୋଷୀୟ କର୍ତ୍ତବ୍ୟ ସମ୍ପାଦନ କରିବାପାଇଁ ପର୍ଯ୍ୟାପ୍ତ ପରିମାଣର ରାଜସ୍ୱ ଆବଶ୍ୟକ କରିଥା’ନ୍ତି । ଆଧୁନିକ ରାଷ୍ଟ୍ରଗୁଡ଼ିକ କଲ୍ୟାଣକାରୀ ହୋଇଥିବାରୁ ଜନମଙ୍ଗଳ ପାଇଁ ଏହାକୁ ବିଭିନ୍ନ ଦିଗରେ ବ୍ୟୟ କରିଥାନ୍ତି । ତେଣୁ ସ୍ଵାଭାବିକଭାବେ, ସରକାରୀ ବ୍ୟୟ ବହୁଗୁଣିତ ହୋଇଥାଏ । ଏଥିପାଇଁ ସରକାର ଯଥେଷ୍ଟ ସମ୍ବଳ ଆବଶ୍ୟକ କରିଥା’ନ୍ତି । ଏକ ବିତ୍ତୀୟ ଯୋଜନା ସାହାଯ୍ୟରେ ବଜେଟ୍ ଏହି ଲକ୍ଷ୍ୟ ପୂରଣ କରିବାରେ ସମର୍ଥ ହୋଇଥାଏ । ସରକାରଙ୍କ କାର୍ଯ୍ୟକଳାପ ପାଇଁ ଆବଶ୍ୟକ ହେଉଥିବା ସମ୍ବଳର ଉତ୍ସମାନ ବିଜେଟ୍‌ରେ ସ୍ପଷ୍ଟଭାବେ ଉଲ୍ଲେଖ ଥାଏ ।

ଦ୍ଵିତୀୟତଃ, ବଜେଟ୍‌ରେ ଉଲ୍ଲେଖ ଥିବା ଆୟ-ବ୍ୟୟ, କୃଷି ଓ ଶିଳ୍ପ କ୍ଷେତ୍ରରେ ଆର୍ଥନୀତିକ କାର୍ଯ୍ୟକଳାପକୁ ବ୍ୟାପକଭାବେ ପ୍ରଭାବିତ କରିଥା’ନ୍ତି । ଟିକସ ରିହାତି ପ୍ରଦାନ କରି ଏବଂ ଉଚିତ ଟିକସ ବସାଇ କୃଷି ଓ ଶିଳ୍ପ କ୍ଷେତ୍ରରେ ଉତ୍ପାଦନ ବୃଦ୍ଧି ପାଇଁ ବଜେଟ୍ ସହାୟକ ହୋଇଥାଏ । ଅଗ୍ରାଧ୍ୟାର ଲାଭ କରିଥିବା ଶିଳ୍ପମାନଙ୍କୁ ଆକର୍ଷିତ କରିବାପାଇଁ ଏହିସବୁ ଶିଳ୍ପକୁ ବଜେଟ୍‌ରେ ଟିକସ ରିହାତି ଦିଆଯାଇପାରେ । ସେହିପରି ମାଗଣା ବା ରିହାତି ଦରରେ କୃଷି ଉପକରଣ, ସାର, ପୋକମରା ଔଷଧ ଇତ୍ୟାଦି ସାଧନମାନ ଯୋଗାଇ ଦେବାପାଇଁ ବଜେଟ୍‌ରେ ବ୍ୟବସ୍ଥା କଲେ କୃଷି ଉତ୍ପାଦନ ବୃଦ୍ଧି ହୋଇଥାଏ ।

ତୃତୀୟତଃ, ମାନବୀୟ ପୁଞ୍ଜି ଗଠନ ହେଉଛି ଦେଶର ଆର୍ଥନୀତିକ ବିକାଶର ଚାବିକାଠି । ଅର୍ଥବିକଶିତ ଦେଶମାନଙ୍କରେ ଶିକ୍ଷା, ସ୍ବାସ୍ଥ୍ୟ ଆଦି କ୍ଷେତ୍ରରେ ମାନବ ସମ୍ବଳ ଯୋଗାଣର ସ୍ତର ଅତ୍ୟନ୍ତ ନିମ୍ନ ମାନର । ନାଗରିକମାନେ ଶିକ୍ଷିତ ଓ ସ୍ୱାସ୍ଥ୍ୟବାନ ନ ହେଲେ କାର୍ଯ୍ୟଦକ୍ଷ ଶ୍ରମିକ ହୋଇପାରନ୍ତି ନାହିଁ ଓ ସେମାନଙ୍କ ଉତ୍ପାଦନଶୀଳତା ବୃଦ୍ଧି ପାଇପାରେ ନାହିଁ । ବଜେଟ୍ ବ୍ୟବସ୍ଥା ମାଧ୍ୟମରେ ଏହି କ୍ଷେତ୍ରରେ ଉନ୍ନତି ଅଣାଯାଇପାରେ ।

ଏହିସବୁ କ୍ଷେତ୍ରରେ ମାନବ ସମ୍ବଳ ବିକାଶ ପାଇଁ ଅଧିକ ପୁଞ୍ଜି ବିନିଯୋଗ ଆବଶ୍ୟକ ହେଉଥିବାରୁ ଏବଂ ଏଥିପାଇଁ ଅଧିକ ସମୟ ଆବଶ୍ୟକ ହେଉଥିବାରୁ ଘରୋଇ କ୍ଷେତ୍ରରୁ ଏଥୁକୁ ଅଧ‌ିକ ପୁଞ୍ଜି ଆସିନଥାଏ । ତେଣୁ କେବଳ ସରକାର ହିଁ ବଜେଟ୍ ବ୍ୟବସ୍ଥା ମାଧ୍ୟମରେ ବୈଷୟିକ ଶିକ୍ଷା ଓ ସ୍ବାସ୍ଥ୍ୟ ଆଦି କ୍ଷେତ୍ରରେ ମାନବସମ୍ବଳ ବିକାଶ ପାଇଁ ପୁଞ୍ଜି ବିନିଯୋଗ କରିଥା’ନ୍ତି ।

ଚତୁର୍ଥତଃ, ଉପଯୁକ୍ତ ଆର୍ଥନୀତିକ ଭିତ୍ତିଭୂମିର ଅଭାବ ହେଉଛି ଏହିସବୁ ଦରିଦ୍ର ଦେଶର ସ୍ୱଳ୍ପବିକାଶର ପ୍ରମୁଖ କାରଣ । ପରିବହନ ଓ ଯୋଗାଯୋଗ, ବିଜୁଳି ଶକ୍ତି ଉତ୍ପାଦନ, ମୌଳିକ ଶିଳ୍ପର ଅଭାବ ଏବଂ ଶ୍ରମିକ ଓ ଉଦ୍ୟୋକ୍ତାମାନଙ୍କର ଉପଯୁକ୍ତ ପ୍ରଶିକ୍ଷଣ ବିନା ଶିଳ୍ପ ବିକାଶ ସମ୍ଭବ ହୋଇପାରେ ନାହିଁ । ସେହିଭଳି ଉପଯୁକ୍ତ ଜଳସେଚନ ସୁବିଧା, ବନ୍ୟା ନିୟନ୍ତ୍ରଣ ଉପାୟ ପର୍ଯ୍ୟାପ୍ତ ପରିମାଣର ରାସାୟନିକ ସାର, କୀଟନାଶକ ଔଷଧ, ଅଧିକ ଅମଳକ୍ଷମ ବିହନର ଯୋଗାଣ, ନୂତନ କୃଷିପଦ୍ଧତି ବିନା କୃଷି ଉତ୍ପାଦନ ଓ ଉତ୍ପାଦିକା ଶକ୍ତିରେ ଉନ୍ନତି ସମ୍ଭବ ହୋଇପାରେ ନାହିଁ ।

କିନ୍ତୁ ଏହସବୁ ସୁବିଧା ସରକାର ହିଁ ଯୋଗାଇ ଦେଇଥାନ୍ତି । ଏହିସବୁ ସୁବିଧା ଯୋଗାଣର ଖର୍ଚ୍ଚ ଅତ୍ୟଧିକ ହୋଇଥିବାରୁ ବ୍ୟବହାରକା ବ୍ୟବହାରକାରୀମାନଙ୍କଠାରୁ ତାହା ଆଦାୟ କରିବା ଅସମ୍ଭବ ଅଟେ । ତେଣୁ ବଜେଟ୍ ବ୍ୟବସ୍ଥା ମାଧ୍ୟମରେ ସରକାର ଏଥିପାଇଁ ସମ୍ବଳ ଯୋଗାଇ ଦେଇଥା’ନ୍ତି । ଅତଏବ ଶିଳ୍ପ ଓ କୃଷି ଉନ୍ନୟନ କ୍ଷେତ୍ରରେ ବଜେଟ୍ ଗୁରୁତ୍ଵପୂର୍ଣ ଭୂମିକା ଗ୍ରହଣ କରେ ।

ପଞ୍ଚମତଃ, ମୁକ୍ତ ବଜାର ବ୍ୟବସ୍ଥାରେ ଯେଉଁସବୁ ଦ୍ରବ୍ୟ ଉତ୍ପାଦନ ହୋଇଥାଏ, ତାହା ବେସରକାରୀ ଉଦ୍ୟୋକ୍ତାମାନଙ୍କୁ ସର୍ବାଧ୍ଵ ଲାଭ ପ୍ରଦାନ କରିଥାଏ । ତେଣୁ ସାଧାରଣ ଭାବରେ ବେସରକାରୀ ନିବେଶ ବିଳାସ ଦ୍ରବ୍ୟ ଉତ୍ପାଦନରେ ହିଁ ନିୟୋଜିତ ହୋଇଥାଏ । ଏହି ପରିପ୍ରେକ୍ଷୀରେ ଉପରୋକ୍ତ କ୍ଷେତ୍ରରେ ନିୟୋଜିତ ସମ୍ବଳକୁ ସର୍ବସାଧାରଣଙ୍କ ଉପଯୋଗରେ ନିୟୋଜିତ ଅତ୍ୟାବଶ୍ୟକୀୟ ଦ୍ରବ୍ୟ ଉତ୍ପାଦନକୁ ପ୍ରବାହିତ କରିବାର ଆବଶ୍ୟକତା ଅନୁଭୂତ ହୋଇଥାଏ ।

ବଜେଟ୍ ମାଧ୍ୟମରେ ସରକାରୀ ହସ୍ତକ୍ଷେପ ବଳରେ ଏହି କାର୍ଯ୍ୟ ସହଜରେ କରାଯାଇପାରେ । ବିଳାସ ଦ୍ରବ୍ୟ ଓ ସାମାଜିକ ଦୃଷ୍ଟିରୁ କ୍ଷତିକାରକ ଦ୍ରବ୍ୟ ଉପରେ ଅଧୂକ ଟିକସ ବସାଇ ଏବଂ ସାଧାରଣ ବ୍ୟବହାର ଉପଯୋଗୀ ହିତକାରକ ଦ୍ରବ୍ୟ ପାଇଁ ଟିକସ ରିହାତିର ବ୍ୟବସ୍ଥା କରି ବଜେଟ୍ ଏହି ଲକ୍ଷ୍ୟ ପୂରଣ କରିପାରେ ।

ଷଷ୍ଠତଃ, ପ୍ରାନ୍ତୀୟ ପରିବ୍ୟୟ ଓ ଦରର ସମାନତା ମଧ୍ୟରେ ସବୁଠାରୁ ଦକ୍ଷ ସମ୍ବଳ ବିନିଯୋଗ କରାଯାଇଥାଏ । ଅବଶ୍ୟ ଏହା କେବଳ ପୂର୍ଣ୍ଣ ପ୍ରତିଯୋଗିତାରେ ସମ୍ଭବ ହୁଏ । ସ୍ଵଳ୍ପ ବିକଶିତ ଦେଶଗୁଡ଼ିକରେ ସମ୍ବଳର ତ୍ରୁଟିପୂର୍ଣ୍ଣ ବିନିଯୋଗ ହୋଇଥାଏ । ବେସରକାରୀ କ୍ଷେତ୍ରର ବଜାରଗୁଡ଼ିକରେ ଏକାଧିକାର, ଏକାସ୍କାରମୂଳକ ପ୍ରତିଯୋଗିତା ଓ ଅଚ୍ଛାଧ୍ୟାର ବଜାର ଥାଏ । ଏଭଳି ଅସମ ବିନିଯୋଗକୁ ବଦଳାଇବାକୁ ହେଲେ ସରକାରୀ କ୍ଷେତ୍ରରେ ଉତ୍ପାଦନ ବ୍ୟବସ୍ଥା କରିବାକୁ ହୁଏ ।

ଏହା କଲେ ହିଁ ହାରାହାରି ଆୟ (ଦର) ଓ ପ୍ରାନ୍ତୀୟ ପରିବ୍ୟୟ ମଧ୍ୟରେ ଥିବା ପାର୍ଥକ୍ୟ ହ୍ରାସ ପାଏ । ଏହି କାରଣରୁ ଅଧ‌ିକ ନିବେଶ ଆବଶ୍ୟକ କରୁଥିବା ଜନକଲ୍ୟାଣକାରୀ ଶିଳ୍ପଗୁଡ଼ିକ କ୍ରମେ ସରକାରୀ କ୍ଷେତ୍ରଭୁକ୍ତ ହେଉଛନ୍ତି ।

ସପ୍ତମ, ସ୍ଵଳ୍ପ ବିକଶିତ ଦେଶଗୁଡ଼ିକରେ ଆଞ୍ଚଳିକ ବୈଷମ୍ୟ ଉତ୍କଟ ହୋଇଥାଏ । ବେସରକାରୀ କ୍ଷେତ୍ର ଲାଭ ମନୋବୃତ୍ତି ଦ୍ଵାରା ପରିଚାଳିତ ହେଉଥିବାରୁ ଏହି କ୍ଷେତ୍ରର ଶିଳ୍ପଗୁଡ଼ିକ ସହରାଞ୍ଚଳ ବା ବିକଶିତ ଅଞ୍ଚଳରେ ଗଢ଼ିଉଠନ୍ତି । ଏହି ବୈଷମ୍ୟ ଦୂରକରିବା ପାଇଁ ସରକାରୀ କ୍ଷେତ୍ରର ଶିଳ୍ପସଂସ୍ଥାଗୁଡ଼ିକୁ ପଛୁଆ ଅଞ୍ଚଳରେ ସ୍ଥାପନ କରାଯାଇଥାଏ ଏବଂ ସରକାରୀ ସହାୟତା, ଭିତ୍ତିଭୂମି ଯୋଗାଣ ଓ ଅନ୍ୟାନ୍ୟ ସରକାରୀ ପ୍ରୋତ୍ସାହନଦ୍ଵାରା କୃଷି ଓ ଗ୍ରାମ୍ୟ ଶିଳ୍ପର ବିକାଶ ମଧ୍ଯ ସମ୍ଭବ ହୋଇପାରିବ ।

ଏହା କଲେ ଗ୍ରାମାଞ୍ଚଳର ଅର୍ଥନୀତି ବିକଶିତ ହୋଇଥାଏ ଏବଂ ଏଥିପାଇଁ ବଜେଟ୍‌ରେ ବ୍ୟବସ୍ଥା କରି ଏହି ଲକ୍ଷ୍ୟ ପୂରଣ କରାଯାଇପାରେ ।

ଅଷ୍ଟମ, ସ୍ଵଳ୍ପବିକଶିତ ଦେଶଗୁଡ଼ିକ ଅଳ୍ପ ଆୟକାରୀ ହୋଇଥିବାରୁ ତା’ର ଜନସାଧାରଣ ଦରିଦ୍ର ହୋଇଥା’ନ୍ତି ଏବଂ ସେଠାରେ ସଞ୍ଚୟ ଓ ନିବେଶ କମ୍ ହୋଇଥାଏ । ତେଣୁ ବଜେଟ୍‌ରେ ବ୍ୟବସ୍ଥା କରି ଜାତୀୟ ଆୟକୁ ବହୁଗୁଣିତ କରାଯାଇପାରେ, ଫଳରେ ଫଳପ୍ରଦ ଚାହିଦା ବୃଦ୍ଧି ପାଏ । ଏହା ଅଧ୍ବକ ନିବେଶ ଓ ନିୟୋଜନ ପାଇଁ ପ୍ରୋତ୍ସାହିତ କରେ । ରାଷ୍ଟ୍ରୀୟ ନିୟୋଜନ ପରିମାଣ ବହୁଗୁଣିତ ହୁଏ । ତେଣୁ, ବେକାର ଶ୍ରମିକମାନଙ୍କୁ ନିଯୁକ୍ତି ପ୍ରଦାନ କରି ପ୍ରାକୃତିକ ସମ୍ବଳର ଇଷ୍ଟତମ ବିନିଯୋଗ କରାଯାଇପାରେ ।

2. ବଜେଟ୍ କ’ଣ ? ବିଭିନ୍ନ ପ୍ରକାର ବଜେଟ୍‌ର ବୈଶିଷ୍ଟ୍ୟ ପ୍ରତିପାଦନ କର ।
Answer:
ବଜେଟ୍ ଶବ୍ଦଟି ଫ୍ରାନ୍ସ ଭାଷାରେ ‘Bougett’ ଶବ୍ଦରୁ ଉଦ୍ଧୃତ ଯାହାର ଅର୍ଥ କ୍ଷୁଦ୍ର ଚମଡ଼ା ବ୍ୟାଗ । ଅର୍ଥଶାସ୍ତ୍ରୀମାନେ ବଜେଟ୍ ସମ୍ପର୍କରେ ବିଭିନ୍ନ ଅର୍ଥନୈତିକ ବିଭିନ୍ନ ସଂଜ୍ଞା ନିରୂପଣ କରିଛନ୍ତି । ଏହା ସରକାରୀ ରାଜସ୍ବ ଓ ବ୍ୟୟର ପ୍ରାଥମିକ ଅନୁମୋଦିତ ଯୋଜନା ସମ୍ପର୍କିତ ନଥୂପତ୍ର । ସଂକ୍ଷେପରେ କହିବାକୁ ଗଲେ ‘ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ବର୍ଷ ପାଇଁ ସରକାରଙ୍କ ଆୟ ଓ ବ୍ୟୟର ରୂପରେଖ’, ବଜେଟ୍‌ରେ ସ୍ଥାନ ପାଇଥାଏ । ସରକାରୀ ଆୟ-ବ୍ୟୟର ଅଟକଳ ବଜେଟ୍‌ର ମୁଖ୍ୟ ଅଂଶ ହୋଇ ରହିଥାଏ ।

ଅନ୍ୟ ଅର୍ଥରେ ପ୍ରକାଶ କଲେ ବଜେଟ୍ ହେଉଛି ସରକାରଙ୍କଦ୍ଵାରା ପ୍ରତ୍ୟାଶିତ ଆୟ ଓ ପ୍ରସ୍ତାବିତ ବ୍ୟୟର ଏକ ଉପସ୍ଥାପନା ଯାହା ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ବର୍ଷ ପାଇଁ ଉଦ୍ଦିଷ୍ଟ ।

• ବଜେଟ୍ ସରକାରଙ୍କ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ବର୍ଷ ପାଇଁ ଆୟବ୍ୟୟର ଅଟକଳ ।
• ଏହା ସରକାରୀ କର୍ତ୍ତୃପକ୍ଷଙ୍କଦ୍ୱାରା ଅନୁମୋଦିତ ।
• ଏହା ଆୟ ସଂଗ୍ରହର ଉତ୍ସ ଓ ପ୍ରକ୍ରିୟା ଏବଂ ବ୍ୟୟ ପରିଚାଳନା ସମ୍ପର୍କରେ ସୂଚନା ଦେଇଥାଏ ।
• ଏହା ଅର୍ଥନୈତିକ ଲକ୍ଷ୍ୟ ହାସଲ ପାଇଁ ଉଦ୍ଦିଷ୍ଟ ।

ବଜେଟ୍‌ର ପ୍ରସ୍ତୁତି ଓ ଉପସ୍ଥାପନା, ଯୋଜନାର ସଫଳ ରୂପାୟନ, ପୁଞ୍ଜି ସଂଗ୍ରହ, ବ୍ୟୟ ପରିଚାଳନା, ଉପାଦାନମାନଙ୍କର ସୁବିନିଯୋଗ ଏବଂ ବିଶେଷଭାବରେ ଅର୍ଥନୈତିକ ବିକାଶ ପାଇଁ ଅପରିହାର୍ଯ୍ୟ ହୋଇଥାଏ ।

ପ୍ରକାରଭେଦ – ସରକାରୀ ବଜେଟ୍‌କୁ ସାଧାରଣତଃ ତିନୋଟି ଶ୍ରେଣୀରେ (ପ୍ରକାରରେ) ବିଭାଗୀକରଣ କରାଯାଇଥାଏ ।

1. ସମତୁଲ ବଜେଟ୍ (Balanced Budget)
2. ନିଅଣ୍ଟିଆ ବଜେଟ୍ (Deficit Budget)
3. ବଳକା ବଜେଟ୍ (Surplus Budget)

ସମତୁଲ ବଜେଟ୍ :
ଯେଉଁ ବଜେଟ୍‌ରେ ସରକାରୀ ଆୟର ପରିମାଣ ଏହାର ବ୍ୟୟ ପରିମାଣ ସହ ସମତୁଲ ହୋଇଥାଏ, ତାହାକୁ ସମତୁଲ ବଜେଟ୍ କୁହାଯାଏ । ସେହି ନିର୍ଦ୍ଦିଷ୍ଟ ବର୍ଷ ପାଇଁ ପ୍ରସ୍ତୁତ ସରକାରୀ ବ୍ୟୟ ଅଟକଳରେ ବିଭିନ୍ନ ସୂତ୍ରରୁ ସଂଗୃହୀତ ହେବାକୁ ଥିବା ପ୍ରତ୍ୟାଶିତ ଆୟ ଓ ବିଭିନ୍ନ ଉଦ୍ଦେଶ୍ୟରେ ହେବାକୁ ଥିବା ପ୍ରସ୍ତାବିତ ବ୍ୟୟ ସମାନ ହୋଇଥାଏ । ସଂକ୍ଷେପରେ ଉପସ୍ଥାପନ କରାଗଲେ ଯେଉଁ ସରକାରୀ ବ୍ୟୟ ଅଟକଳ ସରକାରୀ ପ୍ରତ୍ୟାଶିତ ଆୟ ସହ ସମାନ ତାହାକୁ ସମତୁଲ ବଜେଟ୍ କୁହାଯାଏ ।

ଏହି ବଜେଟ୍‌ରେ କେତେକ ସୁପ୍ରଭାବ ପରିଲକ୍ଷିତ ହୋଇଥାଏ ଯାହା ନିମ୍ନରେ ବର୍ଣ୍ଣନା କରାଗଲା ।

• ସମତୁଲ ବଜେଟ୍, ସରକାରୀ କର୍ତ୍ତୃପକ୍ଷଙ୍କଦ୍ୱାରା ହେଉଥିବା ଅନାବଶ୍ୟକ ଅଦରକାରୀ ବ୍ୟୟକୁ ନିୟନ୍ତ୍ରଣ କରିଥାଏ ।
• ଏହା ଅର୍ଥନୈତିକ ସମସ୍ୟାପାଇଁ ଏକ ସତର୍କ ଘଣ୍ଟି ସଦୃଶ ।
• ମାନ୍ଦାବସ୍ଥା ସମୟରେ ସମତୁଲ ବଜେଟ୍ ବିଶେଷ ସହଯୋଗୀ ହୋଇଥାଏ ।
• ଏହା ମୁଦ୍ରାଙ୍ଗୀତି ଘଟାଇ ନଥାଏ ।

ଏହି ସୁଗୁଣ ସତ୍ତ୍ବେ ଏହାର କେତେକ ସୀମାବଦ୍ଧତା ପରିଲକ୍ଷିତ ହୋଇଥାଏ; ଯଥା –

• ସମତୁଲ ବଜେଟ୍‌ରେ ଆୟବ୍ୟୟ ସମାନ ହୋଇଥିବାରୁ ଏହା ଅର୍ଥନୈତିକ ଦୃଷ୍ଟିକୋଣରୁ ପ୍ରଭାବଶୂନ୍ୟ ହୋଇଥାଏ । ତେଣୁ ଅର୍ଥନୈତିକ ଅଭିବୃଦ୍ଧି ଘଟାଇବା କ୍ଷେତ୍ରରେ ଏହି ବଜେଟ୍ ଅନୁକୂଳ ବା ଲାଭଦାୟକ ନୁହେଁ ।
• ଅର୍ଥନୈତିକ ସଙ୍କଟର ମୁକାବିଲା କରିବା ଦିଗରେ ଏହି ବଜେଟ୍ ଅନୁପଯୁକ୍ତ ହୋଇଥାଏ, କାରଣ ଏହାର ବ୍ୟୟ ବିଶେଷଭାବରେ ସଂକୁଚିତ ।
• ଏହା ସରକାରୀ କର୍ତ୍ତୃପକ୍ଷଙ୍କର ସ୍ବାଧୀନତା କ୍ଷୁଣ୍ଣ କରିଥାଏ ।
• ବାସ୍ତବରେ ଏହି ବଜେଟ୍ ମାନ୍ଦାବସ୍ଥା ଦୂର କରିବା କ୍ଷେତ୍ରରେ ଅନୁପଯୁକ୍ତ ।

ଅନ୍ୟ ପ୍ରକାରଭେଦରେ ବଜେଟ୍ ଅସମତୁଲ ହୋଇଥାଏ, ଯେଉଁଥରେ ସରକାରୀ ଆୟବ୍ୟୟରେ ବୈଷମ୍ୟ ପରିଲକ୍ଷିତ ହୋଇଥାଏ । ଏହି ସରକାରୀ ଆୟବ୍ୟୟର ପାର୍ଥକ୍ୟକୁ ବିଚାର କରି ଅସମତୁଲ ବଜେଟ୍‌କୁ ଦୁଇଟି ଶ୍ରେଣୀରେ ବିଭକ୍ତ କରାଯାଏ; ଯଥା – ନିଅଣ୍ଟିଆ ବଜେଟ୍ ଓ ଉଦ୍‌ବୃତ୍ତ (ବଳକା ବଜେଟ) ।

ନିଅଣ୍ଟିଆ ବଜେଟ୍ (Deficit Budget) :
ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ବର୍ଷ ପାଇଁ ଯଦି ସରକାରଙ୍କର ପ୍ରସ୍ତାବିତ ବ୍ୟୟ ଅଟକଳ ପ୍ରତ୍ୟାଶିତ ଆୟଠାରୁ ଅଧିକ ହୁଏ, ତେବେ ସେ ବଜେଟ୍‌ ନିଅଣ୍ଟିଆ ବଜେଟ୍ କୁହାଯାଏ । ଏହି ଏକ ଅସମତୁଲ ବଜେଟ୍ ଯେଉଁଥିରେ ସରକାରୀ ବ୍ୟୟ ସରକାରୀ ଆୟଠାରୁ ଅତ୍ୟଧିକ ହୋଇଥାଏ ।

ବ୍ୟୟ ଅଧ‌ିକ ହେଲେ ହେଁ ଆଧୁନିକ ଅର୍ଥବ୍ୟବସ୍ଥାରେ ଏହା ଅନେକ ସୁଫଳ ପ୍ରଦାନ କରିଥାଏ; ଯଥା –

• ନିଅଣ୍ଟିଆ ବଜେଟ୍ ଆୟ ସ୍ତର ଓ ନିଯୁକ୍ତି ସ୍ତର ବୃଦ୍ଧି କରିବାରେ ସହାୟକ ହୋଇଥାଏ ।
• ବେକାରୀ ସମସ୍ୟା ଦୂରୀକରଣ କ୍ଷେତ୍ରରେ ଏହା ଏକ ଶକ୍ତିଶାଳୀ ଆୟୁଧ ।
• ଏହା ଅବସ୍କ୍ରୀତି ଦୂର କରିବା ଦିଗରେ ସହାୟକ ହୋଇଥାଏ ।
• ଅର୍ଥନୈତିକ ଅଭିବୃଦ୍ଧି ହାସଲ ଦିଗରେ ଏହି ବଜେଟ୍ ଅନେକାଂଶରେ ସଫଳ ହୋଇଥାଏ ।

ଏତଦ୍‌ଭିନ୍ନ ଏହି ବଜେଟ୍‌ରେ କେତେକ ଦୋଷତ୍ରୁଟି ପରିଲକ୍ଷିତ ହୋଇଥାଏ; ଯଥା –
ନିଅଣ୍ଟିଆ ବଜେଟ୍‌ରେ ବ୍ୟୟର ମାତ୍ରା ଅତ୍ୟଧିକ ହେଲେ ଏହା ମୁଦ୍ରାଙ୍ଗୀତି ଘଟାଇଥାଏ ଯାହା ଅର୍ଥନୈତିକ ଲକ୍ଷ୍ୟ ହାସଲପାଇଁ ନିରୁତ୍ସାହିତ ହୋଇଥାଏ । ଏହି ଅବସ୍ଥାରେ ଆୟ ତାରତମ୍ୟ ବୃଦ୍ଧି ଘଟିବାରେ ଆଶଙ୍କା ରହିଥାଏ ଏବଂ ବଡ଼ଖର୍ଚ୍ଚକୁ ପ୍ରୋତ୍ସାହନ ଦେଇଥାଏ ।

ବଳକା ବଜେଟ୍ (Surplus Budget) :
ଯେଉଁ ବଜେଟ୍‌ରେ ସରକାରୀ ଆୟ, ସରକାରୀ ବ୍ୟୟଠାରୁ ଅଧିକ ହୁଏ, ତାହାକୁ ବଳକା ବଜେଟ୍ (Surplus Budget) କୁହାଯାଏ । ଏ କ୍ଷେତ୍ରରେ ସରକାରୀ ପ୍ରତ୍ୟାଶିତ ଆୟ ପ୍ରସ୍ତାବିତ ବ୍ୟୟଠାରୁ ଅଧିକ ହୋଇଥାଏ, ଫଳରେ ସରକାରୀ ଆୟର ଏକ ଅଂଶ ସରକାରଙ୍କଦ୍ଵାରା ଉପଯୋଗ ନ ହୋଇ ଗଚ୍ଛିତ ହୋଇ ରହିଥାଏ । ତେଣୁ ଏହାକୁ ବଳକା ବଜେଟ୍ କୁହାଯାଏ ।

ଏହି ବଜେଟ୍‌ର ବ୍ୟାବହାରିକ ଗୁରୁତ୍ଵ ବିଶେଷ ଉପଲବ୍‌ଧି କରାଯାଇ ନଥାଏ । ତେଣୁ ଏହି ବଜେଟ୍‌ରେ ପ୍ରୟୋଗାତ୍ମକ ଓ ବ୍ୟାବହାରିକ ଦିଗଟି ଅତିମାତ୍ରାରେ ସୀମିତ । ତଥାପି ଏହି ବଜେଟ୍‌ର କେତେକ ସୁଫଳ ପରିଲକ୍ଷିତ ହୁଏ ।

ବଳକା ବଜେଟ୍ ମୁଦ୍ରାଙ୍ଗୀତିକୁ ଅବଦମିତ କରିବା କ୍ଷେତ୍ରରେ ଏକ ଉପଯୁକ୍ତ ବଜେଟ୍ ଭାବରେ ଗ୍ରହଣ କରାଯାଏ । ଦ୍ଵିତୀୟରେ ଏହା ସରକାରୀ ଖର୍ଚ୍ଚରେ ଅଙ୍କୁଶ ଲଗାଏ ଓ ଅନାବଶ୍ୟକ ବ୍ୟୟକୁ ନିରୁତ୍ସାହିତ ବା ନିୟନ୍ତ୍ରଣ କରିଥାଏ ।

ମାତ୍ର ଏହି ବଜେଟ୍‌ରେ ବ୍ୟୟର ପରିସର ସୀମିତ ହୋଇଥିବାରୁ ଅର୍ଥନୈତିକ ଅଭିବୃଦ୍ଧି ଘଟିପାରେ ନାହିଁ । ସରକାରୀ ଆୟର ଏକ ଅଂଶ (ଯାହା ଖର୍ଚ୍ଚ ହୋଇ ନଥାଏ) ଅଣଉତ୍ପାଦନଶୀଳ ହୋଇ ରହିଥାଏ ।

ବାସ୍ତବ ଦୃଷ୍ଟିକୋଣରୁ ଅନୁନ୍ନତ ଦେଶମାନଙ୍କର ଅର୍ଥନୈତିକ ପ୍ରଗତି ହାରକୁ ତ୍ୱରାନ୍ବିତ କରିବା କ୍ଷେତ୍ରରେ ଏହି ବଜେଟ୍ ଅନୁପଯୁକ୍ତ । ଲକ୍ଷ୍ୟ କରାଯାଏ; କାରଣ ଏହା ଅର୍ଥନୈତିକ ବିକାଶ ଧାରାକୁ ଅବ୍ୟାହତ ଓ ନିରବଚ୍ଛିନ୍ନ ରଞ୍ଝାରେ ସାହାଯ୍ୟ କରେ ।

Odisha State Board BSE Odisha 8th Class Science Solutions Chapter 16 ଆଲୋକ Textbook Exercise Questions and Answers.

BSE Odisha Class 8 Science Solutions Chapter 16 ଆଲୋକ

Question 1.
ମନେକର ତୁମେ ଏକ ଅନ୍ଧାରଘରେ ଅଛ । ସେତେବେଳେ ସେହି ଘରେ ଥ‌ିବା ବସ୍ତୁଗୁଡ଼ିକୁ ତୁମେ ଦେଖିପାରିବ କି ? ଘର ବାହାରେ ଥ‌ିବା ବସ୍ତୁଗୁଡ଼ିକୁ ଦେଖୁରିବ କି ? ଉଭୟ ଉତ୍ତର ପାଇଁ ବିଜ୍ଞାନସମ୍ମତ ଯୁକ୍ତିଯୁକ୍ତ କାରଣ ଲେଖ ।
ଉ-
(i) ଆମେ ଅନ୍ଧାରଘରେ ଥ‌ିବା ସମୟରେ ଯଦି ସେଠାରେ କୌଣସି ଏକ ବସ୍ତୁ ଥାଏ; ତେବେ ତାହାକୁ ଦେଖିହେବ ନାହିଁ । କାରଣ ବସ୍ତୁଟି ଅନ୍ଧାରଘରେ ଥ‌ିବା ସମୟରେ ସେଥ୍ରେ କୌଣସି ଆଲୋକ ପଡ଼ିପାରେ ନାହିଁ କିମ୍ବା ବସ୍ତୁଟିର କୌଣସି ନିଜର ଆଲୋକ ନଥାଏ ବା ଏହା କୌଣସି ଆଲୋକକୁ ବିକିରଣ କରିପାରେ ନାହିଁ । ତେଣୁ ଅନ୍ଧାରଘରେ ଥ‌ିବା କୌଣସି ବସ୍ତୁକୁ ଦେଖୁହେବ ନାହିଁ ।

(ii) ବାହାରେ ଥ‌ିବା ବସ୍ତୁରୁ ଆଲୋକ ଆମ ଚକ୍ଷୁକୁ ଆସିଲେ ହିଁ ବସ୍ତୁଟି ଦେଖୁହୁଏ । ଏହି ଆଲୋକ ବସ୍ତୁର ନିଜର ଆଲୋକ ହୋଇପାରେ କିମ୍ବା ବସ୍ତୁଟିରୁ ପ୍ରତିଫଳିତ ହୋଇ ଆସୁଥ‌ିବା ଆଲୋକ ହୋଇପାରେ ।

Question 2.
ସମ ଓ ଅସମ ପ୍ରତିଫଳନ ମଧ୍ୟରେ ଥ‌ିବା ଦୁଇଟି ପାର୍ଥକ୍ୟ ଲେଖ ।
ଉ-

Question 3.
ଆଲୋକ ରଶ୍ମି ନିମ୍ନରେ ଦିଆଯାଇଥ‌ିବା ବସ୍ତୁଗୁଡ଼ିକରେ ଆପତିତ ହେଲେ ସମ ବା ଅସମ ପ୍ରତିଫଳନ ହେବ କି ନାହିଁ ଲେଖ । ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ରରେ ନିଜର ବିଜ୍ଞାନସମ୍ମତ ଯୁକ୍ତି ଉପସ୍ଥାପନ କର ।
(a) ମସୃଣ କାଠ ଟେବୁଲର ପୃଷ୍ଠ
(b) କାର୍ଡବୋର୍ଡର ପୃଷ୍ଠ
(c) ଚକ୍ ପାଉଡ଼ର
(d) ମାର୍ବଲ ଚଟାଣରେ ପାଣି ଥିଲେ
(e) ଖଣ୍ଡେ କାଗଜ
(f) ଦର୍ପଣ
ଉ-
(a) ମସୃଣ କାଠ ଟେବୁଲର ପୃଷ୍ଠ- ଆଲୋକରଶ୍ମି ମସୃଣ କାଠ ଟେବୁଲର ପୃଷ୍ଠ ଉପରେ ପଡ଼ି ଆପତିତ ହେଲେ ସମ ପ୍ରତିଫଳନ ସୃଷ୍ଟି ହେବ କାରଣ –

• କାଠ ଟେବୁଲର ପୃଷ୍ଠ ମସୃଣ ବା ସମତଳ ହୋଇଥିବାରୁ ଏଥ‌ିରେ ଥିବା ଅଭିଲମ୍ବଗୁଡ଼ିକ ସମାନ୍ତରରେ ଅବସ୍ଥାନ କରିବେ ।
• ଫଳରେ ପ୍ରତିଫଳିତ ରଶ୍ମିଗୁଡ଼ିକ ସମାନ୍ତରରେ ଗତିକରିବେ ଏବଂ ଏଥ‌ିରେ ସମ ପ୍ରତିଫଳନ ସୃଷ୍ଟି ହେବ ।

(b) କାର୍ଡବୋର୍ଡର ପୃଷ୍ଠ- କାର୍ଡବୋର୍ଡ଼ର ପୃଷ୍ଠରେ ଆଲୋକ ରଶ୍ମି ପଡ଼ିଲେ ସମ ପ୍ରତିଫଳନ ସୃଷ୍ଟି ହେବ; କାରଣ

• ଏହାର ପ୍ରତିଫଳନ ପୃଷ୍ଠ ସମତଳ ହୋଇଥିବାରୁ ଆପତନ ପରେ ଉତ୍ପନ୍ନ ଅଭିଲମ୍ବଗୁଡ଼ିକ ସମାନ୍ତର ଭାବରେ ଅବସ୍ଥାନ କରିଥା’ନ୍ତି ।
• ଫଳରେ ପ୍ରତିଫଳନ ରଶ୍ମିଗୁଡ଼ିକ ସମାନ୍ତର ଭାବରେ ଗତି କରିଥାଆନ୍ତି । ତେଣୁ ସମ ପ୍ରତିଫଳନ ସୃଷ୍ଟି ହେବ ।

(c) ଚକ୍ ପାଉଡ଼ର – ଏଥରେ ଆଲୋକ ରଶ୍ମି ପଡ଼ିଲେ ଅସମ ପ୍ରତିଫଳନ ସୃଷ୍ଟି ହେବ; କାରଣ-

• ଚକ୍ ପାଉଡ଼ରର ପୃଷ୍ଠ ଅସମତଳ ହୋଇଥାଏ ।
• ଏଥିରେ ଉତ୍ପନ୍ନ ପ୍ରତିଫଳିତ ରଶ୍ମି ଅସମାନ୍ତର ଭାବରେ ଗତି କରିଥାଏ ।

(d) ମାର୍ବଲ ଚଟାଣରେ ପାଣି ଥିଲେ – ମାର୍ବଲ ଚଟାଣରେ ପାଣି ଥିଲେ ଯଦି କୌଣସି ଆଲୋକ ରଶ୍ମି ଆପତିତ ହୁଏ; ତେବେ ଅସମ ପ୍ରତିଫଳନ ସୃଷ୍ଟି ହେବ । କାରଣ ଏହାର ପୃଷ୍ଠ ଉପରେ ପାଣି ଥିବାରୁ ଏହା ଅସମତଳ ହୋଇଥାଏ ଓ ପ୍ରତିଫଳିତ ରଶ୍ମିଗୁଡ଼ିକ ଅସମାନ୍ତର ଭାବରେ ଗତି କରିଥା’ନ୍ତି ।

(e) ଖଣ୍ଡେ କାଗଜ

• କାଗଜ ଖଣ୍ଡ ଯଦି ପତଳା ହୋଇଥାଏ; ତେବେ ଏହାର ପୃଷ୍ଠ ସମତଳ ହୋଇଥାଏ ଓ ଏଥିରେ ଆଲୋକ ରଶ୍ମି ଆପତିତ ହେଲେ ପ୍ରତିଫଳିତ ହୋଇ ସମ ପ୍ରତିଫଳନ ସୃଷ୍ଟି ହୁଏ ।
• ଯଦି କାଗଜର ପୃଷ୍ଠ ମୋଟା ହୋଇଥାଏ; ତେବେ ଏହାର ପୃଷ୍ଠ ଅସମତଳ ହୋଇଥାଏ । ଏଥିରେ ଉତ୍ପନ୍ନ

(f) ଦର୍ପଣ – ଦର୍ପଣ ପୃଷ୍ଠରେ ଆଲୋକ ରଶ୍ମି ପଡ଼ିଲେ ଆପତିତ ପରେ ସମ ପ୍ରତିଫଳନ ହୋଇଥାଏ । କାରଣ ଦର୍ପଣର ପୃଷ୍ଠ ମସୃଣ ଓ ସମତଳ ହୋଇଥିବାରୁ ଉତ୍ପନ୍ନ ପ୍ରତିଫଳିତ ରଶ୍ମିଗୁଡ଼ିକ ସମାନ୍ତର ଭାବରେ ଗତି କରିଥା’ନ୍ତି । ତେଣୁ ଏହା ସମ ପ୍ରତିଫଳନ ସୃଷ୍ଟି କରିଥାଏ ।

Question 4.
ଆଲୋକ ପ୍ରତିଫଳନର ନିୟମଗୁଡ଼ିକ ଲେଖ ।
ଉ-

• ଆପତନ କୋଣ ଓ ପ୍ରତିଫଳନ କୋଣ ପରସ୍ପର ସହ ସମାନ ।
• ପତିତ ରଶ୍ମି, ଆପତନ ବିନ୍ଦୁରେ ଅଙ୍କିତ ଅଭିଲମ୍ବ ଓ ପ୍ରତିଫଳିତ ରଶ୍ମି ଏକ ସମତଳରେ ଅବସ୍ଥାନ କରନ୍ତି ।

Question 5.
ଗୋଟିଏ ‘ତୁମପାଇଁ କାମ’ ଉଲ୍ଲେଖ କର, ଯେଉଁଥିରେ ଆପତିତ ରଶ୍ମି, ପ୍ରତିଫଳିତ ରଶ୍ମି ଓ ଆପତନ ବିନ୍ଦୁରେ ଅଭିଲୟ ଏକ ସମତଳରେ ଅବସ୍ଥାନ କରୁଥିବାର ଦେଖୁହେବ ।
ଉ-
ପତିତ ରଶ୍ମି, ପ୍ରତିଫଳିତ ରଶ୍ମି ଆପତନ ବିନ୍ଦୁରେ ଅଭିଲମ୍ବ ଏକ ସମତଳରେ ଅବସ୍ଥାନ କରୁଥିବାର ପରୀକ୍ଷଣ-
ଉ-

• ଗୋଟିଏ ଡ୍ରଇଂ ବୋର୍ଡ ନେଇ ଏହା ଉପରେ ଗୋଟିଏ ଧଳା ଡ୍ରଇଂ ସିଟ୍ କ୍ଲିପ୍‌ଦ୍ୱାରା ଚପାଇ ରଖାଯାଉ । ଯେପରି ଡ୍ରଇଂ ସିଟ୍ ଡ୍ରଇଂ ବୋର୍ଡ଼ ବାହାରକୁ ହିବ ।
• ଏହା ଉପରେ ପେନ୍ ସିଲ୍ ଦ୍ଵାରା ଗୋଟିଏ ସରଳରେଖା ‘MN’ ଅଙ୍କନ କରାଯାଉ ।
• ଏହି ସରଳରେଖା MN ଉପରେ ଭୂଲମ୍ବ ଭାବରେ ଗୋଟିଏ ସମତଳ ଦର୍ପଣ ରଖାଯାଉ ।
• ଦୁଇଟି ପିନ୍ କଣ୍ଟା A ଓ B ଦର୍ପଣର ଏକ ପାର୍ଶ୍ଵରେ ପୋତି ରଖ । ଯେପରିକି ଦର୍ପଣ ଭିତରେ ଏହାର ପ୍ରତିଫଳନ ଦେଖାଯିବ ।
• ଦର୍ପଣ ଭିତରେ ଉତ୍ପନ୍ନ କଣ୍ଟାକୁ ସିଧା ଭାବରେ ଲକ୍ଷ୍ୟ କରି ତା’ର ଆଉ ଦୁଇଟି ପିନ୍ କଣ୍ଟା କାଗଜ ଉପରେ ପୋତ ଯେପରିକି ତାହା ଏକ ସରଳରେଖାରେ ଅବସ୍ଥାନ କରିବ ।
• ବର୍ତ୍ତମାନ A ଓ Bକୁ ଦର୍ପଣ ପୃଷ୍ଠସହ ଯୋଗ କର ଏବଂ C ଓ Dକୁ ଯୋଗକଲେ, ତାହା ମଧ୍ୟ ଦର୍ପଣ ପୃଷ୍ଠ ଉପରେ ଗୋଟିଏ ବିନ୍ଦୁ ‘O’ ଉପରେ ରହିବ ।
• ଏଠାରେ AO ଆପତିତ ରଶ୍ମି ଓ OD ପ୍ରତିଫଳିତ ରଶ୍ମି ‘O’ ବିନ୍ଦୁରେ ଅଭିଲମ୍ବ ସହିତ ଏକ ବିନ୍ଦୁରେ ଅବସ୍ଥାନ କରିବ ।

Question 6.
ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(a) ତୁମ ସାଙ୍ଗ ଗୋଟିଏ ସମତଳ ଦର୍ପଣଠାରୁ ଏକ ମିଟର ଦୂରତାରେ ଠିଆହୋଇଥିଲେ ………………. ତାହାର ପ୍ରତିବିମ୍ବ ଦର୍ପଣ ଠାରୁ ମିଟର ଦୂରରେ ସୃଷ୍ଟି ହେବ ।
(b) ତୁମେ କ୍ଷୀଣ ଆଲୋକରେ କୌଣସି ବସ୍ତୁକୁ ଦେଖ‌ିଲେ ତୁମର ମୁକୁରିକାର ଆକାର ………………… ହୁଏ ।
(c) ରାତ୍ରିଚର ପକ୍ଷୀର ଚକ୍ଷୁର ରସ ଅପେକ୍ଷା କୋନ୍ ସଂଖ୍ୟା …………………… ଅଟେ ।

Answers:
(a) ଏକ
(b) ବଡ଼
(c) କମ୍

Question 7.
ନିମ୍ନୋକ୍ତ ପ୍ରଶ୍ନଗୁଡ଼ିକରେ ପ୍ରତ୍ୟେକ ଉକ୍ତିପାଇଁ ଚାରୋଟି ସମ୍ଭାବ୍ୟ ଉତ୍ତର ଦିଆଯାଇଛି । ଠିକ୍ ଉତ୍ତରଟି ବାଛି ଲେଖ ।
ଉ-
(a) ଆପତନ କୋଣର ପରିମାଣ ପ୍ରତିଫଳନ କୋଣର ପରିମାଣ ସହ ସମାନ ।
(i) ସବୁବେଳେ
(ii) ସମୟେ ସମୟେ
(iii) ନିର୍ଦ୍ଦିଷ୍ଟ ସର୍ଭରେ
(iv) ଆଦୌ ନୁହେଁ

(b) ସମତଳ ଦର୍ପଣରେ ସୃଷ୍ଟି ହେଉଥିବା ପ୍ରତିବିମ୍ବଟି ହେଲା
(i) ଦର୍ପଣର ପଛ ପାଖରେ ସୃଷ୍ଟି ହେଉଥ‌ିବା ବଡ଼ ଆଭାସୀ ପ୍ରତିବିମ୍ବ ।
(ii) ଦର୍ପଣର ପଛ ପାଖରେ ସୃଷ୍ଟି ହେଉଥ‌ିବା ବସ୍ତୁପରି ସମାନ ଆକାରର ଆଭାସୀ ପ୍ରତିବିମ୍ବ ।
(iii) ଦର୍ପଣ ପୃଷ୍ଠରେ ଗଠିତ ହେଉଥ‌ିବା ଏକ ବଡ଼ ବାସ୍ତବ ପ୍ରତିବିମ୍ବ ।
(iv) ଦର୍ପଣର ପଛ ପାଖରେ ଗଠିତ ହେଉଥ‌ିବା ବାସ୍ତବ ଓ ସମାନ ଆକାରର ପ୍ରତିବିମ୍ବ ।
ଉ-
(i) ସବୁବେଳେ
(ii) ଦର୍ପଣର ପଛ ପାଖରେ ସୃଷ୍ଟି ହେଉଥ‌ିବା ବସ୍ତୁପରି ସମାନ ଆକାରର ଆଭାସୀ ପ୍ରତିବିମ୍ବ ।

Question 8.
ଗୋଟିଏ ମାନବ ଚକ୍ଷୁର ନାମାଙ୍କିତ ଚିତ୍ର ଅଙ୍କନ କର ।
ଉ-

Question 9.
ତୁମ ସାଙ୍ଗ ତୁମସହ ମିଶି ତୁମ ପାଠ୍ୟପୁସ୍ତକର ‘‘ତୁମପାଇଁ କାମ’? 16.7 କରିବାକୁ ଚାହୁଁଛି, ଶିକ୍ଷକ ତୁମକୁ ଲେଜର ଟର୍ଚ୍ଚ ଏଥ‌ିପାଇଁ ବ୍ୟବହାର ନ କରିବାକୁ କହିଲେ । ଶିକ୍ଷକ କାହିଁକି ଏପରି ଉପଦେଶ ଦେଲେ ? ତାହାର ଲେଖ ।
ଉ-
(i) ଲେଜର ରଶ୍ମି ଚକ୍ଷୁରେ ଥ‌ିବା ମୁକୁରିକାକୁ ନଷ୍ଟ କରିଦିଏ ।
(ii) ଲେଜର ଟର୍ଚ୍ଚରୁ ଶକ୍ତିଶାଳୀ ଆଲୋକ ରଶ୍ମି ବାହାରୁଥ‌ିବାରୁ ଏହାଦ୍ଵାରା ଚକ୍ଷୁରେ ଥ‌ିବା ସ୍ନାୟୁକୋଷ ନଷ୍ଟ ହେବାର ସମ୍ଭାବନା ଥାଏ ।

Question 10.
ତୁମେ ଚକ୍ଷୁର କିପରି ଯତ୍ନ ନେବ ?
ଉ-

• ଚକ୍ଷୁରେ କୌଣସି ଅସୁବିଧା ହେଲେ ସଙ୍ଗେ ସଙ୍ଗେ ଚକ୍ଷୁ ବିଶେଷଜ୍ଞଙ୍କ ନିକଟକୁ ଯାଇ ଚକ୍ଷୁ ପରୀକ୍ଷା କରାଇବା ଆବଶ୍ୟକ । ନିୟମିତ ଚକ୍ଷୁ ପରୀକ୍ଷା କରାଇବା ଉଚିତ ।
• ଚକ୍ଷୁ ବିଶେଷଜ୍ଞ ଚଷମା ପିନ୍ଧିବାକୁ କହିଲେ, ଉପଯୁକ୍ତ ମାପର ଚଷମା ବ୍ୟବହାର କରିବା ଉଚିତ ।
• ଅତି ଉଜ୍ଜଳ କିମ୍ବା ଅତି କ୍ଷୀଣ ଆଲୋକ ଚକ୍ଷୁ ପାଇଁ କ୍ଷତିକାରକ । ଅତି କ୍ଷୀଣ ଆଲୋକ ଚକ୍ଷୁ ଉପରେ ଚାପ ଦିଏ ଏବଂ ମୁଣ୍ଡ ବିନ୍ଧେ । ଅତ୍ୟଧିକ ଆଲୋକ; ଯଥା –
• ସୂର୍ଯ୍ୟଙ୍କୁ କିମ୍ବା କୌଣସି ଶକ୍ତିଶାଳୀ ଆଲୋକ ଉତ୍ସକୁ ଖାଲି ଆସ୍‌ରେ ସିଧାସଳଖ ଦେବା ଉଚିତ ନୁହେଁ ।
• କୌଣସି ଧୂଳିକଣା ଚକ୍ଷୁ ମଧ୍ୟରେ ପ୍ରବେଶକଲେ, ସଙ୍ଗେ ସଙ୍ଗେ ପରିଷ୍କାର ପାଣିରେ ଚକ୍ଷୁକୁ ଧୋଇ ଦେବା ଆବଶ୍ୟକ । ଯଦି ତଦ୍ୱାରା କୌଣସି ଉପଶମ ନ ହୁଏ; ତାହାହେଲେ ଚକ୍ଷୁ ଡାକ୍ତରଙ୍କ ପରାମର୍ଶ ନେବା ଆବଶ୍ୟକ ।
• ସ୍ପଷ୍ଟ ଦର୍ଶନର ନିମ୍ନତମ ଦୂରତାରେ ଚକ୍ଷୁଠାରୁ ବହିଟି ରଖ୍ ପଢ଼ାପଢ଼ି କରିବା ଉଚିତ ।
• ଖାଦ୍ୟରେ ଭିଟାମିନ୍ – A ର ଅଭାବ ହେଲେ ଚକ୍ଷୁରେ ଅନେକ ରୋଗ ଦେଖାଯାଏ । ଅନ୍ଧାରକଣା ସେମାନଙ୍କ ମଧ୍ୟରୁ ଅନ୍ୟତମ । ତେଣୁ ଆମର ପ୍ରତିଦିନ ଖାଦ୍ୟରେ ଭିଟାମିନ୍ – A ଯୁକ୍ତ ଖାଦ୍ୟ ରହିବା ଉଚିତ ।

Question 11.
ପ୍ରତିଫଳିତ ରଶ୍ମି, ଆପତିତ ରଶ୍ମି ସହ ସମକୋଣ କରି ରହିଲେ ତାହାର ଆପତନ କୋଣର ପରିମାଣ କେତେ ?
ଉ-
ପ୍ରତିଫଳିତ ରଶ୍ମି, ଆପତିତ ରଶ୍ମି ସହ ସମକୋଣ କରି ରହିଲେ ତାହାର ଆପତନ କୋଣର ପରିମାଣ । \(\frac{90^{\circ}}{2}=45^{\circ} \) ହେବ

Question 12.
ପରସ୍ପରସହ 30 ସେ.ମି. ଦୂରତାରେ ଦୁଇଟି ସମତଳ ଦର୍ପଣକୁ ସମାନ୍ତରାଳ ଭାବରେ ରଖ । ସେ ଦ୍ବୟ ମଧ୍ୟରେ ଗୋଟିଏ ମହମବତି ଜଳାଅ । ଦର୍ପଣ ଦ୍ଵୟରେ କେତୋଟି ପ୍ରତିବିମ୍ବ ସୃଷ୍ଟି ହେବ ।
ଉ-
ଦୁଇଟି ସମତଳ ଦର୍ପଣକୁ ପରସ୍ପରସହ 30 ସେ.ମି. ଦୂରତାରେ ସମାନ୍ତର ଭାବରେ ରଖ୍ ସେ ଦ୍ଵୟ ମଧ୍ଯରେ ଏକ ମହମବତି ଜଳାଇଲେ ଦର୍ପଣ ମଧ୍ୟରେ ଅସଂଖ୍ୟ ପ୍ରତିବିମ୍ବ ସୃଷ୍ଟି ହେବ; କାରଣ –

• ଉକ୍ତ ଦର୍ପଣ ମଧ୍ଯରେ ଉତ୍ପନ୍ନ କୋଣ ୦° ।
• ଦୁଇଟି ଆନତ ଦର୍ପଣର ପ୍ରତିବିମ୍ବ ସଂଖ୍ୟା =\(\frac{360^{\circ}}{\theta}-1\)
• ଏଠାରେ ୫ = ୦° ହୋଇଥିବାରୁ \(\frac{360^{\circ}}{0^{\circ}}-1=\infty-1=\infty^{\circ}\) ଅର୍ଥାତ୍‌ ଉତ୍ପନ୍ନ ପ୍ରତିବିମ୍ବ ସଂଖ୍ୟା ଅସଂଖ୍ୟ ହେବ ।

ତୁମେ ଜାଣିଛ କି ?

Question 1.
ଚକ୍ଷୁଦାନ ଏକ ମହତ୍ ଦାନ । ଜଣେ ସୁସ୍ଥ ବ୍ୟକ୍ତି ପୁରୁଷ ବା ନାରୀ ହେଲେ ମଧ୍ୟ ଏବଂ ଚଷମା ବ୍ୟବହାର କରୁଥିଲେ ମଧ୍ୟ ଚକ୍ଷୁଦାନ କରି ପାରିବେ ? ମାତ୍ର ସେ ବ୍ୟକ୍ତି ଏଡ୍‌ସ, ହେପାଟାଇଟିସ୍ B ବା C, ଲ୍ୟୁକୋମିଆ, ଟିଟାନସ୍ ଓ କଲେରା ଇତ୍ୟାଦି ରୋଗଗ୍ରସ୍ଥ ହୋଇଥିଲେ ସେ ଚକ୍ଷୁକୁ ଦାନ ଆକାରରେ ନ ନେବା ଉଚିତ ।
ଉ-
ପିଲାମାନେ ନିଜେ କରିବାକୁ ଚେଷ୍ଟା କର ।

Question 2.
ମୃତ୍ୟୁର 4-6 ଘଣ୍ଟା ମଧ୍ୟରେ ଚକ୍ଷୁକୁ ଦାନ କରାଯାଏ । ବ୍ୟକ୍ତି ବଞ୍ଚିବା ସମୟରେ ଯେ କୌଣସି ଚକ୍ଷୁ ବ୍ୟାଙ୍କକୁ ଏ ବିଷୟରେ ସନନ୍ଦ ପତ୍ର କରାଇଥିବା ଆବଶ୍ୟକ । ଆଉ ମଧ୍ୟ ସେ ଏହାକୁ ନିଜ ଉତ୍ତରାଧୀକାରୀଙ୍କ ଅବଗତ କରାଇଥିବା ଆବଶ୍ୟକ । ବ୍ୟକ୍ତି ନିଜ ଘରେ କିମ୍ବା ଡାକ୍ତରଖାନାରେ ମୃତ୍ୟୁବରଣ କରିଥିଲେ ମଧ୍ୟ ଚକ୍ଷୁ ବ୍ୟାଙ୍କର ଲୋକମାନେ ସେଠାକୁ ଯାଇ ଏହାକୁ ସଂଗ୍ରହ କରନ୍ତି ।
ଉ-
ପିଲାମାନେ ନିଜେ କରିବାକୁ ଚେଷ୍ଟା କର ।

Question 3.
ତୁମର କେହି ସାଙ୍ଗସାଥୀଙ୍କୁ ତୁମେ ବ୍ରେଲ କିଟସ୍‌କୁ ଉପହାର ଆକାରରେ ଦେଇପାରିବ । ଗୋଟିଏ ଏହିପରି କିର ମୂଲ୍ୟ ପାଖାପାଖ୍ ଟ. 750.00 । ଏ ବିଷୟରେ ଅଧ୍ଵ ଜାଣିବାକୁ ଚାହିଁଲେ,
Give India, National Association for the Blind ସଂସ୍ଥା ସହ ପତ୍ରାଳାପ କରାଯାଇପାରେ ।
ଉ-
ପିଲାମାନେ ନିଜେ କରିବାକୁ ଚେଷ୍ଟା କର ।

ପରୀକ୍ଷା ଉପଯୋଗୀ ଅତିରିକ୍ତ ପ୍ରଶ୍ନୋତ୍ତର

ବସ୍ତୁନିଷ୍ଠ ପ୍ରଶ୍ନେ। ଭର

1. ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(i) ଯେଉଁ ବସ୍ତୁଗୁଡ଼ିକ ଆଲୋକ ପ୍ରଦାନ କରନ୍ତି, ସେମାନଙ୍କୁ ……………………… ବସ୍ତୁ କୁହାଯାଏ ।
(ii) ଯେଉଁ ବସ୍ତୁଗୁଡ଼ିକ ଆଲୋକ ପ୍ରଦାନ କରନ୍ତି ନାହିଁ, ସେମାନଙ୍କୁ ……………………… ବସ୍ତୁ କୁହାଯାଏ ।
(iii) ଯାହା ମଧ୍ୟଦେଇ ଆଲୋକ ଗତି କରିପାରେ, ତାହାକୁ ……………………… କୁହାଯାଏ ।
(iv) ଯାହା ମଧ୍ୟଦେଇ ଆଲୋକ ଗତି କରିପାରେ ନାହିଁ, ……………………… କୁହାଯାଏ ।
(v) ପ୍ରତିଫଳନ ପୃଷ୍ଠଉପରେ ପତିତ ଆଲୋକ ରଶ୍ମିକୁ ……………………… କୁହାଯାଏ ।
(vi) ପ୍ରତିଫଳନ ପୃଷ୍ଠର ଆପତନ ବିନ୍ଦୁରେ ଟଣାଯାଇଥିବା ……………………… କୁହାଯାଏ ।
(vii) ଆପତନ କୋଣର ପରିମାଣ ……………………… ର ପରିମାଣ ସହ ସମାନ ।
(viii) ଯେଉଁ ପ୍ରତିବିମ୍ବକୁ ପରଦାରେ ଧରି ରଖ୍ ହୁଏ ନାହିଁ, ତାହାକୁ ……………………… ପ୍ରତିବିମ୍ବ କୁହାଯାଏ ।
(ix) ଯେଉଁସବୁ ବସ୍ତୁ ଅନ୍ୟ ବସ୍ତୁର ଆଲୋକରେ ଆଲୋକିତ ହୁଅନ୍ତି, ତାହାକୁ ……………………… ବସ୍ତୁ କୁହାଯାଏ ।
(x) ପ୍ରିଜିମ୍‌ଦ୍ୱାରା ଆଲୋକର ପ୍ରତିସରଣକୁ ……………….. ରହିଥାଏ ।
(xi) ସ୍ୱଚ୍ଛପଟଳର ପଛକୁ ଥିବା ଧୂସର ରଙ୍ଗର ମାଂସଳ ……………………….. କୁହାଯାଏ ।
(xii) ନେତ୍ରସ୍ନାୟୁ ଓ ମୁକୁରିକାର ମିଳନସ୍ଥଳକୁ ……………………….. କୁହାଯାଏ ।
(xiii) ସମୀପ ଦୃଷ୍ଟି ଦୋଷ ସଂଶୋଧନ ପାଇଁ ………………….. ଲେନ୍ସର ଚଷମା ବ୍ୟବହାର କରାଯାଏ ।
(xiv) ବ୍ରେଲ୍ ପଦ୍ଧତିରେ …………………… ଟି ଡଟ୍ ପ୍ୟାଟର୍ଶ ଥାଏ ।
(xv) ……………………. ଯୋଗୁଁ କଲିଡୋସ୍କୋପ୍‌ରରେ ସୁନ୍ଦର ଡିଜାଇନ୍ ସୃଷ୍ଟି ହୁଏ ।
(xvi) ……………….. ଯୁକ୍ତ ଖାଦ୍ୟ ଅଭାବରେ ଅନ୍ଧାରକଣା ରୋଗ ହୁଏ ।

Answers:
(i) ଦୀପ୍ତିମାନ
(ii) ଅଦୀପ୍ତମାନ
(iii) ସ୍ଵଚ୍ଛ
(iv) ଅସ୍ବଚ୍ଛ
(v) ପତିତ ରଶ୍ମି
(vi) ଅଭିଳମ୍ବ
(vii) ପ୍ରତିଫଳନ କୋଣ
(viii) ଆଭାସୀ
(ix) ଆଲୋକିତ
(xiii) ଅବତଳ
(x) ପ୍ରକୀର୍ତ୍ତନ
(xi) କନୀନିକା
(xii) ଅନ୍ଧବିନ୍ଦୁ
(xiv) 63
(xv) ବହୁ ପ୍ରତିଫଳନ
(xvi) ଭଟାପିନ୍ – A

2. ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(i) ବ୍ରେଲ ପଦ୍ଧତିରେ ………………… ଟି ବିନ୍ୟାସ ଥାଏ । (26, 63, 16, 100)
(ii) ସୁସ୍ଥ ଚକ୍ଷୁର ସ୍ପଷ୍ଟ ଦର୍ଶନର ସର୍ବନିମ୍ନ ଦୂରତା ……………….. ସେ .ପି. । (10, 20, 25, 30)
(iii) ଚକ୍ଷୁର ମୁକୁରିକାରେ ବସ୍ତୁର ପ୍ରତିବିମ୍ବର ଧାରଣା ………………….. ସେକେଣ୍ଡ ।
(iv) ପ୍ରତିଫଳିତ ରଶ୍ମି, ଆପତିତ ରଶ୍ମି ସହ ସମକୋଣ କରି ରହିଲେ, ତାହାର ଆପତନ କୋଣର ପରିମାଣ ……………………… ହେବ । (90°, 60°, 45°, 30°)
(v) …………………….. ଭିଟାମିନ୍ ଅଭାବରେ ଅନ୍ଧାରକଣା ରୋଗ ହୁଏ । (A, D, E, K)
(vi) ……………….. ଜୀବର ଚକ୍ଷୁର ମୁକୁରିକାରେ ଅଧ୍ଯକ ସଂଖ୍ୟକ ରଡ଼ସ୍ ଓ ଅଳ୍ପ ସଂଖ୍ୟକ କୋନ୍ସ ଥାଏ । (ଚିଲ, ପେଚା, ଇଗଲ, ମନୁଷ୍ୟ)
(vii) ବ୍ରେଲି ପଦ୍ଧତି ……………………………. ମସିହାରେ ପ୍ରକାଶିତ ହୋଇଥିଲା । (1821, 1819, 1720, 2000)
(viii) କେଉଁ ଜୀବର ସ୍ୱଚ୍ଛପଟଳ ଓ ନେତ୍ରପିତୁଳା ବଡ଼ ? (ଚିଲ, ଇଗଲ୍, ମଣିଷ, ପେଚା)

Answers:
(i) 63,
(ii) 25,
(iii) \(=\frac{10}{1000}\)
(iv) 45°,
(v) A,
(vi) ପେଚା,
(vi) 1821,
(viii) ପେଚା,

3. ବାମ ପାର୍ଶ୍ୱସ୍ଥ ସମ୍ପର୍କକୁ ଅନୁଧ୍ୟାନ କରି ଦକ୍ଷିଣ ପାର୍ଶ୍ୱସ୍ଥ ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର
(i) ଉଜ୍ଜ୍ବଳ ଆଲୋକ : କୋସ : : କ୍ଷୀଣ ଆଲୋକ : …………………… ।
(ii) ପ୍ରତିବିମ୍ବ : ପ୍ରତିଫଳନ : : ବର୍ଣ୍ଣାଳୀ : …………………… ।
(iii) ପ୍ରତିଫଳିତ ରଶ୍ମି ସମାନ୍ତର : ସମ ପ୍ରତିଫଳନ : : ପ୍ରତିଫଳନ ରଶ୍ମି ଅସମାନ୍ତର : …………………… ।
(iv) ନିଜର ଆଲୋକ ଥିଲେ : ଦୀପ୍ତିମାନ ବସ୍ତୁ : : ନିଜର ଆଲୋକ ନଥିଲେ : …………………… ।
(v) ପ୍ରତିଫଳନ ପୂର୍ବରୁ : ଆପତିତ ରଶ୍ମି : : ପ୍ରତିଫଳନ ପରେ : …………………… ।
(vi) ଦୃଷ୍ଟିର ଅବିଚଳତା : \(=\frac{1}{16}\) ସେକେଣ୍ଡ : : ସ୍ପଷ୍ଟ ଦର୍ଶନର ନ୍ୟୁନତମ ଦୂରତା : …………………… ।
(vii) ସୂର୍ଯ୍ୟ : ଦୀପ୍ତିମାନ ବସ୍ତୁ : : ଚନ୍ଦ୍ର : …………………… ।
(viii) ଆପତନ କୋଣ : 68° : : …………………… : 68° ।

Answers:
(i) ରଡ୍‌ସ୍
(ii) ପ୍ରକୀର୍ଣ୍ଣନ
(iii) ଅସମ ପ୍ରତିଫଳନ
(iv) ଅଦୀପ୍ତମାନ ବସ୍ତୁ
(v) ପ୍ରତିଫଳିତ ରଶ୍ମି
(vi) 25 ସେ.ମି.
(vi) ଆଲୋକିତ ବସ୍ତୁ
(viii) ପ୍ରତିଫଳନ କୋଣ

4. ‘କ’ ସ୍ତମ୍ଭରେ ଥ‌ିବା ଶବ୍ଦ ସହିତ ‘ଖ’ ସ୍ତମ୍ଭରେ ଥ‌ିବା ସମ୍ପର୍କିତ ଶବ୍ଦକୁ ମିଳାଅ ।

‘କ’ ସ୍ତମ୍ଭ	‘ଖ’ ସ୍ତମ୍ଭ
(i) କାଲ୍ଲିଡୋସ୍କୋପ	(i) କଙ୍କଡ଼ା
(ii) ଦୃଷ୍ଟିରହିତ ବ୍ୟକ୍ତି	(ii) ପ୍ରଜାପତି
(iii) ସମତଳ ପୃଷ୍ଠ	(iii) ସେଚା
(iv) ଚକ୍ଷୁ ବଡ଼	(iv) ବ୍ରେଲ୍ ପଦ୍ଧତି
(v) ଅସମତଳ ପୃଷ୍ଠ	(v) ଅବତଳ ଲେନ୍ସ
(vi) ଚକ୍ଷୁ ଅତିଛୋଟ	(vi) ବହୁପ୍ରତିଫଳନ
(vii) ଭଲ ଦେଖୂପାରନ୍ତି	(vii) ଉତ୍ତଳ ଲେନ୍ସ
(viii) ରାତିରେ ଦେଖିପାରେ	(viii) ସମ ପ୍ରତିଫଳନ
(ix) ସମୀପଦୃଷ୍ଟି ଦୋଷ ସଂଶୋଧନ	(ix) ଅସମ ପ୍ରତିଫଳନ
(x) ଦୂର ସମୀପଦୃଷ୍ଟି ଦୋଷ ସଂଶୋଧନ	(x)  ଚିଲ ଓ ଇଗଲ

Answer:

‘କ’ ସ୍ତମ୍ଭ	‘ଖ’ ସ୍ତମ୍ଭ
(i) କାଲ୍ଲିଡୋସ୍କୋପ	(vi) ବହୁପ୍ରତିଫଳନ
(ii) ଦୃଷ୍ଟିରହିତ ବ୍ୟକ୍ତି	(iv) ବ୍ରେଲ୍ ପଦ୍ଧତି
(iii) ସମତଳ ପୃଷ୍ଠ	(viii) ସମ ପ୍ରତିଫଳନ
(iv) ଚକ୍ଷୁ ବଡ଼	(ii) ପ୍ରଜାପତି
(v) ଅସମତଳ ପୃଷ୍ଠ	(ix) ଅସମ ପ୍ରତିଫଳନ
(vi) ଚକ୍ଷୁ ଅତିଛୋଟ	(i) କଙ୍କଡ଼ା
(vii) ଭଲ ଦେଖୂପାରନ୍ତି	(x)  ଚିଲ ଓ ଇଗଲ
(viii) ରାତିରେ ଦେଖିପାରେ	(iii) ସେଚା
(ix) ସମୀପଦୃଷ୍ଟି ଦୋଷ ସଂଶୋଧନ	(v) ଅବତଳ ଲେନ୍ସ
(x) ଦୂର ସମୀପଦୃଷ୍ଟି ଦୋଷ ସଂଶୋଧନ	(vii) ଉତ୍ତଳ ଲେନ୍ସ

 

Odisha State Board BSE Odisha 9th Class Odia Solutions Chapter 4 ମଣିଷ ଭାଇ Textbook Exercise Questions and Answers.

BSE Odisha Class 9 Odia Solutions Chapter 4 ମଣିଷ ଭାଇ

ପାଠ୍ୟପୁସ୍ତକସ୍ଥ ପ୍ରଶ୍ନାବଳୀର ଉତ୍ତର
ସଂକ୍ଷିପ୍ତ ଉତ୍ତରମୂ ଳକ ପ୍ରଶ୍ନୋତ୍ତର

Question ୧।
ଚିନ୍ତାବା, ଝୋଲା ମାରିବା, ବୁଝିବା, ଝୁରିବା, ସ୍ମରଣ କରିବା –ଏହି ଶବ୍ଦଗୁଡ଼ିକ ମଧ୍ୟରୁ କେଉଁଟି ଶୋକ କରିବା ଅର୍ଥ ପ୍ରକାଶ କରୁଛି ?
Answer:
ଝୁରିବା ।

Question ୨।
ବନ୍ଧନୀ ମଧ୍ୟରେ ଥ‌ିବା ଶବ୍ଦଗୁଡ଼ିକରୁ ଉପଯୁକ୍ତ ଶବ୍ଦ ବାଛି ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(ନିବିଡ଼, ଲାଞ୍ଛିତ, ନିୟତି, ଟୀକା, ପୀଡ଼ିତ)
(କ) ବ୍ୟକ୍ତି ନିଜର ଭବିଷ୍ୟତକୁ ___________________ ଉପରେ ଛାଡ଼ି ଦିଅନ୍ତି ।
(ଖ) ଗାନ୍ଧାରୀଙ୍କ ଆଶୀର୍ବାଦ ଲାଭ କରି ଦୁର୍ଯ୍ୟୋଧନ ମହାଭାରତ ଯୁଦ୍ଧରେ ବିଜୟର ________________ ହାସଲ କରିବେ ବୋଲି ଆଶାପୋଷଣ କରିଥିଲେ ।
(ଗ) ___________________ ବ୍ୟକ୍ତିଙ୍କ ଉନ୍ନତି ନିମନ୍ତେ ଗାନ୍ଧିଜୀ ସର୍ବଦା ଚେଷ୍ଟିତ ଥିଲେ ।
(ଘ) ପଦ୍ମ ଓ ସୂର୍ଯ୍ୟ ମଧ୍ୟରେ ________________________ ସମ୍ପର୍କ ଅଛି ।
(ଙ) ଉତ୍କଳମଣି ଗୋପବନ୍ଧୁ _________________ ଜନତାଙ୍କ ସେବା ପାଇଁ ନିଜକୁ ଉତ୍ସର୍ଗ କରିଥିଲେ ।
Answer:
(କ) ନିୟତି (ଖ) ଟୀକା (ଗ) ଲାଞ୍ଛିତ (ଘ) ନିବିଡ଼ (ଡ) ପୀଡ଼ିତ

Question ୩।
ନିମ୍ନଲିଖ ଶବ୍ଦଗୁଡ଼ିକର ଗଦ୍ୟରୂପ ଲେଖ ।
ଜନମି, ନୁହଇ, ଅରପି, କରମ, ପରାଣରେ
Answer:
ପଗଦ୍ୟରୂ – ଗଦ୍ୟରୂପ

ଜନମି – ଜନ୍ମି/ଜନ୍ମହୋଇ
ନୁହଇ – ନୁହେଁ
ଅରପି – ଅର୍ପି / ଅର୍ପଣ କରି
କରମ – କର୍ମ
ପରାଣରେ – ପ୍ର।ଣରେ

Question ୪।
ନିମ୍ନଲିଖତ ଶବ୍ଦଗୁଡ଼ିକ ମଧ୍ୟରୁ ଯେଉଁଗୁଡ଼ିକ ମାନବିକ ସୁଗୁଣର ମହତ୍ତ୍ବ ଦର୍ଶାଉଛି, ସେଗୁଡ଼ିକୁ ଚିହ୍ନଟ କର ।
କ୍ରୋଧ, କ୍ଷମା, ଲୋଭ, ସହନଶୀଳତା, ହତାଶ, ସେବା, ନମ୍ରତା, ପରଶ୍ରୀକାତରତା, ଭକ୍ତି, ହିଂସା ।
Answer:
କ୍ଷମା, ସହନଶୀଳତା, ସେବା, ନମ୍ରତା, ଭକ୍ତି ।

Question ୫।
କବିତା ଅନୁସରଣରେ ନିମ୍ନରେ ଦିଆଯାଇଥ‌ିବା ଉକ୍ତିଗୁଡ଼ିକ ମଧ୍ୟରୁ ଠିକ୍ ଉକ୍ତି ବାଛି ଲେଖ ।
(କ) ଦୁଃଖ ଆମର ଭାଗ୍ୟଲିପି ।
(ଖ) ଚାଲ, ଜୀବନକୁ ମଉଜ ମଜଲିସ୍‌ରେ ବିତେଇ ଦେବା ।
(ଗ) ମଣିଷ ତା’ ଭିତରେ ଲୁଚି ରହିଥ‌ିବା ଶତ୍ରୁକୁ ଦମନ କଲେ ଦେବତାର ଆସନ ଲାଭ କରିପାରିବ ।
(ଘ) ଏ ପୃଥ‌ିବୀ ନିରନ୍ତର ଧ୍ୱଂସ ପଥରେ ଆଗେଇ ଚାଲିଛି ।
(ଙ) ବିଧାତାର ବରପୁତ୍ରମାନେ ଦୀନହୀନ ଭାବରେ ଜୀବନ ଯାପନ କରନ୍ତି ।
Answer:
(ଗ) ମଣିଷ ତା’ ଭିତରେ ଲୁଚି ରହିଥ‌ିବା ଶତ୍ରୁକୁ ଦମନ କଲେ ଦେବତାର ଆସନ ଲାଭ କରିପାରିବ ।

Question ୬।
ବିପରୀତାର୍ଥବୋଧକ ଶବ୍ଦ ଲେଖ ।
ଅନ୍ଧାର, ଶୃଙ୍ଖଳିତ, ଅମୃତ, ମୃତ୍ୟୁ, ବିଚାର, ସୁନ୍ଦର, ଶୁଭ ।
Answer:
ପ୍ରଶ୍ନ।ପ୍ରଦତ୍ତ ଶବ୍ଦ – ବିପରୀତାର୍ଥବୋଧକ ଶବ୍ଦ

ଅନ୍ଧାର – ଆଲୋକ / ଆଲୁଅ
ଶୃଙ୍ଖଳିତ – ମୁକ୍ତ / ବିଶୃଙ୍ଖଳିତ
ଅମୃତ – ବିଷ
ମୃତ୍ୟୁ – ଜନ୍ମ
ବିଚାର – ଅବିଚାର
ସୁନ୍ଦର – ଅସୁଦର / କଦାକାର
ଶୁଭ – ଅଶୁଭ

Question ୭ ।
‘କ’ ସ୍ତମ୍ଭର ଶବ୍ଦ ସହିତ ‘ଖ’ ସ୍ତମ୍ଭର ଉପଯୁକ୍ତ ଶବ୍ଦ ଯୋଗକରି ବାକ୍ୟ ଗଢ଼ ।

Answer:

ବାକ୍ୟ:

ନିବିଡ଼ ଅନ୍ଧାର ରାତି ମନରେ ଭୟ ସଞ୍ଚାର କରେ ।
ଏ ବିଶାଳ ଜଗତୀରେ ବହୁ ବିସ୍ମୟକର ଦୃଶ୍ୟ ପ୍ରତୀୟମାନ ହୁଏ ।
ଏ ସଂସାର ମାନବ ପାଇଁ ବିଳାସର ଲୀଳା ନିକେତନ ନୁହେଁ ।
ବିଧାତା-ବିଚାରରେ ପକ୍ଷପାତିତା ନ ଥାଏ ।
ମାନବର ଜୀବନ-ସୂତ୍ର ସର୍ବଦା ପରମେଶ୍ଵରଙ୍କ ହାତରେ ସୁରକ୍ଷିତ ରହିଛି ।

Question ୮।
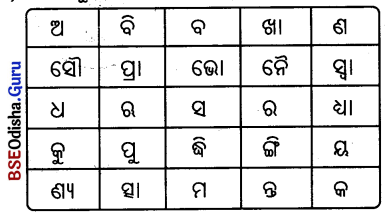
ଅକ୍ଷରଗୁଡ଼ିକ ସଜାଇ ସାର୍ଥକ ଶବ୍ଦରେ ପରିଣତ କର ।
ଶୂଳିଙ୍ଖତ , ତନିକେନ, ବାଶ୍ଵସୀବି, ପନମାଅ, ରଚରାଚ ।
Answer:
ଶୂଳିଙ୍ଖତ – ଶୂଙ୍ଖଳିତ
ତନିକେନ – ନିକେତନ
ବାଶ୍ଵସୀବ – ବାଶ୍ଵବସୀ
ପନମାଅ – ଅପନମା
ରଚରାଚ – ଚରାଚର

Question ୯।
ଅଭିଧାନ ନିୟମ ଅନୁସାରେ ସଜେଇ ଲେଖ ।
ଜୀବନ, ଦେବତା, ଅରିନ୍ଦମ, ଅହମିକା, ନିକେତନ, ସନ୍ତାନ, ଜନମ ।
Answer:
ଅରିନ୍ଦମ, ଅହମିକା, ଜନମ, ଜୀବନ, ଦେବତା, ନିକେତନ, ସନ୍ତାନ ।

Question ୧୦ ।
ନିମ୍ନଲିଖତ ଶବ୍ଦଗୁଡ଼ିକର ଦୁଇଟି ଲେଖାଏଁ ପ୍ରତିଶବ୍ଦ ଲେଖ ।
ମନୁଷ୍ୟ, ବିଧାତା, ଦେବତା, ଶୋଣତ, ନିକେତନ
Answer:
ମନୁଷ୍ୟ – ମାନବ,ନର
ବିଧାତା – ଦୈବ,ବିଧ୍
ଦେବତା – ସୁର,ତ୍ରିଦଶ,ବିବୁଧ
ଶୋଣତ – ରକ୍ତ, ଲହୁ, ରୁଧ୍ର
ନିକେତନ – ଗୃହ,ଘର

Question ୧୧ ।
ଅର୍ଥଗତ ପାର୍ଥକ୍ୟ ଦର୍ଶାଇ ନିମ୍ନୋକ୍ତ ସମୋଚ୍ଚାରିତ ଶବ୍ଦଗୁଡ଼ିକୁ ସାର୍ଥକ ବାକ୍ୟରେ ପରିଣତ କର ।
ଦୀନ-ଦିନ, କାଳି-କାଳୀ, ବଳି-ବଳୀ
Answer:
ଦୀନ – ଦରିଦ୍ର – ଗୋପବନ୍ଧୁ ବାସ୍ତବରେ ଥିଲେ ଦୀନଜନର ବନ୍ଧୁ ।
ଦିନ – ଦିବସ – ଦିନବେଳା ଶୋଇବା ସ୍ୱାସ୍ଥ୍ୟ ପକ୍ଷେ ଅହିତକର ।
କାଳି – ବାକି ସାଧୁ ସାହୁ କାଳିରେ ଜିନିଷ ଦିଏ ନାହିଁ ।
ସ୍ୟାହି-ଶିକ୍ଷକ ନାଲି କାଳିରେ ଖାତା ଦେଖନ୍ତି ।
କାଳୀ – ଦେବୀ ଆଦ୍ୟାଶକ୍ତି – ଦୀପାବଳି ଦିନ ମା’ କାଳୀଙ୍କର ପୂଜା ହୁଏ ।
ପ୍ରାଣୀ ହତ୍ୟା – ପୂର୍ବେ ଦେବୀ ପୀଠରେ ଛାଗ ବଳି ଦିଆଯାଉ ଥିଲା ।
ବଳି –ଦୈତ୍ୟରାଜ – ବାମନ ବଳିରାଜାଙ୍କୁ ତ୍ରିପାଦ ଭୂମି ଦାନ ମାଗିଥିଲେ ।
ବଳୀ – ବଳବାନ୍ – ଭୀମ ମହାବଳୀ ଥିଲେ ।

କ୍ଷୁଦ୍ର ଭତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର

Question ୧୨ ।
ମଣିଷ- ମଣିଷ ମଧ୍ୟରେ ବିଭିନ୍ନ ସମ୍ପର୍କ ଥିବା ସତ୍ତ୍ବେ ‘ଭାଇ’ ସମ୍ବୋଧନ କରାଯାଇଛି କାହିଁକି ?
Answer:
‘ବସୁଧୈବ କୁଟୁମ୍ବକମ୍’ ନ୍ୟାୟରେ ସମଗ୍ର ମାନବଜାତି ଗୋଟିଏ ପରିବାର । ସୁତରାଂ ଜଣେ ଅନ୍ୟ ଜଣଙ୍କର ଭାଇ । ତେଣୁ କବିତାରେ ମଣିଷକୁ ‘ଭାଇ’ ବୋଲି ସମ୍ବୋଧନ କରାଯାଇଛି ।

Question ୧୩ ।
କବି ‘ମଣିଷ ଭାଇ’ ବୋଲି କେଉଁମାନଙ୍କୁ ସମ୍ବୋଧନ କରିଛନ୍ତି ?
Answer:
ସମାଜରେ ଶୋଷିତ, ଲାଞ୍ଛିତ ଓ ନିଷ୍ପେଷିତ ମଣିଷମାନଙ୍କୁ କବି ‘ମଣିଷ ଭାଇ’‘ବୋଲି ସମ୍ବୋଧନ କରିଛନ୍ତି ।

Question ୧୪ ।
ମଣିଷ କେଉଁଥିପାଇଁ ଜନ୍ମଲାଭ କରିନାହିଁ ବୋଲି କବି କହିଛନ୍ତି ?
Answer:
ମଣିଷ ଝୁରି ମରିବାକୁ କିମ୍ବା ବୁଡ଼ି ମରିବାକୁ ଜନ୍ମଲାଭ କରିନାହିଁ ବୋଲି କବି କହିଛନ୍ତି ।

Question ୧୫ ।
ନୈରାଶ୍ୟକୁ ଅନ୍ଧାର ରୂପେ କବି କାହିଁକି ଦେଖୁଛନ୍ତି ?
Answer:
ମଣିଷ ଆଶାଶୂନ୍ୟ ହୋଇଗଲେ, ତାକୁ ଚାରିଆଡ଼ ଅନ୍ଧାର ଦେଖାଯାଏ, ତେଣୁ କବି ନୈରାଶ୍ୟକୁ ଅନ୍ଧାର ରୂପେ ବର୍ଣ୍ଣନା କରିଛନ୍ତି ।

Question ୧୬ ।
ମଣିଷର ଭାଗ୍ୟ କାହା ମଧ୍ୟରେ ସୀମାବଦ୍ଧ ନୁହେଁ ବୋଲି କବି କହିଛନ୍ତି ?
Answer:
ମଣିଷର ଭାଗ୍ୟ ଲାଞ୍ଛନା, ପ୍ରବଞ୍ଚନା ତଥା ଦୁଃଖଯନ୍ତ୍ରଣା ମଧ୍ଯରେ ସୀମାବଦ୍ଧ ନୁହେଁ ।

Question ୧୭ ।
ହତୋତ୍ସାହ ହୋଇପଡ଼ିଥ‌ିବା ମନୁଷ୍ୟ ପୃଥ‌ିବୀକୁ କେଉଁ ଦୃଷ୍ଟିରେ ଦେଖନ୍ତି ?
Answer:
ହତୋତ୍ସାହ ହୋଇପଡ଼ିଥି ମନୁଷ୍ୟ ଏ ପୃଥ‌ିବୀକୁ ‘ଧ୍ଵଂସର ଯାତ୍ରୀ ତଥା ମୃତ୍ୟୁର ଧାତ୍ରୀ’ ରୂପେ ଦେଖନ୍ତି ।

Question ୧୮।
‘ଅମୃତର ସନ୍ତାନ’ ବୋଲି କେଉଁମାନଙ୍କୁ କୁହାଯାଇଛି ?
Answer:
‘ଅମୃତର ସନ୍ତାନ’ ବୋଲି ମାନବମାନଙ୍କୁ କୁହାଯାଇଛି ।

Question ୧୯ ।
ବିଶାଳ ଜଗତର ସୃଷ୍ଟି କ’ଣ ପାଇଁ ନୁହେଁ ବୋଲି କବି କହିଛନ୍ତି ?
Answer:
ବିଶାଳ ଜଗତ କାହାରି ବିଳାସର ଲୀଳାକ୍ଷେତ୍ର ନିମନ୍ତେ ସୃଷ୍ଟି ନୁହେଁ ବୋଲି କବି କହିଛନ୍ତି ।

Question ୨୦ ।
କେଉଁ ଧରଣର ପିପାସା ମେଣ୍ଟେ ନାହିଁ ?
Answer:
ଦୁର୍ବଳକୁ ପଦଦଳିତ କରି ନିର୍ଦ୍ଦୟଭାବରେ ତା’ପ୍ରତି ଅତ୍ୟାଚାର କରି ତା`ର ରକ୍ତକ୍ଷୟ କରିବାର ପିପାସା କେବେହେଲେ ମେଣ୍ଟେ ନାହିଁ ।

Question ୨୧ ।
ବିଶ୍ୱ କେଉଁମାନଙ୍କ ପାଇଁ ସୁନ୍ଦର ନୁହେଁ ?
Answer:
ନୈରାଶ୍ୟଦଗ୍‌ଧ ହୋଇ ସଂସାରକୁ ଧ୍ବଂସାଭିମୁଖୀ ତଥା ଜୀବନକୁ ମୃତ୍ୟୁପଥର ଯାତ୍ରୀ ବୋଲି ବିବେଚନା କରୁଥିବା ମାନବ ପାଇଁ ଏ ବିଶ୍ଵ ସୁନ୍ଦର ନୁହେଁ ।

Question ୨୨ ।
ବିଧାତାଙ୍କ ବିଚାରରେ କେଉଁ କାର୍ଯ୍ୟ ଉଚିତ ନୁହେଁ ?
Answer:
ବିଶ୍ୱକୁ ବିଳାସ କ୍ଷେତ୍ର ମନେକରି ଦୁର୍ବଳକୁ ପଦଦଳିତ କରି ନିଜକୁ ନିଜେ ବିନାଶ କରିବା ବିଧାତାଙ୍କ ବିଚାର ନୁହେଁ ।

Question ୨୩ ।
କବି କିଭଳି ସଂସାରର ପରିକଳ୍ପନା କରିଛନ୍ତି ?
Answer:
କବି ସଂସାରକୁ କର୍ମର ଶୁଭ ଭୁବନ ଭାବେ ପରିକଳ୍ପନା କରିଛନ୍ତି ।

Question ୨୪ ।
ମଣିଷ କେତେବେଳେ ବୀରତ୍ବର ଟୀକା ଲାଭ କରିପାରିବ ?
Answer:
ଲଜ୍ଜା, ଭୟ, ଅପମାନ ଓ ଅହଂକାରକୁ ତ୍ୟାଗକରି ପଶୁତ୍ଵ-ଦେବତ୍ୱ ପରୀକ୍ଷାରେ ବିଜୟୀ ହେବାପରେ ମନୁଷ୍ୟ ବୀରତ୍ବର ଟୀକା ଲାଭ କରିପାରିବ ।

Question ୨୫ ।
କବି ଏହି ପୃଥ‌ିବୀକୁ କାହାର ଭୁବନ ବୋଲି ଦର୍ଶାଇଛନ୍ତି ?
Answer:
କବି ଏହି ପୃଥ‌ିବୀକୁ କର୍ମର ଶୁଭଭୁବନ ବୋଲି ଦର୍ଶାଇଛନ୍ତି ।

Question ୨୬ ।
ମଣିଷର କେଉଁ ପ୍ରବୃତ୍ତିଗୁଡ଼ିକୁ ତ୍ୟାଗ କରିବାପାଇଁ କବି ଆହ୍ବାନ ଦେଇଛନ୍ତି ?
Answer:
କବି ମଣିଷକୁ ଲଜ୍ଜା, ଭୟ, ଅପମାନ ଓ ଅହମିକା ପ୍ରଭୃତି କୁପ୍ରବୃତ୍ତିଗୁଡ଼ିକୁ ତ୍ୟାଗ କରିବାପାଇଁ ଆହ୍ୱାନ ଦେଇଛନ୍ତି ।

Question ୨୭ ।
ଭଗବାନଙ୍କୁ କେତେବେଳେ ଋଣୀ କରାଯାଇପାରିବ ?
Answer:
ବିଶ୍ୱଜୀବନର କଲ୍ୟାଣ ନିମନ୍ତେ ଆୟୋତ୍ସର୍ଗ କରିପାରିଲେ ହିଁ ଭଗବାନଙ୍କୁ ଋଣୀ କରାଯାଇପାରିବ ।

Question ୨୮ ।
ମଣିଷ ଭାଇକୁ କବି ‘ଅରିନ୍ଦମ’ ବୋଲି କାହିଁକି ସମ୍ବୋଧନ କରିଛନ୍ତି ?
Answer:
ମାନବ ହିଁ କାମ, କ୍ରୋଧ, ଲୋଭ, ମୋହ, ମଦ ଓ ମାସ୍କର୍ଯ୍ୟ ପ୍ରଭୃତି ଷଡ଼ରିପୁଙ୍କୁ ଜୟ କରିପାରେ ବୋଲି କବି ତାକୁ ‘ଅରିନ୍ଦମ’ ବୋଲି କହିଛନ୍ତି ।

Question ୨୯ ।
ମଣିଷ କେତେବେଳେ ଦେବତା ରୂପେ ପୂଜିତ ହୋଇପାରିବ ?
Answer:
ମାନବ ଯେତେବେଳେ କାମ-କ୍ରୋଧାଦି ଷଡ଼ରିପୁକୁ ଜୟକରି ବିଶ୍ୱଜୀବନର କଲ୍ୟାଣ ନିମନ୍ତେ ଆୟୋତ୍ସର୍ଗ କରିବାକୁ ସମର୍ଥ ହେବ, ସେତେବେଳେ ସେ ଦେବତାରୂପେ ପୂଜିତ ହୋଇପାରିବ ।

Question ୩୦ ।
ମଣିଷ ଦୀନ-ହୀନ ଭାବରେ କେତେବେଳେ ଜୀବନ ଯାପନ କରିଥାଏ ?
Answer:
ମାନବ ଯେତେବେଳେ ମାନବିକତାକୁ ଭୁଲି ପଶୁତ୍ୱର ଅଧିକାରୀ ହୋଇଯାଏ, ସେତେବେଳେ ସେ ଯାବତୀୟ ହିଂସାତ୍ମକ କାର୍ଯ୍ୟକରି ଆପଣାକୁ କଳୁଷ କାଳିମାରେ କଳଙ୍କିତ କରିବା ସହ ସଂସାରରେ ଦୀନହୀନ ଭାବରେ କାଳଯାପନ କରେ ।

Question ୩୧ ।
କବି ‘ବରପୁତ୍ର’ ସମ୍ବୋଧନ କାହାକୁ ଏବଂ କାହିଁକି କରିଛନ୍ତି ?
Answer:
କବି ମାନବକୁ ବିଧାତାର ବରପୁତ୍ର ବୋଲି ସମ୍ବୋଧନ କରିଛନ୍ତି, କାରଣ ମାନବ ହିଁ ଦିବ୍ୟ ମାନବୀୟ ଗୁଣାବଳୀରେ ଭୂଷିତ ହୋଇ ଦେବତ୍ୱର ଅଧିକାରୀ ହୋଇପାରେ ।

Question ୩୨ ।
ଜୀବନ କେତେବେଳେ ସୁରୁଖୁରୁରେ ଅତିବାହିତ ହୋଇପାରିବ ବୋଲି କବି କହିଛନ୍ତି ?
Answer:
ମୃତ୍ୟୁ ରଜ୍ଜୁକୁ ଛିନ୍ନ କରି ଜୀବନ ସୂତ୍ରକୁ ଧରି ସ୍ବକର୍ତ୍ତବ୍ୟ ପଥରେ ଗତିକଲେ ଜୀବନ ସୁରୁଖୁରୁରେ ଅତିବାହିତ ହୋଇପାରିବ ବୋଲି କବି କହିଛନ୍ତି ।

ସପ୍ରସଙ୍ଗ ସରଳାର୍ଥ ଲେଖ

Question ୩୩ ।
ଶୁଣ ହେ ମଣିଷ ଭାଇ !
ଅମୃତ ଦୀପ୍ତି ସନ୍ତାନ ତୁମେ ମରଣ ତୁମର କାହିଁ ?
Answer:
ଶୁଣ ହେ …………………………. ତୁମର କାହିଁ ?
ଶଂସିତ ପଦ୍ୟାଶଟି ଉତ୍କଳ ଭାରତୀ କୁନ୍ତଳା କୁମାରୀ ସାବତଙ୍କ ରଚିତ ‘ସ୍ଫୁଲିଙ୍ଗ’ କବିତା ପୁସ୍ତକରୁ ସଂଗୃହୀତ ‘ମଣିଷ ଭାଇ’ ଶୀର୍ଷକ କବିତାରୁ ଉଦ୍ଧୃତ ।
ଜାଗରଣଧର୍ମୀ ଆହ୍ବାନ ଦେଇଛନ୍ତି ।
ବିଦେଶୀ ଶାସକବର୍ଗର ଅର୍ଥନୈତିକ ଶୋଷଣ, ନିପୀଡ଼ନ,ଦେଶବାସୀଙ୍କ ଉତ୍କଟ ଦାରିଦ୍ର୍ୟ, ଜମିଦାର ତଥା ବିଦେଶୀ
ଏଠାରେ କବୟିତ୍ରୀ ପରାଧୀନ ଓଡ଼ିଆ ଜାତିର ନୈରାଶ୍ୟଦଗ୍ଧ ପ୍ରାଣରେ ଆଶା ଓ ଆତ୍ମବିଶ୍ଵାସ ଭରିଦେବାପାଇଁ ଜାଗରଣଧର୍ମୀ ଆହ୍ବାନ ଦେଇଛନ୍ତି ।

ଶାସକଙ୍କ ପଦଲେହନକାରୀ ବିଶ୍ୱାସଘାତକଙ୍କ କୂଟ ଚକ୍ରାନ୍ତର ଶିକାର ହୋଇ ଓଡ଼ିଶାର ଜନଜୀବନ ବ୍ୟତିବ୍ୟସ୍ତ ହୋଇପଡ଼ିଥିଲା । ଦୁଃଖ, ଯନ୍ତ୍ରଣା ଓ ଅନୁଶୋଚନାର ତୀବ୍ର ମାନସିକ ଜ୍ଵଳନ ମଧ୍ୟରେ ମଣିଷ ଭାଗ୍ୟକୁ ଧକ୍‌କାର କରି ଏଥୁରୁ ନିସ୍ତାର ପାଇବାପାଇଁ ମୃତ୍ୟୁକୁ ଶ୍ରେୟସ୍କର ବୋଲି ବିଚାର କରୁଥିଲା । ଦୁର୍ଦ୍ଦଶାଗ୍ରସ୍ତ ଜନତାଙ୍କ ପାଇଁ କବୟିତ୍ରୀଙ୍କ ମନର କୋମଳ କାରୁଣ୍ୟ କବିତାରେ ରୂପାୟିତ ହୋଇଛି । ତେଣୁ କବୟିତ୍ରୀ ମଣିଷର ଦୁଃଖରେ ବ୍ୟଥ୍‌ତ ହୋଇ ତା’ ମନରେ ଆଶାର ଅସରନ୍ତି ବିଶ୍ୱାସ ଭରିଦେବାକୁ ଯାଇ କହିଛନ୍ତି ଯେ ମଣିଷ ଈଶ୍ବରଙ୍କ ସୃଷ୍ଟିରେ ଅମୃତର ସନ୍ତାନ ।

ତେଣୁ ଭାଗ୍ୟକୁ ନିନ୍ଦାକରି ନିଜକୁ ମୃତ୍ୟୁପଥର ଯାତ୍ରୀ ବୋଲି ଚିନ୍ତା କରିବା ଆଦୌ ସମୀଚୀନ ନୁହେଁ । ସୁଖ-ଦୁଃଖ, ହସ-କାନ୍ଦ ମାନବ ଜୀବନର ଚିର ସହଚର । ଦୁଃଖ, ନିର୍ଯାତନା, ଦାରିଦ୍ର୍ୟ ଓ କଷଣରୁ ମୁକ୍ତି ପାଇବାପାଇଁ ମୃତ୍ୟୁକୁ ଶେଷ ପନ୍ଥା ବୋଲି ବିବେଚନା କରି କର୍ମବିମୁଖ ହେବା ଏବଂ ଏ ସଂସାରକୁ ଧ୍ବଂସପଥ ଅଭିମୁଖୀ ବୋଲି ବିବେଚନା କରିବା ଅବିବେକିତାର ପରିଚୟ । ମଙ୍ଗଳମୟ ପରମେଶ୍ୱରଙ୍କ ଦିବ୍ୟସୃଷ୍ଟିରେ ନିଜକୁ ଅମୃତର ସନ୍ତାନ ମନେକରି ସମସ୍ତ କର୍ମକୁ ଈଶ୍ବରୀୟ ବୋଲି ଗ୍ରହଣ କରିବାକୁ କବୟିତ୍ରୀ ଉପଦେଶ ଦେଇଛନ୍ତି ।

Question ୩୪ ।
ଏ ନୁହେଁ ବିଧାତା ବିଚାର,
ଧ୍ଵଂସର ଯାତ୍ରୀ, ମୃତ୍ୟୁର ଧାତ୍ରୀ ନୁହେଁ ଏ ସୁନ୍ଦର ସଂସାର ।
Answer:
ଏ ନୁହେଁ ………………….. ସୁନ୍ଦର ସଂସାର ।
ପ୍ରଦତ୍ତ” ପଦ୍ୟାଶଟି ପ୍ରଖ୍ୟାତ ନାରୀକବି କୁନ୍ତଳା କୁମାରୀ ସାବତଙ୍କ କବିତା ପୁସ୍ତକ ‘ସ୍କୁଲିଙ୍ଗ’ରୁ ସଂଗୃହୀତ ‘ମଣିଷ ଭାଇ’ ଶୀର୍ଷକ କବିତାରୁ ଆନୀତ ।

ଏଠାରେ କବୟିତ୍ରୀ ପରମେଶ୍ଵରଙ୍କ ଅମୃତମୟ ସୃଷ୍ଟିରେ ନିୟତିର ବିଚିତ୍ର ବିଧାନ ଉପରେ ଆଲୋକପାତ କରିଛନ୍ତି । ପ୍ରାକ୍ ସ୍ବାଧୀନତା କାଳରେ ବିଦେଶୀ ଶାସକଙ୍କ ରାଜନୈତିକ ସ୍ୱେଚ୍ଛାଚାରିତା, କ୍ଷମତାଧିକାରୀଙ୍କ ଶୋଷଣ ଓ ଅତ୍ୟାଚାରରେ ଅତିଷ୍ଠ ହୋଇପଡ଼ିଥିଲା ତତ୍‌କାଳୀନ ଜନଜୀବନ । ବିପର୍ଯ୍ୟସ୍ତ ହୋଇପଡ଼ିଥିଲା ଓଡ଼ିଶାର ସାମାଜିକ ଜୀବନ । ଏତଦ୍‌ଭିନ୍ନ ବନ୍ୟା ଓ ମରୁଡ଼ିର କରାଳ ଗ୍ରାସରେ ଓଡ଼ିଶାର ଜନସାଧାରଣଙ୍କ ଜୀବନ-ଜୀବିକା ବିପର୍ଯ୍ୟସ୍ତ ହୋଇପଡ଼ିଥିଲା ।

ଦୁଃଖ, ଯନ୍ତ୍ରଣା ଓ ଦାରିଦ୍ର୍ୟର କଷାଘାତରେ ଅତିଷ୍ଠ ହୋଇପଡ଼ିଥିଲା ଜନଜୀବନ । ଶୋଷଣ, କଷଣ, ଅତ୍ୟାଚାର ଓ ନିର୍ଯାତନା ଅସହ୍ୟ ହୋଇପଡ଼ିଥିଲା । ମଣିଷ ଏସବୁକୁ ଭାଗ୍ୟର ବିଡ଼ମ୍ବନା ବୋଲି ଧରିନେଇ ମୃତ୍ୟୁକୁ ଶ୍ରେୟସ୍କର ମଣିଥିଲା । କବୟିତ୍ରୀ କୁନ୍ତଳା କୁମାରୀ ମଣିଷର ଏତାଦୃଶ ଦୁରବସ୍ଥା ଦର୍ଶନରେ ମ୍ରିୟମାଣ ହୋଇପଡ଼ିଛନ୍ତି । ନିଜକୁ ଅସହାୟ ବୋଧ କରୁଥିବା ଚିର ନିଷ୍ପେଷିତ, ଲାଞ୍ଚ, ବଞ୍ଚତ ମାନବ ଜାତିର ଏ ଦୁର୍ଦ୍ଦିନରେ ସମ୍ବେଦନଶୀଳ ହୋଇ ତା’ର ନୈରାଶ୍ୟଦଗ୍ଧ ପ୍ରାଣରେ ଆଶା, ଆଶ୍ୱାସନା ସଞ୍ଚାର କରିବାକୁ ଯାଇ କବି କହିଛନ୍ତି ଯେ ବିଧାତାର ବିଚାର ସର୍ବଦା ନ୍ୟାୟୋଚିତ ଓ ମଙ୍ଗଳକାରକ । ଈଶ୍ୱରଙ୍କ ମହନୀୟ ସୃଷ୍ଟିରେ ମଣିଷ ହେଉଛି ଅମୃତର ସନ୍ତାନ ।

ପରମେଶ୍ବର ମଣିଷକୁ କର୍ମତତ୍ପୁର ରହି କର୍ତ୍ତବ୍ୟ ସମ୍ପାଦନରେ ବ୍ରତୀ ହେବା ନିମନ୍ତେ ଏ ସଂସାରକୁ ପଠାଇଛନ୍ତି । ସୁଖ-ଦୁଃଖ ଓ ହସ-କାନ୍ଦର ଚିର ପରିବର୍ତ୍ତନଶୀଳ ଦୁନିଆରେ ଦୁଃଖ, ଯନ୍ତ୍ରଣା, ଦାରିଦ୍ର୍ୟ, ଲଜ୍ଜା ଓ ଅପମାନରେ ମଣିଷ ଯେ ଚିରକାଳ ଦଗ୍ଧଭୂତ ହେଉଥ‌ିବ– ଏହା ନିୟତିର ବିଧାନ ନୁହେଁ । ଶୋଷଣ, କଷଣ, ଅଭାବ, ଅନଟନ ଯେତେ ଯନ୍ତ୍ରଣାଦାୟକ ହେଲେ ମଧ୍ୟ ତା’ର ଗତି ମୃତ୍ୟୁ ନୁହେଁ କି ଏ ସଂସାର କଦାପି ଧ୍ୱଂସାଭିମୁଖୀ ନୁହେଁ । ସମୟର ଚକ୍ର ଚିର ଘୂର୍ଣ୍ଣନଶୀଳ । ଦୁଃଖ ପରେ ସୁଖର ସମୟ ଅବଶ୍ୟ ଉପଗତ ହେବ । ଏଣୁ ମନରୁ ନୈରାଶ୍ୟ ଓ ହୀନମନ୍ୟତା ପରିହାର କରି କର୍ମରେ ନିଜକୁ ନିୟୋଜିତ କରିବାକୁ କବୟିତ୍ରୀ ଆହ୍ବାନ ଦେଇଛନ୍ତି ।

Question ୩୫ ।
ଶୁଣ ଶୁଣ ବିଶ୍ବବାସି !
କରମର ଶୁଭ ଭୁବନ ଏହିଟି, କରମରେ ଶ୍ରମ ନାଶି ।
Answer:
ଶୁଣ ଶୁଣ……………………….ଶ୍ରମ ନାଶି ।
ଶଂସିତ ପଦ୍ୟାଶଟି ନାରୀକବି କୁନ୍ତଳା କୁମାରୀ ସାବତଙ୍କ ରଚିତ ‘ସ୍ଫୁଲିଙ୍ଗ’ କବିତା ପୁସ୍ତକରୁ ସଂଗୃହୀତ ‘ମଣିଷ ଭାଇ’ ଶୀର୍ଷକ କବିତାରୁ ଉଦ୍ଧୃତ ।
ଏଠାରେ କବୟିତ୍ରୀ କର୍ମର ଜୟଗାନ କରି କର୍ମକୁ ଜୀବନର ମାନଦଣ୍ଡ ଭାବେ ଗ୍ରହଣ କରିବାକୁ ମନୁଷ୍ୟକୁ ଆହ୍ଵାନ ଦେଇଛନ୍ତି । ପରାଧୀନ ଦେଶବାସୀ ବିଦେଶୀ ଶାସକଙ୍କ ଶୋଷଣ, କଷଣ ଓ ଅତ୍ୟଚାରରେ ଅତିଷ୍ଠ ହୋଇ ଭାଗ୍ୟକୁ ଧିକ୍‌କାର କରିବା ପୂର୍ବକ ମୃତ୍ୟୁକୁ ଶ୍ରେୟସ୍କର ବୋଲି ବିବେଚନା କରୁଥିଲେ । କବୟିତ୍ରୀ କୁନ୍ତଳା କୁମାରୀ ମଣିଷର ନୈରାଶ୍ୟଦଗ୍ଧ ପ୍ରାଣରେ ଆଶା ଓ ଆତ୍ମବିଶ୍ଵାସ ସୃଷ୍ଟି କରିବାପାଇଁ ତାକୁ ଭାଗ୍ୟବାଦୀ ନ ହୋଇ କର୍ମରେ ନିୟୋଜିତ ହେବାକୁ ପରାମର୍ଶ ଦେଇଛନ୍ତି ।

ଈଶ୍ବର ମଣିଷକୁ କର୍ମ କରିବାପାଇଁ ଏ ଧରାଧାମରେ ଜନ୍ମ ଦେଇଛନ୍ତି । ଫଳ ବାଞ୍ଛା ନ କରି ସର୍ବଦା କର୍ମରତ ରହିଲେ ମନ ମଧ୍ୟକୁ କୁଭାବନା ପ୍ରବେଶ କରିପାରେ ନାହିଁ । ନିରାଶା, ଦୁଃଖ ଓ ଯନ୍ତ୍ରଣାରୁ ମୁକ୍ତି ପାଇବାର ଏକମାତ୍ର ପଥ ହେଉଛି କର୍ମତତ୍ପରତା । ଏ ସଂସାର ହେଉଛି ମାନବର କର୍ମଭୂମି । ତେଣୁ ନିଜକୁ ମଣିଷ କର୍ମରେ ଜଡ଼ିତ କରି ପରମେଶ୍ଵରଙ୍କ ଅମୃତମୟ ସୃଷ୍ଟିକୁ ମହନୀୟ କରିବାକୁ କବୟିତ୍ରୀ ପରାମର୍ଶ ଦେଇଛନ୍ତି । ବାସ୍ତବିକତା ଦୃଷ୍ଟିରୁ କର୍ମଠ ଜୀବନ ମାନସିକ ସନ୍ତୁଳନ ସୁରକ୍ଷା ଓ କାୟିକ ସୁସ୍ଥତା ରକ୍ଷାରେ ସହାୟକ ହୁଏ । ତେଣୁ ଜୀବନର ସବୁ ମାନ-ଅପମାନ, ଲଜ୍ଜା-ଭୟ, ଅଶ୍ରୁ-ଅଭିଳାଷ, ଦୁଃଖ-ଅବସୋସକୁ ବିଭୁ ପଦାରବିନ୍ଦରେ ସମର୍ପଣପୂର୍ବକ କର୍ମରେ ବିନିଯୁକ୍ତ ହେବାକୁ ମଣିଷ ଭାଇକୁ ନାରୀକବି ଆହ୍ୱାନ କରିଛନ୍ତି ।

Question ୩୬ ।
ବିଧାତାର ବରପୁତ୍ର
ଯୁଗାନ୍ତ-ମୃତ୍ୟୁ ରଜ୍ଜୁ ଛିଣ୍ଡାଇ ଧର ହେ ଜୀବନ ସୂତ୍ର ।
Answer:
ବିଧାତାର …………………..ଜୀବନ ସୂତ୍ର ।
ପ୍ରୋକ୍ତ ପଦ୍ୟାଶଟି ଉତ୍କଳ ଭାରତୀ କୁନ୍ତଳା କୁମାରୀ ସାବତଙ୍କ ରଚିତ ‘ସ୍ଫୁଲିଙ୍ଗ’ କବିତା ପୁସ୍ତକ ଅନ୍ତର୍ଗତ ‘ମଣିଷ ଭାଇ’ ଶୀର୍ଷକ କବିତାରୁ ଉଦ୍ଧୃତ ।
ଏଠାରେ କବୟିତ୍ରୀ ଦୁଃଖ, ଯନ୍ତ୍ରଣା, ଦାରିଦ୍ର୍ୟ ଓ ଅପମାନରେ ବ୍ୟଥୂତ ମୃତ୍ୟୁକାମୀ ମଣିଷ ଭାଇକୁ ତା’ର ମହାର୍ଘ ଜୀବନର ମହତ୍ତ୍ବ ରକ୍ଷାରେ ପ୍ରୟାସୀ ହେବାକୁ ଆହ୍ଵାନ କରିଛନ୍ତି । ଅନନ୍ତ ମରଣ ଯେ ମଣିଷର କପାଳ ଲିଖନ ନୁହେଁ, ଜୀବନର ଶେଷ ଗତି ନୁହେଁ କବୟିତ୍ରୀ ଏହି ଭାବନା ମଣିଷ ମନରେ ଭରିଦେବାକୁ ତାଙ୍କ କବିତା ମାଧ୍ୟମରେ ଆହ୍ଵାନ କରିଛନ୍ତି । ମନର ସମସ୍ତ ନୈରାଶ୍ୟ ଓ ହତାଶବୋଧ ଦୂର କରିବାପାଇଁ କର୍ମରେ ନିମଜ୍ଜିତ ରହିବା ହିଁ ଶ୍ରେଷ୍ଠ ବିକଳ୍ପ । କବୟିତ୍ରୀଙ୍କ ମତରେ ମାନବ ହେଉଛି ବିଧାତାଙ୍କ ଶ୍ରେଷ୍ଠ ବରପୁତ୍ର ।

ଜୀବନ ଯୁଦ୍ଧରେ କ୍ଷତାକ୍ତ ହୋଇଗଲେ ମୃତ୍ୟୁକୁ ଶେଷ ଗତି ବୋଲି ଭାବି ନୀରବରେ ଅଶୁ ବିସର୍ଜନ କରିବା ବୀରତ୍ୱର ପରିଚାୟକ ନୁହେଁ । ସାମାନ୍ୟ ରକ୍ତପାତରେ ଜୀବନ କ୍ଷୀଣ ବା ଦୁର୍ବଳ ହୋଇଯାଏ ନାହିଁ କିମ୍ବା ଲଜ୍ଜା ଓ ଅପମାନର କଳଙ୍କ କାଳିମାରେ ମନୁଷ୍ୟ ଦୀନହୀନ ହୋଇଯାଏ ନାହିଁ । ବରଂ ସମସ୍ତ ବିଷାଦ-ବ୍ୟର୍ଥତା, ଦୁଃଖ-କାତରତା ଓ ହୀନମନ୍ୟତାର ବଳୟ ମଧ୍ୟରୁ ମୁକ୍ତି ପାଇବାର ପ୍ରକୃଷ୍ଟ ପନ୍ଥା ହେଉଛି କର୍ମତତ୍ପରତା । ସଂସାର ରୂପକ ଏହି ବିଶାଳ କର୍ମଭୂମିରେ ବିଭୁ ପ୍ରେରିତ କର୍ମୀ ବୋଲି ନିଜକୁ ମନେକରି କର୍ମରେ ନିୟୋଜିତ ରହିଲେ ମଣିଷ ଜୀବନ-ସୂତ୍ର ଧାରଣରେ ସମର୍ଥ ହୋଇପାରିବ । ମୃତ୍ୟୁକାମୀ ମାନବ ମନରେ ଆତ୍ମବିଶ୍ଵାସ ଭରିଦେବାରେ କବୟିତ୍ରୀଙ୍କ ଆଶାବାଦୀ ଆହ୍ବାନ ଓ ମାନବ ଦରଦୀ ଭାବୋଚ୍ଛାସ ପ୍ରଣିଧାନଯୋଗ୍ୟ ।

ଦୀର୍ଘ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର

Question ୩୭ ।
ହତୋତ୍ସାହିତ ହୋଇପଡ଼ିଥିବା ମଣିଷଙ୍କୁ କବି କି ପ୍ରକାର ପ୍ରେରଣା ଯୋଗାଇଛନ୍ତି, ପଠିତ କବିତା ଅନୁସରଣରେ ଆଲୋଚନା କର ।
କିମ୍ବା, ନୈରାଶ୍ୟବାଦୀ ମନରେ ଆଶାର ସଞ୍ଚାର କରିବା ଥିଲା ଉତ୍କଳ-ଭାରତୀ କୁନ୍ତଳା କୁମାରୀଙ୍କର ରଚନାର ବୈଶିଷ୍ଟ୍ୟ – ଏହା କେତେଦୂର ଯଥାର୍ଥ ଆଲୋଚନା କର ।
କିମ୍ବା, ଦୁଃଖ, ଦୈନ୍ୟ ଓ ଦୁର୍ଦ୍ଦଶା ପ୍ରପୀଡ଼ିତ ମାନବ ସମାଜ ପାଇଁ କବି କୁନ୍ତଳା କୁମାରୀଙ୍କର ଅକୁଣ୍ଠ ଦରଦ ସମ୍ପର୍କରେ ପଠିତ କବିତାରୁ ଏକ ସମୀକ୍ଷାମୂଳକ ତଥ୍ୟ ପ୍ରଦାନ କର।
Answer:
ଓଡ଼ିଆ ସାହିତ୍ୟର ବାଣୀ-ବିତାନରେ ଉତ୍କଳ-ଭାରତୀ କୁନ୍ତଳା କୁମାରୀଙ୍କ ସାହିତ୍ୟ ସାଧନା ଓ ସୃଷ୍ଟି ଓଡ଼ିଆ ସାହିତ୍ୟର ଇତିହାସ ପୃଷ୍ଠାରେ ଏକ ଉଲ୍ଲେଖନୀୟ ସ୍ଥାନ ଅଧିକାର କରିଛି । ଜୀବନର ସ୍ବଳ୍ପକାଳ ମଧ୍ୟରେ ପ୍ରତିଭାର ସୁବିନିଯୋଗ କରି ଓଡ଼ିଆ ସାହିତ୍ୟ କ୍ଷେତ୍ରରେ ନିଜର ଅମଳିନ ପରିଚୟ ରଖୁ ଯାଇଛନ୍ତି ନାରୀକବି । କବୟିତ୍ରୀଙ୍କ କାବ୍ୟ ପରିକ୍ରମାରେ ପରିଣତ ପର୍ଯ୍ୟାୟରେ ତାଙ୍କୁ ବାସ୍ତବବାଦୀ ହୋଇପଡ଼ିଥିବା ଦେଖିବାକୁ ମିଳେ । ଭାଷା ଓ ଭାବର ପ୍ରାଞ୍ଜଳତାରେ, ବର୍ଣ୍ଣିତ କଥା- ବସ୍ତୁର ବାସ୍ତବବାଦୀ କାରୁଣ୍ୟରେ ତଥା ବର୍ଣ୍ଣନାଭଙ୍ଗୀର ନିରାଭରଣ ସାବଲୀଳତାରେ କବୟିତ୍ରୀଙ୍କ କବିତାମାନ ଅଧିକ ପ୍ରାଣବନ୍ତ ହୋଇଛି ।

ଅବିନଶ୍ବର ପ୍ରତିଭାଦୀପ୍ତ ଏହି ପ୍ରଜ୍ଞାପରିମିତାଙ୍କ ସୃଷ୍ଟିନିଚୟ ବାସ୍ତବବାଦ ସହ ଆଶାବାଦର ମଧୁର ସମନ୍ବୟରେ ଯେଭଳି ଅନୁରଣିତ ହୋଇଛି ତା’ର ପଟାନ୍ତର ନାହିଁ । କବୟିତ୍ରୀଙ୍କ ଲେଖନୀ ନିଃସୃତ ‘ଅଞ୍ଜଳି’, ‘ଉଲ୍ଲାସ’, ‘ଅର୍ଜନା’, ‘ସ୍ଫୁଲିଙ୍ଗ’ ଓ ‘ଆହ୍ବାନ’ ଆଦି କବିତା ପୁସ୍ତକ; ‘ଭ୍ରାନ୍ତି’, ‘ନ’ତୁଣ୍ଡୀ, ‘ପରଶମଣି, ‘ରଘୁ ଅରକ୍ଷିତ’, ‘କାଳୀବୋହୂ’ଆଦି ଉପନ୍ୟାସ ତାଙ୍କ ଅମଳିନ ବହୁମୁଖୀ ପ୍ରତିଭାର ବଳିଷ୍ଠ ନିଦର୍ଶନ । ଡାକ୍ତରୀ ବିଦ୍ୟା ତାଙ୍କର ବୃତ୍ତି ଥିଲେ ମଧ୍ୟ ସାହିତ୍ୟ ସାଧନକୁ ନିଜର ବ୍ରତ ଭାବେ ଗ୍ରହଣ କରି ନେଇଥିଲେ କବୟିତ୍ରୀ । ବିଶ୍ବଜନୀନତା, ସେବାପରାୟଣତା, ଭଗବତ୍ ବିଶ୍ଵାସ ଓ କର୍ତ୍ତବ୍ୟପରାୟଣତାକୁ ଆଧାର କରି କାବ୍ୟକବିତା ରଚନା କରିବାରେ କବୟିତ୍ରୀଙ୍କ ଲେଖନୀ ଶତମୁଖ ହୋଇଥିଲା ।

‘ମଣିଷ ଭାଇ ଶୀର୍ଷକ କବିତା କବୟିତ୍ରୀଙ୍କ ‘ସ୍ଫୁଲିଙ୍ଗ’କବିତା ପୁସ୍ତକରୁ ସଂଗୃହୀତ । ଏହି ପୁସ୍ତକର ରଚନାକାଳ ପ୍ରାକ୍- ସ୍ଵାଧୀନତାକାଳୀନ, ଯେତେବେଳେ ବିଦେଶୀ ଶାସକର ସ୍ବେଚ୍ଛାଚାରିତା, ଶୋଷଣ ଓ ଅତ୍ୟାଚାର, ଜମିଦାର ଶ୍ରେଣୀ ବ୍ୟକ୍ତି- ବିଶେଷଙ୍କ ଜୁଲମ ଓ ନାଲିଆଖୁ ଓଡ଼ିଶାର ସାଧାରଣ ଜନଜୀବନକୁ ଦୁର୍ବିସହ କରିଦେଇଥିଲା । ନିଷ୍ପେଷିତ, ଲାଞ୍ଛିତ ମଣିଷ ନିନ୍ଦା, ଅପମାନ, ଲଜ୍ଜା ଓ ଭୟରେ କାକୁସ୍ଥ ହୋଇ ଦୁଃଖ ଓ ଯନ୍ତ୍ରଣାରେ ଅତିଷ୍ଠ ହୋଇଉଠିଥିଲା ।

ଏତଦ୍‌ଭିନ୍ନ ବନ୍ୟା ଓ ମରୁଡ଼ି ପରି ପ୍ରାକୃତିକ ବିପର୍ଯ୍ୟୟ ରାଜ୍ୟବାସୀଙ୍କୁ ଦାରିଦ୍ର୍ୟ ମଧ୍ୟକୁ ଠେଲିଦେଇ ଏକ ହାହାକାରମୟ ପରିସ୍ଥିତି ସୃଷ୍ଟି କରିଥିଲା । ରାଜ- ପ୍ରପୀଡ଼ନର ଦୁଃଖ, ଦୁର୍ଦ୍ଦଶା ସହ ଦାରିଦ୍ର୍ୟର କଷାଘାତରେ ଜର୍ଜରିତ ମଣିଷର ଦୁର୍ବିପାକ ସନ୍ଦର୍ଶନରେ କବୟିତ୍ରୀଙ୍କ ମାନବ- ଦରଦୀ ମନ ଚହଲି ଯାଇଛି । ସାମାଜିକ ଜୀବନର ବିପର୍ଯ୍ୟସ୍ତ ପରିସ୍ଥିତି ଓ ମଣିଷ ଭାଇ ହୃଦୟରେ ବସା ବାନ୍ଧିଥ‌ିବା ନୈରାଶ୍ୟ ଅବଲୋକନରେ କବୟିତ୍ରୀ ମ୍ରିୟମାଣ ହୋଇପଡ଼ିଛନ୍ତି । ଉତ୍କଟ ବାସ୍ତବବାଦୀ କବିତାଟିରେ କୁନ୍ତଳା କୁମାରୀଙ୍କ ଓଡ଼ିଆ ଜାତିପ୍ରୀତି, ଦୁର୍ଦ୍ଦଶାଗ୍ରସ୍ତ ମଣିଷ ଭାଇ ପ୍ରତି ସମ୍ବେଦନଶୀଳତା ତଥା ଆଶାବାଦର ସୁମଧୁର ସମନ୍ୱୟ କବିତାକୁ ଅଧିକ ପ୍ରାଣବନ୍ତ ଓ ମନୋଜ୍ଞ କରିଛି ।

ରାଜନୈତିକ ତଥା ସାମାଜିକ ଜୀବନର ସମସ୍ତ ପ୍ରତିକୂଳତାର ସମ୍ମୁଖୀନ ହୋଇ ମଣିଷ ଭାଗ୍ୟବାଦୀ ହେବାକୁ ବାଧ୍ୟ ହୋଇଛି । ଦୁଃଖ, ଲାଞ୍ଛନା, ଅପମାନ ଓ ଅପବାଦକୁ ଭାଗ୍ୟଲିପି ବୋଲି ଧରିନେଇ ସଂସାରକୁ ଧ୍ବଂସପଥର ଯାତ୍ରୀ ଓ ମୃତ୍ୟୁ ପଥର ଧାତ୍ରୀ ବୋଲି ଚିନ୍ତା କରିଛି । ମୃତ୍ୟୁରେ ହିଁ ଦୁଃଖପୂର୍ଣ୍ଣ ଜୀବନର ପରିସମାପ୍ତି ବୋଲି ତା’ର ମନରେ ଦୃଢ଼ ଧାରଣା ସୃଷ୍ଟି ହୋଇଛି । ସେମାନଙ୍କ ନୈରାଶ୍ୟଦଗ୍ଧ ପ୍ରାଣରେ ଆଶା ଓ ଆତ୍ମବିଶ୍ଵାସ ଭରିଦେବା ପାଇଁ କବୟିତ୍ରୀଙ୍କ ଲେଖନୀରୁ ଝରିପଡ଼ିଛି କବିତା ‘ ମଣିଷ ଭାଇଁ । ସେମାନଙ୍କ ଦୁଃଖରେ ସମଦୁଃଖୀ ହୋଇ କବି ଗାଇ ଉଠିଛନ୍ତି –

‘‘ ଶୁଣ ହେ ମଣିଷ ଭାଇ ! ଝୁରି ମରିବାକୁ ବୁଡ଼ି ମରିବାକୁ
ମଣିଷ ଜନମି ନାହିଁ ।”

ହତୋତ୍ସାହିତ ମଣିଷ ଭାଇକୁ ବଞ୍ଚିବାର ରାହା ଦେଖାଇବାକୁ ଯାଇ କବୟିତ୍ରୀ କେତୋଟି ମୂଲ୍ୟବାନ୍ ପରାମର୍ଶ ଦେବା ସଙ୍ଗେ ସଙ୍ଗେ ଆଶାବାଦୀ ଅନୁପ୍ରେରଣାରେ ସେମାନଙ୍କ ମନରେ ଆତ୍ମବିଶ୍ଵାସ ଜାଗ୍ରତ କରିବାକୁ ପ୍ରୟାସ କରିଛନ୍ତି । ପ୍ରଥମେ ଦୁଃଖ ଦୁର୍ଦ୍ଦଶାକୁ ବିଧ ଅଭିପ୍ରେତ ବୋଲି ବିବେଚନା କରି ଭାଗ୍ୟକୁ ଧ୍କାର ନ କରିବାକୁ କି ଶତ ହତଶ୍ବାସରେ ଜୀବନକୁ ଅଧିକ ଯନ୍ତ୍ରଣା ଜର୍ଜରିତ ନ କରିବାକୁ କବୟିତ୍ରୀ ସମ୍ବେଦନଭରା ଆଶ୍ବାସନା ବାଣୀ ଶୁଣାଇଛନ୍ତି ।

କବୟିତ୍ରୀଙ୍କ ମତରେ ମାନବ ନିୟତିର ଅଧୀନ ହେଲେ ମଧ୍ୟ ଜଣେ ଯନ୍ତ୍ରଣାଦଗ୍ଧ ଅନ୍ଧକାର କାରାଗୃହରେ ଚିର ଶୃଙ୍ଖଳିତ, ଲାଞ୍ଛିତ ଓ ବଞ୍ଚିତ ଜୀବନ ଅତିବାହିତ କରୁଥୁବ; ଏହା ବିଧ୍ୱନିର୍ଦ୍ଦିଷ୍ଟ ନୁହେଁ । ମାନବ ଜାତି କଦାପି ଧ୍ୱଂସପଥର ଯାତ୍ରୀ ନୁହେଁ କି ଏ ସଂସାର ମୃତ୍ୟୁର ମରଣଯନ୍ତା ନୁହେଁ । ଈଶ୍ଵର ସୃଷ୍ଟ ଏ ନିଷ୍ଫଳ ବିଶ୍ବ ହେଉଛି ମାନବର କର୍ମଭୂମି । ଅମୃତର ସନ୍ତାନ ମନୁଷ୍ୟ ପରମେଶ୍ଵରଙ୍କ ମହନୀୟ ସୃଷ୍ଟି । ହସ- କାନ୍ଦ, ସୁଖ-ଦୁଃଖ, ଭଲ-ମନ୍ଦର ସଦା ପରିବର୍ତ୍ତିତ ସମୟକୁ ନେଇ ଏ ସଂସାରରେ ସବୁକିଛି ଆତଯାତ ହେଉଛି । ତେଣୁ ସୁଖ- ସ୍ଵପ୍ନଭରା ଅତୀତକୁ ଝୁରି ତଥା ସାମ୍ପ୍ରତିକ ଦୁଃଖ – ଯନ୍ତ୍ରଣାର କାରୁଣ୍ୟରେ ହୃଦୟକୁ ଭାରାକ୍ରାନ୍ତ କରି ପଳାୟନପନ୍ଥୀ ପରି ନୈରାଶ୍ୟଦଗ୍ଧ ଜୀବନ ଅତିବାହିତ କରିବା ବିବେକୀର ଲକ୍ଷଣ ନୁହେଁ ।

ନାରୀକବିଙ୍କ ମତରେ ଏ ସଂସାର ହେଉଛି ମାନବ ପାଇଁ କର୍ମଭୂମି । ସଦା କର୍ମତତ୍ପର ରହି କର୍ତ୍ତବ୍ୟ ସମ୍ପାଦନ କରିଯିବାକୁ ପରମେଶ୍ୱର ଏହି ସୁନ୍ଦର ସଂସାରକୁ ଆମକୁ ପଠାଇଛନ୍ତି । ଫଳ ବାଞ୍ଛା ନ କରି କର୍ମ ସମ୍ପାଦନ କରି ଚାଲିଲେ ଲାଞ୍ଛନା, ଅପମାନ, ଅପବାଦକୁ ବିସ୍ତୃତ ହେବା ସଙ୍ଗେ ସଙ୍ଗେ ମନରୁ କୁଭାବନା ଦୂରେଇ ରହିବ । ମନରେ ଅହମିକା ପୋଷଣ କରି କ୍ରୋଧଯୁକ୍ତ ହେଲେ କିମ୍ବା ପ୍ରତିଶୋଧପରାୟଣ ମନୋବୃତ୍ତି ପୋଷଣ କଲେ ତା’ର ବିଷକ୍ରିୟାରେ ମନକୁ ପାଶବିକତା ଗ୍ରାସ କରିବ । ଜୀବନର ସବୁ ମାନ – ଅପମାନ, ଦୁଃଖ-ଯନ୍ତ୍ରଣାକୁ ବିଭୁ ପଦାରବିନ୍ଦରେ ସମର୍ପଣ ପୂର୍ବକ ନିଜକୁ କର୍ମତତ୍ପର ରଖୁରିଲେ ହିଁ ଈଶ୍ୱରଙ୍କ ଆଶୀର୍ବାଦ ପ୍ରାପ୍ତ ହେବ ।

ପଶୁତ୍ଵ-ଦେବତ୍ୱର ପରୀକ୍ଷାରେ ଉତ୍ତୀର୍ଣ୍ଣ ହେବାପାଇଁ ଅନ୍ତଃରିପୁ ଦମନ ପ୍ରତି ଯତ୍ନଶୀଳ ହେବାକୁ ମଧ୍ୟ କବୟିତ୍ରୀ ପରାମର୍ଶ ଦେଇଛନ୍ତି । ତାଙ୍କ ମତରେ କାମ, କ୍ରୋଧ, ଲୋଭ, ମୋହ, ମଦ, ମାସର୍ଯ୍ୟାଦି ଷଡ଼ରିପୁ ତଥା ଇନ୍ଦ୍ରିୟ ସୁଖ ଲାଳସା ମାନବାତ୍ମାକୁ କଳୁଷିତ କରି ପାପାତ୍ମାରେ ପରିଣତ କରିଥାଏ । ତେଣୁ ସେହି ଷଡ଼ରିପୁ ଦମନରେ ପ୍ରୟାସୀ ହେଲେ ମଣିଷ ଦିବ୍ୟଜୀବନ ଲାଭ କରିବାରେ ସମର୍ଥ ହୋଇ ଦେବତ୍ୱର ଅଧିକାରୀ ହୋଇପାରିବ । ପରମେଶ୍ବରଙ୍କୁ ଋଣୀ କରିବାପାଇଁ ମାନବୀୟ ଧର୍ମର ଯଥାଯଥ ପାଳନ ଅନିବାର୍ଯ୍ୟ । ତେଣୁ ଈଶ୍ବରଙ୍କ ଏହି ମହନୀୟ ସୃଷ୍ଟିର ସୌନ୍ଦର୍ଯ୍ୟ ବୃଦ୍ଧିରେ ନିଜକୁ ଉତ୍ସର୍ଗ କରି ଜୀବନକୁ ସତ୍ଵକର୍ମରେ ବିନିଯୁକ୍ତ କରିବାକୁ ନାରୀକବି ଆହ୍ୱାନ ଦେଇଛନ୍ତି । ତାଙ୍କ ଭାଷାରେ –

‘‘ଋଣୀ କର ଭବରାଣେ
ତା’ଙ୍କ ରଚା ଚରାଚର ପରାଣରେ ବଳି ଦିଅ ନିଜ ପ୍ରାଣେ ।’’

ମଙ୍ଗଳମୟ ପରମେଶ୍ବର ତାଙ୍କ ଅମୃତମୟ ସୃଷ୍ଟିର ଅଭିନବ ବିକାଶ ଦର୍ଶନରେ ଚିର ଆଗ୍ରହୀ । ସେ ହିଁ ମଣିଷର ସବୁ ବିଷାଦ -ବ୍ୟର୍ଥତା, ଦୁଃଖ – କାତରତା ତଥା ଯାବତୀୟ ହୀନମନ୍ୟତା ରୂପକ କଳଙ୍କ କାଳିମାକୁ ତାଙ୍କ ଦିବ୍ୟସ୍ପର୍ଶରେ ଧୋଇଦେଇ ତାକୁ ଅମୃତ ପିପାସୀ କରାଇବେ । ତେଣୁ ମୃତ୍ୟୁକାମୀ ମଣିଷ ଭାଇ ମନରୁ ସମସ୍ତ ନୈରାଶ୍ୟ ଓ ଅସହାୟବୋଧ ଭାବନାକୁ ପରିହାର କରି ଜୀବନ ସୂତ୍ର ଧାରଣ କରିବାକୁ ନାରୀକବି ଆହ୍ୱାନ ଦେଇଛନ୍ତି । ନାରୀକବିଙ୍କ ମାନବପ୍ରେମୀ ଆଭିମୁଖ୍ୟ ଆଶାବାଦିତାର ଉଜ୍ଜ୍ବଳ ମୟୂଖରେ ଯେ ଚିର ଦୀପ୍ତିମାନ, ଆଲୋଚ୍ୟ କବିତାରୁ ତାହା ସ୍ପଷ୍ଟ ପରିଦୃଷ୍ଟ ହୁଏ ।

Question ୩୮ ।
କବି ଜଣେ ମାନବବାଦୀ – ଏ ଭକ୍ତିର ଯଥାର୍ଥତା ‘ମଣିଷ ଭାଇ’ କବିତା ଅବଲମ୍ବନରେ ପ୍ରତିପାଦନ କର ।
କିମ୍ବା, ନାରୀକବି କୁନ୍ତଳାକୁମାରୀଙ୍କ ଲେଖନୀ ମୁନରେ ମାନବବାଦର ଯେଉଁ ଜ୍ଵଳନ୍ତ ସ୍ଫୁରଣ ଘଟିଛି, ତାହା ଆଲୋଚନା କର ।
କିମ୍ବା, କୁନ୍ତଳାକୁମାରୀଙ୍କର ‘ମଣିଷ ଭାଇ’ କବିତା ଆମୂଳଚୂଳ ମାନବବାଦର ଆଦର୍ଶରେ ଭରପୂର– ଏହାର ଯଥାର୍ଥତା ପ୍ରତିପାଦନ କର ।
Answer:
ଆଧୁନିକ ଓଡ଼ିଆ ସାହିତ୍ୟର ପ୍ରବହମାନ କାଳ ବକ୍ଷରେ ସବୁଜ ଯୁଗ ଓ ପ୍ରଗତିବାଦର ସନ୍ଧିକ୍ଷଣରେ ବାସ୍ତବବାଦ, ଆତ୍ମଭୌତିକ ଚେତନା ଓ ରହସ୍ୟବାଦକୁ ଆଧାର କରି ସ୍ଵକୀୟ ଲେଖନୀ ଚାଳନା କରିଥିଲେ ମାନବବାଦୀ କବୟିତ୍ରୀ ଉତ୍କଳ ଭାରତୀ କୁନ୍ତଳା କୁମାରୀ ସାବତ । ବିଶେଷତଃ ପ୍ରାକ୍-ସ୍ବାଧୀନତା କାଳରେ ଜଣେ ଏକକ ନାରୀକଣ୍ଠର ସ୍ବର – ସମ୍ଭାର ତତ୍‌କାଳୀନ ଓଡ଼ିଶାବାସୀଙ୍କୁ କେବଳ ଯେ ଚମତ୍କୃତ କରିଥିଲା ତାହା ନୁହେଁ, ବରଂ ପ୍ରତିଷ୍ଠିତ ସାହିତ୍ୟିକମାନଙ୍କୁ ତାଙ୍କ ସାରସ୍ବତ ସୃଷ୍ଟିନିଚୟ ବିସ୍ମିତ କରିଥିଲା ।

ବୃତ୍ତିରେ ଚିକିତ୍ସକ ଓ ପ୍ରବୃତ୍ତିରେ ସାହିତ୍ୟ ସାଧନା; କବୟିତ୍ରୀଙ୍କ ବହୁମୁଖୀ ପ୍ରତିଭାର ଉଜ୍ଜ୍ଵଳ ନିଦର୍ଶନ । ମାତ୍ର ୩୮ ବର୍ଷର ସ୍ୱଳ୍ପ ଜୀବନକାଳ ମଧ୍ୟରେ ପ୍ରତିଭାର ସୁବିନିଯୋଗ କରି ସେ ଓଡ଼ିଆ ସାହିତ୍ୟ କ୍ଷେତ୍ରରେ ନିଜର ଅମଳିନ ପରିଚୟ ରଖିଯାଇଛନ୍ତି । କବୟିତ୍ରୀଙ୍କ ସାରସ୍ବତ ସୃଷ୍ଟିସମ୍ଭାର ମଧ୍ୟରେ ‘ଅଞ୍ଜଳି, ‘ଉଲ୍ଲାସ, ‘ଅର୍ଜନା’, ‘ସ୍କୁଲିଙ୍ଗ ଓ ‘ ଆହ୍ୱାନ ପରି କବିତା ପୁସ୍ତକ; ‘ ଭ୍ରାନ୍ତି’, ‘ନ’ତୁଣ୍ଡୀ, ‘ ପରଶମଣି, ‘ରଘୁ ଅରକ୍ଷିତ ଓ ‘ କାଳୀବୋହୂ’ ଆଦି ଉପନ୍ୟାସ ନାରୀକବିଙ୍କ ସାରସ୍ବତ ପ୍ରତିଭାର ବଳିଷ୍ଠ ନିଦର୍ଶନ । ବିଶ୍ୱଜନୀନତା, ସେବାପରାୟଣତା, କର୍ତ୍ତବ୍ୟପରାୟଣତା, ଭଗବତ୍ ବିଶ୍ୱାସ ଓ ସର୍ବୋପରି ମାନବିକ ମୂଲ୍ୟବୋଧ କବିଙ୍କ କାବ୍ୟକବିତାର ବୈଶିଷ୍ଟ୍ୟ ।

ଆଲୋଚ୍ୟ ‘ମଣିଷ ଭାଇ କବିତାଟି କବୟିତ୍ରୀଙ୍କ କବିତାଗୁଚ୍ଛ ‘ସ୍ଫୁଲିଙ୍ଗ’ରୁ ସଂଗୃହୀତ । କବୟିତ୍ରୀଙ୍କ ପ୍ରାକ୍- ସ୍ଵାଧୀନତାକାଳୀନ ଏହି କବିତାରେ ତତ୍‌କାଳୀନ ସମାଜ ଓ ଜନଜୀବନର ନିଚ୍ଛକ ଚିତ୍ର ପ୍ରକାଶ ପାଇଛି । ପରାଧୀନ ଓଡ଼ିଶାରେ ବିକଟ ଦାରିଦ୍ର୍ୟ ଓ ନିପୀଡ଼ିତ ଜୀବନ ନେଇ ଓଡ଼ିଆ ଜାତି ନୈରାଶ୍ୟର ଘନ ଅନ୍ଧକାର ମଧ୍ଯରେ ସଢ଼ୁଥିଲାବେଳେ ସେମାନଙ୍କ ବ୍ୟର୍ଥିତ ପ୍ରାଣରେ ଆଶାର ସଞ୍ଜୀବନୀ ବାରି ବର୍ଷଣ କରିବାକୁ କୁନ୍ତଳା କୁମାରୀଙ୍କ କାଳଜୟୀ ଲେଖନୀ ଆଗେଇ ଆସିଛି। ସମ୍ବେଦନଶୀଳ କବି ହୃଦୟରୁ ମାନବ ପ୍ରୀତି ଝରିପଡ଼ିଛି କବିତା ‘ମଣିଷ ଭାଇ’ରେ ।

ଶୋଷିତ, ଲାଞ୍ଛିତ ଜନଜୀବନର ଦାରିଦ୍ର୍ୟ, କଷଣ, ରୋଗବ୍ୟାଧ୍ ଓ ଅଭାବ ଅନଟନଜନିତ ଅସହାୟବୋଧ, ନାରୀକବିଙ୍କ ଦରଦୀ ପ୍ରାଣରେ ବ୍ୟଥା ଓ ବିଷାଦ ଭରିଦେଇଛି । ତାଙ୍କ ଆୟୋପଲବ୍ଧି ଓ ମାନବୀୟ ମହତ୍ତ୍ଵ ଯେ ଗଭୀର ଆଶାବାଦିତାର ଉଜ୍ଜ୍ବଳ ମୟୂଖରେ ଦୀପ୍ତିମାନ ହୋଇଉଠିଛି ତାହା କବିତାର ପଂକ୍ତିଗୁଡ଼ିକରେ ସ୍ପଷ୍ଟ ରୂପାୟିତ । ମଣିଷ ଭାଇକୁ ହତାଶାବୋଧର ଘୂର୍ତ୍ତି ମଧ୍ୟରୁ ରକ୍ଷା କରିବାପାଇଁ କବୟିତ୍ରୀଙ୍କ ପ୍ରେରଣାପୂର୍ଣ ଆହ୍ବାନ ତଥା ଉପଯୁକ୍ତ ଦିଗ୍‌ଦର୍ଶନ ପ୍ରଦାନ, ତାଙ୍କ ଦୃଢ଼ ମାନସିକତା, ମାନବିକ ମୂଲ୍ୟବୋଧ ତଥା ପ୍ରଗାଢ଼ ଆଶାବାଦିତାର ପରିଚୟ ଦେଇଥାଏ ।

କବିତା ‘ ମଣିଷ ଭାଇ’ରେ ନୈରାଶ୍ୟଦଗ୍ଧ ମଣିଷକୁ କବୟିତ୍ରୀ ଯେଉଁ ପରାମର୍ଶଗୁଡ଼ିକ ଦେଇଛନ୍ତି, ସେଥୁରୁ ସ୍ପଷ୍ଟ ଭାବେ ପ୍ରତୀତ ହୁଏ ଯେ, ସେ ଥିଲେ ଜଣେ ସଫଳ ମନୋବିଜ୍ଞାନୀ । କବୟିତ୍ରୀ ଅନୁଭବ କରିଥିଲେ ଯେ ତତ୍‌କାଳୀନ ସାମାଜିକ ପରିସ୍ଥିତି ମଣିଷକୁ ମାନସିକ ଭାବେ ଦୁର୍ବଳ କରିଦେଇଛି । ତେଣୁ ତା’ ମନରେ ପ୍ରଥମେ ସାହସ ଓ ଧୈର୍ଯ୍ୟ ଭରିଦେବାକୁ ବାଣୀ ପ୍ରୟୋଗ କରିଛନ୍ତି । କବୟିତ୍ରୀଙ୍କ ଭାଷାରେ –

‘‘ଶୁଣ ହେ ମଣିଷ ଭାଇ ! ଝୁରି ମରିବାକୁ ବୁଡ଼ି ମରିବାକୁ
ମଣିଷ ଜନମି ନାହିଁ । ”
ଅମୃତ ଦୀପ୍ତି ସନ୍ତାନ ତୁମେ ମରଣ ତୁମର କାହିଁ ?”’

ତତ୍‌ପରେ କବୟିତ୍ରୀ ଅନୁଭବ କରିଛନ୍ତି ଯେ ଅସହାୟ ମଣିଷ ମନରେ କର୍ମମୁଖର ଜୀବନର ଜୟଗୀତି ଶୁଣାଇବାକୁ ହେବ । କର୍ମରେ ନିୟୋଜିତ ରହିଲେ ମଣିଷ ଯେ ଦୁଃଖ, ଅବସାଦ, ଅପମାନ, ଲଜ୍ଜା ଓ ଭୟ ଆଦି ମାନସିକ ଦୌର୍ବଲ୍ୟଜନିତ ବସ୍ତୁତ ହେବ, କବୟିତ୍ରୀ ଏହା ଆତ୍ମପଲବ୍ଧିରୁ ଅବଗତ ଥିଲେ । ତେଣୁ କର୍ମର ଜୟଗାନ କରି ସେ ଗାଇଛଠିଛନ୍ତି –

‘‘ ଶୁଣ ଶୁଣ ବିଶ୍ୱବାସୀ ! କରମର ଶୁଭ ଭୁବନ ଏହିଟି,
କରମରେ ଶ୍ରମ ନାଶି । ’’

କବିୟତ୍ରୀଙ୍କ ମତରେ ଏ ସଂସାର ହେଉଛି ମାନବର କର୍ମଭୂମି । ଫଳବାଞ୍ଛାବିହୀନ କର୍ମରେ ନିଯୁକ୍ତ ରହିବାକୁ ପରମେଶ୍ୱର ଆମକୁ ଏ ବିଶାଳ ସଂସାରକୁ ପ୍ରେରଣ କରିଛନ୍ତି । ମଣିଷ କର୍ମତତ୍ପର ରହି ସ୍ଵକର୍ତ୍ତବ୍ୟ ସମ୍ପାଦନ କରିଚାଲିଲେ ଈଶ୍ବର ସୃଷ୍ଟିର ସାର୍ଥକତାରେ ପରମ ପ୍ରୀତ ହେବେ । ଅନନ୍ତ ମରଣକୁ କପାଳଲିଖନ ବୋଲି ବିବେଚନା ନ କରି କର୍ମକୁ ଜୀବନର ମାନଦଣ୍ଡ ଭାବେ ଗ୍ରହଣ କରିବାକୁ କବୟିତ୍ରୀ ପରାମର୍ଶ ଦେଇଛନ୍ତି । ସମସ୍ତ ମାନସିକ ସ୍କାନିକୁ ଦୂର କରିବାପାଇଁ ଜଣେ ସଫଳ କର୍ମଯୋଗୀ ଭାବେ ଜୀବନ ଯାପନ କରିବାକୁ କବୟିତ୍ରୀଙ୍କ ଦିବ୍ୟ ପରାମର୍ଶ ହିଁ ବାସ୍ତବିକ ଉଲ୍ଲେଖଯୋଗ୍ୟ । ଦୁଃଖ, ଯନ୍ତ୍ରଣାକୁ କର୍ମହୀନ ଜୀବନ ବହୁଗୁଣିତ କରିଥାଏ ।

ଆଳସ୍ୟପୂର୍ଣ୍ଣ ଜୀବନ ମାନବକୁ ଅନ୍ତଃରିପୁମାନଙ୍କ ଦୌରାତ୍ମ୍ୟ ମଧ୍ୟକୁ ଠେଲି ଦେଇଥାଏ । କାମ, କ୍ରୋଧ, ଲୋଭ, ମୋହ, ମଦ ଓ ମାସର୍ଯ୍ୟାଦିର ଅଧୀନ ହୋଇଗଲେ ତା’ ମନରେ ପାଶବିକ ପ୍ରବୃତ୍ତିର ଅଭ୍ୟୁଦୟ ଘଟେ, ପରବର୍ତ୍ତୀ ସମୟରେ କ୍ରୋଧ ଓ ପ୍ରତିଶୋଧପରାୟଣ ମନୋବୃତ୍ତି ତା’ ପୁଣ୍ୟ ମାନବାତ୍ମାରେ କଳୁଷ କାଳିମାର କଳଙ୍କ ଲଗାଇ ପାପାତ୍ମାରେ ପରିଣତ କରେ । ସଂସାରକୁ ଧ୍ବଂସପଥର ଯାତ୍ରୀ ବୋଲି ଚିନ୍ତା କରୁଥିବା ଅସହାୟ ମଣିଷକୁ ଅମୃତର ସନ୍ତାନ ଭାବେ ବର୍ଣ୍ଣନା କରି ସକଳ କର୍ମ ମଧ୍ଯରେ ‘ଆଧାତ୍ମିକତାର ପୀୟୂଷ ପାନ କରିବାକୁ କବୟିତ୍ରୀଙ୍କ ମହାପରାମର୍ଶ ଲାଜ, ଭୟ, ଅପମାନ ଓ ଲାଞ୍ଛନା ପରି ମାନସିକ ଅସନ୍ତୁଳନତାର ମହାନ୍ ଦାନ କହିଲେ ଅତ୍ୟୁକ୍ତି ହେବ ନାହିଁ । ନାରୀକବିଙ୍କ ଭାଷାରେ –

‘‘ ଉଠ ଦେବ ତେଜେ ତେଜି ଲାଜ ଭୟ ଅପମାନ ଅହମିକା,
ପଶୁତ୍ବ ଦେବତ୍ୱ ପରୀକ୍ଷାରେ ଜୟୀ ଲଭ ବୀରତ୍ଵର ଟୀକା
ଋଣୀ କର ଭବରାଣେ
ତା’ଙ୍କ ରଚା ଚରାଚର ପରାଣରେ ବଳିଦିଅ ନିଜ ପ୍ରାଣେ ।’’

ଭାଗ୍ୟବାଦୀ ମଣିଷକୁ ନିୟତି ବିଚାରର ନିରପେକ୍ଷତା ତଥା ପରିବର୍ତ୍ତନଶୀଳ ଦୁନିଆର ବହମାନ ସ୍ରୋତରେ ସୁଖ- ଦୁଃଖ, ହସ-କାନ୍ଦ ଓ ସମ୍ପଦ– ଦାରିଦ୍ର୍ୟର ପଟ୍ଟ ପରିବର୍ତ୍ତନ ରୂପ ସ୍ମରଣ କରାଇଛନ୍ତି । ତେଣୁ ନିଜକୁ ହୀନମନ୍ୟ ଚିନ୍ତାଚେତନାରୁ ମୁକ୍ତ କରି ଜୀବନକୁ ଅମୃତଅନ୍ଵେଷୀ କରିବା ଯେ ମାନବୋଚିତ ଧର୍ମ ଏହି ପରାମର୍ଶ ଦେଇ ନିରାଶାନ୍ଧକାରରେ ପଥଚ୍ୟୁତ ମଣିଷକୁ ନାରୀକବି ଆହ୍ୱାନ ଦେଇଛନ୍ତି । ମୃତ୍ୟୁ ଯେ ଜୀବନର ଶେଷ ଗତି ନୁହେଁ ଏହି ଦିବ୍ୟ ଭାବନାକୁ ହୃଦୟରେ ଧାରଣ କରି କର୍ମପ୍ରବଣ ଜୀବନ ଯାପନରେ ପ୍ରୟାସୀ ହେଲେ ଜୀବନ ଅଧ୍ବକ ଉପଭୋଗ୍ୟ ହୋଇଉଠିବ ବୋଲି ନାରୀକବିଙ୍କ ମହାନ୍ ଉପଦେଶ ତାଙ୍କ ମାନବବାଦୀ ଦୃଷ୍ଟିଭଙ୍ଗୀର ବଳିଷ୍ଠ ପ୍ରମାଣ ପ୍ରଦାନ କରେ ।

Question ୩୯ ।
ଅମୃତର ସନ୍ତାନ ମଣିଷ କିପରି ତା’ର ଜୀବନକୁ ସରସ ସୁନ୍ଦର କରିପାରିବ ବୋଲି କବି ପ୍ରେରଣା ଦେଇଛନ୍ତି ?
କିମ୍ବା, ମଣିଷ, ଅମୃତର ସନ୍ତାନ– ଏହି ଆଶାବାଦମୂଳକ ଆୟୋପଲବ୍ଧିକୁ କବି ମଣିଷ ମନରେ ସଞ୍ଚାର କରିବାକୁ କି ଦିଗ୍‌ଦର୍ଶନ ଦେଇଛନ୍ତି, ପଠିତ କବିତା ଅବଲମ୍ବନରେ ବର୍ଣ୍ଣନା କର ।
Answer:
ଉତ୍କଳ ସାରସ୍ଵତ ଗଗନର ଅନ୍ୟତମ ଜ୍ୟୋତିର୍ମୟ ଜ୍ୟୋତିଷ୍କ, ଆଧ୍ୟାତ୍ମିକ ଚେତନାର ବାର୍ତ୍ତାବହ ତଥା ମାନବବାଦର ଯଥାର୍ଥ ରୂପକାର ନାରୀକବି ଉତ୍କଳ ଭାରତୀ କୁନ୍ତଳା କୁମାରୀ ସାବତ ପ୍ରାକ୍-ସ୍ଵାଧୀନତା କାଳର ଏକ ସୁଦୂରପ୍ରସାରୀ ନାମ । ବିପ୍ଳବର ଅନିର୍ବାଣ ଅଗ୍ନିଶିଖା ତଥା ମାନବତାର ପରିପୂର୍ଣ୍ଣ ଉତ୍ସ କୁନ୍ତଳା କୁମାରୀ ଉଭୟ ଗୁଣ ଓ ପରିଣାମରେ ପ୍ଲାବନ କଲାଭଳି ଏପରି ଏକ ସାହିତ୍ୟିକ ବ୍ୟକ୍ତିତ୍ବ, ଯାହା ଏ ପର୍ଯ୍ୟନ୍ତ ଓଡ଼ିଆ ନାରୀ ଜଗତରେ ଦେଖା ଦେଇନାହିଁ ।

କବିତା, ପ୍ରବନ୍ଧ ଓ ଉପନ୍ୟାସ ଆଦି ସାହିତ୍ୟର ବିଭିନ୍ନ ଦିଗକୁ ତାଙ୍କ ଲେଖନୀ ସ୍ପର୍ଶ କରିଛି । ପୂର୍ବଗୌରବାନୁଚିନ୍ତା, ଦେଶାତ୍ମବୋଧ, ପ୍ରେମ, ପ୍ରକୃତିପ୍ରାଣତା, ବିଭୁଚେତନା ପ୍ରଭୃତି କାବ୍ୟକବିତାର ବିଭିନ୍ନ ବିଭାଗ ମଧ୍ୟରେ ତାଙ୍କ ଲେଖନୀର ଜୟଯାତ୍ରା ପରିଲକ୍ଷିତ ହୁଏ । କବୟିତ୍ରୀଙ୍କ ସାରସ୍ବତ ସୃଷ୍ଟିନିଚୟ ମଧ୍ୟରେ ‘ଅଞ୍ଜଳି’, ‘ଉଲ୍ଲାସ’, ‘ଅର୍ଜନା’, ‘ସ୍କୁଲିଙ୍ଗ’, ‘ଆହ୍ବାନ’ ଆଦି କବିତା ପୁସ୍ତକ; ‘ଭ୍ରାନ୍ତି’, ‘ନ’ତୁଣ୍ଡୀ’, ‘ପରଶମଶି’, ‘ରଘୁ ଅରକ୍ଷିତ’, ‘କାଳୀବୋହୂ’ ଆଦି ଉପନ୍ୟାସ ତାଙ୍କ ସୃଷ୍ଟି ନୈପୁଣ୍ୟର ପରିଚାୟକ ।

କବିତା ‘ ମଣିଷ ଭାଇଁ ନାରୀକବିଙ୍କ କବିତା ପୁସ୍ତକା ‘ସ୍ଫୁଲିଙ୍ଗ’ ଅନ୍ତର୍ଭୁକ୍ତ ଏକ ଆହ୍ୱାନଧର୍ମୀ ସମ୍ବୋଧୀ କବିତା । ସ୍ଵାଧୀନତା ପ୍ରାପ୍ତି ପୂର୍ବରୁ ଦେଶବାସୀ ବିଦେଶୀ ଶାସକର ଶୋଷଣ, ଅତ୍ୟାଚାରରେ ଅତିଷ୍ଠ ହୋଇ ଦୟନୀୟ ଜୀବନ ଯାପନ କରୁଥିଲେ । ଭୂମିକା, ରୋଗବ୍ୟାଧ, ବନ୍ୟା ଓ ମରୁଡ଼ିଜନିତ ପ୍ରାକୃତିକ ବିପର୍ଯୟ ଆଦି ନାନାବିଧ ପ୍ରତିକୂଳ ପରିସ୍ଥିତି ମଧ୍ୟଦେଇ ଘୋର ନୈରାଶ୍ୟପୂର୍ଣ୍ଣ ଜୀବନ ଅତିବାହିତ କରୁଥିଲେ । ଅସହାୟ ମଣିଷ ନିଜ ଦୁରବସ୍ଥା ପାଇଁ ଭାଗ୍ୟକୁ ଦାୟୀ କରି ଓ ମୃତ୍ୟୁରେ ହିଁ ଜୀବନଯନ୍ତ୍ରଣାର ମଣିଷକୁ ମଣିଷପରି ବଞ୍ଚିବାପାଇଁ କବିତାଟିରେ ରହିଛି ନାରୀକବିଙ୍କର ଆଶାନ୍ବିତ ଆହ୍ୱାନ।

ଅମୃତର ସନ୍ତାନ ମଣିଷ ପାଇଁ ନାରୀ କବିଙ୍କର ଆତ୍ମବିଶ୍ବାସଭରା ଆଶା ଆଶ୍ବାସନାର ଦିବ୍ୟବାଣୀ ରହିଛି କବିତାଟିରେ । ଦୁଃଖ ଦୁର୍ଦ୍ଦଶାକୁ କପାଳ ଲିଖନ ବୋଲି ବିବେଚନା କପାଳ ଲିଖନ ବୋଲି ବିବେଚନା କରି ଶତ ହତଶ୍ଵାସରେ ଭାଗ୍ୟକୁ ଧିକ୍‌କାର କରି ଓ ଜୀବନକୁ ମୃତ୍ୟୁପଥର ଯାତ୍ରୀ ବୋଲି ଧରିନେଇ ଘୋର ନୈରାଶ୍ୟ ମଧ୍ୟରେ ଛଟପଟ ହେଉଥ‌ିବା ମଣିଷ ପ୍ରତି ନାରୀକବି ସମ୍ବେଦନଶୀଳ ହୋଇଛନ୍ତି । ତାଙ୍କ ମତରେ ମାନବ ଜୀବନ ନିୟତି ଅଧୀନ ହେଲେ ମଧ୍ୟ ଚିର ଶୃଙ୍ଖଳିତ ଜୀବନ ନେଇ ମାନବ ଯେ ଯନ୍ତ୍ରଣାର କାରାଗାରରେ ଚିର ବନ୍ଦୀ ହୋଇ ପଡ଼ିଥିବ ଏହା କଦାପି ଭାଗ୍ୟଲିପି ନୁହେଁ ମାନବ ଜାତି କଦାପି ହଂସପଥର ଯାତ୍ରୀ ନୁହେଁ କି ଏ ସଂସାର ମୃତ୍ୟୁଯନ୍ତା ନୁହେଁ ।

ଦୁଃଖ, ଯାତନା ଓ ଅନୁଶୋଚନାର ତୀବ୍ର ଜ୍ଵଳନକୁ ନତଶିର ହୋଇ ଚିରଦିନ ସହ୍ୟ କରିବା ମାନବର ନିୟତି ନୁହେଁ । ସେହିପରି ଧନୀ, ପୁଞ୍ଜିପତି ଓ କ୍ଷମତାଧ୍ୟାକାରୀ ଅତ୍ୟାଚାରୀ ଶାସକ ଦୁର୍ବଳ ନିରୀହ ଜନତା ଉପରେ ଚିର ଆଧୂପତ୍ୟ ବିସ୍ତାର କରି ଶୋଷଣ, କଷଣରେ ଜୀବନକୁ ଦୁର୍ବିଷହ କରିଚାଲିଥବ, ଏହା କଦାପି ବିଧାତା ବିଧାନ ନୁହେଁ । ନାରୀକବିଙ୍କ ଭାଷାରେ –

କୁର ଅତ୍ୟାଚାରେ ଦଳିବ ଦୁର୍ବଳେ ରକ୍ତ ପିପାସା ଶମିବ
ନତଶିରେ ସୁଖେ ଶ୍ରୀପାଦେ ଅରପି ଆପଣାକୁ ଆପେ ବଧୂବ
ଏ ନୁହେଁ ବିଧାତା ବିଚାର,
ଧ୍ଵଂସର ଯାତ୍ରୀ, ମୃତ୍ୟୁର ଧାତ୍ରୀ ନୁହେଁ ଏ ସୁନ୍ଦର ସଂସାର ।’’

ନାରୀକବିଙ୍କ ମତରେ ପରମେଶ୍ବରଙ୍କ ସୃଷ୍ଟ ଏ ସଂସାର ଚିର ଆନନ୍ଦମୟ ଓ ମଙ୍ଗଳମୟ । ସଂସାରବାସୀ ହେଉଛନ୍ତି ଅମୃତର ସନ୍ତାନ । ମଣିଷ ଚାହିଁଲେ ତା’ ଜୀବନକୁ ମଧୁମୟ, ସରସ ଓ ସୁନ୍ଦର କରିପାରିବ । ତେଣୁ ମୃତ୍ୟୁପଥର ଯାତ୍ରୀ ବୋଲି ଭାବି ମଣିଷ ସ୍ଵକର୍ତ୍ତବ୍ୟ ସମ୍ପାଦନରୁ ନିବୃତ୍ତ ରହିବା ଅବିବେକତାର ପରିଚୟ । ନାରୀକବି ବିଶ୍ବବାସୀଙ୍କୁ ସଦା କର୍ମତତ୍ପର ରହି କର୍ତ୍ତବ୍ୟ କରିଯିବାକୁ ଉପଦେଶ ଦେଇଛନ୍ତି । କର୍ମରେ ନିମଜ୍ଜିତ ରହିଲେ ମନ ଭିତରୁ ନୈରାଶ୍ୟ ଓ ହତାଶାବୋଧ ଦୂରକରିବା ସମ୍ଭବ ।

ମନ ମଧ୍ଯରୁ ଲଜ୍ଜା, ଭୟ, ଅପମାନ ଓ ଅପବାଦକୁ ବିସ୍ମୃତ ହେବାପାଇଁ କର୍ମଯୋଗ ହିଁ ଶ୍ରେଷ୍ଠ ଉପଚାର । ମନରେ ଅହମିକା ପୋଷଣ କରି କ୍ରୋଧଯୁକ୍ତ ହେଲେ ବା ପ୍ରତିଶୋଧପରାୟଣ ଭାବନା ମନରେ ଧାରଣ କଲେ ଆତ୍ମା କଳୁଷିତ ହୁଏ । କାମ, କ୍ରୋଧ, ଲୋଭ, ମୋହ, ମଦ, ମାସର୍ଯ୍ୟାଦି ଅନ୍ତଃରିପୁମାନଙ୍କୁ ଦୃଢ଼ ଭାବେ ଦମନ କରି ମାନବୀୟ ଗୁଣାବଳୀରେ ଭୂଷିତ ହେଲେ ପରମେଶ୍ୱରଙ୍କ ଆଶୀର୍ବାଦ ପ୍ରାପ୍ତ ହୁଏ । ଇନ୍ଦ୍ରିୟଲାଳସା ପରିହାର କରି ମନରେ ଦିବ୍ୟଚେତନା ଜାଗ୍ରତ କଲେ ମାନବ ଦେବତ୍ୱର ଅଧିକାରୀ ହେବ । ନୈତିକତାପୂର୍ଣ୍ଣ ଜୀବନ ଶୈଳୀକୁ ପାଥେୟ କରି ଓ ମନରେ ଫଳପ୍ରାପ୍ତି ବାଞ୍ଛା ନ କରି କର୍ମରେ ନିୟୋଜିତ ରହିଲେ ସବୁ ସମସ୍ୟା ସହଜରେ ସମାହିତ ହୋଇପାରିବ ବୋଲି କବୟିତ୍ରୀ ଦୃଢୋକ୍ତି ପ୍ରକାଶ କରିଛନ୍ତି ।

କର୍ମମୟ ସଂସାରରେ କର୍ତ୍ତବ୍ୟ ସମ୍ପାଦନରେ ବ୍ରତୀ ହେବା ହିଁ ମାନବିକତାର ଶ୍ରେଷ୍ଠ ପରିଚୟ । କର୍ମତତ୍ପରତାଦ୍ବାରା ଈଶ୍ଵରଙ୍କ ଇଚ୍ଛା ପୂର୍ଣ କରାଯାଇପାରିବ ଓ ପଶୁତ୍ଵ- ଦେବତ୍ୱର ଭୀଷଣ ପରୀକ୍ଷାରେ ସଫଳତାର ସହିତ ଉତ୍ତୀର୍ଣ୍ଣ ହୋଇ ମଣିଷ ମାନବିକ ମୂଲ୍ୟବୋଧର ବିଜୟ ବୈଜୟନ୍ତୀ ଉଡ଼ାଇପାରିବ । ଫଳତଃ ପରମେଶ୍ଵର ତାଙ୍କ ସୃଷ୍ଟିର ସାର୍ଥକତା ଅବଲୋକନ କରି ଚିର ସନ୍ତୁଷ୍ଟ ହେବେ ଓ ମାନବ ନିକଟରେ ଚିର ଋଣୀ ରହିବେ । ତାଙ୍କ ଅମୃତମୟ ସୃଷ୍ଟିକୁ ସୁନ୍ଦରତର କରିବାରେ ମଣିଷ ନିଜକୁ ଉତ୍ସର୍ଗ କରିବାକୁ କବୟିତ୍ରୀ ଆହ୍ବାନ ଦେଇଛନ୍ତି । ତାଙ୍କ ଭାଷାରେ –

‘‘ଉଠ ଦେବ ତେଜେ ତେଜି ଲାଜ ଭୟ ଅପମାନ ଅହମିକା,
ପଶୁତ୍ଵ ଦେବତ୍ୱ ପରୀକ୍ଷାରେ ଜୟୀ ଲଭ ବୀରତ୍ଵର ଟୀକା
ଋଣୀ କର ଭବରାଣେ
ତା’ଙ୍କ ରଚା ଚରାଚର ପରାଣରେ ବଳି ଦିଅ ନିଜ ପ୍ରାଣେ ।’’

କବିଙ୍କ ମତରେ ମାନବ ହେଉଛି ବିଧାତାର ବରପୁତ୍ର । ଜୀବନ ଯୁଦ୍ଧରେ ସାମାନ୍ୟ କ୍ଷତାକ୍ତ ହୋଇଗଲେ ସେ ନିଜକୁ କ୍ଷୀଣ ବା ଦୁର୍ବଳ ମନେକରିବା ଅନୁଚିତ । ଦୁଃଖ, ଯନ୍ତ୍ରଣା, ଲଜ୍ଜା, ଅପମାନ, ଅପବାଦରେ ନିଜକୁ ଦୀନ-ହୀନ ମନେକରିବା ମଧ୍ୟ ଅନୁଚିତ । ଧୈର୍ଯ୍ୟ, ସାହସ ଓ ବିକ୍ରମ ସହ ଜୀବନ ସଂଗ୍ରାମର ସମ୍ମୁଖୀନ ହେବା ବୀରୋଚିତ ଲକ୍ଷଣ । କାରଣ ପରମେଶ୍ଵର ତାଙ୍କ ଅମୃତମୟ ସୃଷ୍ଟିର ଅଭିନବ ବିକାଶ ଦର୍ଶନରେ ଚିର ଆଗ୍ରହୀ, ଅମୃତ ସନ୍ତାନ ମାନବର ଆଧ୍ୟାତ୍ମିକ ବିକାଶ ଦର୍ଶନରେ ସେ ସଦା ସନ୍ତୁଷ୍ଟ ।

ତେଣୁ ମଣିଷର ସବୁ ବିଷାଦ – ବ୍ୟର୍ଥତା, ଦୁଃଖ – କାତରତା, ତଥା ଯାବତୀୟ ହୀନମନ୍ୟତା ରୂପକ କଳଙ୍କ କାଳିମାକୁ ଧୋଇଦେଇ କ୍ଷତାକ୍ତ ମାନବାତ୍ମାକୁ ସେ ତାଙ୍କ ସୁଧାସ୍ପର୍ଶରେ ନବରୂପ ପ୍ରଦାନ ପୂର୍ବକ ତାକୁ ପୀୟୂଷ ପିପାସୀ କରାଇବେ । ଫଳରେ ଜୀବନ ହୋଇଉଠିବ ସରସ, ସୁନ୍ଦର, ଆନନ୍ଦମୟ ଓ ଅମୃତମୟ । ମଣିଷ ମନରେ ଆତ୍ମଚୈତନ୍ୟ, ପ୍ରାଣପ୍ରାଚୁର୍ଯ୍ୟ ତଥା କର୍ମମୟ ଜୀବନରେ ଉନ୍ମାଦନା ଭରିଦେବାରେ ‘ମଣିଷ ଭାଇ’ କବିତା ଯେ ନାରୀକବିଙ୍କର ଏକ ସାର୍ଥକ ସୃଷ୍ଟି ଏଥରେ ଦ୍ବିରୁକ୍ତି ନାହିଁ ।

Question ୪୦ ।
ବିଷାଦଗ୍ରସ୍ତ ହୋଇପଡ଼ିଥିବା ତୁମର ଜଣେ ବନ୍ଧୁଙ୍କୁ କବିତା ଅନୁସରଣରେ ଆଶ୍ୱାସନାର ବାଣୀ ଦେଇ ପତ୍ରଟିଏ ଲେଖ ।
Answer:

କଟକ
ତା ୨୫.୩.୨୦୧୮

ପ୍ରିୟ ସାଥୀ ସ୍ବାତୀ,
ଶୁଭେଚ୍ଛା ନେବୁ । ମଉସା, ମାଉସୀଙ୍କୁ ମୋର ପ୍ରଣାମ ଜଣାଇବୁ ଓ ତୋ’ ଗେହ୍ଲା ଭାଇ ସୁମନକୁ ମୋର ସ୍ନେହ । କାଲି ତୋ’ ଚିଠି ପାଇଲି । ତୋ’ ଜେଜେଙ୍କ ମୃତ୍ୟୁରେ ତୁ’ ଯେ ଗଭୀର ଭାବେ ମର୍ମାହତ ତାହା ମୁଁ ଅନୁଭବ କଲି । ତୋ’ ଦୁଃଖରେ ସମବେଦନା ଜଣାଇବାକୁ ଦୁଇଧାଡ଼ି ଲେଖୁଛି । ତତେ ଉପଦେଶ ଦେଉଛି ବୋଲି ଭାବିବୁନି । ଏହା ଅବଶ୍ୟ ସତ ଯେ ମଣିଷ ଯାହାଠାରୁ ବେଶୀ ସ୍ନେହ ଆଦର ପାଇଥାଏ ତା’ ବିୟୋଗରେ ମନ ଭିତରେ ଯେଉଁ ଶୂନ୍ୟସ୍ଥାନ ସୃଷ୍ଟି ହୁଏ ତାହା ଅପୂରଣୀୟ। ତାଙ୍କର ସେହି ସ୍ନେହବୋଳା ଡାକ, ମମତାଭରା କଥାପଦେ ତୁ ଆଉ ଶୁଣିବୁନି ।

କିନ୍ତୁ ଏକଥା ମଧ୍ୟ ସତ ଯେ ‘ଜାତସ୍ୟ ହି ଧ୍ରୁବମୃତ୍ୟୁ ।’’ ମଣିଷ ଦିନେ ନା ଦିନେ ଧରାଧାମରୁ ବିଦାୟ ନେବ ଏବଂ ଏହା ବିଧ୍ଵନିର୍ଦ୍ଦିଷ୍ଟ । ସାର୍ କହୁଥିଲେ, ଆତ୍ମାର ମୃତ୍ୟୁ ନାହିଁ । ଜରାଜୀର୍ଣ୍ଣ ପୋଷାକ ପରିବର୍ତ୍ତନ କରି ଏକ ନୂତନ ପୋଷାକ ପରିଧାନ କରିବା ପରି ଆତ୍ମା କେବଳ ଘଟ ପରିବର୍ତ୍ତନ କରେ । ସ୍ୱର୍ଗରେ ଥାଇ ତାଙ୍କ ଆତ୍ମା ତୋ’ ଉପରେ ନିଶ୍ଚୟ ଆଶିଷ ବର୍ଷା କରିବେ ଏଥ‌ିରେ ସନ୍ଦେହ ନାହିଁ । ତା’ ଛଡ଼ା ତାଙ୍କ ପାଇଁ ମନକୁ ବିଷାଦିତ କରି ବସିରହିବା ମଧ୍ୟ ବିବେକୀର ଲକ୍ଷଣ ନୁହେଁ ।

ମନ ଭାରାକ୍ରାନ୍ତ ରହିଲେ କୌଣସି କାମରେ ଉତ୍ସାହ ଆସେନାହିଁ ସତ୍ୟ; ମାତ୍ର କର୍ତ୍ତବ୍ୟରେ ଅବହେଳା କଲେ ତା’ର ପରିଣାମ ଆମକୁ ହିଁ ଭୋଗିବାକୁ ପଡ଼ିବ । ଯିଏ ଯେତେଦିନ ପାଇଁ ଆସିଛନ୍ତି ସେଥୁରୁ ମୁହୂର୍ଭେ ଅଧିକ ସମୟ ରଖୁବା କଦାପି ସମ୍ଭବ ନୁହେଁ । ଜନ୍ମ ଓ ମୃତ୍ୟୁ ପରି ଜୀବନର ଦୁଇ ମହାସତ୍ୟକୁ ଆମକୁ ମାନିବାକୁ ହେବ । ଠିକ୍ ଅନୁରୂପଭାବେ ଆମ କର୍ମମୟ ଜୀବନକୁ କିପରି କର୍ତ୍ତବ୍ୟ ସମ୍ପାଦନ ପୂର୍ବକ ଅଧ୍ଵ ସାର୍ଥକ କରିହେବ ତାହା ଚିନ୍ତା କରିବାକୁ ହେବ । କର୍ମ ହିଁ ଜୀବନ । କର୍ମତତ୍ପର ରହିବାଦ୍ୱାରା ଆମେ ଆମ ମନର ସବୁ ଦୁଃଖ ଭୁଲିଯାଇ ପାରିବା ।

ତା’ ଛଡ଼ା ମନର ସୁସ୍ଥତା ରହିଲେ କର୍ମରେ ଉତ୍ସାହ ଆସେ । ତୁ’ ତ ଜାଣୁ, ଯେ ଆମେ ଯେତେବେଳେ କୌଣସି ଏକ କାମରେ ନିୟୋଜିତ ରହୁ, ସେତେବେଳେ ଅନ୍ୟକୌଣସି ଭାବନା ମନକୁ ଆସେନାହିଁ । ତୁମର ମଧ୍ଯ କୁନ୍ତଳା କୁମାରୀଙ୍କ ‘ମଣିଷ ଭାଇ’ କବିତା ପଢ଼ା ସରିଥିବ । ନାରୀକବି କର୍ମର ଜୟଗାନ କରି ଯେଉଁ ପରାମର୍ଶଗୁଡ଼ିକ ଦେଇଛନ୍ତି ସେଗୁଡ଼ିକ ବହୁତ ମନଛୁଆଁ ନା ! ଈଶ୍ବରଙ୍କ ଏହି ଚିରଶୋଭାମୟ ସଂସାର ହେଉଛି ମାନବର କର୍ମଭୂମି । ତାଙ୍କ ପଦାରବିନ୍ଦରେ ସବୁ ଦୁଃଖ, ଦୁର୍ଭାବନାକୁ ସମର୍ପଣ କରି କର୍ମରେ ନିୟୋଜିତ ରହିଲେ, ସେ ସବୁ ସମସ୍ୟାର ସମାଧାନ କରିଦେବେ ।

ସ୍ୱାତୀ, ତୋ’ ପଢ଼ାପଢ଼ି ବିଷୟରେ ଲେଖୁ ଜଣାଇବୁ । ମାସିକ ପରୀକ୍ଷାଗୁଡ଼ିକରେ କେମିତିସବୁ ନମ୍ବର ଆସୁଛି ଜଣାଇବୁ । ଗଲା ପରୀକ୍ଷାରେ ଗଣିତରେ ମୋର ଭଲ ହେଲା; କିନ୍ତୁ ବିଜ୍ଞାନରେ ଭଲ ପ୍ରସ୍ତୁତି ନ ଥିବାରୁ ବହୁତ ଖରାପ ନମ୍ବର ଆସିଲା । ଭଲ ମନ୍ଦ ଜଣାଇ ମଝିରେ ମଝିରେ ଚିଠି ଖଣ୍ଡେ ଖଣ୍ଡେ ଦେଉଥୁବୁ । ରହୁଛି ।

ତୋର ସାଙ୍ଗ

ଠିକଣା
ପ୍ରେରକ :	ପ୍ରାପ୍ତେଷୁ : [ଉ।କଟିକଟ]
ପୂଜା ପ୍ରିୟଦଶିନୀ ମାଫିତ୍ – ସଂଗ୍ରାମ ପଟ୍ଟନାୟକ ସେକ୍ଟର – ୬ ସି.ଡି.ଏ. ମର୍କତ ନଗର, କଟକ – ୭୫୩୦୧୪	ସ୍ୱ।ତୀ ସ୍ୱ।ଗତିକା ମାଫିତ – ପ୍ରବୀର ମହାପାତ୍ର କ୍ବାଟର ନମ୍ବର – ସି ୯୫ ଛେଣ୍ଡ କଲୋନୀ ରାଉରକେଲା – ୭୫୯୦୦୨

ତୁମପାଇଁ କାମ

୪୧ । କୁନ୍ତଳା କୁମାରୀଙ୍କ ରଚନାଗୁଡ଼ିକ ସଂଗ୍ରହ କରି ପଢ଼ ।
୪୨ । କୁନ୍ତଳା କୁମାରୀଙ୍କ ସମସାମୟିକ କବିମାନଙ୍କର ଏକ ତାଲିକା ପ୍ରସ୍ତୁତ କର ।
୪୩ । ମାନବିକ ମୂଲ୍ୟବୋଧ ପ୍ରକାଶ କରୁଥ‌ିବା ପଦଗୁଡ଼ିକୁ ବାଛି ଟିପାଖାତାରେ ଟିପି ରଖ ।

ପରୀଷା ଉପଯୋଗୀ ଅତିରିକ୍ତ ପ୍ରଶୋତ୍ତର
ଅତିସଂକ୍ଷିପ୍ତ ଓ ବସ୍ତୁନିଷ୍ଠ ପ୍ରଶ୍ନୋତ୍ତର
A ଗୋଟିଏ ବାକ୍ୟରେ ଉତ୍ତର ଲେଖ ।
1. କବି ‘ବରପୁତ୍ର’ ବୋଲି ସମ୍ବୋଧନ କାହାକୁ କରିଛନ୍ତି ?
Answer:
କବି ମାନବକୁ ବିଧାତାର ବରପୁତ୍ର ବୋଲି ସମ୍ବୋଧନ କରିଛନ୍ତି ।

2. କବି ମାନବକୁ ‘ବରପୁତ୍ର’ ବୋଲି କାହିଁକି କହିଛନ୍ତି ?
Answer:
ମାନବ ଦିବ୍ୟ ମାନବୀୟ ଗୁଣାବଳୀରେ ଭୂଷିତ ହୋଇ ଦେବତ୍ୱର ଅଧିକାରୀ ହୋଇପାରେ । କବି ମାନବକୁ ବରପୁତ୍ର ବୋଲି କହିଛନ୍ତି ।

3. ହୋଇପାରିବ ବୋଲି କବି କହିଛନ୍ତି ?
Answer:
ମୃତ୍ୟୁରଜୁକୁ ଛିନ୍ନ କରି ଜୀବନ ସୂତ୍ରକୁ ଧରି ସ୍ଵକର୍ତ୍ତବ୍ୟ ପଥରେ ଅଗ୍ରସର ହେଲେ ଜୀବନ ସୁରୁଖୁରୁରେ ଅତିବାହିତ ହୋଇପାରିବ ବୋଲି କବି କହିଛନ୍ତି ।

4. କବି ‘ମଣିଷ ଭାଇ’ ବୋଲି କେଉଁମାନଙ୍କୁ ସମ୍ବୋଧନ କରିଛନ୍ତି ?
Answer:
ସମାଜରେ ଶୋଷିତ, ଲାଞ୍ଛିତ ଓ ନିଷ୍ପେଷିତ ମଣିଷମାନଙ୍କୁ କବି ‘ମଣିଷ ଭାଇ’ ବୋଲି ସମ୍ବୋଧନ କରିଛନ୍ତି ।

5. ମଣିଷ କେଉଁପାଇଁ ଜନ୍ମଲାଭ କରିନାହିଁ ବୋଲି କବି କହିଛନ୍ତି ?
Answer:
ମଣିଷ ଝୁରି ମରିବାକୁ କିମ୍ବା ବୁଡ଼ି ମରିବାକୁ ଜନ୍ମଲାଭ କରିନାହିଁ ବୋଲି କବି କହିଛନ୍ତି ।

6. ନୈରାଶ୍ୟକୁ ଅନ୍ଧାର ରୂପେ କବି କାହିଁକି ଦେଖୁଛନ୍ତି ?
Answer:
ମଣିଷ ଆଶାଶୂନ୍ୟ ହୋଇଗଲେ, ତାକୁ ଚାରିଆଡ଼ ଅନ୍ଧାର ଦେଖାଯାଏ, ତେଣୁ କବି ନୈରାଶ୍ୟକୁ ଅନ୍ଧାର ରୂପେ ବର୍ଣ୍ଣନା କରିଛନ୍ତି ।

7. ମଣିଷର ଭାଗ୍ୟ କାହା ମଧ୍ୟରେ ସୀମାବଦ୍ଧ ବୋଲି କବି କହିଛନ୍ତି ?
Answer:
ମଣିଷର ଭାଗ୍ୟ ଲାଞ୍ଛନା, ପ୍ରବଞ୍ଚନା ତଥା ଦୁଃଖଯନ୍ତ୍ରଣା ମଧ୍ୟରେ ସୀମାବଦ୍ଧ ନୁହେଁ ।

8. ହତୋତ୍ସାହ ହୋଇପଡ଼ିଥି ମନୁଷ୍ୟ ପୃଥ‌ିବୀକୁ କେଉଁ ଦୃଷ୍ଟିରେ ଦେଖେ ?
Answer:
ହତୋତ୍ସାହ ହୋଇପଡ଼ିଥି ମନୁଷ୍ୟ ଏ ପୃଥ‌ିବୀକୁ ‘ଧ୍ୱଂସର ଯାତ୍ରୀ ତଥା ମୃତ୍ୟୁର ଧାତ୍ରୀ’ ରୂପେ ଦେଖେ ।

୨. ‘ ଅମୃତର ସନ୍ତାନ’ ବୋଲି କେଉଁମାନଙ୍କୁ କୁହାଯାଇଛି ?
Answer:
‘ଅମୃତର ସନ୍ତାନ’ ବୋଲି ମାନବମାନଙ୍କୁ କୁହାଯାଇଛି ।

10. ବିଶାଳ ଜଗତର ସୃଷ୍ଟି କ’ଣ ପାଇଁ ନୁହେଁ ବୋଲି କବି କହିଛନ୍ତି ?
Answer:
ବିଶାଳ ଜଗତ କାହାରି ବିଳାସର ଲୀଳାକ୍ଷେତ୍ର ନିମନ୍ତେ ସୃଷ୍ଟି ନୁହେଁ ବୋଲି କବି କହିଛନ୍ତି ।

11. କେଉଁ ଧରଣର ପିପାସା ମେଣ୍ଟେ ନାହିଁ ?
Answer:
ଦୁର୍ବଳକୁ ପଦଦଳିତ କରି ନିର୍ଦ୍ଦୟଭାବରେ ତା’ପ୍ରତି ଅତ୍ୟାଚାର କରି ତା’ର ରକ୍ତକ୍ଷୟ କରିବାର ପିପାସା କେବେହେଲେ ମେଣ୍ଟେ ନାହିଁ ।

12. ବିଶ୍ବ କେଉଁମାନଙ୍କ ପାଇଁ ସୁନ୍ଦର ନୁହେଁ ?
Answer:
ନୈରାଶ୍ୟଦଗ୍‌ଧ ହୋଇ ସଂସାରକୁ ଧ୍ୱଂସାଭିମୁଖୀ ତଥା ଜୀବନକୁ ମୃତ୍ୟୁପଥର ଯାତ୍ରୀ ବୋଲି ବିବେଚନା କରୁଥିବା ମାନବ ପାଇଁ ଏ ବିଶ୍ଵ ସୁନ୍ଦର ନୁହେଁ ।

13. ବିଧାତାଙ୍କ ବିଚାରରେ କେଉଁ କାର୍ଯ୍ୟ ଉଚିତ ନୁହେଁ ?
Answer:
ବିଶ୍ବକୁ ବିଳାସ କ୍ଷେତ୍ର ମନେକରି ଦୁର୍ବଳକୁ ପଦଦଳିତ କରି ନିଜକୁ ନିଜେ ବିନାଶ କରିବା ବିଧାତାଙ୍କ ବିଚାର ନୁହେଁ ।

14. କବି କିଭଳି ସଂସାରର ପରିକଳ୍ପନା କରିଛନ୍ତି ?
Answer:
କବି ସଂସାରକୁ କର୍ମର ଶୁଭ ଭୁବନ ଭାବେ ପରିକଳ୍ପନା କରିଛନ୍ତି ।

15. ମଣିଷ କେତେବେଳେ ବୀରତ୍ଵର ଟୀକା ଲାଭ କରିପାରିବ ?
Answer:
ଲଜ୍ଜା, ଭୟ, ଅପମାନ ଓ ଅହଂକାରକୁ ତ୍ୟାଗକରି ପଶୁତ୍ଵ-ଦେବତ୍ଵ ପରୀକ୍ଷାରେ ବିଜୟୀ ହେବାପରେ ମନୁଷ୍ୟ ବୀରତ୍ଵର ଟୀକା ଲାଭ କରିପାରିବ ।

16. କବି ଏହି ପୃଥ‌ିବୀକୁ କାହାର ଭୁବନ ବୋଲି ଦର୍ଶାଇଛନ୍ତି ?
Answer:
କବି ଏହି ପୃଥ‌ିବୀକୁ କର୍ମର ଶୁଭ ଭୁବନ ବୋଲି

17. ମଣିଷକୁ କେଉଁ ପ୍ରବୃତ୍ତିଗୁଡ଼ିକୁ ତ୍ୟାଗ କରିବାପାଇଁ କବି ଆହ୍ୱାନ ଦେଇଛନ୍ତି ?
Answer:
କବି ଲଜ୍ଜା, ଭୟ, ଅପମାନ ଓ ଅହମିକା ପ୍ରଭୃତି କୁପ୍ରବୃତ୍ତିଗୁଡ଼ିକୁ ତ୍ୟାଗ କରିବାପାଇଁ ମଣିଷକୁ ଆହ୍ଵାନ ଦେଇଛନ୍ତି ।

18. ଭଗବାନଙ୍କୁ
ଋଣୀ କରାଯାଇପାରିବ ?
Answer:
ବିଶ୍ବ ଜୀବନର କଲ୍ୟାଣ ନିମନ୍ତେ ଆୟୋତ୍ସର୍ଗ କରିପାରିଲେ ହିଁ ଭଗବାନଙ୍କୁ ଋଣୀ କରାଯାଇପାରିବ ।

19. ମଣିଷ ଭାଇକୁ କବି ‘ଅରିନ୍ଦମ’ ବୋଲି କାହିଁକି ସମ୍ବୋଧନ କରିଛନ୍ତି ?
Answer:
ମାନବ ହିଁ କାମ, କ୍ରୋଧ, ଲୋଭ, ମୋହ, ମଦ ଓ ମାସ୍କର୍ଯ୍ୟ ପ୍ରଭୃତି ଷଡ଼ରିପୁଙ୍କୁ ଜୟ କରିପାରେ ବୋଲି କବି ତାକୁ ‘ଅରିନ୍ଦମ’ ବୋଲି କହିଛନ୍ତି ।

20. ମଣିଷ କେତେବେଳେ ଦେବତା ରୂପେ ପୂଜିତ ହୋଇପାରିବ ?
Answer:
ମାନବ ଯେତେବେଳେ କାମ-କ୍ରୋଧାଦି ଷଡ଼ରିପୁକୁ ଜୟକରି ବିଶ୍ୱଜୀବନର କଲ୍ୟାଣ ନିମନ୍ତେ ଆୟୋତ୍ସର୍ଗ କରିବାକୁ ସମର୍ଥ ହେବ, ସେତେବେଳେ ସେ ଦେବତାରୂପେ ପୂଜିତ ହୋଇପାରିବ ।

B ଗୋଟିଏ ଶବ୍ଦରେ ଉତ୍ତର ଲେଖ ।
1. ବ୍ୟକ୍ତି ନିଜର ଭବିଷ୍ୟତକୁ କାହା ଉପରେ ଛାଡ଼ିଦିଏ ?
Answer:
ନିୟତି ଉପରେ

2. କିଏ ଝୁରି ମରିବାକୁ ବୁଡ଼ି ମରିବାକୁ ଜନମି ନାହିଁ ବୋଲି କବି କହିଛନ୍ତି ?
Answer:
ମାନବ

3. ଏ ବିଶାଳ ଜଗତୀ କାହାର ଯାତ୍ରୀ ନୁହେଁ ?
Answer:
ଧ୍ବଂସର

4. ଏ ସଂସାରକୁ କବି କାହାର ଶୁଭ ଭୁବନ ବୋଲି ବର୍ଣ୍ଣନା କରିଛନ୍ତି ?
Answer:
କର୍ମର

5. କେଉଁ ପରୀକ୍ଷାରେ ବିଜୟୀ ହୋଇ ବୀରତ୍ଵର ଟୀକା ଲାଭ କରିବାକୁ କବି କହିଛନ୍ତି ?
Answer:
ପଶୁତ୍ଵ -ଦେବତ୍ୱ

6. ପଶଉତ୍ସ- ଦେବତ୍ୱ ପରୀକ୍ଷାରେ ବିଜୟୀ ହୋଇ କାହାକୁ ଋଣୀ କରିବାକୁ କବି କହିଛନ୍ତି ?
Answer:
ଈଶ୍ବରଙ୍କୁ

7. ଏ ସାରା ସଂସାରର ରଚୟିତା କିଏ ?
Answer:
ଈଶ୍ବର

8. କବି କାହାକୁ ବିଧାତାର ବରପୁତ୍ର ବୋଲି କହିଛନ୍ତି ?
Answer:
ମଣିଷକୁ

9. କବି ମଣିଷ ଭାଇକୁ କେଉଁ ରଜ୍ଜୁ ଛିଣ୍ଡାଇବାକୁ କହିଛନ୍ତି ?
Answer:
ଯୁଗାନ୍ତ-ମୃତ୍ୟୁ ରଜ୍ଜୁ

10. କେଉଁ ସୂତ୍ର ଧରିବାକୁ କବି ମଣିଷ ଭାଇକୁ ନିବେଦନ କରିଛନ୍ତି ?
Answer:
ଜୀବନ ସୂତ୍ର

11. ଅମୃତ ଦୀପ୍ତି ସନ୍ତାନ ଭାବେ କବି କାହାକୁ ବର୍ଣନା କରିଛନ୍ତି ?
Answer:
ମଣିଷମାନଙ୍କୁ

12. କାହାକୁ କବି ଅନ୍ଧକାର ରୂପେ ବର୍ଣ୍ଣନା କରିଛନ୍ତି ?
Answer:
ନୈରାଶ୍ୟ

13. ‘ନିକେତନ’ ଶବ୍ଦର ଅର୍ଥ କ’ଣ ?
Answer:
ଗୃହ

14. ବିଧାତାଙ୍କ ବିଚାରରେ କେଉଁ କାର୍ଯ୍ୟ ଉଚିତ ନୁହେଁ ?
Answer:
ଆପଣାକୁ ଆପେ ବଧୂ

15. ଏ ସଂସାର କେଉଁମାନଙ୍କ ପାଇଁ ସୁନ୍ଦର ନୁହେଁ ?
Answer:
ଧ୍ଵଂସର ଯାତ୍ରୀ ଓ ମୃତ୍ୟୁର ଧାତ୍ରୀ

16. କାହାକୁ ଋଣୀ କରିବାକୁ କବି ମନୁଷ୍ୟମାନଙ୍କୁ କହିଛନ୍ତି ?
Answer:
ଭବରାଣଙ୍କୁ

17. ‘ମଣିଷ ଭାଇ’ କବିତାର କବି କିଏ ?
Answer:
କୁନ୍ତଳାକୁମାରୀ ସାବତ୍

18. ‘ମଣିଷ ଭାଇ’ କବିତାଟି କବିଙ୍କର କେଉଁ କବିତା ପୁସ୍ତକରୁ ଆସିଅଛି ?
Answer:
ସ୍ଫୁଲିଙ୍ଗ

19. କୁନ୍ତଳାକୁ ମାରୀ କେଉଁ ଉପାଧ୍ଧରେ ଭୂଷିତ ହୋଇଥିଲେ ?
Answer:
ଉତ୍କଳ ଭାରତୀ

20. କବିତାରେ କବି କାହାକୁ ଭାଇଁ ବୋଲି ସମ୍ବୋଧନ କରିଛନ୍ତି ?
Answer:
ମଣିଷକୁ

C ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
1. କବିଙ୍କ ମତରେ ମଣିଷ ହେଉଛି ବିଧାତାର _______________।
Answer:
ବରପୁତ୍ର

2. କବିଙ୍କ ମତରେ ପରମେଶ୍ବରଙ୍କ ସୃଷ୍ଟ ଏ ସଂସାର ଚିର ଆନନ୍ଦମୟ ଓ ________________ ।
Answer:
ମଙ୍ଗଳମୟ

3. କର୍ମର ଶୁଭ ଭୁବନ ବୋଲି କବି ____________ କୁ କହିଛନ୍ତି ।
Answer:
ସଂସାର

4. କବି ଅରିନ୍ଦମ ବୋଲି __________________ କୁ ସମ୍ବୋଧନ କରିଛନ୍ତି ।
Answer:
ମଣିଷ

5. __________________ ର ଆସନ ତାରା ଦଳେ ବୋଲି କବି କହିଛନ୍ତି ।
Answer:
ମଣିଷ

6. _______________ ପ୍ରବୃତ୍ତିଗୁଡ଼ିକୁ ତ୍ୟାଗ କରିବାକୁ କବି ମଣିଷକୁ ଆହ୍ବାନ ଦେଇଛନ୍ତି ।
Answer:
ଲାଜ, ଭୟ, ଅପମାନ

7. ମଣିଷ ନିଜ ଭିତରେ ଥ‌ିବା _______________ ଗୁଡ଼ିକୁ ଦମନ କଲେ ଦେବତାର ଆସନ ଲାଭ କରିପାରିବ ।
Answer:
ଅନ୍ତଃଶତ୍ରୁ

8. ଏ ପୃଥ‌ିବୀ ନିରନ୍ତର ________________ ପଥରେ ଆଗେଇ ଚାଲିଛି ।
Answer:
ଧ୍ବଂସ

9. ‘ଚରାଚର’ କହିଲେ _____________________ କୁ ବୁଝାଏ ।
Answer:
ସାରା ସଂସାର

10. କୁନ୍ତଳାକୁମାରୀଙ୍କର ବୃତ୍ତି ______________ ଥିଲା ।
Answer:
ଡାକ୍ତରି

11. ଦେବତା ପୂଜିତ ______________ ରେ ତବାସନ ବୋଲି କବି ମଣିଷକୁ କହିଛନ୍ତି ।
Answer:
ଆକାଶ

12. ________________ କାଳିରେ ଦୀନହୀନ ନ ହେବାକୁ କବି ମଣିଷ ଭାଇକୁ କହିଛନ୍ତି ।
Answer:
କଳୁଷର କଳଙ୍କ

13. କବିତାରେ କବି ______________ କୁ ଭାଇ ବୋଲି ସମ୍ବୋଧନ କରିଛନ୍ତି ।
Answer:
ମଣିଷ

14. ମଣିଷ ______________ ପାଇଁ ଜନ୍ମଲାଭ କରିନାହିଁ ବୋଲି କବି କହିଛନ୍ତି ।
Answer:
ଝୁରି ମରିବାକୁ

15. କବି ନୈରାଶ୍ୟକୁ _____________ ରୂପରେ ବର୍ଣ୍ଣନା କରିଛନ୍ତି ।
Answer:
ଅନ୍ଧାର

16. ମଣିଷର ନିୟତି _____________ ମଣିଷର ନିୟତି ବୋଲି କବି କହିଛନ୍ତି ।
Answer:
କଷଣ କାରା

17. ହତୋତ୍ସାହ ହୋଇପଡ଼ିଥି ମନୁଷ୍ୟ ପୃଥ‌ିବୀକୁ ___________ ଦୃଷ୍ଟିରେ ଦେଖନ୍ତି ।
Answer:
ମୃତ୍ୟୁର ଧାତ୍ରୀ

18. କବି ______________ ମାନଙ୍କୁ ଅମୃତର ସନ୍ତାନ ବୋଲି କହିଛନ୍ତି ।
Answer:
ମଣିଷ

19. ଏ ବିଶାଳ ଜଗତୀ ______________ ର ଧାତ୍ରୀ ନୁହେଁ ।
Answer:
ମୃତ୍ୟୁ

20. କବିଙ୍କ ମତରେ _______________ ର ମରଣ ନାହିଁ ।
Answer:
ଅମୃତଦୀପ୍ତ ସନ୍ତାନ

D ଠିକ୍ କିମ୍ବା ଭୁଲ୍ ଲେଖ ।
1. ପଶୁ ଝୁରି ମରିବାକୁ ବୁଡ଼ି ମରିବାକୁ ଜନମି ନାହିଁ ବୋଲି
Answer:
ଭୁଲ୍

2. ଏ ସଂସାରକୁ କବି ଭାଗ୍ୟର ଶୁଭ ଭୁବନ ବୋଲି ବର୍ଣ୍ଣନା କରିଛନ୍ତି ।
Answer:
ଭୁଲ୍

3. ପଶୁତ୍ଵ-ଦେବତ୍ୱ ପରୀକ୍ଷାରେ ବିଜୟୀ ହୋଇ ମଣିଷକୁ ଋଣୀ କରିବାକୁ କବି କହିଛନ୍ତି ।
Answer:
ଭୁଲ୍

4. କବି ମଣିଷକୁ ବିଧାତାର ବରପୁତ୍ର ବୋଲି କହିଛନ୍ତି ।
Answer:
ଠିକ୍

5. ଜୀବନ ସୂତ୍ର ଧରିବାକୁ କବି ମଣିଷ ଭାଇକୁ ନିବେଦନ କରିଛନ୍ତି ।
Answer:
ଠିକ୍

6. ନୈରାଶ୍ୟକୁ କବି ଅନ୍ଧକାର ରୂପେ ବର୍ଣ୍ଣନା କରିଛନ୍ତି ।
Answer:
ଠିକ୍

7. ବିଧାତାଙ୍କ ବିଚାରରେ ଆପଣାକୁ ଆପେ ବାଧିବା କାର୍ଯ୍ୟ ଉଚିତ ନୁହେଁ ।
Answer:
ଠିକ୍

8. ଭବରାଣଙ୍କୁ ଋଣୀ କରିବାକୁ କବି ମନୁଷ୍ୟମାନଙ୍କୁ କହିଛନ୍ତି ।
Answer:
ଠିକ୍

9. କବିତାରେ କବି ଭଗବାନକୁ ଭାଇ ବୋଲି ସମ୍ବୋଧନ କରିଛନ୍ତି ।
Answer:
ଭୁଲ୍

10. କବିଙ୍କ ମତରେ ପରମେଶ୍ବରଙ୍କ ସୃଷ୍ଟି ଏ ସଂସାର ଚିର ଆନନ୍ଦମୟ ଓ ମଙ୍ଗଳମୟ ।
Answer:
ଠିକ୍

11. କବି ଅରିନ୍ଦମ ବୋଲି ଭଗବାନକୁ ସମ୍ବୋଧନ କରିଛନ୍ତି ।
Answer:
ଭୁଲ୍

12. ଲାଜ, ଭୟ, ଅପମାନ ପ୍ରବୃତ୍ତିଗୁଡ଼ିକୁ ତ୍ୟାଗ କରିବାକୁ କବି ମଣିଷକୁ ଆହ୍ଵାନ ଦେଇଛନ୍ତି ।
Answer:
ଠିକ୍

13. ଏ ପୃଥ‌ିବୀ ନିରନ୍ତର ଅଗ୍ରସର ପଥରେ ଆଗେଇ ଚାଲିଛି ।
Answer:
ଭୁଲ୍

14. କୁନ୍ତଳାକୁମାରୀଙ୍କର ବୃତ୍ତି ଚାକିରି ଥିଲା ।
Answer:
ଭୁଲ୍

E ଚାରୋଟି ବିକଳ୍ପ ମଧ୍ୟରୁ ଠିକ୍ ଉତ୍ତରଟି ବାଛି ଲେଖ ।
1. ବ୍ୟକ୍ତି ନିଜର ଭବିଷ୍ୟତକୁ କାହା ଉପରେ ଛାଡ଼ି ଦିଅନ୍ତି ?
(A) କର୍ମ
(B) କର୍ତ୍ତବ୍ଯ
(C) ନିୟତି
(D) ଭଗବାନ୍
Answer:
(C) ନିୟତି

2. କିଏ ଝୁରି ମରିବାକୁ ବୁଡ଼ି ମରିବାକୁ ଜନମି ନାହିଁ ବୋଲି କବି କହିଛନ୍ତି ?
(A) ମାନବ
(B) ମହାମାନବ
(C) ପରମପୁରୁଷ
(D) ପୁରୁଷୋତ୍ତମ
Answer:
(A) ମାନବ

3. ଏ ବିଶାଳ ଜଗତୀ କାହାର ଯାତ୍ରୀ ନୁହେଁ ?
(A) ମୃତ୍ୟୁର
(B) ଧ୍ବଂସର
(C) ଦାରିଦ୍ର୍ୟର
(D) ଅନଟନର
Answer:
(B) ଧ୍ବଂସର

4. ଏ ସଂସାରକୁ କବି କାହାର ଶୁଭ ଭୁବନ ବୋଲି ବର୍ଣ୍ଣନା କରିଛନ୍ତି ?
(A) କର୍ମର
(B) ଧର୍ମର
(C) ତ୍ଯାଗର
(D) ଉପକାରର
Answer:
(A) କର୍ମର

5. କେଉଁ ପରୀକ୍ଷାରେ ବିଜୟୀ ହୋଇ ବୀରତ୍ଵର ଟୀକା ଲାଭ କରିବାକୁ କବି କହିଛନ୍ତି ?
(A) ପଶୁତ୍ଵ-ଦେବତ୍ଵ
(B) ଦେବତ୍ୱ-ମାନବତ୍ଵ
(C) ମାନବତ୍ବ-ପଶୁତ୍ଵ
(D) ଦେବତ୍ୱ-ଦାନବତ୍ୱ
Answer:
(A) ପଶୁତ୍ଵ-ଦେବତ୍ଵ

6. ପରୀକ୍ଷାରେ ବିଜୟୀ ହୋଇ କାହାକୁ ଋଣୀ କରିବାକୁ କବି କହିଛନ୍ତି ?
(A) ପୃଥିବୀବାସୀଙ୍କୁ
(B) ଦେବତାଙ୍କୁ
(C) ଈଶ୍ବରଙ୍କୁ
(D) ସଂସାରକୁ
Answer:
(C) ଈଶ୍ବରଙ୍କୁ

7. ଏ ସାରା ସଂସାରର ରଚୟିତା କିଏ ?
(A) ସୂର୍ଯ୍ୟ
(B) ଈଶ୍ବର
(C) କର୍ମ
(D) ଚନ୍ଦ୍ର
Answer:
(B) ଈଶ୍ବର

8. କବି କାହାକୁ ବିଧାତାର ବରପୁତ୍ର ବୋଲି କହିଛନ୍ତି ?
(A) ମହାପୁରୁଷମାନଙ୍କୁ
(B) ସଜ୍ଜନଙ୍କୁ
(C) ମଣିଷକୁ
(D) ଦେବତାଙ୍କୁ
Answer:
(C) ମଣିଷକୁ

9. କବି ମଣିଷ ଭାଇକୁ କେଉଁ ରଜ୍ଜୁ ଛିଣ୍ଡାଇବାକୁ କହିଛନ୍ତି ?
(A) ଜୀବନ ରଜ୍ଜୁ
(B) ବନ୍ଧୁତ୍ଵ ରଜୁ
(C) ଯୁଗାନ୍ତ-ମୃତ୍ୟୁ ରଜ୍ଜୁ
(D) ସମ୍ପର୍କ ରଜ୍ଜୁ
Answer:
(C) ଯୁଗାନ୍ତ-ମୃତ୍ୟୁ ରଜ୍ଜୁ

10. କେଉଁ ସୂତ୍ର ଧରିବାକୁ କବି ମଣିଷ ଭାଇକୁ ନିବେଦନ କରିଛନ୍ତି ?
(A) ସମ୍ପର୍କ ସୂତ୍ର
(B) ଜନ୍ମ ସୂତ୍ର
(C) ଜୀବନ ସୂତ୍ର
(D) ମୃତ୍ୟୁ ସୂତ୍ର
Answer:
(C) ଜୀବନ ସୂତ୍ର

11. କେଉଁ ଧରଣର ପିପାସା ମେଣ୍ଟେ ନାହିଁ ?
(A) ଜଳ ପିପାସା
(B) ସୁରା ପିପାସା
(C) ରକ୍ତ ପିପାସା
(D) କେଉଁଟି ନୁହେଁ
Answer:
(D) କେଉଁଟି ନୁହେଁ

12. କେଉଁଟି ମାନବର ଷଡ଼ରିପୁ ମଧ୍ୟରୁ ଏକ ଶତ୍ରୁ ନୁହେଁ ?
(A) କାମ
(B) କ୍ରୋଧ
(C) ଲୋଭ
(D) କ୍ଷମା
Answer:
(D) କ୍ଷମା

13. କର୍ମର ଶୁଭ ଭୁବନ ବୋଲି କବି କାହାକୁ କହିଛନ୍ତି ?
(A) ସଂସାରକୁ
(B) ପାତାଳକୁ
(C) ସ୍ବର୍ଗକୁ
(D) ତ୍ରିଲୋକକୁ
Answer:
(A) ସଂସାରକୁ

14. କବି ଅରିନ୍ଦମ ବୋଲି କାହାକୁ ସମ୍ବୋଧନ କରିଛନ୍ତି ?
(A) ଈଶ୍ବରଙ୍କୁ
(B) ସବଳକୁ
(C) ଦୁର୍ବଳକୁ
(D) ମଣିଷକୁ
Answer:
(D) ମଣିଷକୁ

15. ତାରା ଦଳେ କାହାର ଆସନ ବୋଲି କବି କହିଛନ୍ତି ?
(A) ଚନ୍ଦ୍ରଙ୍କର
(B) ସୂର୍ଯ୍ୟଙ୍କର
(C) ସପ୍ତର୍ଷିମଣ୍ଡଳର
(D) ମଣିଷର
Answer:
(D) ମଣିଷର

16. ମଣିଷର କେଉଁ ପ୍ରବୃତ୍ତିଗୁଡ଼ିକୁ ତ୍ୟାଗ କରିବାକୁ କବି ଆହ୍ବାନ ଦେଇଛନ୍ତି ?
(A) ସତ୍ୟ, ଧର୍ମ, ନ୍ୟାୟ
(B) କ୍ରୋଧ, ଲୋଭ, ମୋହ
(C) ଲାଜ, ଭୟ, ଅପମାନ
(D) ଦୟା, କ୍ଷମା, ସଂଯମ
Answer:
(C) ଲାଜ, ଭୟ, ଅପମାନ

17. ମଣିଷ କେତେବେଳେ ଦେବତାର ଆସନ ଲାଭ କରିପାରିବ ?
(A) ସ୍ଵର୍ଗଜୟ କଲେ
(B) ପୃଥ‌ିବୀର ରାଜା ହେଲେ
(C) ତା’ ଭିତରେ ଥ‌ିବା ଅନ୍ତଃ ଶତ୍ରୁଗୁଡ଼ିକୁ ଦମନ କଲେ
(D) ସୁକାର୍ଯ୍ୟ କଲେ
Answer:
(C) ତା’ ଭିତରେ ଥ‌ିବା ଅନ୍ତଃ ଶତ୍ରୁଗୁଡ଼ିକୁ ଦମନ କଲେ

18. ଏ ପୃଥ‌ିବୀ ନିରନ୍ତର କେଉଁ ପଥରେ ଆଗେଇ ଚାଲିଛି ?
(A) ଅବନତି ପଥରେ
(B) ଉନ୍ନତି ପଥରେ
(C) ଧ୍ବଂସପଥରେ
(D) ଗତିପଥରେ
Answer:
(C) ଧ୍ବଂସପଥରେ

19. ‘ରୋଚର’ କହିଲେ କ’ଣ ବୁଝ ?
(A) ଚାରଣ ଭୂମି
(B) ଗୋଚର ଭୂମି
(C) ମରୁଭୂମି
(D) ସାରା ସଂସାର
Answer:
(D) ସାରା ସଂସାର

20. କୁନ୍ତଳାକୁମାରୀଙ୍କର ବୃତ୍ତି କ’ଣ ଥିଲା ?
(A) ସାହିତ୍ୟ
(B) ସମାଜସେବା
(C) ଡାକ୍ତରି
(D) କାରିଗରି
Answer:
(C) ଡାକ୍ତରି

କବୟିତ୍ରୀଙ୍କ ସମ୍ବନ୍ଧରେ :
ଓଡ଼ିଆ ସାହିତ୍ୟରେ ନାରୀକବି ଉତ୍କଳଭାରତୀ କୁନ୍ତଳା କୁମାରୀ ସାବତ ଏକ ସୁଦୂରପ୍ରସାରୀ ନାମ । ଚିତ୍ତାକର୍ଷକ ବ୍ୟକ୍ତିତ୍ଵ, ବିପ୍ଳବର ଅନିର୍ବାଣ ଅଗ୍ନିଶିଖା, ମାନବିକତାର ଏକ ପରିପୂର୍ଣ୍ଣ ଉତ୍ସ ଏହି ମହୀୟସୀ କବୟିତ୍ରୀଙ୍କ ଲେଖନୀ କବିତା, ପ୍ରବନ୍ଧ, ଉପନ୍ୟାସ ପ୍ରଭୃତି ସାହିତ୍ୟର ବିଭିନ୍ନ ଦିଗକୁ ସ୍ପର୍ଶ କରିଛି । ପୂର୍ବ ଗୌରବାନୁଚିନ୍ତା, ଦେଶାତ୍ମବୋଧ ପ୍ରେମ, ପ୍ରକୃତି, ଭଗବାନ ପ୍ରଭୃତିଙ୍କୁ ଆଧାର କରି କାବ୍ୟ କବିତାର ବିଭିନ୍ନ ବିଭାଗ ମଧ୍ୟରେ ତାଙ୍କ ଲେଖନୀର ଜୟଯାତ୍ରା । ତାଙ୍କ କବିତାରେ ଓଡ଼ିଆ ପ୍ରୀତି ଓ ଓଡିଆ ଭାଷା ପ୍ରୀତିର ଅପୂର୍ବ ନମୁନା ପରିଦୃଷ୍ଟ ହୁଏ । କୁନ୍ତଳା କୁମାରୀଙ୍କ ଜନ୍ମ ୧୯୦୧ ଖ୍ରୀଷ୍ଟାବ୍ଦ ଫେବୃୟାରୀ ୮ ତାରିଖରେ ଓଡ଼ିଶାର ଏକ ବିଚ୍ଛିନ୍ନାଞ୍ଚଳ ବସ୍ତର ଗଡ଼ଜାତରେ ।

ସାରସ୍ଵତ ପ୍ରତିଭାର ଉଜ୍ଜଳତର ସ୍ବାକ୍ଷର ଦେବାକୁ ଯାଉଥିଲାବେଳେ ୧୯୩୮ ମସିହାରେ ସେ ଇହଧାମରୁ ବିଦାୟ ନେଇଥିଲେ । ତେରବର୍ଷ ପର୍ଯ୍ୟନ୍ତ ଓଡ଼ିଆ ବର୍ଣ୍ଣ ପରିଚୟ ପାଇ ନ ଥିବା ଏହି ଅସାଧାରଣ ଧୀଶକ୍ତିସମ୍ପନ୍ନା ଅଳ୍ପ କେତୋଟି ଦିନ ମଧ୍ୟରେ ଓଡ଼ିଆ ଭାଷା ଶିକ୍ଷା କରି ଓଡ଼ିଆ ସାହିତ୍ୟ କ୍ଷେତ୍ରରେ ଯେଉଁ ଗୌରବର ଅଧିକାରୀ ହୋଇପାରିଥିଲେ ତାହା ବାସ୍ତବିକ ବିସ୍ମୟକର । ବୃତ୍ତିରେ ଡାକ୍ତର ଥିଲେ ମଧ୍ୟ ତାଙ୍କ ପ୍ରବୃତ୍ତି ଥିଲା ସାରସ୍ବତ ସାଧନା । କେବଳ ଓଡ଼ିଆ ସାହିତ୍ୟ ନୁହେଁ ହିନ୍ଦୀ ସାହିତ୍ୟରେ ମଧ୍ୟ ତାଙ୍କର ଗଭୀର ପ୍ରବେଶ ଥିଲା । ହିନ୍ଦୀରେ ‘ବରମାଲା’ ନାମକ ଏକ ଗୀତିଗୁଚ୍ଛ ରଚନା କରି ତଥା ବହୁ ହିନ୍ଦୀ ପତ୍ରିକାର ସମ୍ପାଦନା ଦାୟିତ୍ଵରେ ରହି ସେ ହିନ୍ଦୀ ସାହିତ୍ୟ କ୍ଷେତ୍ରରେ ସୁପ୍ରତିଷ୍ଠିତା ହୋଇ ପାରିଥିଲେ ।

ଭାଷଣ ଦେବାର ଗୌରବ ଲାଭ କରିଥିଲେ ସେ । ପ୍ରତିଷ୍ଠାର ଉଚ୍ଚତମ ଶିଖରରେ ଥିଲାବେଳେ ତାଙ୍କୁ ସଂସାର ତ୍ୟାଗ କରିବାକୁ ପଡ଼ିଥିଲା । ମାତ୍ର ୩୮ ବର୍ଷର ସ୍ୱଳ୍ପ ଜୀବନକାଳ ମଧ୍ୟରେ ନିଜ ପ୍ରତିଭାର ସୁବିନିଯୋଗ କରି ସେ ଓଡ଼ିଆ ସାହିତ୍ୟ କ୍ଷେତ୍ରରେ ନିଜର ଅମଳିନ ପରିଚୟ ରଖ୍ଯାଇଛନ୍ତି । ‘ଅଞ୍ଜଳି’, ‘ଉଲ୍ଲାସ’, ‘ଅର୍ଜନା’, ‘ସ୍କୁଲିଙ୍ଗ’ ଓ ‘ଆହ୍ବାନ’ ଆଦି କବିତା ପୁସ୍ତକ; ‘ଭ୍ରାନ୍ତି’, ‘ନ’ ତୁଣ୍ଡୀ’, ‘ପରଶମଣି’, ‘ରଘୁ ଅରକ୍ଷିତ’, ‘କାଳୀବୋହୂ’ ଆଦି ଉପନ୍ୟାସ ତାଙ୍କ ଉଜ୍ଜ୍ଵଳ ପ୍ରତିଭାର ନିଦର୍ଶନ । ତାଙ୍କ ସାରସ୍ବତ କୃତି ପାଇଁ ପୁରୀର ‘ମହିଳା ବନ୍ଧୁ’ ଅନୁଷ୍ଠାନ ତାଙ୍କୁ ‘ଉତ୍କଳ ଭାରତୀ’ ଉପାଧ୍ ପ୍ରଦାନ କରିଥିଲେ । ବିଶ୍ୱଜନୀନତା, ସେବାପରାୟଣତା, ଭଗବତ୍ ବିଶ୍ଵାସ, ମାନବିକ ମୂଲ୍ୟବୋଧ ଓ କର୍ତ୍ତବ୍ୟପରାୟଣତାକୁ ଆଧାର କରି ସାହିତ୍ୟ ସୃଷ୍ଟିରେ ତାଙ୍କ ଲେଖନୀ ଶତମୁଖ ହୋଇଉଠିଛି ।

କବିତାର ପୃଷ୍ଠଭୂମି :
ଓଡ଼ିଶାର ସ୍ଵାଧୀନତା ଲୋପଠାରୁ ନବ ସ୍ଵାଧୀନତା ଲାଭ ପର୍ଯ୍ୟନ୍ତ ଉତ୍କଳୀୟମାନଙ୍କ ଜୀବନ ଥିଲା ଦୁର୍ଦ୍ଦିନ ରାତ୍ରିର ତିମିରିତ କାଳ । ବିକଟ ଦାରିଦ୍ର୍ୟ ଓ ନିପୀଡ଼ିତ ଜୀବନ ନେଇ ଓଡ଼ିଆ ଜାତି ନୈରାଶ୍ୟର ଘନ ଅନ୍ଧକାର ମଧ୍ଯରେ ହା-ହୁତାଶମୟ ଜୀବନ ଅତିବାହିତ କରୁଥିଲା । ଏହି ସମୟରେ କୁନ୍ତଳା କୁମାରୀ ଓଡ଼ିଆମାନଙ୍କ ମୁମୂର୍ଷୁ ଧମନୀକୁ ସ୍ପନ୍ଦିତ କରିବାପାଇଁ ଆଶାର ସଙ୍ଗୀତ ଶୁଣାଇଛନ୍ତି । ସେମାନଙ୍କ ନୈରାଶ୍ୟଦଗ୍ଧ ପ୍ରାଣରେ ଆଶାର ଅସୁମାରି ସ୍ବପ୍ନ ଭରିଦେଇ ଧୈର୍ଯ୍ୟ ଧାରଣପୂର୍ବକ କର୍ମମୟ ଜୀବନରେ ଉନ୍ମାଦନା ଓ ଆତ୍ମଚୈତନ୍ୟ ଜାଗରଣ କରିବାକୁ କବୟିତ୍ରୀ ଆହ୍ବାନ ଜଣାଇଛନ୍ତି ।

ବୀର ଓଡ଼ିଆଜାତିର ସ୍ମାରକୀ ବାରବାଟୀ ଭାଙ୍ଗି ପଡ଼ିଥିଲେ ମଧ୍ୟ, ଓଡ଼ିଆ ଶିଳ୍ପୀ ଓ ସ୍ଥପତିଙ୍କ ଅତୁଳନୀୟ କାରୁକଳାର ପ୍ରତୀକ କୋଣାର୍କ ମାଟିରେ ଲୋଟିଥିଲେ ମଧ୍ୟ, ଓଡ଼ିଆ ସାଧବ ପୁଅର ନୌବାଣିଜ୍ୟ ବିଭବ ଲୋପ ପାଇଯାଇଥିଲେ ମଧ୍ୟ, ଏପରିକି ବନ୍ୟା, ବାତ୍ୟା ଓ ଦୁର୍ଭିକ୍ଷ ପରି ପ୍ରକୃତିର କ୍ରୂର ପରିହାସରେ ଜନଜୀବନ ବିପର୍ଯ୍ୟସ୍ତ ହୋଇପଡ଼ିଥିଲେ ମଧ୍ୟ ଉତ୍କଳରୁ ମନୁଷ୍ୟତା ନିଃଶେଷ ହୋଇଯାଇ ନାହିଁ । ଜାତିର ମାନବିକ ମୂଲ୍ୟବୋଧ ଉପରେ କବୟିତ୍ରୀଙ୍କର ନିବିଡ଼ ଆସ୍ଥା ରହିଛି ।

ଅସହାୟ ଓଡ଼ିଆ ଜାତିପ୍ରାଣରେ ଆଶା ଓ ଉଦ୍ଦୀପନାର ସୁଧାବାରି ସିଞ୍ଚନ କରିବାକୁ ଯାଇ କବୟିତ୍ରୀ ସୃଷ୍ଟି କରିଛନ୍ତି କବିତା ‘ମଣିଷ ଭାଇ’। କବିତାଟି କବୟିତ୍ରୀଙ୍କ କବିତା ପୁସ୍ତକ ସ୍ଫୁଲିଙ୍ଗ ରୁ ଉଦ୍ଧୃତ ହୋଇଛି, ଯାହାର ରଚନାକାଳ ୧୯୨୯ ମସିହା । ତତ୍‌କାଳୀନ ରାଜନୈତିକ ଓ ସାମାଜିକ ପରିସ୍ଥିତି ଥିଲା ଉତ୍ତେଜନାପ୍ରବଣ । ବିଦେଶୀ ଶାସକଙ୍କ ଅର୍ଥନୈତିକ ଶୋଷଣ, ନିପୀଡ଼ନ, ଦେଶବାସୀଙ୍କ ଉତ୍କଟ ଦାରିଦ୍ର୍ୟ, ରୋଗବ୍ୟାଧ, ରାଜା ଜମିଦାରଙ୍କ ବିଳାସବ୍ୟସନ, ବିଦେଶୀ ପଦଲେହନକାରୀଙ୍କର ବିଶ୍ୱାସଘାତୀ ଭୂମିକା ପ୍ରଭୃତି ଦେଶର ଘୋର ଅସହାୟ ଅବସ୍ଥାରେ ସାଧାରଣ ଜନଜୀବନ ବ୍ୟତିବ୍ୟସ୍ତ ହୋଇପଡ଼ିଥିଲା ।

ଧନୀ-ନିର୍ଜନ, ଶୋଷକ ଓ ଶୋଷିତ ମଧ୍ୟରେ ଥ‌ିବା ଯୁଗ ‘ଯୁଗର ବ୍ୟବଧାନ ନାରୀକବିଙ୍କ ଦୃଷ୍ଟିକୁ ଏଡ଼ାଇ ଯାଇ ପାରି ନ ଥିଲା । ମଣିଷର ଦୁଃଖରେ କବୟିତ୍ରୀ କେଉଁଠାରେ ବ୍ୟଥ୍‌ତା ତ କେଉଁଠି ଜାତୀୟ ଜୀବନର ଦୁର୍ଗତି ଲକ୍ଷ୍ୟ କରି ଅବସାଦଗ୍ରସ୍ତା । ଶୋଷିତ, ଲାଞ୍ଛିତ ତଥା ଦାରିଦ୍ର୍ୟର କଷାଘାତରେ ଜର୍ଜରିତ ଜନତାର ଦୁର୍ଦ୍ଦଶା ମୋଚନ ପାଇଁ ତାଙ୍କ କାବ୍ୟସ୍ୱରରେ ଉଗ୍ରତା ନାହିଁ; ମାତ୍ର ଅଭିଯୋଗ ଅଛି । ଦୁର୍ଦ୍ଦଶାଗ୍ରସ୍ତ ଜନତାଙ୍କ ପାଇଁ କବୟିତ୍ରୀଙ୍କ ମନର କୋମଳ କାରୁଣ୍ୟ କବିତାରେ ରୂପାୟିତ ହୋଇଛି । ଏହି ଗ୍ଳାନିକର ପରିସ୍ଥିତି ଭିତରେ କବୟିତ୍ରୀଙ୍କ ଅନ୍ତରରେ ଆଶାର ଅସରନ୍ତି ବିଶ୍ବାସ ସୃଷ୍ଟି ହୋଇପାରିଛି ଓ ମଣିଷର ମହାନତାକୁ ଘୋଷଣା କରି ସେ ଗାଇଛନ୍ତି –

‘ଶୁଣ ହେ ମଣିଷ ଭାଇ !
ଝୁରି ମରିବାକୁ ବୁଡ଼ି ମରିବାକୁ
ମଣିଷ ଜନମି ନାହିଁ ।”

କବିତାର ସାରମମ :
ନାରୀକବି କୁନ୍ତଳା କୁମାରୀଙ୍କ କାବ୍ୟସ୍ୱରରେ ମଣିଷ ପାଇଁ ଅଶେଷ ସ୍ନେହ ଓ ଦିବ୍ୟାଶୀର୍ବାଦର ଧାରା ଉତ୍ସାରିତ ହୋଇଛି । ସମାଜର ଦଳିତ, ଲାଞ୍ଛିତ, ପତିତ ଓ ନିପୀଡ଼ିତ ମଣିଷ ଜାତି ପାଇଁ ତାଙ୍କ ଚିତ୍ତର କୋମଳ କାରୁଣ୍ୟ କବିତାରେ ଭରିଦେଇଛି ଅଫୁରନ୍ତ ପ୍ରାଣପ୍ରାଚୁର୍ଯ୍ୟ । ମାନବ ସମାଜର ଐକ୍ୟ, ପ୍ରୀତି ଓ କଲ୍ୟାଣ କାମନାରେ କବୟିତ୍ରୀଙ୍କ ସାହିତ୍ୟରେ ଅମୃତର ବାର୍ତ୍ତା ପରିବେଷିତ ହୋଇଛି ।
କୁନ୍ତଳା କୁମାରୀଙ୍କ ସମ୍ଭୋଧୀ କବିତା ‘ମଣିଷ ଭାଇ’ ଅମୃତର ସନ୍ତାନ ମଣିଷ ପାଇଁ ଆତ୍ମବିଶ୍ଵାସଭରା ଆଶା, ଆଶ୍ୱାସନାର ଦିବ୍ୟବାଣୀ ଶୁଣାଇଛି । ସୁଖସ୍ଵପ୍ନଭରା ଅତୀତ ସ୍ମୃତିର ରୋମନ୍ଥନ କରି ତଥା ସାମ୍ପ୍ରତିକ ଦୁଃଖ, ଯନ୍ତ୍ରଣାର କାରୁଣ୍ୟରେ ହୃଦୟକୁ ଅଯଥା ଭାରାକ୍ରାନ୍ତ ନ କରି ଉପସ୍ଥିତ ପରିସ୍ଥିତିକୁ ସାହସର ସହିତ ସାମନା କରିବା ବିବେକୀର କାର୍ଯ୍ୟ ।

ସମୟ ଚକ୍ରରେ ଚିର ଘୂର୍ଣ୍ଣନଶୀଳ ଦୁଃଖର ଅମାରାତ୍ରି ପରେ ନବ ପ୍ରଭାତର ନବୀନ ସୁଖ-ସୂର୍ଯ୍ୟର ଉଦୟ ଅବଶ୍ୟମ୍ଭାବୀ । ତେଣୁ ଦୁଃଖ-ଦୁର୍ଦ୍ଦଶାକୁ କପାଳ ଲିଖନ ବୋଲି ବିବେଚନା ନ କରି ଓ ଭାଗ୍ୟକୁ ସ୍ଵୀକାର କରି ଶତ ହତଶ୍ଵାସରେ ଜୀବନକୁ ଅଧିକ ଜନ୍ତ୍ରଣାଜର୍ଜର ନ କରିବାକୁ କବୟିତ୍ରୀ ସମ୍ବେଦନଶୀଳ ଆଶ୍ୱାସନା ବାଣୀ ଶୁଣାଇଛନ୍ତି । କାରଣ ଅନାଗତ ଭବିଷ୍ୟତ ନିଶ୍ଚିତଭାବେ ଜୀବନକୁ ନୂତନ ଆଶା ଓ ନିବ ଉନ୍ମାଦନାରେ ସ୍କନ୍ଦିତ କରିବ । ଯେହେତୁ ପରିବର୍ତ୍ତନ ଧାରାର ପ୍ରବହମାନତାରେ ବିଧାତାଙ୍କ ସୃଷ୍ଟି ଚିର ମଙ୍ଗଳମୟ, ମାନବ ଜୀବନ ,ଯେ ନିୟତିର ଅଧୀନ, ଏକଥା ସତ୍ୟ । ମାତ୍ର ଯନ୍ତ୍ରଣା ପରିପୂର୍ଣ୍ଣ କାରାଗାରରେ ଚିର ଶୃଙ୍ଖଳିତ ଜୀବନ ଧରି ମାନବ ଯେ କେବଳ । ଲାଞ୍ଛନା, ଦୁଃଖ, ଅପମାନ ଓ ଅତ୍ୟାଚାରକୁ ନୀରବରେ ସହ୍ୟ କରି ଚାଲିଥିବ ଏହା କଦାପି ନିୟତିର ବିଧାନ ନୁହେଁ । ମାନବ ଜାତି କେବେ ବି ଧ୍ୱଂସପଥର ଯାତ୍ରୀ ନୁହେଁ କି ଏ ସଂସାର ତା’ ପାଇଁ ମୃତ୍ୟୁର ମହାକାଳ ନୁହେଁ ।

ଈଶ୍ବର ସୃଷ୍ଟ ଏ ବିଶାଳ ଜଗତ ହେଉଛି ଅମୃତ ସନ୍ତାନ, ମାନବର ଲୀଲାକ୍ଷେତ୍ର, ଯେଉଁଠି ତା’ ଜୀବନର ସୁଖ -ଦୁଃଖ, ହସ – କାନ୍ଦ ଗୋଟିଏ ଘୂର୍ଣାୟମାନ ମୁଦ୍ରାର ଦୁଇପାର୍ଶ୍ଵ ସଦୃଶ । ସମୟାନୁକ୍ରମେ ମୁଦ୍ରାର ପଟ ପରିବର୍ତ୍ତନରେ ଦୁଃଖ – ଦୁର୍ଦ୍ଦଶାର ପତନ ଘଟିବ ଏବଂ ସୁଖ-ସମୃଦ୍ଧିର ପ୍ରାଚୁର୍ଯ୍ୟରେ ଜୀବନପାତ୍ର ଭରିଉଠିବ । ପରମେଶ୍ଵରଙ୍କ ଅମୃତମୟ ସୃଷ୍ଟିରେ ଏ ଜଗତ ମଧ୍ଯ କାହାରି ପାଇଁ ଚିର ବିଳାସର ମଧୁକୁଞ୍ଜ ନୁହେଁ । ଧନ, ସମ୍ପଦ ଓ କ୍ଷମତାରେ ମଦମତ୍ତ ହୋଇ ଦଳେ ବିଳାସ, ବ୍ୟସନ ଓ ସୁଖ ସମ୍ଭୋଗରେ ଚିର ମତୁଆଲା ହେଉଥ‌ିବେ ଅଥଚ ଅନ୍ୟ ଦଳକ ଶୋଷଣ, କଷଣ, ଅତ୍ୟାଚାର ଓ ଦାରିଦ୍ର୍ୟର କଷାଘାତରେ ଚିର ଜର୍ଜରିତ ହୋଇ ଭାଗ୍ୟ ଆଦରି ନୀରବରେ ସବୁ ସହ୍ୟ କରି ଚାଲିଥିବେ, ଏହା କଦାପି ନିୟତିର ବିଧାନ ନୁହେଁ ।

ଧନୀ, ପୁଞ୍ଜିପତି, ସ୍ୱେଚ୍ଛାଚାରୀ ଶାସକ ସଦାବେଳେ ଦୁର୍ବଳ, ନିରୀହ ମନୁଷ୍ୟ ଉପରେ ଚିର ଆଧୂପତ୍ୟ ବିସ୍ତାର କରି କଷଣ, ପେଷଣରେ ତା’ର ଜୀବନକୁ ଦୁର୍ବିଷହ କରି ଚାଲିଥିବ; ଏହାକୁ ବିଧ୍ଵନିର୍ଦ୍ଦିଷ୍ଟ ବୋଲି କଦାପି କୁହାଯାଇ ନ ପାରେ । ଦୁଃଖ, ବେଦନା ଓ ଅନୁଶୋଚନାର ତୀବ୍ର ତାଡ଼ନା ମଧ୍ୟରେ ସବୁ ଯନ୍ତ୍ରଣାକୁ ନତଶିରେ ସହ୍ୟ କରି ମନୁଷ୍ୟ କେବଳ ଲୋତକ ବର୍ଷଣ କରିଚାଲିଥବ ଓ ଜୀବନ ଯୁଦ୍ଧରେ ପରାଜିତ ସୈନିକ ପରି ହତଭାଗ୍ୟ ବୋଲି ନିଜକୁ ଶତ ଧକ୍‌କାର କରି ଚାଲିଥବ, ଏହାକୁ ଭାଗ୍ୟଲିପି ବୋଲି କହି ମୃତ୍ୟୁ ଅପେକ୍ଷାରେ ପଡ଼ିରହିବାକୁ ଶ୍ରେୟ ମନେକରୁଥିବା ମଣିଷ ମନରେ ଆଶା ଓ ବିଶ୍ୱାସ ଭରିଦେବାକୁ କବୟିତ୍ରୀ ଆପ୍ରାଣ ଉଦ୍ୟମ କରିଛନ୍ତି । କବୟିତ୍ରୀଙ୍କ ମତରେ ଈଶ୍ବରଙ୍କ ସୃଷ୍ଟି ଏ ସଂସାର ସଦା ଶୋଭାମୟ ଓ ଚିର ଆନନ୍ଦମୟ ।

ମଙ୍ଗଳମୟଙ୍କ ସୃଷ୍ଟିରେ ଏ ସଂସାରବାସୀ ହେଉଛନ୍ତି ବିଶ୍ଵନିୟନ୍ତାଙ୍କ ଅମୃତ ସନ୍ତାନ । ତେଣୁ ଭାଗ୍ୟକୁ ଆଦରି ମାନବ ନିଜକୁ କେବଳ ମୃତ୍ୟୁପଥର ଯାତ୍ରୀ ବୋଲି ଭାବି ସ୍ଵକର୍ତ୍ତବ୍ୟ ସମ୍ପାଦନରୁ ନିବୃତ୍ତ ରହିବା ସର୍ବାଦୌ ଅନୁଚିତ । କବୟିତ୍ରୀଙ୍କ ମତରେ ଏ ବିଶାଳ ଜଗତ କଦାପି ହଂସାଭିମୁଖୀ ନୁହେଁ ଏବଂ ଅମୃତର ସନ୍ତାନ ମନୁଷ୍ୟ ମୃତ୍ୟୁ-ପଥର ଯାତ୍ରୀ ନୁହେଁ । କବୟିତ୍ରୀଙ୍କ ମତରେ ଏ ବିଶାଳ ଜଗତ କଦାପି ଧ୍ୱଂସାଭିମୁଖୀ ନୁହେଁ ଏବଂ ଅମୃତର ସନ୍ତାନ ମନୁଷ୍ୟ ମୃତ୍ୟୁ-ପଥର ଯାତ୍ରୀ ନୁହେଁ । କବୟିତ୍ରୀଙ୍କ ଭାଷାରେ –

‘ନତଶିରେ ସୁଖେ ଶ୍ରୀପାଦେ ଅରପି ଆପଣାକୁ ଆପେ ବଧୂବ
ଏ ନୁହେଁ ବିଧାତା ବିଚାର,
ଧ୍ଵଂସର ଯାତ୍ରୀ, ମୃତ୍ୟୁର ଧାତ୍ରୀ ନୁହେଁ ଏ ସୁନ୍ଦର ସଂସାର ।’’

କବୟିତ୍ରୀ ବିଶ୍ବବାସୀଙ୍କୁ ସଦା କର୍ମତତ୍ପର ରହି କର୍ତ୍ତବ୍ୟ ସମ୍ପାଦନ କରିଯିବାପାଇଁ ଉପଦେଶ ଦେଇଛନ୍ତି । କବୟିତ୍ରୀଙ୍କ ମତରେ ଏ ଜଗତ ହେଉଛି କର୍ମମୟ । ଏହି କର୍ମମୟ ଜଗତରେ ମାନବ ନିଜକୁ ଜଣେ ସଟ କର୍ମୀ ମନେକରି କର୍ମକୁ ଜୀବନର ମାନଦଣ୍ଡ ଭାବେ ଗ୍ରହଣ କରିବା ଉଚିତ ବୋଲି କହି କବୟିତ୍ରୀ କର୍ମର ଜୟଗାନ କରିଛନ୍ତି । କର୍ମରେ ନିମଜ୍ଜିତ ରହିଲେ ମନରୁ ନୈରାଶ୍ୟ ଓ ହତାଶାବୋଧ ଆପେ ଦୂରେଇଯିବ । ମାନସିକ ଗ୍ଳାନିର ବିସ୍କରଣ ପାଇଁ କର୍ମତତ୍ପର ଜୀବନ ହିଁ ପ୍ରକୃଷ୍ଟ ମାର୍ଗ ବୋଲି କବୟିତ୍ରୀ କହିଛନ୍ତି ।

ନିଜକୁ ଅସହାୟ ମନେକରୁଥିବା ଚିର ନିଷ୍ପେଷିତ, ଲାଞ୍ଛିତ, ବଞ୍ଚିତ ମଣିଷ ଭାଇ ଯେତେବେଳେ ନିଜକୁ ଧ୍ବଂସ ପଥର ଯାତ୍ରୀ ବୋଲି ଚିନ୍ତାକରି ଆତ୍ମଗ୍ଳାନିରେ ମ୍ରିୟମାଣ ହୋଇପଡ଼ିଛି, ସେତେବେଳେ ମାନବିକ ଦରଦ ନେଇ ଭରିଦେବାକୁ କବି ମଣିଷ ଭାଇକୁ କର୍ତ୍ତବ୍ୟ କର୍ମରେ ବୁଡ଼ି ରହିବାକୁ ଉପଦେଶ ଦେଇଛନ୍ତି । ଅନନ୍ତ ମରଣ ଯେ ମାନବର ଶେଷଗତି ନୁହେଁ ଏହି ଭାବନାକୁ ମାନବ ହୃଦୟରେ ଭରିଦେବାକୁ କବୟିତ୍ରୀ ଆପ୍ରାଣ ଉଦ୍ୟମ କରିଛନ୍ତି । ତାଙ୍କ ମତରେ ସବୁ ଲାଜ, ଭୟ, ଅପମାନ ଆଦି ମାନସିକ ଗ୍ଳାନିର ବିସ୍କରଣ ପାଇଁ ତାକୁ କର୍ମଯୋଗୀର ଜୀବନ ଆଦରି ନେବାକୁ ହେବ ।

ମନରେ ଅହମିକା ପୋଷଣ କରି କ୍ରୋଧ ଓ ପ୍ରତିଶୋଧପରାୟଣ ହେବା ପଶୁତ୍ଵର ପରିଚାୟକ । ଅପରନ୍ତୁ ଜୀବନର ସବୁ ମାନ-ଅପମାନ, ଲଜ୍ଜା-ଭୟ, ଅଶ୍ରୁ-ଅଭିଳାଷ, ହା-ହତାଶ, ଦୁଃଖ – ଅବସୋସକୁ ବିଭୁଙ୍କ ପଦାରବିନ୍ଦରେ ସମର୍ପଣ କରିଦେଇ ପରମେଶ୍ଵରଙ୍କ କର୍ମମୟ ସଂସାରରେ କେବଳ କର୍ତ୍ତବ୍ୟ ସମ୍ପାଦନରେ ବ୍ରତୀ ହେବା ହିଁ ମାନବିକତାର ପରିଚାୟକ । ଫଳପ୍ରାପ୍ତିରେ ଆଶା ନ ରଖ୍ କର୍ମରେ ଲିପ୍ତ ହେବାରେ ଜୀବନର ସାର୍ଥକତା ବିଦ୍ୟମାନ ।

ତଦ୍ବାରା ହିଁ ଈଶ୍ଵରଙ୍କ ଇଚ୍ଛା ପୂର୍ଣ ହୋଇପାରିବ ଓ ମଣିଷ ପଶୁତ୍ଵ- ଦେବତ୍ଵର ଭୀଷଣ ପରୀକ୍ଷାରେ ସସମ୍ମାନେ ଉତ୍ତୀର୍ଣ୍ଣ ହୋଇ ମାନବିକ ମୂଲ୍ୟବୋଧର ବିଜୟ ବୈଜୟନ୍ତୀ ଉଡ଼ାଇ ପାରିବ । ପରମେଶ୍ଵର ମଧ୍ଯ ତାଙ୍କ ସୃଷ୍ଟିର ସାର୍ଥକତାରେ ଚିରସନ୍ତୁଷ୍ଟ ହୋଇ ମାନବ ଜାତି ନିକଟରେ ଚିର ଋଣୀ ରହିବେ । ତେଣୁ ତାଙ୍କ ରଚିତ ଅନୁପମ ସୃଷ୍ଟିକୁ ସୁନ୍ଦରତର କରିବାପାଇଁ ମଣିଷ ଭାଇ ନିଜକୁ ଉତ୍ସର୍ଗ କରୁ ବୋଲି କବୟିତ୍ରୀ କାମନା କରିଛନ୍ତି । କବୟିତ୍ରୀଙ୍କ ଭାଷାରେ –

‘‘ପଶୁତ୍ବ ଦେବତ୍ୱ ପରୀକ୍ଷାରେ ଜୟୀ ଲଭ ବୀରତ୍ଵର ଟୀକା
ଋଣୀ କର ଭବରାଣେ
ତା’ଙ୍କ ରଚା ଚରାଚର ପରାଣରେ ବଳି ଦିଅ ନିଜ ପ୍ରାଣେ ।’’

ବୁଦ୍ଧି ଓ ବିବେକର ଅଧିକାରୀ ମାନବ ହିଁ ବିଧାତାଙ୍କ ସୃଷ୍ଟିରେ ଶ୍ରେଷ୍ଠ ପ୍ରାଣୀ । ତା’ ଜୀବନର ଚିର ଶତ୍ରୁ କାମ, କ୍ରୋଧ, ଲୋଭ, ମୋହ, ମଦ, ମାତ୍ସର୍ଯ୍ୟକୁ ଦୃଢ଼ତାର ସହ ଦମନ କଲେ ହିଁ ସେ ଜୀବନର ସାର୍ଥକତା ପ୍ରତିପାଦନ କରିପାରେ ଓ ତା’ ଜୀବନ ଧନ୍ୟ ହୁଏ । ଶତ୍ରୁଞ୍ଜୟ ଜୀବନ ତା’ର ଦିବ୍ୟତାରେ ଭରିଉଠେ, ଶାଶ୍ବତ ଜ୍ଞାନରେ ମାନବାତ୍ମା ତା’ର ଦୀପ୍ତିମନ୍ତ ହୋଇଉଠେ । ତା’ର ପ୍ରତିଟି କର୍ମରେ ସେ ଅନୁଭବ କରେ ଈଶ୍ବରସତ୍ତା । ସାତ୍ତ୍ଵିକ ଜୀବନାଦର୍ଶକୁ ପାଥେୟ କରୁଥିବା ମାନବାତ୍ମା ପରିଣତ ହୁଏ ଦିବ୍ୟାତ୍ମାରେ । ମୃତ୍ୟୁ ପରେ ସେହି ଜୀବାତ୍ମା ଅନନ୍ତ ଗଗନରେ ସୁଦୀପ୍ତ ତାରକାର ଆସନ ଅଳଙ୍କୃତ କରେ । କବୟିତ୍ରୀଙ୍କ ମତରେ –

‘ଶୁଣ ଶୁଣ ଅରିନ୍ଦମ ! ଷଡ଼ରିପୁଜିତ, ଦେବତା ପୂଜିତ
ତାରାଦଳେ ତବାସନ ।’’

କବୟିତ୍ରୀଙ୍କ ମତରେ ମାନବ ହେଉଛି ବିଧାତାର ବରପୁତ୍ର । ତେଣୁ କୌଣସି ପରିସ୍ଥିତିରେ ସେ ନିଜକୁ ପରାଜିତ ମନେକରିବା ଅନୁଚିତ୍ । ଜୀବନ ଯୁଦ୍ଧରେ କ୍ଷତାକ୍ତ ହୋଇଗଲେ ମଧ୍ଯ ସାହସ ଓ ବିକ୍ରମ ସହ ଶତ୍ରୁର ମୁକାବିଲା କରିବା ହେଉଛି ବୀରୋଚିତ କାର୍ଯ୍ୟ । ସାମାନ୍ୟ ରକ୍ତପାତରେ ସେ ନିଜକୁ କ୍ଷୀଣ ବା ଦୁର୍ବଳ ମନେକରିବା ଅନୁଚିତ । କଳୁଷିତ ଜୀବନର କଳଙ୍କ କାଳିମାରେ ଦୀନହୀନ ହୋଇଯାଏ ନାହିଁ । ଦେବତ୍ୱର ମହିମାରେ ଦୀପ୍ତିମନ୍ତ ହୋଇ ତା’ର ପୁନରୁତ୍‌ଥାନ ଅବଶ୍ୟ ଘଟିଥାଏ ।

କାରଣ ବିଶ୍ଵନିୟନ୍ତା ପରମେଶ୍ଵର ତାଙ୍କ ଅମୃତମୟ ସୃଷ୍ଟିର ଅଭିନବ ବିକାଶ ଦର୍ଶନରେ ତୃପ୍ତ ହୁଅନ୍ତି । ତେଣୁ ମଣିଷ ଜୀବନର ସମସ୍ତ ବିଷାଦ, ବ୍ୟର୍ଥତା, ଦୁଃଖ, କାତରତା ତଥା ଯାବତୀୟ ହୀନମନ୍ୟତାକୁ ଧୋଇଦେଇ କ୍ଷତାକ୍ତ ଶରୀରକୁ ତାଙ୍କ ସୁଧାସ୍ପର୍ଶରେ ନବ ରୂପ ପ୍ରଦାନପୂର୍ବକ ତାକୁ ଅମୃତପିପାସୀ କରାଇବେ । ତେଣୁ ଭାଗ୍ୟବାଦୀ ମୃତ୍ୟୁକାମୀ ମାନବ ନିଜ ମନରୁ ଅସହାୟବୋଧତାକୁ ପରିହାର କରି ଜୀବନ ସୂତ୍ର ଧାରଣରେ ବ୍ରତୀ ହେବାକୁ କବୟିତ୍ରୀ ଆହ୍ବାନ ଦେଇଛନ୍ତି । କବୟିତ୍ରୀଙ୍କ ଆୟୋପଲବ୍ଧି ଓ ଜୀବନ ଦର୍ଶନ ଯେ ଗଭୀର ଆଶାବାଦିତାର ଉଜ୍ଜ୍ବଳ ମୟୂଖରେ ଚିର ଦୀପ୍ତିମାନ, ଆଲୋଚ୍ୟ କବିତାରୁ ତାହା ସ୍ପଷ୍ଟ ପରିଦୃଷ୍ଟ ହୁଏ । ଆବେଗଧର୍ମୀ ପ୍ରାଣବନ୍ତ ଭାଷାବିନ୍ୟାସ କବୟିତ୍ରୀଙ୍କ ଭାବୋଚ୍ଛାସକୁ ଅଧିକ ଜୀବନ୍ତ କରିଛି ଏଥରେ ଦ୍ବିମତ ନାହିଁ ।

ବିଷୟଗତ ଶବ୍ଦ ଓ ଅର୍ଥ :

• ଝୁରି ମରିବା – ଶୋକ କରିବା / ଗୁଣ ସ୍ମରଣ କରି ଦୁଃଖ
• ନିରାଶେ – ଦୁଃଖରେ / ଆଶାଶୂନ୍ୟ ଭାବରେ ।
• ଲାଞ୍ଛିତ – ଅପମାନିତ ।
• ପୀଡ଼ିତ – ରୋଗଗ୍ରସ୍ତ / ଦୁଃଖୁତ ।
• କାରାରେ – ବନ୍ଦୀଶାଳରେ / ଜେଲଖାନାରେ ।
• ଧ୍ୱଂସର ଯାତ୍ର। – ନଷ୍ଟ ପଥର ପଥୁ ।
• ବିଶାଳ ଜଗତ – ବିରାଟ ପୄଥ୍କ
• ସନ୍ତ।ନ – ପୁତ୍ର ।
• ବିଳାସ – ସୁଖ ଭୋଗ ।
• ବିଶ୍ୱ – ପୃଥ‌ିବୀ ।
• କୂ୍ର – ନିଷ୍ଠୁର ।
• ଦଳିବ – ଚାପିଦେବା, ଦମନ କରିବା ।
• ରକ୍ତପିପାସା – ରକ୍ତତୃଷ୍ଣା ।
• ନତଶିରେ – ମଥା ନୁଆଇଁ ।
• ବଧ୍ବ – ମାରିବ ।
• ଭୁବନ – ଘର ।
• ଦେବ ତେଜେ – ପରାକ୍ରମରେ
• ଅହମିକା – ଅହଂଭାବ / ଗର୍ବ ।
• ଦେବତ୍ୱ – ଦେବଭାବ ସ୍ବଭାବ ।
• ଭବଗ।ଣ – ଈଶ୍ବର, ଭଗବାନ୍ ।
• ରଚା – ସୃଷ୍ଟି ହୋଇଥବା, ରଚିତ ହୋଇଥିବା ।
• ଚର।ଚର – ସାରା ସଂସାର ।
• ଅରିଦମ – ଶତ୍ରୁ ଦମନକାରୀ ।
• ପ୍ର।ଣ – ଜୀବନ ।
• ଷଡ଼ରିପୁ – କାମ, କ୍ରୋଧ, ଲୋଭ, ମୋହ, ମଦ, ମାସ୍କର୍ଯ୍ୟ ପ୍ରଭୃତି ମାନବର ଛଅଗୋଟି ଶତ୍ରୁ ।
• ତବାସନ – ତୁମରି ଆସନ ବା ସ୍ଥାନ ।
• ଶୋଣିତ ଶ୍ରାବ – ରକ୍ତଧାର
• ହତଶ୍ୱ।ସେ- ହତାଶ ଭାବରେ ।
• ନିବିଡ଼ – ଘନ ।
• ବୟତି – ବାଦ୍ ଯିବା, ଅପ୍ରାପ୍ତି ।
• କଷଣ – କଷ୍ଟ ।
• ନିୟତି – ଭାଗ୍ୟ ।
• ମୃତ୍ୟୁର ଧାତ୍ରୀ – ମରଣର ସହଚରୀ ।
• ଅମୃତ ଦୀପ୍ତି – ଅମୃତର ତେଜ, ଜ୍ୟୋତି, ଉଜ୍ଜ୍ବଳତା ।
• ନର-ନାରୀ – ପୁରୁଷ -ସ୍ତ୍ରୀ ।
• ନିକେତନ – ଗୃହ ।
• ସତତ – ସବୁବେଳ ପାଇଁ ।
• ଅତ୍ୟ।ଚାର – ଅମାନୁଷିକ ଆଚରଣ ।
• ଦୁର୍ବଳେ – ବଳହୀନରେ ।
• ଶମିବ – ଶାନ୍ତ ହେବ ।
• ଅରପି – ଅର୍ପଣ କରି ।
• ବିଧାତା ବିଚାର – ନିୟତିର ବିଚାର ବା ଇଚ୍ଛା ।
• ବିଶ୍ୱବାସୀ- ପୃଥ‌ିବୀର ଜୀବଗଣ ।
• ଶ୍ରମ – ପରିଶ୍ରମ ।
• ଶୌର୍ଯ୍ୟ – ଶକ୍ତି, ବୀରତ୍ଵ।
• ପଶୁତ୍ୱ – ପଶୁବୃତ୍ତି ବା ସ୍ଵଭାବ ।
• ପୀକା – ସଙ୍କେତ, ଚିତା
• ପରାଣେ – ପ୍ରାଣରେ ।
• ବଳିଦିଅ – ଉତ୍ସର୍ଗ କରିବା ।
• କ୍ଷତଶିରେ – ଖଣ୍ତିଆ ମଥାରେ
• କ୍ଳୀଷ୍ନ – ଯନ୍ତ୍ରଣାପୀଡ଼ିତ, କ୍ଳେଶଜର୍ଜରିତ
• କ୍ଷୀଣ – କମିଯିବା, ପତଳା ହେବା ।
• କଳଙ୍କ – ଅପଯଶ
• ଦୀନ – ଦରିଦ୍ର (ଏଠାରେ ଦୈନ୍ୟ -ନିକୃଷ୍ଟ) ।
• ଯୁଗ।ନ୍ତ – ଯୁଗ ଯୁଗ ଧରି ।
• ଛିଣ୍ଡ।ଇ – ନଷ୍ଟ କରି ।
• କଳୁଷ – ପାପ ।
• ହୀନ – ସାନ ।
• ବିଧାତାର ବରପୁତ୍ର – ଈଶ୍ବରଙ୍କ ଶ୍ରେଷ୍ଠ ସନ୍ତାନ ।
• ମୃତୁ୍ୟରତୁ – ମରଣର ଡୋରି ।
• ଜୀବନସୂତ୍ର – ବଞ୍ଝାର ଡୋର ।
• ନିୟତି – ଭାଗ୍ୟ ।
• ଧାତ୍ରି – ଧାଈ / ଉପମାତା ।
• ଜଗତୀ – ଅଟ୍ଟାଳିକା / ଭବନ । (ଏଠାରେ ଏ ଶବ୍ଦଟି ପୃଥ‌ିବୀ ଅର୍ଥରେ ବ୍ୟବହୃତ ହୋଇଛି ।)
• ଦୀପ୍ତି – ତେଜ ।
• ପିପ।ସା – ପିଇବାର ଇଚ୍ଛା/ଶୋଷ ।
• ନତ – ନଇଁବା ।
• ଭବରାଣ – ଈଶ୍ବର ।
• ଯୁଗ।ନ୍ତ – ଯୁଗର ଅନ୍ତ ।
• ରଜୁ – ଦଉଡ଼ି ।
• ଶୃଙ୍ଖଳିତ – ଶୃଙ୍ଖଳରେ ବନ୍ଦୀ ।
• ଶୋଣିତ – ରକ୍ତ ।
• ନିରାଶେ – ଆଶାଶୂନ୍ୟ ଭାବରେ ।
• ପୀଡ଼ିତ – ରୋଗଗ୍ରସ୍ତ, ଦୁଃଖ୍

Odisha State Board CHSE Odisha Class 12 Economics Solutions Chapter 16 ରାଷ୍ଟ୍ରବିତ୍ତ Long Answer Questions.

CHSE Odisha 12th Class Economics Chapter 16 Long Answer Questions in Odia Medium

ଦୀର୍ଘ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର

1. ରାଷ୍ଟ୍ରବିତ୍ତ କ’ଣ ? ରାଷ୍ଟ୍ରବିତ୍ତ ଓ ବ୍ୟକ୍ତିବିତ୍ତ ମଧ୍ଯରେ ପାର୍ଥକ୍ୟ ଦର୍ଶାଅ ।
Answer:
ଆଧୁନିକ ରାଷ୍ଟ୍ରକୁ କଲ୍ୟାଣକାରୀ ରାଷ୍ଟ୍ର ଆଖ୍ୟା ଦିଆଯାଇଥାଏ । ଏକ ଆଧୁନିକ କଲ୍ୟାଣକାରୀ ରାଷ୍ଟ୍ରର କାର୍ଯ୍ୟାବଳୀ ବହୁଗୁଣରେ ବୃଦ୍ଧି ପାଇଛି । ଏହିସବୁ କାର୍ଯ୍ୟାବଳୀର ସୁଗ୍ଧ ସମ୍ପାଦନ ନିମନ୍ତେ ରାଷ୍ଟ୍ର ସମ୍ବଳ ଆବଶ୍ୟକ କରିଥାଏ । ତେଣୁ ରାଷ୍ଟ୍ରବିତ୍ତ କହିଲେ, କେନ୍ଦ୍ରୀୟ, ରାଜ୍ୟ ବା ସ୍ଥାନୀୟ ସ୍ତରରେ ବିଭିନ୍ନ ସର୍ବସାଧାରଣ ସଂସ୍ଥାମାନେ ଆବଶ୍ୟକ କରୁଥିବା ବିଭକୁ ବୁଝାଏ ।

ଏଠାରେ ସର୍ବସାଧାରଣ ସଂସ୍ଥା କହିଲେ କେନ୍ଦ୍ର ସରକାର, ରାଜ୍ୟ ସରକାର ଓ ପୌରସଭା ବା ପଞ୍ଚାୟତ ସମିତି ପରି ସ୍ୱାୟତ୍ତଶାସନ ସଂସ୍ଥା ଇତ୍ୟାଦିକୁ ବୁଝାଏ ।

ରାଷ୍ଟ୍ରବିଭକୁ ଲୋକବିର ମଧ୍ୟ କୁହାଯାଏ । ‘ବିଭ’’ ଶବ୍ଦଟି ଏଠାରେ ଅର୍ଥସଂକ୍ରାନ୍ତୀୟ ପ୍ରଶାସନ ଓ ପରିଚାଳନାକୁ ମଧ୍ଯ ସୂଚୀତ କରିଥାଏ । ତେଣୁ ରାଷ୍ଟ୍ରବିତ୍ତ କହିଲେ ସର୍ବସାଧାରଣ କର୍ତ୍ତୃପକ୍ଷଙ୍କର ଆର୍ଥିକ କ୍ରିୟାକଳାପର ନିୟନ୍ତ୍ରଣ ଓ ପରିଚାଳନାକୁ ମଧ୍ୟ ସୂଚୀତ କରିଥାଏ ।

ତେଣୁ ରାଷ୍ଟ୍ରବିତ୍ତ କହିଲେ ସର୍ବସାଧାରଣ କର୍ତ୍ତୃପକ୍ଷଙ୍କର ଆର୍ଥିକ କ୍ରିୟାକଳାପର ନିୟନ୍ତ୍ରଣ ଓ ପରିଚାଳନାକୁ ବୁଝାଇଥାଏ । ଏହା ଅର୍ଥଶାସ୍ତ୍ରର ସେହି ବିଭାଗର ସୂଚନା ଦିଏ; ଯାହା ସର୍ବସାଧାରଣ କର୍ତ୍ତୃପକ୍ଷଙ୍କର ଆୟ, ବ୍ୟୟ ଓ ତତ୍ ସଂକ୍ରାନ୍ତୀୟ ନିୟମାବଳୀ ସମସ୍ୟା ଓ ନୀତି ଇତ୍ୟାଦି ସହିତ ସମ୍ପୃକ୍ତ ।

ଅନେକ ଆଧୁନିକ ଅର୍ଥଶାସ୍ତ୍ରୀ ରାଷ୍ଟ୍ରବିତ୍ତକୁ ସରକାରୀ ଚିର (Government finance) ଭାବରେ ମଧ୍ଯ ନାମିତ କରିଛନ୍ତି । ଏହି ସରକାର ଜାତୀୟ ସ୍ତରରେ, ରାଜ୍ୟସ୍ତରରେ ବା ସ୍ଥାନୀୟ ସ୍ତରରେ କାର୍ଯ୍ୟ କରିପାରେ । ପ୍ରତ୍ୟେକ ସରକାର ବିଭିନ୍ନ କାର୍ଯ୍ୟ ସମ୍ପାଦନ ନିମନ୍ତେ ବିପୁଳ ପରିମାଣ ଅର୍ଥ ଆବଶ୍ୟକ କରନ୍ତି । ଏହି ଅର୍ଥ ସଂଗ୍ରହର ଉପାୟ ଓ ଅର୍ଥବ୍ୟୟର ପଦ୍ଧତି ରାଷ୍ଟ୍ରବିତ୍ତର ପ୍ରଧାନ ଆଲୋଚ୍ୟ ବିଷୟବସ୍ତୁ ।

ବାଷ୍ଟାବଲଙ୍କ ମତରେ, ‘‘ରାଷ୍ଟ୍ରବିତ୍ତ ସର୍ବସାଧାରଣ କର୍ତ୍ତୃପକ୍ଷଙ୍କର ବ୍ୟୟ ଓ ଆୟ ଓ ସେମାନଙ୍କର ପାରସ୍ପରିକ ସମ୍ପର୍କ ଓ ଆର୍ଥିକ ପ୍ରଶାସନ ଓ ନିୟନ୍ତ୍ରଣକୁ ବୁଝାଏ ।’’

ଶ୍ରୀମତୀ ଉତ୍ସୁଳା ହିକ୍‌ସ୍ କହିଛନ୍ତି ଯେ- ‘ଯେଉଁ ଉପାୟ ସାହାଯ୍ୟରେ ସରକାର ଅଭାବର ସମଷ୍ଟିଗତ ପରିତୃପ୍ତି ସାଧନ କରିଥାନ୍ତି ଓ ସେମାନଙ୍କ ଉଦ୍ଦେଶ୍ୟ ପୂରଣ ନିମନ୍ତେ ଆବଶ୍ୟକୀୟ ପାଣ୍ଠି ଆହରଣ କରନ୍ତି । ଅର୍ଥଶାସ୍ତ୍ର ପ୍ରଧାନତଃ ତାହାର ପର୍ଯ୍ୟାଲୋଚନା ଓ ମୂଲ୍ୟାୟନ ସହିତ ସମ୍ପୃକ୍ତ ।’’

ଅଧ୍ୟାପକ ଫିଣ୍ଡଲେ ସିରାଜଙ୍କ ମତରେ ସର୍ବସାଧାରଣ କର୍ତ୍ତୃପକ୍ଷଙ୍କ ଦ୍ୱାରା ପାଣ୍ଠି ସଂଗ୍ରହ ଓ ବ୍ୟୟ ସଂକ୍ରାନ୍ତୀୟ ନୀତିର ଅଧ୍ୟୟନ ହିଁ ରାଷ୍ଟ୍ରୀୟ କର୍ତ୍ତୃପକ୍ଷଙ୍କ ଆୟ ବ୍ୟୟ ଓ ସେଗୁଡ଼ିକର ପାରସ୍ପରିକ ସମଯୋଜକ ସହିତ ସମ୍ପୃକ୍ତ ।’’ (Public finance is concerned with the income and expenditure of public authorities and with the adjustment of one to the other).

ଉପରୋକ୍ତ ଆଲୋଚନାରୁ ଜଣାପଡ଼େ ଯେ ରାଷ୍ଟ୍ରବିତ୍ତ କେନ୍ଦ୍ରୀୟ, ରାଜ୍ୟ ଓ ସ୍ଥାନୀୟ ସମସ୍ତ ସ୍ତରରେ କାର୍ଯ୍ୟ କରୁଥିବା ସରକାରଙ୍କର ଆୟ ଓ ବ୍ୟୟ ସମ୍ପର୍କରେ ଅନୁଧ୍ୟାନ କରିଥାଏ ।

ରାଷ୍ଟ୍ରବିତ୍ତ ଓ ବ୍ୟକ୍ତିବିର :- ରାଷ୍ଟ୍ରବିତ୍ତ ବା ସରକାରଙ୍କ ବିର ସହିତ ବ୍ୟକ୍ତିବିତ୍ତ ବା ଘରୋଇବିତ୍ତର ତୁଳନାରୁ ରାଷ୍ଟ୍ରବିତ୍ତର ଅଧ୍ୟୟନ ଓ ଅନୁଧ୍ୟାନ ସହଜ ହୁଏ । ଏହି ତୁଳନାରୁ ଆମେ ରାଷ୍ଟ୍ରର ଓ ବ୍ୟକ୍ତିର ଆର୍ଥିକ ସମ୍ପର୍କରେ ଅବଗତ ହୋଇଥାଉ ।

ପାର୍ଥକ୍ୟ :
(୧) ବ୍ୟକ୍ତିବିଶେଷ ନିଜର ବ୍ୟୟକୁ ଆୟ ସହିତ ସମତୁଲ କରିବାକୁ ଚେଷ୍ଟା କରିଥାଏ । ତାହାର ବ୍ୟୟ, ଆୟ ଦ୍ବାରା ନିର୍ଦ୍ଧାରିତ ହୋଇଥାଏ । ତାହାର ଆୟ ଅଧ‌ିକ ହେଲେ, ସେ ଅଧିକ ବ୍ୟୟ କରିବାକୁ ସକ୍ଷମ ହୁଏ । ଅବଶ୍ୟ ସାମୟିକ ଭାବରେ ସେ ନିଜ ଆୟରୁ ଅଧିକ ବ୍ୟୟ କରିପାରେ । କିନ୍ତୁ ଅନିର୍ଦ୍ଦିଷ୍ଟ କାଳପର୍ଯ୍ୟନ୍ତ ଅଧ୍ବକ ବ୍ୟୟ କରି ଚାଲି ବା ତାଙ୍କ ପକ୍ଷରେ ସମ୍ଭବପର ନୁହେଁ । ତେଣୁ ସେ ନିଜର ସୀମିତ ସାଧନ ମଧ୍ଯରେ ଜୀବନ ନିର୍ବାହ କରନ୍ତି ।

ସେ ତାଙ୍କର କନାର ପରିମାଣ ଅନୁଯାୟୀ ଜାମାର ଆବର ସ୍ଥିର କରନ୍ତି । କିନ୍ତୁ ସରକାରଙ୍କ କ୍ଷେତ୍ରରେ ବ୍ୟୟ, ଆୟର ପରିମାଣ ନିର୍ଦ୍ଧାରଣ କରିଥାଏ । ସରକାର ପ୍ରଥମେ ସମ୍ଭାବ୍ୟ ବ୍ୟୟକୁ ଅଟକଳ କରି ତାହାପରେ ସେହି ବ୍ୟୟ ନିର୍ବାହ କରିବାପାଇଁ ସଂଗ୍ରହ କରନ୍ତି । ବ୍ୟକ୍ତି ବିଶେଷଙ୍କର ଆୟ ପ୍ରାୟ ସୀମିତ ହୋଇଥିବାରୁ, ଲଗାମଛଡ଼ା ବ୍ୟୟ ତାଙ୍କ ପକ୍ଷରେ ସମ୍ଭବପର ନୁହେଁ; କିନ୍ତୁ ସରକାର ଇଚ୍ଛା କଲେ ବିଭିନ୍ନ ସୂତ୍ରରୁ ଅତିରିକ୍ତ ସମ୍ବଳ ସଂଗ୍ରହ କରିପାରନ୍ତି ।

ଅବଶ୍ୟ ବେଳେବେଳେ ବ୍ୟକ୍ତିବିଶେଷ କରି ସରକାରଙ୍କୁ ମଧ୍ୟ ନିଜ ଆୟ ଅନୁସାରେ ବ୍ୟୟ କରିବାକୁ ପଡ଼େ । ସରକାର ଯେତେବେଳେ ଅନୁଭବ କରନ୍ତି ଯେ ବିଭିନ୍ନ ସୂତ୍ରରୁ ଅତିରିକ୍ତ ସମ୍ବଳ ସଂଗ୍ରହ ଆଉ ସମ୍ଭବପର ନୁହେଁ, ସେତେବେଳେ ସରକାରଙ୍କୁ ମଧ୍ୟ ଖର୍ଚ୍ଚ କାଟ କରିବାକୁ ପଡ଼େ । ଅନ୍ୟ ପକ୍ଷରେ ବ୍ୟକ୍ତିବିଶେଷ ମଧ୍ଯ ବେଳେବେଳେ ତାଙ୍କର ବ୍ୟୟ ନିର୍ଦ୍ଧାରଣ କରି ସେହି ଆର୍ଥିକ ଦାୟିତ୍ବ ତୁଲାଇବାପାଇଁ ଅଧିକ ଆୟ ଉପାର୍ଜନ କରିବାକୁ ଚେଷ୍ଟା କରିଥା’ନ୍ତି ।

କୌଣସି ବ୍ୟକ୍ତିଙ୍କର ଆର୍ଥିକ ଦାୟିତ୍ଵ ଅଧୂକ ହୋଇଥିଲେ, ସେ କଠିନ ପରିଶ୍ରମ କରି ଅଧୂକ ଉପାର୍ଜନ କରିବାକୁ ବ୍ରତୀ ହୁଅନ୍ତି । ଅବଶ୍ୟ ବେଳେବେଳେ ବ୍ୟକ୍ତିବିଶେଷ କରି ସରକାରଙ୍କୁ ମଧ୍ୟ ନିଜ ଆୟ ଅନୁସାରେ ବ୍ୟୟ କରିବାକୁ ପଡ଼େ । ସରକାର ଯେତେବେଳେ ଅନୁଭବ କରନ୍ତି ବିଭିନ୍ନ ସୂତ୍ରରୁ ଅତିରିକ୍ତ ସମ୍ବଳ ସଂଗ୍ରହ ଆଉ ସମ୍ଭବପର ନୁହେଁ, ସେତେବେଳେ ସରକାରଙ୍କୁ ମଧ୍ୟ ଖର୍ଚ୍ଚ କାଟ କରିବାକୁ ପଡ଼େ ।

ଅନ୍ୟପକ୍ଷରେ ବ୍ୟକ୍ତିବିଶେଷ ମଧ୍ଯ ବେଳେବେଳେ ତାଙ୍କର ବ୍ୟୟ ନିର୍ଦ୍ଧାରଣ କରି ସେହି ଆର୍ଥିକ ଦାୟିତ୍ଵ ଅଧ୍ଵ ହୋଇଥିଲେ, ସେ କଠିନ ପରିଶ୍ରମ କରି ଅଧ୍ବକ ଉପାର୍ଜନ କରିବାକୁ ବ୍ରତୀ ହୁଅନ୍ତି ।

(୨) ବେଳେବେଳେ ନିଅଣ୍ଟିଆ ଭରଣା କରିବାପାଇଁ ଉଭୟ ସରକାର ଓ ବ୍ୟକ୍ତିବିଶେଷଙ୍କୁ ଋଣର ଆଶ୍ରୟ ଗ୍ରହଣ କରିବାକୁ ପଡ଼ିଥାଏ । ତେଣୁ ଆର୍ଥିକ ଅସୁବିଧା ସୃଷ୍ଟି ହେଲେ ସରକାର ନିଜର ନାଗରିକମାନଙ୍କଠାରୁ ଆଭ୍ୟନ୍ତରୀଣ ଋଣ ସଂଗ୍ରହ କରିପାରନ୍ତି ।

ସେହିପରି ସରକାର ବିଦେଶରୁ ମଧ୍ୟ ବୈଦେଶିକ ଋଣ ନେଇପାରନ୍ତି, କିନ୍ତୁ ବ୍ୟକ୍ତିବିଶେଷଙ୍କ ପକ୍ଷରେ ଆଭ୍ୟନ୍ତରୀଣ ଋଣ ସଂଗ୍ରହ ସମ୍ଭବ ନୁହେଁ । ଅର୍ଥାତ୍ ସେ ନିଜେ ନିଜ ପାଖରୁ ଋଣ ନେଇପାରନ୍ତି ନାହିଁ । ସେ କେବଳ ଅନ୍ୟମାନଙ୍କ ନିକଟରୁ ଅର୍ଥାତ୍ ବାହ୍ୟିକ ଋଣ ଗ୍ରହଣ କରିପାରନ୍ତି ।

(୩) ସରକାର ଆର୍ଥିକ ସମସ୍ୟାର ସମ୍ମୁଖୀନ ହେଲେ, ନୋଟ୍ ଛପାଇ ତାହାର ସମାଧାନ କରିପାରନ୍ତି । ଅଧ‌ିକ ନୋଟ ପ୍ରଚଳନ, ସରକାରୀ ଆୟର ଏକ ଅତିରିକ୍ତ ଉତ୍ସ ଭାବରେ କାର୍ଯ୍ୟ କରେ । ଯୁଦ୍ଧକାଳୀନ ଅବସ୍ଥାରେ ବା କ୍ରମାଗତ ନିଅଣ୍ଟିଆ ବଜେଟ୍ ଭରଣାପାଇଁ ସରକାର ଅତିରିକ୍ତ ମୁଦ୍ରା ପ୍ରଚଳନ କରି ଆର୍ଥିକ ସଙ୍କଟର ମୁକାବିଲା କରିଥା’ନ୍ତି । କିନ୍ତୁ ବ୍ୟକ୍ତିବିଶେଷଙ୍କ ପକ୍ଷରେ ଅତିରିକ୍ତ ମୁଦ୍ରା ପ୍ରଚଳନ ସମ୍ଭବ ନୁହେଁ ।

(୪) ସରକାର ତାଙ୍କ ବଜେଟ୍ ବା ଆୟବ୍ୟୟର ଅଟକଳ ବାର୍ଷିକ ଭିଭିରେ ପ୍ରସ୍ତୁତ କରନ୍ତି । ଏହି ବଜେଟ୍ ଏକ ଆର୍ଥିକ ବର୍ଷପାଇଁଉଦ୍ଦିଷ୍ଟ ହୋଇଥାଏ । କିନ୍ତୁ ବ୍ୟକ୍ତିବିଶେଷଙ୍କ କ୍ଷେତ୍ରରେ ଏପରି କୌଣସି ସମୟ ସୀମା ନ ଥାଏ । ତାଙ୍କ ଆୟବ୍ୟୟର ଅଟକଳ ସ୍ଵଳ୍ପକାଳୀନ ଦୀର୍ଘକାଳୀନ ହୋଇପାରେ ।

(୫) ସରକାର ଓ ବ୍ୟକ୍ତିବିଶେଷଙ୍କର ବ୍ୟୟର ଉଦ୍ଦେଶ୍ୟରେ ମଧ୍ୟ ପାର୍ଥକ୍ୟ ଦେଖାଯାଏ । ପ୍ରତ୍ୟେକ ବ୍ୟକ୍ତି ଲାଭପାଇଁ ଲାଳାୟିତ । ବ୍ୟକ୍ତିଗତ ଲାଭକୁ ସର୍ବାଧ‌ିକ କରିବା ତାଙ୍କର ବ୍ୟବସାୟିକ କାର୍ଯ୍ୟାବଳୀର ପ୍ରଧାନ ଉଦ୍ଦେଶ୍ୟ । ଅନ୍ୟପକ୍ଷରେ ରାଷ୍ଟ୍ରୀୟ ବ୍ୟୟ ସାମୂହିକ କଲ୍ୟାଣ ବୃଦ୍ଧିର ଉଦ୍ଦେଶ୍ୟ ଦ୍ବାରା ପରିଚାଳିତ । ତେଣୁ ଯେଉଁ ସବୁ କ୍ଷେତ୍ରରେ ଦୀର୍ଘକାଳ ପରେ ଲାଭର ଉଦ୍ଭବ ହୁଏ; ସେ ସବୁ କ୍ଷେତ୍ରରେ ଘରୋଇ ବିନିଯୋଗରେ ସମ୍ଭାବନା କ୍ଷୀଣ ହୋଇଥାଏ ।

ବ୍ୟକ୍ତିବିଶେଷ କୌଣସି ଅନୁନ୍ନତ ଅଞ୍ଚଳରେ ରେଳରାସ୍ତା ନିର୍ମାଣ କରିବାକୁ ଆଦୌ ଆଗ୍ରହ ହେବ ନାହିଁ । କାରଣ ଏ ଧରଣର ପ୍ରକଳ୍ପରୁ ଲାଭର ପ୍ରତ୍ୟାଶା ଅତି କ୍ଷୀଣ । କିନ୍ତୁ ସାମାଜିକ ଦୃଷ୍ଟିକୋଣରୁ ସେହି ରେଳରାସ୍ତାର ଆବଶ୍ୟକତା ଥିଲେ ସରକାରଙ୍କୁ ତାହାର ନିର୍ମାଣ ଦାୟିତ୍ଵ ଗ୍ରହଣ କରିବାକୁ ପଡିପାରେ ।

(୬) ଲୋକମାନେ ସର୍ବଦା ନିଜ ଆୟ ବ୍ୟୟ ସମ୍ପର୍କରେ ଗୋପନୀୟତା ରକ୍ଷା କରିବାକୁ ଚାହାନ୍ତି । ଜଣେ ବ୍ୟକ୍ତି ସର୍ବଦା ନିଜର ଆୟର ପରିମାଣ ବା ଋଣ ପରିମାଣ ଅନ୍ୟମାନଙ୍କ ନିକଟରୁ ଗୋପନ ରଖୁବାକୁ ଚେଷ୍ଟା କରିଥାଏ । କିନ୍ତୁ ରାଷ୍ଟ୍ରବିତ୍ତ କ୍ଷେତ୍ରରେ ଗୋପନୀୟତା ରକ୍ଷାର କୌଣସି ପ୍ରଶ୍ନ ନ ଥାଏ । ସର୍ବସାଧାରଣଙ୍କ ଗୋଚରାର୍ଥେ ସରକାର ବାର୍ଷିକ ବଜେଟ୍ ଉପସ୍ଥାପିତ କରିଥା’ନ୍ତି ।

ସରକାରଙ୍କ ଆୟ ବ୍ୟୟ ସଂକ୍ରାନ୍ତରେ ସଂସଦରେ ବିଶଦ ଆଲୋଚନା ହୁଏ । ଖବରକାଗଜ, ଟି.ଭି. ଓ ରେଡ଼ିଓ ପ୍ରଭୃତି ମାଧ ଜରିଆରେ ବଜେଟ୍‌ର ବିଭିନ୍ନ ଦିଗକୁ ଘେରି ଆଲୋଚନା ହୋଇଥାଏ । ତେଣୁ ରାଷ୍ଟ୍ରବିତ୍ତଙ୍କୁ ସର୍ବସାଧାରଣ ବିତ୍ତ ଓ ବ୍ୟକ୍ତିବିରକୁ ଘରୋଇ (ଗୋପନୀୟ) ବିତ୍ତ ଆଖ୍ୟା ଦିଆଯାଇଥାଏ ।

(୭) ଜଣେ ସାଧାରଣ ବ୍ୟକ୍ତି ହାତରେ ମୋଟ୍ ବ୍ୟୟ ଉପରେ କିଛି ବଳକା ଆୟ ରହିଲେ, ତାହା ତାଙ୍କର ବିଜ୍ଞତା ବୋଲି ବିଚାର କରାଯାଏ । ସେ ଆୟଠାରୁ ବ୍ୟୟ କମ୍ କରିବାକୁ ଚେଷ୍ଟା କରେ । ଅଧ‌ିକ ସଞ୍ଚୟ କରି ଜଣେ ବ୍ୟକ୍ତି ବିତ୍ତଶାଳୀ ହୋଇ ନିଜ ସାମାଜିକ ପଦମର୍ଯ୍ୟାଦା ବୃଦ୍ଧି କରିପାରେ । କିନ୍ତୁ ରାଷ୍ଟ୍ରବିତ୍ତରେ ବଳକା ବଜେଟ୍ ସର୍ବଦା ଶୁଭପ୍ରଦ ବୋଲି ଗୃହୀତ ହୁଏନାହିଁ ।

ଉଦାହରଣସ୍ୱରୂପ ଦେଶରେ ମାନ୍ଦାବସ୍ଥା ବିଦ୍ୟମାନ ଥିଲେ ନିଅଣ୍ଟିଆ ବଜେଟ୍ ହିଁ ବାଞ୍ଛନୀୟ । ସରକାର ମୋଟ ବ୍ୟୟର ପରିମାଣ ବର୍ଷିତ କଲେ, ଅଧ୍ଵକ କ୍ରୟକ୍ଷମତା ସୃଷ୍ଟି ହୁଏ । ମୋଟ ଚାହିଦା ବୃଦ୍ଧି ପାଏ । ଅଧ୍ୟାପକ କେନସ୍ ମତ ଦେଇଥିଲେ ଯେ ସରକାର ସର୍ବଦା ନିଅଣ୍ଟିଆ ବଜେଟ୍ କରିବା ଉଚିତ୍ । ସାଧାରଣ ପରିସ୍ଥିତିରେ ସରକାର ବଳକା ବଜେଟ୍ କରିପାରନ୍ତି ।

(୮) ରାଷ୍ଟ୍ର ଏବଂ ବ୍ୟକ୍ତିବିଶେଷ ଉଭୟ ସେମାନଙ୍କ ବ୍ୟୟରୁ ଲବ୍‌ଧ ଉପଯୋଗିତାକୁ ସର୍ବାଧ୍ଵକ କରିବାକୁ ତତ୍ପର ହୋଇଥାଆନ୍ତି । ସମସୀମାନ୍ତ ଉପଯୋଗିତା ସୂତ୍ରର ନୀତିକୁ ଅନୁସରଣ କରି ପରିତୃପ୍ତିକୁ ସର୍ବାଧ୍ଵ କରାଯାଇପାରେ । ଜଣେ ବ୍ୟକ୍ତି ତାହାର ବ୍ୟୟକୁ ଏପରି ଭାବରେ ବିନ୍ୟାସ କରେ, ତଦ୍ବାରା ସେ ପ୍ରତ୍ୟେକ ପ୍ରକାର ବ୍ୟୟରୁ ସମାନ ଉପଯୋଗିତା ଲାଭ କରିଥାଏ । ଅର୍ଥାତ୍ ବ୍ୟକ୍ତି ପକ୍ଷରେ ସମସୀମାନ୍ତ ଉପଯୋଗିତା ସୂତ୍ରକୁ ଯଥାଯଥ ଭାବରେ ପାଳନ କରିବା ସମ୍ଭବପର ହୋଇଥାଏ ।

ସରକାର ମଧ୍ୟ ଏହି ନିୟମ ଅନୁସାରେ ଚଳୁଥିଲେ ସୁଦ୍ଧା, ସର୍ବଦା ଏହାକୁ ଯଥାଯଥ ଭାବରେ ମାନିବା ସମ୍ଭବ ହୁଏ ନାହିଁ । କାରଣ ସରକାର ଅନେକ ସମୟକ ହୁଏନାହିଁ । କାରଣ ସରକାର ଅନେକ ସମୟରେ ଅଣ-ଅର୍ଥନୈତିକ କାରଣ ଦ୍ଵାରା ପ୍ରଭାବିତ ହୋଇଥାନ୍ତି । ବିଭିନ୍ନ ରାଜନୈତିକ ଓ ଅର୍ଥନୈତିକ ଗୋଷ୍ଠୀର ଅଯୌକ୍ତିକ ଚାହିଦା ଆଗରେ ସରକାର ରେଲେଇଲେ ନୀରି ସ୍ଵୀକାର କରିବାକୁ ବାଧ୍ୟ ହୁଅନ୍ତି ।

(୯) ବ୍ୟକ୍ତିବିଶେଷ ଆୟ ସଂଗ୍ରହ ନିମନ୍ତେ କାହାକୁ ବାଧ୍ୟ କରିପାରନ୍ତି ନାହିଁ । କିନ୍ତୁ ସରକାରଙ୍କର ବଳପ୍ରୟୋଗର କ୍ଷମତା ରହିଛି । ସରକାର କାହାରି ଉପରେ କରଧାର୍ଯ୍ୟ କଲେ, ସେ କର ଦେବାକୁ ଅସ୍ବୀକାର କରିପାରିବେ ନାହିଁ ।

(୧୦) ବ୍ୟକ୍ତିବିଶେଷଙ୍କ ପକ୍ଷରେ ଦେବାଳିଆ ହୋଇଯିବା ସମ୍ଭବ । ତାଙ୍କର ମୋଟ ଦେୟର ପରିମାଣ ଯଦି ମୋଟ ପରିସମ୍ପତ୍ତି ଠାରୁ ବଳିଯାଏ; ତେବେ ତାଙ୍କୁ ଦେବାଳିଆ ଘୋଷଣା କରାଯାଏ; କିନ୍ତୁ କୌଣସି ରାଷ୍ଟ୍ରର ପରିସମ୍ପତ୍ତିକୁ ଏତେ ସହଜରେ ନିର୍ଦ୍ଧାରିତ କରିହୁଏ ନାହିଁ । କୌଣସି ରାଷ୍ଟ୍ରର ମୋଟ ପରିସମ୍ପତ୍ତିର ପରିମାଣ ତାହାର ନାଗରିକମାନଙ୍କର ମୋଟ ପରିସମ୍ପତ୍ତି ସହିତ ସମାନ । ତେଣୁ ସାଧାରଣ ଅର୍ଥରେ କୌଣସି ରାଷ୍ଟ୍ରର ଦେବାଳିଆ ହେବା ସମ୍ଭବ ନୁହେଁ ।

(୧୧) ବ୍ୟକ୍ତିବିଶେଷଙ୍କ ପକ୍ଷରେ ଭବିଷ୍ୟତ ଅପେକ୍ଷା ବତ୍ତର୍ମାନ ଅଧିକ ଗୁରୁତ୍ଵପୂର୍ଣ୍ଣ । ଭବିଷ୍ୟତକୁ ସେମାନେ ଅବହେଳା କରିଥାଆନ୍ତି । ସେମାନେ ତେଣୁ ସତ୍ତ୍ବର ଲାଭ ପାଇବାକୁ ତତ୍ପର । ସେମାନଙ୍କ ନିକଟରେ ଭବିଷ୍ୟତର ଆୟ ଅପେକ୍ଷା ବର୍ତ୍ତମାନର ଆୟ ଅଧୁକ କାମ୍ୟ । କିନ୍ତୁ ରାଷ୍ଟ୍ରର କଥା ଅଲଗା । ରାଷ୍ଟ୍ର ଏକ ଚିରସ୍ଥାୟୀ ଅନୁଷ୍ଠାନ । ତେଣୁ ରାଷ୍ଟ୍ରର ଉଭୟ ବର୍ତ୍ତମାନ ଓ ଭବିଷ୍ୟତ ପିଢ଼ି ପ୍ରତି ସମାନ ଦାୟିତ୍ଵ ରହିଥାଏ । ତେଣୁ ଅନେକ ସମୟରେ ସରକାର କେବଳ ବର୍ତ୍ତମାନ ପାଇଁ ବ୍ୟୟ ନିର୍ବାହ ନ ଭାର ନ୍ୟସ୍ତ ହୁଏ ସତ, କିନ୍ତୁ ଭବିଷ୍ୟତରେ ତାହାର ସୁଫଳ ମିଳେ ।

2. ରାଷ୍ଟ୍ରୀୟ ଆୟର ବିଭିନ୍ନ ଉତ୍ସଗୁଡ଼ିକ ବର୍ଣ୍ଣନା କର ।
Answer:
ରାଷ୍ଟ୍ରୀୟ ଆୟ ବା ରାଜସ୍ବ ରାଷ୍ଟ୍ରବିତ୍ତର ଏକ ପ୍ରଧାନ ଅଂଶ । ସମୂହ କଲ୍ୟାଣ ଉଦ୍ଦେଶ୍ୟରେ ରାଷ୍ଟ୍ର ବିପୁଳ ପରିମାଣର ସମ୍ବଳ ବା ରାଜସ୍ବ ଦରକାର କରିଥାଏ । ସାଧାରଣଭାବେ ବର୍ଣ୍ଣନା କଲେ ସରକାର ନିଜର ଆର୍ଥିକ ଆବଶ୍ୟକତାର ପରିପୂରଣ ନିମନ୍ତେ ସମସ୍ତ ସୂତ୍ରରୁ ସଂଗୃହୀତ ଅର୍ଥକୁ ରାଷ୍ଟ୍ରୀୟ ଆୟର ଆଖ୍ୟା ଦିଆଯାଇଥାଏ । ବ୍ୟାପକ ଅର୍ଥରେ ସରକାରୀ ଋଣ, ଅଧିକ ନୋଟ୍ ପ୍ରଚଳନ, ସରକାରୀ ଉଦ୍ୟୋଗରୁ ମିଳୁଥିବା ଲାଭାଂଶ ଇତ୍ୟାଦି ରାଷ୍ଟ୍ରୀୟ ଆୟପ୍ରାପ୍ତିର ଅନ୍ତର୍ଭୁକ୍ତ । କିନ୍ତୁ ରାଷ୍ଟ୍ରୀୟ ରାଜସ୍ଵ ଏକ ସୀମିତ ଧାରଣ କାରଣ କେତେକ ବିଧ‌ିବଦ୍ଧ ସୂତ୍ରରୁ ମିଳୁଥିବା ଆୟ ହିଁ ରାଷ୍ଟ୍ରୀୟ ରାଜସ୍ବର ଅନ୍ତର୍ଭୁକ୍ତ ।

ସରକାରୀ ରାଜସ୍ବକୁ ସାଧାରଣଭାବେ ନିମ୍ନଲିଖ ଶ୍ରେଣୀରେ ବିଭକ୍ତ କରାଯାଇଥାଏ ।
(1) କର (Tax) – କର ହେଉଛି ସରକାରୀ ରାଜସ୍ବର ଏକ ସର୍ବବୃହତ୍ ଅଂଶ । ‘ଜଣେ ବ୍ୟକ୍ତି ବା ବ୍ୟକ୍ତସମୂହ ସରକାରଙ୍କ ସେବା ନିମନ୍ତେ ନିଜ ସମ୍ପରିରୁ ଯେଉଁ ବାଧ୍ୟତାମୂଳକ ଦେୟ ପ୍ରଦାନ କରନ୍ତି, ତାହାକୁ କର କୁହାଯାଏ ।’’ ଅନ୍ୟ ଅର୍ଥରେ, ‘କୌଣସି ବିଶେଷ ସୁବିଧା ସହ ସମ୍ପର୍କ ନ ଥାଇ ସର୍ବସାଧାରଣ ସ୍ଵାର୍ଥ ଦୃଷ୍ଟିରୁ ବ୍ୟୟ ନିର୍ବାହ ନିମନ୍ତେ ବ୍ୟକ୍ତିବିଶେଷ ସରକାରଙ୍କୁ ଯେଉଁ ବାଧ୍ୟତାମୂଳକ ଦେୟ ଦିଅନ୍ତି, ତାହାକୁ ‘କର’ କୁହାଯାଏ ।’’

କର ଏକ ବାଧ୍ୟତାମୂଳକ ଦେୟ ହୋଇଥିବାରୁ କରଦାତାଙ୍କର ଏହା ଏକ ଆଇନଗତ କର୍ତ୍ତବ୍ୟ ବୋଲି ବିଚାର କରାଯାଏ । ଏହାକୁ ପ୍ରତ୍ୟାଖ୍ୟାନ କଲେ ଆଇନ ଦୃଷ୍ଟିରେ ଏହା ଅପରାଧ ବୋଲି ବିବେଚିତ ହୋଇଥାଏ । କରରୁ ସଂଗୃହୀତ ଅର୍ଥ ସାମୂହିକ କଲ୍ୟାଣ ଉଦ୍ଦେଶ୍ୟରେ ବ୍ୟୟ କରାଯାଇଥାଏ । କର ପ୍ରଦାନ ବ୍ୟକ୍ତିମାନଙ୍କର ଏକ ନିଜସ୍ବ ଦାୟିତ୍ଵ ।

(2) ପ୍ରଶାସନିକ ରାଜସ୍ଵ (Administrative Revenue) – ପି, ଲାଇସେନ୍ସ ଫି, ଜୋରିମାନା, ବାଜ୍ୟାପ୍ତି, ବିଶେଷ ନିର୍ଦ୍ଧାରଣ (Special Assessment) ଆଦିକୁ ପ୍ରଶାସନିକ ରାଜସ୍ୱ କୁହାଯାଏ ।
(a) ଫିଜ୍ (Fees) – ସର୍ବସାଧାରଣ ସ୍ଵାର୍ଥ ନିହିତ ଥିବା ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ସେବା ନିମନ୍ତେ ଦିଆଯାଉଥିବା ବାଧ୍ୟତାମୂଳକ ଦେୟକୁ ଫିଜ୍ କୁହାଯାଏ । ଫିଦାତାଙ୍କୁ ଫିଜର ପ୍ରତିବଦଳରେ ପ୍ରତ୍ୟକ୍ଷ ସୁବିଧା, ପ୍ରାପ୍ତି ହୋଇଥାଏ । ଉଦାହରଣ ସ୍ଵରୂପ, କଲେଜ ଫି, କଲେଜରେ ପଢୁଥିବା ଛାତ୍ରଙ୍କ ନିମନ୍ତେ ଏକ ବାଧ୍ୟତାମୂଳକ ଦେୟ ଅଟେ ।

(b) ଲାଇସେନ୍ସ ଫିଜ୍ (Licence Fees) – ସରକାର ନିଜେ କୌଣସି ନିର୍ଦ୍ଦିଷ୍ଟ କାର୍ଯ୍ୟ ସମ୍ପାଦନ ନ କରି ଫିଦାତାଙ୍କୁ କୌଣସି ନିର୍ଦ୍ଦିଷ୍ଟ କାର୍ଯ୍ୟ ନିମନ୍ତେ ଅନୁମତି ବା ବିଶେଷ ସୁବିଧା ପ୍ରଦାନ କରିଥା’ନ୍ତି; ଯଥା – ଏକ ମୋଟରଚାଳକ ଗାଡ଼ି ଚଳାଇବା ପାଇଁ ଲାଇସେନ୍ସ ଫି ପ୍ରଦାନ କରି ସରକାରଙ୍କଠାରୁ ବିଶେଷ ଅନୁମତି ପ୍ରାପ୍ତ ହୋଇଥା’ନ୍ତି । କେତେକ ଧରଣର କାର୍ଯ୍ୟକଳାପ ନିୟନ୍ତ୍ରଣ କରିବା ଏହି ଫି’ର ପ୍ରଧାନ ଉଦ୍ଦେଶ୍ୟ । ମାଦକ ଦ୍ରବ୍ୟର ବିକ୍ରୟ ନିମନ୍ତେ ଲାଇସେନ୍ସ ପ୍ରଚଳନ କରିବାର ମୁଖ୍ୟ ଉଦ୍ଦେଶ୍ୟ ହେଲା, ସେସବୁ ଦ୍ରବ୍ୟର କ୍ରୟ ବିକ୍ରୟ ଉପରେ ଯଥେଷ୍ଟ ନିୟନ୍ତ୍ରଣ ଜାରି କରିବା ।

(c) ଜୋରିମାନା (Penalty) କୌଣସି ବ୍ୟକ୍ତି ବା ଅନୁଷ୍ଠାନ ଆଇନର ବିରୁଦ୍ଧାଚରଣ କଲେ ତାହାର ଶାସ୍ତି ସ୍ବରୂପ କର୍ତ୍ତୃପକ୍ଷଙ୍କଦ୍ୱାରା ଅର୍ଥଦଣ୍ଡରେ ଦଣ୍ଡିତ ହୋଇଥା’ନ୍ତି । ଏହା ଜୋରିମାନା ନାମରେ ପରିଚିତ । ଏହାଦ୍ୱାରା ସରକାର କିଛି ରାଜସ୍ୱ ସଂଗ୍ରହ କରିଥା’ନ୍ତି ।

(d) ବାଜ୍ୟାପ୍ତି (Forleitures) – କେତେକ କ୍ଷେତ୍ରରେ ଚୁକ୍ତିଭଙ୍ଗ ଯୋଗୁଁ ବା ଦାୟିତ୍ୱ ପାଳନରେ ଅକ୍ଷମତା ଯୋଗୁଁ ଅର୍ଥଦଣ୍ଡ ଭାବରେ ବାଜ୍ୟାପ୍ତି କାର୍ଯ୍ୟ କରେ । ଏହା ରାଜସ୍ୱ ସଂଗ୍ରହର ଏକ ନଗଣ୍ୟ ଉତ୍ସ ।

(e) ବିଶେଷ ନିର୍ଦ୍ଧାରଣ (Special Assessment) – ସରକାରଙ୍କ ରାସ୍ତାଘାଟ ନିର୍ମାଣ, ନଦୀବନ୍ଧ ନିର୍ମାଣ ପରି କେତେକ ସ୍ଥାନୀୟ ଉନ୍ନତିମୂଳକ କାର୍ଯ୍ୟ ନିମନ୍ତେ ଉପକୃତ ହେଉଥିବା ସ୍ଥାନୀୟ ଅଧିବାସୀଙ୍କଠାରୁ ଏକ ସମୁନ୍ନତ କର ଆଦାୟ କରିଥା’ନ୍ତି ଯାହାକୁ ବିଶେଷ ନିର୍ଦ୍ଧାରଣ କୁହାଯାଏ । ଏହି ରାଜସ୍ବ ସାଧାରଣଭାବେ ସରକାରୀ କାର୍ଯ୍ୟକ୍ରମରୁ ଲାଭବାନ୍ ହେଉଥିବା ବ୍ୟକ୍ତିମାନଙ୍କଠାରୁ ସଂଗୃହୀତ ହୋଇଥାଏ ।

(3) ବାଣିଜ୍ୟିକ ରାଜସ୍ୱ (Commercial Revenue) – ବାଣିଜ୍ୟିକ ରାଜସ୍ଵ ଦୁଇଟି ଉତ୍ସରୁ ସୃଷ୍ଟି ହୋଇଥାଏ; ଯଥା – ସରକାରୀ ସମ୍ପତ୍ତି କିମ୍ବା ସରକାରୀ ଉଦ୍ୟୋଗ ।
(a) ସରକାରୀ ସମ୍ପରି ରାଜସ୍ବ – ପ୍ରତ୍ୟେକ ଦେଶରେ ଭୂମି, ଖଣି, ଜଙ୍ଗଲ ପରି କେତେକ ସମ୍ପରି ସରକାରଙ୍କ ଅଧିକାରଭୁକ୍ତ ହୋଇଥାଏ । ଏସବୁ ସମ୍ପତ୍ତି ବିକ୍ରୟ କରି କିମ୍ବା ଲିଜ୍ ପ୍ରଦାନ କରି ସରକାର ରାଜସ୍ୱ ଆହରଣ କରିଥା’ନ୍ତି ।

(b) ସରକାରୀ ଉଦ୍ୟୋଗ ରାଜସ୍ଵ – ଆଧୁନିକ ମିଶ୍ରିତ ଅର୍ଥନୀତିରେ ସରକାର ବିଭିନ୍ନ ଦ୍ରବ୍ୟ ସାମଗ୍ରୀ ଓ ସେବାର ଉତ୍ପାଦନ ଓ ବିକ୍ରୟ କରିଥା’ନ୍ତି । ଏହା ସରକାରୀ ଉଦ୍ୟୋଗଲବ୍‌ଧ ଆୟ ଭାବରେ ବିବେଚିତ ହୋଇଥାଏ । ରେଳବାଇ, ଡାକ ବ୍ୟବସ୍ଥା, ରାଷ୍ଟ୍ରୀୟ ପରିବହନ ଓ ଅନ୍ୟାନ୍ୟ ଶିକ୍ଷୋଦ୍ୟୋଗ ପ୍ରଭୃତିରୁ ଲାଭକୁ ସରକାରୀ ରାଜସ୍ବର ଅନ୍ତର୍ଭୁକ୍ତ କରାଯାଇଥାଏ ।

(4) ଦାନ ଏବଂ ଅନୁଦାନ (Gifts & Grants) – ବ୍ୟକ୍ତିବିଶେଷ, ଘରୋଇ ସଂସ୍ଥା କିମ୍ବା ଅନୁଷ୍ଠାନମାନଙ୍କ ନିକଟରୁ ଦାନ ମିଳିଥାଏ ଯାହା ସମ୍ପୂର୍ଣ ସ୍ବେଚ୍ଛାକୃତ ଅଟେ । ବାତ୍ୟା, ବନ୍ୟା, ମରୁଡ଼ି ପ୍ରପୀଡ଼ିତଙ୍କୁ ସହାୟତା ପ୍ରଦାନ ପ୍ରଭୃତି ନିର୍ଦ୍ଦିଷ୍ଟ କାରଣ ନିମନ୍ତେ ଏହି ଦାନ ମିଳିଥାଏ । ସେହିପରି ଜାତୀୟ ପ୍ରତିରକ୍ଷା ପାଣ୍ଠି, ମୁଖ୍ୟମନ୍ତ୍ରୀ ଓ ପ୍ରଧାନମନ୍ତ୍ରୀଙ୍କ ରିଲିଫ୍ ଫଣ୍ଡକୁ ମଧ୍ଯ ଦାନ ମିଳିଥାଏ । ଏହା ସରକାରୀ ରାଜସ୍ବର ଅନ୍ତର୍ଭୁକ୍ତ ।

କୌଣସି ସରକାର ଅନ୍ୟ ଏକ ସରକାରଙ୍କୁ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ କାର୍ଯ୍ୟ ପାଇଁ ଦେଇଥିବା ଆର୍ଥିକ ସହାୟତାକୁ ଅନୁଦାନ କୁହାଯାଏ । କେନ୍ଦ୍ର ସରକାର ରାଜ୍ୟ ସରକାରଙ୍କୁ କେତେକ କ୍ଷେତ୍ରରେ ଅନୁଦାନ ପ୍ରଦାନ କରିଥା’ନ୍ତି । ସେହିପରି ବିଦେଶୀ ରାଷ୍ଟ୍ର ବା ସଂସ୍ଥା ଅନୁଦାନ ପ୍ରଦାନ କରିଥା’ନ୍ତି ଯାହା ସରକାରୀ ରାଜସ୍ବର ଅଂଶବିଶେଷ ହୋଇଥାଏ ।

ଉପରୋକ୍ତ ଆଲୋଚନାରୁ ପ୍ରତୀୟମାନ ହୁଏ ଯେ, ସରକାରୀ ରାଜସ୍ବର ଶ୍ରେଣୀ ପ୍ରକରଣ କଠୋର ନୁହେଁ, ବରଂ ବିଭିନ୍ନ ରାଜସ୍ବ ମଧ୍ୟରେ ଥିବା ପାର୍ଥକ୍ୟ ଅତ୍ୟନ୍ତ କ୍ଷୀଣ ।

3. ପ୍ରତ୍ୟକ୍ଷ କର କାହାକୁ କୁହାଯାଏ ? ପ୍ରତ୍ୟକ୍ଷ କରର ସୁବିଧା ଓ ଅସୁବିଧାଗୁଡ଼ିକ ସଂକ୍ଷେପରେ ବର୍ଣ୍ଣନା କର ।
Answer:
କୌଣସି କରର ସଂଘାତ (ପ୍ରାରମ୍ଭିକ ବୋଝ) ଓ ଆପାତ ( ଅନ୍ତିମ ବୋଝ) ଯେତେବେଳେ ଜଣେ ବ୍ୟକ୍ତିଙ୍କ ଉପରେ ପଡ଼େ, ସେତେବେଳେ ସେହି କରକୁ ପ୍ରତ୍ୟକ୍ଷ କର କୁହାଯାଏ । ପ୍ରକାରାନ୍ତରେ କହିଲେ, ଯେଉଁ କରର ବୋଝକୁ ହସ୍ତାନ୍ତର କରାଯାଇପାରେ ନାହିଁ, ତାହାକୁ ପ୍ରତ୍ୟକ୍ଷ କର କୁହାଯାଏ । ଅଧ୍ୟାପକ ଡାଲ୍‌ଟନ୍‌ ଏହି ପ୍ରକାର ଶ୍ରେଣୀବିଭାଜନକୁ ସମର୍ଥନ କରନ୍ତି ନାହିଁ । ତାଙ୍କ ମତରେ, ବ୍ୟକ୍ତିଗତ ସେବା ବ୍ୟତୀତ ଅନ୍ୟ ଯେଉଁସବୁ ଦ୍ରବ୍ୟ ଓ ସେବା କ୍ରୟବିକ୍ରୟ ଉପରେ କରଧାର୍ଯ୍ୟ କରାଯାଏ ତାହାକୁ ପରୋକ୍ଷ କର ଏବଂ ଅନ୍ୟ ସମସ୍ତ କରକୁ ପ୍ରତ୍ୟକ୍ଷ କର କୁହାଯାଏ ।

ପ୍ରତ୍ୟକ୍ଷ କରର ନିମ୍ନଲିଖ୍ ସୁବିଧାମାନ ପରିଲକ୍ଷିତ ହୁଏ :
(a) ନ୍ୟାୟୋଚିତ – ପ୍ରତ୍ୟକ୍ଷ କର ଧାର୍ଯ୍ୟ କଲାବେଳେ ବ୍ୟକ୍ତିବିଶେଷଙ୍କ ଆୟ ଓ ସଞ୍ଚୟକୁ ବିଚାର କରାଯାଇ କରଧାର୍ଯ୍ୟ କରାଯାଉଥିବାରୁ ଏହି କର ନ୍ୟାୟୋଚିତ ବିବେଚିତ ହୁଏ । ଏହାଫଳରେ ଧନୀଲୋକମାନଙ୍କ ଉପରେ ଅଧିକ ହାରରେ କର ଧାର୍ଯ୍ୟ କରାଯାଇପାରେ ଅଥବା କରମୁକ୍ତ କରାଯାଇପାରେ । ମୋଟ ଉପରେ କରଦାତାଙ୍କ ସାମର୍ଥ୍ୟ ଅନୁଯାୟୀ ଏହି କର ଧାର୍ଯ୍ୟ କରାଯାଉଥିବାରୁ ଏହାକୁ ନ୍ୟାୟୋଚିତ ବିବେଚନା କରାଯାଏ ।

(b) ନିଶ୍ଚିତତା – କର କର୍ତ୍ତୃପକ୍ଷ ଓ କରଦାତା ଉଭୟ କର ବିଷୟରେ ନିଶ୍ଚିତଭାବରେ ଜାଣିଥା’ନ୍ତି । ଅର୍ଥାତ୍ କେତେ କର ଦେବାକୁ ହେବ ତାହା କରଦାତାମାନଙ୍କୁ ଜଣାଥାଏ । ସେହିପରି ପ୍ରତ୍ୟକ୍ଷ କରସୂତ୍ରରୁ କେତେ ରାଜସ୍ୱ ଆଦାୟ ହେବ ତାହା ସରକାର ଜାଣିଥା’ନ୍ତି । ତେଣୁ କର ଦେୟ ଓ ଆଦାୟରେ ନିଶ୍ଚିତତା ପ୍ରତ୍ୟକ୍ଷ କରର ଏକ ପ୍ରଧାନ ସୁବିଧା ।

(c) ମିତବ୍ୟୟିତା – ପ୍ରତ୍ୟକ୍ଷ କର ଆଦାୟ କରିବାରେ ମିତବ୍ୟୟିତା ଆଚରଣ କରାଯାଇପାରେ । ଏହି ପ୍ରକାର କରକୁ ଆୟର ଉତ୍ପତ୍ତିସ୍ଥଳରୁ ଆଦାୟ କରାଯାଉଥିବାରୁ ଏଥୁ ନିମନ୍ତେ ପ୍ରଶାସନିକ ଖର୍ଚ୍ଚ ସ୍ଵଳ୍ପ ହୋଇଥାଏ ।

(d) ସ୍ଥିତିସ୍ଥାପକ – ପ୍ରତ୍ୟକ୍ଷ କର ସାହାଯ୍ୟରେ ସରକାରଙ୍କ ପକ୍ଷରେ ସହଜରେ ଅଧ୍ବକ ସମ୍ବଳ ସଂଗ୍ରହ କରିବା ସମ୍ଭବପର ହେଉଥିବାରୁ ଏହି କରକୁ ସ୍ଥିତିସ୍ଥାପକ ବୋଲି ବିଚାର କରାଯାଏ । ଉଦାହରଣସ୍ୱରୂପ, ଆୟ କର ବା ମୃତ୍ୟୁ କର ହାର ହ୍ରାସବୃଦ୍ଧି ହୁଏ । କର ହାର ବୃଦ୍ଧି ହେବା ଭୟରେ କେହି ଅଧୁକ ଆୟ କରିବାକୁ ସଙ୍କୁଚିତ ହୁଅନ୍ତି ନାହିଁ ।

(e) ନାଗରିକ ଚେତନାର ବିକାଶ – ପ୍ରତ୍ୟକ୍ଷ କର ନାଗରିକ ଚେତନାର ବିକାଶ ଘଟାଏ । କରଦାତା କରବୋଝ ପ୍ରତ୍ୟକ୍ଷଭାବରେ ବହନ କରୁଥିବାରୁ ସରକାରଙ୍କ ରାଜସ୍ୱ କିପରି ଭାବରେ ଓ କେଉଁ ଉଦ୍ଦେଶ୍ୟରେ ବ୍ୟୟିତ ହେଉଛି ସେଥ୍ୟପ୍ରତି ସଜାଗ ଦୃଷ୍ଟି ରଖୁ’ନ୍ତି ।

ଅସୁବିଧା – ପ୍ରତ୍ୟକ୍ଷ କରର ନିମ୍ନଲିଖତ ଅସୁବିଧାମାନ ଦୃଷ୍ଟିଗୋଚର ହୁଏ ।
(1) ଅସୁବିଧାଜନକ – ପ୍ରତ୍ୟକ୍ଷ କର ମୋଟା ଆକାରରେ ଦେବାକୁ ହୋଇଥାଏ । ଏକକାଳୀନ ବହୁପରିମାଣରେ କର ଦେବାକୁ ହେଉଥିବାରୁ କରଦାତାଙ୍କୁ ଏହି କର ସୁବିଧାଜନକ ମନେହୁଏ ନାହିଁ । ପୁନଶ୍ଚ କରଦାତାଙ୍କୁ କର ସମ୍ବନ୍ଧୀୟ ନିୟମ ବିଷୟରେ ଅବଗତ ହେବାକୁ ପଡ଼ିଥାଏ ଏବଂ ତଦନୁଯାୟୀ ଆୟର ବିବରଣୀ ସରକାରଙ୍କୁ ଦାଖଲ କରିବାକୁ ହୁଏ । ଏହା ମଧ୍ୟ କରଦାତାଙ୍କୁ କେତେକ ଅସୁବିଧାର ସମ୍ମୁଖୀନ କରାଇଥାଏ ।

(2) ସାଧୁତା ଉପରେ ଏକ କର – ଯେଉଁମାନେ ସରକାରଙ୍କୁ ଆୟ ସମ୍ବନ୍ଧୀୟ ଭୁଲ୍ ତଥ୍ୟ ଦେଇ କର ଫାଙ୍କିଦେବାକୁ ସମର୍ଥ ହୁଅନ୍ତି, ସେମାନେ କରବୋଝରୁ ନିସ୍ତାର ପାଆନ୍ତି । ମାତ୍ର ଯେଉଁମାନେ ଆୟର ସଠିକ୍ ବିବରଣୀ ସରକାରଙ୍କୁ ଦିଅନ୍ତି ଏବଂ କର ଦେବାରେ ସାଧୁତା ଆଚରଣ କରନ୍ତି ସେମାନଙ୍କୁ କରବୋଝ ବହନ କରିବାକୁ ହୁଏ । ଏହି କାରଣରୁ ସମାଲୋଚକମାନେ କରନ୍ତି, ତାହା ମନମୁଖୀ ହୋଇଥାଏ ।

(4) ପ୍ରୋତ୍ସାହନ ଅଭାବ – ଉଚ୍ଚ ହାରରେ ପ୍ରତ୍ୟକ୍ଷ କର ଆରୋପିତ ହେଉଥିବାରୁ ଲୋକମାନଙ୍କର ସଞ୍ଚୟ ଓ ବିନିଯୋଗ ଶକ୍ତି ହ୍ରାସପ୍ରାପ୍ତ ହୁଏ । ଫଳତଃ ଦେଶରେ ପୁଞ୍ଜି ଗଠନ ବାଧାପ୍ରାପ୍ତ ହୁଏ ଓ ଉତ୍ପାଦନ ହ୍ରାସ ପାଏ ।

(5) ଲୋକପ୍ରିୟତାର ଅଭାବ – ପ୍ରତ୍ୟକ୍ଷ କର କରଦାତାମାନଙ୍କ ମଧ୍ୟରେ ଆଦୃତ ହୁଏ ନାହିଁ । କାରଣ ସରକାର ବର୍ଦ୍ଧିଷ୍ଣୁ ଆବଶ୍ୟକତାକୁ ମେଣ୍ଟାଇବାପାଇଁ କର ହାର ବାରମ୍ବାର ପରିବର୍ତ୍ତନ କରିଥା’ନ୍ତି । ପ୍ରତିଥର କର ହାର ବୃଦ୍ଧି ପାଉଥିବାରୁ କରଦାତାଙ୍କ ତରଫରୁ ପ୍ରତିବାଦ ପ୍ରକାଶ ପାଏ । ତେଣୁ ପ୍ରତ୍ୟକ୍ଷ କର ଲୋକପ୍ରିୟ ହୋଇପାରେ ନାହିଁ ।

(6) ପାତରଅନ୍ତର ବିଚାର – ଆୟ ଓ ସମ୍ପଦ ଉପରେ କରଧାର୍ଯ୍ୟ କଲାବେଳେ ସରକାର କେତେକଙ୍କୁ କର ପରିସରଭୁକ୍ତ କଲାବେଳେ ଅନ୍ୟ କେତେକଙ୍କୁ କରମୁକ୍ତ କରିଥା’ନ୍ତି । ଏକ ଗଣତାନ୍ତ୍ରିକ ରାଷ୍ଟ୍ରରେ ସମସ୍ତେ ସମାନ ସୁବିଧା ଓ ସୁଯୋଗର ଅଧିକାରୀ ହୋଇଥିବାରୁ ସମସ୍ତଙ୍କର କିଛି ନା କିଛି ତ୍ୟାଗ ସ୍ବୀକାର କରିବା ଉଚିତ ।

4. ପ୍ରତ୍ୟକ୍ଷ କର ଓ ପରୋକ୍ଷ କର ପରସ୍ପର ପ୍ରତିଯୋଗୀ ନୁହଁନ୍ତି, ସହଯୋଗୀ – ଆଲୋଚନା କର ।
Answer:
ପରୋକ୍ଷ କର ଓ ପ୍ରତ୍ୟକ୍ଷ କର ପରସ୍ପର ପ୍ରତିଯୋଗୀ ନୁହଁନ୍ତି । କର ବ୍ୟବସ୍ଥାରେ ସେମାନେ ପରସ୍ପରକୁ ସହାୟତା କରିଥା’ନ୍ତି । ପରୋକ୍ଷ କରର ସୁବିଧା ଓ ଅସୁବିଧା ସମୂହ ଆଲୋଚନା କଲେ ଏହି ଉକ୍ତିର ସତ୍ୟତା ପ୍ରତିପାଦନ ହୁଏ ।
(1) ସୁବିଧାଜନକ – ପରୋକ୍ଷ କର ସାଧାରଣତଃ ଦ୍ରବ୍ୟ ଓ ସାମଗ୍ରୀ ଉପରେ ଧାର୍ଯ୍ୟ କରାଯାଇଥାଏ । ବିକ୍ରେତା କରକୁ ଦ୍ରବ୍ୟର ଦାମ୍ରେ ଅନ୍ତର୍ଭୁକ୍ତ କରି ଦ୍ରବ୍ୟକୁ ବର୍ଦ୍ଧିତ ଦାମରେ ବିକ୍ରୟ କରିଥା’ନ୍ତି । କ୍ରେତାମାନେ ଦ୍ରବ୍ୟ କ୍ରୟ କଲାବେଳେ ବର୍ଣ୍ଣିତ ଦାମ୍ ଦେଇ କ୍ରୟ କରୁଥିବାରୁ ସେମାନେ କର ବୋଝ ବହନ କରୁଥିବା ଅନୁଭବ କରନ୍ତି ନାହିଁ; କିନ୍ତୁ ପ୍ରତ୍ୟକ୍ଷ କର ଦେବାରେ କରଦାତା କରର ବୋଝ ବିଷୟରେ ସଚେତନ ଥାଆନ୍ତି ।

(2) ପ୍ରଶସ୍ତ ଭିତ୍ତି – ପରୋକ୍ଷ କରର ଉତ୍ସ ବ୍ୟାପକ ଏବଂ ଭିଭି ପ୍ରଶସ୍ତ । କାରଣ ଦେଶରେ ଧନୀ, ଦରିଦ୍ର ସମସ୍ତେ ଏହି କର ପରିସରଭୁକ୍ତ ହୋଇଥା’ନ୍ତି । ଯେଉଁମାନେ ଅଧିକ ପରିମାଣରେ ଦ୍ରବ୍ୟ କ୍ରୟ କରନ୍ତି, ସେମାନଙ୍କୁ ଅଧିକ କରବୋଝ ବହନ କରିବାକୁ ହୋଇଥାଏ ଏବଂ ଯେଉଁମାନେ କମ୍ ପରିମାଣର ଦ୍ରବ୍ୟ କ୍ରୟ କରନ୍ତି, ସେମାନେ କମ୍ କର ଦେଇଥା’ନ୍ତି । ମାତ୍ର ଧନୀ, ଦରିଦ୍ର ସମସ୍ତଙ୍କୁ ଏହି କର ଦେବାକୁ ହୋଇଥାଏ ।

(3) ସ୍ଥିତିସ୍ଥାପକ – ପରୋକ୍ଷ କରରୁ ମିଳୁଥିବା ଆୟ ଅପେକ୍ଷାକୃତ ଅଧ୍ଵ ସ୍ଥିତିସ୍ଥାପକ । ସରକାର ଚାହିଁଲେ କର ପରିସର ବୃଦ୍ଧି କରି ବା କର ହାର ବୃଦ୍ଧି କରି ଅକ୍ଳେଶରେ ଅଧୂକ ସମ୍ବଳ ସଂଗ୍ରହ କରିପାରନ୍ତି । ଉଦାହରଣସ୍ୱରୂପ, ଅତ୍ୟାବଶ୍ୟକ ଦ୍ରବ୍ୟ ଉପରେ କର ବସାଇ ସରକାର ଅଧିକ ସମ୍ବଳ ସଂଗ୍ରହ କରିବାକୁ ସମର୍ଥ ହୋଇଥା’ନ୍ତି । କାରଣ ଅତ୍ୟାବଶ୍ୟକ ଦ୍ରବ୍ୟର ଚାହିଦା ଅସ୍ଥିତିସ୍ଥାପକ ହୋଇଥିବାରୁ କରଜନିତ ଦାମ୍ ବୃଦ୍ଧି ହେଲେ ସେସବୁର ଚାହିଦା ହ୍ରାସ ହୁଏ ନାହିଁ । ତେଣୁ ଅଧିକ ସମ୍ବଳ ସଂଗ୍ରହ କରିବାପାଇଁ ସରକାର ପରୋକ୍ଷ କର ଉପରେ ଭରସା କରିଥା’ନ୍ତି।

(4) କ୍ଷତିକାରକ ଦ୍ରବ୍ୟର ନିୟନ୍ତ୍ରଣ – ପରୋକ୍ଷ କର ସାହାଯ୍ୟରେ ସରକାର କ୍ଷତିକାରକ ମାଦକ ଦ୍ରବ୍ୟର ଉତ୍ପାଦନ ଓ ଉପଭୋଗକୁ ନିୟନ୍ତ୍ରଣ କରିଥା’ନ୍ତି । ମାଦକ ଦ୍ରବ୍ୟ ଉପରେ କର ହାର ବୃଦ୍ଧି ହେଲେ ତାହାର ଦାମ୍ ବୃଦ୍ଧି ହୋଇ ଚାହିଦାକୁ ହ୍ରାସ କରାଏ । ଏହି କାରଣରୁ ପରୋକ୍ଷ କରକୁ ବ୍ୟୟ ନିୟନ୍ତ୍ରଣକାରୀ କର କୁହାଯାଏ ।

(5) କର ଫାଙ୍କିବା କଷ୍ଟକର – ପରୋକ୍ଷ କରକୁ ଫାଙ୍କିଦେବା ସହଜ ନୁହେଁ । ପରୋକ୍ଷ କର ଦ୍ରବ୍ୟସାମଗ୍ରୀ ଉପରେ ଆରୋପିତ ହେଉଥିବାରୁ କ୍ରେତା ଦ୍ରବ୍ୟ କ୍ରୟ କଲାବେଳେ କର ଦେବାକୁ ବାଧ୍ୟ ହୋଇଥା’ନ୍ତି । ଦ୍ରବ୍ୟ ଉପଭୋଗରୁ ଯେଉଁମାନେ ବିରତ ହୋଇପାରନ୍ତି କେବଳ ସେହିମାନେ କରରୁ ମୁକ୍ତି ପାଇଥା’ନ୍ତି । ସୁତରାଂ ପରୋକ୍ଷ କରକୁ ଫାଙ୍କିଦେବା ସହଜସାଧ୍ୟ ନୁହେଁ ।

(6) ଆୟ ବୈଷମ୍ୟ ହ୍ରାସ – ପ୍ରଗାମୀ ପରୋକ୍ଷ କରକୁ ଆୟ ବୈଷମ୍ୟ ଦୂର କରିବାପାଇଁ ଅସ୍ତ୍ରରୂପେ ବ୍ୟବହାର କରାଯାଇପାରେ । ଧନିକ ଶ୍ରେଣୀ ଉପଭୋଗ କରୁଥିବା ବିଳାସ ସାମଗ୍ରୀ ଉପରେ ଉଚ୍ଚହାରରେ କର ଆରୋପ କରି ଏବଂ ଅତ୍ୟାବଶ୍ୟକ ଦ୍ରବ୍ୟକୁ କରମୁକ୍ତ କରି ସରକାର ଧନୀ ଓ ଦରିଦ୍ର ମଧ୍ୟରେ ଥିବା ଆୟର ବୈଷମ୍ୟକୁ ଦୂର କରିଥା’ନ୍ତି ।

(7) ଦେଶଜ ଶିଳ୍ପର ସୁରକ୍ଷା – ଆମଦାନି କରାଯାଉଥିବା ଦ୍ରବ୍ୟ ଉପରେ କର ଧାର୍ଯ୍ୟ କରି ସରକାର ଦେଶୀୟ ଶିଳ୍ପକୁ ଉତ୍ସାହିତ କରିପାରନ୍ତି । ଆମଦାନୀ ଶୁଳ୍‌କ ଆରୋପିତ ହେବା ଫଳରେ ବିଦେଶାଗତ ଦ୍ରବ୍ୟର ଦାମ୍ ବୃଦ୍ଧି ହୋଇ ଚାହିଦାକୁ ହ୍ରାସ କରାଏ । ଏହାଫଳରେ ଦେଶଜ ଦ୍ରବ୍ୟର ଚାହିଦା ବୃଦ୍ଧି ହେବା ସଙ୍ଗେ ସଙ୍ଗେ ଉତ୍ପାଦନ ଓ ନିଯୁକ୍ତି କ୍ଷେତ୍ର ସାମ୍ପ୍ରସାରିତ ହୁଏ ।

ପରୋକ୍ଷ କରର ଅସୁବିଧା:
(1) ଅନ୍ୟାୟୋଚିତ – ପରୋକ୍ଷ କର ଧନୀ ଓ ଦରିଦ୍ର ନିର୍ବିଶେଷରେ ଆରୋପିତ ହେଉଥିବାରୁ ଅପେକ୍ଷାକୃତ ସ୍ଵଚ୍ଛ ଆୟକାରୀମାନେ ଅଧିକ ଆକ୍ରାନ୍ତ ହୁଅନ୍ତି । କରର ବାସ୍ତବ ବୋଝ ଦରିଦ୍ର ଲୋକମାନଙ୍କ ଉପରେ ଅଧିକ ପରିମାଣରେ ପଡୁଥିବାରୁ ଏହି କରକୁ ଅନ୍ୟାୟୋଚିତ ବୋଲି ସମାଲୋଚକମାନେ ମତ ଦେଇଥା’ନ୍ତି ।

(2) ଆୟ ଅନିଶ୍ଚିତ – ପରୋକ୍ଷ କରରୁ ମିଳୁଥିବା ଆୟ ଅନିଶ୍ଚିତ ହୋଇଥାଏ । କାରଣ ଏହି ସୂତ୍ରରୁ ମିଳୁଥିବା ଆୟ ଦ୍ରବ୍ୟ ପାଇଁ ଚାହିଦାର ସ୍ଥିତିସ୍ଥାପକତା ଉପରେ ନିର୍ଭର କରେ । ଦ୍ରବ୍ୟ ପାଇଁ ଚାହିଦା ଯଦି ସ୍ଥିତିସ୍ଥାପକ ହୋଇଥାଏ, ତେବେ କରଜନିତ ଯେଉଁ ଦାମ୍ ବୃଦ୍ଧି ହୁଏ ତାହା ଚାହିଦାକୁ ବହୁଳାଶରେ ଅଥବା ସମ୍ପୂର୍ଣ୍ଣଭାବରେ ହ୍ରାସ କରିଥାଏ । ଚାହିଦା ହ୍ରାସ ହେଲେ ସରକାରଙ୍କ ପରୋକ୍ଷ କର ସୂତ୍ରରୁ ଆୟ ଅନିଶ୍ଚିତ ହୋଇଥାଏ ।

(3) ଅମିତବ୍ୟୟିତା – ପରୋକ୍ଷ କର ପରିସର ଅତି ବ୍ୟାପକ ହୋଇଥିବାରୁ କରି ପ୍ରଶାସନ ବ୍ୟୟବହୁଳ ହୋଇଥାଏ । କାରଣ ବହୁସଂଖ୍ୟକ କର୍ମଚାରୀଙ୍କୁ କର ଆଦାୟ କରିବା ଓ କର ଫାଙ୍କିବାରୁ ନିରୁତ୍ସାହିତ କରିବାପାଇଁ ନିଯୁକ୍ତି କରିବାକୁ ହୁଏ । ସେମାନଙ୍କ ବେତନ ଓ ଭତ୍ତା ବାବଦ ସରକାରଙ୍କୁ ଅଧିକ ଖର୍ଚ୍ଚାନ୍ତ ହେବାକୁ ହୁଏ । ଏପରି ଘୋଡ଼ା ଛ’ଟଙ୍କାକୁ ଦାନା ନ’ଟଙ୍କା ହେଲାଭଳି ଅବସ୍ଥା ସୃଷ୍ଟି ହୁଏ ।

(4) ସାମାଜିକ ଚେତନା – ପରୋକ୍ଷ କର ନାଗରିକମାନଙ୍କ ମଧ୍ୟରେ ସାମାଜିକ ଚେତନା ଓ ସ୍ଵଦେଶବତ୍ସଳତା ସୃଷ୍ଟି କରିପାରେ ନାହିଁ । କାରଣ କର ଦ୍ରବ୍ୟର ଦାମ୍‌ରେ ଲୁକ୍‌କାୟିତ ହୋଇ ରହିଥାଏ । ଦେଶବାସୀ କରି ଦେଉଥୁବାଜନିତ ବୋଝକୁ ଅନୁଭବ କରନ୍ତି ନାହିଁ । ତେଣୁ ସେମାନଙ୍କ ମଧ୍ୟରେ ସାମାଜିକ ଚେତନା ବିକାଶଲାଭ କରିପାରେ ନାହିଁ ।

(5) ସମ୍ବଳ ବଣ୍ଟନ କ୍ଷେତ୍ରରେ କୁଫଳ – ପରୋକ୍ଷ କର ଦେଶରେ ସମ୍ବଳ ବଣ୍ଟନର ଧାରାକୁ ବିଶୃଙ୍ଖଳିତ କରିବାର ଆଶଙ୍କା ରହିଥାଏ । ସେଥ୍ପାଇଁ ଏହି କରକୁ ବିଜ୍ଞତାର ସହିତ ପରିଚାଳନା କରିବା ଆବଶ୍ୟକ ହୁଏ । ସରକାର କରଧାର୍ଯ୍ୟ କଲାବେଳେ କେଉଁ ଦ୍ରବ୍ୟ କର ପରିସରଭୁକ୍ତ ହେବା ବାଞ୍ଛନୀୟ ଓ କେଉଁ ଦ୍ରବ୍ୟ ନୁହେଁ, ତାହା ବିଚାରକୁ ନେଇ ନ ଥା’ନ୍ତି । କରଧାର୍ଯ୍ୟ ହେବା ଫଳରେ କରଭୁକ୍ତ ଦ୍ରବ୍ୟର ଦାମ୍ ବୃଦ୍ଧି ହୋଇ ଚାହିଦା ହ୍ରାସ କରାଏ ।

ଚାହିଦା ହ୍ରାସ ହେଲେ ଉତ୍ପାଦନ ହ୍ରାସ ହୁଏ । ଉତ୍ପାଦନର ଉପାଦାନସମୂହ ନିଯୁକ୍ତି କ୍ଷେତ୍ରରୁ ବିତାଡ଼ିତ ହୋଇଥା’ନ୍ତି । ଫଳରେ ବେକାର ସମସ୍ୟା ଦେଖାଦିଏ । ଉପାଦାନସମୂହ ଅବାଞ୍ଛିତ ଦିଗକୁ ପରିଚାଳିତ ହେବା ଆଶଙ୍କା ମଧ୍ୟ ସର୍ବଦା ରହିଥାଏ ।

ଏହି ଦୁଇ ପ୍ରକାରର କର ମଧ୍ୟରେ ତୁଳନାତ୍ମକ ବିଚାର କଲେ ଜଣାଯାଏ ଯେ ପ୍ରତ୍ୟକ୍ଷ କର ସପକ୍ଷରେ ଯୁକ୍ତି ଖୁବ୍ ବଳିଷ୍ଠ । କାରଣ ପ୍ରତ୍ୟକ୍ଷ କର ବିପକ୍ଷରେ ଥିବା ଯୁକ୍ତି ସଂଶୋଧନକ୍ଷମ । ସରକାର ଅବଶ୍ୟ କେତେକ ଦୃଷ୍ଟିରୁ ପ୍ରତ୍ୟକ୍ଷ କର ଉପରେ ଗୁରୁତ୍ୱ ଆରୋପ କରିଥା’ନ୍ତି । ମାତ୍ର ଏହାର ତାତ୍ପର୍ଯ୍ୟ ନୁହେଁ ଯେ କେବଳ ପ୍ରତ୍ୟକ୍ଷ କର ଜରିଆରେ ଦେଶର ସମ୍ବଳ ବୃଦ୍ଧି କରାଯାଇପାରେ । ରାଜସ୍ୱ ସଂଗ୍ରହ ବ୍ୟତୀତ ଅନ୍ୟାନ୍ୟ ଦୃଷ୍ଟିକୋଣରୁ ପରୋକ୍ଷ କର ବାଞ୍ଛନୀୟ ବିବେଚିତ ହୁଏ ।

ଉଦାହରଣସ୍ୱରୂପ, ଆମଦାନିକୁ ନିୟନ୍ତ୍ରଣ କରିବା ଓ ରପ୍ତାନିକୁ ଉତ୍ସାହିତ କରିବା, କ୍ଷତିକାରକ ଦ୍ରବ୍ୟ ଉତ୍ପାଦନ ନିୟନ୍ତ୍ରଣ କରିବା ଓ ଦେଶୀୟ ଶିଳ୍ପକୁ ସୁରକ୍ଷା ପ୍ରଦାନ କରିବା ପ୍ରଭୃତି କାରଣରୁ ଦେଶରେ ପରୋକ୍ଷ କରର ଗୁରୁତ୍ଵ ବୃଦ୍ଧି ପାଇବାରେ ଲାଗିଛି । ତେଣୁ ପରୋକ୍ଷ କର ଓ ପ୍ରତ୍ୟକ୍ଷ କର – ଉଭୟର ଦେଶ ପାଇଁ ଆବଶ୍ୟକତା ରହିଛି । ଏହି ଅର୍ଥବ୍ୟବସ୍ଥାରେ ପ୍ରତ୍ୟକ୍ଷ କର, ପରୋକ୍ଷ କର ପରସ୍ପର ସହଯୋଗୀ ରୂପେ କାର୍ଯ୍ୟ କରନ୍ତି ।

5. ସରକାରୀ ବ୍ୟୟ କହିଲେ କ’ଣ ବୁଝ ? ରାଜସ୍ଵ ବ୍ୟୟ (Revenue expenditure) ଓ ପୁଞ୍ଜି ବ୍ୟୟ (Capital expenditure) ସମ୍ପର୍କରେ ଆଲୋକପାତ କର ।
Answer:
ସରକାରୀ ବ୍ୟୟ କହିଲେ ସରକାରୀ କର୍ତ୍ତୃପକ୍ଷ, ଯଥା – କେନ୍ଦ୍ର ସରକାର, ରାଜ୍ୟ ସରକାର ଓ ସ୍ଥାନୀୟ ସରକାର (ପୌର ପରିଷଦ, ଗ୍ରାମପଞ୍ଚାୟତ)ଙ୍କ ଦ୍ବାରା ସାମୁହିକ ଅଭାବ ବା ଆବଶ୍ୟକତାର ପରିତୃପ୍ତି ପାଇଁ କିମ୍ବା ଅର୍ଥନୈତିକ ଏବଂ ସାମାଜିକ କଲ୍ୟାଣ ସାଧନ ପାଇଁ କରାଯାଉଥିବା ଖର୍ଜଗୁଡ଼ିକୁ ହିଁ ବୁଝାଇଥାଏ ।

ସରକାରୀ ବ୍ୟୟ ରାଷ୍ଟ୍ରବିତ୍ତର ଏକ ପ୍ରମୁଖ ଅଂଶ ଯାହା ଆଧୁନିକ ଅର୍ଥବ୍ୟବସ୍ଥାର ସାମୂହିକ ଅର୍ଥନୈତିକ ତଥା ସାମାଜିକ କଲ୍ୟାଣ ସାଧନ ନିମନ୍ତେ ଉଦ୍ଦିଷ୍ଟ । ବର୍ତ୍ତମାନ ପରିସ୍ଥିତିରେ ରାଷ୍ଟ୍ରର ଅର୍ଥନୈତିକ କ୍ରିୟା ଦୃତଗତିରେ ବୃଦ୍ଧିପାଇ ଚାଲୁଥିବାରୁ ସରକାରୀ ବ୍ୟୟର ପ୍ରାଧାନ୍ୟ ବହୁଗୁଣିତ ହୋଇଛି; ଯଥା –
(1) ରାଷ୍ଟ୍ରଦ୍ୱାରା ସମ୍ପାଦିତ ଅର୍ଥନୈତିକ କ୍ରିୟାର ଦୃତ ସମ୍ପ୍ରସାରଣ ।
(2) ସରକାରୀ ବ୍ୟୟ ଅର୍ଥନୈତିକ ପ୍ରକ୍ରିୟାଗୁଡ଼ିକ; ଯଥା – ଉତ୍ପାଦନ, ବଣ୍ଟନ ଓ ସାଧାରଣ ଅର୍ଥନୈତିକ କାର୍ଯ୍ୟକଳାପକୁ ବହୁଭାବରେ ପ୍ରଭାବିତ କରୁଅଛି । ଉପରୋକ୍ତ କାରଣରୁ ସରକାରୀ ବ୍ୟୟର ଅର୍ଥ ପ୍ରକରଣ କରାଗଲେ କୁହାଯାଇ ପାରିବ ଯେ ସରକାରଙ୍କ ପରିଚାଳନା ନିମନ୍ତେ ଓ ସାମାଜିକ କଲ୍ୟାଣର ସୁରକ୍ଷା ନିମନ୍ତେ ଯେଉଁ ବ୍ୟୟ ସଂଘଟିତ ହୁଏ ତାହାହିଁ ସରକାରୀ ବ୍ୟୟ ।

ଏହି ବ୍ୟୟ ସାଧାରଣଭାବେ ସରକାରଙ୍କଦ୍ଵାରା କରାଯାଇଥାଏ ଏବଂ ଦ୍ଵିତୀୟରେ ଏହା ସାମୂହିକ କଲ୍ୟାଣ ସାଧନ ନିମନ୍ତେ ଉଦ୍ଦିଷ୍ଟ । ବାସ୍ତବରେ ସରକାର ନିଜର ସାମାଜିକ ଓ ଅର୍ଥନୈତିକ ପରିସୀମାର ପ୍ରଶସ୍ତୀକରଣ ନିମନ୍ତେ ଏହି ସରକାରୀ ବ୍ୟୟ ଘଟାଇଥା’ନ୍ତି ।

ମୁଖ୍ୟତଃ ସରକାରୀ ବ୍ୟୟକୁ ଦୁଇଟି ଭାଗରେ ବିଭକ୍ତ କରାଯାଇଥାଏ ; ଯଥା –
(a) ରାଜସ୍ବ ହିସାବ ଫର୍ଦ୍ଦରେ ବ୍ୟୟ ( ରାଜସ୍ବ ବ୍ୟୟ)
(b) ପୁଞ୍ଜି ହିସାବ ଫର୍ଦ୍ଦରେ ବ୍ୟୟ (ପୁଞ୍ଜି ବ୍ୟୟ)

(a) ରାଜସ୍ଵ ହିସାବ ଫର୍ଦ୍ଦରେ ବ୍ୟୟ ରାଜସ୍ୱ ବ୍ୟୟ (Revenue Expenditure) – ଯେଉଁ ବ୍ୟୟ ସରକାରଙ୍କଦ୍ଵାରା ସଂଗୃହୀତ ଅର୍ଥଦ୍ଵାରା ସଂଘଟିତ ହୋଇଥାଏ, ତାହାକୁ ରାଜସ୍ୱ ବ୍ୟୟ କୁହାଯାଏ । ଏହି ବ୍ୟୟ ସାଧାରଣତଃ ସରକାରଙ୍କ ଚିରାଚରିତ ରାଜସ୍ବ ଉତ୍ସରୁ ପ୍ରାପ୍ତ ଅର୍ଥରୁ ହିଁ ବହନ କରାଯାଇଥାଏ । ସରକାରଙ୍କ ବିଭିନ୍ନ ବିଭାଗ ଓ ପ୍ରାଶାସନ ତଥା ଅନ୍ୟାନ୍ୟ ସ୍ଥାୟୀ ସେବା ପ୍ରଦାନକାରୀ କ୍ଷେତ୍ରର ସ୍ଵାଭାବିକ ପରିଚାଳନା ନିମନ୍ତେ ରାଜସ୍ବ ବ୍ୟୟ କରାଯାଇଥାଏ ।

ସଂକ୍ଷେପରେ କହିବାକୁ ଗଲେ, ସରକାରଙ୍କ ଯେଉଁ ବ୍ୟୟ ପରିସମ୍ପତ୍ତି ବା ସମ୍ପଦ ସୃଷ୍ଟି କରିବାରେ ଉପଯୋଗ ହୁଏ ନାହିଁ, ତାହାକୁ ରାଜସ୍ୱ ବ୍ୟୟ କୁହାଯାଏ । ସରକାରଙ୍କର ପରିଚାଳନା ବାବଦ ବ୍ୟୟ, ବିଭିନ୍ନ ସ୍ଥାୟୀ ସେବା କ୍ଷେତ୍ର ନିମନ୍ତେ ବ୍ୟୟ, ସରକାରୀ ଋଣ ଉପରେ ସୁଧ ପ୍ରଦାନଜନିତ ବ୍ୟୟ, ରାଜ୍ୟ ସରକାରଙ୍କୁ ଅନୁଦାନ ପ୍ରଦାନଜନିତ ବ୍ୟୟ ଆଦି ଏହି ରାଜସ୍ୱ ବ୍ୟୟର ଅନ୍ତର୍ଭୁକ୍ତ । ରାଜସ୍ବ ବ୍ୟୟର ଗଠନ – ନିମ୍ନଲିଖତ ସରକାରୀ କାର୍ଯ୍ୟ ସାଧନ ନିମନ୍ତେ ଏହି ରାଜସ୍ବ ବ୍ୟୟ କରାଯାଇଥାଏ ।

(1) ସାଧାରଣ ସେବା (General Services) – ପାର୍ଲାମେଣ୍ଟ ପରିଚାଳନା, ନ୍ୟାୟପାଳିକା, ନିର୍ବାଚନ, ମୁଖ୍ୟ ହିସାବ ନିରୀକ୍ଷକଙ୍କ ପରିଚାଳନା ଓ ସରକାଙ୍କଦ୍ୱାରା ନିୟନ୍ତ୍ରିତ ଓ ପରିଚାଳିତ ଅନୁଷ୍ଠାନମାନଙ୍କ ନିମନ୍ତେ ଖର୍ଚ୍ଚ ଏହି ଶ୍ରେଣୀର ଅନ୍ତର୍ଭୁକ୍ତ । ଅନ୍ୟ ସାଧାରଣ ସେବା ଅନ୍ତର୍ଭୁକ୍ତ ବ୍ୟୟଗୁଡ଼ିକ ହେଲା – କର ସଂଗ୍ରହଜନିତ ବ୍ୟୟ, ନୋଟ୍ ପ୍ରଚଳନଜନିତ ବ୍ୟୟ ଓ ସରକାରୀ ଋଣ ଉପରେ ସୁଧ ପ୍ରଦାନଜନିତ ବ୍ୟୟ । ଏତଦ୍‌ବ୍ୟତୀତ ପ୍ରଶାସନିକ ସେବା, ପୋଲିସ୍, ଜେଲ୍, ଯୋଗାଣ, ଜନସ୍ୱାସ୍ଥ୍ୟ ସେବା, ବୈଦେଶିକ ବ୍ୟାପାର ନିମନ୍ତେ ବ୍ୟୟ ଏହି ସାଧାରଣ ସେବାଜନିତ ବ୍ୟୟର ଅନ୍ତର୍ଭୁକ୍ତ ହୋଇଥାଏ ।

(2) ପ୍ରତିରକ୍ଷା ବାବଦ ବ୍ୟୟ (Defence Expenditure) – ବାହ୍ୟଶକ୍ତିଙ୍କ ଆକ୍ରମଣରୁ ରାଷ୍ଟ୍ରକୁ ସୁରକ୍ଷା ଦେବା ନିମନ୍ତେ ପ୍ରତିରକ୍ଷା ବିଭାଗର ଭୂମିକା ଅତ୍ୟନ୍ତ ଗୁରୁତ୍ଵପୂର୍ଣ୍ଣ । ଜାତୀୟ ସମ୍ପତ୍ତିର ସୁରକ୍ଷା, ଦେଶ ଭିତରେ ଶୃଙ୍ଖଳା ରକ୍ଷା ପାଇଁ ପ୍ରତିରକ୍ଷା ବିଭାଗ ବାବଦ ଖର୍ଚ୍ଚ ଏକାନ୍ତ ଅପରିହାର୍ଯ୍ୟ । ଆଧୁନିକ ଯୁଦ୍ଧ ସରଞ୍ଜାମ କ୍ରୟ, ସ୍ଥଳସେନା, ଜଳସେନା ଓ ବାୟୁସେନା ବାହିନୀଙ୍କ ନିମନ୍ତେ ବିପୁଳ ବ୍ୟୟ ଏହି ଶ୍ରେଣୀଭୁକ୍ତ ହୋଇଥା’ନ୍ତି । ସେନାବାହିନୀରେ କାର୍ଯ୍ୟରତ ଯବାନମାନଙ୍କର ଦରମା, ଭତ୍ତା ବାବଦରେ ଖର୍ଚ୍ଚ ଏହି ବ୍ୟୟଭୁକ୍ତ ହୋଇଥାଏ ।

(3) ସାମାଜିକ ସେବା (Social Services) – ଏହି ବିଭାଗର ବ୍ୟୟ ସାଧାରଣଭାବେ ସଚିବାଳୟ, ଶିକ୍ଷା ଓ ସାମାଜିକ କଲ୍ୟାଣ, ସ୍ଵାସ୍ଥ୍ୟ ଓ ପରିବାର କଲ୍ୟାଣ, ଶ୍ରମ ଓ ନିଯୁକ୍ତି, ଆଣବିକ ଶକ୍ତି ଆଦି ମନ୍ତ୍ରଣାଳୟ ନିମନ୍ତେ ସଂଘଟିତ ହୋଇଥାଏ ।

(4) ଅର୍ଥନୈତିକ ସେବା (Economic Services) – ଅର୍ଥନୈତିକ ପ୍ରଗତି ତଥା ଅଭିବୃଦ୍ଧି ହାରକୁ ଦୃତଗତିରେ ତ୍ୱରାନ୍ବିତ କରିବା ନିମନ୍ତେ ସରକାର ଅର୍ଥନୈତିକ ସେବାକ୍ଷେତ୍ର ନିମନ୍ତେ ବ୍ୟୟବହନ କରିଥା’ନ୍ତି । ଏଥସହ ସଂପୃକ୍ତ ବିଭାଗଗୁଡ଼ିକ ହେଲା – ବାଣିଜ୍ୟ, ପରିବହନ, ଜାହାଜ ଚଳାଚଳ, ଜଳସେଚନ, ଶକ୍ତି, ରାସାୟନିକ ସାର, ଶିଳ୍ପ, କୃଷି, ଇଲେକ୍‌ଟ୍ରୋନିକ୍‌ସ । ଏହି ବିଭାଗ ନିମନ୍ତେ ବ୍ୟୟ ଅର୍ଥନୈତିକ ସେବା ଅନ୍ତର୍ଭୁକ୍ତ ହୋଇଥାଏ ।

(5) ରାଜ୍ୟମାନଙ୍କୁ ଅନୁଦାନ (Grants-in Aid to States) – ରାଜ୍ୟମାନଙ୍କର ପ୍ରଶାସନିକ ସୁପରିଚାଳନା ନିମନ୍ତେ କେନ୍ଦ୍ର ସରକାର ରାଜ୍ୟ ସରକାରମାନଙ୍କୁ ଅନୁଦାନ ପ୍ରଦାନ କରିଥା’ନ୍ତି; ଯାହା ରାଜ୍ୟରେ କାର୍ଯ୍ୟରତ ସରକାରୀ ସର୍ମଚାରୀମାନଙ୍କ ବେତନ ଓ ଭତ୍ତା ନିମନ୍ତେ ବ୍ୟୟ କରାଯାଇଥାଏ ।

ଏତଦ୍‌ବ୍ୟତୀତ ସରକାରୀ ଋଣ ଉପରେ ସୁଧ ପ୍ରଦାନଜନିତ ବ୍ୟୟ ଓ କରସଂଗ୍ରହଜନିତ ବ୍ୟୟ ରାଜସ୍ବ ବ୍ୟୟର ଅନ୍ୟତମ ଉପାଂଶ ।

ପୁଞ୍ଜି ବ୍ୟୟ (Capital Expenditure) – ଯେଉଁ ବ୍ୟୟ ପୁଞ୍ଜି ସଂଗ୍ରହଜନିତ ପ୍ରାପ୍ତି (ଆୟ); ଯଥା – ଖୋଲାବଜାର ଋଣ, ରିଜର୍ଭ ବ୍ୟାଙ୍କଦ୍ୱାରା ସରକାରଙ୍କୁ ପ୍ରଦତ୍ତ ଋଣ ଏବଂ ଦେଶ ଭିତରେ ଓ ବାହାରେ ଥିବା ଅନୁଷ୍ଠାନମାନଙ୍କଦ୍ୱାରା ପ୍ରଦତ୍ତ ଋଣଦ୍ୱାରା ଭରଣା କରାଯାଇଥାଏ, ତାହାକୁ ପୁଞ୍ଜି ବ୍ୟୟ ବା ପୁଞ୍ଜି ହିସାବ ଫର୍ଦ୍ଦରେ ବ୍ୟୟ (Expenditure on Capital Account) କୁହାଯାଏ ।

ଏତଦ୍‌ବ୍ୟତୀତ ଏହି ବ୍ୟୟ ଭାର ବୈଦେଶିକ ଋଣ, ଆନ୍ତର୍ଜାତୀୟ ଅନୁଷ୍ଠାନମାନଙ୍କଦ୍ୱାରା ପ୍ରଦତ୍ତ ଋଣ ଓ ରାଜ୍ୟ ସରକାରଙ୍କଦ୍ବାରା ପରିଶୋଧ କରାଯାଇଥିବା ଋଣଦ୍ଵାରା ମଧ୍ୟ ବହନ କରାଯାଇଥାଏ । ଏହି ବ୍ୟୟ ସାଧାରଣଭାବେ ଭୂମି ଅଧ୍ଵକୃତ, କୋଠାବାଡ଼ି ନିର୍ମାଣ, ଯନ୍ତ୍ରପାତି ଓ କଳକବ୍‌ଜା କ୍ରୟ, ଅଂଶଧନରେ ବିନିଯୋଗ ଏବଂ ରାଜ୍ୟ ସରକାରଙ୍କ ଅଗ୍ରୀମ ନିମନ୍ତେ କରାଯାଇଥାଏ ।

(b) ପୁଞ୍ଜି ବ୍ୟୟର ଗଠନ :
(1) ସାଧାରଣ ସେବା (General Services) – କେନ୍ଦ୍ର ସରକାରଙ୍କଦ୍ୱାରା ପରିଚାଳିତ ମୁଦ୍ରା ପ୍ରସ୍ତୁତି, ଆନ୍ତର୍ଜାତିକ ମୁଦ୍ରା ପାଣ୍ଠି ଓ ଅନ୍ୟାନ୍ୟ ଆନ୍ତର୍ଜାତୀୟ ଅନୁଷ୍ଠାନମାନଙ୍କୁ ଚାନ୍ଦା ପ୍ରଦାନ ନିମନ୍ତେ କରାଯାଉଥିବା ବ୍ୟୟ ଏହି ସାଧାରଣ ସେବାଜନିତ ବ୍ୟୟର ଅଂଶବିଶେଷ ଅଟେ । ଅଧିକନ୍ତୁ ଏହି ବ୍ୟୟ କାର୍ଯ୍ୟାଳୟ, ପ୍ରଶାସନିକ ଗୃହ, ଜନସମ୍ପର୍କିତ କାର୍ଯ୍ୟ ନିମନ୍ତେ ମଧ୍ୟ କରାଯାଇଥାଏ ।

(2) ପ୍ରତିରକ୍ଷା ବାବଦ ଖର୍ଚ (Defence Expenditures) – କେନ୍ଦ୍ର ସରକାରଙ୍କଦ୍ଵାରା ପରିଚାଳିତ ସ୍ଥଳ, ଜଳ ଓ ଆକାଶ ବାହିନୀ ନିମନ୍ତେ ଖର୍ଜ ଏହି ଶ୍ରେଣୀଭୁକ୍ତ । ଏହାଛଡ଼ା ବିଭିନ୍ନ କାର୍ଯ୍ୟାଳୟ, ଗୋଳାବାରୁଦ କାରଖାନା, ମେସିନ୍, ଯନ୍ତ୍ରପାତି ଉଦ୍ଦେଶ୍ୟରେ ଏହି ବ୍ୟୟ ସଂଘଟିତ ହୋଇଥାଏ ।

(3) ସାମାଜିକ ସେବା (Social Services) – ମାନବ ସମ୍ବଳର ଦକ୍ଷତା ଓ ଉତ୍ପାଦନଶୀଳତାର ବୃଦ୍ଧି ନିମନ୍ତେ ସାମଜିକ ସେବା ଏକାନ୍ତ ଆବଶ୍ୟକ । ଏହା ମଧ୍ୟ ଜୀବନଧାରଣ ମାନର ଉନ୍ନତି ସାଧନ ନିମନ୍ଦେ ଉଦ୍ଦିଷ୍ଟ । ତେଣୁ ଶିକ୍ଷା, ସଂସ୍କୃତି, ସ୍ୱାସ୍ଥ୍ୟସେବା, ପରିବାର କଲ୍ୟାଣ, ଜଳଯୋଗାଣ , ପରିମଳ ବ୍ୟସସ୍ଥା, ଗୃହନିର୍ମାଣ, ନଗର ଉନ୍ନୟନ, ସାମଜିକ ନିରାପତ୍ତା, ବିଜ୍ଞାନର ବିକାଶ ଆଦି କ୍ଷେତ୍ରରେ ସରକାର ବ୍ୟୟ ବହନ କରିଥା’ନ୍ତି ।

(4) ଅର୍ଥନୈତିକ ସେବା (Economic Services) – ଏହି ବ୍ୟୟ ସାଧାରଣଭାବେ ବୈଦେଶିକ ବାଣିଜ୍ୟ, କୃଷି ଓ ଅନ୍ୟାନ୍ୟ ଆନୁଷଙ୍ଗିକ ସେବା; ଯଥା – କ୍ଷୁଦ୍ର ଜଳସେଚନ, ପଶୁପାଳନ, ମତ୍ସ୍ୟଚାଷ ନିମନ୍ତେ କରାଯାଇଥାଏ । ଏତଦ୍‌ଭିନ୍ନ ଶିଳ୍ପ ଓ ଖଣିଜଦ୍ରବ୍ୟର ବିକାଶ, ଡାକ ଓ ତାର ବିଭାଗ, ପରିବହନ ଓ ଯୋଗାଯୋଗ ଆଦି କ୍ଷେତ୍ରରେ ଏହି ବ୍ୟୟ କରାଯାଇଥାଏ । ଏହାବ୍ୟତୀତ ରାଜ୍ୟ ସରାକାରଙ୍କୁ କେନ୍ଦ୍ର ସରକାରଙ୍କଦ୍ଵାରା ପ୍ରଦତ୍ତ ଋଣ ମଧ୍ୟ ଏହି ବ୍ୟୟଭୁକ୍ତ ହୋଇଥାଏ ।

Odisha State Board BSE Odisha 9th Class Physical Science Notes Chapter 4 ପରମାଣୁ ଗଠନ will enable students to study smartly.

BSE Odisha Class 9 Physical Science Notes Chapter 4 ପରମାଣୁ ଗଠନ

→ ପରିଚୟ (Introduction):
(i) ଡାଲ୍‌ନ୍‌ଙ୍କ ପରମାଣୁ ତତ୍ତ୍ବ ଅନୁଯାୟୀ, ‘‘ପରମାଣୁ ହେଉଛି ମୌଳିକର କ୍ଷୁଦ୍ରତମ, ଅବିଭାଜ୍ୟ, ଅବିଧ୍ୱଂସୀ କଣିକା ଏବଂ ଏହି କଣିକାଟି ରାସାୟନିକ ପରିବର୍ତ୍ତନରେ ଅଂଶ ଗ୍ରହଣ କରିଥାଏ ।
(ii) ଊନବିଂଶ ଶତାବ୍ଦୀରେ ପଦାର୍ଥର ବୈଦ୍ୟୁତିକ ପ୍ରକୃତିକୁ ଭିଭିକରି ବୈଜ୍ଞାନିକମାନେ ମତଦେଲେ ଯେ, ପରମାଣୁ କ୍ଷୁଦ୍ରତମ କଣିକା ନୁହେଁ, ପରମାଣୁ ମଧ୍ଯରେ କ୍ଷୁଦ୍ରତର କଣିକା ବା ଇଲେକ୍‌ଟ୍ରନ, ପ୍ରୋଟନ ଓ ନିଉଟ୍ରନ ପରି ଅବପରମାଣୁ କଣିକା (Subatomic particles) ଦ୍ଵାରା ଗଠିତ । ଏହି କଣିକାଗୁଡ଼ିକୁ

→ ପରମାଣୁର ଗଠନ (Structure of an Atom) :
(i) ପରମାଣୁ ଭିତରେ ଇଲେକ୍‌ଟ୍ରନ୍‌ ଓ ପ୍ରୋଟନ୍‌ ଗୁଡ଼ିକ କିପରି ସଜ୍ଜିତ ହୋଇ ରହିଛନ୍ତି ତାହା ଜାଣିବାପାଇଁ ଏବଂ ଏହାକୁ ବୁଝାଇବା ପାଇଁ ଅନେକ ବୈଜ୍ଞାନିକ ବିଭିନ୍ନ ପରମାଣୁ ମଡ଼େଲ ପ୍ରସ୍ତାବ କରିଥିଲେ ।
(ii) ବୈଜ୍ଞାନିକ ଜେ.ଜେ. ଟମସନ୍ ସର୍ବପ୍ରଥମେ ପରମାଣୁ ଗଠନର ଏକ ମଡ଼େଲର ପ୍ରସ୍ତାବ ଦେଇଥିଲେ ।

→ ଥୋମସନ୍ ର ପରମାଣୁର ମଡେଲ୍  (Thomson’s Model of an Atom):
(i) ଟମ୍‌ସନ୍ ଙ୍କ ପରମାଣୁ ମଡ଼େଲ ଅନୁ ଯାୟୀ ପରମାଣୁଟି ଯୁକ୍ତାତ୍ମକ ଚାର୍ଜ ରହିଥ‌ିବା ଏକ ଗୋଲକ । ଇଲେକ୍‌ଟ୍ରଗୁଡ଼ିକ ଏହା ଭିତରେ ବାଣ୍ଟି ହୋଇ ରହିଥା’ନ୍ତି ।
(ii) ପରମାଣୁର ଯୁକ୍ତାତ୍ମକ ଚାର୍ଜ ବିସ୍ତାରିତ ହୋଇଥିବା ବେଳେ ପରମାଣୁରେ ଇଲେକ୍‌ଟ୍ରନ୍‌ ଗୁଡ଼ିକ ବିଚ୍ଛୁରିତ ହୋଇ ରହିଥାନ୍ତି ।

ଟମସନ୍‌ଙ୍କ ପ୍ରସ୍ତାବ ଅନୁ ସାରେ :
(i) ପରମାଣୁ ଏକ ଯୁକ୍ତାତ୍ମକ ଚାର୍ଜ ଧାରଣ କରିଥିବା ଗୋଲକ ଏବଂ ଏଥିରେ ଇଲେକ୍‌ଟ୍ରଗୁଡ଼ିକ ସବୁଆଡ଼େ ଦୃଢ଼ଭାବରେ ସଂଯୁକ୍ତ ହୋଇ ରହିଥା’ନ୍ତି ।
(ii) ପରମାଣୁରେ ଯୁକ୍ତାତ୍ମକ ଚାର୍ଜ ଓ ବିଯୁକ୍ତାତ୍ମକ ଚାର୍ଜ ସମାନ ପରିମାଣରେ ଥାଏ । ତେଣୁ ପରମାଣୁଟି ବିଦ୍ୟୁତ୍ ନିରପେକ୍ଷ (neutral) ।

→ ରଥରଫୋର୍ଡର ଏକ ପରମାଣୁର ମଡେଲ୍ । (Rutherford’s Model of an Atom) : ବୈଜ୍ଞାନିକ ରଦରଫୋର୍ଡ଼ ଏକ ପରୀକ୍ଷାର ପରିକଳ୍ପନା କରିଥିଲେ । ଏହି ପରୀକ୍ଷାରେ ଖଣ୍ଡିଏ ଅତି ପତଳା ସୁନାପାତିଆ ଉପରେ ତୀବ୍ର ବେଗରେ ଗତି କରୁଥିବା α କଣିକାକୁ ନିକ୍ଷେପ କରାଗଲା । α, କଣିକା ହେଉଛି । ହିଲିୟମ୍ ଆୟନ (He⁺⁺) ଯାହା ଦ୍ଵି ଯୁକ୍ତାତ୍ମକ ଚାର୍ଜ (++) ବହନ କରେ ଏବଂ ଏହାର ବସ୍ତୁତ୍ଵ 4u ହୋଇଥିବାରୁ ଏଥିରେ ଯଥେଷ୍ଟ ପରିମାଣରେ ଶକ୍ତି ରହିଥାଏ।
ପର୍ଯ୍ୟବେକ୍ଷଣ :
(i) ଅଧିକାଂଶ -କଣିଳା ସନାପାନିଆ ମଧ୍ୟଦେଇ ସାଧାସଳଖ ଭାବରେ ଗତକଲା
(ii) କିଛି α-କଣିକାର ଗତିପଥ ବଙ୍କେଇ ହୋଇଗଲା ।
(iii) ଅଳ୍ପକିଛି α-କଣିକା ସୁନାପାତିଆକୁ ଭେଦ ନକରି ଯେଉଁ ଦିଗରେ ଯାଇଥିଲା ଠିକ୍ ତା’ର ବିପରୀତ ଦିଗରେ ପଛକୁ ଫେରିଆସଲା

ସିଦ୍ଧାନ୍ତ :
(i) ଅଧିକାଂଶ α- କ ଣିକ। ସୁନା ପାତିଆ ମଧ୍ୟଦେଇ ଗଳି ଯାଉଥ୍ ବା ରୁ ଭିତରେ ଅସ୍ଵୀକାଂଶ ସ୍ଥାନ ଫମ୍ପା (empty) ।
(ii) ଖୁବ୍ କମ୍ ସଂଖ୍ୟକ α-କଣିକା ଗତିପଥରେ ବଙ୍କାଇ ଯାଉଥିବାରୁ ପରମାଣୁର ଯୁକ୍ତାତ୍ମକ ଚାର୍ଜ କମ୍ ସ୍ଥାନ ଦଖଲ କରିଛି ।
(iii) ଅତି ଅଳ୍ପ ନଂ-କଣିକା ସୁନାପାତିଆକୁ ଭେଦକରି ନପାରି ପଛକୁ ଫେରିଆସିବାରୁ ସୂଚନା ମିଳୁଛି ଯେ, ସୁନା ପରମାଣୁର ସମସ୍ତ ଯୁକ୍ତାତ୍ମକ ଚାର୍ଜ ଓ ବସ୍ତୁତ୍ଵ କେନ୍ଦ୍ରୀଭୂତ ହୋଇ ପରମାଣୁ ମଧ୍ୟରେ ଖୁବ୍ କମ୍ ସ୍ଥାନ ଆଧ୍କାର କରିଛି ।

ରଦରଫୋର୍ଡ଼ଙ୍କ ପ୍ରସ୍ତାବ ଅନୁସାରେ :
(i) ପରମାଣୁରେ ଏକ ଯୁକ୍ତାତ୍ମକ ଚାର୍ଜିତ କେନ୍ଦ୍ର ରହିଛି, ଯାହାକୁ ନ୍ୟୁକ୍ଲିୟସ୍ କୁହାଯାଏ । ପରମାଣୁର ପ୍ରାୟ ସମସ୍ତ ବସ୍ତୁତ୍ଵ ଏହି ନ୍ୟୁକ୍ଲିୟସ୍‌ରେ କେନ୍ଦ୍ରୀଭୂତ ହୋଇ ରହିଛି । ନ୍ୟୁକ୍ଲିୟସ୍ ଚାରିପଟେ ବହୁତ ଫାଙ୍କା
(ii) ଇଲେକ୍‌ଟ୍ରଗୁଡ଼ିକ ନ୍ୟୁକ୍ଲିୟସ୍ ଚାରିପଟେ ଥିବା ଫାଙ୍କା ସ୍ଥାନରେ ନିର୍ଦ୍ଦିଷ୍ଟ କକ୍ଷପଥରେ ଘୂରନ୍ତି ।
(iii) ପରମାଣୁର ଅକାର ତୁଳନାରେ ନ୍ୟୁକ୍ଲିୟସ୍‌ର ଆକାର ଖୁବ୍‌ ଛୋଟ ।

→ ରଥରଫୋର୍ଡର ମଡେଲର ପରମାଣୁର ତ୍ରୁଟି (Drawbacks of Rutherford’s Model of Atom):
(i) ପରମାଣୁ ମଧ୍ୟରେ ନ୍ୟୁକ୍ଲିୟସ୍ ଚାରିପଟେ ଘୂର୍ଣ୍ଣନ କରୁଥିବା ଇଲେକ୍‌ଟ୍ରନ୍‌ ତ୍ଵରଣ ଥିବାରୁ ଘୂର୍ଣ୍ଣନରତ ଇଲେକ୍‌ଟ୍ରନ୍ ଏକ ତ୍ଵରାନ୍ଵିତ ଚାର୍ଜିତ କଣିକା ।
(ii) ତ୍ଵରାନ୍ଵିତ ଚାର୍ଜିତ କଣିକାରୁ ଶକ୍ତି ବିକିରଣ ହୁଏ । ତେଣୁ ପରମାଣୁ ଭିତରେ ନ୍ୟୁକ୍ଲିୟସ୍ ଚାରିପଟେ ଘୂରି ବୁଲୁଥିବା ଇଲେକ୍‌ଟ୍ରନ୍‌ରୁ ଅନବରତ ଶକ୍ତି ବିକିରିତ ହେବା ଆଶା କରାଯାଏ । ଫଳରେ ଇଲେକ୍‌ଟ୍ରନ୍‌ର ଶକ୍ତିସ୍ତର ଅନବରତ ହ୍ରାସ ପାଇବ ।
(iii) ଏହି କାରଣରୁ ଇଲେକ୍‌ଟ୍ରନ୍ ବୃତ୍ତାକାର କକ୍ଷପଥରେ ନ ଘୂରି କୁଣ୍ଡଳାୟିତ ପଥରେ ଘୂରି ଘୂରି ଶେଷରେ ନ୍ୟୁକ୍ଲିୟସ୍‌ରେ ମିଶିଯିବ । ଏହାଦ୍ଵାରା ଇଳେକ୍‌ଟ୍ରନ୍ ବର୍ଭୁଳପଥରେ ସ୍ଥାୟୀ ହୋଇ ରହିବ ନାହିଁ ।
(iv) ମାତ୍ର ଇଲେକ୍‌ଟ୍ରନ୍ ପରମାଣୁ ମଧ୍ୟରେ କୁଣ୍ଡଳାୟିତ ପଥରେ ଘୂରି ଘୂରି ନ୍ୟୁକ୍ଲିୟସରେ ମିଶିଯାଏ ନାହିଁ । ରଦରଫୋର୍ଡ଼ ଏହାର କାରଣ ବୁଝାଇପାରିଲେ ନାହିଁ ।

→ ବୋ’ରଙ୍କ ପରମାଣୁ ମଡ଼େଲ (Bohr’s Model of Atom):
ରଦରଫୋର୍ଡ଼ଙ୍କ ମଡ଼େଲରେ ଥିବା ତ୍ରୁଟିକୁ ଦୂର କରିବାପାଇଁ 1913 ମସିହାରେ ବୈଜ୍ଞାନିକ ବୋ’ର ଏକ ନୂଆ ପରମାଣୁ ମଡ଼େଲ ଉପସ୍ଥାପନ କଲେ । ବୋ’ରଙ୍କ ପରମାଣୁ ମଡ଼େଲର ରଦରଫୋର୍ଡ଼ଙ୍କ ପରମାଣୁ ମଡ଼େଲ ସହିତ ଅନେକ ସାମଞ୍ଜସ୍ୟ ଥିଲା । ବୋ’ରଙ୍କ ମଡ଼େଲ୍ ଅନୁ ସାରେ ଏକ ଯକ୍ତା ମକ କେନ୍ଦ୍ର ସ୍ଥଳୀ ଥାଏ. ଏକ ଯୁକ୍ତାତ୍ମକ କେନ୍ଦ୍ର ସ୍ଥଳୀ ଥାଏ, ଯାହାକୁ ନ୍ୟୁକ୍ଲିୟସ୍ କୁହାଯାଏ । ନ୍ୟୁକ୍ଲ ୟସ୍ ଚାରି ପଟେ ଥିବ । ଶୂନ୍ୟସ୍ଥାନରେ ଇଲେକ୍ ଟ୍ରନ୍ ଗୁଡ଼ିକ କେ ବ ଳ କେ ତେ ଗୁ ଡ଼ିଏ ନି ର୍ଦ୍ଦିଷ୍ଟ କେତେ ବର୍ଭୁ ଳାକାର କକ୍ଷପଥରେ ନ୍ୟୁକ୍ଲିୟସ୍ଚାରିପଟେ ଘୂର୍ଣ୍ଣନ କରନ୍ତି ।’’

ବୋ’ରଙ୍କ ସ୍ଵୀକାର :
(i) ନ୍ୟୁକ୍ଲିୟସ୍ ଚାରିପଟେ କେବଳ କେତେକ ନିର୍ଦ୍ଦିଷ୍ଟ କକ୍ଷପଥରେ ଇଲେକ୍‌ଟ୍ରଗୁଡ଼ିକ ଘୂର୍ଣ୍ଣନ କରେ ।
(ii) କ କ୍ଷ ପଥରେ ଘୂରୁ ଥ୍ ବି । ବେ ଳେ ନିର୍ଦିଷ୍ଠ କପଥରେ ଘୁରୁଥ୍ଚାବେ କେ ଇଲେକ୍‌ଟ୍ରଗୁଡ଼ିକ ଶକ୍ତି ବିକିରଣ କରନ୍ତି ନାହିଁ । ତେଣୁ ସେହି କକ୍ଷପଥକୁ ବିକିରଣବିହୀନ (non-radiating) କକ୍ଷ କୁହାଯାଏ ।
(iii) ଏହି କକ୍ଷପଥ ବା ସେଲ୍ (shell) ଗୁଡ଼ିକୁ ଶକ୍ତିସ୍ତର (energy level) କୁହାଯାଏ ।
(iv) କକ୍ଷପଥ ବା ସେଲ୍‌ଗୁଡ଼ିକୁ ନ୍ୟୁକ୍ଲିୟସ୍ଠାରୁ ଦୂରତା କ୍ରମରେ ଯଥାକ୍ରମେ K, L, M, N ଇତ୍ୟାଦି ଅକ୍ଷରଦ୍ଵାରା ବା 1, 2, 3, 4 ଇତ୍ୟାଦି ସଂଖ୍ୟାଦ୍ଵାରା ସୂଚିତ କରାଯାଏ ।

→ ନିଉଟ୍ରନ୍ (Neutron):
(i) 1932 ମସିହାରେ ବ୍ରିଟିଶ୍ ବୈଜ୍ଞାନିକ ଜେମ୍‌ସ ଚାଦଉଇକ୍ ପରମାଣୁ ଭିତରେ ଥ‌ିବା ‘ନିଉଟ୍ରନ୍’ କଣିକାର ଆବିଷ୍କାର କରିଥିଲେ ।
(ii) ନିଉଟ୍ରନ୍ ଚାର୍ଜବିହୀନ ଏବଂ ଏହାର ବସ୍ତୁତ୍ଵ ପ୍ରୋଟନ୍‌ର ବସ୍ତୁତ୍ଵ ସହ ପ୍ରାୟ ସମାନ ।
(iii) ହାଇଡ୍ରୋଜେନ୍ ବ୍ୟତୀତ ଅନ୍ୟସବୁ ପରମାଣୁର ନ୍ୟୁକ୍ଲିୟସ୍ ଭିତରେ ନିଉଟ୍ରନ୍ ରହିଥାଏ ।
(iv) ପ୍ରୋଟନ୍‌ ବା ନିଉଟ୍ରନ୍‌ର ବସ୍ତୁତ୍ଵ ତୁଳନାରେ ଇଲେକ୍‌ଟ୍ରିନ୍‌ର ବସ୍ତୁତ୍ଵ ନଗଣ୍ୟ

ପରମାଣୁରେ ଥିବା ମୁଖ୍ୟ କଣିକାର ପ୍ରତୀକ, ଚାର୍ଜ ଓ ବସ୍ତୁତ୍ଵ

କଷପଥ ମଧ୍ୟରେ ଇକେକ୍ଟ୍ରନ୍‌ ମାନଙ୍କର ସଜ୍ଵ ।
ପରମାଣୁର ବିଭିନ୍ନ କକ୍ଷପଥରେ ଇଲେକ୍‌ଟ୍ରନ୍ ଗୁଡ଼ିକ କିପରି ବାଣ୍ଟିହୋଇ ରହିବେ, ତାହା ବୋ’ର ଏବଂ ବରି ପ୍ରସ୍ତାବ ଦେଇଥିଲେ ।
(i) କୌଣସି ସେଲ୍‌ରେ ରହୁଥ‌ିବା ସର୍ବାଧ‌ିକ ଇଲେକ୍‌ଟ୍ରନ୍ ସଂଖ୍ୟା 2n² ଅଟେ । n ହେଉଛି କକ୍ଷମାନଙ୍କର କ୍ରମିକ ସଂଖ୍ୟା ବା ଶକ୍ତିସ୍ତର ସୂଚନାଙ୍କ (n = 1, 2, 3…) ।

(ii) ପରମାଣୁର ବାହ୍ୟତମ କକ୍ଷରେ ସର୍ବାଧ‌ିକ 8ଟି ଇଲେକ୍‌ଟ୍ରନ୍ ରହିପାରିବ । ଯଦି ଗୋଟିଏ ପରମାଣୁର ତୃତୀୟ କକ୍ଷଟି ବାହ୍ୟତମ କକ୍ଷ ହୋଇଥାଏ, ତେବେ ସେଥ‌ିରେ ୫ଟିରୁ ଅଧୂକ ଇଲେକ୍‌ଟ୍ରନ୍ ରହିପାରିବ ନାହିଁ । ଚତୁର୍ଥ କକ୍ଷ ଯଦି ବାହ୍ୟତମ କକ୍ଷ ହୁଏ, ତେବେ ସେଥ‌ିରେ ମଧ୍ୟ ୫ଟି ଇଲେକ୍‌ଟ୍ରନ୍ ରୁ ଅଧିକ ରହିବ ନାହିଁ।

→ ସଂଯୋଜକ ଇଲେକ୍‌ଟ୍ରନ୍‌ (Valency Electron) :
(i) ଯେଉଁ ମୌଳିକଗୁଡିକର ପରମାଣୁର ବାହ୍ୟତମ ସେଲ୍‌ରେ ସର୍ବା ଧୂକ (୫ଟି) ଅର୍ଥାତ୍ ସଂପୂର୍ଣ୍ଣ ମାତ୍ରା । ରେ (completely filled) ଇଲେକ୍‌ଟ୍ରନ୍ ରହିଥାଏ, ସେଗୁଡ଼ିକ ନିଷ୍କ୍ରିୟ ଏବଂ ସେମାନଙ୍କର ସଂଯୋଜନ କ୍ଷମତା ବା ଯୋଗ୍ଯତା ହେଉଛି ଶୂନ ।
(ii) ଏହିପରି ନିଷ୍କ୍ରିୟ ମୌଳିକଗୁଡ଼ିକ ମଧ୍ୟରେ ହିଲିୟମ୍ ପରମାଣୁର ବାହ୍ୟତମ କକ୍ଷରେ ଦୁଇଟି ଇଲେକ୍‌ଟ୍ରନ୍ ରହିଛି ଏବଂ ଅନ୍ୟ ନିଷ୍କ୍ରିୟ ମୌଳିକ; ଯଥା-ନିୟନ, ଆରଗନ୍, କ୍ରିପ୍‌ଟନ୍, ଜେନନ୍, ରାଡ଼ନ୍ ଆଦି ପରମାଣୁର ବାହ୍ୟତମ କକ୍ଷରେ 8 ଟି ଇଲେକ୍‌ଟ୍ରନ୍ ରହିଥାଏ ।
(iii) ବାହ୍ୟତମ କକ୍ଷରେ ୫ଟି ଇଲେକ୍‌ଟ୍ରିନ୍ ରହିଲେ ତାକୁ ଅଗ୍ନେଟ (octet) ସ୍ଥିତି କୁହାଯାଏ ।
(iv) ଅଣୁ ଗଠନବେଳେ ପ୍ରତ୍ୟେକ ପରମାଣୁ ତାହାର ନିକଟତମ ନିଷ୍କ୍ରିୟ ମୌଳିକ ପରମାଣୁ ସଂରଚନାରେ ରହିବାକୁ ଚେଷ୍ଟା କରେ ।
କେତେକ ପରମାଣୁ ଇଲେକ୍‌ଟ୍ରନ୍ ତ୍ୟାଗକରି, କେତେକ ପରମାଣୁ ଇଲେକ୍‌ଟ୍ରନ୍‌ ଗ୍ରହଣ କରି ଏବଂ ଅନ୍ୟ କେତେକ ପରମାଣୁ ଭିନ୍ନ ପରମାଣୁ ସହ ମିଳିତ ଭାବେ ଇଲେକ୍‌ଟ୍ରନ୍ ସହଭାଗ (share) କରି ଅଣୁ ଗଠନ କରନ୍ତି ।
(vi) ନିକଟତମ ନିଷ୍କ୍ରିୟ ମୌଳିକ ପରମାଣୁର ସଂରଚନାପାଇଁ କିମ୍ବା ଅକ୍ଟିସ୍ଥିତି ପାଇଁ ପରମାଣୁ ତ୍ୟାଗ କରୁଥିବା, ଗ୍ରହଣ କରୁଥିବା କିମ୍ବା ଭାଗ କରୁଥିବା ଇଲେକ୍‌ଟ୍ରମ୍ ସଂଖ୍ୟାରୁ ସିଧାସଳଖ ମୌଳିକର ସଂଯୋଜନ କ୍ଷମତା ବା ଯୋଗ୍ୟତା ଜଣାପଡ଼େ ।

ଉଦାହରଣ :
(a) ଲିଥ୍ୟମ୍ ଓ ସୋଡ଼ିୟମ୍ ପରମାଣୁ ପ୍ରତ୍ୟେକର’ ବାହ୍ୟତମ ସେଲ୍‌ରେ ଗୋଟିଏ ଇଲେକ୍‌ଟ୍ରିନ୍ ଥାଏ । ଲିଥୁମ୍ ପରମାଣୁ ହିଲିୟମ୍ ପରମାଣୁର ସଂରଚନାରେ ଏବଂ ସୋଡ଼ିୟମ୍ ପରମାଣୁ ନିୟନ ପରମାଣୁର ସଂରଚନାରେ ରହିବାକୁ ଚାହେଁ । ତେଣୁ ଲିଥୁମ୍ ଓ ସୋଡ଼ିୟମ୍ ମୌଳିକର ଯୋଗ୍ୟତା । ।
(b) ମ୍ୟାଗ୍ନେସିୟମ୍ ଓ ଏଲୁମିନିୟମ୍‌ର ବାହ୍ୟତମ ସେଲ୍‌ରେ ଯଥାକ୍ରମେ 2ଟି ଓ 3ଟି ଇଲେକ୍‌ଟ୍ରନ୍ ଥୁବାରୁ ଏମାନଙ୍କର ଯୋଗ୍ୟତା ଯଥାକ୍ରମେ 2 ଓ 3 ।
(vii) ଗୋଟିଏ ପରମାଣୁର ବାହ୍ୟତମ ସେଲ୍‌ର ଇଲେକ୍‌ଟ୍ରନ୍‌ ସଂଖ୍ୟା ତାହାର ପୂର୍ଣ୍ଣ (ସର୍ବାଧ‌ିକ) କ୍ଷମତାର ପାଖାପାଖୁ ବା ନିକଟତର ହୋଇଥାଏ, ତାହାର ଯୋଗ୍ୟତା ଭିନ୍ନ ପ୍ରକାରେ ନିର୍ଣ୍ଣୟ କରାଯାଏ ।

ଉଦାହରଣ :
କ୍ଲୋରିନ୍ ପରମାଣୁର ବାହ୍ୟତମ ସେଲ୍‌ରେ 7ଟି ଇଲେକ୍‌ଟ୍ରନ୍ ଅଛି । କ୍ଲୋରିନ୍ ପାଇଁ 7ଟି ଇଲେକ୍‌ଟ୍ରନ୍‌ ତ୍ୟାଗ କରିବା ଅପେକ୍ଷା ଗୋଟିଏ ଇଲେକ୍‌ଟ୍ରନ୍ ଗ୍ରହଣ କରିବା ସହଜ ହୋଇଥାଏ । ତେଣୁ ଅକ୍ଟେଟ୍ (8)ରୁ 7ଟି ଇଲେକ୍‌ଟ୍ରନ୍ ବିୟୋଗ କରି ଏହାର ଯୋଗ୍ୟତା ନିର୍ଣ୍ଣୟ କରାଯାଏ । ତେଣୁ କ୍ଲୋରିନ୍‌ର ଯୋଗ୍ୟତା l ହୋଇଥାଏ । ସେହିପରି ଅକ୍‌ସିଜେନ୍‌ର ଯୋଗ୍ୟତା 2 ଅଟେ ।
(viii) ପ୍ରତ୍ୟେକ ମୌଳିକର ପରମାଣୁର ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ସଂଯୋଜନ କ୍ଷମତା ରହିଛି । ଏହାକୁ ମୌଳିକର ଯୋଗ୍ଯତା
କୁହାଯାଏ ।

→ ପରମାଣୁ କ୍ରମାଙ୍କ (Atomic Number):
(i) ବିଭିନ୍ନ ପ୍ରକାର ପରମାଣର ନ୍ୟୁକ୍ଲିୟସରେ ପ୍ରୋଟନ ସଂଖ୍ୟା ଭିନ୍ନ ଭିନ୍ନ ହୋଇଥାଏ ।
(ii) ପରମାଣୁ କ୍ରମାଙ୍କକୁ Z ଦ୍ଵାରା ସୂଚିତ କରାଯାଏ ।
(iii) ପ୍ରତ୍ୟେକ ମୌଳିକର କେବଳ ଗୋଟିଏ ପରମାଣୁ କ୍ରମାଙ୍କ ଥାଏ I

ଉଦାହରଣ :
(a) ହାଇଡ୍ରୋଜେନ୍ ପରମାଣୁର ନ୍ୟୁକ୍ଲିୟସ୍‌ରେ କେବଳ ଗୋଟିଏ ପ୍ରୋଟନ୍ ଥ‌ିବାରୁ ତାହାର ପରମାଣୁ କ୍ରମାଙ୍କ । ।
(b) କାର୍ବନ ପରମାଣୁର ନ୍ୟୁକ୍ଲିୟସ୍‌ରେ ଟେ ପ୍ରୋଟନ୍ ଥ‌ିବାରୁ କାର୍ବନର ପରମାଣୁ କ୍ରମାଙ୍କ 6 ।

ବିଭିନ୍ନ – ସେଲ୍‌ରେ ଇଲେକ୍‌ଟ୍ରନ୍ ବଣ୍ଟନ ସହ ପ୍ରଥମ କେତୋଟି ମୌଳିକର ପରମାଣୁ ଗଠନ

→ ବସ୍ତୁତ୍ୱ ସଂଖ୍ୟା (Mass Number) :
(i) ପରମାଣୁ ମଧ୍ୟରେ ପ୍ରୋଟନ୍, ନିଉଟ୍ରନ୍ ଓ ଇଲେକ୍‌ଟ୍ରିନ୍ ଥାଏ । ପ୍ରୋଟନ୍‌ ବା ନିଉଟ୍ରନ୍‌ର ବସ୍ତୁତ୍ଵ ତୁଳନାରେ ଇଲେକ୍‌ଟ୍ରିନ୍‌ର ବସ୍ତୁତ୍ଵ ନଗଣ୍ୟ ହୋଇଥିବାରୁ ପରମାଣୁର ବସ୍ତୁତ୍ଵ ନିଶ୍ଚୟ କଲାବେଳେ ଅନେକ କ୍ଷେତ୍ରରେ ଇଲେକ୍‌ଟ୍ରିନ୍‌ର ବସ୍ତୁତ୍ୱକୁ ଉପେକ୍ଷା କରାଯାଏ ।
(ii) ପରମାଣୁର ନ୍ୟୁକ୍ଲିୟସ୍‌ରେ ରହିଥ‌ିବାରୁ ପ୍ରୋଟନ୍ ଓ ନିଉଟ୍ରନ୍‌କୁ ନ୍ୟୁକ୍ଲିୟନ୍ (Neucleon) କୁହାଯାଏ ।
(iii) ପରମାଣୁର ବସ୍ତୁତ୍ଵ ଏହାର ନ୍ୟୁକ୍ଲିୟସ୍‌ରେ ନିହିତ ଥାଏ ।

ଉଦାହରଣ :
(a) ନାଇଟ୍ରୋଜେନ୍‌ର ପ୍ରୋଟନ୍‌ ସଂଖ୍ୟା = 7 ଓ ନ୍ୟୁଟ୍ରନ୍‌ ସଂଖ୍ୟା = 7
∴ ନାଇଟ୍ରୋଜେନ୍ ର ବସ୍ତୁତ୍ଵ = 7u + 7u = 14u
(b) ସୋଡ଼ିୟମ୍‌ର ପ୍ରୋଟନ୍‌ ସଂଖ୍ୟା = 11 ଓ ନିଉଟ୍ରନ୍ ସଂଖ୍ୟା = 12
∴ସୋଡ଼ିୟମ୍‌ର ବସ୍ତୁତ୍ଵ = 11u + 12u = 23u
(v) ଗୋଟିଏ ପରମାଣୁ ପାଇଁ ସଙ୍କେତନ (notation) ରେ ମୌଳିକର ପରମାଣୁ କ୍ରମାଙ୍କ, ବସ୍ତୁତ୍ୱ ସଂଖ୍ୟା ଓ ପ୍ରତୀକ ନିମ୍ନ ପ୍ରକାରେ ପ୍ରକାଶ କରାଯାଏ ।

ଉଦାହରଣ :
(a) ସୋଡ଼ିୟମକୁ ²³₁₁Na ରୂପେ ପ୍ରକାଶ କରାଯାଏ । ଏଥୁରୁ ବୁଝାଯାଏ ସୋଡ଼ିୟମ୍‌ର ପରମାଣୁ କ୍ରମାଙ୍କ 11 ଓ ବସ୍ତୁତ୍ୱ ସଂଖ୍ୟା 23 1
(b) କାର୍ବନ ପରମାଣୁର ଟି ପ୍ରୋଟନ୍ ଓ ଟିଂ ନିଉଟ୍ରନ୍ ରହିଛି । ତେଣୁ କାର୍ବନର ବସ୍ତୁତ୍ଵ ସଂଖ୍ୟା 12 । ଏହାକୁ ସଂକ୍ଷେପରେ ¹²₆C ଲେଖାଯାଏ ।

ଏ ଆଇସୋଟୋପ୍ (Isotope) :
(i) ଅନେକ ମୌଳିକ ଆଜସେ ଟେ। ପଗୁଡ଼ିକର ମିଶ୍ରଣରେ ଗଠିତ ହୋଇଥାଏ । ଗୋଟିଏ ମୌଳିକର ପ୍ରତ୍ୟେକଟି ଆଇସୋଟୋପ୍ ଏକ ବିଶୁଦ୍ଧ ପଦାର୍ଥ ଅଟେ ।
(ii) ଆଇସୋଟୋପ୍‌ଗୁଡ଼ିକର ରାସାୟନିକ ଧର୍ମରେ ପାର୍ଥକ୍ୟ ଦେଖାଯାଏ ନାହିଁ, କିନ୍ତୁ ସେମାନଙ୍କର ଭୌତିକ ଧର୍ମଗୁଡ଼ିକ ଭିନ୍ନ ଅଟେ ।
(iii) ଯେଉଁ ମୌଳିକର ଆଇସୋଟୋପ୍ ନାହିଁ, ସେହି ମୌଳିକର ପାରମାଣବିକ ବସ୍ତୁତ୍ଵ, ଏହାର ପରମାଣୁରେ ଥିବା ପ୍ରୋଟନ୍ ସଂଖ୍ୟା ଓ ନିଉଟ୍ରନ୍ ସଂଖ୍ଯାର ସମଷ୍ଟି ସହିତ ସମାନ ।

ଉଦାହରଣ :
(a) ହାଇଡ୍ରୋଜେନ୍‌ର 3ଟି ଆଇସୋଟୋପ୍ ହେଲା- ହାଇଡ୍ରୋଜେନ୍ ବା ପ୍ରୋଟିୟମ୍ (¹₁H), ଡିଉଟେରିୟମ୍ (²₁H ବା D) ଏବଂ ଟ୍ରାଇଟିୟମ୍ (³₁H ବା T) ।
(b) ନାଇଟ୍ରୋଜେନ୍ ର 2ଟି ଆଇସୋଟୋପ୍ ହେଲା – ¹⁴₇N ଏବଂ ¹⁵₇N ।
(c) ଅକ୍‌ସିଜେନ୍ ର 3ଟି ଆଇସୋଟୋପ୍ ହେଲା – ¹⁶₈O, ¹⁷₈O ଏବଂ ¹⁸₈O ।
(d) କ୍ଲୋରିନ୍‌ ର 2ଟି ଆଇସୋଟୋପ୍ ହେଲା – ³⁵₁₇Cl ଏବଂ ³⁷₁₇Cl ।
(e) ପୋଟାସିୟମ୍‌ର 3ଟି ଆଇସୋଟୋପ୍ ହେଲା – ³⁹₁₉K, ⁴⁰₁₉K ଏବଂ ⁴¹₁₉K

ଆଇସୋଟୋପ୍‌ର ବସ୍ତୁତ୍ଵ ନିରୂପଣ :
(i) ଯେଉଁ ମୌଳିକର ଆଇସୋଟୋପ୍ ରହିଛି, ତାହାର ବସ୍ତୁତ୍ଵ ନିରୂପଣ କରିବାପାଇଁ ଆଇସୋଟୋପ୍‌ଗୁଡ଼ିକର ଶତକଡ଼ା ଅନୁପାତ ଜାଣିବା ଆବଶ୍ୟକ ।
(ii) ³⁵₁₇Cl ଏବଂ ³⁷₁₇Cl ପ୍ରକୃତିରେ ଯଥାକ୍ରମେ 75% ଓ 25% ଅନୁପାତରେ ମିଳେ ।
(iii) କ୍ଲୋରିନ୍‌ ପରମାଣୁର ହାରାହାରି ପାରମାଣବିକ ବସ୍ତୁତ୍ଵ
= 35 × \(\frac{75}{00}+37 \times \frac{25}{100}=\frac{105}{4}+\frac{37}{4}=\frac{142}{4}\) = 35.5u
(iv) ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ପରିମାଣର କ୍ଲୋରିନ୍‌ରେ ଦୁଇଟିଯାକ ଆଇସୋଟୋପ୍ ରହିଥାଏ ଏବଂ କ୍ଲୋରିନ୍‌ ହାରାହାରି ବସ୍ତୁତ୍ଵ ହେଉଛି 35.5u ।

→ ଆଇସୋବାର୍ (Isobar):
ସମାନ ବସ୍ତୁତ୍ଵ ସଂଖ୍ୟା କିନ୍ତୁ ଭିନ୍ନ ପରମାଣୁ କ୍ରମାଙ୍କର ପରମାଣୁଗୁଡ଼ିକୁ ଆଇସୋବାର୍ କୁହାଯାଏ ।
ଉଦାହରଣ :
⁴⁰₁₉K ଓ ⁴⁰₂₀Ca ଆଇସୋବାର୍‌ ଅଟନ୍ତି ।

Odisha State Board BSE Odisha 8th Class Odia Solutions Chapter 7 ଗୁରୁ-ଶିଷ୍ୟ ସମ୍ପର୍କ Textbook Exercise Questions and Answers.

BSE Odisha Class 8 Odia Solutions Chapter 7 ଗୁରୁ-ଶିଷ୍ୟ ସମ୍ପର୍କ

ପାଠ୍ୟପୁସ୍ତକସ୍ଥ ଅଭ୍ୟାସ କାର୍ଯ୍ୟର ଉତ୍ତର

Question ୧ ।
ଆସ, କଥାବାର୍ତ୍ତା ହେବା :
(କ) କେଉଁ ଭାବନାଟି ପୁରାଣ ଯୁଗରେ ଗୁରୁକୂଳ ଶିକ୍ଷାର ପ୍ରାଣସ୍ୱରୂପ ଥିଲା ?
Answer:
‘ଗୁରୁଙ୍କୁ ନମଣିବ ନର, ଗୁରୁହିଁ ସାକ୍ଷାତ୍‌ ଈଶ୍ବର ।’’ଏହି ଭାବନାଟି ପୁରାଣଯୁଗରେ ଗୁରୁକୁଳ ଶିକ୍ଷାର ପ୍ରାଣ ସ୍ବରୂପ ଥିଲା ।

(ଖ) ଗୁରୁଶିଷ୍ୟ ସମ୍ପର୍କ ଆଜି କିପରି ଅବସ୍ଥାରେ ଅଛି ?
Answer:
ଗୁରୁ ଶିଷ୍ୟର ସମ୍ପର୍କ ଆଜି ବଦଳି ଯାଇଛି । ଗୁରୁର ଗୁରୁ ପଦବାଚ୍ୟ ହେବାର ବାସନା ନାହିଁ ଏବଂ ଶିଷ୍ୟ ଶାସନ

(ଗ) ମୂଳ ପ୍ରକୃତି କେଉଁ ଦୁଇଟି କ୍ଷେତ୍ରରେ ଅତୁଟ ରହିଛି ?
Answer:
ମୂଳ ପ୍ରକୃତି ଦୁଇଟି କ୍ଷେତ୍ରରେ ଅତୁଟ ରହିଛି, ତାହା ହେଉଛି ସମ୍ପର୍କରେ ଅଭେଦତ୍ବ, ଅର୍ଥାତ୍ ଯେ ଗୁରୁ ସେ ଶିଷ୍ୟ ଓ ଯେ ଶିଷ୍ୟ ସେ ଗୁରୁ ।

(ଘ) ଶିକ୍ଷା କ୍ଷେତ୍ରରେ କାହାକୁ କେନ୍ଦ୍ରସ୍ଥାନ ଦିଆଯାଏ ?
Answer:
ଶିକ୍ଷାକ୍ଷେତ୍ରରେ ଶିଷ୍ୟକୁ କେନ୍ଦ୍ରସ୍ଥାନ ଦିଆଯାଏ ।

(ଙ) ପୁସ୍ତକ କୈନ୍ଦ୍ରିକ ଶିକ୍ଷାର ଅର୍ଥ କ’ଣ ?
Answer:
ପୁସ୍ତକ କୈନ୍ଦ୍ରିକ ଶିକ୍ଷାର ଅର୍ଥ ହେଉଛି, ମୁଖସ୍ଥ୍ୟକରଣଦ୍ୱାରା ପରୀକ୍ଷାରେ କୃତକାର୍ଯ୍ୟ ହୋଇ ପ୍ରମାଣ ପତ୍ର ହାସଲ କରିବା, ଯାହାଦ୍ୱାରା ଶିକ୍ଷାର୍ଥୀ ଓ ଅଭିଭାବକ ନିଜକୁ ଶ୍ରେୟ ମନେକରିବ । ପୁସ୍ତକ ବିଦ୍ୟା ଭିନ୍ନ ଅନ୍ୟ ବିଷୟ ପ୍ରତି ଉଦାସୀନ ହେବା ।

Question ୨ ।
ଆସ, ତଳଲିଖ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଦୁଇ ବା ତିନୋଟି ବାକ୍ୟରେ ଲେଖୁବା ।
(କ) ଶିକ୍ଷକଙ୍କ ଶିକ୍ଷା ଚିରନ୍ତନ – ଏପରି କାହିଁକି କୁହାଯାଇଛି ?
Answer:
ଶିକ୍ଷକ ଜୀବନ ବ୍ୟାପୀ କୋଟି କୋଟି ପ୍ରାଣକୁ ପ୍ରଭାବିତ କରୁଥିବାରୁ, ତାଙ୍କର ପ୍ରଭାବ ଅନନ୍ତ, କାଳଜୟୀ ଓ ଅସରନ୍ତି । ଏହା କାଳାତୀତ ଓ କାଳଲିପିକୁ ପ୍ରଭାବିତ କରେ । ତେଣୁ ଶିକ୍ଷକଙ୍କ ଶିକ୍ଷାକୁ ଚିରନ୍ତନ କୁହାଯାଇଛି ।

(ଖ) ‘ଗୋଟିଏ ଦୀପ ଅନ୍ୟ ଏକ ଦୀପକୁ ଜାଳିବାର’ ତାତ୍ପର୍ଯ୍ୟ କ’ଣ ?
Answer:
ଗୋଟିଏ ଜ୍ଵଳନ୍ତ ଦୀପରୁ ଅନ୍ୟ ଏକ ଦୀପ ପ୍ରଜ୍ଜ୍ୱଳିତ ହୋଇଥାଏ । ମାତ୍ର ମୂଳ ଦୀପର ଜ୍ୟୋତି କ୍ଷୀଣ ହୁଏ ନାହିଁ । ସେହିପରି ଶିକ୍ଷକଙ୍କ ଶିକ୍ଷା ଚିରନ୍ତନ ଯାହା କାଳାତୀତ ଓ କାଳଲିପିକୁ ପ୍ରଭାବିତ କରେ । ପଠନ ଓ ପାଠନର ସତ୍ୟନିଷ୍ଠ ସାଧନା ଶିକ୍ଷାର ଇତିହାସକୁ ମହିମାନ୍ବିତ କରିଥାଏ ।

(ଗ) ‘ଗୁରୁଙ୍କର ଜୀବନ ଜୀବନ୍ତ ହୁଏ’ କହିବାର କାରଣ କ’ଣ ?
Answer:
ପଠନ ଓ ପାଠନର ସତ୍ୟନିଷ୍ଠ ସାଧନା ଶିକ୍ଷାକୁ ମହିମାନ୍ଵିତ କରେ । ପ୍ରଭାବକାରୀ ପ୍ରାଣର ପ୍ରାଚୁର୍ଯ୍ୟ ଗୁରୁଜୀବନକୁ ଗରୀୟାନ୍ କରେ। କେବଳ ଏହି ଆଦର୍ଶଦ୍ବାରା ଗୁରୁର ଜୀବନ ଧନ୍ୟ ହୁଏ ଓ ଶିକ୍ଷାପ୍ରକ୍ରିୟା ସଂକ୍ରମଣରେ ସହାୟକ ହୋଇଥିବାରୁ, ଗୁରୁଙ୍କର ଜୀବନ ଜୀବନ୍ତ ହୋଇଥାଏ ।

(ଘ) ‘ତେଜସ୍ବିନାବାଧୀତମସ୍ତୁ’ ଉକ୍ତିରୁ ଗୁରୁଶିଷ୍ୟଙ୍କ ସମ୍ପର୍କରେ କ’ଣ ଜଣାପଡୁଛି ?
Answer:
ଏହା ‘କଠୋପନିଷଦ୍’ ଅନ୍ତର୍ଗତ ଶାନ୍ତିପାଠର ଏକ ଅଂଶ । ଯାହାର ଅର୍ଥ ଆମ ଗୁରୁ ଶିଷ୍ୟଙ୍କ ଦ୍ୱାରା ଅଧ୍ୟୟନ କରାଯାଉଥ‌ିବା ବିଦ୍ୟା ତେଜୋମୟୀ ହେଉ । ଏହି ଉକ୍ତିରୁ ଗୁରୁଶିଷ୍ୟଙ୍କ ସମ୍ପର୍କରେ ନିବିଡ଼ତା ରହିଥ‌ିବା ଜଣାପଡ଼ୁଛି ।

(ଙ‍) ଶିକ୍ଷାର ସାମାଜିକ ଲକ୍ଷ୍ୟ କ’ଣ ହେବା ଆବଶ୍ୟକ ?
Answer:
ପୁସ୍ତକକୈନ୍ଦ୍ରିକ ଶିକ୍ଷା ସମ୍ପ୍ରତି ଯୋଗ୍ୟତାର ମାପକାଠିଭାବେ ଗୃହୀତ ହେବା ଫଳରେ ଏହା ସାମାଜିକ ଲକ୍ଷ୍ୟଠାରୁ ଦୂରେଇ ଯାଉଛି । ଶିକ୍ଷା ସାମାଜିକ ତଥା ଆର୍ଥନୀତିକ ବିକାଶର ଅଙ୍ଗଭାବେ ପରିଗଣିତ ହେଲେ ଲକ୍ଷ୍ୟ ପୂରଣରେ ସଫଳ ସମାନ ସେବାର ଏକ ଅବିଚ୍ଛେଦ୍ୟ ଅଙ୍ଗଭାବେ ଗୃହୀତ ହେବା ଆବଶ୍ୟକ ।

(ଚ) ଏବେ ଗୁରୁଶିଷ୍ୟର ସମ୍ପର୍କ କିପରି ହେବା ଉଚିତ ବୋଲି ଲେଖକ କହିଛନ୍ତି ?
Answer:
ସମ୍ପ୍ରତି ଗୁରୁଶିଷ୍ୟଙ୍କର ସମ୍ପର୍କ ପ୍ରାଧ୍ୟାକାରଭିଭିକ ନ ହୋଇ, ସହଯୋଗୀ ଓ ଉତ୍ସାହପ୍ରଦ ହେବା ଉଚିତ । ଉଭୟ ଗୁରୁ ଓ ଶିଷ୍ୟ ପାଠ୍ୟତାଲିକା, ପାଠ୍ୟପୁସ୍ତକ ଓ ପରୀକ୍ଷାର ଦାସ ନହୋଇ ଏକ ଉନ୍ମ କ୍ତ ପରିବେଶରେ କାର୍ଯ୍ୟ କରିବାର ସୁଯୋଗ ଲାଭ କଲେ ଏ ସମ୍ପର୍କରେ ଉନ୍ନତି ସାଧୁ ହେବ । ଶିକ୍ଷାଳୟ ପାରମ୍ପରିକ କାର୍ଯ୍ୟଧାରାରୁ ମୁକ୍ତ ହୋଇ ଏକ ସାମାଜକ ଗବେଷଣାଗାରରେ ଗୁରୁ ଶିଷ୍ୟ ଉଭୟ ଯନ୍ତୀଭାବେ ପରସ୍ପର ସହଯୋଗୀ ହେବା ଉଚିତ୍ ବୋଲି ଲେଖକ କହିଛନ୍ତି ।

Question ୩ ।
ଆସ, ସରଳ ଭାଷାରେ ବୁଝାଇ ଲେଖୁ ।
(କ) ଏକଥା ସତ୍ୟ ଯେ କୌଣସି ଦେଶର ଗୌରବ, ସେ ଦେଶର ଲୋକ ଚରିତ୍ର ଉପରେ ନିର୍ଭର କରେ । ତଦ୍ବାରା ଦେଶ ବଳୀୟାନେ ହୁଏ ।
Answer:
“ଏକଥା ସତ୍ୟ ………………….. ବଳୀୟାନ୍ ହୁଏ ।’’
ଶଂସିତ ମୃଦ୍ୟାଶଟି ପ୍ରଫେସର ଶତ୍ରୁଘ୍ନ ନାଥଙ୍କ ରଚିତ ‘ଜୀବନ ଶିକ୍ଷା’ ପୁସ୍ତକରୁ ‘ଗୁରୁ-ଶିଷ୍ୟ ସମ୍ପକ ପ୍ରବନ୍ଧରୁ ଆନୀତ । ଏଠାରେ ଲେଖକ ଲୋକ ଚରିତ୍ର କିପରି ଦେଶର ଗୌରବ ବୃଦ୍ଧିରେ ସହାୟକ ହୁଏ ତାହା ଉପରେ ଆଲୋକପାତ କରିଛି୍ତି ।

ସମ୍ପ୍ରତି ଗୁରୁଶିଷ୍ୟ ସମ୍ପର୍କ ଯେପରିଭାବେ କଳୁଷିତ ହୋଇପଡ଼ିଛି ତାହାର କାରଣ ନିର୍ଦ୍ଧାରଣ କରିବାକୁ ପ୍ରାବନ୍ଧିକ ଶିକ୍ଷାର କେତୋଟି ଗୁରୁତ୍ଵପୂର୍ଣ୍ଣ ଦିଗ ପ୍ରତି ଅଙ୍ଗୁଳି ନିର୍ଦ୍ଦେଶ କରିଛନ୍ତି । ଆଜିକାଲି ଶିକ୍ଷକ ଗୁରୁଭାବେ ପରିଚିତ ହେବାକୁ ଇଚ୍ଛା କରୁନାହାନ୍ତି । ଶିଷ୍ୟ ମଧ୍ୟ ଆଜି ଶାସନ ବିରୋଧରେ ବିଦ୍ରୋହୀ ଓ ବିପ୍ଳବୀ ହୋଇଉଠିଛି । କାଳର କରାଳ ଗତିରେ ମୂଲ୍ୟବୋଧର ଅବକ୍ଷୟ ଘଟିଛି । ସମାଜରେ ପରିଦୃଷ୍ଟ ସ୍ଖଳନ ଓ ଭ୍ରଷ୍ଟାଚାର ଏଥିପାଇଁ ବହୁଭାବେ ଦାୟୀ । ବିକାଶମୂଳକ କାର୍ଯ୍ୟକ୍ରମଦ୍ୱାରା ସାମାଜିକ ଜୀବନ ବହୁଭାବେ ପ୍ରଭାବିତ ହେଉଅଛି । ସମାଜରେ ନୈତିକତା ଓ ଆଧ୍ୟାତ୍ମିକତା କ୍ରମଶଃ ବିଲୁପ୍ତ ହେବାକୁ ବସିଲାଣି । ଯଦ୍ଵାରା ଦେଶର ସଂସ୍କୃତି ଓ ପରମ୍ପରା ବିପର୍ଯ୍ୟସ୍ତ ହୋଇଉଠୁଛି ।

ଲୋକ ଚରିତ୍ର ଉପରେ ଦେଶ ଓ ଜାତିର ସମୃଦ୍ଧି ଓ ସୁନାମ ନିର୍ଭର କରିଥାଏ । ଏହା ଦେଶକୁ ବଳୀୟାନ୍ କରେ । ଲୋକ ଚରିତ୍ର କ୍ରମେ ମାନବିକ ମୂଲ୍ୟବୋଧରୁ ଦୂରେଇ ଯାଇ ସ୍ବାର୍ଥସର୍ବସ୍ଵ ଓ ଆତ୍ମକୈନ୍ଦ୍ରିକ ହୋଇଉଠୁଛି । ଏହା ପ୍ରଚଳିତ ଶିକ୍ଷା ବ୍ୟବସ୍ଥା ଉପରେ ମଧ୍ୟ ପ୍ରଭାବ ପକାଉଛି । ଜୀବନ ସୌଧର ମୂଳଭିଭି ଶିକ୍ଷାଳୟରେ ପଡ଼ିଥାଏ । ଜାତିର ଜୟଗାଥାର ମୂଳପିଣ୍ଡ ହେଉଛି ଜୀବନ । କେବଳ ଲୋକ ଚରିତ୍ର ମର୍ଯ୍ୟାଦାପୂର୍ଣ୍ଣ ହେଲେ ହିଁ ଦେଶ ଓ ଜାତିର ଗୌରବ ବୃଦ୍ଧି ହେବା ସମ୍ଭବ ।

(ଖ) ‘ମୁଁ ମୋର ଜନ୍ମ ପାଇଁ ପିତାମାତାଙ୍କ ସମୀପରେ ଋଣୀ, କିନ୍ତୁ ମୋର ଜୀବନପାଇଁ ଗୁରୁଙ୍କ ସମୀପରେ ଋଣୀ ।
Answer:
‘ମୁଁ ମୋର ଜନ୍ମ …………………………….. ସମୀପରେ ଋଣୀ ।’’
ଶଂସିତ ଗଦ୍ୟାଂଶଟି ପ୍ରଫେସର ଶତ୍ରୁଘ୍ନ ନାଥଙ୍କ ରଚିତ ‘ଜାବନ ଶିକ୍ଷା’ ପୁସ୍ତକରୁ ସଂଗୃହାତ ‘ଗୁରୁ – ଶିଷ୍ୟ ସମ୍ପକ’ ଶୀର୍ଷକ ପ୍ରବନ୍ଧରୁ ଆନୀତ । ଏଠାରେ ପ୍ରାବନ୍ଧିକ ଜନୈକ ଗୁରୁପରାୟଣ ମହାମନୀଷୀଙ୍କ ମହନୀୟ ସ୍ବୀକାରୋକ୍ତି ଉପରେ ଥିଲେ।କପାତ କରିଛନ୍ତି। ପିତାମାତା ଆମକୁ ଜନ୍ମ ଦିଅନ୍ତି । ସେଥ‌ିପାଇଁ ଆମେ ତାଙ୍କଠାରେ କୃତଜ୍ଞ । ସଂସାରକୁ ଆଣିବାରେ ତାଙ୍କର ଅବଦାନ ପାଇଁ ଆମେ ସେମାନଙ୍କ ପାଖରେ ଋଣୀ । କିନ୍ତୁ ମଣିଷ ପରି ମଣିଷଟିଏ ଗଢ଼ିବାରେ ଶିକ୍ଷକଙ୍କ ଗୁରୁତ୍ଵପୂର୍ଣ୍ଣ ଭୂମିକା ଅନସ୍ବୀକାର୍ଯ୍ୟ । ଜୀବନ ଗଠନରେ ଗୁରୁଙ୍କ ବିରଳ ଆତ୍ମତ୍ୟାଗ ଶିଷ୍ୟ ଜୀବନକୁ ଧନ୍ୟ କରେ । ଶିଷ୍ୟକୁ ଉପଯୁକ୍ତ ଜ୍ଞାନ ଦାନ କରି ସମାଜ ପାଇଁ ଜଣେ ଉପଯୋଗୀ ନାଗରିକ ଭାବେ ଗଢ଼ିଥାଆନ୍ତି ଗୁରୁ ।

ଜୀବନକୁ ସତ୍ୟ-ଶିବ-ସୁନ୍ଦର କରିବାରେ ଗୁରୁଙ୍କ ଅବଦାନର ମହତ୍ତ୍ବ ଯେ ଅପରିସୀମ ଏହା ଶିଷ୍ୟ ଆଜୀବନ ଅନୁଭବ କରିଥାଏ । ଗୁରୁଙ୍କର ଗୋଟିଏ ଗୋଟିଏ କଥା ଶିଷ୍ୟର ଜୀବନକୁ ମହିମାବନ୍ତ କରେ । ଗୁରୁଙ୍କ ଜ୍ଞାନ ପ୍ରଦୀପର ଶିଖାଦ୍ଵାରା ଶିଷ୍ୟର ଜୀବନଦୀପ ପ୍ରଜ୍ଜ୍ୱଳିତ ହୋଇ ତା’ ଅନ୍ତରର ଅଜ୍ଞାନ ଅନ୍ଧକାର ଦୂର କରିଥାଏ ଏବଂ ସେହି ଆଲୋକର ଦୀପ୍ତି ଆଜୀବନ ଜାଜ୍ୱଲ୍ୟମାନ ରହିଥାଏ । ସେଥ‌ିପାଇଁ ଗୁରୁଙ୍କଠାରେ ଚିରକୃତଜ୍ଞ ଜଣେ ମହାମନୀଷୀ ମୁକ୍ତକଣ୍ଠରେ ଏହି ମହାନ୍ ବାଣୀ ପ୍ରକାଶ କରି ନଜ ଗୁରୁଙ୍କ ଯଶଗାନ କରିଛନ୍ତି ।

(ଗ) ଗୁରୁ ଓ ଶିଷ୍ୟ ହେବେ ସାମାଜିକ ଇଞ୍ଜିନିୟର ।
Answer:
ଉକ୍ତ ଗଦ୍ୟାଂଶଟି ପ୍ରଫେସର ଶତ୍ରୁଘ୍ନ ନାଥଙ୍କ ରଚିତ ‘ଚ୍ଚାବନ ଶିକ୍ଷା’ ପୁସ୍ତକରୁ ସଂଗୃହାତ ‘ଗୁରୁ – ଶିଷ୍ୟ ସମ୍ପର୍କ’ ଶୀର୍ଷକ ପ୍ରବନ୍ଧରୁ ଗୃହିତ । ପ୍ରାବନ୍ଧିକ ଶିକ୍ଷାଳୟକୁ ପାରମ୍ପରିକ ଭୂମିକା ତ୍ୟାଗ କରି ଏକ ସାମାଜିକ ଗବେଷଣାଗାରର ଭୂମିକା ଗ୍ରହଣ କରିବାକୁ ପରାମର୍ଶ ଦେଇଛନ୍ତି । ସେଠାରେ ଗୁରୁ ଓ ଶିଷ୍ୟ ଉଭୟେ ଯନ୍ତ୍ରୀରୂପେ କାର୍ଯ୍ୟ କରିବେ । ସେଠାରେ ଚିରାଚରିତ ଓ ଚିରନ୍ତନ ମୂଲ୍ୟବୋଧରେ ପୁନଃ ମୂଲ୍ୟାୟନ କରାଯିବ । ସାମଜର ସୁରକ୍ଷା ଓ ନୂତନ ସୃଷ୍ଟି ପାଇଁ ଉଭୟ ଦିଗରେ ଗରୁଶିଷ୍ୟ କାର୍ଯ୍ୟ କରିବେ ବୋଲି ଲେଖକ କହିଛନ୍ତି । ପାଠ୍ୟପୁସ୍ତ, ପାଠ୍ୟତାଲିକା ଆଦି ଏପରି ଭାବେ ପ୍ରସ୍ତୁତ ହେବ ଯେପରି ପରୀକ୍ଷାରୀ ଦାସ ନହୋଇ ଗୁରୁ ଓ ଶିଷ୍ୟ ଏକ ଉନ୍ମକ୍ତ ପରିବେଶରେ କାର୍ଯ୍ୟ କରିବାକୁ ଆଗ୍ରହ ପ୍ରକାଶ କରିବେ ।

ସେ ସବୁର ସମାଧାନ ଦିଗରେ ଶିକ୍ଷାୟତନ ରୂପକ ଗବେଷଣାଗାରରେ ଚିନ୍ତା ଓ ସାମର୍ଥ୍ୟ ସଞ୍ଚାର କରାଯାଇପାରି । ଇଞ୍ଜିନିୟର ବା ଯନ୍ତ୍ରୀ ଯେପରି ଯୋଜନାବଦ୍ଧ ଭାବେ, ଦୂରଦୃଷ୍ଟି ସମ୍ପନ୍ନ ହୋଇ ସ୍ଥପତି ବା କରିଗରୀକୁ ପରିଚାଳନା କରେ, ଠିକ୍ ସେହିପରି ଉନ୍ନତ ସମାଜ ପାଇଁ ଗୁରୁଶିଷ୍ୟ ଅନୁରୂପ ଭୂମିକା ଗ୍ରହଣ କରିବେ । ଯାହା ଫଳରେ ସେମାନେ ହେବେ ସୁସ୍ଥ ସମାଜରେ କାରଣ ଓ ନିୟାମକ । ବାସ୍ତବିକ ପ୍ରାବନ୍ଧିକ ଅନୁଚିନ୍ତା ପ୍ରଣିଧାନ ଯୋଗ୍ୟ।

Question ୪ ।
ତଳ ଲିଖ୍ତ ଅନୁଚ୍ଛେଦଟିକୁ ଉତ୍ତର ଭାବି ସେଥୁରୁ ପ୍ରଶ୍ନ ତିଆରି କରିବା ।
ସେଥ‌ିପାଇଁ ଗୁରୁଙ୍କ ସ୍ଥାନ ଉଚ୍ଚରେ । ଶିକ୍ଷା ପଦ୍ଧତିର ସର୍ବୋର୍ଡ଼ରେ । ଯୁଗେ ଯୁଗେ ସେ କେବଳ ଶିକ୍ଷାର୍ଥୀଙ୍କର ନୁହେଁ, ସମଗ୍ର ସମାଜର ନମସ୍ୟ, ଜଣେ ମନୀଷା ଏହି ଭାବନାକୁ ସ୍ୱୀୟ ବାଣୀରେ ପ୍ରକାଶ କରିଛନ୍ତି । ତାହା ହେଉଛି, ‘‘ମୁଁ ମୋର ଜନ୍ମ ପାଇଁ ପିତାମାତାଙ୍କ ସମୀପରେ ଋଣୀ, କିନ୍ତୁ ମୋର ଜୀବନ ପାଇଁ ଗୁରୁଙ୍କ ସମୀପରେ ଋଣୀ’’ । ଗୁରୁ ପ୍ରାଣ ପ୍ରତିଷ୍ଠା କରନ୍ତି । ଶ୍ରେଣୀ କୋଠରି ନଥାଇପାରେ । ଉପକରଣ ନଥାଉ ଆଡ଼ମ୍ବର ଦୂରେଇ ଯାଉ । ସେ ହିଁ ସବୁ । ଗୁରୁଙ୍କର ମାତ୍ର ପଦଟିଏ କଥା ଶିଷ୍ୟମାନଙ୍କର କୋଟି କୋଟି ପ୍ରାଣରେ କୋଟି କୋଟି ରୂପରେ ଉଦ୍ଭାସିତ ହୁଏ ।
Answer:
(କ) କାହାର ସ୍ଥାନ ଉଚ୍ଚରେ ?
(ଖ) ଶିକ୍ଷା ପଦ୍ଧତିର ସ୍ଥାନ କେଉଁଠାରେ ?
(ଗ) କେଉଁମାନେ ସମାଜର ନମସ୍ୟ ?
(ଘ) ସମଗ୍ର ସମାଜର ଗୁରୁ ନମସ୍ୟ ବୋଲି କିଏ କହିଥିଲେ ?
(ଙ‍) ମନୀଷୀ ନିଜର ଭାବନାକୁ ପ୍ରକାଶ କରି କ’ଣ କହିଥିଲେ ?
(ଚ) କିଏ ପ୍ରାଣ ପ୍ରତିଷ୍ଠା କରନ୍ତି ?
(ଛ) ଗୁରୁଙ୍କର ପଦୁଟିଏ କଥା କିପରି ଉଦ୍‌ଭାସିତ ହୋଇଥାଏ ।

Question ୫।
‘ରୂପାନ୍ତର’ ଶବ୍ଦଟିର ଅର୍ଥ ‘ରୂପ ପରିବର୍ତ୍ତନ’ ବା ‘ଅନ୍ୟରୂପ’ । ‘ରୂପାନ୍ତର’ ଶବ୍ଦ ପରି ଆଉ ଚାରୋଟି ଶବ୍ଦ ଲେଖୁ ଓ ସେଗୁଡ଼ିକୁ ବାକ୍ୟରେ ବ୍ୟବହାର କରିବା ।
Answer:
ଗ୍ରାମାନ୍ତର, ଦେଶାନ୍ତର, ଭାଷାନ୍ତର, ଘଟାନ୍ତର ।
ଗ୍ରାମାନ୍ତର – ମେଳା ଦେଖ‌ିବାକୁ ଗ୍ରାମ, ଗ୍ରାମାନ୍ତର ଲୋକେ ବହୁସଂଖ୍ୟାରେ ଆସିଥାଆନ୍ତି ।
ଦେଶାନ୍ତର – ଦେଶଦ୍ରୋହ ଅପରାଧ ପାଇଁ ତାଙ୍କୁ ଦେଶାନ୍ତର ହେବାର ଦଣ୍ଡ ପ୍ରଦାନ କରାଗଲା ।
ଭାଷାନ୍ତର – ଭାଷାନ୍ତର, ସାହିତ୍ୟ ସାଧନାର ଏକ ଅଙ୍ଗ ।
ଘଟାନ୍ତର – ମୃତ୍ୟୁ ପରେ ମଣିଷର ଘଟାନ୍ତର ହୋଇଥାଏ ବୋଲି ବିଶ୍ଵାସ କରାଯାଏ ।

Question ୬ ।
ଆସ, କୋଠରିରୁ ଅକ୍ଷର ନେଇ ଶବ୍ଦ ଗଢ଼ିବା ।

Answer:
ସୌଧ, ଅବିର, ବଖାଣ, ଅପ୍ରାସଙ୍ଗିକ, ବିଭୋର, ଋଦ୍ଧିମନ୍ତ, ସ୍ୱାଧ୍ୟାୟ, କୁତ୍ସା, ନୈପୁଣ୍ୟ

Question ୭।
ଆରମ୍ଭରେ ‘ଅ’ ଅକ୍ଷର ଯୋଗକରି ପାଞ୍ଚଗୋଟି ଶବ୍ଦ ଲେଖୁବା ।
ନୂତନ ଶବ୍ଦ ଏଠାର ଲେଖୁ ।
୧._________
୨. _________
୩. _________
୪. _________
୫. _________
ସେହି ଶବ୍ଦଗୁଡ଼ିକୁ ନେଇ ବାକ୍ୟ ଗଠନ କରି ଲେଖୁବା ।
୧. _________
୨. _________
୩. _________
୪. _________
୫. _________
Answer:

ନୂତନ ଶବ୍ଦ :	ବାକ୍ୟ :
୧. ଅବାସ୍ତବ	୧। ବିଜ୍ଞାନ ବଳରେ ଅନେକ ଅବାସ୍ତବ କଥା ସତ୍ୟରେ ପରିଣତ ହେଲାଣି ।
୨. ଅବିଭାଜ୍ୟ	୨। ବାପା ନିଜର ସମ୍ପତ୍ତିକୁ ଅବିଭାଜ୍ୟ କରି ରଖୁବାକୁ ଚାହିଁଥିଲେ ।
୩. ଅସଭ୍ୟ	୩ । ପ୍ରାଚୀନ ଯୁଗରେ ମଣିଷ ଅସଭ୍ୟ ଥିଲା ।
୪. ଅଭେଦ୍ୟ	୪। ରାଜାଙ୍କର ଅଭେଦ୍ୟ ଦୁର୍ଗକୁ ଶତ୍ରୁମାନେ ତଶିପାରୁନଥିଲେ।
୫. ଅକାଟ୍ୟ	୫। ଦାର୍ଶନିକଙ୍କର ଯୁକ୍ତି ଅକାଟ୍ୟ ଥିଲା ।

Question ୮।
କୋଠରି ଭିତରେ ଥ‌ିବା ଶବ୍ଦରେ ଇକ ପ୍ରତ୍ୟୟ ଯୋଗ କରାଯାଇଛି । ଆସ ମୂଳ ଶବ୍ଦଗୁଡ଼ିକୁ ଲେଖୁବା ।
_________ + ଇକ = ସାମାଜିକ
_________ + ଇକ = ଆର୍ଥନୀତିକ
_________ + ଇକ = ପ୍ରାସଙ୍ଗିକ
Answer:
ସମାଜ + ଇକ = ସାମାଜିକ
ଅର୍ଥନୀତି + ଇକ = ଆର୍ଥନୀତିକ
ପ୍ରସଙ୍ଗ + ଇକ = ପ୍ରାସଙ୍ଗିକ

Question ୯।
ତଳେ ଦିଆଯାଇଥ‌ିବା ଶବ୍ଦମାନଙ୍କ ମଧ୍ୟରେ ‘ବିଶେଷ୍ୟ’ ଓ ‘ବିଶେଷଣ’ ପଦ ମିଶିକରି ରହିଛି । ସେମାନଙ୍କୁ ଅଲଗା କରି ବାକ୍ୟରେ ବ୍ୟବହାର କରିବା ।
ଜାଗ୍ରତ, ଶାସନ, ଯନ୍ତ୍ରଣାଦାୟକ, ଗୌରବ, ଅନୁରାଗୀ, ସମାଜ, ବିଭେଦ, ବ୍ୟବଧାନ, ଉପଯୋଗ
Answer:
ଏଥ‌ିରେ ଥ‌ିବା ବିଶେଷ୍ୟ ପଦ – ଶାସନ, ଗୌରବ, ସମାଜ,ବିଭେଦ, ବ୍ୟବଧାନ, ଉପଯୋଗ, ପରିବର୍ତ୍ତନ ।
ଶାସନ – ଶିଶୁମାନଙ୍କୁ ଅଯଥା ଶାସନ କର ନାହିଁ ।
ଗୌରବ – ପରିବାର ସମାଜର ଏକ ଅଂଶ ।
ସମାଜ – ସାମଜିକ ବିଭେଦ ବିଶୃଙ୍ଖଳାର କାରଣ ।
ବିଭେଦ – ପରିବାରରେ ପୁତ୍ରକନ୍ୟାମାନଙ୍କ ମଧ୍ୟରେ ବ୍ୟବଧାନ ରହିବା ଉଚିତ ନୁହେଁ ।
ଭରଯୋଗ – ନିଜର ଶକ୍ତିକୁ ଯଥାର୍ଥ ଉପଯୋଗ କର ।
ପରିବର୍ତ୍ତନ – ସୃଷ୍ଟି ସଦା ପରିବର୍ତ୍ତନଶୀଳ ।
ଏଥିରେ ଥିବା ବିଶେଷଣ ପଦ – ଜାଗ୍ରତ, ଯନ୍ତ୍ରଶାଦାୟକ, ଅନୁରାଗା ।
ଜାଗ୍ରତ – ସୈନିକମାନେ ଆମ ଦେଶର ଜାଗ୍ରତ ପ୍ରହରୀ ।
ଯନ୍ତ୍ରଣାଦାୟକ – ଶରୀର କଷ୍ଟ ଅପେକ୍ଷା ମନର କଷ୍ଟ ଅଧ୍ଵ ଯନ୍ତ୍ରଣାଦାୟକ ।
ଅନୁରାଗା – ଶିକ୍ଷକମାନେ ଛାତ୍ରଛାତ୍ରୀଙ୍କ ଅନୁରାଗା ହେବା ଉଚିତ୍।

Question ୧୦ ।
ତଳେ ପ୍ରତ୍ୟେକ ଧାଡ଼ିରେ ଦିଆଯାଇଥ‌ିବା ଶବ୍ଦମାନଙ୍କ ମଧ୍ୟରେ ଗୋଟିଏ ଭିନ୍ନ ଜାତୀୟ ଶବ୍ଦ ରହିଛି । ସେହି ଶବ୍ଦଟିକୁ ବାଛି ଖାତାରେ ଲେଖ ।
(କ) ଶ୍ଵାସରୁଦ୍ଧ, ବାଷ୍ପରୁଦ୍ଧ, ଅବରୁଦ୍ଧ, ବାରୁଦ୍ଧ
Answer:
ଅବରୁଦ୍ଧ

(ଖ) ଦୃଷ୍ଟିପାତ, ବୃଷ୍ଟିପାତ, ଉଲ୍‌କାପାତ, ଅନୁପାତ
Answer:
ଅନୁପାତ

Question ୧୧।
ଆସ, ତଳଲିଖ୍ ଶବ୍ଦରୁ ନାମଧାତୁ କ୍ରିୟା ଗଠନ କରିବା ।
ଯେପରି ମନ – ମନେଇବା ହୁଏ ସେହିପରି କ’ଣ ହେବ ?
ଦୂର _________
ଫେଶ _________
ଫଳ _________
ଛୋଟ _________
ଗାତଳ _________
Answer:
ହରେଇବା
ଫେଣେଇବା
ଫଳାଇବା / ଫଳେଇବା
ଛେ।ଟେଇବା / ଛୋଟାଇବା
ଶାଢଳେଇବା / ଶାଢଳାଇବା

Question ୧୨ ।
ଯାହାର ରୂପାନ୍ତର ଘଟି ନ ଥାଏ ତାହାକୁ ଭିନ୍ନ ରୂପରେ ପ୍ରକାଶ କରିବା କାମକୁ କୁହାଯାଏ ‘ରୂପାନ୍ତରୀକରଣ’ । ସେହିପରି
ହୃଦଭାବରେ ନଥ‌ିବା ବସ୍ତୁକୁ ଦୃଢ଼ କରିବା ଦୃଢ଼ୀକରଣ
(କ) ବନ ନ ଥ‌ିବା ସ୍ଥାନରେ ବନ ସୃଷ୍ଟି କରିବା ।
(ଖ) ବାଷ୍ପ ହୋଇ ନଥ‌ିବା ପଦାର୍ଥକୁ ବାଷ୍ପରେ ପରିଣତ କରିବା ।
(ଗ) ଦୃଷ ଭାବରେ ନଥ‌ି ବସ୍ତୁକୁ ଦୃଢ଼ କରିବା ।
(ଘ) ଭାଗଭାଗ ହୋଇ ନ ଥ‌ିବା ପଦାର୍ଥକୁ ବିଭିନ୍ନ ବିଭାଗରେ ପରିଣତ କରିବା ।
Answer:
(କ) ବନୀକରଣ
(ଖ) ବାଷ୍ଟାକରଶ
(ଘ) ବିଭାଗାକରଣ

Question ୧୩।
ଯାହାକୁ ବିଚ୍ଛେଦ କରି ହେବ ନାହିଁ ତାହାକୁ ଗୋଟିଏ ଶବ୍ଦରେ କୁହାଯାଏ । ‘ଅବିଚ୍ଛେଦ୍ୟ’ । ସେହିପରି ନିମ୍ନରେ ଦିଆଯାଇଥବା ପ୍ରତ୍ୟେକ ଉକ୍ତିକୁ ଗୋଟିଏ ଶବ୍ଦରେ ପ୍ରକାଶ କରି ଲେଖୁବା ।
(କ) ଯାହାକୁ ଭାଗଭାଗ କରିହେବ ନାହିଁ ।
(ଖ) ଯାହାକୁ କାଟି ହେବ ନାହିଁ ।
(ଗ) ଯାହାକୁ ଭେଦ କରି ହେବ ନାହିଁ ।
(ଘ) ଯାହାକୁ ଛେଦନ କରିହେବ ନାହିଁ ।
Answer:
(କ) ଅବିଭାଜ୍ୟ
(ଖ) ଅକାଟ୍ୟ
(ଗ) ଅଭେଦ୍ୟ
(ଘ) ଅଛେଦ୍ୟ

Question ୧୪ ।
ଭୁଲଥୁବା ଶବ୍ଦକୁ ଠିକ୍ କରି ଲେଖୁ ।

ଭୁଲ୍ ଶବ୍ଦ	ଠିକ୍ ଶବ୍ଦ
ଗୁରୁକୂଳ	ଗୁରୁକୁଳ
ମନୀଷି	ମନୀଷା
ନୈପୂଣ୍ୟ	ନୈପୁଣ୍ୟ
ପ୍ରାଧୀକାର	ପ୍ରାଧିକାର
ପରିସିମା	ପରିସାମା
କର୍ପୁର	କର୍ପୁର
କାଳାତିତ	କାକାତାତ
ପ୍ରତିଦ୍ବନ୍ଦିତା	ପ୍ରତିଦ୍ୱନ୍ଦ୍ୱାତା

ତୁମ ପାଇଁ କାମ:

(କ) ଆସ ପ୍ରବନ୍ଧର ଗୋଟିଏ ଲେଖାଏ ଅନୁଚ୍ଛେଦ ଜଣ ଜଣ କରି ଶ୍ରେଣୀରେ ଉଚ୍ଚ ପଠନ କରିବା ।
(ଖ) ଶିକ୍ଷକଙ୍କ ସହିତ ଆଲୋଚନା କରି ଆସ ପୁରାଣରେ ବର୍ଣ୍ଣିତ ଦୁଇଜଣ ଗୁରୁଭକ୍ତ ଶିଷ୍ୟଙ୍କ କାହାଣୀ ସଂଗ୍ରହ କରିବା ଓ ଖାତାରେ ଲେଖୁ ।
(ଗ) ନିଜ ଶିକ୍ଷକଙ୍କ ସହିତ ଥ‌ି ତୁମର ସମ୍ପର୍କକୁ ଆଧାର କରି ଗୋଟିଏ ଅନୁଚ୍ଛେଦ ଲେଖିବା ।

ପରାକ୍ଷା ଉପଯେ।ଗା ଅତିରିକ୍ତ ପ୍ରଶ୍ନୋତ୍ତର

ସଂକ୍ଷିପ୍ତ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନେ।ତ୍ତର

Question ୧ ।
କେଉଁ ନୀତି ଗୁରୁକୁଳର ଶିକ୍ଷାକୁ ପରିଚାଳିତ କରୁଥୁଲା ?
Answer:
ଶିକ୍ଷାଳୟକୁ ସତ୍ୟ, ଶିବ, ସୁନ୍ଦର କରିବାରେ ଶିକ୍ଷକଙ୍କର ଯେଉଁ ବଳିଷ୍ଠ ଦାୟିତ୍ଵ ରହିଛି ତାହାକୁ କର୍ମକ୍ଷେତ୍ରରେ ପ୍ରୟୋଗ କରିବା ଦରକାର । ଏହି ନୀତି ଆଧାରରେ ଗୁରୁକୁଳର ଶିକ୍ଷା ପରିଚାଳିତ ହେଉଥିଲା ।

Question ୨ ।
‘ଗୁରୁ-ଶିଷ୍ୟ ସମ୍ପର୍କ’ ପ୍ରବନ୍ଧର ପ୍ରାବନ୍ଧିକ କିଏ ? ତାଙ୍କ ଆତ୍ମଜୀବନୀର ନାମ କ’ଣ ?
Answer:
ପ୍ରଫେସର ଶତ୍ରୁଘ୍ନ ନାଥ ହେଉଛନ୍ତି ‘ଗୁରୁ-ଶିଷ୍ୟ ସଂପର୍କ’ ପ୍ରବନ୍ଧର ପ୍ରାବନ୍ଧିକ । ତାଙ୍କ ଆତ୍ମଜୀବନୀର ନାମ

Question ୩ ।
ବିଦ୍ୟା ଆଉ ମୁକ୍ତିକାମୀ ବୋଲି ବିବେଚିତ ହେଉନାହିଁ କାହିଁକି ?
Answer:
ଅଧୁନା ‘ଗୁରୁ’ ଓ ‘ଶିଷ୍ୟ’ ଶବ୍ଦ ଦୁଇଟି ଆଭିଧାନିକ ଶବ୍ଦରେ ରୂପାନ୍ତରିତ ହୋଇଛି । ଏବେ ଗୁରୁ ଓ ଶିଷ୍ୟ ଉଭୟ ଶଠତା, ସଂକୀର୍ଣ୍ଣତା, ସ୍ୱାର୍ଥାନ୍ଧତା, ହିଂସା ଓ ହୁଙ୍କାର ଆଦି ଆଚରଣର ଭୂମିକା ଗ୍ରହଣ କରୁଛନ୍ତି । ଗୁରୁ ଆଉ ଶିଷ୍ୟର ପ୍ରାଣ ପରିଚାୟକ ହେଉନାହିଁ । ତେଣୁ ବିଦ୍ୟା ଆଉ ମୁକ୍ତିକାମୀ ଭାବେ ବିବେଚିତ ହେଉନାହିଁ ।

Question ୪।
ଗୁରୁ-ଶିଷ୍ୟ ସଂପର୍କର ମୂଳମନ୍ତ୍ର କିପରି ପ୍ରକାଶିତ ହେବ ?
Answer:
ଶିଷ୍ୟ ଶ୍ରଦ୍ଧାବାନ୍ ହେବା ସହ ସ୍ବାଧ୍ୟାୟୀ ହେବା ଆବଶ୍ୟକ । ସେମାନେ ବିଦ୍ୟାନୁରାଗୀ ହେବା ଆବଶ୍ୟକ । ଗୁରୁ ଶିଷ୍ୟପରାୟଣ ଓ ଶିଷ୍ୟ ଗୁରୁପରାୟଣ ହେବା ଆବଶ୍ୟକ । ଏପରି ହେଲେ ଗୁରୁ-ଶିଷ୍ୟ ସଂପର୍କର ମୂଳମନ୍ତ୍ର କାର୍ଯ୍ୟତଃ ପ୍ରକାଶିତ ହେବ ।

Question ୫।
ଶିଷ୍ୟତ୍ ଇଚ୍ଛେତ୍ ପରାଜୟମ୍ – ଏହା ଅର୍ଥ ବୁଝାଇଲେଖ ।
Answer:
ଜଣେ ଆଦର୍ଶ ଗୁରୁ ସବୁବେଳେ ନିଜ ଶିଷ୍ୟକୁ ଶୀର୍ଷତମ ସୋପାନରେ ପହଞ୍ଚାଇବାର ଅଭିଳାଷ ପୋଷଣ କରିଥାଏ । ଏକମାତ୍ର ଗୁରୁ ହିଁ ଶିଷ୍ୟଠାରୁ ପରାଜିତ ହେବାର ମନୋବାଞ୍ଛା ରଖୁଥାଏ । ଅନ୍ୟ କୌଣସି ବ୍ୟକ୍ତି କାହା ନିକଟରେ ପରାଜୟ ସ୍ୱୀକାର କରିବାକୁ ଆଗ୍ରହୀ ନଥାନ୍ତି । କେବଳ ଜଣେ ଆଦର୍ଶ ଗୁରୁ ହିଁ ଏଭଳି ମନୋବାଞ୍ଛା ପୋଷଣ କରିପାରେ ।

Question ୬ ।
‘ଅତୀତକୁ ଉଦ୍‌ବୋଧଇ ବୃଥା ଭାଳି ଭାଳି’ – ଏହା କେଉଁ କବିଙ୍କ କେଉଁ କବିତାର ଏକ ଅଂଶ ? ଏହାର ତାତ୍ପର୍ଯ୍ୟ କ’ଣ ?
Answer:
ଉପରୋକ୍ତ ଧାଡ଼ିଟି ମଧୁସୂଦନ ରାଓଙ୍କ ରଚିତ ବିଖ୍ୟାତ କବିତା ‘ଜୀବନ ଚିନ୍ତା’ କବିତାର ଏକ ଧାଡ଼ି । ଏହାର ଅର୍ଥ ହେଉଛି ଅତୀତ କାଳର ସୁଖସଂପଦ ବିଷୟରେ ବୃଥା ଚିନ୍ତା କରିବା । ଏହା ଏକ ଅମୂଳକ ଚିନ୍ତାଧାରା । ବର୍ତ୍ତମାନ କିପରି ସୁଖସଂପଦ ପ୍ରାପ୍ତି ହୋଇପାରିବ ସେଥ‌ିପାଇଁ ଉଦ୍ୟମ ନକରି ଅତୀତକୁ ଝୁରିହେବା ମୁର୍ଖମିର ପରିଚାୟକ ।

ଲେଖକ ପରିଚୟ :

ଜଣେ ସ୍ୱନାମଧନ୍ୟ ଶିକ୍ଷାବିତ୍ ଓ ପ୍ରାବନ୍ଧିକ ଭାବେ ପ୍ରଫେସର ଶତ୍ରୁଘ୍ନ ନାଥ ଓଡ଼ିଆ ଭାଷା ସାହିତ୍ୟ କ୍ଷେତ୍ରରେ ଉଚ୍ଚ ବ୍ୟକ୍ତିତ୍ୱର ଅଧିକାରୀ । ଭଦ୍ରକ ଜିଲ୍ଲାର ଉତ୍ତରବାହିନୀ ଗ୍ରାମରେ ୧୯୧୫ ମସିହାରେ ସେ ଜନ୍ମଗ୍ରହଣ କରିଥିଲେ । ଜଣେ ଉଚ୍ଚକୋଟୀର ଶିକ୍ଷା-ପ୍ରଶାସକ ଓ ଚିନ୍ତାମୂଳକ ପ୍ରବନ୍ଧ ଲେଖକଭାବେ ପ୍ରଫେସର ନାଥ ବହୁ ପ୍ରସିଦ୍ଧି ଅର୍ଜନ କରିଛନ୍ତି । ମୌଳିକ ଶିକ୍ଷା ସଂଗଠକ, ଶିକ୍ଷା ଅଧ୍ୟାପକ ତଥା ଶିକ୍ଷକ-ପ୍ରଶିକ୍ଷଣ ମହାବିଦ୍ୟାଳୟ ଏବଂ ରାଜ୍ୟ ଶିକ୍ଷା ପ୍ରତିଷ୍ଠାନର ଅଧ୍ୟକ୍ଷ ଭାବରେ କାର୍ଯ୍ୟ କରି ସେ ସରକାରୀ କାର୍ଯ୍ୟରୁ ଅବସର ଗ୍ରହଣ କରିଥିଲେ । ତାଙ୍କର ଲିଖ ପୁସ୍ତକଗୁଡ଼ିକ ମଧ୍ୟରେ ‘ଜଗତରେ ଭାରତ’, ‘ପିଲାଙ୍କ ବିଲାତ କଥା’, ‘ଆମ ଭାଷା ବିଭବ’, ‘ବିଶ୍ବ ଓ ବ୍ୟକ୍ତି’, ‘ଶିକ୍ଷାର ଧାରା’ ଓ ‘ଜୀବନ ‘ଶିକ୍ଷାର ଧାରା’ ଓ ‘ଜୀବନ ଶିକ୍ଷା’ ପ୍ରଭୃତି ପ୍ରଧାନ । ‘ଚରାଚୟ ହିତାୟ’ ପୁସ୍ତକଟି ପ୍ରଫେସର ନାଥଙ୍କ ଆତ୍ମଜୀବନୀ ।

ପ୍ରବନ୍ଧର ପୃଷ୍ଠଭୂମି :

ସଂପ୍ରତି ସମାଜରେ ଗୁରୁ ଓ ଶିଷ୍ୟର ସମ୍ପର୍କ ମଧ୍ୟରେ ବ୍ୟବଧାନ ବଢ଼ିବାରେ ଲାଗିଛି । ପୂର୍ବର ସେହି ମମତ୍ୱବୋଧ କ୍ରମଶଃ ଲୋପ ହୋଇ ତାହା ବ୍ୟାବସାୟିକ ହୋଇଉଠୁଛି । ପ୍ରାବନ୍ଧିକ ଏହା ଉପରେ ଗୁରୁତ୍ଵ ଦେଇ ପ୍ରତିକାର ସ୍ବରୂପ କିଛି ମୂଲ୍ୟବାନ୍ ପରାମର୍ଶ ପ୍ରଦାନ କରିଛନ୍ତି । ଶିକ୍ଷାବିତ୍ ଓ ବୁଦ୍ଧିଜୀବୀମାନେ ମଧ୍ୟ ଗୁରୁ ଓ ଶିଷ୍ୟ ମଧ୍ୟରେ ଉତ୍ତମ ସମ୍ପର୍କର ଆବଶ୍ୟକତା ଓ ମହତ୍ତ୍ଵ ଉପରେ ଗୁରୁତ୍ବ ଆରୋପ କରୁଛନ୍ତି । ଯଦିଓ ପ୍ରାଚୀନ କାଳର ଗୁରୁ-ଶିଷ୍ୟ ପରମ୍ପରା ସାମ୍ପ୍ରତିକ ଯୁଗରେ ସମ୍ଭବ ନୁହେଁ; ତଥାପି ଆଜିର ବସ୍ତୁବାଦୀ ସମାଜରେ ଏ ଦିଗରେ କିଛି ଆଦୃଶିଆ ପଦକ୍ଷେପ ନିଆ ନଗଲେ ଶିକ୍ଷା ବ୍ୟବସ୍ଥା ନିମ୍ନମୁଖୀ ହୋଇପଡ଼ିବ । ଛାତ୍ରର ଅନ୍ତର୍ନିହିତ ପ୍ରତିଭା ବିକଶିତ କରାଇବାରେ ଶିକ୍ଷକ ଓ ଛାତ୍ର ମଧ୍ୟରେ ସମ୍ପର୍କରେ ଉନ୍ନତି ଅବଶ୍ୟମ୍ଭାବୀ ହୋଇପଡ଼ିଛି । ଏହି ଗୁରୁତ୍ବପୂର୍ଣ୍ଣ ବିଷୟ ଉପରେ ପ୍ରବନ୍ଧଟି ଆଧାରିତ । ଏହା ପ୍ରାବନ୍ଧିକଙ୍କ ‘ଜୀବନ ଶିକ୍ଷା’ ଶୀର୍ଷକ ପୁସ୍ତକରୁ ଗୃହୀତ ।

ପ୍ରବନ୍ଧର ସାରକଥା :
ଗୁରୁଙ୍କୁ ଈଶ୍ବର ଜ୍ଞାନ କରିବା ଗୁରୁକୁଳ ପରମ୍ପରାର ଆଦର୍ଶ ଥିଲେ ମଧ୍ୟ ଆଜିର ଯୁଗରେ ଏହା ଅବାସ୍ତବ, ଅବାନ୍ତର ଓ ଅପ୍ରାସଙ୍ଗିକ ବିବେଚିତ ହେଉଅଛି । ବୟୋବୃଦ୍ଧମାନେ ପୂର୍ବକାଳର ଶିକ୍ଷା ବ୍ୟବସ୍ଥା ଓ ଗୁରୁ-ଶିଷ୍ୟ ସମ୍ପର୍କ ସ୍ମରଣ କରି ହତୋତ୍ସାହିତ ହୋଇପଡୁଛନ୍ତି । ସମ୍ପ୍ରତି ଶିକ୍ଷକମାନେ ଗୁରୁ ରୂପେ ପରିଚିତ ହେବା ପରି କାର୍ଯ୍ୟରେ ଆଗ୍ରହୀ ନୁହଁନ୍ତି କିମ୍ବା ଆଜିକାଲି ଶାସନ ବିରୋଧରେ ବିଦ୍ରୋହୀ ଓ ବିପ୍ଳବୀ ହୋଇ ଉଠୁଛନ୍ତି । ସେମାନଙ୍କ ପାଇଁ ଶାସନ ସମ୍ଭବତଃ ଅପ୍ରାସଙ୍ଗିକ ଓ ଆଜିକାଲି ଶାସନ ବିରୋଧରେ ବିଦ୍ରୋହୀ ଓ ବିପ୍ଳବୀ ହୋଇ ଉଠୁଛନ୍ତି । ସେମାନଙ୍କ ପାଇଁ ଶାସନ ସମ୍ଭବତଃ ଅପ୍ରାସଙ୍ଗିକ ଓ ପ୍ରଗତିର ପରିପନ୍ଥୀ ଭାବେ ଗୃହୀତ ହୋଇଛି ।

ଗୁରୁ ଓ ଶିଷ୍ୟ ଶବ୍ଦ ଦ୍ଵୟ ଏବେ କେବଳ ଅଭିଧାନର ଦୁଇଟି ଶବ୍ଦରେ ରୂପାନ୍ତରିତ ହୋଇଛି । ସମ୍ପ୍ରତି ଗୁରୁ ଓ ଶିଷ୍ୟ ଉଭୟ ଶଠତା, ସଂକୀର୍ଣ୍ଣତା, ସ୍ବାର୍ଥାନ୍ଧତା, ହିଂସା ଓ ହୁଙ୍କାର ଆଦି ଆଚରଣର ଭୂମିକା ଗ୍ରହଣ କରୁଛନ୍ତି । କାଳର କରାଳ ଗତିରେ ମୂଲ୍ୟବୋଧର ଅବକ୍ଷୟ ଘଟିଛି । ଗୁରୁ, ଶିଷ୍ୟର ପ୍ରାଣ ପରିଚାୟକ ହେଉନାହିଁ କି ବିଦ୍ୟା ମଧ୍ୟ ଆଉ ମୁକ୍ତିକାମୀ ବୋଲି ବିବେଚିତ ହେଉନାହିଁ । ଗୁରୁ-ଶିଷ୍ୟ ସମ୍ପର୍କର ଅଧୋଗତି ହେବାରେ ଲାଗିଛି ।

କୌଣସି ଦେଶର ଗୌରବ, ସେ ଦେଶର ଲୋକଚରିତ୍ର ଉପରେ ନିର୍ଭର କରେ । ଜାତିର ଜୟଗାଥାର ମୂଳପିଣ୍ଡ ହେଉଛି ଜୀବନ । ସେହି ଜୀବନର ନିର୍ମାଣ ବିଦ୍ୟାଳୟରେ ହିଁ ହୋଇଥାଏ । ଜୀବନ ସୌଧର ମୂଳଭିଭି ଶିକ୍ଷାଳୟରେ ପଡ଼ିଥାଏ । ସେଠାରେ ବିଧ୍ଵବଦ୍ଧ ଭାବେ ଚରିତ୍ର ଗଠନ ହୁଏ । ଶିକ୍ଷକ ହିଁ ଶିକ୍ଷାୟତନକୁ ସତ୍ୟ-ଶିବ-ସୁନ୍ଦରରେ ପରିଣତ କରନ୍ତି । ଏହି ନୀତି ଗୁରୁକୁଳର ଶିକ୍ଷାକୁ ପରଚାଳିତ କରୁଥିଲା । ସମ୍ପ୍ରତି ସମାଜ ଯେପରି ଜଟିଳତା ଦିଗକୁ ଅଗ୍ରସର ହେବାରେ ଲାଗିଛି, ଗୁରୁ-ଶିଷ୍ୟ ସମ୍ପର୍କର ପୁନଃସ୍ଥାପନ ଗୁରୁତ୍ଵପୂର୍ଣ୍ଣ ହୋଇଉଠିଛି ।

ପିତାମାତା ଜନ୍ମଦାତା । ଜନ୍ମଦାନ ପରେ ତାଙ୍କ କର୍ତ୍ତବ୍ୟର ସମାପ୍ତି । ମାତ୍ର ପରବର୍ତୀ ଦାୟିତ୍ଵ ଶିକ୍ଷକଙ୍କର । ଶିକ୍ଷକଙ୍କ ଶିକ୍ଷା ଚିରନ୍ତନ । ଜୀବନ-ବ୍ୟାପୀ କୋଟି କୋଟି ପ୍ରାଣ ଶିକ୍ଷକଙ୍କଦ୍ବାରା ଗଠିତ ଓ ପ୍ରଭାବିତ ହୁଏ । ଏହି କାଳଜୟୀ ପ୍ରଭାବ ବିଷୟରେ ଶିକ୍ଷାୟତନର ସଚେତନତା ସର୍ବାଦୌ ଆବଶ୍ୟକ । ପ୍ରାଚୀନ କାଳରୁ ଶିକ୍ଷକଙ୍କ ବିରଳ ଆତ୍ମତ୍ୟାଗର ଦୃଷ୍ଟାନ୍ତ ଶିକ୍ଷା ଓ ସେବା କ୍ଷେତ୍ରକୁ ବହୁଳ ଭାବେ ଋଦ୍ଧିମନ୍ତ କରିଛି । ପଠନ-ପାଠନର ସତ୍ୟନିଷ୍ଠ ସାଧନା ଶିକ୍ଷାର ଇତିହାସକୁ ମହିମାନ୍ବିତ କରିଛି । ଆଜିର ଦୁନିଆରେ ପଠନ ବିରହିତ ପାଠନ କେବଳ ଶୁଷ୍କ ବକ୍ତୃତା ବା ବଖାଣରେ ପରିଣତ ହୋଇଛି ।

ପ୍ରଭାବକାରୀ ପ୍ରାଣର ପ୍ରାଚୁର୍ଯ୍ୟ ଗୁରୁ ଜୀବନକୁ ଗରୀୟାନ କରେ । ଆଦର୍ଶର ମହିମାରେ ତାହା ଜୀବନ୍ତ ହୁଏ । ସେଥ‌ିପାଇଁ ଗୁରୁଙ୍କ ସ୍ଥାନ ବହୁ ଉଚ୍ଚରେ, ଶିକ୍ଷାପଦ୍ଧତିର ବହୁ ଊର୍ଦ୍ଧ୍ବରେ । ତେଣୁ ଯୁଗେ ଯୁଗେ ସେ କେବଳ ଶିକ୍ଷାର୍ଥୀଙ୍କର ନୁହଁନ୍ତି, ସମଗ୍ର ସମାଜର ନମସ୍ୟ । ଗୁରୁଙ୍କର ମାତ୍ର ପଦୁଟିଏ କଥା ଶିଷ୍ୟ ପ୍ରାଣରେ ବହୁଭାବେ ଉଦ୍ଭାସିତ ହୁଏ । ଗୁରୁଙ୍କର ସତ୍ୟ ପ୍ରତି ସମର୍ପଣ ଓ ନିଷ୍ଠାପର ଜ୍ଞାନଦାନରେ ଶିଷ୍ୟର ଜ୍ଞାନପିପାସା ବୃଦ୍ଧି ପାଏ । ଶିକ୍ଷା ପ୍ରକ୍ରିୟାର କେନ୍ଦ୍ରରେ ଅବସ୍ଥିତ ଶିଷ୍ୟର ଶିକ୍ଷା ପ୍ରତି ଶ୍ରଦ୍ଧା ରହିବା ଆବଶ୍ୟକ । ତେଣୁ କୁହାଯାଇଛି

‘ଶ୍ରଦ୍ଧାବାନ ଲଭତେ ଜ୍ଞାନମ୍’’

ଶିଷ୍ୟ ଶ୍ରଦ୍ଧାବାନ ହେବା ସହ ସ୍ୱାଧ୍ୟାୟୀ ହେବେ ଓ ବିଦ୍ୟାନୁରାଗୀ ହେବେ । ଏହାଦ୍ଵାରା ଗୁରୁ-ଶିଷ୍ୟ ସମ୍ପର୍କର ମୂଳମନ୍ତ୍ର କାର୍ଯ୍ୟତଃ ପ୍ରକାଶ ପାଇବ । ଗୁରୁ ‘ଶିଷ୍ୟପରାୟଣ’ ହେବେ ଓ ଶିଷ୍ୟ ମଧ୍ୟ ‘ଗୁରୁପରାୟଣ’ ହେବେ । ଉଭୟ ଗୁରୁ ଓ ଶିଷ୍ୟ ‘ବିଦ୍ୟାପରାୟଣ’ ହେବେ ଓ ସେମାନଙ୍କ ବିଦ୍ୟା ‘ସେବାପରାୟଣ’ ହେବ । କାରଣ ଅଧ୍ୟୟନ ବିନା ଅଧ୍ୟାପନା କଦାପି ସଫଳ ହୋଇପାରିବ ନାହିଁ । ଏହି ଶିକ୍ଷାରେ ଗୁରୁ, ଶିଷ୍ୟ, ଅଭିଭାବକ ଓ ସମାଜ ଜଡ଼ିତ ହେବା ବାଞ୍ଛନୀୟ ।

ସାମ୍ପ୍ରତିକ ଯୁଗରେ ଗୁରୁ-ଶିଷ୍ୟ ସମ୍ପର୍କର ନିବିଡ଼ତା କ୍ରମକ୍ଷୟିଷ୍ଣୁ ହୋଇ କଳୁଷିତ ହେବାରେ ଲାଗିଛି । ସନ୍ଦେହ, ଶଙ୍କା, କୁତ୍ସା ଓ କଳଙ୍କ-କାଳିମାରେ ଶିକ୍ଷାର ସ୍ବରୂପ କୁରୂପ ଧାରଣ କରୁଛି । ଶିକ୍ଷାର ପ୍ରସାର ଓ ଶିକ୍ଷାୟତନର ସଂଖ୍ୟା ବୃଦ୍ଧି ସଙ୍ଗେ ସଙ୍ଗେ ଗୁରୁ ଓ ଶିଷ୍ୟ ମଧ୍ୟରେ ଦୂରତ୍ବ ବୃଦ୍ଧି ପାଉଛି । ଫଳରେ ବ୍ୟକ୍ତିର ପ୍ରତିଭା ଓ ଜାତୀୟ ନୈପୁଣ୍ୟର ବିକାଶ ହୋଇପାରୁ ନାହିଁ । ଶିକ୍ଷାଳୟ ସମାଜଠାରୁ ଦୂରେଇଯାଉଛି । ବିଦ୍ୟା ପ୍ରତି ଶ୍ରଦ୍ଧା ପରିବର୍ତ୍ତେ ଜୀବନ, ସମୟ, ଶକ୍ତି ଓ ଅର୍ଥ ଶ୍ରାଦ୍ଧ ହିଁ ସାର ହେଉଛି । ଆଧ୍ୟାତ୍ମିକ ଶକ୍ତିର ସଞ୍ଚାର ଘଟିବା ପରିବର୍ତ୍ତେ ଆସୁରିକ ଶକ୍ତିର ତାଣ୍ଡବଲୀଳା ସଂଗଠିତ ହେଉଛି । ଛାତ୍ର, ଶିକ୍ଷକ, ଅଭିଭାବକ ଓ ସମାଜ ମଧ୍ୟରେ ସହଯୋଗ ସୂତ୍ର କ୍ରମେ ବିଲୁପ୍ତ ହେଉଛି । ବରଂ ସଂକୀର୍ଣ୍ଣ ସ୍ବାର୍ଥ ସାଧନ ପାଇଁ ପ୍ରତିଦ୍ବନ୍ଦିତା ଚାଲିଛି । ଶିକ୍ଷା ଆଉ ଗଣପ୍ରକ୍ରିୟା ନ ହୋଇ ମୁଷ୍ଟିମେୟ ଲୋକଙ୍କ ବ୍ୟବସାୟରେ ପରିଣତ ହେଉଛି ।

ସମ୍ପ୍ରତି ଶିକ୍ଷା ପୁସ୍ତକ-କୈନ୍ଦ୍ରିକ ହୋଇଉଠିଛି । ମୁଖସ୍ଥକରଣ ଖୁବ୍ ଗୌରବ ଅର୍ଜନ କରିଛି । ଏହା ଗୁରୁ-ଶିଷ୍ୟ ସମ୍ପର୍କ ସ୍ଥାପନର ପରିପନ୍ଥୀ ଅଟେ । କାମର ଜଗତ ଓ ପାଠର ଜଗତ ମଧ୍ୟରେ ବ୍ୟବଧାନ ବଢ଼ି ବଢ଼ି ଚାଲିଛି । ଶିକ୍ଷାୟତନର ସୌଧ ସମାଜଠାରୁ କ୍ରମେ ବିଚ୍ଛିନ୍ନ ହେବାରେ ଲାଗିଛି । ଶିକ୍ଷା ପ୍ରଣାଳୀ, ପରୀକ୍ଷା ଓ ପ୍ରଶାସନ ଆଦି ସକଳ କ୍ଷେତ୍ର ଗୁରୁ ଓ ଶିଷ୍ୟ

ମଧ୍ୟରେ ସମ୍ପର୍କ ପ୍ରତିଷ୍ଠାରେ ସହାୟକ ହେଉନାହିଁ । ସବୁ କ୍ଷେତ୍ରରେ ରାଜନୀତିର କଳୁଷିତ ଅନୁପ୍ରବେଶ ଏ କ୍ଷେତ୍ରରେ ପ୍ରଧାନ ଅନ୍ତରାୟ ସାଜିଛି । ଶିକ୍ଷା ଯେ ଏକ ସହଯୋଗୀ ବିକାଶମୂଳକ କାର୍ଯ୍ୟକ୍ରମ – ଏହା ସାବ୍ୟସ୍ତ ହୋଇପାରୁନାହିଁ । କେବଳ କାଗଜପତ୍ରରେ ବିକାଶ ରୂପ ନେଉଛି; ମାତ୍ର ପ୍ରତିଭା ପରିପୂର୍ଣ୍ଣ ପରିପ୍ରକାଶ କ୍ଵଚିତ୍ ଦେଖାଯାଉଚ୍ଛା

ଗୁରୁ-ଶିଷ୍ୟ ସମ୍ପର୍କରେ ଉନ୍ନତି ଆଜିର ଚରମ ଆବଶ୍ୟକତା । ଏ ଦୃଷ୍ଟିରୁ ପ୍ରତ୍ୟେକ ଅନୁଷ୍ଠାନକୁ ସାମାଜିକ ଦାୟିତ୍ୱ ବହନ କରିବାକୁ ପଡ଼ିବ । ଏକ ସାମାଜିକ ଲକ୍ଷ୍ୟ ନେଇ ଶିକ୍ଷା ବ୍ୟବସ୍ଥାର ପରିବର୍ତ୍ତନ ଆବଶ୍ୟକ, ଯେପରି ଶିକ୍ଷା ପ୍ରତ୍ୟେକ ସ୍ତରରେ ସମାଜସେବାର ଏକ ଅଙ୍ଗଭାବେ ପରିଗଣିତ ହେବ । ଶିକ୍ଷାନୁଷ୍ଠାନରେ ଶ୍ରେଣୀ ଅନ୍ତର୍ଗତ ଓ ବହିର୍ଭୂତ କାର୍ଯ୍ୟଗୁଡ଼ିକ ସାମାଜିକ ସମସ୍ୟା ଓ ପ୍ରସଙ୍ଗ ସହ ସମ୍ପର୍କୀକୃତ ହେବ । ଫଳତଃ ସମସ୍ତ କାର୍ଯ୍ୟ ଗତିଶୀଳ ହେବ । ଶିକ୍ଷାୟତନର ସମସ୍ତ ସମୟ ଯଦି କେତେ ଖଣ୍ଡ ପାଠ୍ୟପୁସ୍ତକକୁ ବାରମ୍ବାର ପୁନରାବୃତ୍ତି କରିବାରେ ଆବଦ୍ଧ ହେବ ତେବେ ସମସାମୟିକ ସମାଜ ପ୍ରତି ଏହା ଅର୍ଥହୀନ ହୋଇପଡ଼ିବ ।

ପରିବର୍ତ୍ତନଶୀଳ ସମାଜରେ ବିକାଶମୂଳକ କାର୍ଯ୍ୟକ୍ରମଦ୍ୱାରା ସାମାଜିକ ଜୀବନ ନିରନ୍ତର ପ୍ରଭାବିତ ହେବାରେ ଲାଗିଛି । ଜ୍ଞାନର ପରିସୀମା ଦ୍ରୁତଗତିରେ ବିସ୍ତାରିତ ହେଉଛି । ସଂସ୍କୃତିର ସ୍ଵରୂପ ସମୃଦ୍ଧ ହେବାରେ ଲାଗିଛି । ତେଣୁ ଗୁରୁ- ଶିଷ୍ୟ ଓ ଅଭିଭାବକଙ୍କ ସମ୍ମିଳିତ ଉଦ୍ୟମରେ ବିଭିନ୍ନ ପ୍ରକଳ୍ପ ପ୍ରସ୍ତୁତ କରି ତାହା ଯେପରି ସାମାଜିକ ପ୍ରଗତିରେ ସହାୟକ ହେବ ଏବଂ ଛାତ୍ରର ଅନ୍ତର୍ନିହିତ ଗୁଣାବଳୀ ତଥା ପ୍ରତିଭାର ପୂର୍ଣ୍ଣ ବିକାଶ ହେବା ସହ ଶିକ୍ଷାର ଲକ୍ଷ୍ୟ ସାଧୂତ ହେବ ସେ ଦିଗରେ ଦୃଷ୍ଟି ଦିଆଯିବା ଆବଶ୍ୟକ । ସମ୍ପ୍ରତି ବିଜ୍ଞାନ ଓ କାରିଗରୀ ବିଦ୍ୟାର ଦ୍ରୁତ ବିକାଶର ପ୍ରଭାବରେ ରେଡ଼ିଓ, ଟେଲିଭିଜନ ଓ ଚଳଚ୍ଚିତ୍ର ଆମୋଦ ଓ ଆନନ୍ଦ ପ୍ରଦାନରେ ସହାୟକ ହେବା ସହ ଶିକ୍ଷାର ଏକ ଅଭିନବ ଉତ୍ସଭାବେ କାର୍ଯ୍ୟ କରୁଛି । ପୂର୍ବଭଳି ଗୁରୁ ଏକ ମାତ୍ର ଜ୍ଞାନଦାତା ହୋଇ ରହିନାହାନ୍ତି କିମ୍ବା ଶ୍ରେଣୀଗୃହ ଜ୍ଞାନାର୍ଜନର ଏକମାତ୍ର ପରିସର ହୋଇ ରହିନାହିଁ ।

ତେଣୁ ଏପରିସ୍ଥଳେ ଗୁରୁ-ଶିଷ୍ୟ ମଧ୍ୟରେ ସମ୍ପର୍କ ଶିକ୍ଷାଲାଭରେ ପ୍ରାସ୍କାର-ଭିଭିକ ନହୋଇ ସହାୟକ ଓ ସହଯୋଗୀ ହେବା ବାଞ୍ଛନୀୟ । ଶିକ୍ଷାଳୟ କେବଳ ଏକ ପାରମ୍ପରିକ ଅନୁଷ୍ଠାନ ନହୋଇ ଏକ ସାମାଜିକ ଗବେଷଣାଗାର ହୋଇଉଠିବା ଆବଶ୍ୟକ । ଫଳତଃ ସମାଜର ସୁରକ୍ଷା ଓ ନୂତନ ସମାଜର ସୃଷ୍ଟି କରିବା ଦିଗରେ ଏହା କାର୍ଯ୍ୟ କରିଚାଲିବ । ପାଠ୍ୟପୁସ୍ତକ, ପାଠ୍ୟ ତାଲିକା ଓ ପରୀକ୍ଷାର ଦାସ ନ ହୋଇ ଗୁରୁ ଓ ଶିଷ୍ୟ ଉଭୟ କିପରି ଉନ୍ମୁକ୍ତ ପରିବେଶରେ ସାମାଜିକ ସମସ୍ୟା ସମାଧାନରେ ସହାୟକ ହୋଇପାରିବେ ସେ ଦିଗରେ ଦୃଷ୍ଟିଦେବା ଆବଶ୍ୟକ, ଯଦ୍ବାରା ଉଭୟ ଗୁରୁ ଓ ଶିଷ୍ୟ ଶିକ୍ଷାର ପୁନର୍ଗଠନରେ ସହାୟକ ହୋଇପାରିବୋ

ସୂଚନା ଓ କଠିନ ଶବ୍ଦାର୍ଥ :

• ଗୁରୁକୁଳ – ପ୍ରାଚାନ ସମୟର ଶିକ୍ଷାଳୟ। ପୂର୍ବେ ଜଣେ ଜଣେ ଗୁରୁଙ୍କ ଦତ୍ତାବଧାନରେ ଥାଇ ଶିଷ୍ୟମାନେ ଶିକ୍ଷା ପ୍ରରୁଥ୍ ଲୋ
• କାଳାତାତ – ଯାହା କୌଶସି ନିର୍ଦ୍ଦିଷ୍ଟ ସମୟର ସାମା ମଧ୍ୟରେ ଆବଦ୍ଧ ହୋଇ ରହିଥାଏ।
• ଇତିବୃତ୍ତ – ଇତିହାସ / ପ୍ରାଚୀନ କଥା ।
• ସମାପ – ନିକଟା
• ଉନୁଖ – ଉସ୍କୁକ / ତାପର / ଆଗ୍ରହା ।
• ପରିପନ୍ଥା – ବିରୋଧୀ / ବିପକ୍ଷ / ପ୍ରତିରୋଧକା
• ଘ।ତକ – ହତ୍ୟାକାରା ।
• ଚିରନ୍ତନ – ଅତି ଉତ୍ଵଳା
• ବିରହିତ – ବିହାନ / ବିଯୁକ୍ତ
• ମୂଲ୍ୟବୋଧ – ଗୁରୁକୁଳ – ପ୍ରାଚାନ ସମୟର ଶିକ୍ଷାଳୟ। ପୂର୍ବେ ଜଣେ ଜଣେ ଗୁରୁଙ୍କ ତତ୍ତ୍। ବଧାନରେ ଥାଇ ଶିଷ୍ୟମାନେ ଶିକ୍ଷା ଗ୍ରହଣ କରୁଥ୍ଲେ।
• ଅବିଛେଦ୍ୟ – ଯାହାକୁ ବିଚ୍ଛିନ୍ନ ବା ଅଲଗା କରିହୁଏ ନାହିଁ ।
• ନିୟାମକ – ଯେ ନିୟମ ନିର୍ଦ୍ଧାରଣ କରେ | ପରିଚାଳକ ।
• ସୃଷ୍ଟିମେୟ -ଅଳ୍ପ ସଂଖ୍ୟକ / ଗୋଟିଏ ମୁଠା ଭିତରେ ମାପି ହେଉଥୁବା ଭଳି ପରିମାଣ ।
• ସଂସୃତି – ଲୋକ ଚଳଣି (ଭାଷା, ରୁଚି, ନୀତି, ଖାଦ୍ୟପେୟ, ବେଶଭୂଷା, କଳା, ଭାସ୍କର୍ଯ୍ୟ, ଧର୍ମଧାରା ଇତ୍ୟାଦି ସଂସ୍କୃତିର ଅନ୍ତଭୁକ୍ତ ।)
• ‘‘ଅତୀତକୁ ଉଦ୍‌ବୋଧଇ ବୃଥା ଭାଳି ଭାଳି’’– ଅତୀତର ପ୍ରାପ୍ତି ବା ସୁଖସମ୍ପଦ ସମ୍ବନ୍ଧରେ ଭାଳିହେବା । ଏହି ଅଂଶଟି ମଧୁସୂଦନ ରାଓଙ୍କ ବିଖ୍ୟାତ କବିତା ‘ଜୀବନ ଚିନ୍ତା ର ଏକ ଧାଡ଼ି ।
• ଶିଷ୍ୟତ୍ ଇଚ୍ଛେତ୍ ପରାଜୟମ୍ – ଶିଷ୍ୟଠାରୁ ଗୁରୁ ନିଜର ପରାଜୟ ଇଚ୍ଛା କରିବା ଆବଶ୍ୟକ । ଏହା ହେଉଛି ଜଣେ ଆଦର୍ଶ ଗୁରୁର ଅର୍ଭିଳାଷା
• ତେଜସ୍ବିନାବଧୀତମସ୍ତୁ – ‘କଠୋପନିଷଦ୍’ ଅନ୍ତର୍ଗତ ଶାନ୍ତିପାଠର ଅଂଶବିଶେଷ । (ନୌ ଅଧୀତମ୍ ତେଜସ୍ୱ ଅସ୍ତୁ) ଆମ ଗୁରୁ ଓ ଶିଷ୍ୟଙ୍କ ଦ୍ଵାରା ଅଧ୍ୟୟନ କରାଯାଇଥ‌ିବା ବିଦ୍ୟା ତେଜୋମୟୀ ହେଉ । ପୂରାକାଳରେ ଗୁରୁ ଓ ଶିଷ୍ୟ ଶାନ୍ତିପାଠ
• କରିବା ସମୟରେ ମିଳିତ ଭାବରେ ଏହି ବାଣୀ ଉଚ୍ଚାରଣ କରୁଥିଲେ ।

କେତୋଟି ନୂତନ ଶବ୍ଦ ଓ ଏହାର ଅର୍ଥ :

• ବିଭୋର – କୌଣସି ଚିନ୍ତାରେ ବୁଡ଼ି ରହିବା / ନିମଜ୍ଜିତ ହୋଇ ରହିବା
• ଅପ୍ରାସଙ୍ଗକ – ଯାହା ପ୍ର।ସଙ୍ଗିକ ନୁହେଁ / ମୂଲ୍ୟହାନ
• ବିଭୋର – କୌଶସି ଚିନ୍ତ୍ର।ରେ ଚୁଡି ରହିବା / ନିମଜ୍ଜିତ ହୋଇ ରହିବା
• ରଦ୍ଧିମନ୍ତ – ଭାଗ୍ୟବାନ୍ / ସମୃଦ୍ଧିଶାଳା
• ମାନାଷା – ମହାପୁରୁଷ / ବିଜ୍ଞ ବ୍ୟକ୍ତି
• କୁତ୍ସା – ନିନ୍ଦା / ଗାଳି
• ପ୍ରାଧ୍ କାର – ଅଧିକାର
• ଅଭେଦତ୍ଵ ସୌଧ – ଏକତା ବା ସମତାର ସୌଧ
• ବଖାଣ – କହିବା / ମୁଖରେ ଆବୃତ୍ତି କରିବା
• ସ୍ଵାଧଧ୍ୟ୍ୟାୟ – ନିଜେ ଅଧ୍ୟୟନ
• ନୈପୁଣ୍ୟ – ନିପୁଣଭାବ / ସିଦ୍ଧହସ୍ତ

Odisha State Board CHSE Odisha Class 12 Economics Solutions Chapter 16 ରାଷ୍ଟ୍ରବିତ୍ତ Short Answer Questions.

CHSE Odisha 12th Class Economics Chapter 16 Short Answer Questions in Odia Medium

ସଂକ୍ଷିପ୍ତ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
A. ଦୁଇଟି / ତିନୋଟି ବାକ୍ୟରେ ଉତ୍ତର ଦିଅ ।

1. ରାଷ୍ଟ୍ରବିତ୍ତ କାହାକୁ କୁହାଯାଏ ?
Answer:
ସମସ୍ତ ସରକାରୀ ସଂସ୍ଥାର ଆୟ-ବ୍ୟୟ ସମ୍ବନ୍ଧୀୟ ବିଜ୍ଞାନ ହିଁ ରାଷ୍ଟ୍ରବିତ୍ତ । ଅତଏବ ରାଷ୍ଟ୍ରୀୟ ବିତ୍ତ କହିଲେ ସରକାରୀ କର୍ତ୍ତୃପକ୍ଷଙ୍କ ସମ୍ପଦ ବିନିଯୋଗ, ଏହାର ବଣ୍ଟନ, ଆର୍ଥିକ ସ୍ଥିରତା ଏବଂ ଜନକଲ୍ୟାଣ କାର୍ଯ୍ୟକୁ ବୁଝାଏ । ଅର୍ଥାତ୍ ଏହା ସରକାରଙ୍କ ଆୟବ୍ୟୟ କାର୍ଯ୍ୟାବଳୀର ଆଲୋଚନା କରେ ।

2. ଉନ୍ନୟନ ବ୍ୟୟ କ’ଣ ?
Answer:
ଯେଉଁ ସରକାରୀ ବ୍ୟୟ ଅର୍ଥନୈତିକ ବିକାଶ ନିମନ୍ତେ ସହାୟତା ପ୍ରଦାନ କରେ, ତାହା ଉନ୍ନୟନ ବ୍ୟୟ । ଜାତୀୟ ଆୟ ବୃଦ୍ଧି ସହିତ ସାମାଜିକ ଓ ଅର୍ଥନୈତିକ ବିକାଶ ଉନ୍ନୟନ ବ୍ୟୟର ପ୍ରମୁଖ ଆଭିମୁଖ୍ୟ । କୃଷି, ଶିଳ୍ପ, ସ୍ବାସ୍ଥ୍ୟ, ଶିକ୍ଷା, ଗମନାଗମନ ଇତ୍ୟାଦିର ଉନ୍ନତି ପାଇଁ ହେଉଥ‌ିବା ସରକାରୀ ବ୍ୟୟକୁ ଉନ୍ନୟନ ବ୍ୟୟ କୁହାଯାଏ ।

3. ଅଣଉନ୍ନୟନ ବ୍ୟୟ କ’ଣ ?
Answer:
ସରକାର ଏପରି କେତେକ ନିର୍ଦ୍ଦିଷ୍ଟ ଉଦ୍ଦେଶ୍ୟରେ ବ୍ୟୟ କରିଥା’ନ୍ତି ଯେଉଁଗୁଡ଼ିକ ଅତ୍ୟାବଶ୍ୟକ ହୋଇଥିଲେ ମଧ୍ୟ ବିକାଶ କ୍ଷେତ୍ରରେ ସହାୟତା ପ୍ରଦାନ କରନ୍ତି ନାହିଁ । ଏପରି ସମସ୍ତ ସରକାରୀ ବ୍ୟୟକୁ ଅଣଉନ୍ନୟନ ବ୍ୟୟ କୁହାଯାଏ । ଆଇନ ଓ ଶୃଙ୍ଖଳା, ପ୍ରତିରକ୍ଷା, ପ୍ରଶାସନ ଇତ୍ୟାଦି ପାଇଁ ସରକାର କରୁଥିବା ବ୍ୟୟ ଅଣଉନ୍ନୟନ ବ୍ୟୟରେ ଅନ୍ତର୍ଭୁକ୍ତ ।

4. ରାଜସ୍ବ ବ୍ୟୟ କ’ଣ ?
Answer:
ରାଷ୍ଟ୍ରର ଦୈନନ୍ଦିନ ଆବଶ୍ୟକତା ପୂରଣ କରିବା ନିମନ୍ତେ କରାଯାଉଥ‌ିବା ରାଷ୍ଟ୍ରୀୟ ବ୍ୟୟକୁ ରାଜସ୍ୱ ବ୍ୟୟ କୁହାଯାଏ । କୌଣସି ପରିସମ୍ପତ୍ତି ସୃଷ୍ଟି ଏହାର ଉଦ୍ଦେଶ୍ୟ ନୁହେଁ । ବିଭିନ୍ନ ସରକାରୀ ବିଭାଗର ସାଧାରଣ କାର୍ଯ୍ୟ ସମ୍ପାଦନ ପାଇଁ ରାଜସ୍ଵ ବ୍ୟୟ କରାଯାଏ ।

5. ପୁଞ୍ଜି ବ୍ୟୟ କ’ଣ ?
Answer:
ରାଷ୍ଟ୍ର ପରିସମ୍ପତ୍ତି ସୃଷ୍ଟି ପାଇଁ ଯେଉଁ ବ୍ୟୟ କରିଥାଏ, ତାହାକୁ ପୁଞ୍ଜି ବ୍ୟୟ କୁହାଯାଏ । ଏହି ବ୍ୟୟ ରାଷ୍ଟ୍ରର ଉତ୍ପାଦନ କ୍ଷମତା ବୃଦ୍ଧି କରିବା ପାଇଁ ସହାୟତା ପ୍ରଦାନ କରେ । ବିଭିନ୍ନ ବିକାଶମୂଳକ ପ୍ରକଳ୍ପ ପାଇଁ ରାଷ୍ଟ୍ର ଯେଉଁ ବ୍ୟୟ ବରାଦ କରିଥାଏ, ତାହା ପୁଞ୍ଜି ବ୍ୟୟରେ   ଅନ୍ତର୍ଭୁକ୍ତ ।

6. ଯୋଜନା ବ୍ୟୟ କ’ଣ ?
Answer:
ଯେଉଁ ବ୍ୟୟ ପାଇଁ ରାଷ୍ଟ୍ରୀୟ ଯୋଜନାର ଅନୁମୋଦନ ଆବଶ୍ୟକ, ତାହା ଯୋଜନା ବ୍ୟୟ । ବିଭିନ୍ନ ମନ୍ତ୍ରଣାଳୟ ଓ ବିଭାଗର ଆବଶ୍ୟକତା ଅନୁସାରେ ନୂତନ ଭାବେ ପ୍ରସ୍ତାବିତ ଓ ଅନୁମୋଦିତ ବ୍ୟୟକୁ ଯୋଜନା ବ୍ୟୟ କୁହାଯାଏ । ନୂତନ ରାସ୍ତା, ବନ୍ଧ ଇତ୍ୟାଦିର ନିର୍ମାଣଜନିତ ବ୍ୟୟ ହେଉଛି ଯୋଜନା ବ୍ୟୟ ।

7. ଅଣଯୋଜନା ବ୍ୟୟ କ’’ଣ ?
Answer:
ଯେଉଁ ସରକାରୀ ବ୍ୟୟ ନିମନ୍ତେ ରାଷ୍ଟ୍ରୀୟ ଯୋଜନାର ଅନୁମୋଦନ ଆବଶ୍ୟକ ହୋଇନଥାଏ, ତାହା ଅଣଯୋଜନା ବ୍ୟୟ । ଏହି ବ୍ୟୟଭାର ବହନ କରିବାପାଇଁ ସରକାର ବାଧ୍ୟ । ସ୍ଥାୟୀ କର୍ମଚାରୀମାନଙ୍କ ଦରମା ଓ ପେନ୍‌ସନ୍, ସୁଧ, ପରିଶୋଧ, ଦେଶରକ୍ଷା ପାଇଁ ହେଉଥ‌ିବା ବ୍ୟୟ ହେଉଛି ଅଣଯୋଜନା ବ୍ୟୟ ।

8. କରାଘାତ କ’ଣ ?
Answer:
କରାଘାତ ହେଉଛି କରର ମୂଳ ବୋଝ । ଏହା ମୂଳ କର ଧାର୍ଯ୍ୟ ବିନ୍ଦୁ । ଯେଉଁ ବ୍ୟକ୍ତି ପ୍ରଥମେ କରର ବୋଝ ବହନ କରେ କିମ୍ବା ସରକାରଙ୍କୁ ପ୍ରତ୍ୟକ୍ଷ ଭାବେ କର ପ୍ରଦାନ କରେ, ତାଙ୍କ ଉପରେ କରାଘାତ ହେଲା ବୋଲି କୁହାଯାଏ ।

9. କରାପାତ କ’ଣ ?
Answer:
ପରିଶେଷରେ କର ବୋଝ ବହନ କରୁଥିବା ବ୍ୟକ୍ତିଙ୍କ ଉପରେ କରାପାତ ହୋଇଥାଏ । ଏହା କର ସ୍ଥାନାନ୍ତରଣର ଅନ୍ତିମ ପରିଣାମ । କରାନ୍ତକରଣର ଶେଷ ବିନ୍ଦୁ ହେଉଛି କରାପାତ ।

10. କର ସ୍ଥାନାନ୍ତରଣ କ’ଣ ?
Answer:
ଯେଉଁ ପ୍ରକ୍ରିୟାରେ କରଭାର ବାରମ୍ବାର ସ୍ଥାନାନ୍ତର ଘଟେ, ତାହାକୁ କର ସ୍ଥାନାନ୍ତରଣ କୁହାଯାଏ । କ୍ରୟ-ବିକ୍ରୟ ମାଧ୍ୟମରେ ସ୍ଥାନାନ୍ତରଣ ସମ୍ଭବ ହୋଇଥାଏ । ଯଦି କରଭାର ଉତ୍ପାଦନକାରୀଠାରୁ ଖାଉଟି ନିକଟକୁ ସ୍ଥାନାନ୍ତର ଘଟେ, ତାହାକୁ ଅଗ୍ରଗାମୀ ସ୍ଥାନାନ୍ତରଣ କୁହାଯାଏ । ଯେତେବେଳେ କରଭାର ଉତ୍ପାଦନକାରୀଠାରୁ କଞ୍ଚାମାଲ ମାଲିକ ନିକଟକୁ ସ୍ଥାନାନ୍ତର ଘଟେ, ତାହାକୁ ପଶ୍ଚାତ୍ମାମୀ ସ୍ଥାନାନ୍ତରଣ
କୁହାଯାଏ ।

11. ପ୍ରତ୍ୟକ୍ଷ କର କ’ଣ ?
Answer:
ଯେଉଁ କରର କରାଘାତ ଓ କରାପାତ ଜଣେ ବ୍ୟକ୍ତି ହିଁ ବହନ କରନ୍ତି, ତାହାକୁ ପ୍ରତ୍ୟକ୍ଷ କର କୁହାଯାଏ । ଏଠାରେ କର ସ୍ଥାନାନ୍ତରଣ ସମ୍ଭବ ନୁହେଁ । ପ୍ରତ୍ୟକ୍ଷ କରର ଦାତା ଓ ବୋଝ ବହନକାରୀ ଜଣେ । ଆୟକର ପ୍ରତ୍ୟକ୍ଷ କରର ଉଦାହରଣ ।

12. ପରୋକ୍ଷ କର କ’ଣ ?
Answer:
ଯେଉଁ କରର କରାଘାତ ଓ କରାପାତ ବିଭିନ୍ନ ବ୍ୟକ୍ତି ବହନ କରିଥା’ନ୍ତି, ତାହାକୁ ପରୋକ୍ଷ କର କୁହାଯାଏ । ଏଠାରେ ‘କରଦାତା’ ଓ କରଭାର ବହନକାରୀ ଭିନ୍ନ ବ୍ୟକ୍ତି ଅଟନ୍ତି । ପରୋକ୍ଷ କର ସ୍ଥାନାନ୍ତରକ୍ଷମ । ତେଣୁ ଜଣେ ବ୍ୟକ୍ତି ଉପରେ କରାଘାତ ହେଲାବେଳେ ଅନ୍ୟ ଜଣେ ବ୍ୟକ୍ତି ଉପରେ କରାପାତ ହୋଇଥାଏ ।

13. ପ୍ରଗାମୀ କର କ’ଣ ?
Answer:
ଯେଉଁ କ୍ଷେତ୍ରରେ ଆୟର ବୃଦ୍ଧି ସଙ୍ଗେ ସଙ୍ଗେ କରର ହାର ବୃଦ୍ଧି ହୁଏ, ସେହି କରକୁ ପ୍ରଗାମୀ କର କୁହାଯାଏ । ଆୟକର ପ୍ରଗାମୀ କରର ଏକ ଜ୍ଵଳନ୍ତ ଉଦାହରଣ । ଏଠାରେ ବିଭିନ୍ନ ଆୟ ସ୍ତର ପାଇଁ ବିଭିନ୍ନ କର ହାର ପ୍ରଚଳିତ ହୋଇଥାଏ ।

14. ପ୍ରତିଗାମୀ କର କ’ଣ ?
Answer:
ଆୟ ବୃଦ୍ଧି ହେଲେ ଯଦି କରର ହାର ହ୍ରାସ ହୁଏ, ତେବେ ଏହି କରକୁ ପ୍ରତିଗାମୀ କର କୁହାଯାଏ । ପ୍ରତିଗାମୀ କର କ୍ଷେତ୍ରରେ କରଦାତାଙ୍କର ଆୟ ବୃଦ୍ଧି ହେବାଫଳରେ କରର ହାର ହ୍ରାସ ହୁଏ ଏବଂ ଆୟ ହ୍ରାସ ହେବା ଫଳରେ କରର ହାର ବୃଦ୍ଧି ହୁଏ । ଏହି କରର ବୋଝ ଧନୀମାନଙ୍କ ଉପରେ କମ୍ ଓ ଦରିଦ୍ରମାନଙ୍କ ଉପରେ ବେଶି ପଡ଼ିଥାଏ । ବିକ୍ରିକର, ଅବକାରୀ ଶୁଳ୍‌କ ପ୍ରଭୃତି ପ୍ରତିଗାମୀ କରର ଉଦାହରଣ ।

15. ଆନୁପାତିକ କର କ’ଣ ?
Answer:
ଯେତେବେଳେ କରହାର ଆୟର ହ୍ରାସ ଓ ବୃଦ୍ଧି ସହିତ ସମ୍ପର୍କିତ ନ ହୋଇ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ କାଳ ପାଇଁ ସ୍ଥିର ରହେ, ସେହି ପ୍ରକାର କରକୁ ଆନୁପାତିକ କର କୁହାଯାଏ । ଏ କ୍ଷେତ୍ରରେ କରଦାତାଙ୍କୁ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ହାରରେ କର ଦେବାକୁ ହୋଇଥାଏ । ବ୍ୟକ୍ତିବିଶେଷଙ୍କର ଆୟ ବୃଦ୍ଧି ସଙ୍ଗେ ସଙ୍ଗେ କର ଆଦାୟ ବୃଦ୍ଧି ହୁଏ; କିନ୍ତୁ କରର ହାରରେ କୌଣସି ପରିବର୍ତ୍ତନ ହୁଏ ନାହିଁ ।

16. ଫିଡ୍ କ’ଣ ?
Answer:
କୌଣସି ନିର୍ଦ୍ଦିଷ୍ଟ ସେବା ନିମନ୍ତେ ସରକାରଙ୍କୁ ଦିଆଯାଉଥିବା ବାଧ୍ୟତାମୂଳକ ଦେୟକୁ ଫିଜ୍ କୁହାଯାଏ । ଫିଦାତାଙ୍କୁ ବିଶେଷ ସୁବିଧା ଦେବାପାଇଁ ହେଉଥ‌ିବା ବ୍ୟୟର କିଛି ଅଂଶ ସରକାର ଫିଜ୍ ଆକାରରେ ଆଦାୟ କରିଥା’ନ୍ତି । କୋର୍ଟ ଫିଡ୍ ରେଜିଷ୍ଟ୍ରୀକରଣ ଫିଜ୍, ଲାଇସେନ୍ସ ଫିଜ୍ ଇତ୍ୟାଦି ଫିଜ୍‌ର ଉଦାହରଣ ।

17. ଜୋରିମାନା କ’ଣ ?
Answer:
ନ୍ୟାୟପ୍ରଦାନ ଓ ସୁସ୍ଥ ପ୍ରଶାସନ ପାଇଁ ସରକାର ଜୋରିମାନା ଆଦାୟ କରିଥା’ନ୍ତି । ଏହା ଆଇନ ଭଙ୍ଗକାରୀଙ୍କ ପାଇଁ ଅର୍ଥଦଣ୍ଡ । ଜୋରିମାନା ରାଷ୍ଟ୍ରୀୟ ରାଜସ୍ବର ଏକ ଅଂଶ ହେଲେ ମଧ୍ୟ ମୋଟ ରାଜସ୍ୱରେ ଏହାର ଅଂଶ ଖୁବ୍ କମ୍ ।

18. ବାଜ୍ୟାପ୍ତି କ’ଣ ?
Answer:
ଚୁକ୍ତିଭଙ୍ଗ କିମ୍ବା ସ୍ଥିରୀକୃତ କାର୍ଯ୍ୟ ସମ୍ପାଦନ କରିନଥିବା ବ୍ୟକ୍ତିବିଶେଷଙ୍କଠାରୁ ସରକାର ଦଣ୍ଡସ୍ଵରୂପ ସେମାନେ ଅମାନତ ରୂପେ ରଖୁଥ‌ିବା ଅର୍ଥ ଫେରସ୍ତ କରନ୍ତି ନାହିଁ । ତାହାକୁ ବାଜ୍ୟାପ୍ତି କୁହାଯାଏ । ଉଦାହରଣସ୍ୱରୂପ, ସାଧାରଣ ନିର୍ବାଚନରେ ପ୍ରତ୍ୟେକ ପ୍ରାର୍ଥୀ କିଛି ଅମାନତ ଜମା ଦିଅନ୍ତି । ସର୍ଭେ ମୁତାବକ ଯଦି ଜଣେ ପ୍ରାର୍ଥୀ ମୋଟ ଭୋଟର ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଶତାଂଶ ଭୋଟ ଆକାରରେ ପାଆନ୍ତି ନାହିଁ, ତେବେ ରଖୁଥ‌ିବା ଅମାନତରୁ ସେ ବଞ୍ଚତ ହୁଅନ୍ତି ଏବଂ ଉକ୍ତ ଅମାନତ ରାଷ୍ଟ୍ରୀୟ ରାଜସ୍ବର ଏକ ଅଂଶରେ ପରିଣତ ହୁଏ ।

19. ରାଜଭୁକ୍ତି କ’ଣ ?
Answer:
ଆଇନାନୁମୋଦିତ ଉତ୍ତରାଧିକାରୀ ନଥ‌ିବା କୌଣସି ବ୍ୟକ୍ତିର ମୃତ୍ୟୁ ଘଟିଲେ ତାଙ୍କ ସମ୍ପରି ସରକାରଙ୍କଦ୍ୱାରା ଅଧିକୃତ ହୋଇଥାଏ । ଏହାକୁ ରାଜଭୁକ୍ତି କୁହାଯାଏ । ଆଇନ ଶୃଙ୍ଖଳା ରକ୍ଷା ପାଇଁ ସରକାର ଉତ୍ତରାଧ୍ୟାକାରୀ ବିହୀନ ସମ୍ପରିକୁ ନିଜ ମାଲିକାନାକୁ ଆଣନ୍ତି ।

20. କର କ’ଣ ?
Answer:
କର ରାଷ୍ଟ୍ରୀୟ ରାଜସ୍ବର ସର୍ବବୃହତ୍ ଉତ୍ସ । କୌଣସି ବିଶେଷ ସୁବିଧା ସହ ସମ୍ପର୍କ ନଥାଇ, ସର୍ବସାଧାରଣଙ୍କ ସ୍ବାର୍ଥରେ ବ୍ୟୟ କରିବାପାଇଁ ବ୍ୟକ୍ତିବିଶେଷ ସରକାରଙ୍କୁ ଦେଉଥ‌ିବା ବାଧ୍ୟତାମୂଳକ ଦେୟକୁ କର କୁହାଯାଏ । ତେଣୁ, କୌଣସି ପ୍ରତ୍ୟକ୍ଷ ସୁବିଧାର ଆଶା ନରଖ୍ ଜନସାଧାରଣ ସରକାରଙ୍କୁ ଦେଉଥ‌ିବା ବାଧ୍ୟତାମୂଳକ ଦେୟକୁ କର କହନ୍ତି ।

B. ନିମ୍ନଲିଖ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ପାଞ୍ଚଟି| / ଛଅଟି ବାକ୍ୟରେ ଦିଅ ।

1. ବିଶେଷ ନିର୍ଦ୍ଧାରଣ କ’ଣ ?
Answer:
ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଅଞ୍ଚଳର ଜନସାଧାରଣଙ୍କୁ ସ୍ୱତନ୍ତ୍ର ସୁବିଧା ପ୍ରଦାନ କରି ସରକାର ସେମାନଙ୍କଠାରୁ ଯେଉଁ ଦେୟ ଆଦାୟ କରନ୍ତି, ତାହାକୁ ବିଶେଷ ନିର୍ଦ୍ଧାରଣ କୁହାଯାଏ । ରାସ୍ତା ନିର୍ମାଣ, ଜଳଯୋଗାଣ, ନଦୀବନ୍ଧ ନିର୍ମାଣ ଇତ୍ୟାଦି ଉନ୍ନୟନମୂଳକ କାର୍ଯ୍ୟକ୍ରମଦ୍ୱାରା ନିର୍ଦ୍ଦିଷ୍ଟ ଅଞ୍ଚଳର ବିକାଶ ଘଟେ । କେତେକ ନିର୍ଦ୍ଦିଷ୍ଟ ସମ୍ପତ୍ତି ମାଲିକ ସ୍ଵତନ୍ତ୍ର ସୁବିଧା ପାଆନ୍ତି ।

ସେମାନଙ୍କ ସମ୍ପତ୍ତିର ମୂଲ୍ୟରେ ହଠାତ୍‌ ବୃଦ୍ଧି ଘଟେ । ସ୍ଵତନ୍ତ୍ର ସୁବିଧା ପାଉଥବା ସମ୍ପଭି ମାଲିକଙ୍କଠାରୁ ସରକାର ଆନୁପାତିକ ହାରରେ ସ୍ୱତନ୍ତ୍ର ନିର୍ଦ୍ଧାରଣ ଆଦାୟ କରନ୍ତି । ଏହା ଉନ୍ନୟନମୂଳକ କାର୍ଯ୍ୟରେ ହୋଇଥିବା ସରକାରୀ ବ୍ୟୟର ଏକ ଅଂଶ । ଏହାକୁ ସମନ୍ବିତ କର ମଧ୍ୟ କୁହାଯାଏ ।

2. ପ୍ରତ୍ୟକ୍ଷ କର କ’ଣ ?
Answer:
ଯେଉଁ କରର କରାଘାତ ଓ କରାପାତ ଜଣେ ବ୍ୟକ୍ତି ହିଁ ବହନ କରନ୍ତି, ତାହାକୁ ପ୍ରତ୍ୟକ୍ଷ କର କୁହାଯାଏ । ଏଠାରେ କର ସ୍ଥାନାନ୍ତରଣ ସମ୍ଭବ ନୁହେଁ । ପ୍ରତ୍ୟକ୍ଷ କରର ଦାତା ଓ ବୋଝ ବହନକାରୀ ଜଣେ । ତେଣୁ ଯେଉଁ ବ୍ୟକ୍ତିବିଶେଷଙ୍କ ଉପରେ ସରକାର ପ୍ରତ୍ୟକ୍ଷ କର ଧାର୍ଯ୍ୟ କରନ୍ତି ସେ ନିଜେ କରଦାତା ଓ କରଭାର ବହନକାରୀ ।

ଆୟକର, ସମ୍ପରି କର, ବୃତ୍ତି କର ଇତ୍ୟାଦି ପ୍ରତ୍ୟକ୍ଷ କରର ଉଦାହରଣ । ପ୍ରତ୍ୟକ୍ଷ କର କ୍ଷେତ୍ରରେ ନାଗରିକ ମୂଲ୍ୟବୋଧର ବିକାଶ ସାଧୂ ହୋଇଥାଏ । ଫଳରେ ସେ ସରକାରଙ୍କ କାର୍ଯ୍ୟକଳାପ୍ ପ୍ରତି ସଚେତନ ରହେ ।

3. ପ୍ରତ୍ୟକ୍ଷ କର ସାଧୁତା ଉପରେ ଏକ କର – ଏପରି କାହିଁକି କୁହାଯାଏ ?
Answer:
ପ୍ରତ୍ୟକ୍ଷ କର କ୍ଷେତ୍ରରେ କରାଘାତ ଓ କରାପାତ ଜଣେ ବ୍ୟକ୍ତି ବହନ କରନ୍ତି । ପ୍ରତ୍ୟକ୍ଷ କରର ଦାତା ଓ ବୋଝ ବହନକାରୀ ଜଣେ । ପ୍ରତ୍ୟକ୍ଷ କର କରଦାତାଙ୍କ ନିଜସ୍ୱ ଆୟ ଓ ସମ୍ପତ୍ତି ସମ୍ବନ୍ଧୀୟ ସ୍ଵେଚ୍ଛାକୃତ ଘୋଷଣା ଉପରେ ପର୍ଯ୍ୟବସିତ । ତେଣୁ ଅସାଧୁ ବ୍ୟକ୍ତିଙ୍କ ପାଇଁ କର ଠକେଇର ସମ୍ଭାବନା ଅଧିକ ।

ପ୍ରକୃତରେ, ଜଣେ ସାଧୁ ଓ ସଟ କିମ୍ବା ନିଜ ଆୟ ବା ସମ୍ପତ୍ତି ଲୁଚାଇ ପାରୁନଥିବା ବ୍ୟକ୍ତି ପ୍ରତ୍ୟକ୍ଷ କର ଦେଇଥାନ୍ତି । ତେଣୁ, କୁହାଯାଏ ଯେ ପ୍ରତ୍ୟକ୍ଷ କର ସାଧୁତା ଉପରେ ଏକ କର ।

4. ବିନିଯୋଗରେ ରାଷ୍ଟ୍ରର ଆଭିମୁଖ୍ୟ କିପରି ହୋଇଥାଏ ?
Answer:
ଜଣେ ବ୍ୟକ୍ତି ପାଇଁ ଭବିଷ୍ୟତ ସର୍ବଦା ଅନିଶ୍ଚିତ । ତାଙ୍କ ପାଇଁ ବର୍ତ୍ତମାନର ଗୁରୁତ୍ଵ ଅଧିକ । ଭବିଷ୍ୟତର ଆୟ ଅପେକ୍ଷା ବର୍ତ୍ତମାନର ଆୟ ଅଧିକ କାମ୍ୟ । କିନ୍ତୁ, ରାଷ୍ଟ୍ରର ଆଭିମୁଖ୍ୟ ସ୍ୱତନ୍ତ୍ର । ରାଷ୍ଟ୍ର ଚିରସ୍ଥାୟୀ । ଏହାର ଉଭୟ ବର୍ତ୍ତମାନ ଓ ଭବିଷ୍ୟତ ପିଢ଼ୀ ପ୍ରତି ସମାନ ଦାୟିତ୍ୱ ରହିଛି । ତେଣୁ ରାଷ୍ଟ୍ର କେବଳ ବର୍ତ୍ତମାନ ପାଇଁ ବିନିଯୋଗ ନ କରି ଭବିଷ୍ୟତ ପାଇଁ ମଧ୍ଯ ବିନିଯୋଗ କରିଥାଏ । ରାଷ୍ଟ୍ରୀୟ ବିନିଯୋଗ ଉଭୟ ସ୍ଵଳ୍ପକାଳୀନ ଓ ଦୀର୍ଘକାଳୀନ ହୋଇପାରେ ।

5. କିପରି ରାଷ୍ଟ୍ରୀୟ ରାଜସ୍ବ ରାଷ୍ଟ୍ରୀୟ ଆୟର ଏକ ଅଂଶବିଶେଷ ।
Answer:
ଆଧୁନିକ ରାଷ୍ଟ୍ର ଜନକଲ୍ୟାଣକାରୀ । ଜନକଲ୍ୟାଣ ପାଇଁ ପ୍ରତ୍ୟେକ ରାଷ୍ଟ୍ର ପ୍ରଚୁର ଆୟ ଆବଶ୍ୟକ କରିଥାଏ । ଯେଉଁ ରାଷ୍ଟ୍ରର ଆୟ ଯେତେ ଅଧ୍ଯକ, ସେହି ରାଷ୍ଟ୍ରର ବ୍ୟୟ ପରିସୀମା ସେତେ ବ୍ୟାପକ । ରାଷ୍ଟ୍ରୀୟ ରାଜସ୍ଵ, ରାଷ୍ଟ୍ରୀୟ ଆୟର ଏକ ଅଂଶ । ରାଷ୍ଟ୍ରୀୟ ଆୟ ସରକାରଙ୍କ ସମସ୍ତ ପ୍ରାପ୍ତିକୁ ବୁଝାଏ ।

ରାଜସ୍ୱ ସହିତ ରାଷ୍ଟ୍ରୀୟ ଋଣ, ଅଧ‌ିକ ନୋଟ୍ ପ୍ରଚଳନ, ସରକାରୀ ଉଦ୍ୟୋଗରୁ ହେଉଥ‌ିବା ଲାଭ ଇତ୍ୟାଦି ରାଷ୍ଟ୍ରୀୟ ଆୟର ଅନ୍ତର୍ଭୁକ୍ତ । ସରକାର କେତେକ ନିର୍ଦ୍ଦିଷ୍ଟ କ୍ଷେତ୍ରରୁ କରୁଥିବା ଆୟ ହିଁ ରାଷ୍ଟ୍ରୀୟ ରାଜସ୍ବ । ଏହା ଏକ ସୀମିତ ଧାରଣା । ରାଷ୍ଟ୍ରୀୟ ରାଜସ୍ବର ବିଭିନ୍ନ ଉତ୍ସ ରହିଛି ।

6. କର କ’ଣ ?
Answer:
କର ରାଷ୍ଟ୍ରୀୟ ରାଜସ୍ବର ସର୍ବବୃହତ୍ ଉତ୍ସ । ସର୍ବସାଧାରଣଙ୍କ ସ୍ବାର୍ଥରେ ବ୍ୟୟ କରିବାପାଇଁ ବ୍ୟକ୍ତିବିଶେଷ ସରକାରଙ୍କୁ ଦେଉଥ‌ିବା ବାଧ୍ୟତାମୂଳକ ଦେୟକୁ କର କୁହାଯାଏ । କର ସରକାରଙ୍କ ପ୍ରତି ଜନସାଧାରଣଙ୍କ ଏକ ବାଧ୍ୟତାମୂଳକ ଦେୟ । କର ନ ଦେବା ଆଇନତଃ ଏକ ଦଣ୍ଡନୀୟ ଅପରାଧ । କର ପ୍ରଦାନ କରି କରଦାତା କୌଣସି ସ୍ଵତନ୍ତ୍ର ସୁବିଧା ପାଇନଥାଏ । ଅର୍ଥାତ୍, କର ବିନିମୟରେ ସରକାର କରଦାତାଙ୍କୁ କୌଣସି ପ୍ରତ୍ୟକ୍ଷ ସୁବିଧା ପ୍ରଦାନ କରନ୍ତି ନାହିଁ । କରପ୍ରଦାନ ଏକ ବ୍ୟକ୍ତିଗତ ଦାୟିତ୍ଵ ।

7. ରାଷ୍ଟ୍ରୀୟ ବ୍ୟୟ କ’ଣ ?
Answer:
ଆଧୁନିକ ରାଷ୍ଟ୍ର ଏକ ଜନକଲ୍ୟାଣକାରୀ ରାଷ୍ଟ୍ର । ଜନସାଧାରଣଙ୍କ କଲ୍ୟାଣ ନିମନ୍ତେ ସରକାର ବିଭିନ୍ନ କାର୍ଯ୍ୟକ୍ରମ ହାତକୁ ନିଅନ୍ତି ଏବଂ ସେଥ‌ିପାଇଁ ବ୍ୟୟ କରିଥା’ନ୍ତି । ଏହାକୁ ରାଷ୍ଟ୍ରୀୟ ବ୍ୟୟ ବା ସରକାରୀ ବ୍ୟୟ କୁହାଯାଏ । ସୁତରାଂ, ସର୍ବସାଧାରଣଙ୍କ ସାମାଜିକ ଓ ଅର୍ଥନୈତିକ କଲ୍ୟାଣ ନିମନ୍ତେ ରାଷ୍ଟ୍ର ଯେଉଁ ବ୍ୟୟ କରେ, ତାହାକୁ ରାଷ୍ଟ୍ରୀୟ ବ୍ୟୟ କୁହାଯାଏ ।

ରାଷ୍ଟ୍ରୀୟ ବ୍ୟୟ ସମୟରେ ପ୍ରତ୍ୟେକ ସରକାର ବିଚାରବନ୍ତ ହେବା ଉଚିତ । ତେଣୁ ରାଷ୍ଟ୍ର ନିଜସ୍ଵ ସମ୍ବଳକୁ ଏପରି ବାଣ୍ଟିବା ଆବଶ୍ୟକ ଯଦ୍ବାରା ଜନସାଧାରଣଙ୍କର ମୋଟ ସୁବିଧା ସର୍ବାଧ‌ିକ ହୋଇପାରିବ ।

8. ବାଣିଜ୍ୟିକ ରାଜସ୍ୱ କ’ଣ ?
Answer:
ସରକାର ଏକ ଉଦ୍ୟୋକ୍ତା ମଧ୍ୟ । ସରକାରୀ ଉଦ୍ୟୋଗରେ ଉତ୍ପାଦିତ ବିଭିନ୍ନ ଦ୍ରବ୍ୟ ଓ ସେବା! ବିକ୍ରୟ କରି ସରକାର ଯେଉଁ ରାଜସ୍ଵ ପାଇଥା’ନ୍ତି, ତାହାକୁ ବାଣିଜ୍ୟିକ ରାଜସ୍ୱ କୁହାଯାଏ । ସରକାରୀ ଦ୍ରବ୍ୟ ଓ ସେବା ପ୍ରତିବଦଳରେ ଜନସାଧାରଣ ଦର ଦେଇଥା’ନ୍ତି । ତେଣୁ ଦର ବାଣିଜ୍ୟିକ ରାଜସ୍ବର ଅନ୍ୟ ନାମ ।

ରେଳବାଇ, ଡାକ ବ୍ୟବସ୍ଥା, ରାଷ୍ଟ୍ରୀୟ ପରିବହନ ବ୍ୟବସ୍ଥା, ସରକାରୀ ଉଦ୍ୟୋଗ,ଖଣି ଜଙ୍ଗଲ ଇତ୍ୟାଦିରୁ ମିଳୁଥିବା ରାଜସ୍ବ ବାଣିଜ୍ୟିକ ରାଜସ୍ଵର ଅଂଶବିଶେଷ । ଏହା ରାଷ୍ଟ୍ରୀୟ ରାଜସ୍ବର ଏକ ପ୍ରମୁଖ ଉତ୍ସ ।

9. ଫିଜ୍ କ’ଣ ?
Answer:
କୌଣସି ନିର୍ଦ୍ଦିଷ୍ଟ ସେବା ନିମନ୍ତେ ସରକାରଙ୍କୁ ଦିଆଯାଉଥ‌ିବା ବାଧ୍ୟତାମୂଳକ ଦେୟକୁ ଫିଜ୍ କୁହାଯାଏ । ଫିଦାତାଙ୍କୁ ବିଶେଷ ସୁବିଧା ଦେବାପାଇଁ ହେଉଥ‌ିବା ବ୍ୟୟର କିଛି ଅଂଶ ସରକାର ଫିଜ୍ ଆକରରେ ଆଦାୟ କରିଥା’ନ୍ତି ! ଫିଜ୍ ପ୍ରଦାନକାରୀ ପ୍ରତ୍ୟକ୍ଷ ସୁବିଧା ପାଇଥା’ନ୍ତି । ସୁବିଧା ଓ ଫିଜ୍ ସମାନୁପାତିକ ନୁହଁନ୍ତି ।

ଫିଲ୍ମ୍ ଅପେକ୍ଷା ସୁବିଧାର ମୂଲ୍ୟ ଅଧିକ । କେବଳ ବିଶେଷ ସୁବିଧା ଲାଭ କରୁଥିବା ବ୍ୟକ୍ତିଙ୍କ ପାଇଁ ଫିଜ୍ ଏକ ବାଧ୍ୟତାମୂଳକ ଦେୟ । କୋର୍ଟ ଫିଜ୍, ରେଜିଷ୍ଟ୍ରୀକରଣ ଫିଜ୍, ଲାଇସେନ୍ସ ଫିଜ୍ ଇତ୍ୟାଦି ଫିଜ୍‌ର ଉଦାହରଣ ।

10. ପ୍ରତ୍ୟକ୍ଷ କର କ’ଣ ?
Answer:
ଯେଉଁ କରର କରାଘାତ ଓ କରାପାତ ଜଣେ ବ୍ୟକ୍ତି ହିଁ ବହନ କରନ୍ତି ତାହାକୁ ପ୍ରତ୍ୟକ୍ଷ କର କୁହାଯାଏ । ପ୍ରତ୍ୟକ୍ଷ କରର ଦାତା ଓ ବୋଝ ବହନକାରୀ ଜଣେ । ପ୍ରତ୍ୟକ୍ଷ କର କରାଦାତାର ଦେଇ ପାରିବାର ସାମର୍ଥ୍ୟ ଉପରେ ପର୍ଯ୍ୟବସିତ । ତେଣୁ ଧନୀକ ଶ୍ରେଣୀ ଅଧ୍ଵ କର ଦେଇଥା’ନ୍ତି । ଫଳରେ ପ୍ରତ୍ୟକ୍ଷ କର ସମାନତା ସହିତ ସାମାଜିକ ନ୍ୟାୟ ପ୍ରତିଷ୍ଠା କ୍ଷେତ୍ରରେ ସହାୟତା ପ୍ରଦାନ କରେ ।

ପ୍ରତ୍ୟକ୍ଷ କର କ୍ଷେତ୍ରରେ କରଦାତା ଓ ସରକାରଙ୍କ ମଧ୍ୟରେ ପ୍ରତ୍ୟକ୍ଷ ସମ୍ପର୍କ ରହିଥାଏ । ସେ ସରକାରଙ୍କ କାର୍ଯ୍ୟକଳାପ ପ୍ରତି ସଚେତନ ରହେ । ଫଳରେ ନାଗରିକ ମୂଲ୍ୟବୋଧର ବିକାଶ ସାଧୂତ ହୋଇଥାଏ ।

11. ପରୋକ୍ଷ କର କ’ଣ ?
Answer:
ଯେଉଁ କରର କରାଘାତ ଓ କରାପାତ ବିଭିନ୍ନ ବ୍ୟକ୍ତି ବହନ କରିଥା’ନ୍ତି; ତାହାକୁ ପରୋକ୍ଷ କର କୁହାଯାଏ । ଏଠାରେ କରଦାତା ଓ କରଭାର ବହନକାରୀ ଭିନ୍ନ ବ୍ୟକ୍ତି ଅଟନ୍ତି । ପରୋକ୍ଷ କର ସ୍ଥାନାନ୍ତରଣକ୍ଷମ । ତେଣୁ ଜଣେ ବ୍ୟକ୍ତି ଉପରେ କରାଘାତ ହେଲାବେଳେ ଅନ୍ୟ ଜଣେ ବ୍ୟକ୍ତି ଉପରେ କରାପାତ ହୋଇଥାଏ ।

ଦ୍ରବ୍ୟକର ଉତ୍ପାଦନକାରୀ ପ୍ରଥମେ ସରକାରଙ୍କ ନିକଟରେ ପଇଠ କରିଥା’ନ୍ତି । କିନ୍ତୁ, ତତ୍ପରେ ଦ୍ରବ୍ୟର ଦାମ୍‌ରେ କର ମିଶାଇ ଖାଉଟିକୁ ଅଧିକ ଦରରେ ବିକ୍ରି କରିବାଦ୍ୱାରା କର ସ୍ଥାନାନ୍ତରଣ ହୋଇଥାଏ । ତେଣୁ ଦ୍ରବ୍ୟକର ଏକ ପରୋକ୍ଷ କର । ବିକ୍ରିକର, ଉତ୍ପାଦନ ଶୁଳ୍‌କ, ସୀମା ଶୁଳ୍‌କ, ପ୍ରମୋଦ କର, ମୂଲ୍ୟଯୁକ୍ତ କର ଇତ୍ୟାଦି ପରୋକ୍ଷ କରର ଉଦାହରଣ ।

12. ରାଜସ୍ବ ବ୍ୟୟ କ’ଣ ?
Answer:
ସରକାର ନିଜର ଦୈନନ୍ଦିନ କାର୍ଯ୍ୟନିର୍ବାହ ସକାଶେ ଯେଉଁ ବ୍ୟୟ ବରାଦ କରିଥା’ନ୍ତି, ତାହାକୁ ରାଜସ୍ବ ବ୍ୟୟ ବୋଲି କୁହାଯାଏ । ଉକ୍ତ ବ୍ୟୟଦ୍ବାରା ରାଷ୍ଟ୍ରର କୌଣସି ପରିସମ୍ପତ୍ତି ସୃଷ୍ଟି ହେବାର ସମ୍ଭାବନା ନଥାଏ । ସରକାରଙ୍କ ଅନ୍ତିମ ଉପଭୋଗ ବ୍ୟୟ ଏହି ଶ୍ରେଣୀଭୁକ୍ତ ହୋଇଥାଏ । ବିଭିନ୍ନ ସରକାରୀ ବିଭାଗର ସାଧାରଣ କାର୍ଯ୍ୟ ସମ୍ପାଦାନ ପାଇଁ ରାଜସ୍ବ ବ୍ୟୟ କରାଯାଏ ।

ଅତଏବ ଲୋକମାନଙ୍କୁ ବିଭିନ୍ନ ପ୍ରକାର ସେବା ଯୋଗାଇବାପାଇଁ ସରକାରୀ ବିଭାଗଗୁଡ଼ିକ ଯେଉଁ ଦୈନନ୍ଦିନ ବ୍ୟୟ କରିଥା’ନ୍ତି, ତାହାକୁ ରାଜସ୍ବ ବ୍ୟୟ ବୋଲି କୁହାଯାଏ । ଏହି ରାଜସ୍ବ ବ୍ୟୟ, ରାଜସ୍ବ ଆୟରୁ ଭରଣା କରାଯାଇଥାଏ ।

13. ଉନ୍ନୟନ ବ୍ୟୟ କ’ଣ ?
Answer:
ଯେଉଁ ସରକାରୀ ବ୍ୟୟଦ୍ୱାରା ଦେଶରେ ଉତ୍ପାଦନ ଓ ବାସ୍ତବ ଆୟ ବୃଦ୍ଧି ହୋଇ ଆର୍ଥନୀତିକ ଅଭିବୃଦ୍ଧି ହୋଇଥାଏ, ସେହି ବ୍ୟୟକୁ ଉନ୍ନୟନ ବ୍ୟୟ କୁହାଯାଏ । ଏହାକୁ ମଧ୍ୟ ଉତ୍ପାଦୀ ବ୍ୟୟ କୁହାଯାଇଥାଏ । ଭାରତ ଭଳି ଏକ ବିକାଶମୁଖୀ ରାଷ୍ଟ୍ରରେ ଉନ୍ନୟନ ବ୍ୟୟର ଗୁରୁତ୍ଵ ସର୍ବାଧ‌ିକ ।

ମୋଟ ଜାତୀୟ ଆୟ ଓ ମୁଣ୍ଡପିଛା ଆୟ ବୃଦ୍ଧିର ଲକ୍ଷ୍ୟ ଆମ ଦେଶର ଆର୍ଥିକ ନୀତିର ମୁଖ୍ୟ ଉଦ୍ଦେଶ୍ୟ । ୧୯୫୧ ମସିହାଠାରୁ ଆମ ଦେଶରେ ଏହି ବ୍ୟୟର ଗୁରୁତ୍ବ ବୃଦ୍ଧି ପାଇଅଛି । ଶିକ୍ଷା, ସ୍ୱାସ୍ଥ୍ୟ, ପରିବାର କଲ୍ୟାଣ, ଶ୍ରମ ଓ ନିଯୁକ୍ତି, କୃଷି, ଶିଳ୍ପ, ପରିବହନ ଇତ୍ୟାଦି ବିଭିନ୍ନ ଉନ୍ନୟନମୂଳକ କାର୍ଯ୍ୟ ପାଇଁ ବହନ କରାଯାଉଥ‌ିବା ସରକାରୀ ଖର୍ଚ୍ଚକୁ ଉନ୍ନୟନ ବ୍ୟୟ ବୋଲି ବିଚାର କରାଯାଇଥାଏ ।

C. ପାଞ୍ଚଟି/ଛଅଟି ବାକ୍ୟରେ ନିମ୍ନଲିଖ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଦିଅ ।

1. ଦାନ ଓ ଅନୁଦାନ :
Answer:
ବ୍ୟକ୍ତିବିଶେଷ କୌଣସି ନିର୍ଦ୍ଦିଷ୍ଟ ଉଦ୍ଦେଶ୍ୟରେ ସ୍ୱେଚ୍ଛାକୃତ ଭାବେ ସରକାରଙ୍କୁ ଦେଉଥ‌ିବା ଅର୍ଥ ବା ସମ୍ପତ୍ତିକୁ ଦାନ କୁହାଯାଏ । ସାଧାରଣତଃ କୌଣସି ବିପତ୍ତିର ମୁକାବିଲା ପାଇଁ ବଦାନ୍ୟ ବ୍ୟକ୍ତିବିଶେଷ ସରକାରଙ୍କୁ ଦାନ ଦେଇଥା’ନ୍ତି । ଯୁଦ୍ଧ, ବାତ୍ୟା, ବନ୍ୟା ଇତ୍ୟାଦିର ମୁକାବିଲା ପାଇଁ ଦାନ ସରକାରଙ୍କୁ ସହାୟତା ଯୋଗାଇଥାଏ । ଅବଶ୍ୟ, ରାଷ୍ଟ୍ରୀୟ ରାଜସ୍ୱରେ ଦାନର ଗୁରୁତ୍ଵ ନଗଣ୍ୟ ।

ଅନ୍ୟପକ୍ଷରେ ଗୋଟିଏ ସରକାର ଅନ୍ୟ ଏକ ସରକାରଙ୍କୁ କୌଣସି ନିର୍ଦ୍ଦିଷ୍ଟ ଉଦ୍ଦେଶ୍ୟରେ ହେଉଥ‌ିବା ସହାୟତାକୁ ଅନୁଦାନ କୁହାଯାଏ । ଆମ ଦେଶରେ କେନ୍ଦ୍ର ସରକାର ସ୍ବାସ୍ଥ୍ୟ ଓ ଶିକ୍ଷାର ବିକାଶ, ରାସ୍ତା ଓ ଗୃହ ନିର୍ମାଣ ଇତ୍ୟାଦି ନିମନ୍ତେ ରାଜ୍ୟମାନଙ୍କୁ ଅନୁଦାନ ଦେଇଥା’ନ୍ତି । ଆମ ଦେଶ ମଧ୍ୟ ବିଦେଶରୁ ଅନୁଦାନ ପାଇପାରେ । ଏହାକୁ ବିଦେଶୀ ଅନୁଦାନ କୁହାଯାଏ । ଅନୁଦାନ ରାଷ୍ଟ୍ରୀୟ ରାଜସ୍ଵରେ ଗୁରୁତ୍ବପୂର୍ଣ୍ଣ ଭୂମିକା ଗ୍ରହଣ କରେ ।

2. କର ଓ ସ୍ୱତନ୍ତ୍ର ନିର୍ଦ୍ଧାରଣ :
Answer:
କର ସମସ୍ତଙ୍କ ପାଇଁ ଏକ ବାଧ୍ୟତାମୂଳକ ଦେୟ; କିନ୍ତୁ ସ୍ୱତନ୍ତ୍ର ନିର୍ଦ୍ଧାରଣ କେବଳ ସ୍ବତନ୍ତ୍ର ସୁବିଧା ପାଉଥ‌ିବା ବ୍ୟକ୍ତିବିଶେଷଙ୍କ ପାଇଁ ବାଧ୍ୟତାମୂଳକ ଦେୟ । କର କରଦାତାଙ୍କୁ କୌଣସି ପ୍ରତ୍ୟକ୍ଷ ସୁବିଧା ଦେଇନଥାଏ; କିନ୍ତୁ ବିଶେଷ ନିର୍ଦ୍ଧାରଣରୁ ସ୍ୱତନ୍ତ୍ର ସୁବିଧା ମିଳିଥାଏ । କରର ପରିସର ସମଗ୍ର ରାଷ୍ଟ୍ର । ସରକାର ସମଗ୍ର ରାଷ୍ଟ୍ରରୁ କର ଆଦାୟ କରନ୍ତି; କିନ୍ତୁ ସ୍ବତନ୍ତ୍ର କରିଥା’ନ୍ତି । କର ସର୍ବଦା ସମାନୁପାତୀ ହୋଇନଥାଏ; କିନ୍ତୁ ସ୍ବତନ୍ତ୍ର ନିର୍ଦ୍ଧାରଣ ସର୍ବଦା ସମାନୁପାତୀ ହୋଇଥାଏ । କର ବାରମ୍ବାର ଧାର୍ଯ୍ୟ କରାଯାଏ କିନ୍ତୁ ସ୍ବତନ୍ତ୍ର ନିର୍ଦ୍ଧାରଣ ଥରେ ମାତ୍ର ଧାର୍ଯ୍ୟ କରାଯାଏ ।

3. ଫିଜ୍ ଓ ସ୍ଵତନ୍ତ୍ର ନିର୍ଦ୍ଧାରଣ :
Answer:
ଫିଲ୍ମର ପରିଚାଳନା କ୍ଷେତ୍ର ବ୍ୟାପକ । ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ସେବା ପାଇଁ ଯେକୌଣସି ସ୍ଥାନରେ ଏହା ଧାର୍ଯ୍ୟ କରାଯାଏ; କିନ୍ତୁ ସ୍ବତନ୍ତ୍ର ନିର୍ଦ୍ଧାରଣର ପରିଚାଳନା କ୍ଷେତ୍ର ସୀମିତ । ଏହା ଆଞ୍ଚଳିକ ଉନ୍ନୟନ ନିମନ୍ତେ ଧାର୍ଯ୍ୟ କରାଯାଇଥାଏ । ନିର୍ଦ୍ଦିଷ୍ଟ ସୁବିଧା ଉପଭୋଗ ପାଇଁ ପ୍ରତ୍ୟେକ ଥର ଫିଜ୍ ଦେବାକୁ ହୋଇଥାଏ । ତେଣୁ ଫିଜ୍ ବାରମ୍ବାର ଦିଆଯାଏ; କିନ୍ତୁ ବିଶେଷ ନିର୍ଦ୍ଧାରଣ ଥରେ ମାତ୍ର ଦେବାକୁ ହୋଇଥାଏ ।

ଯେକୌଣସି ବ୍ୟକ୍ତିବିଶେଷ ନିର୍ଦ୍ଦିଷ୍ଟ ସେବାପାଇଁ ସରକାରଙ୍କଦ୍ଵାରା ଧାର୍ଯ୍ୟ ଫିଜ୍ ଦେଇଥା’ନ୍ତି; କିନ୍ତୁ ସ୍ବତନ୍ତ୍ର ନିର୍ଦ୍ଧାରଣ କେବଳ ବିଶେଷ ସୁବିଧା ଲାଭ କରିଥିବା ବ୍ୟକ୍ତିମାନଙ୍କ ପାଇଁ ଧାର୍ଯ୍ୟ କରାଯାଏ ।

4. କର ଓ ଦର :
Answer:
କରି ସମସ୍ତଙ୍କ ପାଇଁ ଏକ ବାଧ୍ୟତାମୂଳକ ଦେୟ; କିନ୍ତୁ ଦର ସମସ୍ତଙ୍କ ପାଇଁ ବାଧ୍ୟତାମୂଳକ ନୁହେଁ । କେବଳ ସରକାରଙ୍କଦ୍ଵାରା ପ୍ରସ୍ତୁତ ଦ୍ରବ୍ୟ ଓ ସେବା କ୍ରୟ କରୁଥିବା ବ୍ୟକ୍ତିବିଶେଷ ଦର ଦେଇଥା’ନ୍ତି । ଏହା ସ୍ୱେଚ୍ଛାକୃତ । କର କରଦାତାଙ୍କୁ କୌଣସି ପ୍ରତ୍ୟକ୍ଷ ସୁବିଧା ଦେଇନଥାଏ; କିନ୍ତୁ ଦର ପ୍ରତ୍ୟକ୍ଷ ସୁବିଧା ଦେଇଥାଏ । ସେବା ପରିବ୍ୟୟ ସହ କରର କୌଣସି ସମ୍ପର୍କ ନଥାଏ, କିନ୍ତୁ ସେବା ପରିବ୍ୟୟ ସହିତ ଦରର ପୂର୍ଣ ସମ୍ପର୍କ ରହିଛି । ସର୍ବସାଧାରଣଙ୍କ କଲ୍ୟାଣ ନିମନ୍ତେ କର ଦିଆଯାଏ; କିନ୍ତୁ କେବଳ ବ୍ୟକ୍ତିଗତ ସନ୍ତୋଷ ନିମନ୍ତେ ଦର ଦିଆଯାଏ ।

5. କର ଓ ଫିଜ୍ :
Answer:
କର ସମସ୍ତଙ୍କ ପାଇଁ ଏକ ବାଧ୍ୟତାମୂଳକ ଦେୟ; କିନ୍ତୁ, ଅନ୍ୟପକ୍ଷରେ କୌଣସି ନିର୍ଦ୍ଦିଷ୍ଟ ସେବା ଉପଭୋଗ କରୁଥିବା ବ୍ୟକ୍ତିବିଶେଷଙ୍କ ପାଇଁ ଫିଜ୍ ଏକ ବାଧ୍ୟତାମୂଳକ ଦେୟ । ସରକାରଙ୍କ ବ୍ୟୟ ତୁଲାଇବା ନିମନ୍ତେ କର ଆଦାୟ କରାଯାଏ; କିନ୍ତୁ ପ୍ରଶାସନିକ ନିୟନ୍ତ୍ରଣ ଫିଜ୍ ଆଦାୟର ମୁଖ୍ୟ ଉଦ୍ଦେଶ୍ୟ । ସାଧାରଣ ସୁବିଧା ପାଇଁ କର ଧାର୍ଯ୍ୟ କରାଯାଇଥାଏ; କିନ୍ତୁ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ସୁବିଧା ପାଇଁ ଫିଜ୍ ଧାର୍ଯ୍ୟ କରାଯାଏ । ସରକାରଙ୍କଦ୍ୱାରା ପ୍ରଦତ୍ତ ସେବା ପାଇଁ ଦେଉଥ‌ିବା ବ୍ୟୟ ସହିତ କରର କୌଣସି ସମ୍ପର୍କ ନଥିଲାବେଳେ ସେବା ପରିବ୍ୟୟ ସହିତ ଫିଡ୍‌ର ସମ୍ପର୍କ ଦେଖ‌ିବାକୁ ମିଳେ ।

6. ରାଜସ୍ଵ ବ୍ୟୟ ଓ ପୁଞ୍ଜି ବ୍ୟୟ :
Answer:
ଯେଉଁ ବ୍ୟୟ ସରକାରଙ୍କଦ୍ଵାରା ସଂଗୃହୀତ ରାଜସ୍ୱ; ଯଥା – କର, ରେଳବାଇ, ଡାକ ଓ ତାର, ଅନ୍ୟାନ୍ୟ ସରକାରୀ କାର୍ଯ୍ୟରୁ ସଂଗୃହୀତ ଅର୍ଥଦ୍ଵାରା ସଂଘଟିତ ହୋଇଥାଏ, ତାହାକୁ ରାଜସ୍ବ ବ୍ୟୟ କୁହାଯାଏ । ସରକାରଙ୍କ ବିଭିନ୍ନ ବିଭାଗ ଓ ପ୍ରଶାସନ ତଥା ଅନ୍ୟାନ୍ୟ ସ୍ଥାୟୀ ସେବା ପ୍ରଦାନକାରୀ କ୍ଷେତ୍ରରେ ସ୍ଵାଭାବିକ ପରିଚାଳନା ନିମନ୍ତେ ରାଜସ୍ୱ ବ୍ୟୟ କରାଯାଇଥାଏ ।

ସଂକ୍ଷେପରେ କହିବାକୁ ଗଲେ ସରକାରଙ୍କ ଯେଉଁ ବ୍ୟୟ ପରିସମ୍ପତ୍ତି ବା ସମ୍ପଦ ସୃଷ୍ଟି କରିବାରେ ଉପଯୋଗ ହୁଏ ନାହିଁ, ତାହାକୁ ରାଜସ୍ବ ବ୍ୟୟ କୁହାଯାଏ । ସରକାରଙ୍କର ପରିଚାଳନା ବାବଦ ବ୍ୟୟ, ବିଭିନ୍ନ ସ୍ଥାୟୀ ସେବାକ୍ଷେତ୍ର ନିମନ୍ତେ ବ୍ୟୟ, ସରକାରୀ ଋଣ ଉପରେ ସୁଧ ପ୍ରଦାନଜନିତ ବ୍ୟୟ, ରାଜ୍ୟ ସରକାରଙ୍କୁ ପ୍ରଦାନ କରାଯାଉଥ‌ିବା ଅନୁଦାନ ଏହାର ଅନ୍ତର୍ଭୁକ୍ତ ।

ଯେଉଁ ବ୍ୟୟ, ପୁଞ୍ଜି ସଂଗ୍ରହଜନିତ ପ୍ରାପ୍ତି; ଯଥା – ଖୋଲାବଜାର ରଣ, ରିଜର୍ଭ ବ୍ୟାଙ୍କଦ୍ୱାରା ସରକାରଙ୍କୁ ପ୍ରଦତ୍ତ ଋଣ ଓ ଦେଶ ଭିତରେ ଓ ବାହାରେ ଥ‌ିବା ଅନୁଷ୍ଠାନମାନଙ୍କଦ୍ଵାରା ପ୍ରଦତ୍ତ ଋଣଦ୍ବାରା ଭରଣା କରାଯାଇଥାଏ, ତାହାକୁ ପୁଞ୍ଜି ବ୍ୟୟ କୁହାଯାଏ । ଏହି ବ୍ୟୟଭାର ବୈଦେଶିକ ଋଣ, ଆନ୍ତର୍ଜାତୀୟ ଅନୁଷ୍ଠାନମାନଙ୍କଦ୍ୱାରା ପ୍ରଦତ୍ତ ଋଣ ଓ ରାଜ୍ୟ ସରକାରଙ୍କଦ୍ବାରା ପରିଶୋଧ କରାଯାଉଥ‌ିବା ଋଣଦ୍ଵାରା ମଧ୍ୟ ବହନ କରାଯାଇଥାଏ । ଏହି ବ୍ୟୟ ସାଧାରଣଭାବେ ଭୂମି ଅଧୃତ, କୋଠାବାଡ଼ି ନିର୍ମାଣ, ଯନ୍ତ୍ରପାତି ଓ କଳକବ୍‌ଜା କ୍ରୟ, ଅଂଶଧନରେ ବିନିଯୋଗ ଏବଂ ରାଜ୍ୟ ସରକାରଙ୍କ ଅଗ୍ରିମ ନିମନ୍ତେ କରାଯାଇଥାଏ ।

7. ପ୍ରତ୍ୟକ୍ଷ କର ଓ ପରୋକ୍ଷ କର :
Answer:
ଯେଉଁ ବ୍ୟକ୍ତି ଉପରେ କର ଧାର୍ଯ୍ୟ କରାଯାଇଥାଏ ସେ ଯଦି କରଭାର ବହନ କରେ, ତାହାହେଲେ ସେ ପ୍ରକାର କର ଏକ ପ୍ରତ୍ୟକ୍ଷ କର । ସେ ଅନ୍ୟ କୌଣସି ବ୍ୟକ୍ତିଙ୍କୁ କରଭାର ହସ୍ତାନ୍ତର କରିପାରେ ନାହିଁ । ଆୟକର ଏକ ପ୍ରତ୍ୟକ୍ଷ କରର ଦୃଷ୍ଟାନ୍ତ । ଏହାର କରାଘାତ ଓ କରାପାତ ସମାନ ବ୍ୟକ୍ତି ଉପରେ ପଡ଼େ । ଡାଲଟନ୍‌ଙ୍କ ଭାଷାରେ, ‘ପ୍ରତ୍ୟକ୍ଷ କର ତାହାକୁ କୁହାଯାଏ ଯେଉଁ କ୍ଷେତ୍ରରେ, ଆଇନ ଅନୁଯାୟୀ ଯେଉଁ ବ୍ୟକ୍ତି ଉପରେ ଟିକସ ଧାର୍ଯ୍ୟ କରାଯାଏ, ସେହିଁ ପ୍ରକୃତରେ ଏହା ଭରଣା କରେ ।’

ଯେଉଁ କରଗୁଡ଼ିକ ପ୍ରଥମେ ଜଣେ ବ୍ୟକ୍ତି ଦେଇଥା’ନ୍ତି; କିନ୍ତୁ ପରେ ଅନ୍ୟ କୌଣସି ଜଣେ ବ୍ୟକ୍ତିଙ୍କ ଉପରକୁ ଖସାଇ ଦିଆଯାଇଥାଏ, ସେଗୁଡ଼ିକୁ ପରୋକ୍ଷ କର କୁହାଯାଏ । ଏଠାରେ କରାଘାତ ପ୍ରଥମ ବ୍ୟକ୍ତି ଉପରେ ପଡ଼ିଥାଏ ଓ କରାପାତ ଦ୍ବିତୀୟ ବ୍ୟକ୍ତିଙ୍କ ଉପରେ ପଡ଼ିଥାଏ । କେତେକ କ୍ଷେତ୍ରରେ ମୋଟ କରାପାତ ଦ୍ବିତୀୟ ବ୍ୟକ୍ତି ଉପରେ ପୂରା ଭାବରେ ପଡ଼ିନଥାଏ ।

ଡାଲଟନ୍‌ଙ୍କ ମତରେ, ‘ପରୋକ୍ଷ କର ଜଣେ ବ୍ୟକ୍ତି ଉପରେ ବସାଯାଏ, କିନ୍ତୁ ପ୍ରକୃତ କରଦାତା ଓ ଅନ୍ୟାନ୍ୟ ସମ୍ପର୍କୀୟ ପୂର୍ବ ସର୍ଭାବଳୀରେ ଏକ ଆନୁଷଙ୍ଗିକ ପରିବର୍ତ୍ତନ ଯୋଗୁଁ ନିର୍ଦ୍ଧାରିତ କରର ପୁରା ଭାଗ ବା ଏହାର କିଛି ଅଂଶ ପ୍ରକୃତରେ ଅନ୍ୟକୁ ଦେବାକୁ ପଡ଼ିଥାଏ ।’

8. କରାଘାତ ଓ କରାପାତ :
Answer:
କରଧାର୍ଯ୍ୟ ହେବା ପରେ ଯେଉଁମାନଙ୍କୁ ପ୍ରଥମେ କର ଦେବାକୁ ହୋଇଥାଏ ସେମାନଙ୍କ ଉପରେ କରାଘାତ ହେଲା ବୋଲି କୁହାଯାଏ । ଅନ୍ୟପକ୍ଷରେ ଯେଉଁମାନେ ପରିଶେଷରେ କର ଭାର ବହନ କରନ୍ତି ସେମାନଙ୍କ ଉପରେ କରାପାତ ହୋଇଥାଏ । କରାଘାତ କହିଲେ କରର ଧାର୍ଯ୍ୟ ବିନ୍ଦୁକୁ ବୁଝାଉଥିବାବେଳେ କରାଘାତ କହିଲେ କରର ଅନ୍ତିମ ଭାରବିନ୍ଦୁକୁ ବୁଝାଇଥାଏ । କରାପାତ କର ସ୍ଥାନାନ୍ତରଣ ଅନ୍ତିମ ପରିଣାମ ।

ଯେଉଁ ଲୋକମାନଙ୍କ ଉପରେ କରାଘାତ ହୁଏ, ସେମାନେ କରର ପ୍ରାଥମିକ ଭାର ବହନ କରନ୍ତି । ଅନ୍ୟ ପକ୍ଷରେ ଯେଉଁମାନଙ୍କ ଉପରେ କରାପାତ ହୁଏ ସେମାନେ କରର ଅନ୍ତିମ ଭାର କରଥା’ନ୍ତି ।

9. ଉପାର୍ଜିତ ରାଜସ୍ଵ ଓ ଅନୁପାର୍ଜିତ ରାଜସ୍ଵ :
Answer:
ରାଷ୍ଟ୍ର ନିଜ ମାଲିକାନାରେ ଥିବା ପ୍ରାକୃତିକ ସମ୍ବଳଗୁଡ଼ିକର ଉପଯୋଗ କରି ଯେଉଁ ରାଜସ୍ୱ ସଂଗ୍ରହ କରିଥାଏ, ତାହାକୁ ଉପାର୍ଜିତ ରାଜସ୍ୱ ଆଖ୍ୟା ଦିଆଯାଇଥାଏ । ଏତଦ୍‌ବ୍ୟତୀତ ରାଷ୍ଟ୍ରାୟତ୍ତ ବାଣିଜ୍ୟିକ ଓ ଔଦ୍ୟୋଗିକ ସଂସ୍ଥାମାନଙ୍କରୁ ରାଷ୍ଟ୍ର ଯେଉଁ ଆୟ ଅର୍ଜନ କରିଥାଏ, ତାହାକୁ ଉପାର୍ଜିତ ରାଜସ୍ୱ କୁହାଯାଏ । ସରକାର ମଧ୍ୟ ଏକ ଉଦ୍ୟୋକ୍ତା । ସରକାରୀ ଉଦ୍ୟୋଗରେ ଉତ୍ପାଦିତ ବିଭିନ୍ନ ଦ୍ରବ୍ୟ ଓ ସେବା ବିକ୍ରୟ କରି ସରକାର ଯେଉଁ ରାଜସ୍ବ ପାଇଥା’ନ୍ତି, ତାହାକୁ ଉପାର୍ଜିତ ରାଜସ୍ୱ କୁହାଯାଏ ।

ଅନ୍ୟପକ୍ଷରେ ରାଷ୍ଟ୍ରର ଅନୁପାର୍ଜିତ ରାଜସ୍ବ ମୁଖ୍ୟତଃ ବ୍ୟକ୍ତି, ପରିବାର ଓ ପ୍ରତିଷ୍ଠାନମାନଙ୍କଠାରୁ ମିଳିଥାଏ । କର, ପ୍ରଶାସନିକ ଆୟ, ଉପହାର ଓ ଅନୁଦାନ ଆଦିକୁ ସରକାରଙ୍କ ଅନୁପାର୍ଜିତ ଆୟ ବୋଲି କୁହାଯାଇଥାଏ ।

10. ରାଷ୍ଟ୍ରବିତ୍ତ ଓ ବ୍ୟକ୍ତିବିର :
Answer:
ଜଣେ ବ୍ୟକ୍ତିଙ୍କ ଆୟ ପ୍ରାୟତଃ ସ୍ଥିର, ତେଣୁ ତାଙ୍କୁ ଆୟ ଅନୁସାରେ ବ୍ୟୟ କରିବାକୁ ପଡ଼େ; କିନ୍ତୁ ରାଷ୍ଟ୍ର ପ୍ରଥମେ ବ୍ୟୟ ପରିମାଣ ଆକଳନ କରି ବ୍ୟୟ ଭରଣା ପାଇଁ ବିଭିନ୍ନ ଆୟର ପନ୍ଥା ନିର୍ଦ୍ଧାରଣ କରେ ।

ଜଣେ ବ୍ୟକ୍ତି ପାଇଁ ଲାଭ ବ୍ୟୟର ମୁଖ୍ୟ ଉଦ୍ଦେଶ୍ୟ; କିନ୍ତୁ ଲାଭ ପ୍ରତ୍ୟାଶା ରାଷ୍ଟ୍ରର ମୁଖ୍ୟ ଆଭିମୁଖ୍ୟ ନୁହେଁ । ସର୍ବାଧିକ ଜନକଲ୍ୟାଣ ରାଷ୍ଟ୍ର ବ୍ୟୟର ଲକ୍ଷ୍ୟ ।

ଜଣେ ବ୍ୟକ୍ତିର ବଜେଟ୍ ତା’ର ନିଜସ୍ବ । ଏହା ସାଧାରଣରେ ପ୍ରକାଶିତ ହୋଇନଥାଏ ଏବଂ ଗୋପନ ରହିଥାଏ; କିନ୍ତୁ ସରକାରୀ ବଜେଟ୍ ଗୋପନୀୟ ନୁହେଁ ଏବଂ ଏହା ସର୍ବସାଧାରଣ ପାଇଁ ଖୋଲା ।

11. ଯୋଜନା ବ୍ୟୟ ଓ ଅଣଯୋଜନା ବ୍ୟୟ :
Answer:
ଯେଉଁ ବ୍ୟୟ ପାଇଁ ରାଷ୍ଟ୍ରୀୟ ଯୋଜନାର ଅନୁମୋଦନ ଆବଶ୍ୟକ, ତାହା ଯୋଜନା ବ୍ୟୟ । ବିଭିନ୍ନ ମନ୍ତ୍ରଣାଳୟ ଓ ବିଭାଗର ଆବଶ୍ୟକତା ଅନୁସାରେ ନୂତନ ଭାବେ ପ୍ରସ୍ତାବିତ ଓ ଅନୁମୋଦିତ ବ୍ୟୟକୁ ଯୋଜନା ବ୍ୟୟ କୁହାଯାଏ । ନୂତନ ରାସ୍ତା, ବନ୍ଧ ଇତ୍ୟାଦିର ନିର୍ମାଣଜନିତ ବ୍ୟୟ ହେଉଛି ଯୋଜନା ବ୍ୟୟ ଅଟେ ।

ଯେଉଁ ସରକାରୀ ବ୍ୟୟ ନିମନ୍ତେ ରାଷ୍ଟ୍ରୀୟ ଯୋଜନାର ଅନୁମୋଦନ ଆବଶ୍ୟକ ହୋଇନଥାଏ ତାହା ଅଣଯୋଜନା ବ୍ୟୟ । ଏହି ବ୍ୟୟଭାର ବହନ କରିବାପାଇଁ ସରକାର ବାଧ୍ୟ । ସ୍ଥାୟୀ କର୍ମଚାରୀମାନଙ୍କ ଦରମା ଓ ପେନ୍‌ସନ୍, ସୁଧ ପରିଶୋଧ, ଦେଶରକ୍ଷା ଇତ୍ୟାଦି ପାଇଁ ହେଉଥିବା ବ୍ୟୟ ହେଉଛି ଅଣଯୋଜନା ବ୍ୟୟ ।

12. ଉନ୍ନୟନ ବ୍ୟୟ ଓ ଅଣଉନ୍ନୟନ ବ୍ୟୟ :
Answer:
ଯେଉଁ ସରକାରୀ ବ୍ୟୟ ଅର୍ଥନୈତିକ ବିକାଶ ନିମନ୍ତେ ସହାୟତା ପ୍ରଦାନ କରେ, ତାହା ଉନ୍ନୟନ ବ୍ୟୟ । ଜାତୀୟ ଆୟ ବୃଦ୍ଧି ସହିତ ସାମାଜିକ ଓ ଅର୍ଥନୈତିକ ବିକାଶ ଉନ୍ନୟନ ବ୍ୟୟର ପ୍ରମୁଖ ଆଭିମୁଖ୍ୟ । କୃଷି, ଶିଳ୍ପ, ସ୍ବାସ୍ଥ୍ୟ, ଗମନାଗମନ ଇତ୍ୟାଦିର ଉନ୍ନତି ପାଇଁ ହେଉଥ‌ିବା ସରକାରୀ ବ୍ୟୟକୁ ଉନ୍ନୟନ ବ୍ୟୟ କୁହାଯାଏ ।

ସରକାର ଏପରି କେତେକ ନିର୍ଦ୍ଦିଷ୍ଟ ଉଦ୍ଦେଶ୍ୟରେ ବ୍ୟୟ କରିଥା’ନ୍ତି ଯେଉଁଗୁଡ଼ିକ ଅତ୍ୟାବଶ୍ୟକ ହୋଇଥିଲେ ମଧ୍ୟ ବିକାଶ କ୍ଷେତ୍ରରେ ସହାୟତା ପ୍ରଦାନ କରନ୍ତି ନାହିଁ । ଏପରି ସମସ୍ତ ସରକାରୀ ବ୍ୟୟକୁ ଅଣଉନ୍ନୟନ ବ୍ୟୟ କୁହାଯାଏ । ଆଇନ୍ ଓ ଶୃଙ୍ଖଳା, ପ୍ରତିରକ୍ଷା, ପ୍ରଶାସନ ଇତ୍ୟାଦି ପାଇଁ ସରକାର କରୁଥିବା ବ୍ୟୟ ଅଣଉନ୍ନୟନ ବ୍ୟୟର ଅନ୍ତର୍ଭୁକ୍ତ ।

Odisha State Board BSE Odisha 8th Class Science Solutions Chapter 15 କେତେକ ପ୍ରାକୃତିକ ଘଟଣା Textbook Exercise Questions and Answers.

BSE Odisha Class 8 Science Solutions Chapter 15 କେତେକ ପ୍ରାକୃତିକ ଘଟଣା

Question 1.
ନିମ୍ନୋକ୍ତ ପ୍ରତ୍ୟେକ ପ୍ରଶ୍ନର ଠିକ୍ ଉତ୍ତର ବାଛି ଲେଖ ।
(i) କେଉଁଟି ଘର୍ଷଣ ଦ୍ବାରା ସହଜରେ ଚାର୍ଜିତ ହୁଏ ନାହିଁ ?
(a) ଏକ ପ୍ଲାଷ୍ଟିକ୍ ସ୍କେଲ୍
(b) ଏକ ତମ୍ବା ଦଣ୍ଡ
(c) ଏକ ଫୁଙ୍କା ହୋଇଥ‌ିବା ବେଲୁନ୍
(d) ଏକ ପଶମ କପଡ଼ା
ଉ-
(b) ଏକ ତମ୍ବା ଦଣ୍ଡ

(ii) ଏକ କାଚଦଣ୍ଡକୁ ଛୋଟ ରେଶମ କପଡ଼ାରେ ଘଷିଲେ ।
(a) ଦଣ୍ଡ ଏବଂ କପଡ଼ା ଉଭୟ ଯୁକ୍ତଚାର୍ଜ ଗ୍ରହଣକରନ୍ତି ।
(b) ଦଣ୍ଡଟି ଯୁକ୍ତଭାବେ ଚାର୍ଜିତ ଓ କପଡ଼ାଟି ବିଯୁକ୍ତ ଭାବେ ଚାର୍ଜିତ ହୁଏ ।
(c) ଦଣ୍ଡ ଏବଂ କପଡ଼ା ଉଭୟ ବିଯୁକ୍ତ ଭାବେ ଚାର୍ଜିତ ହୁଅନ୍ତି ।
(d) ଦଣ୍ଡଟି ବିଯୁକ୍ତ ଭାବେ ଚାର୍ଜିତ ହୁଏ ଓ କପଡ଼ା ଯୁକ୍ତଭାବେ ଚାର୍ଜିତ ହୁଏ ।
ଉ-
(b) ଦଣ୍ଡଟି ଯୁକ୍ତ ଭାବେ ଚାର୍ଜିତ ହୁଏ ଓ କପଡ଼ା ବିଯୁକ୍ତଭାବେ ଚାର୍ଜିତ ହୁଏ ।

Question 2.
ନିମ୍ନ ଉକ୍ତିଗୁଡିକ ଠିକ୍ ଥିଲେ T, ଭୁଲ୍ ଥିଲେ I ଲେଖ ।
(a) ସମ ଚାର୍ଜ ପରସ୍ପରକୁ ଆକର୍ଷଣ କରନ୍ତି ।
(b) ଏକ ଚାର୍ଜିତ କାଚଦଣ୍ଡ ଏକ ଚାର୍ଜିତ ପ୍ଲାଷ୍ଟିକ୍ ଷ୍ଟ୍ରକୁ ଆକର୍ଷଣ କରେ ।
(c) ବିଜୁଳି ପରିଚାଳକ ଏକ କୋଠାଘରକୁ ବିଜୁଳି ଆଘାତରୁ ରକ୍ଷା କରି ପାରିବ ନାହିଁ ।
(d) ଭୂକମ୍ପର ପୂର୍ବାନୁମାନ କରି ହେବ ।

Answers
(a) F
(b) T
(c) F
(d) F

Question 3.
ଶୀତଦିନେ ସ୍ଟେଟର ଓହ୍ଲାଇବା ବେଳେ କାହିଁକି ଚଡ୍ ଚଡ୍ ଶବ୍ଦ ହୁଏ, ବୁଝାଅ ।
ଉ-
ସ୍ଵେଟର ପଶମରେ ନିର୍ମିତ ହୋଇଥାଏ । ଏହାକୁ ଓହ୍ଲାଇବା ସମୟରେ ଏହା ଶରୀରରେ ଲୋମସହ ଘର୍ଷଣ ହୋଇ ସ୍ପାର୍କ ସହ ଚଡ଼ ଚଡ଼ ଶବ୍ଦ ହୋଇଥାଏ ।

Question 4.
ଚାର୍ଜିତ ବସ୍ତୁକୁ ହାତରେ ଛୁଇଁଲେ ଏହା କାହିଁକି ଚାର୍ଜ ହରାଇ ଥାଏ, ବୁଝାଅ ।
ଉ-
ଆମ ଶରୀର ବିଦ୍ୟୁତ୍ ସୁପରିବାହୀ ହୋଇଥିବାରୁ ଚାର୍ଜିତ ବସ୍ତୁକୁ ହାତରେ ଛୁଇଁଲେ ଚାର୍ଜ ଆମ ଶରୀର ମଧ୍ୟରେ ଭୂପୃଷ୍ଠକୁ ସ୍ଥାନାନ୍ତରିତ ହୁଏ; ଫଳରେ ଚାର୍ଜିତ ବସ୍ତୁ ଚାର୍ଜ ହରାଇଥାଏ ।

Question 5.
ବିଜୁଳି ଆଘାତରୁ ରକ୍ଷାପାଇବାପାଇଁ ତିନୋଟି ପ୍ରତିକାର ବ୍ୟବସ୍ଥା ଲେଖ ।
ଉ-
(a) ବଡ଼ ବଡ଼ କୋଠାଘରମାନଙ୍କରେ ବିଦ୍ୟୁତ୍ ଚାଳକ ସଂଯୁକ୍ତ କରିବା ଆବଶ୍ୟକ ।
(b) ବିଜୁଳି ଘଡ଼ଘଡ଼ି ହେଉଥ‌ିବାବେଳେ ନିରାପଦ ସ୍ଥାନରୁ ବାହାରକୁ ନ ଯାଇ କିଛି ସମୟ ଅପେକ୍ଷା କରିବା ଉଚିତ ।
(c) ଏ ସମୟରେ କୌଣସି ଘର କିମ୍ବା କୋଠାଘର ନିରାପଦ ସ୍ଥାନ ।

Question 6.
ଏକ ଚାର୍ଜିତ ବେଲୁନ୍ ଆଉ ଏକ ଚାର୍ଜିତ ବେଲୁନ୍‌କୁ କାହିଁକି ବିକର୍ଷଣ କରେ ଏବଂ ଏକ ଚାର୍ଜ ନଥ‌ିବା ବେଲୁନ୍ ଆଉ ଏକ ଚାର୍ଜିତ ବେଲୁକୁ କାହିଁକି ଆକର୍ଷଣ କରେ, ବୁଝାଅ ।
ଉ-
ଏକା ଚାର୍ଜଥିବା ଦୁଇଟି ବେଲୁନ ପରସ୍ପରକୁ ବିକର୍ଷଣ କରନ୍ତି, କାରଣ ‘ସମପ୍ରକାର ଚାର୍ଜ ପରସ୍ପରକୁ ବିକର୍ଷଣ କରନ୍ତି’ ଓ ‘ଏକା ଚାର୍ଜ ହୀନ ଦୁଇଟି ବେଲୁନ ଚାର୍ଜ ଗ୍ରହଣ କରିବା ପାଇଁ ଆଉ ଏକ ଚାର୍ଜିତ ବେଲୁନ୍‌କୁ ଆକର୍ଷଣ କରନ୍ତି’ ।

Question 7.
ଚାର୍ଜିତ ବସ୍ତୁ ବିଷୟରେ ଜାଣିହେଉଥ‌ିବା ଯନ୍ତ୍ରଟିର ନାମ ଲେଖ ଓ ଚିତ୍ରସହ ଏହାର ଗଠନ ବର୍ଣ୍ଣନା କର ।
ଉ-
ଚାର୍ଜିତ ବସ୍ତୁ ବିଷୟରେ ଜାଣିହେଉଥ‌ିବା ଯନ୍ତ୍ରଟିର ନାମ ‘ସରଳ ଇଲେକ୍ଟ୍ରୋସ୍କୋପ୍’ ।
ଗଠନ :

• ଗୋଟିଏ ଖାଲି କାଚ ବୋତଲ ଉପରେ ଏହାର ମୁହଁଠାରୁ ସାମାନ୍ୟ ବଡ଼ ଗୋଟିଏ କାର୍ଡ଼ବୋର୍ଡ଼ ରଖାଯାଇଥାଏ ।
• କାର୍ଡ଼ବୋର୍ଡ଼ ମଝିରେ ଗୋଟିଏ ରନ୍ଧ୍ର କରାଯାଇଥାଏ ।
• ରନ୍ଧ୍ର ବାଟେ ଗୋଟିଏ ଧାତବ କ୍ଲିପରେ ଦୁଇଟି ପତଳା ଆଲୁମିନିୟମ୍ ଫଏଲ ଝୁଲାଇ ରଖାଯାଇଥାଏ ।
• ଆଲୁମିନିୟମ୍ ଫଏଲର ଦୈର୍ଘ୍ୟ 4 ସେ.ମି. ଓ ପ୍ରସ୍ଥ । ସେ.ମି. ହୋଇଥାଏ ।
• ଧାତବ କ୍ଲିପଟି କାର୍ଡ଼ବୋର୍ଡ଼ ସହ ଲମ୍ବ ଭାବରେ ଅବସ୍ଥାନ କରିଥାଏ ।
• କ୍ଲିପ୍‌ର ଯେଉଁ ପ୍ରାନ୍ତରେ ଫଏଲ ଝୁଲାଯାଏ ତାହା ବୋତଲ ଭିତରକୁ ଓ ଅନ୍ୟ ପ୍ରାନ୍ତଟି କାର୍ଡ଼ବୋର୍ଡ଼ ଉପରକୁ ରହିଥାଏ ।

Question 8.
ଭାରତର ତିନୋଟି ଭୂକମ୍ପ ପୀଡ଼ିତ ରାଜ୍ୟର ନାମ ଲେଖ ।
ଉ-
ଜାମ୍ମୁ ଓ କାଶ୍ମୀର, ରାଜସ୍ଥାନ, ଗୁଜରାଟ

Question 9.
ମନେକର ତୁମେ ଘର ବାହାରେ ଅଛ । ହଠାତ୍‌ ଭୂମିକମ୍ପ ହେଲା, ନିଜର ସୁରକ୍ଷା ପାଇଁ କି ପ୍ରକାର ପ୍ରତିକାର ବ୍ୟବସ୍ଥା ଗ୍ରହଣକରିବ, ଲେଖ ।
ଉ-

• ଖୋଲାଜାଗା ଦେଖୁ ରହିବୁ; ଗଛ, କୋଠାଘର ଏବଂ ଉପରେ ଯାଇଥିବା ବିଦ୍ୟୁତ୍ ଲାଇନ୍ ଇତ୍ୟାଦିଠାରୁ ଦୂରରେ ରହିବୁ, ଯଥାସମ୍ଭବ ଦୂରରେ ଭୂମି ଉପରେ ଆଣ୍ଠୁ ମଝିରେ ମୁହଁ ପୋତି ବସିରହିବୁ ।
• ବସ୍ କିମ୍ବା କାରରେ ଥିଲେ ଭିତରୁ ବାହାରକୁ ଆସିବା ଉଚିତ ନୁହେଁ । ଧୀରେ ଗାଡ଼ି ଚଳାଇ ନିକଟସ୍ଥ କୌଣସି ଖୋଲାଜାଗାକୁ ଯିବୁ ଏବଂ ଭୂମିକମ୍ପ ବନ୍ଦ ନହେବା ପର୍ଯ୍ୟନ୍ତ ଗାଡ଼ି ଖୋଲିବା ଉଚିତ ନୁହେଁ ।

Question 10.
ପାଣିପାଗ ବିଭାଗ ଦ୍ବାରା ସୂଚନା ଦିଆଗଲା ଯେ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଦିନରେ ଝଡ଼ ହେବ, ତୁମକୁ ସେଦିନ ବାହାରକୁ ଯିବାକୁ ଅଛି, ତୁମେ ସାଥୀରେ ଛତା ନେଇ ଯିବ କି, ବୁଝାଅ ।
ଉ-
ବିଜୁଳି ଓ ଘଡ଼ଘଡ଼ି ସହ ବର୍ଷାବେଳେ ଛତାଧରି ଯିବା ବିପଦ ଅଟେ; କାରଣ

• ଛତାର ମଧ୍ୟଭାଗରେ ଥ‌ିବା ବେଣ୍ଟ ସାଧାରଣତଃ ଲୁହାରେ ତିଆରି ହୋଇଥାଏ ।
• ଛତାର ଗୋଟିଏ ପ୍ରାନ୍ତକୁ ଆମେ ହାତରେ ଧରୁଥିବାବେଳେ ଅନ୍ୟ ପ୍ରାନ୍ତଟି ଗୋଜିଆ ହୋଇ ଉପର ଆଡ଼କୁ ରହିଥାଏ ।
• ଛତାର ଏହି ମୁନ ବାଟ ଦେଇ ବିଦ୍ୟୁତ୍ ବିସର୍ଜନ ପ୍ରକ୍ରିୟା ସହଜ ହୁଏ ଓ ବାୟୁମଣ୍ଡଳରୁ ବିଦ୍ୟୁତ୍ ଚାର୍ଜ ଶରୀରକୁ  ଆସିବାର ସମ୍ଭାବନା ରହିଥ‌ିବା ସହ ଦୂର୍ଘଟଣା ଘଟିବାର ମଧ୍ୟ ଆଶଙ୍କା ରହିଥାଏ ।

ପରୀକ୍ଷା ଉପଯୋଗୀ ଅତିରିକ୍ତ ପ୍ରଶ୍ନୋତ୍ତର

ବସ୍ତୁନିଷ୍ଠ ପ୍ରଶ୍ନେ। ଭର

1. ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

(i) ବିଜୁଳି ଓ ଘଡ଼ଘଡ଼ି ପ୍ରକୃତିରେ ଘଟୁଥ‌ିବା ଏକପ୍ରକାର ………………….. ଅଟେ ।
(ii) ଅମ୍ବର ଏକପ୍ରକାର ପ୍ରାକୃତିକ ପଲିମର୍ ବା …………………… ଅଟେ ।
(iii) ଘର୍ଷଣଦ୍ଵାରା ପଦାର୍ଥକୁ …………………. କରାଯାଇପାରେ ।
(iv) ସମପ୍ରକାର ଚାର୍ଜ ପରସ୍ପରକୁ …………………… କରନ୍ତି ।
(v) ଅସମ ପ୍ରକାରର ଚାର୍ଜ ପରସ୍ପରକୁ ………………….. କରନ୍ତି ।
(vi) କାଚଦଣ୍ଡକୁ ରେଶମ କନାରେ ଘଷିଲେ କାଚଦଣ୍ଡରେ ……………………… ଚାର୍ଜ ସୃଷ୍ଟି ହୁଏ ।
(vii) କାଚଦଣ୍ଡକୁ ରେଶମ କନାରେ ଘଷିଲେ ରେଶମ କନାରେ …………………….. ଚାର୍ଜ ସୃଷ୍ଟି ହୁଏ ।
(viii) ଘର୍ଷଣଜନିତ ପଦାର୍ଥରେ ସୃଷ୍ଟ ଚାର୍ଜକୁ …………………… ଚାର୍ଜ କୁହାଯାଏ ।
(ix) ଯେଉଁ ସାଧନ ଦ୍ଵାରା ବସ୍ତୁଟି ଚାର୍ଜ ହୋଇଛି …………………. କୁହାଯାଏ ।

(xi) ବିଜୁଳି ଦେଖାଯିବାର କିଛି ସମୟପରେ …………………… ଶବ୍ଦ ଶୁଭେ ।
(xii) ବିଜୁଳି ଘଡ଼ଘଡ଼ି ସହ ବର୍ଷାବେଳେ …………………. ଧରି ଯିବା ବିପଦ ଅଟେ ।
(xiii) ବଜ୍ରପାତର ପ୍ରଭାବରୁ ସୁରକ୍ଷାପାଇଁ କୋଠାଘରଗୁଡ଼ିକରେ ……………………. ସଂଯୁକ୍ତ କରାଯାଇଥାଏ ।
(xiv) ବର୍ତ୍ତମାନ ସୁଦ୍ଧା ……………………… ପରି ପ୍ରାକୃତିକ ବିପର୍ଯ୍ୟୟ ବିଷୟରେ କୌଣସି ପୂର୍ବାନୁମାନ କରାଯାଇପାରୁ ନାହିଁ ।
(xv) 2005 ମସିହା ଅକ୍ଟୋବର ……………………….. ତାରିଖରେ ଉତ୍ତର କାଶ୍ମୀରରେ ବଡ଼ଧରଣର ଭୂମିକମ୍ପ ହୋଇଥିଲା ।
(xvi) 2001 ମସିହା ଜାନୁଆରୀ …………………….. ତାରିଖରେ ଉତ୍ତର କାଶ୍ମୀରରେ ବଡ଼ଧରଣର ଭୂମିକମ୍ପ ହୋଇଥିଲା ।
(xvii) ପୃଥ‌ିବୀପୃଷ୍ଠ ହଠାତ୍ ଥରିବାକୁ ଆରମ୍ଭକଲେ ………………….. ଅନୁଭୂତ ହୁଏ ।
(xviii) ବନ୍ୟା, ଭୂସ୍ଖଳନ ଓ ସୁନାମି …………………… ର ପ୍ରଭାବରେ ହୋଇଥାଏ ।
(xix) ପୃଥ‌ିବୀର ବାହ୍ୟ ଆବରଣ ଅନେକ ସ୍ତରରେ ଗଠିତ । ପ୍ରତ୍ୟେକ ସ୍ତରକୁ ………………….. କୁହାଯାଏ ।
(xx) ଭୂକମ୍ପ ତରଙ୍ଗକୁ …………………. ଲିପିବଦ୍ଧ କରାଯାଏ ।

Answer:
(i) ଷ୍ଟାର୍କ
(ii) ରେ ଚ୍ଚିନ୍
(iii) ଚାର୍ଜିତ
(iv) ବିକର୍ଷଣ
(v) ଆକର୍ଷଣ
(vi) ଯୁକ୍ତ
(vii) ବିଯୁକ୍ତ
(viii) ସ୍ଥିର ବିଦ୍ୟୁତ୍
(ix) ଇଲେକ୍‌ଷ୍ଟୋପ
(xiii) ବିଜୁଳି ଚାଳକ
(xii) ଭୂକମ୍ପ
(x) 212
(xi) ଘଡ଼ଘଡ଼ି
(xii) ଛତା
(Xiv) ଭୂମିକମ୍ପ ଓ ସୁନାମି
(xv) 8
(xvi) 26
(xviii) ଭୂମିକମ୍ପ
(xix) ପ୍ଲେଟ୍
(xx) ସେସ୍‌ମୋଗ୍ରାଫ୍

2. ବନ୍ଧନୀ ମଧ୍ଯରୁ ଉପଯୁକ୍ତ ଶବ୍ଦ ବାଛି ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

(i) ……………….. ଗୋଟିଏ ପ୍ରାକୃତିକ ଘଟଣା ନୁହେଁ ! (ବନ୍ୟା, ବାତ୍ୟା, ଭୂମିକମ୍ପ, ପରମାଣୁ ବୋମା ପରୀକ୍ଷଣ )
(ii) ବିଜୁଳି ଓ ଘଡ଼ଘଡ଼ି ଯୋଗୁଁ କୋଠାଘର ଫାଟିଗଲେ ଏହାକୁ ……………………….. କୁହାଯାଏ । (ଭୂମିକମ୍ପ, ସୁନାମି, ବଜ୍ରପାତ, ବାତ୍ୟା)
(iii) ର୍କ ଓ ବିଜୁଳି ପ୍ରାୟ ଏକାପ୍ରକାରର । ଏହା ବୈଜ୍ଞାନିକ …………………. ଦର୍ଶାଇଥିଲେ । (ଫ୍ରାଙ୍କ୍‌ଲିନ୍, ଆଇନ୍‌ଷ୍ଟାଇନ୍, ନିଉଟନ୍, ବ୍ଲାକ୍‌ମ୍ୟାନ୍)
(iv) ସମପ୍ରକାର ଚାର୍ଜ ପରସ୍ପରକୁ …………………… କରନ୍ତି । (ଆକର୍ଷଣ, ବିକର୍ଷଣ, ନିରପେକ୍ଷ, କୌଣସିଟି ନୁହେଁ)
(v) ଅସମ ପ୍ରକାର ଚାର୍ଜ ପରସ୍ପରକୁ …………………. କରନ୍ତି । ( ଆକର୍ଷଣ, ବିକର୍ଷଣ, ନିରପେକ୍ଷ, କୌଣସିଟି ନୁହେଁ )
(vi) କାଚଦଣ୍ଡକୁ ରେଶମ କନାରେ ଘଷିଲେ କାଚଦଣ୍ଡରେ …………………….. ଚାର୍ଜ ସୃଷ୍ଟି ହୁଏ । (ଧନାତ୍ମକ, ରଣାତ୍ମକ, ନିରପେକ୍ଷ, କୌଣସିଟି ନୁହେଁ)
(vii) କାଚଦଣ୍ଡକୁ ରେଶମ କନାରେ ଘଷିଲେ ରେଶମ କନାରେ ………………….. ଚାର୍ଜ ସୃଷ୍ଟି ହୁଏ । (ଧନାତ୍ମକ, ଋଣାତ୍ମକ, ନିରପେକ୍ଷ, କୌଣସିଟି ନୁହେଁ)
(viii) ଘର୍ଷଣଜନିତ ପଦାର୍ଥରେ ସୃଷ୍ଟ ଚାର୍ଜକୁ …………………… ଚାର୍ଜ କୁହାଯାଏ । (ଧନାତ୍ମକ, ଋଣାତ୍ମକ, ସ୍ଥିର ବିଦ୍ୟୁତ୍ ଚାର୍ଜ, କୌଣସିଟି ନୁହେଁ)
(ix) ଇଲେକ୍ଟ୍ରୋସ୍କୋପ୍‌ରେ ……………………. ସମ୍ବକ୍ଷରେ ପରୀକ୍ଷଣ କରାଯାଏ । (ଚାର୍ଜ, ବିଦ୍ୟୁତ୍ ସ୍ରୋତ, ବିଭବ ପାର୍ଥକ୍ୟ, ପ୍ରତିରୋଧ )
(x) ଗୋଟିଏ ଚାର୍ଜ ହୋଇଥ‌ିବା ବସ୍ତୁରୁ ପୃଥ‌ିବୀମଧ୍ୟକୁ ଚାର୍ଜର ସ୍ଥାନାନ୍ତରଣକୁ …………………… କୁହାଯାଏ । (ବିଦ୍ୟୁତ୍ ବିସର୍ଜନ, ସ୍ଥର ବିଦ୍ୟୁତ୍, ବଜ୍ରପାତ, ଆଣ୍ଟିଂ)

Answer:
(i) ପରମାଣୁ ବୋମା ପରୀକ୍ଷଣ
(ii) ବଜ୍ରପାତ
(iii) ଫ୍ରାଙ୍କ୍‌ଲିନ୍‌
(iv) ବିକର୍ଷଣ
(v) ଆକର୍ଷଣ
(vi) ଧନାତ୍ମକ
(vii) ଋଣାତ୍ମକ
(viii) ସ୍ଥିର ବିଦ୍ୟୁତ୍ ଚାର୍ଜ
(ix) ଚାର୍ଜ
(x) ଆର୍ଥି

3. ବାମ ପାର୍ଶ୍ୱସ୍ଥ ଶବ୍ଦପୁଞ୍ଜକୁ ଲକ୍ଷ୍ୟ କରି ଦକ୍ଷିଣ ପାର୍ଶ୍ଵରେ ଥ‌ିବା ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

(i) ମେଘ : ବିଯୁକ୍ତାତ୍ମକ :: ଭୂପୃଷ୍ଠ : …………………….।
(ii) ଆଲୋକ : ବିଜୁଳି :: ଶବ୍ଦ : …………………….।
(iii) ଆଲୋକ : ଶୀଘ୍ର :: ଶବ୍ଦ : …………………….।
(iv) ଯୁକ୍ତାତ୍ମକ ଚାର୍ଜ : ମେଘର ଉପର ସ୍ତର :: ବିଯୁକ୍ତାତ୍ମକ ଚାର୍ଜ : …………………….।
(v) 2005 : କାଶ୍ମୀରର ୟୁରି :: 2001 : …………………….।
(vi) ବିଦ୍ୟୁତ୍ ଚାର୍ଜ : ଇଲେକ୍‌ଟ୍ରୋସ୍କୋପ୍ :: ସେସ୍‌ମିକ୍ ତରଙ୍ଗ : …………………….।
(vii) କ୍ଷୟକ୍ଷତି କମ୍ : ରୁ କମ୍ :: କ୍ଷୟକ୍ଷତି ଅଧୂକ : …………………….।
(viii) ସମ ପ୍ରକାର ଚାର୍ଜ : ବିକର୍ଷଣ :: ଅସମ ପ୍ରକାର ଚାର୍ଜ :
(ix) ଯୁକ୍ତାତ୍ମକ : କାଚଦଣ୍ଡ :: ଋଣାତ୍ମକ : …………………….।
(x) ପେନ୍‌ସିଲ : ପଶମକନା :: ପ୍ଲାଷ୍ଟିକ୍ ପାନିଆ : …………………….।

Answer:
(i) ଧନ। ମୂକ
(ii) ଘଡ଼ଘଡ଼ି
(iii) ଡେରି
(iv) ମେଘର ତଳ ସ୍ତର
(v) ଗୁଜରାଟର ଭୁଜ୍
(vi) ସେସ୍‌ମୋଗ୍ରାଫ୍
(vii) ରୁ ଅଧିକ
(viii) ଆକର୍ଷଣ
(ix) ରେଶମ କନା
(x) ଶୁଷ୍କ କେଶ

4. ‘କ’ସ୍ତମ୍ଭରେ ଥ‌ିବା ଶବ୍ଦ ସହିତ ‘ଖ’ ସ୍ତମ୍ଭରେ ଥିବା ସମ୍ପର୍କିତ ଶବ୍ଦକୁ ମିଳାଅ ।

‘କ’ ସ୍ତମ୍ଭ	‘ଖ’ ସ୍ତମ୍ଭ
(i) ଆମ୍ବର	(i) ଇଲେକ୍‌ଟ୍ରୋସ୍କୋପ୍
(ii) ର୍କ – ବିଜୁଳି	(ii) ପଣମକନା
(iii) ବ୍ୟବହୃତ ରିଫିଲ	(iii) ବିଜୁଳି ଚାଳକ
(iv) ଚାର୍ଜର ସ୍ଥାନାନ୍ତରଣ	(iv) ଚୁର୍ କି
(v) ବଜ୍ରପାତ	(v) ଆଣବିକ ବୋମା ବିସ୍ଫୋରଣ
(vi) ଭୂମିକମ୍ପର ମାତ୍ରା	(vi) ପ୍ଲେଟ୍
(vii) C.B.R.I.	(vii) ସେସ୍‌ମିକ୍ ଜୋନ୍
(viii) ପୃଥ‌ିବୀ ବାହ୍ୟ ଆବରଣ ସ୍ତର	(viii) ଫ୍ରାଙ୍କଲିନ୍
(ix) ଭୂକମ୍ପନ	(ix) ରେଜିନ୍
(x) ଦୁର୍ବଳ ଜୋନ୍	(x) ରିକ୍ଟର

Answer:

‘କ’ ସ୍ତମ୍ଭ	‘ଖ’ ସ୍ତମ୍ଭ
(i) ଆମ୍ବର	(ix) ରେଜିନ୍
(ii) ର୍କ – ବିଜୁଳି	(viii) ଫ୍ରାଙ୍କଲିନ୍
(iii) ବ୍ୟବହୃତ ରିଫିଲ	(ii) ପଣମକନା
(iv) ଚାର୍ଜର ସ୍ଥାନାନ୍ତରଣ	(i) ଇଲେକ୍‌ଟ୍ରୋସ୍କୋପ୍
(v) ବଜ୍ରପାତ	(iii) ବିଜୁଳି ଚାଳକ
(vi) ଭୂମିକମ୍ପର ମାତ୍ରା	(x) ରିକ୍ଟର
(vii) C.B.R.I.	(iv) ଚୁର୍ କି
(viii) ପୃଥ‌ିବୀ ବାହ୍ୟ ଆବରଣ ସ୍ତର	(vi) ପ୍ଲେଟ୍
(ix) ଭୂକମ୍ପନ	(v) ଆଣବିକ ବୋମା ବିସ୍ଫୋରଣ
(x) ଦୁର୍ବଳ ଜୋନ୍	(vii) ସେସ୍‌ମିକ୍ ଜୋନ୍