Odisha State Board BSE Odisha 8th Class Sanskrit Solutions Chapter 4 କୃଷକଃ Textbook Exercise Questions and Answers.
BSE Odisha Class 8 Sanskrit Solutions Chapter 4 କୃଷକଃ
एकपदेन उत्तरं कुरुत । (ଏକପଦେନ ଉତ୍ତରଂ କୁରୁତ ।)
(ଗୋଟିଏ ପଦରେ ଉତ୍ତର ଦିଅ ।)
(क) कृषकस्य श्रमः कस्याः मूलम् ?
କୃଷକସ୍ୟ ଶ୍ରମଃ କନ୍ୟା ମୂଲମ୍ ?
उत्तर:
ଶ୍ୟାମଳତାୟା

(ख) कृषकः केन भूमिं कर्षति ?
କୃଷକ କେନ ଭୂମି କର୍ଷତି ?
उत्तर:
ହଳେନ
(ग) कदा कृषिकार्यस्य आरम्भः भवति ?
କଦା କୃଷିକାର୍ଯ୍ୟସ୍ୟ ଆରମ୍ଭ ହବତି ?
उत्तर:
ଅକ୍ଷୟତୃତୀୟାତଃ
(घ) कै: क्षेत्रं रमणीयं भवति ?
କୈ କ୍ଷେତ୍ର ରମଣୀୟଂ ଭବତି ।
उत्तर:
ଶାକାଦିଭିଂ
(ङ) कस्मै नम: ?
କର୍ଣ୍ଣେ ନମଃ ?
उत्तर:
କୃଷକାୟ
(हलेन, कृषकाय, श्यामलतायाः, अक्षयतृतीयातः, शाकादिभि,:)
(ହଳେନ, କୃଷକାୟ, ଶ୍ୟାମଳତାୟା, ଅକ୍ଷୟତୃତୀୟାତଃ, ଶାକାଦିଭି)

2. शून्यस्थानं पूरयत (ଶୂନ୍ୟସ୍ଥାନଂ ପୂରୟତ ।)
(ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।)
(क) ………… ओडिशाप्रदेशः ।
…………… ଓଡ଼ିଶା ପ୍ରଦେଶଃ ।
उत्तर:
ଏଷ
(ख) हलं नाम ………… |
ହଳଂ ନାମ ………………
उत्तर:
ଲାଙ୍ଗଳମ୍
(ग) कृषकः ………… कष्टं करोति ।
କୃଷକଃ ……….. ଓଡ଼ିଶା ପ୍ରଦେଶଃ ।
उत्तर:
ସ୍ବୟଂ
(घ) पण्यद्रव्याणि ………… आनयति ।
ପଣ୍ୟଦ୍ରବ୍ଯାଣି………….. ଆନୟତି ।
उत्तर:
ବିପଣୀମ୍
(ङ) अतः ………… कृषकाय नम:।
ଅତଃ ………………. କୃଷକାୟ ନମଃ ।
उत्तर:
ଏତଦ୍ଵୈ
(एषः, एतस्मै, विपणीम, लाङ़लम्स्व,यम्)
(ଏଷ, ଏତଦ୍ଵୈ, ବିପଣୀମ୍, ଲାଙ୍ଗଳମ୍, ସ୍ଵୟମ୍)

3. मांतृभाषया अनुवादं कुरुत : (ମାତୃଭାଷୟା ଅନୁବାଦଂ କୁରୁତ ।)
(ମାତୃଭାଷାରେ ଅନୁବାଦ କର ।)
(क) बहवः नद्यः अस्मिन् प्रदेशे प्रवहन्ति ।
(ବହବ ନମଃ ଅସ୍ମିନ୍ ପ୍ରଦେଶେ ପ୍ରବହନ୍ତି ।)
उत्तर:
ବହୁତ ନଈ ଏହି ପ୍ରଦେଶରେ ପ୍ରବାହିତ ।
(ख) नदी-प्रवाहात् एतस्याः भूमिः उर्वरा ।
(ନଦୀ ପ୍ରବାହାତ୍ ଏତସ୍ୟା ଭୂମି ଉର୍ବରା ।)
उत्तर:
ନଦୀ ପ୍ରବାହରୁ ଏହାର ମାଟି ଉର୍ବର ।
(ग) शाकादिभि:क्षेत्रं रमणीयं भवति ।
(ଶାକାଦିରଃ କ୍ଷେତ୍ର ରମଣୀୟଂ ଭବତି।)
उत्तर:
ଶାଗାଦିଦ୍ୱାରା ଜମି ସୁନ୍ଦର ହୋଇଥାଏ ।
(घ) पण्यद्रव्याणि विपणीम् आनयति ।
(ପଣ୍ୟଦ୍ରବ୍ଯାଣି ବିପଣୀମ୍ ଆନୟତି ।)
उत्तर:
ବିକ୍ରୟଯୋଗ୍ୟ ଦ୍ରବ୍ୟ ବଜାରକୁ ଆଣେ ।
(ङ) अतः एतस्मै कृषकाय नमः ।(ଅତଃ ଏତକୈ କୃଷକାୟ ନମଃ ।)
उत्तर:
ଏଣୁ ଏହି ଲକ୍ଷଇଲ ମଥାଏ ।
(च) जयतु कृषकः । जयतु सैनिकः । (ଜୟତୁ କୃଷକଃ ଜୟତୁ ସୈନିକଃ )
उत्तर:
କୃଷକର ଜୟହେଉ । ସୈନିକର ଜୟ ହେଉ ।
उदाहरणम्-ता श्या म ल या:-श्यामलताया:
ଉଦାହରଣମ୍ – ତା ଶ୍ୟା ମ ଳ ୟା – ଶ୍ୟାମଳତାୟା
(१) प्र शे दे …………
ପ୍ର ନ ଧା ମ୍ – ପ୍ରଧାନମ୍
(२) भूण चक:…………
ଭୂ ଣ ଚ କଃ – ଭୂଚଣକଃ
(३) प्र न धा म् …………
ପ୍ର ନ ଧା ମ୍ – ପ୍ରଧାନମ୍
(४) का ले शी त …………
କାଳେ ଶୀତ – ଶୀତକାଳେ
(५) श्रा ण व स्य …………
ଶ୍ରା ଣ ବ ସ୍ୟ – ଶ୍ରାବଣସ୍ୟ
(६) वि णी प म् …………
ବି ଣୀ ପ ମ୍ – ବିପଣୀମ୍

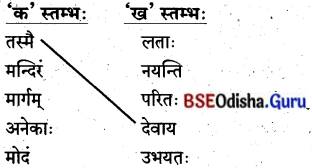
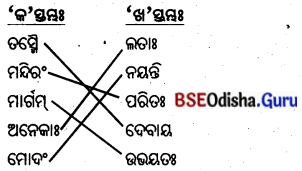
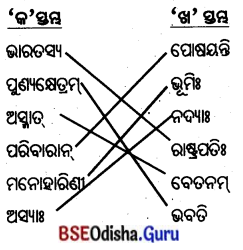
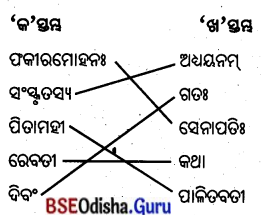
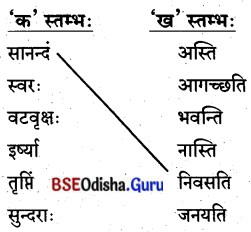
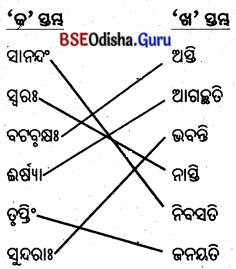
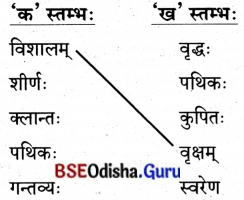
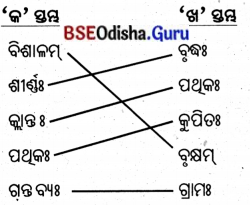
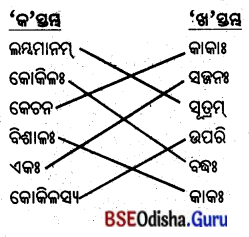
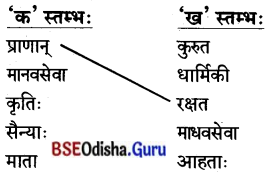
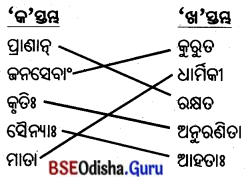
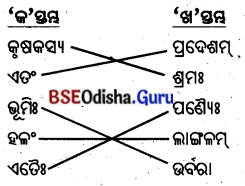
5. स्तम्भमेलनं कुरुत (ସ୍ତମ୍ଭମେଳନଂ କୁରୁତ ।)
(ସ୍ତମ୍ଭ ମିଳନ କର ।)

उत्तर:
6. रेखाक्कितपदस्य संशोधनं कुरुत। (ରେଖାଙ୍କିତପଦସ୍ୟ ସଂଶୋଧନଂ କୁରୁତ ।)
(ରେଖାଙ୍କିତ ପଦର ସଂଶୋଧନ କର ।)
(क) भोजनव्यवस्था रुचिकरा भवति ।
ଭୋଜନବ୍ୟବସ୍ଥା ରୁଚିକରା ଭବତି ।
उत्तर:
ଭୋଜନବ୍ୟବସ୍ଥା ରୁଚିକରୀ ଭବତି।
(ख) एतस्मै कृषकं नमः।
ଏତ କୃଷକଂ ନମଃ ।
उत्तर:
ଏତସ୍କି କୃଷକାୟ ନମଃ ।
(ग) एषा आड़िशाप्रदेशः।
ଏଷା ଓଡ଼ିଶାପ୍ରଦେଶଃ ।
उत्तर:
ଏତଃ ଓଡ଼ିଶାଦେଶଃ ।
(घ) बहुनि नद्य:प्रवहन्ति ।
ବହୁନି ନଦ୍ୟ ପ୍ରବହନ୍ତି ।
उत्तर:
ବହନଃ ନମଃ ପ୍ରବହନ୍ତି |
(ङ) कृषकः स्वयं कष्टं कुर्वन्ति ।
କୃଷକଃ ସ୍ଵୟଂ କଷ୍ଟ କୁହଁନ୍ତି ।
उत्तर:
କୃଷକଃ ସ୍ଵୟଂ କଷ୍ଟ କରୋତି ।

7. वाक्यानि रचयत ।
आनयति, नमः, करोति, भवति, जना:
उत्तर:
आनयति (ଆନୟତି) – ବାଳିକା ପୁଷ୍ପମ୍ ଆନୟତି ।
नमः (ନମଃ) – ଶ୍ରୀଜଗନ୍ନାଥାୟ ନମଃ ।
करोति (କରୋତି) – ଗୋପାଳ କିଂ କରୋତି ?
भवति (ଭବତି) – ଅତ୍ର ମେଳା ଭବତି ।
जना: (ଜନା) – ଜନଃ ବିପଣୀ ଗଛନ୍ତି ।
8. सन्थिविच्छेदं कुरुत। (ସନ୍ଧିବିଚ୍ଛେଦଂ କୁରୁତ।)
(ସନ୍ଧିବିଚ୍ଛେଦ କର ।)
चणकादीनि, प्रारम्भः, शाकादिभि:
उत्तर:
चणकादीनि (ଚଣକାଦୀନି) – ଚଣକ + ଆଦୀନି
प्रारम्भः (ପ୍ରାରମ୍ଭ) – ପ୍ର + ଆରମ୍ଭ
शाकादिभि: (ଶାକାଦିଭି) – ଶାକ + ଆଦିଭିଂ
तव कृते करणीयम् ତୁମ ପାଇଁ କାମ)
पश्यत, उच्चैः पठत (ଦେଖ, ପାଟିକରି ପଢ଼ ।)
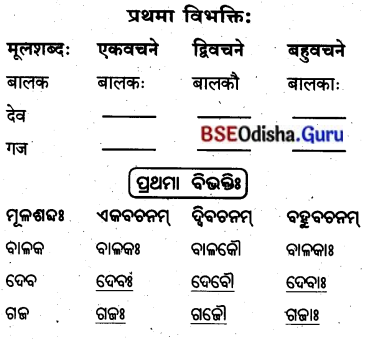
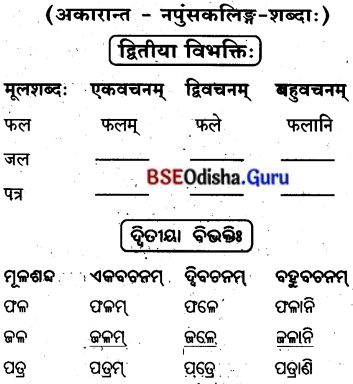
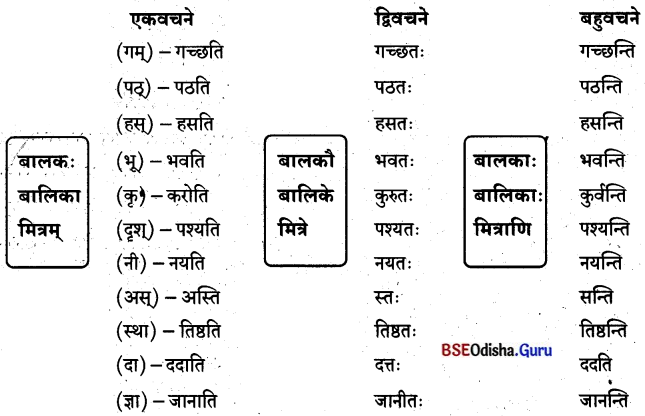
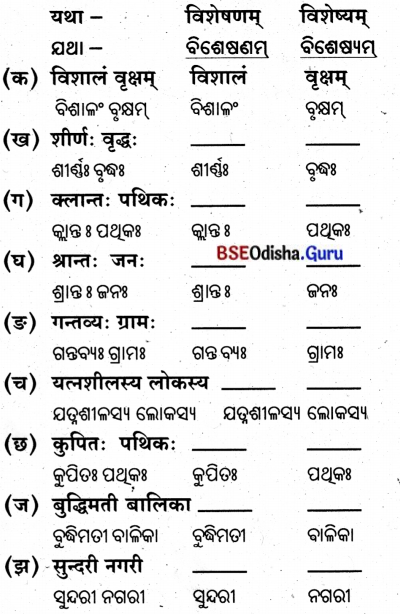
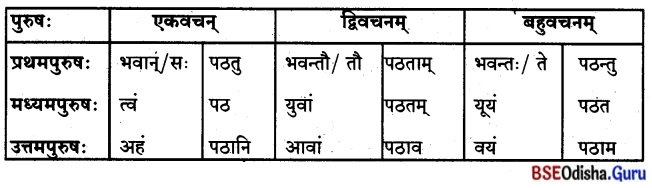
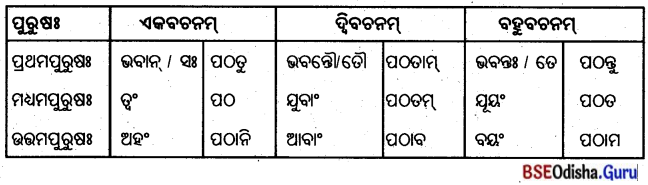
प्रथमा विभक्तिः (ପ୍ରଥମା ବିଭଭି)
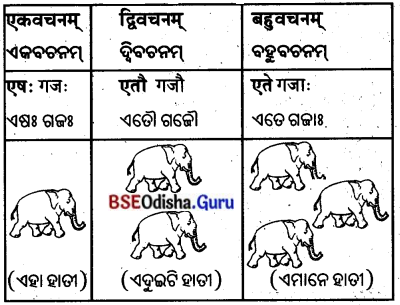
शून्यस्थानानि पूरयत –

ଶୂନ୍ୟସ୍ଥାନାନି ପୂରୟତ । (ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।)

‘एतद्’ शब्दस्य पुंलिङ्गे ‘ଏତଦ୍’ ଶବ୍ଦସ୍ୟ ପୁଂଲିଙ୍ଗେ
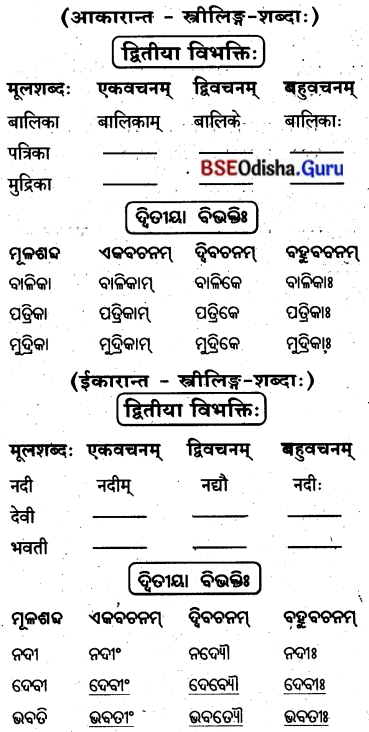
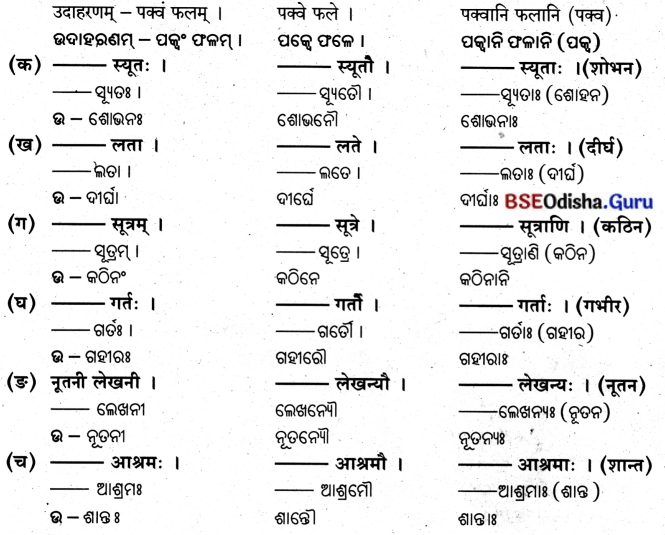
द्वितीया विभक्ति: (ଦ୍ବିତୀୟା ବିଭବାଃ)

शून्यस्थानानि पूरयत –

ଶୂନ୍ୟସ୍ଥାନାନି ପୂରୟତ । (ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।)


‘एतद्’ शब्दस्य पुंलिझें’ ‘ଏତଦ୍’ ଶବ୍ଦସ୍ୟ ପୁଂଲିଙ୍ଗେ
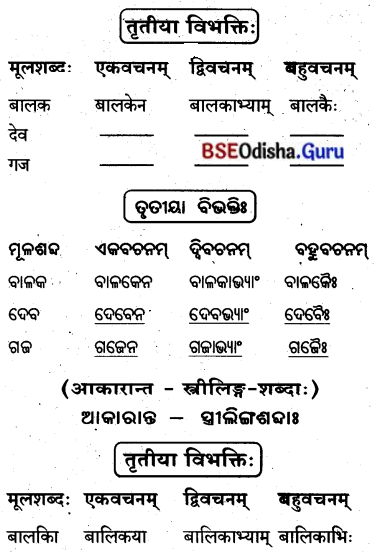
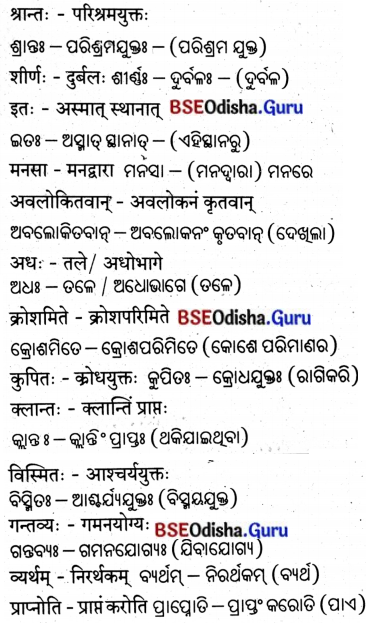
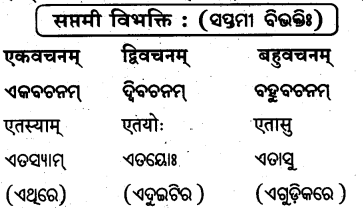
तृतीया विभक्तिः : (ତୃତୀୟା ବିଭବାଃ)
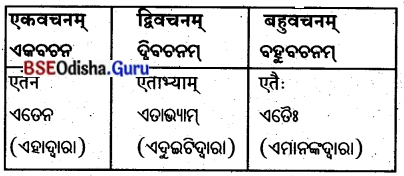
शून्यस्थानानि पूरयत –

ଶୂନ୍ୟସ୍ଥାନାନି ପୂରୟତ । (ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।)

‘एतद्’ शब्दस्य पुंलिङ्रे – ‘ଏତଦ୍’ ଶବ୍ଦସ୍ୟ ପୁଂଲିଙ୍ଗେ
शून्यस्थानानि पूरयत –

ଶୂନ୍ୟସ୍ଥାନାନି ପୂରୟତ । (ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

‘एतद्’ शब्दस्य पुंलिक्रे ‘ଏତଦ୍’ ଶବ୍ଦସ୍ୟ ପୁଂଲିଙ୍ଗେ
शून्यस्थानानि पूरयत –


ଶୂନ୍ୟସ୍ଥାନାନି ପୂରୟତ । (ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।)

‘एतद्र’ शब्दस्य पुंलिङ्ने
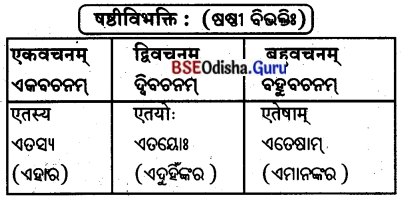
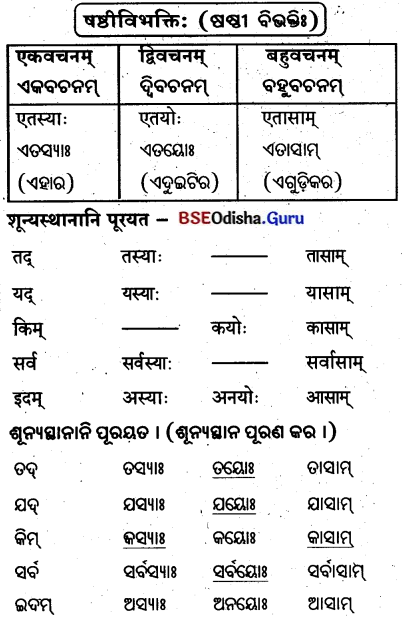
शून्यस्थानानि पूरयत – तद् – तस्य – तेषाम्

ଶୂନ୍ୟସ୍ଥାନାନି ପୂରୟତ । (ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।)

‘एतद्’ शब्दस्य पुंलिङ्ने -‘ଏତଦ୍’ ଶବ୍ଦସ୍ୟ ପୁଂଲିଙ୍ଗେ
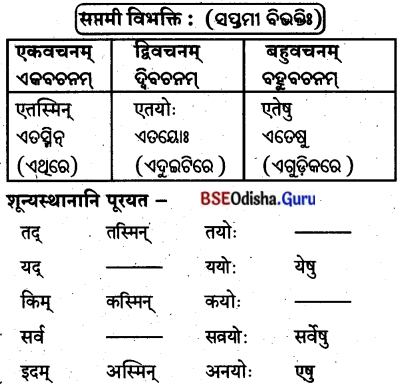
ଶୂନ୍ୟସ୍ଥାନାନି ପୂରୟତ । (ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।)

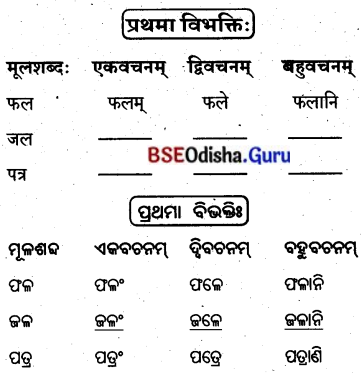
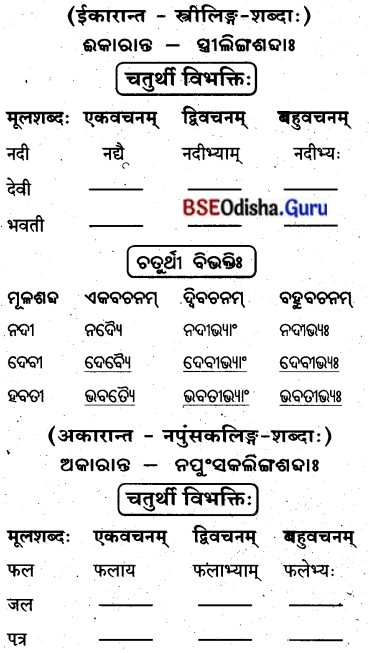
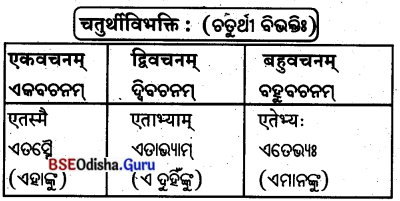
‘एतद्’ शब्दस्य नपुंसकलिङ़्रे – (‘ଏତଦ୍’ ଶବ୍ଦସ୍ୟ ନପୁଂସକଲିଙ୍ଗ)
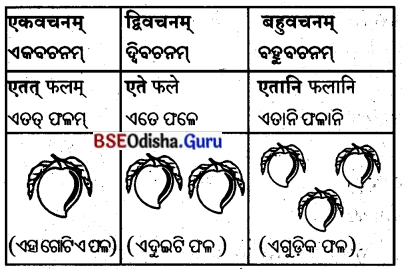
प्रथमाविभक्तिः

ପ୍ରଥମ ବିଭବାଃ


द्वितीया विभक्ति:

ଦ୍ଵିତୀୟା ବିଭନିଃ

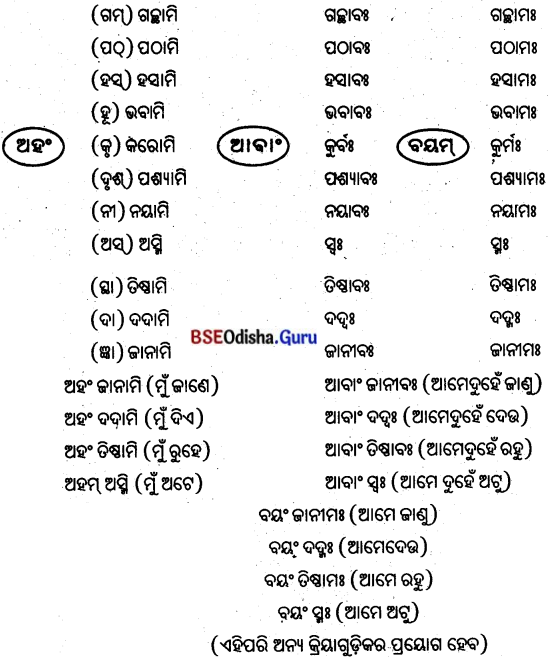
तृतीयात्: सम़मीं यावत् पुंलिङ्ग्नव्
(ତୃତୀୟାତଃ ସପ୍ତମୀ ଯାବତ୍ ପୁଂଲିଙ୍ଗବତ୍)
(ତୃତୀୟାଠାରୁ ସପ୍ତମୀ ପର୍ଯ୍ୟନ୍ତ ପୁଂଲିଙ୍ଗ ପରି)
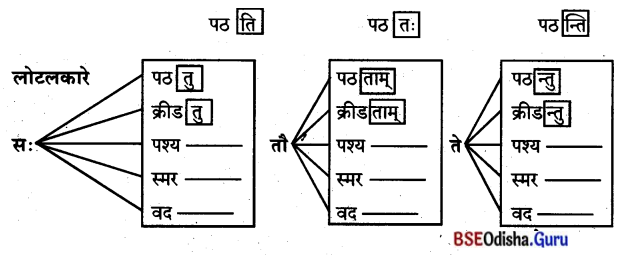
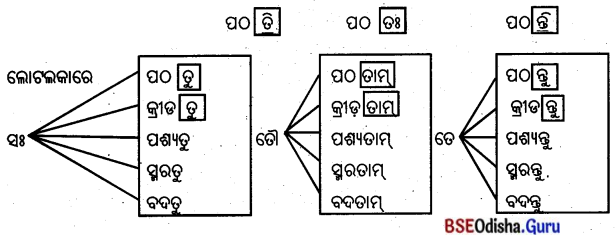
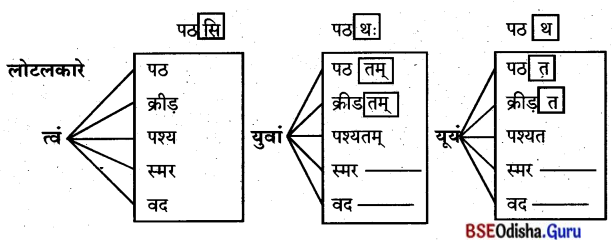
पश्यत,लिखत-ପଶ୍ୟତ ଲିଖତ (ଦେଖ ଓ ଲେଖ)
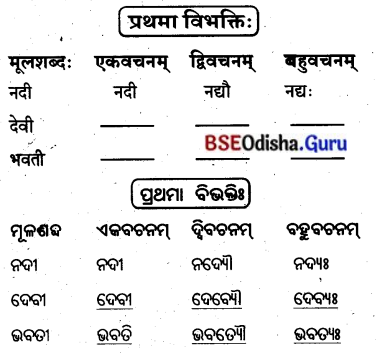
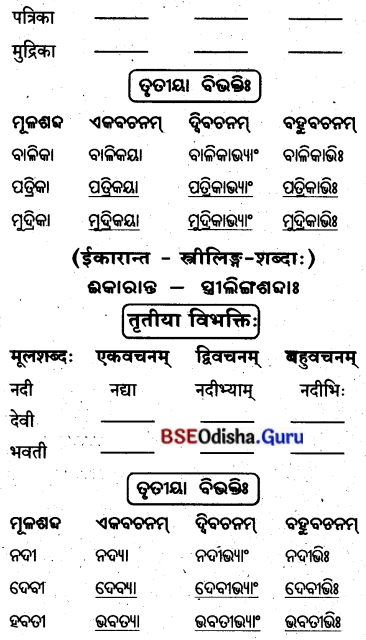
‘एतद्'शब्दस्य स्रीलिझे़्ग़-(ଏତଦ୍ ଶବ୍ଦସ୍ୟ ସ୍ତ୍ରୀଲିଙ୍ଗେ)
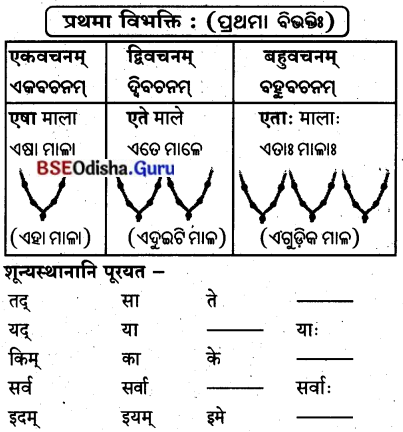


‘एतद्’ शब्दस्य स्वीलिझे – ‘ଏତଦ୍’ ଶବ୍ଦସ୍ୟ ସ୍ତ୍ରୀଲିଙ୍ଗେ
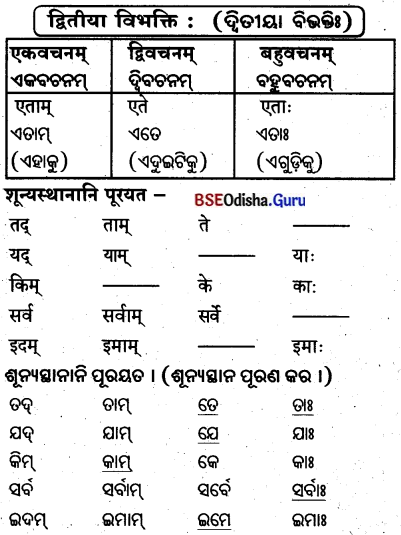
‘एतद्’ शब्दस्य स्रीलिङ्रे (‘ଏତଦ୍’ ଶବ୍ଦସ୍ୟ ସ୍ତ୍ରୀଲିଙ୍ଗେ)
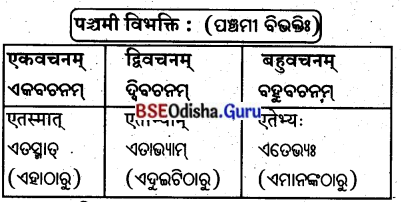
तृतीया विभक्ति : (ତୃତୀୟା ବିଭବାଃ)
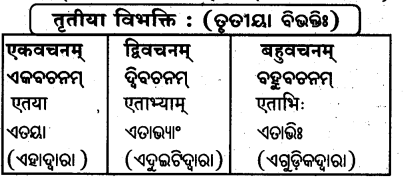
शून्यस्थानानि पूरयत –

ଶୂନ୍ୟସ୍ଥାନାନି ପୂରୟତ । (ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।)

‘एतद्’ शब्दस्य स्रीलिझे़ –
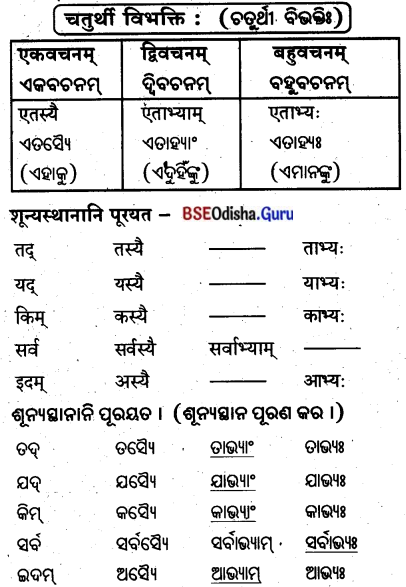
‘एतद्’ शब्दस्य स्रीलिझ्रे – (‘ଏତଦ୍’ ଶବ୍ଦସ୍ୟ ସ୍ତ୍ରୀଲିଙ୍ଗେ)
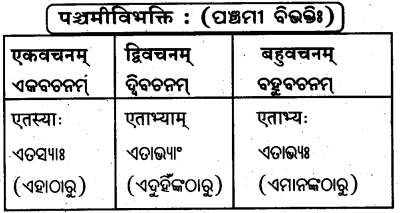


‘एतद्’ शब्दस्य स्रीलिझे -(‘ଏତଦ୍’ ଶବ୍ଦସ୍ୟ ସ୍ତ୍ରୀଲିଙ୍ଗେ)
‘एतद्’ शब्दस्य स्रीलिझे़ – (‘ଏତଦ୍’ ଶବ୍ଦସ୍ୟ ସ୍ତ୍ରୀଲିଙ୍ଗେ)
शून्यस्थानानि पूरयत –


एकपदेन उत्तरं लिखत ।
(ଏକପଦେନ ଉତ୍ତରଂ ଲିଖତ ।)
1. केषां सौन्दर्यम् एतं प्रदेशं मण्डयति ?
କେଷା ସୌନ୍ଦର୍ଯ୍ୟମ୍ ଏବଂ ପ୍ରଦେଶଂ ମଣ୍ଡୟତି ?
उत्तर:
ଶସ୍ୟଶ୍ୟାମଳକ୍ଷେତ୍ରାମାଂ
2. कस्य श्रम: श्यामलताया: मूलम् ?
କସ୍ୟ ଶ୍ରମଃ ଶ୍ୟାମଳତାୟା ମୂଳମ୍ ?
उत्तर:
କୃଷକସ୍ଯ
3. प्रायतः कति प्रतिशतं जनाः कृषिद्वारा जीवन्ति?
ପ୍ରାୟତଃ କତି ପ୍ରତିଶତଂ ଜନଃ କୃଷିଦ୍ୱାରା ଜୀବନ୍ତି ?
उत्तर:
ଅଶୀତିଃ
4. एतस्य प्रदेशस्य प्रधानम् उत्पादनं किम् ?
ଏତସ୍ୟ ପ୍ରଦେଶସ୍ୟ ପ୍ରଧାନମ୍ ଉତ୍ପାଦନଂ କିମ୍ ?
उत्तर:
ଧାନ୍ୟମ୍

5. कृषिकार्यस्य आरम्भः कस्मात् भवति ?
କୃଷିକାର୍ଯ୍ୟସ୍ୟ ଆରମ୍ଭ କସ୍ମାତ୍ ଭବତି ?
उत्तर:
ଅକ୍ଷୟତୃତୀୟାତଃ
6. अक्षयतुतीयातः कस्य आरम्भः भवति ?
ଅକ୍ଷୟତୃତୀୟାତଃ କସ୍ୟ ଆରମ୍ଭ ଭବତି ?
उत्तर:
କୃଷିକାର୍ଯ୍ୟସ୍ଯ
7. शाकादिभि:किं रमणीयं भवति ?
ଶାକାଦିଭିଂ କିଂ ରମଣୀୟଂ ଭବତି ?
उत्तर:
କ୍ଷେତ୍ରମ୍
8. कृषकः प्रणयद्रव्याणि कुत्र आंनयति ?
କୃଷକଃ ପଣ୍ୟଦ୍ରବ୍ଯାଣି କୁତ୍ର ଆନୟତି ?
उत्तर:
ବିପଣୀମ୍
9. कृषकः कानि विपणीम् आनयति ?
କୃଷକଃ କାନି ବିପଣୀମ୍ ଆନୟତି ?
उत्तर:
ପଣ୍ୟଦ୍ରବ୍ଯାଣି
10. कै:अस्माकं भोजनव्यवस्था रुंचिकरी भवति ?
କୈ ଅସ୍ମାକଂ ଭୋଜନବ୍ୟବସ୍ଥା ରୁଚିକରୀ ଭବତି ?
उत्तर:
ପଣ୍ୟ
11. पणयै: अस्माकं का रुचिकरी भवति ?
ପଶୌ ଅସ୍ମାକଂ କା ରୁଚିକରୀ ଭବତି ?
उत्तर:
ଭୋଜନବ୍ୟବସ୍ଥା
12. जना: केन जीवन्ति ?
ଜନାଃ କେନ ଜୀବନ୍ତି ?
उत्तर:
କୃଷିଦ୍ୱାରା
13. कृषिद्वारा के जीवन्ति ?
କୃଷିଦ୍ୱାରା କେ ଜୀବନ୍ତି ?
उत्तर:
ଜନାଃ

14. हलं नाम किम् ?
ହଳଂ ନାମ କିମ୍ ?
उत्तर:
ଲାଙ୍ଗଳମ୍
15. किं नाम हलम् ?
କିଂ ନାମ ହଳମ୍ ?
उत्तर:
ଲାଙ୍ଗଳମ୍
16. कस्य राज्यस्य प्रधानम् उत्पादनं धान्यम् ?
କସ୍ୟ ରାଜ୍ୟସ୍ୟ ପ୍ରଧାନମ୍ ଉତ୍ପାଦନଂ ଧାନ୍ୟମ୍ ?
उत्तर:
ଓଡ଼ିଶାରାଜ୍ୟସ୍ୟ
17. कः स्वयं कष्टं करोति ?
କଂ ସ୍ବୟଂ କଷ୍ଟ କରୋତି ?
उत्तर:
କୃଷକ
18. कदा क्षेत्रं रमणीयं भवति ?
କଦା କ୍ଷେତ୍ର ରମଣୀୟଂ ଭବତି ?
उत्तर:
ଶୀତକାଳେ

19. शीतकाले क्षेत्रं किं भवति ?
ଶୀତକାଳେ କ୍ଷେତ୍ର କିଂ ଭବତି ?
उत्तर:
ରମଣୀୟମ୍
बन्धनीमध्यात् शून्यस्थानं पूररयत।
(ବନ୍ଧନୀମଧ୍ଯାତ୍ ଶୂନ୍ୟସ୍ଥାନଂ ପୂରୟତ।)
1. ता:नर्त्तक्य:। ………… नर्त्तकीनां नृत्यम् अद्य अस्ति। (एतेषाम्,एतासां,तासाम्)
……………. ନର୍ତ୍ତକୀନାଂ ନୃତ୍ୟମ୍ ଅଦ୍ୟ ଅସ୍ତି । (ଏତେଷାମ୍, ଏତାସାଂ, ତାସାମ୍)
उत्तर:
ତାସାଂ
2. तौ चतुरौ। ………… चतुराभ्यां परितोषिकं ददामि।
ତୌ ଚତୁରୌ ……………. ଚତୁରାଭ୍ୟା ପରିତୋଷିକଂ ଦଦାମି । (ଏତାଭ୍ୟାମ୍, ତାଙ୍ଖ୍ୟା, ଆଭ୍ୟାମ୍)
उत्तर:
ତାଙ୍ଖ୍ୟା
3. सा नदी। ………… नद्यां वहवः मकराः सन्ति । (तस्मिन,तस्यां,एतस्याम्)
ସା ନଦୀ ………………… ନଦ୍ୟା ବହନଃ ମକରା ସନ୍ତି । (ତସ୍ମିନ୍, ତସ୍ୟା, ଏତସ୍ୟାମ୍)
उत्तर:
ତଥ୍ଯା

4. एते छात्रा:। ………… छात्रेषु कः चतुरः स्यात् ? (एतेषु,एषु,तेषु)
ଏତେ ଛାତ୍ରା । ……………. ଛାତ୍ରେଷୁ କଃ ଚତୁରଃ ସ୍ୟାତ୍ ? (ଏତେଷୁ, ଏଷୁ, ତେଣୁ)
उत्तर:
ଏତେଷୁ
5. स: पर्वतः। ………… पर्वतात्’तिस्र: नद्यः प्रभवन्ति। (अस्मात्, तस्मात्, एतस्मातं)
ସ୍ୱ ପର୍ବତଃ ………………….. ପର୍ବତାତ୍ ତିନଃ ନମଃ ପ୍ରଭବର୍ତ୍ତି ? (ଅସ୍ନାତ୍, ତସ୍ମାତ୍, ଏତସ୍ମାତ୍)
उत्तर:
ତସ୍ମାତ୍
6. इमे शिक्षिके । ………… शिक्षिकयो : पाठनेन छात्रा: तुष्यन्ति। (अनयो:, एतयो:, एतसाम्प)
ଇମେ ଶିକ୍ଷିକେ ………………..ଶିକ୍ଷିକ ପାଠନେନ ଛାତ୍ରା ତୁଷ୍ଯତି ? (ଅନୟୋ, ଏତ, ଏତସାମ୍)
उत्तर:
ଅନୟୋ
7. ते शिक्षका: । ………… शिक्षकान् वयं प्रणमामः।. (एताः, इमान, तान् )
ତେ ଶିକ୍ଷକା । ……………….ଶିକ୍ଷକାନ୍ ବୟଂ ପ୍ରଣମାମଃ ( ଏତଃ, ଇମାନ, ତାନ)
उत्तर:
ତାନ୍
8. तानि फलानि । ………… फलेभ्यः एकं भवान् त्रेयंतुं। (ताभ्यः; तेभ्यः, एभ्यः)
ତାନି ଫଳାନି । ……………… ଫଳେଭ୍ୟ ଏବଂ ଭବାନ୍ ନିର୍ୟତ୍ବ। (ତାଜ୍ୟ, ତେଭ୍ୟ, ଏଭ୍ୟ)
उत्तर:
ତେବାଃ
9. ते घटाः। ………… घटानां वर्ण्णः समानः। (तासाम्, तेषाम्, एथाम्)
ତେ ଘଟା ……………ଘଟାନାଂ ବହିଃ ସମାନଃ ? (ତାସାମ, ତେଷାମ୍, ଏଷାମ୍)
उत्तर:
ତେଷା
10. इमा: नालिका:। ………… नालिकाभ्यः जलं स्त्रववि। (आभ्य:, एभ्य:, ताभ्य:)
ଇମା ନାଳିକା । ……….. ନାଳିକାଭ୍ୟ ଜଳଂ ସୁବତି । (ଆଭ୍ୟ, ଏଭ୍ୟ, ତାଭ୍ୟ)
उत्तर:
ଆଭ୍ୟ

11. अयं मार्गः। ………… मार्गेण गच्छति चेत् नगरं प्राप्नोति। (एतेन, अनेन, अनया)
ଅୟଂ ମାର୍ଗ । ……….. ମାର୍ଗେଣ ଗଚ୍ଛତି ଚେତ୍ ନଗରଂ ପ୍ରାଷ୍ଟୋତି ? (ଏତେନ, ଅନେନ, ଅନୟା)
उत्तर:
ଅନେନ
12. इमे वाहने। …………वाहनयो :भवत्यै किं रोचते ? (अनयो, एतांसां, तयो:)
ଇମେ ବାହନେ । ………………… ବାହନୟୋ ଭବତ୍ୟେ କିଂ ରୋବତେ ? ( ଅନୟୋ, ଏତାସାଂ, ତ)
उत्तर:
ଅନୟୋ
13. एताः शाटिकाः। …………शाटिकानां विन्यासः मनोहरः अस्तिः।(आसाम्,एतासाम्,तासाम्)
ଏତଃ ଶାଟିକା । ………….. ଶାଟିକାନାଂ ବିନ୍ୟା ପଃ ମନୋହରଃ ଅସ୍ଥି। (ଆସାମ, ଏତାସାମ୍, ତାସାମ)
उत्तर:
ଆସାଂ
14. इयं मम लेखनी …………लेखन्य पंचविशतिरूप्यकाणि अदाम्।(अस्मैं,अस्यै,एतस्यै)
ଇୟଂ ମମ ଲେଖନୀ ………………..ଲେଖନୈ ପଞ୍ଚବିଂଶତିରୂପ୍ୟକାଣି ଅଦଦାମ୍ । (ଅସ୍ଥି, ଅସ୍ୟ, ଏତତ୍ସ୍ୟ)
उत्तर:
ଅସ୍ଯ
15. इमौ चषकौ …………चषकाभ्याम् अतिथिभ्यः फलरसं ददातु ।(एताभ्याम्,आभ्याम्,एभ्याम्)
ଇମୌ ଚଷକୌ । …………………. କାଲ୍ୟାମ୍ ଅତିଥ୍ ଫଳରସଂ ଦଦାତୁ ? ( ଏତାଭ୍ୟାମ୍, ଆଭ୍ୟାମ୍, ଏଭ୍ୟାମ୍)
उत्तर:
ଆଭ୍ଯା
उत्तरचयनं कुरुत ।
(ଉତ୍ତରଚୟନଂ କୁରୁତ।)
प्रश्न 1.
केषां सौन्दर्य्यम् एतं प्रदेशं मण्डयति?
କେଷା ସୌନ୍ଦର୍ଯ୍ୟମ୍ ଏବଂ, ପ୍ରଦେଶଂ ମଣ୍ଡୟତି ?
(A) ଶସ୍ୟଶ୍ୟାମଳକ୍ଷେତ୍ରାଣାମ୍
(B) କ୍ଷେତ୍ରାଣାମ୍
(C) ଭୂମିନୀମ୍
(D) ଶସ୍ୟକ୍ଷେତ୍ରାଣାମ
उत्तर:
(A) ଶସ୍ୟଶ୍ୟାମଳକ୍ଷେତ୍ରାଣାମ୍

प्रश्न 2.
उत्तरचयनं कुरुत ।
ଶ୍ୟାମଲତାୟା ମୂଳଂ କିମ୍ ?
(A) କର୍ମୀ
(B) ଶ୍ରମଃ
(C) ଧର୍ମଃ
(D) ବିଶ୍ରାମଃ
उत्तर:
(B) ଶ୍ରମଃ
प्रश्न 3.
प्रायतः कतिजनाः कृषिद्वारा जीवन्ति?
ପ୍ରାୟତଃ କତିଜନଃ କୃଷିଦ୍ୱାରା ଜୀବନ୍ତି ?
(A) ପ୍ରତିଶତମ୍ ପଞ୍ଚଦଶ
(B) ପ୍ରତିଶତମ୍ ପଞ୍ଚାଶିତ୍
(C) ପ୍ରତିଶତମ୍ ଅଶୀତିଃ
(D) ପ୍ରତିଶତମ୍ ନବତଃ
उत्तर:
(C) ପ୍ରତିଶତମ୍ ଅଶୀତିଃ
प्रश्न 4.
कृषकः केन भूमिं कर्षति?
‘କୃଷତଃ କେନ ଭୂମି କର୍ଷତି ?
(A) ହସ୍ତନ
(B) ଦୁଃଖେନ
(C) ଶକଟେନ
(D) ହଳେନ
उत्तर:
(D) ହଳେନ
प्रश्न 5.
एतस्य प्रदेशस्य प्रधानम् उत्पादनं किम्?
ଏତସ୍ୟ ପ୍ରଦେଶସ୍ୟ ପ୍ରଧାନମ୍ ଉତ୍ପାଦନଂ କିମ୍ ?
(A) ଧାନ୍ୟମ
(B) ମୁଦ୍ଗମ୍
(C) ମାଷମ୍
(D) ଚଣକମ୍
उत्तर:
(A) ଧାନ୍ୟମ

प्रश्न 6.
कदा कृषिकार्यस्य आरम्भः भवति?
କଦା କୃଷିକାର୍ଯ୍ୟସ୍ୟ ଆରମ୍ଭ ଭବତି ?
(A) ତୃତୀୟାତଃ
(B) ଅକ୍ଷୟତୃତୀୟାତଃ
(C) ଦୋଳପାର୍ବଣତଃ
(D) ଦଶହରାତଃ
उत्तर:
(B) ଅକ୍ଷୟତୃତୀୟାତଃ
प्रश्न 7.
कै:क्षेत्रं रमणीयं भवति?
କୈ କ୍ଷେତ୍ର ରମଣୀୟଂ ଭବତି ?
(A) ଶାକାଦିର୍ଭି
(B) ପୁଚ୍ଚୈଃ
(C) ଫଲୈ
(D) ବୃକ୍ଷି
उत्तर:
(A) ଶାକାଦିଭି
प्रश्न 8.
कृषकः पणयद्रव्याणि कुत्र आनयति ?
କୃଷକ ପଣ୍ୟଦ୍ରବ୍ଯାଣି କୁତ୍ର ଆନୟତି ?
(A) ଗୃହମ୍
(B) କାର୍ଯ୍ୟାଳୟମ୍
(C) ବିପଣୀମ୍
(D) ଆପଣମ
उत्तर:
(C) ବିପଣୀମ୍
प्रश्न 9.
पणयै:अस्माकं का रुचिकरी भवति?
ପଣ୍ୟ ଅସ୍ମାକଂ କା ରୁଚିକରୀ ଭବତି’?
(A) ବ୍ୟଞ୍ଜନମ୍
(B) ଅନ୍ନମ୍
(C) ଭୋଜନମ୍
(D) ଭୋଜନବ୍ୟବସ୍ଥା
Answer:
(D) ଭୋଜନବ୍ୟବସ୍ଥା
प्रश्न 10.
कस्मै नम:?
କର୍ଣ୍ଣେ ନମଃ ?
(A) କୃଷକାୟ
(B) ତସ୍ମି
(C) ସୈନିକାୟ
(D) ମାନବାୟ
उत्तर:
(A) କୃଷକାୟ

प्रश्न 11.
कृषिद्वारा के जीवन्ति?
କୃଷିଦ୍ୱାରା କେ ଜୀବନ୍ତି ?
(A) ପୁରୁଷା
(B) ଜନାଃ
(C) ଲୋକା
(D) ମାନବାଃ
उत्तर:
(B) ଜନାଃ
प्रश्न 12.
किं नाम हलम्?
କିଂ ନାମ ହଳମ୍ ?
(A) ଜଳମ୍
(B) ଫଳମ୍
(C) ଲଙ୍ଗଳମ୍
(D) ଯୁଗଳମ୍
उत्तर:
(C) ଲଙ୍ଗଳମ୍
प्रश्न 13.
धान्यं कस्य राज्यस्य प्रधानम् उत्पादनम्?
ଧାନ୍ୟ କସ୍ୟ ରାଜ୍ୟସ୍ୟ ପ୍ରଧାନମ୍ ଉତ୍ପାଦନମ୍ ?
(A) ଓଡ଼ିଶା
(B) କର୍ଣାଟକ
(C) ବିହାର
(D) ହିମାଳୟ
उत्तर:
(A) ଓଡ଼ିଶା
प्रश्न 14.
कः स्वयं कष्टं करोति?
କଃ ସ୍ଵୟଂ କଷ୍ଟ କରୋତି ?
(A) କୃଷକଃ
(B) ଗ୍ରାହକଃ
(C) ଯୁବକଃ
(D) ଶ୍ରମିକଃ
उत्तर:
(A) କୃଷକଃ

प्रश्न 15.
कदा क्षेत्रं रमणीयं भवति?
କଦା କ୍ଷେତ୍ର ରମଣୀୟଂ ଭବତି ?
(A) ଆତପକାଳେ
(B) ଶୀତକାଳେ
(C) ବସନ୍ତକାଳେ
(D) ଶରଦି
उत्तर:
(B) ଶୀତକାଳେ
रेखांकित पदानां संशोधनं वुरुत।
(ରେଖାଙ୍କିତପଦାନାଂ ସଂଶୋଧନଂ କୁରୁତ।)
1. एषा ओड़िशा प्रदेशम् ।
ଏଷା ଓଡ଼ିଶା ପ୍ରଦେଶମ୍ ।
उत्तर:
ଏଷ ଓଡ଼ିଶାପ୍ରଦେଶଃ ।
2. प्रतिशतम् अशीतिः जनः कृषिद्वारा जीवन्ति।
ପ୍ରତିଶତମ୍ ଅଶୀତଃ ଜନଃ କୃଷିଦ୍ୱାରା ଜୀବନ୍ତି ।
उत्तर:
ପ୍ରତିଶତମ୍ ଅଶୀତିଃ ଜନଃ କୃଷିଦ୍ୱାରା ଜୀବନ୍ତି ।
3. बहवं: नदी अस्मिन् प्रदेशे प्रवहन्ति ।
ବହନଃ ନଦୀ ଅସ୍ମିନ୍ ପ୍ରଦେଶେ ପ୍ରବହନ୍ତି ।
उत्तर:
ବହନଃ ନଦ୍ୟ ଅସ୍ମିନ୍ ପ୍ରଦେଶ ପ୍ରବହନ୍ତି।
4. नदी प्रवाहात् एतस्या: भूंमि: उर्वरः।
ନଦୀ ପ୍ରବାହାତ୍ ଏତସ୍ୟା ଭୂମି ଊର୍ବରଃ ।
उत्तर:
ନଦୀ ପ୍ରବାହାତ୍ ଏତସ୍ୟା ଭୂମି ଉର୍ବରା ।
5. एतद् भूमि: उत्पादनयोग्या भवति।
ଏତଦ୍ ଭୂମି ଉତ୍ପାଦନଯୋଗ୍ୟା ଭବତି ।
उत्तर:
ଏତେନ ଭୂମି ଉତ୍ପାଦନଯୋଗ୍ୟ ଭବତି ।

6. धान्यम् एतस्य प्रदेशस्य प्रधानः उत्पादनम्।
ଧାନ୍ୟମ ଏତସ୍ୟ ପ୍ରଦେଶସ୍ୟ ପ୍ରଧାନଃ ଉତ୍ପାଦନମ୍ ।
उत्तर:
ଧାନ୍ୟମ୍ ଏତସ୍ୟ ପ୍ରଦେଶସ୍ୟ ପ୍ରଧାନମ୍ ଉତ୍ପାଦନମ୍ ।
7. कृषकः रौद्रतापस्य सहनं कुर्वन्ति ।
କୃଷକ ରୌଦ୍ରତାପସ୍ୟ ସହନଂ କୁର୍ବନ୍ତି ।
उत्तर:
କୃଷକ ରୌଦ୍ରତାପସ୍ୟ ସହନଂ କରୋତି।
8. शाकादिभि: क्षेत्रं रमणीया भवति।
ଶାକାଦିଭିଂ କ୍ଷେତ୍ର ରମଣୀୟା ଭବତି ।
उत्तर:
ଶାକାଦିଭିଂ କ୍ଷେତ୍ର ରମଣୀୟଂ ଭବତି ।
9. क़षकाः स्वयं कष्टं करोति ।
କୃଷକ ସ୍ଵୟଂ କଷ୍ଟ କରୋତି ।
उत्तर:
କୃଷକଃ ସ୍ଵୟଂ କର୍ଡିଂ କରୋତି ।
10. एतस्मै कृषकं नमः।
ଏତକୈ କୃଷକଂ ନମଃ ।
उत्तर:
ଏତସ୍ରେ କୃଷକାୟ ନମଃ ।
सन्धिविच्छेदं कुरुत।
(ସନ୍ଧିବିଚ୍ଛେଦଂ କୁରୁତ।)
- भूचणकादीन् (ଭୂଚଣକାଦୀନ) = ଭୂଚଣକ + ଆଦିନ :
- प्रारम्भ: (ପ୍ରାରମ୍ଭ) = ପ୍ର + ଆରମ୍ଭ = ପ୍ରାରମ୍ଭ
- शाकादिभि: (ଶାକାଦିଭି) = ଶାକ + ଆଦିଭିଂ
सन्थिं कुरुत
(ସନ୍ଧି କୁରୁତ।)
- शाक + आदिभि: = शाकादिभि: ଶାକ + ଆଦିଭିଂ = ଶାକାଦିଭି
- प्र + आरम्भ: = प्रारम्भ: ପ୍ର + ଆରମ୍ଭ = ପ୍ରାରମ୍ଭ
क्रियापदं निर्वाचयत (କ୍ରିୟାପଦଂ ନିର୍ବାଚୟତ।)
मण्डयति, प्रायतः, जीवन्ति, भूमि:, कर्षति, भवन्ति, कृषक:, करोति, स्वयम्, धान्यम् । कर्तृपदं चिनुत ।
ମଣ୍ଡୟତି, ପ୍ରାୟତଃ, ଜୀବନ୍ତ, ଭୂମି, କର୍ଷତି, ଭବତି, କୃଷକ, କରୋତି, ସ୍ଵୟମ୍, ଧାନ୍ୟମ୍ ।
उत्तर: ମଣ୍ଡୟତି, ଜୀବନ୍ତି, କର୍ଷନ୍ତି, ଭବନ୍ତି, କରୋତି

कर्तृपदं चिनुत (କର୍ତ୍ତୃପଦଂ ଚିନୁତ।)
ओड़िशाप्रदेशः, श्रम, मण्डयति, जनाः, जीवन्ति, नद्यः, प्रवहन्ति, कर्षन्ति, कृषक:, धान्यम् ।
ଓଡ଼ିଶାପ୍ରଦେଶଃ, ଶ୍ରମ, ମଣ୍ଡୟିତ, ଜନା, ଜୀବନ୍ତି, ନଦ୍ୟ, ପ୍ରବହନ୍ତି, କର୍ଷନ୍ତି, କୃଷକ, ଧାନ୍ୟମ୍ ।
उत्तर: ଓଡ଼ିଶାପ୍ରଦେଶଃ, ଜନା, ନଦ୍ୟ, କୃଷକଃ, ଧାନ୍ୟମ୍ ।
शब्दानां मातृभाषया अर्थान् ल्लिखत।
(ଶବ୍ଦାନାଂ ମାତୃଭାଷୟା ଅର୍ଥାନ୍ ଲିଖତ ।)
- मण्डयति (ମଣ୍ଡୟତି) – ମଣ୍ଡନ କରିଛି
- बहवः (ବହବ) – ବହୁତ
- मुद्गः (ମୁଦ୍ଗ) – ମୁଗ
- भूब (ରୌଦ୍ରତାପସ୍ୟ) – ଟାଣଖରାର
- सिक्तः (ସିଲ୍ଲୀ) – ଓଦାହୋଇ
- उषाठशः (ବାର୍ଭାକ) – ବାଇଗଣ
- विपिणीम् (ବିପଣୀମ) – ବଜାରକୁ
निजभाषया प्रायशः दशभि: वाक्यै : उत्तरं लिखत ।
(ନିଜଭାଷୟ ପ୍ରାୟଶଃ ଦଶତିଃ ବାର୍କେ ଉତ୍ତରଂ ଲିଖତ ।)
कृषकः देशरक्षकः कथं भवति ?
କୃଷକଃ ଦେଶରକ୍ଷତଃ କଳଂ ଭବତି ?
उत्तर:
ଓଡ଼ିଶା ଆମ ପ୍ରଦେଶ। ଶସ୍ୟଶ୍ୟାମଳକ୍ଷେତ୍ରର ସୌନ୍ଦର୍ଯ୍ୟରେ ପରିପୂର୍ଣ୍ଣ ଆମ ଦେଶ । ଏହି ଶ୍ୟାମଳତାର ମୂଳ ହେଉଛି କୃଷକର ଶ୍ରମ। ଏଠାରେ ପ୍ରାୟ ଅଶୀ ପ୍ରତିଶତ ଲୋକମାନେ କୃଷିଦ୍ଵାରା ଜୀବନଯାପନ କରନ୍ତି । ଏଠାରେ ଅନେକ ନଦୀ ପ୍ରବାହିତ ହେଉଛି ଏବଂ ନଦୀ ପ୍ରବାହଦ୍ବାରା ଭୂମି ଉର୍ବର ହେଉଛି । କୃଷକ ଏହି ଭୂମିକୁ ହଳଦ୍ଵାରା କର୍ଷଣ କରେ । ଯେତେବେଳେ ଏହା . ଉତ୍ପାଦନଯୋଗ୍ୟ ହୋଇଯାଏ କୃଷକ ନିଜ କଠୋର ପରିଶ୍ରମରେ ଧାନ, ମୁଗ, ବିରି, କୋଳଥ ଆଦି ଶସ୍ୟ ଉତ୍ପାଦନ କରିଥାଏ।

ଧାନ ହେଉଛି ଆମ ପ୍ରଦେଶର ପ୍ରଧାନ ଉତ୍ପାଦନ ଶସ୍ୟ । ଅକ୍ଷୟତୃତୀୟା ଦିନଠାରୁ ଏଠାରେ କୃଷିକାର୍ଯ୍ୟ ଆରମ୍ଭ ହୋଇଥାଏ । କୃଷକ ପ୍ରଚଣ୍ଡଖରାକୁ ସହି ଶ୍ରାବଣର ବୃଷ୍ଟିଧାରାରେ ଭିଜି କୃଷିକାର୍ଯ୍ୟ ସ୍ଵାଦନ କରେ। ଋତୁ ଅନୁଯାୟୀ ପନିପରିବା ଋଷ କରିଥାଏ । ଶୀତଦିନେ ଆଳୁ, ବାଇଗଣ, ପିଆଜ, ରସୁଣ, ମୂଳା, ଶାଗ ଆଦିରେ କ୍ଷେତ୍ର ଅତ୍ୟନ୍ତ ରମଣୀୟ ଦେଖାଯାଏ । କୃଷକ ଦିନରାତି ପରିଶ୍ରମ କରି ବିଭିନ୍ନ ଶସ୍ୟ ତଥା ପନିପରିବା
मातृभाषयाअनुवादं कुरुत ।
(ମାତୃଭଷୟା ଅନୁବାଦଂ କୁରୁତ ।)
1. एष: ओड़िशाप्रदेशः।
ଏଷ ଓଡ଼ିଶାପ୍ରଦେଶଃ ।
ଅନୁବାଦ: ଏହା ଓଡ଼ିଶା ପ୍ରଦେଶ ।
2. शस्यश्यामलक्षेत्राणां सौन्दर्यम् एतं प्रदेशं मण्डयति ।
ଶସ୍ୟଶ୍ୟାମଳକ୍ଷେତ୍ରାଣା ସୌନ୍ଦର୍ଯ୍ୟମ୍ ଏବଂ ପ୍ରଦେଶଂ ମଣ୍ଡୟତି ।
ଅନୁବାଦ: ଶସ୍ୟଶାମଳକ୍ଷେତ୍ରର ସୌନ୍ଦର୍ଯ୍ୟ ଏହି ପ୍ରଦେଶକୁ ମଣ୍ଡନ କରେ।
3. प्रायतः प्रतिशतम् अशीतिः जनाः कृषिद्वारा जीवन्ति ।
ପ୍ରାୟତଃ ପ୍ରତିଶତମ୍ ଅଶୀତଃ ଜନଃ କୃଷିଦ୍ୱାରା ଜୀବନ୍ତି ।
ଅନୁବାଦ: ପ୍ରାୟ ଶହେରୁ ଅଶୀଭାଗ ଲୋକ କୃଷିଦ୍ୱାରା ଜୀବନ ଧାରଣ କରନ୍ତି ।
4. कृषकः हलेन भूमिं कर्षति ।
କୃଷକ ହଳେନ ଭୂମି କର୍ଷତି ।
ଅନୁବାଦ: କୃଷକ ହଳରେ ଭୂମି ଚାଷ କରେ।
5. एतेन भूमिः उत्पादनयोग्या भवति ।
ଏତେନ ଭୂମି ଉତ୍ପାଦନଯୋଗ୍ୟ ଭବତି ।
ଅନୁବାଦ: ଏହାଦ୍ଵାରା ଭୂମି ଉତ୍ପାଦନଯୋଗ୍ୟ ହୋଇଥାଏ।
6. हलं नाम लाइलम्।
ହଳଂ ନାମ ଲାଙ୍ଗଳମ୍ ।
ଅନୁବାଦ: ହଳର ଅର୍ଥ ଲଙ୍ଗଳ।
7. कृषिक्षेत्रात् धान्य-मुद्र-माष-भूचकणकादीनि शस्यानिं उत्पादितानि भवन्ति ।
କୃଷିକ୍ଷେତ୍ରାତ୍ର ଧାନ୍ୟ-ମୁଦ୍ଗ-ମାଷ-ଭୂଚକଣକାଦୀନି ଶସ୍ୟାନି ଉତ୍ପାଦିତାନି ଭାବନ୍ତି ।
ଅନୁବାଦ: କୃଷିକ୍ଷେତ୍ରରୁ ଧାନ, ମୁଗ, ବିରି, ବାଦାମ ପ୍ରଭୃତି ଶସ୍ୟ ଉତ୍ପନ୍ନ ହୁଏ ।
8. अक्षयतृतीयातः एतस्मिन् प्रदेशे कृषिकार्यस्य प्रारम्भ: भवति ।
ଅକ୍ଷୟତୃତୀୟାତଃ ଏତସ୍ମିନ୍ ପ୍ରଦେଶ କୃଷିକାର୍ଯ୍ୟସ୍ୟ ପ୍ରାରମ୍ଭ ଭବତି ।
ଅନୁବାଦ: ଅକ୍ଷୟ ତୃତୀୟାରୁ ଏହି ପ୍ରଦେଶରେ କୃଷିକାର୍ଯ୍ୟ ଆରମ୍ଭ ହୁଏ ।

9. कृषकः रौद्रतापस्य सहनं करोति ।
କୃଷକ ରୌଦ୍ରତାପସ୍ୟ ସହନଂ କରୋତି ।
ଅନୁବାଦ: କୃଷକ ଖରାର ତାତିକୁ ସହନ କରେ।
10. श्रावणस्य वृष्टिद्वारा सिक्तः सन् कृषिकार्यं सम्पादयति।
ଶ୍ରାବଣସ୍ୟ ବୃଷ୍ଟିଦ୍ୱାରା ସିଫ୍ଟ ସନ୍ କୃଷିକାର୍ଯ୍ୟ ସ୍ନାଦୟତି ।
ଅନୁବାଦ: ଶ୍ରାବଣର ବୃଷ୍ଟିଦ୍ୱାରା ଓଦାହୋଇ କୃଷିକାର୍ଯ୍ୟ ସ୍ନାଦନ କରେ ।
11. शीतकाले आलुक-वार्ताक, पलाण्डु, मूलक शाकादिभि: क्षेत्रं रमणीयं भवति ।
ଶୀତକାଳେ ଆଳୁକ-ବାର୍ତାକ, ପଲାଣ୍ଡୁ, ମୂଳକ ଶାକାଦିର୍ଭି କ୍ଷେତ୍ର ରମଣୀୟଂ ଭବତି ।
ଅନୁବାଦ: ଶୀତଦିନେ ଆଳୁ, ବାଇଗଣ, ପିଆଜ, ମୂଳା, ଶାଗ ପ୍ରଭୃତି ଦ୍ଵାରା କ୍ଷେତ୍ର ରମଣୀୟ ହୋଇଥାଏ।
12. कृषकः स्वयं कष्ट करोर्ति ।
କୃଷକଃ ସ୍ବୟଂ କଷ୍ଟ କରୋତି ।
ଅନୁବାଦ: କୃଷକ ନିଜେ କଷ୍ଟକରେ ।
13. एतै : पणयै : अस्माकं भोजनव्यवस्था रुचिकरी भवति।
ଏତଃ ପଣ୍ୟ ଅସ୍ତ୍ରାକଂ ଭୋଜନବ୍ୟବସ୍ଥା ରୁଚିକରୀ ଭବତି ।
ଅନୁବାଦ: ଏହି ପଣ୍ୟଦ୍ରବ୍ୟଦ୍ଵାରା ଆମ ଭୋଜନ -ବ୍ୟବସ୍ଥା ରୁଚିକର ହୋଇଥାଏ।
संस्कृतभाषया अनुवादं कुरुत।
(ସଂସ୍କୃତଭାଷିୟା ଅନୁବାଦଂ କୁରୁତ ।)
1. ଲୋକମାନେ କୃଷିଦ୍ୱାରା ଜୀବନଧାରଣ କରନ୍ତି ।
उत्तर:
जना: कृषिद्वारा जीवन्ति।
ଜନଃ କୃଷିଦ୍ୱାରା ଜୀବନ୍ତି |

2. ନଦୀଗୁଡ଼ିକ ଏହି ପ୍ରଦେଶରେ ବହିଥାନ୍ତି।
उत्तर:
नद्य:अस्मिन् प्रदेशे प्रवहन्ति।
ନଦ୍ୟ ଅସ୍ମିନ୍ ପ୍ରଦେଶେ ପ୍ରବହନ୍ତି ।
3. ଲଙ୍ଗଳରେ ଭୂମି କର୍ଷଣ ହୁଏ ।
उत्तर:
लाङ्गलेन भूमिकर्षणं भवति।
ଲାଙ୍ଗଳେନ ଭୂମିକର୍ଷଣଂ ଭବତି ।
4. ଧାନ ଓଡ଼ିଶାର ପ୍ରଧାନ ଶସ୍ୟ ।
उत्तर:
धान्यम् उत्कलस्य प्रधानं शस्यम्।
ଧାନ୍ୟମ୍ ଉତ୍କଳସ୍ୟ ପ୍ରଧାନଂ ଶସ୍ୟମ୍ ।
5. କୃଷକ ନିଜେ କଷ୍ଟ କରେ।
उत्तर:
कृषक: स्वयं कष्टं करोति।
କୃଷକଃ ସ୍ଵୟଂ କଷ୍ଟ କରୋତି। .
6. ପଣ୍ୟଦ୍ରବ୍ୟଗୁଡ଼ିକୁ ବଜାରକୁ ନେଇଥାଏ।
उत्तर:
पण्यानि विपणं नयति।
ପଣ୍ୟାନି ବିପଣଂ ନୟତି।
7. ପରିବାଗୁଡ଼ିକ ଦ୍ୱାରା ଆମର ଭୋଜନ ବ୍ୟବସ୍ଥା ରୁଚିକର ହୁଏ ।
उत्तर:
पण्यै: अस्माकं भोजनव्यवस्था रुचिकरी भवति।
ପଶୌ ଅସ୍ପୃକଂ ଭୋଜନବ୍ୟବସ୍ଥା ରୁଚିକରୀ ଭବତି।
अनुच्छेद: (ଅନୁ ଚ୍ଛେ ଦଃ )
एषः ओडिशाप्रदेशः । शस्यश्यामलक्षेत्राणां सौन्दर्यम् एतं प्रदेशं मण्डयति । एतस्याः श्यामलतायाः मूलं कृषकस्य श्रमः एव ।प्रायतः प्रतिशतम् अशीतिः जनाः कृषिद्वारा जीवन्ति । बहवः नद्यः अस्मिन् प्रदेशे प्रवहन्ति । नदीप्रवाहात् एतस्याः भूमिः उर्वरा । कृषकः हलेन भूमिं कर्षति । एतेन भूमि: उत्पादनयोग्या भवति । हलं नाम लाङ्लम्। एतस्मात् कृषिक्षेत्रात् धान्य-मुद्र-माष-कुल्माष-भूचणकादीनि शस्यानि उत्पादितानि भवन्ति ।
धान्यम् एतस्य प्रदेशस्य प्रधानम् उत्पादनम् । अक्षयतृतीयातः एतस्मिन् प्रदेशे कृषिकार्यस्य प्रारम्भः भवति । कृषकः रौद्रतापस्य सहनं करोति । एषः श्रावणस्य वृष्टिद्वारा सिक्तः सन् कृषिकार्यं सम्पादयति । शीतकाले आलुक-वार्ताक-पलाण्डु-लसुन-हरित-मूलक-रक्तवार्ताक-शाकादिभिः क्षेत्रं रमणीयं भवति । कृषकः स्वयं कष्टं करोति । पण्यद्रव्याणि विपणीम् आनयति । एतैः पण्यैः अस्माकं भोजनव्यवस्था डुचिकरी भवति । अतः एतस्मै कृषकाय नमंः ।
“जयतु कृषकः। जयतु सैनिकः।”

ଏଷ ଓଡ଼ିଶାପ୍ରଦେଶଃ । ଶସ୍ୟଶ୍ୟାମଳକ୍ଷେତ୍ରାଣଂ ସୌନ୍ଦର୍ଯ୍ୟମ୍ ଏବଂ ପ୍ରଦେଶଂ ମଣ୍ଡୟତି । ଏତସ୍ୟା ଶ୍ୟାମଳତାୟାଂ ମୂଳ କୃଷକସ୍ୟ ଶ୍ରମ ଏବ । ପ୍ରାୟତଃ ପ୍ରତିଶତମ୍ ଅଶୀତଃ ଜନଃ କୃଷି ଦ୍ଵାରା ଜୀବନ୍ତି । ବହନଃ ନଦ୍ୟ ଅସ୍ମିନ୍ ପ୍ରଦେଶେ ପ୍ରବହନ୍ତି । ନଦୀପ୍ରବାହାତ୍ ଏତସ୍ୟା

ଭୂମି ଉର୍ବରା । କୃ
ଷକଃ ହଳେନ ଭୂମି କର୍ଷତି । ଏତେନ ଭୂମି ଉତ୍ପାଦନଯୋଗ୍ୟ ଭବତି । ହଳଂ ନାମ ଲାଙ୍ଗଳମ୍ । ଏତସ୍ମାତ୍ କୃଷିକ୍ଷେତ୍ରାତ୍ ଧାନ୍ୟ – ମୁଗ୍ଧ – ମାଷ – କୁଳ୍ମଷ – ଭୂଚଣକାଦୀନି ଶସ୍ୟାନି ଉତ୍ପାଦିତାନି ଭାବନ୍ତି । ଧାନ୍ୟମ ଏତସ୍ୟ ପ୍ରଦେଶସ୍ୟ ପ୍ରଧାନମ ଉତ୍ପାଦନମ୍ । ଅକ୍ଷୟତୃତୀୟାତଃ ଏତସ୍ମିନ୍ ପ୍ରଦେଶେ କୃଷିକାର୍ଯ୍ୟସ୍ୟ ପ୍ରାରମ୍ଭ ଭବତି। କୃଷକଃ ରୌଦ୍ରତାପସ୍ୟ ସହନଂ କରୋତି । ଏଷ ଶ୍ରାବଣସ୍ୟ ଦୃଷ୍ଟିଦ୍ୱାରା ସିଦୁଃ ସନ୍ କୃଷିକାର୍ଯ୍ୟ ସମ୍ପାଦୟତି। ଶୀତକାଳେ ଆଳୁକ – ବାର୍ତାକ – ପଲାଣ୍ଡୁ – ଲସୁନ –ହରିତ – ମୂଳକ – ରକ୍ତବାର୍ତାକ – ଶାକାଦିଭିଂ କ୍ଷେତ୍ର ରମଣୀୟଂ ଭବତି। କୃଷକଃ ସ୍ଵୟଂ କଷ୍ଟ କରୋତି’’ ପଣ୍ୟଦ୍ରବ୍ଯାଣି ବିପଣୀମ୍ ଆନୟତି।ଏତଃ ପଣ୍ୟ ଅସ୍ନାକଂ ଭୋଜନବ୍ୟବସ୍ଥା ରୁଚିକରୀ ଭବତି। ଅତଃ ଏତସ୍ମି କୃଷକାୟ ନମଃ ।
‘‘ଜୟତୁ କୃଷକଃ । ଜୟତୁ ସୈନିକ ।’’
ସନ୍ଧି ବିଚ୍ଛେଦ
ଭୂଚଣକାଦୀନି = ଭୂଚଣକ + ଆଦୀନ, ପ୍ରାରମ୍ଭ = ପ୍ର + ଆରମ୍ଭ, ଶାକାଦିଭିଂ = ଶାକ + ଆଦିଭିଂ ।
ଶବ୍ଦାର୍ଥ
ଏଷ – ଏହି, ଏବଂ ପ୍ରଦେଶମ୍ – ଏହି ପ୍ରଦେଶକୁ, ଏତସ୍ୟା | ଶ୍ୟାମଳତାୟା – ଏହି ଶ୍ୟାମଳତାର, ଶ୍ରମ – ପରିଶ୍ରମ, ଏବ – ହିଁ | ନିଶ୍ଚୟ, ପ୍ରାୟତଃ – ପ୍ରାୟ, ପ୍ରତିଶତମ୍ – ଶତକଡ଼ା, ପ୍ରବାହୀଦ୍ – ପ୍ରବାହହେତୁ, ଭୂମିଂ – ମାଟିକୁ, ନାମ – ଅର୍ଥାତ୍, ଚ – ଏବଂ, ଧାନ୍ୟ – ଧାନ, ମୁଗ୍ଧ – ମୁଗ, ମାଷ – ବିରି, କୁଳ୍ମଷ – କୋଳଥ, ଭୂଚଣକ – ବାଦାମ, ରୌଦ୍ରତାପସ୍ୟ – ସୂର୍ଯ୍ୟଙ୍କ ଉତ୍ତାପର, ସିଧଃ ସନ୍ – ଓଦାହୋଇ, ଆଳୁକ – ଆଳୁ, ବାର୍ଭାକ – ବାଇଗଣ, ଲସୁନ – ରସୁଣ, ହରିତ – ବନ୍ଧାକୋବି, ମୂଳକ – ମୂଳା, ରକ୍ତବାର୍ଭାକ – ବିଲାତି, ଶାକ – ଶାଗ, ରମଣୀୟଂ – ସୁନ୍ଦର, ସ୍ଵୟଂ – ନିଜେ, ପଣ୍ୟଦ୍ରବ୍ଯାଣି ବିକ୍ରିଯୋଗ୍ୟ ବସ୍ତୁ, ବିପଣୀମ୍ – ବଜାରକୁ, ରୁଚିକରୀ – ସ୍ଵାଦିଷ୍ଟ, ଏତଦ୍ଵୈ କୃଷକାୟ – ଏହି କୃଷକକୁ, ନମଃ – ପ୍ରଣାମ, ଜୟତୁ – ଜୟହେତୁ ।
ଅନୁବାଦ
ଏହା ଓଡ଼ିଶା ପ୍ରଦେଶ । ଶସ୍ୟଶ୍ୟାମଳକ୍ଷେତର ସୌନ୍ଦର୍ଯ୍ୟ ଏହି ପ୍ରଦେଶକୁ ମଣ୍ଡନ କରେ । ଏହି ଶ୍ୟାମଳତାର ମୂଳ ହିଁ କୃଷକର ପରିଶ୍ରମ । ପ୍ରାୟ ଶହେରେ ଅଶି ପ୍ରତିଶତ ଲୋକ କୃଷି ଦ୍ଵାରା ଜୀବନ ଧାରଣ କରନ୍ତି । ବହୁତ ନଈ ଏହି ପ୍ରଦେଶରେ ପ୍ରବାହିତ ହୁଏ । ନଦୀପ୍ରବାହରୁ ଏହାର ଭୂମି ଉର୍ବର । କୃଷକ ହଳରେ ଭୂମି ଚାଷ କରେ । ଏହାଦ୍ଵାରା ଭୂମି ଉତ୍ପାଦନ ଯୋଗ୍ୟ ହୋଇଥାଏ । ହଳ ଅର୍ଥ ଲଙ୍ଗଳ । ଏହି କୃଷିକ୍ଷେତରୁ ଧାନ, ମୁଗ, ବିରି, କୋଳଥ, ବାଦାମ ପ୍ରଭୃତି ଶସ୍ୟ ଉତ୍ପନ୍ନ ହୁଏ । ଧାନ ଏହି ପ୍ରଦେଶର ପ୍ରଧାନ ଉତ୍ପାଦନ। ଅକ୍ଷୟତୃତୀୟାରୁ ଏହି ପ୍ରଦେଶରେ କୃଷିକାର୍ଯ୍ୟ ଆରମ୍ଭ ହୁଅନ୍ତି । କୃଷକ ଖରା ସହନ କରେ । ଇଏ ଶ୍ରାବଣର ବୃଷ୍ଟିଦ୍ୱାରା ଓଦା ହୋଇ କୃଷିକାର୍ଯ୍ୟ କରେ । ଶୀତଦିନେ ଆଳୁ, ବାଇଗଣ, ପିଆଜ, ରସୁଣ, ବନ୍ଧାକୋବି, ମୂଳା, ବିଲାତି, ଶାଗ ପ୍ରଭୃତିଦ୍ଵାରା କ୍ଷେତ ରମଣୀୟ ହୋଇଥାଏ । କୃଷକ ନିଜେ କଷ୍ଟ କରେ । ପଣ୍ୟଦ୍ରବ୍ୟ ବଜାରକୁ ଆଣେ । ଏହି ପଣ୍ୟଦ୍ରବ୍ୟ ଦ୍ୱାରା ଆମ ଭୋଜନ ବ୍ୟବସ୍ଥା ସ୍ଵାଦିଷ୍ଟ ହୋଇଥାଏ । ଏଣୁ ଏହି କୃଷକକୁ ପ୍ରଣାମ ।

मण्डयति, उर्वरा, कुल्माष:, सिक्त:, वार्ताकम्, विपणीम्, पणयै:
कर्तृपदानि :
जना:, नद्या, शस्यानि, कृषक:, धान्यम्।
क्रियापदानि :
मण्डयति, जीवन्ति, प्रवहन्ति, कर्षति, संपादयति।
शब्दार्थ:

![]()
![]()
![]()
![]()


![]()
 पिता (ପିତା) ବାପା
पिता (ପିତା) ବାପା