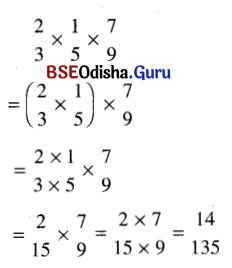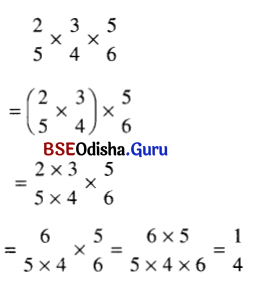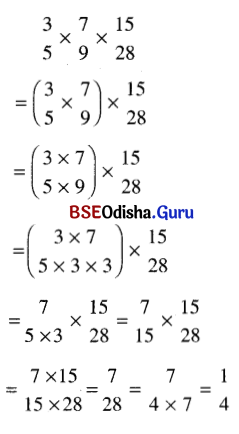Odisha State Board BSE Odisha 8th Class Maths Solutions Algebra Chapter 5 ସୂଚକ ତତ୍ତ୍ଵ Ex 5(b) Textbook Exercise Questions and Answers.
BSE Odisha Class 8 Maths Solutions Algebra Chapter 5 ସୂଚକ ତତ୍ତ୍ଵ Ex 5(b)
Question 1.
ନିମ୍ନଲିଖ ରାଶିଗୁଡ଼ିକୁ ଏକ ଆଧାର ବିଶିଷ୍ଟ ଘାତ ରାଶି ରୂପେ ପ୍ରକାଶ କର ।
(i) 36 × 34
(ii) \(\left(\frac{1}{2}\right)^6 \times\left(\frac{1}{2}\right)^5\)
(ii) \(\left(\frac{2}{3}\right)^7 \times\left(\frac{2}{3}\right)^3\)
(iv) (4)6 × (-4)-3
(v) \(\left(\frac{3}{2}\right)^5 \times\left(\frac{2}{3}\right)^4\)
(vi) (-4)6 × (4)3
(vii) (9)3 × (27)4
(viii) (8)3 × (-4)4
(ix) (7)8 × (-7)5
(x) (8)5 ÷ (4)4
(xi) {(5)3}4
(xii) {(-2)3}4
(xiii) \(\frac{7^4}{3^4}\)
(xiv) (3)9 + (4)9
(xv) \(\left(\frac{a}{b}\right)^7 \div\left(\frac{b}{a}\right)^3\)
(xvi) \(\left(\frac{a}{b}\right)^7 \div\left(\frac{-b}{a}\right)^3\)
ସମାଧାନ :
(i) 36 × 34 = (3 × 3 × 3 × 3 × 3 × 3) × (3 × 3 × 3 × 3)
= 3 × 3 × 3 × 3 × 3 × 3 × 3 × 3 × 3 × 3 = 310
ବିକଳ୍ପ ପ୍ରଣାଳୀ : 36 × 34 = 36+4 = 310
(ii) \(\left(\frac{1}{2}\right)^6 \times\left(\frac{1}{2}\right)^5=\left(\frac{1}{2}\right)^{6+5}=\left(\frac{1}{2}\right)^{11}\)
(iii) \(\left(\frac{2}{3}\right)^7 \times\left(\frac{2}{3}\right)^3=\left(\frac{2}{3}\right)^{7+3}=\left(\frac{2}{3}\right)^{10}\)
(iv) (4)6 × (-4)-3 = (4)6 × (-1 × 4)3
= (4)6 × (-1)3 × (4)3 = (-1)3 × (4)6 × (4)3
= (-1) × 46+3 = (-1)9 × 49 = (-1 × 4)9 = (-4)9
(v)
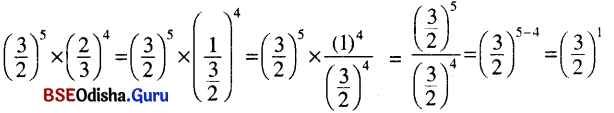
(vi) (-4)6 × (4)3 = (-1 × 4)6 × (4)3
= (-1)3 × (4)6 × (4)3 = 1 × 46+3 = (4)9
(vii) (9)3 × (27)4 = (32)3 × (33)4
= 32×3 × 33×4
= 36 × 312 = 36+12 = 318
(viii) (8)3 × (-4)4 = (8)3 × (-1 × 4)4 = (8)3 × (-1)4 × (4)4
= (-1)4 × 83 × (4)4 = 1 × (23)3 × (22)4 = 29 × 28 = 29+8 = 217
(ix) (7)8 × (-7)5 = 78 × (-1 × 7)5
= 78 × (-1)5 × 75 = (-1)5 × 78 × 75 = -1 × 78+5
= -1 × 713 = (-1)13 × 713 = (-1 × 7)13 4= (-7)13
(x) (8)5 ÷ (4)4 = ((2)3)5 ÷ ((2)2)4 = (2)15 ÷ (2)8 = 215-8 = 27
![]()
(xi) {(5)3}4 = 53×4 = 512
(xii) {(-2)3}4 = (-2)3×4 = (-2)12
(xiii) \(\frac{7^4}{3^4}\) = \((\frac{7}{3})^4\)
(xiv) (3)9 ÷ (4)9 = \((\frac{3}{4})^9\)
(xv)
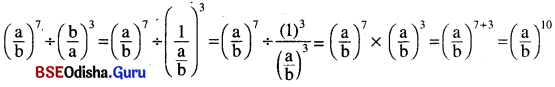
(xvi) \(\left(\frac{a}{b}\right)^7 \div\left(\frac{-b}{a}\right)^3\)
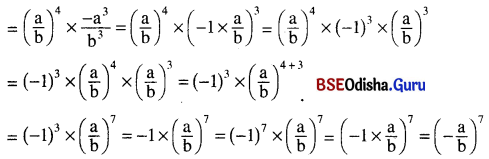
Question 2.
ମାନ ନିର୍ଣ୍ଣୟ କର ।
(i) 34 × 33 ÷ 35
(ii) (311 × 45) ÷ (44 × 36)
(iii) (43 × 42 × 4) ÷ (24 × 23 × 22)
(iv) 211 ÷ 83 × 42
(v) \(\left(\frac{3}{2}\right)^6 \div\left(\frac{2}{3}\right)^2\)
ସମାଧାନ :
(i) 34 × 33 ÷ 35
= \(3^4 \times\left(\frac{3^3}{3^5}\right)=3^4 \times \frac{1}{3^{5-3}}=3^4 \times \frac{1}{3^2}=\frac{3^4}{3^2}=3^{4-2}=3^2=9\)
(ii) (311 × 45) ÷ (44 × 36)
= \(\frac{3^{11} \times 4^5}{4^4 \times 3^6}=\frac{3^{11}}{3^6} \times \frac{4^5}{4^4}=3^{11-6} \times 4^{5-4}\) = 35 × 4 = 243 × 4=972
(iii) (43 × 42 × 4) ÷ (24 × 23 × 22)
= 43+2+1 ÷ 24+3+2 = 46 ÷ 29
= (2²)6 ÷ 29 = 212 ÷ 29 = 212 – 9 = 23 = 8
(iv) 211 ÷ 83 × 42 = 211 ÷ (23)3 × (22)2
= 211 ÷ 23×3 × 22×2 = 211 ÷ 29 × 24 = 211-9 × 24 = 22 × 24 = 22+4 = 26 = 62
(v)
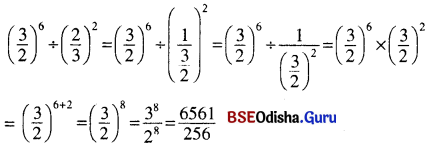
Question 2.
ସରଲ କର ।
(i) (22 × 2)3
(ii) (ab)5 × a3 × b2
(iii) \(\left(\frac{a}{b}\right)^7 \times a^6 \times b^5 \times\left(\frac{b}{a}\right)^6\)
(iv) 39 × 35+ 97
(v) \(\left(\frac{2}{3}\right)^5 \div\left(\frac{2}{3}\right)^8 \times\left(\frac{2}{3}\right)^3\)
ସମାଧାନ :
(i) (22 × 2)3 = (22+1)3 = (23)3 = 23×3 = 29 = 512
(ii) (ab)5 × a3 × b2 = a5 × b5 × a3 × b2
= (a5 × a3) × (b5 × b2) = a5+3 × b5+2 =a8b7
(iii) \(\left(\frac{a}{b}\right)^7 \times a^6 \times b^5 \times\left(\frac{b}{a}\right)^6\) = \(\left(\frac{a^7}{b^7}\right) \times a^6 \times b^5 \times\left(\frac{b^6}{a^7}\right)\)
(iv) 39 × 35 ÷ 97 = 39 × 35 ÷ (3²)7 = 39 × 35 ÷ 32×7
= 39 × 35 ÷ 314 = 39 × \(\frac{3^5}{3^14}\) = 39 × \(\frac{1}{3^14-5}\) = \(\frac{3^9}{3^9}\) = 1
(v)
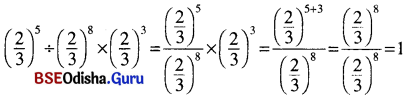
![]()
Question 4.
ମୌଳିକ ଆଧାର ବିଶିଷ୍ଟ ଘାତରାଶିରେ ପ୍ରକାଶ କର ।
(i) (64)3
(ii) (9)7
(iii) (125)m-1
(iv) (-8)11
ସମାଧାନ :
(1) 643 = (26)3 = 26×3 = 218 [∵ 64 ର ଏକ ମୌଳିକ ଗୁଣନୀୟକ 2]
(ii) (9)7 = (32)7 = 32×7 = 314 [∵ 9 ର ଏକ ମୌଳିକ ଗୁଣନୀୟକ 3]
(iii) (125)m-1 = (53)m-1 = 53(m-1) = 53m-3 [125 ର ଏକ ମୌଳିକ ଗୁଣନୀୟକ 5]
(iv) (-8)11 = {(-2)11}11 = (-2)11 = (-2)11 [(-8) ର ମୌଳିକ ଗୁଣନୀୟକ -2]
Question 5.
ନିମ୍ନଲିଖ୍ତ ଉକ୍ତି ମଧ୍ୟରୁ ଠିକ୍ ଉକ୍ତି ପାଇଁ (T) ଓ ଭୁଲ୍ ଉକ୍ତି ପାଇଁ (F) ଲେଖ ।
(i) 23 × 35 = 68
(ii) 35 × 55 = 155
(iii) (43)4 = (4)7
(iv) (52)3 = 56
(v) (3)3 × (3)2 = 36
(vi) (a3 . b5) = (ab)15
(vii) (23 × 33) = 63
(viii) \(\left(\frac{3}{4}\right)^6 \div\left(\frac{4}{3}\right)^2=\left(\frac{3}{4}\right)^4\)
(ix) (3)4 × (3)5 × (-3)2 = (-3)11
(x) -34 × 33 = -37
ସମାଧାନ :
(i) F
(ii) T
(iii) F
(iv) T
(v) T
(vi) F
(vii) T
(viii) F
(ix) F
(x) F
Question 6.
କେଉଁ କ୍ଷେତ୍ରରେ n ଏକ ଗଣନ ସଂଖ୍ୟା ହେବ ?
(i) 2n = 32
(n) 5n = loo
(iii) 4n = 512
(iv) 4n = 1024
(v) 3n = 729
(vi) 5n = 1250
(vii) 7n = 343
(viii) (\(\frac{1}{2}\))n = \(\frac{1}{64}\)
(ix) (\(\frac{2}{3}\))n = \(\frac{32}{15}\)
(x) (-2)n = -512
ସମାଧାନ :
ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ରରେ ଉଭୟ ପାର୍ଶ୍ଵର ଆଧାର ସମାନ କରି ଘାତଦ୍ଵୟ ମଧ୍ଯରେ ସମ୍ବନ୍ଧ ନିରୂପଣ କର ଏବଂ ଉଦ୍ଧୃତ ସମ୍ବନ୍ଧରୁ ‘n’ କେଉଁ ପ୍ରକାରର ସଂଖ୍ୟା ସ୍ଥିର କର ।
(i) 2n = 32 ⇒ 2n=2n ⇒ n = 5, ଏଠାରେ n ଏକ ଗଣନ ସଂଖ୍ୟା ।
(ii) 5n = 100 ⇒ 5n = 52 × 4, ଏଠାରେ n ଏକ ଗଣନ ସଂଖ୍ୟା ନୁହେଁ ।
(iii) 4n = 512 ⇒ (22)n = 29 ⇒ 2n = 9 ⇒ n =
(iv) 4n = 1024 ⇒ (22)n = 210 ⇒ 22n = 210 ⇒ 2n = 10 ⇒ n = 5, ଏଠାରେ n ଏକ ଗଣନ ସଂଖ୍ୟା ।
(v) 3n = 729 ⇒ 3n = 36 ⇒ n = 6, ଏଠାରେ n ଏକ ଗଣନ ସଂଖ୍ୟା ।
(vi) 5n = 1250 ⇒ 5n = 54 × 2, ଏଠାରେ n ଏକ ଗଣନ ସଂଖ୍ୟା ନୁହେଁ ।
(vii) 7n = 343 ⇒ 7n = 73 ⇒ n = 3, ଏଠାରେ n ଏକ ଗଣନ ସଂଖ୍ୟା ।
(viii) \(\left(\frac{1}{2}\right)^{\mathrm{n}}=\frac{1}{64} \Rightarrow\left(\frac{1}{2}\right)^{\mathrm{n}}=\left(\frac{1}{2}\right)^6\) ⇒ n = 6, ଏଠାରେ n ଏକ ଗଣନ ସଂଖ୍ୟା ।
(ix) (\(\frac{2}{3}\))n = \(\frac{32}{15}\) ⇒ (\(\frac{2}{3}\))n = \(\frac{2^5}{3×5}\) ଏଠାରେ n ଏକ ଗଣନ ସଂଖ୍ୟା ନୁହେଁ ।
(x) (-2)n = -512 ⇒ (-2)n = (-2)9 ⇒ n = 9, ଏଠାରେ n ଏକ ଗଣନ ସଂଖ୍ୟା ।