BSE Odisha 8th Class Maths Solutions Algebra Chapter 3 ବୀଜଗାଣିତିକ ପରିପ୍ରକାଶ ଓ ଅଭେଦ Ex 3(c)

Odisha State Board BSE Odisha 8th Class Maths Solutions Algebra Chapter 3 ବୀଜଗାଣିତିକ ପରିପ୍ରକାଶ ଓ ଅଭେଦ Ex 3(c) Textbook Exercise Questions and Answers.

BSE Odisha Class 8 Maths Solutions Algebra Chapter 3 ବୀଜଗାଣିତିକ ପରିପ୍ରକାଶ ଓ ଅଭେଦ Ex 3(c)

Question 1.
ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(i) 3 × 5x = (…………)
(ii) 3x² × 2x² = (…………)
(iii) 2 {x} × 0 = (…………)
(iv) 3x³ × 1 = (…………)
ସମାଧାନ :
(i) 3 × 5x = (15 x)
(ii) 3x² × 2x² = 6×4
(iii) 2x × 0 = 0
(iv) 3x³ × 1 = 3x³

Question 2.
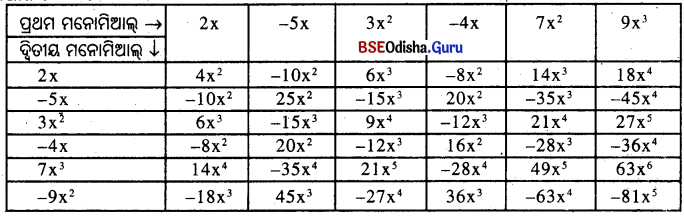
ନିମ୍ନ ସାରଣୀଟିକୁ ପୂରଣ କର ।

ସମାଧାନ :

Question 3.
ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
3 × (2x – 7) = 3 × 2x + 3 × (………)
(-2) × ( 3x + 1) = (-2) × 3x + (-2) × (………)
(2x – 6) × (-x) = 2x × (……..) + (……..) (-x)
(-3x²) (2x + 4) = (…….) × 2x + (-3x²) × (…….)
ସମାଧାନ :
3 × (2x – 7) = 3 × 2x + 3 × (2) : a(b + c) = a × b + a × c
(-2) × ( 3x + 1) = (-2) × 3x + (-2) × (1)
(2x – 6) × (-x) = 2x × (-1) + (-6) (-x)
(-3x²) (2x + 4) = (-3x²) × 2x + (-3x²) × (4)

Question 4.
ଗୁଣଫଳ ନିର୍ଣ୍ଣୟ କର ।
(i) (x – 1) × ( x + 1)
(ii) (x – 1) × (x² + x + 1)
(iii) (x + 1) × (x² – x + 1)
(iv) (2x + 1) × (x – 2)
(v) (2x + 3) × (x² – 2x + 5)
(vi) (-x – 3) × (x² – 5x – 2)
(vii) (x² + 1) × ( x² – 1)
(viii) (x² + 1) × (2x² – x + 1)
(ix) (x² – 1) × (x² + x + 1)
ସମାଧାନ :
(i) (x – 1) × ( x + 1)
= (x – 1) x + ( x – 1)1 (ବଣ୍ଟନ ନିୟମର ପ୍ରୟୋଗ )
= x² – x + x – 1 = x² – 1

(ii) (x – 1) × (x² + x + 1) = (x – 1)x² + (x – 1) x + (x – 1) 1
= x³ – x² + x² – x + x – 1 = x³ – 1

(iii) (x + 1) × (x² – x + 1) = (x + 1)x² – (x + 1) + (x + 1) 1
= x³ + x² – x² – x + x + 1 = x³ + 1

(iv) (2x + 1) × (x – 2) = (2x + 1)x – (2x +1)2 (ବଣ୍ଟନ ନିୟମର ପ୍ରୟୋଗ )
= 2x² + x – 4x – 2 = 2x² – 3x – 2

(v) (2x +3) x (x² – 2x + 5 )= x² (2x + 3) – 2x (2x + 3) +5 (2x + 3) (ବଣ୍ଟନ ନିୟମର ପ୍ରୟୋଗ )
= 2x³ + 3x² – 4x² – 6x + 10x + 15
= 2x³ – x² + 4x + 15

(vi) (- x – 3) x (x² – 5x – 2) = x² (-x – 3) – 5x (-x – 3) – 2(- x – 3)
= – x³ – 3x² + 5x² + 15x + 2x + 6 = – x³ + 2x² + 17x +6

(vii) (x² +1) x.(x² – 1) = x² (x² +1) – 1 (x² + 1) = x⁴ + x² – x² – 1 = x⁴ – 1

(viii) (x²+1)(2x² – x + 1) = 2x²(x² + 1) – x(x² + 1) + 1(x² + 1)
= 2x⁴ + 2x² – x³ – x + x² + 1
=2x⁴ – x³ + 2x² + x² – x + 1 = 2x⁴ – x³ + 3x² – x + 1

(ix) (x² – 1) (x² + x + 1) = x² (x² – 1) + x (x² – 1) + 1(x² – 1)
= x⁴ – x² + x³ – x + x² – 1
= x⁴ + x³ – x² + x² – x – 1 = x⁴ + x³ – x – 1