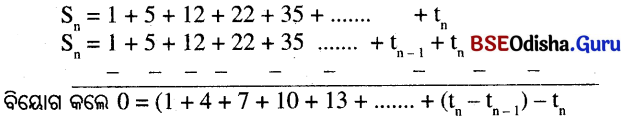Odisha State Board BSE Odisha 10th Class Maths Solutions Geometry Chapter 2 ବୃତ୍ତ Ex 2(a) Textbook Exercise Questions and Answers.
BSE Odisha Class 10 Maths Solutions Geometry Chapter 2 ବୃତ୍ତ Ex 2(a)
Question 1.
ଉକ୍ତିଟି ଠିକ୍ ଥିଲେ T ଏବଂ ଭୁଲ ଥିଲେ F ଲେଖ ।
(i) ଏକ ସମତଳରେ ଥିବା ଏକ ବକ୍ରରେଖାର ପ୍ରତ୍ୟେକ ବିନ୍ଦୁ ଉକ୍ତ ସମତଳ ଉପରିସ୍ଥ ଏକ ଦତ୍ତ ବିନ୍ଦୁଠାରୁ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଦୂରତାରେ ଥିଲେ ବକ୍ରରେଖାଟିକୁ ବୃତ୍ତ କୁହାଯାଏ ।
(ii) ବୃତ୍ତର ପ୍ରତ୍ୟେକ ବିନ୍ଦୁ କୌଣସି ଏକ ବ୍ୟାସାର୍କର ଏକ ପ୍ରାନ୍ତ ବିନ୍ଦୁ ଅଟେ ।
(iii) ଏକ ବୃତ୍ତର ଅସଂଖ୍ୟ ବ୍ୟାସ ରହିଛି ।
(iv) କେନ୍ଦ୍ର, ବୃତ୍ତର ଏକମାତ୍ର ବିନ୍ଦୁ ଯାହା ବୃତ୍ତର ପ୍ରତ୍ୟେକ ବ୍ୟାସ ଉପରେ ଅବସ୍ଥିତ ।
(v) ଏକ ଜ୍ୟା ବୃତ୍ତର ଅନ୍ତର୍ଦେଶକୁ ଯେଉଁ ଦୁଇ ଅଂଶରେ ବିଭକ୍ତ କରେ ସେମାନେ ପ୍ରତ୍ୟେକ ଉତ୍ତଳ ସେଟ୍ ଅଟନ୍ତି ।
(vi) ବୃତ୍ତର ଏକ ବ୍ୟାସ ଗୋଟିଏ ଜ୍ୟାକୁ ସମଦ୍ବିଖଣ୍ଡ କଲେ ସେମାନେ ପରସ୍ପର ପ୍ରତି ଲମ୍ବ ଅଟନ୍ତି ।
(vii) ପ୍ରତ୍ୟେକ ତ୍ରିଭୁଜର ପରିକେନ୍ଦ୍ର ଏହାର ଏକ ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ ।
(vii) ଏକ ବୃତ୍ତର କେନ୍ଦ୍ର, ଏହାର ଏକମାତ୍ର ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ ଯାହାଠାରୁ ବୃତ୍ତର ପ୍ରତ୍ୟେକ ବିନ୍ଦୁର ଦୂରତା ସମାନ ।
(ix) ଏକ ରଶ୍ମି ବୃତ୍ତକୁ ଗୋଟିଏ ମାତ୍ର ବିନ୍ଦୁରେ ଛେଦ କରେ । ତେବେ ରଶ୍ମିର ଆଦ୍ୟ ବିନ୍ଦୁଟି ବୃତ୍ତର ଏକ ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ
(x) ଏକ ତ୍ରଭରେ \(\overline{\mathrm{AB}}\) ଓ \(\overline{\mathrm{BC}}\) ହୁକଟି ସବସମ କ୍ୟା 6ହ6ଲ B ଦିନ୍ଦନାମ କ୍ୟାମଣ ∠ABC କୁ ସମଦ୍ୱଖଣ୍ଡ ହେବ ।
(xi) ଗୋଟିଏ ବିନ୍ଦୁ ଦୁଇ ବା ତତୋଽଧ୍ଵକ ବୃତ୍ତର କେନ୍ଦ୍ର ହୋଇପାରିବ ନାହିଁ ।
(xii) ଗୋଟିଏ ସରଳରେଖା ଗୋଟିଏ ବୃତ୍ତରକୁ ସର୍ବଦା ଦୁଇଟି ବିନ୍ଦୁରେ ଛେଦ କରେ ।
Solution:
(i) F (ବକ୍ରରେଖାଟି ଏକ ବୃତ୍ତର ଚାପ ହୋଇପାରେ ।)
(ii) T (ଏକ ବ୍ୟାସାର୍କର ଦୁଇଟି ପ୍ରାନ୍ତ ବିନ୍ଦୁ ମଧ୍ୟରୁ ଗୋଟିଏ ବିନ୍ଦୁ କେନ୍ଦ୍ର ଓ ଅନ୍ୟଟି ବୃତ୍ତ ଉପରିସ୍ଥ ।)
(iii) T (ବୃତ୍ତ ଉପରିସ୍ଥ )
(iv) F
(v) T
(vi) T (ବ୍ୟାସରେ କେନ୍ଦ୍ର ଅବସ୍ଥିତ । କେନ୍ଦ୍ର ଓ ଜ୍ୟାର ମଧ୍ୟବିନ୍ଦୁକୁ ଯୋଗ କରୁଥିବା ରେଖାଖଣ୍ଡ ଜ୍ୟା ପ୍ରତି ଲମ୍ବ ।)
(vii) F (ସ୍ଥୂଳକୋଣୀ ତ୍ରିଭୁଜ ଓ ସମକୋଣୀ ତ୍ରିଭୁଜର ପରିକେନ୍ଦ୍ର ତ୍ରିଭୁଜର ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ ନୁହେଁ ।)
(viii) T (ବୃତ୍ତର ସଂଜ୍ଞା ଅନୁସାରେ ।)
(ix) F (ରଶ୍ମିଟି ବୃତ୍ତପ୍ରତି ସ୍ପର୍ଶକ ହେବ ।)
(x) T (O ବୃତ୍ତର କେନ୍ଦ୍ର ହେଲେ A OAB = A OCB ହେବ ।
(xi) F (ଏକକୈନ୍ଦ୍ରିକ ବୃତ୍ତମାନଙ୍କର ଗୋଟିଏ କେନ୍ଦ୍ରବିନ୍ଦୁ ।)
(xii) F (ଆଦୌ ଛେଦ ନକରିପାରେ ବା ଗୋଟିଏ ବିନ୍ଦୁରେ ଛେଦ କରିପାରେ ।)
![]()
Question 2.
ପ୍ରଦତ୍ତ ସମ୍ଭାବ୍ୟ ଉତ୍ତରରୁ ଠିକ୍ ଉତ୍ତରଟି ବାଛି ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(i) ଦୁଇଟି ଅସମାନ୍ତର ଜ୍ୟାର ଛେଦବିନ୍ଦୁ …………………. ଅଟେ ।
(a) ବୃତ୍ତର ଏକ ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ
(b) ବୃତ୍ତର ଏକ ବହିଃସ୍ଥ ବିନ୍ଦୁ
(c) ବୃତ୍ତ ଉପରିସ୍ଥ ଏକ ବିନ୍ଦୁ
(d) ବୃତ୍ତ ଉପରିସ୍ଥ କିମ୍ବା ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ
Solution:
ହଉ ଭପରିମ୍କ କିମ୍ଵା ଆନ୍ତଃମ ଦିନ୍ଦୁ
(ii) P ବିନ୍ଦୁ ବୃତ୍ତର ଏକ ବହିଃସ୍ଥ ବିନ୍ଦୁ ହେଲେ ବୃତ୍ତ ଉପରେ P ଠାରୁ ସମଦୂରବର୍ତ୍ତୀ ……………………… ଯୋଡ଼ା ବିନ୍ଦୁ ଅଛି ।
(a) 1
(b) 2
(c) 8
(d) ଅସଂଖ୍ୟ
Solution:
ଅସଂଖ୍ୟ
(iii) 6ଗାଟିଏ ରେଖାଖଣ୍ଡ ସଦାଧକ ………….. ଟି ବୃତ୍ତର ଜ୍ୟା ହୋଇପାରିବ ।
(a) 1
(b) 2
(c) 4
(d) ଅସଂଖ୍ୟ
Solution:
2
(iv) 6ଗାଟିଏ ରେଖାଖଣ୍ଡ ସଦାଧକ ………….. ବ୍ୟାସାର୍ଦ୍ଧ ହୋଇ ପାରିବ ।
(a) 1
(b) 2
(c) 4
(d) ଅସଂଖ୍ୟ
Solution:
ଅଫଖ୍ୟ
(v) ଗୋଟିଏ ବୃତ୍ତରେ ଏକ ଜ୍ୟାର ଗୋଟିଏ ପ୍ରାନ୍ତବିନ୍ଦୁ କେନ୍ଦ୍ରଠାରୁ 5 ସେ.ମି. ଦୂରରେ ଏବଂ ଜ୍ୟାଟିର ମଧ୍ୟବିନ୍ଦୁ କେନ୍ଦ୍ରଠାରୁ 3 ସେ.ମି. ଦୂରରେ ଅଛି । ଜ୍ୟାଟିର ଦୈର୍ଘ୍ୟ …………….. 6ପ.ମି.
(a) 8
(b) 12
(c) 16
(d) 20
Solution:
8
Question 3.
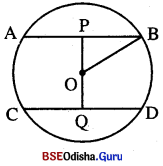
ଏକଭର 16 6ସ.ମି. ଦେଣ୍ୟ ବିଶିଷ୍ଟ 6ଟାଟିଏ ବ୍ୟା ଏକ ବ୍ୟାସାଶୁ \(\overline{OP}\) ଦାରା D ଜିନ୍ଦୁ 6ର ପମଦ୍ୱିଖଣ୍ଡତ ହୁଏ | ହୁଇର ଦ୍ୟାସାରୁ 10 6ସ.ମି. 6ଦ୍ର6କ DP ର 6ଦିଶ୍ୟ ନିଣ୍ଟଯ କର |
Solution:
ଦକ ହଉ6ର AB ର୍ଯ୍ୟର 6ଦିଣ୍ୟ = 16 ପେ.ମି.
⇒ AD = \(\frac { 16 }{ 2 }\) ପେ.ମି. = 8 ପେ.ମି. (AD = \(\frac { 1 }{ 2 }\) AB)
ହଉର ଦ୍ୟାସାର୍ଦ (OA) = 10 ପେ.ମି. = OP
∴ △ODA 6ର OD = \(\sqrt{\mathrm{OA}^2-\mathrm{AD}^2}\) = \(\sqrt{\mathrm{10}^2-\mathrm{8}^2}\) = \(\sqrt{100-64}\) = \(\sqrt{36}\) = 6 6ସ.ମି. |
DP = OP – OD = 10 6ସ.ମି. – 6 6ସ.ମି. = 4 6ସ.ମି. |
∴ \(\overline{DP}\) ର 6ଦିଖ୍ୟ 4 6ସ.ମି. |
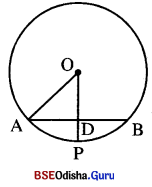
Question 4.
6ଟାଟିଏ ତ୍ରଭର 6କହ୍ O | ଏକ ଲ୍ୟା \(\overline{\mathbf{AB}}\) ର ମଧ୍ୟଦିନୁ D 6ହ6ଲ ପ୍ରମାଣୀ କର ଯେ \(\overline{\mathbf{OD}}\) , ∠AOB କୁ ସମଦ୍ୱିଖଣ୍ କ6ର |
Solution:
ଦଇ : ହଉର 6କହ O | ଖ୍ୟା AB ର ମଧ୍ୟଦିନ୍ଦୁ D |
ପ୍ରାମାଣ୍ୟ : \(\overline{\mathbf{OD}}\), ∠AOB କୁ ସମଦିଖଣ୍ଡକ କ6ର |
ପ୍ରମାଣ : △AOD ଓ △BOD ମଧ୍ୟ6ର
AO = BO (ଏକା ଦୃତ୍ତର ବନ୍ଦ୍ୟାସାଦଁ)
AD = BD (ଦଇ)
\(\overline{\mathbf{OD}}\) ସାଧାରଣ ଦାନ୍ଦୁ
△AOD ≅ △BOD (ଦା.ଦା.ଦା. ସଦପମତା)
⇒ ∠AOD ≅ ∠BOD (ର୍ଥ ନୁର୍ପ କୋଣ)
⇒ \(\overline{\mathbf{OD}}\) , ∠AOB କୁ ସମଦ୍ୱିଖଣ୍ଡ କରେ |
![]()
Question 5.
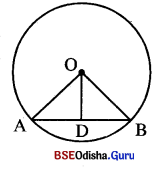
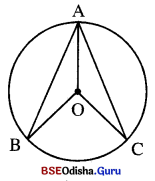
6ଟାଟିଏ ତ୍ରଭର 6କହ୍ O | ଏକ ଲ୍ୟା \(\overline{\mathbf{AB}}\) ଓ \(\overline{\mathbf{AC}}\) ର ମଧ୍ୟଦିନୁ D 6ହ6ଲ ପ୍ରମାଣୀ କର ଯେ \(\overline{\mathbf{OA}}\) , ∠BAC କୁ ସମଦ୍ୱିଖଣ୍ କ6ର |
Solution:
ଦଇ : O, ABC ହଉର 6କହ ଏକ AB = AC | (ତ୍ୟାଦୟ ସଦଂସମ)
ପ୍ରାମାଣ୍ୟ : \(\overline{\mathbf{OA}}\), ∠BAC କୁ ସମଦିଖଣ୍ଡ କ6ର |
ଆଥାତ୍ m∠OAB = m∠OAC
ର୍ଥଙନ : \(\overline{\mathbf{OB}}\) ଏବଂ \(\overline{\mathbf{OC}}\) ଅଳନ କର |
ପ୍ରମାଣ : △AOB ଓ △AOC ମଧ୍ୟରେ
AB = AC (ଦଇ)
OB = OC (ଗୋଟିଏ ହଭର ବ୍ୟାପୀ ବଂ)
\(\overline{\mathbf{OA}}\) ସାଧାରଣ ଦାନ୍ଦୁ
△AOB ≅ △AOD (ଦା.ଦା.ଦା. ସଦପମତା)
⇒ m∠OAB = m∠OAC (ର୍ଥ ନୁର୍ପ କୋଣ)
Question 6.
ଗୋଟିଏ ବୃତ୍ତର କେନ୍ଦ୍ର O ଏବଂ \(\overline{\mathbf{AB}}\) ଓ CD ଏହାର ଦୁଇଟି ସମାନ୍ତର ଜ୍ୟା । P ଓ Q ଯଥାକ୍ରମେ AB ଓ CDର ମଧ୍ୟବିନ୍ଦୁ ହେଲେ ପ୍ରମାଣ କର ଯେ ( ବିନ୍ଦୁ, \(\stackrel{\leftrightarrow}{P}\) ଉପରିସ୍ଥ ହେବ ।
Solution:
ଦତ୍ତ : AB ଓ CD ବୃତ୍ତର ଯେକୌଣସି ଦୁଇଟି ସମାନ୍ତର ଜ୍ୟା । P ଓ Q ଯଥାକ୍ରମେ AB ଏବଂ CD ଜ୍ୟାର ମଧ୍ୟବିନ୍ଦୁ ।
ପ୍ରାମାଣ୍ୟ : ବୃତ୍ତର କେନ୍ଦ୍ର ‘O’, \(\overline{\mathbf{PQ}}\) ଉପରିସ୍ଥ ହେବ ।
ପ୍ରମାଣ : ମନେକର ବୃତ୍ତର କେନ୍ଦ୍ର ‘O’, PQ ଉପରିସ୍ଥ ନୁହେଁ ।
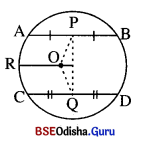
OP ଓ \(\overline{\mathbf{OQ}}\) ଅଙ୍କନ କର । O ବିନ୍ଦୁରେ AB ସହ ସମାନ୍ତର କରି \(\overrightarrow{\mathrm{OR}}\) ଅଙ୍କନ କର।
m∠APO = 90° (∵ 0 କେନ୍ଦ୍ର ଏବଂ AB ଜ୍ୟାର ମଧ୍ୟବିନ୍ଦୁ P)
∴ m∠POR = 90° (∵ AB || OR ଏବଂ \(\overline{\mathbf{PO}}\) ହେଲେ)
ସେହିପରି m∠CQO = 90° ଏବଂ m∠ROQ = 90° (\(\overline{\mathbf{CD}}\) || \(\overline{\mathbf{OR}}\) ଏବଂ QO ଛେଦକ)
∴m∠POR + m∠ROQ = 180°
⇒ P, O ଓ Q ଏକରେଖୀୟ ।
⇒ O, \(\overline{\mathbf{PQ}}\) ଉପରିସ୍ଥ ଏକ ବିନ୍ଦୁ ହେବ ।
Question 7.
ଗୋଟିଏ ସମବାହୁ ତ୍ରିଭୁଜର ପରିକେନ୍ଦ୍ରଠାରୁ ତ୍ରିଭୁଜର ବାହୁମାନେ ସମଦୂରବର୍ତ୍ତୀ – ପ୍ରମାଣ କର ।
Solution:
ଆମେ ଜାଣୁ ସମବାହୁ ତ୍ରିଭୁଜର ବାହୁମାନଙ୍କର ଦୈର୍ଘ୍ୟ ସମାନ ।
ପୁନଶ୍ଚ ଏକ ବୃତ୍ତରେ ସମାନ ଦୈର୍ଘ୍ୟବିଶିଷ୍ଟ ଜ୍ୟାମାନ କେନ୍ଦ୍ରଠାରୁ ସମଦୂରବର୍ତ୍ତୀ ।
ତେଣୁ ସମବାହୁ ତ୍ରିଭୁଜର ପରିକେନ୍ଦ୍ରଠାରୁ ତ୍ରିଭୁଜର ବାହୁମାନ ସମଦୂରବର୍ତ୍ତୀ । (ପ୍ରମାଣିତ)
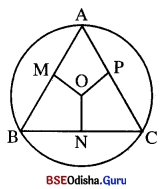
ବିକଳ୍ପ ପ୍ରମାଣ :
ଦତ୍ତ : A ABCର ବାହୁମାନ କେନ୍ଦ୍ରଠାରୁ ସମୟଦୂରବର୍ତ୍ତୀ ।
ପ୍ରମାଣ : \(\overline{\mathbf{AB}}\), BC ଓ CA ର ସମଦ୍ଵିଖଣ୍ଡକ ଲମ୍ବମାନଙ୍କର ଛେଦବିନ୍ଦୁ O ।
ତେଣୁ O ପରିବୃତ୍ତର କେନ୍ଦ୍ର ।
AB, BC ଓ CA ହେତୁ ଜ୍ୟାମାନ କେନ୍ଦ୍ରଠାରୁ ସମଦୂରବର୍ତ୍ତୀ
କାରଣ AB = BC = CA (ଉପପାଦ୍ୟ – 8)
Question 8.
ପ୍ରମାଣ କର ଯେ ବୃତ୍ତରେ ଏକ ବ୍ୟାସ ଏହାର ବୃହତ୍ତମ ଜ୍ୟା । (ସୂଚନା : ଏକ କ୍ୟାର କେନ୍ଦ୍ରଠାରୁ ଦୂରତା d ≥ 0 ) ଏବଂ ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ r ହେଲେ, ଜ୍ୟାର ଦୈର୍ଘ୍ୟ \(2 \sqrt{r^2-d^2} \leq 2 r\) = ବ୍ୟାସ) ।
Solution:
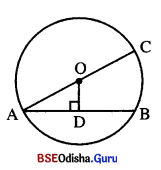
ଦତ୍ତ : ABC ବୃତ୍ତର \(\overline{\mathbf{AC}}\) ବ୍ୟାସ । O ବୃତ୍ତର କେନ୍ଦ୍ର ।
ପ୍ରାମାଣ୍ୟ : AC ବୃହତ୍ତମ ଜ୍ୟା ।
ଅଙ୍କନ : AB ଜ୍ୟା ଅଙ୍କନ କର । OD ⊥ AB ଅଙ୍କନ କର ।
ପ୍ରମାଣ : △AODରେ m∠ADO = 90°
⇒ AO > AD
⇒ 2AO > 2AD ⇒ AC > AB
ସେହିପରି ପ୍ରମାଣ କରାଯାଇ ପାରେ ଯେ, \(\overline{\mathbf{AC}}\) ର ଦୈର୍ଘ୍ୟ
ଅନ୍ୟ ଯେକୌଣସି ଜ୍ୟାର ଦୈର୍ଘ୍ୟଠାରୁ ବୃହତ୍ତର ।
∴ AC ବ୍ୟାସ ବୃତ୍ତର ବୃହତ୍ତମ ଜ୍ୟା । (ପ୍ରମାଣିତ)
Question 9.
ଗୋଟିଏ ବୃତ୍ତରେ ଦୁଇଟି ସମାନ୍ତର ଜ୍ୟାର ଏକ ପାର୍ଶ୍ବରେ ବୃତ୍ତର କେନ୍ଦ୍ର ଅବସ୍ଥିତ । ପ୍ରମାଣ କର ଯେ ଜ୍ୟା ଦ୍ଵୟ ସର୍ବସମ ନୁହଁନ୍ତି ।
Solution:
S ବୃତ୍ତର O କେନ୍ଦ୍ର । କେନ୍ଦ୍ରର ଏକ ପାର୍ଶ୍ବରେ AB ଓ CD ଦୁଇଟି ଜ୍ୟା | AB || CD |
ପ୍ରାମାଣ୍ୟ : AB ≠ CD ଅର୍ଥାତ୍ AB ଓ CD ଜ୍ୟା ଦ୍ଵୟ ସର୍ବସମ ନୁହଁନ୍ତି ।
ଅଙ୍କନ : OM ⊥ CD ଅଙ୍କନ କର ଏବଂ OA ଓ OC ଅଙ୍କନ କର ।
ପ୍ରମାଣ : OM ⊥ AB ⇒ OM ⊥ CD
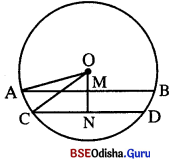
△OAM ରେ OA2 = OM2 + AM2 ….(i)
△ONC ରେ OC2 = ON2 + CN2 ….(ii)
OA = OC 6ହତ୍ର (i) ଓ (ii) ବ୍ ପାଲାଟା OM2 + AM2 = ON2 + CN2
⇒ AM2 – CN2 = ON2 – OM2 > 0 (∵ ON > OM)
⇒ CN < AM = \(\frac { 1 }{ 2 }\) CD < \(\frac { 1 }{ 2 }\) Ab
⇒ CD < AM ⇒ AB ≠ CD (ପ୍ରମାଣିତ) (∵ ON > OM ⇒ CD < AB)
![]()
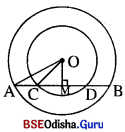
Question 10.
AB ଓ CD ଗୋଟିଏ ବୃତ୍ତର ଦୁଇଟି ସମାନ୍ତର ଜ୍ୟା । AB = CD = 8 ସେ.ମି. । ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ 5 ସେ.ମି. ହେଲେ ଜ୍ୟାଦ୍ଵୟର ମଧ୍ୟବର୍ତ୍ତୀ ଦୂରତା ନିର୍ଣ୍ଣୟ କର ।
Solution:
AB = CD ଓ AB || CD
ହେତୁ ଜ୍ୟାଦ୍ଵୟ କେନ୍ଦ୍ରର ବିପରୀତ ପାର୍ଶ୍ଵରେ ରହିବେ ।
AB = 8 6ସ.ମି. ⇒ BP \(\frac { 1 }{ 2 }\) × 8 ସେ.ମି. = 4 ସେ.ମି. |
OB = 5 ସେ.ମି., OP ⊥ AB ଓ OQ ⊥ CD ହେଉ ।
POB ସମ6କାଣା ତ୍ରିକୁଲ6ର OP = \(\sqrt{\mathrm{OB}^2-\mathrm{BP}^2}\) = \(\sqrt{5^2-4^2}\) = \(\sqrt{9}\) = 3
∴ PQ = OP + OQ = 3 ସେ.ମି. + 3 ସେ.ମି. = 6 ସେ.ମି. |
∴ ଜ୍ୟାଦ୍ବୟର ମଧ୍ୟବର୍ତ୍ତୀ ଦୂରତା 6 ସେ.ମି. |
Question 11.
10 ସେ.ମି. ବ୍ୟାସାର୍ଦ୍ଧ ବିଶିଷ୍ଟ ଗୋଟିଏ ବୃତ୍ତର ଦୁଇଟି ସମାନ୍ତର ଜ୍ଯା \(\overline{\mathbf{AB}}\) ଓ \(\overline{\mathbf{CD}}\) ମଧ୍ୟରେ ଦୂରତା 10 ସେ.ମି. | \(\overline{\mathbf{AB}}\) କ୍ୟା କେନ୍ଦ୍ରଠାରୁ 6 ସେ.ମି. ଦୂରରେ ଅବସ୍ଥିତ ହେଲେ \(\overline{\mathbf{AB}}\) ଓ \(\overline{\mathbf{CD}}\) ର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
Solution:
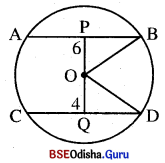
ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ = 10 ସେ.ମି.
\(\overline{\mathbf{AB}}\) ଓ \(\overline{\mathbf{CD}}\) ମଧ୍ୟରେ ଦୂରତା = 10 ସେ.ମି. |
∴ \(\overline{\mathbf{AB}}\) ଓ \(\overline{\mathbf{CD}}\) କେନ୍ଦ୍ରର ବିପରୀତ ପାର୍ଶ୍ଵରେ ଅବସ୍ଥିତ ।
ମନେକର O ବୃତ୍ତର କେନ୍ଦ୍ର ।
OP ⊥ AB ଓ OQ ⊥ CD |
PQ = 10 ସେ.ମି. , OP = 6 ସେ.ମି.
∴ OQ = (10 – 6) 6 ସେ.ମି. . = 4 ସେ.ମି. |
A OBP ରେ BP = \(\sqrt{\mathrm{OB}^2-\mathrm{OP}^2}\) = \(\sqrt{10^2-6^2}\) ସେ.ମି. = \(\sqrt{64}\) ସେ.ମି. = 8 ସେ.ମି.
⇒ AB = 2BP = 16 ସେ.ମି. |
△OQD ରେ QD = \(\sqrt{\mathrm{OD}^2-\mathrm{OQ}^2}\) = \(\sqrt{10^2-4^2}\) ସେ.ମି. = \(\sqrt{84}\) ସେ.ମି.
= 2√21 ସେ.ମି. |
∴CD = 2QD = 4√21 ସେ.ମି. |
Question 12.
ଗୋଟିଏ ବୃତ୍ତରେ △ABC ଅନ୍ତର୍ଲିଖ୍ ହୋଇଛି । ଯଦି AB = ÀC ହୁଏ, ପ୍ରମାଣ କର ଯେ ∠BACର ସମଦ୍ବିଖଣ୍ଡକ ରଶ୍ମି ବୃତ୍ତର କେନ୍ଦ୍ର ବିନ୍ଦୁଗାମୀ ଅଟେ ।
Solution:
: O, ABC ଦ୍ରଦ୍ଭର କେନ୍ଦ୍ର ଏବଂ AB = AC |
ପ୍ରାମାଣ୍ୟ : AO, ZBACର ସମଦ୍ଵିଖଣ୍ଡକ ।
ଅଙ୍କନ : OB ଓ OC ଅଙ୍କନ କର ।
ପ୍ରମାଣ : △ABO ଓ △ACO ମଧ୍ୟରେ
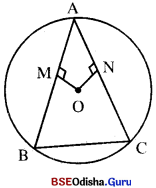
AB = AC (ଦତ୍ତ)
AO (ସାଧାରଣ ବାହୁ)
OB = OC (ଏକା ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ)
⇒ △ABO ≅ △ACO (ବା. ବା. ଦା . ସବଂସମତା)
m∠BAO = m∠CAO (ଅନୁରୁପ କୋଣ)
⇒ ∠BACର ସମଦ୍ବିଖଣ୍ଡକ ରଶ୍ମି \(\overrightarrow{\mathrm{AO}}\) ବୃତ୍ତର କେନ୍ଦ୍ରବିନ୍ଦୁଗାମୀ ।
Question 13.
ଗୋଟିଏ ବୃତ୍ତର ଦୁଇଟି ଜ୍ୟା ଏକ ବ୍ୟାସ ଦ୍ବାରା ସମଦ୍ବିଖଣ୍ଡିତ ହେଲେ ପ୍ରମାଣ କର ଯେ ଜ୍ୟା ଦୁଇଟି ସମାନ୍ତର ।
Solution:
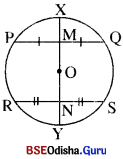
ଦତ୍ତ : ବୃତ୍ତର କେନ୍ଦ୍ର O । PQ ଓ RS ଜ୍ୟା ଦ୍ବୟ XY ବ୍ୟାସଦ୍ବାରା ଯଥାକ୍ରମେ M ଓ N ବିନ୍ଦୁରେ ସମଦ୍ବିଖଣ୍ଡିତ
ପ୍ରାମାଣ୍ୟ : PQ||\(\overline{\mathbf{RS}}\)
ପ୍ରମାଣ : PQ ର ମଧ୍ୟବିନ୍ଦୁ M ।
⇒ OM ⊥ PQ ⇒ m∠QMO = 90°
ସେହିପରି RS ର ମଧ୍ୟବିନ୍ଦୁ N |
⇒ ON ⊥ RS ⇒ m∠ONR = 90° |
∴ m∠QMO = m∠ONR = 90° |
ମାତ୍ର ଏହି କୋଣଦ୍ଵୟ ଏକାନ୍ତର, ତେଣୁ PQ || RS |
Question 14.
ପ୍ରମାଣ କର ଯେ ଗୋଟିଏ ବୃତ୍ତର ଦୁଇଟି ଜ୍ୟା କେନ୍ଦ୍ର ହେବ । (ସୂଚନା : ଅସମ୍ଭବାୟବ ପ୍ରଣାଳୀ ପରସ୍ପରକୁ ସମଦ୍ବିଖଣ୍ଡ କଲେ ସେମାନଙ୍କ ଛେଦବିନ୍ଦୁ ବୃତ୍ତର (Method of contradiction) ବ୍ୟବହାର କର)
Solution:
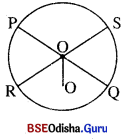
ଦତ୍ତ : PQ ଓ RS ଜ୍ୟା ଦ୍ବୟ ପରସ୍ପରକୁ O ବିନ୍ଦୁରେ ସମଦ୍ଵିଖଣ୍ଡ କରନ୍ତି ।
ପ୍ରାମାଣ୍ୟ : ‘O’ ବୃତ୍ତର କେନ୍ଦ୍ର ।
ପ୍ରମାଣ : ମନେକର ‘O’ ବୃତ୍ତର କେନ୍ଦ୍ର ନୁହେଁ । O’ ବୃତ୍ତର କେନ୍ଦ୍ର ହେଉ । O’ O ଅଙ୍କନ କର ।
O, RS ଜ୍ୟାର ମଧ୍ୟବିନ୍ଦୁ ⇒ m∠O′OS = 90°
ସେହିପରି O, PQ ଜ୍ୟାର ମଧ୍ୟବିନ୍ଦୁ ⇒ m∠O’OQ = 90°
∴ m∠O’OS = m∠O’OQ = 90°
କିନ୍ତୁ ଏହା ଅସମ୍ଭବ ।
କାରଣ Q ଓ S ବିନ୍ଦୁ O’O ର ଏକ ପାର୍ଶ୍ଵରେ ଅବସ୍ଥିତ ।
∴ O’ ଓ O ବିନ୍ଦୁଦ୍ଵୟ ଏକ ଓ ଅଭିନ୍ନ ।
⇒ PQ ଓ RS ଜ୍ୟା ଦ୍ଵୟର ଛେଦବିନ୍ଦୁ, ‘O’ ବୃତ୍ତର କେନ୍ଦ୍ର ହେବ ।
15. ଗୋଟିଏ ବୃତ୍ତର ଦୁଇଟି ଜ୍ଯା AB ଓ BC, B ଠାରେ ୨୦ କୋଣ ଉତ୍ପନ୍ନ କରନ୍ତି । ବୃତ୍ତର କେନ୍ଦ୍ର O ହେଲେ ପ୍ରମାଣ କର ଯେ A, O ଏବଂ C ଏକ ଏକରେଖୀୟ ।
Solution:
ଦତ୍ତ : ( କେନ୍ଦ୍ର ବିଶିଷ୍ଟ ଏକ ବୃତ୍ତର \(\overline{\mathrm{AB}}\) ଓ \(\overline{\mathrm{BC}}\) ଦୁଇଟି ଜ୍ୟା ।
m∠ABC = 90°
ପ୍ରାମାଣ୍ୟ : A – 0 – C ଅର୍ଥାତ୍ \(\overline{\mathrm{AC}}\) ବ୍ୟାସ ।
ଅଙ୍କନ : \(\overline{\mathrm{BO}}\) ଅଙ୍କନ କର ।
ପ୍ରମାଣ : △ABO ରେ AO = BO ⇒ m∠OAB = m∠ABO = θ (ମ6ନକର)
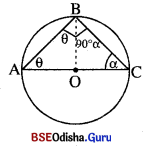
△BOC ରେ BO = CO ⇒ m∠OBC = m∠OCB = α (ମ6ନକର)
∴ θ + α = 90° (·.· m∠ABC = 90°)
△ABO ରେ m∠AOB = 180° – 2θ ଏବଂ △BOC ରେ m∠BOC = 180° – 2α
∴ m∠AOB +m∠BOC = 360 – 2(θ + α) = 360° – 2(90°) (∵ θ + α = 90°) = 180°
⇒ A – O – C = \(\overline{\mathrm{AC}}\) ଏକ ବ୍ୟାସ ।
Question 16.
ପ୍ରମାଣ କର ଯେ ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜରେ କର୍ପୂର ମଧ୍ୟବିନ୍ଦୁ, ଏହାର ପରିବୃତ୍ତର କେନ୍ଦ୍ର ଅଟେ ।
Solution:
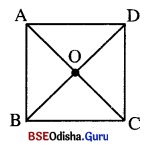
ଦତ୍ତ : △ABC ର m∠ABC = 90° । ‘O’ \(\overline{\mathrm{AC}}\) କର୍ପୂର ମଧ୍ୟବିନ୍ଦୁ ।
ପ୍ରାମାଣ୍ୟ : A ABC ର ପରିବୃତ୍ତର କେନ୍ଦ୍ର O ।
ଅଙ୍କନ : \(\overrightarrow{\mathrm{BO}}\) ଅଙ୍କନ କର । \(\overrightarrow{\mathrm{BO}}\) ଉପରିସ୍ଥ ‘D’ ଏପରି ଏକ ବିନ୍ଦୁ ଯେପରିକି BO = OD |
DC ଅଙ୍କନ କର ।
ପ୍ରମାଣ : △OBC ଓ △ODC ଦ୍ଵୟରେ AO = OC (∵ O, \(\overline{\mathrm{AC}}\) ର ମଧ୍ୟବିନ୍ଦୁ)
BO = OD (ଅଙ୍କନ), m∠AOB = m∠COD (ପ୍ରତୀପ)
△ABO = △CDO ⇒ m∠BAO = m∠OCD 19° AB = CD
⇒ ମାତ୍ର ଏହି କୋଣଦ୍ଵୟ ଏକାନ୍ତର ⇒ \(\overline{\mathrm{AB}}\) || \(\overline{\mathrm{CD}}\)
ପୁନଶ୍ଚ, m∠ABC = 90° ହେତୁ ABCD ଏକ ଆୟତଚିତ୍ର ।
∴ AC = BD = \(\frac { 1 }{ 2 }\) AC = \(\frac { 1 }{ 2 }\) BD ⇒ AO = BO
∴ AO = BO = CO
ଏଠାରେ ଠ ବିନ୍ଦୁଠାରୁ A, B ଓ C ବିନ୍ଦୁତ୍ରୟ ସମଦୂରବର୍ତ୍ତୀ ।
⇒ O ବିନ୍ଦୁ △ABC ର ପରିବୃତ୍ତର କେନ୍ଦ୍ର ।
Question 17.
PQ ବୃତ୍ତର ଜ୍ୟା । P ଓ Q ଠାରେ ଉକ୍ତ ଜ୍ୟା ରେ ଅଙ୍କିତ ଲମ୍ବଦ୍ଵୟ R ଓ S ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି । ପ୍ରମାଣ କର ଯେ PQSR ଏକ ଆୟତ ଚିତ୍ର |
Solution:
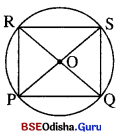
ଦତ୍ତ : \(\overline{\mathrm{PQ}}\) ଜ୍ୟାର P ଓ Q ଠାରେ ଅଙ୍କିତ ଲମ୍ବଦ୍ଵୟ ବୃତ୍ତକୁ R ଓ S ବିନ୍ଦୁରେ ଛେଦ କ6ର |
ପ୍ରାମାଣ୍ୟ : PQSR ଏକ ଆୟତଚିତ୍ର ।
ଅଙ୍କନ : \(\overline{\mathrm{RQ}}\) ଓ \(\overline{\mathrm{PS}}\) ଅଙ୍କନ କର ।
ପ୍ତମାଣ : △PRQ ରେ m∠RPQ = 90° ⇒ RQ ଏବ ଦ୍ୟାସ ….(i)
△SPQ ରେ m∠PQS = 90° ⇒ PQ ଏବ ଦ୍ୟାସ ….(ii)
ଆମେ ଜାଣିଛେ, ବ୍ୟାସଦ୍ଵୟ ପରସ୍ପରକୁ କେନ୍ଦ୍ର ‘O’ରେ ସମଦ୍ଵିଖଣ୍ଡ କରନ୍ତି ।
∴ PORS ଏକ ଆୟତଚିତ୍ର ।
ବିକଳ୍ପ ପ୍ରମାଣ:
PQRS ଦ୍ରଭନ୍ନକଖତ ଚତୁରୁଢର m∠P + m∠S = 180°
⇒ m∠S = 90° (∴ \(\overline{\mathrm{RQ}}\) ବୃତ୍ତର ଏକ ବ୍ୟାସ)
⇒ m∠P = 90°, 6ସଦ୍ରପତି m∠R = 90° |
∴ PQSR ଏକ ଆୟତଚିତ୍ର ।
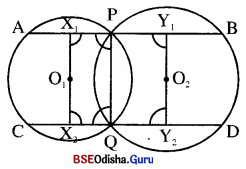
![]()
Question 18.
ଚିତ୍ରରେ A ଓ B ଦୁଇଟି ପରସ୍ପର ଛେଦୀ ବୃତ୍ତର କେନ୍ଦ୍ର ଏବଂ P ଓ Q ବୃତ୍ତ ଦ୍ଵୟର ଛେଦବିନ୍ଦୁ ଅଟନ୍ତି । ପ୍ରମାଣ କର ଯେ,
(i) \(\stackrel{\leftrightarrow}{\mathbf{AB}}\), \(\overline{\mathrm{PQ}}\) ସାଧାରଣ ଜ୍ୟାକୁ ସମର୍ଦ୍ଦିଖଣ୍ଡ କରେ ।
ଏବଂ (ii) \(\stackrel{\leftrightarrow}{\mathbf{A B}}\) ⊥ \(\overline{\mathrm{PQ}}\)
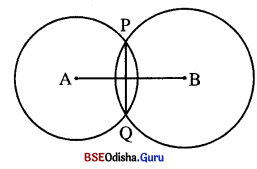
Solution:
ଦତ୍ତ : A ଓ B ଦୁଇଟି ପରସ୍ପରଛେଦୀ ବୃତ୍ତର କେନ୍ଦ୍ର ।
P ଓ Q ବୃତ୍ତଦ୍ଵୟର ଛେଦବିନ୍ଦୁ ।
ପ୍ରାମାଣ୍ୟ : (i) \(\stackrel{\leftrightarrow}{\mathbf{AB}}\), \(\overline{\mathrm{PQ}}\) କୁ ସମର୍ଦ୍ଦିଖଣ୍ଡ କରେ । (ii) \(\stackrel{\leftrightarrow}{\mathbf{A B}}\) ⊥ \(\overline{\mathrm{PQ}}\)
ଅଙ୍କନ : \(\overline{\mathrm{PA}}\), \(\overline{\mathrm{AQ}}\), \(\overline{\mathrm{BQ}}\) ଏବଂ \(\overline{\mathrm{BP}}\) ଅଙ୍କନ କର ।
ପ୍ରମାଣ : △APB ଏବଂ △AQB ଦ୍ବୟରେ
PA = AQ (ଏକା ଦ୍ୱଭର ବ୍ୟାସାକିଂ), BP = BQ
ଏବଂ \(\overline{\mathrm{AB}}\) ସାଧାରଣ ବାହୁ ।
∴△APB ≅ △AQB (ଦା .ଦା. ଦା)
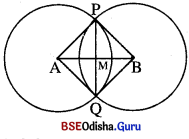
⇒ m∠PAM = m∠QAM (ଅନୁରୂପ କୋଣ)
ବର୍ତ୍ତମାନ △APM ଏବଂ △AQM ଦ୍ବୟରେ
PA = AQ, m∠PAM = m∠QAM ଏବଂ \(\overline{\mathrm{AM}}\) ସମତ୍ତିଖଣ୍ଡ କରିବ ।
∴ △APM ≅ △AQM (ଦା .ଦା. ଦା)
PM = MQ ⇒ \(\overleftrightarrow{\mathrm{AB}}\), \(\overline{\mathrm{PQ}}\) ….. (ii) (ପ୍ରମାଣିତ)
ଏବଂ m∠AMP = m∠AMQ
କିନ୍ତୁ ଏମାନେ ସନ୍ନିହିତ ପରିପୂରକ ହେତୁ m∠AMP = m∠AMQ = 90°
⇒ \(\overleftrightarrow{\mathrm{AB}}\) ⊥ \(\overline{\mathrm{PQ}}\) ….. (ii) (ପ୍ରମାଣିତ)
Question 19.
ଚିତ୍ରରେ ଦୁଇଟି ବୃତ୍ତ ପରସ୍ପରକୁ P ଓ Q ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି । P ଠାରେ PQ ପ୍ରତି ଅଙ୍କିତ ଲମ୍ବ ବୃତ୍ତ ଦ୍ଵୟକୁ A ଓ B ଠାରେ ଛେଦ କରେ ଓ ସେହିପରି () ଠାରେ PQ ପ୍ରତି ଅଙ୍କିତ ଲମ୍ବ ବୃତ୍ତଦ୍ଵୟକୁ C ଓ D ଠାରେ ଛେଦ କରେ । ପ୍ରମାଣ କର ଯେ, AB = CD ।
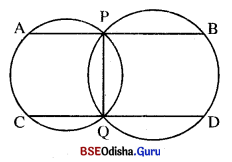
Solution:
ଦତ୍ତ : ଦୁଇଟି ବୃତ୍ତ ପରସ୍ପରକୁ P ଓ Q ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି । P ଠାରେ PQ ପ୍ରତି ଅଙ୍କିତ ଲମ୍ବ ବୃତ୍ତଦ୍ଵୟକୁ A ଓ B ଠାରେ ଛେଦକରେ Q ଠାରେ PQ ପ୍ରତି ଅଙ୍କିତ ଲମ୍ବ ବୃତ୍ତଦ୍ଵୟକୁ C ଓ D ଠାରେ ଛେଦ କରେ ।
ପ୍ରାମାଣ୍ୟ : AB = CD
ଅଙ୍କନ : ବୃତ୍ତଦ୍ଵୟର କେନ୍ଦ୍ର O1 ଓ O2 ନିଆ | O1X1 ⊥ AP ଏବଂ
O2 Y1 ⊥ PB ଅଙ୍କନ କର ।
X1 O1, ଓ Y1 O2, CDକୁ ଯଥାକ୍ରମେ X2 ଓ Y2 ରେ ଛେଦକରୁ ।
ପ୍ରମାଣ : AB || CD = X1 Y1 || X2 Y2
ପୁନଶ୍ଚ X1 X2 || Y1 Y2
∵ m∠X2X1Y1 +m∠X1Y1Y2 = 180°
⇒ X1Y1Y1X2 ଏକ ଆପ୍ତତତିତ୍ର |
X1Y1 = X2Y2
AB = AP + PB = 2PX1 + 2PY1
= 2(PX1 + PY1) = 2 X1Y1 = 2X2Y2
= 2(X2Q + QY2) = 2QX2 + 2QY2 = CQ + QD = CD (ପ୍ରମାଣିତ)
Question 20.
A ଓ B କେନ୍ଦ୍ର ବିଶିଷ୍ଟ ଦୁଇଟି ବୃତ୍ତ ପରସ୍ପରକୁ P ଓ ଠୁ ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି । P ମଧ୍ୟ ଦେଇ AB ସହିତ ସମାନ୍ତର ସରଳରେଖା ବୃତ୍ତ ଦ୍ଵୟକୁ M ଓ N ବିନ୍ଦୁରେ ଛେଦ କଲେ ପ୍ରମାଣ କର ଯେ, MN = 2AB | (ସୂଚନା : \(\overline{\mathbf{AC}}\) ଓ \(\overline{\mathbf{BD}}\), \(\overline{\mathbf{MN}}\) ପ୍ରତି ଲମ୍ବ ଅଙ୍କନ କରି ଦର୍ଶାଅ ଯେ, AB = CD)
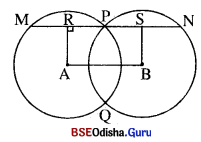
ସମାଧାନ :
ଦତ୍ତ : A ଓ B କେନ୍ଦ୍ର ବିଶିଷ୍ଟ ଦୁଇଟି ବୃତ୍ତ ପରସ୍ପରକୁ P ଓ Q ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି ।
P ବିନ୍ଦୁ ମଧ୍ୟଦେଇ ଅଙ୍କିତ \(\overline{\mathbf{MN}}\), \(\overline{\mathbf{AB}}\) ସହ ସମାନ୍ତର ।
ପ୍ରାମାଣ୍ୟ : MN = 2AB
ଅଙ୍କନ : AR ⊥ MP ଏବଂ BS ⊥ PN
ପ୍ରମାଣ : AR ⊥ MP ⇒ RP = \(\frac { 1 }{ 2 }\) MP
ସେହିପରି BS ⊥ NP ⇒ PS = \(\frac { 1 }{ 2 }\) PN
∴ RP + PS = \(\frac { 1 }{ 2 }\) (MP + PN) ⇒ RS = \(\frac { 1 }{ 2 }\) MN ……(i)
କିନ୍ତୁ RABS ଏକ ଆୟତଚିତ୍ର ⇒ RS = AB ….(ii)
(i) ଓ (ii) ରୁ AB = \(\frac { 1 }{ 2 }\), MN (ପ୍ରମାଣିତ)
Question 21.
ଚିତ୍ରରେ ଗୋଟିଏ ସରଳରେଖା ଦୁଇଟି ଏକ କେନ୍ଦ୍ରିକ ବୃତ୍ତ S1 ଓ S2 କୁ ଯଥାକ୍ରମେ A, C, D ଓ B ବିନ୍ଦୁରେ ଛେଦ କରୁଛି । ପ୍ରମାଣ କର ଯେ, AC = DB |
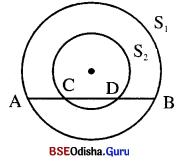
Solution:
ଦତ୍ତ : S1 ଓ S2 ଦୁଇଟି ଏକ କେନ୍ଦ୍ରିକ ବୃତ୍ତ । ଏକ ସରଳରେଖା ବୃତ୍ତଦ୍ଵୟକୁ ଯଥାକ୍ରମେ A, C, D ଓ B ବିନ୍ଦୁରେ ଛେଦ କରୁଛି |
ପ୍ରାମାଣ୍ୟ : AC = DB
ଅଙ୍କନ : OM ⊥ AB ଅଙ୍କନ କର । \(\overline{\mathbf{OC}}\) ଏବଂ \(\overline{\mathbf{OA}}\) କୁ ଯୋଗକର ।
ପ୍ରମାଣ : \(\overline{\mathbf{OM}}\) ⊥ \(\overline{\mathbf{AB}}\) ଏବଂ \(\overline{\mathbf{OM}}\) ⊥ \(\overline{\mathbf{CD}}\)
∴ AM = MB ଏବଂ CM = MD
⇒ AM – CM = MB – MD ⇒ AC = BD
Question 22.
ଗୋଟିଏ ବୃତ୍ତର ଏକ ବହିଃସ୍ଥ ବିନ୍ଦୁ P ମଧ୍ୟ ଦେଇ ଅଙ୍କିତ ଦୁଇଟି ଛେଦକ ବୃତ୍ତକୁ A, B ଏବଂ C, D ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି ଯେପରି P – A – B ଏବଂ P – C – D। ଯଦି AB = CD ହୁଏ, ପ୍ରମାଣ କର ଯେ, PA = PC ଏବଂ AC || BD |
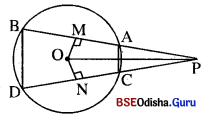
Solution:
ଦତ୍ତ : ବୃତ୍ତର ବହିଃସ୍ଥ ବିନ୍ଦୁ P ମଧ୍ୟଦେଇ ଏକ ଛେଦକ ବୃତ୍ତକୁ A, B ଏବଂ C, D ବିନ୍ଦୁରେ ଛେଦ କରୁଛନ୍ତି । AB = CD
ପ୍ରାମାଣ୍ୟ : (i) PA = PC (ii) \(\overline{\mathbf{AC}}\)||\(\overline{\mathbf{BD}}\)
ଅଙ୍କନ : କେନ୍ଦ୍ର O ଠାରୁ \(\overline{\mathbf{AB}}\) ଓ DC ପ୍ରତି ଯଥାକ୍ରମେ OM ଏବଂ ON ଲମ୍ବ ଅଙ୍କନ କର । OP ଅଙ୍କନ କର ।
ପ୍ରମାଣ : AB = CD = \(\frac { 1 }{ 2 }\) AB = \(\frac { 1 }{ 2 }\) CD ⇒ AM = NC ଏବଂ MB = ND… (i)
△OMP ଏବଂ △ONP ଦ୍ୱୟରେ m∠OMP = m∠ONP (ପ୍ରତ୍ୟେକ ସମକୋଣ)
OM = ON ( ସମାନ ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ଜ୍ୟା ମାନ କେନ୍ଦ୍ରଠାରୁ ସମଦୂରବର୍ତ୍ତୀ), \(\overline{\mathbf{OP}}\) ସାଧାରଣ ବାହୁ ।
△OMP ≅ △ONP
⇒ MP= NP ⇒ MP – AM = NP – NC [(i)ରୁ] → PA = PC (ପ୍ରମାଣିତ) …(ii)
ପୁନଶ୍ଚ MP + MB = NP + ND [(i)ରୁ]
⇒ PB = PD ⇒ △PBD ସମଦିବାହୁ (ii) ରୁ PA = PC → A PAC ଏକ ସମଦ୍ବିବାହୁ ।
△PBD ରେ PB = PD ⇒ m∠PBD = m∠PDB = θ (ମନେକର)
ସେହିପରି △PAC m∠PAC = m∠ACP = α (ମନେକର)
∴ △PBD ରେ θ + θ + m∠BPD = 180°
⇒ 2θ + m∠BPD = 180° ….(iii)
ପେଦ୍ୱିପରି △PAC ରେ, 2α + m∠APC = 180° …(iv)
(iii) 2θ = 2α
Question 23.
ABC ବୃତ୍ତର କେନ୍ଦ୍ର O । ଏହାର ଦୁଇଟି ସର୍ବସମ ଜ୍ୟା ପରସ୍ପରକୁ ଏକ ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ P ଠାରେ ଛେଦ କରନ୍ତି । B ଓ C, \(\overline{\mathbf{OP}}\) ର ଏକ ପାର୍ଶ୍ୱସ୍ଥ ହେଲେ ପ୍ରମାଣ କର ଯେ, (i) PA = PC ଏବଂ (ii) \(\overline{\mathbf{AC}}\) || \(\overline{\mathbf{BD}}\) | (ସୂଚନା : \(\overline{\mathbf{OE}}\) L \(\overline{\mathbf{AB}}\) ଏବଂ \(\overline{\mathbf{OF}}\) ⊥ \(\overline{\mathbf{CD}}\) ଅଙ୍କନ କରି O, P ଯୋଗ କର)
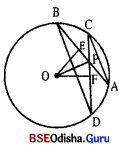
ସମାଧାନ :
ଦତ୍ତ : ବୃତ୍ତର କେନ୍ଦ୍ର ( 1 AB = CD, AB ଓ CD ଜ୍ୟା ଦ୍ଵୟର ଛେଦବିନ୍ଦୁ P ।
B ଓ C, \(\overline{\mathbf{OP}}\) ର ଏକ ପାର୍ଶ୍ଵରେ ଅବସ୍ଥିତ ।
ପ୍ତାମଣ୍ୟ : (i) PA = PC (ii) \(\overline{\mathbf{AC}}\) || \(\overline{\mathbf{BD}}\)
ଅଙ୍କନ : \(\overline{\mathbf{OE}}\) L \(\overline{\mathbf{AP}}\) ଏବଂ \(\overline{\mathbf{OD}}\) L \(\overline{\mathbf{CD}}\) ଅଙ୍କନ କର ।
ପ୍ରମାଣ : AB = CD ⇒ \(\frac { 1 }{ 2 }\) AB = \(\frac { 1 }{ 2 }\) CD ⇒ AE = CF ଏବଂ BE = FD
△OPE ଏବଂ OPF ଦଯ6ର m≤OEP = m≤OFP = 90°, OE = OF (∵ ଲ୍ୟା ଦ୍ବାଦାସମ)
\(\overline{\mathbf{OP}}\) ସାଧାରଣ ∴ △OPE ≅ △OPE ⇒ PE = PF
⇒ AE – PE = CF – PF ⇒ AP = CP ….(i)
⇒ △APC ସମଦିବାହୁ ।
ପୁନଶ୍ଚ BE + PE = DF + FP ⇒ PB = PD ⇒ △PBD ସମଦ୍ବିବାହୁ ।
△APC ସମଦିବାହୁ ।
m∠PAC = m∠PCA = θ (ମ6ନକର) ⇒ 2θ + m∠CPA = 180° ……(1)
△PBD ସମଙ୍ଗିବାହୁ = m∠PBD = m∠PDB = α (ମନେକର)
⇒ 2α + m∠BPD = 180° …..(2)
(1) ଓ (2)ରୁ 2θ + m∠CPA = 2α + m∠BPD (∵ m∠CPA = m∠BPD ପ୍ରତୀପ)
⇒ 2θ = 2α ⇒ θ = α ⇒ m∠PAC = m∠PBD
ମାତ୍ର ଏହି କୋଣଦ୍ଵୟ ଏକାନ୍ତର, ତେଣୁ \(\overline{\mathbf{AC}}\) || \(\overline{\mathbf{BD}}\) ……. (ii)