Odisha State Board BSE Odisha 10th Class Maths Notes Algebra Chapter 4 ସମ୍ଭାବ୍ୟତା will enable students to study smartly.
BSE Odisha Class 10 Maths Notes Algebra Chapter 4 ସମ୍ଭାବ୍ୟତା
→ ଉପକ୍ରମଣିକା (Introduction) :
- କୌଣସି ଏକ ଘଟଣାର ସମ୍ଭାବନାର ପରିମାପରୁ ସମ୍ଭାବ୍ୟତା ତତ୍ତ୍ବ (Probability Theory)
- ପ୍ରତ୍ୟେକ ସମ୍ଭାବ୍ୟତା ଏକ ପଶାଖେଳ, ଏଥରେ ଆମେ ବାଜି ଜିତିପାରୁ କିମ୍ବା ହାରିପାରୁ ।
- ଗଣିତଜ୍ଞ Blaise Pascal (1623-1662) ଓ Pierre Formal (1601-1665) ବାଜି ଜିତିବାର ସମ୍ଭାବ୍ୟତାର ସମାଧାନର ସୂତ୍ର ଉପସ୍ଥାପନ କରିଥିଲେ ।
- A.N. Kalmogorov ଏବଂ A.A. Markov ସମ୍ଭାବ୍ୟତା ତତ୍ତ୍ଵକୁ ଆଧୁନିକ ଗଣିତର ରୂପ ପ୍ରଦାନ କରିଛନ୍ତି ।
- ବିଭିନ୍ନ ବୈଜ୍ଞାନିକ କ୍ଷେତ୍ରରେ, ଯୋଜନା ପ୍ରକରଣ, ପାଣିପାଗର ପୂର୍ବାନୁମାନରେ ସମ୍ଭାବ୍ୟତା ସୂତ୍ର ପ୍ରୟୋଗ
![]()
→ ଅନୁଭବିକ ଏବଂ ତତ୍ତ୍ଵାଧାରିକ ସମ୍ଭାବ୍ୟତା (Empirical and Theoretical Probability) :
(i) ସମ୍ଭାବ୍ୟତାର ଧାରଣା ସାଧାରଣତଃ, ପରୀକ୍ଷଣ (Experiments) ଓ ପର୍ଯ୍ୟବେକ୍ଷଣ (observation) ଉପରେ ଆଧାରିତ ହୁଏ ।
ମନେରଖ : ମୁଦ୍ରା ଟସ୍ରେ ମୁଦ୍ରାଟି ସର୍ବଦା ଅପ୍ରବଣ ଓ ସମତୁଲ୍ୟ । ଏହି Adjective ଦ୍ଵୟକୁ ବ୍ୟବହାର ନକଲେ ମଧ୍ୟ ଆମେ ମୁଦ୍ରାଟିକୁ ଅପ୍ରବଣ ଓ ସମତୁଲ୍ୟ ବୋଲି ଧରିନେବା ।
(ii) ପରୀକ୍ଷଣରୁ ଉଦ୍ଭବ ଫଳାଫଳର ପ୍ରକୃତ, ଉପସ୍ଥାପନା କରାଯାଇ ଘଟଣାଟିର ସତ୍ୟତା ଉପସ୍ଥାପନା କରାଯାଇ ଘଟଣାଟିର ସତ୍ୟତା ନିରୂପଣ ସଂଖ୍ୟାଦ୍ଵାରା କରାଗଲେ ଏହି ପ୍ରକାର ସମ୍ଭାବ୍ୟତାକୁ ଅନୁଭବ ସିଦ୍ଧ ବା ଆନୁଭବିକ (Empirical) ସମ୍ଭାବ୍ୟତା କୁହାଯାଏ ।
(iii) ମୁଦ୍ରା ଟସ୍ କରିବା, ଲୁଡୁଗୋଟି ଗଡ଼ାଇବା ଭଳି ପରୀକ୍ଷଣରୁ ଆମେ ସମ୍ଭାବ୍ୟତାର ସ୍ପଷ୍ଟ ଧାରଣା ପାଇପାରିବା ।
(iv) ମୁଦ୍ରାକୁ ଟିସ୍ କଲେ ଆମେ H କିମ୍ବା T ପାଇପାରିବା । ଟସ୍ କରିବାର ପୂର୍ବରୁ ଆମେ କହିପାରିବା କି ପଡ଼ିଥିବା ପାର୍ଶ୍ୱଟି H କିମ୍ବା T ହେବ । କାରଣ ଏଠାରେ ଫଳାଫଳ କୌଣସି ନିୟମର ଅଧୀନ ନୁହେଁ ।
(v) 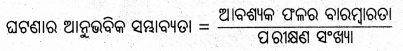
ଏକଥର ମୁଦ୍ରା ଟସ୍ରେ P(H) = P(T) = \(\frac{1}{2}\)
ସେହିପରି ଏକଥର ଲୁଡୁଗୋଟି ଗଡ଼ାଇବାରେ P(1) = P(2) = …….. P(6) = \(\frac{1}{6}\)
(vi) ଆନୁଭବିକ ସମ୍ଭାବ୍ୟତା, ତତ୍ତ୍ଵାଧାରିକ ସମ୍ଭାବ୍ୟତା ପାଇଁ ଏକ ଧାରକ ହୋଇଥାଏ । ପ୍ରଥମଟି ପରୀକ୍ଷଣ ସିଦ୍ଧ ହୋଇଥବାବେଳେ, ଦ୍ୱିତୀୟ ପ୍ରକାରର ସମ୍ଭାବ୍ୟତା ପରୀକ୍ଷଣରୁ ଉଦ୍ଭବ ସିଦ୍ଧାନ୍ତ ଉପରେ ଆଧାରିତ ହୋଇଥାଏ ।
(vii) ଗୋଟିଏ ଘଟଣା E ହେଲେ ତତ୍ତ୍ଵାଧାରିକ ସମ୍ଭାବ୍ୟତା ଅନୁଯାୟୀ

ଏଠାରେ m = ଫଳର ବାରମ୍ବାରତା ଓ n = ସମୁଦାୟ ଗୋଟି ପଡ଼ିବାର ସଂଖ୍ୟା ।
![]()
→ ଦ୍ରଷ୍ଟବ୍ୟ :
- ପରୀକ୍ଷଣରେ ଯଦି ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଫଳ ଯଦି ନିଶ୍ଚିତ ଭାବେ ଘଟେ, ତେବେ ଉକ୍ତ ଫଳର ସମ୍ଭାବ୍ୟତା 1 ସହ ସମାନ ହେବ ।
- ପରୀକ୍ଷଣରେ ଯଦି ଫଳ ନ ଉପୁଜେ ତେବେ ଏହାର ସମ୍ଭାବ୍ୟତା ‘0’ ।
∴ 0 ≤ P(E) ≤ 1
→ ସେଟ୍ ତତ୍ତ୍ବ ଉପରେ ଆଧାରିତ ସମ୍ଭାବ୍ୟତାର ଧାରଣା :
ଅପେକ୍ଷାକୃତ ଏକ ଉତ୍କୃଷ୍ଟ ପନ୍ଥା । ଏଥିପାଇଁ ପ୍ରଥମେ ମୁଦ୍ରା ଟସ୍ ଉଦାହରଣ ନେବା ।
ସେଟ୍ ମାଧ୍ୟମରେ ସମ୍ଭାବ୍ୟତାର ସଂଜ୍ଞା ଓ ଧାରଣା ଗଣିତଜ୍ଞ Kalmogorov ପ୍ରଦାନ କରିଥିଲେ ।
(i) ମନେକର ଏକ ଅପ୍ରବଣ ମୁଦ୍ରାକୁ ଟସ୍ କରାଗଲା । ଫଳ H ଓ Tରୁ ଯେକୌଣସି ଗୋଟିଏ ପଡ଼ିବ ।
(ii) ସମସ୍ତ ଫଳାଫଳମାନଙ୍କୁ ନେଇ ଗଠିତ ସେଟ୍କୁ S (Sample Space) କୁହାଯାଏ ।
(iii) ଗୋଟିଏ ମୁଦ୍ରାକୁ ଦୁଇଥର ଟସ୍ କଲେ S = {HH, HT, TH, TT}
(iv) ସେହିପରି ଗୋଟିଏ ଲୁଡୁ ଗୋଟିକୁ ଦୁଇଥର ଗଡ଼ାଇବା ଦ୍ଵାରା ବା ଦୁଇଟି ଲୁଡୁଗୋଟିକୁ ଏକ ସଙ୍ଗେ ଗଡ଼ାଇବାଦ୍ୱାରା ଆମେ ଯେଉଁ sample spaceଟି ପାଇବା ତାହା ନିମ୍ନରେ ପ୍ରଦତ୍ତ ।
S = {11, 12, 13, 14, 15, 16
21, 22, 23, 24, 25, 26
31, 32, 33, 34, 35, 36
41, 42, 43, 44, 45, 46
51, 52, 53, 54, 55, 56
61, 62, 63, 64, 65, 66}
(v)ଗୋଟିଏ ମୁଦ୍ରାକୁ ଦୁଇଥର ଟସ୍କକଲେ Sample Spaceର ସମ୍ଭାବ୍ୟ ଫଳ ସଂଖ୍ୟା 2² । ସେହିପରି nଥର ଟସ୍ କଲେ | S | = 2<sub>n</sub> ହେବ ।
(vi) ଗୋଟିଏ ଲୁଡୁଗୋଟିକୁ ଦୁଇଥର ଗଡ଼ାଇଲେ Sample space ର ସମ୍ଭାବ୍ୟ ଉତ୍ତର ସଂଖ୍ୟା 6² = 36 1 ସେହିପରି nଥର ଗଡ଼ାଇଲେ ସମ୍ଭାବ୍ୟ ଫଳାଫଳ | S | = 6<sub>n</sub> ହେବ ।
![]()
ନିମ୍ନ ଚିତ୍ର ମାଧ୍ୟମରେ ଥରେ, ଦୁଇଥର ଓ ତିନିଥର ମୁଦ୍ରା ଟସ୍ର ଫଳାଫଳ ସ୍ଥିରିକୃତ ହୋଇଛି ।
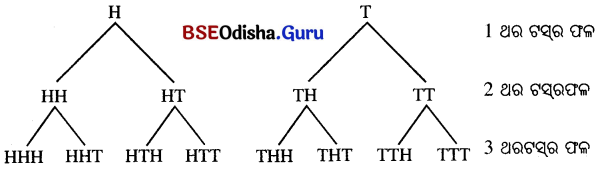
ଗୋଟିଏ ଲୁଡୁଗୋଟିକୁ ଥରେ ଗଡ଼ାଇଲେ ଗଠିତ ସେଟ୍ {H, T}
ଦୁଇଥର ଗଡ଼ାଇଲେ ଗଠିତ ସେଟ୍ = {HH, HT, TH, TT}
ତିନିଥର ଗଡ଼ାଇଲେ ଗଠିତ ସେଟ୍ = {HHH, HHT, HTH, HTT, THH, THT, TIH, TIT}
ଏକ ପରୀକ୍ଷଣରେ ସମ୍ଭାବ୍ୟ ସମସ୍ତ ଫଳାଫଳଗୁଡିକୁ ନେଇ ଗଠିତ ସେଟ୍କୁ ପରୀକ୍ଷଣର Sample Set କୁହାଯାଏ ।
→ ଘଟଣା (Event) :
ପରୀକ୍ଷଣରେ ଲବ୍ଧ Sample space S ହେଲେ, ଏହାର କୌଣସି ଉପସେଟ୍ E ।
ମନେକର ଘଟଣା E ‘ଅତି କମ୍ରେ ଗୋଟିଏ T ଥିବାକୁ’ ସୂଚାଏ ।
ଏଠାରେ Sରେ ଥିବା ଫଳାଫଳ ମାନଙ୍କ ମଧ୍ୟରୁ {HT, TH, TT} ଫଳ ତିନୋଟି E ଘଟଣାର ଅନୁକୂଳ ଅର୍ଥାତ୍ E ଦ୍ଵାରା ଅନୁଗୃହୀତ ଫଳାଫଳ ଅଟନ୍ତି ।
ସୁତରାଂ E = {HT, TH, TT}
