Odisha State Board BSE Odisha 10th Class Maths Solutions Algebra Chapter 1 ସରଳ ସହସମୀକରଣ Ex 1(c) Textbook Exercise Questions and Answers.
BSE Odisha Class 10 Maths Solutions Algebra Chapter 1 ସରଳ ସହସମୀକରଣ Ex 1(c)
Question 1.
ଦୁଇଟି ସଂଖ୍ୟାର ଯୋଗଫଳ 137 ଓ ସେମାନଙ୍କର ବିୟୋଗଫଳ 43। ତେବେ ସଂଖ୍ୟାଦ୍ୱୟ ନିରୂପଣ କର ।
ସମାଧାନ:
ମନେକର ସଂଖ୍ୟାଦ୍ଵୟ x ଓ y ।
ପ୍ରଶ୍ନନୁସାରେ x + y = 137 ……..(i) ଏବଂ x – y = 43 …….(ii)
ସମୀକରଣ (i) ଓ (ii) କୁ ପ୍ରୟୋଗକଲେ,
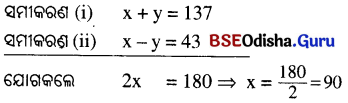
x ର ମାନ ସମୀକରଣ (i) ରେ ସ୍ଥାପନ କଲେ, x + y = 137
⇒ 90 + y = 137 ⇒ y = 137 – 90 ⇒ y = 47
∴ ସଂଖ୍ୟାଦ୍ଵୟ 90 ଓ 47।
Question 2.
ସମବାହୁ ତ୍ରିଭୁଜର ବାହୁ ତ୍ରୟର ଦୈର୍ଘ୍ୟ x + 4 ସେ.ମି., 4x – y ସେ.ମି. ଓ y + 2 ସେ.ମି. ହେଲେ ବାହୁର ଦୈର୍ଘ୍ୟ ସ୍ଥିର କର ।
ସମାଧାନ :
ସମବାହୁ ତ୍ରିଭୁଜର ବାହୂତ୍ରୟର ଦୈର୍ଘ୍ୟ ସମାନ । ଅର୍ଥାତ୍ x + 4 = 4x – y = y + 2
⇒ x + 4 = y + 2 = x – y = 2 – 4
⇒ x – y = -2 … (i)
ପୁନଶ୍ଚ 4x – y = y + 2 ⇒ 4x – y – y = 2 ⇒ 4x – 2y = 2
⇒ 2(2x – y) = 2 ⇒ 2x – y = 1 …… (ii)
ସମୀକରଣ (ii)ରୁ ସମୀକରଣ (i)କୁ ବିୟୋଗ କଲେ,
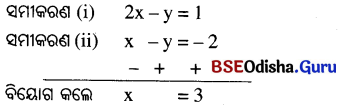
x ର ମାନ ସମୀକରଣ (i) ରେ ସ୍ଥାପନ କଲେ, 3 – y = – 2
⇒ – y = -2 – 3 = -5 ⇒ y = 5
∴ ସମବାହୁ ତ୍ରିଭୁଜର ଏକ ବାହୁର ଦୈର୍ଘ୍ୟ = y + 2 = 5 + 2 = 7 ସେ.ମି.
![]()
Question 3.
ABCD ଅ।ୟତକ୍ଷେତ୍ରର AB = 3x + y ସେ.ମି, BC = 3x + 2 ସେ.ମି, CD = 3y – 2x ସେ.ମି, ଓ DA = y + 3 ସେ.ମି. ହେଲେ ଆୟତକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ ନିରୂପଣ କର ।
ସମାଧାନ :
ଆୟତଚିତ୍ରର ବିପରୀତ ବାହୁମାନଙ୍କର ଦୈର୍ଘ୍ୟ ପରସ୍ପର ସମାନ ।
ତେଣୁ ABCD ଆୟତଚିତ୍ରରେ AB = CD ଏବଂ BC = AD ହେବ ।
AB = CD ହେଲେ, 3x + y = 3y – 2x ⇒ 3x + 2x = 3y – y ⇒ 5x – 2y=0 (i)
ସେହିପରି BC = AD ହେଲେ, 3x + 2 = y + 3
⇒ 3x – y = 3 – 2 ⇒ 3x – y =1 …..(ii)

‘x’ ର ମାନ ସମୀକରଣ (ii) ରେ ପ୍ରୟୋଗ କଲେ, 3 × 2 – y = 1 ⇒ 6 – 1 = y ⇒ y = 5
∴ AB = 3x + y = 3 × 2 + 5 = 11 ସେ.ମି
BC = 3x + 2 = 3 × 2 + 2 = 8 ସେ.ମି
∴ ଆୟତକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = AB × BC = 11 × 8 = 88
Question 4.
ଦୁଇ ଅଙ୍କ ବିଶିଷ୍ଟ ଗୋଟିଏ ସଂଖ୍ୟା, ତାହାର ଅଙ୍କଦ୍ଵୟର ଯୋଗଫଳର 4 ଗୁଣ । କିନ୍ତୁ ସଂଖ୍ୟାଟିରେ 18 ଯୋଗ କଲେ ଅଙ୍କଦ୍ଵୟର ସ୍ଥାନ ବଦଳିଯାଏ । ତେବେ ସଂଖ୍ୟାଟି କେତେ ?
ସମାଧାନ :
ମନେକର ଦୁଇଅଙ୍କ ବିଶିଷ୍ଟ ସଂଖ୍ୟାଟିର ଦଶକ ଏବଂ ଏକକ ସ୍ଥାନୀୟ ଅଙ୍କଦ୍ଵୟ ଯଥାକ୍ରମେ x ଏବଂ y l .:. ସଂଖ୍ୟାଟି = 10x + y
ପ୍ରଶ୍ନନୁସାରେ, ସଂଖ୍ୟାଟି ତାହାର ଅଙ୍କ ଦ୍ବୟର ଯୋଗଫଳର 4 ଗୁଣ ।
⇒ 10x + y = 4(x + y) ⇒ 10x + y = 4x + 4y ⇒ 10x – 4x + y – 4y = 0
⇒ 6x – 3y = 0 ⇒ 3(2x – y) = 0 … (i)
⇒2x – y = 0
ପ୍ରଶ୍ନନୁସାରେ ସଂଖ୍ୟାଟିରେ 18 ଯୋଗକଲେ ଅଙ୍କ ଦୁଇଟିର ସ୍ଥାନ ବଦଳିଯାଏ ।
⇒ 10x + y + 18 = 10y + x ⇒ 10x – x + y – 10y = -18
⇒ 9(x- y) = -18 ⇒ x – y = \(\frac{-18}{9}=-2\)
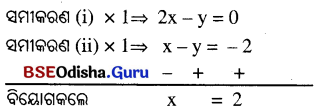
x ର ମାନ ସମୀକରଣ (i)ରେ ସଂସ୍ଥାପନ କଲେ, 2x – y = 0
⇒ 4 – y = 0 ⇒ y=4
∴ ସଂଖ୍ୟାଟି = 10x + y = 10 × 2 + 4 = 24
Question 5.
ଦୁଇଅଙ୍କ ବିଶିଷ୍ଟ ଗୋଟିଏ ସଂଖ୍ୟା ଓ ତାହାର ଅଙ୍କଦ୍ଵୟର ସ୍ଥାନ ବଦଳାଇ ଲେଖୁଲେ ଯେଉଁ ସଂଖ୍ୟା ମିଳିବ, ସେ ଦୁହିଁଙ୍କର ଯୋଗଫଳ 99 ଓ ଅଙ୍କଦ୍ୱୟର ଅନ୍ତର 3 ହେଲେ ସଂଖ୍ୟାଟି କେତେ ?
ସମାଧାନ :
ମନେକର ଦୁଇଅଙ୍କ ବିଶିଷ୍ଟ ସଂଖ୍ୟାର ଦଶକ ଓ ଏକକ ସ୍ଥାନୀୟ ଅଙ୍କ ଦ୍ବୟ ଯଥାକ୍ରମେ x ଓ y
∴ ସଂଖ୍ୟାଟି = 10x + y
ଅଙ୍କଦ୍ୱୟର ସ୍ଥାନ ବଦଳାଇ ଲେଖୁଲେ ସଂଖ୍ୟାଟି ହେବ = 10y + x
ପ୍ରଶ୍ନନୁସାରେ, 10x + y + 10y + x = 99
⇒ 11x + 11y = 99 ⇒ x + y = \(\frac{99}{11}=9\) ………(i)
ଅଙ୍କଦ୍ୱୟର ଅନ୍ତର 3 ।
ଅର୍ଥାତ୍ x – y = 3 ବା y – x = 3 … (ii)
ଯଦି x – y = 3 ହୁଏ,
∴ x = \(\frac{x+y+x-y}{2}=\frac{9+3}{2}=\frac{12}{2}=6\)
y = 9 – x = 9 – 6 = 3
∴ ସଂଖ୍ୟାଟି = 10x + y = 10 × 6 + 3 = 63
ଯଦି ଆମେ ଦ୍ବିତୀୟ ସମୀକରଣକୁ y – x = 3 ନେବା ତେବେ ସଂଖ୍ୟାଟି 36 ହେବ ।
∴ ସଂଖ୍ୟାଟି 63 ବା 36 ।
![]()
Question 6.
ଦୁଇଟି ସଂଖ୍ୟାର ସମଷ୍ଟି, ସେମାନଙ୍କ ବିୟୋଗଫଳର 4 ଗୁଣ ଏବଂ ସଂଖ୍ୟା ଦୁଇଟିର ଯୋଗଫଳ 8 । ତେବେ ସଂଖ୍ୟା ଦୁଇଟି କେତେ ?
ସମାଧାନ :
ମନେକର ସଂଖ୍ୟାଦ୍ଵୟ x ଓ y
ପ୍ରଶ୍ନନୁସାରେ, x + y = 4 (x – y)
⇒ 4x – 4y – x – y = 0 ⇒ 3x – 5y = 0 … (i)
ପୁନଶ୍ଚ ପ୍ରଶ୍ନନୁସାରେ x + y = 8 …… (ii)
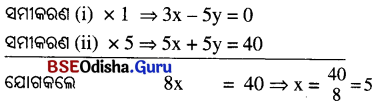
x ର ମାନ ସମୀକରଣ (ii)ରେ ସଂସ୍ଥାପନ କଲେ, x + y = 8
⇒ y = 8 – x = 8 – 5 = 3
∴ ସଂଖ୍ୟାଦ୍ୱୟ 5 ଓ 3 ।
Question 7.
ଦୁଇଅଙ୍କ ବିଶିଷ୍ଟ ସଂଖ୍ୟାର ଅଙ୍କମାନଙ୍କର ସମଷ୍ଟି 10; କିନ୍ତୁ ଅଙ୍କଗୁଡ଼ିକର ସ୍ଥାନ ବଦଳାଇ ଲେଖୁଲେ ଉତ୍ପନ୍ନ ସଂଖ୍ୟାଟି ମୂଳ ସଂଖ୍ୟାର ଦୁଇ ଗୁଣରୁ 1 ଊଣା ହୁଏ, ସଂଖ୍ୟାଟି ସ୍ଥିର କର ।
ସମାଧାନ :
ମନେକର ସଂଖ୍ୟାଟିର ଦଶକ ସ୍ଥାନୀୟ ଅଙ୍କ ଏବଂ ଏକକ ସ୍ଥାନୀୟ ଅଙ୍କ ଯଥାକ୍ରମେ x ଏବଂ y ।
∴ ସଂଖ୍ୟାଟି 10x + y ହେବ ।
ଅଙ୍କଗୁଡ଼ିକର ସ୍ଥାନ ବଦଳିଗଲେ ଉତ୍ପନ୍ନ ସଂଖ୍ୟାଟି 10y + x ହେବ ।
ପ୍ରଶ୍ନନୁସାରେ, ଅଙ୍କଗୁଡ଼ିକର ଯୋଗଫଳ 10 । x + y = 10 … (i)
ପୁନଶ୍ଚ ଉତ୍ପନ୍ନ ସଂଖ୍ୟାଟି, ମୂଳ ସଂଖ୍ୟାର ଦୁଇଗୁଣରୁ 1 କମ୍ ।
ଅର୍ଥାତ୍ 10y + x = 2(10x + y) – 1 = 10y + x = 20x + 2y – 1
⇒ 8y – 19x = -1 ⇒ 19x – 8y = 1 … (ii)
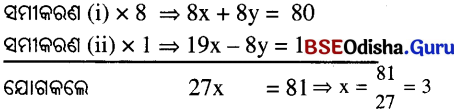
‘x’ ର, ମାନ ସମୀକରଣ (i) ରେ ପ୍ରୟୋଗ କଲେ, 3 + y = 10 ⇒ y = 10 -3 = 7
∴ ସଂଖ୍ୟାଟି = 10x + y = 10 × 3 + 7 = 37
Question 8.
ଦୁଇଟି ସଂଖ୍ୟା ମଧ୍ୟରୁ ପ୍ରଥମଟିର 3 ଗୁଣରୁ ଦ୍ବିତୀୟଟିର 2 ଗୁଣ ବିୟୋଗ କଲେ ବିୟୋଗଫଳ 2 ହେବ ଏବଂ ଦ୍ଵିତୀୟଟିରେ 7 ଯୋଗ କଲେ ଯୋଗଫଳ ପ୍ରଥମଟିର 2 ଗୁଣ ହେବ। ସଂଖ୍ୟାଦ୍ଵୟ ସ୍ଥିର କର ।
ସମାଧାନ :
ମନେକର ପ୍ରଥମ ସଂଖ୍ୟା ଓ ଦ୍ୱିତୀୟ ସଂଖ୍ୟା ଯଥାକ୍ରମେ x ଏବଂ y ହେଉ ।
ପ୍ରଥମଟିର 3 ଗୁଣରୁ ଦ୍ବିତୀୟଟିର 2 ଗୁଣ ବିୟୋଗକଲେ ବିୟୋଗଫଳ 2 ହେବ ।
ଅର୍ଥାତ୍ 3x – 2y = 2 …(i)
ସେହିପରି ଦ୍ବିତୀୟ ସଂଖ୍ୟାରେ 7 ଯୋଗକଲେ, ଯୋଗଫଳ ପ୍ରଥମ ସଂଖ୍ୟାର 2 ଗୁଣ ସଙ୍ଗେ ସମାନ ହେବ ।
ଅର୍ଥାତ୍ y + 7 = 2x = 2x – y = 7 …(ii)

‘x’ ର, ମାନ ସମୀକରଣ (i) ରେ ପ୍ରୟୋଗ କଲେ, 3 × 12 – 2y = 2 ⇒ 36 – 2y = 2
⇒ 2y = 34 ⇒ y = 17
∴ ପ୍ରଥମ ସଂଖ୍ୟାଟି 12 ଏବଂ ଦ୍ବିତୀୟ ସଂଖ୍ୟାଟି 17 ।
Question 9.
ଗୋଟିଏ ଭଗ୍ନାଂଶର ଲବ ଓ ହରରେ 2 ଯୋଗକଲେ ତାହା \(\frac{9}{11}\) ହୁଏ । ମାତ୍ର ଲବ ଓ ହରରେ 3 ଯୋଗକଲେ \(\frac{5}{6}\)
ହୁଏ । ତେବେ ଭଗ୍ନାଂଶଟି କେତେ ?
ସମାଧାନ :
ମନେକର ଭଗ୍ନସଂଖ୍ୟାର ଲବ x ଓ ହର y
ଭଗ୍ନସଂଖ୍ୟାଟି \(\frac{x}{y}\)
ପ୍ରଶ୍ବାନୁସାରେ, \(\frac{x+2}{y+2}=\frac{9}{11}\)
⇒ 11x + 22 = 9y + 18 ⇒ 11x – 9y = – 4 (i)
ପୁନଶ୍ଚ ପ୍ରଶ୍ନନୁସାରେ, \(\frac{x+3}{y+3}=\frac{5}{6}\)
⇒ 6x + 18 = 5y + 15 ⇒ 6x – 5y = – 3 … (ii)
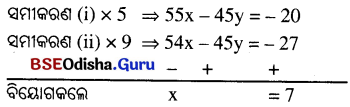
x ର ମାନ ସମୀକରଣ (i)ରେ ସଂସ୍ଥାପନ କଲେ, 11 × 7 – 9y = -4
⇒77 – 9y = 4 ⇒ – 9y = – 4 – 77 = – 81 ⇒ y =\(\frac{81}{9}=9\)
∴ ଭଗ୍ନ ସଂଖ୍ୟାଟି \(\frac{x}{y}=\frac{7}{9}\)
![]()
Question 10.
ଗୋଟିଏ ଭଗ୍ନାଂଶର ଲବର 3 ଗୁଣ ଓ ହରରୁ 3 ବିୟୋଗ କଲେ ଭଗ୍ନାଂଶଟି \(\frac{18}{11}\) ହୁଏ । ମାତ୍ର ଲବରେ 8 ଯୋଗକଲେ ଓ ହରକୁ 2 ଗୁଣ କଲେ ତାହା \(\frac{2}{5}\) ହୁଏ । ତେବେ ଭଗ୍ନାଂଶ କେତେ ?
ସମାଧାନ :
ମନେକର ଭଗ୍ନସଂଖ୍ୟାର ଲବ x ଓ ହର y
∴ ଭଗ୍ନ ସଂଖ୍ୟାଟି \(\frac{x}{y}\)
ପ୍ରଶ୍ନନୁସାରେ, \(\frac{3x}{y-3}=\frac{18}{11}\)
⇒ 33x= 18y – 54 ⇒ 33x – 18y = – 54 ……..(i)
ପୁନଶ୍ଚ ପ୍ରଶ୍ନନୁସାରେ, \(\frac{x+8}{2y}=\frac{2}{5}\)
⇒ 5x + 40 = 4y ⇒ 5x – 4y = -40 ……….(ii)
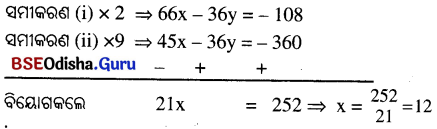
x ର ମାନ ସମୀକରଣ (i)ରେ ବସାଇଲେ,
⇒ 33 × 12 – 18y = 54 ⇒ -18y = -54 – 396
⇒ 18y = 450 ⇒ y = \(\frac{450}{18}=25\)
∴ ଭଗ୍ନସଂଖ୍ୟାଟି \(\frac{x}{y}=\frac{12}{25}\)
Question 11.
5ଟି କଲମ ଓ ଟି ପେନ୍ସିଲ୍ର ଦାମ୍ ମିଶି ୨ ଟଙ୍କା ଏବଂ 3ଟି କଲମ ଓ 2ଟି ପେନ୍ସିଲ୍ର ଦାମ୍ ମିଶି 5 ଟଙ୍କା ହୁଏ । ତେବେ ଗୋଟିଏ କଲମ ଓ ଗୋଟିଏ ପେନ୍ସିଲ୍ର ଦାମ୍ କେତେ ?
ସମାଧାନ :
ମନେକର ଗୋଟିଏ କଲମର ଦାମ୍ x ଟଙ୍କା ଓ ଗୋଟିଏ ପେନ୍ସିଲ୍ର ଦାମ୍ y ଟଙ୍କା ।
ପ୍ରଶ୍ନନୁସାରେ, 5x + 6y = 9 …… (i)
3x + 2y = 5 …….. (ii)
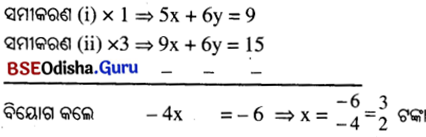
xର ମାନ ସମୀକରଣ (ii)ରେ ବସାଇଲେ, 3 × \(\frac{3}{2}\) + 2y = 5
⇒ 2y = 5 – \(\frac{9}{2}\) ⇒ 2y = \(\frac{10-9}{2}\)
⇒ y = \(\frac{1}{4}\) ଟଙ୍କା ।
∴ ଗୋଟିଏ କଲମର ଦାମ୍ \(\frac{3}{2}\) ଟଙ୍କା ଓ ଗୋଟିଏ ପେନ୍ସିଲ୍ର ଦାମ୍ \(\frac{1}{4}\) ଟଙ୍କା ।
Question 12.
ପିତାଙ୍କ ବୟସ ପୁତ୍ର ବୟସର 3 ଗୁଣ । 12 ବର୍ଷ ପରେ ପିତାଙ୍କ ବୟସ ପୁତ୍ର ବୟସର 2 ଗୁଣ ହେବ । ତେବେ ପିତା ଓ ପୁତ୍ରର ବର୍ତ୍ତମାନ ବୟସ କେତେ ?
ସମାଧାନ :
ମନେକର ପିତାଙ୍କର ବୟସ x ବର୍ଷ ଓ ପୁତ୍ରର ବୟସ y ବର୍ଷ |
ପ୍ରଶ୍ନନୁସାରେ, x = 3y … (i)
ପୁନଶ୍ଚ 12 ବର୍ଷ ପରେ ପିତାଙ୍କର ବୟସ (x + 12) ବର୍ଷ ଓ ପୁତ୍ରର ବୟସ (y + 12) ବର୍ଷ |
ପ୍ରଶ୍ନନୁସାରେ x + 12 = 2 (y + 12) ……..(ii)
ସମୀକରଣ (i)ର ମାନ ସମୀକରଣ (ii)ରେ ସଂସ୍ଥାପନ କଲେ,
3y +12 = 2 (y + 12) ⇒ 3y + 12 = 2y + 24
⇒3y – 2y = 24 – 12
⇒ y = 12 ବର୍ଷ |
ସମୀକରଣ (i)ରେ y = 12 ପ୍ରୟୋଗ କଲେ
x = 3y = 3 × 12 = 36 ବର୍ଷ |
∴ ପିତାଙ୍କର ବର୍ତ୍ତମାନ ବୟସ 36 ବର୍ଷ ଓ ପୁତ୍ରର ବର୍ତ୍ତମାନ ବୟସ 12 ବର୍ଷ ।
Question 13.
ଏକ ଆୟତ କ୍ଷେତ୍ରର ଦୈର୍ଘ୍ୟକୁ 5 ସେ.ମି. କମାଇ ପ୍ରସ୍ଥକୁ 3 ସେ.ମି. ବଢ଼ାଇବା ଦ୍ଵାରା ଏହାର କ୍ଷେତ୍ରଫଳ 9 ବର୍ଗ ସେ.ମି. କମିଯାଏ । ଆୟତକ୍ଷେତ୍ରର ଦୈର୍ଘ୍ୟକୁ 3 ସେ.ମି. ଓ ପ୍ରସ୍ଥକୁ 2 ସେ.ମି. ବଢ଼ାଇବା ଦ୍ୱାରା କ୍ଷେତ୍ରଫଳ 67 ବର୍ଗ ସେ.ମି. ବଢ଼ିଯାଏ । ଆୟତକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ ସ୍ଥିର କର ।
ସମାଧାନ :
ମନେକର ଆୟତକ୍ଷେତ୍ରର ଦୈର୍ଘ୍ୟ x ସେ.ମି. ଓ ପ୍ରସ୍ଥ y ସେ.ମି. ।
∴ ଆୟତକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = xy ବର୍ଗ ସେ.ମି.
ପ୍ରଶ୍ନନୁସାରେ, (x – 5) (y + 3) = xy – 9 ⇒ 3x – 5y – 6 = 0 … (i)
ପୁନଶ୍ଚ (x + 3) (y + 2) = xy + 67 = 2x +3y – 61 = 0 …….(ii)

⇒ \(\frac{x}{323}=\frac{y}{171}=\frac{1}{19}\)
⇒ x = \(\frac{323}{19}\) = 17 ଏବଂ y = \(\frac{171}{19}\) = 9
∴ ଆୟତକ୍ଷେତ୍ରର ଦୈର୍ଘ୍ୟ 17 ସେ.ମି. ଓ ପ୍ରସ୍ଥ 9 ସେ.ମି. ।
∴ ଆୟତକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = ଦୈର୍ଘ୍ୟ × ପ୍ରସ୍ଥ = 17 × 9 = 153 ବର୍ଗ ସେ.ମି. ।
![]()
Question 14.
2 ଜଣ ପୁରୁଷ ଓ 3 ଜଣ ସ୍ତ୍ରୀ ଲୋକ ଏକତ୍ର ଗୋଟିଏ କାର୍ଯ୍ୟକୁ 5 ଦିନରେ ଶେଷ କରିପାରନ୍ତି । ସେହି କାର୍ଯ୍ୟକୁ 4 ଜଣ ପୁରୁଷ ଓ ୨ ଜଣ ସ୍ତ୍ରୀ ଲୋକ ଏକତ୍ର 2 ଦିନରେ ଶେଷ କରିପାରନ୍ତି । ତେବେ ଜଣେ ସ୍ତ୍ରୀ ଲୋକ କିମ୍ବା ଜଣେ ପୁରୁଷ ସେହି କାର୍ଯ୍ୟକୁ କେତେ ଦିନରେ ଶେଷ କରିପାରବେ ?
ସମାଧାନ :
ମନେକର ଜଣେ ପୁରୁଷ ଏବଂ ଜଣେ ସ୍ତ୍ରୀ ଗୋଟିଏ କାର୍ଯ୍ୟକୁ ଯଥାକ୍ରମେ x ଓ y ଦିନରେ ଶେଷ କରିପାରିବେ ।
∴ ଜଣେ ପୁରୁଷ ଏବଂ ଜଣେ ସ୍ତ୍ରୀ 1 ଦିନରେ କାର୍ଯ୍ୟର ଯଥାକ୍ରମେ \(\frac{1}{x}\) ଅଂଶ ଏବଂ \(\frac{1}{y}\) ଅଂଶ କରିବେ ।
2 ଜଣ ପୁରୁଷ ଓ 3 ଜଣ ସ୍ତ୍ରୀ 1 ଦିନରେ କାର୍ଯ୍ୟର = \(\frac{2}{x}\) + \(\frac{3}{y}\) ଅଂଶ କରିବେ ।
କିନ୍ତୁ 2 ଜଣ ପୁରୁଷ ଓ 3 ଜଣ ସ୍ତ୍ରୀ କାର୍ଯ୍ୟଟିକୁ 5 ଦିନରେ କରନ୍ତି ।
1 ଦିନରେ କାର୍ଯ୍ୟଟିର କରିବେ = \(\frac{1}{5}\) ଅଂଶ ।
ପ୍ରଶାନୁସାରେ, \(\frac{2}{x}+\frac{3}{y}=\frac{1}{5}\) ……….(i)
ପୁନଶ୍ଚ, 4 ଜଣ ପୁରୁଷ ଓ 9 ଜଣ ସ୍ତ୍ରୀ 1 ଦିନରେ କାର୍ଯ୍ୟର କରିବେ = \(\frac{4}{x}\) + \(\frac{9}{y}\) ଅଂଶ ।
କିନ୍ତୁ 4 ଜଣ ପୁରୁଷ ଓ 9 ଜଣ ସ୍ତ୍ରୀ କାର୍ଯ୍ୟଟିକୁ 2 ଦିନରେ କରନ୍ତି ।
1 ଦିନରେ କାର୍ଯ୍ୟଟିର କରିବେ = \(\frac{1}{2}\) ଅଂଶ ।
ପୁନଶ୍ଚ, ପ୍ରଶ୍ନନୁସାରେ, \(\frac{4}{x}+\frac{9}{y}=\frac{1}{2}\)

⇒ \(– \frac{3}{y}=\frac{4-5}{10}=\frac{-1}{10}\) ⇒ \(\frac{3}{y}=\frac{1}{10}\)
⇒ y = 30
y ର ମାନ ସମୀକରଣ (i) ରେ ପ୍ରୟୋଗ କଲେ,
⇒ \(\frac{2}{x}+\frac{3}{30}=\frac{1}{5}\) ⇒ \(\frac{2}{x}+\frac{1}{10}=\frac{1}{5}\)
\(\frac{2}{x}+\frac{1}{5}-\frac{1}{10}\) ⇒ \(\frac{2}{x}=\frac{1}{10}\) ⇒ x = 20
∴ ଜଣେ ପୁରୁଷ କିମ୍ବା ଜଣେ ସ୍ତ୍ରୀ ସେହି କାର୍ଯ୍ୟକୁ ଯଥାକ୍ରମେ 20 ଦିନରେ କିମ୍ବା 30 ଦିନରେ କରିବେ ।
Question 15.
A ଓ B ଏକତ୍ର କାମ କରି ଗୋଟିଏ କାର୍ଯ୍ୟକୁ 8 ଦିନରେ ଶେଷ କରିପାରନ୍ତି । ସେମାନେ ଏକତ୍ର କାର୍ଯ୍ୟ ଆରମ୍ଭ କରି 3 ଦିନ କାର୍ଯ୍ୟ କରିବା ପରେ A ଚାଲିଗଲା ଓ ଅବଶିଷ୍ଟ କାର୍ଯ୍ୟକୁ B ଏକା ଆଉ 15 ଦିନରେ ଶେଷ କଲା । ପ୍ରତ୍ୟେକ ଏକାକୀ କାମ କଲେ କେତେ ଦିନରେ କାର୍ଯ୍ୟକୁ ଶେଷ କରିପାରିବେ ?
ସମାଧାନ :
ମନେକର A ଓ B କାର୍ଯ୍ୟକୁ ଯଥାକ୍ରମେ x ଓ y ଦିନରେ କରିପାରିବେ ।
A ଓ B 1 ଦିନରେ କାର୍ଯ୍ୟଟିର ଯଥାକ୍ରମେ \(\frac{1}{x}\) ଅଂଶ ଏବଂ \(\frac{1}{y}\) ଅଂଶ କରିପାରିବେ ।
A ଓ B ମିଶି 1 ଦିନରେ କାର୍ଯ୍ୟଟିର \(\frac{1}{x}+\frac{1}{y}\) ଅଂଶ କରିପାରିବେ ।
କିନ୍ତୁ ପ୍ରଶ୍ନ ଅଛି A ଓ B କାର୍ଯ୍ୟଟିକୁ 8 ଦିନରେ କରିପାରନ୍ତି ।
∴ 1 ଦିନରେ କରିବେ = \(\frac{1}{8}\) ଅଂଶ ।
ପ୍ରଶ୍ନନୁସାରେ, \(\frac{1}{x}+\frac{1}{y}=\frac{1}{8}\) …….. (i)
A ଓ B ଏକତ୍ର କାର୍ଯ୍ୟ ଆରମ୍ଭ କରିବାର 3 ଦିନ ପରେ A ଚାଲିଗଲା ।
ଅବଶିଷ୍ଟ କାର୍ଯ୍ୟଟିକୁ B ଆଉ 15 ଦିନରେ ଶେଷକଲା ।
ଅର୍ଥାତ୍ A, 3 ଦିନ ଓ B (15 + 3) = 18 ଦିନ କାର୍ଯ୍ୟ କଲାପରେ କାର୍ଯ୍ୟଟି ସମ୍ପୂର୍ଣ ହେଲା ।
∴ A, 3 ଦିନରେ କାର୍ଯ୍ୟଟିର କରିବ = \(\frac{3}{x}\) ଅଂଶ । B, 18 ଦିନରେ କାର୍ଯ୍ୟଟିର କରିବ \(\frac{18}{y}\) ଅଂଶ ।
ପୁନଶ୍ଚ ପ୍ରଶ୍ନନୁସାରେ, \(\frac{3}{x}+\frac{18}{y}=1\) ……….(ii)

⇒ \(– \frac{15}{y}=\frac{3-8}{8}\) ⇒ \(– \frac{15}{y}=\frac{-5}{8}\)
⇒ \(\frac{3}{y}=\frac{1}{8}\) ⇒ y = 24
y ର ମାନ ସମୀକରଣ (i) ରେ ପ୍ରୟୋଗ କଲେ,
⇒ \(\frac{1}{x}+\frac{1}{24}=\frac{1}{8}\) ⇒ \(\frac{1}{x}=\frac{1}{8}-\frac{1}{24}\)
\(\frac{1}{x}=\frac{3-1}{24}=\frac{2}{24}=\frac{1}{12}\) ⇒ x = 12
∴ A ଏକାକୀ କାର୍ଯ୍ୟଟିକୁ 12 ଦିନରେ ଓ B ଏକାକୀ କାର୍ଯ୍ୟଟିକୁ 24 ଦିନରେ ଶେଷ କରିପାରିବେ ।
![]()
Question 16.
A ଓ Bର ଆୟର ଅନୁପାତ 8 : 7 ଓ ବ୍ୟୟର ଅନୁପାତ 19 : 16 । ଯଦି ଉଭୟେ 1250 ଟଙ୍କା ସଞ୍ଚୟ କରିପାରନ୍ତି, ତେବେ ସେମାନଙ୍କର ଆୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ :
A ଓ B ର ଆୟର ଅନୁପାତ 8 : 7 ।
ମନେକର A ଓ B ର ଆୟ ଯଥାକ୍ରମେ 8x ଟଙ୍କା ଏବଂ 7x ଟଙ୍କା ।
ସେହିପରି A ଓ B ର ବ୍ୟୟର ଅନୁପାତ 19 : 16 |
ତେଣୁ ମନେକର A ଓ B ର ବ୍ୟୟ ଯଥାକ୍ରମେ 19y ଟଙ୍କା ଏବଂ 16y ଟଙ୍କା ।
ପ୍ରଶ୍ନନୁସାରେ A ର ସଞ୍ଚୟ = 1250 ଟଙ୍କା ⇒ 8x – 19y = 1250 ……..(i)
ସେହିପରି B ର ସଞ୍ଚୟ = 1250 ଟଙ୍କା ⇒ 7x – 16y = 1250 ……….(ii)
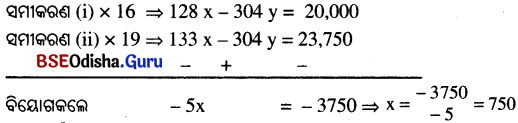
∴ A = 8x = 8 × 750 = 6000 ଟଙ୍କା । ଏବଂ Bର ଆୟ = 7x = 7 × 750 = 5250 ଟଙ୍କା ।
Question 17.
5 ବର୍ଷ ପରେ ପିତାର ବୟସ ପୁତ୍ରର ବୟସର ତିନିଗୁଣ ହେବ ଓ 5 ବର୍ଷ ପୂର୍ବେ ପିତାର ବୟସ ପୁତ୍ର ବୟସର ସାତଗୁଣ ଥିଲା । ତେବେ ସେମାନଙ୍କର ବର୍ତ୍ତମାନ ବୟସ ସ୍ଥିର କର ।
ସମାଧାନ :
ମନେକର ପିତାର ବର୍ତ୍ତମାନ ବୟସ x ବର୍ଷ ଓ ପୁତ୍ରର ବର୍ତ୍ତମାନ ବୟସ y ବର୍ଷ ।
5 ବର୍ଷ ପରେ ପିତାର ବୟସ ହେବ = (x + 5) ବର୍ଷ ଓ ପୁତ୍ରର ବୟସ ହେବ = (y + 5) ବର୍ଷ
ପ୍ରଶ୍ନନୁସାରେ, x + 5 = 3(y + 5)
⇒ x + 5 = 3y + 15 ⇒ x – 3y = 10 …(i)
ପୁନଶ୍ଚ, 5 ବର୍ଷ ପୂର୍ବେ ପିତାର ବୟସ ଥିଲା = (x – 5) ବର୍ଷ ଓ ପୁତ୍ରର ବୟସ ଥିଲା = (y – 5) ବର୍ଷ
ପ୍ରଶ୍ନନୁସାରେ, (x – 5) = 7(y – 5)
⇒ x -5 = 7y – 35 ⇒ x – 7y = -30 …(ii)
ସମୀକରଣ (i)ରୁ ସମୀକରଣ (ii)କୁ ବିୟୋଗ କଲେ, (x – 3y) – (x – 7y) = 10 – (-30)
⇒ x – 3y – x + 7y = 40 ⇒ 4y = 40 ⇒ y = 10
ସମୀକରଣ (i) ରେ y = 10 ସ୍ଥାପନ କଲେ, x – 3 × 10 = 10 ⇒ x = 40
∴ ପିତାର ବର୍ତ୍ତମାନ ବୟସ 40 ବର୍ଷ ଓ ପୁତ୍ରର ବର୍ତ୍ତମାନ ବୟସ 10 ବର୍ଷ ।
Question 18.
ଗୋଟିଏ ଆୟତକ୍ଷେତ୍ରର ଦୈର୍ଘ୍ୟ 2 ମି. ଅଧ୍ଵ ଓ ପ୍ରସ୍ଥ 2ମି. କମ୍ ହେଲେ, କ୍ଷେତ୍ରଫଳ 28 ବ.ମି. କମିଯାଏ; ମାତ୍ର ଦୈର୍ଘ୍ୟ 1 ମି. କମ୍ ଓ ପ୍ରସ୍ଥ 2 ମି. ଅଧ୍ବକ ହେଲେ କ୍ଷେତ୍ରଫଳ 33 ବ. ମି. ବଢ଼ିଯାଏ । ମୂଳ ଆୟତକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ ସ୍ଥିର କର ।
ସମାଧାନ :
ମନେକର ଆୟତକ୍ଷେତ୍ରର ଦୈର୍ଘ୍ୟ ଓ ପ୍ରସ୍ଥ ଯଥାକ୍ରମେ x ମି. ଓ Y ମି. ।
∴ କ୍ଷେତ୍ରଫଳ = ଦୈର୍ଘ୍ୟ × ପ୍ରସ୍ଥ = xy ବର୍ଗ ମି. ।
ପ୍ରଶ୍ନନୁସାରେ, ଦୈର୍ଘ୍ୟ 2 ମି. ଅଧୂକ ଏବଂ ପ୍ରସ୍ଥ 2 ମି. କମ୍ ହେଲେ କ୍ଷେତ୍ରଫଳ 28 ବର୍ଗ ମି. କମିଯାଏ ।
ତେଣୁ ପରିବର୍ତ୍ତିତ ଦୈର୍ଘ୍ୟ ଏବଂ ପ୍ରସ୍ଥ ଯଥାକ୍ରମେ (x + 2) ମି. ଏବଂ (y – 2) ମି. ହେବ ।
(x + 2) (y – 2) = xy – 28 ⇒ xy + 2y – 2x – 4 = xy – 28
⇒ 2y – 2x = -28 + 4 ⇒ y – x = \(\frac{-24}{2}\) ⇒ y – x = -12
⇒ x – y = 12 … (i)
ସେହିପରି ଦୈର୍ଘ୍ୟ 1 ମି. କମ୍ ଓ ପ୍ରସ୍ଥ 2 ମି. ଅଧ୍ଯକ ହେଲେ, କ୍ଷେତ୍ରଫଳ 33 ବର୍ଗ ମି. ବୃଦ୍ଧିପାଏ ।
∴ ପରିବର୍ତ୍ତିତ ଦୈର୍ଘ୍ୟ ଏବଂ ପ୍ରସ୍ଥ ଯଥାକ୍ରମେ (x – 1) ମି, ଏବଂ (y + 2) ମି. ହେବ ।
∴ (x – 1) (y + 2) = xy + 33 ⇒ xy + 2x – y – 2 = xy + 33
⇒ 2x – y = 33 +2 ⇒ 2x – y = 35 ……(ii)
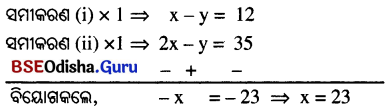
‘x’ ର ମାନ ସମୀକରଣ (i) ରେ ପ୍ରୟୋଗ କଲେ 23 – y = 12 = y = 11
∴ ଆୟତକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = xy ବର୍ଗ ମି. = (23 × 11) ବର୍ଗ ମି. = 253 ବର୍ଗ ମି. ।
![]()
Question 19.
50କୁ ଏପରି ଦୁଇଟି ସଂଖ୍ୟାର ସମଷ୍ଟି ରୂପେ ପ୍ରକାଶ କର ଯେପରିକି ସଂଖ୍ୟା ଦ୍ଵୟର ବ୍ୟକ୍ରମର ସମଷ୍ଟି \(\frac{1}{12}\) ହେବ ।
ସମାଧାନ :
ମନେକର ସଂଖ୍ୟା ଦୁଇଟି x ଓ y ।
ସଂଖ୍ୟା ଦୁଇଟିର ସମଷ୍ଟି 50 । ⇒ x + y = 50 ….. (i)
x ଓ y ର ବ୍ୟକ୍ରମ ଯଥାକ୍ରମେ \(\frac{1}{x}\) ଓ \(\frac{1}{y}\) ।
ପ୍ରଶାନୁସାରେ, \(\frac{1}{x}+\frac{1}{y}=\frac{1}{12}\) ……..(ii)
⇒ \(\frac{1}{x}+\frac{1}{y}=\frac{1}{12}\) ⇒ \(\frac{x+y}{xy}=\frac{1}{12}\) ⇒ \(\frac{50}{xy}=\frac{1}{12}\) (∵ x + y = 50)
⇒ xy = 600 ……..(iii)
ଆମେ ଜାଣିଛେ, x – y = \(\sqrt{(x+y)^2-4xy}\) = \(\sqrt{(50)^2-4×600}\) = \(\sqrt{100}\)
⇒ x – y = 10 ……(iv)
ସମୀକରଣ (i) ଓ (iv)କୁ ଯୋଗକଲେ, 2x = 60 ⇒ x = 30
ସମୀକରଣ (i)ରେ x = 30 ସ୍ଥାପନ କଲେ, 30 + y = 50 ⇒ y = 20
∴ ସଂଖ୍ୟାଦ୍ବୟ 30 ଓ 20 ।
Question 20.
ଗୋଟିଏ ଭଗ୍ନ ସଂଖ୍ୟାର ଲବ ଓ ହରକୁ ଯୋଗକରି ଯୋଗଫଳର ଏକ-ତୃତୀୟାଂଶ ନେଲେ, ତାହା ହରଠାରୁ 4 ଊଣା ହୁଏ ଓ ହରରେ 1 ଯୋଗକରି ଭଗ୍ନ ସଂଖ୍ୟାଟିକୁ ଲଘିଷ୍ଠ ଆକାରରେ ଲେଖୁଲେ ତାହା \(\frac{1}{4}\) ହୁଏ । ଭଗ୍ନ ସଂଖ୍ୟାଟି କେତେ ?
ସମାଧାନ :
ମନେକର ଭଗ୍ନସଂଖ୍ୟାଟି \(\frac{x}{y}\), ଯାହାର ଲବ x ଏବଂ ହର y ।
ପ୍ରଶ୍ନନୁସାରେ, ଲବ ଓ ହରକୁ ଯୋଗକରି ଯୋଗଫଳର ଏକତୃତୀୟାଂଶ ନେଲେ ତାହା ହରଠାରୁ 4 ଊଣା ହୁଏ ।
\(\frac{1}{3}\)(x+y) = y – 4 ⇒ x + y = 3y – 12 ⇒ x – 2y= – 12 …….. (i)
ପୁନଶ୍ଚ ହରରେ 1 ଯୋଗକରି ଭଗ୍ନାଂଶଟିକୁ ଲଘିଷ୍ଠ ଆକାରକୁ ଆଣିଲେ ତାହା \(\frac{1}{4}\) ହୁଏ ।
\(\frac{x}{y+1}=\frac{1}{4}\) ⇒ 4x = y + 1 ⇒ 4x – y = 1 ……….(ii)
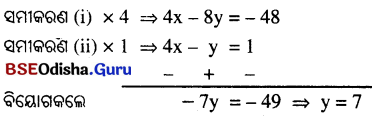
‘y’ ର ମାନ ସମୀକରଣ (i) ରେ ପ୍ରୟୋଗ କଲେ, x – 2 × 7 = -12
⇒ x – 14 = -12 ⇒ x = 2
∴ ଭଗ୍ନାଂଶଟି \(\frac{x}{y}=\frac{2}{7}\)
