CHSE Odisha Class 12 Math Solutions Chapter 9 Integration Ex 9(a)

Odisha State Board Elements of Mathematics Class 12 Solutions CHSE Odisha Chapter 9 Integration Ex 9(a) Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 9 Integration Exercise 9(a)

Question 1.
(i) ∫2 dx
Solution:
∫2 dx = 2x + C

(ii) ∫3x² dx
Solution:
∫3x² dx = 3 \(\frac{x^3}{3}\) + C = x³ + C

(iii) ∫4x³ dx
Solution:
∫4x³ dx = 4 \(\frac{x^4}{4}\) + C = x⁴ + C

(iv) ∫x⁵ dx
Solution:
∫x⁵ dx = \(\frac{x^6}{6}\) + C

(v) ∫x³¹ dx
Solution:
∫x³¹ dx = \(\frac{x^{32}}{32}\) + C

(vi) ∫\(\left(2 \sqrt{x}+\frac{3}{\sqrt{x}}\right)\) dx
Solution:

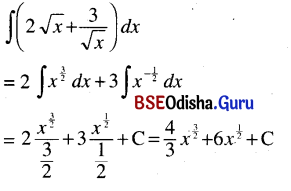
(vii) ∫\(\frac{1}{x \sqrt{x}}\) dx
Solution:

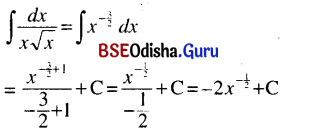
(viii) ∫\(\left(x^{\frac{4}{7}}+\frac{1}{x^{\frac{1}{3}}}\right)\) dx
Solution:

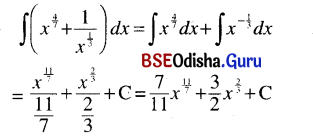
(ix) ∫\(\frac{4}{x}\) dx
Solution:
∫\(\frac{4}{x}\) dx = 4 ln |x| + C

(x) ∫\(\left(\frac{3}{x^2}+\frac{1}{x^{12}}\right)\) dx
Solution:

(xi) ∫(x² + √x)² dx
Solution:

(xii) ∫(x + 3) (2 – x) dx
Solution:
∫(x + 3) (2 – x) dx
= ∫(2x + 6 – x² – 3x) dx
= ∫(-x² – x + 6) dx
= –\(\frac{1}{3}\)x³ – \(\frac{1}{2}\)x² + 6x + C

(xiii) ∫\(\frac{(\sqrt{x}+2)^2}{x^4}\) dx
Solution:

(xiv) ∫\(\frac{(x+\sqrt{x})(2 x+1)}{x^2}\) dx
Solution:

Question 2.
(i) ∫cos dx
Solution:
∫cos dx = sin x + C

(ii) ∫\(\frac{d x}{\cos ^2 x}\)
Solution:
∫\(\frac{d x}{\cos ^2 x}\) = ∫sec² x dx = tan x + C

(iii) ∫\(\frac{d x}{1-\cos ^2 x}\)
Solution:
∫\(\frac{d x}{1-\cos ^2 x}\) = ∫\(\frac{d x}{\sin ^2 x}\)
= ∫cosec² x dx
= -cot x + C

(iv) ∫\(\frac{\sin x}{\cos ^2 x}\) dx
Solution:
∫\(\frac{\sin x}{\cos ^2 x}\) dx = ∫\(\frac{\sin x}{\cos x} \cdot \frac{1}{\cos x}\) dx
= ∫sec x . tan x dx = sec x + C

(v) ∫\(\frac{2 \cos x}{1-\cos ^2 x}\) dx
Solution:

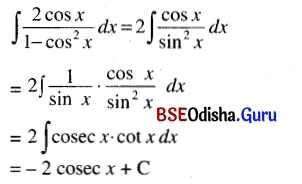
(vi) ∫\(\frac{1-\sin ^3 x}{\sin ^2 x}\) dx
Solution:
∫\(\frac{1-\sin ^3 x}{\sin ^2 x}\) dx = ∫(cosec² x – sin x) dx
= -cot x + cos x + C

(vii) ∫\(\frac{\sin ^2 x}{1+\cos x}\) dx
Solution:

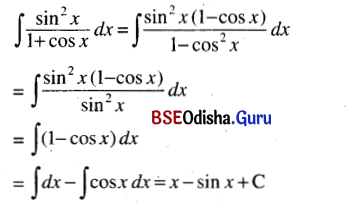
(viii) ∫\(\frac{\cos 2 x}{\cos x+\sin x}\) dx
Solution:

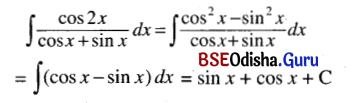
(ix) ∫\(\frac{\cos ^4 x-\sin ^4 x}{\cos x-\sin x}\) dx
Solution:

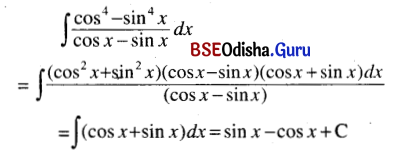
(x) ∫\(\frac{\cos 2 x}{\sin ^2 x \cdot \cos ^2 x}\) dx
Solution:

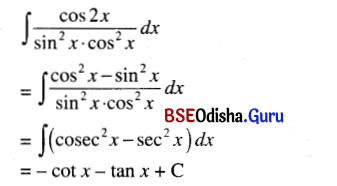
(xi) ∫\(\frac{a^2 \sin ^2 x+b^2 \cos ^2 x}{\sin ^2 2 x}\) dx
Solution:

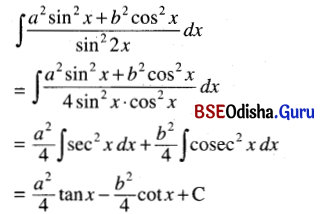
(xii) ∫(tan x + cot x)² dx
Solution:

(xiii) ∫\(\frac{1-\cos 2 x}{1+\cos 2 x}\) dx
Solution:

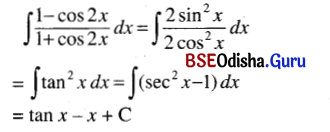
(xiv) ∫sec² x . cosec² x dx
Solution:

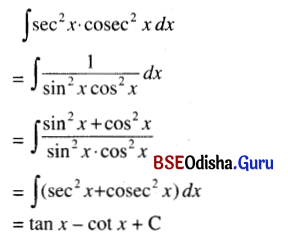
(xv) ∫\(\frac{\sin ^3 x+b \cos ^3 x}{\sin ^2 x \cos ^2 x}\) dx
Solution:

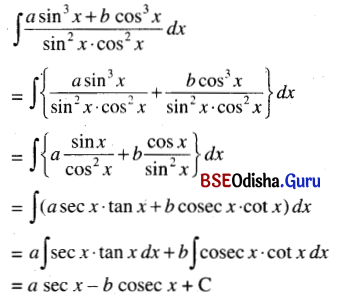
(xvi) ∫\(\sqrt{1+\sin 2 x}\) dx
Solution:

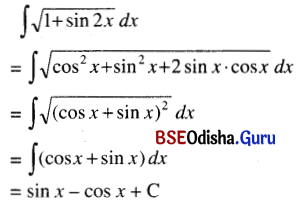
(xvii) ∫\(\sqrt{1-\cos 2 x}\) dx
Solution:

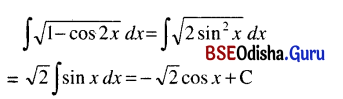
(xviii) ∫\(\sqrt{1+\cos 2 x}\) dx
Solution:
∫\(\sqrt{1+\cos 2 x}\) dx = ∫√2 cos x dx
= √2 sin x + C

(xix) ∫\(\frac{\cos 3 x \cos 2 x+\sin 3 x \sin 2 x}{1-\cos ^2 x}\) dx
Solution:

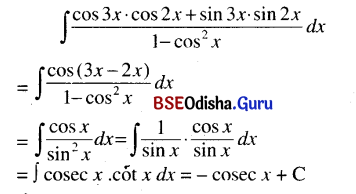
(xx) ∫(a cot x + b tan x)² dx
Solution:
∫(a cot x + b tan x)² dx
= ∫{a² cot² x + b² tan² x + 2ab cot x – tanx} xdx
= ∫(a² cot² x + b² tan² x + 2ab) dx
= a² ∫cot² x dx + b² ∫tan² x dx + 2ab ∫dx
= a² ∫(cosec² x – 1) dx + b² ∫(sec² x – 1) dx + 2ab x + C
= a² (-cot x – x) + b² (tan x – x) + 2ab x + C
= b² tan x – a² cot x – x (a² + b² – 2ab) + C
= b² tan x – a² cot x – (a – b)² x + C
= b² tan x – a² cot x + C

Question 3.
(i) ∫(e^x + 2) dx
Solution:
∫(e^x +2) dx = ∫e^x dx + 2 ∫dx
= e^x + 2x + C

(ii) ∫3^x dx
Solution:
∫3^x dx = ∫\(\frac{3^x}{\ln 3}\) + C

(iii) ∫a^x+2 dx
Solution:
∫a^x+2 dx = ∫a^x a² dx
= a² . \(\frac{a^x}{\ln a}\) + C
= \(\frac{a^{x+2}}{\ln a}\) + C

(iv) ∫a^3x dx
Solution:
∫a^3x dx = \(\frac{1}{3} \frac{a^{3 x}}{\ln a}\) + C

(v) ∫\(\frac{e^{2 x}+1}{e^x}\) dx
Solution:
∫\(\frac{e^{2 x}+1}{e^x}\) dx = ∫(e^x + e^-x) dx
= e^x – e^-x + C

Question 4.
(i) ∫\(\left(\frac{5}{\sqrt{1-x^2}}+\frac{7}{1+x^2}\right)\) dx
Solution:

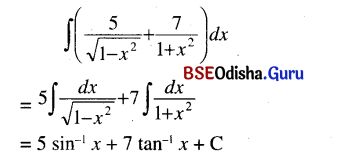
(ii) ∫\(\frac{3 x^2}{x^2+1}\) dx
Solution:

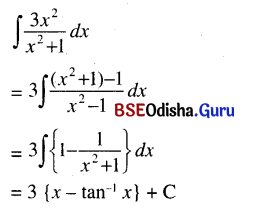
(iii) ∫\(\frac{x^6}{x^2+1}\) dx
Solution:

(iv) ∫\(\frac{x^4+x^3+x^2+x+2}{x^2+1}\) dx
Solution:

(v) ∫\(\left(\sqrt{1-x^2}+\frac{x^2}{\sqrt{1-x^2}}\right)\) dx
Solution:

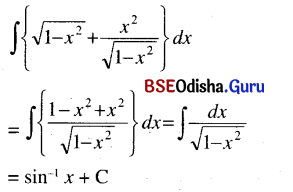
(vi) ∫\(\frac{x^2+\sqrt{x^2+1}}{x^3 \sqrt{x^2-1}}\) dx
Solution:

Question 5.
Find the unique antiderivative F(x) of f(x) = 2x² + 1, whese F(o) = -2.
Solution:
F(x) = ∫f(x) dx = ∫(2x² + 1) dx
= \(\frac{2}{3}\)x³ + x + C
But F(0) = -2
∴ -2 = C
Thus F(x) = \(\frac{2}{3}\)x³ + x – 2