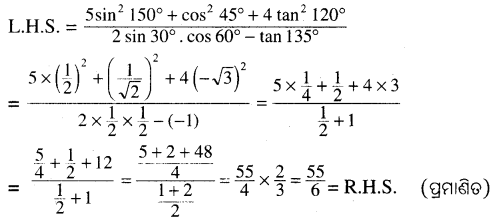BSE Odisha 10th Class Maths Solutions Geometry Chapter 4 ତ୍ରିକୋଣମିତି Ex 4(a)

Odisha State Board BSE Odisha 10th Class Maths Solutions Geometry Chapter 4 ତ୍ରିକୋଣମିତି Ex 4(a) Textbook Exercise Questions and Answers.

BSE Odisha Class 10 Maths Solutions Geometry Chapter 4 ତ୍ରିକୋଣମିତି Ex 4(a)

Question 1.
ବନ୍ଧନୀ ମଧ୍ଯରୁ ଠିକ୍ ଉତ୍ତରଟି ବାଛି ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
1. (a) sin 80° = _____ [sin 10°, sin 20°, cos 10°, cos 20°]
(b) cos 65° = _____ [sin 25°, sin 35°, cos 25°, cos 35°]
(c) sin 180° = _____ [1, −1, 0, ± 1]
(d) cos 90° = _____ [1, -1, 0, ± 1]
(e) cos 110° + sin 20° = _____ [2 cos 110°, 2 sin 20°, 0, 1]
(f) sin 75° – cos 15° = _____ [\(\frac{\sqrt{3}}{2}\) , \(\frac { 1 }{ 2 }\) , 0, 1]
(g) sin 0° = _____ [cos 0°, sin 90°, sin 180°, cos 180°]
(h) sin 15° + cos 105° = _____ [0, 1, -1, ± 1]
(i) cos 121° + sin 149° = _____ [1, -1, 0, ± 1]
(j) tan 102° – cot 168° = _____ [0, −1, 1, ± 1]
Solution:
(a) cos 10° [sin 80° = sin (90° – 10°) = cos 10°]
(b) sin 25° [cos 65° = cos (90° – 25°) = sin 25°]
(c) 0
(d) 0
(e) 0 [cos 110° + sin 20° = cos (90° + 20°) + sin 20° = − sin 20° + sin 20° = 0]
(f) 0 [sin 75° – cos 15° = sin (90° – 15°) – cos 15° = cos 15° – cos 15° = 0]
(g) sin 180°
(h) 0 [sin 15° + cos 105° = sin 15° + cos (90° + 15°) = sin 15° sin 15° = 0]
(i) 0 [cos 121° + sin 149° = cos (90° + 31°) + sin (180° – 31°) = sin 31° + sin 31° = 0]
(j) 0 [tan 102° – cot 168° = tan (90° + 12°) – cot (180° – 12°). =-cot 12° – (- cot 12°) = 0].

Question 2.
90° + 0 ଳାମ୍ବା 90° – 0 ଳାମ୍ବା 180° – θ ତ୍ରିକୋଣମିତିକ ଅନୁପାତ ରୂପରେ ପ୍ରକାଶ କର । (0° < 0 < 90°) |
(i) sin 111°
(ii) cos 122°
(iii) tan 99°
(iv) cot 101°
(v) sin 91°
(vi) cosec 93°
(vii) cos 128°
(viii) cosec 132°
(ix) cot 131°
Solution:
(i) sin 111° = sin (90° + 21°) = cos 21°
ଳାମ୍ବା sin (180° – 69°) = sin 69° = sin (90° – 21°) = cos 21°

(ii) cos 122° = cos (90° + 32°) = – sin 32°
ଳାମ୍ବା, cos (180° – 58°) = − cos 58° = cos (90° + 32°) = – sin 32°

(iii) tan 99° = tan (90° + 9) = – cot 9°
ଳାମ୍ବା tan (180° – 81°) = – tan 81° = − tan (90° – 9°) = – cot 9°

(iv) cot 101° cot (90° +21°) = tan 21°
ଳାମ୍ବା cot (180° – 79°) = – cot 79° = -cot (90° – 21°) = – tan 21°

(v) sin 91° = sin (90° + 1°) = cos 1°
ଳାମ୍ବା sin (180° – 89°) = sin 89° = sin (90° – 1°) = cos 1°

(vi) cosec 93° = cosec (90° + 3°) = sec 3°
cosec (180° – 87°) = cosec 87° cosec (90° – 3°) = sec 3°

(vii) cos 128° = cos (90° + 38°) = – sin 38°
ଳାମ୍ବା, cos (180° – 52°) = cos 52° = − cos (90° – 38°) = – sin 38°

(viii) cosec 132° = cosec (90° + 42°) = sec 42°
ଳାମ୍ବା, cosec (180° – 48°) = cosec 48° = cosec (90° – 42°) = sec 42°

(ix) cot 131° = cot (90° + 41°) = – tan 41°
ଳାମ୍ବା, cot (180° – 49°) = — cot 49° = -cot (90° – 41°) = – tan 41°

Question 3.
ନମ୍ନମ ପଦଗୁପିକ୍ନ 0° ଏବ 45° କୋଣ ପରିମାଣ ମଧ୍ଯସ୍ଥ ତ୍ରିକୋଣମିତିକ ଅନୁପାତରେ ପ୍ରକାଶ କର ।
(i) cos 85° + cot 85°
(ii) sin 75° + tan 75°
(iii) cot 65° + tan 49°
Solution:
(i) cos 85° + cot 85° = cos (90° -5°) + cot (90° -5°) = sin 5° + tan 5°
(ii) sin 75° + tan 75° = sin (90° – 15°) + tan (90° – 15°) = cos 15° + cot 15°
(iii) cot 65° + tan 49° = cot (90° – 25°) + tan (90° – 41°) = tan 25° + cot 41°

Question 4.

Solution:

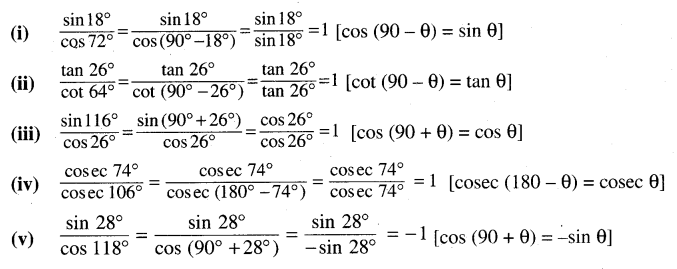
Question 5.
ସରକ କର:
(i) cosec 31° – sec 59°
(ii) sin (50° + θ) — cos (40° − θ)
(iii) sin2 59° + sin2 31°
(iv) tan (55°-0) – cot (35° + 0)
(v) cos 1°. cos 2° …… cos 180°

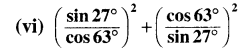
(vii) cot 112°. cot 158°
(viii) cos² (90° + α) + cos² (180° – α)
(ix) sec² (105° + α) – tan² (75° – α)
(x) sin² (110° + α) + cos² (70° – α)
Solution:
(i) cosec 31° – sec 59° = cosec 31° – sec (90° – 31°) = cosec 31° – cosec 31° = 0

(ii) sin (50° + θ) — cos (40° – θ)
= sin (50° + θ) – cos (90° – (50° + θ)} = sin (50° + θ) – sin (50° + θ) = 0

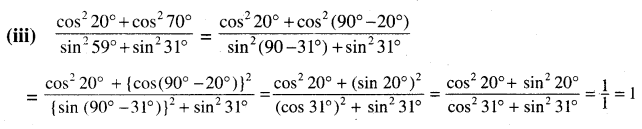
(iv) tan (55° – θ) — cot (35° + θ)
= tan (55° – θ) — cot {90° – (55° – θ)}
= tan (55° – θ) — tan (55° – θ) = 0 [(∵ cot (90° – θ) = tan θ]

(v) cos 1°. cos 2° ………… cos 180°
= cos 1° × cos 2° × …… cos 90° ×……. cos 180°
= cos 1° × cos 2° × …….0 ×…….cos 180° = 0
(‘.’ cos 90° = 0)

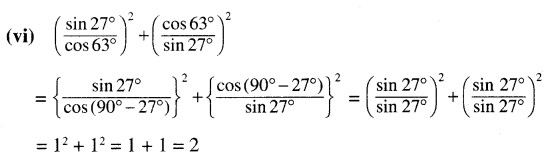
(vii) cot 112° × cot 158° = cot (90° + 22°) × cot (180° – 22°)
= (- tan 22°) × (- cot 22°) = 1
[‘.’ cot (90° + θ) = tan θ ଏବଂ cot (180° – θ) = – cot θ]

(viii) cos² (90° + α) + cos² (180° – α)
= {cos (90° + α)}² + {cos (180° – α)}²
= (- sin α)² + (- cos α)² = sin² a + cos² α = 1
= [‘.’ cos (90° + θ) = – sin θ)]

(ix) sec² (105° + α) – tan2 (75° – α)
= [sec {180° – (75° – α)}]² – tan² (75° – α)
= sec² (75° – α) – tan² (75° – α) = 1
[‘.’ sec (180° – θ) = – sec θ]

(x) sin² (110° +α) + cos² (70° – α)
= [sin {180° – (70° – α)}]² + cos² (70° – α)
= sin² (70° – α) + cos² (70° – α) = 1
[‘.’ sin (180° – θ) = sin θ]

Question 6.
ପାନ ନିଣ୍ଡଯ କର |

Solution:

Question 7.
ପ୍ରମାଣ କର|
(i) cos (90° – θ). cosec (180° – θ) = 1

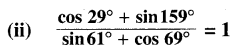
(iii) sin² 70° + cos2 110° = 1
(iv) sin² 110° + sin2 20° = 1
(v) sec² θ + cosec² (180° – θ) = sec² θ. cosec² θ
(vi) 2 sinθ. sec (90° + 0). sin 30°. tan 135° = 1
Solution:

Question 8.
(i) cos² 135° – 2 sin² 180° + 3cot² 150° – 4 tan² 120° = \(\frac { -5 }{ 2 }\)
(ii) tan 30°. tan 135°. tan 150°. tan 45° = \(\frac { 1 }{ 3 }\)

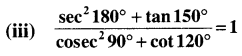
(iv) sin² 135° + cos² 120° – sin² 120° + tan² 150° = \(\frac { 1 }{ 3 }\)
Solution:

Question 9.
ମ୍ଭକ୍ୟ ନିର୍ପଣ କର:
(i) tan 10° × tan 20° × tan 30° ×…….× tan 70° × tan 80°
(ii) cot 12°. cot 38°. cot 52°. cot 60°. cot 78°
(iii) tan 5°. tan 15°. tan 45°. tan 75°. tan 85°
Solution:
ସମାଧାନ :
(i) tan 10° × tan 20° × tan 30° × tan 40° × tan 50° × tan 60° × tan 70° × tan 80° = tan 10° × tan 20° × tan 30° × tan 40° × tan (90 – 40°) × tan (90 – 30°) × tan (90° – 20°) × tan (90° – 10°)
= tan 10° × tan 20° × tan 30° × tan 40° × cot 40° × cot 30° × cot 20° × cot 10° =(tan 10° × cot 10°) × (tan 20° × cot 20°) × (tan 30° × cot 30°) × (tan 40° × cot 40°) = 1 × 1 × 1 × 1 = 1

(ii) cot 12°. cot 38°. cot 52°. cot 60°. cot 78°
= cot 12° × cot 38° × cot (90° – 38°) × \(\frac{1}{\sqrt{3}}\) × cot (90° – 12°)
= cot 12° × cot 38° × tan 38° × \(\frac{1}{\sqrt{3}}\) × tan 12°
= tan 12° × cot 12° × cot 38° × tan 38° × \(\frac{1}{\sqrt{3}}\)
= 1 × 1 × \(\frac{1}{\sqrt{3}}\) × \(\frac{1}{\sqrt{3}}\)

(iii) tan 5°. tan 15°. tan 45°. tan 75°. tan 85°
= tan 5° × tan 15° × 1 × tan (90° – 15°) × tan (90° – 5°)
= tan 5° × tan 15° × cot 15° × cot 5°
= tan 5° × 1 × cot 5° = (tan 5° × cot 5o) × 1 = 1

Question 10.
ପ୍ରମାଣ କର :

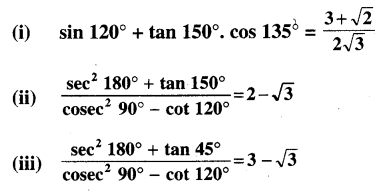
Solution:

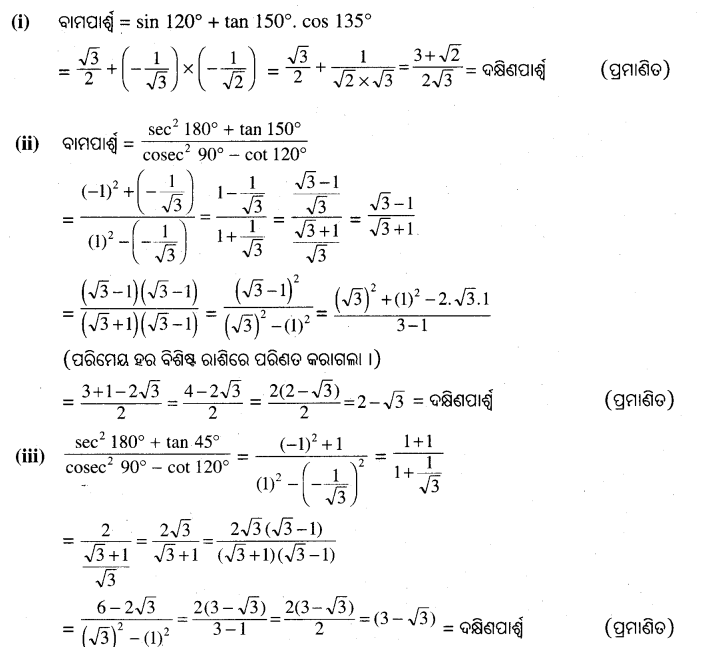
Question 11.
ସରକ କର:
(i) sin (180° – θ). cos (90° – θ) + sin (90° – θ). cos (180° – θ)

Solution:

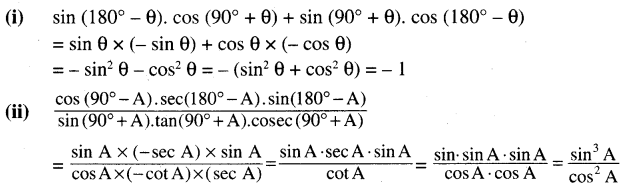
Question 12.
△ABC ରେ m∠B = 90° ହେଲେ ପ୍ରାମାଣ କାର ଯେ, sin²A + sin²C = 1|
Solution:
△ABC ରେ m∠B = 90° ⇒ m∠A + m∠C = 90°
⇒ A = (90° – C)
⇒ sin A = sin(90° – C) = cos C
∴ ଦାମପାଣ = sin² A + sin² C = (cos C)² + sin² C (∵ sin A = cos C)
= cos² C + sin² C = 1 = ଦଯିିଣପାଣ

Question 13.
△ABC ରେ ପ୍ରମାଣ କର ଯେ , cos (A + B) + sin C = sin (A + B) – cos C |
Solution:
△ABC ରେ A + B + C = 180° ⇒ A + B = 180° – C
L.H.S. = cos (A + B) + sin C = cos (180° – C) + sin C = -cos C + sin C
R.H.S. = sin (A + B) – cos C = sin (180° – C) + cos C = sin C + cos C
∴ L.H.S. = R.H.S.

Question 14.
A ଓ B ଦୁଇଟି ପରସ୍ପର ଅନୁପୂରକ କୋଣ ହେଲେ sin A. cos B + cos A. sin B ର ମାନ ନିର୍ଣ୍ଣୟ କର ।
Solution:
A + B + 90° ⇒ A = (90° – B)
∴ sin A × cos B + cos A × sin B
= sin (90° – B) × cos B + cos (90° – B) × sin B
= cos B × cos B + sin B × sin B = cos²B + sin²B = 1

Question 15.
ABCD ବୃତ୍ତାନ୍ତର୍ଲିଖ୍ ଚତୁର୍ଭୁଜ ହେଲେ tan A + tan C ର ମାନ ନିର୍ଣ୍ଣୟ କର ।
Solution:
ABCD ବୃତ୍ତାନ୍ତର୍ଲିଖ୍ ଚତୁର୍ଭୁଜହେ A + C = 180°
⇒ A = (180° – C)
∴ tan A + tan C = tan (180° – C) + tan C = – tan C + tan C = 0

Question 16.

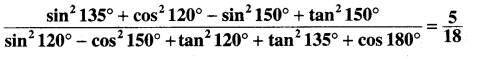
Solution:

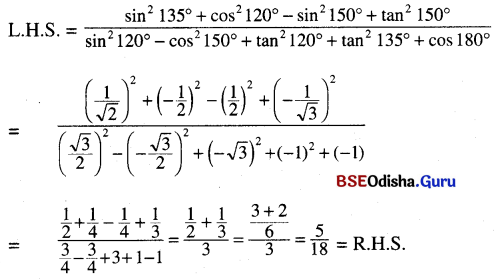
Question 17.

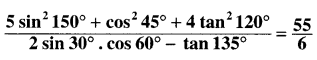
Solution: