BSE Odisha 6th Class Maths Solutions Chapter 10 ବୀଜଗଣିତ ସହିତ ପରିଚିତ InText Questions

Odisha State Board BSE Odisha 6th Class Maths Solutions Chapter 10 ବୀଜଗଣିତ ସହିତ ପରିଚିତ InText Questions Textbook Exercise Questions and Answers.

BSE Odisha Class 6 Maths Solutions Chapter 10 ବୀଜଗଣିତ ସହିତ ପରିଚିତ InText Questions

ନିମ୍ନ ପ୍ରଶ୍ନମାନଙ୍କର ଉତ୍ତର ଲେଖ:
(କ) ଗୋଟିଏ ବର୍ଗଚିତ୍ରର ଗୋଟିଏ ବାହୁର ଦୈର୍ଘ୍ୟ 5 ସେ.ମି. ହେଲେ, P = 4 × a ସୂତ୍ର ବ୍ୟବହାର କରି ଉକ୍ତ ବର୍ଗଚିତ୍ରର ପରିସୀମା ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ଏଠାରେ a = 5 ସେ.ମି. 
p = 4 × a = (4 × 5) ସେ.ମି. =20 ସେ.ମି. ।

(ଖ) ଜଣେ ସାଇକେଲ ସ୍ଖଳକ ମିନିଟ୍ ପ୍ରତି 220 ମିଟର ସାଇକେଲ ଚଳାଇ ପାରନ୍ତି । ତେବେ 8 ମିନିଟ୍ ସମୟରେ କେତେ ଦୂରତା ଅତିକ୍ରମ କରିପାରିବେ ।
ସମାଧାନ:
ଏଠାରେ s = 220 ମିଟର ।
d = s × t = 220 × 8 = 1760 ମିଟର ।

ନିଜେ କରି ଦେଖ:
ଆକୃତି ବିଶିଷ୍ଟ ଗୋଟିଏ ଚିତ୍ରପାଇଁ ଆବଶ୍ୟକ ଦିଆସିଲି କାଠି ସଂଖ୍ୟାକୁ ବିଚାରକୁ ନେଇ ଏକ ସୂତ୍ର ଗଠନ କର, ଯାହାଦ୍ବାରା ଯେକୌଣସି ସଂଖ୍ୟକ ଚିତ୍ର ସୃଷ୍ଟିପାଇଁ କେତେ ସଂଖ୍ୟକ କାଠି ଦରକାର ସ୍ଥିର କରିହେବ । (ଚିତ୍ର ସଂଖ୍ୟା ଲାଗି ñ ଓ ଦିଆସିଲି କାଠି ସଂଖ୍ୟା ଆଦି s ସଂକେତ ବ୍ୟବହାର କର ।) 
ସମାଧାନ:
s = 3n

ଆକୃତି ବିଶିଷ୍ଟ ଗୋଟିଏ ଚିତ୍ର ଗଠନପାଇଁ ଆବଶ୍ୟକ ଦିଆସିଲି କାଠି ସଂଖ୍ୟାକୁ ବିଚାରକୁ ନେଇ ଏକ ସୂତ୍ର ଗଠନ କର, ଯାହାକୁ ବ୍ୟବହାର କରି ଯେକୌଣସି ସଂଖ୍ୟକ ଚିତ୍ର ଗଠନ ପାଇଁ ଆବଶ୍ୟକ ଦିଆସିଲି କାଠି ସଂଖ୍ୟା ନିର୍ଣ୍ଣୟ କରିହେବ ।
ସମାଧାନ:
s = 3n

x + 10 ଏକ ପରିପ୍ରକାଶ ଯେଉଁଥରେ ‘x’ ଏକ ଚଳରାଶି । ‘x + 10’ କୁ କିପରି ପଢ଼ାଯିବ ?
ସମାଧାନ:
x ଠାରୁ 10 ଅଧିକ ।

ଉତ୍ତର ଲେଖ:
କୌଣସି ଏକ ବିଦ୍ୟାଳୟରେ ଛାତ୍ରୀ ସଂଖ୍ୟା, ଛାତ୍ର ସଂଖ୍ୟାଠାରୁ 35 ଅଧିକ । 
ଛାତ୍ର ସଂଖ୍ୟା ଯଦି ‘x’ (ଚଳରାଶି) ହୁଏ । ତେବେ ବିଦ୍ୟାଳୟରେ ଛାତ୍ରୀସଂଖ୍ୟା କେତେ ହେବ ।
(i) ଛାତ୍ରୀ ସଂଖ୍ୟା ଜାଣିବାପାଇଁ ପରିପ୍ରକାଶକୁ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ଛାତ୍ରୀ ସଂଖ୍ୟା = x + 35

(ii) ଯଦି ଛାତ୍ରୀ ସଂଖ୍ୟା 75 ହୋଇଥାଏ । ତେବେ ପରିପ୍ରକାଶକୁ ବ୍ୟବହାର କରି ଛାତ୍ରୀ ସଂଖ୍ୟା ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ଛାତ୍ରୀ ସଂଖ୍ୟା = 75 + 35 = 110 ଜଣ ।

ନିଜେ କରି ଦେଖ:
ଗୋଟିଏ ସମବାହୁ ତ୍ରିଭୁଜର ବାହୁର ଦୈର୍ଘ୍ୟ l ଚଳରାଶି ରୂପନେଇ ଏହାର ପରିସୀମାକୁ l ମାଧ୍ୟମରେ ପ୍ରକାଶ କର ।

ସମାଧାନ:
3l

ଗୋଟିଏ ସୁଷମ ଷଡ଼ଭୁଜର ବାହୁର ଦୈର୍ଘ୍ୟକୁ l ଚଳରାଶି ରୂପେ ନେଇ ଏହାର ପରିସୀମାକୁ l ମାଧ୍ୟମରେ ପ୍ରକାଶ କର ।

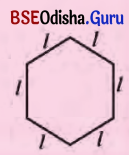
ସମାଧାନ:
6l

ନିମ୍ନଲିଖ୍ତ ଉକ୍ତିଗୁଡ଼ିକୁ କିପରି ଲେଖାଯିବ ?
a ଓ 4 ର ଯୋଗଫଳ 
ସମାଧାନ:
a + 4

5 ଅପେକ୍ଷା x ଅଧିକ
ସମାଧାନ:
5 + x

x ଠାରୁ y ଅଧିକ
ସମାଧାନ:
x + y

(x + y) ଠାରୁ 6 ଅଧିକ
ସମାଧାନ:
(x + y) + 6

ଆଧାର a ଓ ଘାତାଙ୍କ 8 ନେଇ ଘାତାନ୍ବିତ ବୀଜଟି କେତେ ?
ସମାଧାନ:
a⁸

x³z² ଓ z²x³ ସମାନ କି ? କାରଣ ସହ ଲେଖ ।
ସମାଧାନ:
x³z² = z²x³ କାରଣ
x³z² = x × x × x × z × z
z²x³ = z × z × x × x × x
ଉଭୟରେ x, 3 ଥର ଓ z, 2 ଥର ଅଛି ।

କହିଲ ଦେଖ୍: 
x⁵ ଗୋଟିଏ ଘାତାନ୍ବିତ ରାଶି ହେଲେ ଏହାର ଆଧାର କେତେ ଓ ଘାତାଙ୍କ କେତେ ?
ସମାଧାନ:
ଏହାର ଆଧାର x ଓ ଘାତାଙ୍କ 5 ।

ତୁମେ ଏକପଦ ବିଶିଷ୍ଟ ରାଶି, ଦୁଇପଦ ବିଶିଷ୍ଟ ରାଶି ଓ ବହୁପଦ ବିଶିଷ୍ଟ ରାଶିର ଦୁଇଟି ଲେଖାଏଁ ଉଦାହରଣ ଦିଅ ।
ସମାଧାନ:

ଏକପଦ ବିଶିଷ୍ଟ ରାଶି	ଦୁଇପଦ ବିଶିଷ୍ଟ ରାଶି	ବହୁପଦ ବିଶିଷ୍ଟ ରାଶି
x	5x + y	3m + z – n
4y	4z + p	4a + 3b – 7

3x – y + 5b ରେ ଥିବା ଭିନ୍ନ ଭିନ୍ନ ପଦମାନଙ୍କ ସହଗ ଲେଖ ।
ସମାଧାନ:
3x – y + 5b ରେ ଥିବା 3x ରେ x ର ସହଗ 3,
y ରେ ସହଗ 1 ଏବଂ 5 ରେ b ର ସହଗ 5 ।