Odisha State Board BSE Odisha 7th Class Maths Solutions Chapter 12 ଜ୍ୟାମିତିକ ଅଙ୍କନ Ex 12.2 Textbook Exercise Questions and Answers.
BSE Odisha Class 7 Maths Solutions Chapter 12 ଜ୍ୟାମିତିକ ଅଙ୍କନ Ex 12.2
Question 1.
ଗୋଟିଏ ଲେଖାଏ ସମକୋଣୀ, ସୂକ୍ଷ୍ମକୋଣୀ ଓ ସ୍ଥୁଳକୋଣୀ ତ୍ରିଭୁଜ ଅଙ୍କନ କର । ପ୍ରତ୍ୟେକ ତ୍ରିଭୁଜରେ ତିନୋଟି ଲେଖାଏଁ ମଧ୍ୟମା ଅଙ୍କନ କର ।
ସମାଧାନ:
ସମକୋଣୀ ତ୍ରିଭୁଜରେ ମଧ୍ୟମା ଅଙ୍କନ:

(i) ABC ନାମକ ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜ ଅଙ୍କନ କର ।
(ii) Δ ABC ର B͞C କୁ ସମଦ୍ବିଖଣ୍ଡ କରିବା ପାଇଁ B ଉପରେ କମ୍ପାସର କଣ୍ଟାମୁନ ରଖ୍ BCର ମାପର ଅର୍ଦ୍ଧେକରୁ ଅଧିକ ଅଧ୍ଵବ୍ୟାସାର୍ଦ୍ଧ ନେଇ ଏକ ଚାପ ଅଙ୍କନ କର, ଯାହା BC ର ଉଭୟ ପାର୍ଶ୍ଵରୁ ବିସ୍ତୃତ ହୋଇ ରହିବ ।
(iii) ପୂର୍ବ ସୋପାନରେ କମ୍ପାସରେ ନେଇଥିବା ଚାପକୁ ପରିବର୍ତ୍ତନ ନକରି କମ୍ପାସର କଣ୍ଟାମୁନକୁ C ଉପରେ ରଖ୍ ଆଉ ଏକ ଚାପ ଅଙ୍କନ କର, ଯାହା ପୂର୍ବରୁ ଅଙ୍କାଯାଇଥିବା ଚାପକୁ X ଓ Y ବିନ୍ଦୁରେ ଛେଦ କରିବ ।
(iv) X ଓ Y ର ସଂଯୋଜକ ରେଖା ଅଙ୍କନ କର । \(\overleftrightarrow{\mathrm{XY}}\), ହେଉଛି BC ର ସମଦ୍ୱିଖଣ୍ଡକ ଲମ୍ବ । \(\overleftrightarrow{\mathrm{XY}}\), BC କୁ D ବିନ୍ଦୁରେ ଛେଦକରୁ ।
(v) D ହେଉଛି BC ର ମଧ୍ୟବିନ୍ଦୁ । BC ର ବିପରୀତ ଶୀର୍ଷବିନ୍ଦୁ A ସହିତ D କୁ ଯୋଗକର । A͞D ହେଉଛି ABC ତ୍ରିଭୁଜର ଗୋଟିଏ ମଧ୍ୟମା ।
(vi) ସେହିପରି B ବିନ୍ଦୁରେ AC ପ୍ରତି B͞E ମଧ୍ୟମା ଓ C ବିନ୍ଦୁରେ AB ପ୍ରତି CF ମଧ୍ୟମା ଅଙ୍କନ କର ।
ସୂକ୍ଷ୍ମକୋଣୀ ତ୍ରିଭୁଜରେ ମଧ୍ୟମା ଅଙ୍କନ:
ସମକୋଣୀ ତ୍ରିଭୁଜରେ ମଧ୍ୟମା ଅଙ୍କନକୁ ଅନୁସରଣ କରି Δ PQR ସୂକ୍ଷ୍ମକୋଣୀ ତ୍ରିଭୁଜର ମଧ୍ୟମା ଅଙ୍କନ କର ।
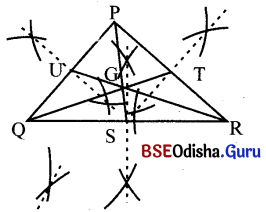
ସ୍ଥୂଳକୋଣୀ ତ୍ରିଭୁଜରେ ମଧ୍ୟମା ଅଙ୍କନ:
ସମକୋଣୀ ତ୍ରିଭୁଜରେ ମଧ୍ୟମା ଅଙ୍କନକୁ ଅନୁସରଣ କରି XYZ ସ୍ଥୂଳକୋଣୀ ତ୍ରିଭୁଜର ମଧ୍ୟମା ଅଙ୍କନ କର ।
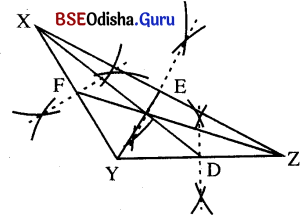
![]()
Question 2.
Δ POR ନିଅ ।
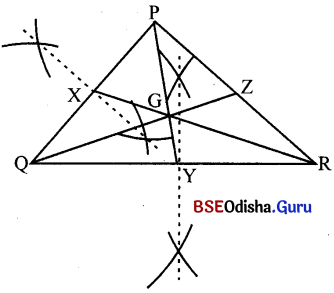
(କ) ଏହାର P͞Q ର ମଧ୍ୟବିନ୍ଦୁ X ନିଅ । R͞X ମଧ୍ୟମା ଅଙ୍କନ କର ।
ସମାଧାନ:
ପୂର୍ବ ଉତ୍ତରକୁ ଅନୁସରଣ କରି R ବିନ୍ଦୁରେ P͞Q ପ୍ରତି R͞X ମଧ୍ୟମା ନିର୍ଣ୍ଣୟ କର ।
(ଖ) Q͞R ର ମଧ୍ୟବିନ୍ଦୁ Y ନିଅ । P͞Y ମଧ୍ୟମା ଅଙ୍କନ କର ।
ସମାଧାନ:
ସେହିପରି P ବିନ୍ଦୁରେ QR ପ୍ରତି P͞Y ମଧ୍ୟମା ନିର୍ଣ୍ଣୟ କର ।
(ଗ) ଏବେ R͞P ର ମଧ୍ୟବିନ୍ଦୁ ନିର୍ୟୟନ କରି ତୁମେ Q͞Z ମଧ୍ୟମା ଅଙ୍କନ କରି ପାରିବ କି ? କିପରି ?
ସମାଧାନ:
ଏବେ R͞P ର ମଧ୍ୟବିନ୍ଦୁ ନିଶ୍ଚୟ ନ କରି ଆମେ Q͞Z ମଧ୍ୟମା ପାଇପାରିବା ।
(i) P͞Y ଓ R͞X ର ଛେଦବିନ୍ଦୁର ନାମ G ଦିଅ ।
(ii) \(\overrightarrow{\mathrm{QG}}\) ଅଙ୍କନ କର ।
(iii) \(\overrightarrow{\mathrm{QG}}\) ଓ P͞R ର ଛେଦବିନ୍ଦୁର ନାମ Z ଦିଅ । ଓ QZ ଆବଶ୍ୟକ ମଧ୍ୟମା ।
