Odisha State Board BSE Odisha 7th Class Maths Solutions Chapter 12 ଜ୍ୟାମିତିକ ଅଙ୍କନ Ex 12.4 Textbook Exercise Questions and Answers.
BSE Odisha Class 7 Maths Solutions Chapter 12 ଜ୍ୟାମିତିକ ଅଙ୍କନ Ex 12.4
Question 1.
A XYZ ଅଙ୍କନ କର ଯାହାର XY = 4.8 ସେ.ମି, YZ=5.3 ସେ.ମି. ZX=5.6 ସେ. ମି । ଏହାର ଶୀର୍ଷବିନ୍ଦୁ X ରୁ \(\overline{\mathbf{Y Z}}\) ପ୍ରତି ଲମ୍ବ ଅଙ୍କନ କରି ତା’ର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ଅଙ୍କନ ପ୍ରଣାଳୀ :
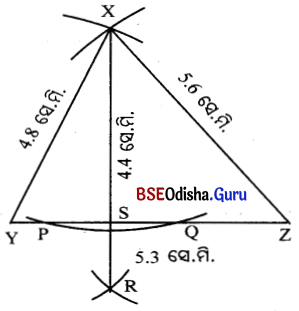
(i) 5.3 ସେ.ମି. ଦୈର୍ଘ୍ୟର YZ ରେଖାଖଣ୍ଡ ଅଙ୍କନ କର ।
(ii) Y କୁ କେନ୍ଦ୍ରକରି 4.8 ସେ.ମି. ବ୍ୟାସାର୍କ ବିଶିଷ୍ଟ ଏକ ଚାପ ଅଙ୍କନ କର ।
(iii) କୁ କେନ୍ଦ୍ରକରି 5.6 ସେ.ମି. ବ୍ୟାସାର୍ଦ୍ଧ ବିଶିଷ୍ଟ ଆଉ ଏକ ଚାପ ଅଙ୍କନ କର, ଯେପରି ତାହା ପୂର୍ବରୁ ଅଙ୍କା ହୋଇଥିବା ଚାପକୁ ଛେଦ କରିବ । ଛେଦବିଦୁର ନାମ X ହେଉ ।
(iv) \(\overline{\mathbf{X Y}}\) ଓ \(\overline{\mathbf{Z X}}\) ଅଙ୍କନ କର ΔXYZ ସଂପୁର୍ଣ୍ୱ କର
(v) X ବିନ୍ଦୁକୁ କେନ୍ଦ୍ର ଓ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ବ୍ୟାସାର୍ଦ୍ଧ ନେଇ ଏପରି ଏକ ଚାପ ଅଙ୍କନ କର ଯେପରି, ଚାପଟି \(\overline{\mathbf{Y Z}}\) କୁ ଦୁଇଟି ବିନ୍ଦୁରେ ଛେଦକରିବ । ବିନ୍ଦୁ ଦ୍ବୟର ନାମ P ଓ Q ହେଉ ।
(vi) P ଓ Q କୁ ଯଥାକ୍ରମେ କେନ୍ଦ୍ରରୂପେ ନେଇ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ବ୍ୟାସାର୍ଦ୍ଧ ବିଶିଷ୍ଟ ଦୁଇଟି ଚାପ ଅଙ୍କନ କର ଯେପରି ଚାପଦ୍ବୟ \(\overline{\mathbf{Y Z}}\) ର ଯେଉଁପାର୍ଶ୍ବରେ X ଅଛି ତା’ର ବିପରୀତ ପାର୍ଶ୍ବରେ ପରସ୍ପରକୁ ଛେଦକରିବେ । ଛେଦବିନ୍ଦୁର ନାମ R ଦିଅ ।
(vii) \(\overline{\mathbf{X R}}\) ଅଙ୍କନ କର । \(\overleftrightarrow{\mathrm{XR}}\) ଓ \(\overleftrightarrow{\mathrm{YZ}}\) ପରସ୍ପରକୁ S ବିନ୍ଦୁରେ ଛେଦ କରିବେ । \(\overleftrightarrow{\mathrm{XS}}\) ର ଦୈର୍ଘ୍ୟ ମାପିଲେ XS = 4.4 ସେ.ମି. ହେଉ ।
Question 2.
(କ) ଗୋଟିଏ ସମବାହୁ ତ୍ରିଭୁଜ ଅଙ୍କନ କର, ଯାହାର ପ୍ରତ୍ୟେକ ବାହୁ 5.5 ସେ.ମି। ଏହାର ପ୍ରତ୍ୟେକ କୋଣର ପରିମାଣ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ଅଙ୍କନ ପ୍ରଣାଳୀ :
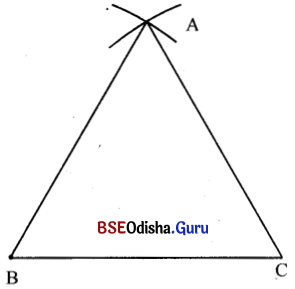
(i) \(\overline{\mathrm{BC}}\) ଅଙ୍କନ କର ଯାହାର ଦୈର୍ଘ୍ୟ 5.5 ସେ.ମି. ।
(ii) B କୁ କେନ୍ଦ୍ରକରି 5.5 ସେ.ମି. ବ୍ୟାସାର୍ଦ୍ର ବିଶିଷ୍ଟ ଏକ ଚାପ ଅଙ୍କନ କର ।
(iii) C କୁ କେନ୍ଦ୍ରକରି 5.5 ସେ.ମି. ବ୍ୟାସାର୍ଷ ବିଶିଷ୍ଟ ଏକ ଚାପ ଅଙ୍କନ କର, ଯାହା ଅଙ୍କିତ ଚାପକୁ ଏକ ବିନ୍ଦୁରେ ଛେଦକରିବ । ଛେଦ ବିନ୍ଦୁଟିର ନାମ A ହେଉ ।
(iv) AB ଓ \(\overline{\mathrm{AC}}\) ଅଙ୍କନ କରି Δ ABC ସଂପୂର୍ଣ୍ଣ କର । ∠A, ∠B, ∠C ର ପରିମାଣ ମାପିଲେ m∠A = 60°, m∠B = 60° ଓ m∠C = 60° ହେଉ
(ଖ) 6 ସେ.ମି. ବାହୁ ବିଶିଷ୍ଟ ସମବାହୁ ତ୍ରିଭୁଜ ଅଙ୍କନ କରି ଏହାର ପ୍ରତ୍ୟେକ କୋଣର ପରିମାଣ ମାପି ନିଷ୍କ୍ରିୟ କର ।
ସମାଧାନ:
ଅଙ୍କନ ପ୍ରଣାଳୀ :
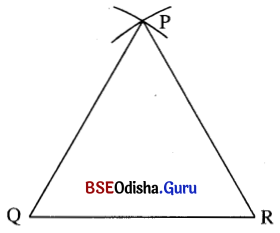
2 (କ) ଅଙ୍କନ ପ୍ରଣାଳୀକୁ ଅନୁସରଣ କରି POR ସମବାହୁ ତ୍ରିଭୁଜ ଅଙ୍କନ କର ।
Δ PQR ର m∠P = m∠Q= m∠R = 60° ହେଉ ।
![]()
Question 3.
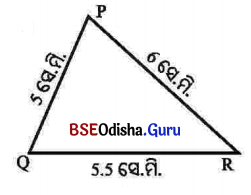
Δ POR ର PQ=5 ସେ.ମି. QR=5.5 ସେ.ମି. RP= 6 ସେ.ମି. ।
(କ) ଚିତ୍ର-କ ନକ୍ସାକୁ ବ୍ୟବହାର କରି POR ତ୍ରିଭୁଜ ଅଙ୍କନ କର ।
ସମାଧାନ:
ଅଙ୍କନ ପ୍ରଣାଳୀ :
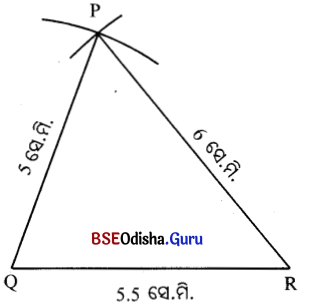
(i) 5.5 ସେ.ମି. ଦୈର୍ଘ୍ୟର QR ରେଖାଖଣ୍ଡ ଅଙ୍କନ କର ।
(ii) Qକୁ ବ୍ୟାସାର୍ଦ୍ଧ ନେଇ 5 ସେ.ମି. (PQ) ବ୍ୟାସାର୍ଦ୍ଧ ବିଶିଷ୍ଟ ଏକ ଚାପ ଅଙ୍କନ କର ।
(iii) Rକୁ କେନ୍ଦ୍ର କରି 6 ସେ.ମି. (PR) ବ୍ୟାସାର୍ଷ ବିଶିଷ୍ଟ ଚାପ ଅଙ୍କନ କର, ଯେପରି ତାହା ପୂର୍ବରୁ ଅଙ୍କା ହୋଇଥିବା ଚାପକୁ ଛେଦ କରିବ । ଛେଦବିନ୍ଦୁର ନାମ P ହେଉ ।
(iv) \(\overline{\mathrm{PQ}}\) ଓ PR ଅଙ୍କନ କରି Δ POR ସଂପୂର୍ଣ୍ଣ କର ।
(ଖ) ପାର୍ଶ୍ଵସ୍ଥ ନକ୍ସା ଅନୁଯାୟୀ Δ POR ଅଙ୍କନ କର । ଉଭୟ ଅଙ୍କନରେ ସମାନ ଆକାରର ତ୍ରିଭୁଜ ମିଳିଲା କି? କାରଣ କ’ଣ ଲେଖ ।
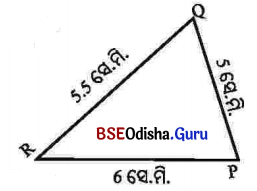
ସମାଧାନ:
ଅଙ୍କନ ପ୍ରଣାଳୀ :
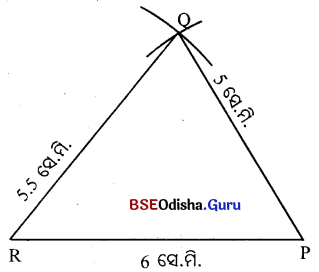
3(କ)ର ‘ଅଙ୍କନ ପ୍ରଣାଳୀ’ ଅନୁସରଣ କରି A QPR ଅଙ୍କନ କର ।
ଉଭୟ ଅଙ୍କନରେ ସମାନ ଆକାରର ତ୍ରିଭୁଜ ମିଳିଲା । କାରଣ ତ୍ରିଭୁଜ ଦ୍ଵୟ ବା-ବା-ବା ସର୍ବସମତା ଯୋଗୁ ସର୍ବସମ ଅଟେ ।
Question 4.
ଉମେଶ BC = 5 ସେ.ମି., CA = 3 ସେ.ମି. ଓ AB = 8.5 ସେ.ମି. ନେଇ A ABC ଅଙ୍କନ କରିବାକୁ ଚେଷ୍ଟା କଲେ । ତୁମେ ଏହି ମାପକୁ ନେଇ A ABC ଅଙ୍କନ କରିବାକୁ ଚେଷ୍ଟା କର । ତ୍ରିଭୁଜ ଅଙ୍କନ କରିବା ସମ୍ଭବ ହେଲା କି ? ତୁମ ଉତ୍ତର ସପକ୍ଷରେ କାରଣ ବୁଝାଇ ଲେଖ ।
ସମାଧାନ :
ଏଠାରେ BC + CA = 5 ସେ.ମି. + 3 ସେ.ମି. = 8 ସେ.ମି. BC + CA < AB
∴ ତ୍ରିଭୁଜ ଅଙ୍କନ ସମ୍ଭବ ନୁହେଁ । କାରଣ BC + CA < AB
