Odisha State Board BSE Odisha 7th Class Maths Solutions Chapter 3 ମୌଳିକ ଜ୍ୟାମିତିକ ଚିତ୍ର Ex 3.2 Textbook Exercise Questions and Answers.
BSE Odisha Class 7 Maths Solutions Chapter 3 ମୌଳିକ ଜ୍ୟାମିତିକ ଚିତ୍ର Ex 3.2
Question 1.
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ \(\overleftrightarrow{A B}\) ଓ \(\overleftrightarrow{C D}\) ପରସ୍ପରକୁ O ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି ।
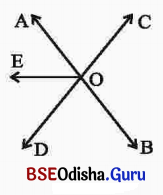
(କ) ∠AOC କୋଣ ସନ୍ନିହିତ ହୋଇଥିବା ଗୋଟିଏ କୋଣର ନାମ ଲେଖ। ଏଭଳି ଅନ୍ୟ କୌଣସି କୋଣ ଅଛି କି? ଯଦି ଅଛି, ତା’ର ନାମ ଲେଖ ।
ସମାଧାନ:
∠AOE, ∠BOC ଏବଂ ∠AOD
(ଖ) ∠AOC ଏବଂ ∠AOB କୋଣ ଦ୍ଵୟ ପରସ୍ପର ସନ୍ନିହିତ କୋଣ ଅଟନ୍ତି କି?
ସମାଧାନ:
ନୁହେଁ
(ଗ) ∠COB ସହ ଅନ୍ୟ ଯେଉଁ କୋଣ ସରଳ ଯୋଡ଼ି ଗଠନ କରେ ତା’ର ନାମ ଲେଖ ।
ସମାଧାନ:
∠BOD ଏବଂ ∠AOC
(ଘ) ∠AOD ସହ ପରସ୍ପର ପରିପୂରକ ହୋଇଥବା ଗୋଟିଏ କୋଣର ନାମ ଲେଖ ।
∠AOD ସହ ପରସ୍ପର ପରିପୂରକ ହୋଇଥବା ଅନ୍ୟ କୋଣ ଅଛି କି? ଯଦି ଥାଏ, ତେବେ ତା’ର ନାମ ଲେଖ ।
ସମାଧାନ:
∠BOD, ∠AOC
(ଙ) ∠AOC କୋଣଟି ଯେଉଁ କୋଣର ପ୍ରତୀପ କୋଣ ତା’ର ନାମ ଲେଖ ।
ସମାଧାନ:
∠BOD
![]()
(ଚ) ଚିତ୍ରରେ ∠AOD କୋଣର ପ୍ରତୀପ କୋଣ ଥିଲେ, ତା’ର ନାମ ଲେଖ।
ସମାଧାନ:
∠BOC
(ଛ) ଚିତ୍ରରେ ∠BOD ର ପ୍ରତୀପ କୋଣ ଥୁଲେ, ତା’ର ନାମ ଲେଖ ।
ସମାଧାନ:
∠AOC
Question 2.
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ \(\overleftrightarrow{A C}\) ଓ \(\overleftrightarrow{B D}\) ରେଖାଦ୍ୱୟ ପରସ୍ପରକୁ O ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି ।
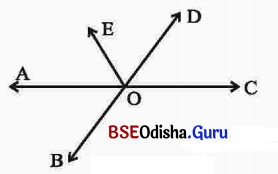
(କ) ଦୁଇ ଯୋଡ଼ା ପରସ୍ପର ପ୍ରତୀପ କୋଣର ନାମ ଲେଖ।
ସମାଧାନ:
∠AOB ଓ ∠COD ପରସ୍ପର ପ୍ରତୀପ ଏବଂ ∠AOD ଓ ∠BOC ପରସ୍ପର ପ୍ରତୀପ ।
(ଖ) ଚାରିଯୋଡ଼ା ସରଳ ଯୋଡ଼ି କୋଣର ନାମ ଲେଖ ।
ସମାଧାନ:
∠DOC ଓ ∠DOA, ∠DOC ଓ ∠BOC, ∠BOC ଓ ∠AOB, ∠AOB ଓ ∠AOD ସରଳ ଯୋଡ଼ି କୋଣ ।
(ଗ) m∠AOE = 75°, m∠EOD = 40° ହେଲେ
m∠AOB, m∠BOC, m∠COD ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
m∠AOE = 75°, m∠EOD = 40°
∴ m∠AOD = m∠AOE + m∠EOD = 75° + 40° = 115°
m∠AOB = 180° – m∠AOD = 180° – 115° = 65° (ସରଳ ଯୋଡ଼ି କୋଣ)
m∠BOC = m∠AOD = 115° (ପ୍ରତୀପ କୋଣ)
m∠COD = m∠AOB = 65° (ପ୍ରତୀପ କୋଣ)
Question 3.
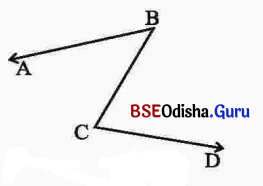
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ର 3.17 ରେ ∠ABC ଓ ∠BCD ପରସ୍ପର ସନ୍ନିହିତ କୋଣ ଅଟନ୍ତି କି ? ତୁମ ଉତ୍ତର ଲାଗି କାରଣ ଦର୍ଶାଅ ।
ସମାଧାନ:
∠ABC ଓ ∠BCD ପରସ୍ପର ସନ୍ନିହିତ କୋଣ ନୁହଁନ୍ତି
କାରଣ ∠ABC ଓ ∠BCD କୋଣଦ୍ୱୟର କୌଣସି ସାଧାରଣ ଶୀର୍ଷବିନ୍ଦୁ ନାହିଁ ।
Question 4.
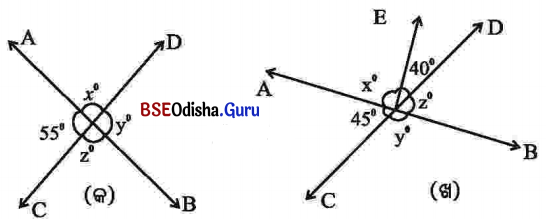
ଉପରିସ୍ଥ ଚିତ୍ର (କ) ଏବଂ ଚିତ୍ର (ଖ) ରେ \(\overleftrightarrow{A B}\) ଓ \(\overleftrightarrow{C D}\) ପରସ୍ପରକୁ ଛେଦ କରୁଛନ୍ତି । ଚିତ୍ର (କ) ରେ ଗୋଟିଏ କୋଣର ପରିମାଣ ଓ ଚିତ୍ର (ଖ) ରେ ଦୁଇଟି କୋଣର ପରିମାଣ ଲେଖାଯାଇଛି । ପ୍ରତ୍ୟେକ ଚିତ୍ରରେ ଥିବା କୋଣ ପରିମାଣ,x, y ଓ z ର ମୂଲ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
(କ) x = 180° – 55° = 125° (ସରଳଯୋଡ଼ି କୋଣ)
y° = 55° (ପ୍ରତୀପ କୋଣ), z° = x° = 125° (ପ୍ରତୀପ କୋଣ)
(ଖ) x = 180° – 45° – 40° = 95° (ସରଳଯୋଡ଼ି କୋଣ)
y° = x° + 40° = 95° + 40° = 135° (ପ୍ରତୀପ କୋଣ), z° = 45° (ପ୍ରତୀପ କୋଣ)
![]()
Question 5.
ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(କ) ଦୁଇଟି କୋଣର ପରିମାଣର ସମଷ୍ଟି………….. ହେଲେ, କୋଣ ଦୁଇଟି ପରସ୍ପର ଅନୁପୂରକ ।
ସମାଧାନ:
90°
(ଖ) ଦୁଇଟି ପରସ୍ପର ପରିପୂରକ କୋଣ ପରିମାଣର ସମଷ୍ଟି……. ।
ସମାଧାନ:
180°
(ଗ) ଗୋଟିଏ ସରଳ ଯୋଡ଼ି ଗଠନ କରୁଥିବା କୋଣ ଦୁଇଟି ପରସ୍କାର…… ।
ସମାଧାନ:
ପରିପୂରକ
(ଘ) ଦୁଇଟି ରେଖା ପରସ୍ପରକୁ ଛେଦ କଲେ ପ୍ରତୀପ କୋଣ ଦ୍ଵୟର ପରିମାଣ……. |
ସମାଧାନ:
ସମାନ
(ଙ) ଦୁଇଟି ପରସ୍ପର ଛେଦୀ ରେଖା ଦ୍ଵାରା ଗଠିତ ଗୋଟିଏ ଯୋଡ଼ା ପ୍ରତୀପ କୋଣ ପ୍ରତ୍ୟେକ ସୂକ୍ଷ୍ମ କୋଣ ହେଲେ, ଅନ୍ୟ ଯୋଡ଼ା ପ୍ରତୀପ କୋଣ ମଧ୍ୟରୁ ପ୍ରତ୍ୟେକ……… ।
ସମାଧାନ:
ସ୍ଥୂଳକୋଣ
Question 6.
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ \(\overleftrightarrow{A B}\) ଓ \(\overleftrightarrow{C D}\) ପରସ୍ପରକୁ O ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି ।
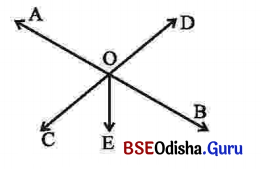
(କ) ଯେଉଁ ପ୍ରତୀପ କୋଣଦ୍ୱୟ ସ୍ଥୁଳକୋଣ ସେ ଦୁଇଟିର ନାମ ଲେଖ ।
ସମାଧାନ:
∠AOD ଓ ∠BOC ପ୍ରତୀପ କୋଣଦ୍ବୟ ସ୍ଥୂଳକୋଣ ।
(ଖ) ଯେଉଁ ସନ୍ନିହିତ କୋଣମାନ ସରଳ ଯୋଡ଼ି ନୁହନ୍ତି ସେଗୁଡ଼ିକର ନାମ ଲେଖ । ଏଭଳି କେତେ ଯୋଡ଼ା ସନ୍ନିହିତ କୋଣ ଅଛନ୍ତି?
ସମାଧାନ:
∠EOC ଓ ∠BOE, ∠AOC ଓ ∠COE, ∠BOE ଓ ∠BOD, ∠DOE ଓ ∠AOE ସନ୍ନିହିତ କୋଣମାନ ସରଳଯୋଡ଼ି ନୁହନ୍ତି ।
ଏଭଳି 4 ଯୋଡ଼ା ସନ୍ନିହିତ କୋଣ ଅଛନ୍ତି ।
Question 7.
ନିମ୍ନରେ ଡିଗ୍ରୀ-ପରିମାଣଗୁଡ଼ିକ ମଧ୍ୟରୁ କେଉଁ ଯୋଡ଼ିଗୁଡିକ ଅନୁପୂରକ କୋଣର ପରିମାଣ ଓ କେଉଁ ଯୋଡ଼ିଗୁଡ଼ିକ ପରିପୂରକ କୋଣର ପରିମାଣକୁ ସୁଖନ୍ତି ଚିହ୍ନଟ କର ।
(କ) 55°, 125°
(ଖ) 43°, 47°
(ଗ) 112°, 68°
(ଘ) 62°, 28°
(ଙ) 40°, 140°
(ଚ) 70°, 20°
(ଛ) 15°, 165°
(ଜ)90°, 90°
ସମାଧାନ:
| ଅନୁପୂରକ କୋଣ ଯୋଡ଼ି | ପରିପୂରକ କୋଣ ଯୋଡ଼ି |
| (ଖ) 43°, 47° | (କ) 55°, 125° |
| (ଘ) 62°, 28° | (ଗ) 112°, 68° |
| (ଚ) 70°, 20° | (ଙ) 40°, 140° |
| (ଛ) 15°, 165° | |
| (ଜ)90°, 90° |
Question 8.
(କ) ଯେଉଁ କୋଣଟି ନିଜର ପରିପୂରକ, ସେ କୋଣଟିର ପରିମାଣ କେତେ?
ସମାଧାନ:
90°
(ଖ) ଯେଉଁ କୋଣଟି ନିଜର ଅନୁପୂରକ, ସେ କୋଣଟିର ପରିମାଣ କେତେ?
ସମାଧାନ:
45°
![]()
Question 9.
ଦୁଇଟି ପରସ୍ପର ପରିପୂରକ କୋଣ ମଧ୍ୟରୁ ଗୋଟିଏ କୋଣର ପରିମାଣକୁ 10° ଅଧିକ କରି ଦିଆଗଲା । ଅନ୍ୟ କୋଣର ପରିମାଣରେ କି ପରିବର୍ତ୍ତନ କଲେ, ନୂତନ କୋଣ ଦୁଇଟି ମଧ୍ଯ ପରସ୍ପର ପରିପୂରକ ହେବ?
ସମାଧାନ:
ଗୋଟିକର ପରିମାଣକୁ 10° ଅଧିକ କଲେ ଅନ୍ୟଟିର ପରିମାଣକୁ 10° କମାଇଲେ ନୂତନ କୋଣଦ୍ବୟ ପରସ୍ପର ପରିପୂରକ ହେବେ ।
Question 10.
ପରସ୍ପର ପରିପୂରକ ହୋଇଥିବା ଦୁଇଟି କୋଣ ମଧ୍ୟରୁ ଉଭୟ
(କ) ସୂକ୍ଷ୍ମ କୋଣ ହୋଇ ପାରିବେ କି?
ସମାଧାନ:
ନାହଁ
(ଖ) ସ୍ଥଳ କୋଣ ହୋଇ ପାରିବେ କି?
ସମାଧାନ:
ନାହଁ
(ଗ) ଉଭୟ ସମକୋଣ ହୋଇପାରିବେ କି?
ସମାଧାନ:
ହଁ
(ଘ) ଗୋଟିଏ ସୂକ୍ଷ୍ମ ଓ ଅନ୍ୟଟି ସମକୋଣ ହୋଇ ପାରିବେ କି?
ସମାଧାନ:
ନାହଁ
(ଡ) ଗୋଟିଏ ସୂକ୍ଷ୍ମ ଓ ଅନ୍ୟଟି ସ୍ଥୁଳକୋଣ ହୋଇ ପାରିବେ କି?
ସମାଧାନ:
ହଁ
Question 11.
(କ) ଦୁଇଟି ପରସ୍ପର ପରିପୂରକ କୋଣ ମଧ୍ୟରୁ ଗୋଟିକର ପରିମାଣ ଅନ୍ୟଟିର ପରିମାଣର ପାଞ୍ଚ ଗୁଣ ହେଲେ, କୋଣଦୁଇଟିର ପରିମାଣ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ଗୋଟିଏ କୋଣର ପରିମାଣ l ଗୁଣ । ତେବେ ଅନ୍ୟ କୋଣର ପରିମାଣ 5 ଗୁଣ
1 ଗୁଣ + 5 ଗୁଣ = 180° (କୋଣଦ୍ଵୟ ପରିପୂରକ)
6 ଗୁଣକୁ = 180° ବା 1 ଗୁଣକୁ \(\frac{180°}{6}\) = 30°
5 ଗୁଣକୁ 30° × 5 = 150° ବା ∴ କୋଣ ଦୁଇଟିର ପରିମାଣ 30° ଓ 150° ।
(ଖ) ଦୁଇଟି ପରସ୍ପର ଅନୁପୂରକ କୋଣ ମଧ୍ୟରୁ ଗୋଟିକର ପରିମାଣ ଅନ୍ୟଟିର ଋରି ଗୁଣ ହୋଇଥିଲେ, କୋଣଦୁଇଟିର ପରିମାଣ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ଗୋଟିଏ କୋଣ ପରିମାଣ l ଗୁଣ । ତେବେ ଅନ୍ୟ କୋଣଟିର ପରିମାଣ 4 ଗୁଣ ।
1 ଗୁଣ + 4 ଗୁଣ = 90° (କୋଣଦ୍ଵୟ ପରସ୍ପର ଅନୁପୂରକ)
5 ଗୁଣକୁ = 90° ବା 1 ଗୁଣକୁ \(\frac{90°}{6}\) = 18°
4 ଗୁଣକୁ 18° × 4 = 72° ∴ କୋଣ ଦୁଇଟିର ପରିମାଣ 18° ଓ 72° ।
