Odisha State Board BSE Odisha 8th Class Maths Notes Geometry Chapter 1 ଜ୍ୟାମିତିର ମୌଳିକ ଧାରଣ will enable students to study smartly.
BSE Odisha Class 8 Maths Notes Geometry Chapter 1 ଜ୍ୟାମିତିର ମୌଳିକ ଧାରଣ
→ ଉପକ୍ରମଣିକା (Introduction) :
- Geometry ଶବ୍ଦଟି ଦୁଇଟି ଗ୍ରୀକ୍ ଶବ୍ଦ Geo (ପୃଥ୍ବୀ) ଓ Metron (ମାପ)ରୁ ଉତ୍ପନ୍ନ ହୋଇଛି । ଜ୍ୟାମିତି ପଦଟିରେ ‘ଜ୍ୟା’ର ଅର୍ଥ ପୃଥିବୀ ଓ ‘ମିତି’ର ଅର୍ଥ ମାପ । ଜମି ମାପ କରିବାର ଆବଶ୍ୟକତାକୁ ଭିଭିକରି ଜ୍ୟାମିତିର ସୃଷ୍ଟି ।
- ଆନୁମାନିକ ଖ୍ରୀଷ୍ଟପୂର୍ବ 800 ରୁ ଖ୍ରୀଷ୍ଟପୂର୍ବ 500 ମଧ୍ୟରେ ଭାରତରେ ରଚିତ ‘ଶୁଲ୍ବ ସୂତ୍ର’ ହେଉଛି ଏକ ଜ୍ୟାମିତି ଶାସ୍ତ୍ର । ଶୁକ୍ଳବ ଅର୍ଥାତ୍ ଦଉଡ଼ି ସାହାଯ୍ୟରେ ମାପ ସମ୍ବନ୍ଧୀୟ ବିଭିନ୍ନ ସୂତ୍ରକୁ ନେଇ ଏହି ଶାସ୍ତ୍ର ସମୃଦ୍ଧ ।
- ଗ୍ରୀକ୍ ଗଣିତଜ୍ଞ ଥାଲେସ୍ (ଖ୍ରୀଷ୍ଟପୂର୍ବ 640-546) ପ୍ରଥମେ ଜ୍ୟାମିତିରେ ତର୍କଶାସ୍ତ୍ରର ପ୍ରୟୋଗକରି ପୂର୍ବରୁ ପିଥାଗୋରାସ୍ (ଖ୍ରୀଷ୍ଟପୂର୍ବ 580-500) ଓ ତାଙ୍କ ପରେ ସକ୍ରେଟିସ୍ (ଖ୍ରୀଷ୍ଟପୂର୍ବ 468-390), ପ୍ଲାଟୋ (ଖ୍ରୀଷ୍ଟପୂର୍ବ 430-339) ଓ ଆରିଷ୍ଟଟଲ୍ (ଖ୍ରୀଷ୍ଟପୂର୍ବ 384-322) ଆଦି ଗ୍ରୀକ୍ ବିଦ୍ଵାନଗଣ ଏହି ଧାରାକୁ
- ଖ୍ରୀଷ୍ଟପୂର୍ବ ଚତୁର୍ଥ ଶତାବ୍ଦୀରେ ଆଲେକ୍ଜାଣ୍ଡ୍ରିୟା (ଗ୍ରୀସ୍)ର ଗଣିତଜ୍ଞ ଇଉକ୍ଲିଡ୍ (Euclid) ତାଙ୍କ ଅନବଦ୍ୟ ଗ୍ରନ୍ଥ Elementsରେ ଦର୍ଶାଇଲେ ଯେ ଜ୍ୟାମିତିକ ସିଦ୍ଧାନ୍ତଗୁଡ଼ିକ ପ୍ରତ୍ୟେକ ଗୋଟିଏ ଗୋଟିଏ ସ୍ବତନ୍ତ୍ର ତଥ୍ୟ ନୁହଁନ୍ତି, ଅଳ୍ପ କେତେଗୁଡ଼ିଏ ତଥ୍ୟକୁ ସ୍ଵୀକାର କରିଗଲେ ବାକି ସମସ୍ତ ଜ୍ୟାମିତିକ ସିଦ୍ଧାନ୍ତ ଏହି ସ୍ବୀକୃତ ତଥ୍ୟ
ଯଥାର୍ଥରେ ଜ୍ୟାମିତିର ଜନକ ବୋଲି ସ୍ବୀକାର କରାଯାଏ । ତାଙ୍କରି ନାମାନୁଯାୟୀ ଜ୍ୟାମିତିକୁ ଇଉକ୍ଲିଡ଼ିୟ ଜ୍ୟାମିତି (Euclidean Geometry) କୁହାଯାଏ । - ପରବର୍ତ୍ତୀ କାଳରେ ଭାରତୀୟ ଗଣିତଜ୍ଞମାନଙ୍କ ମଧ୍ୟରେ ଭାସ୍କର (ଜନ୍ମ 114 ଖ୍ରୀଷ୍ଟାବ୍ଦ), ଆର୍ଯ୍ୟଭଟ୍ଟ (ଜନ୍ମ 580 ଖ୍ରୀଷ୍ଟାବ୍ଦ) ଜ୍ୟାମିତି ଶାସ୍ତ୍ରକୁ ସମୃଦ୍ଧ କରିଥିଲେ ।
→ ସଂଜ୍ଞାବିହୀନ ପଦ ଓ ତତ୍ସମ୍ପର୍କୀୟ ସ୍ଵୀକାର୍ଯ୍ୟ (Undefined terms and related postulates) :
- ପ୍ରତ୍ୟେକ ବିଷୟରେ କେତେକ ବିଶେଷ ପ୍ରକାର ଶବ୍ଦ ନିର୍ଦ୍ଦିଷ୍ଟ ଅର୍ଥରେ ବ୍ୟବହାର କରାଯାଏ ଓ ସେଗୁଡ଼ିକୁ ସେହି ବିଷୟ ସମ୍ବନ୍ଧୀୟ ପଦ (term) କୁହାଯାଏ ।
- ବିନ୍ଦୁ, ରେଖା, ସମତଳ, ରଶ୍ମି, ତ୍ରିଭୁଜ, ବୃତ୍ତ ଆଦି ଜ୍ୟାମିତିଶାସ୍ତ୍ରର ଗୋଟିଏ ଗୋଟିଏ ‘ପଦ’ ।
- ବିନ୍ଦୁ, ରେଖା ଓ ସମତଳ ଏହି ପଦ ତିନୋଟିକୁ ‘ମୌଳିକ ପଦ’ ବା ‘ସଂଜ୍ଞାବିହୀନ ପଦ’ (undefined term) ରୂପେ ଗ୍ରହଣ କରି, ଏହି ପଦ ଓ ତତ୍ସମ୍ବନ୍ଧୀୟ ସ୍ଵୀକାର୍ଯ୍ୟ ସାହାଯ୍ୟରେ ନୂତନ ପଦଗୁଡ଼ିକର ସଂଜ୍ଞା ନିରୂପଣ କରାଯାଇଥାଏ ।
→ ବିନ୍ଦୁ (Point) :
ଏହା ଏକ ସଂଜ୍ଞାବିହୀନ ପଦ । ଏହାକୁ ଇଂରାଜୀ ବର୍ଣ୍ଣମାଳା A, B, C… ଦ୍ବାରା ଏଠାରେ A, B, ଓ C ତିନୋଟି ବିନ୍ଦୁ ଅଟନ୍ତି ।
![]()
![]()
→ ରେଖା ବା ସରଳରେଖା (Line) :
ଏହା ଉଭୟ ଦିଗରେ ସୀମାହୀନ ଭାବରେ ଲମ୍ବିଥାଏ । ଏହାର ଆରମ୍ଭ କିମ୍ବା ଶେଷ ନଥାଏ । ତେଣୁ ଏହାର ଦୁଇ ପ୍ରାନ୍ତକୁ ତୀର ଚିହ୍ନଦ୍ୱାରା ଦର୍ଶାଯାଇଥାଏ ।
![]()
‘L’ ଏକ ସରଳ ରେଖା ।
- L ସରଳରେଖାରେ ଏକାଧ୍ଵ ବିନ୍ଦୁ ଥାଏ ।
L = \(\overleftrightarrow{\mathrm{AB}}\) = \(\overleftrightarrow{\mathrm{BA}}\)
→ ସ୍ବୀକାର୍ଯ୍ୟ – 1 : ସରଳରେଖା ବିନ୍ଦୁମାନଙ୍କର ସମାହାର ବା ସେଟ୍ ।
- ଏକ କାଗଜ ଉପରେ ଦୁଇଟି ବିନ୍ଦୁ ନେଇ ଏହାକୁ ଯୋଗକଲେ
ଏଥିରେ ଗୋଟିଏ ମାତ୍ର ସରଳରେଖା ହେବ ।
A ଓ B, L ସରଳରେଖାର ଦୁଇଟି ବିନ୍ଦୁ ହେଲେ, ଏହାକୁ \(\overleftrightarrow{\mathrm{AB}}\) ଦ୍ବାରା ଲେଖାଯାଏ ।
→ ସ୍ବୀକାର୍ଯ୍ୟ – 2 : ଦୁଇଟି ପୃଥକ୍ ବିନ୍ଦୁକୁ ଧାରଣ କରୁଥିବା କେବଳ ମାତ୍ର ଗୋଟିଏ ସରଳରେଖା ଅବସ୍ଥିତ ।
- ତିନି ବା ତତୋଽଧିକ ସଂଖ୍ୟକ ବିନ୍ଦୁ ଯଦି ଗୋଟିଏ ସରଳରେଖାରେ ଅବସ୍ଥିତ ହୁଅନ୍ତି, ତେବେ ସେମାନଙ୍କୁ ସରଳରେଖ୍ ବିନ୍ଦୁ ବା ଏକରେଖୀ ବିନ୍ଦୁ (Collinear Points) କୁହାଯାଏ ।
- ଯେଉଁସବୁ ବିନ୍ଦୁ ଗୋଟିଏ ସରଳରେଖାରେ ନ ଥା’ନ୍ତି, ସେମାନଙ୍କୁ ନୈକରେଖୀ ବା ଅଣସରଳରେଖ୍ ବିନ୍ଦୁ (non-collinear points) କୁହଯାଏ ।
→ ସ୍ବୀକାର୍ଯ୍ୟ – 3 : ସମତଲ ଦିନ୍ଦୁମାନକର ସେଟ୍ ଅଟେ |
→ ସ୍ବୀକାର୍ଯ୍ୟ – 4 : ଯେକୋଣସି ତିନିଗୋଟି ନୈକଲେଖା ଦନ୍ଦୁ ଦେଲ ଗୋଟିଏ ମାତ୍ର ସମତଲ ଅଦମ୍ବିତ |
- ଗୋଟିଏ ସମତଳର ନାମକରଣ ସେହି ସମତଳରେ ଥିବା ଯେକୌଣସି ତିନିଗୋଟି ନୈକରେଖା ବିନ୍ଦୁ ସାହାଯ୍ୟରେ କରାଯାଏ ।
→ ସ୍ବୀକାର୍ଯ୍ୟ – 5 :
ଏକ ସମତଲମ ଦୁଲ ପୃଥକ୍ ଦିନ୍ଦୁକୁ ଧାରଣ କରୁଥିବା ସରଲରେଖା ଉକ୍ତ ସମତଳର ଅଦମ୍ବିତ |
→ ସମାନ୍ତର ସରଳରେଖା (Parallel Lines) :
- ଏକ ସମତଲରେ ଅଦସ୍ଥିତ ଦୁଇଟି ସରଲରେଖାର ସାଧାରଣ ବିନ୍ଦୁକୁ ସେମାନଙ୍କର ଛେଦବିନ୍ଦୁ (point of intersection) କୁହାଯାଏ ।
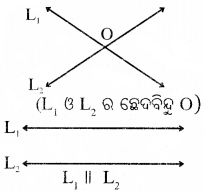
- ଏକ ସମତଲରେ ଥ୍ବା ଦୁଲଟି ସରଲରେଖା ପରସ୍ପରକୁ ଛେଦ ନ କଲେ, ସେ ଦୁଇଟିକୁ ସମାନ୍ତର ରେଖା କୁହାଯାଏ ।
→ ତୁମେ କୁହ :
(a) ଏକ ସମତଳରେ ଅବସ୍ଥିତ ଦୁଇଟି ସରଳରେଖାର ଅତିବେଶିରେ କେତୋଟି ଛେଦବିନ୍ଦୁ ରହିପାରିବ ?
(b) ଏକ ସମତଳରେ ଅବସ୍ଥିତ ତିନୋଟି ସରଳରେଖାର ଅତିବେଶିରେ କେତୋଟି ଛେଦବିନ୍ଦୁ ରହିପାରିବ ?
(c) ଏକ ସମତଳରେ ଅବସ୍ଥିତ ତାରୋଟି ସରଳରେଖାର ଅତିବେଶିରେ କେତୋଟି ଛେଦବିନ୍ଦୁ ରହିପାରିବ ?
ଉତ୍ତର : (a) ଗୋଟିଏ, (b) ତିନୋଟି, (c) ଛଅଗୋଟି
→ ଦୁଇ ବିନ୍ଦୁ ମଧ୍ୟସ୍ଥ ଦୂରତା, ସରଳରେଖା ଓ ବାସ୍ତବ ସଂଖ୍ୟା ସେଟ୍ ମଧ୍ୟରେ ସମ୍ପର୍କ :
- ଗୋଟିଏ ବିନ୍ଦୁର ତା’ ନିଜଠାରୁ ଦୂରତା ଯେକୌଣସି ସ୍କେଲ୍ରେ ଶୂନ ହୁଏ ।
ଦୂରତା ମାପ ପାଇଁ ବ୍ୟବହୃତ ସଂଖ୍ୟା ସର୍ବଦା ଅଣଋଣାତ୍ମକ ଅର୍ଥାତ୍ ଶୂନ ବା ଧନାତ୍ମକ ରାଶି । ଦୁଇଟି ବିନ୍ଦୁ ଅଭିନ୍ନ ହେଲେ ଦୂରତା ଶୂନ ହେବ ।
![]()
ସ୍ବୀକାର୍ଯ୍ୟ – 6 : ରୁଲାର୍ ସ୍ଵୀକାର୍ଯ୍ୟ (Ruler Postulate) : ଗୋଟିଏ ସମତଳରେ ଥିବା ବିନ୍ଦୁ ଗୋଟିଏ ଅଣରଣାତ୍ମକ ବାସ୍ତବ ସଂଖ୍ୟା ସହ ସମ୍ପୃକ୍ତ, ଯାହାକୁ ବିଦୁ୍ୟଦ୍ବ ମଧ୍ୟସ୍ଥ ଦୂରତା ମଧ୍ୟସ୍ଥ ଦୂରତା ଉପରେ ନିର୍ଭର କରି ଏକ ସରଳରେଖାର ବିନ୍ଦୁସମୂହ ଓ ବାସ୍ତବ ସଂଖ୍ୟା ବିଶେଷ ପ୍ରକାର ସମ୍ପର୍କ ସମ୍ଭବ ହୁଏ ।
ସ୍ବୀକାର୍ଯ୍ୟ – 6ର ପରିଣାମ ସ୍ଵରୂପ :
- ଏକ ସରଳରେଖାର ବିନ୍ଦୁଗୁଡ଼ିକ ପ୍ରତ୍ୟେକେ ଗୋଟିଏ ଗୋଟିଏ ନିର୍ଦ୍ଦିଷ୍ଟ ବାସ୍ତବ ସଂଖ୍ୟା ସହ ସମ୍ପୃକ୍ତ । ପରୋକ୍ଷରେ ବାସ୍ତବ ସଂଖ୍ୟାଗୁଡ଼ିକ ମଧ୍ୟ ପ୍ରତ୍ୟେକେ ଏହି ରେଖା ଉପରିସ୍ଥ ଗୋଟିଏ ଗୋଟିଏ ନିର୍ଦ୍ଦିଷ୍ଟ ବିନ୍ଦୁସହ ସମ୍ପୃକ୍ତ ।
- ସରଳରେଖା ଉପରିସ୍ଥ ଯେକୌଣସି ଦୁଇ ବିନ୍ଦୁ ମଧ୍ୟସ୍ଥ ଦୂରତା, ସେମାନଙ୍କ ସହିତ ସମ୍ପୃକ୍ତ ବାସ୍ତବ ସଂଖ୍ୟାଦ୍ବୟର ଅନ୍ତରର ପରମମାନ ସହ ସମାନ ହୁଏ ।
→ ଦୁଇ ବିନ୍ଦୁ ମଧ୍ୟସ୍ଥ ଦୂରତା :
ଏକ ସରଳରେଖାରେ ଦୁଇଟି ବିନ୍ଦୁ P ଓ Q ର ସ୍ଥାନାଙ୍କ p ଓ q ଦ୍ଦେଲେ
P ଓ Q ମଧ୍ୟସ୍ଥ ଦୂରତା = | p – q | ହେବ ।
ମନେରଖ : x ର ପରମ ମାନ । x | = x ଯଦି x ଶୂନ ବା ଧନାତ୍ମକ ବାସ୍ତବ ସଂଖ୍ୟା = -x ଯଦି x ଋଣାତ୍ମକ ବାସ୍ତବ ସଂଖ୍ୟା ।
- ସରଳରେଖା ଅଫଖ୍ୟ ଦିନ୍ଦୁବିଶିଶୁ |
- ସରଳରେଖାର ଆଦ୍ୟ ଓ ପ୍ରାନ୍ତବିନ୍ଦୁ ନଥାଏ ।
- ସରଳରେଖା ନିରଦନ୍ଥିନି ଭାବରେ ପରିବ୍ୟାପ୍ତ |
ଦୁଇଟି ବିନ୍ଦୁ P ଓ Q ମଧ୍ୟରେ ଦୂରତା ଯାହା Q ଓ P ମଧ୍ୟରେ ଦୂରତା ତାହା, ଆଦ୍ୟ PQ = QP
→ ମଧ୍ୟବର୍ତ୍ତିତା (Betweenness) :
- ଯଦି ତିନୋଟି ବିନ୍ଦୁ A, B ଓ C (i) ପରସ୍ପରଠାରୁ ପୃଥକ୍ ଅଟନ୍ତି, (ii) ଏକ ସରଳରେଖାରେ ଅବସ୍ଥାନ କରି ଥାଆନ୍ତି ଏବଂ (iii) AB + BC AC ହୋଇଥାଏ, ତେବେ Bକୁ A ଓ C ଦିନ୍ଦୁଦୟର ମଧ୍ୟଦାଭା ବିନ୍ଦୁ କତ୍ତିନ୍ତି |
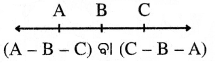
→ ରେଖାଖଣ୍ଡ (Line Segment or Segment) :
- ଦୁଇଟି ପୃଥକ୍ ବିନ୍ଦୁ A, B ଓ ସେମାନଙ୍କର ମଧ୍ୟବର୍ତ୍ତୀ ବିନ୍ଦୁମାନଙ୍କର ସେଟ୍କୁ A ଓ B ଦ୍ୱାରା ନିରୂପିତ ରେଖାଖଣ୍ଡ କୁହାଯାଏ ଏବଂ ଏହାକୁ \(\overline{\mathrm{AB}})\) ଦ୍ଵାରା ସୂଚିତ କରାଯାଏ । ସେଟ୍ ପରିଭାଷାରେ \(\overline{\mathrm{AB}})\) ⊂ \(\overleftrightarrow{A B}\) | A ଓ Bକୁ \(\overline{\mathrm{AB}})\) ର ପ୍ରାନ୍ତବିନ୍ଦୁ କୁହାଯାଏ ।
IMG - କୋଣସି ରେଖାଖପ୍ରର ପ୍ରାନ୍ତଦିଦ୍ଵୟର ହରତାଜ୍ମ ରେଖାଖପ୍ରର ଦୈର୍ଘ୍ୟ କୁହାଯାଏ । ରେଖାଖଣ୍ଡର ଦୈର୍ଘ୍ୟ ସର୍ବଦା ଏକ ଧନାତ୍ମକ ସଂଖ୍ୟା ।
- ଏକ ରେଖାଖପ୍ରର ଗୋଟିଏ ମାତ୍ରା ମଧ୍ୟଦିନ୍ଦୁ ଥାଏ |
AB ର ପ୍ରାନ୍ତବିଦ୍ୟୁଦ୍ଵୟ A ଓ B, \(\overleftrightarrow{A B}\) ର କୌଣସି ପ୍ରାନ୍ତବିନ୍ଦୁ ନଥାଏ |
→ ରେଖାଖଣ୍ଡର ମଧ୍ୟବିନ୍ଦୁ :
M, \(\overline{\mathrm{AB}})\) ଉପରେ ଏକ ବିନ୍ଦ ଏବଂ AM = MB ହେଲେ, M କୁ AB ର ମଧ୍ୟବିନ୍ଦୁ କୁହାଯାଏ ।
∴ AM = MB = 1/2 AB.
→ ରଶ୍ମି (Ray) :
- AB ରେଖାଖଣ୍ଡ ( AB ) ଓ B ପରବର୍ତ୍ତୀ ସମସ୍ତ ବିନ୍ଦୁମାନଙ୍କୁ ନେଇ ଗଠିତ ରେଖାର ଅଂଶ ହେଉଛି ଏକ ରଶ୍ମି (ray) । AB ରଶ୍ମିକୁ ସାଙ୍କେତିକ ଚିହ୍ନରେ \(\overrightarrow{\mathrm{AB}}\) ବୋଲି ଲେଖାଯାଏ । AB ର ଶୀର୍ଷବିନ୍ଦୁ ହେଉଛି A ଏବଂ \(\overrightarrow{\mathrm{BA}}\) ର ଶୀର୍ଷବିନ୍ଦୁ ହେଉଛି B |
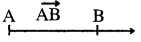
- ଏକ ରଶ୍ମିର ଶୀର୍ଷବିନ୍ଦୁକୁ ଆଦ୍ୟବିନ୍ଦୁ (Initial Point) ମଧ୍ୟ କୁହାଯାଏ ।
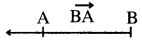
- ଦୁଇଟି ରଶ୍ମି ଏକ ସରଳରେଖାର ଅଂଶ ହେଲେ, ସେମାନଙ୍କୁ ଏକରେଖୀ ବା ସରଳରେଖକ ରଶ୍ମି (Collinear rays) କୁହାଯାଏ । ଦୁଇଟି ରଶ୍ମି ସରଳରେଖ ନ ହେଲେ, ସେମାନଙ୍କୁ ନୈକରେଖୀ ରଶ୍ମି (non-collinear rays) କୁହାଯାଏ ।
→ ରେଖାଖଣ୍ଡ, ରଶ୍ମି ଓ ସରଳରେଖା ମଧ୍ଯରେ ସମ୍ପର୍କ :
![]()
ଚିତ୍ରରୁ ଏହା ସୁସ୍ପଷ୍ଟ ଯେ AB ରେଖାଖଣ୍ଡର ସମସ୍ତ ବିନ୍ଦୁ ‘AB ରଶ୍ମି’ରେ ଏବଂ AB ରଶ୍ମିର ସମସ୍ତ ବିନ୍ଦୁ ‘AB ସରଳରେଖା’ରେ ରହିଛନ୍ତି । ତେଣୁ ସେଟ୍ ଭାଷାରେ \(\overline{\mathrm{AB}})\) ⊂ \(\overrightarrow{\mathrm{AB}}\) ⊂ \(\overrightarrow{\mathrm{AB}}\) । ସେହି ପରି BA ⊂ \(\overrightarrow{\mathrm{BA}}\) ⊂ \(\overrightarrow{\mathrm{AB}}\)
![]()
→ ନିଲେ କାର :
ତୁମ ଖାତାରେ ତିନୋଟି ରଶ୍ମି \(\overrightarrow{\mathrm{OA}}\), \(\overrightarrow{\mathrm{OB}}\) ଓ \(\overrightarrow{\mathrm{OC}}\) ଅଙ୍କନ କର, ଯେପରି
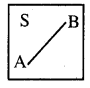
(a) କୌଣସି ଦୁଇଟି ରଶ୍ମି ବିପରୀତ ରଶ୍ମି ହୋଇ ନଥିବେ ।
(b) ଦତ୍ତ ରଶ୍ମିଗୁଡ଼ିକ ମଧ୍ୟରୁ ଯେକୌଣସି ଦୁଇଟି ରଶ୍ମି ପରସ୍ପରର ବିପରୀତ ରଶ୍ମି ହୋଇଥିବେ ।
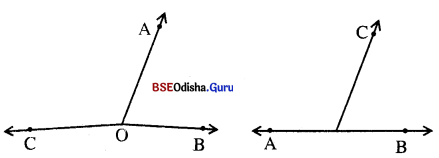
ନିଲେ କାର :
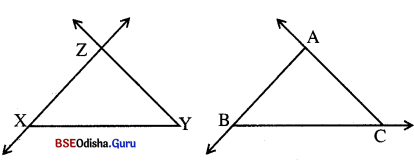
(a) ତୁମ ଖାତାରେ ତିନୋଟି ନୈକରେଖୀ ବିନ୍ଦୁ X, Y, Z ଚିହ୍ନଟ କର ଓ XY, YZ, XZ ଅଙ୍କନ କର ।
(b) ତୁମ ଖାତାରେ ତିନୋଟି ନେକରେଖୀ ବିନ୍ଦୁ A, B ଓ C ଚିହ୍ନଟ କର । \(\overrightarrow{\mathrm{AB}}\), \(\overrightarrow{\mathrm{BC}}\), \(\overrightarrow{\mathrm{CA}}\) ଅଙ୍କନ କର ।
ନିଜେ କର : କିଏ କାହାର ଉପସେଟ୍ ଲେଖ ।
(i) (a) \(\overline{\mathrm{PQ}})\) ଓ \(\overrightarrow{\mathrm{PQ}}\) (b) \(\stackrel{\leftrightarrow}{\mathrm{CD}}\) ଓ \(\overline{\mathrm{CD}})\) (c) AB ଓ \(\overrightarrow{\mathrm{BA}}\)
(ii) A-P-B ହେଲେ, \(\stackrel{\leftrightarrow}{\mathrm{AB}}\) ଉପରିସ୍ଥ ଦୁଇଟି ବିପରୀତ ରଶ୍ମିର ନାମ ଲେଖ ।
ଭ :
(i) (a) \(\overline{\mathrm{PQ}})\) ⊂ \(\overrightarrow{\mathrm{PQ}}\) (b) \(\overline{\mathrm{CD}})\) ⊂ \(\stackrel{\leftrightarrow}{\mathrm{CD}}\) (c) AB ⊂ \(\overrightarrow{\mathrm{BA}}\)
(ii) ![]()
\(\overrightarrow{\mathrm{PA}}\) ଓ \(\overrightarrow{\mathrm{PB}}\), \(\stackrel{\leftrightarrow}{\mathrm{AB}}\) ଉପରିସ୍ଥ ଦୁଇଟି ବିପରୀତ ରଶ୍ମି ।
→ ଉତ୍ତଳ ସେଟ୍ (Convex Set) :
- ସେଟ୍ ସ୍ତର ଯେକୌଣସି ଦୁଇଟି ବିନ୍ଦୁ A ଓ B ହେଲେ, ଯଦି AB c S ହୁଏ, ତେବେ Sକୁ ଏକ ଉତ୍ତଳ ସେଟ୍ କୁହାଯାଏ ।
ଉଦାହରଣ – ରଶ୍ମି, ସରଳରେଖା ଓ ସମତଳ ।
→ ତୁମ ପାଇ କାମ :
ନିମ୍ନଲିଖ ଚିତ୍ରଗୁଡ଼ିକ ମଧ୍ୟରୁ କେଉଁଟି ଉତ୍ତଳ ସେଟ୍ ଦର୍ଶାଅ |
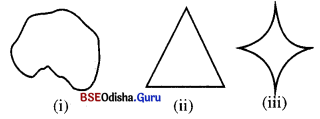
ଉତ୍ତଳ ସେଟ୍ ସମ୍ବନ୍ଧୀୟ କେତୋଟି ତଥ୍ୟ :
(i) ଦୁଇଟି ଉତ୍ତଳ ସେଟ୍ ଛେଦ ମଧ୍ଯ ଏକ ଉତ୍ତଳ ସେଟ୍ ।
(ii) ଦୁଇଟି ଉତ୍ତଳ ସେଟ୍ର ସଂଯୋଗ ଉତ୍ତଳ ସେଟ୍ ନ ହୋଇପାରେ ।
- ଦୁଇଟି ଉତ୍ତଳ ସେଟ୍ର ଛେଦ ମଧ୍ଯ ଏକ ଉତ୍ତଳ ସେଟ୍ ।
- ଦୁକଟି ଭରଲ ସେଟର ଫଯୋଗ ଭଳକ ସେଟ ନ ହୋଇ ପାରେ |
→ ସରଳରେଖାର ପାର୍ଶ୍ଵ (Side of a Line) :
- କୌଣସି ସରଳରେଖାର ଏକ ପାର୍ଶ୍ଵର ନାମକରଣ ସେହି ପାର୍ଶ୍ବରେ ଥିବା ଯେକୌଣସି ବିନ୍ଦୁକୁ ନେଇ କରାଯାଇପାରିବ । L ସରଳରେଖାର ଯେଉଁ ପାର୍ଶ୍ଵରେ A ବିନ୍ଦୁ ଅଛି, ତାକୁ L ସରଳରେଖାର A ପାର୍ଶ୍ଵ ଏବଂ ଯେଉଁ ପାର୍ଶ୍ଵରେ B ବିନ୍ଦୁ ଅଛି, ତାକୁ L ସରଳରେଖାର B ପାର୍ଶ୍ବ କୁହାଯାଏ ।
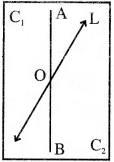
AB ରେଖାଖଣ୍ଡ ବା \(\overrightarrow{\mathrm{AB}}\) ରଶ୍ମିର ଭୁଲ ପାଣ୍ଠି କହଲେ ଆମେ ସରଲ ହି ହ୍ରଖବା |
![]()
→ ସ୍ବୀକାର୍ଯ୍ୟ 7 : ସମତଳ ବିଭାଜନ (Plane Separation) ସ୍ଵୀକାର୍ଯ୍ୟ :
ମନେକର L ସରଳରେଖାଟି P ସମତଳରେ ଅବସ୍ଥିତ । ସମତଳର ଯେଉଁ ବିନ୍ଦୁଗୁଡ଼ିକ L ସରଳରେଖାରେ ନାହାନ୍ତି, ସେମାନଙ୍କୁ ଦୁଇଟି ସେଟ୍ C ଓ C ରେ ବିଭକ୍ତ କରାଯାଇପାରିବ ଯେପରି :
(i) C, ଏବଂ C ପ୍ରତ୍ୟେକ ଗୋଟିଏ ଗୋଟିଏ ଉତ୍ତଳ ସେଟ୍ ହେବେ,
(ii) ଦୁଇଟି ପୃଥକ୍ ବିନ୍ଦୁ A ଓ B ଯଥାକ୍ରମେ C ଓ C, ସେଟ୍ରେ ରହିଲେ, A ଓ Bର ସଂଯୋଗକାରୀ ରେଖାଖଣ୍ଡ ଅର୍ଥାତ୍ AB, L ସରଳରେଖାକୁ ଛେଦ କରିବ ।
→ କୋଣ (Angle) :
- ତିନୋଟି ପୃଥକ୍ ବିନ୍ଦୁ A, B ଓ C ଯଦି ଏକ ସରଳରେଖାରେ ଅବସ୍ଥିତ ନ ହୁଅନ୍ତି; ତେବେ \(\overrightarrow{\mathrm{BA}}\) ଓ \(\overrightarrow{\mathrm{BC}}\) ରଶ୍ମିଦ୍ଵୟର ସଂଯୋଗ (Union)କୁ ଗୋଟିଏ କୋଣ କୁହାଯାଏ (ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ର ଦେଖ) । ଏହାକୁ ∠ABC ବା ∠CBA ସଙ୍କେତଦ୍ବାରା ଲେଖାଯାଏ ଏବଂ ‘ABC କୋଣ’ ବା ‘CBA କୋଣ’ ବୋଲି ପଢ଼ାଯାଏ । (ସେଟ୍ ପରିଭାଷାରେ ∠ABC = \(\overrightarrow{\mathrm{BA}}\) ∪\(\overrightarrow{\mathrm{BC}}\))
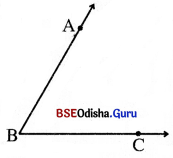
→ ନିଜେ କର :
A, B, ଓ C ଏକ ସରଳରେଖାରେ ଅବସ୍ଥିତ ନଥିବା ତିନୋଟି ବିନ୍ଦୁ, ନିମ୍ନସ୍ଥ ପ୍ରତ୍ୟେକ ଯୋଡ଼ା ରଶ୍ମିର ସଂଯୋଗର ଜ୍ୟାମିତିକ ଚିତ୍ରର ନାମକରଣ କର ।
(i) \(\overrightarrow{\mathrm{AB}}\) ଓ \(\overrightarrow{\mathrm{AC}}\)
(ii) \(\overrightarrow{\mathrm{BA}}\) ଓ \(\overrightarrow{\mathrm{BC}}\)
(iii) \(\overrightarrow{\mathrm{CB}}\) ଓ \(\overrightarrow{\mathrm{CA}}\)
(iv) \(\overrightarrow{\mathrm{AB}}\) ଓ \(\overrightarrow{\mathrm{BA}}\)
(v) \(\overrightarrow{\mathrm{BC}}\) ଓ \(\overrightarrow{\mathrm{CB}}\)
ଉ :
(i) ∠BAC
(ii) ∠ABC
(iii) ∠BCA
(iv) \(\overrightarrow{\mathrm{AB}}\)
(v) \(\stackrel{\leftrightarrow}{\mathrm{BC}}\)
(vi) \(\stackrel{\leftrightarrow}{\mathrm{AC}}\)
→ (a) ∠POR ର ଶୀର୍ଷବିନ୍ଦୁର ନାମ ଲେଖ ।
(b) ∠ABC ର କେତୋଟି ବାହୁ ଅଛନ୍ତି ? ସେମାନଙ୍କର ନାମ ଲେଖ ।
(c) \(\overrightarrow{\mathrm{AB}}\) ଓ \(\overrightarrow{\mathrm{AC}}\) ପରସ୍ପର ବିପରୀତ ରଶ୍ମି ହେଲେ, \(\overrightarrow{\mathrm{AB}}\) ଓ \(\overrightarrow{\mathrm{AC}}\)ର ସଂଯୋଗରେ କ’ଣ ସୃଷ୍ଟି ହେବ ?
(d) A ଶୀର୍ଷ ଏବଂ \(\overrightarrow{\mathrm{AB}}\) ଓ \(\overrightarrow{\mathrm{AC}}\) ବାହୁବିଶିଷ୍ଟ କୋଣର ନାମ କ’ଣ ?
ଉ :
(a) Q
(b) ହୁଲଟି ବାହି \(\overrightarrow{\mathrm{BA}}\) ଓ \(\overrightarrow{\mathrm{BC}}\)
(c) \(\overleftrightarrow{\mathrm{BC}}\)
(d) ∠BAC
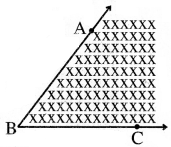
→ କୋଣର ଅନ୍ତର୍ଦେଶ ଓ ବହିର୍ଦେଶ (Interior & Exterior of an angle) :
- ଉତ୍ତଳ ସେଟ୍ର ସଂଜ୍ଞା ଅନୁଯାୟୀ କୋଣର ଅନ୍ତର୍ଦେଶ ଏକ ଉତ୍ତଳ ସେଟ୍, କିନ୍ତୁ ବହିର୍ଦ୍ଦେଶ ନୁହେଁ ।
- କୋଣ ନିଲେ ରଇଲ ସେଟ ନୁରହ |
- ∠ABC, ∠ABC ର ଅନ୍ତର୍ଦେଶ ଓ ∠ABCର ବହିର୍ଦେଶ – ଏହି ତିନୋଟି ସେଟ୍ ପରସ୍ପର ଅଣଛେଦୀ (Mutually disjoint); ଅର୍ଥାତ୍ ସେମାନଙ୍କ ମଧ୍ୟରୁ କୌଣସି ଦୁଇଟି ସେଟ୍ ମଧ୍ୟରେ ସାଧାରଣ ବିନ୍ଦୁ ନାହିଁ ।
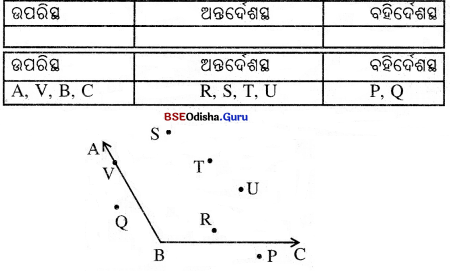
→ ନିଜେ କର :
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ର ଦେଖ୍ A, B, C, P, Q, R, S, T, U, V ବିନ୍ଦୁମାନଙ୍କ ମଧ୍ୟରୁ ∠ABC ର ଉପରିସ୍ଥ, ଅନ୍ତର୍ଦେଶସ୍ଥ ଓ ବହିର୍ଦେଶସ୍ଥ ବିନ୍ଦୁଗୁଡ଼ିକର ନାମ ନିମ୍ନ ସାରଣୀରେ ପୂରଣ କର ।
![]()
→ କୋଣର ମାପ (Measure of an angle) :
∠ABC କୋଣର ପରିମାଣ m∠ABC, ଯାହା ଏକ ବାସ୍ତବ ସଂଖ ମାତ୍ର m∠ABC ହେଉଛି ବିନ୍ଦୁମାନଙ୍କର ସେଟ୍ ।
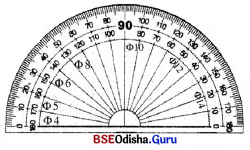
→ ସ୍ଵୀକାର୍ଯ୍ୟ 8 : ପ୍ରୋଟ୍ରାକ୍ଟର ସ୍ଵୀକାର୍ଯ୍ୟ (Protractor Postula ପ୍ରତ୍ୟେକ କୋଣ ସହିତ 0 ରୁ ବଡ଼ ଓ 180 ରୁ ସାନ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ବାସ୍ତବ ସଂଖ୍ୟା ସଂପୃକ୍ତ, ଯାହାକୁ କୋଣର ପରିମାଣ କୁହାଯାଏ । m∠ABC ଏପରି ଭାବରେ ନିରୂପିତ ହୁଏ, ଯେପରି :
- 0 ଠାରୁ ବଡ଼ ଓ 180 ରୁ ସାନ ଯେ କୌଣସି ଏକ ବାସ୍ତବ ସଂଖ୍ୟା x ପାଇଁ ABC ସମତଳରେ \(\overrightarrow{\mathrm{BC}}\) ର ଯେ କୌଣସି ଗୋଟିଏ ପାର୍ଶ୍ଵରେ ବିସ୍ତୃତ ଗୋଟିଏ ମାତ୍ର ରଶ୍ମି \(\overrightarrow{\mathrm{BM}}\) ଅଦନ୍ଥିତ , ଯେପରି m∠MBC = x ହେବ । (ସାଧାରଣତଃ m∠ABC = x°, ଏହିପରି ଲେଖାଯାଏ ।)
- ∠ABCର ଅନ୍ତର୍ଦେଶରେ P ଯେ କୌଣସି ଏକ ବିନ୍ଦୁ ହେଲେ, m∠ABC = m∠ABP + m∠PBC ହେବ ।
→ ପ୍ରୋଟ୍ରାକ୍ଟର ସ୍ଵୀକାର୍ଯ୍ୟରେ :
- କୋଣ ପରିମାଣକୁ 0 ରୁ ବଡ଼ ଓ 180 ରୁ ସାନ ବୋଲି ସ୍ୱୀକାର କଲେ, ଲବ୍ଧ ପରିମାଣକୁ କୋଣର ଡିଗ୍ରୀମାପ କୁହାଯାଏ । ସମ୍ପୃକ୍ତ ପ୍ରୋଟ୍ରାକ୍ଟରକୁ ଡିଗ୍ରୀ-ପ୍ରୋଟ୍ରାକ୍ଟର କୁହାଯାଏ ।
1° = 60 ମିନିଟ୍ ଓ
1 ମିନିଟ୍ = 60 ସେକେଣ୍ଡ
1° = 60′ ଓ 1′ = 60′′ - କୋଣର ପରିମାଣକୁ 0 ରୁ ବଡ଼ ଓ π (pai) (ପାଇ)ରୁ ସାନ ବୋଲି ସ୍ବୀକାରକଲେ, ଲବ୍ଧ ପରିମାଣକୁ ‘ରେଡ଼ିଆନ୍ ମାପ’ କୁହାଯାଏ ।
π ରେଡ଼ିଆନ୍ = 180 ଡିଗ୍ରୀ ।
ମଳେରଣ π ଏକ ଅପରିମେୟ ସଂଖ୍ୟା, ଯାହାର ଆସନ୍ନମାନ 3.1415 | - ଏକାତ୍ମକ କୋଣ ପରିମାଣ ମିଶି 180° ରୁ ଅଧିକ ହୋଇପାରେ; ମାତ୍ର ଆମ ଆଲୋଚନାରେ ଉପୁଜୁଥିବା ଯେ କୌଣସି କୋଣର ମାପ 0ରୁ 180° ମଧ୍ୟରେ
→ କୋଣ ସମଦ୍ବିଖଣ୍ଡକ (Angle-bisector) :
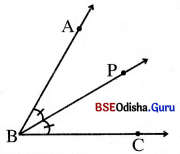
- ∠ABCର ଅନ୍ତର୍ଦେଶରେ P ବିନ୍ଦୁ ଅବସ୍ଥିତ । ଯଦି m∠ABP = M∠PBC ହୁଏ; ତେବେ BP କୁ ∠ABCର ସମଦ୍ରି ଖଣ୍ଡକ କୁହାଯାଏ । ଏ ସ୍ଥଳରେ m∠ABP = m∠PBC = \(\frac { 1 }{ 2 }\)m∠ABC
→ ବିଭିନ୍ନ ପ୍ରକାର କୋଣ (Different types of Angles) :
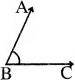
- ସୂକ୍ଷ୍ମକୋଣ – ଯେଉଁ କୋଣର ପରିମାଣ 0° ରୁ ବେଶି ଓ 90° ରୁ କମ୍, ତାହାକୁ ସୂକ୍ଷ୍ମକୋଣ (acute angle) କୁହାଯାଏ ।
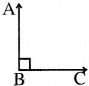
- ସମକୋଣ – ଗୋଟିଏ କୋଣର ପରିମାଣ 90° ସହ ସମାନ ହେଲେ, ତାହାକୁ ସମକୋଣ (right angle) କୁହାଯାଏ ।
- ସ୍ଥୂଳକୋଣ – ଗୋଟିଏ କୋଣର ପରିମାଣ ୨୦ ରୁ ଅଧିକ, କିନ୍ତୁ 180° ରୁ କମ୍ ହେଲେ, ତାହାକୁ ସ୍ଥୂଳକୋଣ (obtuse angle) କୁହଯାଏ ।
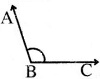
ନିଜେ କର :
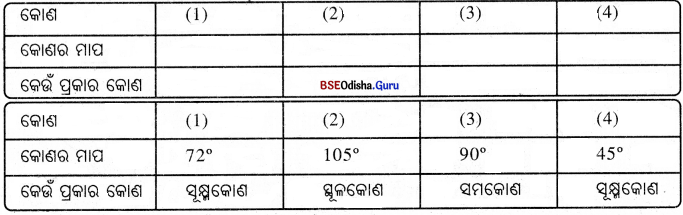
ଚିତ୍ରରେ ଥିବା କୋଣଗୁଡ଼ିକର ପରିମାଣ ପ୍ରୋଟ୍ରାକ୍ଟର ସାହାଯ୍ୟରେ ମାପ ଓ ପରବର୍ତ୍ତୀ ସାରଣୀରେ କୋଣର ମାପ ଓ କେଉଁ ପ୍ରକାର କୋଣ ଲେଖ ।
→ ଦୁଇଟି କୋଣ ମଧ୍ଯରେ ସମ୍ପର୍କ :
- ଦୁଇଟି କୋଣର ପରିମାଣର ସମଷ୍ଟି 90° ହେଲେ, ସେମାନଙ୍କୁ ପରସ୍ପର ଅନୁପୂରକ (Complementary) କୋଣ କୁହାଯାଏ । x° ର ଅନୁପୂରକ କୋଣ = (90° – x°)
- ଉଦାହରଣସ୍ୱରୂପ : 20°, 30°, 63° ପରିମାଣ ବିଶିଷ୍ଟ କୋଣମାନଙ୍କର ଅନୁପୂରକ କୋଣଗୁଡ଼ିକର ପରିମାଣ ଯଥାକ୍ରମେ 70°, 60° ଓ 27° ହେବ ।
- ଦୁଇଟି କୋଣର ପରିମାଣର ସମଷ୍ଟି 180° ହେଲେ, ସେମାନଙ୍କୁ ପରସ୍ପର ପରିପୂରକ (Supplementary) କୋଣ କୁହାଯାଏ । x° ର ପରିପୂରକ କୋଣ = (180° – x°)
- ଉଦାହରଣସ୍ୱରୂପ : 27°, 60°, 135° ଓ x ପରିମାଣ ବିଶିଷ୍ଟ କୋଣମାନଙ୍କର ପରିପୂରକ କୋଣଗୁଡ଼ିକର ପରିମାଣ 153°, 120°, 45° ଓ (180 – x) ହେବ ।
→ ତୁମପାଇଁ କାମ :
ଦତ୍ତ ସାରଣୀରେ କେତେଗୁଡ଼ିଏ କୋଣର ନାମ ଓ ସେମାନଙ୍କର ପରିମାଣ ଦିଆଯାଇଅଛି । କୋଣଗୁଡ଼ିକର ଅନୁପୂରକ ଓ ପରିପୂରକ କୋଣର ପରିମାଣ ନିର୍ଣ୍ଣୟ କରି ସାରଣୀଟି ପୂରଣ କର । ଉତ୍ତର ସମ୍ଭବ ନହେଲେ (X) ଚିହ୍ନ ଦିଅ ।
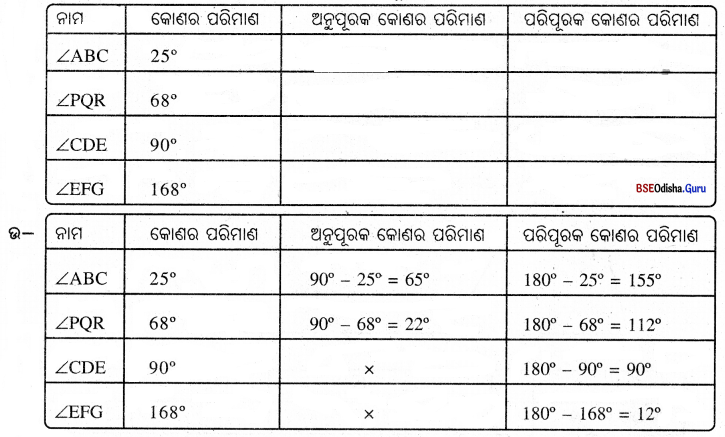
![]()
→ ସନ୍ନିହିତ କୋଣ (Adjacent Angles) :
ମନେରଖ : ଦୁଇଟି କୋଣ ସନ୍ନିହିତ ହେଲେ, ସେମାନଙ୍କର
(i) ଗୋଟିଏ ସାଧାରଣ ଶୀର୍ଷବିନ୍ଦୁ;
(ii) ଗୋଟିଏ ସାଧାରଣ ବାହୁ ଏବଂ
(iii) ସେମାନଙ୍କର ଅନ୍ତର୍ଦେଶଦ୍ଵୟ ଅଣଛେଦୀ ହୁଅନ୍ତି ।
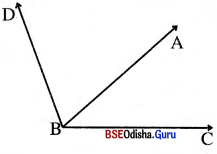
→ ନିଜେ କର :
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ର ଦେଖ୍ ଉତ୍ତର ଦିଅ ।
(i) \(\overrightarrow{\mathrm{AC}}\) ସାଧାରଣ ବାହୁ ଥିବା ଦୁଇଯୋଡ଼ା ସନ୍ନିହିତ କୋଣର ନାମ ଲେଖ ।
(ii) \(\overrightarrow{\mathrm{AD}}\) ସାଧାରଣ ବାହୁଥିବା ଦୁଇଯୋଡ଼ା ସନ୍ନିହିତ କୋଣର ନାମ ଲେଖ ।
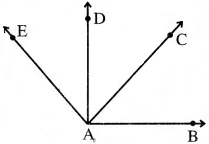
ଦୁଇଟି ସନ୍ନିହିତ କୋଣର ପରିମାଣର ସମଷ୍ଟି 180° ହେଲେ, ସେମାନଙ୍କୁ ସନ୍ନିହିତ ପରିପୂରକ କୋଣ କୁହାଯାଏ ।
→ ପ୍ତତାପ କୋଣ (Vertically Opposite Angles) :
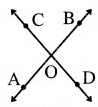
ଦୁଇଟି ସରଳରେଖା \(\stackrel{\leftrightarrow}{\mathrm{AB}}\) ଓ CD ପରସ୍ପରକୁ ୦ ବିନ୍ଦୁରେ ଛେଦକରୁଛନ୍ତି । ଏଠାରେ ∠AOC ଓ ∠BODକୁ ପ୍ରତୀପ କୋଣ କୁହାଯାଏ । ସେହିପରି ∠BOC ଏବଂ ∠DOA ମଧ୍ୟ ପରସ୍ପର ପ୍ରତୀପ କୋଣ ଅଟନ୍ତି ।
→ ନିଜେ କର :
\(\stackrel{\leftrightarrow}{\mathrm{AB}}\) ଓ \(\stackrel{\leftrightarrow}{\mathrm{CD}}\) ପରସ୍ପରକୁ O ବିନ୍ଦୁରେ ଛେଦ କରୁଥିବା ତିନୋଟି ଭିନ୍ନ ଚିତ୍ର ଅଙ୍କନ କର । ଦୁଇଯୋଡ଼ା ପ୍ରତୀପ କୋଣକୁ ପ୍ରୋଟ୍ରାକ୍ଟର ସାହାଯ୍ୟରେ ମାପି ସାରଣୀଟି ପୂରଣ କର ।

ଏହି ସାରଣୀରୁ କ’ଣ ଲକ୍ଷ୍ୟ କରୁଛ ଲେଖ ।
