Odisha State Board BSE Odisha 8th Class Maths Notes Geometry Chapter 2 ତ୍ରିଭୁଜ will enable students to study smartly.
BSE Odisha Class 8 Maths Notes Geometry Chapter 2 ତ୍ରିଭୁଜ
→ ତ୍ରିଭୁଜ, ତ୍ରିଭୁଜର ଶୀର୍ଷବିନ୍ଦୁ, ବାହୁ ଓ କୋଣ :
- A, B ଓ C ତିନୋଟି ବାହୁ ଏକ ସରଳରେଖାରେ ଅବସ୍ଥାନ ନ କଲେ, A ଓ B ବିନ୍ଦୁଦ୍ଵୟକୁ ନେଇ \(\overline{\mathrm{AB}})\) (ରେଖାଖଣ୍ଡ AB), B ଓ C ବିନ୍ଦୁଦ୍ଵୟକୁ ନେଇ BC (ରେଖାଖଣ୍ଡ BC) ଏବଂ C ଓ A ବିନ୍ଦୁଦ୍ୱୟକୁ ନେଇ CA (ରେଖାଖଣ୍ଡ CA) ଅଙ୍କନ କରିବା ସମ୍ଭବ ।
ଏହି ତିନି ରେଖାଖଣ୍ଡଦ୍ଵାରା ଗଠିତ ଚିତ୍ରଟି ହେଉଛି ତ୍ରିଭୁଜ ABC |
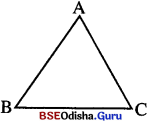
- ତିନୋଟି ବିନ୍ଦୁ A, B ଓ C ଏକ ସରଳରେଖାରେ ଅବସ୍ଥାନ କରୁ ନଥିଲେ, AB, BC ଓ \(\overline{\mathrm{CA}})\) ଏହି ସେତ୍ରୟର ସଂଯୋଗକୁ ତ୍ରିଭୁଜ ABC କୁହାଯାଏ ଓ ସଂକେତରେ △ABC (ବା ABC △) ରୂପେ ଲେଖାଯାଏ |
- \(\overline{\mathrm{AB}})\),\(\overline{\mathrm{BC}})\),\(\overline{\mathrm{CA}})\) ତ୍ପତ୍ୟେଲ ଦିନ୍ଦୁମାନର ସେଟ୍ ହୋଇଥିବା ହେତୁ ସେମାନକଦ୍ୱାରା ଗଠିର ତିରୁକ ମଧ୍ୟ ବିନ୍ଦୁମାନର ସେଟ୍ | △ABC = AB∪BC∪CA
- A, B ଓ C ବିନ୍ଦୁତ୍ରଯକୁ △ABCର କୋମାକ ଦିନ୍ଦୁ ଦା ଶାପଦିହୁ (Vertex) କୁହାଯାଏ | AB, BC ଓ CA କୁ △ABC ର ଗୋଟିଏ ଗୋଟିଏ ଦାଦୁ (side) କ୍ମିହଯାଏ | ∠ABC, ∠BCA ଓ ∠CAB କ △ ABC ର ଗୋଟିଏ ଗୋଟିଏ କୋଣ କୁହାଯାଏ ଓ ସଯେପରେ ଯଥାକ୍ତମେ ∠B, ∠C, ∠A ରୁପେ ଲେଖାଯାଏ |
- ପ୍ତତେଲ ତ୍ରିଭୁଜର ତିନୋଟି ଦାହି ଓ ତିନୋଟି କୋଣା ଥାଏ |
- ∠A କୁ BC ଦ୍ଵାଦୁଇ ସମ୍ମଖାନା କୋଣ (opposite angle) ଓ BC ବାହୁକୁ ∠A ର ସମ୍ମଖାନ ଦାହୁ କୁହାଯାଏ |
- ∠A ଓ ∠B ପ୍ରତ୍ୟେକକୁ ବାହୁ AB ର ସଂଲଗ୍ନ କୋଣ କୁହାଯାଏ ।
- CA ର ସଂଲଗ୍ନ କୋଣ ହେଲେ ∠C ଓ ∠A ଏବଂ BCର ସଂଲଗ୍ନ କୋଣ ହେଲେ, ∠B ଓ ∠C | AB ଓ AC ପ୍ରତ୍ୟେକକୁ ∠Aର ସଂଲଗ୍ନ ବାହୁ ବୋଲି କୁହାଯାଏ ।
![]()
→ ତ୍ରିଭୁଜର ଅନ୍ତର୍ଦେଶ ଏବଂ ବହିର୍ଦେଶ (Interior and Exterior of the Triangle) :
- ଏକ ସରଳରେଖାରେ ନ ଥିବା ତିନୋଟି ବିନ୍ଦୁ ମଧ୍ୟ ଦେଇ ଗୋଟିଏ ମାତ୍ର ସମତଳ ସମ୍ଭବ । ଏଣୁ ତ୍ରିଭୁଜଟିଏ ସର୍ବଦା ଏକ ସମତଳ ଉପରେ ଅବସ୍ଥାନ କରିବ ।
- ଯେଉଁ ବିନ୍ଦୁଗୁଡ଼ିକ ∠A, ∠B ଓ ∠Cର ଅନ୍ତଃସ୍ଥ ତାହା △ABCର ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ ଅଟେ ।
- △ABCର ସମସ୍ତ ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁର ସେଟ୍କୁ ଏହାର (△ABCର) ଅନ୍ତର୍ଦେଶ (Interior) କୁହାଯାଏ ।
- ତ୍ରିଭୁଜର ବହିଃସ୍ଥ ବିନ୍ଦୁମାନଙ୍କର ସେଟ୍କୁ ଏହାର ବହିର୍ଦେଶ (Exterior) କୁହାଯାଏ ।
- ସମତଳ ଉପରିସ୍ଥ ସମସ୍ତ ବିନ୍ଦୁ ତିନୋଟି ସେଟ୍ରେ ଅଛନ୍ତି । ଯଥା
- ତ୍ରିଭୁଜ ଉପରିସ୍ଥ ବିନ୍ଦୁମାନଙ୍କର ସେଟ୍,
- ତ୍ରିଭୁଜର ଅନ୍ତର୍ଦେଶ ଏବଂ
- ତ୍ରିଭୁଜର ବହିର୍ଦେଶ ।
- ତ୍ରିଭୁଜର ବହିର୍ଦେଶ ମଧ୍ୟ ଉତ୍ତଳ ସେଟ୍ ନୁହେଁ ।
- ଏକ ତ୍ରିଭୁଜ ଓ ଏହାର ଅନ୍ତର୍ଦେଶକୁ ଏକତ୍ର ନେଇ ଯେଉଁ ସେଟ୍ ଗଠିତ ହୁଏ, ତାକୁ ତ୍ରିଭୁଜ ଆକୃତିବିଶିଷ୍ଟ କ୍ଷେତ୍ର ଅଥବା ତ୍ରିଭୁଜାକାର କ୍ଷେତ୍ର (Triangular region) କୁହାଯାଏ ।
→ ତୁମାପଇଁ କାପ :
ଚିତ୍ରରେ ଥିବା ∠ABC ଓ ଏହି ସମତଳରେ ଥିବା P, Q, R, S, T, U, V, M, N, ଓ W ବିନ୍ଦୁମାନଙ୍କୁ ଦେଖ୍ ନିମ୍ନସ୍ଥ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଦିଅ । A, B, C ଏବଂ ପୂର୍ବୋକ୍ତ ଆଠଟି ବିନ୍ଦୁମାନଙ୍କ ମଧ୍ୟରୁ –
(i) କେଉଁ ବିନ୍ଦୁ ∠Aର ଅନ୍ତଃସ୍ଥ ?
(ii) କେଉଁ ବିନ୍ଦୁ ∠Bର ଅନ୍ତଃସ୍ଥ ?
(iii) କେଉଁ ବିନ୍ଦୁ ∠Cର ଅନ୍ତଃସ୍ଥ ?
(iv) କେଉଁ ବିନ୍ଦୁ ∠A, ∠B, ∠Cର ଅନ୍ତଃସ୍ଥ ?.
(v) କେଉଁ ବିନ୍ଦୁ A, ∠B, ∠Cର କୌଣସି
(vi) କେଉଁ ବିନ୍ଦୁ △ABC ଉପରିସ୍ଥ ?
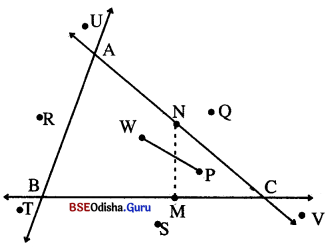
(1) W, P, (ii) W, P, (iii) W, P. (iv) W, P (v) R, T, S, Q, V, U, (vi) N, M
ମନେରଖ : ଯେଉଁ ବିନ୍ଦୁ ∠A, ∠B ଓ ∠Cର ଅନ୍ତଃସ୍ଥ ତାହା △ABCର ଅନ୍ତସ୍ଥ ବିନ୍ଦୁ ଅଟେ ।
→ ବିଭିନ୍ନ ପ୍ରକାର ତ୍ରିଭୁଜ (Types of Triangles) :
- ବାହୁମାନଙ୍କ ଦୈର୍ଘ୍ୟ ସମ୍ବନ୍ଧୀୟ ପ୍ରକାରଭେଦ :
(i) ଯେଉଁ ତ୍ରିଭୁଜର ଦୁଇଟି ବାହୁର ଦୈର୍ଘ୍ୟ ପରସ୍ପର ସମାନ, ତାହା ଏକ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜ ।
(ii) ଯେଉଁ ତ୍ରିଭୁଜର ବାହୁତ୍ରୟର ଦୈର୍ଘ୍ୟ ପରସ୍ପର ସମାନ, ତାହା ଏକ ସମବାହୁ ତ୍ରିଭୁଜ’।
(iii) ଯେଉଁ ତ୍ରିଭୁଜର କୌଣସି ଯୋଡ଼ା ବାହୁର ଦୈର୍ଘ୍ୟ ପରସ୍ପର ସମାନ ନୁହେଁ ତାହା ଏକ ବିଷମବାହୁ ତ୍ରିଭୁଜ । - କୋଣମାନଜ ମାପ ସମଦିୟ ପ୍ରକାରଭେଦ :
(i) ଯେଉଁ ତ୍ରିଭୁଜର ଗୋଟିଏ କୋଣ ସମକୋଣ ବା 90° ସଙ୍ଗେ ସମାନ ତାହା ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜ ।
(ii) ଯେଉଁ ତ୍ରିଭୁଜର ଗୋଟିଏ କୋଣ ସ୍ଥୂଳକୋଣ ବା 90° ରୁ ବେଶୀ ତାହା ଏକ ସ୍ଥୂଳକୋଣୀ ତ୍ରିଭୁଜ ।
(iii) ଯେଉଁ ତ୍ରିଭୁଜର କୋଣତ୍ରୟ ପ୍ରତ୍ୟେକ ସୂକ୍ଷ୍ମକୋଣ ବା 90° ରୁ କମ୍ ତାହା ଏକ ସୂକ୍ଷ୍ମକୋଣୀ ତ୍ରିଭୁଜ ।
ଏକ ସମକୋଣା ତ୍ରିଭୁଜର ସମକୋଣା ଦ୍ୟାବାତ ଅନ୍ୟ କୋଣଦୟ ପ୍ରତେଅଲ ତ୍ପକଲେଣ ଓ ଗୋଟିଏ ସ୍ଥୂଳକୋଣୀ ତ୍ରିଭୁଜର ସ୍ଥୂଳକୋଣ ବ୍ୟତୀତ ଅନ୍ୟ କୋଣଦ୍ଵୟ ପ୍ରତ୍ୟେକ ସୂକ୍ଷ୍ମକୋଣ |
→ ତ୍ରିଭୁଜ ସମ୍ବନ୍ଧୀୟ କେତୋଟି ପରୀକ୍ଷା :
- ବିଷମବାହୁ ତ୍ରିଭୁଜ ଅଙ୍କନ (ସ୍କେଲ୍ ଓ କମ୍ପାସ୍ ସାହାଯ୍ୟରେ) :
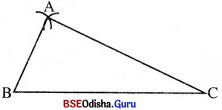
(i) ଯେ କୌଣସି ଦୈର୍ଘ୍ୟବିଶିଷ୍ଟ BC ଅଙ୍କନ କର ।
(ii) Bକୁ କେନ୍ଦ୍ରକରି ଓ BC ଠାରୁ ଭିନ୍ନ ଏକ ଚାପ ଅଙ୍କନ କର ।
(iii) Cକୁ କେନ୍ଦ୍ରକରି ଓ BC ତଥା (ii)ରେ ନେଇଥିବା ବ୍ୟାସାର୍ଷଠାରୁ ପୃଥକ୍ ଏକ ବ୍ୟାସାର୍ଦ୍ଧ ନେଇ ଅନ୍ୟ ଏକ ଚାପ ଅଙ୍କନ କର, ଯେପରି ଏହା ଅଙ୍କିତ ଚାପକୁ ଛେଦ କରିବ । ଛେଦବିଦୁର ନାମ A ଦିଅ । AB ଓ AC ଅଙ୍କନ କର । ବର୍ତ୍ତମାନ ମିଳିଥିବା ତ୍ରିଭୁଜ ଏକ ବିଷମବାହୁ ତ୍ରିଭୁଜ । - ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜ ଅଙ୍କନ :
(i) ଯେ କୌଣସି ଦୈର୍ଘ୍ୟନେଇ BC ଅଙ୍କନ କର ।
(ii) Bକୁ କେନ୍ଦ୍ରକରି BC ସହ ସମାନ ବ୍ୟାସାର୍ଦ୍ଧ ନେଇ ଚାପଟିଏ ଅଙ୍କନ କର ।
(iii) Cକୁ କେନ୍ଦ୍ରକରି BCଠାରୁ ପୃଥକ୍ ଏକ ବ୍ୟାସାର୍ଦ୍ଧ ନେଇ ଚାପଟିଏ ଅଙ୍କନ କର, ଯେପରିକି ଏହା ପ୍ରଥମରେ ଅଙ୍କିତ ଚାପକୁ ଛେଦକରିବ ।
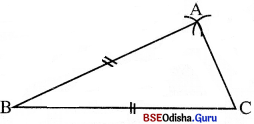
(iv) ଏହି ଅଙ୍କିତ ଚାପଦ୍ଵୟର ଛେଦବିନ୍ଦୁର ନାମ A ଦିଅ । AB ଓ AC ଅଙ୍କନ କର । ବର୍ତ୍ତମାନ AABC ଏକ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜ ।
ଏହାର BC = AB ଏବଂ CA ଏହାର ଭୂମି ।
- ସମବାହୁ ତ୍ରିଭୁଜ ଅଙ୍କନ :
(i) ଯେ କୌଣସି ଦୈର୍ଘ୍ୟନେଇ BC ଅଙ୍କନ କର ।
(ii) B ବିନ୍ଦୁକୁ କେନ୍ଦ୍ରକରି BC ସହ ସମାନ ବ୍ୟାସାର୍ଦ୍ଧ ନେଇ ଚାପଟିଏ ଅଙ୍କନ କର !
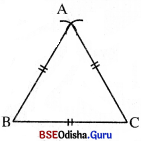
(iii) Cକୁ କେନ୍ଦ୍ରକରି ପ୍ରଥମେ ନେଇଥିବା ବ୍ୟାସାର୍ଦ୍ଧ (BC ସହ ସମାନ) ନେଇ ଚାପଟିଏ ଅଙ୍କନ କର ।
(iv) ଅଙ୍କିତ ଚାପଦ୍ଵୟର ଛେଦ ବିନ୍ଦୁର ନାମ A ଦିଅ । AB ଓ AC ଅଙ୍କନ କର । ବର୍ତ୍ତମାନ △ABC ଏକ ସମବାହୁ ତ୍ରିଭୁଜ । ଏହାର AB = BC = AC | - ସମକୋଣୀ ତ୍ରିଭୁଜ ଅଙ୍କନ :
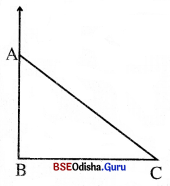
(i) ଯେ କୌଣସି ଦୈର୍ଘ୍ୟବିଶିଷ୍ଟ BC ଅଙ୍କନ କର ।
(ii) BC ସହ ସେୟାରରେ ସମକୋଣ ସଂଲଗ୍ନ ଗୋଟିଏ ଧାର ଲଗାଇ ରଖ ଯେପରି ଏହାର ସମକୋଣ Bଠାରେ ରହିବ । ସେୟାରର ସମକୋଣ ସଂଲଗ୍ନ ଅନ୍ୟ ଧାରକୁ ଲଗାଇ ଏକ ରେଖାଖଣ୍ଡ ଅଙ୍କନ କର ଯାହାର ଗୋଟିଏ ପ୍ରାନ୍ତବିନ୍ଦୁ B, ଏହାର ଅନ୍ୟ ପ୍ରାନ୍ତବିନ୍ଦୁର ନାମ A ଦିଅ ।
(iii) AC ଅଙ୍କନ କର । ବର୍ତମାନ ମିଳିଥିବା △ABC ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜ । - ସ୍ଥୂଳକୋଣୀ ତ୍ରିଭୁଜ ଅଙ୍କନ :
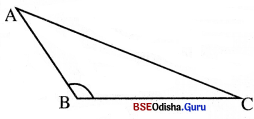
(i) ଯେକୌଣସି ଦୈର୍ଘ୍ୟବିଶିଷ୍ଟ BC ଅଙ୍କନ କର ।
(ii) BC ସହ Bଠାରେ ସ୍ଥୂଳକୋଣ (ଅର୍ଥାତ୍ 90° ରୁ ଅଧିକ ପରି ମାଣବିଶିଷ୍ଟ କୋଣ) ଅଙ୍କନ କରୁଥିବା BA (ଯେକୌଣସି ଦୈର୍ଘ୍ୟବିଶିଷ୍ଟ) ଅଙ୍କନ କର ।
(iii) AC ଅଙ୍କନ କର । ବର୍ତ୍ତମାନ ମିଳିଥିବା △ABC ଏକ ସ୍ଥୂଳକୋଣୀ ତ୍ରିଭୁଜ ।
![]()
→ ଅନୁସିଦ୍ଧାନ୍ତ – 2 :
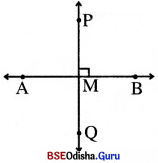
\(\overleftrightarrow{\mathrm{AB}}\) ର ବହିଃସ୍ଥ P ଏକ ବିନ୍ଦୁ ହେଲେ, P ବିନ୍ଦୁ ମଧ୍ୟ ଦେଇ ଗୋଟିଏ ମାତ୍ର PQ ଅଙ୍କନ ହେବ, ଯେପରିକି AB ସହ PQ ଏକ ସମକୋଣ ସୃଷ୍ଟି କରିବ । ଏଠାରେ PQ ଓ AB ପରସ୍ପର ପ୍ରତି ଲମ୍ବ କୁହାଯାଏ । ଯଦି AB ଓ PQ ର ଛେଦବିନ୍ଦୁ M ହୁଏ, ତେବେ \(\overline{\mathrm{PM}})\) କୁ P ବିନ୍ଦୁରୁ \(\overleftrightarrow{\mathrm{AB}}\) ପ୍ରତି ଲମ୍ବ ବୋଲି କୁହାଯାଏ ଏବଂ M ବିନ୍ଦୁକୁ \(\overline{\mathrm{PM}})\) ଲମ୍ବର ପାଦବିନ୍ଦୁ କୁହାଯାଏ ।
- କ୍ତିରୁଲଭ ରକତା (Height of the triangle) :
△ABCରେ A ବିନ୍ଦୁରୁ BC ପ୍ରତି ଗୋଟିଏ ମାତ୍ର ଲମ୍ବ ଅଙ୍କନ ସମ୍ଭବ । \(\overline{\mathrm{AP}})\)ର ଦୈର୍ଘ୍ୟ APକୁ △ABCର A ଶୀର୍ଷବିନ୍ଦୁରୁ \(\overline{\mathrm{BC}})\) ପ୍ରତି ଉଚ୍ଚତା କୁହାଯାଏ । ସେହିପରି BQ ଓ CRକୁ ଯଥାକ୍ରମେ B ବିନ୍ଦୁରୁ AC ପ୍ରତି ଓ C ବିନ୍ଦୁରୁ AB ପ୍ରତି ଉଚ୍ଚତା କୁହାଯାଏ
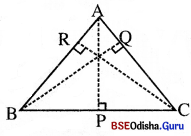
ତ୍ରିଭୁଜର ମଧ୍ୟମା (Medians of a triangle) :
ତ୍ରିଭୁଜର କୌଣସି କୌଣିକ ବିନ୍ଦୁ ଓ ତାହାର ସମ୍ମୁଖୀନ ବାହୁର ମଧ୍ୟବିନ୍ଦୁକୁ ସଂଯୋଗ କରୁଥିବା ରେଖାଖଣ୍ଡକୁ ତ୍ରିଭୁଜର ମଧ୍ୟମା କୁହାଯାଏ । A ର ସମ୍ମୁଖୀନ ବାହୁ BC ର ମଧ୍ୟବିନ୍ଦୁ D ଅଟେ । ତେଣୁ AD ଗୋଟିଏ ମଧ୍ୟମା । ସେହିପରି BE ଓ CF ଅନ୍ୟ ଦୁଇଟି ମଧ୍ୟମା ।
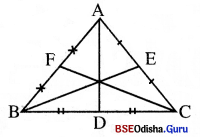
ତ୍ରିଭୁଜର କୋଣମାନଙ୍କ ସମଦ୍ବିଖଣ୍ଡକ (Bisectors of the angles of a triangle or angle-bisectors of a triangle) :
△ABCର କୋଣମାନଙ୍କର ସମଦ୍ଵିଖଣ୍ଡକ ରଶ୍ମିଗୁଡ଼ିକ ହେଲେ, \(\overrightarrow{\mathrm{AX}}\), BY ଏବଂ \(\overrightarrow{\mathrm{CZ}}\)। ସେଗୁଡ଼ିକ ଯଥାକ୍ରମେ ∠A, ∠B ଓ ∠Cର ଅନ୍ତଃସମଦ୍ବିଖଣ୍ଡକ ଅଟନ୍ତି ।
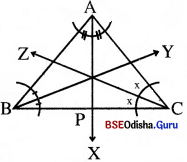
→ ସିଦାନ୍ତ – 2 :
ଏକ ତ୍ରିଭୁଜର ଯେ କୌଣସି ଦୁଇ ବାହୁର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି ଏହାର ତୃତୀୟ ବାହୁର ଦୈର୍ଘ୍ୟଠାରୁ ବୃହତ୍ତର ।
→ ଥନୁସିବାନ୍ତ୍ର
ଏକ ତ୍ରିଭୁଜର ଯେ କୌଣସି ଦୁଇ ବାହୁର ଦୈର୍ଘ୍ୟର ଅନ୍ତର ତୃତୀୟ ବାହୁର ଦୈର୍ଘ୍ୟଠାରୁ କ୍ଷୁଦ୍ରତର ।
→ ସିଦ୍ଧାନ୍ତ – 3 :
ଯେ କୋଣସି ସମଦ୍ୱିବାକୁ ତ୍ରିଭୁଜର ବାହୁଦୂଯଲ ସମ୍ମଖାନ କୋଶମାନର ପରିମାଣ ସମାନ ।
→ ଥନୁସିବାନ୍ତ୍ର
ଏକ ସମବାହୁ ତ୍ରିଭୁଜର କୋଣତ୍ରୟର ପରିମାଣ ସମାନ ଓ ପ୍ରତ୍ୟେକର ପରିମାଣ 60° |
→ ସିଦ୍ଧାନ୍ତ – 4 :
ଏକ ତ୍ରିଭୁଜର ଦୁଇଟି କୋଣର ପରିମାଣ ସମାନ ହେଲେ, ଏହି କୋଣଦ୍ଵୟର ସମ୍ମୁଖୀନ ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ
![]()
→ ତ୍ରିଭୁଜର ବହିଃସ୍ଥ କୋଣ :
- ତ୍ରିଭୁଜର ପ୍ରତ୍ୟେକ ଅନ୍ତଃସ୍ଥ କୋଣର ସନ୍ନିହିତ ପରିପୂରକ କୋଣକୁ ତ୍ରିଭୁଜର ବହିଃସ୍ଥ କୋଣ କୁହାଯାଏ ।
- ତ୍ରିଭୁଜର କୌଣସି ଏକ ଶୀର୍ଷବିନ୍ଦୁରେ ଥିବା ଅନ୍ତଃସ୍ଥ କୌଣ ଓ ଏକ ବହିଃସ୍ଥ କୋଣର ପରିମାଣର ସମଷ୍ଟି 180° |
- △ABC ର ∠B ଓ ∠C କୁ A ଠାରେ ଥିବା ବହିଃସ୍ଥ କୋଣର ଅନ୍ତଃସ୍ଥ ଦୂରବର୍ତ୍ତୀ କୋଣ କୁହାଯାଏ । ସେହିପରି ∠C ଓ ∠A, ∠A ଓ ∠B ଯଥାକ୍ରମେ B ଏବଂ C ଠାରେ ଥିବା ବହିଃସ୍ଥ କୋଣର ଅନ୍ତଃସ୍ଥ ଦୂରବର୍ତ୍ତୀ କୌଣ କୁହାଯାଏ ।
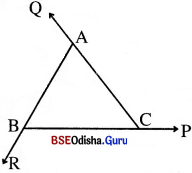
→ ସିଦ୍ଧାନ୍ତ – 5 :
କୋଣସି ଦିରୁକାର ଏକ ଶାୟବିଦୁଲେ ଥିବା ଗୋଟିଏ ଦହିମ କୋଣର ପରିମାଣ ଏହାର ଅନୁମ ଦୁଇ ଦଭା କୋଣଦ୍ଵୟର ପରିମାଣର ସମଷ୍ଟି ସଙ୍ଗେ ସମାନ ।
