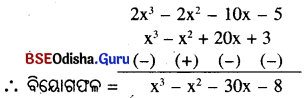Odisha State Board BSE Odisha 8th Class Maths Solutions Algebra Chapter 3 ବୀଜଗାଣିତିକ ପରିପ୍ରକାଶ ଓ ଅଭେଦ Ex 3(b) Textbook Exercise Questions and Answers.
BSE Odisha Class 8 Maths Solutions Algebra Chapter 3 ବୀଜଗାଣିତିକ ପରିପ୍ରକାଶ ଓ ଅଭେଦ Ex 3(b)
Question 1.
ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(i) 5x – 3x = 5x + (………..) = {(………..) + (………..)}x = (………..)
(ii) 3x- (-2x) = 3x + (………..) = {(………..) + (………..)} x = (………..)
(iii) -2x – 3x = -2x + (………..) = {(………..) + (………..)}x = (………..)
(iv) (2 + 3x) – (3 – 2x) = (2 + 3x) + (………..) = (2 – 3) + (3x + ………..) = (………..) + (………..)
(v) (x – 4) – (-3x + 2) = (x – 4) + (………..) = (x + 3x) + (………..) = (………..) + (………..)
ସମାଧାନ :
(i) 5x – 3x = 5x + (-3x) = {(5)+(-3)} x = (2x)
(ii) 3x – (-2x) = 3x + (2x) = {(3)+(2)}x = (5x)
(iii) -2x – 3x = -2x + (-3x) = {(-2) + (-3)} x = (-5x)
(iv) (2 + 3x) – (3 – 2x) = (2 + 3 x) + (2 x – 3)
= (2 – 3)+ {3 x + (2x)} = (-1) + (5x)
(v) (x – 4) – (-3x + 2) = (x – 4) + (3x-2)
= (x + 3x) + (-4 – 2) = (4x) + (-6)
![]()
Question 2.
ବିୟୋଗ କର ।
(i) 12x ରୁ 9x
(ii) 5x ରୁ -3x
(iii) -2 x ରୁ 3x
(iv) -4x ରୁ -6x
(v) (x + 2) ରୁ (3x + 2)
(vi) 3 ରୁ x² + x + 1
(vii) 2x² – 2x – 2 ରୁ x² + 2x + 4
ସମାଧାନ :
(i) 12x – 9x + 12x + (-9x) = {12 + (-9)}x = 3x
(ii) 5x – (-3x) = 5x + 3x = (5+3)x = 8x
(iii) -2x – 3x = -2x + (-3x) = {-2 + (-3)}x = -5x
(iv) -4x – (-6x) = -4x + 6x = {-4 + 6}x = 2x
(v) (x + 2) – (3x + 2) = x + 2 – 3x – 2 = x – 3x + 2 – 2
= x + (-3x) + 2 +(-2)
= {1 + (-3)}x + {2 + (-2)} = -2x
(vi) 3 – (x² + x + 1) = 3 – x² – x – 1 = -x² – x + 3 – 1 = -x² – x + 2
(vii) (2x² – 2x – 2) – (x² + 2x + 4) = 2x² – 2x – 2 – x² – 2x – 4
= 2x² – x² – 2x – 2x – 2 – 4 = 2x² + (-x²) + (-2x) + (-2x) + (-2) + (-4)
= {2+(-1)} x²+{(-2)+(-2)} x+{(-2)+(-4)}
= x² + (-4x) + (-4) = x²- 4x – 4
![]()
Question 3.
ବିୟୋଗଫଳ ନିର୍ଣ୍ଣୟ କର ।
(i) 2x² + 2 x ରୁ 2x²
(ii) 5x² + 3 x ରୁ x² + 3 x
(iii) 2x² – 2 x ରୁ x² + 2 x
(iv) 3x² + 3 x + 2 ରୁ x² + 3 x – 2
(v) 2x² – 5 x – 1 ରୁ x² + 5 x – 1
(vi) 4 + 3 x + 2x² + x³ ରୁ x³ + 2x² – 3 x – 4
(vii) 2x³ – 5 – 2x² – 10 x ରୁ x³ + 20 x – x² + 3
ସମାଧାନ :
(i) (2x² + 2x) – 2x² = 2x² + 2x + (-2x²) = 2x² + (-2x²) + 2 x = 2 x
(ii) (5x² + 3 x)-(x² + 3 x) = 5x² + 3 x + (-x²) + (-3 x)
= 5x² + (-x²) + 3 x + (-3 x) = 4x²
(iii) (2x²-2 x) – (x² + 2 x) = 2x² – 2 x – x² – 2 x = 2x² – x² – 2 x – 2 x = x² – 4 x
(iv) (3x² + 3 x + 2) – (x² + 3 x – 2) = 3x² + 3 x + 2 – x² – 3 x + 2
= 3x² – x² + 3 x – 3 x + 2 + 2 = 2x² + 4
(v) (2x² – 5 x – 1) – (x² + 5 x – 1) = 2x² – 5 x – 1 – x² – 5 x + 1
= 2x² – x² – 5 x – 5 x – 1 + 1 = x² – 10 x
ବିକଳ୍ପ ପ୍ରଣାଳୀ :

(vi) (4 + 3 x + 2x² + x³) – (x³ + 2x² – 3 x – 4)
=4 + 3 x + 2x² + x³ – x³ – 2x² + 3 x + 4
= x³ – x³ + 2x² – 2x² + 3 x + 3 x + 4 + 4
=6 x + 8
ବିକଳ୍ପ ପ୍ରଣାଳୀ :

(vii) (2x³ – 5 – 2x² – 10 x) – (x³ + 20 x – x² + 3)
= 2x² – 5 – 2x² – 10 x – x³ – 20 x + x² – 3
= 2x³ – x³ – 2x² + x² – 10 x – 20x – 5 – 3
= x³ – x² – 30 x – 8
ବିକଳ୍ପ ପ୍ରଣାଳୀ :