Odisha State Board BSE Odisha 8th Class Maths Solutions Algebra Chapter 5 ସୂଚକ ତତ୍ତ୍ଵ Ex 5(d) Textbook Exercise Questions and Answers.
BSE Odisha Class 8 Maths Solutions Algebra Chapter 5 ସୂଚକ ତତ୍ତ୍ଵ Ex 5(d)
Question 1.
ନିମ୍ନଲିଖ ରାଶିଗୁଡ଼ିକୁ ଏକ ଆଧାର ବିଶିଷ୍ଟ ଘାତ ରାଶି ରୂପେ ପ୍ରକାଶ କର ।
(i) \(64^{\frac{2}{3}}\)
(ii) \(16^{1 \frac{1}{4}}\)
(iii) \(125^{1 \frac{2}{3}}\)
(iv) \(\left(\frac{81}{625}\right)^{\frac{1}{4}}\)
(v) \(\left(\frac{1}{216}\right)^{-\frac{2}{3}}\)
(vi) \(\left(\frac{1}{27}\right)^{-1 \frac{2}{3}}\)
ସମାଧାନ :
(i) \(64^{\frac{2}{3}}=\left(4^3\right)^{\frac{2}{3}}=4^{3 \times \frac{2}{3}}=4^2=16\)
(ii) \(16^{1 \frac{1}{4}}=\left(2^4\right)^{\frac{5}{4}}=2^{4 \times \frac{5}{4}}=2^5=32\)
(iii) \(125^{1 \frac{2}{3}}=\left(5^3\right)^{\frac{5}{3}}=5^{3 \times \frac{5}{3}}=5^5=3125\)
(iv) \(\left(\frac{81}{625}\right)^{\frac{1}{4}}=\left\{\left(\frac{3}{5}\right)^4\right\}^{\frac{1}{4}}=\left(\frac{3}{5}\right)^{4 \times \frac{1}{4}}=\frac{3}{5}\)
![]()
(v)
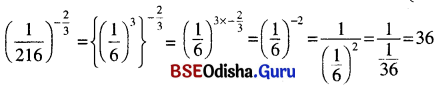
(vi)
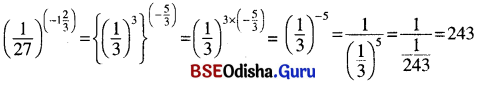
ବିକଳ୍ପ ପ୍ରଣାଳୀ :
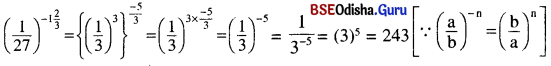
Question 2.
ସରଲ କର ।
(i) \(\sqrt{2} \times \sqrt[3]{2} \times \sqrt[6]{2}\)
(ii) \(8^3 \times 4^{\frac{1}{2}} \div 16^2\)
(iii) \(27^{1 \frac{1}{3}} \times \sqrt{\frac{1}{9}} \div 81^{-\frac{1}{4}}\)
(iv) \(\left(\frac{4}{9}\right)^{\frac{1}{2}} \times 4^0 \times\left(1 \frac{1}{3}\right)^{-1}\)
(v) \((\sqrt[2]{25})^2 \times(125)^{\frac{1}{3}} \times(625)^{\frac{1}{4}}\)
(vi) \((343)^{\frac{1}{3}} \times(49)^{\frac{1}{2}} \div 14\)
ସମାଧାନ :
(i)
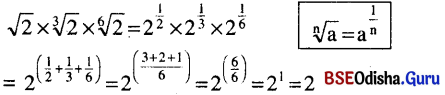
(ii) \(8^3 \times 4^{\frac{1}{2}} \div 16^2\)
= (23)3 × (22)\(\frac{1}{2}\) ÷ (24)2 = 23×3 × 2\(2 \times \frac{1}{2}\) ÷ 24×2 = 29 × 2 ÷ 28 = 29+1-8 = 22 = 4
(iii)
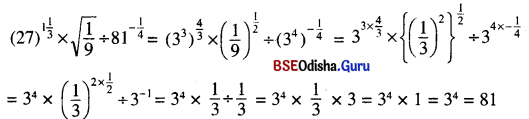
(iv)
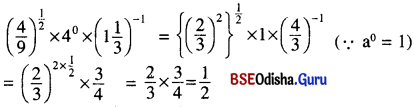
(v)
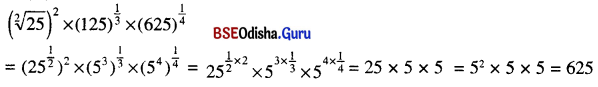
(vi)
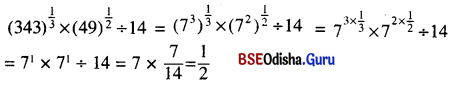
![]()
Question 3.
ସରଲ କର ।
(i) \(\left(\mathbf{a}^l\right)^{\mathrm{m}-\mathrm{n}} \times\left(\mathbf{a}^{\mathrm{m}}\right)^{\mathrm{n}-l} \times\left(\mathbf{a}^{\mathrm{n}}\right)^{l-\mathrm{m}}(\mathbf{a} \neq 0, l, \mathrm{~m}, \mathbf{n} \in \mathbf{Q})\)
(ii) \(\left(\frac{a^p}{a^q}\right)^{p+q} \times\left(\frac{a^q}{a^r}\right)^{q+r} \times\left(\frac{a^r}{a^p}\right)^{r+p}(\mathbf{a} \neq 0, p, q, r \in Q)\)
ସମାଧାନ :
(i)

(ii)
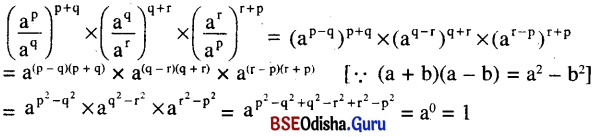
![]()
Question 4.
ଗୁଣଫଳ ସ୍ଥିର କର ।
(i) \(\left(a^{\frac{1}{2}}+b^{\frac{1}{2}}\right)\left(a^{\frac{1}{2}}-b^{\frac{1}{2}}\right)\) (a > 0, b > 0)
(ii) \((\sqrt{x}+\sqrt{y})(\sqrt{x}-\sqrt{y})\) (x > 0, y > 0)
ସମାଧାନ :
(i) \(\left(a^{\frac{1}{2}}+b^{\frac{1}{2}}\right)\left(a^{\frac{1}{2}}-b^{\frac{1}{2}}\right)\)
\(a^{\frac{1}{2}}\) = x ଓ \(b^{\frac{1}{2}}\) = y ନେଲେ ଦତ୍ତ ପରିପ୍ରକାଶଟି ହେବ (x + y) (x – y) = x² – y²
= (\(a^{\frac{1}{2}}\))² – (\(b^{\frac{1}{2}}\))² [x ଓ y ର ମାନ ନେଲେ]
= \(a^{\frac{1}{2} \times 2}-b^{\frac{1}{2} \times 2}\) = a – b
(ii) \((\sqrt{x}+\sqrt{y})(\sqrt{x}-\sqrt{y})\) = \(\left(x^{\frac{1}{2}}+y^{\frac{1}{2}}\right)\left(x^{\frac{1}{2}}-y^{\frac{1}{2}}\right)\)
\(x^{\frac{1}{2}}\) = a ଓ \(y^{\frac{1}{2}}\) = b ନେଲେ ଦତ୍ତ ପରିପ୍ରକାଶଟି ହେବ
(a + b) (a – b) = a² – b² = (\(x^{\frac{1}{2}}\))² – (\(y^{\frac{1}{2}}\))² (a ଓ bର ମାନ ନେଲେ)
= \(x^{\frac{1}{2} \times 2}-y^{\frac{1}{2} \times 2}\) = x – y
