Odisha State Board BSE Odisha 8th Class Maths Solutions Geometry Chapter 3 ଚତୁର୍ଭୁଜ Ex 3(b) Textbook Exercise Questions and Answers.
BSE Odisha Class 8 Maths Solutions Geometry Chapter 3 ଚତୁର୍ଭୁଜ Ex 3(b)
Question 1.
ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(a) ____ ର କର୍ଣ୍ଣଦ୍ଵୟ ପରସ୍ପରକୁ ସମଦ୍ବିଖଣ୍ଡ କରନ୍ତି ।
(b) ______ର କର୍ଣ୍ଣଦ୍ଵୟ ପରସ୍ପର ପ୍ରତି ଲମ୍ବ ଏବଂ ପରସ୍ପରକୁ ସମଦ୍ଵିଖଣ୍ଡ କରନ୍ତି ।
(c) ____ ର କର୍ଣ୍ଣଦ୍ଵୟ ପରସ୍ପର ପ୍ରତି ଲମ୍ବ, ପରସ୍ପରକୁ ସମଦ୍ବିଖଣ୍ଡ କରନ୍ତି ଏବଂ ସମଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ।
(d) ____ ର କର୍ଣ୍ଣଦ୍ଵୟ ସମଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ଏବଂ ପରସ୍ପରକୁ ସମଦ୍ଵିଖଣ୍ଡ କରନ୍ତି ।
(e) ____ ର କର୍ଣ୍ଣଦ୍ଵୟ ପରସ୍ପରକୁ ସମଦ୍ଵିଖଣ୍ଡ କରନ୍ତି; କିନ୍ତୁ ସମଦୈର୍ଘ୍ୟ ନ ହୋଇପାରନ୍ତି ।
(f) ଏକ ଚତୁର୍ଭୁଜର କର୍ଣ୍ଣଦ୍ଵୟ ସମଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ, ପରସ୍ପର ପ୍ରତି ଲମ୍ବ ଏବଂ ପରସ୍ପରକୁ ସମନ୍ଦିଖଣ୍ଡ କରୁଥିଲେ, ସମଷ୍ଟି ____ |
(g) ଏକ ଚତୁର୍ଭୁଜର କର୍ଣ୍ଣଦ୍ଵୟ ସମଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ, ପରସ୍ପର ପ୍ରତି ଲମ୍ବ ଏବଂ ପରସ୍ପରକୁ ସମନ୍ଦିଖଣ୍ଡ କରୁଥିଲେ, ଏହାର ଦୁଇଟି କ୍ରମିକ କୋଣର ପରିମାଣର ସମଷ୍ଟି ____ |
Solution:
(a) ସମଦୈର୍ଘ୍ୟ ଚିତ୍ର
(b) ରମ୍ବସ୍
(c) ବର୍ଗଚିତ୍ର
(d) ଆୟତଚିତ୍ର
(e) ସାମାନ୍ତରିକ ଚିତ୍ର
(f) 180°
(g) 180°
![]()
Question 2.
ନିମ୍ନସ୍ଥ ଉକ୍ତିମାନଙ୍କ ମଧ୍ୟରୁ ସାମାନ୍ତରିକ ଚିତ୍ର ପାଇଁ ଯାହା ସତ୍ୟ ତା’ ପାଖରେ T ଲେଖ ଓ ଯାହା ସତ୍ୟ ନୁହେଁ ତା’ ପାଖରେ F ଲେଖ ।
(a) ବିପରୀତ କୋଣଦ୍ଵୟର ପରିମାଣ ସର୍ବଦା ସମାନ ।
(b) ବିପରୀତ ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ସମାନ ।
(c) କର୍ଣ୍ଣଦ୍ୱୟର ଛେଦବିନ୍ଦୁ ସମ୍ବନ୍ଧୀୟ ନିର୍ଦ୍ଦିଷ୍ଟ ତଥ୍ୟ କିଛି ନାହିଁ ।
(d) ଦୁଇଟି କ୍ରମିକ କୋଣ ପରସ୍ପର ପରିପୂରକ ।
(e) ଦୁଇଟି ସ୍ତମିଳ କୋଣର ପରିମାଣ ପରାମର ସାମାନ |
(f) ପ୍ରଦ୍ୟୋଗ କୋଣ ସମ୍ଭୋଗ |
(g) ଗୋଟିଏ କର୍ଣ୍ଣ ଦ୍ବାରା ଉତ୍ପନ୍ନ ତ୍ରିଭୁଜଦ୍ଵୟ ମଧ୍ୟରୁ ଗୋଟିକର ବାହୁମାନଙ୍କର ଦୈର୍ଘ୍ୟ ଯଥାକ୍ରମେ
Solution:
(a) ✓
(b) ✓
(c) x
(d) ✓
(e) x
(f) x
(g) ✓
Question 3.
ନିମ୍ନ ଉକ୍ତିମାନଙ୍କ ମଧ୍ୟରୁ ଠିକ୍ ଉକ୍ତ ପାଖରେ T ଓ ଭୁଲ୍ ଉକ୍ତି ପାଖରେ F ଲେଖ ।
(a) ପ୍ରତ୍ୟେକ ପ୍ରକାର ସାମାନ୍ତରିକ ଚିତ୍ରର ସମ୍ମୁଖୀନ କୋଣଦ୍ଵୟର ପରିମାଣ ସମାନ ।
(b) ସାମାନ୍ତରିକ ଚିତ୍ରର କଣ୍ଠଦ୍ଵୟ ପରସ୍ପରକୁ ସମକୋଣରେ ସମର୍ଦ୍ଦିଖଣ୍ଡ କରନ୍ତି ।
(c) କୌଣସି କୋଣ ସମକୋଣ ନ ହୋଇଥିବା ଏକ ରମ୍ବସ୍ର କଣ୍ଠଦ୍ଵୟ ସମଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ହେବେ ନାହିଁ।
(d) ସନ୍ନିହିତ ବାହୁର ଦୈର୍ଘ୍ୟ ସମାନ ହୋଇ ନଥିବା ଆୟତଚିତ୍ରର କର୍ଣ୍ଣଦ୍ଵୟ ସମଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ।
(e) ବର୍ଗଚିତ୍ରର କର୍ଣ୍ଣଦ୍ଵୟ ସମଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ଓ ପରସ୍ପରପ୍ରତି ଲମ୍ବ ।
(f) ଏଭଳି ସାମାନ୍ତରିକ ଚିତ୍ର ନାହିଁ ଯାହାର କଣ୍ଠଦ୍ଵୟ ପରସ୍ପରକୁ ସମଦ୍ଵିଖଣ୍ଡ କରନ୍ତି ନାହିଁ ।
Solution:
(a) ✓
(b) x
(c) ✓
(d) ✓
(e) ✓
(f) ✓
Question 4.
ABCD ସାମାନ୍ତରିକ ଚିତ୍ରର m∠A = 70° ହେଲେ, ∠B, ∠C ଏବଂ ∠D ର ପରିମାଣ ସ୍ଥିର କର ।
Solution:
ABCD ସାମାନ୍ତରିକ ଚିତ୍ରର m∠A = 70° (କର)
∴ m∠C = m∠A = 70°
(∵ସାମାନ୍ତରିକ ଚିତ୍ରର ବିପରୀତ କୋଣମାନଙ୍କର ପରିମାଣ ପରସ୍ପର ସମାନ)
ଆମେ ଜାଣିଛେ, m∠A + m∠B + m∠C + m∠D = 360°
⇒ m∠B + m∠D = 360° – 140° ( ∵ m∠A + m∠C = 140°)
⇒ m∠B + m∠D = 220°
କିନ୍ତୁ m∠B = m∠D
(∵ସାମାନ୍ତରିକ ଚିତ୍ରର ବିପରୀତ କୋଣମାନଙ୍କର ପରିମାଣ ସମାନ ।)
∴ m∠B = m∠D = \(\frac { 220° }{ 2 }\) = 110°
Question 5.
ABCD ସାମାନ୍ତରିକ ଚିତ୍ରର ଦୁଇଟି କ୍ରମିକ କୋଣର ପରିମାଣର ଅନୁପାତ 2 : 3 ହେଲେ, ସାମାନ୍ତରିକ ଚିତ୍ରର ପ୍ରତ୍ୟେକ କୋଣର ପରିମାଣ ସ୍ଥିର କର ।
Solution:
ABCD ସାମାନ୍ତରିକ ଚିତ୍ରର m∠A: m∠B = 2 : 3 (କର)
ମନେକର m∠A = 2x° ଓ m∠B = 3x°
ଆମେ ଜାଣିଛି, ସାମାନ୍ତରିକ ଚିତ୍ରର ବିପରୀତ କୋଣମାନକର ପରିମାଣ ପରଖର ସମାନ ।
∴ m∠A = m∠C = 2x° ଏବଂ m∠B = m∠D = 2x°
2x + 3x + 2x + 3x = 360° (∵ ଚତୁର୍ଭୁଜର ଚାରିକୋଣର ପରିମାଣର ସମଷ୍ଟି 360°)
⇒ 10x = 360° ⇒ X = \(\frac { 360° }{ 10 }\) = 36°
∴ କୋଣମାନକର ପରିମାଣ;
m∠A = m∠C = 2x = 2 × 36 = 72°
m∠B = m∠D = 3x = 3 × 36 = 108°
![]()
Question 6.
ଗୋଟିଏ ଚତୁର୍ଭୁଜର କୋଣମାନଙ୍କର ପରିମାଣ ଅନୁପାତ 1 : 3 : 7 : 9 ହେଲେ, ଚତୁର୍ଭୁଜର ପ୍ରତ୍ୟେକ କୋଣର ପରିମାଣ ସ୍ଥିର କର ।
Solution:
ମନେକର ଚତୁର୍ଭୁଜର କୋଣମାନଙ୍କର ପରିମାଣ ଯଥାକ୍ରମେ x°, 3x°, 7x° ଓ 9x° |
ଆମେ ଜାଣିଛୁ, ଚତୁର୍ଭୁଜର କୋଣମାନଙ୍କର ପରିମାଣର ସମଷ୍ଟି 360° |
⇒ x° + 3x° + 7x° + 9x° = 360° ⇒ 20x = 360° ⇒ x = \(\frac { 360 }{ 20 }\) = 18°
ଚତୁର୍ଭୁଜର ଚାରିକୋଣର ପରିମାଣ;
3x = 3 × 18 = 54°; 7x = 7 × 18 = 126°; ଏବଂ 9x = 9 × 18 = 162°
∴ ଚତୁର୍ଭୁଜର ଚାରିକୋଣର ପରିମାଣ 18°, 54°, 126° ଓ 162° |
Question 7.
କୌଣସି ଏକ ଚତୁର୍ଭୁଜର କୋଣଗୁଡ଼ିକର ପରିମାଣ ସମାନ ଏବଂ ଚତୁର୍ଭୁଜର କର୍ଣ୍ଣଦ୍ୱୟ ପରସ୍ପର କୁ ସମକୋଣରେ ସମଦ୍ବିଖଣ୍ଡ କରୁଥିଲେ, ଚତୁର୍ଭୁଜଟି କେଉଁ ପ୍ରକାର ଚିତ୍ର ହେବ କାରଣ ସହ ଦର୍ଶାଅ ।
Solution:
ଚତୁର୍ଭୁଜର ଚାରିକୋଣର ପରିମାଣର ସମଷ୍ଟି 360° |
କୋଣମାନଙ୍କର ପରିମାଣ ସମାନ ହେତୁ, ପ୍ରତ୍ୟେକ କୋଣର ପରିମାଣ = \(\frac { 360° }{ 4 }\) = 90°
ଅର୍ଥାତ୍ ପ୍ରତ୍ୟେକ କୋଣ ସମକୋଣ ।
ଚତୁର୍ଭୁଜର କୋଣଗୁଡ଼ିକର ପରିମାଣ ସମାନ ଏବଂ ଚତୁର୍ଭୁଜର କର୍ଣ୍ଣଦ୍ୱୟ ପରସ୍ପର ଚତୁର୍ଭୁଜଟି ଏକ ବର୍ଗଚିତ୍ର ।
Question 8.
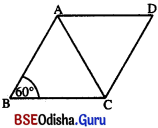
ଗୋଟିଏ ରମ୍ବସ୍ର ଗୋଟିଏ କୋଣର ପରିମାଣ 60° ହେଲେ, ଦର୍ଶାଅ ଯେ, ରମ୍ବସ୍ଟିର କ୍ଷୁଦ୍ରତର କର୍ପୂର ଦୈର୍ଘ୍ୟ ଏହାର ଏକ ବାହୁର ଦୈର୍ଘ୍ୟ ସହ ସମାନ ହେବ ।
Solution:
ଦତ୍ତ : ABCD ଏକ ରମ୍ବସ୍; ଯାହାର m∠B = 60° ଓ AC ଏହାର କ୍ଷୁଦ୍ରତର କର୍ଣ୍ଣ ।
ପ୍ରାମାଣ୍ୟ : ରମ୍ବସ୍ର ଏକ ବାହୁର ଦୈର୍ଘ୍ୟ, କ୍ଷୁଦ୍ରତର କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ ସହ ସମାନ ଅର୍ଥାତ୍ AB = AC |
ପ୍ରମାଣ : AC କର୍ଣ୍ଣ ABCD ରମ୍ବକୁ △ABC ଓ △ADC ରେ ପରିଣତ କରୁଛି ।
△ABC ରେ m∠B = 60° ହେଲେ,
m∠BAC + m∠BCA = 180° – m∠B
= 180° – 60° = 120° (∵ △ର ତିନି କୋଣର ସମସି 180°)
AB = BC (∵ ରମ୍ବସ୍ର ବାହୁ)
⇒ M∠BAC = m∠BCA (ଭୂମିସଂଲଗ୍ନ କୋଣ)
∴ m∠BAC = m∠BCA = \(\frac { 120° }{ 2 }\) = 60°
∴ △ABC ର କୋଣତ୍ରୟର ପରିମାଣ ସମାନ ।
⇒ AB = BC = AC
⇒ AB = AC (ପ୍ରମାଣିତ)
Question 9.
ଗୋଟିଏ ଚତୁର୍ଭୁଜର ଦୁଇଟି କୋଣର ପରିମାଣ ଯଥାକ୍ରମେ 60 ଏବଂ 80° । ଅନ୍ୟ କୋଣଦ୍ଵୟର ପରିମାଣ ସମାନ ହେଲେ, କୋଣମାନଙ୍କର ପରିମାଣ ସ୍ଥିର କର ।
Solution:
ABCD ଚତୁର୍ଭୁଜର m∠A = 60°, m∠B = 80°
ଏବଂ m∠C = m∠D (ଦତ୍ତ)
ଆମେ ଜାଣିଛୁ, ଚତୁର୍ଭୁଜର ଚାରିକୋଣର ପରିମାଣର ସମଷ୍ଟି 360° |
ଆମେ m∠A + m∠B + m∠C + m∠D = 360°
⇒ 60° +80° + m∠C + m∠D = 360° ⇒ m∠C + m∠D = 360° (60° + 80°) = 120°
କିନ୍ତୁ m∠C = m∠D (ଦତ୍ତ)
∴ m∠C = m∠D = \(\frac { 120° }{ 2 }\) = 60°
Question 10.
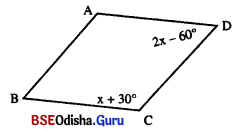
ABCD ସାମାନ୍ତରିକ ଚିତ୍ରରେ ∠C ଓ ∠D ର ପରିମାଣ (ଡିଗ୍ରୀରେ) ଦିଆଯାଇଛି । ଦତ୍ତ ମାପକୁ ନେଇ ପ୍ରତ୍ୟେକ କୋଣର ପରିମାଣ ସ୍ଥିର କର ।
Solution:
ABCD ସାମାନ୍ତରିକ ଚିତ୍ରରେ m∠A = m∠C = x + 30° ଓ m∠B = m∠D = 2x – 60°
(∵ ସାମାନ୍ତରିକ ଚିତ୍ରରେ ବିପରୀତ କୋଣମାନଙ୍କର ପରିମାଣ ସମାନ)
ଚତୁର୍ଭୁଜର ଚାରିକୋଣର ପରିମାଣର ସମଷ୍ଟି 360° |
ନେଇ m∠A + m∠B + m∠C + m∠D = 360°
⇒ x + 30° + 2x – 60° + x + 30° + 2x – 60° = 360°
⇒ 6x – 60° = 360°
⇒ 6x = 360° + 60° = 420°
⇒ x = \(\frac { 420° }{ 6 }\) = 70°
∴ m∠D = 2x – 60° = 2 × 70° – 60° = 80°
ଏବଂ m∠C = x + 30° = 70° + 30° = 100°
Question 11.
ଦଇ ଚିତ୍ରରେ ABCD ଓ PBNM ହୁଲଟି ସାମାନ୍ତରିକ ଚିତ୍ର | m∠D = 70° ହେଲେ, m∠M ଓ m∠MNB କେତେ ସ୍ଥିର କର |
Solution:
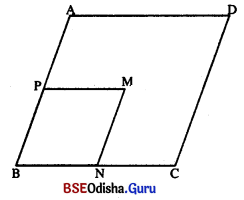
ABCD ସାମାନ୍ତରିକ ଚିତ୍ରରେ m∠D = 70° (ଦଇ)
⇒ m∠B = m∠D = 70° (∵ସାମାନ୍ତରିକ ଚିତ୍ରର ବିପରୀତ କୋଶମାନକର ପରିମାଣ ପରାମର ସମାନ)
PBNM ସାମାନ୍ତରିକ ଚିତ୍ରରେ m∠PBN = 70° (∵m∠B = 70°)
ଦଇ m∠M = m∠PBN (PBNM ସାମାନ୍ତରିକ ଚିତ୍ରରେ କୋଣ)
PBNM ସାମାନ୍ତରିକ ଚିତ୍ରରେ m∠PBN + m∠MNB + m∠M + m∠MPB = 360°
⇒ (m∠PBN + m∠M) + m∠MNB + m∠MPB = 360°
⇒ 70° + 70° + 2m∠MNB = 360° (∵ m∠MNB + m∠MPB = 2m∠MNB)
⇒ 2m∠MNB = 360° – 140° = 220°
∴ m∠MNB = \(\frac { 220° }{ 2 }\) = 110°
![]()
Question 12.
ଗୋଟିଏ ସାମାନ୍ତରିଲ ଚିତ୍ରର ଦୁଇଟି ଲୋଗ ମଧ୍ୟରୁ ଭୋଗକର ପରିମାଣ ଅନ୍ୟ କୋଣର ପରିମାଣର ତିନିଗୁଣ ହେଲେ, ଏହାର କୋଣଗୁଡ଼ିକର ପରିମାଣ ସ୍ଥିର କର ।
Solution:
ABCD ସାମାନ୍ତରିଲ ଚିତ୍ରର m∠A = 3m∠B (ଦଇ)
କିନ୍ତି m∠A = m∠C ଏବଂ m∠B = m∠D
ଆମେ ଜାଣିଛେ, m∠A + m∠C + m∠B + m∠D = 360°
⇒ m∠A + m∠A + m∠B + m∠B = 360° ⇒ 2(m∠A + m∠B) = 360°
⇒ m∠A + m∠B = \(\frac { 360° }{ 2 }\) = 180°
ସାମାନ୍ତରିକ ଚିତ୍ରର ଦୁଇଟି କ୍ରମିକ କୋଣର ପରିମାଣର ସମଷ୍ଟି 180° |
କିନ୍ତି m∠A = 3m∠B
3m∠B + m∠B = 180°
⇒ 4m∠B = 180° ⇒ m∠B = \(\frac { 180° }{ 4 }\) = 45°
∴ m∠B = m∠D = 45°
ଏବଂ m∠A = 3m∠B = 3 × 45° = 135° = m∠C
Question 13.
ଚିତ୍ରରେ ABCD, APOR ଓ TSCV ଗୋଟିଏ ଗୋଟିଏ ସାମାନ୍ତରିକ ଚିତ୍ର ।
(i) APOR ର କେଉଁ କେଉଁ କୋଣର ପରିମାଣ m/C ସହ ସମାନ ?
(ii) TSCV ର କେଉଁ କେଉଁ କୋଣର ପରିମାଣ mZA ସହ ସମାନ ?
(iii) m∠T = 110° ହେଲେ, ABCD ସାମାନ୍ତରିକ ଚିତ୍ରର କୋଣମାନଙ୍କର ପରିମାଣ ସ୍ଥିର କର ।
Solution:
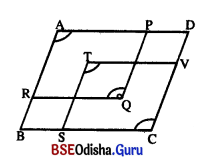
APQR ର ∠A ଓ ∠Q ର ପରିମାଣ ∠C ର ପରିମାଣ ସହ ସମାନ । [ସୂଚନା : m∠A = m∠C]
(∵ ABCD ସାମାନ୍ତରିକ ଚିତ୍ରରେ ବିପରୀତ କୋଣର ପରିମାଣ ସମାନ) କିନ୍ତୁ m∠A = m∠Q
(∵ APOR ସାମାନ୍ତରିକ ଚିତ୍ରର ବିପରୀତ କୋଣର ପରିମାଣ ସମାନ) ∴ m∠A = m∠Q = m∠C]
(ii) TSCV ର ∠T ଓ ∠C ର ପରିମାଣ ∠A ର ପରିମାଣ ସହ ସମାନ । [ସୂଚନା : m∠A = m∠C]
(∵ ABCD ସାମାନ୍ତରିକ ଚିତ୍ରର ବିପରୀତ କୋଣର ପରିମାଣ)
m∠C = m∠T
(∵ TSCV ସାମାନ୍ତରିକ ଚିତ୍ରର ବିପରୀତ କୋଣର ପରିମାଣ)]
(iii) m∠T = 110°
∴ (ii) ର ପୁନଶ୍ଚ ଅନୁଯାଯା m∠T = m∠A = m∠C
∴ m∠A = m∠C = 110°
ପୁନଶ୍ଚ, ପ୍ରଶ୍ନ (12) ର ଉତ୍ତରରୁ ଆମେ ଜାଣିଛେ, ସାମାନ୍ତରିକ ଚିତ୍ରର ଦୁଇଟି କ୍ରମିକ କୋଣର ପରିମାଣର ସମଷ୍ଟି 180° |
∴ ABCD ସାମାନ୍ତରିକ କୋଣର m∠A + m∠B = 180°
⇒ m∠B = 180° – m∠A = 180° – 110° = 70°
କିନ୍ତୁ m∠B = m∠D
∴ m∠D = 70°
∴ସାମାନ୍ତରିକ ଚିତ୍ରର କୋଣର୍ମାନଙ୍କର ପରିମାଣ 110°, 70, 110° ଏବଂ 70° |
Question 14.
ABCD ଆୟତଚିତ୍ରର କର୍ଣ୍ଣଦ୍ୱୟ ପରସ୍ପରକୁ ‘O’ ବିନ୍ଦୁରେ ଛେଦକରନ୍ତି । AO = (2x + 3) ଏକକ ଏବଂ OD = (3x +1) ଏକକ ହେଲେ, xର ମାନ ସ୍ଥିର କର ଏବଂ କର୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ସ୍ଥିର କର ।
Solution:
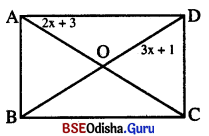
ଆୟତଚିତ୍ରର କର୍ଣ୍ଣଦ୍ଵୟ ସର୍ବସମ ଓ ପରସ୍ପରକୁ ସମଦ୍ବିଖଣ୍ଡ କରନ୍ତି।
⇒ 2x + 3 = 3x + 1 ⇒ 3x – 2x = 3 – 1 ⇒ x = 2
∴ AC = 2(2x + 3) = 2(2 × 2 + 3) = 2(4 + 3) = 2 × 7 = 14 ସେ.ମି.
BD = 2(3x + 1) = 2 (3 × 2 + 1) = 2(6 + 1) = 2 × 7 = 14 ସେ.ମି.
Question 15.
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ ABCD ଏକ ରମ୍ବସ୍ ।
ଚିତ୍ରରୁ x, y ଏବଂ z ର ମାନ ନିରୂପଣ କର ।
Solution:
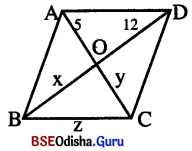
ରମ୍ବସ୍ର କର୍ଣ୍ଣଦ୍ଵୟ ପରସ୍ପରକୁ ସମକୋଣରେ ସମଦ୍ଵିଖଣ୍ଡ କରନ୍ତି ।
ଦତ୍ତ ଚିତ୍ରରେ AOD ସମକୋଣୀ △ ।
⇒ AD = \(\sqrt{5^2+12^2}\) = \(\sqrt{25+144}\) = \(\sqrt{169}\) = 13 ସେ.ମି. |
∴ z = 13 ସେ.ମି. (ରମ୍ବସ୍ର ପ୍ରତ୍ୟେକ ବାହୁ ସର୍ବସମ)
OD = OB = x = 12 ସେ.ମି. |
AO = OC = y = 5 ସେ.ମି. |
Question 16.
(a) ସେୟାର, ସ୍କେଲ୍ ଏବଂ ପ୍ରୋଟ୍ରାକ୍ଟର ବ୍ୟବହାର କରି ଏକ ରମ୍ବସ୍ ଅଙ୍କନ କର, ଯାହାର ଗୋଟିଏ କୋଣର ପରିମାଣ 60° ଏବଂ ବାହୁର ଦୈର୍ଘ୍ୟ 4 ସେ.ମି. |
Solution:
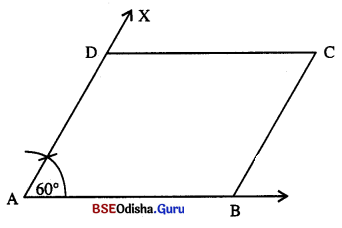
ସୋପାନ :
(i) AB ଅଙ୍କନ କର, ଯାହାର ଦୈର୍ଘ୍ୟ 4 ସେ.ମି. ।
(ii) A ବିନ୍ଦୁରେ ପ୍ରୋଟ୍ରାକ୍ଟର ବ୍ୟବହାର କରି ∠XAB ଅଙ୍କନ କର, ଯାହାର ପରିମାଣ 60° ହେବ ।
(iii) A କୁ କେନ୍ଦ୍ରକରି AB ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ବ୍ୟାସାର୍ଦ୍ଧ ନେଇ ଏକ ଚାପ \(\overrightarrow{\mathrm{AX}}\) କୁ D ବିନ୍ଦୁରେ ଛେଦକରୁ ।
(iv) D ଓ B ବିନ୍ଦୁକୁ କେନ୍ଦ୍ରକରି AB ବ୍ୟାସାର୍କ୍ ନେଇ ଦୁଇଟି ଚାପ୍ ଅଙ୍କନ କର, ଯେପରିକି ଚାପଦ୍ଵୟ ପରସ୍ପରକୁ C ବିନ୍ଦୁରେ ଛେଦକରନ୍ତୁ |
(v) \(\overline{\mathrm{CD}})\) ଓ \(\overline{\mathrm{BC}})\) ଅଳନ କରି ABCD ଉମ୍ଭସ ସମୟ କର ।
(b) ସେୟାର, ସ୍କେଲ୍ ଏବଂ ପ୍ରୋଟ୍ରାକ୍ଟର ବ୍ୟବହାର କରି ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର ଅଙ୍କନ କର, ଯାହାର ଗୋଟିଏ କୋଣର ପରିମାଣ 70° ଏବଂ ଦୁଇ ସନ୍ନିହିତ ବାହୁର ଦୈର୍ଘ୍ୟ 6.3 ସେ.ମି. ଏବଂ 4.5 ସେ.ମି. |
Solution:
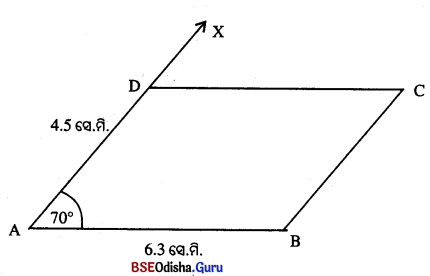
ସୋପାନ :
(i) 6.3 ସେ.ମି. ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ AB ଅଙ୍କନ କର ।
(ii) A ବିନ୍ଦୁରେ ପ୍ରୋଟ୍ରାକ୍ଟର ବ୍ୟବହାର କରି ∠XAB ଅଙ୍କନ କର, ଯେପରିକି ଏହାର ପରିମାଣ 70° ହେବ ।
(iii) A କୁ କେନ୍ଦ୍ର ଏବଂ 4.5 ସେ.ମି. ବ୍ୟାସାର୍ଦ୍ଧ ନେଇ ଏକ ଚାପ \(\overrightarrow{\mathrm{AX}}\) କୁ D ବିନ୍ଦୁରେ ଛେଦକରୁ ।
(iv) D କୁ କେନ୍ଦ୍ର ଏବଂ 6.3 ସେ.ମି. ବ୍ୟାସାର୍ଦ୍ଧ ନେଇ ଏକ ଚାପ ଅଙ୍କନ କର ।
(v) B କୁ କେନ୍ଦ୍ର ଏବଂ 4.5 ସେ.ମି. ବ୍ୟାସାର୍ଦ୍ଧ ବିଶିଷ୍ଟ ଚାପ ପୂର୍ବୋକ୍ତ ଚାପକୁ ଗୋଟିଏ ବିନ୍ଦୁରେ ଛେଦକରୁ । ଛେଦବିଦୁର ନାମ ‘C’ ଦିଅ ।
(vi) \(\overline{\mathrm{DC}})\) ଏବଂ \(\overline{\mathrm{BC}})\) ଅଙ୍କନ କରି ABCD ସାମାନ୍ତରିକ ଚିତ୍ର ସମ୍ପୂର୍ଣ କର ।
(c) ପ୍ରୋଟ୍ରାକ୍ଟର ବ୍ୟବହାର କରି ଏକ ବର୍ଗଚିତ୍ର ଅଙ୍କନ କର, ଯାହାର ବାହୁର ଦୈର୍ଘ୍ୟ 3.2 ସେ.ମି. ହେବ ।
Solution:
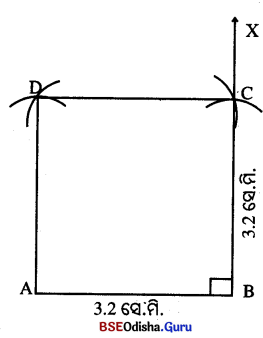
ସୋପାନ :
(i) 3.2 ସେ.ମି. ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ AB ଅଙ୍କନ କର ।
(ii) B ବିନ୍ଦୁରେ ପ୍ରୋଟ୍ରାକ୍ଟର ବ୍ୟବହାର କରି m∠ABX ଅଙ୍କନ କର ଯେପରିକି ଏହାର ପରିମାଣ 90° ହେବ ।
(iii) Bକୁ କେନ୍ଦ୍ରକରି ଏବଂ 3.2 ସେ.ମି. ବ୍ୟାସାର୍କ ବିଶିଷ୍ଟ ଚାପ ନେଇ \(\overline{\mathrm{BX}})\) ରୁ BC = 3.2 ସେ.ମି. ଚାପ କାଟ ଏବଂ ଏହାର ନାମ C ଦିଅ ।
(iv) C ବିନ୍ଦୁ ଓ A ବିନ୍ଦୁରୁ 3.2 ସେ.ମି. ବ୍ୟାସାର୍ଷ ବିଶିଷ୍ଟ ଚାପଦ୍ଵୟ ପରସ୍ପରକୁ D ବିନ୍ଦୁରେ ଛେଦକରନ୍ତୁ ।
(v) CD ଓ AD ଅଙ୍କନ କରି ABCD ବର୍ଗକ୍ଷେତ୍ର ସମ୍ପୂର୍ଣ୍ଣ କର ।
