Odisha State Board BSE Odisha 9th Class Maths Notes Geometry Chapter 1 ରେଖା ଓ କୋଣ will enable students to study smartly.
BSE Odisha Class 9 Maths Notes Geometry Chapter 1 ରେଖା ଓ କୋଣ
ଉପକ୍ରମଣିକା (Introduction):
- ‘Geometry’ ଶବ୍ଦଟି ଦୁଇଟି ଗ୍ରୀକ୍ ଶବ୍ଦ Geo (ପୃଥବୀ) ଓ Metron (ମାପ)ରୁ ସୃଷ୍ଟି ହୋଇଛି । ‘ଜ୍ୟା’ ର ଅର୍ଥ ପୃଥିବୀ ଓ ‘ମିତି’ର ଅର୍ଥ ମାପ ।
- ଜମି ମାପ କରିବାର ଆବଶ୍ୟକତାରୁ ଜ୍ୟାମିତିର ସୃଷ୍ଟି । ମାନବ ସଭ୍ୟତାର ଅଗ୍ରଗତି ସହିତ ଜ୍ୟାମିତିର ଅଭିବୃଦ୍ଧି ଜଡ଼ିତ । ଜ୍ୟାମିତିର ବିକାଶ ସାଧନ କରିଥିବା ପ୍ରାଚୀନତମ ସଭ୍ୟତା ହେଉଛି ମିଶରୀୟ ସଭ୍ୟତା । ବୈଦିକ ଯୁଗରେ ଭାରତୀୟ ମୁନିଋଷିମାନେ ଯଜ୍ଞକୁଣ୍ଡ ଓ ପୂଜାବେଦୀର ନିର୍ମାଣ କାର୍ଯ୍ୟରେ ଜ୍ୟାମିତିକ ଜ୍ଞାନର ପ୍ରୟୋଗ କରୁଥିଲେ ।
- ଆନୁମାନିକ ଖ୍ରୀଷ୍ଟପୂର୍ବ 800 ରୁ ଖ୍ରୀଷ୍ଟପୂର୍ବ 500 ମଧ୍ୟରେ ଭାରତରେ ରଚିତ ‘ଶୁଲ୍ବ ସୂତ୍ର’ ଏକ ଜ୍ୟାମିତି ଶାସ୍ତ୍ର ।
- ପରବର୍ତ୍ତୀ କାଳରେ ଭାସ୍କର, ଆର୍ଯ୍ୟଭଟ୍ଟ, ବ୍ରହ୍ମଗୁପ୍ତ, ମହାବୀର ଆଦି ଭାରତୀୟ ଗଣିତଜ୍ଞଗଣ ଜ୍ୟାମିତି ଶାସ୍ତ୍ରର
- କାଳକ୍ରମେ ଥାଲେସ୍ (Thales), ପିଥାଗୋରାସ୍, ସକ୍ରେଟିସ୍, ପ୍ଲାଟୋ, ଆରିଷ୍ଟଟଲ୍ ଆଦି ଗ୍ରୀକ୍ ବିଦ୍ଵାନଗଣ ତର୍କଶାସ୍ତ୍ରର ପ୍ରୟୋଗ କରି ଜ୍ୟାମିତିକ ତଥ୍ୟ ଉନ୍ମୋଚନ କରିବାର ଧାରା ଆରମ୍ଭ କଲେ ।
- ଖ୍ରୀଷ୍ଟପୂର୍ବ ଚତୁର୍ଥ ଶତାବ୍ଦୀରେ ରଚିତ ଓ ତେରଖଣ୍ଡରେ ବିଭକ୍ତ ଏଲିମେଣ୍ଟସ୍ (Elements) ଗ୍ରନ୍ଥରେ ସମୁଦାୟ ଚାରିଶହ ପଞ୍ଚଷଠିଟି ଉପପାଦ୍ୟ ସନ୍ନିବେଶିତ କରି ଇଉକ୍ଲିଡ୍ ପ୍ରତିପାଦନ କରିବାକୁ ଚେଷ୍ଟା କଲେ ଯେ ଅଳ୍ପ କେତେଗୋଟି ତଥ୍ୟକୁ ସ୍ବୀକାର କରିନେଲେ ବାକି ସମସ୍ତ ସିଦ୍ଧାନ୍ତକୁ ତର୍କଦ୍ୱାରା ପ୍ରଦିପାଦନ କରି ହେବ ।
- ପରୀକ୍ଷାମୂଳକ ତଥ୍ୟ ଆହରଣ ଅପେକ୍ଷା ତତ୍ତ୍ଵ ନିରୂପଣର ମାର୍ଗ ପ୍ରଶସ୍ତ ହେଲା । ତେଣୁ ଇଉକ୍ଲିଙ୍କୁ ଯଥାର୍ଥରେ ଜ୍ୟାମିତିର ଜନକ ଆଖ୍ୟା ଦିଆଯାଏ । ତାଙ୍କ ନାମାନୁଯାୟୀ ‘ଇଉକ୍ଲିଡୀୟ ଜ୍ୟାମିତି? (Euclidean Geometry) ନାମ ପ୍ରଚଳିତ ।
{ଇଉକ୍ଲିଙ୍କୁ ଜ୍ୟାମିତିର ଜନକ କୁହାଯାଏ ।} - ଇଉକ୍ଲିଡ୍ଙ୍କ ଦ୍ଵାରା ପ୍ରଣିତ ଜ୍ୟାମିତିରେ କେତେକ ତାର୍କିକ ଅସଂଗତି ରହିଥିବା କଥା ବିଖ୍ୟାତ ଦାର୍ଶନିକ ଓ ଗଣିତଜ୍ଞ ବଟ୍ରାଣ୍ଡ ରସେଲ୍ ତାଙ୍କର Mathematics and Metaphysics ପ୍ରବନ୍ଧରେ ଦର୍ଶାଇ ଦେବା ପରେ ଜ୍ୟାମିତିକୁ ତ୍ରୁଟିମୁକ୍ତ କରି ଏକ ବଳିଷ୍ଠ ତର୍କସମ୍ମତ ଭିତ୍ତିଭୂମିରେ ପ୍ରତିଷ୍ଠିତ କରିବାର ପ୍ରଚେଷ୍ଟା କରାଗଲା । ଏଥିପାଇଁ ମୁଖ୍ୟଭୂମିକା ଗ୍ରହଣ କରିଥିବା ଦୁଇଜଣ ଗଣିତଜ୍ଞ ହେଉଛନ୍ତି ଆମେରିକାର ଜର୍ଜଡେଭିଡ୍ ବିର୍କଫ୍ ଓ ଜର୍ମାନୀର ଡେଭିଡ୍ ହିଲ୍ବର୍ଟ ।
- ବିରକଫ୍ଙ୍କ ଦ୍ଵାରା ପରିମାର୍ଜିତ ଜ୍ୟାମିତି ବିଦ୍ୟାଳୟ ସ୍ତରପାଇଁ ଅଧିକ ଉପଯୁକ୍ତ । ଏହା ତାଙ୍କର 1932 ମସିହାର ନିବନ୍ଧ ‘A set of postulates for plane-geometry based on scale and protractor’ ଉପରେ ଆଧାରିତ ।
- ଆମେ ବିଦ୍ୟାଳୟ ସ୍ତରରେ ପଢୁଥିବା ଜ୍ୟାମିତି ଇଉକ୍ଲିଡ଼ୀୟ ଜ୍ୟାମିତି ବା ସମତଳ ଜ୍ୟାମିତି ନାମରେ ପରିଚିତ ।
ମୌଳିକ ଅବବୋଧ ଏକ ପୁନରାବୃତ୍ତି (Fundamental concepts – a Recapitulation) :
- ପ୍ରତ୍ୟେକ ପାଠରେ କେତେକ ବିଶେଷ ପ୍ରକାର ଶବ୍ଦ ଗୋଟିଏ ଗୋଟିଏ ନିର୍ଦ୍ଦିଷ୍ଟ ଅର୍ଥରେ ବ୍ୟବହାର କରାଯାଏ । ସେହି ଶବ୍ଦଗୁଡ଼ିକୁ ‘ପଦ’ (term) କୁହାଯାଏ ।
- ଜ୍ୟାମିତି ଶାସ୍ତ୍ର ଅନ୍ତର୍ଗତ ପଦଗୁଡ଼ିକ ଦୁଇ ପର୍ଯ୍ୟାୟଭୁକ୍ତ – ସଂଜ୍ଞାବିହୀନ ପଦ ଓ ସଂଜ୍ଞାକୃତ ପଦ । ସଂଜ୍ଞାବିହୀନ ପଦ ହେଲେ ବିନ୍ଦୁ, ରେଖା ବା ସରଳରେଖା (ଏକ ଅର୍ଥରେ ବ୍ୟବହୃତ) ଓ ସମତଳ । ଏହି ପଦ ବ୍ୟତୀତ ଅନ୍ୟ ସମସ୍ତ ପଦ ସଂଜ୍ଞାକୃତ ।
- ଅର୍ଥନିରୂପକ ବାକ୍ୟକୁ ‘ସଂଜ୍ଞା’ କୁହାଯାଏ । ସଂଜ୍ଞା ନିରୂପଣ ପାଇଁ ଆମ ପାଖରେ ପର୍ଯ୍ୟାପ୍ତ ସଂଖ୍ୟକ ‘ଜଣାପଦ’ ବା ‘ମୌଳିକ ପଦ’ ଥିବା ଆବଶ୍ୟକ ।
- ଜ୍ୟାମିତିରେ ବ୍ୟବହୃତ ସମସ୍ତ ପଦର ଅର୍ଥ ବା ସଂଜ୍ଞା ନିରୂପଣ ପାଇଁ ବିନ୍ଦୁ, ରେଖା ଓ ସମତଳ ଏହି ତିନୋଟି ମୌଳିକ ପଦ ପର୍ଯ୍ୟାପ୍ତ ।
- ପରୀକ୍ଷା ନିରୀକ୍ଷା ମାଧ୍ୟମରେ ଉପଲବ୍ଧ ଅନୁଭୂତିକୁ ଆଧାର କରି ସେମାନଙ୍କର କେତେକ ଧର୍ମକୁ ସ୍ଵୀକାର୍ଯ୍ୟ ଆଖ୍ୟା
![]()
କେତେକ ଉପାଦେୟ ସ୍ବୀକାର୍ଯ୍ୟ :
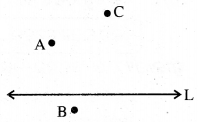
ସ୍ବୀକାର୍ଯ୍ୟ-1 : ସରଳରେଖା ବିନ୍ଦୁମାନଙ୍କର ସମାହର ବା ସେଟ୍ ।
![]()
ଏଠାରେ L ଏକ ସରଳରେଖା ଯିଏକି A, B, C ସମେତ ଅନେକ ବିନ୍ଦୁକୁ ନେଇ ଗଠିତ । ଏଠାରେ L ଏକ ସେଟ୍ ହେଲେ, L = {A, B, C,…..} ଅର୍ଥାତ୍ A ∈ L, B ∈ L, C ∈ L
ଏଠାରେ L ହେଉଛି A, B, C ବିନ୍ଦୁ ମଧ୍ୟଦେଇ ଯାଇଥିବା ସରଳରେଖା ।
ଏକ କାଗଜ ପୃଷ୍ଠାରେ ଦୁଇଟି ବିନ୍ଦୁ P ଓ Q କୁ ନେଇ ପେନ୍ସିଲ୍ ବା କଲମ ଦ୍ବାରା ଗୋଟିଏ ସରଳରେଖା ଅଙ୍କନ କରାଯାଇପାରିବ ।
ସ୍ୱୀକାର୍ଯ୍ୟ-2 : ଦୁଇଟି ପୃଥକ୍ ବିନ୍ଦୁ ମଧ୍ୟଦେଇ ଗୋଟିଏ ଏବଂ କେବଳ ମାତ୍ର ଗୋଟିଏ ସରଳରେଖା ଅବସ୍ଥିତ ।
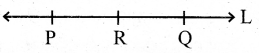
L ସରଳରେଖାର ଦୁଇଟି ପୃଥକ୍ ବିନ୍ଦୁ P ଓ Q ହେଲେ L କୁ \(\overleftrightarrow{\mathrm{PQ}}\) ସଙ୍କେତ ଦ୍ୱାରା ନାମିତ କରିପାରିବା ଓ \(\overleftrightarrow{\mathrm{PQ}}\) କୁ ‘PQ ସରଳରେଖା’ ବୋଲି ପଢ଼ିବା ।
P ∈ L, Q ∈ L, R ∈ L ହେଲେ \(\overleftrightarrow{\mathrm{PQ}}=\overleftrightarrow{\mathrm{PR}}=\overleftrightarrow{\mathrm{QR}}=\overleftrightarrow{\mathrm{RQ}}=\overleftrightarrow{\mathrm{RP}}=\overleftrightarrow{\mathrm{QP}}\) = L
ଏକରେଖୀ ଓ ନୈଳରେଖାର(Collinear and Non-collinear Points):
ସଂଜ୍ଞା – 1 : ତିନି ବା ତାହାଠାରୁ ଅଧିକ ସଂଖ୍ୟକ ବିନ୍ଦୁ ଯଦି ଏକ ସରଳରେଖାରେ ଅବସ୍ଥିତ ହୁଅନ୍ତି, ତେବେ ସେମାନଙ୍କୁ ଏକରେଖୀ ( ବା ସରଳରେଖ୍କ) ବିନ୍ଦୁ (Collinear points) କୁହାଯାଏ ।
ସଂଜ୍ଞା – 2 : ଯେଉଁସବୁ ବିନ୍ଦୁ ଏକ ସରଳରେଖାରେ ଅବସ୍ଥିତ ନୁହଁନ୍ତି, ସେମାନଙ୍କୁ ନୈକରେଖୀ (ବା ଅଣସରଳରେଖ୍କ) ବିନ୍ଦୁ (Non-collinear points) କୁହାଯାଏ ।
ସ୍ଵୀକାର୍ଯ୍ୟ-3 : ସମତଳ ବିନ୍ଦୁମାନଙ୍କର ସେଟ୍ ଅଟେ ।
ମନେକର A, B, C, D ବିନ୍ଦୁଗୁଡ଼ିକ P ସମତଳରେ ଅବସ୍ଥିତ ହେଲେ, A ∈ P, B ∈ P, C ∈ P, D ∈ P ହେବ ।
ସ୍ଵୀକାର୍ଯ୍ୟ-4 : ଗୋଟିଏ ସମତଳରେ ଅନ୍ତତଃ ତିନିଗୋଟି ନୈକରେଖୀ ବିନ୍ଦୁ ଥାଏ ଏବଂ ଯେକୌଣସି ତିନିଗୋଟି ନୈକରେଖୀ ବିନ୍ଦୁ ମଧ୍ୟଦେଇ ଗୋଟିଏ ମାତ୍ର ସମତଳ ଅବସ୍ଥିତ ।
ସମତଳର ନାମକରଣ :
- ଗୋଟିଏ ସମତଳର ନାମକରଣ ସେଥିରେ ଥିବା ଯେକୌଣସି ତିନିଗୋଟି ନେକରେଖୀ ବିନ୍ଦୁ ସାହାଯ୍ୟରେ କରାଯାଏ ।
- A, B, C ଏକ ସମତଳସ୍ଥ ଯେକୌଣସି ତିନୋଟି ନେକରେଖୀ ବିନ୍ଦୁ ହେଲେ ଆମେ ସମତଳଟିକୁ ‘ABC ସମତଳ’ (ବା BAC, CAB ସମତଳ) ବୋଲି ନାମିତ କରିବା ।
ସ୍ଵୀକାର୍ଯ୍ୟ-5 :
ଏକ ସମତଳସ୍ଥ ଦୁଇଟି ପୃଥକ୍ ବିନ୍ଦୁକୁ ଧାରଣ କରୁଥିବା ସରଳରେଖା ଭକ୍ତ ସମତଳରେ ଅବସ୍ଥିତ ।
ଯଦି A ଓ B, P- ସମତଳର ଦୁଇଟି ପୃଥକ୍ ବିନ୍ଦୁ ହୁଅନ୍ତି, ତେବେ ସ୍ବୀକାର୍ଯ୍ୟ ଅନୁଯାୟୀ \(\overleftrightarrow{\mathrm{AB}}\), P ସମତଳରେ ଅବସ୍ଥିତ, ଅର୍ଥାତ୍ ସରଳରେଖାଟିର ସମସୃ ବିନ୍ଦୁ p- ସମତଳରେ ଅବସ୍ଥିତ
ଏହାକୁ ସେଟ୍ରେ ଲେଖିଲେ, \(\overleftrightarrow{\mathrm{AB}}\) ⊂ P, ଅର୍ଥାତ୍ \(\overleftrightarrow{\mathrm{AB}}\), P-ସମତଳର ଉପସେଟ୍ ଅଟେ ।
ଦୁଇବିନ୍ଦୁ ମଧ୍ୟସ୍ଥ ଦୂରତା, ସରଳରେଖା ଓ ବାସ୍ତବ ସଂଖ୍ୟା ସେଟ୍ ମଧ୍ୟରେ ସମ୍ପର୍କ :
ଗୋଟିଏ ସରଳରେଖା ଉପରେ ଦୁଇଟି ପୃଥକ ବିନ୍ଦୁ ରହିଲେ ଏମାନଙ୍କ ମଧ୍ୟରେ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଦୂରତା ଥାଏ । ମାତ୍ର ବିନ୍ଦୁଦ୍ଵୟ ଅଭିନ୍ନ ହେଲେ ଦୂରତା ଶୂନ ହୁଏ । ଗୋଟିଏ ବିନ୍ଦୁର ତା’ ନିଜଠାରୁ ଦୂରତା ଯେକୌଣସି ସ୍କେଲ୍ରେ ଶୂନ ହୁଏ । ଦୂରତା ମାପପାଇଁ ବ୍ୟବହୃତ ସଂଖ୍ୟା ସର୍ବଦା ଅଣରଣାତ୍ମକ, ଅର୍ଥାତ୍ ଶୂନ ବା ଧନାତ୍ମକ ବାସ୍ତବ ସଂଖ୍ୟା ।
ସ୍ଵୀକାର୍ଯ୍ୟ-6 ; ରୁଲର୍ ସ୍ଵୀକାର୍ଯ୍ୟ (Ruler Postulate/Axiom) :
ଗୋଟିଏ ସମତଳରେ ଥିବା ବିନ୍ଦୁଯୋଡ଼ା ଗୁଡ଼ିକ ଗୋଟିଏ ଗୋଟିଏ ଅଣଋଣାତ୍ମକ ବାସ୍ତବ ସଂଖ୍ୟା ସହ ସଂମ୍ପୃକ୍ତ, ଯାହାକୁ ବିନ୍ଦୁଦ୍ଵୟ ‘‘ମଧ୍ୟସ୍ଥ ଦୂରତା’’ କୁହାଯାଏ । ଦୁଇବିନ୍ଦୁ ମଧ୍ୟସ୍ଥ ଦୂରତା ଉପରେ ନିର୍ଭର କରି ଏକ ସରଳରେଖାର ବିନ୍ଦୁସମୂହ ଓ ବାସ୍ତବ ସଂଖ୍ୟା ସେଟ୍ ମଧ୍ୟରେ ଏକ ବିଶେଷ ପ୍ରକାର ସମ୍ପର୍କ ସମ୍ଭବ ହୁଏ ଯଥା –
- ସରଳରେଖା ଉପରେ ଭିନ୍ନ ଭିନ୍ନ ବିନ୍ଦୁ ପାଇଁ ଭିନ୍ନ ଭିନ୍ନ ବାସ୍ତବ ସଂଖ୍ୟା ଓ ଭିନ୍ନ ଭିନ୍ନ ବାସ୍ତବ ସଂଖ୍ୟା ପାଇଁ ଭିନ୍ନ ଭିନ୍ନ ବିନ୍ଦୁ ନିରୂପଣ କରି ପାରିବା ।
- ସରଳରେଖା ଉପରିସ୍ଥ ଯେକୌଣସି ବିଦୁ୍ୟଦ୍ୱୟର ଦୂରତା, ସେମାନଙ୍କ ସହିତ ସଂପୃକ୍ତ ବାସ୍ତବ ସଂଖ୍ୟାଦ୍ବୟର ଅନ୍ତରର ପରମମାନ (ଅଣଋଣାତ୍ମକ ଅନ୍ତର) ସହ ସମାନ ହୁଏ ।
{ରେଖା ଉପରିସ୍ଥ ବିନ୍ଦୁକୁ ଚିହ୍ନଟ କରୁଥିବା ବାସ୍ତବ ସଂଖ୍ୟାଟିକୁ ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ କୁହାଯାଏ ।}
ମଧ୍ୟବର୍ତ୍ତିତା (Betweenness) :
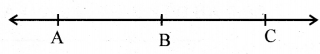 ସଂଜ୍ଞା – ଯଦି ତିନୋଟି ପୃଥକ ବିନ୍ଦୁ A, B,C
ସଂଜ୍ଞା – ଯଦି ତିନୋଟି ପୃଥକ ବିନ୍ଦୁ A, B,C
ଏକ ସରଳରେଖାରେ ଅବସ୍ଥାନ କରନ୍ତି ଓ AB + BC = AC ହୁଏ;
ତେବେ B କୁ A ଓ Cର (କିମ୍ବା C ଓ Aର) ମଧ୍ୟବର୍ତ୍ତୀ ବିନ୍ଦୁ କୁହାଯାଏ ।
ବିଦୁ୍ୟତ୍ରୟର ଏ ପ୍ରକାର ଅବସ୍ଥାନକୁ ସାଙ୍କେତିକ ଭାଷାରେ A – B – C କିମ୍ବା C – B – A ଭାବରେ ଲେଖାଯାଏ ।
ରେଖାଖଣ୍ଡ (Segment or Line segment) :
A ଓ B ଦୁଇଟି ପୃଥକ ବିନ୍ଦୁ ହେଲେ A ଓ B ବିନ୍ଦୁଦ୍ବାରା ନିରୂପିତ ସରଳରେଖା ହେଉଛି \(\overleftrightarrow{\mathrm{AB}}\) ବା \(\overleftrightarrow{\mathrm{BA}}\) ।
ସଂଜ୍ଞା – ଦୁଇଟି ପୃଥକ୍ ବିନ୍ଦୁ A, B ଏବଂ ସେମାନଙ୍କର ମଧ୍ୟବର୍ତ୍ତୀ ବିନ୍ଦୁମାନଙ୍କର ସେଟ୍କୁ A ଓ B ଦ୍ବାରା ନିରୂପିତ \(\overline{A B}\) ବା BA ରେଖାଖଣ୍ଡ କୁହାଯାଏ ।
ସେଟ୍ ଭାଷାରେ \(\overline{A B}\) = {A, B} ∪ {{P: A – P – B}
A ଓ Bର ମଧ୍ୟବର୍ତ୍ତୀ ବିନ୍ଦୁମାନଙ୍କର ପ୍ରତିନିଧ୍ ରୂପେ P ବିନ୍ଦୁକୁ ନିଆଯାଉ ।
![]()
(i) AB କୁ A ଓ Bଦ୍ୱାରା ନିରୂପିତ ରେଖାଖଣ୍ଡ ବା ‘A ଓ Bର ସଂଯୋଜକ ରେଖାଖଣ୍ଡ’ ମଧ୍ୟ କୁହାଯାଏ । ସଂଜ୍ଞାରୁ ଏହା ସ୍ପଷ୍ଟ ହୁଏ ଯେ, AB ଓ BA, ଉଭୟ ଗୋଟିଏ ରେଖାଖଣ୍ଡ ଅଟନ୍ତି ।
(ii) AB ⊂ \(\overleftrightarrow{\mathrm{AB}}\); ଅର୍ଥାତ୍ AB ରେଖାଖଣ୍ଡ, AB ସରଳରେଖାର ଏକ ଅଂଶ ଅଟେ । ଉପରିସ୍ଥ ଚିତ୍ରରେ AB କୁ ସ୍ୱତନ୍ତ୍ର ଭାବରେ ତଥା \(\overleftrightarrow{\mathrm{AB}}\)ର ଅଂଶ ଭାବରେ – ଏ ଦୁଇ ପ୍ରକାରର ଦେଖାଯାଇଛି । ଏହା ସୁସ୍ପଷ୍ଟ ଯେ AB ର ସମସ୍ତ ବିନ୍ଦୁ \(\overleftrightarrow{\mathrm{AB}}\) ରେ ଅବସ୍ଥିତ ।
ରେଖାଖଣ୍ଡର ପ୍ରାନ୍ତବିନ୍ଦୁ (End-points of line segment) : A ଓ Bକୁ ABର ପ୍ରାନ୍ତବିନ୍ଦୁ କୁହାଯାଏ ।
ରେଖାଖଣ୍ଡର ଦୈର୍ଘ୍ୟ (Length of a line segment) :
(i) ପ୍ରାନ୍ତବିନ୍ଦୁଦ୍ଵୟ ମଧ୍ୟସ୍ଥ ଦୂରତାକୁ ରେଖାଖଣ୍ଡର ଦୈର୍ଘ୍ୟ ABAC କୁହାଯାଏ ।
(ii) ତେଣୁ ABର ଦୈର୍ଘ୍ୟ = AB ଅଟେ ।
ରଶ୍ମି ଓ ବିପରୀତ ରଶ୍ମି (Rays and Opposite Rays) :
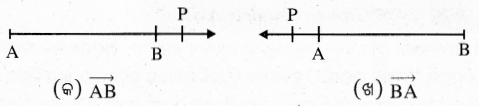
(i) AB ଓ AB ର ବାହାରେ ଥିବା P ଭଳି ସମସ୍ତ ବିନ୍ଦୁକୁ ନେଇ ଚିତ୍ରଟି ଗଠିତ ହୋଇଛି । ଏହାକୁ AB ରଶ୍ମି ବା ସଂକେତରେ \(\overrightarrow{\mathrm{AB}}\) ଲେଖାଯାଏ ।
(ii) ତେଣୁ ସେଟ୍ ଭାଷାରେ AB ରଶ୍ମିର ସଂଜ୍ଞା ହେଉଛି : \(\overrightarrow{\mathrm{AB}}\) = AB ∪ {P: A – B – P}
ସେହିପରି \(\overrightarrow{\mathrm{BA}}\) = AB ∪ (Q: B – A – Q} ବା BA ∪ (Q: B – A – Q}
(iii) \(\overrightarrow{\mathrm{AB}}\) ଓ \(\overrightarrow{\mathrm{BA}}\) ର ସଂଜ୍ଞାରୁ ଏହା ସ୍ପଷ୍ଟ ହୁଏ ଯେ, \(\overrightarrow{\mathrm{AB}}\) ∩ \(\overrightarrow{\mathrm{BA}}\) = AB;
ଅର୍ଥାତ୍ AB ରଶ୍ମି ଓ BA ରଶ୍ମିର ଛେଦ = AB ରେଖାଖଣ୍ଡ ।
![]()
(iv) ଦତ୍ତ ଚିତ୍ରରେ \(\overrightarrow{\mathrm{AP}}, \overrightarrow{\mathrm{AB}}, \overrightarrow{\mathrm{AQ}}, \overrightarrow{\mathrm{AR}}\) ଏ ସମସ୍ତ ଗୋଟିଏ ରଶ୍ମିର ହିଁ ଭିନ୍ନ ଭିନ୍ନ ନାମ ଅଟନ୍ତି ।
\(\overrightarrow{\mathrm{AP}} \subset \overrightarrow{\mathrm{AB}} \subset \overleftrightarrow{\mathrm{AB}}\); ସେହିପରି BA ⊂ \(\overrightarrow{\mathrm{BA}} \subset \stackrel{\leftrightarrow}{\mathrm{BA}}\)
(v) \(\overline{\mathrm{AB}}, \overrightarrow{\mathrm{AB}}, \overleftrightarrow{\mathrm{AB}}\) ଏ ସମସ୍ତେ ହେଉଛନ୍ତି ବିନ୍ଦୁମାନଙ୍କର ସେଟ୍; ମାତ୍ର AB ଗୋଟିଏ ଧନାତ୍ମକ ବାସ୍ତବ ସଂଖ୍ୟା ଯାହା ହେଉଛି A ଓ B ବିନ୍ଦୁ ମଧ୍ୟସ୍ଥ ଦୂରତା ।
![]()
ରଶ୍ମିର ଶୀର୍ଷବିନ୍ଦୁ (Vertex) :
- A କୁ \(\overrightarrow{\mathrm{AB}}\) ର ଶୀର୍ଷବିନ୍ଦୁ କୁହାଯାଏ । ସେହିପରି \(\overrightarrow{\mathrm{BA}}\)ର ଶୀର୍ଷବିନ୍ଦୁ B ଅଟେ । ଶୀର୍ଷବିନ୍ଦୁକୁ ଆଦ୍ୟବିନ୍ଦୁ (Initial Point) ମଧ୍ୟ କୁହାଯାଏ ।
- ବ୍ୟାବହାରିକ ଭାଷାରେ \(\overrightarrow{\mathrm{AB}}\) ରଶ୍ମିକୁ A ବିନ୍ଦୁରୁ ଅଙ୍କିତ ଓ B ବିନ୍ଦୁ ମଧ୍ୟଦେଇ ବିସ୍ତୃତ ରଶ୍ମି ମଧ୍ୟ କୁହାଯାଏ ।
ବିପରୀତ ରଶ୍ମି (Opposite rays) :
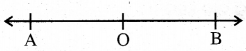
ମନେକର A – O – B, ଅର୍ଥାତ୍ O, A ଓ Bର ଏକ ମଧ୍ୟବର୍ତ୍ତୀ ବିନ୍ଦୁ । ଏ କ୍ଷେତ୍ରରେ \(\overrightarrow{\mathrm{OA}}\) ଓ \(\overrightarrow{\mathrm{OB}}\) କୁ ବିପରୀତ ରଶ୍ମି କୁହାଯାଏ । ତେଣୁ ଏହା ସ୍ପଷ୍ଟ ଯେ,\(\overrightarrow{\mathrm{OA}}\) ଓ \(\overrightarrow{\mathrm{OB}}\) ବିପରୀତ ରଶ୍ମି ହେଲେ \(\overrightarrow{\mathrm{OA}} \cup \overrightarrow{\mathrm{OB}}=\overleftrightarrow{\mathrm{AB}}\)
ଅର୍ଥାତ୍ OA ରଶ୍ମି ଓ OB ରଶ୍ମିର ସଂଯୋଗ AB ସରଳରେଖା ଅଟେ ।
ଏକରେଖୀ ଓ ନୈକରେଖୀ ରଶ୍ମି (Collinear and noncollinear rays) :
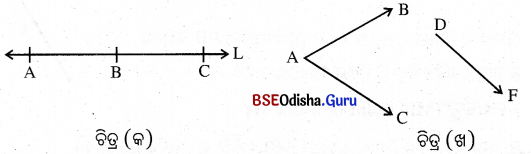
ଯେଉଁସବୁ ରଶ୍ମି ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ରେଖାର ଅଂଶ ବିଶେଷ, ସେମାନଙ୍କୁ ଏକରେଖୀ ବା ସରଳରେଖକ ରଶ୍ମି କୁହାଯାଏ । ଚିତ୍ର (କ) ରେ \(\overrightarrow{\mathrm{AB}}, \overrightarrow{\mathrm{BC}}, \overrightarrow{\mathrm{CA}}, \overrightarrow{\mathrm{BA}}\) ଆଦି L ସରଳରେଖାର ଅଂଶ ହୋଇଥିବାରୁ ଏମାନେ ଏକରେଖୀ ରଶ୍ମି ଅଟନ୍ତି । ମାତ୍ର ଚିତ୍ର (ଖ)ରେ \(\overrightarrow{\mathrm{AB}}, \overrightarrow{\mathrm{AC}}, \overrightarrow{\mathrm{DF}}\) ନୈକରେଖୀ ରଶ୍ମି ଅଟନ୍ତି ।
ସ୍ଥାନାଙ୍କ (Co-ordinates) ସମ୍ବନ୍ଧରେ କେତେକ ପ୍ରୟୋଜନୀୟ ତଥ୍ୟ :
ସରଳରେଖାର ପ୍ରତ୍ୟେକ ବିନ୍ଦୁ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ବାସ୍ତବ ସଂଖ୍ୟା ସହ ସଂପୃକ୍ତ ହୁଏ ଓ ଭିନ୍ନ ଭିନ୍ନ ବିନ୍ଦୁ ଭିନ୍ନ ଭିନ୍ନ ବାସ୍ତବ ସଂଖ୍ୟା ସହ ସମ୍ପୃକ୍ତ ହୁଅନୃି
ଗୋଟିଏ ବିନ୍ଦୁ ସହ ସମ୍ପୃକ୍ତ ବାସ୍ତବ ସଂଖ୍ୟାକୁ ଉକ୍ତ ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ କୁହାଯାଏ ।
(i) ମନେକର A, B ଓ C ସରଳଖୋ L ଉପରିସ୍ଥ ତିନୋଟି ବିନ୍ଦୁ ଓ ସେମାନଙ୍କର ସ୍ଥାନାଙ୍କ ଯଥାକ୍ରମେ a, b ଓ c ହେଉ । ଯଦି A – B – C ଅର୍ଥାତ୍ B, A ଓ C ବିନ୍ଦୁ ଦ୍ବୟର ମଧ୍ୟବର୍ତ୍ତୀ ହୁଏ, ତେବେ a < b <c କିମ୍ବା c< b< a ହେବ ।
![]()
(ii) ଏକ ସରଳରେଖା ଉପରେ ଠ ଏବଂ P ଯେକୌଣସି ଦୁଇଟି ପୃଥକ୍ ବିନ୍ଦୁ ହେଲେ ଉପଯୁକ୍ତ ସ୍ଥାନଙ୍କ ପଦ୍ଧତି ନିର୍ବାଚନ ଦ୍ଵାରା ଠର ସ୍ଥାନାଙ୍କକୁ ଶୂନ ଓ Pର ସ୍ଥାନାଙ୍କକୁ ଧନାତ୍ମକ ନିଆଯାଉ । ଯଦି N – O – P ହୁଏ ତେବେ Nର ସ୍ଥାନାଙ୍କ ଋଣାତ୍ମକ ହେବ । ଏହାକୁ ଆଧାର କରି ସଂଖ୍ୟାରେଖା (Number Line)ରେ ବିନ୍ଦୁମାନଙ୍କର ସ୍ଥାନାଙ୍କ ନିଶ୍ଚିତ ହୁଏ । \(\overrightarrow{\mathrm{OP}}\) ରେ ଅବସ୍ଥିତ ସମସ୍ତ ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ଧନାତ୍ମକ ଓ \(\overrightarrow{\mathrm{ON}}\) ରେ ଅବସ୍ଥିତ ସମସ୍ତ ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ଋଣାତ୍ମକ ହୁଏ ।
![]()
(iii) L ସରଳରେଖା ଉପରେ P ଏକ ବିନ୍ଦୁ ଏବଂ à ଏକ ଧନାତ୍ମକ ବାସ୍ତବ ସଂଖ୍ୟା ହେଲେ L ଉପରେ କେବଳ ମାତ୍ର ଦୁଇଟି ବିନ୍ଦୁ ରହିଛି, ଯାହାର P ଠାରୁ ଦୂରତା a ଅଟେ ।
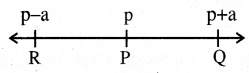
Pର ସ୍ଥାନାଙ୍କ p ହେଲେ ଉକ୍ତ ବିନ୍ଦୁଦ୍ଵୟ ମଧ୍ୟରୁ ଗୋଟିକର ସ୍ଥାନାଙ୍କ p + a ଓ ଅନ୍ୟଟିର ସ୍ଥାନାଙ୍କ p – a ହେବ ।
(iv) ସ୍ଥାନାଙ୍କ ମାଧ୍ୟମରେ ରଶ୍ମି ଓ ରେଖାଖଣ୍ଡର ବିକଳ୍ପ ସଂଜ୍ଞା :
ମନେକର C – A – B ଏବଂ AB ସରଳରେଖାରେ A ଓ Bର ସ୍ଥାନାଙ୍କ ଯଥାକ୍ରମେ x ଓ y ଅଟେ । ଯଦି x < y ହୁଏ, ତେବେ ୯ର ସ୍ଥାନାଙ୍କ xରୁ ସାନ ହେବ ।
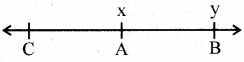
ତେଣୁ \(\overrightarrow{\mathrm{AB}}\) = {P ∈ \(\overleftrightarrow{\mathrm{AB}}\) : Pର ସ୍ଥାନାଙ୍କ ≥ x}, \(\overrightarrow{\mathrm{AC}}\) = {P∈ \(\overleftrightarrow{\mathrm{AB}}\) : Pର ସ୍ଥାନାଙ୍କ ≤ x},
AB = {P∈ \(\overleftrightarrow{\mathrm{AB}}\) : x ≤ Pର ସ୍ଥାନାଙ୍କ ≤ y}
(v) ରେଖାଖଣ୍ଡ ଅଙ୍କନ ଉପପାଦ୍ୟ (Segment-construction Theorem):
r ଏକ ଧନାତ୍ମକ ବାସ୍ତବ ସଂଖ୍ୟା ଓ A, B ଦୁଇଟି ପୃଥକ୍ ବିନ୍ଦୁ ହେଲେ AB ଉପରେ କେବଳ ମାତ୍ର ଗୋଟିଏ ବିନ୍ଦୁ C ନିର୍ଣ୍ଣୟ କରାଯାଇପାରିବ, ଯେପରିକି AC = r ହେବ
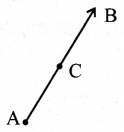
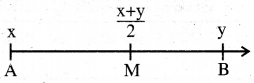
ରେଖାଖଣ୍ଡର ମଧ୍ୟବିନ୍ଦୁ (Mid point of a line-segment) :
ସଂଜ୍ଞା – A͞B ଉପରେ M ଏକ ବିନ୍ଦୁ ଓ AM = M͞B ହେଲେ Mକୁ A͞B ର ମଧ୍ୟବିନ୍ଦୁ କୁହାଯାଏ ।
ଏକ ରେଖାଖଣ୍ଡର ଗୋଟିଏ ମାତ୍ର ମଧ୍ୟବିନ୍ଦୁ ଥାଏ । M, ABର ମଧ୍ୟବିନ୍ଦୁ ହେଲେ, AM = M͞B = 1/2 AB
AB ଉପରେ A ଓ Bର ସ୍ଥାନାଙ୍କ ଯଥାକ୍ରମେ x ଓ y ହେଲେ AB ର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ \(\frac{x+y}{2}\) ଅଟେ ।
କୋଣ ଓ କୋଣ-ପରିମାଣ (Angle and Angle-measure) 
ଜ୍ୟାମିତିରେ ଦୁଇଟି ମୌଳିକ ଶବ୍ଦ ‘ଉତ୍ତଳ ସେଟ୍’ ଓ ‘ସରଳରେଖାର ପାର୍ଶ୍ଵ’ ବିଷୟରେ ଜାଣିବା ଆବଶ୍ୟକ । ଉତ୍ତଳ ସେଟ୍ (Convex set) :
(i) ଏକ ସେଟ୍ S ର ଯେକୌଣସି ଦୁଇଟି ବିନ୍ଦୁ A ଓ B ହେଲେ ଯଦି AB – S ହୁଏ, ତେବେ Sକୁ ଏକ ଉତ୍ତଳ ସେଟ୍ କୁହାଯାଏ । ଏଠାରେ AB c S । ତେଣୁ S ଏକ ଉତ୍ତଳ ସେଟ୍ । ପରବର୍ତୀ ଚିତ୍ରରେ AB ¢ M । ତେଣୁ M ଉତ୍ତଳ ସେଟ୍ ନୁହେଁ ।
(ii) ସମତଳ, ରେଖାଖଣ୍ଡ, ରଶ୍ମି ଓ ସରଳରେଖା ଆଦି ଉତ୍ତଳ ସେଟ୍ ଅଟନ୍ତି ।
(iii) ଏକ ବିନ୍ଦୁ ବିଶିଷ୍ଟ ସେଟ୍ ଓ ଶୂନ୍ୟ ସେଟ୍ ମଧ୍ୟ ଉତ୍ତଳ ସେଟ୍ ବୋଲି ଗ୍ରହଣ କରାଯାଏ ।
{ଦୁଇଟି ଉତ୍ତଳ ସେଟ୍ର ଛେଦ ଏକ ଉତ୍ତଳ ସେଟ୍, ମାତ୍ର ଦୁଇଟି ଉତ୍ତଳ ସେଟ୍ର ସଂଯୋଗ ଉତ୍ତଳ ସେଟ୍ ହୋଇନପାରେ ।}
ସ୍ଵୀକାର୍ଯ୍ୟ 7 : ସମତଳ-ବିଭାଜନ ସ୍ଵୀକାର୍ଯ୍ୟ (Plane-Separation Postulate)
ମନେକର L ସରଳରେଖାଟି P ସମତଳରେ ଅବସ୍ଥିତ । ସମତଳର ଯେଉଁ ବିନ୍ଦୁଗୁଡ଼ିକ ଏହି ସରଳରେଖାରେ ନାହାଁନ୍ତି ସେମାନଙ୍କୁ ଦୁଇଟି ସେଟ୍ H1 ଓ H2 ରେ ବିଭକ୍ତ କରାଯାଇପାରିବ; ଯେପରି 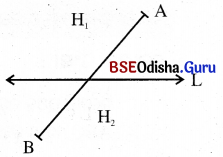
(i) H1 ଓ H2 ପ୍ରତ୍ୟେକ ଗୋଟିଏ ଗୋଟିଏ ଉତ୍ତଳ ସେଟ୍ ହେବ ଏବଂ
(ii) ଦୁଇଟି ପୃଥକ୍ ବିନ୍ଦୁ A ଓ B ଯଥାକ୍ରମେ H1 ଓ H2 ରେ ରହିଲେ,
A ଓ B ର ସଂଯୋଗକାରୀ ରେଖାଖଣ୍ଡ ଅର୍ଥାତ୍ AB,
L ସରଳରେଖାକୁ ଛେଦ କରିବ ।
(a) H1 ≠ Φ ଓ H1 ≠ Φ; ଅର୍ଥାତ୍ H1 ଓ H2 ପ୍ରତ୍ୟେକ ଗୋଟିଏ ଗୋଟିଏ ଅଣଶୂନ୍ୟ ସେଟ୍ ।
(b) H1 ∩ H2 = ଚ୍ ଅର୍ଥାତ୍ H1 ଓ H2, ଦୁଇଟି ଅଣଛେଦୀ ସେଟ୍ ।
ସରଳରେଖା ପାର୍ଶ୍ବ : ସମତଳ-ବିଭାଜନ ସ୍ଵୀକାର୍ଯ୍ୟ ଦ୍ବାରା ନିଶ୍ଚିତ H1 ଓ H2, ସେଟ୍ ଦୁଇଟିକୁ ସରଳରେଖା Lର ଗୋଟିଏ
ଗୋଟିଏ ପାର୍ଶ୍ବ କୁହାଯାଏ । A ଓ B ବିନ୍ଦୁ ଅବସ୍ଥିତ ଥିବା ପାର୍ଶ୍ୱଦ୍ୱୟକୁ ଯଥାକ୍ରମେ Lର A-ପାର୍ଶ୍ବ ଓ B-ପାର୍ଶ୍ବ କୁହାଯାଏ ।
ମନେରଖ :
(i) ଏକ ସରଳରେଖାର ପାର୍ଶ୍ଵଦ୍ଵୟ ଉତ୍ତଳ, ଅଣଶୂନ୍ଯ ଓ ଅଣଛେଦୀ ସେଟ୍ ଅଟନ୍ତି ।
(ii) ସରଳରେଖାର ଉଭୟ ପାର୍ଶ୍ଵକୁ ଅର୍ଦ୍ଧସମତଳ (Half planes) କୁହାଯାଏ ।
(iii) ଗୋଟିଏ ସରଳରେଖାଦ୍ୱାରା ନିର୍ମିତ ଅର୍ଦ୍ଧସମତଳ ଦୁଇଟିକୁ ସରଳରେଖାର ବିପରୀତ ପାର୍ଶ୍ବ ମଧ୍ୟ କୁହାଯାଏ ।
(iv) ସରଳରେଖାକୁ ତାହାଦ୍ୱାରା ନିର୍ମିତ ଅର୍ଦ୍ଧସମତଳ ଦ୍ଵୟର ଧାର (edge) କୁହାଯାଏ ।
![]()
ସମତଳ-ବିଭାଜନ ସ୍ଵୀକାର୍ଯ୍ୟ ଆଧାରିତ କେତେକ ପ୍ରୟୋଜନୀୟ ତଥ୍ୟ :
(i) L ସରଳରେଖା P ସମତଳରେ ଅବସ୍ଥିତ ହେଲେ ସମତଳଟି ତିନୋଟି ଅଣଶୂନ୍ୟ, ଅଣଛେଦୀ ଓ ଉତ୍ତଳ ସେଟ୍ L, H1 ଓ H2 ରେ ବିଭକ୍ତ ହୁଏ, ଅର୍ଥାତ୍ P = L ∪ H1 ∪ H2
(ii) ଉଭୟ ଅର୍ଦ୍ଧସମତଳ H ଓ H, ଅଣଶୂନ୍ୟ ସେଟ୍ ହୋଇଥୁବାରୁ, ଯେକୌଣସି ଅର୍ଦ୍ଧସମତଳ ଉପରିସ୍ଥ ଗୋଟିଏ ବିନ୍ଦୁକୁ L ଉପରିସ୍ଥ ଯେକୌଣସି ବିନ୍ଦୁ ସହ ସଂଯୋଗ କରି ସରଳରେଖାଟିଏ ଅଙ୍କନ କରାଯାଇ ପାରିବ ।
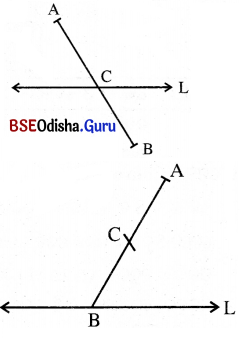
(a) AB ରେଖାଖଣ୍ଡକୁ C ବିନ୍ଦୁରେ ଛେଦ କରେ । ଯଦି C ବିନ୍ଦୁଟି A ଓ B ବିନ୍ଦୁଦ୍ଵୟ ଠାରୁ ପୃଥକ୍ ହୁଏ, ତେବେ A ଓ B ବିନ୍ଦୁଦ୍ଵୟ L ର ବିପରୀତ ପାର୍ଶ୍ଵରେ ଅବସ୍ଥିତ ହେବେ ।
(b) ମନେକର I ସରଳରେଖା ଓ AB ଏକ ସମତଳରେ ଅବସ୍ଥିତ । AB ର ଗୋଟିଏ ପ୍ରାନ୍ତବିନ୍ଦୁ B, L ଉପରେ ଅବସ୍ଥିତ ଓ ଅନ୍ୟ ପ୍ରାନ୍ତବିନ୍ଦୁ A, L ବାହାରେ ଅବସ୍ଥିତ । ତେବେ B – C – A, B – A – C ହେବେ, C ବିନ୍ଦୁ Lର A- ପାର୍ଶ୍ଵରେ ହିଁ ଅବସ୍ଥିତ ହେବେ ।
(c) A ଓ B ବିନ୍ଦୁ Lର ବିପରୀତ ପାର୍ଶ୍ବରେ B ଓ C ବିନ୍ଦୁ Lର ବିପରୀତ ପାର୍ଶ୍ଵରେ ଅବସ୍ଥିତ ହେଲେ A ଓ C ବିଦୁ୍ୟଦ୍ବୟ Lର ସମପାର୍ଶ୍ବରେ ଅବସ୍ଥିତ ହେବେ ।
{ଏକ ରେଖାର ପାର୍ଶ୍ଵଦ୍ଵୟ ଉତ୍ତଳ, ଅଣଶୂନ୍ଯ ଓ ଅଣଛେଦୀ ସେଟ ଅଟନ୍ତି ।}
କୋଣର ସଂଜ୍ଞା : 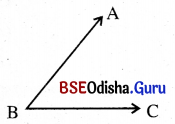
ତିନୋଟି ପୃଥକ୍ ବିନ୍ଦୁ A, B ଓ C ଯଦି ଏକ ସରଳରେଖାରେ ଅବସ୍ଥିତ ନହୁଅନ୍ତି, ତେବେ \(\overrightarrow{\mathrm{BA}}\) ଓ \(\overrightarrow{\mathrm{BC}}\) ର ସଂଯୋଗକୁ ∠ABC କୋଣ କୁହାଯାଏ ଓ ଉକ୍ତ କୋଣକୁ ∠ABC ସଂକେତ ଦ୍ୱାରା ପ୍ରକାଶ କରାଯାଏ ।
(i) ସେଟ୍ ପରିଭାଷାରେ ଆମେ ଲେଖୁ ପାରିବା :
∠ABC = \(\overrightarrow{\mathrm{BA}}\) ∪ \(\overrightarrow{\mathrm{BC}}\)
(ii) ବସ୍ତୁତଃ କୋଣ ହେଉଛି ସାଧାରଣ ଆଦ୍ୟବିନ୍ଦୁ ବିଶିଷ୍ଟ ଦୁଇଟି ନୈକରେଖୀ ରଶ୍ମିର ସଂଯୋଗ ।
(iii) B ବିନ୍ଦୁକୁ ∠ABC ର ଶୀର୍ଷବିନ୍ଦୁ ଏବଂ \(\overrightarrow{\mathrm{BA}}\) ଓ \(\overrightarrow{\mathrm{BC}}\) ରଶ୍ମିଦ୍ୱୟକୁ ∠ABCର ବାହୁ କୁହାଯାଏ ।
କୋଣର ଅନ୍ତର୍ଦେଶ ଓ ବହିର୍ଦେଶ : 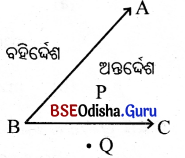
(i) \(\overleftrightarrow{\mathrm{BC}}\) ର A-ପାର୍ଶ୍ବ \(\overleftrightarrow{\mathrm{AB}}\) ର C-ପାର୍ଶ୍ଵର ଛେଦକୁ ∠ABCର ଅନ୍ତର୍ଦେଶ (Interior) କୁହାଯାଏ ।
(ii) ∠ABCର ଅନ୍ତର୍ଦେଶରେ ଥିବା ପ୍ରତ୍ୟେକ ବିନ୍ଦୁକୁ ∠ABCର ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ କୁହାଯାଏ । ଦତ୍ତ ଚିତ୍ରରେ P, ∠ABCର ଗୋଟିଏ ଅନ୍ତସ୍ଥ ବିନ୍ଦୁ ଅଟେ । ଏହିପରି ଅସଂଖ୍ୟ ବିନ୍ଦୁକୁ ନେଇ କୋଣର ଅନ୍ତର୍ଦେଶ ଗଠିତ ।
(iii) ଅନ୍ତର୍ଦେଶରେ ନଥିବା ବିନ୍ଦୁମାନଙ୍କୁ ନେଇ ଗଠିତ ସେଟ୍କୁ କୋଣର ବହିର୍ଦେଶ କୁହାଯାଏ ।
(iv) ବହିର୍ଦେଶରେ ଥିବା ବିନ୍ଦୁକୁ କୋଣର ବହିଃସ୍ଥ ବିନ୍ଦୁ କୁହାଯାଏ । ଦତ୍ତ ଚିତ୍ରରେ Q, ∠ABCର ଗୋଟିଏ ବହିଃସ୍ଥ ବିନ୍ଦୁ ।
{କୋଣର ଅନ୍ତର୍ଦେଶ ଏକ ଉତ୍ତଳ ସେଟ୍, ମାତ୍ର କୋଣ ବା ତାହାର ବହିର୍ଦେଶ ଉତ୍କଳ ସେଟ୍ ନୁହେଁ ।}
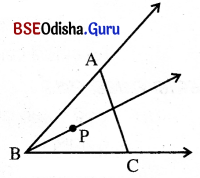
(a) ଗୋଟିଏ କୋଣ, ତାହାର ଅନ୍ତର୍ଦେଶ ଓ ବହିର୍ଦେଶ – ଏହି ତିନୋଟି ପରସ୍ପର ଅଣଛେଦୀ ସେଟ୍; ଅର୍ଥାତ୍ ଏମାନଙ୍କ ମଧ୍ୟରୁ କୌଣସି ଦୁଇଟି ସେଟ୍ ମଧ୍ୟରେ ସାଧାରଣ ବିନ୍ଦୁ ନାହିଁ ।
(b) P, ∠ABCର ଏକ ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ ହେଲେ Bକୁ ଛାଡ଼ି BP ର ଅନ୍ୟ ସମସ୍ତ ବିନ୍ଦୁ ∠ABCର ଅନ୍ତସ୍ଥ ହେବେ । ସେହିପରି A ଓ Cର ମଧ୍ୟବର୍ତ୍ତୀ ଯେକୌଣସି ବିନ୍ଦୁ ମଧ୍ୟ ∠ABCର ଅନ୍ତଃସ୍ଥ ହେବ ।
କୋଣର ପରିମାଣ (Measure of an Angle) :
ସ୍ଵୀକାର୍ଯ୍ୟ-୫ : ପ୍ରୋଟାକ୍ଟର ସ୍ୱୀକାର୍ଯ୍ୟ (Protractor Postulate): 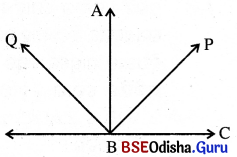
(i) ପ୍ରତ୍ୟେକ କୋଣ (0° ଠାରୁ ବଡ଼ ଓ 180° ଠାରୁ ସାନ) ସହ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଧନାତ୍ମକ ବାସ୍ତବ ସଂଖ୍ୟା ସଂପୃକ୍ତ ଓ ଏହାକୁ ସଂପୃକ୍ତ କୋଣର ପରିମାଣ କୁହାଯାଏ ।
(ii) ∠ABCର ପରିମାଣକୁ m∠ABC ରୂପେ ସୂଚିତ କରାଯାଏ ।
(a) 0 < m∠ABC < 180°
(b) 0 < 8 < 180° ହେଲେ \(\overleftrightarrow{\mathrm{BC}}\) ର ଯେକୌଣସି ପାର୍ଶ୍ଵରେ କେବଳ ମାତ୍ର ଗୋଟିଏ ୫ \(\overleftrightarrow{\mathrm{BQ}}\) ଅବସ୍ଥିତ, ଯେପରି m ∠QBC = θ ହେବ ।
(c) ∠ABCର ଅନ୍ତର୍ଦେଶରେ P ଯେକୌଣସି ଏକ ବିନ୍ଦୁ ହେଲେ m∠ABC = m∠ABP + m∠PBC ହେବ ।
(iii) କୋଣର ପରିମାଣ ୦° ରୁ ବଡ଼ ଓ 180° ରୁ ସାନ (0 < θ < 180°) ପାଇଁ ଲବ୍ଧ କୋଣ ମାପକୁ ଡିଗ୍ରୀମାପ କୁହାଯାଏ । ଯଦି ∠ABCର ମାପ x ହୁଏ, (0 < θ < 180°), ତେବେ ଆମେ ଲେଖୁ m∠ABC = x° 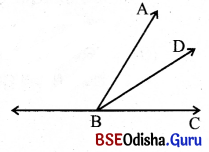
(iv) କୋଣର ପରିମାଣ 0° ରୁ ବଡ଼ ଓ π ରୁ ସାନ (0 < θ < π) ହେଲେ, ଲବ୍ଧ କୋଣ ମାପକୁ ରେଡ଼ିଆନ୍ ମାପ କୁହାଯାଏ ।
(v) କୋଣର ପରିମାଣ 0° ରୁ ବଡ଼ ଓ 200° ରୁ ସାନ (0 < θ < 200) ହେଲେ, ଲବ୍ଧ କୋଣ ମାପକୁ ଗ୍ରେଡ୍ ମାପ କୁହାଯାଏ ।
⇒ π ରେଡ଼ିୟାନ୍ = 180 ଡିଗ୍ରୀ = 200 ଗ୍ରେଡ୍
⇒ 1° 60′ (ମିନିଟ୍)= 60′′ (ସେକେଶୃ)
(vi) ଦୁଇଟି କୋଣର ପରିମାଣ ସମାନ ହେଲେ, ସେମାନଙ୍କୁ ସର୍ବସମ କୋଣ କୁହାଯାଏ ।
(vii) ଯଦି A ଓ D, BC ର ସମପାର୍ଶ୍ୱସ୍ଥିତ ବିନ୍ଦୁ ଓ m∠ABC > m∠DBC ହୁଏ, ତେବେ D, ∠ABC ର ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ ହେବ । 
(viii) A ଓ D, \(\overleftrightarrow{\mathrm{BC}}\) ର ସମପାର୍ଶ୍ୱସ୍ଥିତ ଓ m∠ABD > m∠DBC ତେବେ \(\overrightarrow{\mathrm{BD}}\), ∠ABC ର ଅନ୍ତର୍ଦେଶରେ ବିନ୍ଦୁ ହେବ ।
କୋଣ ସମଦ୍ବିଖଣ୍ଡକ (Angle Bisector) :
(a) ଯଦି ∠ABCର ଅନ୍ତର୍ଦେଶରେ P ଅବସ୍ଥିତ ଏବଂ m∠ABD = m∠DBC
ତେବେ \(\overrightarrow{\mathrm{BD}}\) ∠ABC ସମଦ୍ବିଖଣ୍ଡକ a (Bisector) କୁହାଯାଏ ।
(b) m∠ABD = m∠DBC = 1/2 m∠ABC
ବିଭିନ୍ନ ପ୍ରକାରର କୋଣ (Types of Angles) :
(i) ପରିମାଣ ଭେଦରେ କୋଣଗୁଡ଼ିକୁ ନିମ୍ନମତେ ଶ୍ରେଣୀବିଭାଗ କରାଯାଏ ।
(a) କୌଣସି କୋଣର ପରିମାଣ 90° ଠାରୁ କମ୍ ହେଲେ, ଏହାକୁ ଏକ ସୂକ୍ଷ୍ମକୋଣ (Acute angle) କୁହାଯାଏ ।
(b) କୌଣସି କୋଣର ପରିମାଣ 90° ଠାରୁ ଅଧିକ ହେଲେ, ଏହାକୁ ଏକ ସ୍ଥୂଳକୋଣ (Obtuse angle) କୁହାଯାଏ ।
(c) କୌଣସି କୋଣର ପରିମାଣ 90° ହେଲେ, ଏହାକୁ ଏକ ସମକୋଣ (Right angle) କୁହାଯାଏ ।
![]()
କୋଣ ମଧ୍ଯରେ ସମ୍ପର୍କ :
(ii) ଦୁଇଟି କୋଣର ପରିମାଣର ସମଷ୍ଟି 90° ହେଲେ ସେମାନଙ୍କୁ ପରସ୍ପର ଅନୁପୂରକ (Complementary) କୋଣ କୁହାଯାଏ ।
(iii) ଦୁଇଟି କୋଣର ପରିମାଣର ସମଷ୍ଟି 180° ହେଲେ ସେମାନଙ୍କୁ ପରସ୍ପର ପରିପୁରକ (Supplementary) କୋଣ କୁହାଯାଏ ।
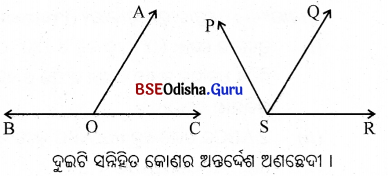
(iv) ଦୁଇଟି କୋଣର ଗୋଟିଏ ସାଧାରଣ ବାହୁ ଓ କୋଣଦ୍ୱୟର ଅନ୍ୟ ବାହୁ ଦୁଇଟି ସାଧାରଣ ବାହୁର ବିପରୀତ ପାର୍ଶ୍ଵରେ ବିସ୍ତୃତ ହେଲେ, ସେମାନଙ୍କୁ ସନ୍ନିହିତ କୋଣ କୁହାଯାଏ । ଦତ୍ତ ଚିତ୍ରରେ ∠AOB ଓ ∠AOC, ∠PSQ ଓ ∠QSR ସନ୍ନିହିତ ଅଟନ୍ତି ।
ସାଧାରଣ ବାହୁର ବିପରୀତ ପାର୍ଶ୍ବରେ ବିସ୍ତୃତ ବାହୁଦ୍ୱୟକୁ ସନ୍ନିହିତ କୋଣମାନଙ୍କର ବହିଃସ୍ଥ ବାହୁ (Exterior side) କୁହାଯାଏ ।
(v) ଗୋଟିଏ କୋଣର ବାହୁଦ୍ୱୟର ବିପରୀତ ରଶ୍ମିମାନଙ୍କ ଦ୍ୱାରା ଗଠିତ କୋଣକୁ ଉକ୍ତ କୋଣର ପ୍ରତୀପ କୋଣ କୁହାଯାଏ । ଦତ୍ତ ଚିତ୍ରରେ ∠AOC ଓ ∠BOD ପରସ୍ପର ପ୍ରତୀପ କୋଣ ଅଟନ୍ତି ।
ସମକୋଣ ସମ୍ପର୍କିତ କେତୋଟି ସଂଜ୍ଞା :
- ପରସ୍ପର ଲମ୍ବ (Mutually perpendicular) ରେଖା ଓ ରଶ୍ମି – ଦୁଇଟି ପରସ୍ପର ଅଣଛେଦୀ ରେଖାଦ୍ଵାରା ସୃଷ୍ଟି ହେଉଥିବା ଚାରିକୋଣ ମଧ୍ୟରୁ କୌଣସି ଗୋଟିଏ କୋଣ ସମକୋଣ ହେଲେ ରେଖାଦ୍ଵୟ ‘ପରସ୍ପର ଲମ୍ବ’’ ଅଟନ୍ତି ।
- ରେଖାଖଣ୍ଡର ସମଦ୍ବିଖଣ୍ଡକ ଲମ୍ବ (Perpendicular bisector) – ଗୋଟିଏ ରେଖାଖଣ୍ଡର ମଧ୍ୟବିନ୍ଦୁ ଦେଇ ଅଙ୍କିତ ଓ ଏହା ପ୍ରତି ଲମ୍ବ ହେଉଥିବା ସରଳରେଖାକୁ ରେଖାଖଣ୍ଡର ସମର୍ଦ୍ଦିଖଣ୍ଡକ ଲମ୍ବ କୁହାଯାଏ ।
ପରିପୂରକ ଓ ପ୍ରତୀପ କୋଣ ସଂପର୍କରେ ପ୍ରୟୋଜନୀୟ ତଥ୍ୟ :
ପରିପୂରକ କୋଣ ସମ୍ବନ୍ଧୀୟ ତଥ୍ୟ :
- ଗୋଟିଏ ରଶ୍ମିର ଶୀର୍ଷବିନ୍ଦୁ ଅନ୍ୟ ଏକ ରେଖାରେ ଅବସ୍ଥିତ ହେଲେ ଯେଉଁ ଦୁଇଟି ସନ୍ନିହିତ କୋଣ ଉତ୍ପନ୍ନ ହୁଏ, ସେମାନେ ପରସ୍ପର ପରିପୂରକ ଅର୍ଥାତ୍ ସେମାନଙ୍କ ପରିମାଣର ସମଷ୍ଟି 180° ଅଟେ।
m∠ACD + m∠BCD = 180° - ବିପରୀତକ୍ରମେ ଦୁଇଟି ସନ୍ନିହିତ କୋଣ ପରସ୍ପର ପରିପୂରକ ହେଲେ, ସେମାନଙ୍କ ବହିଃସ୍ଥ ବାହୁଦ୍ଵୟ ଏକ ସରଳରେଖାରେ ଅବସ୍ଥିତ ଅର୍ଥାତ୍ ପରସ୍ପର ବିପରୀତ ରଶ୍ମି ଅଟନ୍ତି ।
ପ୍ରତୀପ କୋଣ (Vertically Opposite Angles):
\(\overleftrightarrow{\mathrm{AB}}\) ଓ \(\overleftrightarrow{\mathrm{CD}}\) ପରସ୍ପରକୁ ( ବିନ୍ଦୁରେ ଛେଦ କଲେ ଉତ୍ପନ୍ନ ∠AOC ଓ ∠BOD ପରସ୍ପର ପ୍ରତୀପ କୋଣ ଅଟନ୍ତି । କୋଣକୁ ପରସ୍ପର ପ୍ରତୀପକୋଣ କହନ୍ତି । ସେହିପରି ∠BOC ଓ ∠DOA ମଧ୍ୟ
ସଂଜ୍ଞା: ଗୋଟିଏ କୋଣର ବାହୁଦ୍ୱୟର ବିପରୀତ ରଶ୍ମିମାନଙ୍କଦ୍ୱାରା ଗଠିତ କୋଣକୁ ଉକ୍ତ କୋଣର ପ୍ରତୀପକୋଣ କୁହାଯାଏ ।
ଉପପାଦ୍ୟ – 2 : ଦୁଇଟି ସରଳରେଖା ପରସ୍ପରକୁ ଛେଦକଲେ ଉତ୍ପନ୍ନ ହେଉଥିବା ପ୍ରତୀପ କୋଣମାନଙ୍କର ପରିମାଣ ସମାନ ।
ସମାନ୍ତର ସରଳରେଖା (Parallel Lines) :
ସଂଜ୍ଞା – ଏକ ସମତଳରେ ଅବସ୍ଥିତ ଦୁଇଟି ପୃଥକ୍ ସରଳରେଖା ଯଦି ପରସ୍ପରକୁ ଛେଦ କରୁନଥାନ୍ତି, ତେବେ ସେମାନଙ୍କୁ ସମାନ୍ତର ସରଳରେଖା କୁହାଯାଏ । ଦୁଇଟି ସମାନ୍ତର ସରଳରେଖାରେ ଅବସ୍ଥିତ ରଶ୍ମି କିମ୍ବା ରେଖାଖଣ୍ଡକୁ ମଧ୍ୟ ପରସ୍ପର ସମାନ୍ତର କୁହାଯାଏ ।
(i) L1 ଓ L2 ରେଖାଦ୍ବୟ ଯଦି ସମାନ୍ତର ହୁଅନ୍ତି ତେବେ ସଙ୍କେତରେ L1 || L2 ଲେଖାଯାଏ ।
(ii) ସଂଜ୍ଞାନୁଯାୟୀ L1 || L2 ହେଲେ L2 || L1 ହେବ ।
ସ୍ୱୀକାର୍ଯ୍ୟ – 9 : ସମାନ୍ତର ସ୍ୱୀକାର୍ଯ୍ୟ (Parallel Postulate) :
ଗୋଟିଏ ସରଳରେଖାର ବହିଃସ୍ଥ ଏକ ବିନ୍ଦୁ ମଧ୍ୟଦେଇ ତାହାପ୍ରତି ସମାନ୍ତର ହେଉଥିବା କେବଳ ମାତ୍ର ଗୋଟିଏ ସରଳରେଖା ଅବସ୍ଥିତ ।
ଉପପାଦ୍ୟ – 3 : ଏକ ସମତଳରେ ଅବସ୍ଥିତ ଓ ପରସ୍ପର ଠାରୁ ପୃଥକ୍ ଯେଉଁସବୁ ସରଳରେଖା ଅନ୍ୟ ଏକ ସରଳରେଖା ସହ ସମାନ୍ତର, ସେମାନେ ପରସ୍ପର ସମାନ୍ତର ।
ଏ ସମାନ୍ତର ସରଳରେଖା ଓ ସେମାନଙ୍କର ଛେଦକ (Parallel Lines and their transversals) :
(a) ଗୋଟିଏ ସରଳରେଖା ଦୁଇ ବା ତତୋଽଧ୍ଵ ସମାନ୍ତର ରେଖାକୁ ଛେଦ କଲେ ତାହାକୁ ସମ୍ପୃକ୍ତ ସମାନ୍ତର ରେଖାମାନଙ୍କର ଛେଦକ (Transversal) କୁହାଯାଏ ।
(b) ଦୁଇଟି ସମାନ୍ତର ରେଖାକୁ ଗୋଟିଏ ଛେଦକ ଛେଦକଲେ, ଯେଉଁ ଆଠଗୋଟି କୋଣ ସୃଷ୍ଟି ହୁଏ, ସେମାନଙ୍କୁ ଯୋଡ଼ା ଯୋଡ଼ା କରି ଦୁଇପ୍ରକାର ନାମରେ ନାମିତ କରାଯାଏ; ଯଥା – ଏକାନ୍ତର କୋଣ ଓ ଅନୁରୂପ କୋଣ । ଦତ୍ତ ଚିତ୍ରରେ ସଂପୃକ୍ତ କୋଣମାନଙ୍କର ଅନ୍ତର୍ଦେଶଗୁଡ଼ିକ l ରୁ 8 ପର୍ଯ୍ୟନ୍ତ ସଂଖ୍ୟାଦ୍ଵାରା ଚିହ୍ନିତ କରାଯାଇଛି । ଏକାନ୍ତର ଓ ଅନୁରୂପ ଭେଦରେ କୋଣ ଯୋଡ଼ାଗୁଡ଼ିକ ହେଲେ
(i) ଏକାନ୍ତର କୋଣ (Alternate Angles):
- ∠AGH ଓ ∠GHD (ଅନ୍ତର୍ଦେଶ 3 ଓ 6)
- ∠BGH ଓ ∠GHC (ଅନ୍ତର୍ଦେଶ 3 ଓ 6)
(ii) ଅନୁରୂପ କୋଣ (Corresponding Angles) :
- ∠EGB ଓ ∠GHD (ଅନ୍ତର୍ଦେଶ 2 ଓ 6)
- ∠DHF ଓ ∠BGH (ଅନ୍ତର୍ଦେଶ 8 ଓ 4)
- ∠EGA ଓ ∠GHC (ଅନ୍ତର୍ଦେଶ 1 ଓ 5)
- ∠CHF ଓ ∠AGH (ଅନ୍ତର୍ଦେଶ 7 ଓ 3)
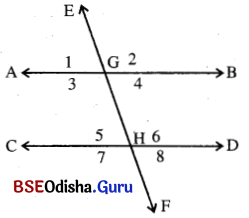
(iii) ଅନ୍ତଃସ୍ଥ କୋଣ (Interior Angles) ଓ ବହିଃସ୍ଥ କୋଣ (Exterior Angles) :
- ଦତ୍ତ ଚିତ୍ରରେ 3, 4, 5 ଓ 6 ଦ୍ୱାରା ଚିହ୍ନିତ ଅନ୍ତର୍ଦେଶ ବିଶିଷ୍ଟ କୋଣଗୁଡ଼ିକୁ ଅନ୍ତଃସ୍ଥ କୋଣ କୁହାଯାଏ ଓ ଅବଶିଷ୍ଟ କୋଣମାନଙ୍କୁ ବହିଃସ୍ଥ କୋଣ କୁହାଯାଏ ।
- ∠AGH, ∠BGH, ∠GHC ଓ ∠GHD ହେଉଛନ୍ତି ଅନ୍ତଃସ୍ଥ କୋଣ ଓ ଅନ୍ୟ ଚାରିଗୋଟି କୋଣ ବହିଃସ୍ଥ ଅଟନ୍ତି ।
କେତେକ ଜ୍ଞାତବ୍ୟ ବିଷୟ :
(a) ଦୁଇଟି ସମାନ୍ତର ସରଳରେଖା ଓ ଗୋଟିଏ ଛେଦକ ଦ୍ବାରା ସୃଷ୍ଟି
(i) ଯେକୌଣସି ଏକାନ୍ତର କୋଣ ଯୋଡ଼ା ସମପରିମାଣ ବିଶିଷ୍ଟ ହୁଅନ୍ତି । ଅର୍ଥାତ୍ ଦତ୍ତ ଚିତ୍ରରେ m∠AGH = m∠GHD ଓ m∠BGH = m∠GHC
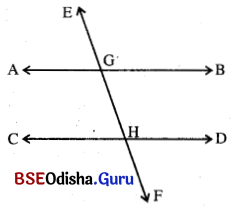
(ii) ଯେକୌଣସି ଅନୁରୂପ କୋଣ ଯୋଡ଼ା ସମପରିମାଣ ବିଶିଷ୍ଟ ହୁଅନ୍ତି, ଅର୍ଥାତ୍ ଦତ୍ତ ଚିତ୍ରରେ
m∠EGB = m∠GHD, m∠DHF = m∠BGH, m∠EGA = m∠GHC ଓ ∠CHF = m∠AGH
(iii) ଯେଉଁ ଅନ୍ତଃସ୍ଥ କୌଣଦ୍ୱୟର ଅନ୍ତର୍ଦେଶ ଛେଦକର ଏକ ପାର୍ଶ୍ଵରେ ଅବସ୍ଥିତ, ସେମାନେ ପରସ୍ପର ପରିପୂରକ, ଅର୍ଥାତ୍ m∠AGH + m∠CHG = 180° ଓ m∠BGH + m∠DHG = 180° ଅଟେ
(b) ଦୁଇଟି ସରଳରେଖା ଓ ସେମାନଙ୍କର ଗୋଟିଏ ଛେଦକ ଦ୍ବାରା ସୃଷ୍ଟି ହେଉଥିବା
(i) ଯେକୌଣସି ଏକାନ୍ତର କୋଣ ଯୋଡ଼ା ଯଦି ସମପରିମାଣ ବିଶିଷ୍ଟ ହୁଅନ୍ତି ।
(ii) ଯେକୌଣସି ଅନୁରୂପ କୋଣ ଯୋଡ଼ା ଯଦି ସମପରିମାଣ ବିଶିଷ୍ଟ ହୁଅନ୍ତି ।
(iii) ଯେଉଁ ଅନ୍ତଃସ୍ଥ କୋଣଦ୍ୱୟର ଅନ୍ତର୍ଦେଶ ଛେଦକର ଏକ ପାର୍ଶ୍ଵରେ ଅବସ୍ଥିତ, ସେମାନେ ଯଦି ପରସ୍ପର ପରିପୂରକ ହୁଅନ୍ତି; ତେବେ ସମ୍ପୃକ୍ତ ରେଖାଦ୍ଵୟ ସମାନ୍ତର ଅଟନ୍ତି ।
![]()
ଉପରୋକ୍ତ ତଥ୍ୟ ଅନୁଯାୟୀ :
(i) m∠AGH = m∠GHD
କିମାୃ, m∠BGH = m∠GHC ⇒ \(\stackrel{\leftrightarrow}{\mathrm{AB}} \| \stackrel{\leftrightarrow}{\mathrm{CD}}\)
(ii) m∠EGB = m∠GHD ବା m∠DHF
= m∠BGH ବା m∠EGA = m∠GHC
ବା m∠CHF = m∠AGH ⇒ \(\stackrel{\leftrightarrow}{\mathrm{AB}} \| \stackrel{\leftrightarrow}{\mathrm{CD}}\)
(iii) m∠AGH + m∠CHG = 180°
କିମାୃ, m∠BGH + m∠DHG = 180° ⇒ \(\stackrel{\leftrightarrow}{\mathrm{AB}} \| \stackrel{\leftrightarrow}{\mathrm{CD}}\)
ଅନୁରୂପ କୋଣ ସ୍ବୀକାର୍ଯ୍ୟ :
ଏକ ସମତଳରେ ଅବସ୍ଥିତ ଦୁଇଟି ସରଳରେଖାକୁ ଏକ ଛେଦକ ଦୁଇଟି ବିନ୍ଦୁରେ ଛେଦକଲେ, ଯଦି ଦୁଇଟି ଅନୁରୂପ କୋଣର ପରିମାଣ ସମାନ ହୁଏ, ତେବେ ସରଳରେଖା ଦୁଇଟି ସମାନ୍ତର ହେବେ ।
ଉପପାଦ୍ୟ – 4 : ଦୁଇଟି ସମାନ୍ତର ସରଳରେଖାକୁ ଏକ ଛେଦକ ଛେଦକଲେ, ଯେକୌଣସି ଦୁଇଟି ଅନୁରୂପ କୋଣର ପରିମାଣ ସମାନ ହୁଏ ।
ଉପପାଦ୍ୟ – 5 : ଦୁଇଟି ସମାନ୍ତର ସରଳରେଖାକୁ ଏକ ଛେଦକ ଛେଦକଲେ ପ୍ରତ୍ୟେକ ଯୋଡ଼ା ଏକାନ୍ତର କୋଣର ପରିମାଣ ସମାନ ହୁଏ ।
ଉପପାଦ୍ୟ – 6 : ଏକ ସମତଳରେ ଥିବା ଦୁଇଟି ସରଳରେଖାକୁ ଏକ ଛେଦକ ଦୁଇଟି ବିନ୍ଦୁରେ ଛେଦକଲେ, ଯଦି ଦୁଇଟି ଏକାନ୍ତର କୋଣର ପରମାଣ ସମାନ ହୁଏ, ତେବେ ସରଳରେଖା ଦୁଇଟି ସମାନ୍ତର ।
ଉପପାଦ୍ୟ -7 : ଦୁଇଟି ସମାନ୍ତର ସରଳରେଖାକୁ ଏକ ଛେଦକ ଛେଦକଲେ, ଛେଦକର ଏକପାର୍ଶ୍ୱସ୍ଥ ଅନ୍ତଃସ୍ଥ କୌଣଦ୍ୱୟର
ପରିମାଣର ସମଷ୍ଟି 180° ।
ଉପପାଦ୍ୟ – 8 : ଏକ ସମତଳରେ ଥିବା ଦୁଇଟି ସରଳରେଖାକୁ ଏକ ଛେଦକ ଦୁଇଟି ବିନ୍ଦୁରେ ଛେଦକଲେ, ଯଦି ଛେଦକର ଏକ ପାର୍ଶ୍ୱସ୍ଥ ଅନ୍ତଃସ୍ଥ କୌଣଦ୍ୱୟର ପରିମାଣର ସମଷ୍ଟି 180° ହୁଏ, ତେବେ ସରଳରେଖାଦ୍ବୟ ସମାନ୍ତର ।
ତ୍ରିଭୁଜର କୋଣ ଏବଂ ଏହାର ବହିଃସ୍ଥ କୋଣ (Angles of a triangle and its exterior angles) :
ଉପପାଦ୍ୟ – 9 : ଗୋଟିଏ ତ୍ରିଭୁଜର ତିନିକୋଣର ପରିମାଣର ସମଷ୍ଟି 180° !
ଅନୁସିଦ୍ଧାନ୍ତ – 1 : ଗୋଟିଏ ସମକୋଣୀ ତ୍ରିଭୁଜର ସୂକ୍ଷ୍ମକୋଣଦ୍ଵୟ ପରସ୍ପର ଅନୁପୂରକ ।
ଅନୁସିଦ୍ଧାନ୍ତ – 2 : ଗୋଟିଏ ତ୍ରିଭୁଜରେ ଗୋଟିକରୁ ଅଧିକ ସମକୋଣ ବା ସ୍ଥୂଳକୋଣ ରହିପାରିବ ନାହିଁ ।
ଅନୁସିଦ୍ଧାନ୍ତ – 3 : ଏକ ଉତ୍ତଳ ଚତୁର୍ଭୁଜର ଚାରିକୋଣର ପରିମାଣର ସମଷ୍ଟି 360° ।
ତ୍ରିଭୁଜର ବହିଃସ୍ଥ କୋଣ (Exterior angle of a triangle) :
ସଂଜ୍ଞା : ତ୍ରିଭୁଜର ଅନ୍ତଃସ୍ଥ କୋଣର ସନ୍ନିହିତ ପରିପୂରକ କୋଣକୁ ତ୍ରିଭୁଜର ବହିଃସ୍ଥ କୋଣ କୁହାଯାଏ ।
ଉପପାଦ୍ୟ – 10 : ତ୍ରିଭୁଜର କୌଣସି ଏକ ବହିଃସ୍ଥ କୋଣର ପରିମାଣ ଏହାର ଅନ୍ତସ୍ଥ ଦୂରବର୍ତ୍ତୀ କୋଣଦ୍ଵୟର ପରିମାଣର ସମଷ୍ଟି ସହ ସମାନ ।
ଅନୁସିଦ୍ଧାନ୍ତ – 1 : ତ୍ରିଭୁଜର କୌଣସି ବହିଃସ୍ଥ କୋଣର ପରିମାଣ, ଏହାର ପ୍ରତ୍ୟେକ ଅନ୍ତଃସ୍ଥ କୋଣ ପରିମାଣଠାରୁ ବୃହତ୍ତର ।
ଅନୁସିଦ୍ଧାନ୍ତ – 2 : ତ୍ରିଭୁଜର ବହିଃସ୍ଥ କୋଣମାନଙ୍କର ପରିମାଣର ସମଷ୍ଟି 360° ।
