BSE Odisha 9th Class Maths Notes Geometry Chapter 6 ଅଙ୍କନ

Odisha State Board BSE Odisha 9th Class Maths Notes Geometry Chapter 6 ଅଙ୍କନ will enable students to study smartly.

BSE Odisha Class 9 Maths Notes Geometry Chapter 6 ଅଙ୍କନ

ତ୍ରିଭୁଜ ଅଙ୍କନ (Construction of Triangles) : 
ନିମ୍ନ କେତେକ ପରିସ୍ଥିତିରେ ତ୍ରିଭୁଜ ଅଙ୍କନ ସମ୍ଭବ ।
ଅଙ୍କନ-1 : ଭୂମିର ଦୈର୍ଘ୍ୟ, ଅନ୍ୟ ଦୁଇବାହୁର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି ଓ ଗୋଟିଏ ଭୂମି ସଂଲଗ୍ନ କୋଣ ପରିମାଣ । 
ଅଙ୍କନ-2 : ଭୂମିର ଦୈର୍ଘ୍ୟ, ଅନ୍ୟ ଦୁଇବାହୁର ଦୈର୍ଘ୍ୟର ଅନ୍ତର ଓ ଗୋଟିଏ ଭୂମି ସଂଲଗ୍ନ କୋଣ ପରିମାଣ 
ଅଙ୍କନ-3 : ତିନିବାହର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି ଓ ଭୂମିସଂଲଗ୍ନ କୋଣଦ୍ବୟର ପରିମାଣ
ଅଙ୍କନ-4 : ଦୁଇବାହୁର ଦୈର୍ଘ୍ୟ ଓ ଗୋଟିଏ କୋଣର ପରିମାଣ
ଅଙ୍କନ-5 : ମଧ୍ଯମାର ଦୈର୍ଘ୍ୟ ଓ ଅନ୍ୟକୌଣସି ଦୁଇଟି ତଥ୍ୟ ।

ଅଙ୍କନ 1:
କୌଣସି ତ୍ରିଭୁଜର ଗୋଟିଏ ବାହୁର ଦୈର୍ଘ୍ୟ, ସେହି ବାହୁ ସଂଲଗ୍ନ କୋଣଦ୍ଵୟ ମଧ୍ୟରୁ ଗୋଟିକର ପରିମାଣ ଓ ଅନ୍ୟ ଦୁଇବାହୁର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି ଦତ୍ତ ଅଛି । ତ୍ରିଭୁଜ ଅଙ୍କନ କରିବାକୁ ହେବ ।
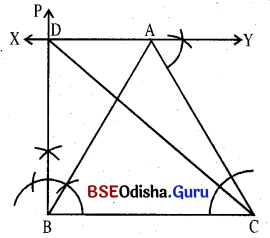
ମନେକର Δ ABCର BC = a ଏକକ, m∠ABC = B°, AC + AB = (b + c) ଏକକ ଦତ୍ତ ଅଛି । Δ ABC ଅଙ୍କନ କରିବାକୁ ହେବ ।
(i) a ଏକକ ପରିମିତ B͞C ଅଙ୍କନ କର ।
(ii) B͞C ଉପରେ B ବିନ୍ଦୁରେ B°
ପରିମିତ ∠CBD ଅଙ୍କନ କର ।
(iii) B͞D ରୁ (b + c) ଏକକ ପରିମିତ B͞D କାଟ ।
DC ଅଙ୍କନ କର ।

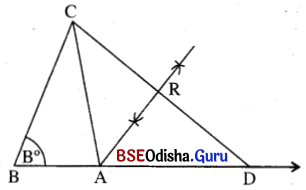
(iv) ବର୍ଭମାନ DCର ସମଦ୍ବିଖଣ୍ଡକ ଲମ୍ବ ଅଙ୍କନ କର । ତାହା BD କୁ ଯେଉଁ ବିନ୍ଦୁରେ ଛେଦ କରିବ ତାହାହିଁ ହେବ A ବିନ୍ଦୁ । (କିମ୍ବା DCର C ବିନ୍ଦୁରେ m∠D = m∠DCA ଅଙ୍କନ କର; \(\overrightarrow{\mathrm{CA}}\), BD କୁ ଯେଉଁ ବିନ୍ଦୁରେ ଛେଦ କରିବ ତାହା ମଧ୍ଯ A ବିନ୍ଦୁ ହେବ ।)
(v) AC ଅଙ୍କନ କର । ବର୍ତ୍ତମାନ Δ ABC ଉଦ୍ଦିଷ୍ଟ ତ୍ରିଭୁଜ ।

ଅଙ୍କନ 2 :
କୌଣସି ତ୍ରିଭୁଜର ଗୋଟିଏ ବାହୁର ଦୈର୍ଘ୍ୟ, ସେହି ବାହୁ ସଂଲଗ୍ନ ଗୋଟିଏ କୋଣ ପରିମାଣ ଓ ଅନ୍ୟ ଦୁଇ ବାହୁର ଦୈର୍ଘ୍ୟର ଅନ୍ତର ଦତ୍ତ ଅଛି । ତ୍ରିଭୁଜ ଅଙ୍କନ କରିବାକୁ ହେବ ।
(a) ମନେକର Δ ABC ର BC = a ଏକକ m∠ABC = B°, AC > AB
AC – AB = (b – c) ଏକକ ଦତ୍ତ ଅଛି । Δ ABC ଅଙ୍କନ କରିବାକୁ ହେବ ।

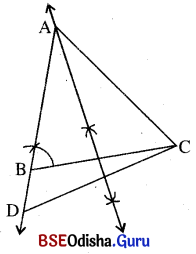
ଅଙ୍କନ ପ୍ରଣାଳୀ :
(i) ଏକ ସରଳରେଖା ଅଙ୍କନ କରି ତହିଁରୁ ଦତ୍ତ à ଏକକ ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ BC କାଟ ।
(ii) B͞C ଉପରେ B ବିନ୍ଦୁରେ B° ପରିମିତ କୋଣ ଅଙ୍କନ କରି ଯେଉଁ ରଶ୍ମି ମିଳିଲା, ତାର ବିପରୀତ ରଶ୍ମି ଉପରେ ବିନ୍ଦୁ ନିଅ ଯେପରି
BD = (b – c) ଏକକ ହେବ ।
(iii) CD ଅଙ୍କନ କର । CDର ସମଦ୍ବିଖଣ୍ଡକ ଲମ୍ବ ଅଙ୍କନ କର । ଏହା \(\overrightarrow{\mathrm{DB}}\) କୁ ଯେଉଁ ବିନ୍ଦୁରେ ଛେଦ କରିବ, ସେ ବିନ୍ଦୁଟି ହେବ A ବିନ୍ଦୁ 
(iv) AC ଅଙ୍କନ କରି Δ ABC ସଂପୂର୍ଣ୍ଣ କର ।

(b) ମନେକର ΔABCରେ BC = a ଏକକ, m∠ABC = B°, AB > AC, AB – AC = (c – b) ଏକକ ଦତ୍ତ ଅଛି । Δ ABC ଅଙ୍କନ କରିବାକୁ ହେବ ।

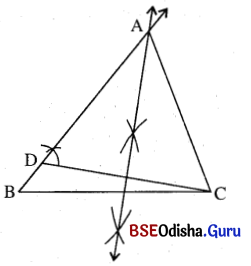
ଅଙ୍କନ ପ୍ରଣାଳୀ :
(i) ଏକ ସରଳରେଖା ଅଙ୍କନ କରି ତହିଁରୁ à ଏକକ ଦୈର୍ଘ୍ୟ ପରିମିତ BC କାଟ ।
(ii) BC ଉପରେ B ବିନ୍ଦୁରେ Bo ପରିମିତ କୋଣ ଅଙ୍କନ କରି ଯେଉଁ ରଶ୍ମି ମିଳିଲା ତା ଉପରେ BD = (c – b) ଏକକ ଛେଦନ କର 
(iii) C͞D ଅଙ୍କନ କର । CD ର ସମଦ୍ବିଖଣ୍ଡକ ଲମ୍ବ ଅଙ୍କନ କର । ତାହା \(\overrightarrow{\mathrm{BD}}\) କୁ ଯେଉଁ ବିନ୍ଦୁରେ ଛେଦ କରିବ ତାହାର ନାମ A ଦିଅ ।
(iv) AC ଅଙ୍କନ କରି Δ ABC ସଂପୂର୍ଣ୍ଣ କର ।

ଅଙ୍କନ –3 :
କୌଣସି ତ୍ରିଭୁଜର ପରିସୀମା ଓ ଦୁଇଟି କୋଣର ପରିମାଣ ଦତ୍ତ ଅଛି । ତ୍ରିଭୁଜଟି ଅଙ୍କନ କରିବାକୁ ହେବ । ମନେକର, Δ ABC ରେ ପରିସୀମା = (a + b + c) ଏକକ, m∠B = B°, m∠C = C° ଦତ୍ତ ଅଛି । Δ ABC ଅଙ୍କନ କରିବାକୁ ହେବ ।

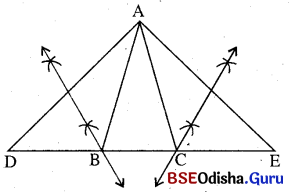
ଅଙ୍କନ ପ୍ରଣାଳୀ :
(i) ଏକ ସରଳରେଖା ଅଙ୍କନ କରି ତହିଁରୁ D͞E ଛେଦନ କର ଯେପରି DE = (a + b + c) ଏକକ ହେବ ।
(ii) D ବିନ୍ଦୁରେ \(\frac{1}{2}\)B° ମାପରେ ∠ADE ଓ E  ବିନ୍ଦୁରେ \(\frac{1}{2}\)C° ମାପରେ ∠AED ଅଙ୍କନ କର ।
(iii) \(\overrightarrow{\mathrm{DA}}\) ଓ \(\overrightarrow{\mathrm{EA}}\) ଯେଉଁ ବିନ୍ଦୁରେ ମିଳିତ ହେବେ ତାହାହିଁ A ବିନ୍ଦୁ ହେବ ।
(iv) AD ର ଲମ୍ବ ସମଦ୍ବିଖଣ୍ଡକ \(\stackrel{\leftrightarrow}{\mathrm{DE}}\) କୁ ଯେଉଁ ବିନ୍ଦୁରେ ଛେଦ କରିବ, ତାହା B ହେବ । \(\stackrel{\leftrightarrow}{\mathrm{AE}}\) ର ଲମ୍ବ ସମର୍ଦ୍ଦିଖଣ୍ଡ ଲମ୍ବ DE କୁ ଯେଉଁ ବିନ୍ଦୁରେ ଛେଦ କରିବ, ତାହା C ହେବ ।
(v) AB ଓ AC ଅଙ୍କନ କରି Δ ABC ସଂପୂର୍ଣ୍ଣ କର ।

ଅଙ୍କନ – 4 :
କୌଣସି ତ୍ରିଭୁଜର ଦୁଇ ବାହୁର ଦୈର୍ଘ୍ୟ ଓ ଗୋଟିଏ କୋଣର ପରିମାଣ ଦତ୍ତ ଅଛି । ତ୍ରିଭୁଜ ଅଙ୍କନ କରିବାକୁ ହେବ । ମନେକର Δ ABCରେ AB = c ଏକକ, BC = a ଏକକ ଏବଂ m∠C = C° ଦତ୍ତ ଅଛି । Δ ABC ଅଙ୍କନ କରିବାକୁ ହେବ ।

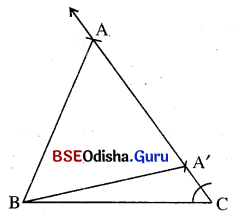
ଅଙ୍କନ ପ୍ରଣାଳୀ :
(i) a ଏକକ ପରିମିତ BC ଅଙ୍କନ କର ଓ C ବିନ୍ଦୁରେ C° ମାପ ବିଶିଷ୍ଟ କୋଣ ଅଙ୍କନ କର ।
(ii) B କୁ କେନ୍ଦ୍ରକରି BA = c ଏକକ ପରିମିତ ବ୍ୟାସାର୍ଦ୍ଧ ନେଇ ଚାପ ଅଙ୍କନ କର । ଏହି ଚାପ ŹCର ଅନ୍ୟ ସ୍ପର୍ଶକରେ, ସ୍ପର୍ଶକ ବିନ୍ଦୁର ନାମ A ଦିଅ ।
(iii) AB ଅଙ୍କନ କରି Δ ABC ସଂପୂର୍ଣ୍ଣ କର ।
(iv) ଏଠାରେ ଲକ୍ଷ୍ୟକର ଏହି ଚାପ, ଉକ୍ତ କୋଣର ବାହୁକୁ ଦୁଇଟି ବିନ୍ଦୁରେ ଛେଦ କରିଛି । ସେ ଦୁଇ ବିନ୍ଦୁର ନାମ A ଓ A’ ଦିଅ । BA ଓ BA’ ଅଙ୍କନ କଲେ, ଯଥାକ୍ରମେ Δ BCA ଓ Δ BCA’ ମିଳିବ ।
ମଧ୍ୟମା ଓ ଅନ୍ୟ ଅଂଶ ଦଉଥ‌ିବା ସ୍ଥଳେ ତ୍ରିଭୁଜ ଅଙ୍କନ :

ଅଙ୍କନ – 5 :
କୌଣସି ତ୍ରିଭୁଜର ଦୁଇବାହୁର ଦୈର୍ଘ୍ୟ ଓ ତୃତୀୟ ବାହୁ ପ୍ରତି ମଧ୍ଯମାର ଦୈର୍ଘ୍ୟ ଦତ୍ତ ଅଛି । ତ୍ରିଭୁଜଟି ଅଙ୍କନ କରିବାକୁ ହେବ । Δ ABCରେ AB = c ଏକକ, AC = b ଏକକ ଓ AM ମଧ୍ଯମାର ଦୈର୍ଘ୍ୟ = x ଏକକ । Δ ABC ଅଙ୍କନ କରିବାକୁ ହେବ ।

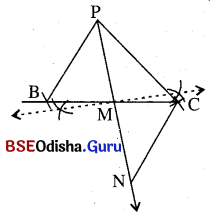
ଅଙ୍କନ ପ୍ରଣାଳୀ :
(i) କୌଣସି ଏକ ସରଳରେଖା ଅଙ୍କନ କରି ଏଥୁରୁ AN ଛେଦନ କର ଯେପରିକି AN = 2x ଏକକ ହେବ ।
(ii) A କୁ କେନ୍ଦ୍ରନେଇ ଓ b ଏକକ (AC ର ଦୈର୍ଘ୍ୟ) ବ୍ୟାସାର୍ଦ୍ଧ ନେଇ ଚାପ କାଟ; Nକୁ କେନ୍ଦ୍ରକରି ଓ NCର ଦୈର୍ଘ୍ୟ (=AB) c ଏକକ ବ୍ୟାସାର୍ଦ୍ଧ ନେଇ ଚାପ କାଟ । ଚାପଦ୍ବୟର ଛେଦବିନ୍ଦୁ C ହେଉ ।
(iii) AN ର ମଧ୍ୟବିନ୍ଦୁ M ନିରୂପଣ କର । C ଓ Mର ସଂଯୋଜକ \(\overrightarrow{\mathrm{CM}}\) ଉପରେ B ଏକ ବିନ୍ଦୁ ନିଅ ଯେପରିକି CM = MB ହେବ। Δ ABC ଆବଶ୍ୟକ ତ୍ରିଭୁଜ ।

ଅଙ୍କନ – 6 :
କୌଣସି ତ୍ରିଭୁଜର ଗୋଟିଏ ବାହୁର ଦୈର୍ଘ୍ୟ, ସେହି ବାହୁ ସଂଲଗ୍ନ କୋଣଦ୍ଵୟ ମଧ୍ୟରୁ ଗୋଟିକର ପରିମାଣ ଓ ଦତ୍ତ ବାହୁ ଭିନ୍ନ ଅନ୍ୟ ଏକ ବାହୁ ପ୍ରତି ମଧ୍ଯମାର ଦୈର୍ଘ୍ୟ ଦତ୍ତ ଅଛି । ତ୍ରିଭୁଜଟି ଅଙ୍କନ କରିବାକୁ ହେବ ।
ମନେକର Δ ABC ରେ AB = c ଏକକ, m∠BAC = A° ମଧ୍ୟମା AMର ଦୈର୍ଘ୍ୟ = x ଏକକ ।

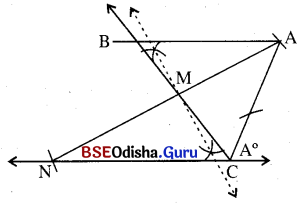
ଅଙ୍କନ ପ୍ରଣାଳୀ :
(i) କୌଣସି ଏକ ସରଳରେଖା ନେଇ ସେଥୁରୁ N͞C ଛେଦନ କର ଯେପରିକି NC = c ଏକକ ହେବ। NC ର C ବିନ୍ଦୁରେ (180 – A)° କୋଣ ଅଙ୍କନ କର । N ବିନ୍ଦୁକୁ କେନ୍ଦ୍ରକରି ଓ 2x ଏକକ ବ୍ୟାସାର୍ଦ୍ଧ ନେଇ ଚାପ କାଟ । ଏହା C ବିନ୍ଦୁରେ ଅଙ୍କିତ ରଶ୍ମିକୁ A ବିନ୍ଦୁରେ ଛେଦ କରୁ । Δ ANC ଅଙ୍କିତ ହେଲା ।
(ii) AN ର ମଧ୍ୟବିନ୍ଦୁ M ନିର୍ଣ୍ଣୟ କର । \(\overrightarrow{\mathrm{CM}}\) ଅଙ୍କନ କର । Mକୁ କେନ୍ଦ୍ରକରି C͞M ସହ ସମାନ ବ୍ୟାସାର୍ଷ ବିଶିଷ୍ଟ ଚାପ କାଟ । ଏହି ଚାପ ଯେଉଁଠି \(\overrightarrow{\mathrm{CM}}\) କୁ ଛେଦ କରିବ ତାହା B ହେବ । A͞B ଅଙ୍କନ କର Δ ABC ମିଳିବ ।

ବିକଳ୍ପ ଅଙ୍କନ ପ୍ରଣାଳୀ :
(i) ନିର୍ଦ୍ଦିଷ୍ଟ ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ AB ଅଙ୍କନ କର ।
(ii) A ବିନ୍ଦୁରେ ଦତ୍ତ ପରିମାଣ ବିଶିଷ୍ଟ ∠XAB ଅଙ୍କନ କର ।
(iii) AB ର ମଧ୍ୟବିନ୍ଦୁ N ଚିହ୍ନଟ କର ଏବଂ N ବିନ୍ଦୁରେ \(\overrightarrow{\mathrm{AX}}\) ସହ ସମାନ୍ତର କରି \(\overrightarrow{\mathrm{NY}}\) ଅଙ୍କନ କର ।
(iv) A ବିନ୍ଦୁକୁ କେନ୍ଦ୍ରକରି AM (ଦତ୍ତ ମଧ୍ଯମାର ଦୈର୍ଘ୍ୟ) ବ୍ୟାସାର୍ଦ୍ଧ ପରିମିତ ଚାପ, \(\overrightarrow{\mathrm{NY}}\) କୁ M ବିନ୍ଦୁରେ ଛେଦ କରୁ ।
(v) \(\overrightarrow{\mathrm{BM}}\), \(\overrightarrow{\mathrm{AX}}\) କୁ C ବିନ୍ଦୁରେ ଛେଦକରୁ । ବର୍ତ୍ତମାନ Δ ABC ଉଦ୍ଦିଷ୍ଟ ତ୍ରିଭୁଜ ।

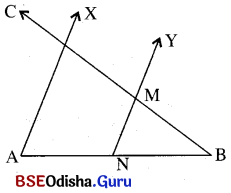
ଚତୁର୍ଭୁଜ ଅଙ୍କନ (Construction of Quadrilaterals) :

ଅଙ୍କନ – 7 :
କୌଣସି ଚତୁର୍ଭୁଜର ଚାରିବାହୁର ଦୈର୍ଘ୍ୟ ଓ ଗୋଟିଏ କୋଣର ପରିମାଣ ଦତ୍ତ ଅଛି, ଚତୁର୍ଭୁଜଟି ଅଙ୍କନ କରିବାକୁ ହେବ । ABCD ଚତୁର୍ଭୁଜର AB = a ଏକକ, BC = b ଏକକ, CD = c ଏକକ, DA = d ଏକକ ଏବଂ m∠A = θ° ଦତ୍ତ ଅଛି, ଚତୁର୍ଭୁଜଟି ଅଙ୍କନ କରିବାକୁ ହେବ ।
ଅଙ୍କନ ପ୍ରଣାଳୀ :

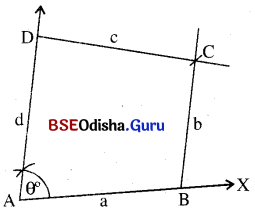
(i) a ଏକକ ପରିମିତ AB ଅଙ୍କନ କରି, A ବିନ୍ଦୁରେ ୫ ମାପରେ ∠BAD ଅଙ୍କନ କର ।
(ii) B ଓ Dକୁ କେନ୍ଦ୍ରକରି ଯଥାକ୍ରମେ b ଓ c ପରିମିତ ବ୍ୟାସାର୍ଦ୍ଧ ନେଇ BAD ର A- ପାର୍ଶ୍ଵର ବିପରୀତ ପାର୍ଶ୍ଵରେ ଦୁଇଟି ଚାପ ଅଙ୍କନ କର ଓ C ସେମାନଙ୍କର ଛେଦବିନ୍ଦୁ ହେଉ ।
(iii) BC ଓ CD ଅଙ୍କନ କର । ବର୍ତ୍ତମାନ ABCD ଉଦ୍ଦିଷ୍ଟ ଚତୁର୍ଭୁଜ ହେବ ।

ଅଙ୍କନ – 8 :
କୌଣସି ଚତୁର୍ଭୁଜର ଚାରିବାହୁର ଦୈର୍ଘ୍ୟ ଓ ଗୋଟିଏ କର୍ପୂର ଦୈର୍ଘ୍ୟ ଦତ୍ତ ଅଛି I ଚତୁର୍ଭୁଜଟି ଅଙ୍କନ କରିବାକୁ ହେବ ।
ମନେକର ABCD ଚତୁର୍ଭୁଜର AB = a ଏକକ, BC = b ଏକକ, CD = c ଏକକ, DA = d ଏକକ ଓ BD କଣ୍ଠର ଦୈର୍ଘ୍ୟ = e ଏକକ ଦତ୍ତ ଅଛି । ଚତୁର୍ଭୁଜଟି ଅଙ୍କନ କରିବାକୁ ହେବ ।

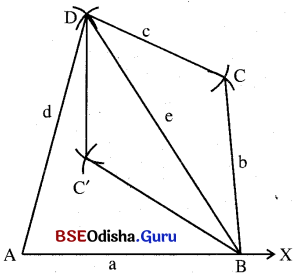
(i) AX ଅଙ୍କନ କରି ସେଥୁରୁ a ଏକ ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ AB ଛେଦନ କର ।
(ii) A ଓ Bକୁ କେନ୍ଦ୍ରକରି ଯଥାକ୍ରମେ d ଓ c ବ୍ୟାସାର୍ଦ୍ଧ ନେଇ AB ର ଏକ ପାର୍ଶ୍ଵରେ ଦୁଇଟି ଚାପ ଅଙ୍କନ କର ଏବଂ ସେମାନେ ପରସ୍ପରକୁ D ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତୁ । A͞D ଓ B͞D ଅଙ୍କନ କର ।
(iii) ପୁଣି B ଓ D ବିନ୍ଦୁକୁ କେନ୍ଦ୍ରକରି ଯଥାକ୍ରମେ b ଓ c ପରିମାଣ ବ୍ୟାସାର୍ଦ୍ଧ ନେଇ ଦୁଇଟି ଚାପ ଅଙ୍କନ କର ଏବଂ ସେମାନେ BD ର ଏକ ପାର୍ଶ୍ବରେ C ବିନ୍ଦୁରେ ଓ ଅପର ପାର୍ଶ୍ଵରେ C’ ବିନ୍ଦୁରେ ପରସ୍ପରକୁ ଛେଦ କରନ୍ତୁ । B͞C   D͞C, B͞C’ ଓ D͞C’ ଅଙ୍କନ କର ।
(iv) ବର୍ତ୍ତମାନ ABCD ବା ABC’D ପ୍ରତ୍ୟେକଟି ଉଦ୍ଦିଷ୍ଟ ଚତୁର୍ଭୁଜ ହେବ । ABCD ଚତୁର୍ଭୁଜଟି ଉତ୍ତଳ ଚତୁର୍ଭୁଜ ହେଉଥିଲା ବେଳେ ABC’D ଚତୁର୍ଭୁଜଟି ଉତ୍ତଳ ଚତୁର୍ଭୁଜ ନୁହେଁ ।

ଅଙ୍କନ – 9 :
କୌଣସି ଚତୁର୍ଭୁଜର ଦୁଇଟି ସନ୍ନିହିତ ବାହୁର ଦୈର୍ଘ୍ୟ ଓ ତିନୋଟି କୋଣର ପରିମାଣ ଦତ୍ତ ଅଛି । ଚତୁର୍ଭୁଜଟି ଅଙ୍କନ କରିବାକୁ ହେବ ।
ମନେକର ABCD ଚତୁର୍ଭୁଜର AB = a ଏକକ, BC = b ଏକକ ଏବଂ ∠A, ∠B, ∠C ଦତ୍ତ ଅଛି I ଚତୁର୍ଭୁଜଟି ଅଙ୍କନ କରିବାକୁ ହେବ ।

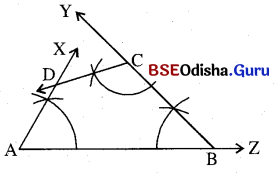
ଅଙ୍କନ ପ୍ରଣାଳୀ :
(i) a ଏକକ ପରିମିତି A͞B ଅଙ୍କନ କରି B ବିନ୍ଦୁରେ m∠B ପରିମିତ କୋଣ ଅଙ୍କନ କର ।
(ii) \(\overrightarrow{\mathrm{BY}}\) ବାହୁରୁ b ଏକକ ଛେଦକଲେ ଚତୁର୍ଭୁଜର C କୌଣିକ ବିନ୍ଦୁ ମିଳିବ ।
(iii) AB ର A ବିନ୍ଦୁରେ ଓ C-ପାର୍ଶ୍ଵରେ m∠A ପରିମାଣ ବିଶିଷ୍ଟ କୋଣ ଓ BC ର C ବିନ୍ଦୁରେ ଓ A-ପାର୍ଶ୍ବରେ m∠C ପରିମାଣ ବିଶିଷ୍ଟ କୋଣ ଅଙ୍କନ କଲେ ସେମାନଙ୍କର ବାହୁମାନ ଯେଉଁ ବିନ୍ଦୁରେ ଛେଦ କରିବେ ତାହା ହେବ D ଓ ଉଦ୍ଦିଷ୍ଟ ଚତୁର୍ଭୁଜ ABCD ମିଳିବ ।

ସମକ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ତ୍ରିଭୁଜ ଅଙ୍କନ :

ଅଙ୍କନ – 10 :
କୌଣସି ଦତ୍ତ ତ୍ରିଭୁଜ ସହ ସମକ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ଏକ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜ ଅଙ୍କନ କରିବାକୁ ହେବ ।
Δ ABC ଗୋଟିଏ ଦତ୍ତ ତ୍ରିଭୁଜ । ଏହାର ସମକ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ଏକ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜ ଅଙ୍କନ କରିବାକୁ ହେବ ।

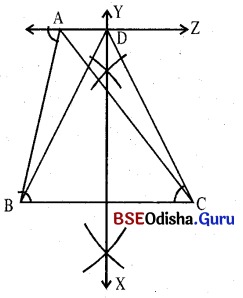
ଅଙ୍କନ ପ୍ରଣାଳୀ :
(i) Δ ABC ଅଙ୍କନ କର ।
(ii) ତତ୍‌ପରେ A ବିନ୍ଦୁ ମଧ୍ୟଦେଇ B͞C ସଙ୍ଗେ ସମାନ୍ତର କରି \(\overleftrightarrow{\mathrm{AZ}}\) ଅଙ୍କନ କର ।
(iii) BC ର ସମଦ୍ବିଖଣ୍ଡକ ଲମ୍ବ \(\overleftrightarrow{\mathrm{XY}}\) ଅଙ୍କନ କର । ତାହା \(\overleftrightarrow{\mathrm{AZ}}\) କୁ D ବିନ୍ଦୁରେ ଛେଦ କରୁ ।
(iv) DB ଓ DCଅଙ୍କନ କର Δ DBC ଆବଶ୍ୟକ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜ ।

ଅଙ୍କନ – 11 :
ଦତ୍ତ ତ୍ରିଭୁଜ ସହ ସମକ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜ ଅଙ୍କନ କରିବାକୁ ହେବ ।
Δ ABC ଗୋଟିଏ ଦତ୍ତ ତ୍ରିଭୁଜ । ଏହାର ସମକ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜ ଅଙ୍କନ କରିବାକୁ ହେବ ।

ଅଙ୍କନ ପ୍ରଣାଳୀ :
(i) Δ ABC ଅଙ୍କନ କର ।
(ii) A ବିନ୍ଦୁ ମଧ୍ୟଦେଇ BC ସହ ସମାନ୍ତର \(\overleftrightarrow{\mathrm{XY}}\) ଅଙ୍କନ କର ।
(iii) B ଏଠାରେ BC ପ୍ରତି BP ଲମ୍ବ ଅଙ୍କନ କର । ଏହା \(\overleftrightarrow{\mathrm{XY}}\) କୁ D ବିନ୍ଦୁରେ ଛେଦ କରୁ ।
(iv) DC ଅଙ୍କନ କର । Δ DBC ଉଦ୍ଦିଷ୍ଟ ତ୍ରିଭୁଜ ।

ଅଙ୍କନ – 12 :
ଏକ ଦତ୍ତ ତ୍ରିଭୁଜର ଭୂମିର ଦୈର୍ଘ୍ୟ ପରିବର୍ତ୍ତନ କରି ସମକ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ଅନ୍ୟ ଏକ ତ୍ରିଭୁଜ ଅଙ୍କନ କରିବାକୁ ହେବ । 
Δ ABC ଗୋଟିଏ ଦତ୍ତ ତ୍ରିଭୁଜ । ଏହାର ସମକ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ଏକ ତ୍ରିଭୁଜ ଅଙ୍କନ କରିବାକୁ ହେବ ।

ଅଙ୍କନ ପ୍ରଣାଳୀ :
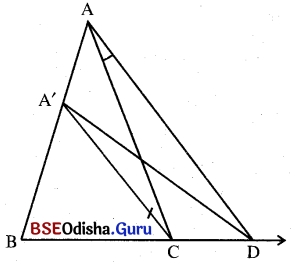
(i) Δ ABC ଅଙ୍କନ କର ।
(ii) Δ ABCର \(\overrightarrow{\mathrm{BC}}\) ଉପରିସ୍ଥ ଏପରି ଏକ ବିନ୍ଦୁ ନିଅ ଯେପରିକି B – C – D  ଏଠାରେ BD > BC ଅଙ୍କନ କର ।
(iii) C ବିନ୍ଦୁରେ AD ସହ ସମାନ୍ତର ଅଙ୍କନ କରି CA’ ଅଙ୍କନ କର ଯାହା AB କୁ A’ ବିନ୍ଦୁରେ ଛେଦ କରିବ ।
(iv) A’D ଅଙ୍କନ କର । ବର୍ତ୍ତମାନ Δ A’BDର କ୍ଷେତ୍ରଫଳ ଦତ୍ତ Δ A’BCର କ୍ଷେତ୍ରଫଳ ସହ ସମାନ ହେବ ।

ଅଙ୍କନ – 13 :
ଏକ ଦତ୍ତ ଚତୁର୍ଭୁଜର ସମକ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ଏକ ତ୍ରିଭୁଜ ଅଙ୍କନ କରିବାକୁ ହେବ ।
ABCD ଏକ ଦତ୍ତ ଚତୁର୍ଭୁଜ । ଏହାର ସମକ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ଏକ ତ୍ରିଭୁଜ ଅଙ୍କନ କରିବାକୁ ହେବ ।

ଅଙ୍କନ ପ୍ରଣାଳୀ :
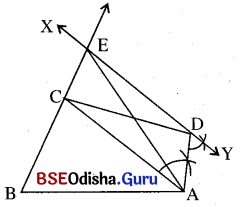
(i) A͞C କର୍ଣ ଅଙ୍କନ କର ।
(ii) D ବିନ୍ଦୁ ଦେଇ AC ସହ ସମାନ୍ତର କରି \(\overleftrightarrow{\mathrm{XY}}\) ଅଙ୍କନ କର । ତାହା \(\overrightarrow{\mathrm{BC}}\) କୁ E ବିନ୍ଦୁରେ ଛେଦ କରୁ ।
(iii) A, Eକୁ ଯୋଗକର ।
(iv) Δ ABE ଆବଶ୍ୟକ ତ୍ରିଭୁଜ ।

ବିକଳ୍ପ ପ୍ରଣାଳୀ :
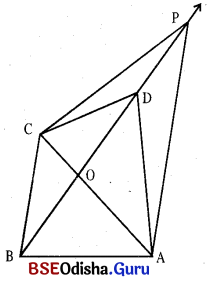
(i) କର୍ଣ୍ଣ CA ଓ BD ଅଙ୍କନ କର ଓ ଛେଦବିନ୍ଦୁର ନାମ ଦିଅ 0 ଦିଅ । \(\overrightarrow{\mathrm{BD}}\) ଅଙ୍କନ କର ।
(ii) D କୁ କେନ୍ଦ୍ର ନେଇ BO ବ୍ୟାସାର୍ଦ୍ଧବିଶିଷ୍ଟ ଚାପ ଅଙ୍କନ କର ଏବଂ ଯେଉଁ ବିନ୍ଦୁରେ ଉକ୍ତ ଚାପ \(\overrightarrow{\mathrm{BD}}\) କୁ ଛେଦ କରିବ ତା’ର ନାମ ଦିଅ P
(iii) PC ଓ P͞A ଅଙ୍କନ କର ।
(iv) ବର୍ତ୍ତମାନ ଆବଶ୍ୟକ ତ୍ରିଭୁଜ ହେଉଛି Δ PCA 

ତ୍ରିଭୁଜର ସମକ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ଆୟତକ୍ଷେତ୍ର ଅଙ୍କନ :

ଅଙ୍କନ – 14 :
କୌଣସି ଦତ୍ତ ତ୍ରିଭୁଜ ସହ ସମକ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ଏକ ଆୟତକ୍ଷେତ୍ର ଅଙ୍କନ କରିବାକୁ ହେବ ।
Δ ABC ଏକ ଦତ୍ତ ତ୍ରିଭୁଜ । ଏହାର ସମକ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ଏକ ଆୟତକ୍ଷେତ୍ର ଅଙ୍କନ କରିବାକୁ ହେବ ।

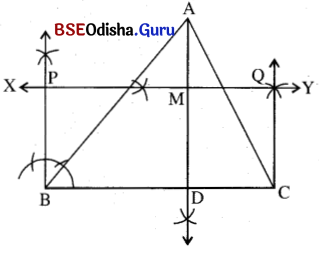
ଅଙ୍କନ ପ୍ରଣାଳୀ (1) :
(i) ଶୀର୍ଷବିନ୍ଦୁ A ରୁ B͞C ପ୍ରତି AD ଲମ୍ବ (ଉଚ୍ଚତା) ଟାଣ । AD ର ସମଦ୍ଵିଖଣ୍ଡକ ଲମ୍ବ \(\overleftrightarrow{\mathrm{XY}}\) ଅଙ୍କନ କର ।
(ii) B ଠାରେ BC ପ୍ରତି \(\overrightarrow{\mathrm{BP}}\) ଲମ୍ବ ଉତ୍ତୋଳନ କର । ତାହା \(\overleftrightarrow{\mathrm{XY}}\) କୁ P ବିନ୍ଦୁରେ ଛେଦ କରୁ ।
(iii) \(\overleftrightarrow{\mathrm{XY}}\) ରୁ BC ର ଦୈର୍ଘ୍ୟ ସଙ୍ଗେ ସମାନ କରି PQ ଅଂଶ ଛେଦନ କର । Q, Cକୁ ଯୋଗକର ।
PBCQ ଆବଶ୍ୟକ ଆୟତକ୍ଷେତ୍ର, ଯାହାର କ୍ଷେତ୍ରଫଳ Δ ABC ର କ୍ଷେତ୍ରଫଳ ସଙ୍ଗେ ସମାନ ।

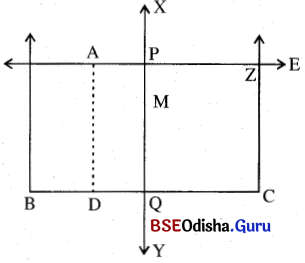
ଅଙ୍କନ ପ୍ରଣାଳୀ (2) :
(i) BC ର ସମଦ୍ବିଖଣ୍ଡକ ଲମ୍ବ \(\overleftrightarrow{\mathrm{XY}}\) ଅଙ୍କନ କର; ତାହା BC କୁ Q ବିନ୍ଦୁରେ ଛେଦକରୁ ।
(ii) A ମଧ୍ୟଦେଇ BC ସଙ୍ଗେ ସମାନ୍ତର କରି \(\overleftrightarrow{\mathrm{AE}}\) ଅଙ୍କନ କର; ତାହା XY କୁ P ବିନ୍ଦୁରେ ଛେଦ କରୁ ।
(iii) \(\overleftrightarrow{\mathrm{AE}}\) ରୁ QC ସଙ୍ଗେ ସମାନ କରି PZ ଅଂଶ ଛେଦନ କର 
PQCZ ଆବଶ୍ୟକ ଆୟତକ୍ଷେତ୍ର, ଯାହାର କ୍ଷେତ୍ରଫଳ Δ ABC ର କ୍ଷେତ୍ରଫଳ ସଙ୍ଗେ ସମାନ ।

ରେଖାଖଣ୍ଡ ବିଭାଜନ :

ଅଙ୍କନ – 15 :
କୌଣସି ଦତ୍ତ ରେଖାଖଣ୍ଡକୁ କେତେକ ସର୍ବସମ ଅଂଶରେ ବିଭକ୍ତ କରିବାକୁ ହେବ ।
A͞B ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ରେଖାଖଣ୍ଡ । ଏହାକୁ କେତେକ ଅଂଶରେ (ମନେକର 3ଟି ସର୍ବସମ ଅଂଶରେ) ବିଭକ୍ତ କରିବାକୁ ହେବ । 
ଅଙ୍କନ ପ୍ରଣାଳୀ :
(AB ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ରେଖାଖଣ୍ଡ । ଏହାକୁ କେତେକ ସର୍ବସମ ଅଂଶରେ (ମନେକର 3ଟି ସର୍ବସମ ଅଂଶରେ) ବିଭକ୍ତ କରିବାକୁ ହେବ ।

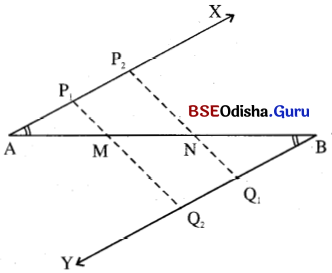
(a) AB ରେଖାଖଣ୍ଡର A ଓ B ବିନ୍ଦୁରେ ଦୁଇଟି ସମାନ ପରିମାଣ ବିଶିଷ୍ଟ କୋଣ ଯଥାକ୍ରମେ ∠XAB ଏବଂ ∠YBA ଅଙ୍କନ କର ।
(b) \(\overrightarrow{\mathrm{AX}}\) ରୁ କୌଣସି ନିର୍ଦ୍ଦିଷ୍ଟ ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ଦୁଇଟି ସର୍ବସମ ଅଂଶ A͞P₁ ଓ \(\overline{\mathrm{P}_1 \mathrm{P}_2}\) ଛେଦକର । (Aକୁ କେନ୍ଦ୍ର ନେଇ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ବ୍ୟାସାଦ୍ଧ ବିଶିଷ୍ଟ ଚାପ ଅଙ୍କନ କର ଯାହା \(\overrightarrow{\mathrm{AX}}\) କୁ P₁ ବିନ୍ଦୁରେ ଛେଦ କରୁ । ପୁନଶ୍ଚ P₁ ବିନ୍ଦୁକୁ କେନ୍ଦ୍ରକରି ପୂର୍ବ ବ୍ୟାସାର୍ଷ ବିଶିଷ୍ଟ ଅନ୍ୟ ଏକ ଚାପ କାଟ; ଯାହା \(\overrightarrow{\mathrm{AX}}\) କୁ P₂ ରେ ଛେଦକରୁ ।) ଏହିପରି କ୍ରମାନ୍ୱୟରେ ଏକାଧିକ ସର୍ବସମ ଅଂଶରେ ବିଭକ୍ତ କରି ପାରିବ ।
(c) ପୂର୍ବ ପ୍ରଣାଳୀ ଅନୁସରଣରେ \(\overrightarrow{\mathrm{BY}}\) ଉପରେ Q₁ ଓ Q₂ ବିନ୍ଦୁ ଚିହ୍ନଟ କର ଯେପରିକି, AP₁ = BQ₁ = BQ₂ ହେବ ।
(d) ବର୍ତ୍ତମାନ \(\overline{\mathrm{P}_2 \mathrm{Q}_1}\) ଏବଂ P₁Q₂ ଅଙ୍କନ କର ଯାହା AB କୁ ଯଥାକ୍ରମେ M ଓ N ବିନ୍ଦୁରେ ଛେଦ କରିବ । ଏଠାରେ AB ଟି ସମାନ ତିନି ସର୍ବସମ ଭାଗରେ ବିଭକ୍ତ ହେଲା ।