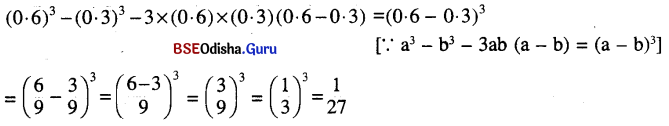BSE Odisha 9th Class Maths Solutions Algebra Chapter 2 ବାସ୍ତବ ସଂଖ୍ୟା Ex 2(a)

Odisha State Board BSE Odisha 9th Class Maths Solutions Algebra Chapter 2 ବାସ୍ତବ ସଂଖ୍ୟା Ex 2(a) Textbook Exercise Questions and Answers.

BSE Odisha Class 9 Maths Solutions Algebra Chapter 2 ବାସ୍ତବ ସଂଖ୍ୟା Ex 2(a)

Question 1.
ଭୁଲ୍ ଥିଲେ (F) ଓ ଠିକ୍ ଥିଲେ (T) ଲେଖ ।

(i) -1 ଦ୍ଵାରା -201 ବିଭାଜ୍ୟ ।
ସମାଧାନ:
T

(ii) 1 ଦ୍ଵାରା 0 ବିଭାଜ୍ୟ ।
ସମାଧାନ:
T

(iii) 0 ଦ୍ଵାରା 5 ବିଭାଜ୍ୟ ।
ସମାଧାନ:
F

(iv) ପୂର୍ଣ୍ଣସଂଖ୍ୟା ପରିମେୟ ନୁହେଁ ।
ସମାଧାନ:
F

(v) -5 < -3 ।
ସମାଧାନ:
T

(vi) 0.9 ଏକ ପରିମେୟ ସଂଖ୍ୟା ।
ସମାଧାନ:
T

(vii) 0 ଏକ ଗଣନ ସଂଖ୍ୟା ।
ସମାଧାନ:
F

(viii) -1/2 ଏକ ପରିମେୟ ସଂଖ୍ୟା ।
ସମାଧାନ:
T

(ix) a, b ∈ N ହେଲେ ab ∈ N ।
ସମାଧାନ:
T

(x) a, b ∈ N ହେଲେ a – b ∈ N ।
ସମାଧାନ:
F

(xi) a, b ∈ N ହେଲେ a – b ∈ Z ।
ସମାଧାନ:
T

(xii) a, b ∈ Z ହେଲେ a/b ∈ Z Q ।
ସମାଧାନ:
F

Question 2.
ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

(i) \(\frac{1}{2}\) ର ଯୋଗାତ୍ମକ ବିଲୋମୀ । _____ ।
ସମାଧାନ:
\(-\frac{1}{2}\)

(ii) -7ରଗୁଣନାତ୍ମକ ବିଲୋମୀ ______ ।
ସମାଧାନ:
\(-\frac{1}{7}\)

(iii) _____ ତା’ ନିଜର ଯୋଗାତ୍ମକ ବିଲୋମୀ ।
ସମାଧାନ:
0

(iv) _____ ତା’ ନିଜର ଯୋଗାତ୍ମକ ବିଲୋମୀ ।
ସମାଧାନ:
1, -1

(v) ପୂର୍ବ ସଂଖ୍ୟା ସେଟ୍‌ରେ ଯୋଗାତ୍ମକ ଅଭେଦ ______
ସମାଧାନ:
0

(vi) ଯୁଗ୍ମ ଓ ଅଯୁଗ୍ମ ସଂଖ୍ୟାର ଯୋଗଫଳ _____
ସମାଧାନ:
ଅଯୁଗ୍ମ

(vii) _____ ଏକମାତ୍ର ଯୁଗ୍ମ ମୌଳିକ ସଂଖ୍ୟା ଅଟେ ।
ସମାଧାନ:
2

(viii) ସର୍ବନିମ୍ନ ଅଯୁଗ୍ମ ମୌଳିକ ସଂଖ୍ୟାଟି _____ ଅଟେ ।
ସମାଧାନ:
3

(ix) ଗୁଣନ ପ୍ରକ୍ରିୟା _____ ପ୍ରକ୍ରିୟାକୁ ବଣ୍ଟନ କରେ ।
ସମାଧାନ:
ପୋଗ

(x) ପ୍ରକ୍ରିୟାକୁ ବଣ୍ଟନ କରେ । ଯୋଗାତ୍ମକ ବିଲୋମୀ ଉପାଦାନକୁ ମିଶାଇଲେ _____ ପକ ଅଟେ ।
ସମାଧାନ:
0

(xi) N ∩ N * = _____।
ସମାଧାନ:
N

(xii) ସେଟ୍‌ରେ – 1ର ଗୁଣନାତ୍ମକ ବିଲୋମୀ _____ ।
ସମାଧାନ:
-1

Question 3.
ନିମ୍ନଲିଖତ ପ୍ରତ୍ୟେକ ପ୍ରଶ୍ନପାଇଁ ପ୍ରଦତ୍ତ ସମ୍ଭାବ୍ୟ ଉତ୍ତରରୁ ଠିକ୍ ଉତ୍ତରଟିକୁ ବାଛ ।

(i) n, m ∈ Z ହେଲେ ନିମ୍ନଲିଖ ମଧ୍ୟରୁ କେଉଁଟି ଅସତ୍ୟ ?
(a) m + n ∈ Z
(b) m – n ∈ Z
(c) m × n ∈ Z
(d) n ÷ m ∈ Z
ସମାଧାନ:
n + m ∈ Z

(ii) Z ସେଟ୍‌ରେ କେଉଁଟି ସତ୍ୟ ?
(a) ଯୋଗାତ୍ମକ ଅଭେଦ 0
(b) ଯୋଗାତ୍ମକ ଅଭେଦ 1
(c) ଗୁଣନାତ୍ମକ ଅଭେଦ 0
(d) ଯୋଗାତ୍ମକ ବିଲୋମୀ (−1)
ସମାଧାନ:
ଯୋଗାତ୍ମକ ଅଭେଦ 0

(iii) ନିମ୍ନଲିଖ ମଧ୍ୟରୁ କେଉଁଟି ସତ୍ୟ ?
(a) ସବୁଠାରୁ କ୍ଷୁଦ୍ରତମ ମୌଳିକ ସଂଖ୍ୟାଟି 3 (b)
(b) ଦୁଇଟି ଅଯୁଗ୍ମ ସଂଖ୍ୟାର ଗୁଣଫଳ ଅଯୁଗ୍ମ
(c) ଦୁଇଟି ଅଯୁଗ୍ମ ସଂଖ୍ୟାର ଗୁଣଫଳ ଅଯୁଗ୍ମ (d)
(d) ଦୁଇଟି ମୌଳିକ ସଂଖ୍ୟାର ଗୁଣଫଳ ମୌଳିକ
ସମାଧାନ:
ଦୁଇଟି ଅଯୁଗ୍ମ ସଂଖ୍ୟାର ଗୁଣଫଳ ଅଯୁଗ୍ମ

(iv) ନିମ୍ନଲିଖ ମଧ୍ୟରୁ କେଉଁଟି ସତ୍ୟ ?
(a) x < y ଓ y < z ହେଲେ x < z
(b) x< y 3 z ∈ Q ହେଲେ xz < yz
(c) x < y ଓ z ∈ Q ହେଲେ x + z < y + z ନ ହୋଇପାରେ ।
(d) ଦୁଇଟି ପରିମେୟ ସଂଖ୍ୟା ମଧ୍ୟରେ ସସୀମ ସଂଖ୍ୟକ ପରିମେୟ ବିଦ୍ୟାମନ ।
ସମାଧାନ:
x < y ଓ y < z ହେଲେ x < z ଓ x < z

(v) ନିମ୍ନଲିଖ ମଧ୍ୟରୁ କେଉଁଟି ଠିକ୍ ?
(a) 0.9999 ……. < 1.0
(b) 1/5 ର ଦଶମିକ ପରିପ୍ରକାଶଟି 0.19999 …….
(c) 1/3 ର ଦଶମିକ ପରିପ୍ରକାଶ
(d) n ଏକ ମୌଳିକ ସଂଖ୍ୟା ହେଲେ 1/n ର ଦଶମିକ ପରିପ୍ରକାଶ ସର୍ବଦା ପୌନଃପୁନିକ ।
ସମାଧାନ:
1/5 ର ଦଶମିକ ପରିପ୍ରକାଶଟି 0.19999 …..

(vi) \(\frac{1}{2}, \frac{2}{3}, \frac{3}{5}, \frac{4}{7}\) ମଧ୍ୟରେ ବୃହତ୍ତମ ପରିମେୟ ସଂଖ୍ୟାଟି କେଉଁଟି ?
(a) \(\frac{1}{2}\)
(b) \(\frac{2}{3}\)
(c) \(\frac{3}{5}\)
(d) \(\frac{4}{7}\)
ସମାଧାନ:
\(\frac{2}{3}\)

(vii) \(\frac{1}{2}, \frac{2}{3}, \frac{3}{5}, \frac{4}{7}\) ମଧ୍ୟରେ କ୍ଷୁଦ୍ରତମ ସଂଖ୍ୟା କେଉଁଟି ?
(a) \(\frac{1}{2}\)
(b) \(\frac{2}{3}\)
(c) \(\frac{3}{5}\)
(d) \(\frac{4}{7}\)
ସମାଧାନ:
\(\frac{1}{2}\)

(viii) 1ର ଯୋଗାତ୍ମକ ବିଲୋମୀ କେଉଁଟି ? 
(a) 1
(b) 0
(c) -1
(d) ଏଥରୁ କୌଣସିଟି ନୁହେଁ
ସମାଧାନ:
-1

(ix) ନିମ୍ନଲିଖ ମଧ୍ୟରୁ କେଉଁ ଉଦ୍ଭଟି ଅସତ୍ୟ ?
(a) p ଓ q ମୌଳିକ ହେଲେ ସେମାନଙ୍କର ଗ.ସା.ଗୁ. = 1 ।
(b) p ଓ ୟୁ ଗଣନ ସଂଖ୍ୟା ହେଲେ p + g + pg ଏକ ଗଣନ ସଂଖ୍ୟା ।
(c) p ଓ ୟୁ ମୌଳିକ ସଂଖ୍ୟା ହେଲେ p + q ମଧ୍ୟ ଏକ ମୌଳିକ ସଂଖ୍ୟା ।
(d) p ଏକ ପୂର୍ବ ସଂଖ୍ୟା ଓ ଠୁ ଏକ ଗଣନ ସଂଖ୍ୟା ହେଲେ pg ଏକ ପୂର୍ଣ୍ଣ ସଂଖ୍ୟା ।
ସମାଧାନ:
p ଓ ୟୁ ମୌଳିକ ସଂଖ୍ୟା ହେଲେ p + g ମଧ୍ଯ ଏକ ମୌଳିକ ସଂଖ୍ୟା ହେବ ।

Question 4.
ପ୍ରତି ଯୁଗ୍ମ ସଂଖ୍ୟା ଯୌଗିକ ଅଟେ କି ? କାରଣ ସହ ଉତ୍ତର ଦିଅ ।
ସମାଧାନ:
2ର ଯୁଗ୍ମସଂଖ୍ୟା ଯାହା ଏକ ମୌଳିକ ସଂଖ୍ୟା ।
ପ୍ରତି ଯୁଗ୍ମସଂଖ୍ୟା ଯୌଗିକ ନୁହେଁ । କାରଣ 2 ବ୍ୟତୀତ ପ୍ରତି ଯୁଗ୍ମ ସଂଖ୍ୟା ଯୌଗିକ ।

Question 5.
କେଉଁ କେଉଁ ବୀଜଗାଣିତିକ ଧର୍ମଗୁଡ଼ିକ ପୂର୍ବ ସଂଖ୍ୟା ସେଟ୍ Zରେ ସତ୍ୟ, ମାତ୍ର ଗଣନ ସଂଖ୍ୟା ସେଟ୍‌ରେ ସତ୍ୟ ନୁହେଁ ସେଗୁଡ଼ିକ ଲେଖ ।
ସମାଧାନ:
ଯୋଗାତ୍ମକ ଅଭେଦ ଧର୍ମ ଏବଂ ଯୋଗାତ୍ମକ ବିଲୋମୀ ଧର୍ମ ଦ୍ଵୟ ପୂର୍ବସଂଖ୍ୟା ସେଟ୍ Zରେ ସତ୍ୟ ହେଲେ ହେଁ ତାହା ଗଣନ ସଂଖ୍ୟା ସେଟ୍ (N) ରେ ସତ୍ୟ ନୁହେଁ ।

Question 6.
କେଉଁ କେଉଁ ବୀଜଗାଣିତିକ ଧର୍ମଗୁଡ଼ିକ ପରିମେୟ ସଂଖ୍ୟା ସେଟ୍ ( ରେ ସତ୍ୟ, ମାତ୍ର ପୂର୍ବ ସଂଖ୍ୟା ସେଟ୍‌ରେ ଅସତ୍ୟ ସେଗୁଡ଼ିକ ଲେଖ ।
ସମାଧାନ:
ଗୁଣନାତ୍ମକ ବିଲୋମୀ ଧର୍ମ ପରିମେୟ ସଂଖ୍ୟା ସେଟ୍ (Q) ରେ ସତ୍ୟ ହେଲେ ହେଁ ପୂର୍ବସଂଖ୍ୟା ସେଟ୍ (Z) ରେ ଅସତ୍ୟ ।

Question 7.
x ଓ y ଅଯୁଗ୍ମ ହେଲେ ପ୍ରମାଣ କର ଯେ, xy ଅଯୁଗ୍ମ ମାତ୍ର x + y ଯୁଗ୍ମ ।
ସମାଧାନ:
ପ୍ରମାଣ : ମନେକର x ଓ y ଅଯୁଗ୍ମ ସଂଖ୍ୟା ଏବଂ x = 2n + 1 ଓ y = 2m + 1 (m, n ∈ Z) ।
xy = (2n + 1) (2m + 1 ) = 4mn + 2m + 2n + 1
= 2 (2 mn + m + n) + 1 (∴ m, n ∈ Z = 2mn + m + n ∈ Z)
x ଓ y ଅଯୁଗ୍ମ ⇒ xy ଅଯୁଗ୍ମ  … (i)  (ପ୍ରମାଣିତ)
x + y = (2n + 1) + (2m + 1 ) = 2n + 2m + 2
= 2(n + m + 1 ) (∴ m, n ∈ Z = m + n + 1 ∈ Z)
∴ x + y ଏକ ଯୁଗ୍ମ ସଂଖ୍ୟା  … (ii)
⇒ x ଓ y ଅଯୁଗ୍ମ = x + y ଯୁଗ୍ମ ।  (ପ୍ରମାଣିତ)
(i) ଓ (ii)ରୁ x ଓ y ଅଯୁଗ୍ମ ହେଲେ xy ଅଯୁଗ୍ମ ଏବଂ x + y ଯୁଗ୍ମ ହେବ ।

Question 8.
ଅଯୁଗ୍ମ ସଂଖ୍ୟାମାନେ ଯୋଗ ଜନିତ ସଂବୃତ୍ତି ନିୟମ ପାଳନ କରନ୍ତି କି ? କାରଣ ସହ ଉତ୍ତର ଦିଅ ।
ସମାଧାନ:
ମନେକର ଦୁଇଟି ଅଯୁଗ୍ମ ସଂଖ୍ୟା, x = 2n + 1 ଏବଂ
y = 2n+ 3 (n ∈ Z)
x + y ଏକ ଅଯୁଗ୍ମ ସଂଖ୍ୟା
ଦର୍ଶାଇବାକୁ ପଡ଼ିବ ।
2n + 1 + 2n + 3 = 4n + 4 = 2 (2n + 2)
ଅର୍ଥାତ୍ x + y ଏକ ଯୁଗ୍ମ ସଂଖ୍ୟା ।
ତେଣୁ ଅଯୁଗ୍ମ ସଂଖ୍ୟାମାନେ ଯୋଗ ଜନିତ ସଂବୃତ୍ତି ନିୟମ ପାଳନ କରନ୍ତି ନାହିଁ ।

Question 9.
15 ଅପେକ୍ଷା ବୃହତ୍ତର ଓ 100 ଠାରୁ କ୍ଷୁଦ୍ରତର ଯେଉଁ ପୂର୍ଣ ସଂଖ୍ୟାଗୁଡ଼ିକର ସାଧାରଣ ରୂପ 3x² +  2, n ∈ Z ସେଗୁଡ଼ିକ ଲେଖ ।
ସମାଧାନ:
ଦତ୍ତ ପୂର୍ଣ୍ଣସଂଖ୍ୟାର ସାଧାରଣ ରୂପ 3x? + 2 (n ∈ Z)
ଏଠାରେ ଲର ମାନ 1, 2, 3, ….. ହେଲେ, ଦତ୍ତ ପୂର୍ଣ୍ଣସଂଖ୍ୟାଗୁଡ଼ିକ ଯଥାକ୍ରମେ….
3(1)² + 2 = 5, 3(2)² + 2 = 12, 3(3)² + 2 = 29, 3(4)² + 2 = 50, 3(5)² + 2 = 77, 3(6)² + 2 = 110,
ଏଠାରେ nର ମାନ 3, 4 ଓ 5 ପାଇଁ ପୂର୍ବସଂଖ୍ୟାର ମାନ ଯଥାକ୍ରମେ 20, 50 ଓ 77 ହେବ ଯହା 15 ଓ 100 ମଧ୍ୟସ୍ଥ ପୂର୍ଣ୍ଣସଂଖ୍ୟା । ପ୍ରକାଶ ଥାଉକି nର ମାନ –3, –4 ଓ –5 ମଧ୍ଯ ପୂର୍ବସଂଖ୍ୟାର ମାନଗୁଡ଼ିକ ଯଥାକ୍ରମେ 29, 50, 77 ପ୍ରତ୍ୟେକ 15 ରୁ ବଡ଼ ଏବଂ 100 ରୁ ସାନ ।

Question 10.
0.123 123 123 …. ସଂଖ୍ୟାଟି ପରିମେୟ ସଂଖ୍ୟା ହେବ କି ? କାରଣ ସହ ଉତ୍ତର ଦିଅ ।
ସମାଧାନ:
0.123 123 123 …..= 0.123
ପନେକବ x = 0. 123 ⇒ 1000 x = 123, \(\overline{123}\)
∴ 1000x -x= 123.0 – 0.0 = 123
⇒ 999x = 123 ⇒ x = \(\frac{123}{999}=\frac{41}{333}\)
ବି.ଦ୍ର. : ଏଥରୁ ସ୍ପଷ୍ଟ ଯେ, 0.123 123 123… ବ ପରିମେୟ ବୁପ \(\frac{41}{333}\) ହେତୁ ଦତ୍ତ ରାଶିଟି ଏକ ପରିମେୟ ସଂଖ୍ୟା ।

Question 11.
0.131 ସଂଖ୍ୟାକୁ, \(\frac{p}{q}\) ପରିମେୟ ରୂପରେ ପ୍ରକାଶ କର ।
ସମାଧାନ:
0.131 = \(\frac{131}{1000}\)
0.131କୁ \(\frac{p}{q}\) ପରିମେୟ ରୂପରେ ପ୍ରକାଶ କଲେ ହେବ \(\frac{131}{1000}\)

Question 12.
\(\frac{1}{3}\) ପରିମେୟ ସଂଖ୍ୟାଟିକୁ ଅସରନ୍ତି ପୌନଃପୁନିକ ଦଶମିକ ରୂପେ ଲେଖ ।
ସମାଧାନ:
\(\frac{1}{3}\) = 1 ÷ 3 = 0. 333333…….= 0.3
∴ \(\frac{1}{3}\) ର ଅସରନ୍ତି ପୌନଃପୁନିକ ଦଶମିକ ରୂପ 0.333333….. ।

Question 13.
\(\frac{1}{3}\) ପରିମେୟ ସଂଖ୍ୟାଟିକୁ ଲଘିଷ୍ଠାକୃତି ନ ହୋଇଥବା \(\frac{100}{q_1}, \frac{p_1}{-102}, \frac{6 \times p_3}{q_3}\) ରୂପରେ ପ୍ରକାଶ କର ।
ସମାଧାନ:

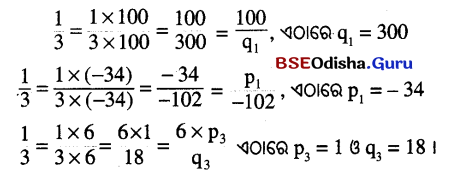
Question 14.
ସମାଧାନ:

ମେହିପରି \(\frac{-15}{15}=\frac{-15}{15}\) = 1 (n = 15 ପାଇଁ)
ପରିମେୟ ସଂଖ୍ୟାମାନ = -15, -7.5, – ….. -1
ଏଠାରେ –15 ଓ –1 ଯଥାକ୍ରମେ କ୍ଷୁଦ୍ରତମ ଏବଂ ବୃହତ୍ତମ ପରିମେୟ ସଂଖା ।

Question 15
ସମାଧାନ:

Question 16.
ସମାଧାନ:

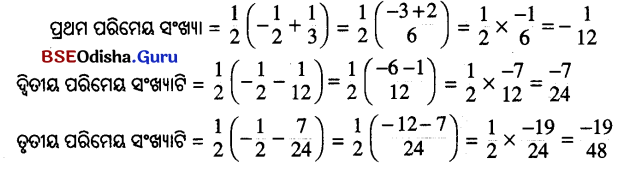
Question 17.
ସମାଧାନ:

Question 18.
(i) \(0 . \overline{9}\) = 1
ସମାଧାନ:
ମନେଳର x = \(0 . \overline{9}\) = 0.999…
⇒ 10 x = 9.999…
∴ 10x – x = 9.9999 …. – 0.999 … = 9
⇒ 9x = 9 ⇒ x = \(\frac{9}{9}\) = 1
∴ \(0 . \overline{9}\) = 1 (ପ୍ରମାଶିତ)

(ii) 1.29 = 1.3
ସମାଧାନ:
ମନେଳର x = 1.29
⇒ 10x = 12.9 = 12.999 ….
⇒ 100x = 129.9
⇒ 100x – 10x = 129.9 – 12.9
⇒ 90x = 117
⇒ x = \(\frac{117}{90}=\frac{13}{10}\) = 1.3
∴ 1.29 = 1.3 (ପ୍ରମାଶିତ)

(iii) 2.349 = 2.35
ସମାଧାନ:
ମନେଳର x = 2.349 ⇒ 100x = 234.9
⇒ 1000 x = 2349.9
∴ 1000 x – 100 x = 2349.9 – 234.9
⇒ 900 x = 2115 ⇒ x = \(\frac{2115}{900}=\frac{235}{100}\) = 2.35
∴ 234.9 = 2.35 (ପ୍ରମାଶିତ)

Question 19.
(i) \(0 . \overline{1}\)
ସମାଧାନ:
ମନେଳର x = \(0 . \overline{1}\) = 0.11111 ….
⇒ 10x = 1.11…. = \(1 . \overline{1}\)
∴ 10x – x = \(1 . \overline{1}\) – \(0 . \overline{1}\)
⇒ 9x = 1 ⇒ x = \(\frac{1}{9}\)
∴ \(0 . \overline{1}\) = \(\frac{1}{9}\)

(ii) \(0 . \overline{11}\)
ସମାଧାନ:
ମନେଳର x = \(0 . \overline{11}\) = 0.11111111….
⇒ 100x = 11.11
∴ 100x – x = 11.11 – 0.11
⇒ 99x = 11 ⇒ x = \(\frac{11}{99}=\frac{1}{9}\)
∴ \(0 . \overline{11}\) \(\frac{1}{9}\)

(iii) \(0 . \overline{89}\)
ସମାଧାନ:
ମନେଳର \(0 . \overline{89}\) = 0.898989 …..
⇒ 10x = \(8 . 9\overline{89}\) = 8.9898989….
⇒ 100 x = 89.898989 …..
∴ 100x – x = 89.898989 ….. – 0.898989 ….
⇒ 99 x = 89
⇒ x = \(\frac{89}{99}\)

(iv) \(0 . \overline{37}\)
ସମାଧାନ:
ମନେଳର x – \(0 . \overline{37}\) = 0.373737….
⇒ 100x = \(37 . \overline{37}\)
∴ 100x – x = 37.37 – 0.37
⇒ 99x = 37 ⇒ x = \(\frac{37}{99}\)
∴ 0.37 = \(\frac{37}{99}\)

(v) \(0 . \overline{123}\)
ସମାଧାନ:
ମନେଳର x = \(0 . \overline{123}\) = 0.123123123….
⇒ 10x = 1.23123 …..
⇒ 100x = 12.3123 …
⇒ 1000x = 123 .123
∴ 1000x – x = 123.123 – 0.123
⇒ 999x = 123 ⇒ x = \(\frac{123}{999}=\frac{41}{333}\)
∴ \(0 . \overline{123}\) = \(\frac{123}{999}=\frac{41}{333}\)

(vi) \(0 . 32\overline{1}\)
ସମାଧାନ:
ମନେଳର \(0 . 32\overline{1}\) = 0.3211111….
⇒ 100x = \(32\overline{1}\) ⇒ 1000x = \(321\overline{1}\)
∴ 1000x – 100x = \(321\overline{1}\) – \(32\overline{1}\)
⇒ 900x = 289 ⇒ x = \(\frac{289}{900}\)
∴ \(0 . 32\overline{1}\) = \(\frac{289}{900}\)

(vii) –\(0. 5\overline{4}\)
ସମାଧାନ:
ମନେଳର x = –\(0. 5\overline{4}\) = -0.5444….
⇒ 10x = –\(5\overline{4}\)
⇒ 100x = –\(54.\overline{4}\)
100x – 10x = –\(54.\overline{4}\) + \(5\overline{4}\)
⇒ 90x = -49 ⇒ x = \(\frac{-49}{90}\)
∴ –\(0. 5\overline{4}\) = \(\frac{-49}{90}\)

(viii) \(6. \overline{89}\)
ସମାଧାନ:
ମନେଳର x = \(6. \overline{89}\) = 6.8999 ….
⇒ 10x = \(68. \overline{9}\)
⇒ 100x = \(689. \overline{9}\)
∴ 100 x – 10 x = \(689. \overline{9}\) – \(68. \overline{9}\)
⇒ 90 x = 621
⇒ x = \(\frac{621}{90}=\frac{69}{10}\)

(ix) –\(0 . \overline{12}\)
ସମାଧାନ:
ମନେଳର –\(0 . \overline{12}\) = – 0.12121212….
⇒ 100x = –\(12 . \overline{12}\)
∴ 100x – x = –\(12 . \overline{12}\) + \(0 . \overline{12}\)
⇒ 99x = -12 ⇒ x = \(\frac{-12}{99}=\frac{-4}{33}\)
∴ –\(0 . \overline{12}\) = \(\frac{-4}{33}\)

(x) \(0 . 013\overline{05}\)
ସମାଧାନ:
ମନେଳର x = \(0 . 013\overline{05}\)
⇒ 1000x = \(13. \overline{05}\)
⇒ 100000 x = 1305.05
⇒ 100000 x – 1000 x = = 1305.05 – 13.05
⇒ 99000 x = 1292
⇒ x = \(\frac{1292}{99000}=\frac{323}{24750}\)

Question 20.
ମୂଲ୍ୟ ନିରୂପଣ କର (ପୂର୍ଣ ସଂଖ୍ୟା କିମ୍ବା ଭଗ୍ନ ସଂଖ୍ୟା ରୂପରେ)
(i) \(0 . \overline{6} + 0 . \overline{3} \)
ସମାଧାନ: 
\(0 . \overline{6} + 0 . \overline{3} \) = \(\frac{6}{9}=\frac{3}{9}\) = \(\frac{6+3}{9}\) = \(\frac{9}{9}\) = 1
(∵ \(0 . \overline{6}\) = \(\frac{6-0}{10-1}\) = \(\frac{6}{9}\))

(ii) \(0 . \overline{6} + (0 . \overline{3}) \) × 2
ସମାଧାନ: 
\(0 . \overline{6} + (0 . \overline{3}) \) × 2 = \(\frac{6}{9}-\frac{3}{9}\) × 2 = \(\frac{6}{9}-\frac{6}{9}\) = 0

(iii) \((0 \cdot \overline{6})^2+(0 \cdot \overline{3})^2+2 \times(0 \cdot \overline{6}) \times(0 \cdot \overline{3})\)
ସମାଧାନ: 

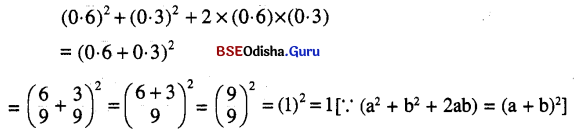
(iv) \((0 . \overline{6})^2+(0 \cdot \overline{3})^2-2 \times(0 . \overline{6}) \times(0 \cdot \overline{3})+0 . \overline{6}\)
ସମାଧାନ: 

(v) \((0 \cdot \overline{6})^2-(0 \cdot \overline{3})^2\)
ସମାଧାନ: 
\((0 \cdot 6)^2-(0 \cdot 3)^2=\left(\frac{6}{9}\right)^2-\left(\frac{3}{9}\right)^2=\frac{36}{81}-\frac{9}{81}=\frac{4}{9}-\frac{1}{9}=\frac{4-1}{9}=\frac{3}{9}=\frac{1}{3}\)

(vi) \((0 \cdot \overline{6})^3+(0 \cdot \overline{3})^3+3 \times(0 \cdot \overline{6}) \times(0 \cdot \overline{3})(0 \cdot \overline{6}+0 \cdot \overline{3})\)
ସମାଧାନ: 

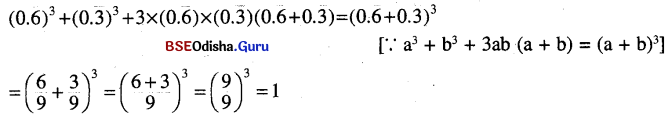
(vii) \((0 . \overline{6})^3-(0 \cdot \overline{3})^3-3 \times(0 \cdot \overline{3}) \times(0 . \overline{6}) \times(0 \cdot \overline{6}-0 . \overline{3})\)
ସମାଧାନ: