CHSE Odisha Class 12 Math Solutions Chapter 9 Integration Ex 9(e)

Odisha State Board Elements of Mathematics Class 12 Solutions CHSE Odisha Chapter 9 Integration Ex 9(e) Textbook Exercise questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 9 Integration Exercise 9(e)

Evaluate the following:
Question 1.
(i) ∫(1 + x) e^x dx
Solution:
∫(1 + x) e^x dx
[Choolse 1 + x as first and ex as second function
= (1 + x) e^x – ∫1 . e^x dx
= ( 1 + x) e^x – e^x + C = xe^x + C

(ii) ∫x³ e^x dx
Solution:
∫x³ e^x dx = x³ e^x – ∫3x² e^x dx
= x³ e^x – 3{x² e^x – ∫2x e^x dx}
= x³ e^x – 3x² e^x + 6 ∫x e^x dx
= x³ e^x – 3x² e^x +6 {x . e^x – ∫1 . e^x dx}
= x³ e^x – 3x² e^x + 6x e^x – 6e^x + C

(iii) ∫x² e^ax dx
Solution:

(iv) ∫(3x + 2)² e^2x dx
Solution:

Question 2.
(i) ∫x sin x dx
Solution:
∫x sin x dx
[x = first function
sin x = 2nd function]
= x (-cosx) – ∫\(\frac{d}{d x}\)(x) . (-cos x) dx
= -x cos x + ∫cos x dx
= -x cos x + sin x + C

(ii) ∫x² cos x dx
Solution:
∫x² cos x dx
[x² = 1st
cos x = 2nd]
= x² . sin x – ∫\(\frac{d}{d x}\)(x²) sin x dx
= x² sin x – ∫2x . sin x dx
[x = 1st
sin x = 2nd]
= x² sin x – 2 {x . (-cos x) – ∫1 . (-cos x) dx}
= x² sin x + 2x cos x – 2∫cos x dx
= x² sin x + 2x cos x – 2 sin x + C

(iii) ∫x² sin ax dx
Solution:

(iv) ∫x cos² x dx
Solution:

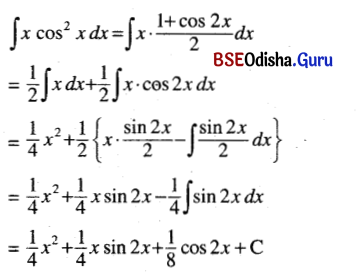
(v) ∫x sin³ x dx
Solution:

(vi) ∫2x sin 2x cos x dx
Solution:

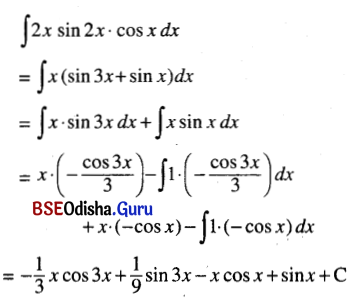
(vii) ∫2x cos 3x cos 2x dx
Solution:

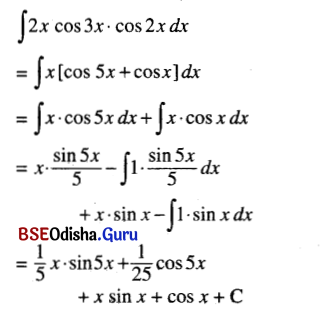
(viii)∫2x³ cos x² dx
Solution:
∫2x³ cos x² dx
[Put x² =t
Then 2x dx = dt]
= ∫x² . cos x² . 2x dx
= ∫t . cos t dt
= t . sin t – ∫1 . sin t dt
= t sin t + cos t + C
= x² sin x² + cos x² + C

(ix) ∫x cosec² x dx
Solution:
∫x cosec² x dx
[x = 1st
cosec² x = 2nd]
= x ∫cosec² x dx – ∫[\(\frac{d}{d x}\)(x) × ∫cosec² x dx] dx
= -x cot x + ∫cot x dx
= -x cot x + ln |sin x| + C

(x) ∫x tan² x dx
Solution:
∫x tan² x dx = ∫x (sec² x – 1) dx
= ∫x sec² x dx – ∫x dx
= x tan x – ∫1 . tan x dx – \(\frac{1}{2}\)x²
[x = 1st
sec² x = 2nd]
= x tan x + ln |cos x| – \(\frac{x^2}{2}\) + C

Question 3.
(i) ∫x ln (1 + x) dx
Solution:

(ii) ∫x⁷ ln x dx
Solution:

(iii) ∫(ln x)³ dx
Solution:

(iv) ∫ln(x² + 1) dx
Solution:
∫ln (x² + 1) dx
= ∫ln (x² + 1) . 1 dx
[Put ln (x² + 1 ) as first function and 1 as the second function.]

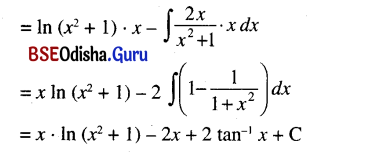
(v) ∫\(\frac{\ln x}{x^5}\) dx
Solution:

(vi) ∫ln (x² + x + 2) dx
Solution:

(vii) ∫ln (x + \(\sqrt{x^2+a^2}\)) dx
Solution:

(viii) ∫ln (x + \(\sqrt{x^2-a^2}\)) dx
Solution:

Question 4.
(i) ∫sin^-1 x dx
Solution:

(ii) ∫x sin^-1 dx
Solution:

(iii) ∫cos^-1 x dx
Solution:

(iv) ∫x tan^-1 dx
Solution:

(v) ∫x² tan^-1 x dx
Solution:

(vi) ∫sec^-1 x dx
Solution:

(vii) ∫x cosec^-1 x dx
Solution:

Question 5.
(i) ∫e^3x cos 2x dx
Solution:

(ii) ∫e^x sin x dx
Solution:

(iii) ∫e^x cos² x dx
Solution:

(iv) ∫x \(e^{x^2}\) sin x² dx
Solution:

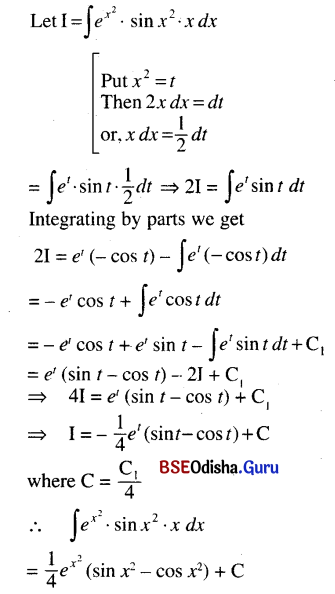
(v) ∫e^ax sin (bx + c) dx
Solution:
Let I = ∫e^ax sin (bx + c) dx
Integrating by parts we get

(vi) ∫(2x² + 1)\(e^{x^2}\) dx
Solution:
I = ∫(2x² + 1)\(e^{x^2}\) dx
= ∫2x² \(e^{x^2}\) dx + ∫\(e^{x^2}\) . 1 dx
= ∫2x² \(e^{x^2}\) dx + x² \(e^{x^2}\) ∫2x\(e^{x^2}\) .x dx
= x\(e^{x^2}\) + C

Question 6.
(i) ∫\(\sqrt{9-x^2}\) dx
Solution:

(ii) ∫\(\sqrt{5-4 x^2}\) dx
Solution:

(iii) ∫\(\sqrt{1-x^2-2 x}\) dx
Solution:

(iv) ∫e^z \(\sqrt{4-e^{2 z}}\) dz
Solution:

(v) ∫cos θ \(\sqrt{5-\sin ^2 \theta}\) dθ
Solution:

Question 7.
(i) ∫\(\sqrt{x^2+4}\) dx
Solution:

(ii) ∫\(\sqrt{7 x^2+2}\) dx
Solution:

(iii) ∫\(\sqrt{4 x^2+12 x+13}\) dx (2x + 3 = z)
Solution:

(iv) ∫e^2z \(\sqrt{e^{4 z}+6}\) dz
Solution:

(v) ∫sec² θ \(\sqrt{\sec ^2 \theta+3}\) dθ
Solution:

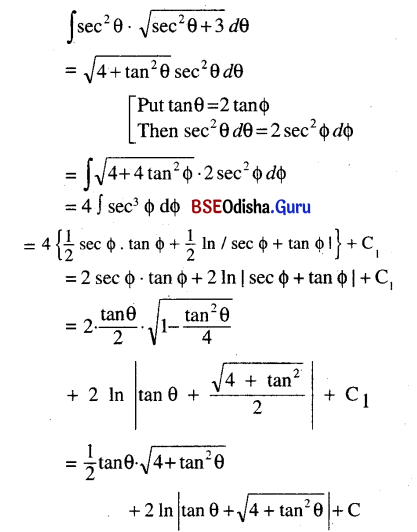
(vi) ∫(2x² +1) \(e^{x^2}\) dx
Solution:
Same as No. 5 (vi).

Question 8.
(i) ∫\(\sqrt{x^2-8}\) dx
Solution:

(ii) ∫\(\sqrt{3 x^2-2}\) dx
Solution:

(iii) ∫\(\sqrt{x^2-4 x+2}\) dx (x – 2 = z)
Solution:

(iv) ∫a^z \(\sqrt{a^{2 z}-4}\) dz
Solution:

(v) ∫sec θ tan θ \(\sqrt{\tan ^2 \theta-3}\) dθ
Solution:

Question 9.
(i)∫e^x (tan x + ln sec x) dx
Solution:
∫e^x (tan x + ln sec x) dx
= ∫e^x tan x dx + ∫e^x ln sec x dx
(Integrating by parts)
= ∫e^x tan x dx + e^x ln sec x – ∫e^x tan x dx
= e^x ln(sec x) + C

(ii) ∫e^x (cot x + ln sin x) dx
Solution:
∫e^x (cot x + ln sin x) dx
[Integrating by parts taking e^x as first function and cot x as second function.]
= ∫e^x ln sin x – ∫e^x ln sin x dx + ∫e^x ln sin x dx + C
= e^x ln sin x + C

(iii) ∫\(\frac{e^x}{x}\) (1 + x ln x) dx
Solution:
∫\(\frac{e^x}{x}\) (1 + x ln x) dx
= ∫\(\frac{e^x}{x}\) dx + ∫\(\frac{e^x}{x}\) e^x ln x dx + C
= e^x ln x + C

(iv) ∫\(\frac{x e^x}{(1+x)^2}\) dx
Solution:

Question 10.
(i) ∫\(\left[\frac{1}{\ln x}-\frac{1}{(\ln x)^2}\right]\) dx
Solution:

(ii) ∫sin (ln x) dx
Solution:
Let I = ∫sin (ln x) dx
[Integrating by parts taking sin (ln x) as first and 1 as second function.]

(iii) ∫sin x ln (cosec x – cot x) dx
Solution:
∫sin x ln (cosec x – cot x) dx
[Integrating by parts taking In (cosec x cot x) as first function and sin x as second function.]
= ln (cosec x – cot x) . – cos x – ∫\(\frac{1}{{cosec} x-\cot x}\)× – cosec x . cot x + cosec² x × – cos x dx
= -cos x . ln (cosec x – cot x) + ∫\(\frac{{cosec} x({cosec} x-\cot x)}{{cosec} x-\cot x}\) . cos x dx
= -cos x . ln (cosec x – cot x) + ∫cot x dx
= -cos x . ln (cosec x – cot x) + ln sin x + C