Odisha State Board BSE Odisha 9th Class Maths Solutions Algebra Chapter 3 ବୀଜଗାଣିତିକ ପରିପ୍ରକାଶ ଓ ଅଭେଦ Ex 3(c) Textbook Exercise Questions and Answers.
BSE Odisha Class 9 Maths Solutions Algebra Chapter 3 ବୀଜଗାଣିତିକ ପରିପ୍ରକାଶ ଓ ଅଭେଦ Ex 3(c)
Question 1.
ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ରରେ ଠିକ୍ ଉତ୍ତରଟିକୁ ବାଛି ଲେଖ ।
(i) x2 – 3x + 2 ର ଉତ୍ପାଦକ ଦ୍ଵୟ
(a) (x – 2) ଓ (x + 1)
(b) (x + 2) ଓ (x – 1)
(c) (x – 2) ଓ (x – 1)
(d) (x + 2) ଓ (x + 1)
ସମାଧାନ:
(x – 2) ଓ (x + 1)
x2 – 3 + 2 = x2 – (2 + 1) x + 2 . 1 = (x – 2) (x – 1)
(ii) ଏକ ଦ୍ୱିଘାତୀ ପଲିନୋମିଆଲ୍ର ଉତ୍ପାଦକ ଦ୍ବୟ (x – 1) ଓ (x – 3) ହେଲେ ପଲିନୋମିଆଲ୍ଟି
(a) x2 – 4x – 3
(b) x2 – 4x + 3
(c) x2 + 4x – 3
(d) x2 + 4x + 3
ସମାଧାନ:
x2 – 4x + 3
(x – 1) (x – 3) = x2 – (1 + 3) x + (1) (3) = x2 – 4x + 3
(iii) x – y ର ଉତ୍ପାଦକ ମାନ
(a) (x2 + y2) (x + y) (x – y)
(b) (x2 – y2) (x – y) (x + y)
(c) (x2 + y2) (x + y)2
(d) (x2 + y2) (x – y)
ସମାଧାନ:
(x2 + y2) (x + y) (x – y)
x4 – y4 = (x2)2 – (y2)2 = (x2 + y2) (x2 – y2) = (x2 + y2) (x + y) (x – y)
(iv) 8a3 – b3 – 12a2b + 6ab2 ର ଉତ୍ପାଦକଗୁଡ଼ିକ
(a) (2a – b), (2a + b), (2a + b)
(b) (2a + b) (2a + b) (2a + b)
(c) (2a – b), (2a – b), (2a + b)
(d) (2a – b), (2a – b), (2a – b)
ସମାଧାନ:
(2a – b) (2a – b) (2a – b)
8a3 – b3 – 12a2b + 6ab2 = (2a)3 – b3 – 3.2a.b(2a – b)
= (2a – b)3 = (2a – b) (2a – b) (2a – b)
(v) 625 + 25x4 + x8 ର ଉତ୍ପାଦକଗୁଡ଼ିକ
(a) (25 + 5x2 + x4) (25 – 5x2 + x4)
(b) (25 + 5x2 + x4) (25 + 5x2 – x4)
(c) (25 + 5x4 + x4) (25 – 5x4 + x4)
(d) (25 – 5x4 + x4)(25 + 5x4 – x4)
ସମାଧାନ:
(25 + 5x2 + x4) (25 – 5x2 + x4)
625 + 25x4 + x8 = 54 + 52(x2)2 + (x2)4
= {52 + 5x2 + (x2)2} {52 – 5x2 + (x2)2} = (25 + 5x2 + x4) (25 – 5x2 + x4)
(vi) 1 – a3 + b3 + 3ab ର ଗୋଟିଏ ଉତ୍ପାଦକ
(a) (1 – a + b)
(b) (1 – a – b)
(c) (1 + a + b)
(d) (1 + a – b)
ସମାଧାନ:
(1 – a + b)
1 – a3 + b3 + 3ab
= (1 – a + b) {12 + a2 + b2 – (1) (-a) – (-a) (b) – (b) (1)}
= (1 – a + b) (1 + a2 + b2 + a + ab – b)
![]()
(vii) (2x – 3y)3 + (3y – 4z)3 + (4z – 2x)3 ର ଉତ୍ପାଦକଗୁଡ଼ିକ ହେଲେ
(a) 6(2x – 3y)(3y – 4z) (2z – x)
(b) 3(2x – 3y) (3y – 4z) (2z – x)
(c) 60xyz
(d) ଏଥୁମଧ୍ୟରୁ କୌଣସିଟି ନୁହେଁ
ସମାଧାନ:
6 (2x – 3y) (3y – 4z) (2z – x)
2x – 3y + 3y – 4z + 4z – 2x = 0
(2x – 3y)3 + (3y – 4z)3 + (4z – 2x)3 = 3 (2x – 3y) (3y – 4z) (4z – 2x)
= 6 (2x – 3y) (3y – 4z) (2z – x)(∵ a + b + c = 0 ହେଲେ a3 + b3 + c3 = 3abc)
(viii) (28)3 + (-15)3 + (-13)3 ର ସରଳୀକୃତ ମାନ
(a) 8190
(b) 16380
(c) 24570
(d) 4095
ସମାଧାନ:
16380
28 – 15 -13 = 0
∴ (28)3 + (-15)3 + (-13)3 = 3 (28) (-15) (-13) = 16380
(∵ a + b + c = 0 ହେଲେ a3 + b3 + c3 = 3abc)
(ix) (a – b)3 + (b – c)3 + (c – a)3 ର ମାନ
(a) 3abc
(b) 3a3b3c3
(c) 3(a – b) (b – c)(c – a)
(d) {a – (b + c)}3
ସମାଧାନ:
3(a – b) (b – c) (c – a)
(a – b)3 + (b – c)3 + (c – a)3 = 3(a – b) (b – c) (c – a)
(∵ (a – b) + (b – c) + (c – a) = 0)
(x) 2x2 – x – 1 ର ଗୋଟିଏ ଉତ୍ପାଦକ
(a) 2x – 1
(b) x + 1
(c) x – 1
(d) x + 2
ସମାଧାନ:
(x – 1)
2x2 – x – 1 = 2x2 – 2x + x – 1
= 2x (x – 1) + 1 (x – 1) = (x – 1) (2x + 1)
∴ 2x2 – x – 1 ର ଏକ ଉତ୍ପାଦକ (x – 1)
Question 2.
ଉତ୍ପାଦକରେ ବିଶ୍ଳେଷଣ କର ।
(i) 2x2 – x – 1
ସମାଧାନ:
2x2 – x – 1 = 2x2 – 2x + x – 1
= 2x(x – 1) + 1(x – 1) = (x – 1) (2x + 1)
(ii) 2x2 – 3x + 1
ସମାଧାନ:
2x2 – 3x + 1 = 2x2 – 2x – x + 1
= 2x (x – 1) – 1 (x – 1) = (x – 1) (2x – 1)
(iii) 5x2 – x – 4
ସମାଧାନ:
5x2 – x – 4 = 5x2 – 5x + 4x – 4
= 5x (x – 1) + 4 (x – 1) = (x – 1) (5x + 4)
(iv) 4x2 – 5x – 6
ସମାଧାନ:
4x2 – 5x – 6 = 4x2 – 8x + 3x – 6
= 4x(x – 2) + 3 (x – 2) = (4x + 3) (x – 2)
(v) 3x2 + 11x + 6
ସମାଧାନ:
3x2 + 11x + 6 = 3x2 + 9x + 2x + 6
= 3x (x + 3) + 2 (x + 3) = (3x + 2) (x + 3)
(vi) 7x2 + x – 6
ସମାଧାନ:
7x2 + x – 6 = 7x2 + 7x – 6x – 6
= 7x (x + 1) – 6 (x + 1) = (7x – 6) (x + 1)
(vii) 2x2 + 5x – 7
ସମାଧାନ:
2x2 + 5x – 7 = 2x2 + 7x – 2x – 7
= x (2x + 7) – 1 (2x + 7) = (2x + 7) (x – 1)
(viii) 4x2 – 5x + 1
ସମାଧାନ:
4x2 – 5x + 1 = 4x2 – 4x – x + 1
= 4x (x – 1) – 1 (x – 1) = (4x – 1) (x – 1)
(ix) 4x2 – 3x – 7
ସମାଧାନ:
4x2 – 3x – 7 = 4x2 – 7x + 4x – 7
= x (4x – 7) + 1 (4x – 7) = (4x – 7) (x + 1)
Question 3.
ଉତ୍ପାଦକରେ ବିଶ୍ଳେଷଣ କର ।
[a3 + b3 = (a + b) (a2 – ab + b2), a3 – b3 = (a – b) (a2 + ab + b2)]
(i) 25a4 – 16b2
ସମାଧାନ:
25a4 – 16b2 = (5a2)2 – (4b)2 = (5a2 + 4b)(5a2 – 4b)
(ii) 9 – 64p2q2
ସମାଧାନ:
9 – 64p2q2 = (3)2 – (8pq)2 = (3 + 8pq)(3 – 8pq)
(iii) 8x3 + 27y3
ସମାଧାନ:
8x3 + 27y3 = (2x)3 + (3y)3 = (2x + 3y){(2x)2 – 2x.3y + (3y)2}
= (2x + 3y)(4x2 – 6xy + 9y2)
(iv) 8x3 – 27y3
ସମାଧାନ:
8x3 – 27y3 = (2x)3 – (3y)3 = (2x – 3y){(2x)2 + 2x.3y + (3y)2}
= (2x – 3y)(4x2 + 6xy + 9y2)
(v) (a + b)2 – 9
ସମାଧାନ:
(a + b)2 – 9 = (a + b)2 – 32 = (a + b + 3) (a + b – 3)
(vi) (2a + 5)2 – 16
ସମାଧାନ:
(2a + 5)2 – 16 = (2a + 5)2 – 42 = (2a + 5 + 4) (2a + 5 – 4) = (2a + 9) (2a + 1)
![]()
(vii) (x + 2y)2 – (x – y)2
ସମାଧାନ:
(x + 2y)2 – (x – y)2 = {(x + 2y) + (x – y)} {x + 2y) – (x – y)}
= (x + 2y + x – y) (x + 2y – x + y) = (2x + y) (3y) = 3y (2x + y)
(viii) 4(a + 2p)2 – 9 (2a – p)2
ସମାଧାନ:
4 (a + 2p)2 – 9 (2a – p)2 = {2 (a + 2p)}2 – {3 (2a – p)}2
= (2a + 4p)2 – (6a – 3p)2 = (2a + 4p + 6a- 3p) (2a + 4p – 6a + 3p) = (8a + p) (7p – 4a)
(ix) 75 (2a – b + 1)2 – 12 (a + b)2
ସମାଧାନ:
75 (2a – b + 1)2 – 12 (a + b)2 = 3 {25 (2a – b + 1)2 – 4 (a + b)2}
= 3 [{5 (2a – b + 1)}2 – {2 (a + b)2}] = 3 {(10a – 5b + 5)2 – (2a + 2b)2]
= 3 (10a – 5b + 5 + 2a + 2b) (10a – 5b + 5 – 2a – 2b) = 3 (12a – 3b + 5) (8a – 7b + 5)
(x) (a + b)3 – 8c3
ସମାଧାନ:
(a + b)3 – 8c3 = (a + b)3 – (2c)3
= (a + b – 2c) {(a + b)2 + (a + b)2c + (2c)2}
= (a + b – 2c) (a2 + 2ab + b2 + 2ca + 2bc + 4c2)
= (a + b – 2c) (a2 + b2 + 4c2 + 2ab + 2bc + 2ca)
(xi) p4 – 27pq6
ସମାଧାନ:
p4 – 27pq6 = p(p3 – 27q6)
= p{p3 – (3q2)3} = p(p – 3q2) {p2 + 3pq2 + (3q2)2} = p(p – 3q2) (p2 + 3pq2 + 9q4)
(xii) 1 – (a + 2)3
ସମାଧାନ:
1 – (a + 2)3 = 13 – (a + 2)3 = (1 – a – 2) {12 + a + 2 + (a + 2)2}
= (- a – 1) (1 + a + 2 + a2 + 4a + 4) = -(a + 1) (a2 + 5a + 7)
(xiii) 8 – (2x – 3)3
ସମାଧାନ:
8 – (2x – 3)3 = 23 – (2x – 3)3 = (2 – 2x + 3) {22 + 2 (2x – 3) + (2x – 3)2}
= (-2x + 5) (4 + 4x – 6 + 4x2 – 12x + 9) = (5 – 2x) (4x2 – 8x + 7)
(xiv) 320p6q – 5p2q7
ସମାଧାନ:
320 p6q – 5p2q7 = 5p2q (64p4 – q6)
= 5p2q {(8p2)2 – (q3)2} = 5p2q (8p2 + q3) (8p2 – q3)
(xv) 1 + (a + 2)3
ସମାଧାନ:
1 + (a + 2)3 = 13 + (a + 2)3 = (1 + a + 2) {12 – 1(a + 2) + (a + 2)2}
= (a + 3) (1 – a – 2 + a2 + 4a + 4) = (a + 3) (a2 + 3a + 3)
(xvi) 8 + (2x – 3)3
ସମାଧାନ:
8 + (2x – 3)3 = 23 + (2x – 3)3 = (2 + 2x – 3) {22 – 2 (2x – 3) + (2x – 3)2}
= (2x – 1) (4 – 4x + 6 + 4x2 – 12x + 9) = (2x – 1) (4x2 – 16x + 19)
(xvii) a3 + 6a2b + 12ab2 + 8b3
ସମାଧାନ:
a3 + 6a2b + 12ab2 + 8b3 = a3 + 3a2 (2b) + 3 . a . (2b)2 + (2b)3
= (a + 2b)3 = (a + 2b) (a + 2b) (a + 2b)
(xviii) a3 + 9a2 + 27a + 27
ସମାଧାନ:
a3 + 9a2 + 27a + 27 = a3 + 3a2 . 3 + 3 . a . 32 + 33 = (a + 3)3
= (a + 3) (a + 3) (a + 3)
(xix) 8 – 36p + 54p2 – 27p3
ସମାଧାନ:
8 – 36p + 54p2 – 27p3 = 23 – 3. 22 3p + 3 . 2 (3p)2 – (3p)3
= (2 – 3p)3 = (2 – 3p) (2 – 3p) (2 – 3p)
(xx) (b – q)3 – (c – q)3 – 3 (b – c) (b – q) (c – q)
ସମାଧାନ:
(b – q)3 – (c – q)3 – 3 (b – c) (b – q) (c – q)
ମନେକର b – q = x ଓ c – q = y
∴ x – y = (b – q) – (c – q) = b – q – c + q = b – c
ପ୍ରଦତ୍ତ ପଲିନୋମିଆଲ୍ଟି x3 – y3 – 3 (x – y) (xy) = x3 – y3 – 3xy (x – y) = (x – y)3
= {(b – q) – (c – q)}3 (x ଓ yର ମାନ ବସାକଳେ)
= (b – c)3 = (b – c) (b – c) (b – c)
Question 4.
ଉତ୍ପାଦକରେ ବିଶ୍ଳେଷଣ କର ।
a4 + a2b2 + b4 = (a2 + ab + b2)(a2 – ab + b2)
(i) a4 + a2 + 1
ସମାଧାନ:
a4 + a2 + 1
= a4 + 1 + a2 = (a2)2 + (1)2 + a2 = (a2 + 1)2 – 2 . a2. 1 + a2
= (a2 + 1)2 – 2a2 + a2 = (a2 + 1)2 – a2 = (a2 + 1 + a) (a2 + 1 – a)
= (a2 + a + 1)(a2 – a + 1)
(ii) a4b4 + a2b2 + 1
ସମାଧାନ:
a4b4 + a2b2 + 1 = (ab)4 + (ab)2 12 + 14
= (a2b2 + ab + 1) (a2b2 – ab + 1)
![]()
(iii) 16a4 + 36a2b2 + 81b4
ସମାଧାନ:
16a4 + 36a2b2 + 81b4 = (4a2)2 + 36a2b2 + (9b2)2
= (4a2)2 + (9b2)2 + 72a2b2 – 72a2b2 + 36a2b2 [72a2b2 ଯେ।ଗ ଓ ବିୟେ।ଗ କରି]
= (4a2 + 9b2)2 – 36a2b2 = (4a2 + 9b2)2 – (6ab)2
= (4a2 + 9b2 + 6ab) (4a2 + 9b2 – 6ab) = (4a2 + 6ab + 9b2) (4a2 – 6ab + 9b2)
ବିକଳ୍ପ ସମାଧାନ –
16a4 + 36a2b2 + 81b4 = (4a2)2 + (9b2)2 + 36a2b2
= (4a2 + 9b2)2 – 2 . 4a2 . 9b2 + 36a2b2 = (4a2 + 9b2)2 – 36a2b2
= (4a2 + 9b2)2 – (6ab)2 = (4a2 + 9b2 + 6ab) (4a2 + 9b2 – 6ab)
= (4a2 + 6ab + 9b2) (4a2 – 6ab + 9b2)
(iv) a8 + a4 + 1
ସମାଧାନ:
a8 + a4 + 1 = (a2)4 + (a2)2 . 12 + 14
= {(a2)2 + a2 . 1 + 12} {(a2)2 – a2 . 1 + 12} = (a4 + a2 + 1) (a4 – a2 + 1)
= (a4 + a2 . 12 + 14) (a4 – a2 + 1) = (a2 + a + 1) (a2 – a + 1) (a4 – a2 + 1)
(v) x4 + 4
ସମାଧାନ:
x4 + 4 = (x2)2 + (2)2 = (x2)2 + (2)2 + 4x2 – 4x2
= (x2 + 2)2 – (2x)2 = (x2 + 2 + 2x) (x2 + 2 – 2x) = (x2 + 2x + 2) (x2 – 2x + 2)
(vi) 2a4 + 8b4
ସମାଧାନ:
2a4 + 8b4 = 2(a4 + 4b4) = 2{(a2)2 + (2b2)2 + 4a2b2 – 4a2b2}
= 2{(a2 + 2b2)2 – (2ab)2} = 2 {a2 + 2b2 + 2ab) (a2 + 2b2 – 2ab)}
= 2(a2 + 2ab + 2b2) (a2 – 2ab + 2b2)
(vii) 36a4 + 9b4
ସମାଧାନ:
36a4 + 9b4 = 9 (4a4 + b4) = 9 {(2a2)2 + (b2)2}
= 9 {(2a2 + b2)2 – 2 (2a2) b2} = 9 {(2a2 + b2)2 – 4a2b2}
= 9 {(2a2 + b2)2 – (2ab)2} = 9(2a2 + b2 + 2ab) (2a2 + b2 – 2ab)
= 9 (2a2 + 2ab + b2) (2a2 – 2ab + b2)
(viii) 4a4 + 7a2 + 16
ସମାଧାନ:
4a4 + 7a2 + 16 = (2a2)2 + (4)2 + 16a2 – 16a2 + 7a2
= (2a2 + 4)2 – 9a2 = (2a2 + 4)2 – (3a)2 = (2a2 + 4 + 3a) (2a2 + 4 – 3a)
= (2a2 + 3a + 4) (2a2 – 3a + 4)
(ix) a4 + 2a2b2 + 9b4
ସମାଧାନ:
a4 + 2a2b2 + 9b4 = a4 + 9b4 + 2a2b2
= (a2)2 + (3b2)2 + 6a2b2 – 6a2b2 + 2a2b2 = (a2 + 3b2)2 – 4a2b2
= (a2 + 3b2)2 – (2ab)2 = (a2 + 3b2 + 2ab) (a2 + 3b2 – 2ab)
= (a2 + 2ab + 3b2) (a2 – 2ab + 3b2)
(x) a4 – 3a2 + 1
ସମାଧାନ:
a4 – 3a2 + 1 = (a2)2 + (1)2 – 3a2
= (a2)2 + (1)2 – 2a2 + 2a2 – 3a2 (2a2 ଯେ।ଗ ଓ ବିୟେ।ଗ କରି)
= (a2 – 1)2 – (a)2 = (a2 – 1 + a) (a2 – 1 – a) = (a2 + a – 1) (a2 – a – 1)
(xi) 25a4 – 19a2b2 + 9b2
ସମାଧାନ:
25a4 – 19a2b2 + 9b4 = (5a2)2 + (3b2)2 – 19a2b2
= (5a2 + 3b2)2 + 2 . 5 a2 . 3b2 – 19 a2b2
= (5a2 + 3b2)2 – 49 a2b2 = (5a2 + 3b2) – (7ab)2
= (5a2 + 3b2 + 7ab) (5a2 + 3b2 – 7ab) = (5a2 + 7ab + 3b2) (5a2 – 7ab + 3b2)
(xii) 9x2 + y2 + 6xy – 4z2
ସମାଧାନ:
9x2 + y2 + 6xy – 4z2 = (3x)2 + y2 + 2 . 3x . y – (2z)2
= (3x + y)2 – (2z)2 = (3x + y + 2z) (3x + y – 2z)
(xiii) 16 – x2 – 24y + 9y2
ସମାଧାନ:
16 – x2 – 24y + 9y2 = 16 – 24y + 9y2 – x2
= 42 – 2 . 4 . 3y + (3y)2 – x2 = (4 – 3y)2 – x2 = (4 – 3y + x) (4 – 3y – x)
(xiv) (a2 – b2) (x2 – y2) – 4abxy
ସମାଧାନ:
(a2 – b2) (x2 – y2) – 4abxy = a2x2 – a2y2 – b2x2 + b2y2 – 4abxy
= a2x2 + b2y2 – 2abxy – a2y2 – b2x2 – 2abxy
= (a2x2 + b2y2 – 2abxy) – (a2y2 + b2x2 + 2abxy)
= {(ax)2 + (by)2 – 2(ax) (by)} – {(ay)2 + (bx)2 + 2(ay) (bx)}
= (ax – by)2 – (ay + bx)2 = (ax – by + ay + bx) (ax – by – ay – bx)
(xv) (a2 + b2)(x2 – y2) – 2ab (x2 + y2)
ସମାଧାନ:
(a2 + b2)(x2 – y2) – 2ab (x2 + y2)
= a2x2 – ay2 + b2x2 – b2y2 – 2abx2 – 2aby2
= a2x2 + b2x2 – 2abx2 – a2y2 – b2y2 – 2aby2
= (a2x2 + b2x2 – 2abx2) – (a2y2 + b2y2 + 2aby2)
= {(ax)2 + (bx)2 – 2ax . bx} – {(ay)2 + (by)2 + 2ay . by}
= (ax – bx)2 – (ay + by)2 = (ax – bx + ay + by) (ax – bx – ay – by)
= {x (a – b) + y (a + b)} {x (a – b) – y(a + b)}
![]()
Question 5.
ଉତ୍ପାଦକରେ ବିଶ୍ଳେଷଣ କର ।
(a3 + b3 + c3 – 3abc = (a + b + c) (a2 + b2 + c2 – ab – bc – ca)
(i) a3 + b3 + x3 – 3abx
ସମାଧାନ:
a3 + b3 + x3 – 3abx
= (a + b + x) (a2 + b2 + x2 – ab – bx – ax)
(ii) 8a3 + b3 + c3 – 6abc
ସମାଧାନ:
8a3 + b3 + c3 – 6abc = (2a)3 + b3 + c3 – 3(2a) (b) (c)
= (2a + b + c) { (2a)2 + b2 + c2 – 2a . b. bc – c . 2a}
= (2a + b + c) (4a2 + b2 + c2 – 2ab – bc – 2ca)
(iii) a3 + b3 – 8 + 6ab
ସମାଧାନ:
a3 + b3 – 8 + 6ab = a3 + b3 + (-2)3 – 3a . b(-2)
= (a + b – 2) { a2 + b2 + (-2)2 – ab – b (-2) – (-2) a}
= (a + b – 2) (a2 + b2 + 4 – ab + 2b + 2a)
(iv) l – 27m3 – n3 – 9 lmn
ସମାଧାନ:
l3 – 27m3 – n3 – 9lmn = l3 + (- 3m)3 + (- n)3 – 3l(-3m) (-n)
= {l + (-3m) + (-n)} {l2 + (-3m)2 + (- n)2 – l(-3m) – (-3m) (-n) – (-n) l}
= (l – 3m – n) (l2 + 9m2 + n2 + 3lm – 3mn + nl)
(v) (a – b)3 + (c – b)3 + (a – c)3 – 3 (a – b) (b – c) (c – a)
ସମାଧାନ:
(a – b)3 + (c – b)3 + (a- c)3 – 3 (a – b) (b – c) (c – a)
ମନେକର a – b = x, b – c = y, c – a = z ⇒ c – b = -y ⇒ a – c = -z
ପ୍ରଦତ୍ତ ପଲିନୋମିଆଲ୍ଟି x3 + (-y)3 + (-z)3 – 3(x) (-y) (-z)
= {x + (-y) + (-z)} {x2 + (-y)2 + (-z)2 – x (-y) – (-y) (-z) – (-z) x}
= (x – y – z) (x2 + y2 + z2 + xy – yz + zx)
= {(a – b) – (b – c) – (c – a)} {(a – b)2 + (b – c)2 + (c – a)2 +(a – b) (b – c) – (b – c) (c – a) + (c – a) (a – b) x, y ଓ zର ମାନ ବସାକଳେ,
= (a – b – b + c – c + a) (a2 – 2ab + b2 + b2 – 2bc + c2 + c2 – 2ca + a2 + ab – ca – b2 + bc – bc + ab + c2 – ca + ca – bc – a2 + ab)
= (2a – 2b) (a2 + b2 + c2 + ab – 3bc – 3ca)
= 2 (a – b) (a2 + b2 + c2 + ab – 3bc – 3ca)
(vi) a6 + 4a3 – 1
ସମାଧାନ:
a6 + 4a3 – 1 = a6 + a3 – 1 + 3a3 = (a2)3 + a3 + (-1)3 – 3. a2 .a(-1)
= (a2 + a – 1) {(a2)2 + (a)2 + (-1)2 – a2.a – a(-1) – (-1)a2}
= (a2 + a – 1) (a4 + a2 + 1 – a3 + a + a2) = (a2 + a – 1)(a4 – a3 + 2a2 + a + 1)
(vii) x3 + 72 – 24x
ସମାଧାନ:
x3 + 72 – 24x = x3 + 64 + 8 – 24x
= x3 + 43 + 23 – 3. x. 4. 2 = (x + 4 + 2)(x2 + 42 + 22 – x. 4 – 4. 2 – 2. X)
= (x + 4 + 2)(x2 + 16 + 4 – 4x – 8 – 2x)
= (x + 6)(x2 + 16 + 4 – 8 – 6x)
= (x + 6)(x2 – 16 + 12)
(viii) m6 + 7m3 – 8
ସମାଧାନ:
m6 + 7m3 – 8 = m6 + m3 – 8 + 6m3
= (m2)3 + m3 + (-2)3 – 3m2 .m(-2)
= (m2 + m – 2) {(m2)2 + m2 + (2)2 – m2 . m – m (-2) – (-2) m2}
= (m2 + m – 2)(m4 + m2 + 4 – m3 + 2m + 2m2)
= (m2 + 2m – m – 2)(m4 – m3 + 3m2 + 2m + 4)
= {m(m + 2) – 1(m + 2)}(m4 – m3 +3m2 + 2m + 4)
= (m + 2)(m – 1)(m4 – m3 + 3m2 + 2m + 4)
(ix) a6 + \(\frac{1}{a^6}\) + 2 (a ≠ 0)
ସମାଧାନ:
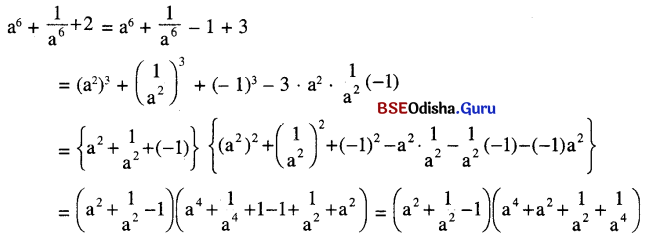
(x) r6 + 45r3 – 8
ସମାଧାନ:
r6 + 45r3 – 8 = r6 + 27r3 – 8 + 18r3
= (r2)3 + (3r)3 + (-2) – 3 . r2 . 3r (-2)
= (r2 + 3r – 2) {(r2)2 + (3r)2 + (2)2 – r2 3r – 3r (-2) – (-2) r2)
= (r2 + 3r – 2)(r4 + 9r2 + 4 – 3r3 + 6r + 2r2)
= (r2 + 3r – 2)(r4 – 3r3 – t – 11r2 + 6r + 4)
(xi) 16x3 – 54y6 – 2z3 – 36xy2z
ସମାଧାନ:
16x3 – 54y6 – 2z3 – 36xy2z = 2 { 8x3 – 27y6 – z3 – 18xy2z)}
= 2 {(2x)3 + (-3y2)3 + (-z)3 – 3 (2x) (-3y2) (-z))
= 2{2x + (-3y2) + (-z)) {(2x)2 + (-3y2)2 + (-z)2 – (2x) (-3y2) – (-3y2) (-z) – (-z) (2x)}
= 2(2x – 3y2 – z) (4x2 + 9y4 + z2 + 6xy2 – 3y2z + 2zx)
(xii) a3 + b3 – \(\frac{1}{27}\) c3 + abc
ସମାଧାନ:

(xiii) 27a3 – 8b6 + 125 c3 + 90ab2c
ସମାଧାନ:
27a3 – 8b6 + 125 c3 + 90 ab2c = (3a)3 + (- 2b2)3 + (5c)3 – 3(3a) (- 2b2) (5c)
= {3a + (-2b2) + 5c} {(3a)2 + (-2b2)2 + (5c)2 – (3a) (-2b2) – (-2b2) (5c) – (5c) (3a)}
= (3a – 2b2 + 5c) (9a2 + 4b4 + 25c2 + 6ab2 + 10b2c – 15 ca)
(xiv) (2x + 3)3 + (3x – 2)3 – (5x + 1)3
ସମାଧାନ:
(2x + 3)3 + (3x – 2)3 – (5x + 1)3
ମନେକର 2x + 3 = a, 3x- 2 = b, 5x + 1 = c
∴ a + b – c = 2x + 3 + 3x – 2 – 5x – 1=0
a + b – c = 0 ହେଲେ a3 + b3 – c3 = -3abc
∴(2x + 3)3 + (3x – 2)3 – (5x + 1)3 = -3 (2x + 3) (3x – 2) (5x + 1)
(a, b ଓ cର ମାନ ବସାକଳେ)
Question 6.
a + b + c = 0 ହେଲେ ଦର୍ଶାଅ ଯେ, a3 + b3 + c3 = 3 abc
ସମାଧାନ:
L.H.S. = a3 + b3 + c3 = a3 + b3 + c3 – 3abc + 3abc
= (a + b + c) (a2 + b2 + c2 – ab – bc – ca) + 3abc
= (0) (a2 + b2 + c2 – ab – bc – ca) + 3abc
= 0 + 3abc = 3abc = R.H.S. (ପ୍ରମାଣିତ)
![]()
Question 7.
(x – y)3 + (y – z)3 + (z – x)3 ର ଉତ୍ପାଦକଗୁଡ଼ିକୁ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର x – y = a, y – z = b, z – x = c
∴ a + b + c = x – y + y – z + z – x ⇒ a + b + c = 0
ପ୍ରଦତ୍ତ ପଲିନୋମିଆଲ୍ଟି = a3 + b3+ c3 = 3abc (∵ a + b + c = 0)
∴ (x – y)3 + (y – z)3 + (z – x)3 = 3(x – y) (y – z) (z – x)
Question 8.
ଦର୍ଶାଅ ଯେ, x3 + y3 + z3 – 3xyz = \(\frac{1}{2}\) {(x – y)2 + (y – z)2 + (z – x)2}
ସମାଧାନ:
x3 + y3 + z3 – 3xyz
= (x + y + z) (x2 + y2 + z2 – xy – yz – zx)
= \(\frac{1}{2}\) (x + y + z) (2x2 + 2y2 + 2z2 – 2xy – 2yz – 2zx)
= \(\frac{1}{2}\) (x + y + z) (x2 – 2xy + y2 + y2 – 2yz + z2 + z2 – 2zx + x2}
= \(\frac{1}{2}\) (x + y + z) {(x – y)2 + (y – z)2 + (z – x)2}
∴ x3 + y3 + z3 = \(\frac{1}{2}\) {(x – y)2 + (y – z)2 + (z – x)2}
