BSE Odisha 9th Class Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(d)

Odisha State Board BSE Odisha 9th Class Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(d) Textbook Exercise Questions and Answers.

BSE Odisha Class 9 Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(d)

Question 1.
ନିମ୍ନଲିଖତ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଦିଅ ।
(i) ଗୋଟିଏ ଟ୍ରାପିଜିୟମ୍‌ର ସମାନ୍ତର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ 3 ସେ.ମି. ଓ 5 ସେ.ମି. । ସେମାନଙ୍କ ମଧ୍ୟରେ ବ୍ୟବଧାନ 3 ସେ.ମି. ହେଲେ ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ କେତେ ?
ସମାଧାନ:
ଟ୍ରାପିଜିୟମ୍‌ର ସମାନ୍ତର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ a  = 3 ସେ.ମି. ଓ b = 5 ସେ.ମି. । 
ସେମାନଙ୍କ ମଧ୍ୟରେ ଦୂରତା = ଉଚ୍ଚତା (h) = 3 ସେ.ମି. । 
ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) h (a + b) ସେ.ମି. ।
∴ ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × 3(3 + 5) ବର୍ଗ’ସେ.ମି. = 12 ବର୍ଗ ସେ.ମି. ।
∴ ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ 12 ବର୍ଗ ସେ.ମି. ।

(ii) ଗୋଟିଏ ଟ୍ରାପିଜିୟମ୍‌ର ସମାନ୍ତର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି 18 ସେ.ମି. ଓ କ୍ଷେତ୍ରଫଳ 36 ବର୍ଗ ସେ.ମି. ହେଲେ, ସେମାନଙ୍କ ମଧ୍ୟରେ ଥ‌ିବା ବ୍ୟବଧାନ କେତେ ?
ସମାଧାନ:
ଟ୍ରାପିଜିୟମ୍ ସମାନ୍ତର ବାହୁର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି = 18 ସେ.ମି. ଓ କ୍ଷେତ୍ରଫଳ = 36 ବର୍ଗ ସେ.ମି. ।
ମନେକର ସମାନ୍ତର ବାହୁଦ୍ୱୟ ମଧ୍ୟରେ ଦୂରତା = x ସେ.ମି. ।
ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × (ସମାନ୍ତର ବାହୁଦ୍ୱୟ ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି × ସମାନ୍ତର ବାହୁଦ୍ଵୟ ମଧ୍ୟରେ ଦୂରତା)
∴ 36 = \(\frac{1}{2}\) × 18 × x
⇒ 9x = 36 ⇒ x = 4 ସେ.ମି. ।
∴ ସମାନ୍ତର ବାହୁଦ୍ଵୟ ମଧ୍ୟରେ ଥିବା ବ୍ୟବଧାନ 4 ସେ.ମି. ।

(iii) ABCD ଟ୍ରାପିଜିୟମ୍‌ରେ A͞B || C͞D । ଯଦି AB = 6 ସେ.ମି., ବ୍ୟବଧାନ AE = 4 ସେ.ମି. ଓ କ୍ଷେତ୍ରଫଳ 28 ବର୍ଗ ସେ.ମି. ହୁଏ, ତେବେ CD କେତେ ?
ସମାଧାନ:

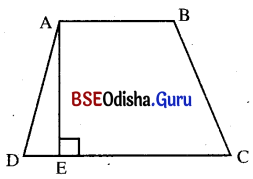
ABCD ଏକ ଟ୍ରାପିଜିୟମ୍‌ରେ A͞B || C͞D ଓ AB = 6 ସେ.ମି. ।
A͞B ଓ C͞D ମଧ୍ୟରେ ବ୍ୟବଧାନ (h) = AE = 4 ସେ.ମି. ।
ମନେକର CD ବାହୁର ଦୈର୍ଘ୍ୟ = x ସେ.ମି. ।
ABCD ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ = 28 ବର୍ଗ ସେ.ମି. ।
ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) h (a + b) ⇒ 28 = \(\frac{1}{2}\) × 4 (AB + CD)
⇒ 28 = 2(6 + x) ⇒ x + 6 = \(\frac{28}{2}\) = 14
⇒ x = 14 – 6 = 8 ସେ.ମି. ।
∴ CD ର ଦୈର୍ଘ୍ୟ 8 ସେ.ମି. ।

(iv) ଏକ ଟ୍ରାପିଜିୟମ୍‌ର ଅସମାନ୍ତର ବାହୁଦ୍ୱୟର ମଧ୍ୟବିନ୍ଦୁକୁ ଯୋଗକରୁଥିବା ସରଳରେଖାର ଦୈର୍ଘ୍ୟ 8 ସେ.ମି. ଓ 
କ୍ଷେତ୍ରଫଳ 40 ବର୍ଗ ସେ.ମି. ହେଲେ, ସମାନ୍ତର ବାହୁଦ୍ୱୟ ମଧ୍ୟରେ ଥ‌ିବା ବ୍ୟବଧାନ କେତେ ?
ସମାଧାନ:
ଟ୍ରାପିଜିୟମ୍ର ଅସମାନ୍ତର ବାହୁଦ୍ୱୟର ମଧ୍ୟବିନ୍ଦୁକୁ ଯୋଗକରୁଥିବା ସରଳରେଖାର ଦୈର୍ଘ୍ୟ = 8 ସେ.ମି. ଓ 
କ୍ଷେତ୍ରଫଳ = 40 ବର୍ଗ ସେ.ମି. ।

∴ ସମାନ୍ତର ବାହୁଦ୍ଵୟ ମଧ୍ଯରେ ବ୍ୟବଧାନ 5 ସେ.ମି. ।

(v) ABCD ଟ୍ରାପିଜିୟମ୍‌ରେ A͞B || C͞D ଓ 2AB = CD । ଯଦି ସମାନ୍ତର ବାହୁମାନଙ୍କ ମଧ୍ୟରେ ଥିବା ବ୍ୟବଧାନ 4 ସେ.ମି. ଓ କ୍ଷେତ୍ରଫଳ 42 ବର୍ଗ ସେ.ମି. ହୁଏ, ତେବେ CD କେତେ ?
ସମାଧାନ:

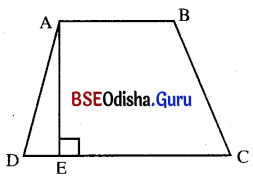
ABCD ଟ୍ରାପିଜିୟମ୍‌ରେ A͞B || C͞D ଓ 2AB = CD ।
ସମାନ୍ତର ବାହୁଦ୍ଵୟ ମଧ୍ୟରେ ବ୍ୟବଧାନ (h) = AE = 4 ସେ.ମି. ।
ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ = 42 ବର୍ଗ ସେ.ମି. ।
⇒ \(\frac{1}{2}\) × AE (AB + CD) = 42
⇒ \(\frac{1}{2}\) × 4 (AB + 2AB) = 42 (∵ CD = 2AB)
⇒ 3AB = \(\frac{42}{2}\) = 21
⇒ AB = \(\frac{21}{3}\) = 7 ସେ.ମି.
CD = 2AB = 2 × 7 ସେ.ମି. = 14 ସେ.ମି.
∴ CD ର ଦୈର୍ଘ୍ୟ 14 ସେ.ମି.

Question 2.
(i) ଗୋଟିଏ ଟ୍ରାପିଜିୟମ୍‌ର ଉଚ୍ଚତା 12 ସେ.ମି. ଏବଂ କ୍ଷେତ୍ରଫଳ 96% ବର୍ଗ ସେ.ମି. ହେଲେ, ସମାନ୍ତର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି କେତେ ?
ସମାଧାନ:
ଟ୍ରାପିଜିୟମ୍‌ର ଉଚ୍ଚତା = 12 ସେ.ମି. ଓ କ୍ଷେତ୍ରଫଳ = 96 ବର୍ଗ ସେ.ମି.

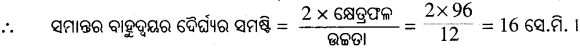
∴ ସମାନ୍ତର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି 16 ସେ.ମି. । 

(ii) ଗୋଟିଏ ଟ୍ରାପିଜିୟମ୍‌ର ସମାନ୍ତର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ଯଥାକ୍ରମେ 5 ମିଟର ଓ 7 ମିଟର ଏବଂ ସେମାନଙ୍କ ମଧ୍ୟରେ ବ୍ୟବଧାନ 6 ମିଟର ହେଲେ, ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ ନିଶ୍ଚୟ କର ।
ସମାଧାନ:
ଟ୍ରାପିଜିୟମ୍‌ର ସମାନ୍ତର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ଯଥାକ୍ରମେ 5 ମିଟର ଓ 7 ମିଟର ।
∴ ସେମାନଙ୍କ ମଧ୍ୟରେ ବ୍ୟବଧାନ ଅର୍ଥାତ୍ ଉଚ୍ଚତା = 6 ମିଟର ।
∴ ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × ଉଚ୍ଚତା × ସମାନ୍ତର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ଯୋଗଫଳ
= \(\frac{1}{2}\) × 6 ମି. × (5ମି. + 7 ମି.) = 3 ମି. × 12 ମି. = 36 ବର୍ଗ ସେ.ମି. ।
∴ ଟ୍ରାପିଜିୟମ୍‌ର ଉଚ୍ଚତା 36 ବର୍ଗ ମିଟର ।

(iii) ABCD ଟ୍ରାପିଜିୟମ୍‌ରେ A͞B ଓ C͞D ପରସ୍ପର ସମାନ୍ତର ଏବଂ AB = 2CD । ଯଦି ଏହାର କର୍ଣ୍ଣଦ୍ଵୟ ପରସ୍ପରକୁ O ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି, ତେବେ Δ AOB ଓ Δ CODର କ୍ଷେତ୍ରଫଳର ଅନୁପାତ କେତେ ହେବ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:

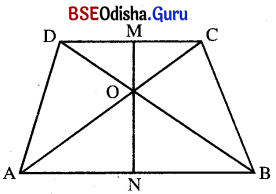
ABCD ଟ୍ରାପିଜିୟମ୍‌ରେ A͞B || C͞D ଏବଂ AB = 2CD
A͞B || C͞D ଓ BD ଛେଦକ m∠ABO = m∠CDO (ଏକାନ୍ତର)
ସେହିପରି m∠OAB = m∠OCD (ଏକାନ୍ତର)
m∠AOB = m∠COD (ପ୍ରତୀପ)
∴ Δ AOB ~ Δ COD
ସଦୃଶ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳର ଅନୁପାତ, ଅନୁରୂପ ବାହୁମାନଙ୍କ ଦୈର୍ଘ୍ୟର ବର୍ଗାନୁପାତୀ ସହ ସମାନ ।


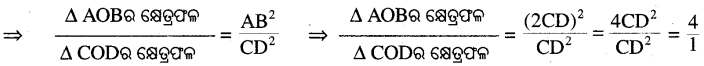
∴ Δ AOB ଓ Δ COD ର କ୍ଷେତ୍ରଫଳର ଅନୁପାତ 4 : 1 ।

Question 3.
ଗୋଟିଏ ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ 384 ବର୍ଗ ସେ.ମି. । ଯଦି ଏହାର ସମାନ୍ତର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ଅନୁପାତ 3 : 5 ହୁଏ ଏବଂ ସେମାନଙ୍କ ମଧ୍ୟରେ ବ୍ୟବଧାନ 12 ସେ.ମି. ହୁଏ ତେବେ କ୍ଷୁଦ୍ରତର ସମାନ୍ତର ବାହୁର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ଟ୍ରାପିଜିୟମ୍‌ର ସମାନ୍ତର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ 3x ସେ.ମି. ଓ 8x ସେ.ମି. ।
ସମାନ୍ତର ବାହୁଦ୍ଵୟ ମଧ୍ୟରେ ବ୍ୟବଧାନ (h) = 12 ସେ.ମି.
ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ = 384 ବର୍ଗ ସେ.ମି. ।
ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × ସମାନ୍ତର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି × ଉଚ୍ଚତା
⇒ 384 = \(\frac{1}{2}\) × (3x + 5x) × 12
⇒ 8x = \(\frac{384}{6}\) = 64
⇒ x = \(\frac{64}{8}\) = 8 ସେ.ମି. ।
କ୍ଷୁଦ୍ରତର ସମାନ୍ତର ବାହୁର ଦୈର୍ଘ୍ୟ = 3x ସେ.ମି. = 3 × 8 ସେ.ମି. = 24 ସେ.ମି. ।
∴ ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷୁଦ୍ରତର ସମାନ୍ତର ବାହୁର ଦୈର୍ଘ୍ୟ 24 ସେ.ମି. ।

Question 4.
ଗୋଟିଏ ଟ୍ରାପିଜିୟମ୍‌ର ସମାନ୍ତର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ଯଥାକ୍ରମେ 58 ମିଟର ଓ 72 ମିଟର । ଏହାର ଉଚ୍ଚତା 15 ମିଟର ହେଲେ, କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ଟ୍ରାପିଜିୟମ୍‌ର ସମାନ୍ତର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ଯଥାକ୍ରମେ 58 ମି. ଓ 78 ମି. ଏବଂ ଉଚ୍ଚତା 15 ମି. ।
∴ ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × ଉଚ୍ଚତା × ସମାନ୍ତର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି
= \(\frac{1}{2}\) × 15 × (58 + 72) ବର୍ଗ ମି. 
= \(\frac{1}{2}\) × 15 × 130 = 975 ବର୍ଗ ମି. ।

Question 5.
ଗୋଟିଏ ଟ୍ରାପିଜିୟମ୍‌ର ସମାନ୍ତର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ଯଥାକ୍ରମେ 55 ମିଟର ଓ 35 ମିଟର । ଏହାର କ୍ଷେତ୍ରଫଳ 810
ବର୍ଗ ମିଟର ହେଲେ, ଉଚ୍ଚତା ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ଟ୍ରାପିଜିୟମ୍‌ର ସମାନ୍ତର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ଯଥାକ୍ରମେ 55 ମି. ଓ 35 ମି. ଏବଂ କ୍ଷେତ୍ରଫଳ 810 ମି. ।
ମନେକର ଉଚ୍ଚତାର ଦୈର୍ଘ୍ୟ = x ମି.
∴ ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × ଉଚ୍ଚତା × ସମାନ୍ତର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି
⇒ 810 = \(\frac{1}{2}\) × x × (55 + 35)
⇒ 810 = \(\frac{90x}{2}\)
⇒ 45x = 810
⇒ x = \(\frac{810}{45}\) = 18 ମିଟର ।
∴ ଟ୍ରାପିଜିୟମ୍‌ର ଉଚ୍ଚତା 18 ମିଟର ।

Question 6.
ଗୋଟିଏ ଟ୍ରାପିଜିୟମ୍‌ର ଦୁଇ ସମାନ୍ତର ବାହୁ ମଧ୍ୟରୁ ଗୋଟିକର ଦୈର୍ଘ୍ୟ ଅନ୍ୟଠାରୁ 20 ସେ.ମି. ବେଶୀ ଓ ଏହି ବାହୁଦ୍ୱୟ ମଧ୍ୟରେ ବ୍ୟବଧାନ 25 ସେ.ମି. । ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ 1250 ବର୍ଗ ସେ.ମି. ହେଲେ, ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର । 
ସମାଧାନ: 
ମନେକର ଟ୍ରାପିଜିୟମ୍‌ର ଗୋଟିଏ ସମାନ୍ତର ବାହୁର ଦୈର୍ଘ୍ୟ = x ସେ.ମି. ।
ପ୍ରଶ୍ନନୁସାରେ, ଅନ୍ୟ ସମାନ୍ତର ବାହୁର ଦୈର୍ଘ୍ୟ = (x + 20) ସେ.ମି. ।
ସମାନ୍ତର ବାହୁଦ୍ଵୟ ମଧ୍ୟରେ ବ୍ୟବଧାନ = 25 ସେ.ମି. = ଉଚ୍ଚତା, କ୍ଷେତ୍ରଫଳ = 1250 ବର୍ଗ ସେ.ମି.
∴ ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × ଉଚ୍ଚତା × ସମାନ୍ତର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି
1250 = \(\frac{1}{2}\) × 25 × (x + x + 20)
⇒ 2500 = 25 (2x + 20)
⇒ 2x + 20 = \(\frac{2500}{25}\) = 100
⇒ 2x = 100 – 20 = 80
⇒ x = \(\frac{80}{2}\) = 40
∴ ଟ୍ରାପିଜିୟମ୍‌ର ଗୋଟିଏ ସମାନ୍ତର ବାହୁର ଦୈର୍ଘ୍ୟ = 40 ସେ.ମି.
ଓ ଅନ୍ୟ ସମାନ୍ତର ବାହୁର ଦୈର୍ଘ୍ୟ = x + 20 = 40 + 20 = 60 ବର୍ଗ ସେ.ମି. ।

Question 7.
ଗୋଟିଏ ଟ୍ରାପିଜିୟମ୍‌ର ସମାନ୍ତର ବାହୁଦ୍ଵୟ ମଧ୍ୟରେ ବ୍ୟବଧାନ 30 ମିଟର ଏବଂ ସେହି ଦୁଇଟିର ଦୈର୍ଘ୍ୟର ଅନୁପାତ 2 : 3 ଅଟେ । ଗୋଟିକର ଦୈର୍ଘ୍ୟ ଅନ୍ୟଠାରୁ 10 ମିଟର ଅଧ‌ିକ ହେଲେ, କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ଟ୍ରାପିଜିୟମ୍‌ର ସମାନ୍ତର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ଯଥାକ୍ରମେ 2x ମି. ଓ 3x ମି. ।
ପ୍ରଶ୍ବାନୁସାରେ, 3x = 2x + 10
⇒ 3x – 2x = 10 ⇒ x = 10
ସମାନ୍ତର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ଯଥାକ୍ରମେ, 2x = 2 × 10 = 20 ମି. ଓ 3x = 3 × 10 = 30 ମି.
ସମାନ୍ତର ବାହୁଦ୍ଵୟ ମଧ୍ୟରେ ବ୍ୟବଧାନ ଅର୍ଥାତ୍ ଉଚ୍ଚତା = 30 ମି.
∴ ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × ଉଚ୍ଚତା × ସମାନ୍ତର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି
= \(\frac{1}{2}\) × 30 × (20 + 30) = 15 × 50 = 750 ବର୍ଗ ସେ.ମି. ।

Question 8.
ଗୋଟିଏ ଟ୍ରାପିଜିୟମ୍ର କ୍ଷେତ୍ରଫଳ 960 ବର୍ଗ ମିଟର । ଏହାର ଉଚ୍ଚତା 6 ମିଟର ଓ ସମାନ୍ତର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ଅନ୍ତର 20 ମିଟର ହେଲେ, ସମାନ୍ତର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ଗୋଟିଏ ସମାନ୍ତର ବାହୁର ଦୈର୍ଘ୍ୟ = x ମି. ।
ପ୍ରଶ୍ନନୁସାରେ, ଅନ୍ୟ ସମାନ୍ତର ବାହୁର ଦୈର୍ଘ୍ୟ = (x + 20) ମି. ।
କ୍ଷେତ୍ରଫଳ = 960 ବର୍ଗ ମି., ଉଚ୍ଚତା = 6 ମି. ।
∴ ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × ଉଚ୍ଚତା × ସମାନ୍ତର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ଯୋଗଫଳ
⇒ 960 = \(\frac{1}{2}\) × 6 × (x + x + 20)
⇒ 960 = 3(2x + 20)
⇒ 2x + 20 = \(\frac{960}{3}\)
⇒ 2x + 20 = 320
⇒ 2x = 300
⇒ x = 150 ମି.
ଅନ୍ୟ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = x + 20 = 150 + 12 = 170 ସେ.ମି.
∴ ସମାନ୍ତର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ 150 ମି. ଓ 170 ସେ.ମି. ।

Question 9.
ଗୋଟିଏ ଟ୍ରାପିଜିୟମ୍‌ର ଏକ ସମାନ୍ତର ବାହୁର ଦୈର୍ଘ୍ୟ 44 ମିଟର ଓ ଅନ୍ୟ ସମାନ୍ତର ବାହୁର ଦୈର୍ଘ୍ୟ ଉଚ୍ଚତାର ଅର୍ଦ୍ଧେକ । ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ 885 ବର୍ଗ ମିଟର ହେଲେ, ଉଚ୍ଚତା ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ: 
 ଗୋଟିଏ ସମାନ୍ତର ବାହୁର ଦୈର୍ଘ୍ୟ = 44 ମି., କ୍ଷେତ୍ରଫଳ = 885 ବ. ମି. ।
ମନେକର ଉଚ୍ଚତାର ଦୈର୍ଘ୍ୟ = x ମି. । 
ପ୍ରଶ୍ନନୁସାରେ, ଅନ୍ୟ ସମାନ୍ତର ବାହୁର ଦୈର୍ଘ୍ୟ = \(\frac{x}{2}\) ମି. I
ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × ଉଚ୍ଚତା × ସମାନ୍ତର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି
⇒ 885 = \(\frac{1}{2}\) × x × (45 + \(\frac{x}{2}\))
⇒ 885 = \(\frac{88 x+x^2}{4}\)
⇒ 3540 = 88x + x²
⇒ x² + 88x – 3540 = 0
⇒ x² + 118x – 30x – 3540 = 0
⇒ x(x + 118) – 30(x + 118) = 0
⇒ (x + 118)(x – 30) = 0
⇒ x + 118 = 0 ବା x – 30 = 0
⇒ x = -118 ଏହା ଅସମ୍ଭବ ଓ x = 30
∴ ଟ୍ରାପିଜିୟମ୍‌ର ଉଚ୍ଚତା 30 ମିଟର ।

Question 10.
ଗୋଟିଏ ଟ୍ରାପିଜିୟମ୍‌ର ଅସମାନ୍ତର ବାହୁଦ୍ୱୟର ମଧ୍ୟବିନ୍ଦୁକୁ ଛେଦ କରୁଥିବା ରେଖାଖଣ୍ଡର ଦୈର୍ଘ୍ୟ 39 ସେ.ମି. । ଏହି ରେଖାଖଣ୍ଡଠାରୁ ବୃହତ୍ତର ସମାନ୍ତର ବାହୁର ଦୂରତା 12 ସେ.ମି. ହେଲେ, କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ଟ୍ରାପିଜିୟମ୍‌ର ସମାନ୍ତର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ଯଥାକ୍ରମେ a ସେ.ମି. ଓ b ସେ.ମି. ।
ଟ୍ରାପିଜିୟମ୍‌ର ଅସମାନ୍ତର ବାହୁଦ୍ୱୟର ମଧ୍ୟବିନ୍ଦୁକୁ ଯୋଗକରୁଥିବା ରେଖାଖଣ୍ଡର ଦୈର୍ଘ୍ୟ = \(\frac{1}{2}\) (a + b) = 39 ସେ.ମି.
ଏହି ରେଖାଖଣ୍ଡଠାରୁ ବୃହତ୍ତର ସମାନ୍ତର ବାହୁର ଦୂରତା = \(\frac{h}{2}\) = 12 ସେ.ମି. ⇒ h = 24 ସେ.ମି. ।
∴ ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) h (a + b) = 24 × 39 = 936 ବର୍ଗ ସେ.ମି. ।

Question 11.
ଗୋଟିଏ ଟ୍ରାପିଜିୟମ୍‌ର ସମାନ୍ତର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ଯଥାକ୍ରମେ 24 ମିଟର ଓ 50 ମିଟର ଓ ସେମାନଙ୍କ ମଧ୍ୟରେ ବ୍ୟବଧାନ 12 ମିଟର । ଅସମାନ୍ତର ବାହୁଦ୍ୱୟର ମଧ୍ୟବିନ୍ଦୁକୁ ଯୋଗ କରୁଥିବା ରେଖାଖଣ୍ଡ ଟ୍ରାପିଜିୟମ୍‌କୁ ଯେଉଁ ଦୁଇଟି ଚତୁର୍ଭୁଜରେ ବିଭକ୍ତ କରେ, ସେମାନଙ୍କର କ୍ଷେତ୍ରଫଳ ନିଶ୍ଚୟ କର ।
ସମାଧାନ:

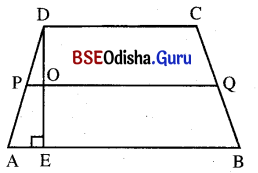
ABCD ଟ୍ରାପିଜିୟମ୍‌ରେ A͞B || C͞D ଏବଂ P ଓ Q ଯଥାକ୍ରମେ A͞D ଓ B͞C ର ମଧ୍ୟବିନ୍ଦୁ ।
ମନେକର D͞E ⊥ A͞B ଓ ଏହା PQ କୁ ଠ ବିନ୍ଦୁରେ ଛେଦ କରୁଛି ।
AB = 50 ମି., CD = 24 ମି. ଏବଂ DE = 12. ମି. ।

Question 12.
ଗୋଟିଏ ଟ୍ରାପିଜିୟମ୍‌ର ସମାନ୍ତର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ଯଥାକ୍ରମେ 35 ମିଟର ଓ 50 ମିଟର । ଏହାର ଅସମାନ୍ତର ବାହୁଦ୍ଵୟଙ୍କ ମଧ୍ୟରୁ ଗୋଟିଏ ସମାନ୍ତର ବାହୁମାନଙ୍କ ପ୍ରତି ଲମ୍ବ ଓ ଅନ୍ୟଟିର ଦୈର୍ଘ୍ୟ 17 ମିଟର ହେଲେ, କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:

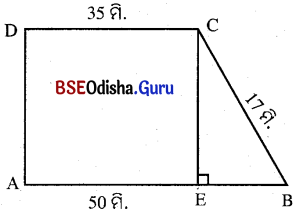
ABCD ଟ୍ରାପିଜିୟମ୍‌ର A͞B || CD ଏବଂ AD
AB ଓ CD ପ୍ରତି ଲମ୍ବ ।
ମନେକର AB = 50 ମି., CD = 35 ମି. ଓ BC = 17 ମି. ।
C ବିନ୍ଦୁରୁ AB ପ୍ରତି C͞E ଲମ୍ବ ଅଙ୍କିତ ହୋଇଛି ।
ବର୍ତ୍ତମାନ AECD ଏକ ଆୟତକ୍ଷେତ୍ର ।
∴ AE = CD = 35 ମି. । ତେଣୁ BE = AB – AE = 50 – 35 = 15 ମି. ।

Question 13.
ଗୋଟିଏ ଟ୍ରାପିଜିୟମ୍ର କ୍ଷେତ୍ରଫଳ 210 ବର୍ଗ ସେ.ମି. । ଏହାର ଅସମାନ୍ତର ବାହୁଦ୍ଵୟ ମଧ୍ୟରୁ ଗୋଟିକର ଦୈର୍ଘ୍ୟ 17 ସେ.ମି. ଓ ଅନ୍ୟଟି ସମାନ୍ତର ବାହୁମାନଙ୍କ ପ୍ରତି ଲମ୍ବ । ଯଦି ଗୋଟିଏ ସମାନ୍ତର ବାହୁର ଦୈର୍ଘ୍ୟ ଅନ୍ୟଠାରୁ 8 ସେ.ମି. ଅଧିକ ହୁଏ, ତେବେ ବାହୁ ତିନୋଟିର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:

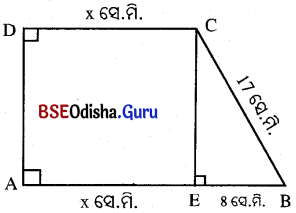
ABCD ଟ୍ରାପିଜିୟମ୍‌ରେ AB || CD ଏବଂ
AD, AB ଓ CD ପ୍ରତି ଲମ୍ବ ।
କ୍ଷେତ୍ରଫଳ = 210 ବର୍ଗ ସେ.ମି. ।
ମନେକର CD = x ସେ.ମି. ।
ପ୍ରଶ୍ନନୁସାରେ, AB = (x + 8) ସେ.ମି.
C ବିନ୍ଦୁରୁ AB ପ୍ରତି CE ଲମ୍ବ ଅଙ୍କିତ ହୋଇଛି ।
ବର୍ତ୍ତମାନ AECD ଏକ ଆୟତକ୍ଷେତ୍ର । ∴ AE = CD = x ସେ.ମି.
ତେଣୁ BE = AB – AE = 8 ସେ.ମି.

CD = x = 10 ସେ.ମି. ଓ AB = x + 8 = 10 + 8 = 18 ସେ.ମି. ।
∴ ଟ୍ରାପିଜିୟମ୍‌ର ସମାନ୍ତର ବାହୁଦ୍ୱୟ ଯଥାକ୍ରମେ 10 ସେ.ମି. ଓ 18 ସେ.ମି. ଏବଂ ଅନ୍ୟ ଅସମାନ୍ତର ବାହୁର ଦୈର୍ଘ୍ୟ 15 ସେ.ମି. ।

Question 14.
ଗୋଟିଏ ଟ୍ରାପିଜିୟମ୍‌ର ଦୁଇ ସମାନ୍ତର ବାହୁର ଦୈର୍ଘ୍ୟ ଯଥାକ୍ରମେ 54 ସେ.ମି. ଓ 30 ସେ.ମି. ଏବଂ ପ୍ରତ୍ୟେକ ଅସମାନ୍ତର ବାହୁର ଦୈର୍ଘ୍ୟ 20 ସେ.ମି. ହେଲେ, କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ABCD ଟ୍ରାପିଜିୟମ୍‌ର AB ||CD ଏବଂ AD ଓ BC ଅସମାନ୍ତର ବାହୁ ।
AB = 54 ସେ.ମି., CD = 30 ସେ.ମି. ଓ AD = BC = 20 ସେ.ମି. ।
ମନେକର CE || AD ଏବଂ CF ⊥ BE ।
ବର୍ତ୍ତମାନ AECD ଏକ ସାମାନ୍ତରିକ କ୍ଷେତ୍ର ।
∴ CE = AD = BC = 20 ସେ.ମି. ଏବଂ AE = CD = 30 ସେ.ମି. ।
∴ BE = AB – AE = 54 – 30 = 24 ସେ.ମି. Δ BCE ରେ BC = EC ।
ତେଣୁ ଏହା ଏକ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜ ।
C ବିନ୍ଦୁରୁ ଭୂମି B͞E ପ୍ରତି C͞F ଲମ୍ବ ।

Question 15.
ଗୋଟିଏ ଟ୍ରାପିଜିୟମ୍‌ର ଗୋଟିଏ କୋଣର ପରିମାଣ 60° ଅଟେ । ଏହାର ପ୍ରତ୍ୟେକ ଅସମାନ୍ତର ବାହୁର ଦୈର୍ଘ୍ୟ 16 ସେ.ମି. ଏବଂ କ୍ଷେତ୍ରଫଳ 336√3 ବର୍ଗ ସେ.ମି. ହେଲେ, ସମାନ୍ତର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ABCD ଟ୍ରାପିଜିୟମ୍‌ର AB || CD ଏବଂ m∠ABC = 60° ।
AD = BC = 16 ସେ.ମି.
C ବିନ୍ଦୁରେ DA ସହ ସମାନ୍ତରଭାବେ ଅଙ୍କିତ ରେଖା AB କୁ E ବିନ୍ଦୁରେ ଛେଦକରୁ ଏବଂ C ବିନ୍ଦୁରୁ AB ପ୍ରତି CF ଲମ୍ବ ଅଙ୍କନ କରାଯାଉ ।
ବର୍ତ୍ତମାନ AECD ଏକ ସାମାନ୍ତରିକ କ୍ଷେତ୍ର ।
AD = CE = 16 ସେ.ମି.
Δ BCE ରେ BC = CE
⇒ m∠CEB = m∠CBE = 60°
∴ m∠BCE = 180° – (m∠CEB + m∠CBE) = 180° – (60° + 60°) = 60°
∴ Δ BCE ଏକ ସମବାହୁ ତ୍ରିଭୁଜ ।
∴ BE = 16 ସେ.ମି.

∴ ସମାନ୍ତର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ 34 ସେ.ମି. ଓ (x + 16) = 50 ସେ.ମି. ।

Question 16.
ଗୋଟିଏ ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ 550√3 ବର୍ଗ ମିଟର ଓ ପ୍ରତ୍ୟେକ ଅସମାନ୍ତର ବାହୁର ଦୈର୍ଘ୍ୟ 20 ମିଟର । ଏହାର ବୃହତ୍ତର ସମାନ୍ତର ବାହୁ ସଂଲଗ୍ନ କୋଣଦ୍ଵୟର ପରିମାଣ ପ୍ରତ୍ୟେକ 60 ହେଲେ ସମାନ୍ତର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ABCD ଟ୍ରାପିଜିୟମ୍‌ର AB || CD ଏବଂ m∠ABC = 60° ।
AB = BC= 20 ମି. ।
C ବିନ୍ଦୁରୁ AD ସହ ସମାନ୍ତରଭାବେ ଅଙ୍କିତ ରେଖା 
AB କୁ E ବିନ୍ଦୁରେ ଛେଦକରୁ ଏବଂ C ବିନ୍ଦୁରୁ
AB ପ୍ରତି CF ଲମ୍ବ ଅଙ୍କନ କରାଯାଉ । 
ବର୍ତ୍ତମାନ AECD ଏକ ସାମାନ୍ତରିକ କ୍ଷେତ୍ର ।
∴ AE = CD ଏବଂ AD = EC = BC = 20 ମି.
Δ BCF ରେ BC = CE, ତେଣୁ m∠CEB = m∠CBE = 60°
∴ m∠BCE = 180° – (m∠CEB + m∠CBE) = 180° – (60° + 60°) = 60°
∴ Δ BCE ଏକ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜ ।
⇒ AD = EC = BC = BE = 20 ମି.

∴ ଟ୍ରାପିଜିୟମ୍‌ର ସମାନ୍ତର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ଯଥାକ୍ରମେ 65 ମି, ଓ 45 ମି. ।

Question 17.
ଗୋଟିଏ ଟ୍ରାପିଜିୟମ୍ର ଦୁଇ ସମାନ୍ତର ବାହୁର ଦୈର୍ଘ୍ୟ ଯଥାକ୍ରମେ 42 ମିଟର ଓ 30 ମିଟର । ଏହାର ବୃହତ୍ତମ ସମାନ୍ତର ବାହୁର ସଂଲଗ୍ନ କୋଣଦ୍ୱୟର ପରିମାଣ 90° ଓ 45° ହେଲେ, ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ ନିଶ୍ଚୟ କର ।
ସମାଧାନ:

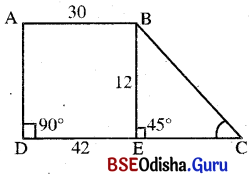
ABCD ଟ୍ରାପିଜିୟମ୍‌ରେ AB = 30 ସେ.ମି., CD = 42 ସେ.ମି.,
m∠ADC = 90° ଓ m∠BCD = 45° ।
B ବିନ୍ଦୁରୁ CD ପ୍ରତି BE ଲମ୍ବ ଅଙ୍କନ କରାଯାଉ । 
∴ AB = DE = 30 ମିଟର, 
CE = CD – DE = 42 ମି. – 30 ମି. = 12 ମି. ।
∴ Δ BCE ସମକୋଣୀ ତ୍ରିର୍ଭୁଜରେ m∠BCE = 45°
m∠CBE = 180° – (m∠BEC + m∠BCE) = 180° – (90° +45°) = 45°
∴ Δ BCE ଏକ ସମକୋଣୀ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜ ।
∴ CE = BE = 12 ମି.
∴ BE ଟ୍ରାପିଜିୟମ୍‌ର ଉଚ୍ଚତା 12 ମି. ।
∴ ABCD ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × ଉଚ୍ଚତା × ସମାନ୍ତର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି
= \(\frac{1}{2}\) × 12 × (30 + 42) = 6 × 72 = 432 ବର୍ଗ ମି. ।
∴ ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ 432 ବର୍ଗ ମିଟର ।